Луч (геометрия) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Луч.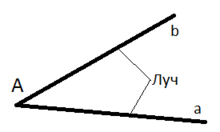
Два луча, образующие уголЛуч (в геометрии) или полупрямая — часть прямой, состоящая из данной точки и всех точек, лежащих по одну сторону от неё. Любая точка на прямой разделяет прямую на два луча[1].
Каждая точка O на прямой разбивает множество точек этой прямой, отличных от O, на две полупрямые, причём точка O лежит между любыми двумя точками прямой, принадлежащими разным подмножествам. Каждое из этих подмножеств называется открытым лучом с началом в O.
Объединение открытого луча с его началом — точкой O — называется лучом с началом в O.
Луч с началом в точке O, содержащий точку A, обозначается «луч
Для любого неотрицательного числа a на заданном луче с началом O существует единственная точка A, находящаяся на расстоянии a от точки O.
Лучами также называют бесконечные промежутки (полупрямые) числовой прямой.
Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча.
Терминология
Строгая терминология для прямой, луча, отрезка была установлена Якобом Штейнером в 1833 году[3].
См. также
Примечания
- ↑ 1 2 Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. Геометрия. 7—9 классы: учебник для общеобразовательных организаций. — М.: Просвещение, 2014. — С. 8. — 383 с. — 170 000 экз. — ISBN 978-5-09-032008-5.
- ↑ Н.Я, Виленкин, К.И. Нешков, С.И. Щварцбурд, А.С. Чесноков, А.Д. Семушин Под редакцией А.И.Маркушевича. Математика. Учебник для 4 класса средней школы.. — 3. — М: Просвещение, 1977. — С. 17.
- ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд., испр. — М.: ЛКИ, 2008. — С. 94. — 248 с. — ISBN 978-5-382-00839-4.
Урок 2. луч и угол — Геометрия — 7 класс
Геометрия
7 класс
Урок № 2
Луч и угол
Перечень рассматриваемых вопросов:
- Угол.
- Луч.
- Внутренняя и внешняя часть угла.
- Развёрнутый угол.
Тезаурус:
Луч – часть прямой, состоящая из всех точек, лежащих по одну сторону от заданной точки и той точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.
Стороны угла – лучи, из которых состоит угол.
Основная литература:
1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Мы уже познакомились с некоторыми геометрическими понятиями: прямая, точка, отрезок. Сегодня мы рассмотрим ещё два понятия, часто встречающиеся в геометрии – это луч и угол.
Для начала, вспомним, как строятся и обозначаются лучи и углы.
Для этого проведём прямую а, отметим на ней точкуО, которая разделит прямую на две части. Эти части прямой называются лучами, исходящими из точки О. А сама точка О, называется началом каждого из лучей.
Луч принято обозначать как одной малой латинской буквой, например, а.
Или двумя большими латинскими буквами, например, ОА.
При этом стоит помнить, что первая буква всегда обозначает начало луча, а вторая– это любая точка на луче.
Теперь рассмотрим понятие угол.
Начнём с определения.
Угол – это часть плоскости, ограниченная двумя лучами с общим началом.
Лучи – это стороны угла.
В данном случае, это стороны ОА и ОВ.
Общее начало сторон, в данном случае О – это вершина угла.
Углы принято обозначать как двумя малыми латинскими буквами, по названию сторон угла, например, ∠hk,
так и тремя большими латинскими буквами, например, тот же угол можно обозначить ∠АОВ, где вершина угла будет стоять в середине обозначения угла.
Или одной большой латинской буквой, обозначающей вершину угла. Например, тот же угол можно обозначить буквой∠О, по вершине угла.
Далее введём понятия, связанные с углами.
Во-первых, рассмотрим угол, который называют развёрнутым, его обе стороны лежат на одной прямой. Например, ∠С– развёрнутый.
В дальнейшем будем рассматривать углы меньше развёрнутого.
Угол также рассматривается как часть плоскости, ограниченная двумя лучами с общим началом.
Во-вторых, плоскость, на которой изображён любой угол, кроме развёрнутого, делится на две области: внутреннюю и внешнюю.
В развёрнутом углу, любая часть считается внутренней.
Решим задачу.
На рисунке изображён угол. Какие из точек лежат внутри угла и вне его?
Решение:
Внутри угла лежат точки: М, Е, К.
Вне угла лежат точки: Р, D, N.
Отметим, что точкиВ и С лежат на сторонах углаО.
Продолжая изучать углы, отметим, что если внутри угла из его вершины провести луч, то он разделит угол на два угла.
Например, луч ОС делит ∠АОВ на два угла – ∠ВОС и ∠АОС.
Итак, сегодня мы повторили некоторые сведения о луче и углах; сформировали представления о внутренней и внешней областях угла, меньше развернутого, познакомились с различными обозначениями луча и угла.
Материал для углубленного изучения
Двугранный угол.
Мы разобрали понятие угол, связанное с планиметрией. Но как отмечалось ранее, у геометрии есть ещё один раздел – стереометрия, который изучается в старших классах. Этот раздел изучает пространственные фигуры, одна из таких фигур–двугранный угол. Дадим ему определение: двугранный угол – пространственнаягеометрическая фигура, образованная двумяполуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями. Двугранный угол имеет стороны (иначе их называют грани), это полуплоскости α и β, и ребро, в данном случае это прямая АВ. Как измерить такие углы и их разновидности, вы узнаете в курсе геометрии 10 класса.
Тренировочные задания.
№ 1. Какие из точек лежат на стороне угла?
Решение:
Посмотрите на рисунок. На нём изображён угол ВОС, соответственно точки B и C лежат на сторонах угла, других точек нет.
Ответ: B и C.
№ 2. Сколько углов изображено на рисунке?
Решение. Перечислим все углы, изображённые на рисунке.
СОВ, ВОА, АОD, DОС и развёрнутые углы СОА и DОВ. Получается 8 углов.
Ответ: 8 углов.
Основная теория — Геометрия: задачи на построение
Найти решение задачи на построение — значит указать конечную последовательность основных построений, после выполнения которых искомая фигура будет считаться построенной в силу принятых аксиом конструктивной геометрии.
Для изображения на рисунке прямой мы пользуемся линейкой, но мы изображаем не всю прямую, а только лишь её кусок. Так как прямая в нашем представлении простирается до бесконечности в обе стороны, то прямая есть бесконечна.
На рисунке представленном выше мы видим, что точки А и С расположены на прямой а. В таких случаях говорят, что точки А и С принадлежат прямой а. Либо говорят, что прямая проходит через точки А и С. При записи принадлежность точки к прямой обозначают специальным значком. А тот факт, что точка не принадлежит прямой, отмечают таким же значком, только зачеркнутым.
В нашем случае точки B и D не принадлежат прямой а.
Как уже отмечалось выше, на рисунке точки А и С принадлежат прямой а. Часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными точками называется отрезком. Другими словами, отрезком называется часть прямой, ограниченная двумя точками.
В нашем случае мы имеем отрезок АB. Точки А и B называются концами отрезка. Для того, чтобы обозначить отрезок указывают его концы, в нашем случае АB. Одним из основных свойств принадлежности точек и прямых является следующее свойство: через любые две точки можно провести прямую, и притом только одну.
Если две прямые имеют общую точку, то говорят, что эти две прямые пересекаются. На рисунке прямые a и b пересекаются в точке A. Прямые а и с не пересекаются.
Любые две прямые имеют только одну общую точку либо не имеют общих точек. Если предположить обратное, что две прямые имеют две общих точки, тогда через них проходили бы две прямые. А это невозможно, так как
Луч (геометрия) — Википедия. Что такое Луч (геометрия)
Материал из Википедии — свободной энциклопедии Два луча, образующие уголЛуч (в геометрии) или полупрямая — часть прямой, состоящая из данной точки и всех точек, лежащих по одну сторону от неё. Любая точка на прямой разделяет прямую на два луча[1].
Каждая точка O на прямой разбивает множество точек этой прямой, отличных от O, на две полупрямые, причём точка O лежит между любыми двумя точками прямой, принадлежащими разным подмножествам. Каждое из этих подмножеств называется открытым лучом с началом в O.
Объединение открытого луча с его началом — точкой O — называется лучом с началом в O.
Луч с началом в точке O, содержащий точку A, обозначается «луч ОА»[1] или [OA)[2].
Для любого неотрицательного числа a на заданном луче с началом
Лучами также называют бесконечные промежутки (полупрямые) числовой прямой.
Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча.
Терминология
Строгая терминология для прямой, луча, отрезка была установлена Якобом Штейнером в 1833 году[3].
См. также
Примечания
- ↑ 1 2 Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. Геометрия. 7—9 классы: учебник для общеобразовательных организаций. — М.: Просвещение, 2014. — С. 8. — 383 с. — 170 000 экз. — ISBN 978-5-09-032008-5.
- ↑ Н.Я, Виленкин, К.И. Нешков, С.И. Щварцбурд, А.С. Чесноков, А.Д. Семушин Под редакцией А.И.Маркушевича. Математика. Учебник для 4 класса средней школы.. — 3. — М: Просвещение, 1977. — С. 17.
- ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд., испр. — М.: ЛКИ, 2008. — С. 94. — 248 с. — ISBN 978-5-382-00839-4.
лучей — Концепция — Геометрия Видео от Brightstorm
Луч является частью линии, имеет одну фиксированную конечную точку и бесконечно проходит вдоль линии от конечной точки. Противоположные математические лучи — лучи с общей конечной точкой, проходящие в противоположных направлениях и образующие линию.
Если бы у нас была линия, которая бесконечно продолжалась
в любом направлении, и я где-то выбрал конечную точку
, и стер все
, выходящие за пределы этой конечной точки
, то я создал только
луч.
Итак, у луча одна конечная точка, и он проходит на
бесконечно от этой конечной точки.
Но как обозначить луч?
Ну, вы начинаете с того, что говорите
, какова ваша конечная точка?
Моя конечная точка этого луча — A, потому что это
, где он начинается, и он простирается от
до точки B. Итак, я собираюсь обозначить этот луч
как линию, но
у меня только одна стрелка.
Итак, стрелка
проходит над B.
Поскольку моя конечная точка — A и обратите внимание, что у меня
нет стрелки над A, которая
сообщает ученику-геометру или учителю геометрии
, что этот луч начинается с
. A и проходит через B.
Теперь у вас также могут быть противоположные лучи,
и противоположные лучи имеют общую конечную точку
.
Итак, если вы посмотрите на эту строку прямо здесь,
содержит X, Y и Z, где X, Y и
Z все коллинеарны.
У нас есть противоположные лучи
, если я выберу точку Y.
Итак, я мог бы сказать, что луч Y, Z — так что
снова я говорю от точки Y до точки
Z. Итак, идите YZ и обратите внимание, как
я выравниваю. здесь стрелка находится на
над Z, потому что она начинается в Y и
, противоположной будет луч
, начинающийся в Y, проходящий с
через X.
Так что я могу обозначить это как луч YX.
Таким образом, противоположные лучи имеют общую конечную точку, а
лучей в целом имеют одну конечную точку, а
бесконечно продолжаются от
этой конечной точки.
Введение в геометрию | SkillsYouNeed
Когда вы начинаете изучать геометрию, важно знать и понимать некоторые основные понятия.
Эта страница поможет вам понять концепцию размеров в геометрии и понять, работаете ли вы в одном, двух или трех измерениях.
Он также объясняет некоторые основные термины и указывает на другие страницы для получения дополнительной информации.
На этой странице представлены точки, линии и плоскости.
На других страницах этой серии рассказывается об углах и формах, включая многоугольники, круги и другие изогнутые формы, а также трехмерные формы.
Что такое геометрия?
Геометрия , н. та часть математики, которая рассматривает свойства точек, линий, поверхностей и твердых тел…
Словарь английского языка Чемберса, издание 1989 г.
Геометрия происходит от греческого, означающего «измерение земли», и представляет собой визуальное изучение форм, размеров и узоров, а также того, как они сочетаются друг с другом в пространстве.Вы обнаружите, что наши страницы с геометрией содержат множество диаграмм, которые помогут вам понять предмет.
Когда вы столкнулись с проблемой, связанной с геометрией, может быть очень полезно нарисовать диаграмму самостоятельно.
Работа в разных размерах
Нет, не континуум пространства-времени! Мы говорим о фигурах в одном, двух и трех измерениях.
То есть объекты, имеющие длину (одно измерение), длину и ширину (два измерения) и длину, ширину и глубину или высоту (три измерения).
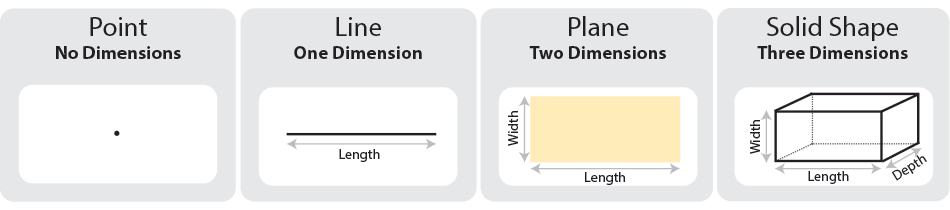
очков: особый случай: без размеров
точка — это отдельная точка в пространстве. Часто он представлен на странице в виде точки, но на самом деле не имеет реального размера или формы.
Вы не можете описать точку с точки зрения длины, ширины или высоты, поэтому она является безразмерной . Однако точка может быть описана координатами. Координаты не определяют ничего о точке, кроме ее положения в пространстве по отношению к контрольной точке с известными координатами.Вы встретите координаты точек во многих приложениях, например, когда вы рисуете графики или читаете карты.
Практически все в геометрии начинается с точки, будь то линия или сложная трехмерная форма.
линий: одно измерение
Линия — кратчайшее расстояние между двумя точками. Он имеет длину, но не ширину, что делает его одномерным.
Везде, где встречаются или пересекаются две или более прямых, есть точка, и говорят, что две линии имеют общую точку:
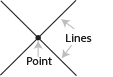
Отрезки и лучи
Есть два типа линий: те, которые имеют определенную начальную и конечную точки, и те, которые продолжаются вечно.
Линии, которые перемещаются между двумя точками, называются отрезками линии . Они начинаются с определенной точки и переходят к другой, конечной точке. Как и следовало ожидать, они нарисованы как линия между двумя точками.
Второй тип линий называется луч , и они продолжаются бесконечно. Их часто проводят в виде линии, начинающейся от точки со стрелкой на другом конце:
Параллельные и перпендикулярные прямые
Есть два типа линий, которые особенно интересны и / или полезны в математике. Параллельные линии никогда не пересекаются и не пересекаются. Они просто идут вечно бок о бок, как железнодорожные пути. Условием показа параллельности линий на диаграмме является добавление «перьев», которые выглядят как наконечники стрелок.
Перпендикулярные линии пересекаются под прямым углом, 90 °:
Плоскости и двумерные формы
Теперь, когда мы разобрались с одним измерением, пора перейти к двум.
Плоскость — это плоская поверхность, также известная как двумерная.Технически он неограничен, что означает, что он продолжается вечно в любом заданном направлении, и поэтому его невозможно нарисовать на странице.
Один из ключевых элементов геометрии — это количество измерений, с которыми вы работаете в любой момент времени. Если вы работаете в одной плоскости, то это либо одна (длина), либо две (длина и ширина). При наличии более чем одной плоскости он должен быть трехмерным, потому что высота / глубина также учитываются.
Двумерные фигуры включают многоугольники, такие как квадраты, прямоугольники и треугольники, у которых есть прямые линии и точки в каждом углу.
Больше о полигонах можно узнать на нашей странице Полигоны . Другие двухмерные формы включают круги и любую другую форму, которая включает кривую. Вы можете узнать больше об этом на нашей странице Curved Shapes .
Три измерения: многогранники и изогнутые формы
Наконец, есть также трехмерных фигур , таких как кубы, сферы, пирамиды и цилиндры.
Чтобы узнать больше об этом, посетите нашу страницу Трехмерные формы .
Знаки, символы и терминология
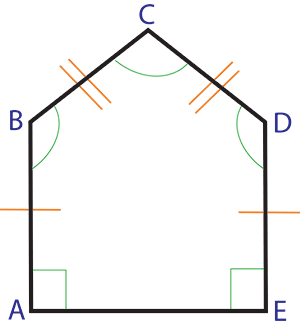
Форма, показанная здесь, представляет собой неправильный пятиугольник, пятиугольный многоугольник с разными внутренними углами и длинами линий (подробнее об этих формах см. Нашу страницу о Многоугольники ).
Градусы ° являются мерой вращения и определяют величину угла между двумя сторонами.
Углы обычно обозначаются в геометрии с использованием сегмента окружности (дуги), если только они не являются прямым углом, когда они «возведены в квадрат».В данном примере угловые метки обозначены зеленым цветом. Смотрите нашу страницу Уголки для получения дополнительной информации.
Отметки (показаны оранжевым цветом) указывают стороны формы, которые имеют одинаковую длину (стороны формы, которые соответствуют или совпадают). Одиночные линии показывают, что две вертикальные линии имеют одинаковую длину, а двойные линии показывают, что две диагональные линии имеют одинаковую длину. Нижняя горизонтальная линия в этом примере отличается по длине от остальных 4 линий и поэтому не отмечена.Отметки также могут называться « штриховок ».
Вершина — это точка пересечения линий (линии также называются лучами или ребрами). Множественное число вершин — это вершины. В этом примере пять вершин помечены как A, B, C, D и E. Называть вершины буквами — обычное дело в геометрии.
В замкнутой форме, такой как в нашем примере, математическое соглашение гласит, что буквы всегда должны располагаться в порядке по часовой стрелке или против часовой стрелки.Нашу форму можно описать как «ABCDE», но было бы неправильно обозначать вершины так, чтобы форма была, например, «ADBEC». Это может показаться несущественным, но в некоторых сложных ситуациях важно избегать путаницы.
Символ угла ‘’ используется как сокращенный символ в геометрии при описании угла. Выражение ∠ABC является сокращением для описания угла между точками A и C в точке B. Средняя буква в таких выражениях всегда является вершиной угла, который вы описываете — порядок сторон не важен. ABC совпадает с CBA, , и оба описывают вершину B в этом примере.
Если вы хотите записать измеренный угол в точке B в сокращенном виде, вы должны использовать:
m∠ABC = 128 ° (m просто означает «мера»)
или
м∠CBA = 128 °
В нашем примере мы также можем сказать:
м∠EAB = 90 °
м∠BCD = 104 °
Почему эти концепции имеют значение?
Точки, линии и плоскости лежат в основе почти всех других геометрических концепций.Углы образуются между двумя линиями, начиная с общей точки. Фигуры, двухмерные или трехмерные, состоят из линий, соединяющих точки. Плоскости важны, потому что двумерные формы имеют только одну плоскость; трехмерные их два и более.
Другими словами, вам действительно нужно понять идеи на этой странице, прежде чем вы сможете перейти к любой другой области геометрии.
,средних точек и конгруэнтных сегментов — концепция
Изучая около средних точек , также важно понимать концепцию конгруэнтных сегментов. Конгруэнтные линейные сегменты — это линейные сегменты одинаковой длины. В отрезке линии есть одна точка, которая разделит отрезок пополам на два совпадающих отрезка. Эта точка называется средней точкой.
Если мы говорим о средней точке линейного сегмента, что означает, что у него есть фиксированные конечные точки, мы сначала должны поговорить об идее конгруэнтности.В геометрии конгруэнтность означает одинаковое расстояние или одно и то же измерение. Перед съемкой я нарисовал два совпадающих отрезка. Они измеряют ровно 9 дюймов. Обратите внимание, что я использую две метки для обозначения дюймов. Если бы я использовал только один из них, это означало бы 9 футов, но я смотрю на это, это определенно не 9 футов. Так что оба они ровно 9 дюймов.
Я собираюсь добавить конечные точки с метками. Итак, я скажу, что это отрезок линии ab, и я скажу, что это отрезок cd. Если бы я возвращался к алгебре, мы любим использовать знаки равенства в алгебре.Итак, я бы сказал, что ab = cd, но теперь, когда мы находимся в геометрии, мы собираемся использовать другой термин, и этот другой термин — конгруэнтность. Итак, я собираюсь сказать, что этот сегмент линии ab, обратите внимание, что у меня здесь нет стрелок, которые говорят мне, что это не луч и не линия, конгруэнтно сегменту линии cd.
Сейчас мы должны обсудить то, что две линии никогда не могут быть конгруэнтными, потому что они бесконечны. Итак, в алгебре мы говорим ab = cd, в геометрии мы говорим, что ab конгруэнтно cd. Единственная разница здесь в том, что у нас есть Mr.Сквиглс, и у меня есть полоса над ab, которая говорит мне, что мы говорим о отрезке линии.
Итак, возвращаясь к нашему отрезку прямой, на этом отрезке есть одна точка, которая разделит его пополам. Я собираюсь это записать. Bisect — это также слово из словаря геометрии. Теперь, что означает деление пополам, это разделит это на две равные части. Как я могу сказать каждому изучающему геометрию, каждому учителю геометрии, каждому математику в мире, что эти двое совпадают?
Я делаю это с помощью знаков.Итак, я собираюсь написать одинаковое количество отметок на любом из этих сегментов. При желании вы можете использовать две оценки, а если вы с ума сошли, можете использовать три оценки. Но это говорит каждому ученику, изучающему геометрию, что эти два отрезка линии должны совпадать.
Уклон (м) прямой (координатная геометрия)
Наклон (м) линии (Координатная геометрия) — Math Open ReferenceОпределение: наклон линии — это число, которое измеряет ее «крутизну», обычно обозначается буквой m. Это изменение y для изменения единицы x вдоль линии.
Попробуй это Отрегулируйте линию ниже, перетащив оранжевую точку в точке A или B. Наклон линии постоянно пересчитывается. Вы также можете перетащить исходную точку на (0,0).
Наклон линии (также называемый градиентом линии) — это число, которое описывает, насколько она «крутая». На рисунке выше нажмите «сброс». Обратите внимание, что для каждого увеличения на одну единицу вправо по горизонтальной оси x, линия опускается на половину единицы. Следовательно, он имеет наклон -0,5. Чтобы попасть из точки А в точку Б по линии, нам нужно переместиться вправо на 30 единиц и вниз на 15. Опять же, это половина единицы на каждую единицу в поперечнике.
Поскольку линия наклоняется вниз вправо, она имеет отрицательный наклон.По мере увеличения x y уменьшается на . Если линия наклонена вверх вправо, наклон будет положительным числом. Отрегулируйте точки выше, чтобы создать положительный наклон.
Формула уклона
Для любых двух точек на прямой ее наклон определяется по формуле  | |
| где: | |
| A x | — координата x точки A |
| A y | — координата y точки A |
| B x | — координата x точки B |
| B y | — координата y точки B |
Пример
На схеме вверху страницы нажмите «сбросить». Подставляя координаты A и B в формулу, получаем
Определение уклона прямой при осмотре
Вместо того, чтобы просто подставлять числа в формулу выше, мы можем найти наклон, поняв концепцию и рассмотрев ее. Обратитесь к линии ниже, определенной двумя заданными точками A, B.Мы видим, что линия наклоняется вверх и вправо, поэтому наклон будет положительным.
- Вычислить dx, горизонтальное расстояние от левой точки до правой точки. Поскольку B находится в точке (15,5), его координата x — это первое число, 15. Координата X точки A равна 30. Таким образом, разница (dx) равна 15.
- Вычислите dy — величину подъема или опускания линии при движении вправо. Поскольку B находится в (15,5)
его координата Y — это второе число или 5.
Координата Y точки A равна 25.Таким образом, разница (dy) составляет +20.
Положительно, потому что линия идет на вверх на , когда вы идете вправо. Иначе было бы отрицательно. - Разделение подъема (dy) на пробег (dx):
Один из способов запомнить этот метод — «подъем через бег». Это «подъем» — разница между точками вверх и вниз, а «бег» — горизонтальный бег между ними. Просто помните, что подъем вниз отрицательный.
Направление откоса
Наклон линии может быть положительным, отрицательным, нулевым или неопределенным.Положительный наклон
Здесь y увеличивается на с увеличением x, поэтому линия наклоняется вверх вправо. Наклон будет
быть положительным числом. Линия справа имеет наклон примерно +0,3, она идет на вверх примерно на 0,3 для каждого шага 1 по оси x.Отрицательный уклон
Здесь y уменьшается на по мере увеличения x, поэтому линия наклоняется вниз вправо. Наклон будет
быть отрицательным числом. Линия справа имеет наклон примерно -0.3, он идет на вниз на примерно на 0,3 для каждого шага 1 по оси x.Нулевой наклон
Здесь y не изменяет при увеличении x, поэтому линия строго горизонтальна. Склон
любой горизонтальной линии всегда равен нулю.
Линия справа не идет ни вверх, ни вниз при увеличении x, поэтому ее наклон равен нулю.Неопределенный уклон
Когда линия строго вертикальна, у нее нет определенного наклона.
Две координаты x одинаковы, поэтому разница равна нулю.Тогда расчет наклона выглядит примерно так: 
Когда вы делите что-либо на ноль, результат не имеет значения.
Линия выше строго вертикальна, поэтому у нее нет определенного наклона.
Мы говорим: «наклон прямой AB не определен».Вертикальная линия имеет уравнение вида x = a, где a — точка пересечения с x. Подробнее об этом см. Наклон вертикальной линии.
Уравнение прямой
Наклон m линии является одним из элементов уравнения линии, если записать ее в форме «наклон и пересечение»: y = mx + b . м в уравнении — это наклон линии, описанной здесь.Подробнее об этом см .:
Наклон в виде угла
Наклон линии также может быть выражен как угол, обычно в градусах или радианах.
На рисунке выше нажмите «Показать угол». Традиционно угол отсчитывается от любой горизонтальной линии (параллельной оси x). Линии с положительным уклоном (вверх и вправо) имеют положительный угол, а отрицательный угол — отрицательный.Измените уклон, перетащив A или B, и убедитесь в этом сами.
Чтобы преобразовать наклон m в угол наклона и обратно:угол = arctan (м)
м = загар (угол)
Tan и его обратный arctan описаны в Обзор тригонометрииЧто попробовать
- На приведенной выше диаграмме перетащите точки A и B и обратите внимание на изменение рассчитанного наклона. Попробуйте получить положительный, отрицательный, нулевой и неопределенный наклон
- Нажмите «скрыть детали».Перетащите A и B в новое место и самостоятельно рассчитайте наклон линии. Затем нажмите «Показать подробности» и посмотрите, насколько близко вы подошли. В качестве бонуса оцените наклон по двум точкам на выбранной вами линии, а не по точкам A и B.
- Отрегулируйте точки A и B, чтобы получить наклон +1 и -1. Что вы заметили в наклоне? (Ответ: наклон 45 ° — линия находится посередине между вертикальной и горизонтальной). Щелкните «Показать угол», чтобы проверить.
Ограничения
Для большей ясности в апплете выше координаты округлены до целых чисел, а длины округлены до одного десятичного знака.Это может привести к небольшому отклонению расчетов.
Подробнее см. Учебные заметки
Прочие разделы о координатной геометрии
(C) Открытый справочник по математике, 2011 г.
Все права защищены.