точка, прямая, отрезок, луч, ломаная линия
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Луч: начальная точка, обозначение лучей
Луч – это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой. Луч также называется
Любой луч имеет начало и направление. Начало луча, начальная точка или вершина луча – это точка, из которой исходит луч. Таким образом, у луча есть начало, но нет конца.
Рассмотрим три луча с общим началом:
Все 3 луча имеют общую начальную точку O, но разные направления. Про каждый из них можно сказать: луч исходит из точки O
или луч исходящий из точки O
.
Дополнительные лучи
Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча:
Дополнительные лучи – это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой. Также можно сказать, что дополнительными называются лучи, дополняющие друг друга до прямой линии.
Обозначение лучей
Луч обозначают одной строчной латинской буквой:
луч h.
Также луч можно обозначить двумя точками, лежащими на нём:
При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором – буква, обозначающая какую-либо другую его точку: луч
Посмотрим на следующий пример:
Луч с началом в точке A можно обозначить как AB или AC.
naobumium.info
Отрезок. Луч / Виды линий / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Виды линий
- Отрезок. Луч
Прежде, чем поговорить о луче и отрезке, повтори тему «Прямая линия» в нашем справочнике.
Отрезок
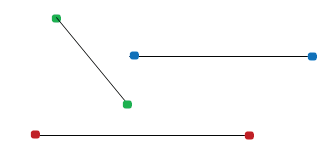
У отрезка есть начало и конец.
Часто отрезки обозначают буквами.
Луч
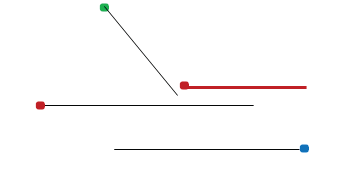
У луча есть начало, но нет конца.
Луч тоже можно обозначать буквами.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точка. Кривая. Прямая линия
Ломаная линия
Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине
Виды линий
Правило встречается в следующих упражнениях:
1 класс
Страница 60, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 68, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 78, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 82, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 84, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 39, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 24, Моро, Волкова, Степанова, Учебник, 2 часть
Страница 25, Моро, Волкова, Степанова, Учебник, 2 часть
Страница 47, Моро, Волкова, Степанова, Учебник, 2 часть
Страница 106, Моро, Волкова, Степанова, Учебник, 2 часть
2 класс
Страница 4, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Задание 25, Моро, Волкова, Рабочая тетрадь, 1 часть
Задание 43, Моро, Волкова, Рабочая тетрадь, 1 часть
Задание 2, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 62, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 5, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 48, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 54, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 107, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 9, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
4 класс
Страница 13, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 63, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 65, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 8, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 29, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 57, Моро, Волкова, Рабочая тетрадь, 1 часть
© budu5.com, 2019
Пользовательское соглашение
Copyright
budu5.com
точка и прямая линия, отрезок, луч, ломаная линия
К основным геометрическим фигурам на плоскости относятся точка и прямая линия. Отрезок, луч, ломаная линия — простейшие геометрические фигуры на плоскости.
Точка — это самая малая геометрическая фигура, которая является основой всех прочих построений (фигур) в любом изображении или чертеже.
Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.
Прямую линию, или прямую, можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком. Отрезок изображается так:
Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:
Если на прямой вы поставили точку, то этой точкой прямая разбивается па два луча, противоположно направленных. Такие лучи называются дополнительными.
Ломаная линия — это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.
Выше изображена трехзвенная ломаная линия.
Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник:
Четырехзвенная замкнутая ломаная линия — четырехугольник
Трехзвенная замкнутая ломаная линия — треугольник
Плоскость, как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную
геометрическую фигуру:
shkolo.ru
Урок-сказка «Луч. Отрезок. Прямая». 2-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- Закрепить представления о понятиях «прямая», «луч», «отрезок»;
- Учить детей распознавать прямые, лучи, отрезки; изображать их с помощью линейки, находить и обозначать точки их пересечения;
- Закреплять навыки сложения и вычитания трехзначных чисел;
- Развивать творческое мышление, интерес к математике.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Слайд 3. Решив данные примеры и расположив ответы в порядке возрастания, вы узнаете, в чье королевство мы сегодня отправимся за новыми знаниями.
| 32 | 440 | 588 | 635 | 744 |
Появляется слово «Точка». «Молодцы!» (Слайд 4)
III. Работа над темой урока. Сказка про Точку.
Слово учителя: Сегодня мы отправимся в увлекательное путешествие по стране Геометрии. Встречает нас здесь королева этой страны, без которой невозможно построить ни одной фигуры, это Точка (Слайд 5).
Жила-была Точка. Она была очень любопытна и хотела все знать. Увидит незнакомую линию и непременно спросит:
— Как эта линия называется?
— Длинная она или короткая?
Подумала однажды Точка: «Как же я смогу все узнать, если всегда буду жить на одном месте? «Отправлюсь-ка я в путешествие!».
— Ребята, вы готовы совершить путешествие вместе с Точкой? (Да).
Сказано — сделано. Вышла точка на прямую и пошла по этой линии (Слайд 6). Долго шла. Устала. Остановилась и говорит: «Долго ли я еще буду идти?».
— Ребята, а скоро ли конец прямой? (У прямой нет конца).
— Тогда я наверное поверну назад, — ответила Точка. Я наверное пошла не в ту сторону.
— Ребята, сможет ли Точка найти концы прямой? (Нет)
Слайд 7.
Без конца и края
Линия прямая!
Хоть сто лет по ней идти —
Не найти конца пути!
— Опечалилась Точка. Что же, так мне и придется идти, идти и идти без конца?
— А что если я позову на помощь Ножницы?
Тут откуда не возьмись, появились Ножницы. Щелкнули перед самым Точкиным носом и разрезали прямую (Слайд 8)
— Ура! Воскликнула Точка. Получился конец, да не один, а целых два, с одной стороны и с другой! Что же стало с моей прямой? (Слайд 9) Как называется получившаяся фигура? (Отрезок). Чем отличается от прямой? (Имеет начало и конец).
— Я запомню это название — «отрезок», сказала Точка. Мне нравится на отрезке, я устрою здесь себе дом::. Но прямая мне тоже нравилась. Жаль, что её не стало. Ведь теперь вместо прямой есть мой отрезок и еще два :.этих::.ну этих::.даже не знаю как назвать. У них конец с одной стороны, а с другой нет конца. Как же они называются? (Лучи). Слайд 10
— А я знаю почему они так называются. Воскликнула Точка. Они похожи на солнечные лучики! Солнечные лучи начинаются на солнце и идут от солнца без конца:.. В Геометрии каждый луч, отрезок, прямая имеют название. Обратите внимание, что луч обозначается либо одной строчной буквой, либо двумя прописными, причем при чтении и записи на первом месте указывается начало луча, а при названии прямой или отрезка порядок не имеет значения. Точка обозначается одной буквой. Давайте правильно прочитаем название фигур (Буквы латинского алфавита). Слайд 11
— В чем отличие прямой от луча? Отрезок от прямой? Луч от отрезка?
Молодцы!!!! Слайд 12.
Слайд 13. Физминутка. Учащиеся танцуют под «Танец маленьких утят».
IV. Закрепление пройденного материала.
Работа по учебнику Л.Г.Петерсон Математика 2 класс. Тема: «Луч. Отрезок. Прямая».
№ 1. Откройте тетради. Обозначьте точку. Сколько можно провести прямых через данную точку? (Слайд 14) Какой можно сделать вывод? Вывод: через одну точку можно провести сколько угодно прямых.
№ 2. Поставьте две точки на расстоянии друг от друга (Слайд 15). Сколько можно провести прямых через эти две точки? Вывод: Через две точки можно провести только одну прямую.
V. Итоги урока.
1. А теперь повторим: о каких геометрических фигурах мы узнали, благодаря нашей гостье Королеве — Точке? (Слайд 16)
2. Что вы узнали о каждой из этих фигур? (Слайд 17)
ПРЯМАЯ — НЕ ИМЕЕТ НИ НАЧАЛА, НИ КОНЦА, МЫ МОЖЕМ НАЧЕРТИТЬ ТОЛЬКО ЧАСТЬ ПРЯМОЙ, ТАК КАК ЕЁ МОЖНО ПРОДОЛЖИТЬ, ПРЯМУЮ ПРИНЯТО ОБОЗНАЧАТЬ ОДНОЙ ИЛИ ДВУМЯ БУКВАМИ.
ЛУЧ — ИМЕЕТ НАЧАЛО, НО НЕ ИМЕЕТ КОНЦА, ЕГО МОЖНО ПРОДОЛЖИТЬ ТОЛЬКО В ОДНУ СТОРОНУ.
ОТРЕЗОК — ИМЕЕТ НАЧАЛО И КОНЕЦ, ЕГО НЕЛЬЗЯ ПРОДОЛЖИТЬ.
НУ ВОТ И ВСЕ, КОНЕЦ! А КТО СЛУШАЛ, МОЛОДЕЦ!!!
urok.1sept.ru
5 класс. Математика. Никольский. Учебник. Ответы к стр. 80
Измерение величин
Прямая. Луч. Отрезок
Ответы к стр. 80
346. Проведите прямую AB и вне ее точку C. Через точку C проведите прямую параллельную прямой AB.
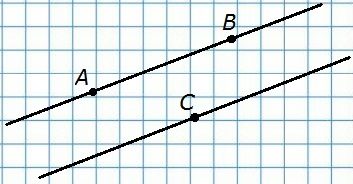
347. Сколько прямых можно провести через одну точку?
Бесконечное множество.
348. Даны три точки, не лежащие на одной прямой. Через каждые две точки проведена прямая. Сколько прямых проведено?
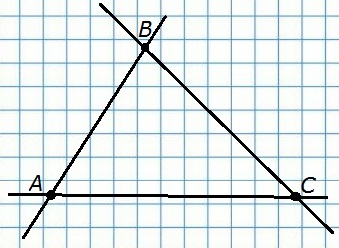
Три прямые.
349. Даны четыре точки так, что никакие три из них не лежат на одной прямой. Через каждые две точки проведена прямая. Сколько прямых проведено?
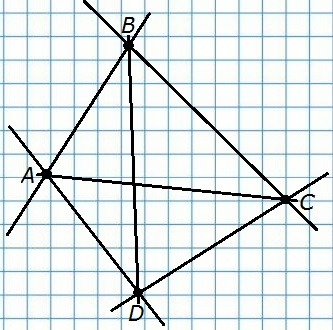
Шесть прямых.
350. На сколько частей прямая делит плоскость?
На две части.
351. На сколько частей делят плоскость две прямые, если они:
а) пересекаются; б) параллельны?
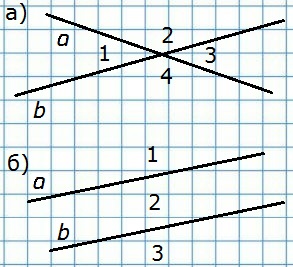
а) на 4 части;
б) на 3 части.
352. На сколько частей можно разделить плоскость тремя прямыми?
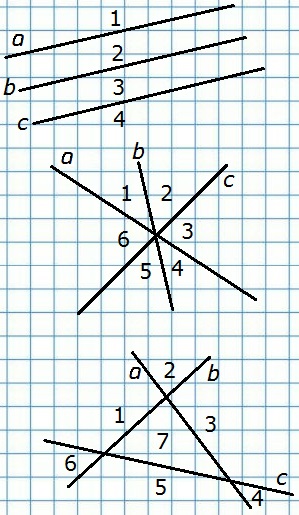
Если прямые параллельны – на 4 части, если пересекаются в одной точке – на 6 частей, если пересекаются не в одной точке – на 7 частей.
353. Отметьте на листе бумаги точку, проведите несколько лучей с началом в этой точке. Сколько таких лучей можно провести?
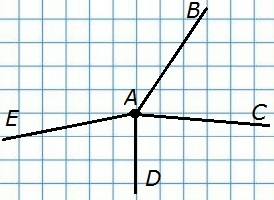
Бесконечно много.
354. Отметьте на прямой две точки A и B. Сколько получилось лучей с началом в этих точках?
Лучи АС, АD, ВС, ВD.
355. Сколько получится лучей, если на прямой отметить:
а) 3 точки; б) 5 точек; в) 100 точек?
Из одной точки выходят два луча.
а) 3 • 2 = 6 лучей;
б) 5 • 2 = 10 лучей;
в) 100 • 2 = 200 лучей.
356. Две прямые пересекаются в одной точке. Сколько лучей с началом в этой точке они образуют?
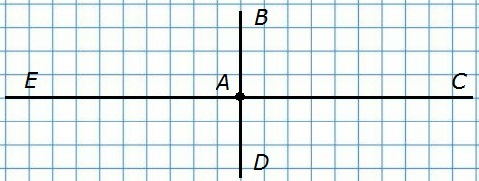
Лучи АС, АD, АЕ, АВ – всего 4 луча.
357. Назовите все лучи с вершиной в точках A, B и C (рис. 47). Сколько лучей получилось.
Лучи АM, АN, BM, ВN, CM, CN – всего 6 лучей.
358. Назовите все отрезки с концами в точках M, N и K (рис. 48). Сколько отрезков получилось?
Отрезки MА, MК, NК – всего 3 отрезка.
359. На прямой отметили четыре точки. Образовалось 6 отрезков с концами в этих точках. Проверьте.
Отрезки АВ, АС, АD, ВС, ВD, СD – всего 6 отрезков.
360. Перечертите рисунок 49 в тетрадь. Обозначьте все точки пересечения прямых, продолжив их, если нужно. На сколько частей разделилась плоскость? Выберите правильный ответ:
A. 10 частей;
Б. 11 частей;
В. 12 частей.
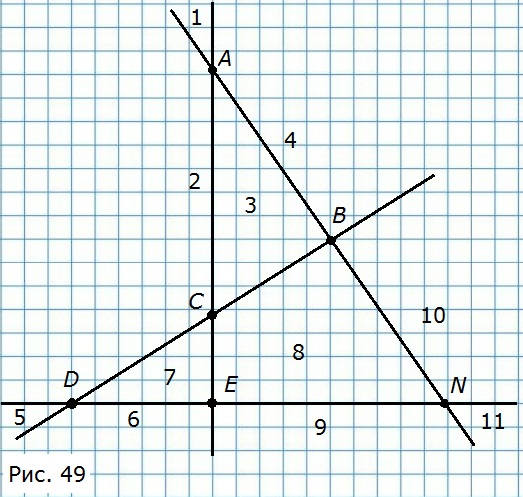
Ответ Б – 11 частей.
Ответы по математике. 5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 5 класс
volzsky-klass.ru
Плоскость. Прямая. Луч
На этом уроке мы познакомимся с понятиями «отрезок», «прямая», «луч» и «плоскость». Рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
На прошлом уроке мы разобрались, как строить отрезок. Мы уже знаем, что отрезок – это прямая линия, ограниченная двумя точками.
Определение
Давайте начертим отрезок MN. Если продлить этот отрезок неограниченно за точку N, то мы получим новую фигуру, которая называется луч. У нас получился луч MN.
Точку М называют началом луча.
Если бы мы продлевали отрезок MN неограниченно за точку М, то у нас бы получился луч NМ, у которого точка N – начало луча.
Заметьте: обозначается луч большими заглавными буквами латинского алфавита, первой буквой записывают его начало, а затем букву, обозначающую какую-либо другую точку луча.
Обратите внимание, что луч имеет начало, но не имеет конца, т. е. он бесконечен в одну сторону.
Для того чтобы представить луч в окружающей среде, достаточно сфотографировать след от самолёта в безоблачном небе, где сам самолёт – это начальная точка, а след, оставленный на небе, – это прямая линия, которая бесконечна.
Либо солнечный луч, где начальная точка – это солнце, а конечной точки нет.
Определение
Если отрезок MN неограниченно продлевать в обе стороны – как за точку М, так и за точку N, то у нас получится фигура, которая называется прямой.
На рисунке у нас получилась прямая MN, также её можно назвать и прямая NМ. Как кому больше нравится!
Заметьте, что прямая не имеет ни начала, ни конца.
Любая точка прямой разделяет её на 2 луча.
В нашем случае точка О разделяет прямую MN на луч ОМ и луч ОN. Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.
Представление о прямой можно получить, если сложить лист бумаги (линия, которая получилась при сгибе, и будет прямой) или туго натянуть верёвку.
В математике прямая представляется идеально ровной и бесконечной в обе стороны.
Прямую можно обозначить двумя вариантами.
1-й вариант: двумя заглавными буквами латинского алфавита, например MN. В таком случае говорят: «Прямая MN».
2-й вариант: прямую обозначают одной малой буквой, например m, и говорят: «Прямая m».
Давайте попробуем провести ещё одну прямую через эти же две точки.
У нас это не получится. Через любые две точки можно провести только одну прямую!
Точки, отрезки, лучи и прямые располагаются в плоскости. Примеры плоскостей в жизни мы встречаем каждый день. Представление о плоскости дают поверхности стола, оконного стекла или замёрзшего водоёма.
Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях. Мы рисуем фигуры на «кусках» плоскости, например в тетрадном листе или на школьной доске.
Теперь давайте рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
На рисунке изображены прямая EF и точки А, L, P и T. Точки А, E, F лежат на отрезке EF, а точки L, P, T не лежат на этом отрезке. Посмотрите, как это записывается.
Точки А, E, F лежат на луче EF, а точки А, E, F, Т лежат на луче FЕ. Посмотрите запись этих утверждений.
Точки А, E, F, Т лежат на прямой EF, а точки А, P, L – на прямой PL.
Обозначается это так:
Точка А лежит между точками Е и F. Точка L не лежит между точками Е и F, она находится вне отрезка EF. Точка Е лежит между точками А и Т, а точка А – между точками P и L.
На следующем рисунке изображены прямая a и прямая b.
Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке. В нашем примере прямые а и b пересекаются в точке О. Точка О делит каждую прямую на две части. Точка О – точка пересечения прямых.
Посмотрите на взаимное расположение прямых m и n:
Они не имеют общих точек. Если прямые не имеют общих точек, то говорят, что они параллельны.
Запомните!
· Прямая бесконечна.
· Отрезок ограничен.
· Луч имеет начало, но не имеет конца.
· Плоскость бесконечна.
Итоги
Итак, на уроке мы с вами разобрались в отличиях понятий «отрезок», «прямая», «луч». Научились их строить. Узнали, что такое плоскость, а также рассмотрели расположение точек, отрезков, прямых и лучей в плоскости.
videouroki.net