Масштаб — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
Масшта́б (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») — в общем случае отношение двух линейных размеров. Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта.
Понятие наиболее распространено в геодезии, картографии и проектировании — отношение величины изображения объекта к его натуральной величине. Человек не в состоянии изобразить большие объекты, например дом, в натуральную величину, поэтому при изображении большого объекта в рисунке, чертеже или макете величину объекта уменьшают в несколько раз: в два, пять, десять, сто, тысячу и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину её изображения в несколько тысяч раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Масштаб в геодезии, картографии и проектировании
Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический.
Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1 : 5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1 : 1 000 крупнее, чем масштаб 1 : 25 000. Иначе говоря, при более крупном масштабе объект изображается крупнее (больше), при более мелком масштабе — тот же объект изображается мельче (меньше).
Именованный масштаб показывает, какое расстояние на местности соответствует 1 см на плане. Записывается, например: «В 1 сантиметре 100 километров», или «1 см = 100 км».
Графические масштабы подразделяются на линейные и поперечные.
- Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части.
- Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла. Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД=0,2 мм, а точность 0,1.
Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).
Масштабы изображений на чертежах должны выбираться из следующего ряда:[1]
| Масштабы уменьшения | 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1 000 |
| Натуральная величина | 1:1 |
| Масштабы увеличения | 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1 |
При проектировании генеральных планов больших объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.
Масштаб в фотографии
При фотосъёмке под масштабом понимают отношение линейного размера изображения, полученного на фотоплёнке или светочувствительной матрице, к линейному размеру проекции соответствующей части сцены на плоскость, перпендикулярную к направлению на камеру.
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Масштаб имеет важное значение при расчете глубины резко изображаемого пространства. Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съемке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).
Под макрофотографией традиционно понимают съёмку в масштабе 1:1 или крупнее. Однако с широким распространением компактных цифровых фотоаппаратов этим термином стали также называть съёмку расположенных близко к объективу (как правило, ближе 50 см) мелких объектов. Связано это с необходимым изменением режима работы системы автофокуса в таких условиях, однако с точки зрения классического определения макросъёмки такое толкование является неверным.
Масштаб в моделизме
Для каждого вида масштабного (стендового) моделизма определены масштабные ряды, состоящие из нескольких масштабов разной степени уменьшения, причём для разных видов моделизма (авиамоделизм, судомоделизм, железнодорожный, автомобильный, военной техники) определены свои, исторически сложившиеся, масштабные ряды, которые обычно не пересекаются.
Масштаб в моделизме исчисляется по формуле:
L / М = Х
Где: L — параметр оригинала, М — требуемый масштаб, Х — искомое значение
Например:
При масштабе 1/72, и параметре оригинала 7500 мм, решение будет выглядеть;
7500 мм / 72 = 104,1 мм.
Полученное значение 104,1 мм, есть искомое значение при масштабе 1/72.
Масштаб времени
В программировании
В операционных системах с разделением времени чрезвычайно важную роль играет предоставление отдельно взятым задачам так называемого «режима реального времени», при котором обработка внешних событий обеспечивается без дополнительных задержек и пропусков. Для этого употребляется также термин «реальный масштаб времени», однако это терминологическая условность, не имеющая к исходному значению слова «масштаб» никакого отношения.
В кинотехнике
Масштаб времени — количественная мера замедления или ускорения движения, равная отношению проекционной частоты кадров к съёмочной. Так, если проекционная частота кадров равна 24 кадра в секунду, а киносъёмка производилась на 72 кадра в секунду, масштаб времени равен 1:3. Масштаб времени 2:1 означает ускоренное вдвое по сравнению с обычным протекание процесса на экране.
В математике
Масштаб — это отношение двух линейных размеров. Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта. В математике масштаб определяется как отношение расстояния на карте к соответствующему расстоянию на реальной местности. Масштаб 1:100 000 означает, что 1 см на карте соответствует 100 000 см = 1 000 м = 1 км на местности.
Напишите отзыв о статье «Масштаб»
Примечания
Отрывок, характеризующий Масштаб
И он ухватил медведя, и, обняв и подняв его, стал кружиться с ним по комнате.Князь Василий исполнил обещание, данное на вечере у Анны Павловны княгине Друбецкой, просившей его о своем единственном сыне Борисе. О нем было доложено государю, и, не в пример другим, он был переведен в гвардию Семеновского полка прапорщиком. Но адъютантом или состоящим при Кутузове Борис так и не был назначен, несмотря на все хлопоты и происки Анны Михайловны. Вскоре после вечера Анны Павловны Анна Михайловна вернулась в Москву, прямо к своим богатым родственникам Ростовым, у которых она стояла в Москве и у которых с детства воспитывался и годами живал ее обожаемый Боренька, только что произведенный в армейские и тотчас же переведенный в гвардейские прапорщики. Гвардия уже вышла из Петербурга 10 го августа, и сын, оставшийся для обмундирования в Москве, должен был догнать ее по дороге в Радзивилов.
Графиня была женщина с восточным типом худого лица, лет сорока пяти, видимо изнуренная детьми, которых у ней было двенадцать человек. Медлительность ее движений и говора, происходившая от слабости сил, придавала ей значительный вид, внушавший уважение. Княгиня Анна Михайловна Друбецкая, как домашний человек, сидела тут же, помогая в деле принимания и занимания разговором гостей. Молодежь была в задних комнатах, не находя нужным участвовать в приеме визитов. Граф встречал и провожал гостей, приглашая всех к обеду.
Графиня подумала и понюхала из золотой табакерки с портретом мужа.
– Замучили меня эти визиты, – сказала она. – Ну, уж ее последнюю приму. Чопорна очень. Проси, – сказала она лакею грустным голосом, как будто говорила: «ну, уж добивайте!»
Высокая, полная, с гордым видом дама с круглолицей улыбающейся дочкой, шумя платьями, вошли в гостиную.
«Chere comtesse, il y a si longtemps… elle a ete alitee la pauvre enfant… au bal des Razoumowsky… et la comtesse Apraksine… j’ai ete si heureuse…» [Дорогая графиня, как давно… она должна была пролежать в постеле, бедное дитя… на балу у Разумовских… и графиня Апраксина… была так счастлива…] послышались оживленные женские голоса, перебивая один другой и сливаясь с шумом платьев и передвиганием стульев. Начался тот разговор, который затевают ровно настолько, чтобы при первой паузе встать, зашуметь платьями, проговорить: «Je suis bien charmee; la sante de maman… et la comtesse Apraksine» [Я в восхищении; здоровье мамы… и графиня Апраксина] и, опять зашумев платьями, пройти в переднюю, надеть шубу или плащ и уехать. Разговор зашел о главной городской новости того времени – о болезни известного богача и красавца Екатерининского времени старого графа Безухого и о его незаконном сыне Пьере, который так неприлично вел себя на вечере у Анны Павловны Шерер.
– Я очень жалею бедного графа, – проговорила гостья, – здоровье его и так плохо, а теперь это огорченье от сына, это его убьет!
– Что такое? – спросила графиня, как будто не зная, о чем говорит гостья, хотя она раз пятнадцать уже слышала причину огорчения графа Безухого.
– Вот нынешнее воспитание! Еще за границей, – проговорила гостья, – этот молодой человек предоставлен был самому себе, и теперь в Петербурге, говорят, он такие ужасы наделал, что его с полицией выслали оттуда.
– Скажите! – сказала графиня.
– Он дурно выбирал свои знакомства, – вмешалась княгиня Анна Михайловна. – Сын князя Василия, он и один Долохов, они, говорят, Бог знает что делали. И оба пострадали. Долохов разжалован в солдаты, а сын Безухого выслан в Москву. Анатоля Курагина – того отец как то замял. Но выслали таки из Петербурга.
– Да что, бишь, они сделали? – спросила графиня.
– Это совершенные разбойники, особенно Долохов, – говорила гостья. – Он сын Марьи Ивановны Долоховой, такой почтенной дамы, и что же? Можете себе представить: они втроем достали где то медведя, посадили с собой в карету и повезли к актрисам. Прибежала полиция их унимать. Они поймали квартального и привязали его спина со спиной к медведю и пустили медведя в Мойку; медведь плавает, а квартальный на нем.
– Хороша, ma chere, фигура квартального, – закричал граф, помирая со смеху.
– Ах, ужас какой! Чему тут смеяться, граф?
Но дамы невольно смеялись и сами.
– Насилу спасли этого несчастного, – продолжала гостья. – И это сын графа Кирилла Владимировича Безухова так умно забавляется! – прибавила она. – А говорили, что так хорошо воспитан и умен. Вот всё воспитание заграничное куда довело. Надеюсь, что здесь его никто не примет, несмотря на его богатство. Мне хотели его представить. Я решительно отказалась: у меня дочери.
– Отчего вы говорите, что этот молодой человек так богат? – спросила графиня, нагибаясь от девиц, которые тотчас же сделали вид, что не слушают. – Ведь у него только незаконные дети. Кажется… и Пьер незаконный.
Гостья махнула рукой.
– У него их двадцать незаконных, я думаю.
Княгиня Анна Михайловна вмешалась в разговор, видимо, желая выказать свои связи и свое знание всех светских обстоятельств.
– Вот в чем дело, – сказала она значительно и тоже полушопотом. – Репутация графа Кирилла Владимировича известна… Детям своим он и счет потерял, но этот Пьер любимый был.
– Как старик был хорош, – сказала графиня, – еще прошлого года! Красивее мужчины я не видывала.
– Теперь очень переменился, – сказала Анна Михайловна. – Так я хотела сказать, – продолжала она, – по жене прямой наследник всего именья князь Василий, но Пьера отец очень любил, занимался его воспитанием и писал государю… так что никто не знает, ежели он умрет (он так плох, что этого ждут каждую минуту, и Lorrain приехал из Петербурга), кому достанется это огромное состояние, Пьеру или князю Василию. Сорок тысяч душ и миллионы. Я это очень хорошо знаю, потому что мне сам князь Василий это говорил. Да и Кирилл Владимирович мне приходится троюродным дядей по матери. Он и крестил Борю, – прибавила она, как будто не приписывая этому обстоятельству никакого значения.
wiki-org.ru
Масштаб — WiKi
Масштаб[1] показывает, во сколько раз каждая линия, нанесённая на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, линейный.
Масштаб в геодезии, картографии и проектировании
Типы Масштабов
Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5000 показывает, что 1 см на плане соответствует 5000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1000 крупнее, чем масштаб 1:25 000.
Именованный масштаб показывает какое расстояние на местности соответствует 1 см на плане. Записывается, например: «В 1 сантиметре 100 километров», или «1 см = 100 км».
Графические масштабы подразделяются на линейные и поперечные.
- Линейный масштаб — графический масштаб в виде масштабной линейки, разделённой на равные части.
- Поперечный масштаб — графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла. Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность 0,1.
Иррациональный масштаб — масштаб представленный в виде иррациональной дроби. Не стандартный вид масштаба. Определителем является простое число исключая 2 и 5.
Десятичный или кратный масштаб — масштаб с определитем кратным 5 и 2. Все стандартные масштабы являются кратными.
Точность масштаба
Точность масштаба — отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооружённым глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1000 см (10 м), 0,1 мм — 100 см (1 м).
Определитель масштаба
Определитель масштаба — число определяющие (показывающие) во сколько раз увеличен или уменьшен натуральный размер.
Определитель масштаба может быть положительным (со знаком «+») или отрицательным (со знаком «-«)
Масштабный Ряд
Масштабы изображений на чертежах должны выбираться из следующего ряда:[1]
| Масштабы уменьшения (правильный масштаб) | 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000 |
| Натуральная величина | 1:1 |
| Масштабы увеличения (цельный масштаб) | 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1 |
При проектировании генеральных планов крупных объектов допускается применять масштабы 1:2000; 1:5000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.
Масштабы Планов и Карт
Традиционно установлено план имеет масштаб крупнее 1 : 5000, а карта мельче 1 : 5000.
Масштаб с точки зрения математики
С точки зрения математики определители масштаба является дробью.
Так же как дроби бывают правильные или цельные, так и масштабы бывают
— правильные 1:Х
— неправильные X:1
Правильные масштабы так, же называю относительными
дробь 1:Х есть отношение 1 к Х.
А неправильные цельными или абсолютными, т.е. Х:1 есть |x|.
Сам масштаб является 1-ой степенью числа.
1:Х — есть -1 степень
Х:1 — есть +1 степень.
Масштаб в фотографии
При фотосъёмке под масштабом понимают отношение линейного размера изображения, полученного на фотоплёнке или светочувствительной матрице, к линейному размеру проекции соответствующей части сцены на плоскость, перпендикулярную к направлению на камеру.
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Масштаб имеет важное значение при расчёте глубины резко изображаемого пространства. Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съёмке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).
Под макрофотографией традиционно понимают съёмку в масштабе 1:1 или крупнее. Однако с широким распространением компактных цифровых фотоаппаратов этим термином стали также называть съёмку расположенных близко к объективу (как правило, ближе 50 см) мелких объектов. Связано это с необходимым изменением режима работы системы автофокуса в таких условиях, однако с точки зрения классического определения макросъёмки такое толкование является неверным.
Масштаб в моделизме
Основная статья: Масштаб (моделизм)
Для каждого вида масштабного (стендового) моделизма определены масштабные ряды, состоящие из нескольких масштабов разной степени уменьшения, причём для разных видов моделизма (авиамоделизм, судомоделизм, железнодорожный, автомобильный, военной техники) определены свои, исторически сложившиеся, масштабные ряды, которые обычно не пересекаются.
Масштаб в моделизме исчисляется по формуле:
L / М = Х
Где: L — параметр оригинала, М — требуемый масштаб, Х — искомое значение
Например:
При масштабе 1/72, и параметре оригинала 7500 мм, решение будет выглядеть;
7500 мм / 72 = 104,1 мм.
Полученное значение 104,1 мм, есть искомое значение при масштабе 1/72.
Масштаб времени
В программировании
В операционных системах с разделением времени чрезвычайно важную роль играет предоставление отдельно взятым задачам так называемого «режима реального времени», при котором обработка внешних событий обеспечивается без дополнительных задержек и пропусков. Для этого употребляется также термин «реальный масштаб времени», однако это терминологическая условность, не имеющая к исходному значению слова «масштаб» никакого отношения.
В кинотехнике
Масштаб времени — количественная мера замедления или ускорения движения, равная отношению проекционной частоты кадров к съёмочной. Так, если проекционная частота кадров равна 24 кадра в секунду, а киносъёмка производилась на 72 кадра в секунду, масштаб времени равен 1:3. Масштаб времени 2:1 означает ускоренное вдвое по сравнению с обычным протекание процесса на экране.
В математике
Масштаб — отношение двух линейных размеров.
Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта. В математике масштаб определяется как отношение расстояния на карте к соответствующему расстоянию на реальной местности.
Масштаб 1:100000 означает, что 1 см на карте соответствует 100000 см = 1000 м = 1 км на местности.
Масштабы изображений на чертежах должны выбираться из следующего ряда (масштабы ГОСТ 2.302-68):
- Масштабы уменьшения 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000
- Натуральная величина 1:1
- Масштабы увеличения 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1
Примечания
- ↑ 1 2 ГОСТ 2.302-68
ru-wiki.org
Для чего нужен масштаб? Какие виды масштабов существуют?
Зачем нужен масштаб?
Ни один географический объект, например реку, мост, поселок, невозможно изобразить на топографическом плане в натуральную величину. В древности люди рисовали уменьшенные изображения местности, на которых разные участки уменьшались произвольно, в разной степени. Поэтому старинные чертежи местности не дают возможности понять, например, каково расстояние между берегами реки, чему равна длина реки и т. д. Чтобы план местности был более точным, необходимо все расстояния уменьшать в одинаковое число раз с сохранением всех пропорций, делать изображение в масштабе.
Масштаб показывает, во сколько раз расстояния на плане уменьшены по отношению к реальным расстояниям.
Длина школы на плане школьного двора в 1000 раз меньше, чем в действительности. Это означает, что на данном плане все расстояния уменьшены в 1000 раз.
Численный и именованный масштабы
Масштаб пишут по-разному. В виде числа масштаб изображается так: 1:100 (это означает, что 1 см плана заменяет 100 см на местности). Это численный масштаб. 100 см — это 1 м, поэтому можно просто написать: в 1 см — 1м. Масштаб, записанный в таком виде, — именованный масштаб.
Линейный масштаб
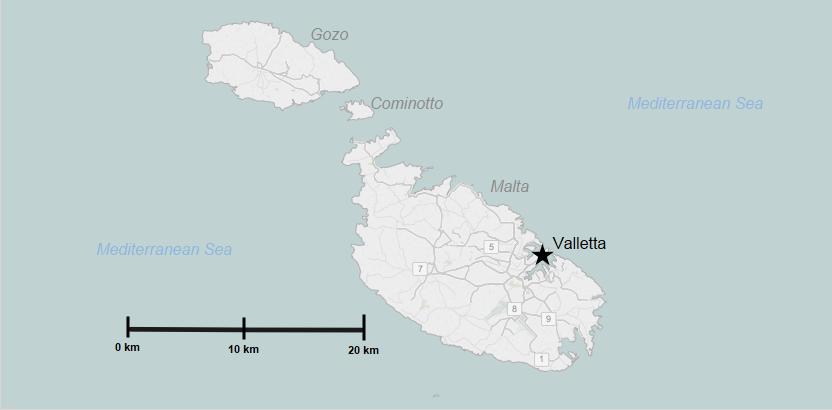
Обычно на планах, кроме численного и именованного масштабов, помещают линейный масштаб. Он представляет собой линию, разделенную на равные отрезки. Отрезки справа от 0 показывают, какому расстоянию на местности соответствуют расстояния на плане в 1 см, 2 см и т. д. Отрезок слева от 0 разделен на равные мелкие части. Зная расстояние на местности, которому соответствует большой отрезок, и количество мелких отрезков, можно вычислить, какому расстоянию на местности соответствует каждый мелкий отрезок. Например, длина большого отрезка слева от 0 на рисунке равна 10м. Этот отрезок разделен на 5 мелких частей, значит, длина одной такой части составляет 10м:5=2 м.
Линейный масштаб позволяет измерять расстояния на плане при помощи циркуля-измерителя или полоски бумаги.
При помощи линейного масштаба можно определять длину кривых линий, например реки, дороги. Для этого надо отметить на полоске бумаги небольшое расстояние или установить небольшой раствор между иглами циркуля-измерителя и переставлять бумагу с отметкой или циркуль вдоль измеряемой линии, считая число перестановок. Определив при помощи линейного масштаба длину одного «шага» в метрах и умножив ее на число перестановок, мы получим длину кривой линии.
Выбор масштаба
Масштаб выбирают в зависимости от величины расстояний. Например, надо изобразить расстояние в 6 км. Тогда масштаб в 1 см — 10 м не годится, потому что это расстояние изображается линией в 600 см, то есть в 6 м; но линию в 6 м нельзя поместить на обычном листе бумаги. Удобнее взять масштаб: в 1 см — 1 км. При таком масштабе расстояние в 6 км будет соответствовать линии в 6 см.
geographyofrussia.com
Точность масштаба: определение, особенности и виды
Среди главных характеристик карт местности чаще всех выделяют данную. Это точность масштаба. В статье мы разберем, что скрывает в себе данное понятие. Также рассмотрим, что такое масштаб вообще, охарактеризуем его основные разновидности. Разберем, как понятие «графическая точность» связано с предметом нашего разговора.
Что это?
Масштаб — это важное уточнение, показывающее, во сколько каждая линия, что была нанесена на чертеж, план, меньше или больше настоящих размеров объекта, который она изображает. Такие уточнения представляются на чертежных документах и картах как численно, так и графически.
Масштабы планов, точность масштабов — понятия, которые можно встретить в самых разнообразных сферах:
- Картография.
- Проектирование.
- Геодезия.
- Фотография.
- Моделизм.
- Программирование.
- Математика.
- Кинотехника.
Некоторые из этих применений, их особенности мы рассмотрим по ходу статьи.
Точность масштаба
И теперь определение ключевого понятия. Точность масштаба — часть горизонтального проложения линии, которая будет означать 0,1 мм на чертеже. Почему выбрано такое значение?
0,1 мм тут принят из-за того, что это наименьший отрезок, который может различить глаз человека на изображении без использования специальной техники, инструментов, приборов.
Приведем конкретный пример. Дано 1:10000. Точность масштаба станет составлять, соответственно, 1 м. Разберем подробнее:
- 1 см на плане или изображении — это 10 000 см (или 100 м) на реальной местности.
- 1 мм на изображении — это 1 000 см (или 10 м).
- 0,1 мм — это 100 см (или 1 м) на реальной местности.
Таким образом несложно определить предельную точность масштаба. Это расстояние реальной поверхности, равное 0,1 мм на карте — минимальному отрезку, который способен различить человек.
Графическая точность
А теперь познакомимся с графической точностью масштабов. Это еще одна значимая характеристика при использовании планов и карт.
Графическая точность связывается с разрешением «и» глаза человека. В свою очередь, оно составляет «Г». Отсюда Г=и.
То есть, если угол «и» между векторами на две точки «В» и «Л» при рассматривании их наблюдателем с нормальным уровнем зрения составляет «Г» или же более, то они будут восприниматься, как две точки. Если же данный угол к понятию разрешения меньше «Г», то «Л» и «В» будут восприниматься человеком как одна точка.
Лучше всего тут познакомиться с определением точности масштаба на конкретном примере. Допустим, человек рассматривает карту с наилучшего расстояния «б», равного 35 см. Значение Г=и. Теперь нужно определить наименьшее расстояние (то есть, графическую точность) между «В» и «Л», при котором они еще будут восприниматься наблюдателем в виде двух разных точек. Тут проводится такое вычисление:
1 — ис! — 1/3438 х 350 мм = 0,1 мм.
1/3438 — это значение угла и=Г, которое в данном случае выражено в радианах (3438′ — количество минут в радиане).
Таким образом, вышедшее значение 0,1 мм — графическая точность плана или карты.
Связь понятий
А теперь посмотрим, как вышеобозначенный термин соотносится с главным. Точность масштаба — это, как мы помним, расстояние на поверхности Земли, что равняется 0,1 мм на документе.
Можно вывести формулу:
Т = гМ = 0,1 М мм.
Расшифруем ее элементы:
- Т — точность масштаба.
- М — знаменатель масштаба.
- г = 0,1 мм — графическая точность.
Отсюда можно вывести и связанную трактовку. Точность масштаба — графическая точность, что выражается в масштабе карты или плана. И что же в итоге? Графическая точность станет выступать константой (0,1 мм) для всех существующих масштабов.
Соответственно, точность масштаба станет изменяться вместе с ним самим. Она будет тем выше, чем крупнее составитель выбрал масштаб.
А теперь разберемся с особенностями такой характеристики, как масштаб, в различных сферах применения.
Проектирование, геодезия и картография
Мы в курсе, что обозначает точность «500» масштаба — 1:500. Рассмотрим теперь, какие его разновидности характерны для сферы проектирования, картографии и геодезии:
- Численный масштаб. Показатель прописывается в виде дроби. В ее числителе будет стоять единица, а в знаменателе — какая-либо степень уменьшения проекции на карте. Для примера возьмем масштаб 1:5 000. Он обозначает, что 1 см на плане, карте — это 5 000 см (или 50 м) на реальной местности. Соответственно, тут будет более крупным тот масштаб, который отличается меньшим знаменателем. Так, 1:1 000 будет крупнее, нежели 1:20 000.
- Именованный масштаб. Составитель карты прописывает на документе, какое расстояние на реальной местности равняется 1 см на плане. Вот пример: «В 1 сантиметре — 1000 километров». Или же кратко: «1 см = 100 км».
- Графический масштаб. В свою очередь, будет разделяться на поперечный и линейный. Разберем их отдельно.

Разновидности графической категории
Какова же точность масштаба — поперечного масштаба? Познакомимся с характеристиками:
- Линейный. Такой графический масштаб на карте представляется в виде линейки, которая будет разделена на реальные части.
- Поперечный. Это графический масштаб, представленный в виде номограммы. Ее построение зиждется на пропорциональности частей параллельных прямых, что пересекают стороны угла. Такой масштаб применим для более точного измерения протяженности линий на планах. Пользуются им таким образом: производят на нижней линии данного поперечного масштаба замер длины так, чтобы правый конец находился на целом расстоянии (ОМ), а левый был за 0. Если при этом левая ножка окажется между десятыми делениями, соответственно, левого отрезка (от 0), то специалист подымает обе ножки измерителя кверху. Пока левая ножка измерителя не встанет уже на пересечении какой-либо горизонтальной линии и какой-либо трансверсали. А вот правая ножка тоже должна быть на этой горизонтальной черте. Минимальная ЦД здесь — 0,2 мм. Соответственно, наименьшая точность — 0,1 мм.
Ряд масштабов изображений в проектировании
Мы уже знаем, что означает точность масштаба 1:500. Но в каких случаях ее выбирает составитель? Разберем и этот вопрос:
- Масштабы уменьшения. Соответственно, используются в случаях, когда на плане нужно изобразить объект, местность, значительно превышающую его по площади. Если же составитель обращается к проектированию генеральных планов особо крупных размеров, то он ему пригодится использование следующих масштабов: 1:2 000, 1:5 000, 1:10 000, 1:20 000, 1:25 000, 1:50 000.
- Натуральная величина. Если требуется изобразить объект на плане так, «как он есть», то обращаются к масштабу «один к одному». Соответственно 1 см реальной длины тут будет соответствовать 1 см длины на плане.
- Масштабы увеличения. Необходимы в случаях, когда требуется изобразить на плане слишком маленький объект для детального ознакомления с его внешним видом, устройством.
В фотографии
Конечно, точность масштаба 1:10 000 более связывается с картографией. Но это применимо и для мира фотосъемки. Под масштабом здесь подразумевается отношение так называемых линейных размеров изображения, полученного на сверхчувствительной матрице или же на фотопленке, к размеру проекции соответствующей зоны проекции на плоскость, которая перпендикулярна к камере.
Есть фотографы, которые измеряют масштаб в виде отношения размеров реального объекта к его размерам на экране, фотобумаге или другом носителе. Но верный способ определения масштаба в фотографии зависит только от контекста, в котором использовано изображение.
В фотосъемке масштаб характеризуется важным значением и при расчете глубины какого-либо резко изображаемого объекта, пространства. Сегодня специалистам доступен весьма широкий выбор диапазонов масштабов от бесконечно малого (применяется при съемке далеких небесных тел) до весьма крупного (без использования специальных оптических насадок, например, сегодня возможно получить снимок масштабом 10:1).
Здесь макрофотографией считается уже съемка в масштабе 1:1 (и, соответственно, крупнее). Но с распространением цифровых компактных фотоаппаратов макросъемкой также стали называть стиль, когда объектив располагают слишком близко к объекту. Если рассматривать классическое определение, то подобное толкование не будет верным.

В моделизме
Для каждого из видов стендового (или масштабного) моделизма определены свои масштабные ряды. Они состоят из нескольких масштабов, характеризующихся определенной степенью уменьшения. Что интересно, для каждого из видов моделизма (железнодорожного, автомобильного, судомоделизма, военной техники, авиамоделизма) есть определенные исторически сформированные масштабные ряды, которые не пересекаются с иными.
Здесь масштаб исчисляется по простой формуле:
L / М = Х.
Расшифруем:
- L — параметры оригинала.
- М — необходимый для работы масштаб.
- Х — нужное значение.
В программировании
В этой сфере будет важен так называемый масштаб времени. Разберемся, что это.
В ОС с разделением времени весьма важную роль имеет предоставление конкретно взятым задачам «режима реального времени». Он отличается тем, что обработка внешних событий идет без дополнительных задержек или пропусков. Здесь важным будет еще одно понятие — «реальный масштаб времени». Но стоит понимать, что к масштабу на картах он прямого отношения не имеет. Это всего лишь терминологическая условность.
В кинотехнике
В кинотехнике тоже важна точность масштаба времени. Под последним подразумевается количественный показатель замедления либо ускорения движения, который будет равняться отношению проекционный частоты кадров к частоте съемочной.
Рассмотрим это на простом примере. Проекционная частота кадров при съемке фильма составляет 24 кадра/сек. Киносъемка производилась при этом «со скоростью» 72 кадра/сек. Масштаб времени в данном случае будет равен 1:3.
А что тогда будет означать, к примеру, 2:1? Это ускоренное в два раза по сравнению со стандартным протеканием происходящего на экране.
В математике
В этой сфере под масштабом понимается линейное соотношение двух размеров. Также во многих практически применимых областях так будет называться отношение размера изображения к реальному размеру изображаемого.
В математике масштаб — это отношение какого-либо расстояния на карте уже к реальному расстоянию на реальной местности. Если рассмотреть на примере, это то же самое, что и в картографии. Допустим, 1:100 000 000. Значит, 1 см на изображении — это 100 000 см в реальности. То есть, тысяча метров или один километр.
Масштаб — широко применимая характеристика. Это стандартная и неотъемлемая составляющая при разработке планов, чертежей объектов, карт местности. Используется при проектировании, в геодезии, картографии, актуальна при фотосъемке, в кинотехнике, программировании и математике. Саму же ее главным образом характеризует точность — отношение реального расстояния к принятому на карте.
fb.ru
Масштаб
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Технологии:
- элементы ИКТ-технологий, технология проблемного обучения,
- технология эвристического обучения,
- здоровьесберегающие технологии.
Цели урока:
- систематизировать и закрепить знания по теме “Масштаб”;
- закрепить умение решать задачи на нахождение расстояний на местности и на карте, зная масштаб карты;
- формировать метапредметные компетенции в ходе выполнении практической работы по вычислению расстояния на местности при помощи программы “Google. Земля” в сети Интернет;
- развивать мыслительную деятельность учащихся на уроке;
- развивать познавательный интерес учащихся на основе межпредметных связей;
- воспитывать трудолюбие.
Оборудование:
- экран;
- мультимедийный проектор;
- персональные компьютеры, подключенные к сети Интернет;
- компьютерная программа “Google. Земля”;
- политическая карта мира.
Приложение:
- презентация “Масштаб”;
- инструкционная карта для работы в программе “Google. Земля”;
- карточки с заданиями для практической работы в программе “Google. Земля”.
Ход урока
I. Организация начала урока
Учитель математики:
(Слайд 2). “Ни одной науке не обходились так дорого знания, как географии. Почти за каждую крупицу знаний заплачено человеческой жизнью”. Эти слова принадлежат знаменитому исследователю Арктики – Георгию Яковлевичу Седову (1877–1914 г.). Будучи сильно больным, он упрямо шел к Северному полюсу, но страшная болезнь цинга оборвала жизнь полярника. Он не достиг Северного полюса, но доказал, что к нему можно продвинуться ближе, чем полагали до него.
Язык карты должен был быть точным. Карты необходимо чертить так, чтобы длина каждой линии на карте соответствовала определенному расстоянию на земле.
Сегодня мы проведем необычный урок – интегрированный урок математики и географии по теме: “Масштаб”. Приложение 3
На прошлых уроках вы познакомились с понятиями отношения и масштаба. В начале урока проверим, как вы усвоили учебный материал. А затем вспомним, как вводится понятие масштаба в географии, и научимся решать географические задачи с использованием математических методов. В конце урока вы выполните практическую работу по математике и по географии и получите оценки по обоим предметам.
II. Актуализация знаний
Учитель географии: На уроках географии мы изучили, что такое план местности.
– Что называют планом местности?
(Ответ: Планом местности называют чертёж, который изображает небольшую часть земной поверхности в уменьшенном виде.)
– Как узнать отношение расстояний на плане к расстояниям на местности?
(Ответ: Для этого надо знать, во сколько раз их следует уменьшить)
– Что такое масштаб? (Слайд 3) – при ответе на вопрос – по щелчку мыши на слайде появляется определение масштаба.
(Ответ: Масштаб – это отношение длины отрезка на карте или плане к его действительной длине на местности)
– Какие виды масштабов мы знаем? (Слайд 4) – при ответах на вопросы – по щелчку мыши заполняются соответствующие ячейки таблицы.
(Ответ: Именованный, численный и линейный)
Заполним вместе следующую таблицу Виды масштабов (заполнить таблицу по результатам фронтальной беседы) (Слайд 5) – при ответах на вопросы – по щелчку мыши заполняются соответствующие ячейки таблицы.
| Виды масштабов | Как изображается | Что показывает | Для чего используется |
| Именованный | Словами и числами | Во сколько раз уменьшается расстояние на карте | Для краткой записи |
| Численный | Дробью | Величину масштаба | Для определения величины масштаба |
| Линейный | Делениями на линии | Соответствующие делениям расстояния на местности | Для измерения расстояний циркулем |
А теперь применим теоретические знания на практике. Выполним несколько заданий.
Переведите численный масштаб в именованный и наоборот (Слайд 6) после решения – по щелчку мыши на слайде возникают правильные ответы.
Численный в именованный
а) 1:1 000 (Ответ: в 1 см – 10 м)
б) 1:75 000 000 (Ответ: в 1 см – 750 км)
Именованный в численный
а) в 1см – 50км (Ответ: 1:5 000 000)
б) в 1см – 200м (Ответ:1:20 000)
– Какой из масштабов крупнее? (Слайд 7).
После ответа на вопрос по щелчку мыши выделяется правильный ответ.
а) 1:25
б) 1:300
в) 1:5000
(Ответ:1:25)
Учитель математики:
Ребята, масштаб и его виды вы рассматривали, изучали на уроках географии.
Почему же в учебнике математики предложена такая тема?
(Ответ: Масштаб – это отношение. А отношение – одно из понятий математики)
– Составим коллективный рассказ об отношениях при помощи вопросов:
(Слайд 8).
Что называют отношением двух чисел?
(Ответ: Отношением двух чисел называют их частное)
– Что показывает отношение двух чисел?
(Ответ: Отношение двух чисел показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго)
– Как иначе можно записать отношение 1 : 100 и что оно показывает?
(Ответ: ; оно показывает, что первое число составляет часть от второго числа или что первое число в 100 раз меньше, чем второе)
– Что показывает отношение 1000 : 1?
(Ответ: Это отношение показывает, что первое число в 1000 раз больше второго)
– Как найти отношение 200 м к 4 см?
(Ответ: Надо выразить величины в одной и той же единице измерения)
– Выразите в см: 450 м; 5 км;
(Ответ: 450 м = 45 000 см; 5 км = 500 000 см)
III. Практическая часть
Учитель математики:
(Слайд 9).
Предлагаются 2 задачи. Решение записывается на доске и в тетрадях с обсуждением.
Задача 1. На карте с масштабом расстояние между деревней и станцией равно 2,8 см. Найти расстояние между ними на местности.
Решение:
Масштаб означает, что расстояние на местности в 150 000 раз больше, чем на карте. Следовательно, искомое расстояние равно
2,8 × 150 000 = 420 000 (см) = 4,2 км.
Ответ: расстояние от деревни до станции на местности равно 4,2 км.
Задача 2. Расстояние между двумя городами равно 280 км. Найти длину отрезка, соединяющего эти города на карте, выполненной в масштабе 1 : 4 000 000.
Решение:
Поскольку расстояние на карте в 4 000 000 раз меньше, чем на местности, то 280 км надо уменьшить в 4 000 000 раз. Вначале выразим это расстояние в см, а затем выполним деление:
280 км = 28 000 000 см,
28 000 000 : 4 000 000 = 7 (см )
Ответ: расстояние между городами на карте 7 см.
Минутка зрительной гимнастики.
Учитель географии: И ещё одна задача:
Измерьте расстояние Мурманск – Париж на карте и с помощью масштаба определите расстояние между этими городами на местности. (Решение записывается на доске и в тетрадях с обсуждением.)
(Переключает презентацию на программу “Google. Земля”) Приложение 2
(Слайд 10).
Учащиеся пересаживаются за компьютерные столы.
А теперь вам предстоит выполнить практическую работу при помощи программы “Google. Земля”. Перед вами карточка с заданиями и инструкционная карта. Вы должны выполнить задания практической работы и записать результаты в карточку, а поможет вспомнить, как работать с программой “Google. Земля”, инструкционная карта.
Первое задание выполняется под руководством учителя.
После выполнения работы программа “Google. Земля” отключается, и мы возвращаемся в презентацию.
IV. Итог урока.
V. Домашнее задание. (Слайд 11).
Построить план своей комнаты вместе с имеющейся там мебелью в масштабе 1 : 20.
Все вычисления произвести в рабочей тетради по математике.
(Слайд 12).
urok.1sept.ru
Что такое масштаб? Виды масштаба и для чего он нужен?
Чтобы изобразить предметы, которые имеют размер больше листа, на котором планируется его рисовать, используется такое понятие, как масштаб. Что такое масштаб? Что обозначает данное понятие и как оно применяется на практике?

Что такое масштаб
С немецкого языка, слово «masstab» дословно переводится, как «мерная палка». Что показывает масштаб? Эта величина показывает, какое соотношение величины оригинального предмета и его изображения. Его принято использовать в математике, географии, картографии, моделировании, программировании, проектировании и других науках. Проще говоря, масштаб – соотношение реального и изображенного размеров.
Какие бывают масштабы
Масштаб, указанный на чертеже или карте, может быть изображен числом или графически. Поэтому выделяют несколько разных видов масштаба:

- Численный. Он изображается в виде дроби и обычно используется при составлении географических карт. Примером может служить топографическая карта, где он выглядит так: 1:1 000. При этом настоящая длина отрезка будет в 1 тысячу раз больше, нежели длина отрезка представленного на этой карте.
- Именованный. Данный вид необходим для того, чтобы можно было узнать, какому значению равен конкретно-взятый масштаб карты. Он выглядит так: 1 см – 1 км и используется в географических картах.
- Линейный. Используется при составлении различных карт местности. С виду – это своеобразная линейка, разделенная на отдельные графы, которые соответствуют нужным размерам.
- Поперечный. Этот вид представляет собой усложненный вариант графического масштаба. Его принято применять для измерений, которые требуют точности.
Как использовать масштаб
Для чего нужен масштаб и что он показывает, уже узнали. Но, как ним правильно пользоваться? К примеру, на карте есть два населенных пункта А и Б, а вам необходимо узнать, какое между ними расстояние. Согласно карте, ее масштаб составляет 1:50 000. Чтобы определить расстояние между населенными пунктами, измеряем при помощи обыкновенной линейки расстояние, которое есть между ними на карте. У нас получилось 5 см. Теперь, нам осталось 5 умножить на 0,5 (так как согласно масштаба в 1 см карты – 0,5 км в реальности). Проведя простые расчеты, мы получили, что расстояние между населенными пунктами А и Б равно 2,5 км.
Разновидности карт
Именно масштаб является одним из основных критериев, по которому принято классифицировать географические карты. Исходя из этого, все карты делят на:
- Крупномасштабные.
- Среднемасштабные.
- Мелкомасштабные.
Местность, показанная на крупномасштабной графической карте, будет более детализована и чем крупнее масштаб нанесен на карте, тем соответственно больше различных объектов мы сможем на ней показать.

Мелкомасштабные географические карты применяются для передачи данных о континентах или полушариях. Среднемасштабные подходят для изображения стран. А на крупномасштабных, принято показывать небольшие по размеру объекты. Обычно их используют туристы, военные и т.д.
Масштаб в черчении
С данным понятием школьная программа знакомит не только на уроках географии, но и в черчении. Здесь он используется для детального изображения различных предметов. От географического масштаба, чертежный отличается тем, что здесь, наоборот, он применяется для увеличения на рисунке мелких деталей или их частей. К примеру, чтобы показать винтик и т.д.

В данном случае, масштабирование нам помогает детальнее рассмотреть мелкий предмет. Записывается масштаб на чертеже, тоже в перевернутом виде 100:1. Это значит, что 100 метрических единиц предмета, который изображен на данном чертеже, соответствуют 1 единице его размера в действительности.
topkin.ru