Онлайн урок: Масштаб по предмету Математика 6 класс
Различают три вида масштаба:
- численный
- именованный
- графический
Графический, в свою очередь, делится на линейный и поперечный.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Численный масштаб представляют в виде дроби, где числитель — это единица, а знаменатель показывает степень уменьшения размеров изображения объектов относительно их реальных размеров.
Численный масштаб — это дробь, поэтому числитель и знаменатель выражены в одинаковых единицах измерения.
При обозначении численного масштаба не указывают единицы измерения, указывают только числа (1:2 000, 1:200 000, 1:100 и т.п.).
Пример 1
Численный масштаб карты 1:15 000 000, что он показывает?
Данный масштаб показывает, что 1 см на карте соответствует 15 000 000 см в действительности.
Нужно помнить, что чем меньше значение знаменателя в масштабе, тем крупнее масштаб.
Пример 2
Масштаб 1:1 000 крупнее, чем 1:15 000, так как знаменатель первого масштаба равен 1 000, а знаменатель второго масштаба 15 000.
1 000 меньше 15 000, следовательно, масштаб 1:1 000 крупнее.
Чем крупнее масштаб, тем больше можно изобразить объектов действительности, карта (план) получается подробней и содержательней.
При большем масштабе хорошо изображать небольшие по площади территории.
Применяется в топографических картах и планах.
На чертежах могут изображаться как уменьшенные изображения реальных объектов, так и увеличенные, если размеры изображаемого объекта слишком малы.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Именованный масштаб— это, по сути, словесное обозначение численного масштаба.
Такой масштаб показывает, сколько одному сантиметру на карте (плане) соответствует метров (километров) на местности.
Расстояние на местности, соответствующее 1 сантиметру на карте (плане), называют величиной масштаба.
Пример 3
Дан именованный масштаб: в 1 см — 250 м (в 1 сантиметре 250 метров).
Такой масштаб означает, что 250 м на местности соответствуют 1 см на карте (плане).
Величина этого масштаба равна 250 м.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Графический масштаб подразделяют на линейный и поперечный.
Линейный масштаб дает возможность определить расстояние и размеры без расчетов и переводов длин из масштабных в реальные, позволяя тем самым ускорить работу с картой.
Линейный масштаб представляет собой отрезок прямой, разделенный на деления (подобно линейке со шкалой).
Эти деления равной длины, но с разным номинальным значением, называют основанием линейного масштаба.
Каждое деление подписано значениями, указывающими размеры соответствующих им отрезков в действительности.
Основание откладывается по всей длине масштабного отрезка (чаще всего с шагом 2 см).
Крайнее левое от нуля основание делят на более мелкие деления — это наименьшее деление линейного масштаба.
Расстояние в действительности, соответствующее номинальному делению масштаба, называют точностью масштаба (т.е. это отрезок на местности, который соответствует одному минимальному значению масштаба).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Поперечный масштаб
Поперечный масштаб это улучшенный вариант линейного масштаба, позволяющий делать максимально точные измерения расстояний и размеров.
Выглядит поперечный масштаб, как сетка, состоящая из горизонтальных линий, пересеченных вертикалями и наклонными линиями (трансверсали).
Используют поперечный масштаб подобно линейному, но измерения откладываются по трем основаниям (горизонталям, вертикалям и трансверсалям).
Для фиксирования длины отрезка на карте также используют циркуль.
Чаще всего поперечный масштаб применяют на специализированных картах.
Этот вид масштаба удобен для определения длинны рек, дорог, горных хребтов и других кривых на карте.
Нередко для удобства на картах приводятся все три вида масштабов: численный, именованный, графический (линейный).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
ladle.ru
Масштаб. 6-й класс
Цели урока:
- Ввести понятие масштаба, научить находить расстояния на карте и на местности, пользуясь масштабом, учить решать задачи, связанные с понятием масштаба
- Развивать мышление, творческую активность, внимание, интерес к математике.
- Создать условия для развития самостоятельности.
Оборудование: компьютер, мультимедиа, презентация (приложение 1), учебник Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда «Математика 6», тетрадь, линейка, карандаши.
Тип урока — урок изучения и первичного закрепления новых знаний
Ход урока
1. Организационный момент. (слайд 2).
Думать — коллективно!
Решать — оперативно!
Отвечать — доказательно!
Бороться — старательно!
И открытия нас ждут обязательно!
2. Сообщение темы урока (слайд 3)
Речь идет о трудной теме. Хотя уже хорошо отработаны понятия: «отношение», «пропорция», говорилось и об отношении расстояний. Теперь надо только по-новому назвать одно специфическое отношение — расстояния на карте между двумя пунктами к расстоянию между теми же пунктами на местности.
3. Устный счет: (слайд 4)
1. Выразите в километрах:
а) 32000000 см,
б) 600000 см,
в) 32000 см,
г) 5000000 см.
2. Выразите в метрах:
а) 32000000 см,
б) 600000 см,
в) 32000 см,
г) 5000000 см.
4. Изучение нового материала.
1) Подготовительная работа. (слайд 5)
— Составьте отношения:
а) 1 см к 5000 м,
б) 1 см к 210 м,
в) 1 см к 54 см,
г) 1 см к 30000 км.
— Что нужно сначала сделать?
Решение:
а) 1 : 500000,
б) 1 : 21000,
в) 1 : 54,
г) 1 : 3000000000.
— Участки земной поверхности, детали машин, план дома и многое другое изображают на бумаге в уменьшенном виде.
— Если на карте, чертеже, плане встретите такие отношения, то это масштаб карты, чертежа, плана. (слайд 6)
2) Работа над новой темой. (слайд 7)
Определение: Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты. (Аналогично можно сказать о чертеже, плане).
Масштаб — жезл размерный или мерило, мерник, размерник, мера линейная, принятая для чертежа или иной работы. (Из толкового словаря В.И.Даля.)
— Объясните, что обозначают данные масштабы. (слайд 8)
Ответ: Если масштаб карты 1 : 500000, то на этой карте длина каждого отрезка уменьшена в 500000 раз. На такой карте расстояние, равное 5 км, будет изображаться отрезком в 1 см.
Масштаб карты 1 : 500000 = Говорят, что карта сделана в масштабе одна пятитысячная.
3) Работа с учебником. (слайд 9)
— Самостоятельно разберите задачу 1 на стр. 134.
Составьте задачу по карте
масштаб карты 1 : 100000 (в 1 см — 1 км)
Задача. Длина отрезка на карте 2 см. Найдите длину соответствующего отрезка на местности, если масштаб карты 1 : 100000. (слайд 10)
Решение:
Пусть х (м) — расстояние на местности.
расстояние |
масштаб |
|
На карте |
2см |
1см |
На местности |
Х см |
100000 см |
2:х = 1:100000
х = 200000
200000см = 2000 м = 2 км
Ответ: 2 км на местности.
5. Физкультминутка.
6. Закрепление изученного материала.
Рассмотрим две задачи из учебника Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда «Математика 6». (слайд 11-12)
Задача. Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности 72 км. Каково расстояние между городами, на этой карте расстояние между ними 12,6 см?
Решение. Составим таблицу. Запись: 72 км = 7 200 000 см — обязательна. Учащиеся должны каждый раз видеть, что вычисляется отношение величин, измеренных одной и той же единицей.
Таблица
На карте |
3,6см |
12,6см |
На местности |
72 км = 7 200 000 см |
Х см |
Затем, проговаривая определение масштаба, заполняем две последние клетки в таблице. Слева появляется запись: «3,6: 7 200 000», а справа — «12,6: х».
— Ребята! А карта у нас одна и та же? Значит, масштаб в обоих случаях один и тот же? Тогда мы можем приравнять два отношения:
3,6: 7 200 000 = 12,6: х.
Вот теперь учащиеся вступают на достаточно известную им дорогу. Они уже отработали способ решения уравнений такого вида. Записывают равенство произведения крайних членов пропорции произведению ее средних членов и находят значение х:
7 200 000 * 12,6 = 3,6 * х,
Х = (7200000 * 12,6):3,6
Здесь, как правило, учащиеся торопятся умножать. Но этого делать не следует. Надо попытаться сначала сократить дробь, воспользовавшись равными отношениями 12,6:3,6 = 126:36 = 7:2. Тогда
7200000 * 7
х = ———————
2
или х = 3600000 * 7 = 25200000(см) = 252(км).
Такой подход демонстрирует учащимся возможность отказаться от калькулятора, не загружая себя скучной вычислительной работой.
Задача . Отрезок на местности длиной 3 км изображен на карте отрезком 6 см. Какова на карте длина отрезка, изображающего отрезок 10 км? Какой отрезок на местности изображает отрезок на карте длиной 1,8 см?
Решение.
Составляем таблицу, аналогичную таблице в предыдущей задаче, подробно разбирая, в какую строчку какое данное записать. При этом вводим две переменные. Это, во-первых, делает наглядной запись условия, а во-вторых, служит подготовкой к решению задач с двумя неизвестными.
Итак, на первом этапе решения появляется таблица. Строка «Масштаб» пока еще не заполнена — она заполняется по ходу решения.
Таблица
| На карте | 6 см | Х см | 1,8 см |
| На местности | 3 км=300000 см | 10 км =1 000000 см | У см |
| Масштаб |
«Что же можно узнать из второй колонки таблицы?» — «Масштаб, он равен: 6 см: 300 000 см = 2: 100 000».
— «А как можно найти масштаб иным способом, из третьей колонки таблицы?»
Ведя такую беседу (и каждый раз проговаривая определение масштаба, что очень важно), получаем вместе с классом уравнение 2: 1 00 000 = х: 1 000 000, отсюда х = 20 (см).
Снова вспоминая понятие масштаба, получаем уравнение
2: 100 000 = 1,8: у,
у = 90 000 (см) = 0,9 (км).
Конечно, в более сильных классах можно не проговаривать определение масштаба каждый раз. Но таблица, облегчающая запись решения задач, думаю, поможет всем учащимся.
7. Самостоятельная работа. (слайд 13)
Найдите расстояние между поселком Найдорф и станицей Нововеличковской если масштаб карты 1: 100000
8. Итог урока. (слайд 14)
— Что называют масштабом карты?
— Где в практической деятельности человек пользуется этим понятием?
— Чему равен масштаб чертежа, если на нем детали увеличены в 5 раз? Уменьшены в 50 раз?
9. Домашнее задание. (слайд 15)
Стр. 137 № 842, 844
Творческое задание: нарисуйте план своего дома в масштабе 1:100 (в 1 см — 1 метр).
Приложение №1 - Презентация к уроку по теме «Масштаб»
urok.1sept.ru
Задачи на тему Масштаб | Математика
1 Длина отрезка на карте 3 см. Найти длину соответствующего отрезка на местности, если масштаб карты 1 : 1000000РЕШЕНИЕ
2 Длина отрезка на местности 4,5 км. Чему равна длина этого отрезка на карте, сделанной в масштабе 1 : 100000
РЕШЕНИЕ
820 Определите по карте расстояние от опушки леса до точки пересечения дороги с рекой. Масштаб карты 1:100 000.
РЕШЕНИЕ
821 Расстояние между городами А и В на карте равно 8,5 см. Найдите расстояние между городами на местности, если масштаб карты 1:1000000.
РЕШЕНИЕ
822 Длина железной дороги Москва — Петербург приближенно равна 650 км. Изобразите отрезком эту дорогу, применив масштаб 1:10 000 000.
РЕШЕНИЕ
823 Расстояние от Бреста до Владивостока более 10 000 км. Уместится ли на одной странице тетради это расстояние в масштабе одна десятимиллионная?
РЕШЕНИЕ
824 На рисунке дан план квартиры в масштабе 1:100. Определите по плану, какие размеры имеют кухня, ванная и комнаты и какова их площадь в действительности.
РЕШЕНИЕ
825 Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности в 72 км. Каково расстояние между городами, если на этой карте между ними 12,6 см?
РЕШЕНИЕ
826 Длина железнодорожной магистрали 3140 км. Какой длины получится линия, изображающая эту магистраль на карте, сделанной в масштабе 1:10 000 000; 1:2 000 000?
РЕШЕНИЕ
827 Отрезок на местности длиной 3 км изображен на карте отрезком 6 см. Какова на карте длина отрезка, изображающего 10 км? Какой отрезок на местности изображает на карте 1,8 см?
РЕШЕНИЕ
828 Длина детали на чертеже, сделанном в масштабе 1:5, равна 7,2 см. Чему будет равна длина этой детали на другом чертеже в масштабе 1:3; 2:1?
РЕШЕНИЕ
829 Вычислите устно.
РЕШЕНИЕ
830 Какое число надо отнять от числителя и знаменателя дроби 31/47, чтобы получить 5/9
РЕШЕНИЕ
831 Составьте три пропорции, используя верное равенство 18 : 2 — 54 : 6; 4,5 : 1,5 = 1,26 : 0,42; 2,8 · 45 = 6,3 · 20; 3,9 · 0,14 — 0.6 · 0,91
РЕШЕНИЕ
832 Две трети от двух третьих числа равны двум третьим. Какое это число?
РЕШЕНИЕ
833 Сколько гектаров в 1 м2? Сколько часов в 1 с; литров в 1 см3?
РЕШЕНИЕ
834 Известно, что объем пирамиды в 3 раза меньше объема призмы такой же высоты и с таким же основанием. Вычислите объем четырехугольной пирамиды, в основании которой прямоугольник со сторонами 2/3 дм и 9/10 дм, а высота 5 дм.
РЕШЕНИЕ
835 Чтобы приготовить 4 порции картофельной запеканки нужно взять 0,44 кг картофеля. Сколько потребуется картофеля чтобы приготовить 12 порций запеканки?
РЕШЕНИЕ
836 Некоторое расстояние ласточка пролетела за 0,5 ч со скоростью 50 км/ч. За сколько минут пролетит то же расстояние стриж, если будет лететь со скоростью 100 км/ч?
РЕШЕНИЕ
837 Начертите окружность и постройте два ее радиуса, угол между которыми 120°. Закрасьте часть круга между этими радиусами. Какая часть окажется закрашенной и останется незакрашенной?
РЕШЕНИЕ
838 1) Сумма двух чисел 7,2, причем 1/3 большего числа равна меньшему. Найдите эти числа. 2) Разность двух чисел 1,5, причем 1/4 большего равна меньшему. Найдите эти числа.
РЕШЕНИЕ
839 Решите уравнение.
РЕШЕНИЕ
840 Найдите с помощью карты расстояние от Москвы до Киева.
РЕШЕНИЕ
841 Измерьте длину и ширину своей комнаты. Начертите в тетради план этой комнаты в масштабе 1:100.
РЕШЕНИЕ
842 Расстояние на местности в 20 м изображено на плане отрезком 1 см. Определите масштаб плана.
РЕШЕНИЕ
843 Длина дома на плане 25 см. Чему равна длина дома на местности, если план сделан в масштабе 1:300?
РЕШЕНИЕ
844 Расстояние между городами на местности равно 1300 км. Каким отрезком будет изображено это расстояние на карте, масштаб которой 1:10 000 000?
РЕШЕНИЕ
845 Длина детали на чертеже, сделанном в масштабе 1:3, равна 2,4 см. Чему будет равна длина этой детали на другом чертеже в масштабе 2:1?
РЕШЕНИЕ
846 Найдите значение выражения.
РЕШЕНИЕ
famiredo.ru
Масштаб
Всем здравствуйте! Решила рассмотреть несколько задачек на масштаб – оказалось, есть такая нужда у моих учеников. Может, и вам пригодится!
Всем нам знакомы карты местности – так или иначе, но каждый встречался с ними, в школе или по жизни. Понятно, что карта – лишь только изображение, и по сравнению с расстоянием на местности объекты на карте должны быть меньше (иначе зачем она нужна?). Масштаб – это как раз отношение, которое показывает, во сколько раз карта меньше, чем реальная местность, то есть во сколько раз расстояние на карте меньше, чем на местности.
Но масштаб призван также и увеличивать что-то маленькое так, чтобы можно было сделать подробный чертеж или внимательно рассмотреть что-то мелкое.
Первый, “уменьшающий”, масштаб, может быть записан, например, так: 1:5. Тогда расстояние на карте (или чертеже) в пять раз меньше, чем в реальности. Масштаб, записанный так: 1: 100 000 означает, что изображение меньше в сто тысяч раз.
“Увеличивающий” масштаб записывается: 100:1, или 1000:1. Это значит, что расстояние увеличили в сто или тысячу раз, чтобы его можно было изобразить.
В зависимости от конкретной задачи выбирают и масштаб: карта не должна быть слишком уж мелкой, а понятной и подробной, но в то же время не должна быть гигантской, а простую, но небольшую деталь вовсе необязательно увеличивать в десятки раз, когда может быть достаточно и пяти.
Когда работаешь с масштабом, очень важно уметь составлять отношения (пропорции). Давайте потренируемся в этом!
1. Расстояние на местности в 20 м изображено на плане отрезком 1 см. Определите масштаб плана.
Чтобы определить масштаб, нужно узнать, во сколько раз расстояние на карте меньше, чем на местности. Для этого нужно расстояние на местности привести к тем же единицам, что и на плане:
20 м = 20*100 см=2000 см.
Тогда, если одному см на карте соответствуют 2000 см на местности, то и масштаб 1:2000, то есть на карте длина отрезка меньше в 2000 раз.
2. Длина дома на плане 25 см. Чему равна длина дома на местности, если план сделан в масштабе 1:300?
Так как масштаб показывает, во сколько раз карта или план меньше действительного расстояния, или, иначе говоря, во сколько дом больше своего изображения, то:
 см, или 75 м.
см, или 75 м.
3. Длина железнодорожной магистрали 3140 км. Какой длины получится линия, изображающая эту магистраль на карте, сделанной в масштабе: а) 1:10 000 000; б) 1:2 000 000?
Обозначим за  расстояние на карте. Переведем длину магистрали в сантиметры:
расстояние на карте. Переведем длину магистрали в сантиметры:
3140 км = 3 140 000 м = 314 000 000 см.
Тогда 

По правилу пропорции  см.
см.
Изображение карты во втором масштабе – крупнее (2 миллиона меньше, чем 10). Так как отношение масштабов – 1:5, то и изображение будет крупнее в пять раз: 157 см. В этом можно убедиться, решив задачу “стандартным” способом.
4. Расстояние от Бреста до Владивостока более 10 000 км. Уместится ли на одной странице тетради это расстояние в масштабе одна десятимиллионная?
Снова за  обозначим расстояние на карте. Тогда
обозначим расстояние на карте. Тогда

 , или
, или  см.
см.
5. Длина железной дороги Москва – Петербург приближенно равна 650 км. Изобразите отрезком эту дорогу, применив масштаб 1:10 000 000.
Переведем километры в сантиметры:
650 км = 650 000 м = 65 000 000 см.
Обозначаем расстояние на карте неизвестной и составляем пропорцию:

 , или
, или  см.
см.
6. Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности в 72 км. Каково расстояние между городами, если на этой карте расстояние между ними 12,6 см?
Такую задачу можно решать длинным путем: определить масштаб карты и затем найти расстояние между городами, зная масштаб.
Тогда масштаб будет таким:

А второе расстояние найдем так:
 .
.
Почему бы тогда не упростить себе задачу, не определяя масштаб, а составить пропорцию сразу:

Отсюда  см, или 25,2 км
см, или 25,2 км
7. Длина детали на чертеже, сделанном в масштабе 1:3, равна 2,4 см. Чему будет равна длина этой детали на другом чертеже, сделанном в масштабе 2:1?
Нам не нужно знать, каковы реальные размеры детали – нас об этом не спрашивают. Поэтому мы и не будем их искать, а найдем новый размер чертежа через отношение масштабов:

 см
см
8. Площадь земельного участка изображается на плане, масштаб которого 1:250, в виде прямоугольника площадью 128 кв. см. Найдите действительную площадь этого земельного участка.
Хорошая задача. Не пугайтесь, что длина и ширина участка неизвестны – нам и не надо знать их. Однако для лучшего понимания все же обозначим их, например,  и
и  . Тогда на карте расстояние
. Тогда на карте расстояние  изображается отрезком
изображается отрезком  , а расстояние
, а расстояние  – отрезком
– отрезком  . Если перемножить длину и ширину изображения участка, то получим как раз 128 кв. см. Но тогда получается, что
. Если перемножить длину и ширину изображения участка, то получим как раз 128 кв. см. Но тогда получается, что  , или
, или  , то есть реальная площадь участка получится, если площадь изображения умножить на квадрат масштаба:
, то есть реальная площадь участка получится, если площадь изображения умножить на квадрат масштаба:  кв. см. Переведем это в кв. метры, для этого нужно разделить не на 100, а на
кв. см. Переведем это в кв. метры, для этого нужно разделить не на 100, а на  : 800 кв. м, а если нужны квадратные километры, тогда еще на
: 800 кв. м, а если нужны квадратные километры, тогда еще на  : 0,0008 кв. км.
: 0,0008 кв. км.
9. Площадь земельного участка прямоугольной формы 6 га. Найдите площадь прямоугольника, изображающего этот участок на плане, масштаб которого 1:5000.
Аналогичная задача. Вспомним, что такое га: это квадрат со стороной 100 м, то есть это 10 000 кв. м. Тогда в сантиметрах это (умножаем на  ) 100 000 000 кв. см. А у нас – 600 000 000 кв. см.Поделим на масштаб в квадрате, чтобы определить площадь этого прямоугольника на карте:
) 100 000 000 кв. см. А у нас – 600 000 000 кв. см.Поделим на масштаб в квадрате, чтобы определить площадь этого прямоугольника на карте:  кв.см.
кв.см.
Нетрудно догадаться, что, если бы речь шла об объеме, то масштаб пришлось бы возводить в куб: в данном случае масштаб – это коэффициент подобия. Площади относятся как квадрат коэффициента подобия, а объемы – как куб коэффициента подобия.
easy-physic.ru
Масштаб (Вольфсон Г.И.). Видеоурок. Математика 6 Класс
На этом уроке вы продолжите изучение темы «Отношение» и познакомитесь с отношением, которое играет важную роль в повседневной жизни человека. Вы узнаете, что такое масштаб, и научитесь использовать его при решении задач.
Тема: Отношения и пропорции
Урок: Масштаб
Рассматривая любую географическую карту, мы обязательно увидим на ней частное двух чисел. Например, отношение 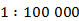 . Карта – это уменьшенное изображение участка земной поверхности. Во сколько раз были уменьшены реальные расстояния, указывают на карте, записывая отношение, называемое масштабом.
. Карта – это уменьшенное изображение участка земной поверхности. Во сколько раз были уменьшены реальные расстояния, указывают на карте, записывая отношение, называемое масштабом.
Данный масштаб означает, что 1 см на карте соответствует отрезок в 100 000 см на местности. Если перевести 100 000 см в более крупные единицы длины, то получим, что
1 см соответствует 1 км.
Действительно, мы знаем, что в 1 м – 100 см. Значит, 100 000 см – это 1000 м, а 1000 м – это и есть 1 км.
Сформулируем определение.

Длина отрезка на карте – 3 см. Найти длину соответствующего отрезка на местности, если масштаб карты 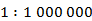 .
.
Решение.
Обозначим за 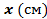 неизвестное.
неизвестное.
Тогда отношение длины отрезка на карте к длине отрезка на местности:
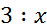
Оно равно масштабу карты:
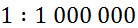
Запишем равенство:
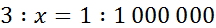
Перед нами пропорция. Найдем ее неизвестный средний член, используя основное свойство пропорции.
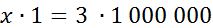
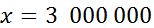
Значит, длина соответствующего отрезка на местности – 3 000 000 см. Переведем это число в более крупные единицы длины. Получим 30 км.
Ответ: 30 км.
Расстояние между поселками на местности – 4,5 км. Чему равна длина соответствующего отрезка на карте, сделанной в масштабе 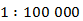 ?
?
Решение.
Переведем сначала 4,5 км в сантиметры.
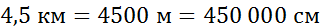
Обозначим длину отрезка на карте буквой 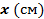 . Составим пропорцию.
. Составим пропорцию.
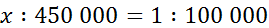
Слева от знака равенства – отношение длины отрезка на карте к расстоянию между поселками, а справа – масштаб. Используя основное свойство пропорции, получим:
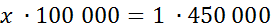
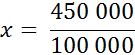
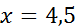
Итак, длина отрезка на карте – 4,5 см.
Ответ: 4,5 см.
Масштаб используют не только для описания географических карт. Его используют для любых уменьшенных по сравнению с реальностью изображений и моделей, например, для описания чертежей. Решим задачу.
Длина детали на чертеже, сделанном в масштабе 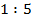 , равна 7,2 см. чему будет равна длина этой же детали на другом чертеже, сделанном в масштабе
, равна 7,2 см. чему будет равна длина этой же детали на другом чертеже, сделанном в масштабе 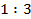 ?
?
Решение.
Узнаем, чему равна длина детали в реальности. Обозначим эту длину за 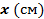 и составим пропорцию.
и составим пропорцию.
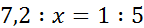
Слева от знака равенства – отношение длины детали на чертеже к длине детали в реальности, а справа – масштаб. Решим пропорцию.
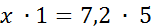
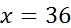
Значит, длина детали – 36 см. Теперь ответим на поставленный в задаче вопрос. Обозначим буквой y (см) длину детали на новом чертеже. Составим и решим пропорцию.
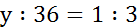
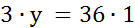
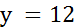
Значит, на втором чертеже длина детали – 12 см.
Ответ: 12 см.
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия, 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. – ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. – Просвещение, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Онлайн тесты по математике (Источник).
- Можно скачать указанные в п.1.2. книги (Источник).
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012. (ссылка см. 1.2)
- Домашнее задание: №824, №840, №844
- Другие задания: №846, №838 (а)
interneturok.ru
Масштаб карты
Каждая карта имеет масштаб – число, которое показывает, сколько сантиметров на местности соответствует одному сантиметру на карте.
 Масштаб карты обычно указан на ней. Запись 1 : 100 000 000 означает, что если расстояние между двумя точками на карте равно 1 см, то расстояние между соответствующими точками её местности равно 100 000 000 см.
Масштаб карты обычно указан на ней. Запись 1 : 100 000 000 означает, что если расстояние между двумя точками на карте равно 1 см, то расстояние между соответствующими точками её местности равно 100 000 000 см.
Масштаб может быть указан в численной форме в виде дроби – численный масштаб (например, 1 : 200 000). А может быть обозначен в линейной форме: в виде простой линии или полосы, разделенной на единицы длины (обычно на километры или мили).
Чем крупнее масштаб карты, тем с более детально могут быть изображены на ней элементы ее содержания, и наоборот, чем мельче масштаб, тем более обширное пространство может быть показано на листе карты, но местность на ней изображается с меньшими подробностями.
Масштаб представляет собой дробь, в числителе которой единица. Чтобы определить, какой из масштабов крупнее и во сколько раз, вспомним правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель.
Отношение расстояния на карте (в сантиметрах) к соответствующему расстоянию на местности (в сантиметрах) равно масштабу карты.
Как же эти знания помогут нам при решении задач по математике?
Пример 1.
Рассмотрим две карты. Расстоянию в 900 км между пунктами А и В соответствует на одной карте расстояние в 3 см. Расстоянию в 1 500 км между пунктами С и D соответствует на другой карте расстояние в 5 см. Докажем, что масштабы карт одинаковы.
Решение.
Найдём масштаб каждой карты.
900 км = 90 000 000 см;
масштаб первой карты равен: 3 : 90 000 000 = 1 : 30 000 000.
1500 км = 150 000 000 см;
масштаб второй карты равен: 5 : 150 000 000 = 1 : 30 000 000.
Ответ. Масштабы карт одинаковы, т.е. равны 1 : 30 000 000.
Пример 2.
Масштаб карты – 1 : 1 000 000. Найдём расстояние между точками А и В на местности, если на карте
АВ = 3,42 см?
Решение.
Составим уравнение: отношение АВ = 3,42 см на карте к неизвестному нам расстоянию х (в сантиметрах) равно отношению между теми же пунктами А и В на местности к масштабу карты:
3,42 : х = 1 : 1 000 000;
х · 1 = 3,42 · 1 000 000;
х = 3 420 000 см = 34,2 км.
Ответ: расстояние между пунктами А и В на местности равно 34,2 км.
 Пример 3
Пример 3
Масштаб карты – 1 : 1 000 000. Расстояние между пунктами на местности 38,4 км. Каково расстояние между этими пунктами на карте?
Решение.
Отношение неизвестного нам расстояния х между пунктами А и В на карте к расстоянию в сантиметрах между теми же пунктами А и В на местности равно масштабу карты.
38,4 км = 3 840 000 см;
х : 3 840 000 = 1 : 1 000 000;
х = 3 840 000 · 1 : 1 000 000 = 3,84.
Ответ: расстояние между пунктами А и В на карте равно 3,84 см.
Остались вопросы? Не знаете, как решать задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Масштаб — это… Что такое Масштаб?
Масшта́б (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») — в общем случае отношение двух линейных размеров. Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта.
Понятие наиболее распространено в геодезии, картографии и проектировании — отношение натуральной величины объекта к величине его изображения. Человек не в состоянии изобразить большие объекты, например, дом, в натуральную величину, поэтому, при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Масштаб в геодезии, картографии и проектировании
Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический.
Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.
Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность — 0,1.
Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).
Масштабы изображений на чертежах должны выбираться из следующего ряда:[1]
| Масштабы уменьшения | 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1 000 |
| Натуральная величина | 1:1 |
| Масштабы увеличения | 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1 |
При проектировании генеральных планов крупных объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.
Масштаб в фотографии
При фотосъёмке под масштабом понимают отношение линейного размера изображения, полученного на фотоплёнке или светочувствительной матрице, к линейному размеру проекции соответствующей части сцены на плоскость, перпендикулярную к направлению на камеру.
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Масштаб имеет важное значение при расчете глубины резко изображаемого пространства. Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съемке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).
Под макрофотографией традиционно понимают съёмку в масштабе 1:1 или крупнее. Однако с широким распространением компактных цифровых фотоаппаратов этим термином стали также называть съёмку расположенных близко к объективу (как правило, ближе 50 см) мелких объектов. Связано это с необходимым изменением режима работы системы автофокуса в таких условиях, однако с точки зрения классического определения макросъёмки такое толкование является неверным.
Масштаб в моделизме
Основная статья: Масштаб (моделизм)
Для каждого вида масштабного (стендового) моделизма определены масштабные ряды, состоящие из нескольких масштабов разной степени уменьшения, причём для разных видов моделизма (авиамоделизм, судомоделизм, железнодорожный, автомобильный, военной техники) определены свои, исторически сложившиеся, масштабные ряды, которые обычно не пересекаются.
Масштаб в моделизме исчисляется по формуле:
L / М = Х
Где: L — параметр оригинала, М — требуемый масштаб, Х — искомое значение
Например:
При масштабе 1/72, и параметре оригинала 7500 мм, решение будет выглядеть;
7500 мм / 72 = 104,1 мм
Полученное значение 104,1 мм, есть искомое значение при масштабе 1/72
Масштаб времени
В программировании
В операционных системах с разделением времени чрезвычайно важную роль играет предоставление отдельно взятым задачам так называемого «режима реального времени», при котором обработка внешних событий обеспечивается без дополнительных задержек и пропусков. Для этого употребляется также термин «реальный масштаб времени», однако это терминологическая условность, не имеющая к исходному значению слова «масштаб» никакого отношения.
В кинотехнике
Масштаб времени — количественная мера замедления или ускорения движения, равная отношению проекционной частоты кадров к съёмочной. Так, если проекционная частота кадров равна 24 кадра в секунду, а киносъёмка производилась на 72 кадра в секунду, масштаб времени равен 1:3. Масштаб времени 2:1 означает ускоренное вдвое по сравнению с обычным протекание процесса на экране.
В математике
Масштаб — это отношение двух линейных размеров. Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта.В математике масштаб определеется как отношение расстояния на карте к соответствующему расстоянию на реальной местности. Масштаб 1: 100000 означает, что 1 см на карте соответствует 100000 см = 1000 м = 1 км на местности.
Масштабы изображений на чертежах должны выбираться из следующего ряда (масштабы ГОСТ 2.302-68): Масштабы уменьшения 1 : 2; 1 : 2,5; 1 : 4; 1 : 5; 1 : 10; 1 : 15; 1 : 20; 1 : 25; 1 : 40; 1 : 50; 1 : 75; 1 : 100; 1 : 200; 1 : 400; 1 : 500; 1 : 800; 1 : 1000 Натуральная величина 1 : 1 Масштабы увеличения 2 : 1; 2.5,5 : 1; 4 : 1; 5 : 1; 10 : 1; 20 : 1; 40 : 1; 50 : 1; 100: 1 см. например Быстро-медленная система
Масштаб-число,показывающее, во сколько раз уменьшены или увеличены настоящие размеры на чертеже.
Примечания
- ↑ ГОСТ 2.302-68
dic.academic.ru