Занимательные факты по алгебре (5 класс) по теме: К.Гаусс
Карл Гаусс
«Математика – царица наук, арифметика – царица математики.» Эти слова принадлежат немецкому математику, астроному и физику Карлу Фридриху Гауссу. Он родился 30 апреля 1777 в Брауншвейге. В три года Карл уже умел считать и выполнять элементарные вычисления. Однажды он обнаружил ошибку в расчетах своего отца, который был водопроводчиком. Расчет был проверен, и число, указанное трехлетним мальчиком было верно. В восьмилетнем возрасте он поразил учителя, сосчитав необычным образом сумму целых чисел от 1 до 100: он сообразил, что сумма пар чисел, равноудаленных от концов, одинакова: 1 + 100 = 2 + 99 = 3 + 98 =… = 50 + 51 = 101, и что таких пар ровно 50, поэтому искомая сумма равна 101*50 = 5050.
В 1788 году Гаусс поступил в закрытую школу Коллегиум Каролинум. Здесь изучают классические языки. Гаусс с удовольствием занимается языками и делает такие успехи, что даже не знает, кем он хочет стать — математиком или филологом. В возрасте 19 лет Гауссу удалось решить задачу, не поддававшуюся усилиям геометров со времен Евклида: он нашел способ, позволяющий построить с помощью циркуля и линейки правильный 17-угольник. Это произвело на Гаусса сильное впечатление, и он решил стать математиком.
К 24 годам Гаусс вошел в число самых известных математиков Европы. Однажды астрономы обнаружили на небе малую планету Цереру. После немногих наблюдений планета была потеряна, и астрономы обратились за помощью к математикам. Гаусс первым откликнулся на этот призыв: по трем наблюдениям он сумел предсказать все будущие положения Цереры. Полвека спустя теория возмущений Гаусса позволила астрономам рассчитать положение на небе еще никем не виданной планеты — Нептуна. В 30 лет Гаусс считался уже «королем» европейских математиков.
Гаусс до старости сохранил юношескую жажду знаний и огромное любопытство. Например, в 62 года он быстро выучил русский язык, чтобы самому разобраться в трудах своего коллеги — Николая Лобачевского.
Внеурочное занятие по математике в 5 классе ЗАДАЧИ КАРЛА ГАУССА
Внеурочное занятие по математике в 5 классе
ЗАДАЧИ КАРЛА ГАУССА
В математике следует помнить
не формулы, а процессы мышления.
В. П. Ермаков
Цель: Показать, что прежде, начинать считать, нужно посмотреть, нет ли более простых и быстрых путей получения результата, познакомить с великими учеными, сделавшими огромный вклад в развитие математики.
Задачи:
— образовательные (формирование познавательных УУД):
знать великих ученых-математиков, вспомнить великих ученых России, узнать об их вкладе в развитие науки в России.
— воспитательные (формирование коммуникативных и личностных УУД):
умение слушать и вступать в диалог, участвовать в обсуждении проблем, интегрироваться в группу со сверстником и строить продуктивное взаимодействие, формировать коммуникативную компетенцию учащихся; воспитывать ответственность и аккуратность.
— развивающие (формирование регулятивных УУД)
умение обрабатывать информацию и ранжировать ее по сложности; представлять информацию в виде алгоритма, выбирать способы решения в зависимости от условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Оборудование: доска, компьютер, мультимедийный проектор, экран.
Ход занятия.
Сосчитайте сумму всех натуральных чисел от 1 до 100
Ответ 101*50=5050
Историческая справка
В Германии в конце 18 –го века и первой половине 19-го веков жил знаменитый ученый Карл Гаусс. Современники называли его «королем математики». Сам ученый шутил, что он считать научился раньше, чем говорить. Рассказывают, что, когда Гауссу было всего три года, он услышал, как его отец вслух делал расчеты, и заметил:
— Папа, счет твой неверен.
У отца от удивления глаза на лоб полезли. «Стоит ли принимать всерьез слова карапуза?» — подумал он, однако проверил свои вычисления и нашел ошибку.
Вот еще одна история из детства Карла Гаусса. Учитель дал первокласснику задачу:
«Вычислите сумму всех натуральных чисел от 1 до 100». Он намеревался, пока ученики считают, заняться каким – то своим делом.
Да не тут – то было. Только он проговорил задание, как услышал голос Карла:
— Учитель, я сосчитал,- сказал Карл и положил на стол свою грифельную доску с правильным ответом.
2. На Елке Мише купили 6 шаров:
Маше купили 7 шаров:
На шарах были указаны цены. Миша схватил калькулятор, чтобы сосчитать стоимость шаров. Маша говорит: «Ты и без калькулятора устно сможешь сосчитать, а вот у меня не больно-то сосчитаешь: один шарик лишний»
Сосчитайте устно стоимость каждой покупки.
Решение: (71+89)*3=160*3=480; (41+59):2*7-350
3. Вычислите произведение: 2*(978*5).
«Вперед делают вычисления в скобках», — бурчит Тима, у которого что – то не заладилось. Множил и так, и эдак, а все с ответом не сходится. Заглянул в тетрадь к соседке, а у нее все иначе и ответ готов.
Как решить задачу иначе, и каков ответ?
Решение: Соседка Тимофея воспользовалась законом математических действий: 9987*(2*5)=987*10=9870.
4. –Дети, в математике существует три закона, которые помогут нам составлять и решать верные равенства: закон Переместительный, закон Сочетательный и правило вычитания суммы. Три равенства записаны на доске. Определите скорее, в соответствии с каким законом составлено каждое из них.
a-(b+c)=a-b-c | Закон переместительный |
a+(b+c)=a+b+c | Закон вычитания суммы |
| a+b=b+a | Закон сочетательный |
5. Сиропчик бросил в щель автомата гривенник (10копеек), и автомат выдал малышу 3 стакана газированной воды с сиропом. Любителю этого напитка показалось, что трех стаканов ему мало. Он хочет выпить еще 21 стакан воды с сиропом. «Если бы я знал цену стакана воды с сиропом, — размышлял малыш, — то подсчитал бы их стоимость. Но как узнать цену? 10 на 3 не делится».
Мимо шел Знайка и сказал Сиропчику: «Если знаешь сочетательный закон, можно сосчитать стоимость и не зная цены».
Скажите, как?
Решение: Цена*21=(цена*3)*7= 10*7=70 коп.
Лекционный материал по теме «решение САЛУ методом Гаусса»
.
Метод Гаусса – это просто!
Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто!
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать!
Систематизируем знания о системах линейных уравнений.
Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья Несовместные системы и системы с общим решением. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся к простейшей системе с урока Как решить систему линейных уравнений?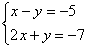
и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы: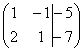
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: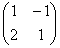 
. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: 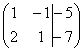. Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: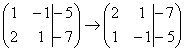 
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу 
. В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: 
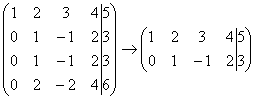
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу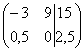 
. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: 
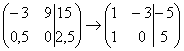. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: 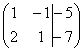. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: 
, и ко второй строке прибавляем первую строку умноженную на –2: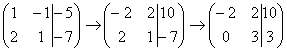 
. Теперь первую строку можно разделить «обратно» на –2: 
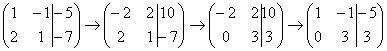. Как видите, строка, которую ПРИБАВЛЯ
На практике так подробно, конечно, не расписывают, а пишут короче:
Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: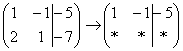 
»
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: 
, и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: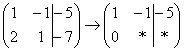 
»
«Теперь второй столбец. Вверху –1 умножаю на –2: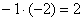 
. Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: 
»
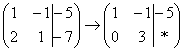«И третий столбец. Вверху –5 умножаю на –2: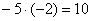 
. Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане».
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!
Вернемся к нашей системе 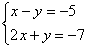. Она практически разобрана по косточкам.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
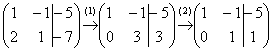
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: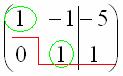 
. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.
В результате элементарных преобразований получена эквивалентная исходной система уравнений: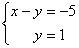
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.
В нижнем уравнении у нас уже готовый результат: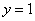 
.
Рассмотрим первое уравнение системы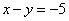 
и подставим в него уже известное значение «игрек»: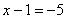
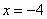
Ответ: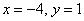 
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример 1
Решить методом Гаусса систему уравнений: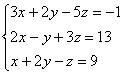
Запишем расширенную матрицу системы: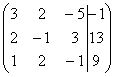
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: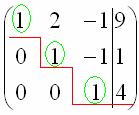
И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число: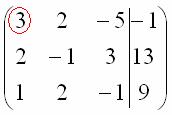 
Почти всегда здесь должна находиться единица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки: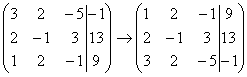
Теперь первая строка у нас останется неизменной до конца решения.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах: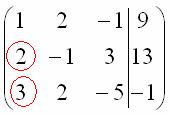
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2: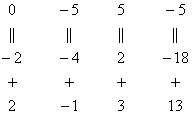
Результат записываем во вторую строку: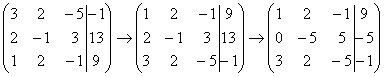
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3: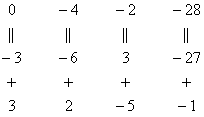
Результат записываем в третью строку: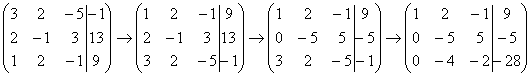
На практике эти действия обычно выполняются устно и записываются в один шаг: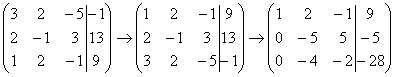
Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО: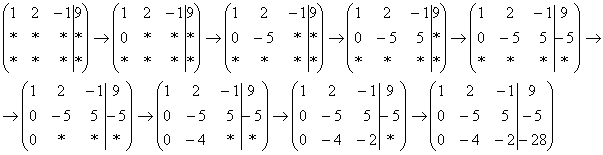
А мысленный ход самих расчётов я уже рассмотрел выше.
Далее нужно получить единицу на следующей «ступеньке»: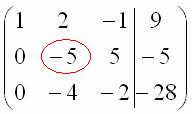
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение: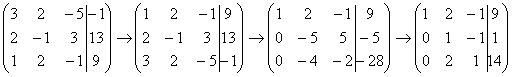
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь: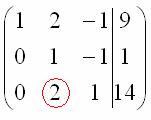
Для этого к третьей строке прибавляем вторую строку, умноженную на –2: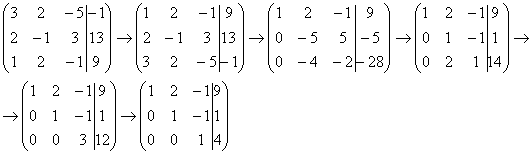
Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: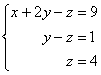
Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат: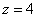 
Смотрим на второе уравнение: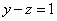 
. Значение «зет» уже известно, таким образом: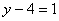
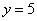
И, наконец, первое уравнение: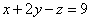 
. «Игрек» и «зет» известны, дело за малым: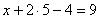
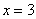
Ответ: 
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.
Пример 2
Решить систему линейных уравнений методом Гаусса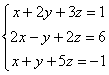
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить систему линейных уравнений методом Гаусса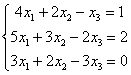
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: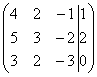
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
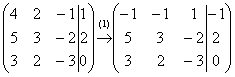
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по накатанной колее: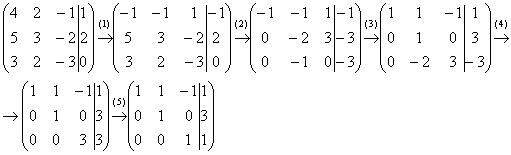
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде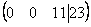 
, и, соответственно, 
, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился: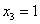
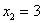
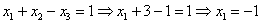
Ответ: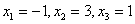 
.
Пример 4
Решить систему линейных уравнений методом Гаусса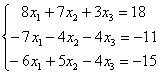
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
Особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: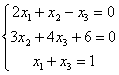
В расширенной матрице системы на месте отсутствующих переменных ставим нули:
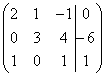
Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.
Вторая особенность
Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: 
.
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Или еще такой условный пример: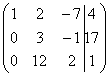 
. Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.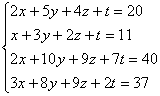
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Решения и ответы:
Пример 2: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.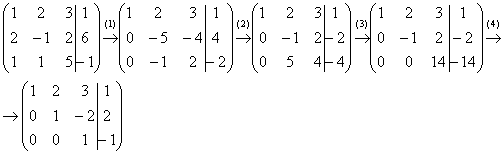
Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание, что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.
Обратный ход: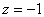 
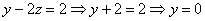
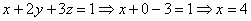
Ответ: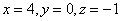 
.
Пример 4: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: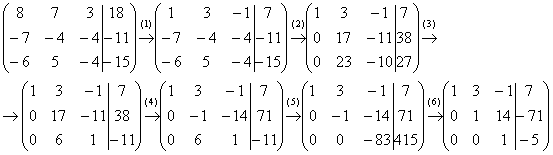
Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.
Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы
(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
Нужная вещь на второй ступеньке получена.
(5) К третьей строке прибавили вторую, умноженную на 6.
(6) Вторую строку умножили на –1, третью строку разделили на -83.
Обратный ход: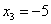 
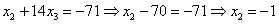
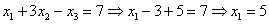
Ответ: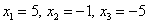 
Пример 5: Решение: Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: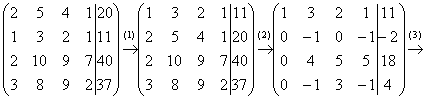
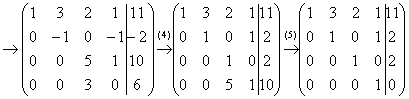
Выполненные преобразования:
(1) Первую и вторую строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.
Обратный ход: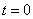
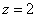
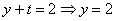
Ответ: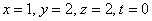 
Практическая работа по теме «Решения систем уравнений методом Гаусса»
Практическая работа по теме «Решения систем уравнений методом Гаусса»
Цели работы:
расширить представление о методах решения СЛУ и отработать алгоритм решения СЛУ методом Гаусса;
развивать логическое мышление студентов, умение находить рациональное решение задачи;
воспитывать у студентов культуру письменной математической речи при оформлении ими своего решения.
Основной теоретический материал.
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной. Пример такой системы — на рисунке сверху.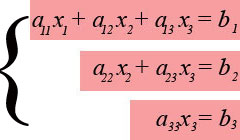 
Решите систему линейных уравнений методом Гаусса. Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент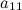 
равнялся 1 (это мы делаем для упрощения вычислений):
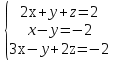
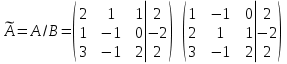
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых: 
Все элементы третьей строки делим на два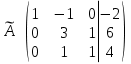 
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
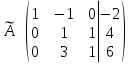От третьей строки отнимаем вторую, умноженную на 3: 
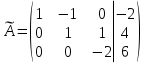Умножив третью строку на 0,5 , получаем: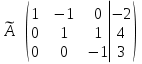
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент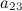 
, для этого от второй строки отнимем третью: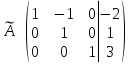 
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую: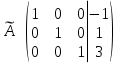 
Полученной матрице соответствует система
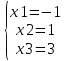Ответ.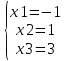
Задания для самостоятельного решения:
ВАРИАНТ 1
Решите системы линейных уравнений методом Гаусса:
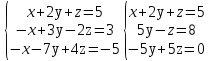
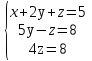
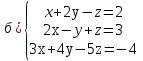. в)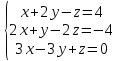
ВАРИАНТ 2
Решите системы линейных уравнений методом Гаусса:
а)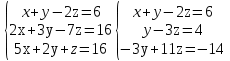 
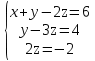
в)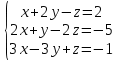
Критерии оценивания:
Работа оценивается на «3»,если: записано решение примера и выполнена проверка решения системы;
самостоятельно методом Гаусса верно решена одна из систем.
Работа оценивается на «4»,если: самостоятельно методом Гаусса верно решены любые две системы.
Работа оценивается на «5»,если: самостоятельно методом Гаусса верно решены три системы.
«Метод Гаусса решения систем линейных уравнений»
Инфоурок › Алгебра ›Презентации›Презентация по математике на тему: «Метод Гаусса решения систем линейных уравнений»Выберите документ из архива для просмотра:
Выбранный для просмотра документ Метод Гауса.ppt
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:Метод Гаусса решения систем линейных уравнений
2 слайд
Описание слайда:Метод Гаусса решения систем линейных уравнений Рассмотрим задачу решения системы линейных уравнений размерностью (m x n). Запишем систему в матричном виде: Если закрепить раз и навсегда нумерацию неизвестных, то можно опустить неизвестные в записи системы и записать ее в виде матрицы, отделяя столбец свободных членов вертикальной чертой. Расширенная матрица системы
3 слайд
Описание слайда:Метод Гаусса решения систем линейных уравнений Следующие действия над расширенной матрицей системы называются элементарными преобразованиями. Умножение или деление элементов строк на одно и то же число, не равное нулю Перестановка местами двух строк Прибавление к элементам строки элементов другой строки, умноженных на произвольный множитель. Конечной целью элементарных преобразований является получение верхнетреугольной матрицы, у которой все элементы, стоящие под главной диагональю равны нулю. Преобразования стараются производить так, чтобы на главной диагонали появлялись единицы.
4 слайд
Описание слайда:Метод Гаусса решения систем линейных уравнений Запишем расширенную матрицу системы К первой строке прибавим вторую строку, умноженную на (-2) Ко второй строке прибавим первую строку, умноженную на (-2), К третьей строке прибавим первую строку, умноженную на (-3). Из третьей строки вычтем вторую строку Ко второй строке прибавим третью строку, умноженную на (-5)
5 слайд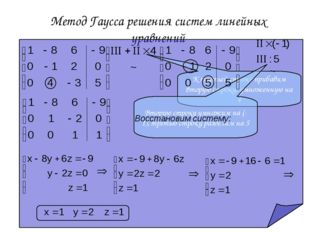
Описание слайда:Метод Гаусса решения систем линейных уравнений К третьей строке прибавим вторую строку, умноженную на 4 Вторую строку умножим на (-1), третью строку разделим на 5 Восстановим систему:
Курс профессиональной переподготовки
Учитель математики
Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДБ-142061
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийПроект «Задача Гаусса» — начальные классы, прочее
Республика Саха (Якутия)
Верхоянский район
МБОУ «Батагайская средняя общеобразовательная школа»
«Задача гениального Гаусса»
Авторы:
ученики 4 «а» класса
Акимова Амалия,
Стручкова Валя
Руководитель:
Ефимова Т.Е.
2016г.
Математика — царица наук. Математика неисчерпаема и многозначна. Одних покоряет её логическая стройность, другие ценят в ней точность, a третьи восхищаются её красотой.
Цель проекта: знакомство с жизнью и деятельностью Карла Фридриха Гаусса, научиться решать задачи, пользуясь способом Гаусса.
Задачи проекта:
найти интересные сведения о его жизни используя различные источники;
уяснить, что подсчет суммы последовательных чисел можно провести через группировку чисел в пары.
Юный Карл Фридрих, по его собственным словам, «научился считать раньше, чем говорить». Рассказывают, когда отец однажды громко подсчитывал заработок своих помощников, трехлетний Карл на слух заметил ошибку в вычислениях и указал на нее отцу.
В 1784 году семилетний Карл начинает учиться в местной однокомплектной (то есть с одним учителем) школе. Первый биограф Гаусса, профессор фон Вальтерсгаузен пишет: «…Душная комната с низким потолком и неровным, потрескавшимся полом. Из одного окна открывается вид на готические башни церкви св. Катарины, из другого — на конюшни. Среди сотни учеников от семи до пятнадцатилетнего возраста взад и вперед расхаживает учитель Бюттнер с хлыстом в руках. Этим беспощадным аргументом своего метода воспитания учитель пользовался достаточно часто — по настроению и по потребности. В этой школе, как бы вырванной из далекого средневековья, юный Гаусс проучился без особых происшествий два года, а затем был переведен в «арифметический класс». Впрочем, «перевод» выразился лишь в том, что девятилетнего мальчика пересадили из одного ряда скамеек в другой. Ученикам, сидевшим в этом ряду, тот же учитель Бюттнер давал меньше заданий по правописанию и больше — по арифметике. Ученик, первым выполнивший заданное вычисление, клал обычно свою грифельную доску на большой стол; поверх нее клал доску второй, и так далее по порядку. Затем кипа досок переворачивалась. Учитель начинал проверку с доски того, кто решил первым.
Вскоре после перевода девятилетнего Гаусса в арифметический класс учитель дал задание: сложить все натуральные числа от 1 до 100. «Едва задание было сформулировано,— продолжает фон Вальтерсгаузен,— как юный Карл объявил: «Я положил свою доску». И пока остальные школьники прилежно складывали и перемножали числа, учитель Бюттнер, исполненный собственного достоинства, расхаживал по классу, бросая время от времени саркастические взгляды на младшего из учеников, который давно выполнил задание. А тот спокойно улыбался, проникнутый непоколебимой уверенностью в правильности полученного результата — эта уверенность овладевала Гауссом после окончания каждой крупной работы в течение всей его жизни… В конце урока на грифельной доске Гаусса обнаружилось единственное число, которое, к общему изумлению, представляло собой правильный ответ на поставленную задачу, тогда как многие другие ответы оказались неверными и подлежали «исправлению с помощью хлыста».
«Вместо того, чтобы складывать последовательно 1+2=3; 3+3=6; 6+4=10; 10+5=15 и т.д., что было бы естественным для любого нормального школьника такого возраста, Гауссу пришло в голову объединить попарно числа с разных концов данного ряда: 1+100=101; 2+99 = 101 и т.д. Таких пар оказалось 50. Затем оставалось лишь выполнить умножение 101х50=5050. Нечего и удивляться: Гауссу не понадобилось много времени, чтобы написать на своей доске это единственное число».
Бюттнер обратил внимание на незаурядные способности своего ученика и достал для него дополнительные пособия. Большую помощь оказал молодой помощник учителя Мартин Бартельс, который также был неравнодушен к математике. Несмотря на восьмилетнюю разницу в возрасте, Гаусс и Бартельс быстро сблизились на почве общего увлечения математикой. Бюттнер и Бартельс убедили отца Гаусса направить сына в гимназию и обещали добиться материальной поддержки: у бедного ремесленника не было возможности платить за обучение сына в гимназии.
В 1788 году Гаусс был принят — небывалый случай! — сразу во второй класс гимназии. Особенно поразил он своих педагогов блестящими способностями к греческому языку и латыни — эти древние языки наряду с историей считались важнейшими в гуманитарном гимназическом образовании. В те времена дети крестьян и ремесленников весьма редко попадали в гимназии и тем более в университеты — образование и получение «привилегированных» профессий было практически недоступно для низших классов общества. Гаусс оказался счастливым исключением.
Чтобы понять, как рассуждал Гаусс, разберем задачу – найдем сумму всех натуральных чисел от 1 до 10.
1.Найти сумму 1 + 2 +3 +4 +5 +6 +7 +8 + 9+10.
Объединим слагаемые в пары – первое с десятым, второе с девятым и т.д. Всего у нас 5 таких пар и каждая пара в сумме дает 11.
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 = (10 +1) 
= 55
Ответ: 55
2. Найти сумму 1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 +11 + 12 +13 + 14
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 +11 + 12 +13 + 14= (1 + 14) 
=85
Ответ: 85
3. Найти сумму чисел 1 + 2 +3 +4 +5 +6 +7 +8 + 9.
(1 + 2 +3 +4 +5 +6 +7 +8) + 9 = (1 + 8) 4 + 9 = 45
1 + 2 +3 +4 +5 +6 +7 +8 + 9 = (1 + 2 +3 +4 +5 +6 +7 +8 + 9 +10) – 10 = 55 – 10 =45
Ответ: 45
А теперь перейдем к задаче маленького Гаусса.
4. Найти сумму чисел от 1 до 100.
1 + 2 + 3 + …+ 98 + 99 + 100.
1 + 2 + 3 + … + 98 + 99 + 100 = (1 + 100) 50 = 5050.
Ответ: 5050.
5. Найти сумму чисел от 1 до 1000.
1 + 2 + 3 + … + 998 + 999 + 1000 = (1 + 1000) ×500 = 500 500.
Ответ: 500 500
6. Найти сумму чисел от 1 до 220.
1 + 2 + 3 + … + 218 +219 + 220 = (1 +220) ×110 = 24 310
Ответ: 24 310
7. Найти сумму чисел от 1 до 221.
(1 + 2 + 3 + … + 218 +219 + 220) + 221 = (1 +220) ×110 + 221= 24 310 + 221 = 24 531
8. Имеется 9 гирь весом 1 г, 2 г, 3 г, 4 г, 5 г, 6 г, 7 г, 8 г, 9 г. Можно ли разложить их на три кучки с равным весом?
Решение.
Найдем сумму гирь методом Гаусса:
1 + 2 +3 +4 +5 +6 +7 +8 + 9 = (1 + 2 +3 +4 +5 +6 +7 +8) + 9 = (1 + 8) 4 + 9 = 45
Сумма масс всех гирек 45 г. Значит, в одной кучке будут гири весом 15г. Попробуем это сделать: 1 г + 9 г + 5 г, 2 г + 6 г + 7 г, 3 г + 4 г + 8 г. Здесь возможны и другие результаты, например: 1 г + 8 г + 6 г, 3 г + 5 г + 7 г, 2 г + 4 г + 9 г.
9. Можете ли вы разделить циферблат часов прямой линией на 2 равные половины так, чтобы суммы чисел на каждой половине были равны?
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 + 11 + 12 = (1 + 12) × 6= 78 – сумма чисел от 1 до 12.
Нужно, чтобы в каждой части было 78 :2 = 39.
Проведем линию между 9 и 10, между 3 и 4.
Проверка: (10 + 3) ×3 = 39 и (9 + 4) × 3=39
10. Проведите на циферблате часов две прямые линии, чтобы в каждой части сумма чисел была одинакова.
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 + 11 + 12 = (1 + 12) × 6= 78 – сумма чисел от 1 до 12.
Нужно, чтобы в каждой части было 78 : 3 = 26.
Проведем линии между а) 10; 11 и 2, 3; б) 8; 9 и 4; 5.
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10
Остроумный ответ Гаусса
Из биографии Гаусса известно, что еще в народной школе он поражал учителя Бюттнера своим умом и остроумием. Однажды учитель спросил ученика: «Карл, я сейчас задам тебе два вопроса. Если на первый ты ответишь правильно, то на второй можешь не отвечать. Итак, скажи мне, сколько иголок на рождественской елке?». Карл без промедления ответил: «67 534». «Как ты так быстро сосчитал иголки?» – изумился учитель. «А это уже второй вопрос, господин учитель», – улыбнулся ученик.
11. Летит стая птиц. Впереди одна птица(вожак), за ней две, потом три, четыре и т.д. Сколько птиц в стае, если в последнем ряду их 20?
Решение: 1 + 2 +3 +4 +5 +6 + … + 18 +19 + 20 = (1 + 20) ×10 = 210
Ответ: 210.
12. Как рассадить 45 кроликов в 9 клетках так, чтобы во всех клетках было разное количество кроликов?
1 + 2 +3 +4 +5 +6 +7 +8 + 9 = (1 + 2 +3 +4 +5 +6 +7 +8) + 9 = (1 + 8) 4 + 9 = 45
Всего 9 слагаемых, значит, в первую –1, во вторую –2, …, в девятую-9.
Ответ: В первую –1, во вторую –2, …, в девятую-9.
13.Набор состоит из 12 гирек массой 1г,2г,…,12г из набора убрали 4 гирек, общая масса которых равна трети общей массы всех гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?
Вес всех гирь равен1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 + 11 + 12 = (1 + 12) × 6= 78
Ее третья часть 78 : 3 = 26
Разобьем все гири на пары 1-12, 2-11, 3-10, 4-9, 5-8, 6-7.
4 9
211
1 12
6 7
5 8
3 10
Если мы уберем 4 гири весом 26 грамм, то при этом мы «разобьем» самое большее четыре пары, а две пары останутся точно нетронутыми, которые составляют тоже треть общей массы.
Таким образом. Мы получили первую четверку убранную, вторую четверку гарантированно оставшуюся (две пары) и третью четверку нетронутую, которая тоже будет весом 26 грамм.
Ответ: Можно.
Вывод:
Работая над этой темой, мы узнали, то в конце 18 века родился великий математик Карл Фридрих Гаусс. Благодаря его трудам, у нас появилась возможность без труда найти ответ в тех задачах, которые на первый взгляд трудно решить или можно потратить очень много времени. Благодаря изучения его жизни и наследия его трудов, мы лишний раз убеждаемся в величие и возможностях человеческого ума.
Литература:
1. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
2. Интернет – ресурсы.
Презентация «Решение СЛАУ методом Гаусса» по дисциплине ЕН.01 МАТЕМАТИКА 2 курс СПО
Инфоурок › Алгебра ›Презентации›Презентация «Решение СЛАУ методом Гаусса» по дисциплине ЕН.01 МАТЕМАТИКА 2 курс СПООписание презентации по отдельным слайдам:
1 слайд
Описание слайда:Толоконников А.В. Преподаватель КРК «Интеграл МЕТОДЫ РЕШЕНИЯ СЛАУ метод Гаусса Государственное бюджетное профессиональное образовательное учреждение «Курсавский региональный колледж «Интеграл» Курсавка 2016 г.
2 слайд
Описание слайда:Цели и задачи: Цель: Научиться решать системы линейных алгебраических уравнений (СЛАУ). Задачи: Изучить решение СЛАУ методом Гаусса Рассмотреть возможные варианты решений системы
3 слайд
Описание слайда:Содержание Правило Крамера Метод Гаусса Матричный способ решения СЛАУ
4 слайд
Описание слайда:Введение Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может: 1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).
5 слайд
Описание слайда:Метод Гаусса Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу!
6 слайд
Описание слайда:Метод Гаусса или метод исключения неизвестных состоит в последовательном исключении во втором уравнении первой неизвестной, в третьем уравнении первой и второй неизвестных и т. д. Пока не получится система треугольного или трапецеидального вида. Метод удобнее применять на расширенной матрице
7 слайд
Описание слайда:Пример Решить методом Гаусса систему уравнений: Запишем расширенную матрицу системы:
8 слайд
Описание слайда:Сначала смотрим на левое верхнее число: Почти всегда здесь должна находиться единица. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
9 слайд
Описание слайда:Теперь нужно получить нули вот на этих местах: Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2:
10 слайд
Описание слайда:Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3.
11 слайд
Описание слайда:Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО:
12 слайд
Описание слайда:Далее нужно получить единицу на следующей «ступеньке»: В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
13 слайд
Описание слайда:Для этого к третьей строке прибавляем вторую строку, умноженную на –2: В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:
14 слайд
Описание слайда:Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх. В третьем уравнении у нас уже готовый результат: z=4 Смотрим на второе уравнение: y-z=1. Y-4=1 Y=5 Значение «зет» уже известно, таким образом: X+2*5-4=9 X=3 Ответ: (3;5;4)
15 слайд
Описание слайда:Выводы: Метод Гаусса универсальный, позволяет решать любую СЛАУ. Слау может иметь единственное решение, если расширенная матрица преобразуется в треугольную, причем имеет уравнение вида а*х=в. Слау может иметь бесконечно много решений, если, если матрица преобразуется в трапецеидальный вид. Слау не имеет решения, если расширенная матрица преобразуется в треугольную, причем имеет уравнение вида 0*х=а
16 слайд
Описание слайда:Спасибо за внимание
Курс профессиональной переподготовки
Учитель математики
Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДБ-503589
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий