Матричный метод решения систем линейных уравнений
Численные методы решения систем линейных уравнений
Содержание
Введение
Численные методы
Матричный метод
Метод Крамера
Метод Гаусса
Итерации для линейных систем
Итерация Якоби
Листинг программы
Введение
Линейная алгебра – часть алгебры, изучающая векторные (линейные) пространства и их подпространства, линейные отображения (операторы), линейные, билинейные, и квадратичные функции на векторных пространствах.
Линейная алгебра, численные методы – раздел вычислительной математики, посвященный математическому описанию и исследованию процессов численного решения задач линейной алгебры.
Среди задач линейной алгебры наибольшее значение имеют две: решение системы линейных алгебраических уравнений определение собственных значений и собственных векторов матрицы. Другие часто встречающиеся задачи: обращение матрицы, вычисление определителя и т.д.
Любой численный метод линейной алгебры можно рассматривать как некоторую последовательность выполнения арифметических операций над элементами входных данных. Если при любых входных данных численный метод позволяет найти решение задачи за конечное число арифметических операций, то такой метод называется прямым. В противоположном случае численный метод называется итерационным. Прямые методы — это такие, как метод Гаусса, метод окаймления, метод пополнения, метод сопряжённых градиентов и др. Итерационные методы – это метод простой итерации, метод вращений, метод переменных направлений, метод релаксации и др. Здесь будут рассматриваться матричный метод, метод Гаусса и метод Крамера.
В данной работе будут рассмотрены численные методы в электронных таблицах Excel и программе MathCAD, Microsoft Visual Basic.
MathCAD.
Программа MathCAD по своему назначению позволяет моделировать в электронном документе научно–технические, а также экономические расчёты в форме, достаточно близкой к общепринятым ручным расчётам. Это упрощает составление программы расчёта, автоматизирует перерасчёт и построение графических иллюстраций подобно электронным таблицам Excel, документирование результатов как в текстовом редакторе Word.
Программа Mathcad известна за лёгкость, с которой математические уравнения, текст, и графика могут быть объединены в одном документе. Кроме того, вычислительные способности Mathcad распространяются от сложения столбца чисел к решению интегралов и производных, решение систем уравнений и больше.
Достоинством MathCAD является также наличие в его составе электронных книг. Одна из них – учебник по самой программе, другие – справочник по различным разделам математики, физики, радиоэлектроники и др.
Microsoft Office Excel.
Если же говорить о программе Excel, которая является одной из наиболее известных в обработке электронных таблиц, то без преувеличения можно утверждать, что ее возможности практически неисчерпаемы.
Обработка текста, управление базами данных — программа настолько мощна, что во многих случаях превосходит специализированные программы — редакторы или программы баз данных. Такое многообразие функций может поначалу запутать, нежели заставить применять их на практике. Но по мере приобретения опыта начинаешь по достоинству ценить то, что границ возможностей Excel тяжело достичь.
За всю историю табличных расчетов с применением персональных компьютеров требования пользователей к подобным программам существенно изменились. В начале основной акцент в такой программе, как, например, Visi Calc, ставился на счетные функции. Сегодня, положение другое. Наряду с инженерными и бухгалтерскими расчетами организация и графическое изображение данных приобретают все возрастающее значение. Кроме того, многообразие функций, предлагаемое такой расчетной и графической программой, не должно осложнять работу пользователя. Программы для Windows создают для этого идеальные предпосылки.
В последнее время многие как раз перешли на использование Windows в качестве своей пользовательской среды. Как следствие, многие фирмы, создающие программное обеспечение, начали предлагать большое количество программ для Windows.
Visual Basic.
Microsoft Visual Basic – это мощная система программирования, позволяющая быстро и эффективно создавать приложения для Microsoft Windows. В отличие от Excel и MathCAD это наиболее удобная программа для решения систем линейных уравнений. Простой пользовательский интерфейс, позволяющий легко переключаться с проекта формы на сам код программы.
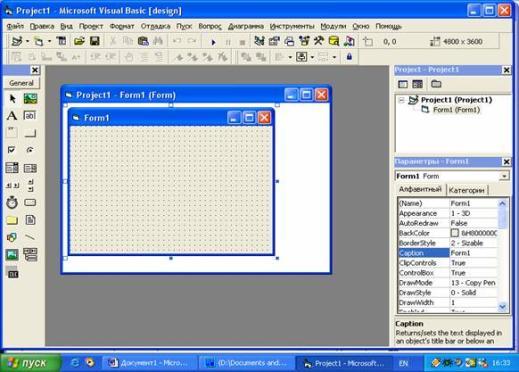
линейная алгебра численный метод
Удобное окно для кода самой программы:
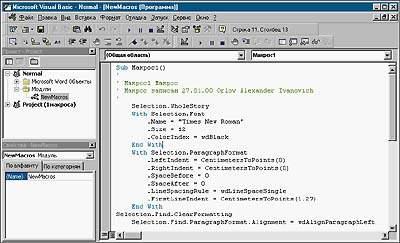
Численные методы
Разрешимость системы линейных уравнений
Когда мы говорим о главной матрице системы линейных уравнений, то всегда имеем в виду квадратную матрицу nЧn, т. е. матрицу с одинаковым количеством строк и столбцов. Это важно.
Если, например, количество строк (количество уравнений в системе) будет меньше, чем количество столбцов (фактически, количества неизвестных), то система будет неопределенной, т. е. мы не сможем однозначно определить все неизвестные (решить систему).
Но это не единственное ограничение. Из векторной алгебры известно, что система линейных уравнений имеет решение (однозначное) тогда и только тогда, когда ее главный определитель не равен нулю: Δ ≠ 0.
Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:
Δ = 0 и каждый из дополнительных определителей Δxi = 0. Это имеет место только тогда, когда коэффициенты при неизвестных xi пропорциональны, т. е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число k. При этом система имеет бесчисленное множество решений.
Δ = 0 и хотя бы один дополнительный определитель Δxi ≠ 0. Это имеет место только тогда, когда коэффициенты при всех неизвестных xi, пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.
Пусть дана система линейных уравнений:
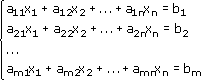
Рассмотрим матрицу, составленную из коэффициентов при неизвестных:
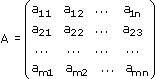
Свободные члены и неизвестные можно записать в виде матрицы столбцов:
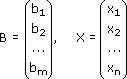
Тогда, используя правило умножение матриц, эту систему уравнений можно записать так:
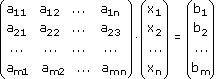
или
A·x = b. (1)
Равенство (1) называется матричным уравнением или системой уравнений в матричном виде.
Матрица А коэффициентов при неизвестных называется главной матрицей системы.
Иногда рассматривают также расширенную матрицу системы, т. е. главную матрицу системы, дополненную столбцом свободных членов, которую записывают в следующем виде:
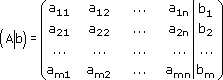
Любую линейную систему уравнений можно записать в матричном виде. Например, пусть дана система:
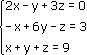
Эта система из двух уравнений с тремя неизвестными – x, y,. В высшей математике можно рассматривать системы из очень большого числа уравнений с большим количеством неизвестных и поэтому неизвестные принято обозначать только буквой х, но с индексами:
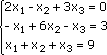
Запишем эту систему в матричном виде:
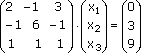
Здесь главная матрица системы:
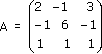
Расширенная матрица будет иметь вид:
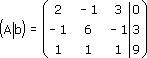
Решения матричных уравнений.
Матричные уравнения решаются при помощи обратных матриц. Уравнение решается следующим образом. Пусть матрица А – невырожденная (D ≠ 0), тогда существует обратная матрица А-1. Умножив на нее обе части матричного уравнения, имеем А-1(АХ) = А-1В. Используя сочетательный закон умножения, перепишем это равенство в виде
(А-1А) Х = А-1В.
Поскольку А-1 А = Е и ЕХ = Х, находим:
Х = А-1В.
Таким образом, чтобы решить матричное уравнение, нужно:
Найти обратную матрицу А-1.
Найти произведение обратной матрицы А-1 на матрицу столбец свободных членов В, т. е А-1В.
Пользуясь определением равных матриц, записать ответ.
При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений.
К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над расширенной матрицей системы. А в методе Крамера – с определителями системы, образованными по специальному правилу.
Метод Крамера
При решении систем линейных уравнений по методу Крамера последовательно выполняется следующий алгоритм:
Записывают систему в матричном виде (если это еще не сделано).
Вычисляют главный определитель системы:
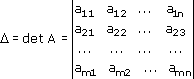
Вычисляют все дополнительные определители системы:

Если главный определитель системы не равен нулю, то выполняют пункт 5. Иначе рассматривают вопрос о разрешимости данной системы (имеет бесчисленное множество решений или не имеет решений). Находят значения всех неизвестных по формулам Крамера для решения системы n линейных уравнений с n неизвестными, которые имеют вид:
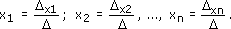
studfile.net
3.1.3. Матричный метод.
Пусть дана система n линейных уравнений с n неизвестными:
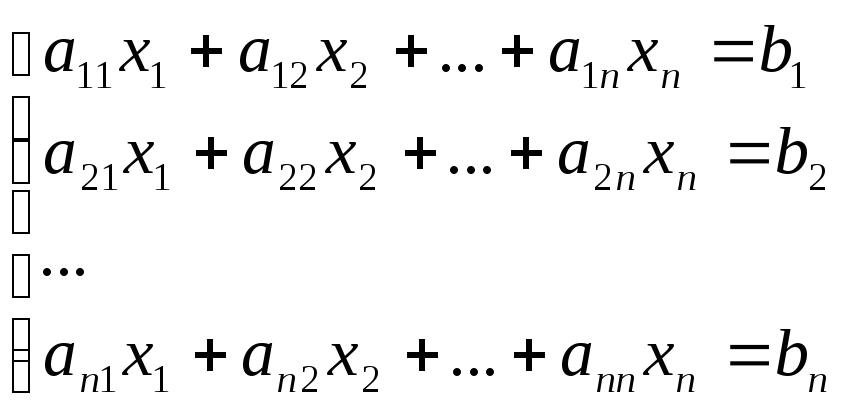 ,
,
которую можно записать в матричной форме, как
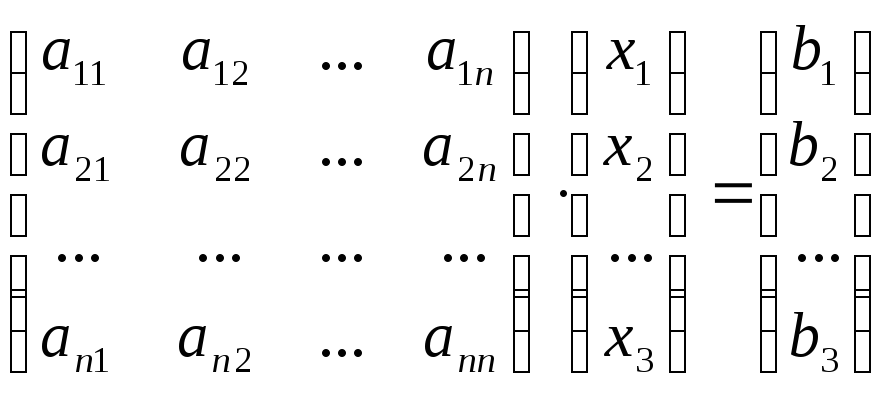 ,
или
,
или 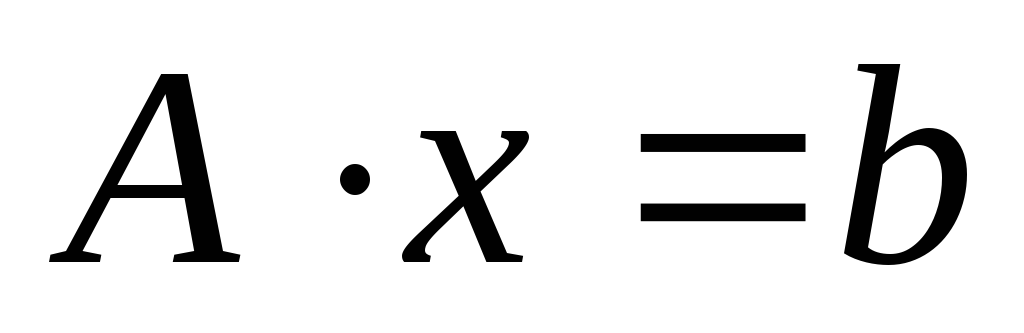 ,
,
где
А= , х =
, х =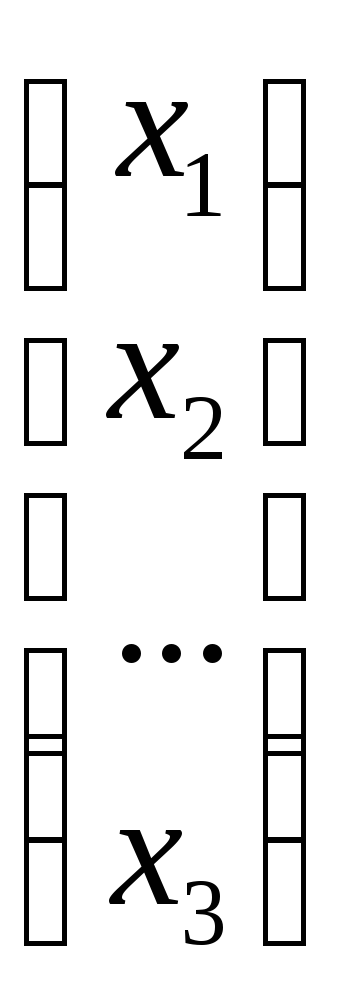 , b =
, b =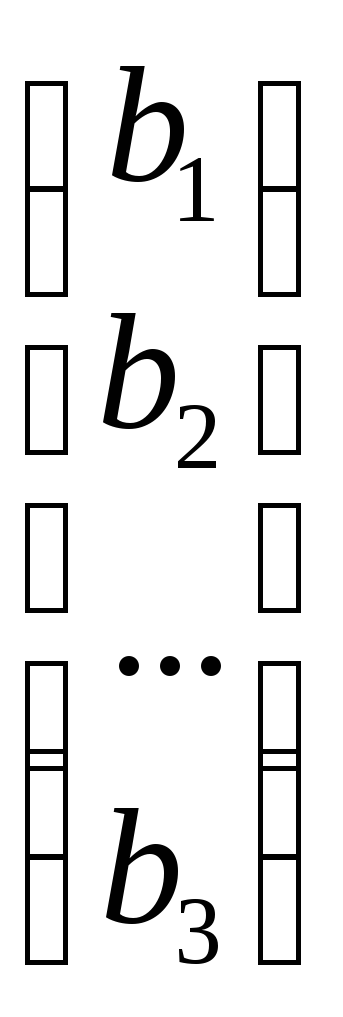 .
.
Предположим,
что 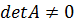 .
В этом случае матрица
.
В этом случае матрица 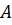 имеет обратную
имеет обратную 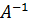 .
Умножим слева обе части системы на
.
Умножим слева обе части системы на 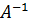 ,
и,
выполнив
преобразования,
,
и,
выполнив
преобразования,
получим:

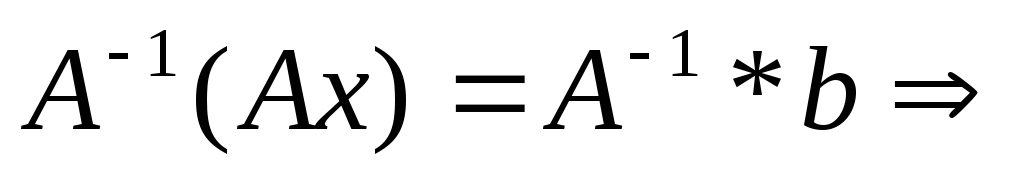
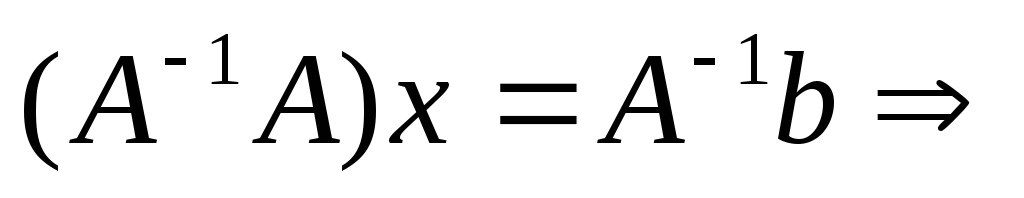
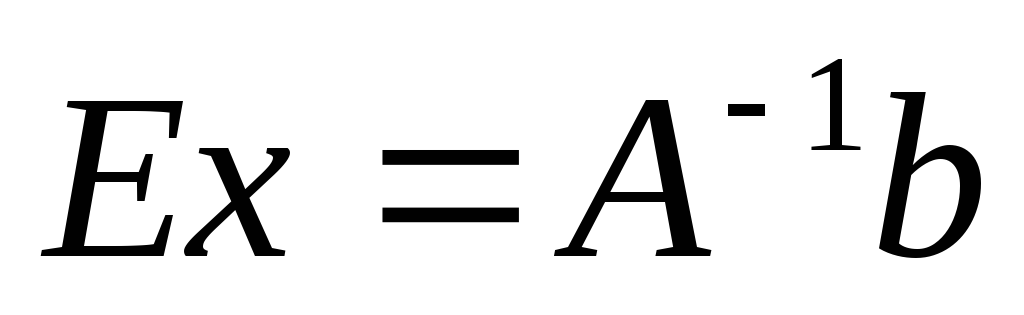 т.е.
т.е. 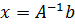 .
.
Данное соотношение и представляет суть матричного метода.
Замечание.
Матричный метод, как и правило Крамера,
применим, если 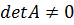 .
.
Пример
4. Решить систему матричным методом 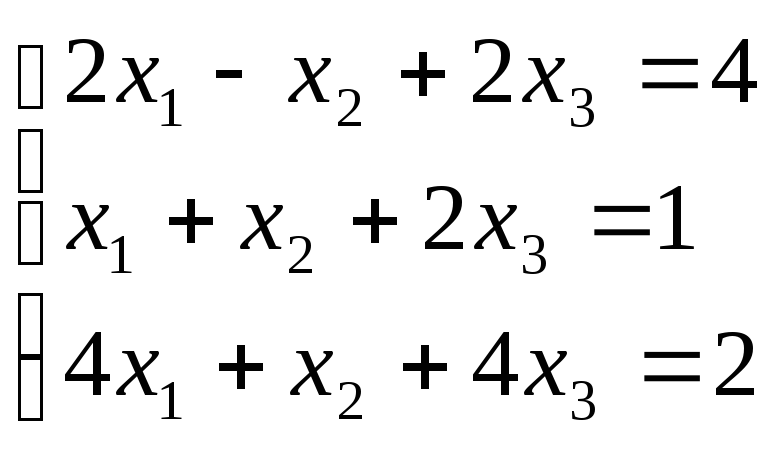 .
.
Решение.
Имеем
 ,
, 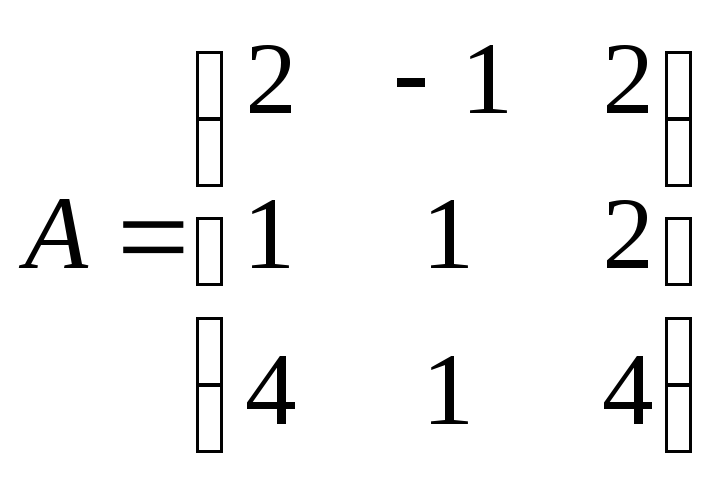 ,
,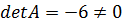 .
.
Таким образом 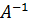 существует. Найдём алгебраические
дополнения:
существует. Найдём алгебраические
дополнения:
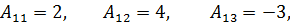
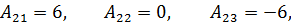
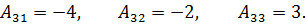
Получим:
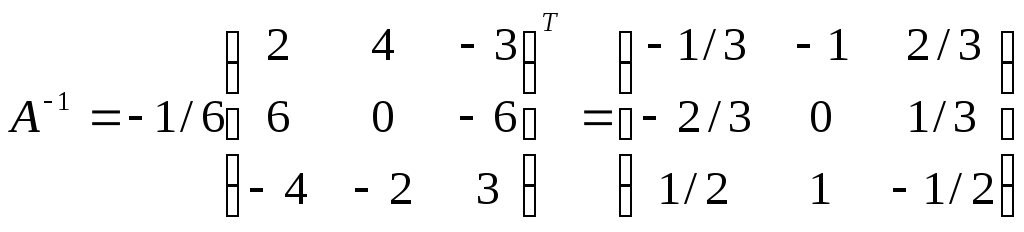 .
.
Следовательно,
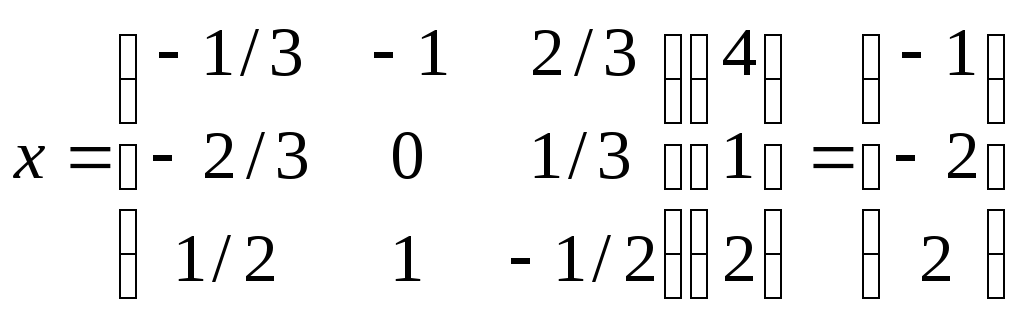
Т.е. 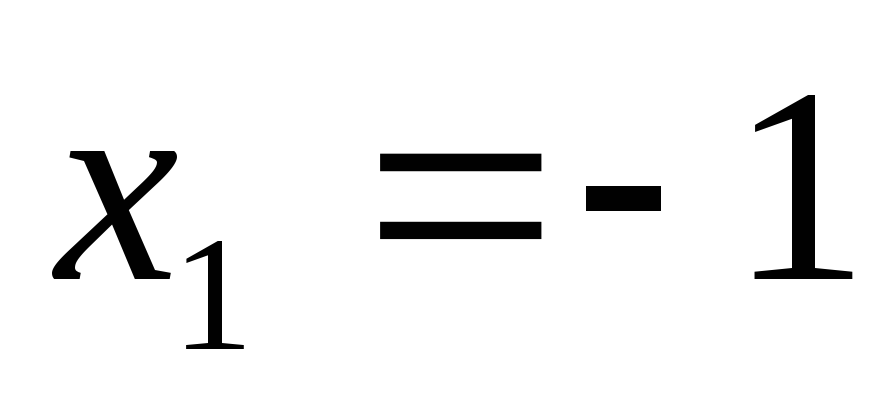 ,
,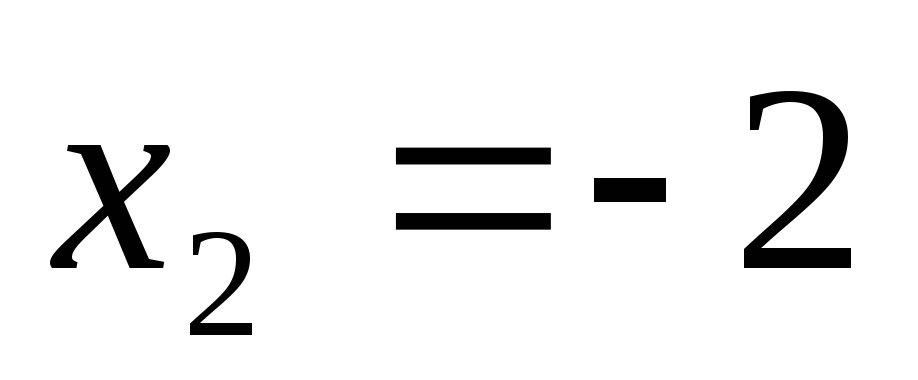 ,
,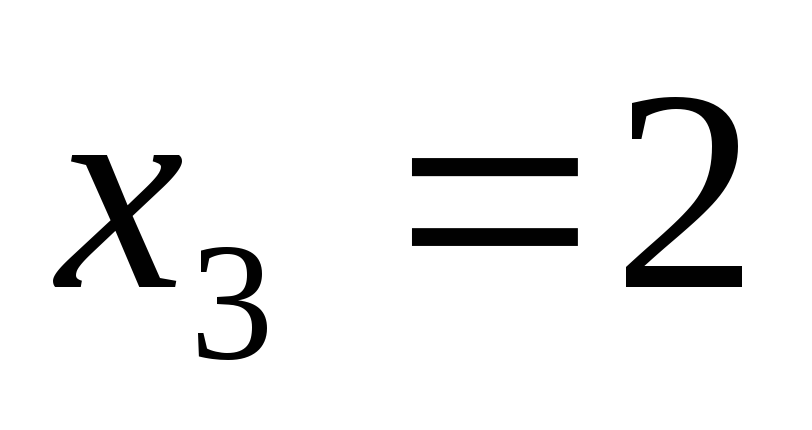 .
.
Выполним проверку.
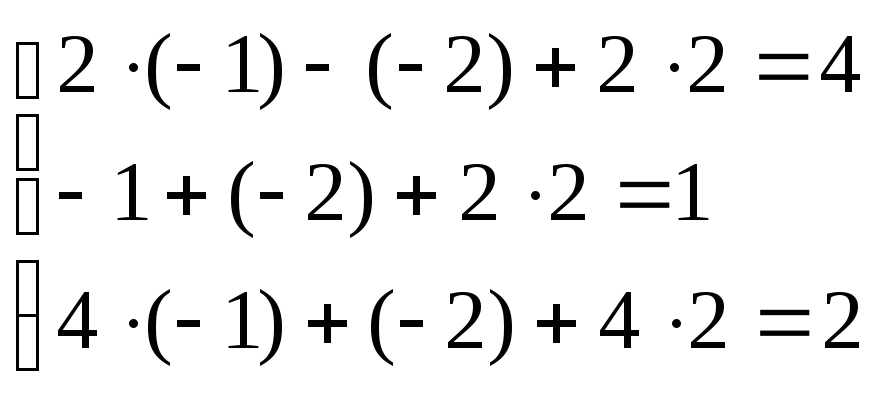
Решение найдено верно.
Ответ. (-1;-2;2).
3.2. Решение типовых примеров
Решить систему линейных алгебраических уравнений двумя способами: матричным методом и по правилу Крамера. Результаты сравнить.
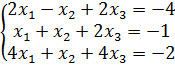
Решение.
Правило Крамера.
Найдем главный определитель системы по правилу треугольников. Имеем
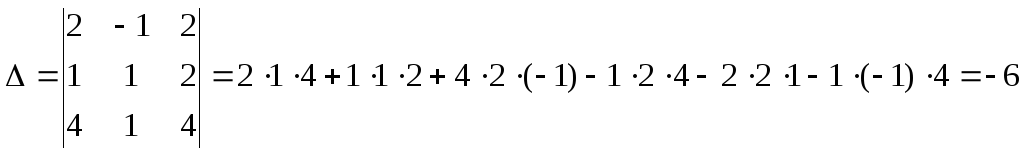 .
.
Определим вспомогательные определители.
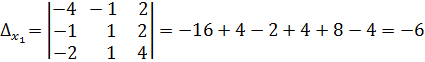 ,
,
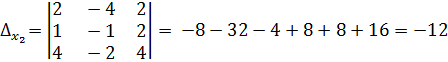 ,
,
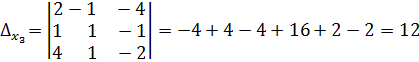 .
.
Найдем значения переменных. Имеем
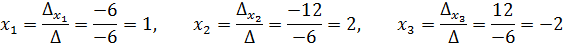 .
.
Матричный метод.
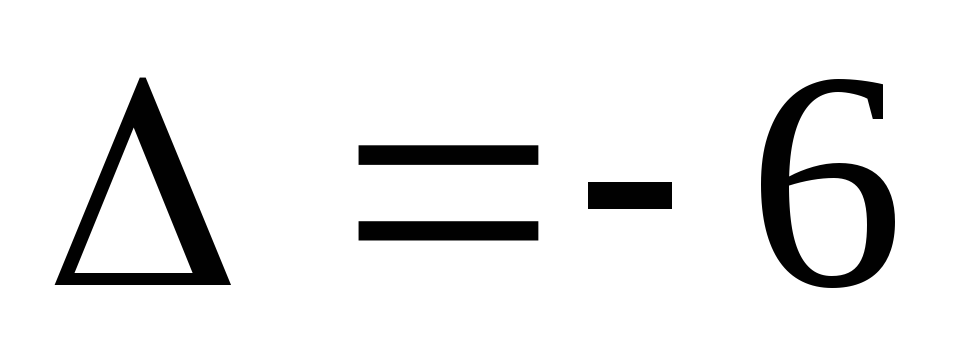
Таким образом 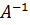 существует. Найдём алгебраические
дополнения:
существует. Найдём алгебраические
дополнения:
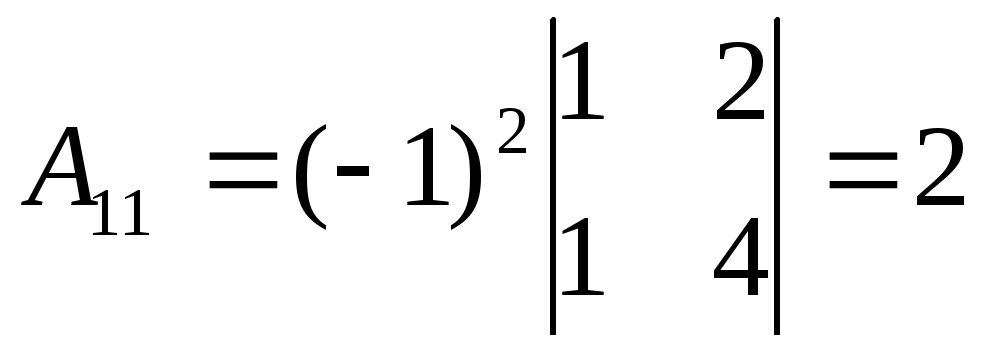 ,
,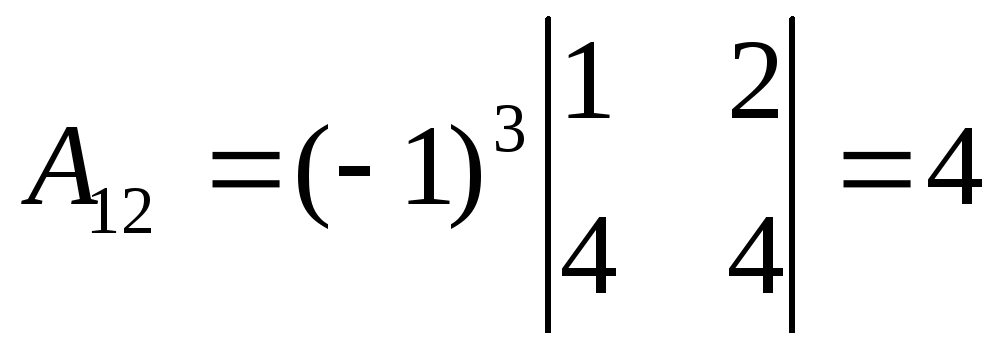 ,
,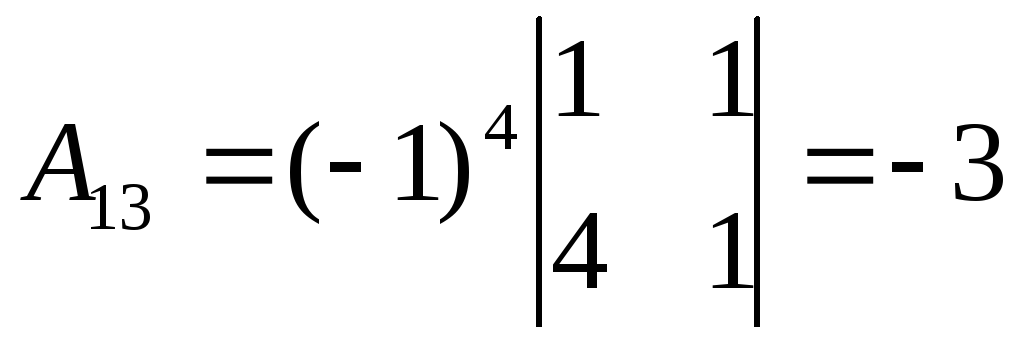 ,
,
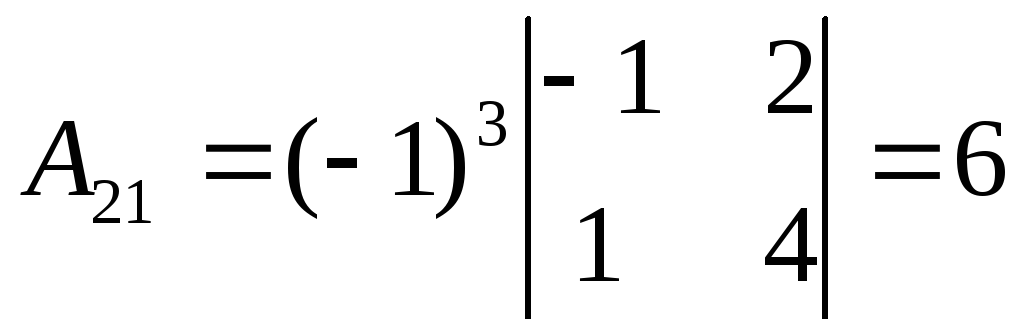 ,
,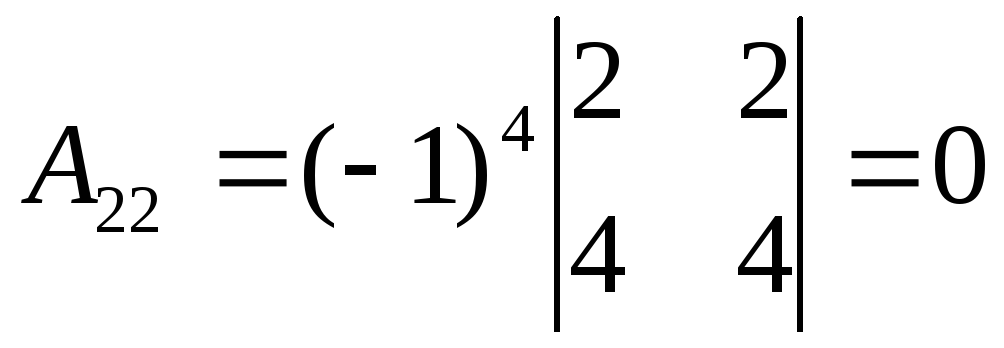 ,
,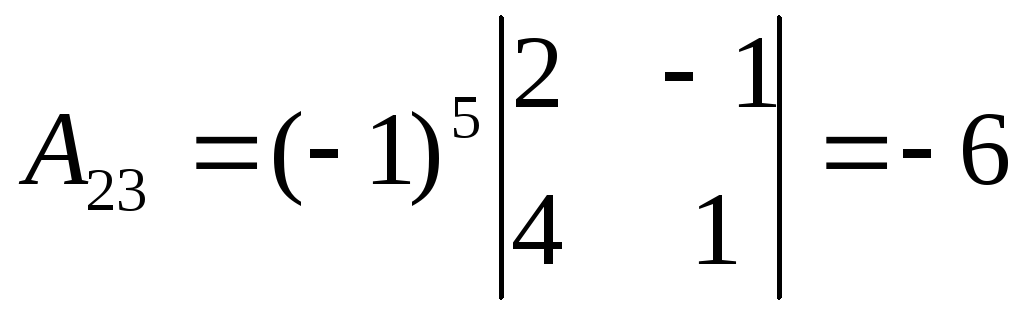 ,
,
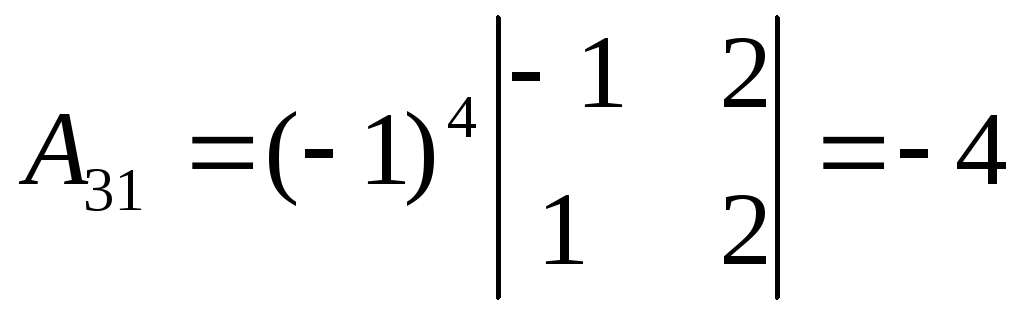 ,
,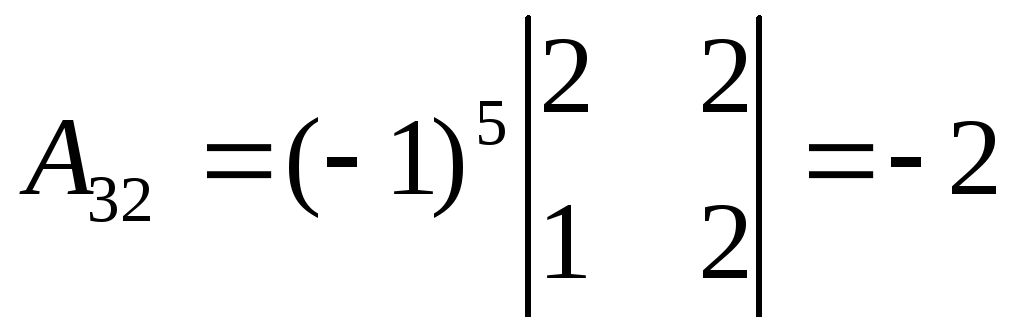 ,
,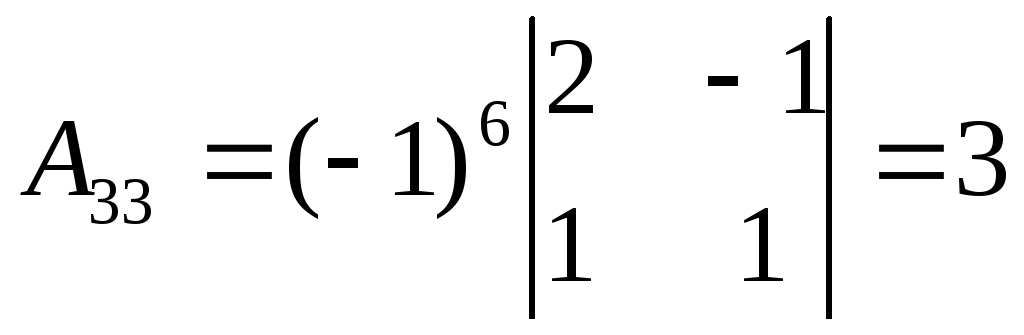
Имеем:
.
Следовательно,
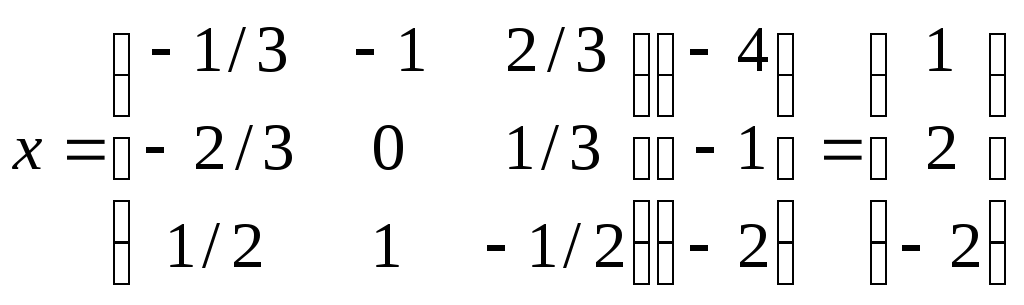 .
.
Т.е. 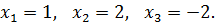
Решив систему двумя способами, мы пришли к одному и тому же ответу (1;2;-2), значит, система решена правильно.
Ответ. (1;2;-2).
2. Решить систему линейных алгебраических уравнений методом Гаусса.
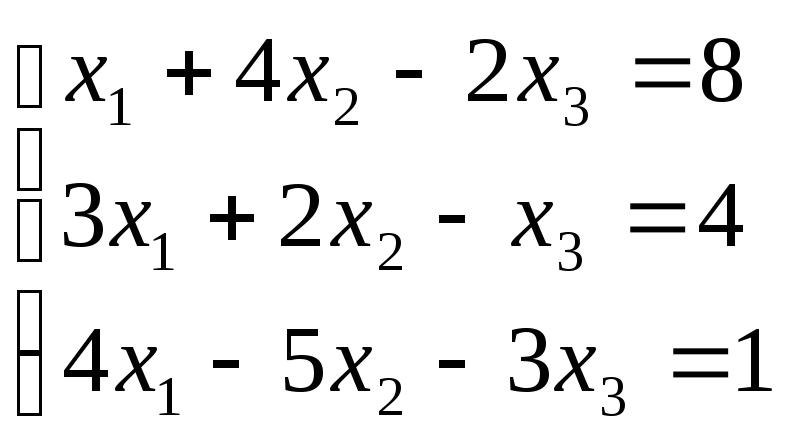
Решение.
Ход решения аналогичен примерам 1,2,3.
Приводим составленную таблицу к ступенчатому виду: умножаем первую строку на (-3), прибавляем к ней вторую, затем умножаем первую строку на (-4) и прибавляем к ней третью; Втору строку умножим на (-21), а третью на (10), результаты сложим. Имеем
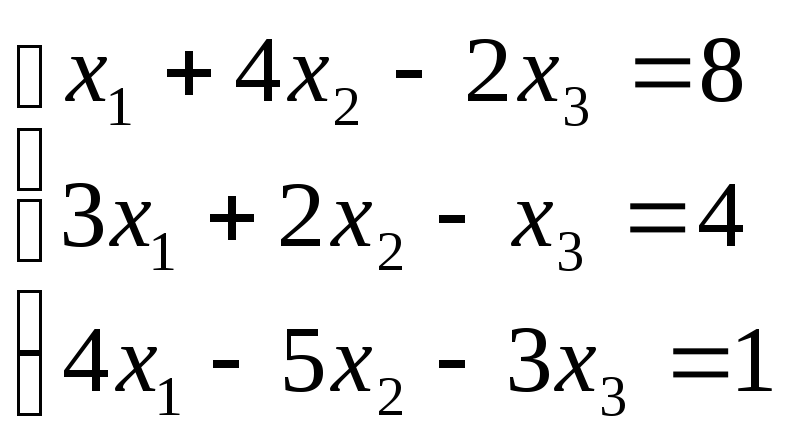

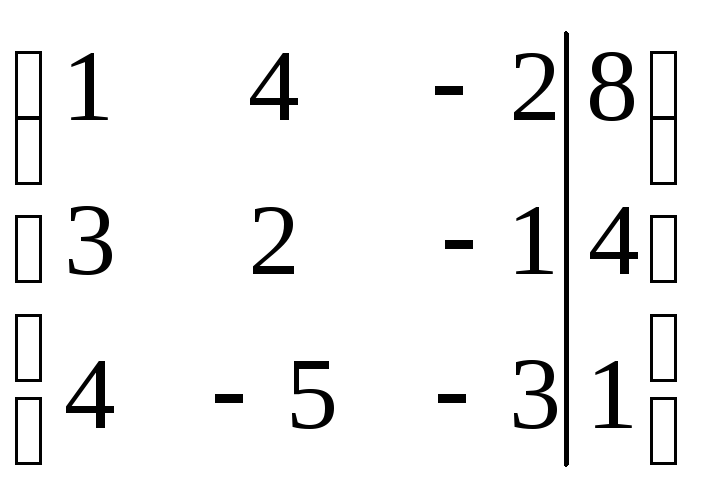
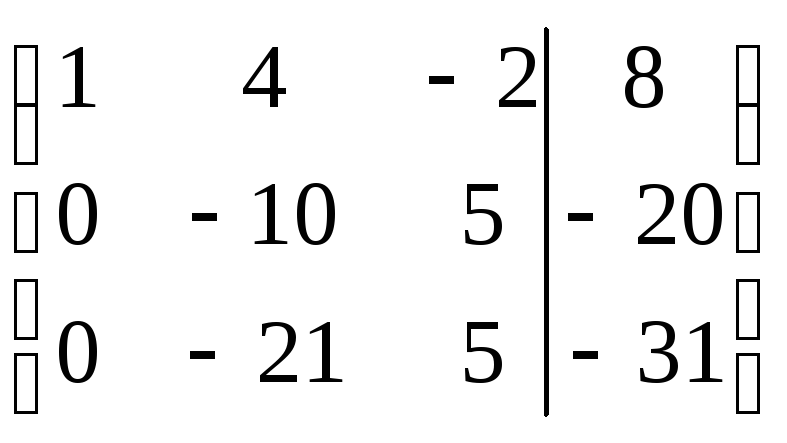
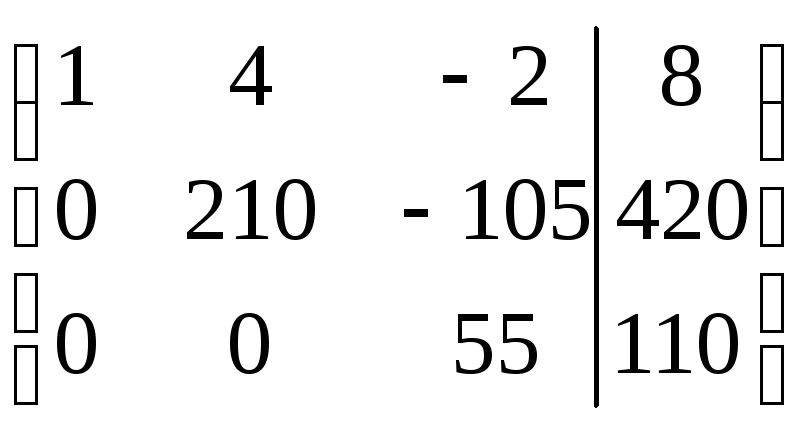
В результате получим следующую систему:
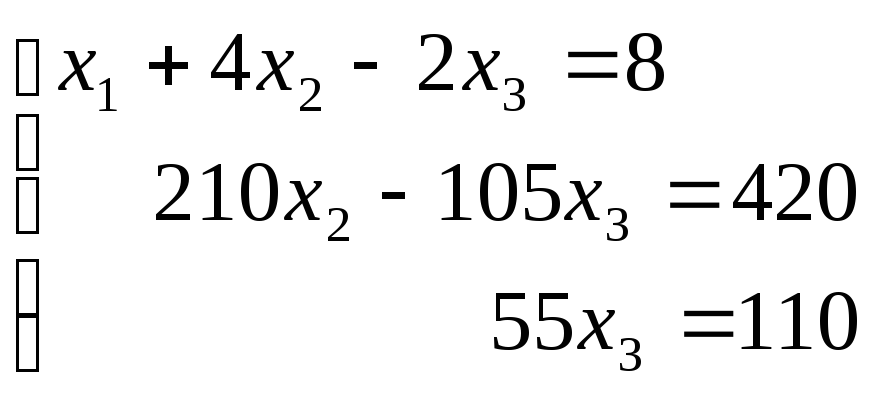
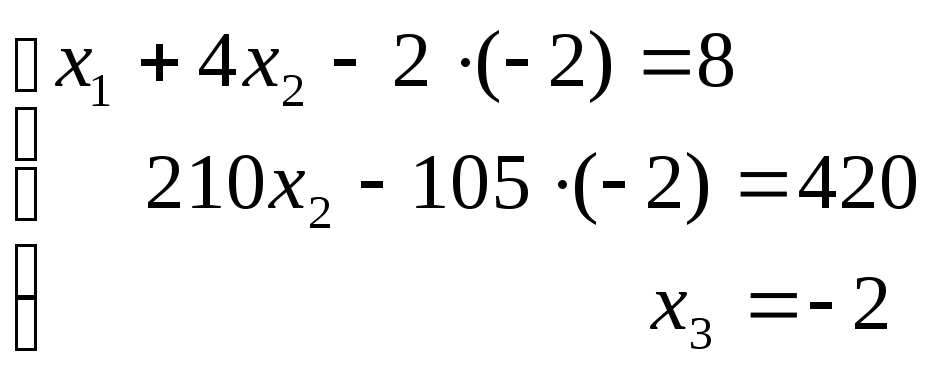
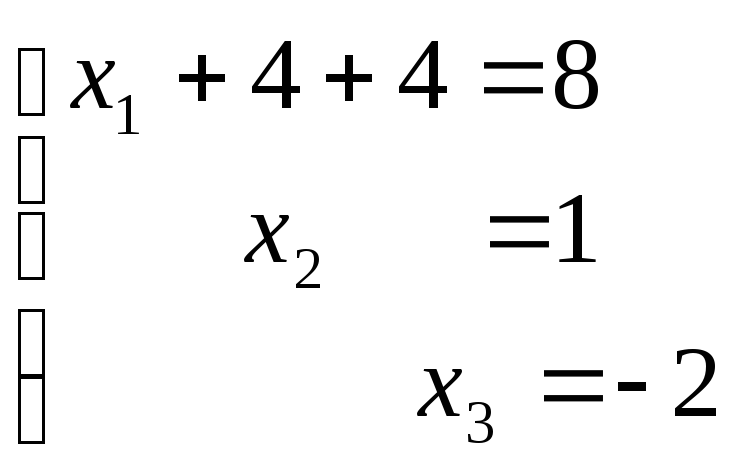
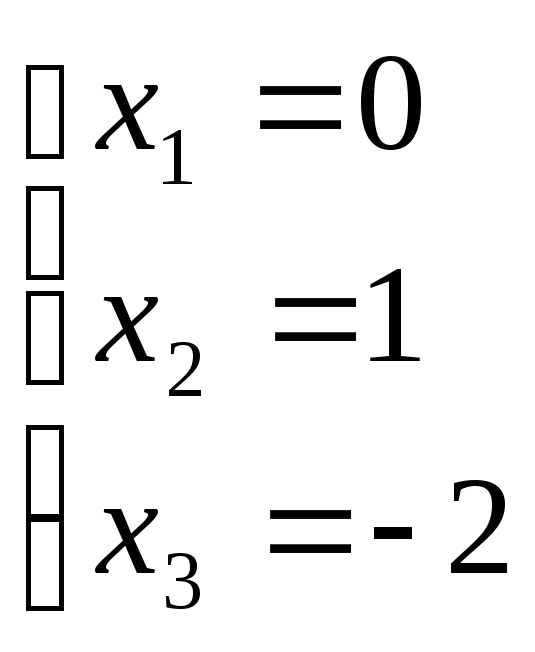
Выполним проверку

Решено верно.
Ответ. (0;1;-2).
3. При каких a и b система имеет 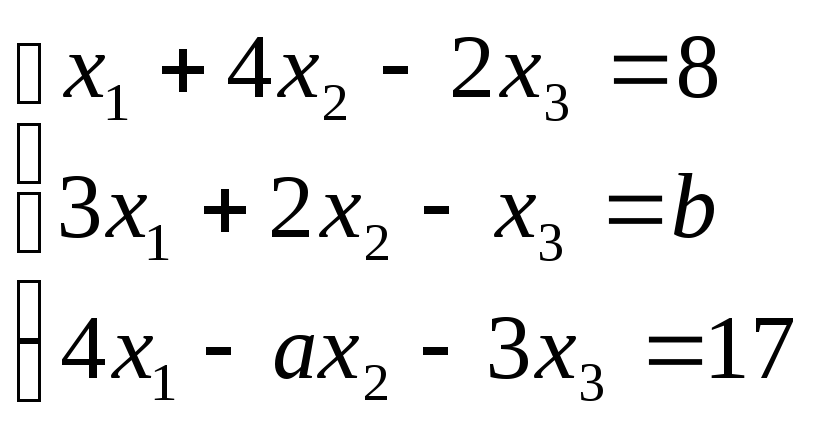
а) единственное решение;
б) не имеет решения;
в) бесчисленное множество решений.
Решение.
Найдём главный определитель системы по правилу Крамера. Если он будет отличен от нуля, тогда система будет иметь лишь одно решение.
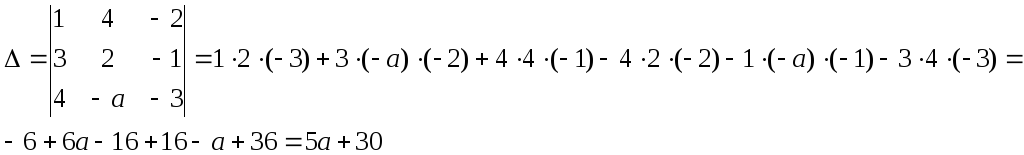
Главный определитель зависит от а. Он обращается в ноль при а=-6.
Если 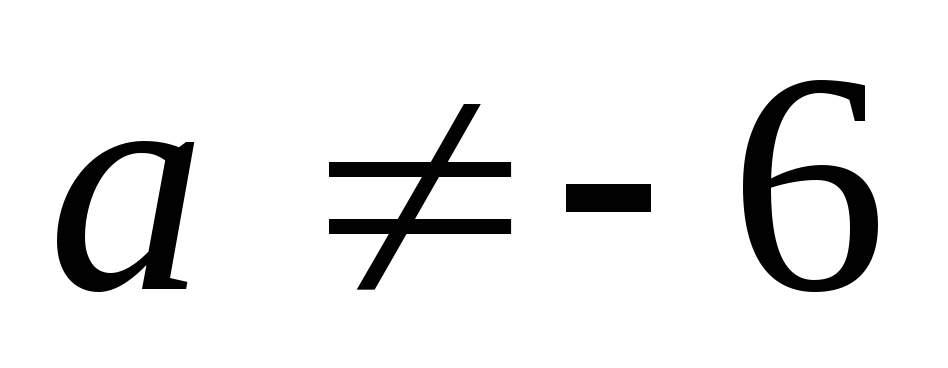 ,
то
,
то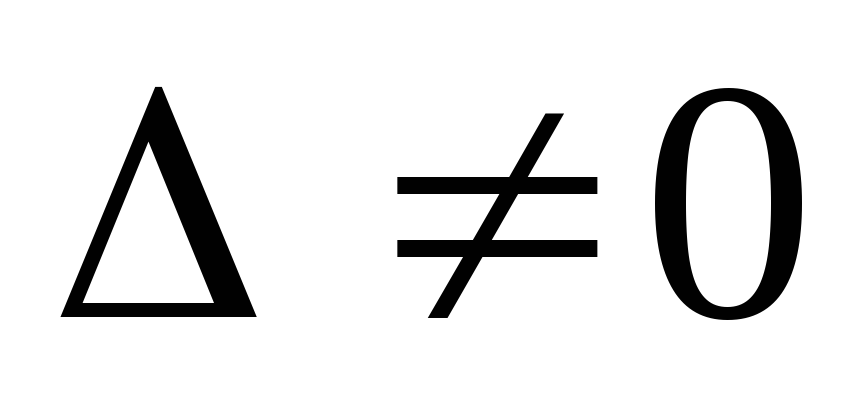 и система имеет только одно решение при
любом
и система имеет только одно решение при
любом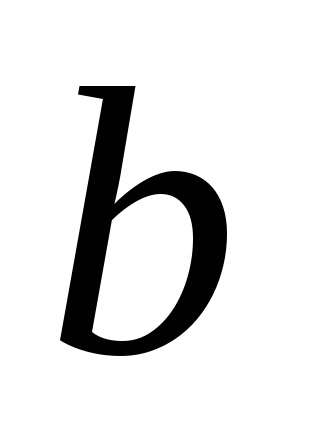 .
.
Если 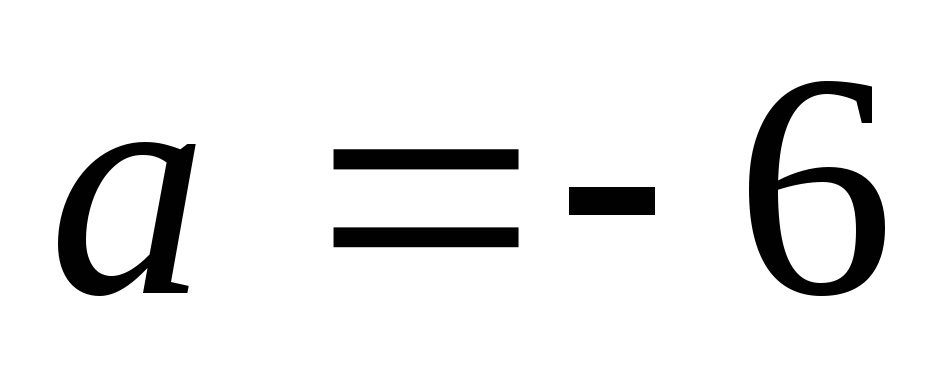 ,
то получим следующую систему линейных
уравнений
,
то получим следующую систему линейных
уравнений 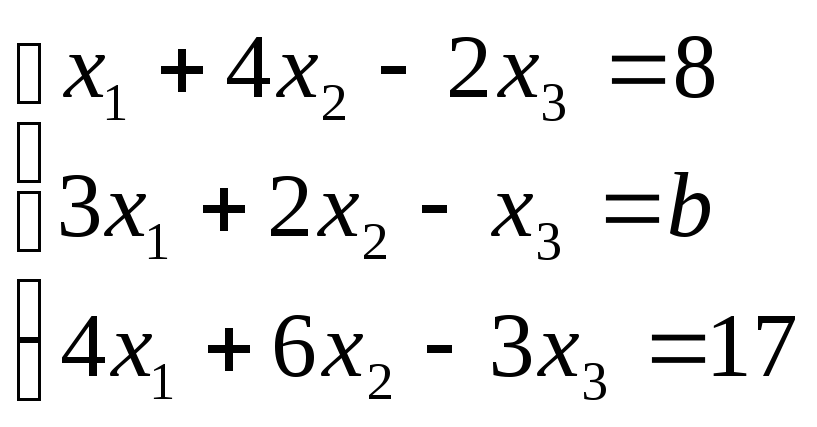 ,
которой соответствует расширенная
матрица
:
,
которой соответствует расширенная
матрица
:
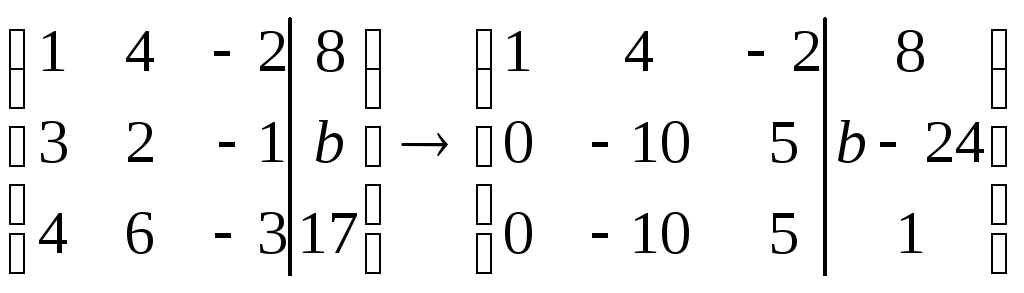
Умножим первую строку на (-3) и сложим со второй, первую строку умножим на (-4) и сложим с третьей.
Заметим, что две последних строки матрицы имеют одинаковую левую часть. Поэтому, чтобы система была совместна необходимо, чтобы правые части также совпадали. При этом возможны следующие варианты.
Если 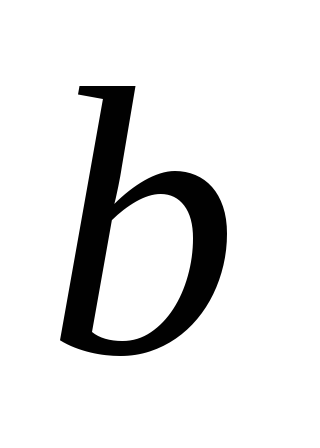 =25,
то два последних уравнения одинаковы.
Опускаем одно из них, в результате чего
исходная система трех уравнений сводится
к системе двух уравнений, но с тремя
неизвестными.
=25,
то два последних уравнения одинаковы.
Опускаем одно из них, в результате чего
исходная система трех уравнений сводится
к системе двух уравнений, но с тремя
неизвестными.
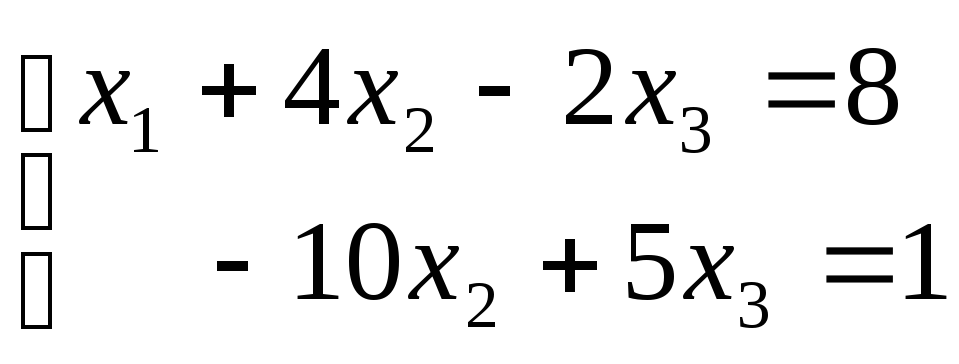
Эта система имеет бесконечное количество решений.
Если же 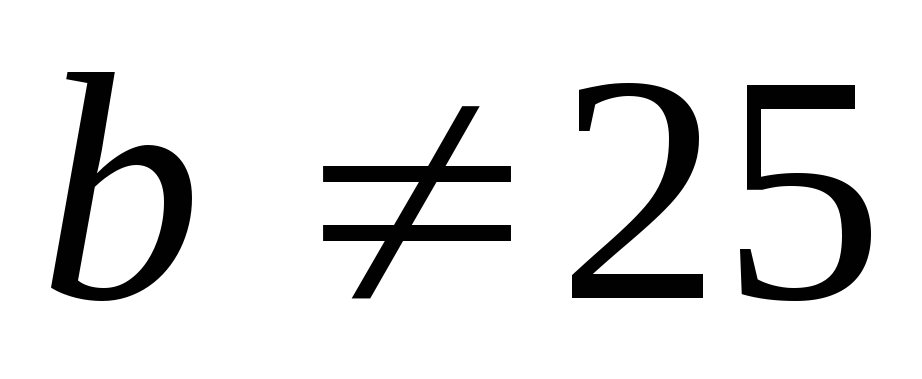 ,
то система несовместна.
,
то система несовместна.
Ответ:
Если 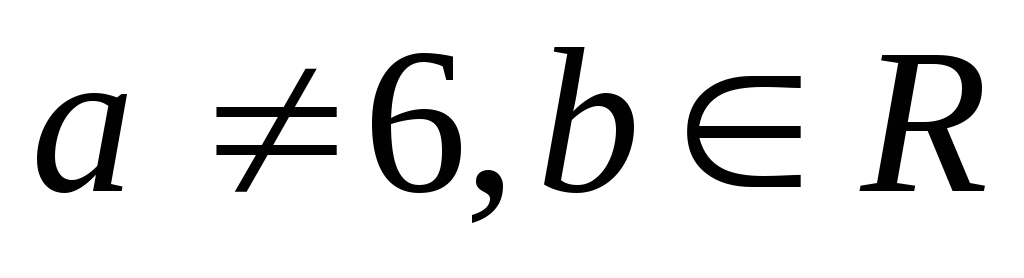 ,
то система имеет единственное решение.
,
то система имеет единственное решение.
Если 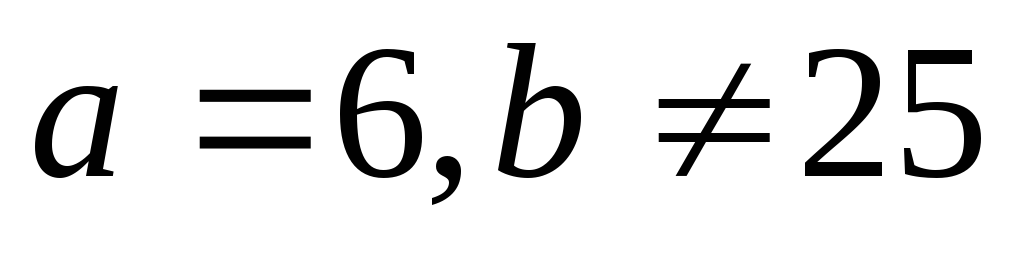 —
система решений не имеет.
—
система решений не имеет.
Если 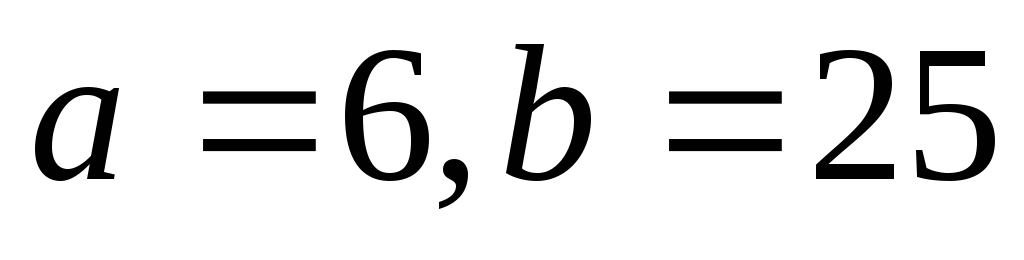 —
система имеет бесконечно много решений.
—
система имеет бесконечно много решений.
4. Составить систему трёх линейных уравнений с тремя неизвестными, имеющую решение (8;7;5). Имеет ли полученная система другие решения?
Решение.
Возьмем
произвольные коэффициенты при
неизвестных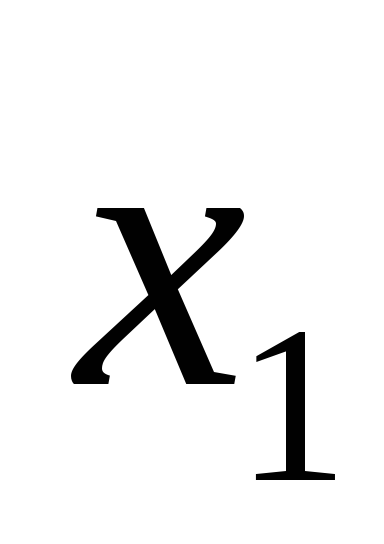 ,
,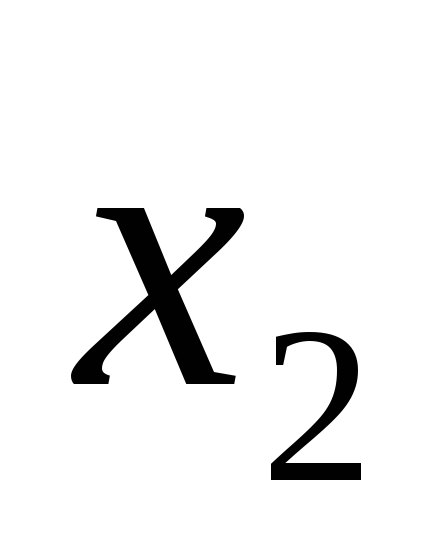 ,
, .и
рассмотрим систему
.и
рассмотрим систему
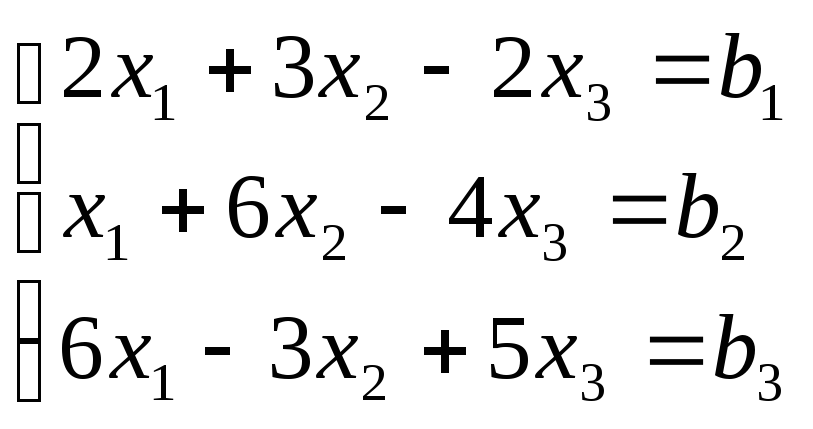 .
.
Теперь,
подставив решение (8;7;5), вычислим коэффициенты 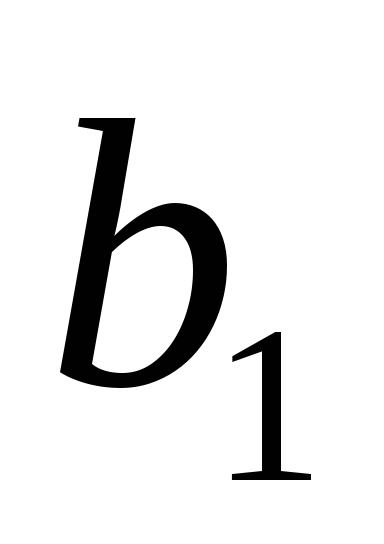 ,
,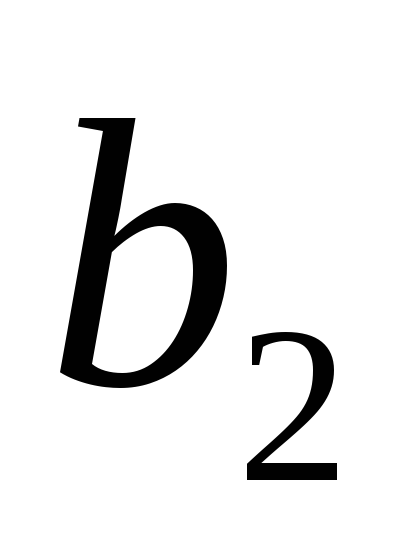 ,
,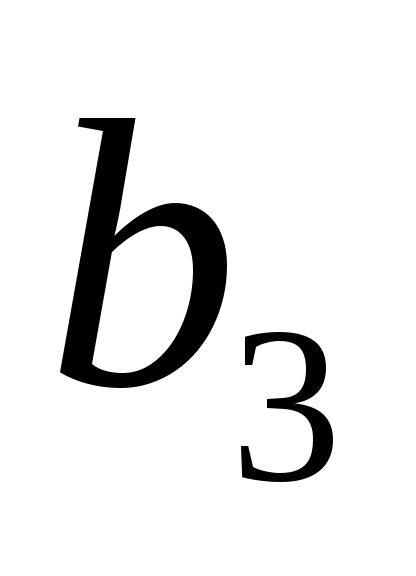
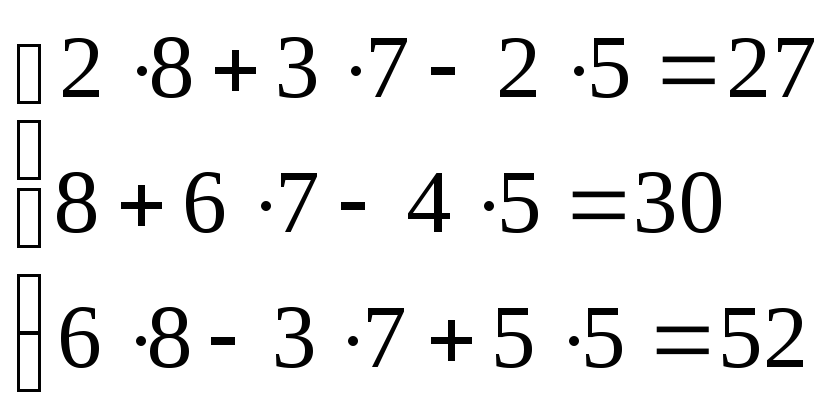 .
.
Таким образом, мы получили систему, которая имеет решение (8;7;5)
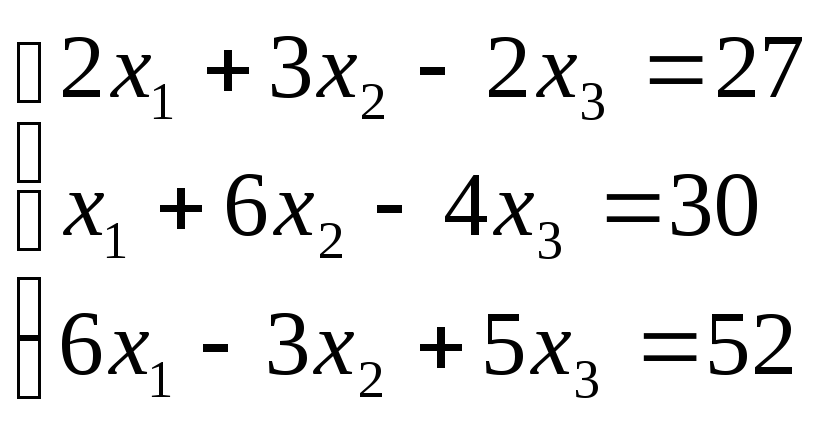 .
.
Проверим эту систему на наличие других решений. С этой целью найдем ее главный определитель
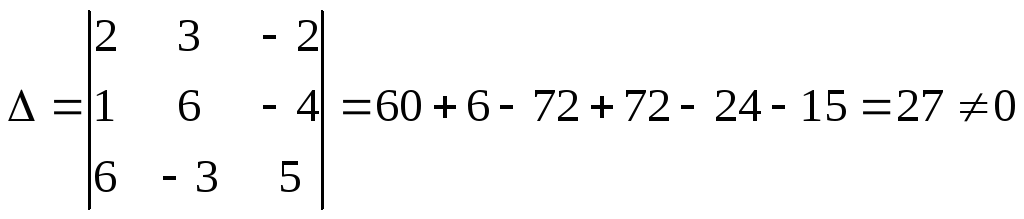 .
.
Так как определитель составленной системы отличен от нуля, то эта система имеет единственное решение (8;7;5).
Замечание.
Если бы 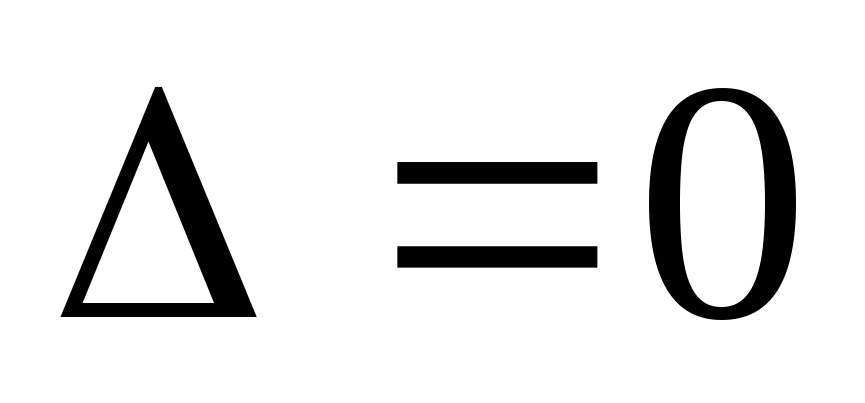 ,
то составленная, таким образом ,система
имела бы бесконечно много решений.
,
то составленная, таким образом ,система
имела бы бесконечно много решений.
Ответ. 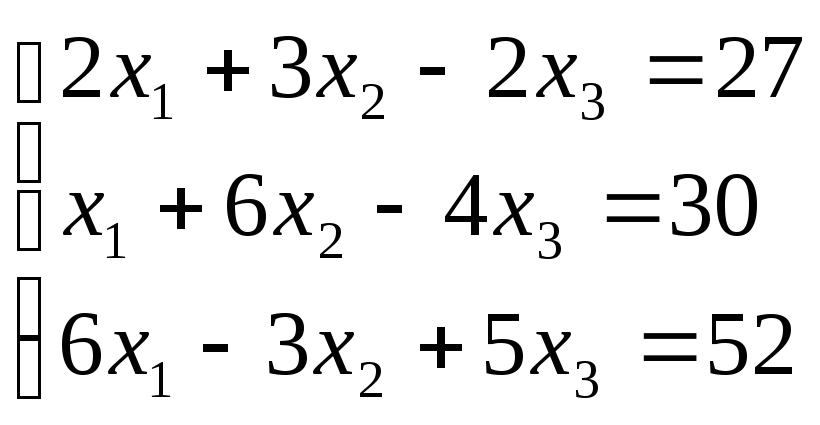 .
.
studfile.net
Обратная матрица. Матричный метод решения СЛАУ.
⇐ ПредыдущаяСтр 4 из 12Следующая ⇒Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с неизвестными (над произвольным полем):
Тогда её можно переписать в матричной форме:
, где — основная матрица системы, и — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на — матрицу, обратную к матрице :
Так как , получаем . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
.
Для однородной системы линейных уравнений, то есть когда вектор , действительно обратное правило: система имеет нетривиальное (то есть ненулевое) решение только если . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
решение системы линейных алгебраических уравнений матричным методом определяется по формуле . Другими словами, решение СЛАУ находится с помощью обратной матрицы .
Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ
С помощью обратной матрицы найдите решение системы линейных уравнений .
Решение.В матричной форме исходная система запишется как , где . Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем , следовательно, для матрицы А может быть найдена обратная матрица . Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как . Итак, задача свелась к построению обратной матрицы . Найдем ее.
Мы знаем, что для матрицы обратная матрица может быть найдена как , где — алгебраические дополнения элементов .
В нашем случае
Тогда
Выполним проверку полученного решения , подставив его в матричную форму исходной системы уравнений . Это равенство должно обратиться в тождество, в противном случае где-то была допущена ошибка.
Следовательно, решение найдено верно.
Ответ:
или в другой записи .
infopedia.su