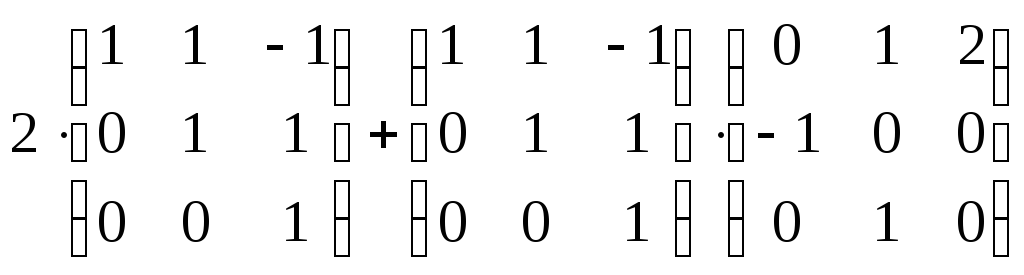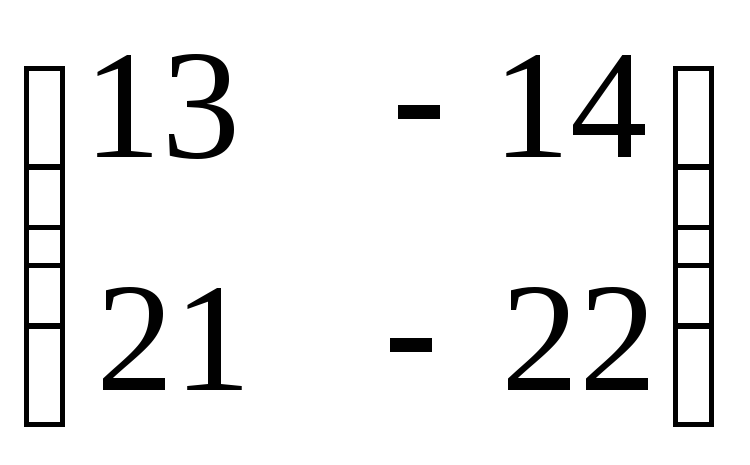Решение матричных уравнений: теория и примеры
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
ax=b,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
A ⋅ X = B
или
X ⋅ A = B,
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A
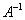 слева:
слева: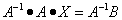 .
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную
матрицу равно единичной матрице: 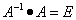 ,
поэтому
,
поэтому
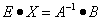 .
.
Так как E — единичная матрица, то E ⋅ X = X. В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A, слева, на матрицу B:
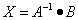 .
.
Как решить матричное уравнение во втором случае?
Если дано уравнениеX ⋅ A = B,
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A, и умножать матрицу B на неё справа:
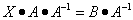 ,
,
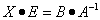 ,
,
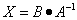 .
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как
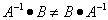 . Обратная к
A матрица умножается на матрицу B
с той стороны, с которой матрица A умножается на неизвестную
матрицу
. Обратная к
A матрица умножается на матрицу B
с той стороны, с которой матрица A умножается на неизвестную
матрицу
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
A ⋅ X ⋅ B = C,
является
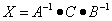 .
.
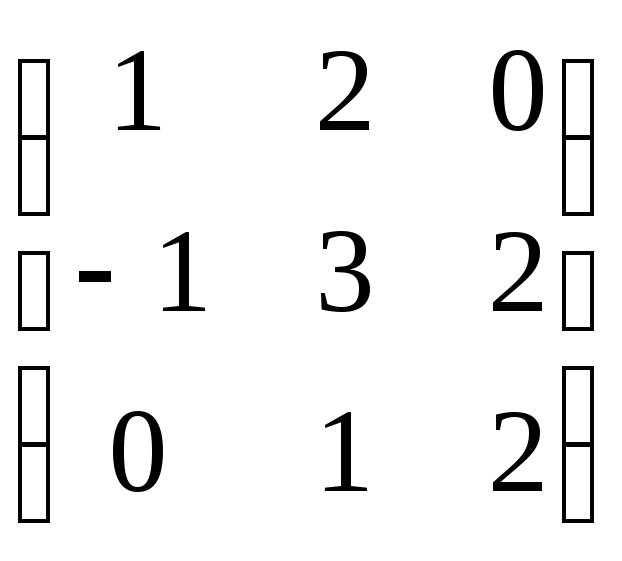
Пример 1. Решить матричное уравнение
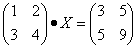
Решение. Данное уравнение имеет вид A ⋅ X = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится слева.
Поэтому решение следует искать в виде 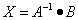 ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A слева. Найдём матрицу, обратную матрице
A.
,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A слева. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
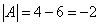 .
.
Найдём алгебраические дополнения матрицы A:
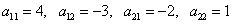 .
.
Составим матрицу алгебраических дополнений:
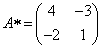
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
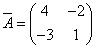 .
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:
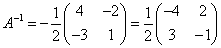 .
.
Наконец, находим неизвестную матрицу:
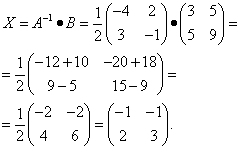
Решить матричное уравнение самостоятельно, а затем посмотреть решение
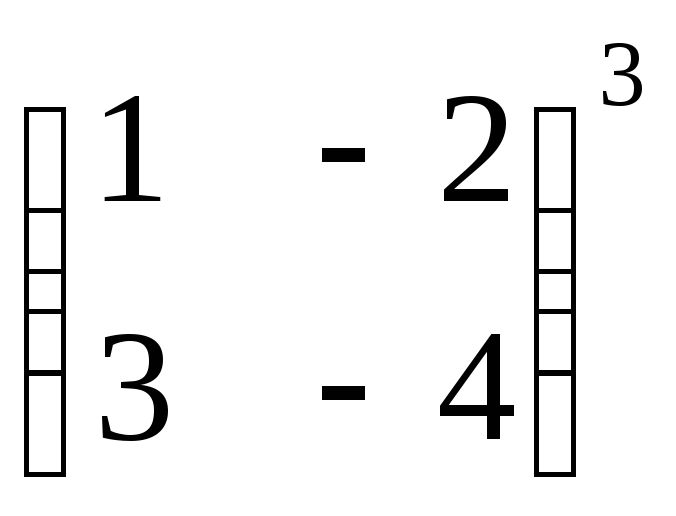
Пример 3. Решить матричное уравнение
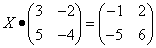 .
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы
X матрица A находится справа. Поэтому решение следует искать в виде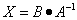 ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A справа. Найдём матрицу, обратную матрице
A.
,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A справа. Найдём матрицу, обратную матрице
A.Сначала найдём определитель матрицы A:
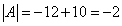 .
.
Найдём алгебраические дополнения матрицы A:
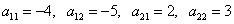 .
.
Составим матрицу алгебраических дополнений:
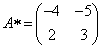 .
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
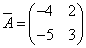
Находим матрицу, обратную матрице A:
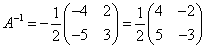 .
.
Находим неизвестную матрицу:
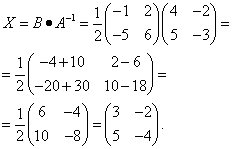
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
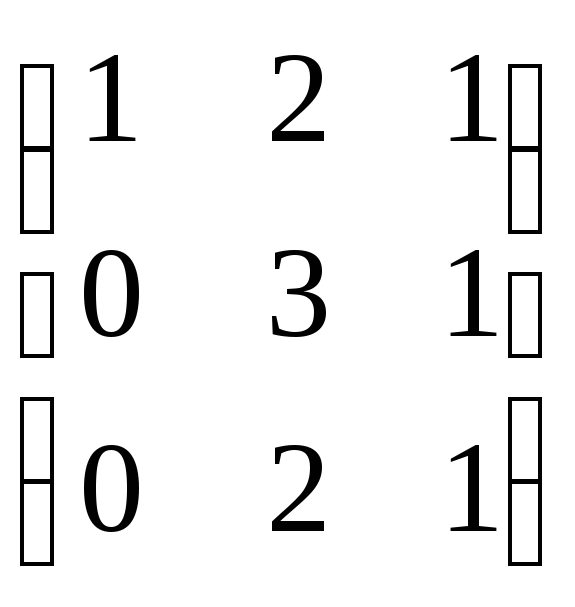
Пример 4. Решить матричное уравнение
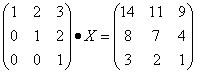 .
.
Решение. Это уравнение первого вида: A ⋅ X = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится слева.
Поэтому решение следует искать в виде 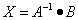 ,
то есть неизвестная матрица равна произведению матрицы
,
то есть неизвестная матрица равна произведению матрицы
Сначала найдём определитель матрицы A:
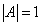 .
.
Найдём алгебраические дополнения матрицы A:
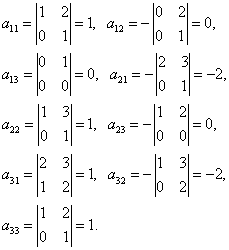
Составим матрицу алгебраических дополнений:
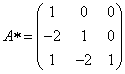
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
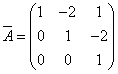 .
.
Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:
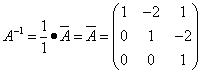 .
.Находим неизвестную матрицу:
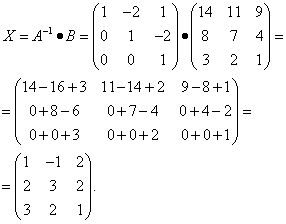
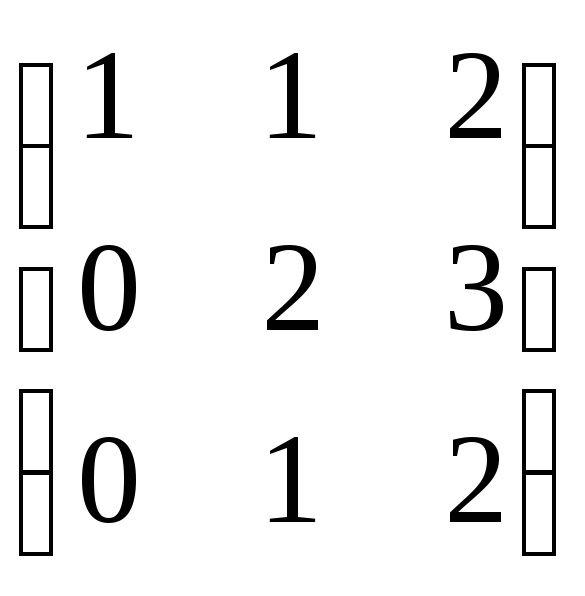
Пример 5. Решить матричное уравнение
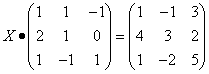 .
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится справа.
Поэтому решение следует искать в виде 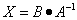 ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A справа. Найдём матрицу, обратную матрице
A.
,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A справа. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
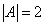
Найдём алгебраические дополнения матрицы A:
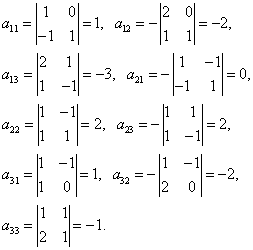
Составим матрицу алгебраических дополнений:
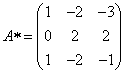 .
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
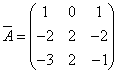 .
.
Находим матрицу, обратную матрице A:
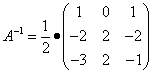 .
.
Находим неизвестную матрицу:
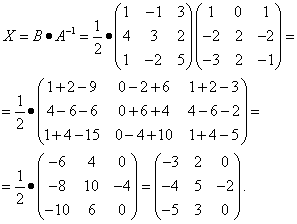
Пример 6. Решить матричное уравнение
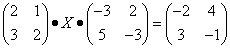
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то
есть неизвестная матрица X находится в середине
произведения трёх матриц. Поэтому решение следует искать в виде
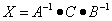 . Найдём матрицу, обратную матрице
A.
. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
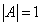 .
.
Найдём алгебраические дополнения матрицы A:
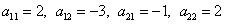 .
.
Составим матрицу алгебраических дополнений:
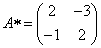 .
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
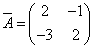 .
.
Находим матрицу, обратную матрице A:
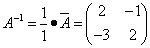 .
.
Найдём матрицу, обратную матрице B.
Сначала найдём определитель матрицы B:
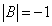 .
.
Найдём алгебраические дополнения матрицы B:
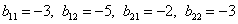
Составим матрицу алгебраических дополнений матрицы B:
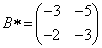 .
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B:
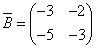 .
.
Находим матрицу, обратную матрице B:
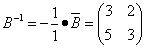 .
.
Находим неизвестную матрицу:
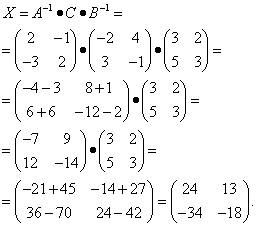

Поделиться с друзьями
Начало темы «Матрицы»
Продолжение темы «Матрицы»
Другие темы линейной алгебры
function-x.ru
Решение матричных уравнений
Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Московский государственный технический университет имени Н.Э. Баумана»
(КФ МГТУ им. Н.Э. Баумана)
Влайков Н.Д.
Решение матричных уравнений
Методические указания для проведения упражнений
по курсу аналитической геометрии
Калуга 2011г.
Содержание.
Цели занятия стр.4
План занятия стр.4
Необходимые теоретические сведения стр.5
Практическая часть стр.6
Контроль освоения пройденного материала стр.10
Домашнее задание стр.11
Количество часов: 2
Цели занятия:
Систематизировать полученные теоретические знания о видах матричных уравнений и способах их решения.
Применить на практике методы решения матричных уравнений.
План занятия:
Кратко изложить теоретический материал.
Решить матричное уравнение вида
 методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы.Решить матричное уравнение вида
 методом,
основанным на элементарных преобразованиях
строк матрицы.
методом,
основанным на элементарных преобразованиях
строк матрицы.Сравнить использованные методы.
Решить матричное уравнение вида
 методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы.Решить матричное уравнение вида
 методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы.Проверить выполнение текущего домашнего задания.
Провести проверочную работу.
Представить тему следующего семинарского занятия.
Выдать текущее домашнее задание.
Необходимые теоретические сведения.
Рассмотрим
два вида матричных уравнений относительно
неизвестной матрицы 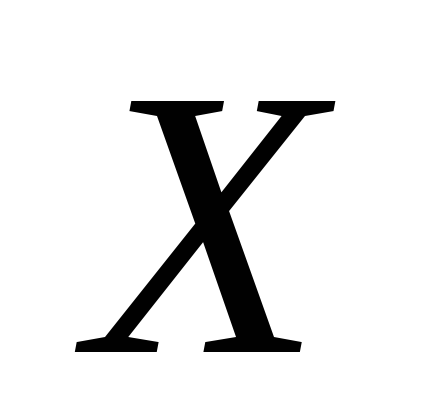 :
: 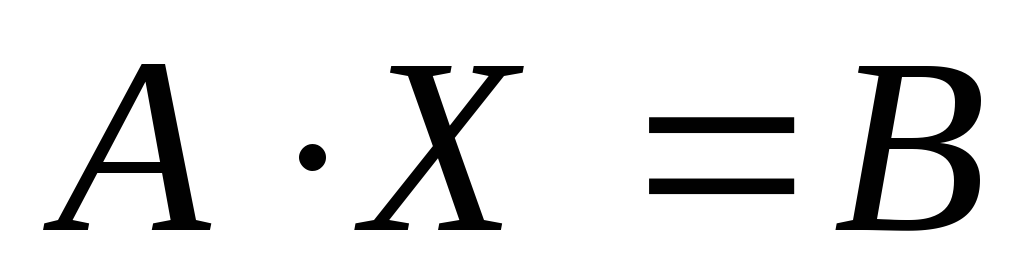 и
и  ,
где матрицы
,
где матрицы  и
и 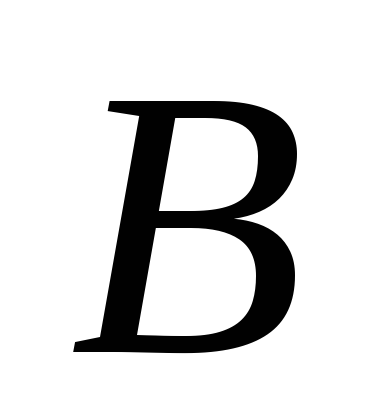 — известны, причем
— известны, причем  — квадратная и невырожденная.
— квадратная и невырожденная.
Опр. Некоторую матрицу называют решением
матричного уравнения относительно
неизвестной матрицы 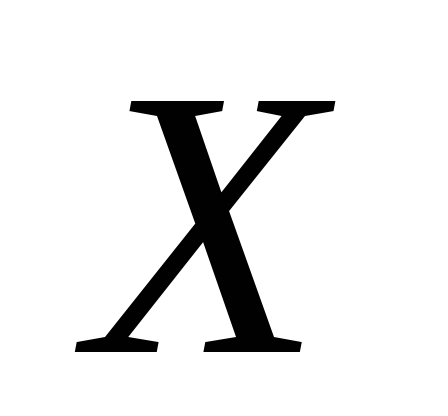 ,
если при ее подстановке вместо
,
если при ее подстановке вместо 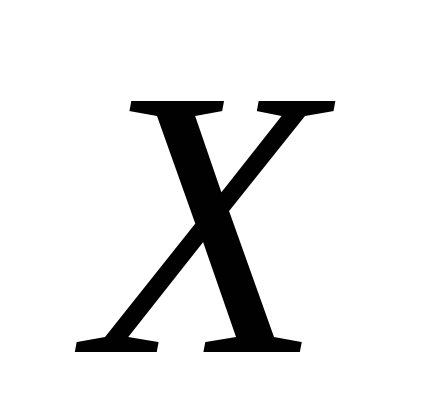 матричное уравнение превращается в
тождество.
матричное уравнение превращается в
тождество.
Рассмотрим
уравнение 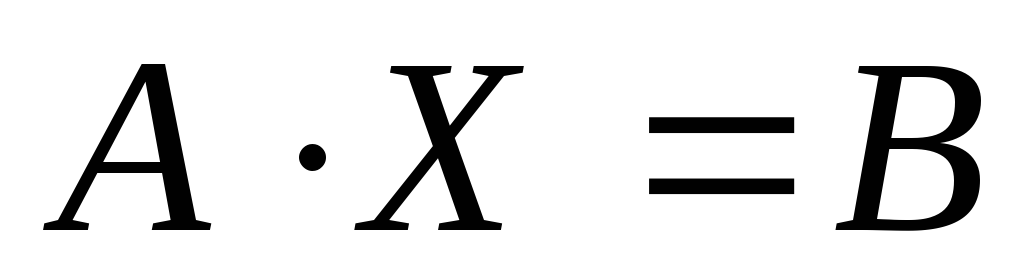 .
.
Первый
метод предполагает
вычисление обратной матрицы 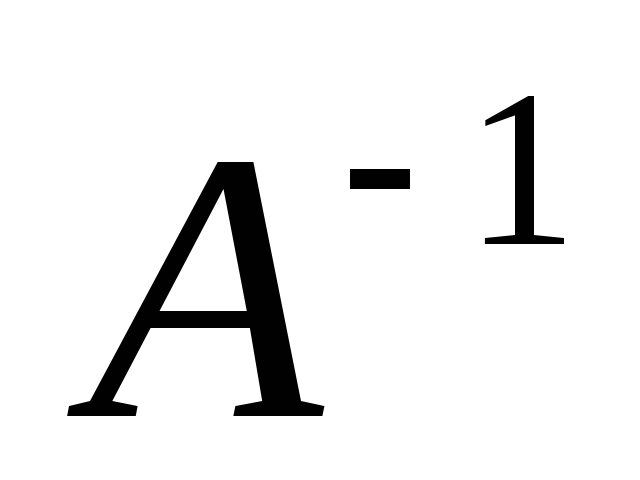 и дает запись решения матричного
уравнения в виде
и дает запись решения матричного
уравнения в виде 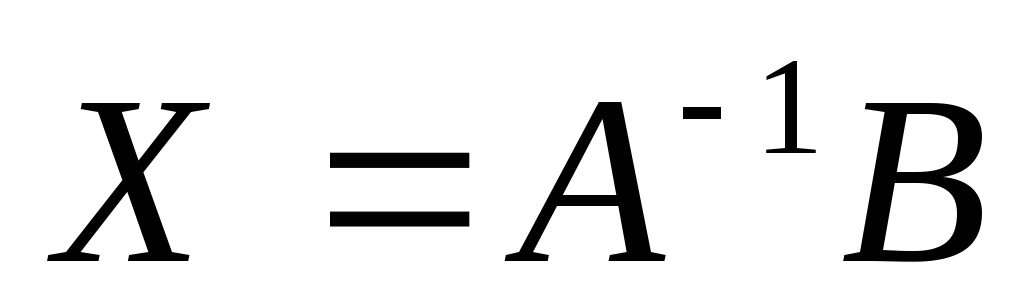 .
Причем данное решение единственно.
.
Причем данное решение единственно.
Второй
метод основан на элементарных преобразованиях
строк блочной матрицы 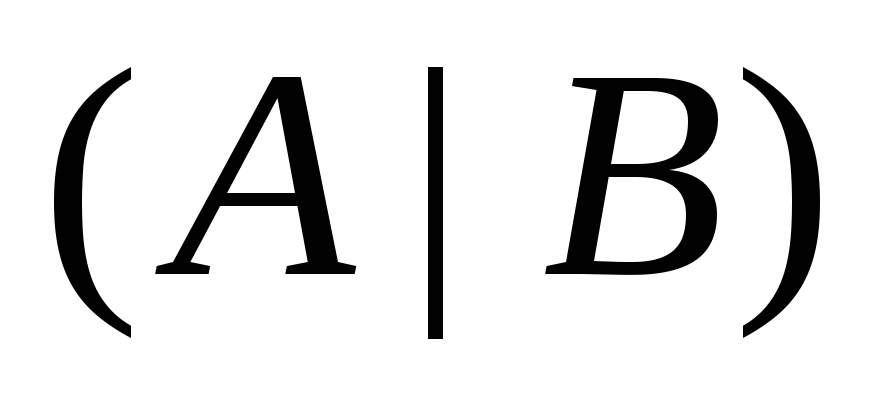 и имеет своей целью преобразование ее
к виду
и имеет своей целью преобразование ее
к виду 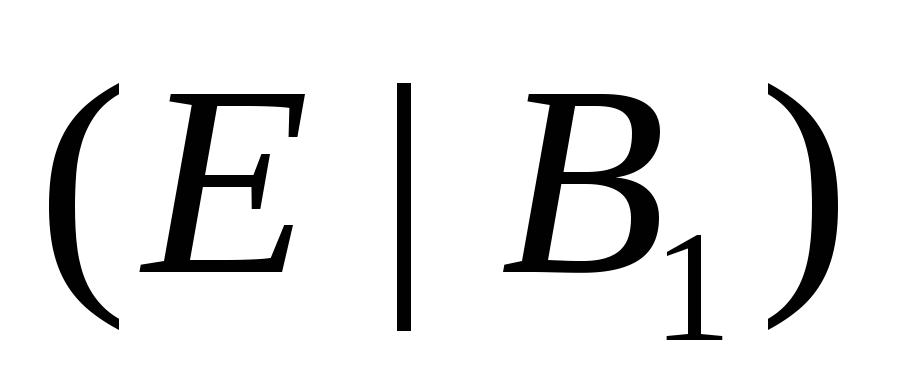 ,
в котором вместо матрицы
,
в котором вместо матрицы  стоит единичная матрица
стоит единичная матрица  .
Тогда матрица
.
Тогда матрица  и будет решением уравнения.
и будет решением уравнения.
Проверка ответа выполняется подстановкой найденного решения в исходное уравнение.
Матричное
уравнение  так же можно решить двумя способами.
Если известна матрица
так же можно решить двумя способами.
Если известна матрица 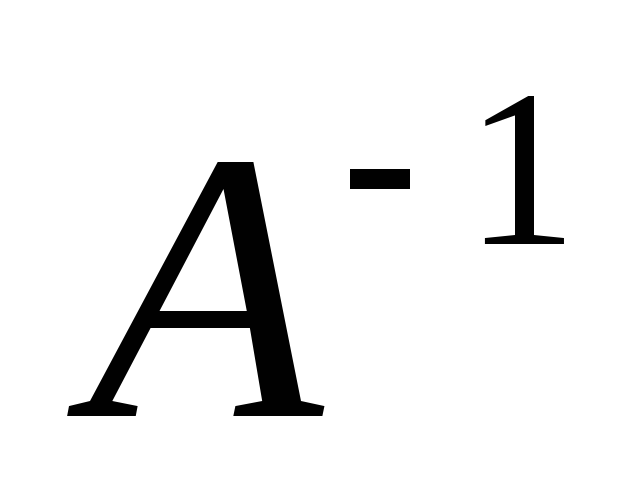 ,
то умножаем справа на
,
то умножаем справа на 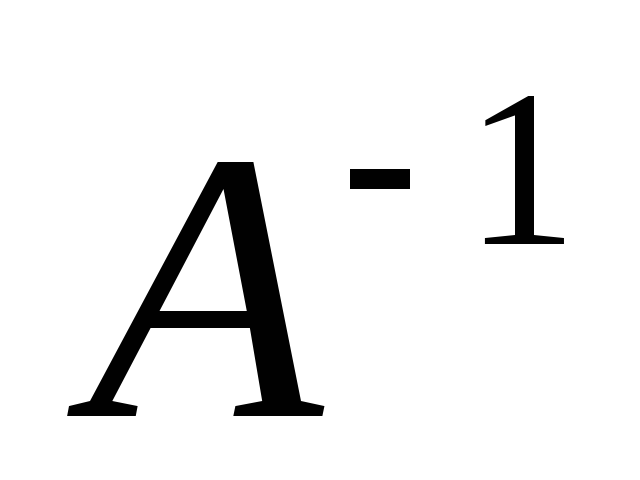 матричное уравнение
матричное уравнение  и после очевидных преобразований
получаем ответ в виде произведения двух
матриц
и после очевидных преобразований
получаем ответ в виде произведения двух
матриц 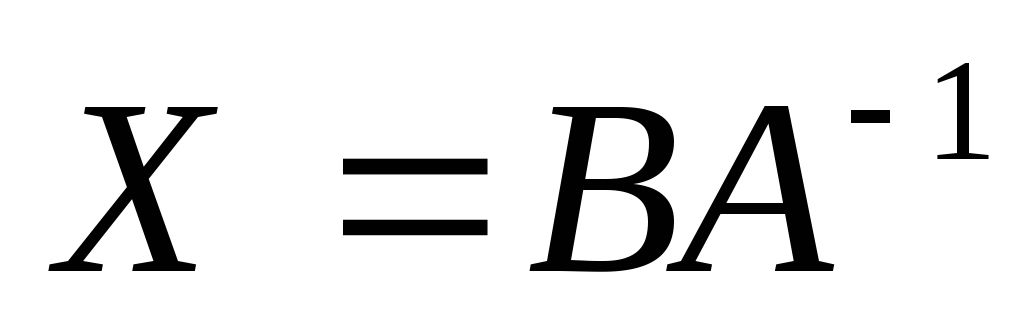 .
Другой метод решения матричного уравнения
.
Другой метод решения матричного уравнения  состоит
в транспонировании его левой и правой
частей
состоит
в транспонировании его левой и правой
частей 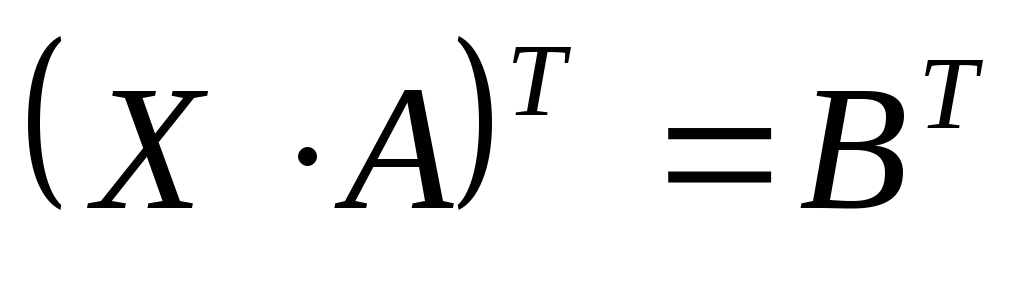 ,
, 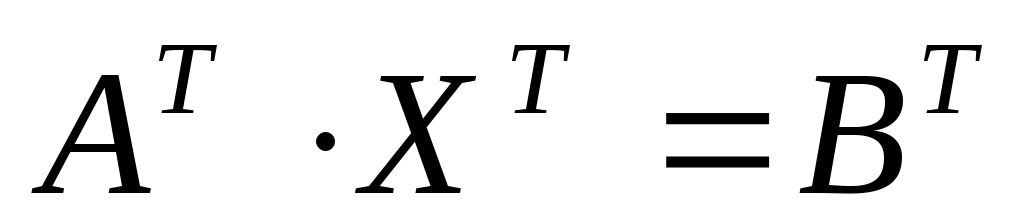 .
После введения новой неизвестной матрицы
.
После введения новой неизвестной матрицы 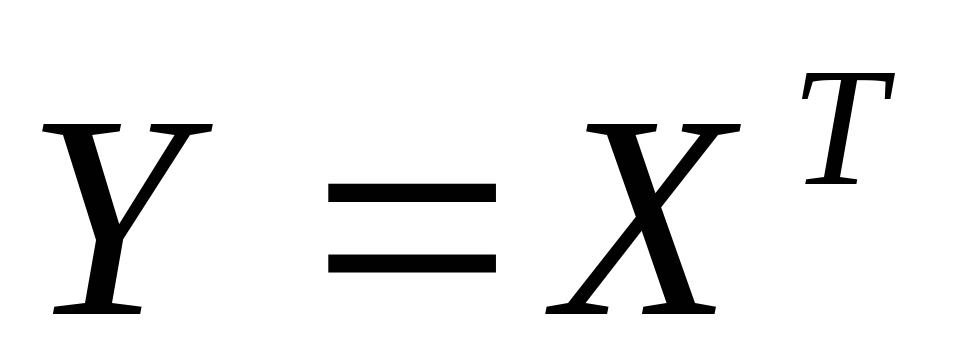 получаем уравнение вида
получаем уравнение вида 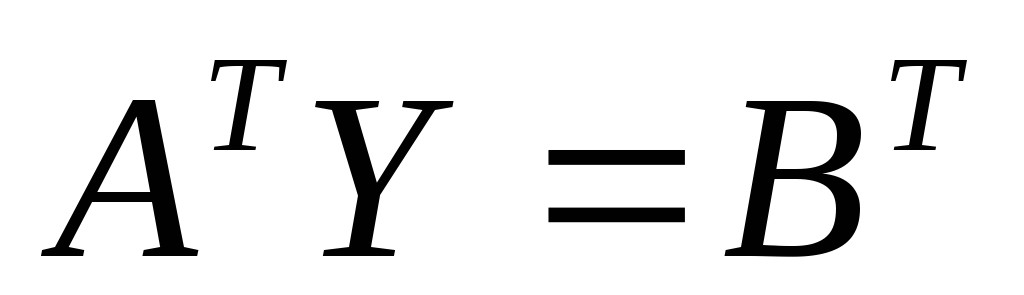 ,
которое решается методом элементарных
преобразований.
,
которое решается методом элементарных
преобразований.
Практическая часть.
Пример
1. Решить
матричное уравнение: 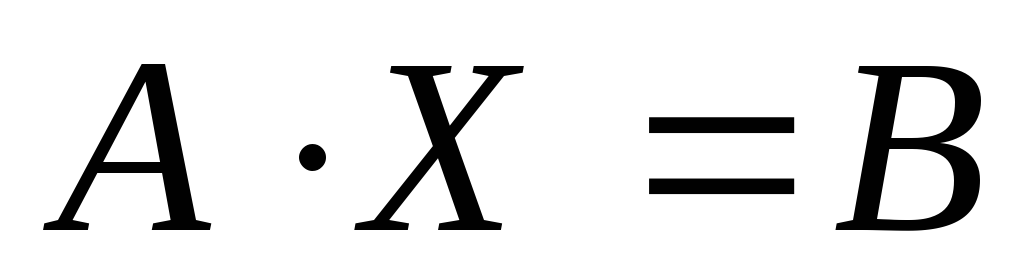 ,
,
где
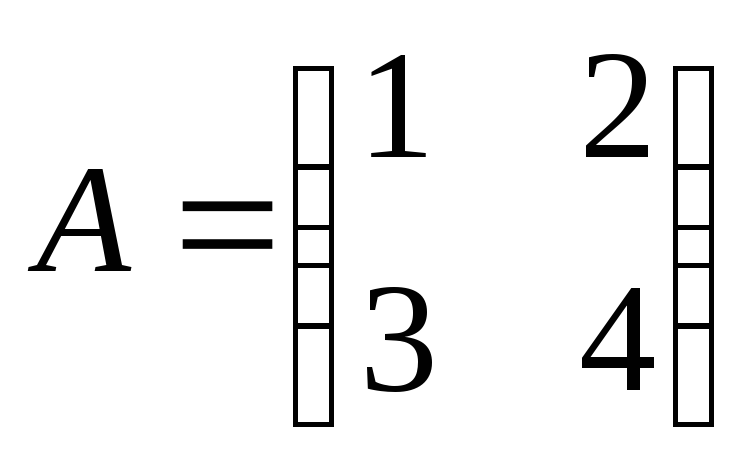 ;
; 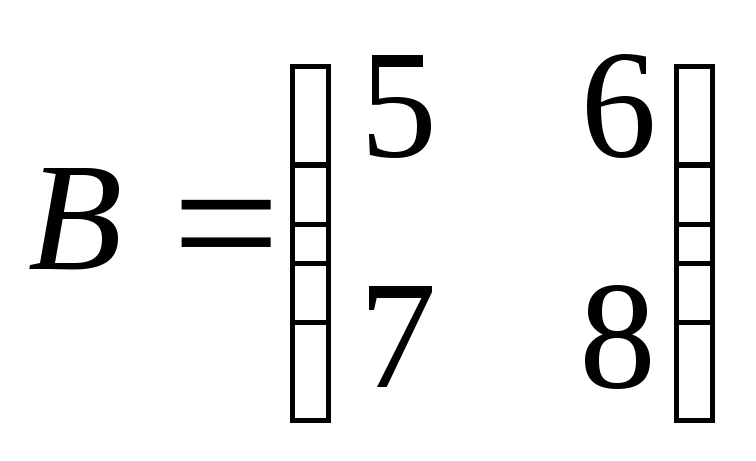 .
.
Решение.
1-ый способ. Найдем решение, используя обратную матрицу:
Решение
ищем в виде 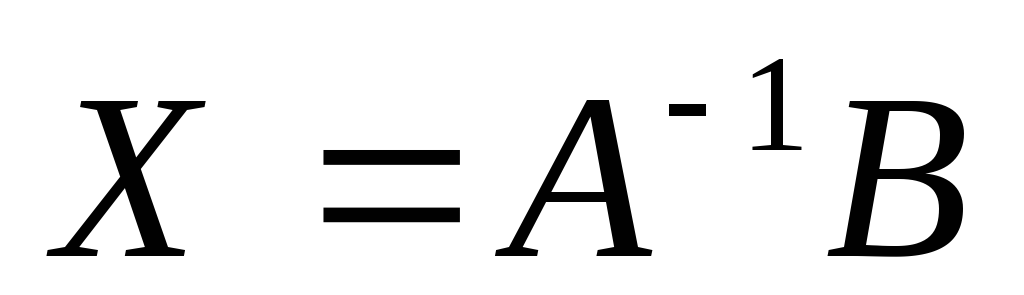 ;
;
Найдем
матрицу 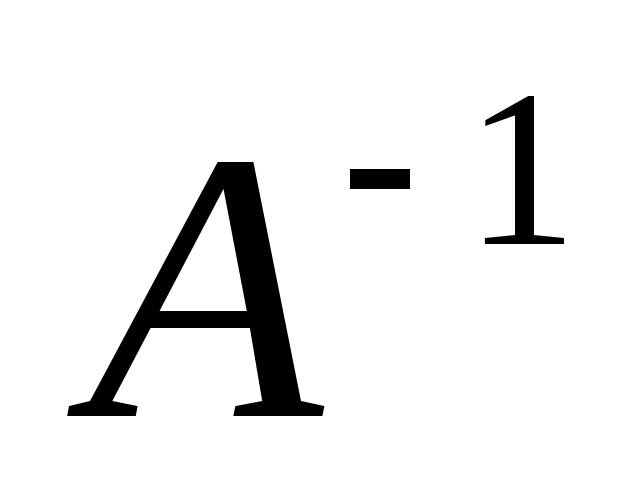 (например, при помощи присоединенной
матрицы)
(например, при помощи присоединенной
матрицы)
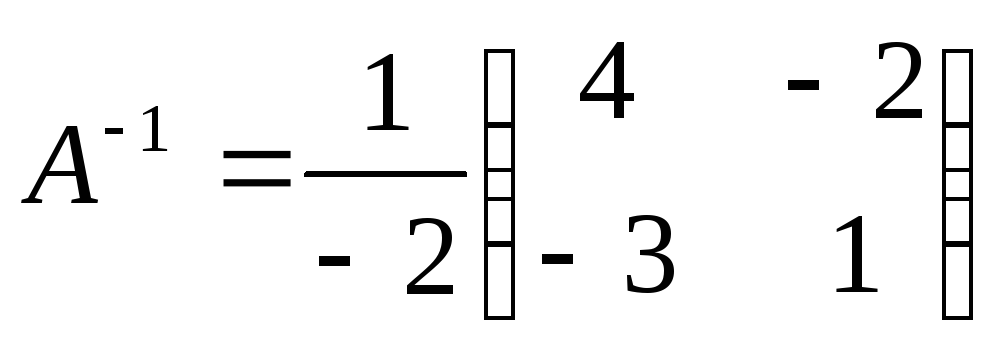 .
.
Таким образом, получим:
 .
.
2-ой способ. Найдем решение методом элементарных преобразований:
Запишем
матрицу 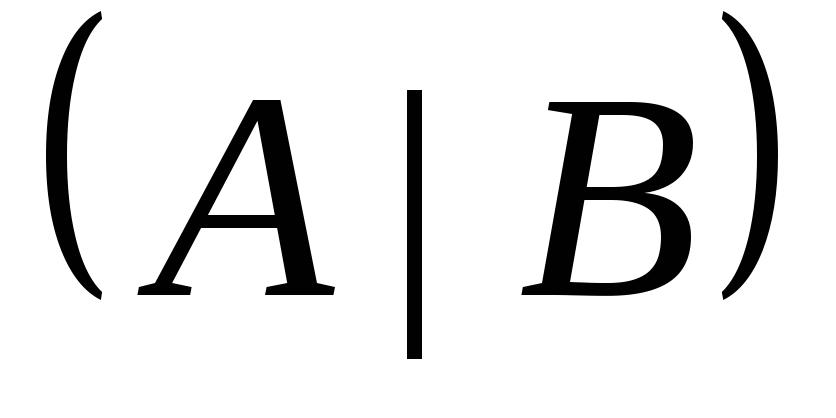 и выполним элементарные преобразования
ее строк с целью привести ее к виду
и выполним элементарные преобразования
ее строк с целью привести ее к виду 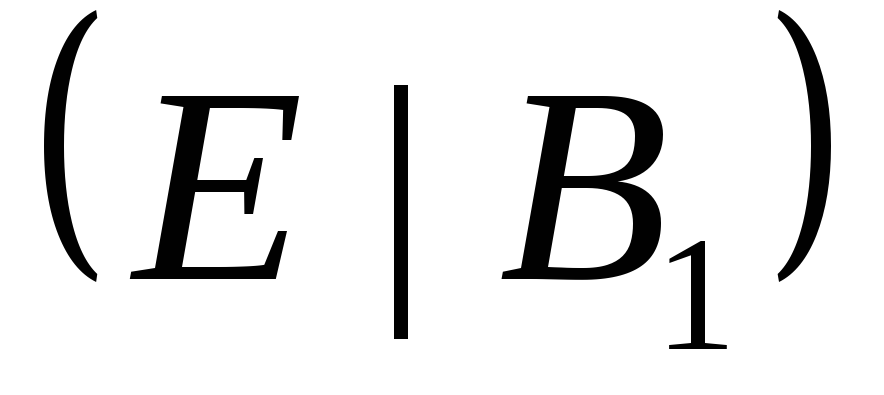 .
.
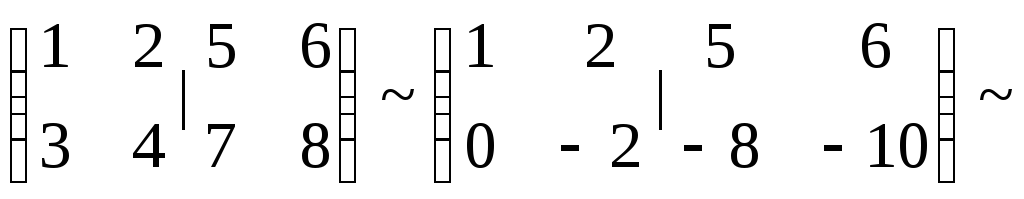
 .
.
Следовательно, 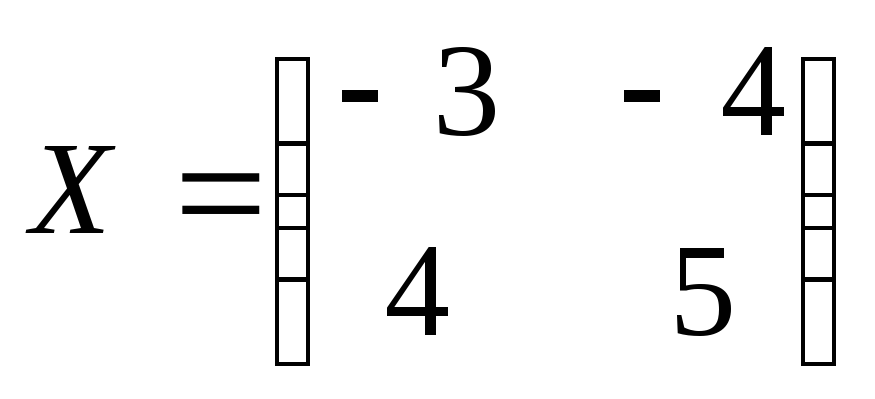 .
.
Проверка осуществляется подстановкой в исходное уравнение:
 —
Верно.
—
Верно.
Пример
2. Решить
матричное уравнение: 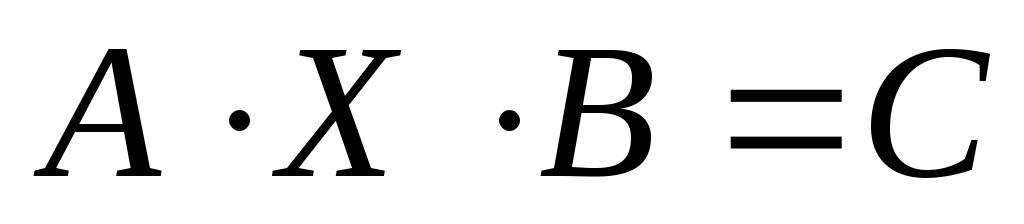 ,
,
где
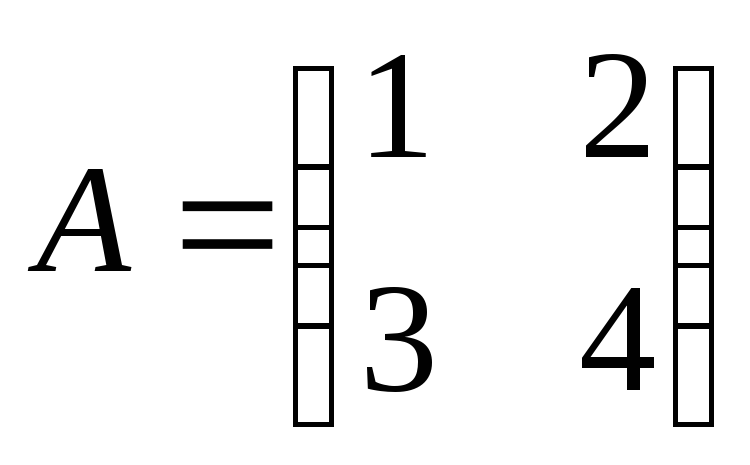 ;
; 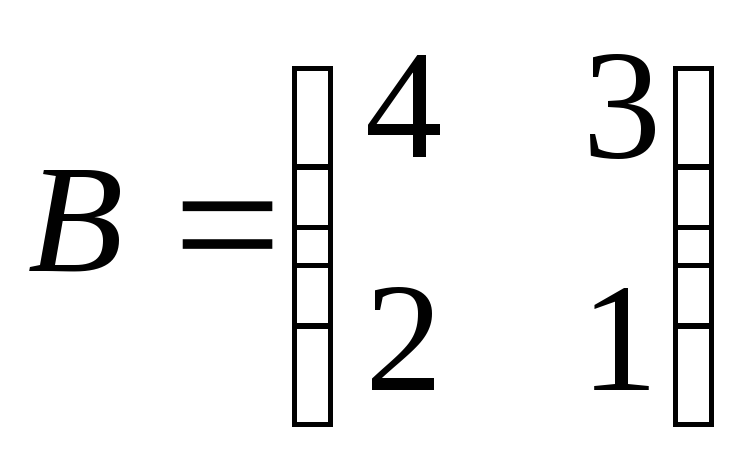 ;
; 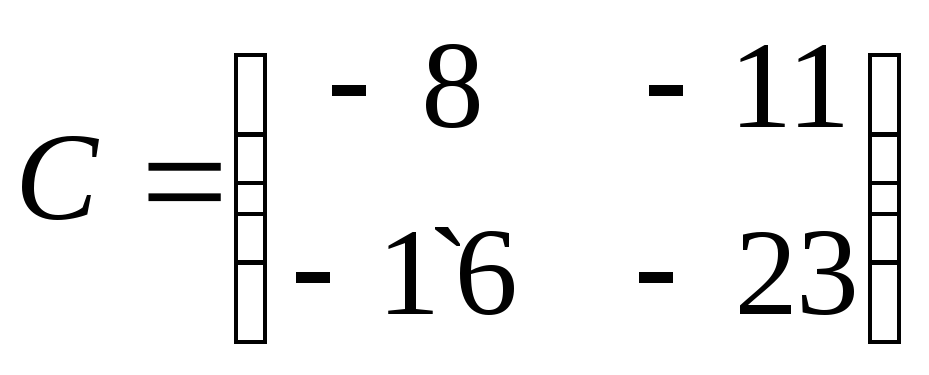 .
.
Решение.
Если
для матриц  и
и 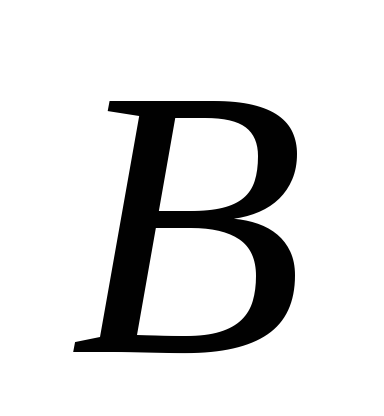 существуют обратные матрицы
существуют обратные матрицы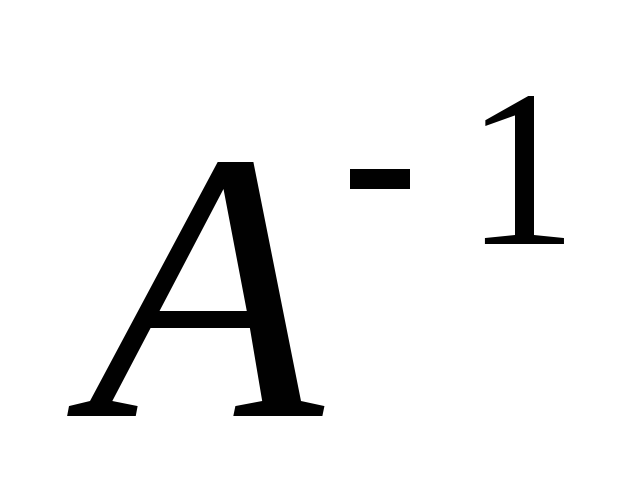 и
и 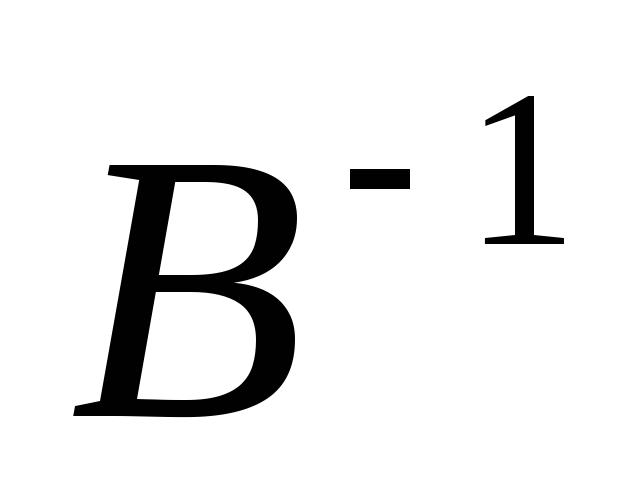 соответственно, умножим обе части
уравнения слева на
соответственно, умножим обе части
уравнения слева на 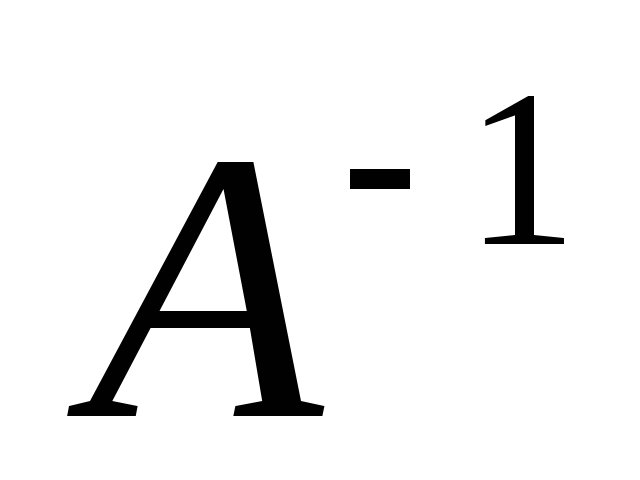 ,
справа на
,
справа на 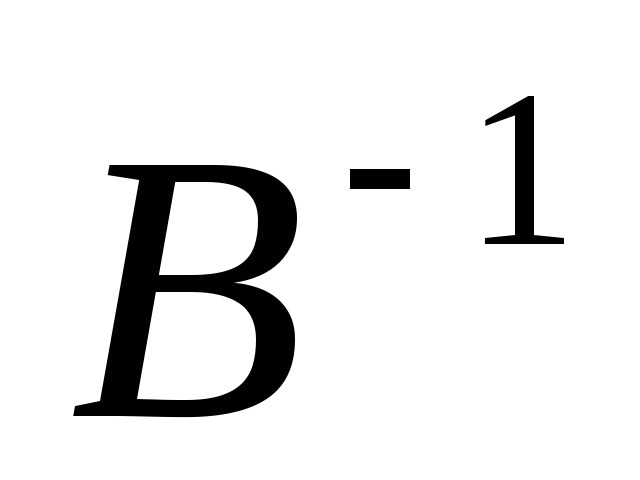 .
В результате получим:
.
В результате получим:
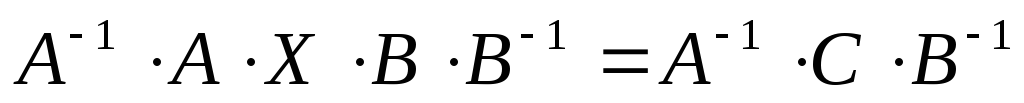 .
Учитывая, что
.
Учитывая, что  ,
, 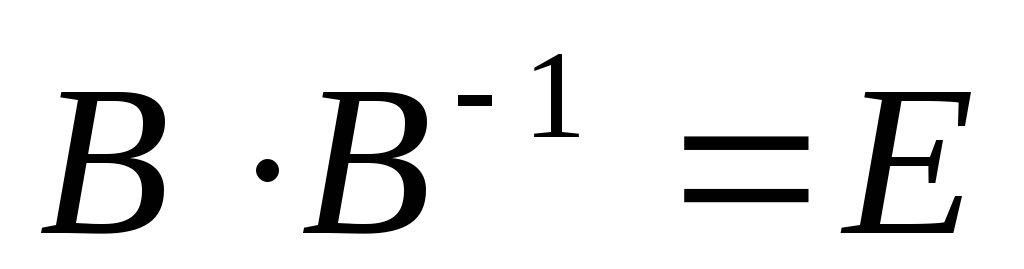
( —
единичная матрица) можно записать:
—
единичная матрица) можно записать: 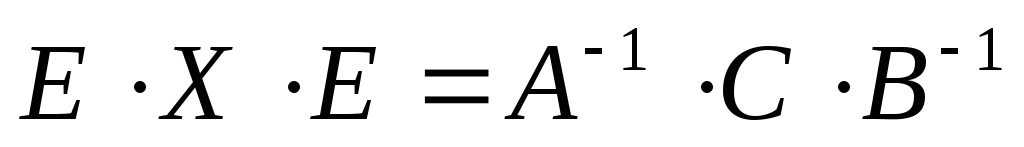 .
Так как
.
Так как
 —
единичная матрица, окончательно имеем
уравнение:
—
единичная матрица, окончательно имеем
уравнение:
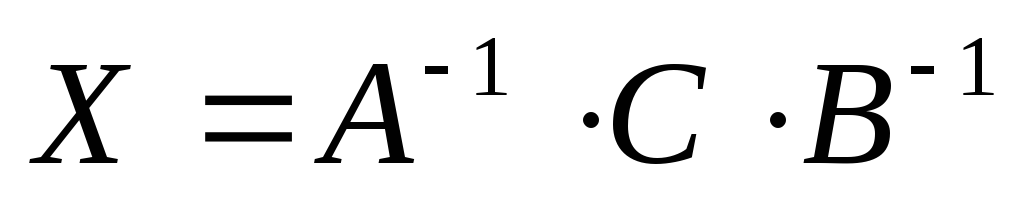
где
матрица 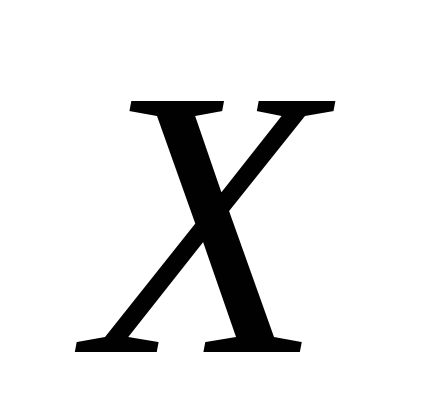 — решение уравнения.
— решение уравнения.
Если
же хотя бы одна из матриц  или
или 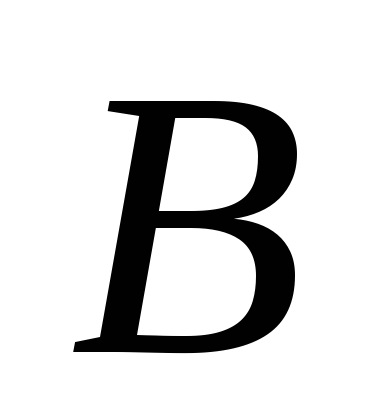 не имеет обратную, уравнение не имеет
решения.
не имеет обратную, уравнение не имеет
решения.
Для
матрицы  найдем
найдем 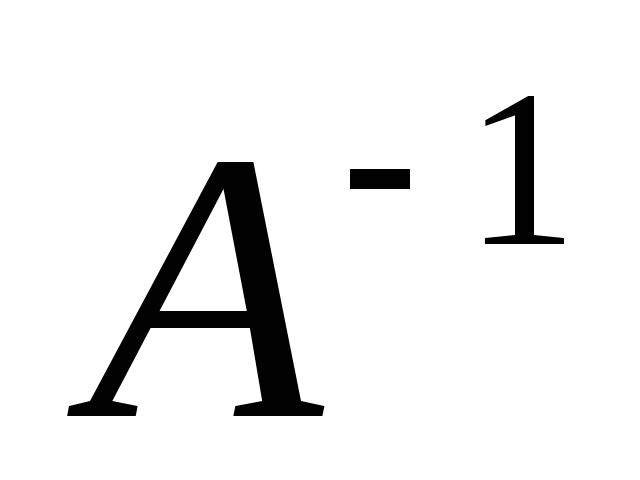 или
докажем, что она не существует.
или
докажем, что она не существует.
а) 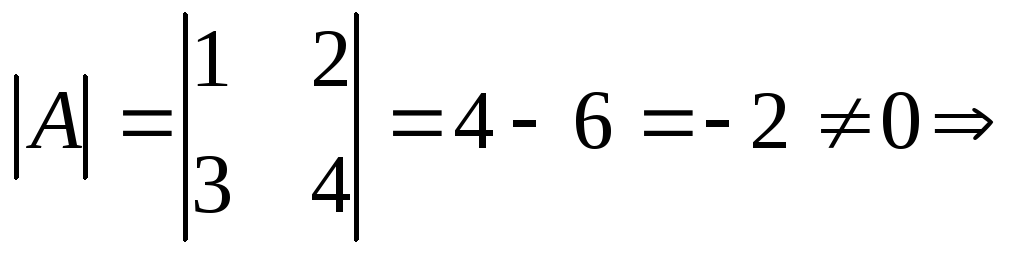 обратная
матрица существует.
обратная
матрица существует.
б) 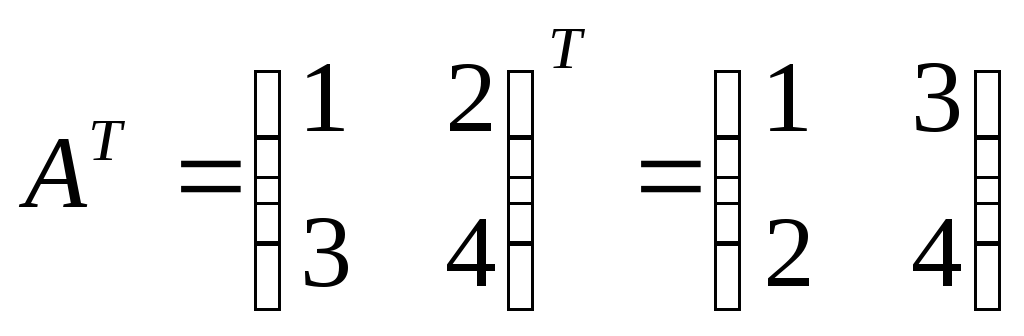 .
.
в) Найдем алгебраические дополнения для
матрицы  и
составим из них присоединенную матрицу
и
составим из них присоединенную матрицу  :
:
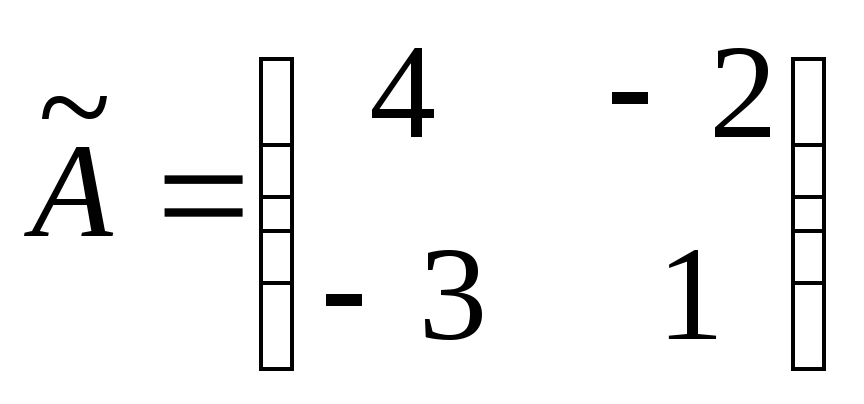 .
.
г) Известно, что 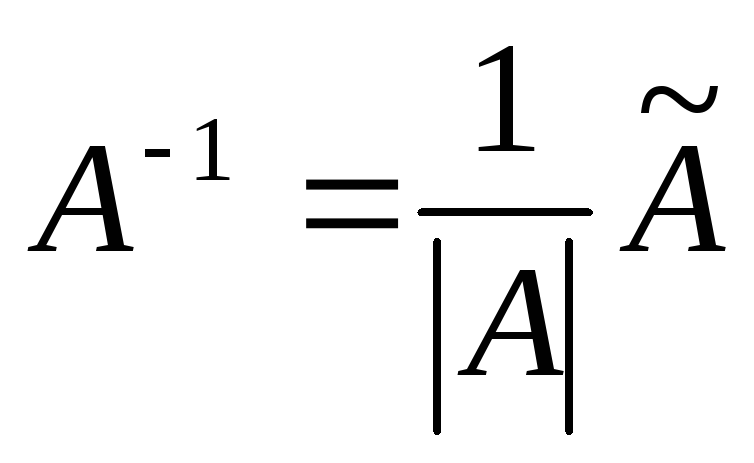 ;
тогда
;
тогда
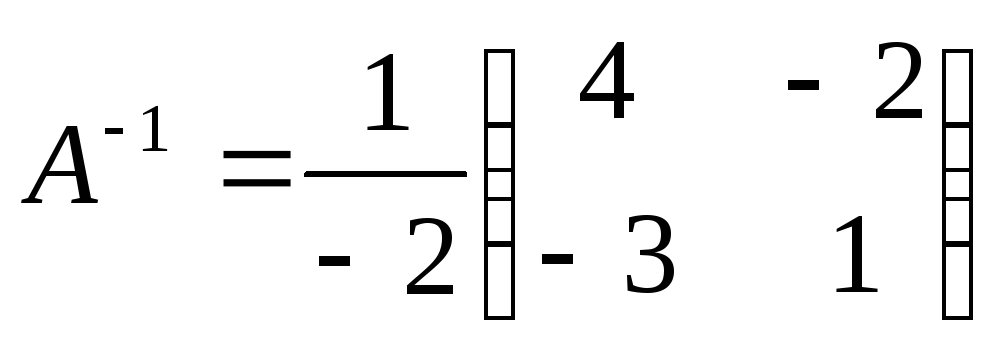 .
.
Для
матрицы 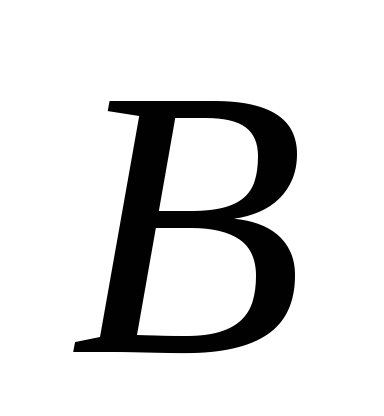 найдем
найдем 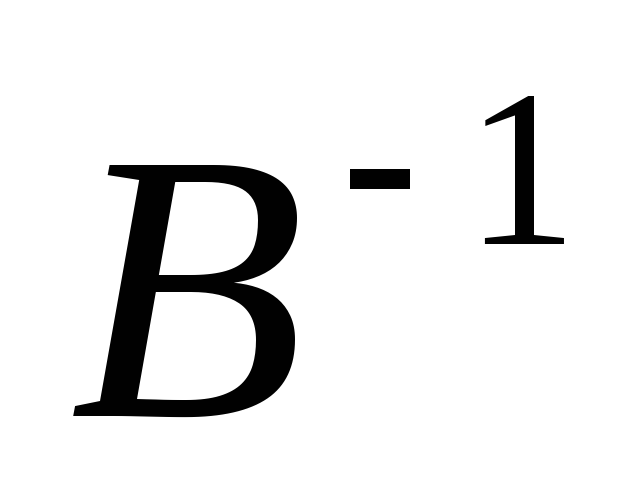 или докажем, что она не существует.
или докажем, что она не существует.
а) 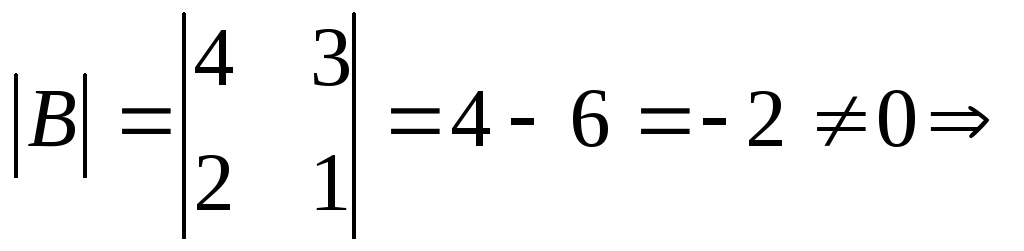 обратная
матрица существует.
обратная
матрица существует.
б) 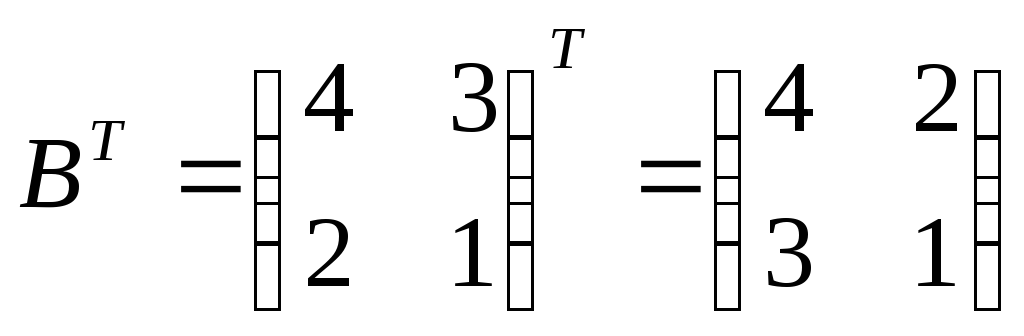 .
.
в) Найдем алгебраические дополнения для
матрицы 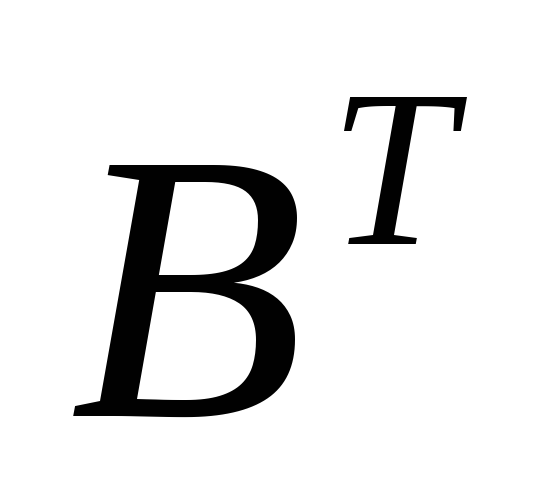 и
составим из них присоединенную матрицу
и
составим из них присоединенную матрицу 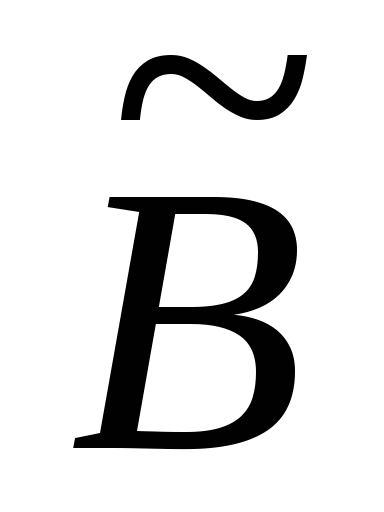 :
:
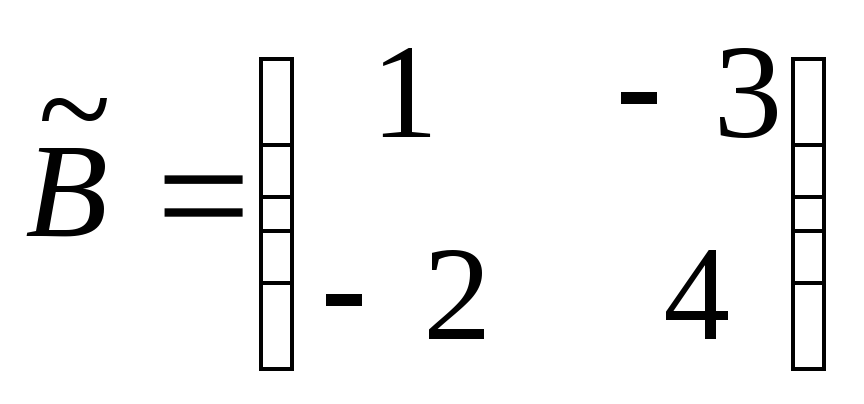 .
.
г) По формуле 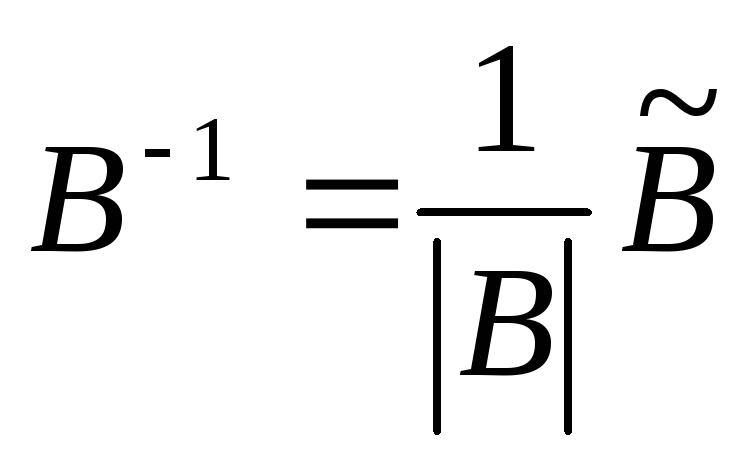 ;
;
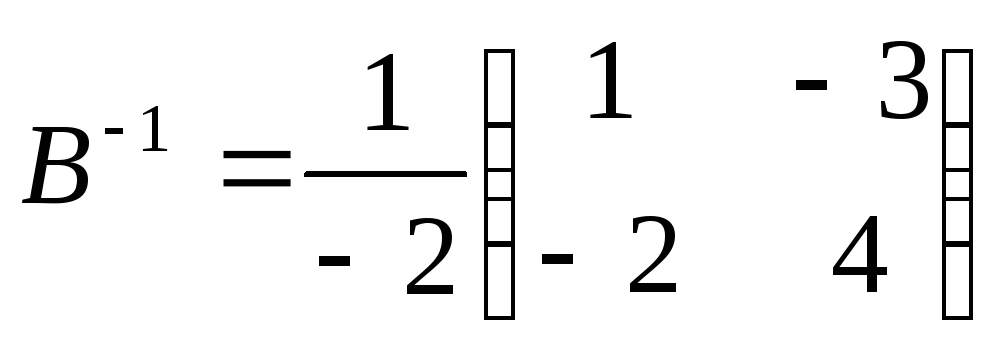 .
.
Найдем
неизвестную матрицу  .
.
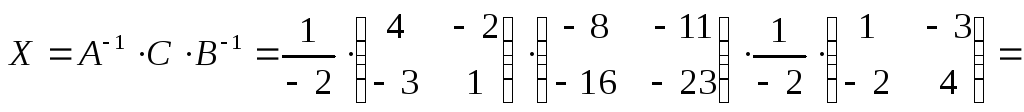
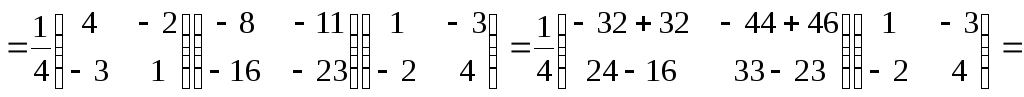
 .
.
Ответ: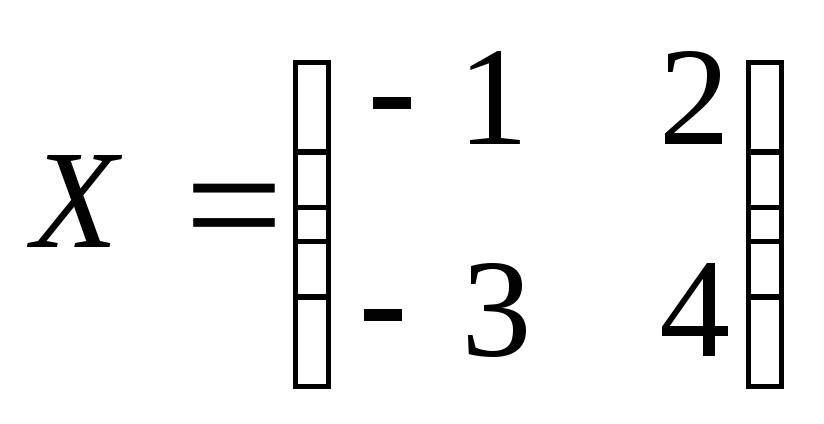 .
.
Решить матричные уравнения:
№2.121(2.39)
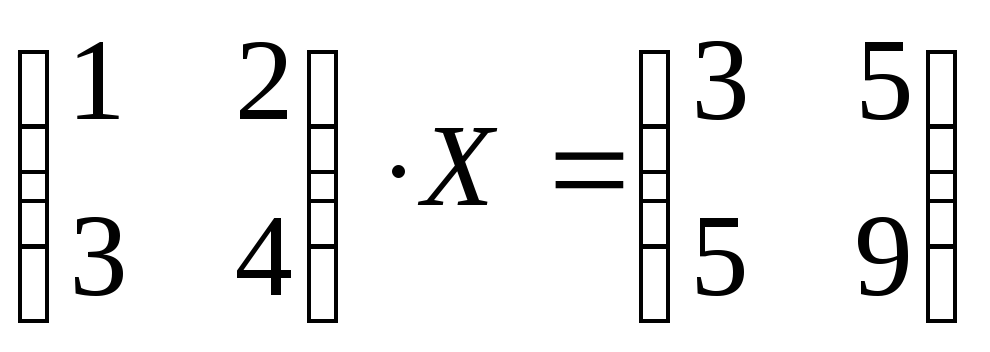 .
Отв.:
.
Отв.: 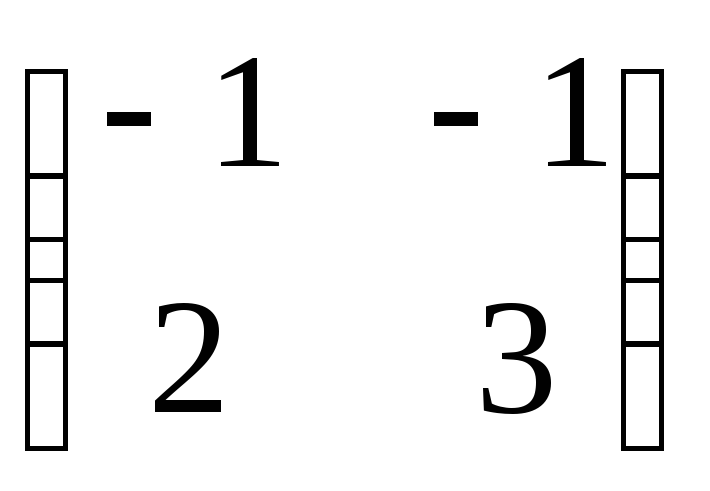
№2.122(2.40)
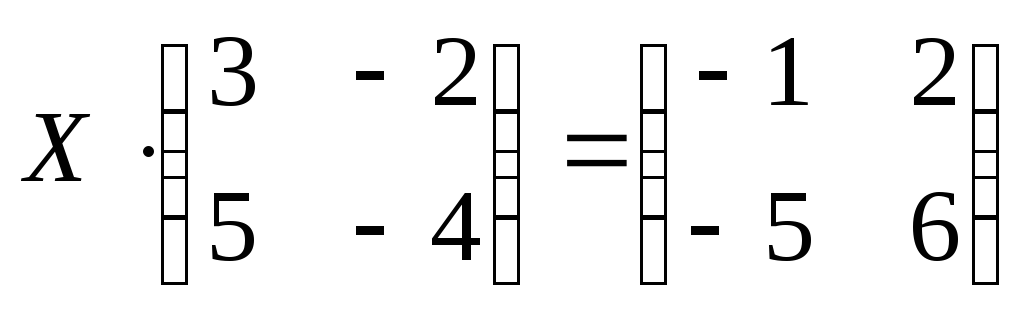 .
Отв.:
.
Отв.: 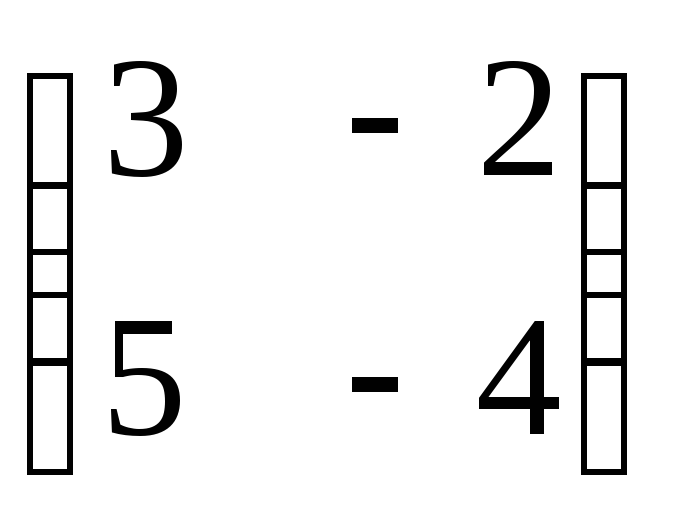
№2.123(2.41)
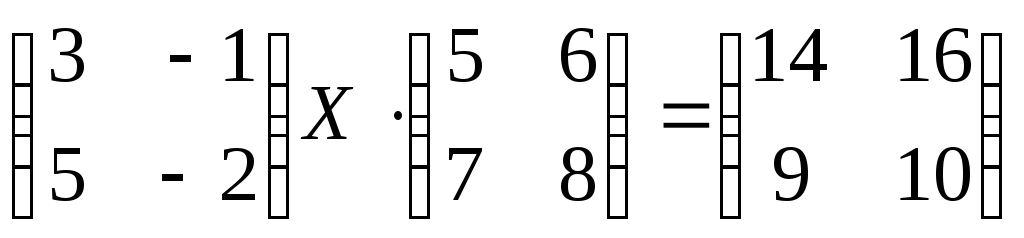 .
Отв.:
.
Отв.: 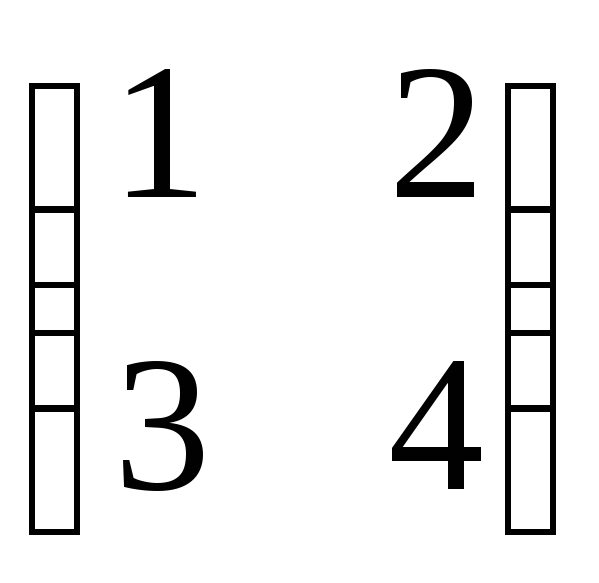
№2.124(2.42)
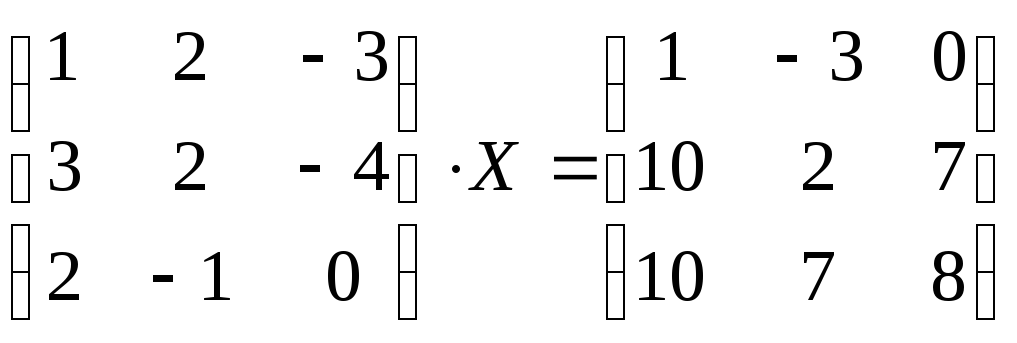 .
Отв.:
.
Отв.: 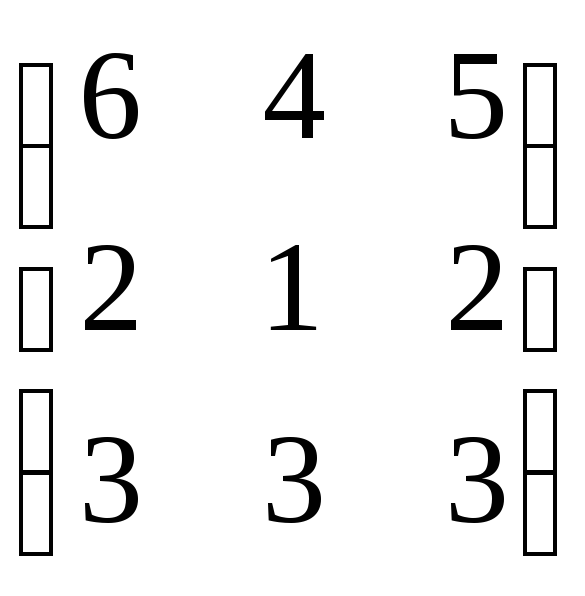
№2.125(2.43)
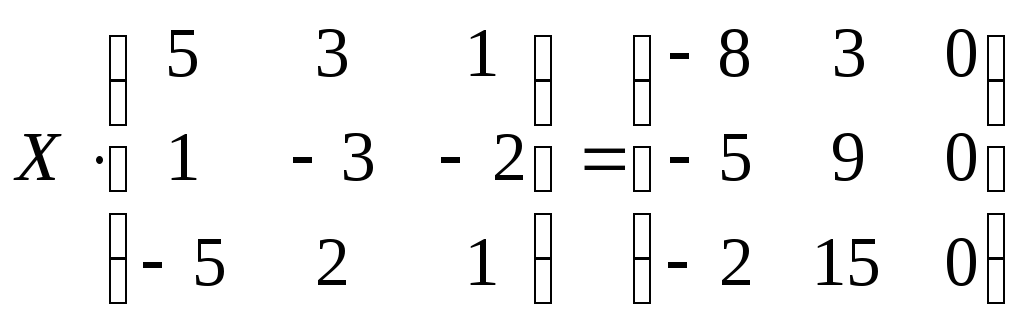 .
Отв.:
.
Отв.: 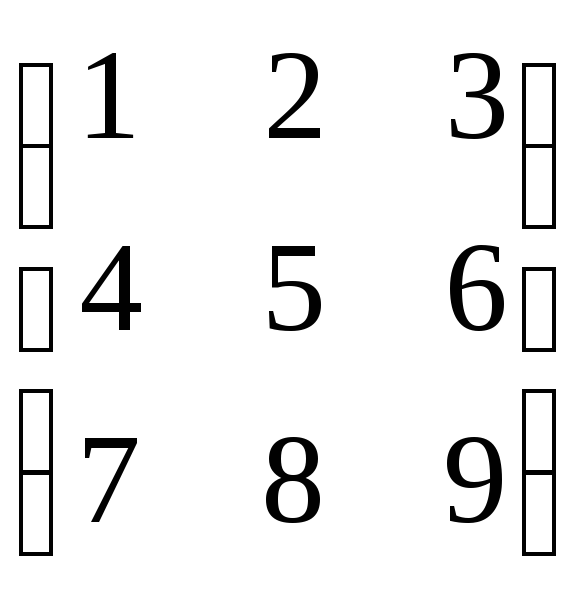
Представление темы следующего семинара.
Решение систем линейных однородных уравнений.
Контроль освоения пройденного материала.
Проверочная работа 5 минут. Участвует 4 студента с четными номерами по журналу, начиная с №10
Задание:
Вар№1 Выполнить действия:
| Вар№2 Выполнить действия:
|
Вар№3 Найти матрицу обратную данной: | Вар№4 Найти матрицу обратную данной:
|
Ответы:
Вар№1 Выполнить действия: | Вар№2 Выполнить действия:
|
Вар№3 Найти матрицу обратную данной: | Вар№4 Найти матрицу обратную данной:
|
Домашнее задание.
1.Решить
матричное уравнение 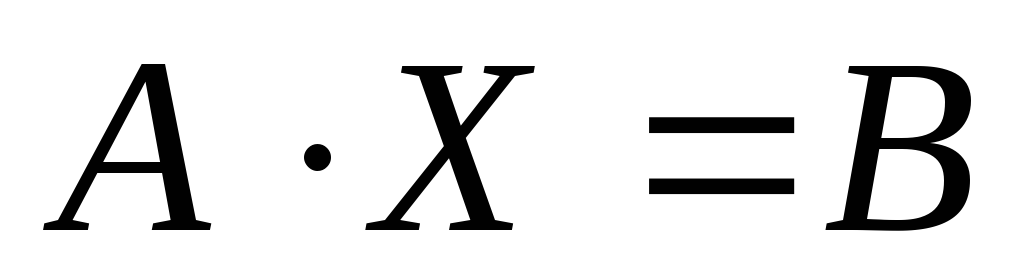 :
:
1) 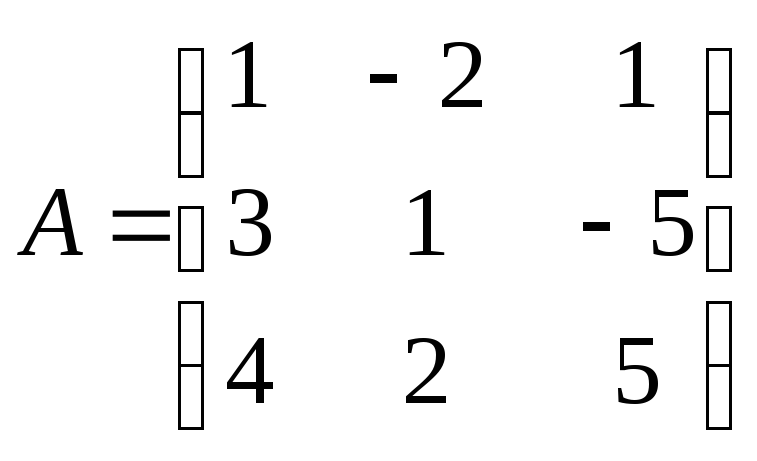 ;
;  .
.
2) 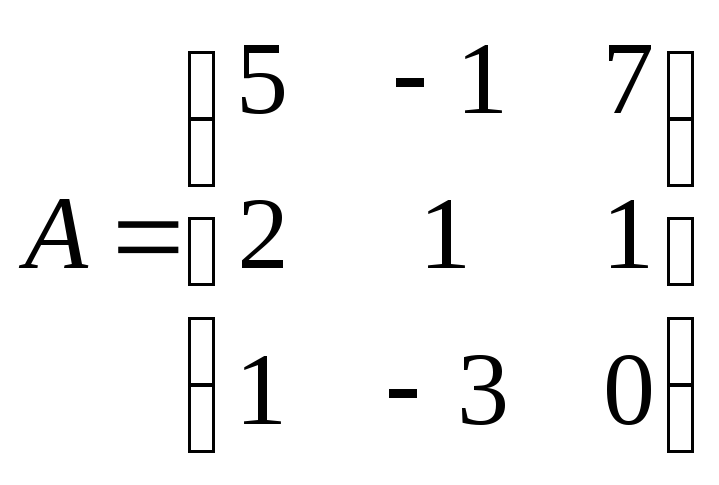 ;
;  .
.
2.Решить
матричное уравнение 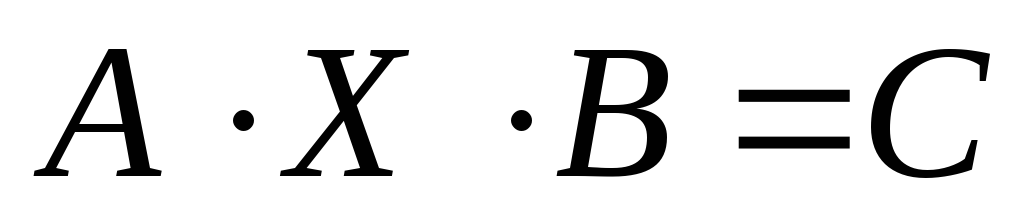 :
:
1) 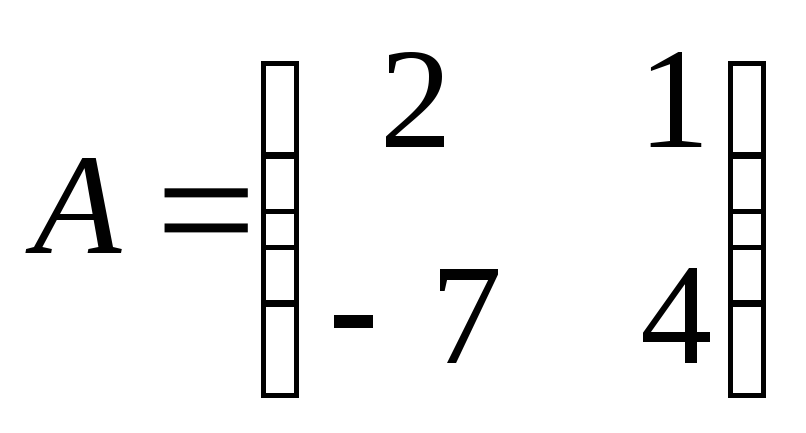 ;
; 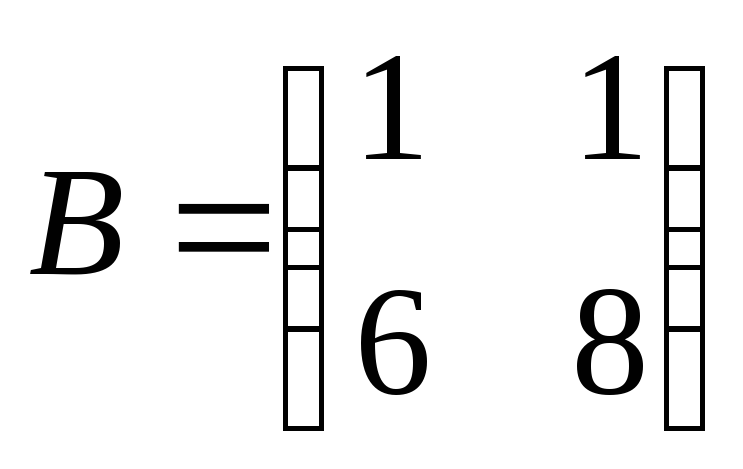 ;
; 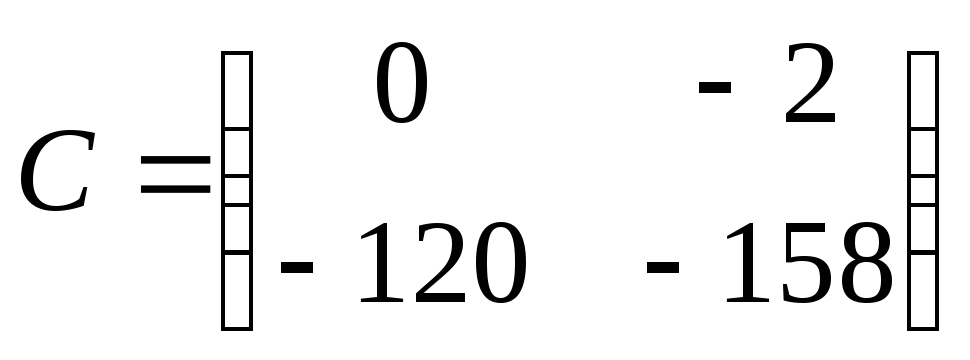 .
.
2) 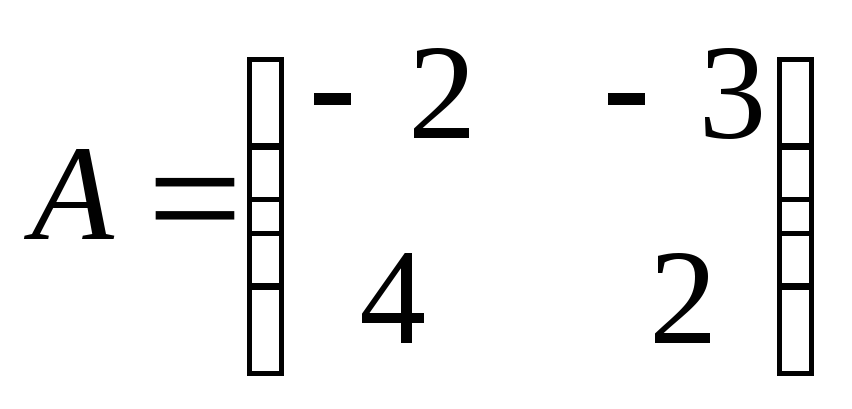 ;
; 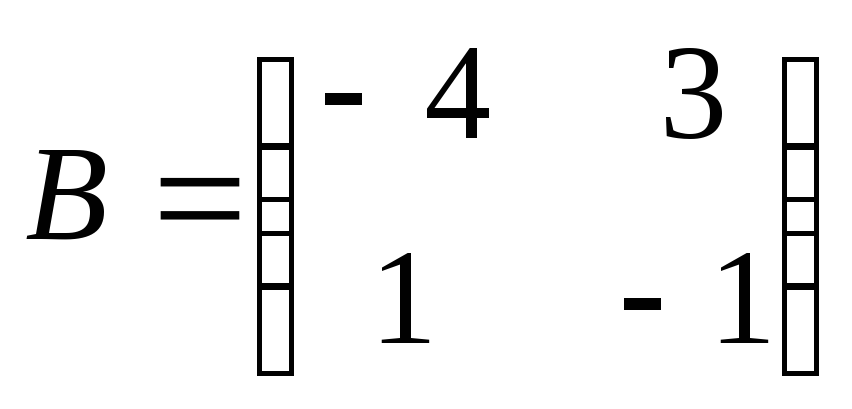 ;
; 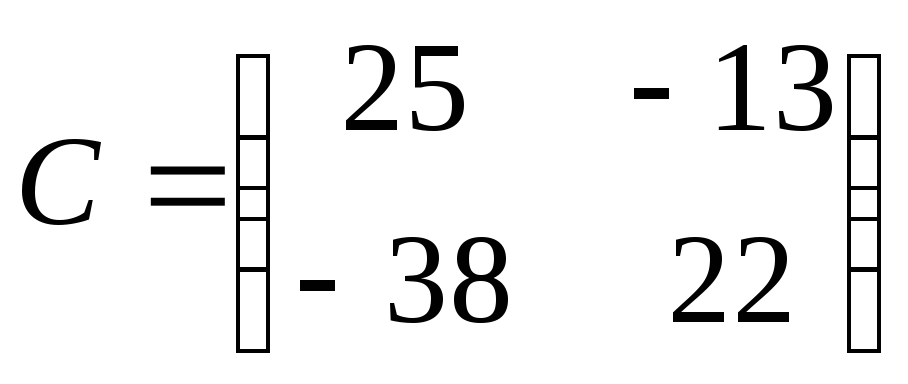 .
.
3.Проработка лекций на темы:
Системы линейных алгебраических уравнений (СЛАУ). Координатная, матричная и векторная формы записи. Критерий Кронекера — Капелли совместности СЛАУ. Однородные СЛАУ. Критерий существования ненулевого решения однородной СЛАУ. Свойства решений однородной СЛАУ. Фундаментальная система решений однородной СЛАУ, теорема о ее существовании. Нормальная фундаментальная система решений. Теорема о структуре общего решения однородной СЛАУ.
11
studfile.net
Матричные уравнения и их решение
Определение и формулы матричных уравнений
ОПРЕДЕЛЕНИЕ Матричным уравнением называется уравнение, состоящее из нескольких матриц-коэффициентов и неизвестной матрицыПростейшим матричным уравнением есть уравнение вида или ,
где — матрицы.
Алгоритм решения матричных уравнений
1. Матричное уравнение приводится к одному из простейших уравнений:
или
где — известные матрицы, — искомая (неизвестная) матрица.
ЗАМЕЧАНИЕ Существует также уравнение вида , но оно является комбинацией методов решения двух первых указанных простейших уравнений.Чтобы привести произвольное матричное уравнение к одному из видов (1), надо все известные матрицы по свойствам уравнений перенести вправо, а неизвестную матрицу в левой части и свести подобные.
2. Разрешаем полученное простейшее уравнение относительно неизвестной матрицы .
2.1 Если в результате преобразований получили простейшее уравнение , то необходимо левую и правую часть этого равенства слева умножить на обратную матрицу к матрице :
ЗАМЕЧАНИЕ
Поскольку умножение матриц некоммутативно, то нужно строго соблюдать умножение слева или справа, иначе это влияет на результат.
2.2 Для простейшего уравнения после умножения справа на обратную матрицу получаем:
ЗАМЕЧАНИЕ Обратная матрица находится либо методом союзной матрицы, либо методом присоединенной матрицы.
3. Далее вычисляется одно из произведений или , что и определяет искомую матрицу.
4. Делаем проверку, для этого подставляем найденную матрицу в исходное уравнение.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
1. Матричные уравнения.
Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом АХ=В, ХА=В, АХС=В.
В этих уравнениях А, В, С, Х – матрицы таких размеров, что все используемые операции возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров.
Если в этих уравнениях матрицы А, В, С – невырожденные, то решения этих уравнений можно записать следующим образом:
АХ=В А-1АХ=А-1В ЕХ=А-1В Х=А-1В.
ХА=В ХАА-1=ВА-1 ХЕ=ВА-1 Х=ВА-1
АХС=В А-1АХСС-1=А-1ХС-1 ЕХЕ=А-1ХС-1 Х=А-1ХС-1
Пример 1. Решить уравнение АХ=Н
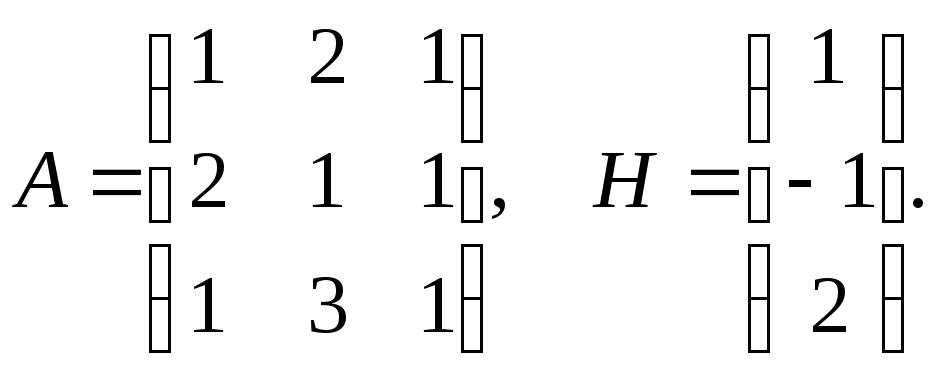
Решение Х=А-1Н
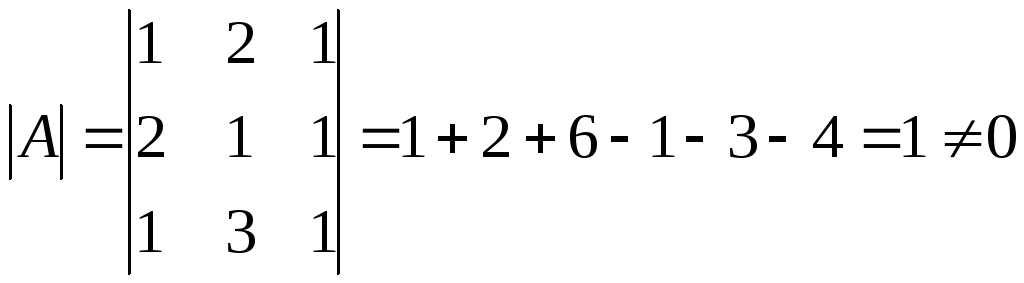 .
Следовательно матрица невырожденная.
.
Следовательно матрица невырожденная.
Найдем обратную матрицу. Составим алгебраические дополнения элементов матрицы А.
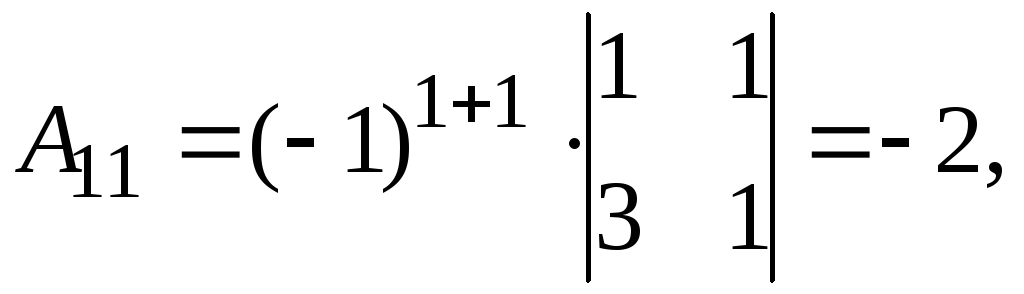
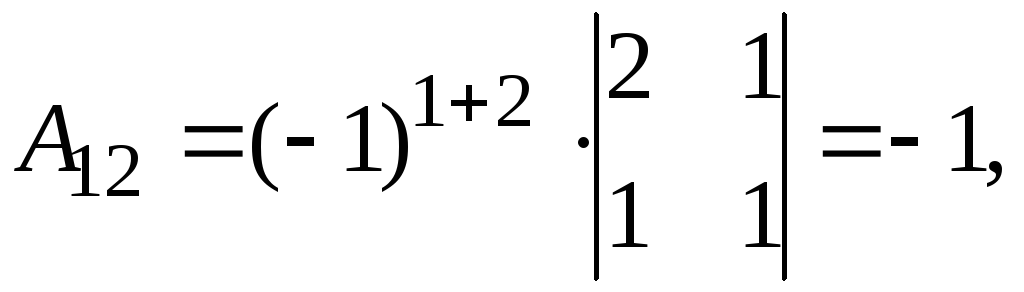
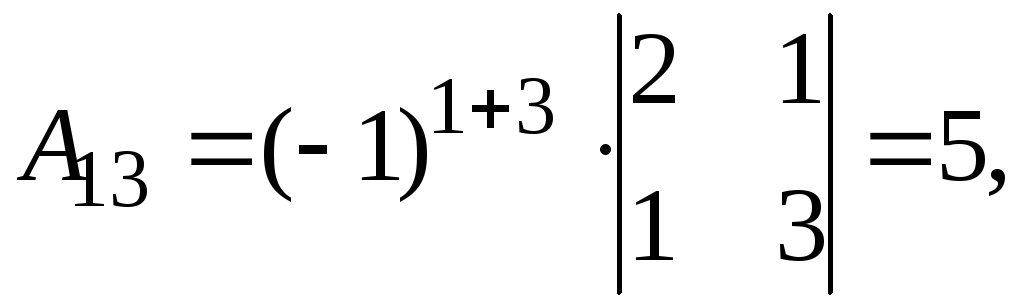
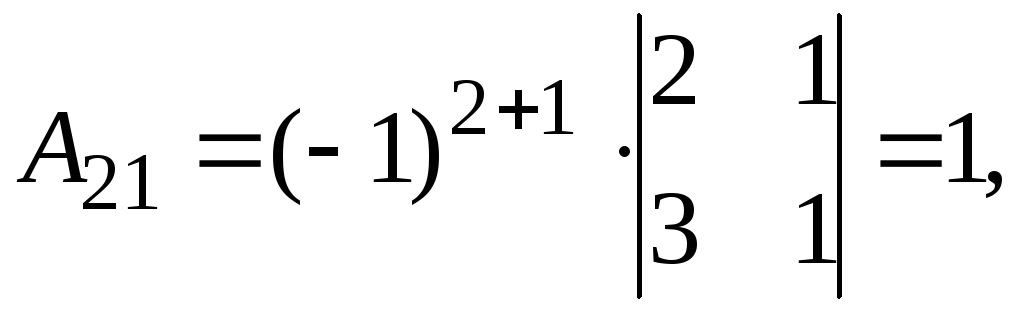
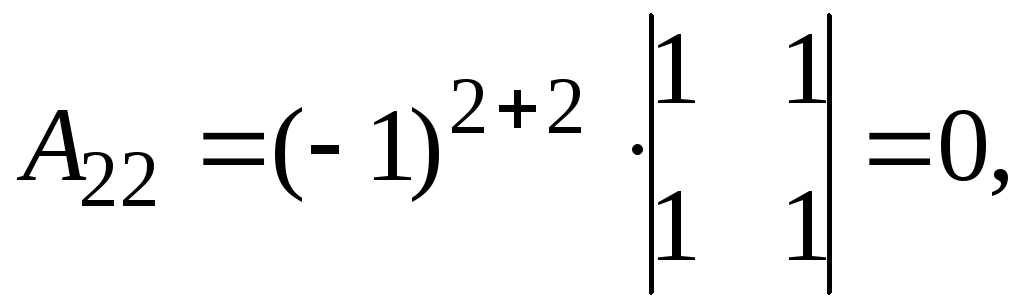
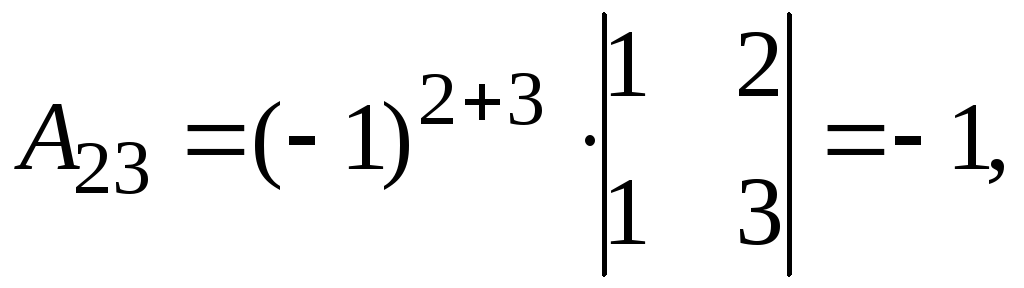
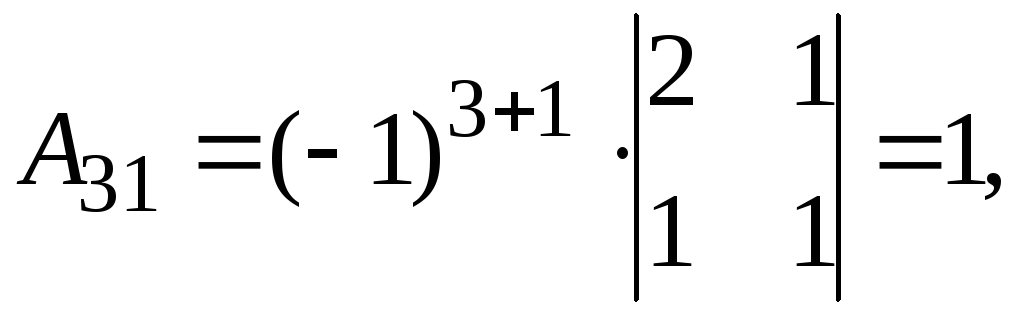
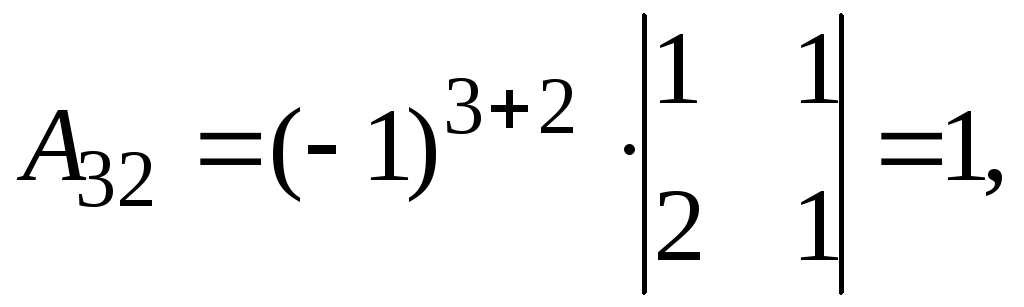
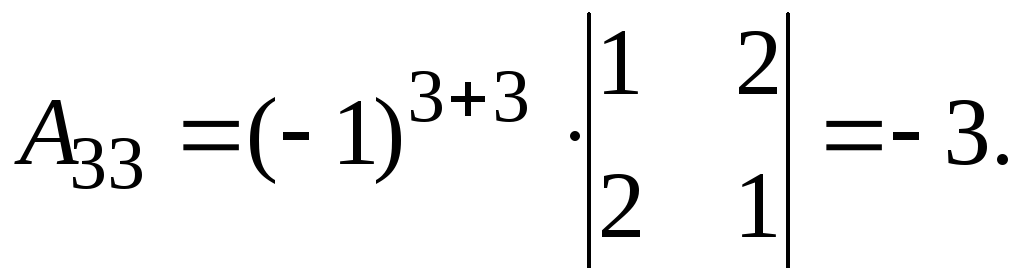
Получаем 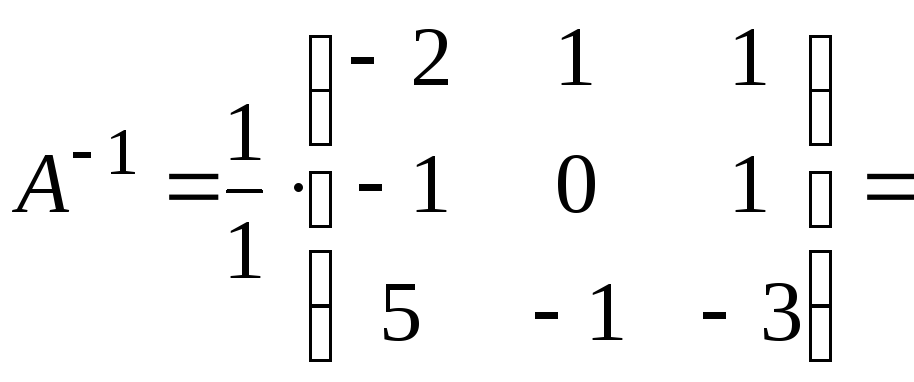
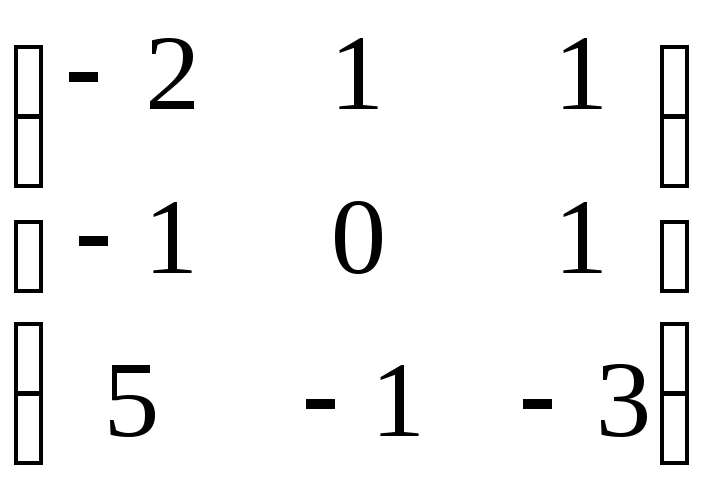 .
.
Следовательно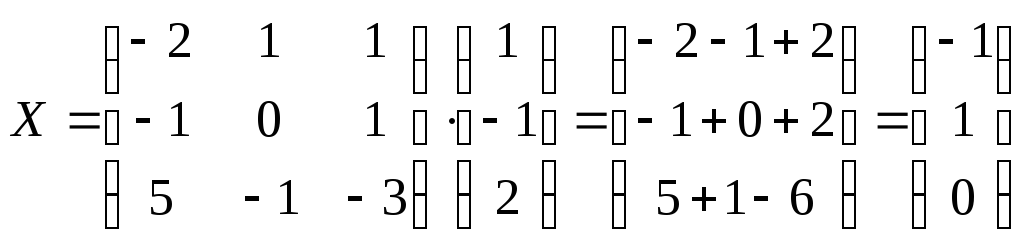
Теория матриц и определителей произвольного порядка строится аналогично изложенной теории матриц и определителей третьего порядка.
2. Системы линейных неоднородных уравнений
Пусть задана система m линейных уравнений с n неизвестными:
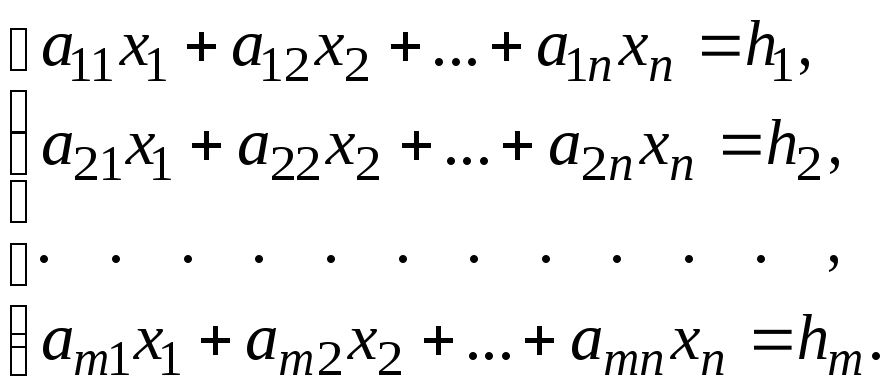 (1)
(1)
Если 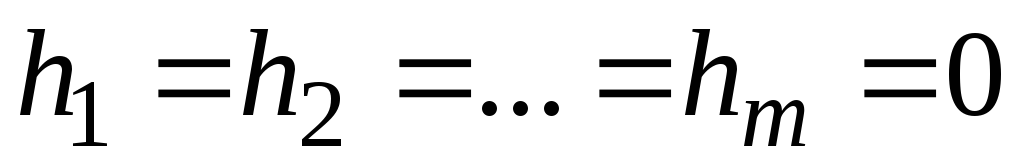 ,
то система (1) называетсяоднородной. Если же хотя бы одно из этих чисел отлично
от нуля, то система неоднородная.
,
то система (1) называетсяоднородной. Если же хотя бы одно из этих чисел отлично
от нуля, то система неоднородная.
Запишем
систему вида (1) в матричном виде, обозначив
матрицу коэффициентов при неизвестных  ,
матрицу столбец свободных членов
,
матрицу столбец свободных членов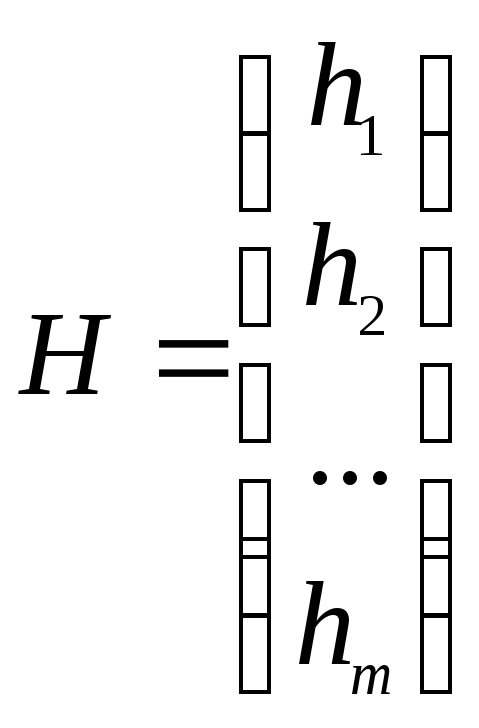 ,
матрицу столбец неизвестных
,
матрицу столбец неизвестных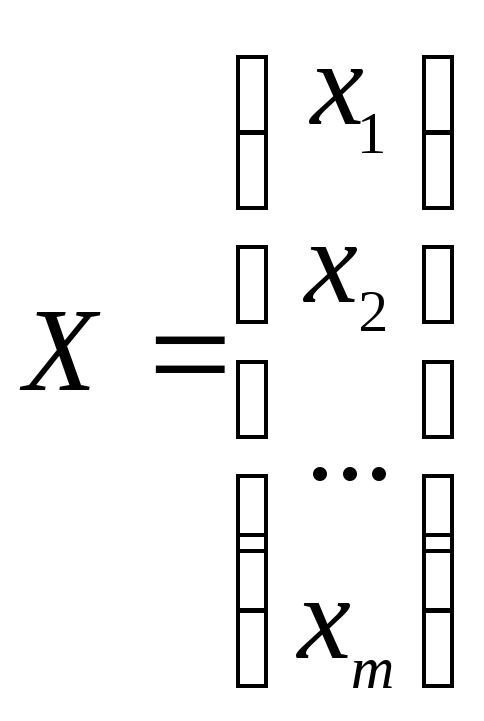 .
Умножая матрицы АХ, получаем новую
матрицу, элементами которой являются
левые части уравнений системы (1). На
основании равенства матриц систему (1)
можно записать систему (1) в виде АХ=В.
.
Умножая матрицы АХ, получаем новую
матрицу, элементами которой являются
левые части уравнений системы (1). На
основании равенства матриц систему (1)
можно записать систему (1) в виде АХ=В.
Определение 1. Решением системы линейных уравнений вида (1), называется такая совокупность n чисел (k1, k2, …, kn), при подстановке которых каждое уравнение обращается в тождество.
Определение 2. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Определение 3. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Вопрос о разрешимости системы уравнений в общем виде рассматривается в следующей теореме.
Теорема Кронекера – Капели:
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
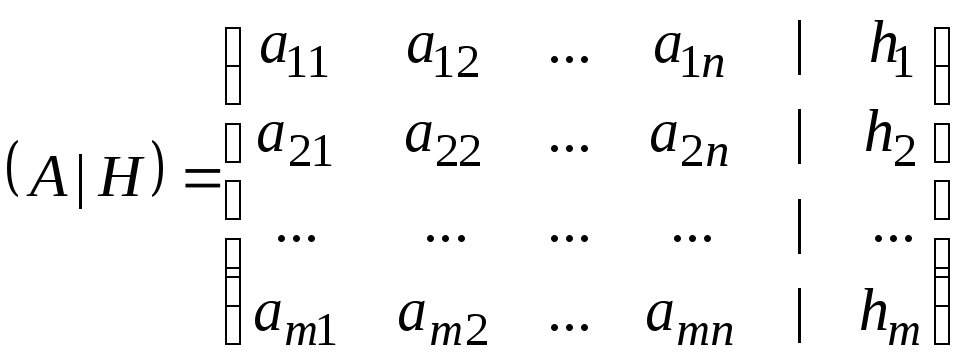 —
расширенная матрица.
—
расширенная матрица.
Для определения рангов обеих матриц достаточно привести расширенную матрицу к ступенчатому виду с помощью элементарных преобразований строк и перестановки столбцов (кроме последнего).
Для совместных систем линейных уравнений верны следующие утверждения:
Если ранг матрицы совместной системы равен числу переменных, т.е. r(A) = n, то система уравнений (1) имеет единственное решение.
Если ранг матрицы совместной системы меньше числа переменных, т.е. r(A) < n, то система (1) неопределенная и имеет бесконечное множество решений.
Схема исследования системы m уравнений с n неизвестными
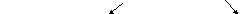
Система совместная, Система несовместная
если r(A) = r(B) = r. Если r(A) r(B).
Ответ: нет решений.

Система определена, Система неопределенна,
если r = n. Если r < n.
Ответ: единственное решение. Ответ: бесконечное множество решений.
Пример
2. Дана система линейных уравнений 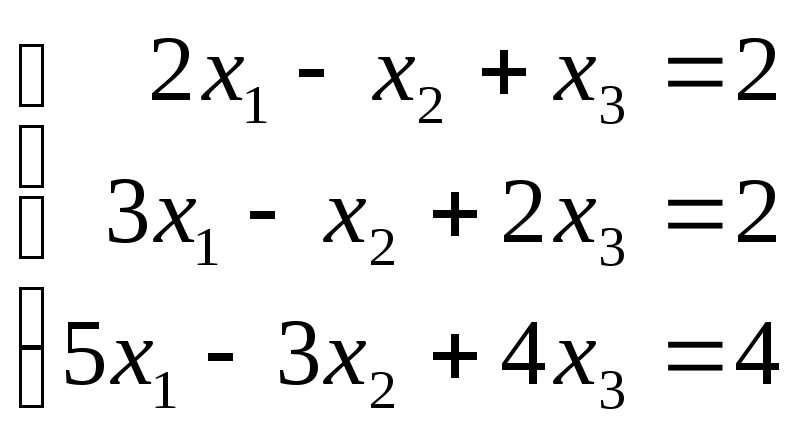 .
Доказать ее совместность.
.
Доказать ее совместность.
Доказательство: Запишем расширенную матрицу системы
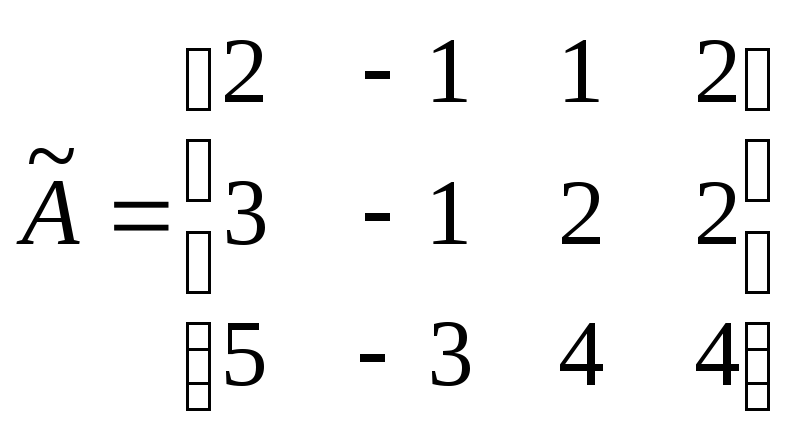
и
найдем ее ранг. Элемент матрицы  ,
стоящий в левом верхнем углу,отличен
от нуля, следовательно
,
стоящий в левом верхнем углу,отличен
от нуля, следовательно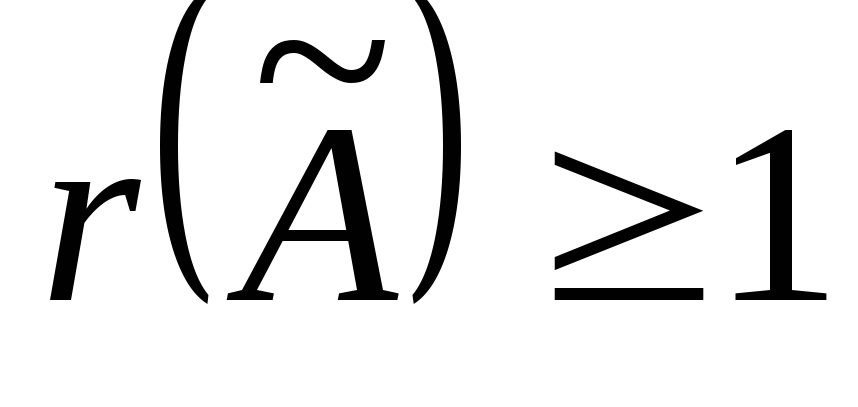 среди миноров второго порядка, окаймляющих
(включающих в себя) этот элемент, также
есть отличные от нуля, например,
среди миноров второго порядка, окаймляющих
(включающих в себя) этот элемент, также
есть отличные от нуля, например,
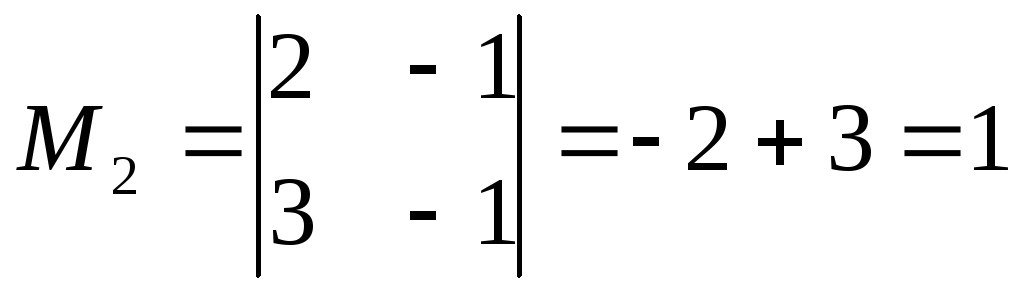 ,
т.е.
,
т.е. 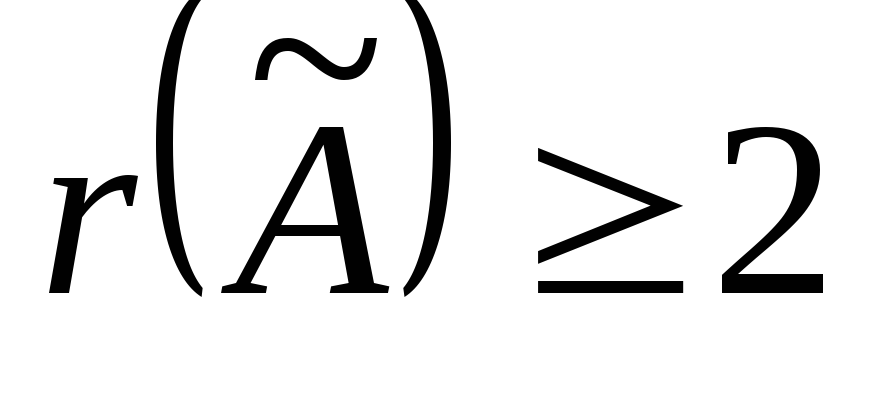 .
.
Из
миноров третьего порядка, окаймляющих  , возьмем минор
, возьмем минор
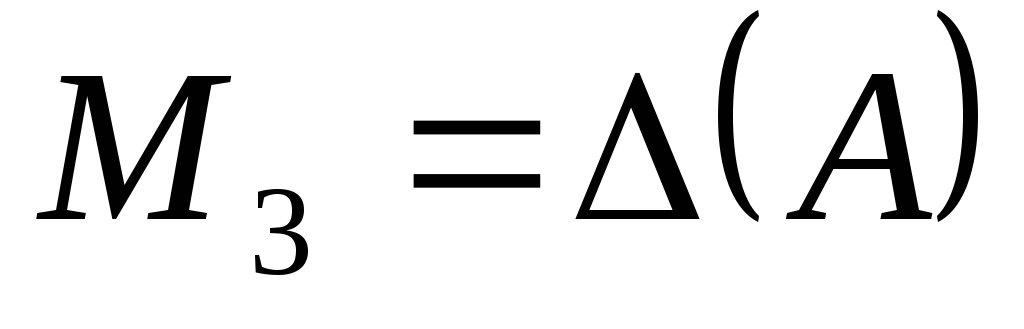 :
:
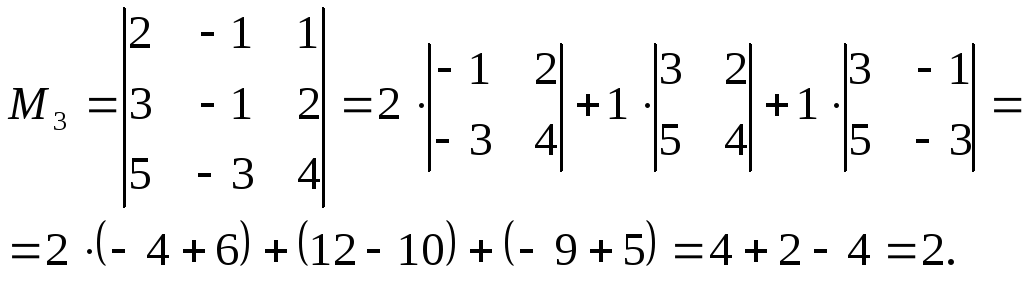
Т.к. 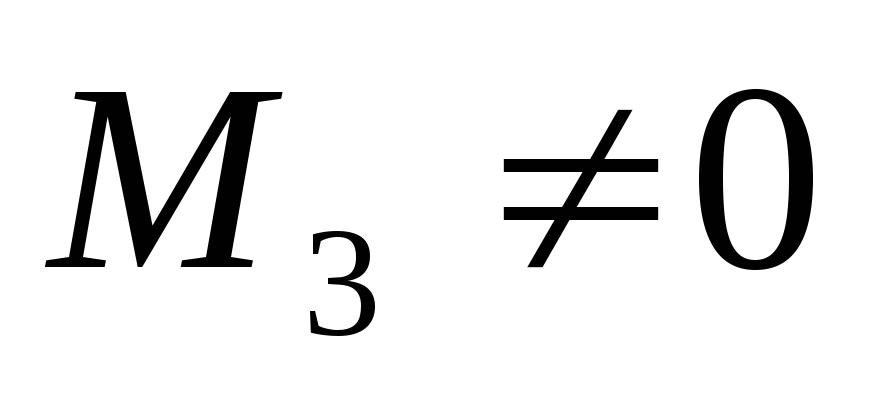 то
то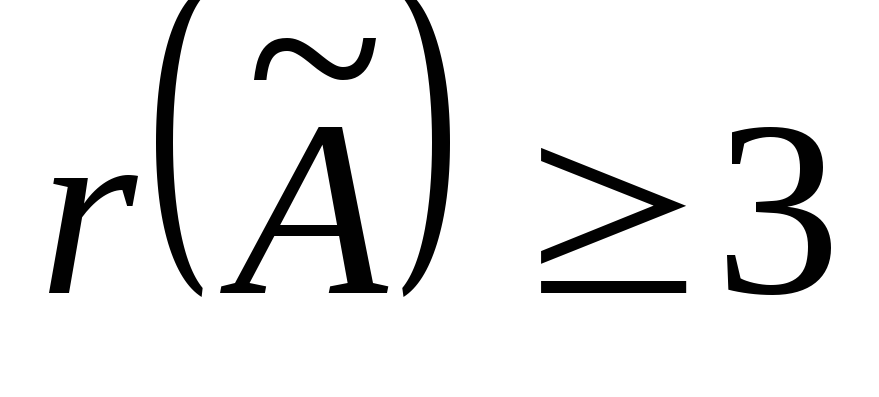 ,
а т.к. у матрицы
,
а т.к. у матрицы миноров 4-го порядка не существует, то
миноров 4-го порядка не существует, то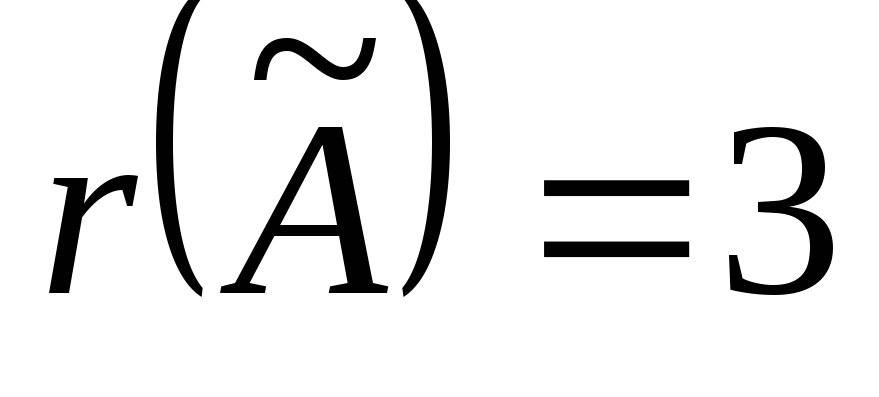 .
Так как
.
Так как 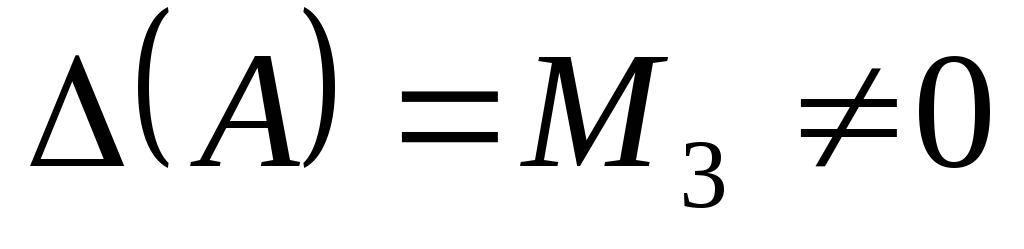 ,
то и
,
то и 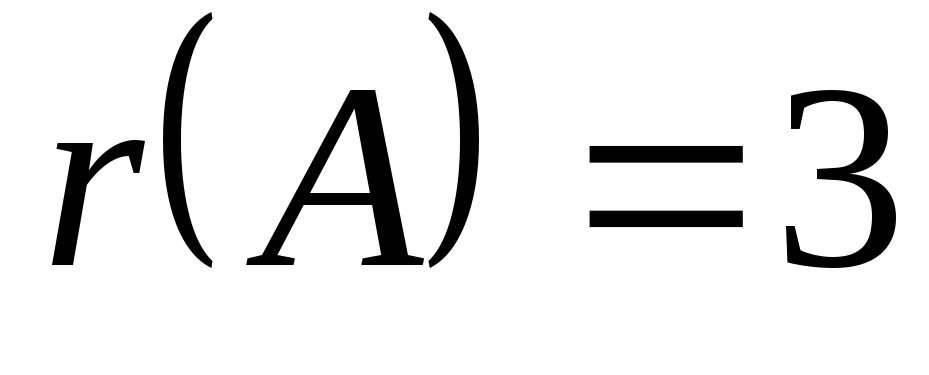 .
Таким образом,
.
Таким образом, 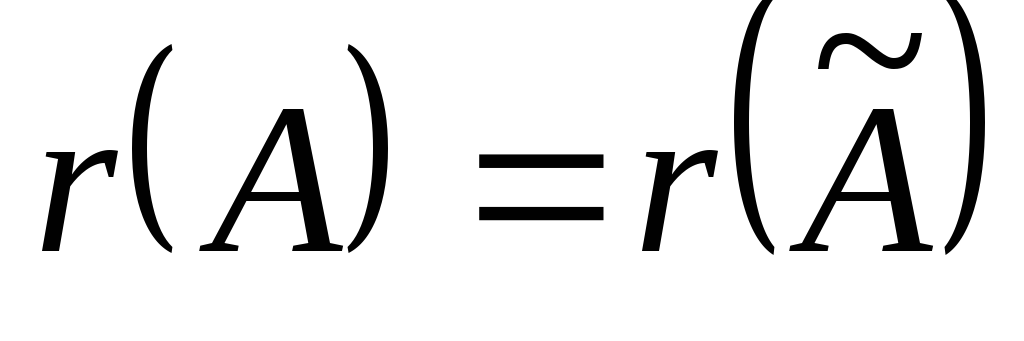 ,
и совместность доказана.
,
и совместность доказана.
Пример
3. Исследовать систему линейных уравнений 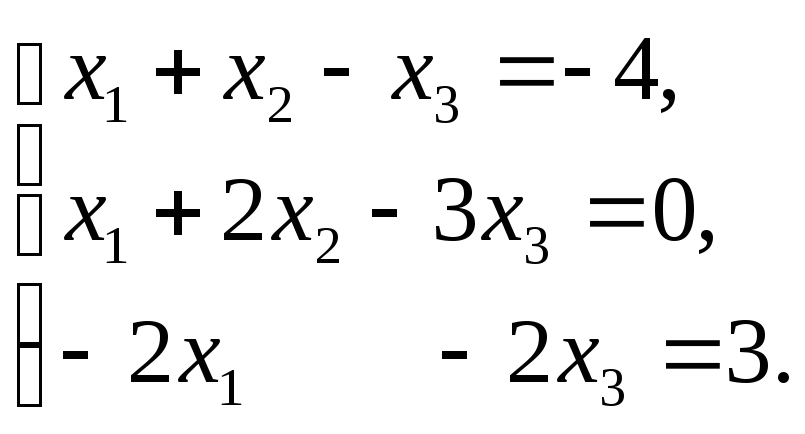
Решение: 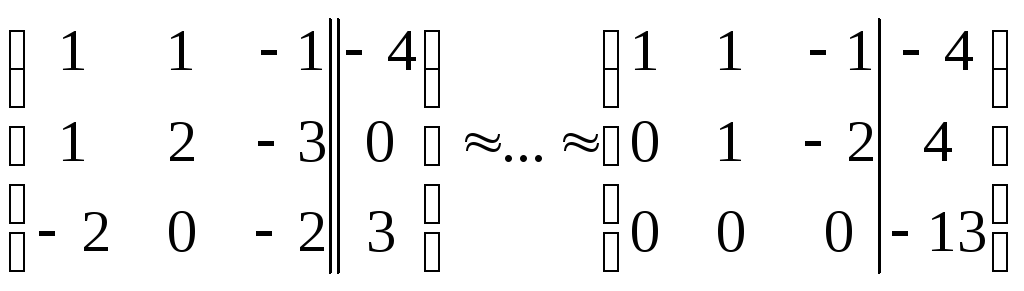 ,
т.к.
,
т.к.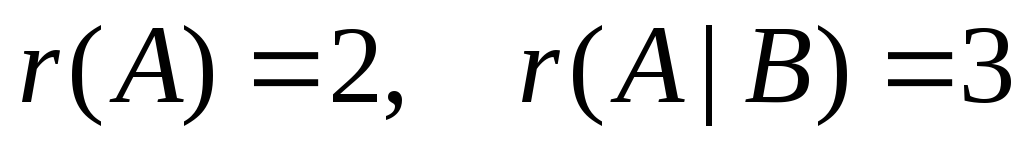 ,
то система несовместна (не имеет решений).
В самом деле, последней строке полученной
расширенной матрицы соответствует
уравнение
,
то система несовместна (не имеет решений).
В самом деле, последней строке полученной
расширенной матрицы соответствует
уравнение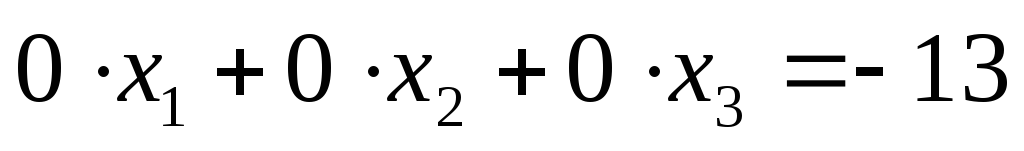 ,
не имеющее решений.
,
не имеющее решений.
Пример 4. Определить совместность системы уравнений:
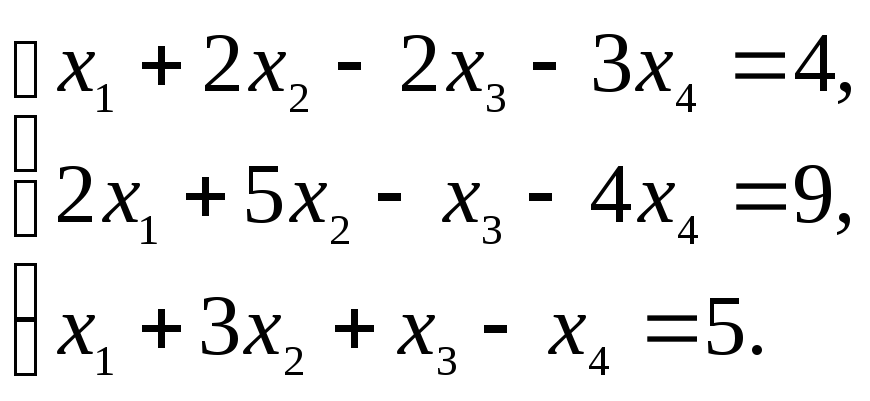
Решение:
Лекция 6. Решение систем линейных уравнений с помощью обратной матрицы.
studfile.net
Матричный метод онлайн
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
 | (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
где
Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.
Умножим матричное уравнение (2) на обратную матрицу A−1. Тогда
Учитывая определение обратной матрицы, имеем A−1A=E, где E— единичная матрица. Следовательно (4) можно записать так:
или, учитывая, что Ex=x:
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
 |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
 . . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
 . . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
 . . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
 . . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
 . . |
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
 . . |
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
 . . |
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
 . . |
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
 . . |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
  . . |
Ответ:
 |
Пример 2. Решить следующую систему линейных уравнений матричным методом:
 . . |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . . |
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
 . . |
Вычислим все алгебраические дополнения матрицы A:
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
 . . |
Обратная матрица вычисляется из следующего выражения:
 |
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
  |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
 |
Ответ:
 |
matworld.ru
Матричные уравнения
Каталин Дэвид
AX = B, где матрица A обратима
Поскольку умножение матриц не всегда коммутативно, умножаем слева обе части уравнения на$ A^{-1}$.
$A^{-1}\cdot|A\cdot X = B$
$A^{-1}\cdot A\cdot X = A^{-1}\cdot B$
$I_{n}\cdot X = A^{-1}\cdot B$
Решение уравнения имеет общий вид
$\color{red}{X =A^{-1}\cdot B}$
Пример 50
Решить уравнение
$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot X \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$
Убедимся, что первая матрица обратима.
$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.
Умножаем слева на обратную ей матрицу.
$\begin{pmatrix} 1 & 3\\ 2 & 5\\ \end{pmatrix}^{-1}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot X= \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$
$I_{2}\cdot X = \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$
$X=\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$
$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}= \begin{pmatrix} -9 & -22\\ 4 & 9 \end{pmatrix}$
XA = B, где матрица A обратима
Поскольку умножение матриц не всегда коммутативно, умножаем справа обе части уравнения на$ A^{-1}$.
$X\cdot A = B |\cdot A^{-1}$
$X\cdot A\cdot A^{-1} = B\cdot A^{-1}$
$X \cdot I_{n} =B\cdot A^{-1}$
Решение уравнения имеет общий вид
$\color{red}{X =B\cdot A^{-1}}$
Пример 51
Решить уравнение
$X \begin{pmatrix} 1 & 3\\ 2 & 5\\ \end{pmatrix}= \begin{pmatrix} 3 & 5\\ 2 & 1\\ \end{pmatrix}$
Убедимся, что первая матрица обратима.
$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.
Умножаем справа на обратную ей матрицу.
$X \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$
$X\cdot I_{2}= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$
$X=\begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$
$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}= \begin{pmatrix} -5 & 4\\ -8 & 5 \end{pmatrix}$
www.math10.com
Решение матриц ℹ️ методы решений и примеров для чайников, формулы вычислений и действий с матрицами

Понятие выражения
Определение гласит, что матрица — это прямоугольная таблица с заключёнными в ней числами. Её название обозначается латинскими прописными буквами (А, В). Таблицы бывают разной размерности — прямоугольной, квадратной, а также в виде строк и столбцов.
От количества строк и столбцов будет зависеть величина таблицы. Матрица размера m*n означает, что в таблице содержится m строк и n столбцов. Допустим, первая строка включает элементы а11, а12, а13, вторая — а21, а22, а23. Тогда элементы, где i = j (а11, а22) образовывают диагональ и называются диагональными.
Различают комплексные матрицы, у которых хотя бы один элемент равен комплексному числу, и действительные, когда все её элементы являются действительными числами. В математике комплексные числа представлены в виде a+b*i, где:
- a — действительная часть числа;
- b — мнимая часть;
- i — мнимая единица (квадратный корень из -1).
На приведенном примере показаны варианты.

Простейшие действия с матрицами могут быть разными. К их числу относятся:
- умножение;
- вычитание;
- умножение на число;
- перемножение между собой;
- транспортирование матриц.
Сложение и вычитание
Действия по сложению возможны только тогда, когда матрицы одинакового порядка равны между собой. В итоге получится новое матричное выражение такой же размерности. Сложение и вычитание выполняются по общей схеме — над соответствующими элементами таблиц проводят необходимые операции. Например, нужно сложить две матрицы А и В размерности 2*2.

Каждый элемент первой строки складывается по порядку с показателями верхней строчки второй матрицы. По аналогии производится вычитание, только вместо плюса ставится минус.

Умножение на число
Любую таблицу чисел можно умножить на число. Тогда каждый её элемент перемножается с этим показателем. К примеру, умножим матричное выражение на 2:

Операция перемножения
Матрицы подлежат перемножению одна на другую, когда количество столбцов первой таблицы равно числу строк второй. Каждый элемент Aij будет равняться сумме произведений элементов i-строки первой таблицы, перемноженных на числа в j-столбце второй. Способ произведения наглядно представлен на примере.

Возведение в степень
Формулу возведения в степень применяют только для квадратных матричных выражений. При этом степень должна быть натуральной. Формула возведения следующая:

Иначе, чтобы выполнить операцию возведения таблицы чисел в степень n, требуется умножить её на себя саму n раз. Для операции возведения в степень удобно применять свойство в соответствии с формулой:

Решение представлено на примере. 1 этап: необходимо возвести в степень, где n = 2.

2 этап: сначала возводят в степень n =2. Согласно формуле перемножают таблицу чисел саму на себя n = 2 раз.

3 этап: в итоге получаем:

Расчёт определителя
В линейной алгебре существует понятие определителя или детерминанта. Это число, которое ставят в соответствие каждой квадратной матрице, вычисленное из её элементов по специальной формуле. Определитель или модуль используется для решения большинства задач. Детерминант самой простой матрицы определяется с помощью вычитания перемноженных элементов из побочной диагонали и главной.
Определителем матрицы А n-энного порядка называется число, которое получают из алгебраической суммы n! слагаемых, попадающих под определённые критерии. Эти слагаемые являются произведением n-элементов, взятых единично из всех столбов и строк.
Произведения могут отличаться друг от друга составом элементов. Со знаком плюс будут включаться в сумму числа, если их индексы составляют чётную подстановку, в противоположном случае их значение меняется на минус. Определитель обозначается символом det A. Круглые скобки матричной таблицы, обрамляющие её элементы, заменяются на квадратные. Формула определителя:

Определитель первого порядка, состоящий из одного элемента, равен самому этому элементу. Детерминант матричной таблицы размером 2*2 второго порядка вычисляется путём перемножения её элементов, расположенных на главной диагонали, и вычитания из них произведения элементов, находящихся в побочной диагонали. Наглядный пример:

Для матрицы также можно найти дискриминант многочлена, отвечающий формуле:

Когда у многочлена имеются кратные корни, тогда дискриминант равен нулю.
Обратная матрица
Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:

По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.
Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.
Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:

Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:

Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.
2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.
При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:


3 этап: находят алгебраические дополнения.

4 этап: определяют транспонированную матрицу.


Итогом будет:
Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.

В рассматриваемом примере получается единичная матрица, когда на главной диагонали находятся единицы, при этом другие элементы равняются нулю. Это говорит о том, что решение было найдено правильно.
Нахождение собственных векторов
Определение собственного вектора и значений матричного выражения легче понять на примере. Для этого задают матричную таблицу чисел и ненулевой вектор Х, называемый собственным для А. Пример выражения:

Согласно теореме собственными числами матричного выражения будут корни характеристического уравнения:

Из однородной системы уравнений можно определить координаты собственного вектора Х, который соответствует значению лямбда.

Метод Гаусса
Методом Гаусса называют способ преобразования системы уравнений линейного вида к упрощённой форме для дальнейшего облегчённого решения. Операции упрощения уравнений выполняют с помощью эквивалентных преобразований. К таким относят:
- действия, когда в системе переставляются местами два уравнения;
- произведение одного из уравнений в системе на действительное ненулевое число;
- сложение первого уравнения со вторым, при этом последнее умножено на произвольное число.
Чтобы понять механизм решения, следует рассмотреть линейную систему уравнений.

Следует переписать эту систему в матричный вид:

А будет являться таблицей коэффициентов системы, b — это правая часть ограничений, а Х — вектор переменных координат, который требуется найти. Для решения используют ранг матрицы. Под ним понимают наивысший порядок минора, который отличается от 0.
В этом примере rang (A) = p. Способ эквивалентных преобразований не изменяет ранг таблицы коэффициентов.
Метод Гаусса предназначен для приведения матричной таблицы коэффициентов А к ступенчатому или диагональному виду. Расширенная система выглядит так:

Допустим, а11 не равен 0. В противном случае, если это не так, то меняют эту строку с другой, где в первом столбце находится элемент, отличный от нуля. Когда подобные строчки отсутствуют, переходят к другому столбцу. Все нижние элементы столбца после а11 обнуляют. Для этих целей выполняют операции сложения строк 2,3…m с первой строчкой, умноженной на а21/а11, -а31/а11….- аm1/a11. В результате система примет вид:

На втором шаге повторяют все действия с элементами столбца 2, которые расположены ниже а22. Если показатель равен нулю, строку также меняют местами со строчкой, лежащей ниже с ненулевым элементом во втором столбце. Затем обнулению подлежат все показатели ниже а22. Для этого складывают строки 2,3 ..m, как описано выше. Выполняя процедуру со всеми элементами, приходят к матричной таблице ступенчатого или диагонального вида. Полученная расширенная таблица будет выглядеть:

Обращают внимание на последние строки.

В этом случае система уравнений имеет решение, но когда хотя бы одно из этих чисел отличается от нуля, она несовместима. Таким образом, система совместима, если ранг таблицы А равен расширенному рангу В (А|b).

Если rang А=rang (A|b), то существует множество решений, где n-p — многообразие. Из этого следует n-p неизвестных Хр+1,…Xn выбираются произвольно. Неизвестные X1, X2,…Xp вычисляют следующим образом: из последнего уравнения выражают Хр через остальные переменные, вставляя в предыдущие выражения. Затем из предпоследнего уравнения получают Хр-1 через прочие переменные и подставляют их в предыдущие выражения. Процедуру повторяют.
Найти быстро ответ и проверить себя позволяет онлайн-калькулятор. Решение матрицы методом Гаусса с помощью такого расчёта показывает подробные этапы операций. Для нахождения достаточно указать количество переменных и уравнений, отметить в полях значения чисел и нажать кнопку «Вычислить».
Способ Крамера
Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:

Её необходимо заменить равноценным матричным уравнением.


Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:

В итоге получают выражения:

Из представленных уравнений выделяют формулы Крамера:

Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:
- Высчитывают определитель дельта базовой матрицы.
- В матричной таблице А замещают первый столбец на вектор свободных элементов b.
- Выполняют расчёт определителя дельта1 выявленной матрицы А1.
- Определяют переменную Х1 = дельта1/дельта.
- Повторяют шаги со 2 по 4 пункт в матрице А для столбов 2,3…n.
Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.
Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.
nauka.club
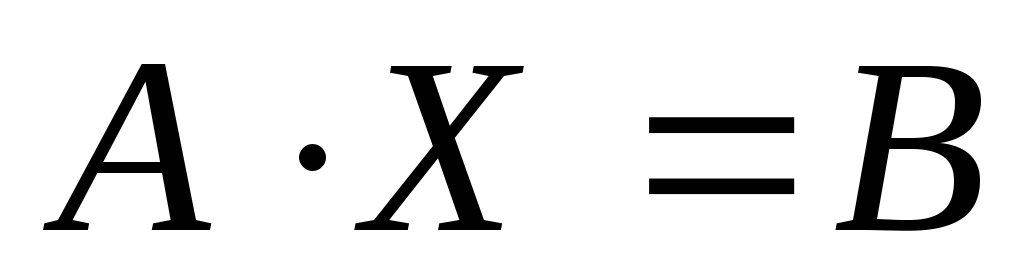 методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы.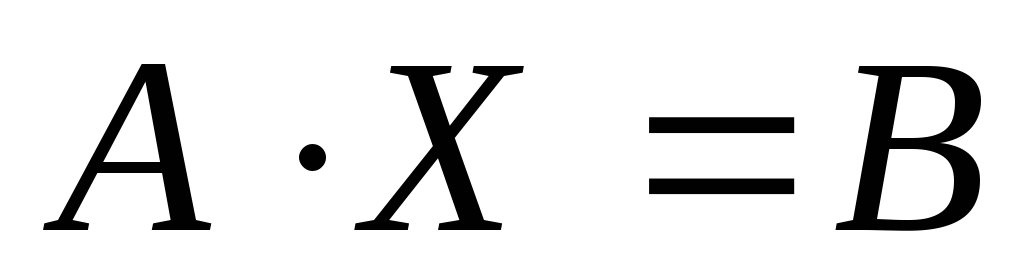 методом,
основанным на элементарных преобразованиях
строк матрицы.
методом,
основанным на элементарных преобразованиях
строк матрицы. методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы.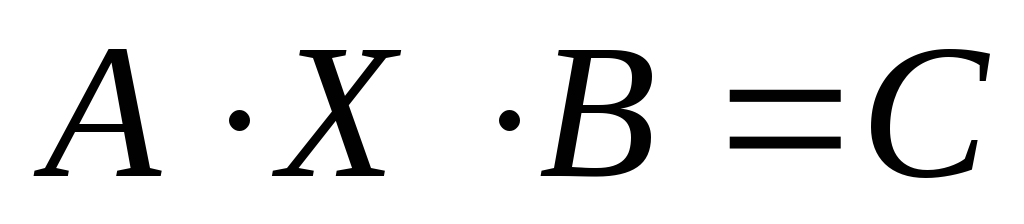 методом с использованием обратной
матрицы.
методом с использованием обратной
матрицы.