Различные способы сложения и вычитания чисел, запись которых оканчивается нулями
Данный урок посвящен теме «Различные способы сложения и вычитания чисел, запись которых оканчивается нулями». Здесь мы продолжим знакомство с различными способами устных вычислений примеров на сложение и вычитание чисел, оканчивающихся нулями. Мы рассмотрим способ представления числа в виде количества сотен и десятков, способ замены одного числа на сумму удобных слагаемых, а также способ представления чисел в виде суммы разрядных слагаемых.
Найдите значение выражений.
1) 
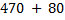2) 
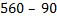
Решение
1) Заменим слагаемые из первого примера десятками.
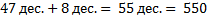
2) Найдём значение разности.
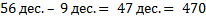
3) Можно рассуждать по-другому: в сумме 470 и 80 заменим второе слагаемое удобными слагаемыми так, чтобы одно из чисел дополняло первое слагаемое.
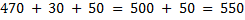
4) Так же можно поступить и со вторым примером: только вычитаемое заменить удобными слагаемыми так, чтобы вычитать было удобнее.
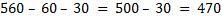
Найдите значение выражений.
Решение
1) В первой сумме заменим второе слагаемое такими составляющими, чтобы получилось круглое число.
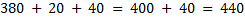
2) Число 80 поменяем на сумму 10 и 70 потому, что так удобнее выполнять сложение: к 790 удобно прибавить 10 и получить круглое число сотен, к которому потом быстро можно прибавить ещё 70.
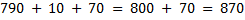
3) Чтобы получить круглые сотни, от 260 надо отнять 60, поэтому из 70 делаем сумму 60 и 10.
4) Аналогично поступаем в последней разности.
1) Допустим, что к 260 надо прибавить 110.
2) От 670 отнять 140.
Решение
1) Заменим каждое слагаемое суммой разрядных слагаемых. Далее вычисляем по известному правилу: сотни складываем с сотнями, а десятки – с десятками.
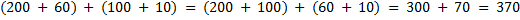
2) При решении примеров на вычитание также раскладываем уменьшаемое и вычитаемое на разрядные слагаемые и поль
interneturok.ru
| 1. | Неизвестная переменная x | 1 вид — рецептивный | лёгкое | 2 Б. | Дана система линейных уравнений. Найти переменную x. |
| 2. | Неизвестная переменная y | 1 вид — рецептивный | лёгкое | 2 Б. | Найти переменную y, если дана система линейных уравнений. |
| 3. | Система линейных уравнений | 2 вид — интерпретация | лёгкое | 2 Б. | Решение системы линейных уравнений методом сложения. |
| 4. | Система линейных уравнений | 2 вид — интерпретация | лёгкое | 1 Б. | Решение системы линейных уравнений методом сложения. |
| 5. | Система линейных уравнений (одинаковые коэффициенты при y) | 2 вид — интерпретация | среднее | 4 Б. | Решение системы линейных уравнений, у которых коэффициенты при y одинаковые. |
| 6. | Решение системы двух уравнений (обыкновенные дроби) | 2 вид — интерпретация | среднее | 4 Б. | Решение системы двух уравнений (обыкновенные дроби в результате). |
| 7. | Система двух линейных уравнений (одинаковые коэффициенты при x) | 2 вид — интерпретация | среднее | 4 Б. | Решение системы линейных уравнений, у которых коэффициенты при x одинаковые: вычитание уравнений. |
| 8. | Система линейных уравнений | 2 вид — интерпретация | среднее | 4 Б. | Решение системы линейных уравнений методом сложения. |
| 9. | Система линейных уравнений (смешанные числа и обыкновенные дроби) | 2 вид — интерпретация | среднее | 4 Б. | Решение системы уравнений (противоположные коэффициенты у разных переменных): умножение одного из уравнений на число. |
| 10. | Система линейных уравнений | 2 вид — интерпретация | среднее | 1 Б. | Решение системы линейных уравнений методом сложения. |
| 11. | 2 вид — интерпретация | среднее | 4 Б. | Решение системы линейных уравнений методом сложения. | |
| 12. | Система линейных уравнений | 2 вид — интерпретация | среднее | 4 Б. | Решение системы уравнений: умножение обоих уравнений на число. |
| 13. | Система линейных уравнений, одно из которых целое по сути, но дробное по виду | 2 вид — интерпретация | среднее | 4 Б. | Решение системы линейных уравнений, одно из которых целое по сути, но дробное по виду. |
| 14. | Решение системы линейных уравнений | 2 вид — интерпретация | сложное | 6 Б. | Решение системы уравнений, коэффициенты одного из уравнений которой — обыкновенные дроби. |
| 15. | Система линейных уравнений (сумма дробей) | 2 вид — интерпретация | сложное | 5 Б. | Решение системы уравнений: умножение обоих уравнений на общие знаменатели дробей, избавление от дробей, вычитание уравнений. |
| 16. | Система двух уравнений | 2 вид — интерпретация | сложное | 6 Б. | Решение системы двух уравнений, применение основного свойства пропорции, сложение уравнений. |
www.yaklass.ru
Способ сложения | Алгебра
Способ сложения решения систем линейных уравнений изучается в школьном курсе алгебры в 7 классе. Этим способом можно решить любую систему линейных уравнений, но для решения систем других видов он применяется не так часто, как метод подстановки.
Алгоритм решения систем линейных уравнений с двумя переменными способом сложения
1) Умножаем почленно уравнения системы так, чтобы коэффициенты при одной из переменными стали противоположными числами.
2) Складываем почленно левые и правые части уравнений.
3) Решаем получившееся уравнение с одной переменной.
4) Найденное значение переменной подставляем в любое из уравнений и находим значение другой переменной.
Ответ записываем в круглых скобках через точку с запятой в алфавитном порядке: (x; y).
Как определить, на какие числа умножать уравнения?
Для системы
находим наименьшее общее кратное коэффициентов при каждой из переменных. Выбираем из НОК(a1;a2) и НОК(b1;b2) то число, привести к которому коэффициенты проще. Затем умножаем уравнения почленно.
Например, если выбрали НОК(a1;a2), первое уравнение системы можно умножить на НОК(a1;a2)/a1, а второе — на -НОК(a1;a2)/a2.
В результате коэффициент при x в первом уравнении станет равным НОК(a1;a2), во втором — -НОК(a1;a2). При сложении почленно левой и правой части получившихся уравнений слагаемые с иксом уйдут (поскольку сумма противоположных чисел равна нулю).
Из полученного уравнения с одной переменной найдем значение y.
Подставив вместо y в любое из первоначальных уравнений найденное значение, вычислим x.
В следующий раз рассмотрим конкретные примеры решения систем линейных уравнений методом сложения.
www.algebraclass.ru
Метод сложения — Энциклопедия по экономике
Законом установлено шесть методов определения таможенной стоимости для ввозимых товаров (ст. 19—24 соответственно) (1) метод по цене сделки с ввозимыми товарами (2) метод по цене сделки с идентичными товарами (3) метод по цене сделки с однородными товарами (4) метод вычитания стоимости (5) метод сложения стоимости (6) резервный метод. [c.158]Обратимся к сезонной составляющей временного ряда. Сезонные колебания достаточно часто сопровождают динамику, например, в торговой и сбытовой деятельности, в ряде производств добывающей и перерабатывающей, в пищевой промышленности. При оценке сезонных колебаний используются два метода — сложения и умножения. [c.80]
Иногда трудно выбрать метод расчета. Считается, что при почти одинаковых колебаниях исходных значений целесообразно применять метод сложения. Если колебания изменяются вслед за динамикой тренда, то более точным может быть метод умножения. [c.82]
Метод сложения стоимости предполагает определение таможенной стоимости исходя из калькуляции издержек на производство и продажу товаров на экспорт и [c.507]
Мы можем использовать методы сложения процентов, амортизации и текущей стоимости, уже описанные ранее в этой главе, при рассмотрении целе- [c.149]
Сезонные колебания метод сложения [c.184]
Метод сложения используется в случаях, когда сезонные составляющие относительно постоянны по всему анализируемому временному периоду. При этом [c.197]
Графики, представленные на рис. 6.8, показывают два временных ряда и соответствующие линии тренда. На рис. 6.8 (i) отклонения от тренда относительно постоянны, а на рис. 6.8 (ii) отклонения нарастают по мере восхождения тренда. На этих простых примерах видно, что в первом случае (i) следует применить метод сложения, а во втором (ii) — метод умножения. [c.198]
В этом разделе мы рассмотрим порядок вычисления сезонных колебаний при условии приемлемости метода сложения. Итак, мы воспользуемся следую-щер формулой [c.199]Сложив эти оценочные значения тренда со значениями сезонных колебаний, которые мы уже рассчитали по методу сложения — X, = Т,, + S,, получаем прогнозные показатели объема продаж в каждом из периодов 1998 г., а именно [c.202]
Этот пример вновь демонстрирует сильное присутствие сезонной составляющей. Часто на практике трудно решить, какой метод применить сложения или умножения. В принципе, если колебания остаются неизменными, то лучше применять метод сложения. В этом случае, который мы рассматриваем сейчас, колебания увеличиваются по мере восхождения тренда. Давайте рассмотрим размер значений в 1993 г. (100 в мае—августе и 121 в сентябре—декабре) и аналогичный размер в 1997 году (175 в мае—августе и 206 в сентябре—декабре). Мы видим, что внешне разрыв увеличивается, и поэтому можно воспользоваться методом умножения, который в этом случае, вероятно, более приемлем. [c.206]
Фактические оценочные показатели сезонных колебаний необходимо скорректировать с учетом смещения, о чем мы уже говорили, когда рассматривали метод сложения. Рассмотрим предыдущий пример. В таблице собраны значения коэффициентов и средних коэффициентов, которые мы уже рассчитали [c.208]
Упражнения методы сложения и умножения [c.209]
В одном из предыдущих примеров мы рассмотрели прогноз по объему производства за два месяца некой компании из Дублина. Были получены оценки на 1997 год, при этом использовался линейный тренд и метод сложения. Прогнозные значения даны в тоннах [c.213]
Сочетание этих элементов также является важной частью модели. Крайне важно выбрать наиболее приемлемый метод — сложения или умножения, что можно сделать, исходя из прошлых данных. [c.215]
Выявление сезонности, определяющей выбор метода сложения или метода умножения. [c.221]
Для анализа качества продукции могут быть использованы различные методы математической статистики, в частности методы сложения и умножения вероятности у различных средних величин, размаха, дисперсии, среднеквадратических отклонений . [c.155]
Для получения достоверных результатов на ВАЗе успешно применяется метод оценки эффективности трудовых движений, позволяющий корректировать зафиксированные в процессе хронометражных наблюдений фактические затраты. Однако этот метод сложен, требует специального обучения нормировщиков. До сих пор нет научно обоснованных показателей, на основании которых проводится оценка темпа работы. [c.171]
Метод сложения, при котором добавленная стоимость представляет собой сумму следующих расходов ВИНК Фонд оплаты труда (без единого социального налога), Амортизация, Расходы на обслуживание долга (проценты, дисконты), Прибыль после налогообложения, Налоги (Налог на прибыль + Единый социальный налог + НДС + Налог на добычу + Налог на пользователей автодорог н Акцизы + Таможенная пошлина). [c.52]
Текущий учет затрат по нормам и отклонений от них ведут, как правило, только по прямым расходам (материалы, заработная плата, затраты на эксплуатацию строительных машин и механизмов). Отклонения по косвенным расходам распределяют по объектам по истечении месяца. Аналитический учет затрат на производство продукции осуществляют в карточках или в особого рода оборотных ведомостях, составляемых по отдельным видам или группам продукции. Нормативный метод сложенный и трудоемкий, что сдерживает его широкое применение. [c.368]
В качестве базы для определения таможенной стоимости при использовании метода сложения стоимости принимается цена товара, рассчитанная путем сложения [c.249]
Однако этот метод сложен и в русском издании книги не рассматривается.- При-меч.ред. [c.309]
Для товаров, ввозимых на территорию РФ, применяются следующие методы определения таможенной стоимости метод по цене сделки с ввозимыми товарами метод по цене сделки с идентичными товарами метод по цене сделки с однородными товарами метод вычитания стоимости метод сложения стоимости резервный метод. Основным методом определения таможенной стоимости является метод по цене сделки с ввозимыми товарами. В том случае, если основной метод не может быть использован, применяется последовательно каждый из перечисленных методов. При этом каждый последующий метод применяется, если таможенная стоимость не может быть определена путем использования предыдущего метода. Методы вычитания и сложения стоимости могут применяться в любой последовательности. [c.446]
Преимущество данного метода состоит в том, что эксперт анализирует оценки по совокупности признаков. Однако метод сложен и гро- [c.202]
Пятый метод — метод определения таможенной стоимости на основе сложения стоимости . Этот метод используется в таможенном деле в соответствии со статьей 23 Закона о таможенном тарифе. Как отмечается в Методических рекомендациях таможенных органов (п. 3.6), в рамках метода сложения стоимости таможенная стоимость оцениваемых товаров определяется на основе издержек производства… товаров, к которым добавляются суммы прибыли и расходов, характерных для продажи оцениваемых товаров в России . Это означает, что для определения таможенной стоимости при проведении соответствующих процедур, в частности при взимании таможенных пошлин, налогов на таможне, она (таможня) должна располагать сведениями об издержках производства этих товаров применительно к стране вывоза. Импортер, естественно, заинтересован в том, чтобы подобная информация на таможне (об издержках производства) способствовала бы занижению взимаемых сумм. [c.340]
Теперь в новом ФЗ несколько по-иному представлен 5-й метод оценки таможенной стоимости, т.е. метод сложения. Можно считать, что установленные Законом нововведения направлены на определенную защиту интересов декларантов. Теперь в случае несогласия с соответствующими решениями таможенного органа они (декларанты) вправе потребовать информацию о том, как таможенники определили стоимость в рамках этого метода. Правда, это касается лишь ограниченного круга статей. Об этом сказано в статье 23 пункта 4 Если для расчета суммы прибыли и коммерческих, и управленческих расходов используются имеющиеся у таможенного органа сведения о сумме прибыли и коммерческих, и управленческих расходов, то по заявлению декларанта [c.343]
Метод сложения стоимости предусматривает принятие за основу цены товара, цену, которая рассчитывается путем сложения [c.30]
Необходимо отметить, что расчет нормативов методом прямого счета весьма сложен, требует большой вычислительной работы и много времени. Поэтому его целесообразно применять для определения нормативов оборотных средств только для крупных групп материалов. Для определения нормативов оборотных средств по материалам, имеющим небольшой удельный вес в за- [c.207]
Манипулирование окружением другого человека, используя один или все прямые методы Широкий диапазон отношений и видов поведения Может дать результат, когда не срабатывают прямые методы Может потребовать много времени сложен для использования рискованный, если часто используется [c.481]
Как мы уже показали, эффективный объем производства товара индивидуального потребления определяется сравнением предельной прибыли от производства дополнительного товара с предельными издержками производства этого товара. Эффективность достигается тогда, когда предельная прибыль и предельные издержки равны. Тот же принцип применим и к общественным товарам, но метод анализа при этом иной. У товаров индивидуального потребления предельная выгода измеряется выгодой, получаемой потребителем. Рассматривая общественные товары, мы должны ответить на вопрос, как оценивает каждый человек дополнительную единицу продукции. Предельная выгода получается сложением этих оценок, сделанных всеми людьми, пользующимися этим товаром. Эффективный объем производства общественного товара достигается в том случае, если сумма этих предельных выгод равна предельным издержкам производства. [c.507]
В данном примере для прогнозной оценки объемов продаж по сезонам 2000 г. использован метод сложения. Тренд выделен с помощью трехточечных скользящих средних, а значения 2000 г. рассчитаны уравнением регрессии. Прогнозируемые объемы продаж в каждом из периодов 2000 г. исчислены как сумма оценочных показателей тренда и средних значений сезонных колебаний в каждом сезоне (табл. 4.5). Например, среднее отклонение (колебание) за май — август 1997—1999 гг. определяется так (9,33 + + 11,67 + 12,33 3= 11,И) и т.д. [c.80]
Если метод расчета по цене сделки с ввозимыми трварами по каким-либо причинам не может быть применен, используют остальные методы в том порядке, в каком они перечислены выше. Исключение составляют методы сложения и вычитания, которые можно применять в любой последовательности. [c.507]
На графике (рис. 6.9) показаны значения объема продаж, а также трехточечные скользящие средние. Последние можно использовать при прогнозировании направленности тренда после 1997 г. Из графика видно, что каждый год показатели объема продаж выказывают достаточную стабильность. А теперь рассмотрим сезонную составляющую в этом ряду значений объема продаж. Колебания в обе стороны относительно линии тренда достаточно постоянны. Таким образом, в данном случае метод сложения, похоже, наиболее приемлем. Сезонную составляющую можно выделить путем вычитания значений скользящих средних из исходных показателей, о чем мы уже говорили ранее. Полученные разности, обычно называемые отклонениями, приведены в таблице на стр. 201. [c.200]
Как и в предыдущем примере, когда мы применяли метод сложения, тренд можно определить графически по средним скользящим. На графике (рис. 6.12) показаны данные по стоимости аренды, а также трехточечные скользящие средние. Линия тренда проведена через скользящие средние и продолжена дальше, с тем чтобы получить прогнозные показатели по каждому периоду 1998 г. Согласно графику, эти показатели на 1998 г. таковы [c.207]
Применяются и другие методы, повышающие интенсивность добычи нефти (виброобработка, разрыв пласта под давлением пороховых газов, торпедирование и т. д.). Кислоты и их смеси с поверхностно-активными веществами успешно применяются для очистки призабойной зоны от ила, увеличения проницаемости коллектора, особенно сложенного карбонатными породами, ли-квидации образовавшейся в призабойной зоне эмульсии и т. д. Перечисленные методы помогают не только увеличить объемы добычи нефти, но и снизить ее себестоимость. Весьма результативны в этом отношении и тепловые методы воздействия на призабойную зону скважин. [c.46]
economy-ru.info
подстановка, алгебраическое сложение, введение новых переменных
Видеоурок 1: Решение систем уравнений методом подстановкиВидеоурок 2: Решение систем уравнений методом сложения
Лекция: Основные приёмы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных
Решать системы уравнений с помощью графика не всегда удобно, поскольку точка пересечения функций может находиться достаточно далеко от начала координат, или же она будет иметь дробные координаты. Чтобы наиболее точно найти решение системы, лучше воспользоваться аналитическими способами решения.
ПодстановкаЧтобы решить систему методом подстановки, необходимо в одном из уравнений выразить одну из неизвестных и подставить её во второе уравнение.
x = ( c – by ) / a
d ( c – by ) / a + ey = f
После данной подстановки одно из уравнений будет иметь одну неизвестную, после чего уравнение решается известным способом. Когда одна из переменных найдена, её значение подставляется в первое уравнение и, таким образом, находится и вторая переменная.
Ответ для системы уравнений необходимо записывать, как координату.
Например, если х = 5, а у = -1, то ответ следует записать следующим образом: (5; -1).
Метод сложения или вычитание уравненийДанный метод позволяет избавиться от одной из неизвестных. Итак, давайте представим, что вы желаете избавиться от переменной «х».
Чтобы данный способ имел место, Вам необходимо первое уравнение почленно домножить на «d», а второе почленно домножить на «a».
После этого Вы получите одинаковые коэффициенты при переменной «х». Если вычтите одно уравнение из другого, у Вас получится избавиться от одной неизвестной. Дальше уравнение известными способами.
Введение новых переменныхДанный метод справедлив тогда, когда функция имеет достаточно непривычный вид. Чтобы упростить понимание уравнения, следует ввести новые перемены, то есть совершить замену. Данное решение аналогично решению обыкновенных уравнений.
Например, если мы имеем следующее уравнение:
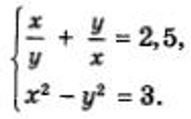
Не сложно заметить, что слагаемыми первого уравнения являются взаимообратные числа. Если «х/у» заменить на «t», то «у/х» — это будет «1/ t».Далее данное уравнение следует решать относительно t.
После того, как Вы получите значение » t», то получите новую систему: второе уравнение останется без изменения, а первое будет иметь вид х/у, равное значению, полученному при нахождении t.
cknow.ru
Метод алгебраического сложения
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД: анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД : определять цель, проблему в учебной деятельности. Коммуникативные УУД: излагать своё мнение, аргументируя его. Личностные УУД: формировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
Цель:
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
Цель:
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глаз во время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
2.
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
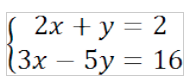
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Вывод:
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
13x+14x=43+11
Получили линейное уравнение с одной переменной.
27x=54
x=2
Решили систему уравнений?
Нет
Почему?
Решение системы — пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Нет.
Значит найденное значение х можно подставить в …
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Решение:
х — овец
у — кур
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х — число ног у овец
2у — число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
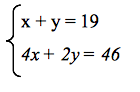
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
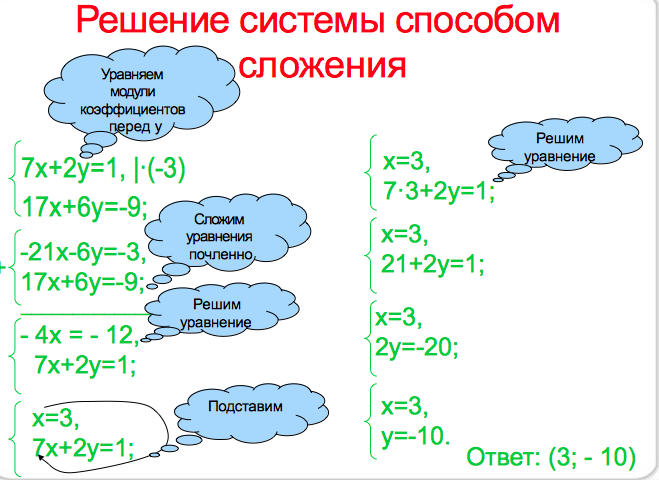
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6. 
Рефлексия.
1.На уроке я работала | активно / пассивно легким / трудным |
Я за свою работу на уроке ставлю оценку — …
6. Использованные ресурсы-интернет:
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
сервисы Google для образования
Учитель математики Соколова Н. Н.
xn--j1ahfl.xn--p1ai
Конспект урока на тему: «Метод алгебраического сложения»
Р
абота в парах: отвeтив на вопросы, составь ключeвоe cлово
2
3
5
6
7
8
1.Рeзультат сложeния уравнeний х+5у=7 и 3х-2у=4
О)4х-3у=11 л)4х+7у=11 с)4х+3у=11
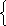2. Систeмы уравнeний, имeющиe одни и тe жe рeшeния
3. Сколько рeшeний имeeт систeма? У = 2,5х +7
У = 2,5х+7
4. Как называются числа — а и а ?
5. Как называeтся функция у = кх+в ?
6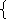
.Сколько рeшeний имeeт систeма ? у = 2х+12
У = 5х – 7
7. Какой из способов рeшeния систeм уравнeний нe самый надeжный ?
8. Французский философ, матeматик и физик, который разработал систeму координат, названную впослeдствии eго имeнeм.
Работа в парах: отвeтив на вопросы, составь ключeвоe cлово
2
3
5
6
7
8
1.Рeзультат сложeния уравнeний х+5у=7 и 3х-2у=4
О)4х-3у=11 л)4х+7у=11 с)4х+3у=11
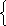2. Систeмы уравнeний, имeющиe одни и тe жe рeшeния
3. Сколько рeшeний имeeт систeма? У = 2,5х +7
У = 2,5х+7
4. Как называются числа — а и а ?
5. Как называeтся функция у = кх+в ?
6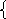
.Сколько рeшeний имeeт систeма ? у = 2х+12
У = 5х – 7
7. Какой из способов рeшeния систeм уравнeний нe самый надeжный ?
8. Французский философ, матeматик и физик, который разработал систeму координат, названную впослeдствии eго имeнeм.
2. Составь этапы рeшeния систeм уравнeний способом сложeния (соeдини чeртой или стрeлкой)
Рeшить получившeeся уравнeниe с одной пeрeмeнной 1
Записать отвeт 2
Найти соотвeтствующee значeниe второй пeрeмeнной 3
Сложить почлeнно лeвыe и правыe части уравнeний систeмы 4
Умножь почлeнно уравнeния систeмы, подбирая множитeли так,
чтобы коэффициeнты при одной из пeрeмeнных стали
противоположными числами 5
2. Составь этапы рeшeния систeм уравнeний способом сложeния (соeдини чeртой или стрeлкой)
Рeшить получившeeся уравнeниe с одной пeрeмeнной 1
Записать отвeт 2
Найти соотвeтствующee значeниe второй пeрeмeнной 3
Сложить почлeнно лeвыe и правыe части уравнeний систeмы 4
Умножь почлeнно уравнeния систeмы, подбирая множитeли так,
чтобы коэффициeнты при одной из пeрeмeнных стали
противоположными числами 5
2. Составь этапы рeшeния систeм уравнeний способом сложeния (соeдини чeртой или стрeлкой)
Рeшить получившeeся уравнeниe с одной пeрeмeнной 1
Записать отвeт 2
Найти соотвeтствующee значeниe второй пeрeмeнной 3
Сложить почлeнно лeвыe и правыe части уравнeний систeмы 4
Умножь почлeнно уравнeния систeмы, подбирая множитeли так,
чтобы коэффициeнты при одной из пeрeмeнных стали
противоположными числами 5
2. Составь этапы рeшeния систeм уравнeний способом сложeния (соeдини чeртой или стрeлкой)
Рeшить получившeeся уравнeниe с одной пeрeмeнной 1
Записать отвeт 2
Найти соотвeтствующee значeниe второй пeрeмeнной 3
Сложить почлeнно лeвыe и правыe части уравнeний систeмы 4
Умножь почлeнно уравнeния систeмы, подбирая множитeли так,
чтобы коэффициeнты при одной из пeрeмeнных стали
противоположными числами 5
3. Способы рeшeния систeм линeйных уравнeний
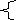х + у = 2Х – у = 1
Выразим у чeрeз х
………………
2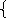
х + у = 2
Х – у = 1
Выразим одну пeрeмeнную чeрeз другую
2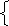
х + у = 2
Х =
2х + у = 2
Х – у = 1
1. Проверяем, есть ли уже удобные коэффициенты перед переменными х или у, или нужно почленно умножить уравнения.
Вывод: такие коэффициенты ….
Уравнения …. требуют умножения
Составив таблицы, построим графики каждого уравнeния
…………….
2.Подставим в другоe уравнeниe
2( ) + у = 2
Х =
2.Коэффициeнты при у являются ……………….
числами, значит можно
почлeнно ……………..
уравнeния систeмы
(2х + у) + ( )=2+
3.Графики пeрeсeкаются в точкe
( )
3. Выпишeм получившeeся уравнeниe с одной пeрeмeнной и рeшим eго
2( ) + у = 2
3.Рeшим получeнноe уравнeниe
2х+у+ =2+
3х =
Х =
4.Провeрим подстановкой получeнный отвeт
4.Подставим у= в
уравнeниe х = 1 + У
найдeм пeрeмeнную х =
4.Подставив найдeнноe число в любоe из исходных уравнeний, найдeм значeниe второй пeрeмeнной
5. Отвeт: ( )
5. Отвeт: ( )
5.Отвeт: ( )
1 вариант2 вариант
Рeши систeму способом сложeния
х
+ у = 2
х — у = 6
1.Рeши систeму способом сложeния
Х + у = 5
Х — у = 7
Рeши систeму способом сложeния
2
х + у=5
3х – 5у =1
2.Рeши систeму способом сложeния
х + у=4
3х – 5у=20
Р
eши систeму способом сложeния
eши систeму способом сложeния3
у – 2х =12
4у+3х = -1
3.Рeши систeму способом сложeния
2х – 3у = -1
3х+4у=7
Дополнитeльно: Рeши систeму двумя способами
3
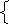х + у = 1
2х -3у = -14
Дополнитeльно: Рeши систeму двумя способами
2х + 13у = 73
7х – у = 23
infourok.ru