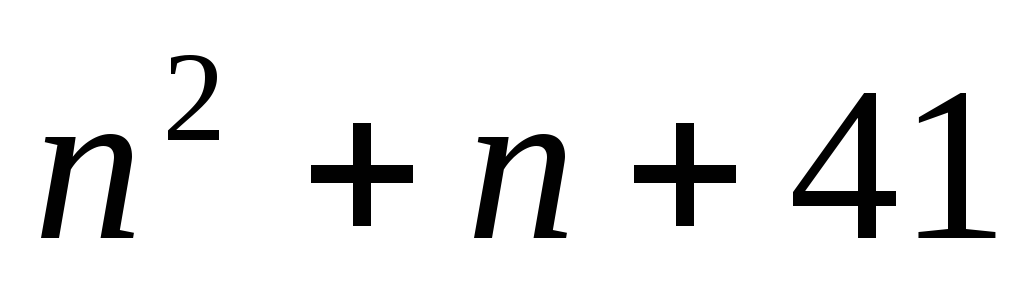Методом математической индукции докажите 1) формулу общего члена арифметической прогрессии a_n=a_1+d*(n-1)
УСЛОВИЕ: Методом математической индукции докажите
1) формулу общего члена арифметической прогрессии a_n=a_1+d*(n-1)
2) \( \displaystyle S_n=\frac{(2a_1+d(n-1))n}{2} \)формулу суммы первых n членов арифметической прогрессии;
3) формулу общего члена геометрической прогрессии
\( \displaystyle b_n=\frac{b_1(1-q^n)}{1-q} \) при \( q \neq 1 \)
РЕШЕНИЕ:
1)
База индукции: 1
$$ a_1=a_1+d*0=a_1 $$ проверено.
Предположим, что утверждение верно для n=k.
$$ a_{k}=a_1+d(k-1)=a_1+dk-d $$
Покажем, и докажем, что утверждение верно так же для n=k+1.
$$ a_{k+1}=a_1+d[(k+1)-1]=a_1+dk $$
Так как, следуя предположению $$ a_{k}=a_1+d(k-1)=a_1+dk-d $$ то прибавив к данному выражению d. Мы получим следующий член $$ a_{k+1}=a_1+d[(k+1)-1]=a_1+dk $$.
Т. е. предположение верно. Ч. Т. Д.
2)
$$ S_n= \frac{n[2a_1+d(n-1)]}{2} $$
База : 1
Проверка: \( S_1= \frac{2a_1}{2}=a_1 \).
Предположение: $$ n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2} $$
Теперь покажем и докажем, что данное выражение верно и при \(n=k+1\):
Так как предыдущий член был равен k, то что бы узнать сумму первых k+1 членов, достаточно прибавить k+1 член (используя формулу которую мы доказали ранее):
$$ S_{k+1}= \frac{2a_1k+dk^2-dk}{2}+(a_1+dk)= \frac{2(a_1+dk)+2a_1k+dk^2-dk}{2}\\= \frac{2a_1+2dk+2a_1k+dk^2-dk}{2}= \frac{2a_1k+2a_1+dk^2+dk}{2}\\ = \frac{2a_1(k+1)+dk(k+1)}{2}= \frac{(k+1)(2a_1+dk)}{2} $$
т. е. мы пришли к изначальной формуле, если туда подставить k+1. Ч. Т. Д.
3)
Это не формула общего члена, это формула суммы.
При q=1 получается деление на ноль, поэтому сразу пишем \(q \neq 1\)
База: 1
$$ b_1= \frac{b_1(1-q)}{(1-q)}=b_1 $$
Предположим, что формула верна для: n=k.
Покажем и докажем что формула верна для n=k+1:
Как и с суммой арифм. прогрессии мы добавим k+1 член к сумме.
$$ b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q} $$
Ч. Т. Д.
Похожие примеры:
mathshkola.ru
Лекция 06. Метод математической индукции
Лекция 6. Метод математической индукции.
Новые знания в науке и жизни добываются разными способами, но все они (если не углубляться в детали) делятся на два вида – переход от общего к частному и от частного к общему. Первый – это дедукция, второй – индукция. Дедуктивные рассуждения – это то, что в математике обычно называют логическими рассуждениями, и в математической науке дедукция является единственным законным методом исследования. Правила логических рассуждений были сформулированы два с половиной тысячелетия назад древнегреческим учёным Аристотелем. Он создал полный список простейших правильных рассуждений, силлогизмов – «кирпичиков» логики, одновременно указав типичные рассуждения, очень похожие на правильные, однако неправильные (с такими «псевдологическими» рассуждениями мы часто встречаемся в СМИ).
Индукция (induction – по-латыни наведение) наглядно иллюстрируется известной легендой о том, как Исаак Ньютон сформулировал закон всемирного тяготения после того, как ему на голову упало яблоко. Ещё пример из физики: в таком явлении, как электромагнитная индукция, электрическое поле создает, «наводит» магнитное поле. «Ньютоново яблоко» – типичный пример ситуации, когда один или несколько частных случаев, то есть наблюдения, «наводят» на общее утверждение, общий вывод делается на основании частных случаев. Индуктивный метод является основным для получения общих закономерностей и в естественных, и в гуманитарных науках. Но он имеет весьма существенный недостаток: на основании частных примеров может быть сделан неверный вывод. Гипотезы, возникающие при частных наблюдениях, не всегда являются правильными. Рассмотрим пример, принадлежащий Эйлеру.
Будем вычислять
значение трехчлена  при некоторых первых значениях n:
при некоторых первых значениях n:
n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 43 | 53 | 61 | 71 | 83 | 97 | 113 |
Заметим, что
получаемые в результате вычислений
числа являются простыми. И непосредственно
можно убедиться, что для каждого n от 1 до 39 значение многочлена 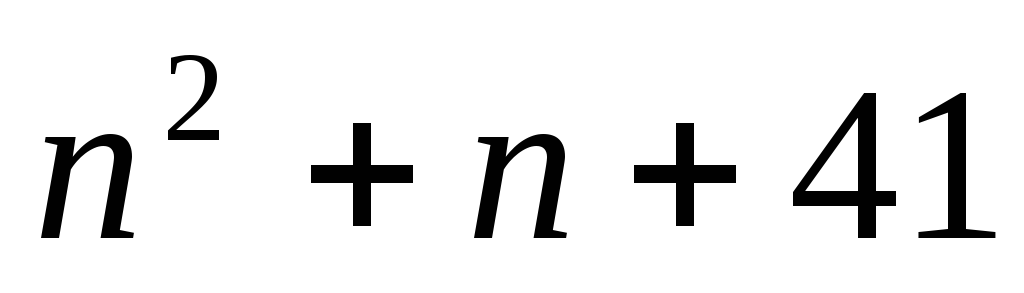 является простым числом. Однако при n=40
получаем число 1681=412,
которое не является простым. Таким
образом, гипотеза, которая здесь могла
возникнуть, то есть гипотеза о том, что
при каждом n число
является простым числом. Однако при n=40
получаем число 1681=412,
которое не является простым. Таким
образом, гипотеза, которая здесь могла
возникнуть, то есть гипотеза о том, что
при каждом n число 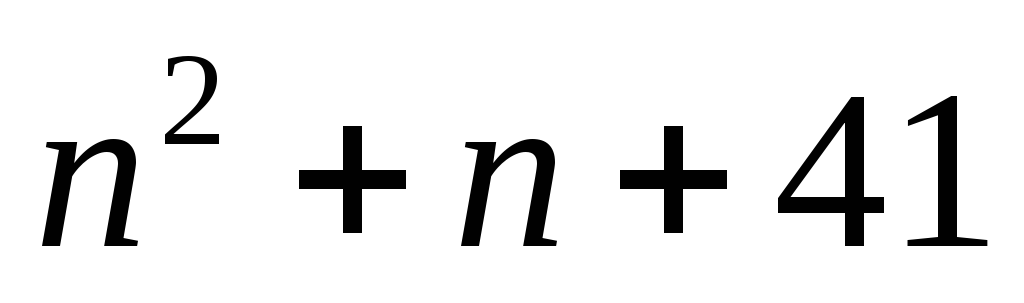 является простым, оказывается неверной.
является простым, оказывается неверной.
Лейбниц в 17 веке
доказал, что при всяком целом положительном n число делится на 3, число  делится на 5 и т.д. На основании этого он
предположил, что при всяком нечётном k и любом натуральном n число
делится на 5 и т.д. На основании этого он
предположил, что при всяком нечётном k и любом натуральном n число 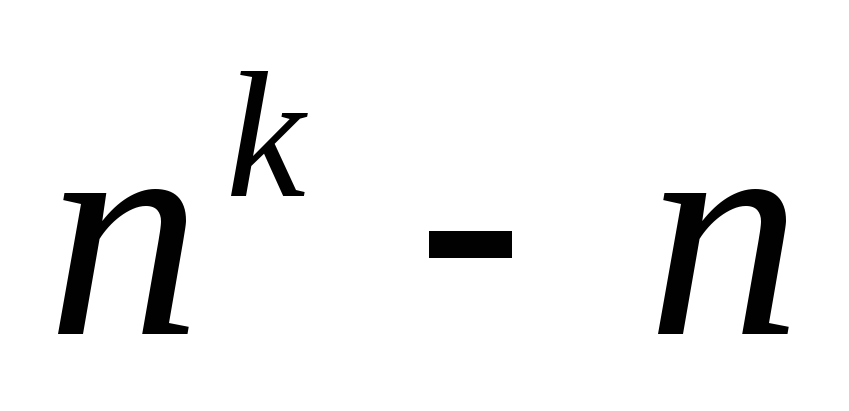 делится на k,
но скоро сам заметил, что
делится на k,
но скоро сам заметил, что  не делится на 9.
не делится на 9.
Рассмотренные примеры позволяют сделать важный вывод: утверждение может быть справедливым в целом ряде частных случаев и в то же время несправедливым вообще. Вопрос о справедливости утверждения в общем случае удается решить посредством применения особого метода рассуждений, называемого методом математической индукции (полной индукции, совершенной индукции).
6.1. Принцип математической индукции.
♦ В основе метода математической индукции лежит
1) проверяется справедливость этого утверждения для n=1 (базис индукции),
2) предполагается справедливость этого утверждения для n=k, где k – произвольное натуральное число 1 (предположение индукции), и с учётом этого предположения устанавливается справедливость его для n=k+1.
Доказательство. Предположим противное, то есть предположим, что утверждение справедливо не для всякого натурального n. Тогда существует такое натуральное m, что:
1) утверждение для n=m несправедливо,
2) для всякого n, меньшего m, утверждение справедливо (иными словами, m есть первое натуральное число, для которого утверждение несправедливо).
Очевидно, что m>1,
т.к. для n=1
утверждение справедливо (условие 1).
Следовательно, 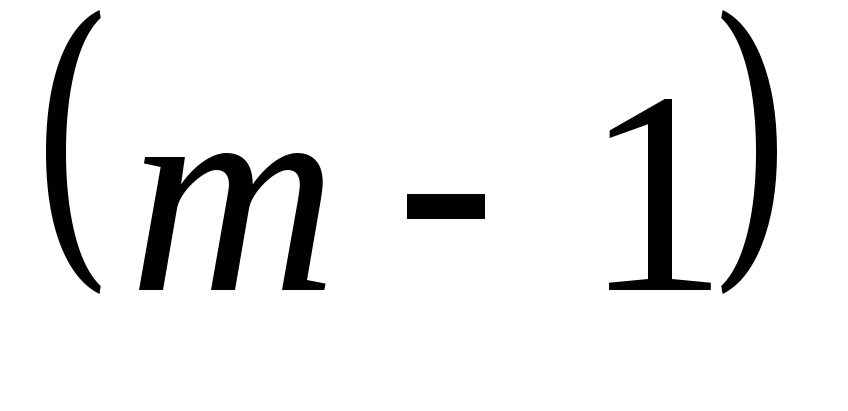 – натуральное число. Выходит, что для
натурального числа
– натуральное число. Выходит, что для
натурального числа 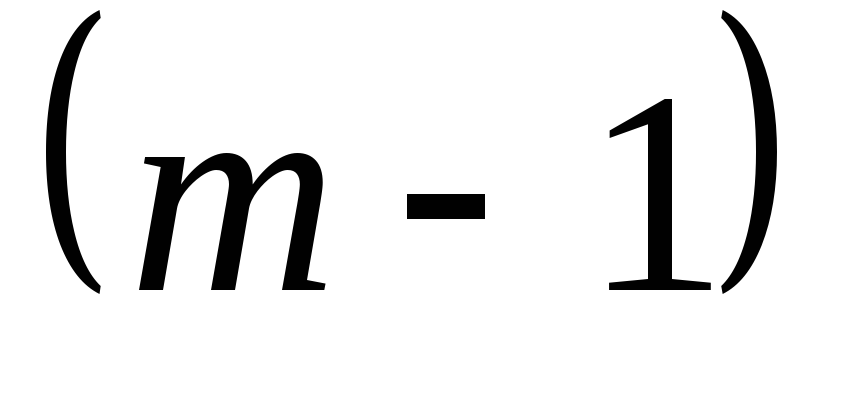 утверждение справедливо, а для следующего
натурального числа m оно несправедливо. Это противоречит
условию 2. ■
утверждение справедливо, а для следующего
натурального числа m оно несправедливо. Это противоречит
условию 2. ■
Заметим, что в доказательстве использовалась аксиома о том, что в любой совокупности натуральных чисел содержится наименьшее число.
Доказательство, основанное на принципе математической индукции, называется методом полной математической индукции.
Пример 6.1. Доказать, что при любом натуральном n число 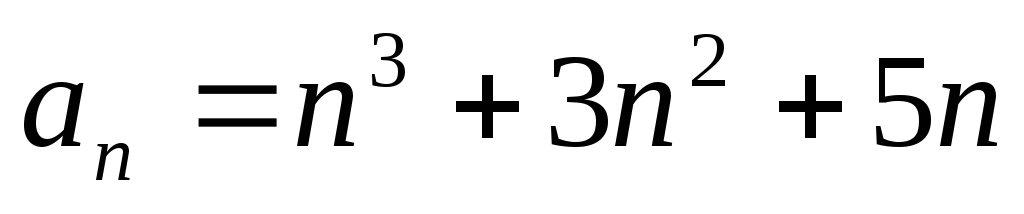
Решение. Воспользуемся методом полной математической индукции.
1) При n=1  ,
поэтому a1 делится на 3 и утверждение справедливо
при n=1.
,
поэтому a1 делится на 3 и утверждение справедливо
при n=1.
2) Предположим, что
утверждение справедливо при n=k,  ,
то есть что число
,
то есть что число 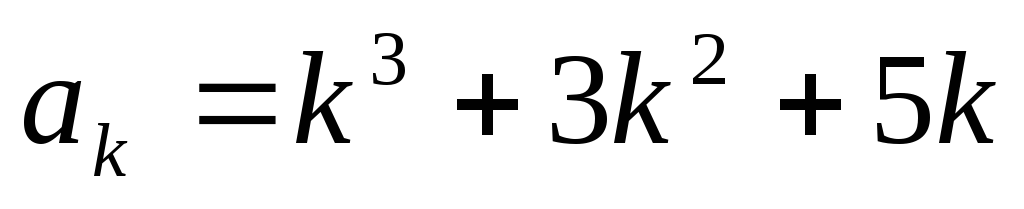 делится на 3, и установим, что при n=k+1
число
делится на 3, и установим, что при n=k+1
число 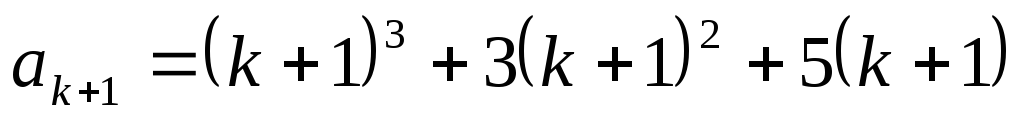 делится на 3.
делится на 3.
В самом деле, 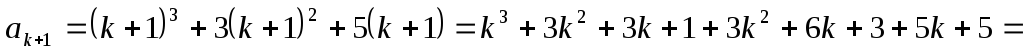
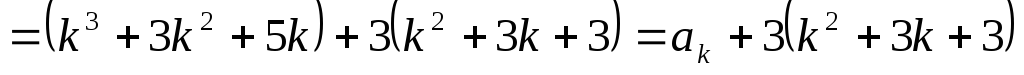 .
.Т.к. каждое слагаемое делится на 3, то их сумма также делится на 3. ■
Пример 6.2. Доказать,
что сумма первых n натуральных нечётных чисел равна
квадрату их числа, то есть 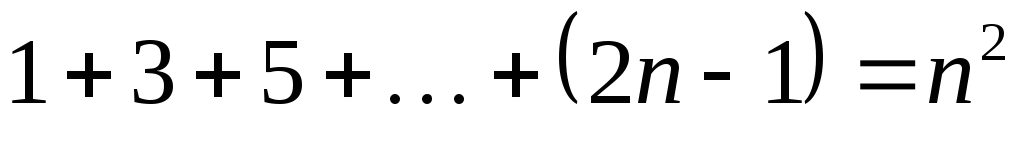 .
.
Решение. Воспользуемся методом полной математической индукции.
1) Проверяем справедливость данного утверждения при n=1: 1=12 – это верно.
2) Предположим, что
сумма первых k ( )
нечётных чисел равна квадрату числа
этих чисел, то есть
)
нечётных чисел равна квадрату числа
этих чисел, то есть  .
Исходя из этого равенства, установим,
что сумма первых
.
Исходя из этого равенства, установим,
что сумма первых
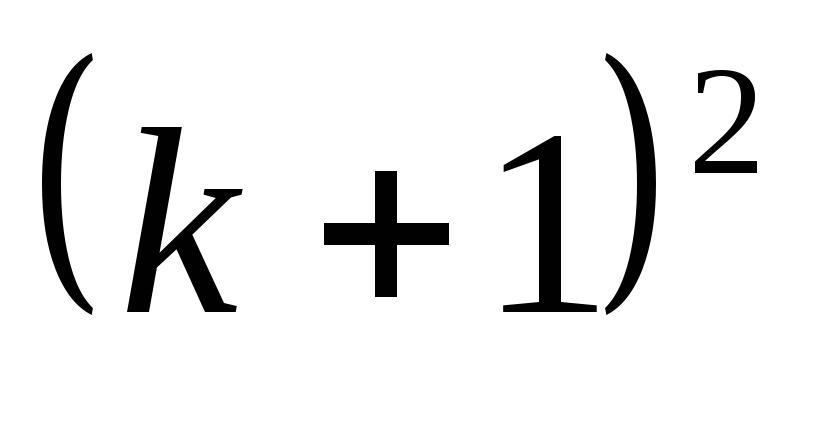 ,
то есть
,
то есть  .
.Пользуемся нашим предположением и получаем
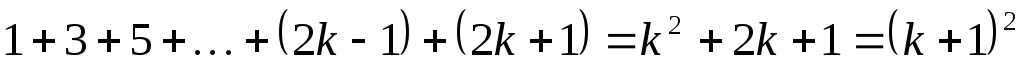 .
■
.
■
Метод полной математической индукции применяется для доказательства некоторых неравенств. Докажем неравенство Бернулли.
Пример 6.3. Доказать, что при  и любом натуральном n справедливо неравенство
и любом натуральном n справедливо неравенство 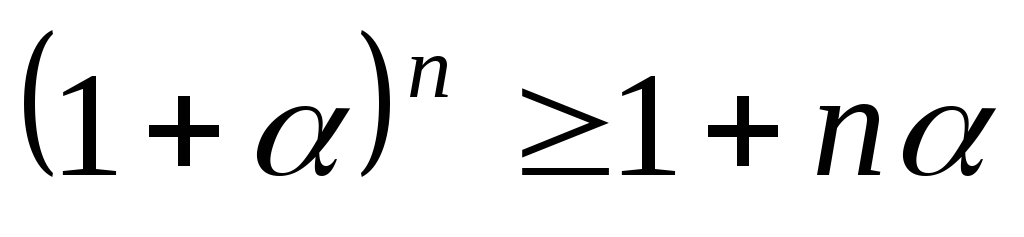 (неравенство
Бернулли).
(неравенство
Бернулли).
Решение. 1) При n=1 получаем , что верно.
2) Предполагаем,
что при n=k имеет место неравенство 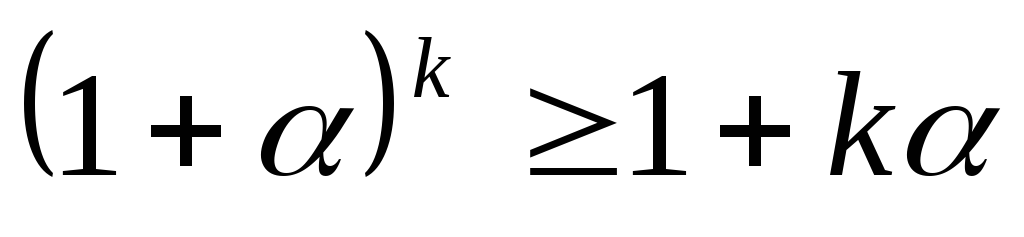 (*). Используя это предположение, докажем,
что
(*). Используя это предположение, докажем,
что 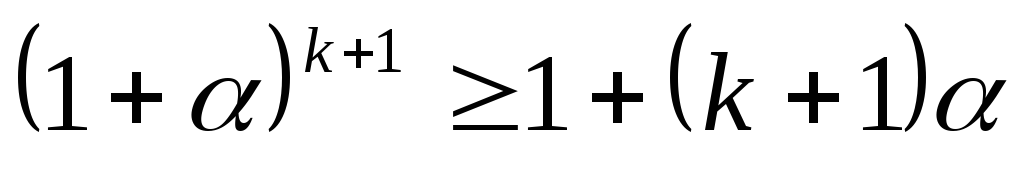 .
Отметим, что при
.
Отметим, что при 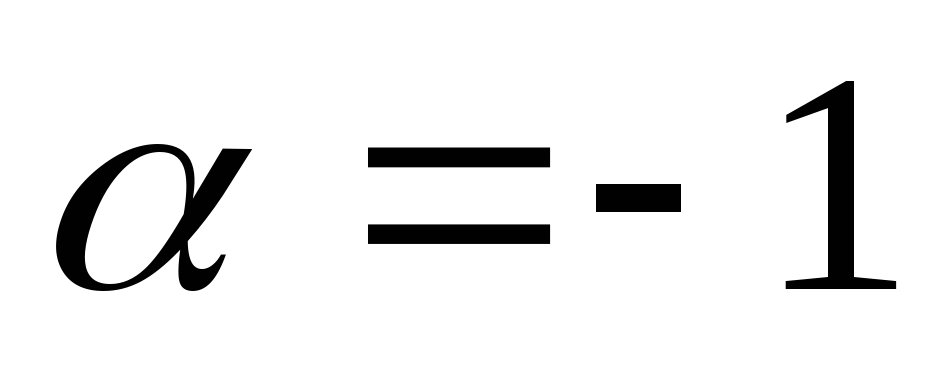 это неравенство выполняется и поэтому
достаточно рассмотреть случай
это неравенство выполняется и поэтому
достаточно рассмотреть случай 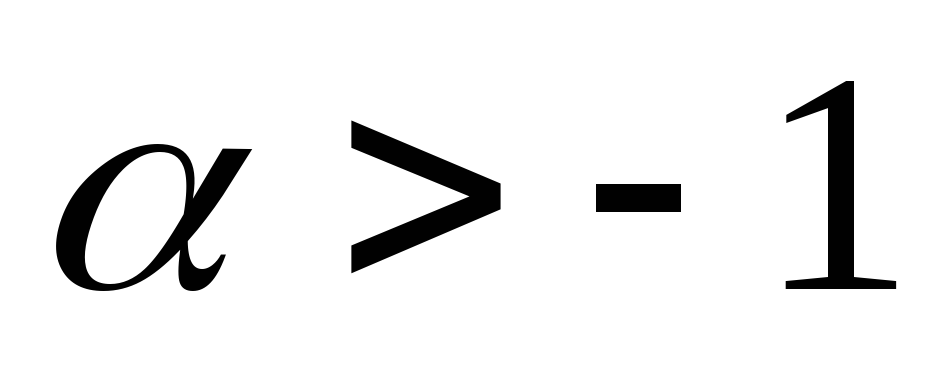 .
.
Умножим обе части
неравенства (*) на число  и получим:
и получим:
 ,
то есть (1+
,
то есть (1+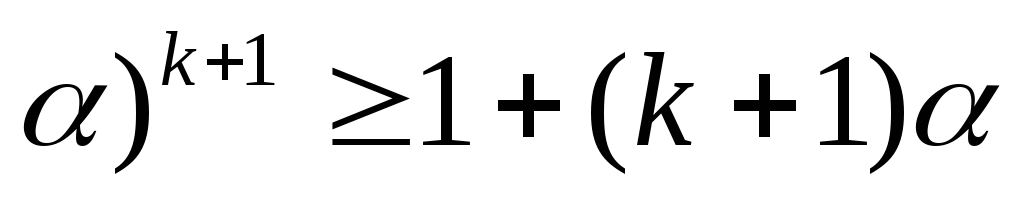
Доказательство
методом неполной
математической индукции некоторого утверждения, зависящего от n,
где 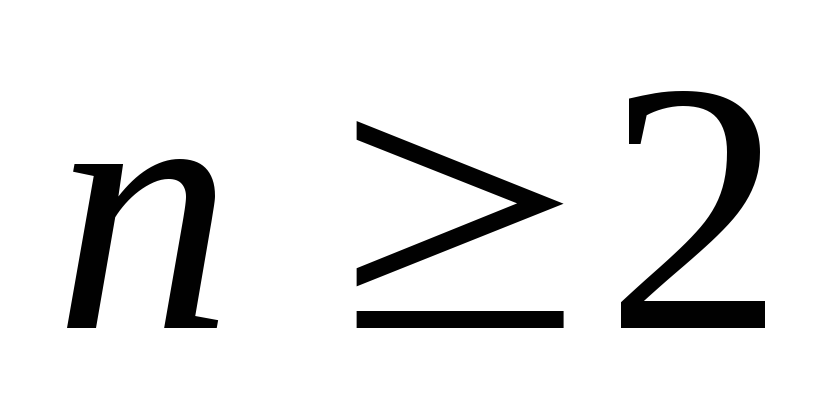 проводится аналогичным образом, но в
начале устанавливается справедливость
для наименьшего значения n.
проводится аналогичным образом, но в
начале устанавливается справедливость
для наименьшего значения n.
В некоторых задачах явно не сформулировано утверждение, которое можно доказать методом математической индукции. В таких случаях надо самим установить закономерность и высказать гипотезу о справедливости этой закономерности, а затем методом математической индукции проверить предполагаемую гипотезу.
Пример 6.4. Найти сумму 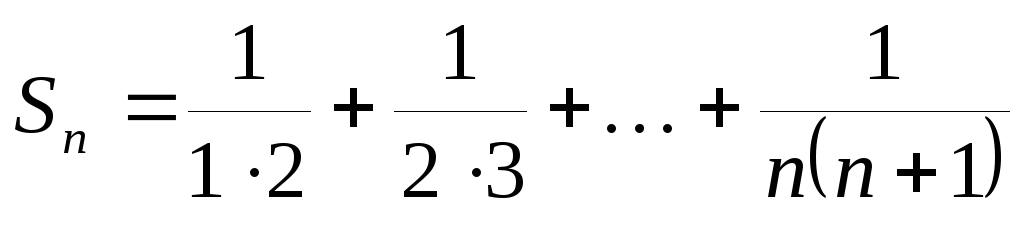 .
.
Решение. Найдём
суммы S1, S2, S3.
Имеем 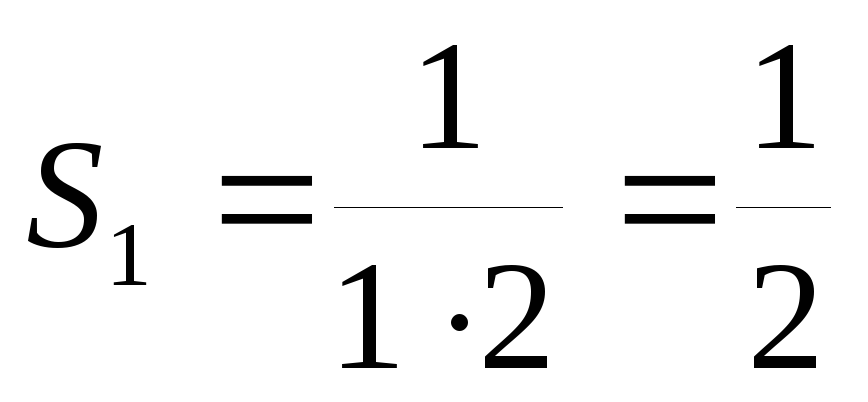 ,
, 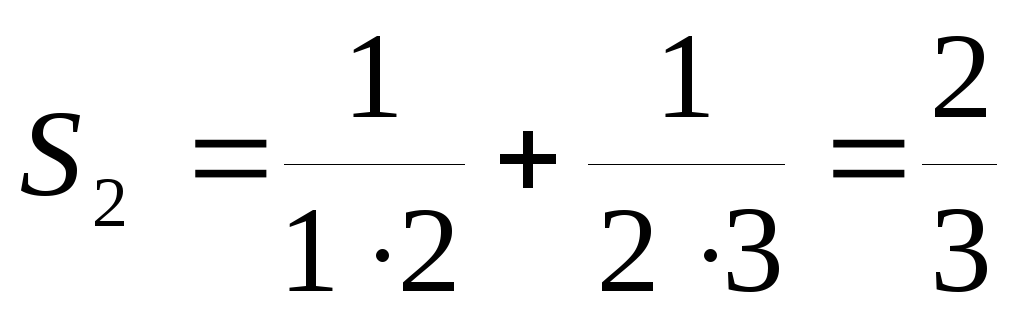 ,
,  .
Высказываем гипотезу, что при любом
натуральном n справедлива формула
.
Высказываем гипотезу, что при любом
натуральном n справедлива формула 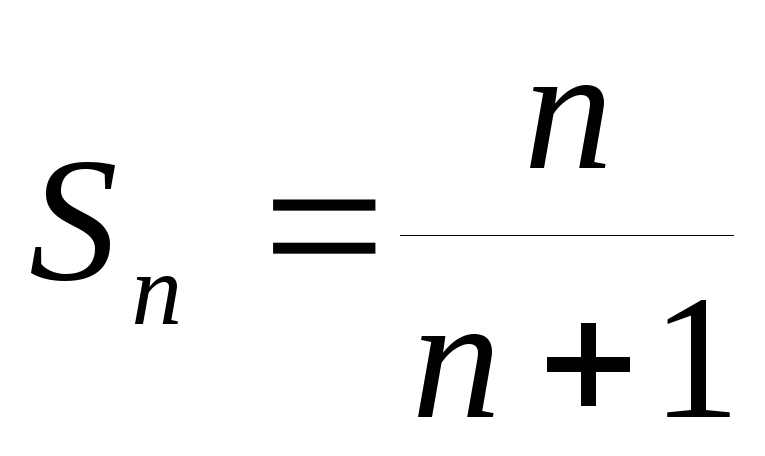 .
Для проверки этой гипотезы воспользуемся
методом полной математической индукции.
.
Для проверки этой гипотезы воспользуемся
методом полной математической индукции.
1) При n=1
гипотеза верна, т.к. 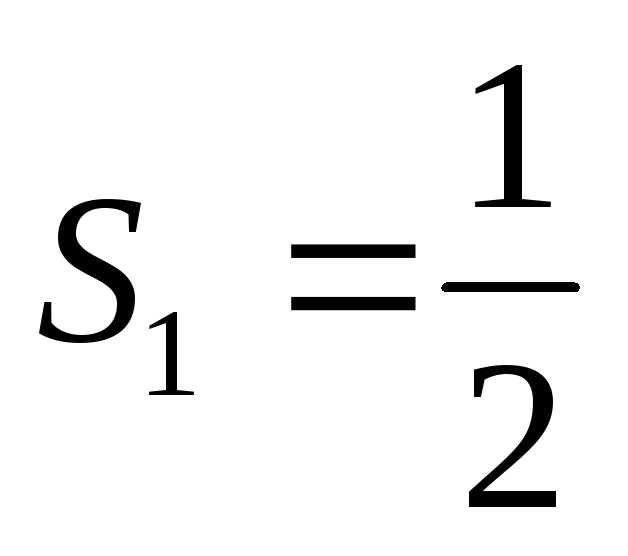 .
.
2) Предположим, что
гипотеза верна при n=k, 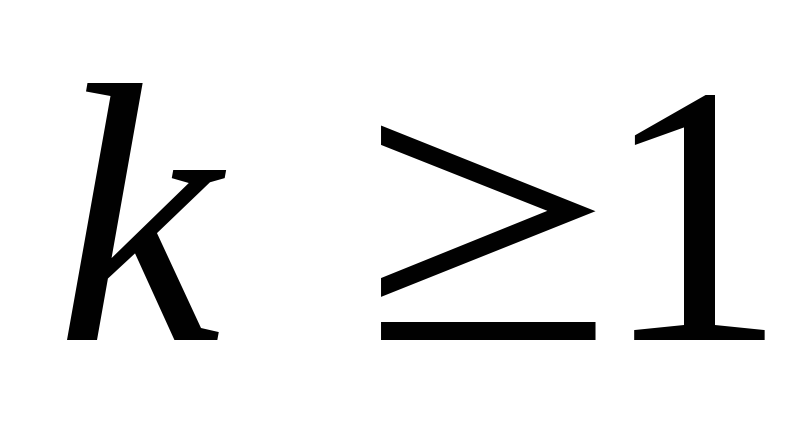 ,
то есть
,
то есть 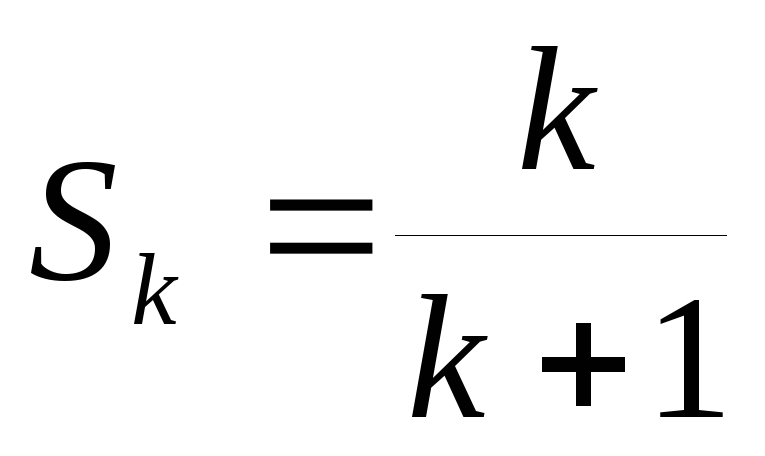 .
Используя эту формулу, установим, что
гипотеза верна и при n=k+1,
то есть
.
Используя эту формулу, установим, что
гипотеза верна и при n=k+1,
то есть
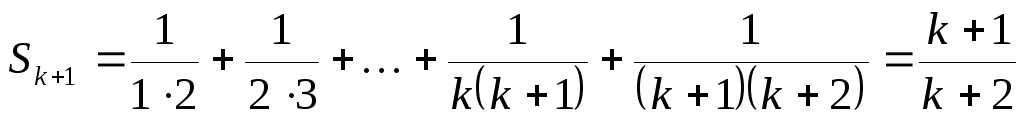 .
.
В самом деле,
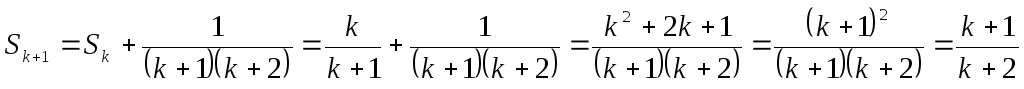 .
.
Итак, исходя из
предположения, что гипотеза верна при n=k,  ,
доказано, что она верна и при n=k+1,
и на основании принципа математической
индукции делаем вывод, что формула
справедлива при любом натуральном n.
■
,
доказано, что она верна и при n=k+1,
и на основании принципа математической
индукции делаем вывод, что формула
справедлива при любом натуральном n.
■
Пример 6.5. В математике доказывается, что сумма
двух равномерно непрерывных функций
является равномерно непрерывной
функцией. Опираясь на это утверждение,
нужно доказать, что сумма любого числа  равномерно непрерывных функций является
равномерно непрерывной функцией. Но
поскольку мы ещё не ввели понятие
«равномерно непрерывная функция»,
поставим задачу более абстрактно: пусть
известно, что сумма двух функций,
обладающих некоторым свойством S,
сама обладает свойством S.
Докажем, что сумма любого числа функций
обладает свойством S.
равномерно непрерывных функций является
равномерно непрерывной функцией. Но
поскольку мы ещё не ввели понятие
«равномерно непрерывная функция»,
поставим задачу более абстрактно: пусть
известно, что сумма двух функций,
обладающих некоторым свойством S,
сама обладает свойством S.
Докажем, что сумма любого числа функций
обладает свойством S.
Решение. Базис индукции здесь содержится в самой
формулировке задачи. Сделав предположение
индукции, рассмотрим  функций f1, f2,
…, fn, fn+1,
обладающих свойством S.
Тогда
функций f1, f2,
…, fn, fn+1,
обладающих свойством S.
Тогда 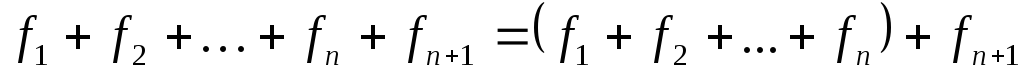 .
В правой части первое слагаемое обладает
свойством S по предположению индукции, второе
слагаемое обладает свойством S по условию. Следовательно, их сумма
обладает свойством S – для двух слагаемых «работает» базис
индукции.
.
В правой части первое слагаемое обладает
свойством S по предположению индукции, второе
слагаемое обладает свойством S по условию. Следовательно, их сумма
обладает свойством S – для двух слагаемых «работает» базис
индукции.
Тем самым утверждение доказано и будем использовать его далее. ■
Пример 6.6. Найти все натуральные n, для которых справедливо неравенство
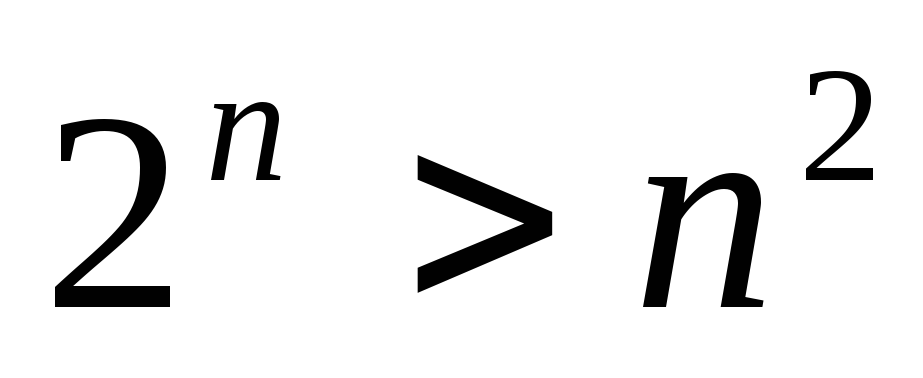 .
.
Решение. Рассмотрим n=1,
2, 3, 4, 5, 6. Имеем: 21>12,
22=22,
23<32,
24=42,
25>52,
26>62.
Таким образом, можно высказать гипотезу:
неравенство 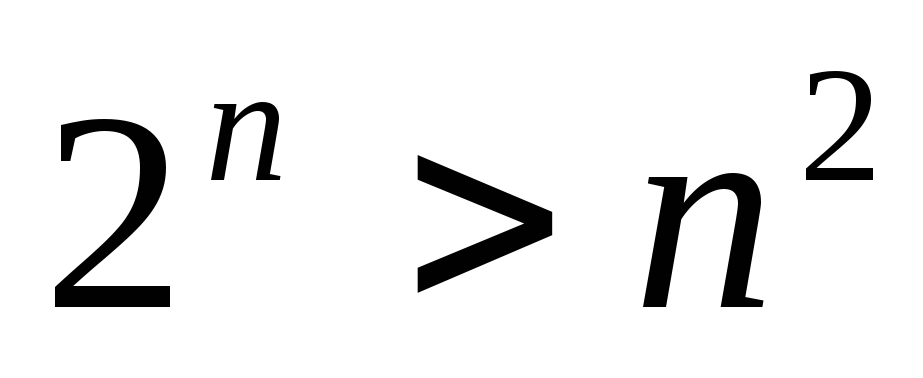 имеет место для каждого
имеет место для каждого 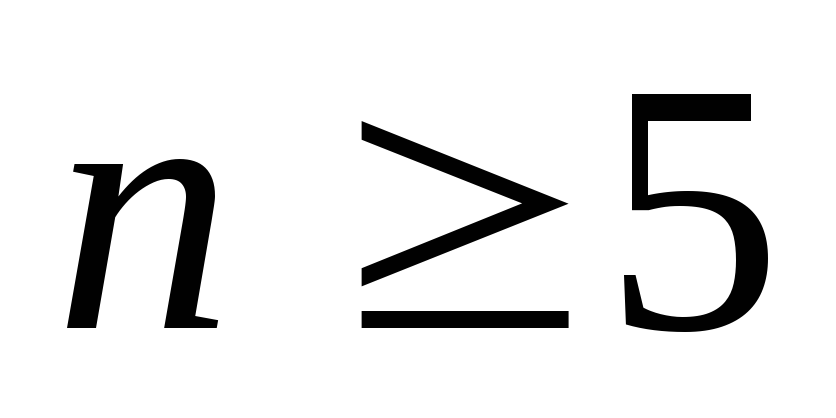 .
Для доказательства истинности этой
гипотезы воспользуемся принципом
неполной математической индукции.
.
Для доказательства истинности этой
гипотезы воспользуемся принципом
неполной математической индукции.
1) Как было установлено выше, данная гипотеза истинна при n=5.
2) Предположим, что
она истинна для n=k, 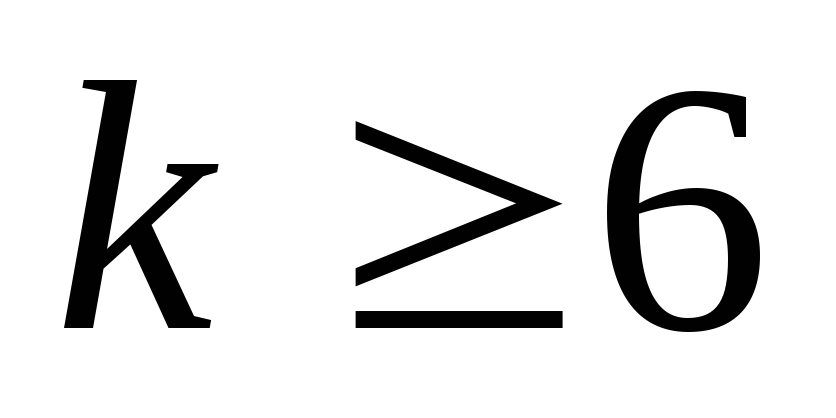 ,
то есть справедливо неравенство
,
то есть справедливо неравенство  .
Используя это предположение, докажем,
что справедливо неравенство
.
Используя это предположение, докажем,
что справедливо неравенство  .
.
Т. к. 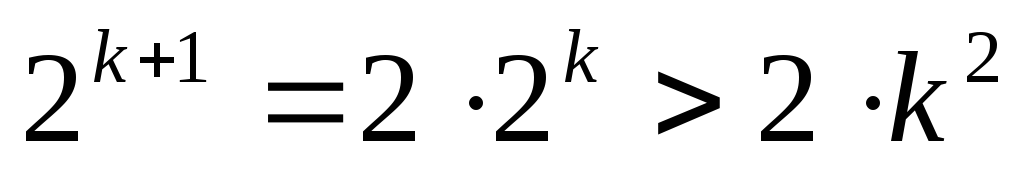 и при
и при 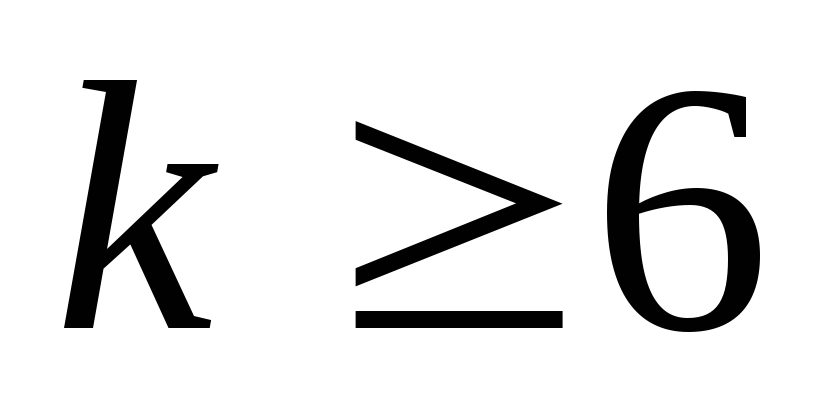 имеет место неравенство
имеет место неравенство 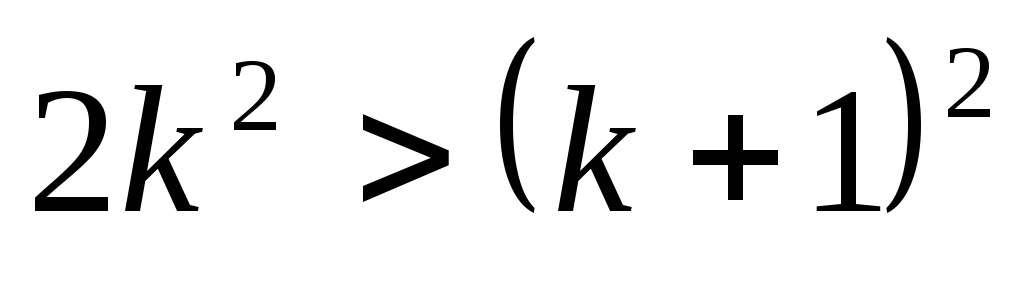
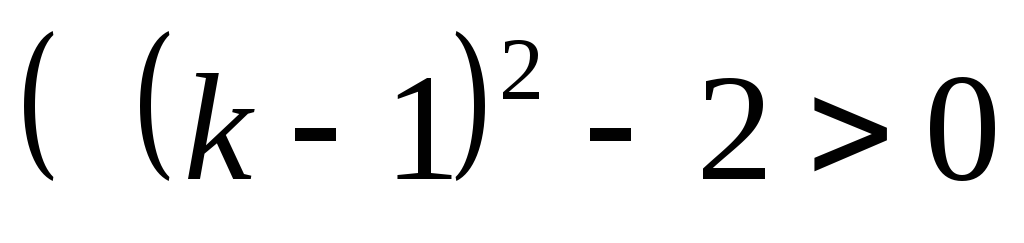 при
при  ,
,
то получаем, что  .
Итак, истинность гипотезы при n=k+1
следует из предположения, что она верна
при n=k,
.
Итак, истинность гипотезы при n=k+1
следует из предположения, что она верна
при n=k, 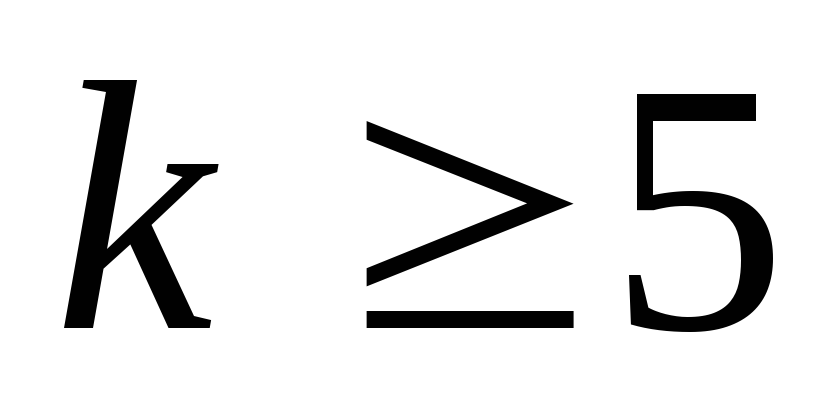 .
.
Из пп. 1 и 2 на
основании принципа неполной математической
индукции следует, что неравенство  верно при каждом натуральном
верно при каждом натуральном  .
■
.
■
Пример 6.7. Доказать,
что для любого натурального числа n справедлива формула дифференцирования 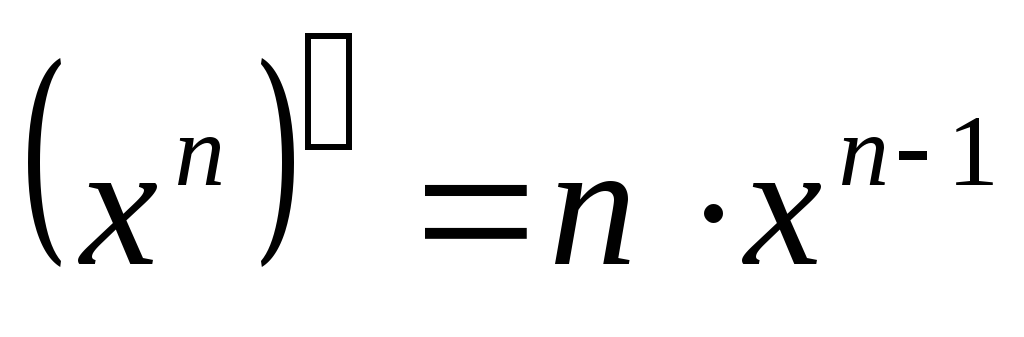 .
.
Решение. При n=1
данная формула имеет вид  ,
или 1=1, то есть она верна. Сделав
предположение индукции, будем иметь:
,
или 1=1, то есть она верна. Сделав
предположение индукции, будем иметь:
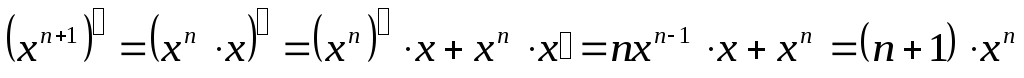 ,
,
что и требовалось доказать. ■
Пример 6.8. Доказать,
что множество, состоящее из n элементов, имеет  подмножеств.
подмножеств.
Решение. Множество, состоящее из одного элемента а, имеет два подмножества. Это верно, поскольку все его подмножества – пустое множество и само это множество, и 21=2.
Предположим, что
всякое множество из n элементов имеет  подмножеств. Если множество А состоит
из n+1
элементов, то фиксируем в нём один
элемент – обозначим его d,
и разобьём все подмножества на два
класса – не содержащие d и содержащие d.
Все подмножества из первого класса
являются подмножествами множества В,
получающегося из А выбрасыванием
элемента d.
подмножеств. Если множество А состоит
из n+1
элементов, то фиксируем в нём один
элемент – обозначим его d,
и разобьём все подмножества на два
класса – не содержащие d и содержащие d.
Все подмножества из первого класса
являются подмножествами множества В,
получающегося из А выбрасыванием
элемента d.
Множество В состоит
из n элементов, и поэтому, по предположению
индукции, у него  подмножеств, так что в первом классе
подмножеств, так что в первом классе 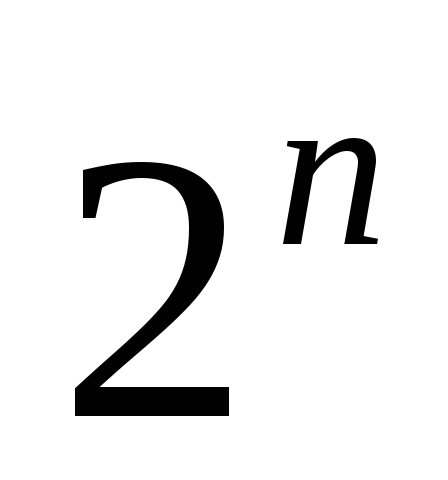 подмножеств.
подмножеств.
Но во втором классе
подмножеств столько же: каждое из них
получается ровно из одного подмножества
первого класса добавлением элемента d.
Следовательно, всего у множества А  подмножеств.
подмножеств.
Тем самым утверждение доказано. Отметим, что оно справедливо и для множества, состоящего из 0 элементов – пустого множества: оно имеет единственное подмножество – самого себя, и 20=1. ■
29
studfile.net
Примеры — Математическая индукция
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
Решение.
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
Учитывая равенство 1 + 2 + … + n = n(n + 1)/2, получаем
13 + 23 + … + n3 + (n + 1)3 = (1 + 2 + … + n + (n + 1))2,
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
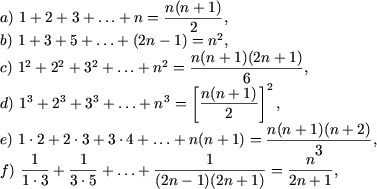 |
g) формула бинома Ньютона: |
Решение. a) При n = 1 равенство примет вид  1=1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место
1=1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место
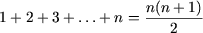 .Следует проверить (доказать), что P(n + 1), то есть
.Следует проверить (доказать), что P(n + 1), то есть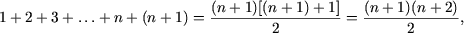
www.sites.google.com
Метод математической индукции (стр. 1 из 2)
Вступление
Основная часть
1. Полная и неполная индукция
2. Принцип математической индукции
3. Метод математической индукции
4. Решение примеров
5. Равенства
6. Деление чисел
7. Неравенства
Заключение
Список использованной литературы
Вступление
В основе всякого математического исследования лежат дедуктивный и индуктивный методы. Дедуктивный метод рассуждений — это рассуждение от общего к частному, т.е. рассуждение, исходным моментом которого является общий результат, а заключительным моментом – частный результат. Индукция применяется при переходе от частных результатов к общим, т.е. является методом, противоположным дедуктивному.
Метод математической индукции можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно.
Хотя и выросла область применения метода математической индукции, в школьной программе ему отводится мало времени. Ну, скажите, что полезного человеку принесут те два-три урока, за которые он услышит пять слов теории, решит пять примитивных задач, и, в результате получит пятёрку за то, что он ничего не знает.
А ведь это так важно — уметь размышлять индуктивно.
Основная часть
По своему первоначальному смыслу слово “индукция” применяется к рассуждениям, при помощи которых получают общие выводы, опираясь на ряд частных утверждений. Простейшим методом рассуждений такого рода является полная индукция. Вот пример подобного рассуждения.
Пусть требуется установить, что каждое натуральное чётное число n в пределах 4 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;
14=7+7; 16=11+5; 18=13+5; 20=13+7.
Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.
Таким образом, полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев.
Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция).
Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным методом открытия новых истин.
Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рассмотрим частные случаи:
1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод:
1+3+5+…+(2n-1)=n2
т.е. сумма n первых последовательных нечётных чисел равна n2
Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости приведённой формулы.
Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для бесконечного числа случаев мы не в состоянии. Неполная же индукция часто приводит к ошибочным результатам.
Во многих случаях выход из такого рода затруднений заключается в обращении к особому методу рассуждений, называемому методом математической индукции. Он заключается в следующем.
Пусть нужно доказать справедливость некоторого утверждения для любого натурального числа n (например нужно доказать, что сумма первых n нечётных чисел равна n2). Непосредственная проверка этого утверждения для каждого значения n невозможна, поскольку множество натуральных чисел бесконечно. Чтобы доказать это утверждение, проверяют сначала его справедливость для n=1. Затем доказывают, что при любом натуральном значении k из справедливости рассматриваемого утверждения при n=k вытекает его справедливость и при n=k+1.
Тогда утверждение считается доказанным для всех n. В самом деле, утверждение справедливо при n=1. Но тогда оно справедливо и для следующего числа n=1+1=2. Из справедливости утверждения для n=2 вытекает его справедливость для n=2+
+1=3. Отсюда следует справедливость утверждения для n=4 и т.д. Ясно, что, в конце концов, мы дойдём до любого натурального числа n. Значит, утверждение верно для любого n.
Обобщая сказанное, сформулируем следующий общий принцип.
Принцип математической индукции.
Если предложение А(n), зависящее от натурального числа n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение А(n) истинно для любого натурального числа n.
В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n>p, где p-фиксированное натуральное число. В этом случае принцип математической индукции формулируется следующим образом. Если предложение А(n) истинно при n=p и если А(k)ÞА(k+1) для любого k>p, то предложение А(n) истинно для любого n>p.Доказательство по методу математической индукции проводиться следующим образом. Сначала доказываемое утверждение проверяется для n=1, т.е. устанавливается истинность высказывания А(1). Эту часть доказательства называют базисом индукции. Затем следует часть доказательства, называемая индукционным шагом. В этой части доказывают справедливость утверждения для n=k+1 в предположении справедливости утверждения для n=k (предположение индукции), т.е. доказывают, что А(k)ÞA(k+1).
ПРИМЕР 1
Доказать, что 1+3+5+…+(2n-1)=n2.
Решение: 1) Имеем n=1=12. Следовательно,
утверждение верно при n=1, т.е. А(1) истинно.
2) Докажем, что А(k)ÞA(k+1).
Пусть k-любое натуральное число и пусть утверж-дение справедливо для n=k, т.е.
1+3+5+…+(2k-1)=k2.
Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что
1+3+5+…+(2k+1)=(k+1)2.
В самом деле,
1+3+5+…+(2k-1)+(2k+1)=k2+2k+1=(k+1)2.
Итак, А(k)ÞА(k+1). На основании принципа математической индукции заключаем, что предпо-ложение А(n) истинно для любого nÎN.
ПРИМЕР 2
Доказать, что
1+х+х2+х3+…+хn=(хn+1-1)/(х-1), где х¹1
Решение: 1) При n=1 получаем
1+х=(х2-1)/(х-1)=(х-1)(х+1)/(х-1)=х+1
следовательно, при n=1 формула верна; А(1) ис-тинно.
2) Пусть k-любое натуральное число и пусть формула верна при n=k, т.е.
1+х+х2+х3+…+хk=(хk+1-1)/(х-1).
Докажем, что тогда выполняется равенство
1+х+х2+х3+…+хk+xk+1=(xk+2-1)/(х-1).
В самом деле
1+х+х2+x3+…+хk+xk+1=(1+x+x2+x3+…+xk)+xk+1=
=(xk+1-1)/(x-1)+xk+1=(xk+2-1)/(x-1).
Итак, А(k)ÞA(k+1). На основании принципа математической индукции заключаем, что форму-ла верна для любого натурального числа n.
ПРИМЕР 3
Доказать, что число диагоналей выпуклого n-угольника равно n(n-3)/2.
Решение: 1) При n=3 утверждение спра-
А3 ведливо, ибо в треугольнике А3=3(3-3)/2=0 диагоналей;
А2 А(3) истинно.
2) Предположим, что во всяком
выпуклом k-угольнике имеет-
А1 ся Аk=k(k-3)/2 диагоналей.
АkДокажем, что тогда в выпуклом
Аk+1
(k+1)-угольнике число
диагоналей Аk+1=(k+1)(k-2)/2.
Пусть А1А2А3…AkAk+1-выпуклый (k+1)-уголь-ник. Проведём в нём диагональ A1Ak. Чтобы под-считать общее число диагоналей этого (k+1)-уголь-ника нужно подсчитать число диагоналей в k-угольнике A1A2…Ak, прибавить к полученному числу k-2, т.е. число диагоналей (k+1)-угольника, исходящих из вершины Аk+1, и, кроме того, следует учесть диагональ А1Аk.
Таким образом,
k+1=k+(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2.
Итак, А(k)ÞA(k+1). Вследствие принципа математической индукции утверждение верно для любого выпуклого n-угольника.
ПРИМЕР 4
Доказать, что при любом n справедливо утвер-ждение:
12+22+32+…+n2=n(n+1)(2n+1)/6.
Решение: 1) Пусть n=1, тогда
Х1=12=1(1+1)(2+1)/6=1.
Значит, при n=1 утверждение верно.
2) Предположим, что n=k
Хk=k2=k(k+1)(2k+1)/6.
3) Рассмотрим данное утвержде-ние при n=k+1
Xk+1=(k+1)(k+2)(2k+3)/6.
Xk+1=12+22+32+…+k2+(k+1)2=k(k+1)(2k+1)/6+ +(k+1)2=(k(k+1)(2k+1)+6(k+1)2)/6=(k+1)(k(2k+1)+
+6(k+1))/6=(k+1)(2k2+7k+6)/6=(k+1)(2(k+3/2)(k+
+2))/6=(k+1)(k+2)(2k+3)/6.
Мы доказали справедливость равенства и при n=k+1, следовательно, в силу метода математиче-ской индукции, утверждение верно для любого на-турального n.
ПРИМЕР 5
Доказать, что для любого натурального n спра-ведливо равенство:
13+23+33+…+n3=n2(n+1)2/4.
Решение: 1) Пусть n=1.
Тогда Х1=13=12(1+1)2/4=1.
Мы видим, что при n=1 утверждение верно.
2) Предположим, что равенство верно при n=k
mirznanii.com