Методы решения геометрических задач.
Методы решения геометрических задач
Сегодня важнейшей задачей школьного математического образования является привлечение внимания школьников и учителей к геометрии, понимание необходимости систематических занятий геометрией, развивающих мышление и пространственные представления. Только такие занятия могут дать необходимое качество математического образования школьников, позволят им не только подготовиться к успешной сдаче экзамена, но и заложат основу для дальнейшей творческой жизни.
Количество геометрических задач, встречающихся в контрольно-измерительных материалах (КИМ) единого экзамена, невелико. Их доля составляет не более 13 % от общего числа задач (3-4 задания). Однако умение решать такие задачи может оказаться решающим аргументом при поступлении в престижные или популярные вузы.
Анализируя результаты решения абитуриентами геометрических задач на вступительных испытаниях по математике, видим печальную статистику: с задачами по геометрии справляются не более 10 % поступающих, решают неправильно – около 30 %, а порядка 60 % абитуриентов полностью игнорируют такие задачи.
Если для большинства задач по алгебре и началам анализа существуют шаблонные подходы и алгоритмы решений, то в геометрии такого нет. Решение почти каждой геометрической задачи – это маленькая исследовательская работа. Чтобы с ней справиться, ученик должен иметь солидный опыт такого рода деятельности. И тут мы сталкиваемся с противоречием – опыт должен быть большой, а часов на изучение геометрии в школьном курсе отводится мало. Частичный выход из этого положения видится в использовании времени, отведенного в средней школе на повторение всего курса геометрии, исключительно для решения геометрических задач, взятых из вариантов ЕГЭ и ГИ
.
Трудности решения геометрических задач обусловлены как объективными, так и субъективными факторами, среди которых
Неалгоритмичность задач
Необходимость выбора метода решения задачи и теоремы для решения конкретной задачи (нескольких теорем) из большого набора известных фактов
Нужно решить довольно много задач, чтобы научиться их решать
Причины ошибок в решении геометрических задач
Незнание и/или непонимание аксиом, определений, теорем;
неумение их применять
невнимательное чтение условия и вопроса задания;
вычислительные ошибки;
нарушения логики в рассуждениях; принятие ошибочных гипотез;
недостатки в работе с рисунком
При решении геометрических задач обычно используются три основных метода:
геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем;
алгебраический – когда искомая геометрическая величина
вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений;
комбинированный – когда на одних этапах
решение ведется геометрическим методом, а на других — алгебраическим.
Метод треугольника
Метод подобия
Метод дополнительного построения
Метод замены
Метод площадей
Метод введения вспомогательного неизвестного
Метод «вспомогательных объёмов»
Координатный метод
Какой бы путь решения ни был выбран, успешность его использования зависит,
естественно, от знания теорем и умения их применять.
Метод дополнительного построения
Всякое геометрическое решение геометрической задачи начинается с работы над
чертежом. При этом иногда на «естественном» чертеже (т.е. на чертеже, на
котором изображено только условие) трудно заметить связи между данными и
искомыми величинами, а если фигуру достроить, эти связи становятся очевидными.

Метод подобия
Подобие треугольников
Две фигуры F и F1 называются подобными, если они переводятся друг в друга преобразованием
подобия, т.е. таким преобразованием, при котором расстояния между точками изменяются
(увеличиваются или уменьшаются) в одно и то же число раз.
Признаки подобия треугольников:
1) Если два угла одного соответственно равны двум углам другого;
2) Если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами равны;
3) Если три стороны одного треугольника пропорциональны трем сторонам другого.


Метод замены Метод
Метод замены широко применяется в алгебре, но не менее эффективно «замена» может быть
применена в геометрии. Сущность этого приема решения геометрических задач состоит в
следующем: фигура, о которой идет речь в условии задачи, так заменяется фигурой с той же
искомой величиной, чтобы найти эту величину было легче.




Метод введения вспомогательного неизвестного
Суть метода заключается в том, что исходя из условия задачи составляют
уравнение (или систему уравнений). В качестве вспомогательных аргументов
удобно выбирать величины, которые вместе с данными из условия задачи дают
набор элементов, однозначно задающих некоторую фигуру.


Метод площадей
В математических задачах часто бывает полезен такой прием: двумя
способами найти одну и ту же величину и приравнять полученные для нее
выражения. Пусть мы, например, двумя способами нашли площадь некоторой
фигуры. Если в одном из выражений для площади входит, скажем синус
какого-либо угла α, то при помощи соотношения из полученного равенства
можно получить некоторое неравенство, порой интересное.


Метод «вспомогательных объёмов»
Для нахождения расстояния от точки до плоскости или при нахождении
углов между прямой и плоскостью метод «вспомогательного объёма» во
многих случаях оказывается наиболее эффективным. Суть метода заключается
в том, что объём некоторой фигуры выражается двумя способами, а затем из
полученных равенств выражается искомая величина. Причём в этом методе
нет необходимости строить проекцию прямой на плоскость или проекцию точки,
что во многих случаях оказывается очень затруднительным.


Векторный метод
Применение критериев коллинеарности и компланарности векторов в решении задач.
Критерии коллинеарности и компланарности векторов служат основной для
применения векторной алгебры в решении стереометрических задач. Они
позволяют выразить в виде векторных равенств различные утверждения о
расположенных точках, прямых и плоскостей в пространстве. Переход от
векторных равенств к скалярным происходит на основе единственности
разложения вектора по двум неколлинеарным и трём некомпланарным векторам.




Координатный метод
Координаты на плоскости и в пространстве можно вводить бесконечным числом
разных способов. И, решая ту или иную геометрическую задачу методом координат,
можно использовать различные координатные системы, выбирая ту из них, в
которой задача решается проще, удобнее. Некоторые виды координатных систем,
отличные от прямоугольных.
1.Косоугольные (аффинные) координаты.
2.Полярные координаты.
4.Сферические координаты.
5.Прямоугольные координаты.
Рассмотрим самые употребительные и простые координаты в пространстве, называемые прямоугольными. Их называют ещё декартовыми по имени Рене Декарта (1596-1650) – французского учёного и философа, впервые ввёдшего координаты в геометрию (на плоскость).


Методические рекомендации «Три метода решения геометрических задач»
Основные этапы решения задач:
а) построение чертежа;
б) выявления особенностей полученной конфигурации;
в) выбор пути и метода решения;
г) анализ полученного решения
2.Методы решения задач
При решении геометрических задач обычно используется три основных метода:
а) геометрический, когда требуемые утверждения выводятся с помощью логических рассуждений из ряда известных теорий;
б) алгебраический, когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнения;
в) комбинированный, когда один из этапов решения ведется геометрическим, а другой – алгебраическим методом.
Две разновидности алгебраического метода:
метод поэтапного решения;
метод составления уравнений.
Сущность первого метода: величины, заданные в условии и те, которые нужно найти, мы связываем цепочкой промежуточных величин, каждая из которых определяется через предыдущие.
Задача: В параллелограмме со сторонами а и в, и углом проведены биссектрисы четырех углов. Найти площадь четырехугольника, ограниченного биссектрисами.
Решение.
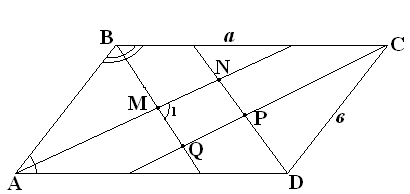
SMNPQ — ?
MNPQ – параллелограмм ( биссектрисы противолежащих углов параллельны)
ВМА=
 MNPQ – прямоугольник
MNPQ – прямоугольникSMNPQ=MN

MN=AN-AM; AM= в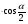 ; AN=а
; AN=а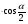
MQ=BQ-BM; BM= в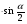 ; BQ= а
; BQ= а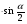
MN= (а- в)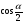 ; MQ= (а- в)
; MQ= (а- в) 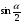
SMNPQ=(а- в)2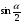
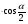
Ответ: SMNPQ=(а- в)2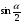
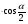
Мы рассмотрели алгебраический метод решения, решали поэтапно, т.е. составляли план решения, а затем его реализовали.
Рассмотрим задачи, решаемые при помощи составления уравнений:
Один и тот же элемент (сторона которого, угол, радиус и т.д.) выражается через известные и неизвестные величины двумя различными способами, полученные выражения приравниваются (опорный элемент)
Задача: Стороны треугольника равны а, в, с. Вычислите высоту hc.
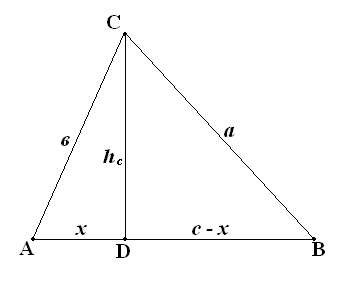
Решение.
Выберем опорный элемент.
hc — общий катет двух прямоугольных треугольников.
∆ АDС
∆СDВ
hc2в2 – х2
а2 – (с – х)2= в2 – х2,
а2 – с2 + 2сх – х2 – в2+х2= 0,
2сх = с2 + в2 – а2,
hc2 = а2 – (с – х)2
а2 – (с-х) 2 = в2— х2,
а2 – с2 + 2cos – x2 – в2 +х2 = 0,
2сх = с2 +в2 –а2,
х = 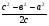
hc = 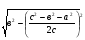
Можно было за опорный элемент выбрать площадь треугольника.
Доказать самостоятельно
S∆=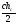 ; S∆=
; S∆=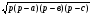
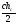 =
=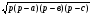
 hc = ?
hc = ?
В этом случае говорят, задача решена методом площадей.
Задача: В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см. и 12см. Найти катеты треугольника.
Решение.
По свойству касательных к окружности, проведенных из одной точки
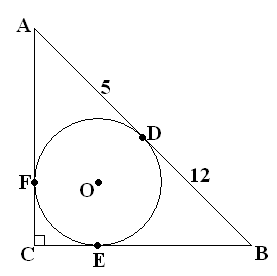
АС — ? СВ — ?
AF = AD =5см
CF=CE
BD=BE=12 см
Пусть CF=x? тогда
AC = x + 5
BC = X + 12
AB = 17
∆ACD, C = 90
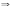 по теореме
по теореме 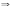
Пифагора
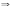 (x2+5)2 + (x+12)2 = 172,
(x2+5)2 + (x+12)2 = 172,
x2 + 10x + 25 +x2 + 24x + 144 – 289 = 0,
2x2 + 34x – 120 = 0,
x2 + 17 – 60 = 0,
Д > 0, x1= -20 – не удовлетворяет условию задачи
x2= 3
AC = 8см, BC = 15 см.
Ответ: AC = 8см, BC = 15 см.
Задача: Найти длину основания равнобедренного треугольника, если S∆ = 25см2, а углы при основании таковы, что tg = 4.
Решение.
AC — ?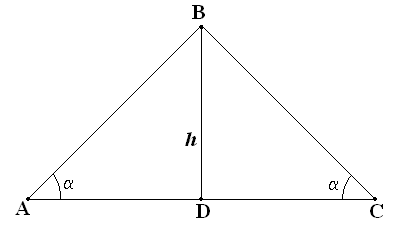
∆ABC : BDAC,
AB=BC? AD=DC
tg = 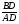
BD=h, AD=a 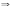 tg =
tg = 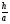 ;
;
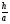 = 4
= 4
S∆ABC = 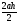 = ah: ah=25
= ah: ah=25
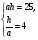
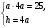
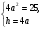
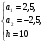 — не имеет смысла
— не имеет смысла
а = 2,5
Ответ: AC=5см
Задача: Один из катетов прямоугольного треугольника равен 15см, а проекция этого катета на гипотенузу равна 16см. найти радиус окружности, вписанной в треугольник.
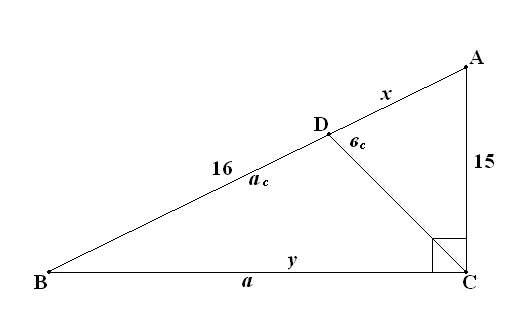
Решение.
r — ?
r = 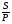 (для произвольного треугольника)
(для произвольного треугольника)
r = 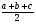 (для прямоугольного треугольника)
(для прямоугольного треугольника)
BC — ?, AB — ?
Пусть = AD=x, BC=y ; ÐC=90 в ∆ACB
 по теореме Пифагора 152+y2=(x=16)2
по теореме Пифагора 152+y2=(x=16)2
∆ABC: DC2=152— x2

 y2-162=152-x2
y2-162=152-x2∆BDC: DC2= y2-162
+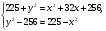
450+y2-x2=x2+32x+256+y2-256
2×2+32x-450=0
x2+16x-225=0
x1=9, x2= — 25 – посторонний корень
y=20, BC=20см, АВ=25см, АС=15см
r =
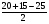 = 5
= 5
Ответ: r=5см.
Задача: В ∆АВС на стороне АС взята точка М такая, что АМ=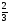 АС, а на стороне ВС взята точка К такая, что ВК=
АС, а на стороне ВС взята точка К такая, что ВК=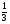 ВС. В каком отношении отрезок ИЬ делит Отрезок АК?
ВС. В каком отношении отрезок ИЬ делит Отрезок АК?
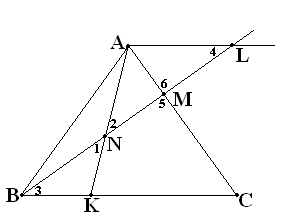
Дано: ∆АВС,
АМ=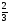 АС; ВК=
АС; ВК=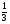 ВС
ВС
Найти: 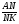
Решение:
Пусть ВК=а, ВС=3а. В каких объектах содержатся AN и NK?
Д.П. AL॥BC, AL∩BM=L
Метод подобия
1) ∆BNK∆LNA (Ð1=Ð2; Ð3=Ð4)
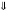
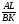 =
=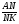 ; AL=?
; AL=?
2) ∆AML∆CMB (Ð5=Ð6, Ð3=Ð4)
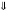
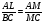 ;
; 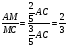 ;
; 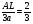 ; AL=2a,
; AL=2a,
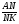 =
=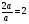
Ответ: 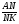 =2
=2
Эту задачу можно решить векторным способом (домашние задание).
Выводы: В качестве основных методов решения геометрических задач рассматривали: а) геометрический (метод подобия, векторный, поэтапное решение) и алгебраический метод.
Недостатки геометрического метода можно отметить следующие: нет алгоритма решения, при решении нужны хорошие чертежи, трудно выбрать из множества теорем нужную.
Преимущества алгебраического метода заключаются в том, что основные его модификации могут быть в достаточной степени алгоритмированы, (метод по этапного решения – аналогия – текстовые арифметические задачи), метод составления уравнений (аналогия — текстовые задачи на составление уравнений).
Не нужно бояться числа неизвестных.
Неизвестные должны полностью определять рассматриваемую в задаче геометрическую фигуру.
Величину какого-либо элемента выражают дважды различными способами через введенные неизвестные.
Возможно, случай составления уравнения является частью общего решения уравнения.
Однако, следует заметить, что, ставя во главу алгебраический метод решения геометрических задач, необходимо избегать чрезмерного увлечения алгеброй и счетам, не забывать – речь идет о геометрических задачах. Поэтому, работая над задачей, нужно искать ее геометрические особенности, учится видеть геометрию.
В алгебраических решениях встречаются различные дополнительные построения, элементы геометрических методов, когда один из этапов решения ведется геометрическим, а другой алгебраическим метом.
Комбинированный метод.
Таким методом мы уже решали задачи, но рассмотрим еще одну задачу.
Задача. На сторонах АD и CD квадрата ABCD со стороной 3см, взяты две точки M и N так, что MD+DN=3см, прямые BM и CD пересекаются в точка Е. найти длину отрезка NЕ, если MЕ=4см.
Решение.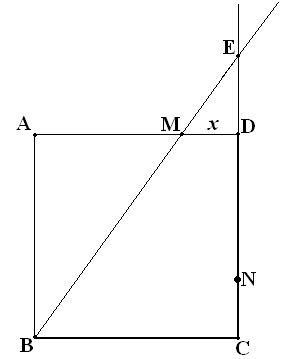
1) ∆DAM∆EMD
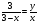
NE=ND+DE=3-x+y
(y-x)=?
2) ∆MDE по теореме Пифагора x2+y2+16
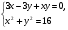
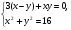
Пусть y-x=z, (1) -3z + xy = 0,
xy = 3z
(2) уравнение: (y-x)2+2xy=16,
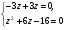
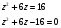 z = 2; z = — 8 – не подходит
z = 2; z = — 8 – не подходит
NE=3+2=5(см)
Ответ: NE=5см
Программа электива для 9 класса «Методы решения геометрических задач»
Темы рефератов для девятиклассников по геометрии
Замечательные точки треугольника.
Задачи на построение.
Геометрические места точек.
Удивительный квадрат.
Некоторые теоремы об окружности.
Решение задач с помощью дополнительных построений.
Геометрические преобразования на плоскости.
Правильные и полуправильные многоугольники.
Вписанные и описанные многоугольники.
Задачи на векторный метод.
Задачи на координатный метод.
Применение подобия к доказательству теорем и решению задач.
Равновеликость и равносоставленность многоугольников.
Геометрические задачи на максимум и минимум.
Симметрия на плоскости.
Задачи Л. Эйлера.
Золотое сечение.
Различные доказательства теоремы Пифагора.
Паркеты из многоугольников.
Тема «Замечательные точки треугольника»
План
1. Четыре замечательные точки треугольника: центр описанной окружности, центр вписанной окружности, центр тяжести (центроид) и ортоцентр.
2. Теорема Чевы.
3. Теорема Менелая.
4. Теоремы о пересечении в одной точке: а) медиан; б) биссектрис; в) высот треугольника. Различные доказательства.
5. Прямая Эйлера.
Литература
1. Александров А.Д. и др. Геометрия для 8-9 классов: Учебное пособие для учащихся школ и классов с углубленным изучением математики. – 3-изд. – М.: Просвещение, 1996, с. 407.
2. Атанасян Л.С. и др. Геометрия: Дополнительные главы к школьному учебнику 8 класса. – М.: Просвещение, 1996, с. 92.
3. Готман Э.Г. Прямая Эйлера /Математический кружок: Геометрия. Выпуск 1. – М.: Бюро Квантум, 1998, с. 23. (Приложение к журналу «Квант». – 1998. — № 1).
4. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 156.
5. Шарыгин И.Ф. Узнайте точку /Математический кружок. – М.: Бюро Квантум, 1999, с. 46. (Приложение к журналу «Квант». – 1999. — № 3).
Тема «Задачи на построение»
План
1. Простейшие задачи на построение.
2. Основные этапы решения задачи на построение.
3. Различные методы решения задач на построение.
4. Примеры решения задач на построение.
Литература
1. Погорелов А.В. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Просвещение, 2000, с. 55.
2. Прасолов В.В. Три классические задачи на построение. – М.: Наука, 1992.
3. Савин А.П. Геометрические построения /Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. Сост. И.Л. Никольская. – М.: Просвещение, 1991, с. 66.
4. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 87.
5. Шарыгин И.Ф. Геометрия. 7-9 классы: Учебник для общеобразовательных учебных заведений. – М.: Дрофа, 1997, с. 79.
Тема «Геометрические места точек»
План
1. Определение геометрического места точек.
2. Сущность метода геометрических мест.
3. Основные геометрические места точек на плоскости.
4. Примеры задач на геометрические места точек.
Литература
1. Погорелов А.В. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Просвещение, 2000, с. 61.
2. Савин А.П. Метод геометрических мест /Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. Сост. И.Л. Никольская. – М.: Просвещение, 1991, с. 74.
3. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 84.
4. Шарыгин И.Ф. Геометрия. 7-9 классы: Учебник для общеобразовательных учебных заведений. – М.: Дрофа, 1997, с. 76.
Тема «Удивительный квадрат»
План
1. Определения квадрата.
2. Замечательные свойства квадрата.
3. Задачи на разрезание квадрата.
4. Построения при помощи перегибания квадратного листа бумаги.
5. Танграм и другие головоломки, связанные с квадратом.
Литература
1. Квадрат //Квант. – 1989. — № 5. – С. 40.
2. Кордемский Б.А., Русалев Н.В. Удивительный квадрат. – М.: Столетие, 1994.
3. Лоповок Л.М. Тысяча проблемных задач по математике: Книга для учащихся. – М.: Просвещение, 1995, с.38.
4. Сергеев И.Н. и др. Примени математику. — М.: Наука, 1989, с.172.
Тема «Некоторые теоремы об окружности»
План
1. Число точек, определяющих окружность.
2. Зависимость длин хорд от их расстояния от центра.
3. Взаимное расположение прямой и окружности.
4. Измерение углов, связанных с окружностью.
5. Взаимное расположение двух окружностей.
Литература
1. Геометрия: Дополнительные главы к школьному учебнику 8 класса / Л.С.Атанасян и др. – М.: Просвещение, 1996, с.121.
2. Габович И.Г. Алгоритмический подход к решению геометрических задач. – М.: Просвещение, 1996, с. 61.
3. Киселев А.П. Элементарная геометрия. – М.: Просвещение, 1996, с. 65.
4. Цукарь А.Я. Дидактические материалы по геометрии с элементами исследования для 8 класса. – М.: Просвещение, 1999, с. 35.
5. Шарыгин И.Ф. Углы и окружности // Квант. – 1994. — № 1. – С. 40.
Тема «Решение задач с помощью дополнительных построений»
План
1. Роль дополнительных построений при решении планиметрических задач.
2. Удвоение медианы треугольника.
3. Проведение вспомогательной биссектрисы треугольника.
4. Проведение прямой, параллельной или перпендикулярной одной из данных прямых.
5. Построение вспомогательной окружности.
Литература
1. Белый С. Учитесь делать дополнительные построения / Практикум абитуриента: Геометрия. Выпуск 1. (Планиметрия) / Под редакцией А.А.Егорова. – М.: Бюро Квантум, 1996, с. 76 (Приложение к журналу «Квант». – 1996. — № 1).
2. Герасимова А.Д. К стратегии поиска дополнительных построений // Математика в школе. – 1996. — № 3. – С. 15.
3. Герасимова А.Д. Обоснование дополнительных построений при доказательстве теорем // Математика в школе. – 1994. — № 5. – С. 30.
4. Готман Э.Г. Вспомогательная окружность //(Приложение к журналу «Квант» №1/1998. – М.: Бюро «Квантум», 1998, с. 11
5. Мордкович А.Г. Беседы с учителями математики. – М: Школа-Пресс, 1995, с. 221.
6. Тарасенкова Н.А. Пропедевтический этап обучения поиску дополнительных построений // Математика в школе. – 2000. — № 4. – С. 32.
Тема «Геометрические преобразования на плоскости»
План
1. Движения и их свойства.
2. Центральная симметрия.
3. Поворот.
4. Осевая симметрия.
5. Параллельный перенос.
6. Равенство фигур.
7. Классификация движений.
8. Задачи по данной теме.
Литература
1. Болтянский В.Г. Геометрические преобразования плоскости /Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. Сост. И.Л. Никольская. – М.: Просвещение, 1991, с. 206.
2. Болтянский В.Г. Движения плоскости / Школа в Кванте. Геометрия / Под редакцией А.А.Егорова. – М.: Бюро Квантум, 1995, с. 4 (Приложение к журналу «Квант» – 1995. — № 1).
3. Готман Э.Г. Задачи по планиметрии и методы их решения. – М.: Просвещение, 1996, с. 5.
4. Дополнительные главы к школьному учебнику геометрии 9 класса / Л.С.Атанасян и др. – М.: Просвещение, 1997, с. 108.
5. Семенов Е.Е. За страницами учебника геометрии. – 2-е изд. – М.: Просвещение, 1999, с. 143.
6. Цукарь А.Я. Дидактические материалы по геометрии с элементами исследования для 9 класса. – М.: Просвещение, 2000, с. 3.
Тема «Правильные и полуправильные многоугольники»
План
1. Определение правильного многоугольника.
2. Равноугольно–полуправильные и равносторонне–полуправильные многоугольники.
3. Построение правильных многоугольников.
4. Элементы симметрии правильных многоугольников.
5. Паркеты из правильных многоугольников.
6. О сумме углов выпуклых и звездчатых многоугольников.
Литература
1. Атанасян Л.С. и др. Дополнительные главы к школьному учебнику геометрии 9 класса. – М.: Просвещение, 1997, с. 86.
2. Киселев А.П. Элементарная геометрия. – М.: Просвещение, 1996, с. 133.
3. Лоповок Л.М. Тысяча проблемных задач по математике. – М.: Просвещение, 1995, с. 49.
4. Сергеев И.Н. и др. Примени математику. – М.: Наука, 1989, с. 139.
5. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 149.
6. Смирнова И.М., Смирнов В.А. О сумме углов звездчатых многоугольников // Математика. – 2002. — № 1. – С. 31.
Тема «Вписанные и описанные многоугольники»
План
1. Вписанные и описанные треугольники.
2. Вписанные окружности.
3. Вписанные и описанные четырехугольники.
4. Правильные многоугольники.
5. Некоторые теоремы, связанные с вписанными и описанными окружностями.
Литература
1. Атанасян Л.С. и др. Дополнительные главы к школьному учебнику геометрии 8 класса. – М.: Просвещение, 1996, с. 149.
2. Гохидзе М.Г. К теме «Вневписанная окружность» //Математика в школе. – 1990. — № 2. – С. 59.
3. Киселев А.П. Элементарная геометрия . – М.: Просвещение, 1996, с. 82.
4. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 149.
5. Хонсбергер Р. Старая японская теорема // Квант. – 1990. — № 7. – С. 54.
6. Шарыгин И.Ф. Геометрия. 7-9 классы: Учебник для общеобразовательных учебных заведений. – М.: Дрофа, 1997, с. 213.
7. Несколько эпизодов из жизни вписанных и описанных окружностей // Квант. – 1990. — № 8. – С. 66.
Тема «Задачи на векторный метод»
План
1. Исторические аспекты векторного исчисления.
2. Понятие вектора.
3. Сложение и вычитание векторов.
4. Умножение вектора на число.
5. Скалярное произведение векторов.
Литература
1. Атанасян Л.С. и др. Дополнительные главы к школьному учебнику геометрии 8 (9 класс). – М.: Просвещение, 1996 (1997), с. 177 (с. 59).
2. Габович И. Векторы помогают на экзамене // Приложение к журналу «Квант» № 1/1996. — М.: Бюро Квантум, 1996, с. 108.
3. Готман Э.Г. Задачи по планиметрии и методы их решения. – М.: Просвещение, 1996, с. 68.
4. Дорофеева А.В. Из истории векторного исчисления // Математика в школе. – 1998. — № 2. – С. 91.
5. Лопшиц А. Векторное решение аффинных задач // Приложение к журналу «Квант» № 1/98. – М.: Бюро Квантум, 1998, с. 90.
6. Семенов Е.Е. За страницами учебника геометрии. – 2-е изд. – М.: Просвещение, 1999, с. 211.
7. Скопец З.А. Геометрические миниатюры. – М.: Просвещение, 1990, с. 28.
Тема «Задачи на координатный метод»
План
1. Жизнь и творчество Р.Декарта.
2. Координаты на прямой.
3. Прямоугольная система координат.
4. Решение задач на координатный метод.
5. Полярная система координат.
Литература
1. Готман Э.Г. Задачи по планиметрии и методы их решения. – М.: Просвещение, 1996, с. 83.
2. Котова А. Жизнь Декарта // Квант. – 1996. — № 3. С. 3.
3. Семенов Е.Е. За страницами учебника геометрии. – 2-е изд. – М.: Просвещение, 1999, с. 137.
4. Смирнова И.М., Смирнов В.А. Полярные координаты /Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 294.
5. Степанов М. Рене Декарт. К 400-летию со дня рождения //Математика. – 1996. — № 12. – С. 15.
6. Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы /Сост. И.Л.Никольская. – М.: Просвещение, 1991, с. 135.
7. Феоктистов И.Е. Материалы по теме «Декартовы координаты на плоскости» // Математика в школе. – 1994. — № 3. – С. 17.
Тема «Применение подобия к доказательству теорем и решению задач»
План
1. Подобие треугольников.
2. Признаки подобия треугольников.
3. Подобие фигур.
4. Понятие гомотетии.
5. Решение задач методом подобия.
Литература
1. Гейдман Б. Гомотетия и замечательные точки в треугольнике //Приложения к журналу «Квант» № 1/1995. — М.: Бюро «Квантум», 1995, с. 18.
2. Готман Э.Г. Задачи по планиметрии и методы их решения. – М.: Просвещение, 1996, с. 23.
3. Дополнительные главы к школьному учебнику геометрии 8 класса /Атанасян Л.С. и др. – М.: Просвещение, 1996, с. 73.
4. Киселев А.П. Элементарная геометрия. – М.: Просвещение, 1996, с. 94.
5. Лоповок Л.М. Тысяча проблемных задач по математике. – М.: Просвещение, 1995, с. 45.
6. Семенов Е.Е. За страницами учебника геометрии. – 2-е изд. – М.: Просвещение, 1999, с. 162.
Тема «Равновеликость и равносоставленность»
План
1. Понятие равновеликости фигур.
2. Понятие равносоставленности фигур.
3. Теорема о равносоставленности равновеликих многоугольников.
4. Задачи на разрезание.
Литература
1. Александров А.Д. и др. Геометрия для 8-9 классов: Учебное пособие для учащихся школ и классов с углубленным изучением математики. – 3-е изд. – М.: Просвещение, 1996, с. 340.
2. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. – 4-е изд. – М.: Просвещение, 1984, с. 114.
3. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995, с. 108.
4. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 253.
5. Энциклопедия для детей. Математика. Том 11. – М.: Аванта+, 2001, с. 363.
Тема «Геометрические задачи на максимум и минимум»
План
1. Понятие экстремальной задачи.
2. Старинные задачи на максимум и минимум.
3. Изопериметрическая задача.
4. Решение экстремальных геометрических задач.
Литература
1. Баврин И.И., Фрибус Е.А. Занимательные задачи по математике. – М.: Владос, 1999, с. 13.
2. Горнштейн П. И др. Геометрические решения экстремальных геометрических задач //Приложение к журналу «Квант» № 3/1996. – М.: Бюро «Квантум», 1996, с. 33.
3. Готман Э.Г. Поиск рационального решения задачи на экстремум //Математика в школе. – 1997. — № 6. – С. 40.
4. Прасолов В.В. Задачи по планиметрии. Часть I. – 2-е изд. – М.: Наука, 1991, с. 282.
5. Тихомиров В.М. Рассказы о максимумах и минимумах. – М.: Наука, 1986 (Библиотечка «Квант», выпуск 56).
Тема «Симметрия на плоскости»
План
1. Понятие о симметрии.
2. Симметрия в окружающем мире.
3. Виды симметрии.
4. Свойства симметрий.
5. Композиции симметрий.
6. Симметрия помогает решать задачи.
Литература
1. Гейдман Б. Осевая симметрия //Приложение к журналу «Квант» № 1/1995. – М.: Бюро «Квантум», 1995, с. 15.
2. Гончарова С.Г., Кукин Г.П. Конструктор «В мире симметрии» //Математика в школе. – 1996. — № 3. – С. 60.
3. Зеркальная симметрия //Квант. – 1992. — № 3. – С. 40.
4. Прасолов В.В. Задачи по планиметрии. Часть I. – 2-е изд. – М.: Наука, 1991, с. 47, с. 56.
5. Тарасов Л.В. Этот удивительно симметричный мир. – М.: Просвещение, 1982.
6. Цукарь А.Я. Дидактические материалы по геометрии с элементами исследования для 9 класса. – М.: Просвещение, 2000, с. 11, с. 30.
Тема «Задачи Л. Эйлера»
План
1. Жизнь и творчество Л. Эйлера.
2. Прямая Эйлера.
3. Окружность Эйлера.
4. Формула Эйлера (связывающая радиусы вписанной и описанной окружностей треугольника с расстоянием между их центрами).
Литература
1. Готман Э. Прямая Эйлера //Приложение к журналу «Квант» № 1/1998. – М.: Бюро «Квантум», 1998, с. 23.
2. Дополнительные главы к школьному учебнику геометрии 8 класса /Атанасян Л.С. и др. – М.: Просвещение, 1996, с. 149.
3. Дополнительные главы к школьному учебнику геометрии 9 класса /Атанасян Л.С. и др. – М.: Просвещение, 1997, с. 78, с. 129.
4. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 110.
5. Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы /Сост. И.Л. Никольская. – М.: Просвещение, 1991, с.96.
6. Шарыгин И.Ф. и др. Окружность девяти точек и прямая Эйлера //Приложение к журналу «Квант» № 1/1998. – М.: Бюро «Квантум», 1998, с. 31.
Тема «Золотое сечение»
План
1. История возникновения «тайны золотой пропорции».
2. Построение золотого сечения.
3. Золотые прямоугольники.
4. Золотые треугольники.
5. Использование золотого сечения в строительстве и искусстве: живописи, архитектуре, строительстве.
Литература
1. Азевич А.И. От золотой пропорции к ее «производным» //Математика в школе. – 1995. — № 3. – С. 55.
2. Васютинский Н.А. Золотая пропорция. – М.: Молодая гвардия, 1990.
3. Волошинов А.В. Математика и искусство. – 2-е изд. – М.: Просвещение, 2000, с. 216.
4. Нафиков Н.Н. Гипотеза об истоке золотого сечения //Математика в школе. – 1994. — № 3. – 76.
5. Смирнова Е.С., Леонидова Н.А. Математическое путешествие в мир гармонии //Математика в школе. – 1993. — № 3. – С.60.
6. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 195.
Тема «Различные доказательства теоремы Пифагора»
План
1. Жизнь и творчество Пифагора.
2. Знаменитая теорема Пифагора.
3. Доказательство Евклида.
4. Древнекитайское доказательство.
5. Древнеиндийское доказательство.
6. Доказательство с помощью листа бумаги и ножниц.
Литература
1. Волошинов А.В. Пифагор. – М.: Просвещение, 1993, с. 165.
2. Глейзер Г.И. История математики в школе. VII-VIII классы. – М.: Просвещение, 1982, с. 196.
3. Изучаем теорему Пифагора //Математика. – 2001. — № 24.
4. Рубинов Р. По следам теоремы Пифагора //Приложение к журналу «Квант» № 3/ 1998. – М.: Бюро «Квантум», 1998, с. 87.
5. Халамайзер А.Я. Пифагор. – М.: Высшая школа, 1994, с. 6, с. 47.
Тема «Паркеты из многоугольников»
План
1. Определение паркета.
2. Паркеты из одноименных правильных многоугольников.
3. Паркеты из различных правильных многоугольников.
4. Паркет из произвольного четырехугольника.
5. Другие паркеты.
Литература
1. Болтянский В.Г. Паркет из четырехугольников //Квант. – 1989. — № 11. – С. 57.
2. Заславский А. Паркеты и разрезания //Квант. – 1999. — № 2. – С. 32.
3. Колмогоров А.Н. Паркеты из правильных многоугольников //Квант. – 1986. — № 8. – С. 3.
4. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995, с. 96.
5. Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М.: Мнемозина, 2005, с. 178.
6. Энциклопедия для детей. Математика. Том 11. – М.: Аванта+, 2001, с. 298.
Некоторые методы решения геометрических задач. Программа элективного курса для профильной подготовки учащихся 9–11-х классов по математике
Пояснительная записка
Если мы действительно что-то знаем, то мы знаем это благодаря изучению математики.
П. Гассенди
Основная функция элективных курсов по выбору в системе предпрофильной и профильной подготовки по математике – формирование представлений об идеях и методах математики, о математике как универсальном языке науки; развитие творческих способностей у школьников, осознанных мотивов учения, подготовка к продолжению образования и сознательному выбору профессии.
Решение геометрических задач вызывает трудности у многих учащихся. Это объясняется прежде всего тем, что редко какая либо задача по геометрии может быть решена с использованием определённой теоремы или формулы. Большинство задач требует применения разнообразных теоретических знаний, доказательства утверждений, справедливых лишь при определенном расположении фигуры, применение различных формул. Приобрести навыки в решении задач можно, лишь решив достаточно большое их количество, ознакомившись с различными методами, приёмами и подходами.
Программа для общеобразовательных школ по геометрии не акцентирует внимание на методах решения задач, особенно на их частные случаи.
Искусство же решать задачи основывается на хорошем знании теоретической части курса, знании достаточного количества геометрических фактов, в овладении определённым арсеналом приёмов и методов решения геометрических задач.
Методы решения геометрических задач обладают некоторыми особенностями, а именно:
- большое разнообразие, трудность формального описания;
- взаимозаменяемость;
- отсутствие чётких границ области применения.
Поэтому целесообразно рассмотреть применение подходов, приёмов, методов при решении конкретных задач.
Знакомство учащихся с методами решения геометрических задач стимулирует анализ учащихся своей деятельности по решению задач, выделению в них общих подходов и методов, их теоретическое осмысление и обоснование, решение задач несколькими способами. Особое внимание уделяется аналитическому способу решения задач, доводится до понимания учащихся, что анализ условия задачи, анализ решения задачи – важнейшие этапы её решения. Учащиеся знакомятся со схемой восходящего анализа.
Знание методов решения геометрических задач позволяет решать, казалось бы, сложные математические задачи просто, понятно и красиво.
Кроме того, предлагаемый курс позволяет создать целостное представление о теме и значительно расширить спектр задач, благодаря пониманию методов, приёмов решения задач.
Конструирование программного содержания на занятиях по курсу может быть проведено по алгоритму:
- обобщение первоначальных знаний;
- систематизация, конкретизация и углубление теоретических знаний;
- проектирование и организация практической деятельности учащихся по применению базисных знаний.
Такая конструкция программного материала, законченность блоков содержания, помогает ученику достигать поставленных перед ним дидактических задач и позволяет осуществлять интеграцию разных видов и форм обучения.
Важное значение при организации учебно-познавательной деятельности имеет обратная связь: внутренняя при взаимоконтроле, самоконтроле и внешняя.
Технологии, используемые в организации изучения элективного курса по геометрии должны быть личностно-ориентированными, направленными на запланированный конечный результат, а именно, содержание материала, поуровневая индивидуализация учебной и дифференциация обучающей деятельности на фоне благоприятного психологического климата дают возможность создать ситуацию выбора для учителя и ученика, помогают ученику сформировать общеучебные умения и навыки, повысить его образовательный уровень, что связано с дальнейшим успешным самообразованием и профессиональным самоопределением.
I. Организационно-методический раздел
Цель курса: расширить представления учащихся о методах, приемах, подходах решения задач по планиметрии в системе предпрофильной и профильной подготовки.
Задачи курса
1. Познакомить учащихся с некоторыми методами решения задач:
а) методом опорного элемента;
б) методом площадей;
в) методом введения вспомогательного параметра;
г) методом восходящего анализа;
д) методом подобия;
е) методом дополнительного построения;
2. Познакомить учащихся с некоторыми теоремами планиметрии и свойствами фигур, не рассматриваемыми в курсе геометрии 7-9 классов.
3. Развивать общеучебные умения учащихся, логическое мышление, алгоритмическую культуру, математическое мышление и интуицию, повысить их уровень обученности.
4. Развивать творческие способности школьников, готовить их к продолжению образования и сознательному выбору профессии.
Место курса в системе профильной подготовки.
Курс направлен на профильную подготовку по математике. Он расширяет и углубляет базовый курс по геометрии, является предметно ориентированным, дает возможность учащимся познакомиться с различными методами, приемами решения задач по геометрии, которые являются не только эффектными, но и эффективными.
Данный элективный курс будет способствовать совершенствованию и развитию знаний и умений по математике, даст возможность учащимся проанализировать свои способности к математической деятельности.
Требования к уровню усвоения содержания курса
Административной проверки усвоения материала курса “Некоторые методы решения геометрических задач” не предполагается. В технологии проведения занятий осуществляется обратная связь при взаимоконтроле и самоконтроле. Возможно проведение обучающих самостоятельных работ и итогового тестирования.
Распределение часов курса по темам
Данный элективный курс предполагает 17 тематических занятий.
Тематический план курса
| № | Тема | Кол-во часов | Форма занятия |
| 1 | Методы решения геометрических задач | 2 | Лекция |
| 2 | Треугольник | 6 | Практикум |
| 3 | Четырехугольники | 7 | Практикум |
| 4 | Итоговое занятие | 2 | Тестирование |
II. Содержание курса
Тема 1. Методы решения геометрических задач
Три основных метода решения геометрических задач: геометрический; алгебраический; комбинированный.
Анализ и синтез. Метод восходящего анализа.
Дополнительные методы и приемы решения задач. Анализ условия задачи, анализ решения задачи – этапы решения задачи.
Решение задач.
Тема 2. Треугольник
Обзор теоретического материала по теме.
Решение задач с использованием методов:
1. метода опорного элемента, метода площадей;
2. метода введения вспомогательного параметра;
3. метода дополнительного построения:
а) проведение прямой параллельной или перпендикулярной одной из имеющихся на рисунке;
б) удвоение медианы треугольника;
в) проведение вспомогательной окружности;
г) проведение радиусов в точки касания окружности и прямой или двух окружностей;
4. использование свойства медиан, биссектрис и высот треугольника;
5. метода подобия;
6. применение тригонометрии (теоремы синусов и теоремы косинусов).
Тема 3. Четырехугольники
Обзор теоретического материала по теме.
Параллелограмм. Вписанные и описанные четырехугольники.
Трапеция. Свойства трапеции определенного вида.
Решение задач с использованием:
1. метода подобия;
2. метода опорного элемента; метода площадей;
3. метода введения вспомогательного параметра;
4. свойств трапеции определенного вида;
5. метода дополнительного построения.
Задания для самостоятельной работы учащихся
Работа с рекомендованной литературой.
Самостоятельное решение предложенных задач с последующим обсуждением вариантов решения.
Самостоятельный подбор задач по теме элективного курса с использованием дополнительной математической литературы.
Самостоятельное конструирование задач по изучаемому курсу и их презентация.
Самоанализ когнитивной и креативной деятельности учащихся.
III. Учебно-методическое обеспечение курса
1. Атанасян Л.С. и др. Геометрия. Учебник для 7-9 кл. общеобразовательных учреждений. – М.: Просвещение, 1998.
2. Габович И.Г. Алгоритмический подход к решению геометрических задач. – М.: Просвещение, 1996.
3. Гусев В.А. и др. Практикум по решению математических задач. – М.: Просвещение, 1985.
4. Пиголкина Т.С. Математическая энциклопедия абитуриента. – М.: изд. Российского открытого университета, 1992.
5. Пойа Д. Как решать задачу. – М.: Просвещение, 1959.
6. Семенов С.В., Хазанкин Р.Г. Математика. Трапеция. – УРЭК, 1997.
7. Шарыгин И.Ф. Геометрия-8. Теория и задачи. – М.: Рост, МИРОС, 1996.
8. Шарыгин И.Ф. Решение задач: учеб. пособие для 10 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.
9. Сборник конкурсных задач по математике для поступающих во ВТУЗы. Под ред. М.И. Сканави. Учеб. пособие. – С.-Петербург, 1994.
Метод дополнительных построений при решении геометрических задач в курсе планиметрии по учебнику Л.С.Атанасяна.
Метод дополнительных построений при решении геометрических задач в курсе планиметрии по учебнику Л.С.Атанасяна.
Суть метода: Решение планиметрической задачи начинается с построения чертежа, аккуратное выполнение которого помогает найти связи между элементами фигуры и наметить дальнейшие действия. Дополнительные линии чаще всего проводятся для того, чтобы свести задачу к ранее решенной или просто более простой задаче. Они позволяют включить в задачу новые фигуры с их свойствами, тем самым увеличить число теорем, которые можно использовать при решении задачи. Одним из эффективных методов решения геометрических задач является метод дополнительных построений. Метод дополнительных построений при решении геометрических задач является непростым, так как нужное дополнительное построение не всегда удается определить с первого взгляда. Но, зная различные способы дополнительных построений и их применение, решение геометрической задачи становится намного проще, так как появляются другие фигуры (чаще те, которые мы изучили), свойства которых нам известны. Иногда условие задачи подсказывает выбор дополнительного построения. Однако увидеть нужное дополнительное построение могут далеко не все. Вместе с тем существуют достаточно типичные дополнительные построения, к выполнению которых учащихся (в подавляющем большинстве) можно подготовить. Дополнительные построения встречаются по всему курсу планиметрии с 7 по 9 классы.
В учебнике геометрии Л.С. Атанасяна имеется теоретический материал (почти половина теорем) и задачный материал, при доказательстве, решении которого применяются различные дополнительные построения А именно в темах: «Треугольники», «Параллельные прямые», «Соотношения между сторонами и углами треугольника», «Четырехугольники», «Площадь», «Подобные треугольники», «Окружность». При этом общее представление о разновидностях дополнительных построений при решении геометрических задач у школьников формируется стихийно. Сейчас в школьном курсе учеников знакомят с разнообразными понятиями и средствами решения задач, но именно их разнообразие оставляет мало времени на приобретение навыков, и вкус к такого рода задачам, которые развивают геометрическое воображение. Чтобы этот процесс сделать целенаправленным, на мой взгляд, в первую очередь необходимо систематизировать разновидности дополнительных построений. Разновидности дополнительных построений:
1)построение прямой, параллельной одной из имеющихся на чертеже;
2) построение прямой, перпендикулярной данной;
3) продолжение медианы;
3) построение окружности.
Основным средством обучения учащихся приему дополнительного построения являются имеющиеся теоремы и набор задач. При изучении планиметрии в 7-8 классах особое внимание нужно уделять построению отрезков (соединение отрезком каких-либо точек, лежащих на сторонах многоугольника, построение высот треугольника или четырехугольника, радиусов или хорд окружности, диагоналей многоугольника, продолжение отрезков до взаимного пересечения между собой и т.д.). В 7 классе можно начинать вводить метод дополнительного построения при изучении темы «Свойства равнобедренного треугольника», при доказательстве признаков параллельности прямых, а также теорем, обратных этим теоремам. Закрепить знакомство можно при доказательстве теоремы о сумме углов треугольника, неравенства треугольника.
В 8 классе при изучении темы «Четырехугольники, площади» можно ознакомить со следующими видами дополнительного построения.
1.Удвоение медианы треугольника с последующим достраиванием треугольника до параллелограмма, то есть продолжить эту медиану на расстояние равное длине медианы, т.е. продлить ее за точку, лежащую на стороне треугольника. Полученная новая точка соединяется с вершиной (вершинами) исходного треугольника, в результате чего образуются равные треугольники. Равенство соответствующих элементов этих треугольников помогает найти неизвестную величину или доказать предложенное утверждение.
2. Стандартное дополнительное построение в задачах на трапецию: проводим либо два перпендикуляра к основанию и получаем прямоугольник и два прямоугольных треугольника, либо проводим отрезок, параллельно боковой стороне, и получаем параллелограмм и произвольный треугольник, либо проводим через середину меньшего основания прямые, параллельные боковым сторонам, либо продливаем боковые стороны до пересечения. Если же в условии задачи говорится о диагоналях трапеции, то стандартным будет дополнительное построение, состоящее в проведении через одну из ее вершин прямой, параллельной диагонали.
Вспомогательные окружности часто облегчают вычисление углов в задачах о «некруглых» фигурах. Этот метод дополнительного построения можно ввести в 9 классе при повторении и подготовки учащихся к ОГЭ.
Приложение 1.
1.Задачи из учебника Л.С. Атанасяна (№160,165,200, задачи на построение).
2. Докажите, что треугольник является равнобедренным, если совпадают проведенные из одной и той же вершины медиана и биссектриса.
3.В прямоугольном треугольнике АВС (С = 90) проведена медиана СД. Докажите, что СД=ДВ (для проверки усвоения метода)
Приложение 2.
1.Задачи из учебника Л.С. Атанасяна (№384,388,393,527, задачи на построение).
2. Найти среднюю линию трапеции, диагонали которой перпендикулярны и равны 6 и 8.
3. Найдите площадь трапеции с основаниями 6 и 7 и диагоналями 5 и 12.
4. Найдите площадь трапеции, если её диагонали равны 17 и 113, а высота равна 15.
5. В трапеции АВСD ВС II AD M N- середины оснований ВС и AD. АС=√15, ВD=1, MN=2. Найдите площадь трапеции.
6.Вычислить площадь трапеции, параллельные стороны которой равны 16 и 44, а непараллельные — 17 и 25.
7.Длины боковой стороны AD и основания CD трапеции ABCD равны 2, а длина основания АВ равна 4. Длина диагонали АС равна √7. Найти длину боковой стороны ВС.
8. Отрезок, соединяющий середины оснований трапеции, равен 3. Углы при большем основании равны 300 и 600, Найдите высоту,
9. В трапеции длина средней линии равна 4, а углы при одном из оснований имеют величины 400 и 500 . Найти длины оснований трапеции, если длина отрезка, соединяющего середины этих оснований, равна 1. 10. Найдите косинус острого угла равнобедренной трапеции, основания которой равны 37 и 49, а боковые стороны равны 15.
Приложение3.
1.Из точки Р, расположенной внутри острого угла с вершиной А, опущены РВ и РС на стороны угла. Известно, что СВР=250. Найдите угол САР.
2.В выпуклом четырехугольнике АВСD диагонали АС и ВD пересекаются в точке О. < АВС = 1110 , <ОВС = 490 , < АСD = 620 . Найти углы САD и АDС
3.В трапеции АВСD с основаниями АD и ВС угол АВD равен углу АСD. Доказать, что АВСD – равнобедренная трапеция.
4.Известно, что ВМ и СN – высоты треугольника АВС, при этом МN=10, и ВС =26. Найдите расстояние между серединами отрезков МN и ВС.
5.В выпуклом четырехугольнике АВСД известно, что ВСД= 800, АСВ=500 и АДВ=300. Найдите АДВ.
6. В выпуклом четырехугольнике АВСD АВД = АСД = 450, ВАС = 300, ВС=1. Найдите АД. 7. В треугольнике АВС проведена высота ВК. Найти длину отрезка, соединяющего точку К с серединой АВ, если АВ = 10 см.
Для проверки усвоения метода можно составить аналогичные задачи.
«ИЗУЧЕНИЕ ГЕОМЕТРИЧЕСКИХ СПОСОБОВ РЕШЕНИЯ НЕГЕОМЕТРИЧЕСКИХ ЗАДАЧ ПРИ ПОДГОТОВКЕ К МАТЕМАТИЧЕСКИМ ОЛИМПИАДАМ»
Государственное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
п.г.т. Осинки муниципального района Безенчукский Самарской области
«ИЗУЧЕНИЕ ГЕОМЕТРИЧЕСКИХ СПОСОБОВ РЕШЕНИЯ НЕГЕОМЕТРИЧЕСКИХ ЗАДАЧ ПРИ ПОДГОТОВКЕ К МАТЕМАТИЧЕСКИМ ОЛИМПИАДАМ»
Выполнила:
Смирнова Раиса Михайловна,
учитель математики
ГБОУ СОШ п.г.т. Осинки.
Самара – 2014
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Решение задач – это сердцевина, смысл и внутренняя пружина самой математики. Сначала появляется задача, и лишь потом строится теория для ее решения.
Нестандартные задачи во все времена привлекали внимание ученых. Среди них много красивых задач, которые интересно и приятно решать. Но в школе их решением занимаются отнюдь не только «из любви к искусству». Такие задачи развивают абстрактное и логическое мышление, познавательные способности. Нетрадиционные приемы решения задач позволяют полнее раскрыть потенциал школьников. Именно поэтому большинство заданий олимпиад различного уровня проверяют способность ребенка видеть нестандартные пути решения. Не секрет, что для получения высокого балла на ЕГЭ также необходимо решать именно такие задачи.
При подготовке к олимпиаде учащиеся столкнулись с решением сложной алгебраической задачи геометрическим методом, открыв для себя красоту этого решения, его наглядность и простоту.
Мы часто встречаем задачи по геометрии, которые решаются с помощью алгебры (различные уравнения, системы уравнений и т.д.). Менее известны другие случаи, когда арифметические и алгебраические задачи удобно решать на геометрическом языке, но в школе они редко рассматриваются. Если такое задание попадется в тексте ЕГЭ, могут возникнуть проблемы. И даже если и сможем решить такую задачу своими способами, то потратим на это уйму времени, а в режиме экзамена каждая минута на вес золота. Нетрадиционные приёмы решения задач позволяют полнее раскрыть потенциал школьника, приобщить его к творчеству, проиллюстрировать внутриматематические связи.
Актуальность выбранной темы.
С одной стороны это расширит возможности решения задач. С другой стороны, многим учащимся геометрия даётся легче, чем алгебра, и им будет интересно решать такие задачи, хотя малое количество задач в материалах ЕГЭ снизил интерес к её изучению. Это объясняет выбор темы.
Цель работы:
Создать формирование у школьников приёмы и способы решений негеометрических задач геометрическим способом. Показать преимущества геометрического способа решения алгебраических задач, заключающиеся в его наглядности и изящности решения.
Для достижения поставленной цели необходимо решить следующие задачи:
1. Выявить алгебраические задачи, решаемые геометрическими методами, используя различные источники.
2. Рассмотреть достоинства и недостатки данного метода.
Решая первую из поставленных задач, выяснилось, что таких заданий много, это привело к постановке новых задач:
3. Классифицировать найденные примеры по темам:
рассмотреть способы решения геометрическими методами задач в тригонометрии;
рассмотреть геометрические методы решения задач, содержащих иррациональность, действия с величинами в отрезках; решение квадратных уравнений с помощью квадрирования прямоугольников; формулы сокращенного умножения; арифметическую прогрессию;
рассмотреть геометрические методы решения систем;
рассмотреть векторный метод решения задач;
рассмотреть способы решения текстовых задач геометрическими методами.
4. Подготовить результаты исследования к виду, готовым к использованию.
Применяя различные методы решения задач, мы тренируем и делаем более гибким своё мышление. Такая тренировка оттачивает навык решения задач, а также способствует более лучшей усвояемости нового материала.
ГИПОТЕЗА: Могут быть сделаны выводы.
Решение алгебраических задач геометрическим способом позволит избежать многих сложных вычислений.
При подборе задач, изучив дополнительную литературу, мы расширили свои знания в точных науках и расширили свой кругозор.
При решении некоторых задач геометрическими методами наблюдалась явно выраженная экономия сил, энергии, а главное времени.
Чтобы решить алгебраическую задачу геометрическим методом необходимо иметь навык и «видение» геометрической интерпретации задачи, что является самым сложным в данном методе.
Во многих разделах алгебры существуют классы задач, решаемых геометрическими методами.
Чтобы решить задачу геометрическими методами необходимо иметь мощную базу знаний по геометрии, т.к. в решении используются: метод площадей, векторная геометрия, свойства геометрических фигур, геометрические неравенства и т.п.
Геометрический подход даёт более быстрое, а главное, красивое решение этих задач.
ПРИЛОЖЕНИЕ
Системы:
Решить систему уравнений:

 ,
,
3ху-10у=3
Найти S=xy+yz, если x>0, y>0, z>0 и
 x2+y2=16,
x2+y2=16,
y2+z2=48,
y2=xz.
Найти M=xy+2yz+3xz, если x>0, y>0, z>0 и


Сколько пар целых чисел (x;y) удовлетворяет системе неравенств



 ?
?
Задания, содержащие иррациональность:
Решить уравнение

Найти наибольшее и наименьшее значения выражения
 , если
, если  .
.Доказать неравенство
 <
<
Доказать, что для положительных a, b, c выполняется неравенство

Текстовые задачи:
Поезд проходит расстояние от города А до города В за 10 час. 40 мин. Если бы скорость поезда была на 10 км/ч меньше, то он пришел бы в В на 2 часа 8мин. позже. Определить расстояние между городами и скорость поезда.
Задания по тригонометрии:
Найти значение выражения:
 .
.Найдите

Векторы помогают алгебре:
Для положительных чисел a, b, c доказать неравенство
 .
.Доказать, что для любых x, y, z выполняется неравенство

Решить уравнение:

РЕШЕНИЕ СИСТЕМЫ
Решая приведенные ниже системы традиционными методами, можно столкнулись с решением уравнений высших степеней и достаточно сложными преобразованиями. Именно поэтому геометрический метод не только упрощает решение, но и делает его прозрачным и изящным. Основной трудностью является увидеть применение данного метода в конкретном примере. В некоторых заданиях, например №1 явно прослеживается неравенство треугольника, а в задании №3 применение данного метода заметить сложно. Недаром этот номер были представлен на всероссийской олимпиаде школьников различных лет.
Задача 1.
Решить систему уравнений:

 ,
,
3ху-10у=3
Решение: На координатной плоскости рассмотрим точки А(2;4), В(5;8) и М(х;у). (рис.1)
 Рис. 1
Рис. 1
Тогда неравенство треугольника МА+МВ АВ в координатной форме выглядит так:
АВ в координатной форме выглядит так:  . Ясно, что равенство возможно лишь в том случае, когда точка М(х;у) принадлежит отрезку АВ. Уравнение прямой АВ имеет вид 4х-3у+4=0. Получаем систему, равносильную исходной:
. Ясно, что равенство возможно лишь в том случае, когда точка М(х;у) принадлежит отрезку АВ. Уравнение прямой АВ имеет вид 4х-3у+4=0. Получаем систему, равносильную исходной:
4

 х-3у+4=0 x=
х-3у+4=0 x= x=3.5
x=3.5
3ху-10у=3 9y2-52y-12=0
2 5 2
5 2 5 y=6
5 y=6
Ответ: (3,5; 6)
Задача 2.
Н айти S=xy+yz, если x>0, y>0, z>0 и
айти S=xy+yz, если x>0, y>0, z>0 и
x2+y2=16,
y2+z2=48,
y2=xz.
Решение:
На отрезке АВ таком, что АВ=АС+СВ, где АС = z, СВ = х. (рис. 2), как на диаметре, построим полуокружность. Далее, через точку С проведем прямую, перпендикулярную АВ и пересекающую полуокружность в точке D.
 Рис. 2
Рис. 2
Тогда с учетом третьего уравнения системы CD = у. Из уравнений х2+у2=16 и у2+z2=48 следует, что BD=4, AD=4 .
.
Имеем S= ху+уz =2 SBCD+2 SACD=2 SADB=16 .
.
Ответ:16 .
.
З адача 3.
адача 3.
Найти M= xy + 2yz +3xz, если x>0, y>0, z>0 и

 Рис. 3
Рис. 3
Решение:
Построим отрезки ОВ= , ОС=z и ОА= х такие, что
, ОС=z и ОА= х такие, что  =90°,
=90°,  СОА=120° и
СОА=120° и  ВОА=150° (рис. 3).
ВОА=150° (рис. 3).
Тогда с учетом условия АВ=5, ВС=4, АС=3 и SABC= . Но SABC=SBOC+SCOA+SBOA=
. Но SABC=SBOC+SCOA+SBOA= .
.
Теперь, умножив обе части равенства  =6 на 4
=6 на 4 , получим М=24
, получим М=24 .
.
Ответ: 24 .
.
Список литературы:
[1] Алфутова Н.Б., Устинов А.В. Алгебра и теория чисел. Сборник задач для математических школ. М.: МЦНМО, 2009 – 264с.
[2] Колесникова С.И. Математика. Решение сложных задач единого государственного экзамена – 2-е изд., испр.- М.: Айрис-пресс, 2006. – 272с. – (Домашний репетитор: Подготовка к ЕГЭ)
[3] Математика. 9-11 классы: Решение заданий ЕГЭ высокой степени сложности. Основные методы и приемы/ Авт.-сост. М.А. Куканов. – Волгоград: Учитель, 2009. – 223с.
[4] Математика. Областные олимпиады. 8-11 классы/ [Н.Х. Агаханов, И.И.Богданов, П.А.Кожевников и др.] – М.: Просвещение, 2010 – 239с.: ил. – (Пять колец).
[5] Островский А.И., Кордемский Б.А. Геометрия помогает арифметике. М.:ФИЗМАТГИЗ, 1960.
[6] Уфановский В.А. Математический аквариум. — Ижевск: НИЦ «Регулярная и хаотическая механика», 2000.
[7] Шарыгин И.Ф., Голубев В.И. Факультативный курс по математике: Решение задач: Учеб. пособие для 11кл. сред. шк. – М.: Просвещение, 1991. – 384с.
[8] Шарыгин И.Ф., Факультативный курс по математике: Решение задач: Учеб. пособие для 10кл. сред. шк. – М.: Просвещение, 1989. – 252с.
[9] Шахно К.У. Сборник задач по элементарной математике повышенной трудности. Изд. 5-е, стереотипное. Минск, «Вышейш. школа», 1969.
[10] Энциклопедия для детей. [Том 11.] Математика. – 2-е изд., перераб. / ред. Коллегия: М. Аксёнова, В. Володин, М. Самсонов. – М.: Мир энциклопедий Аванта+, Астрель, 2007. – 621с.
[11] Якир М.С., Мерзляк А.Г., Полонский В.Б. Неожиданный шаг или сто тринадцать красивых задач. Киев: Агрорифма «Александрия». 1993.
Библиотечка «Квант»
[12] Васильев Н., Сендеров В. Про угол  и
и  // №2. 1996.
// №2. 1996.
[13] Кушнир И. Геометрические решения негеометрических задач // №11. 1989.
[14] Ясиновый Э.Геометрия помогает решать уравнения // №12. 1984.
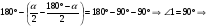 MNPQ – прямоугольник
MNPQ – прямоугольник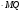
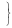

 , если
, если  .
. <
<

 .
.
 .
.
