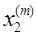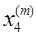Методы решения слау
Рассмотрим систему из трех линейных алгебраических уравнений и трех неизвестных.
 (II.5)
(II.5)
тогда матрица коэффициентов при неизвестных и расширенная матрица коэффициентов имеют вид:
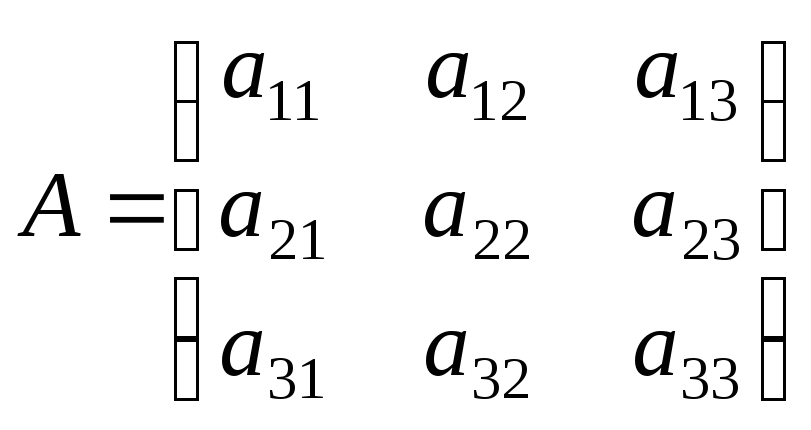 ,
,  .
.
1. Метод Крамера
Для системы (II.5) введем следующие обозначения:
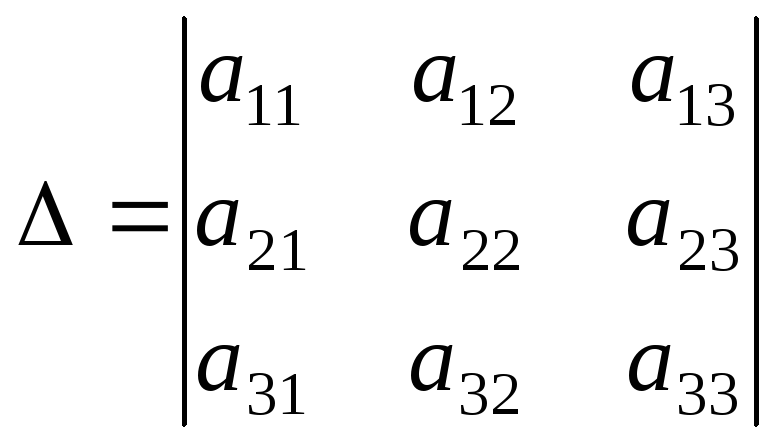 ,
,  ,
,
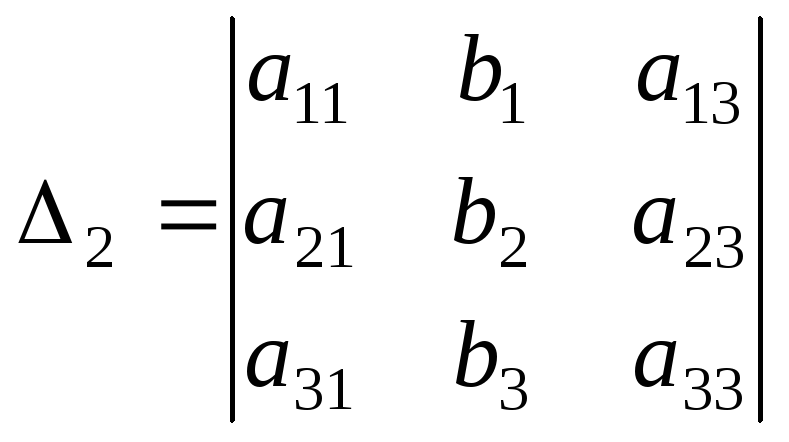
 ,
, где  ,i=1,2,3,
– определители, полученные из исходного
определителя
заменой i-ого
столбца столбцом свободных членов.
,i=1,2,3,
– определители, полученные из исходного
определителя
заменой i-ого
столбца столбцом свободных членов.
Тогда при решении системы методом Крамера 7 возможны следующие случаи:
если 0, то система (II.5) совместна и имеет единственное решение, которое находится по формулам:
 ,
,  ,
, 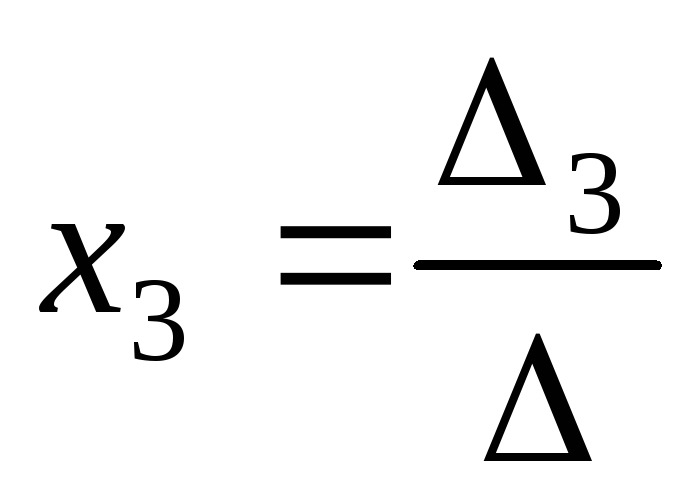 ;
;
если =0, 1=2=3=0, то система (II.5) либо имеет множество решений, либо несовместна;
если =0 и хотя бы один из 1, 2, 3 не равен нулю, то система (II.5) несовместна и решения не имеет.
2. Матричный метод
Пусть для системы (II.5) определитель 0. Запишем ее в матричной форме. Имеем: A – матрица коэффициентов при неизвестных, X – столбец неизвестных, B – столбец свободных членов системы:
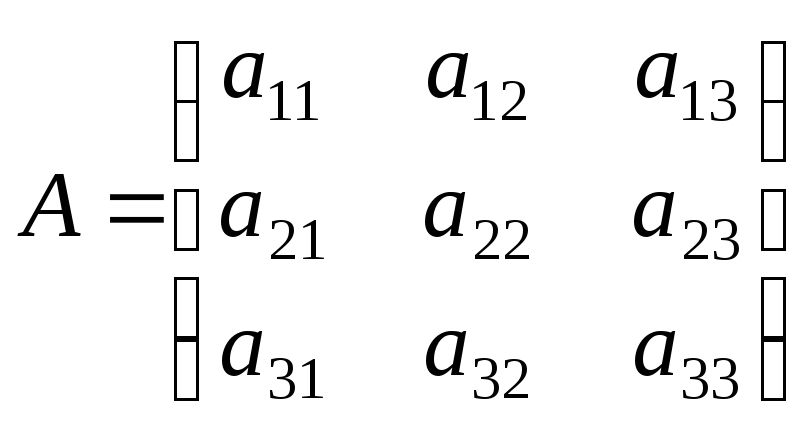 ,
, 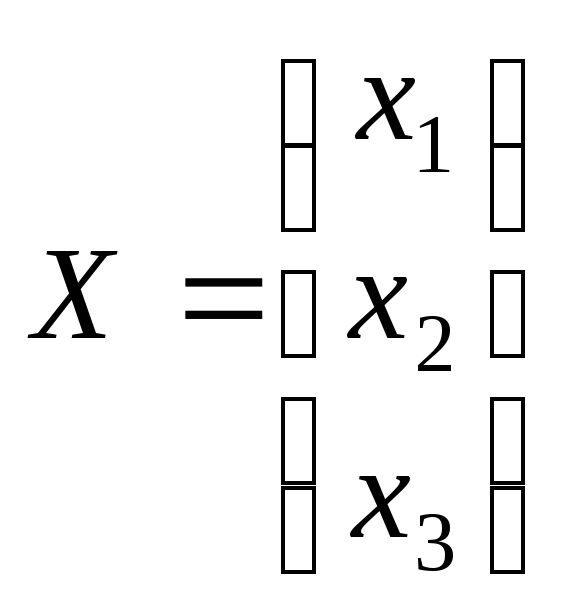 ,
,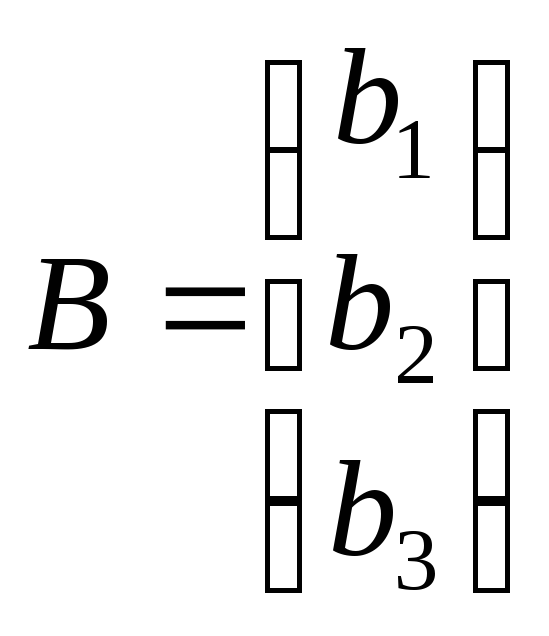 ,
,
тогда
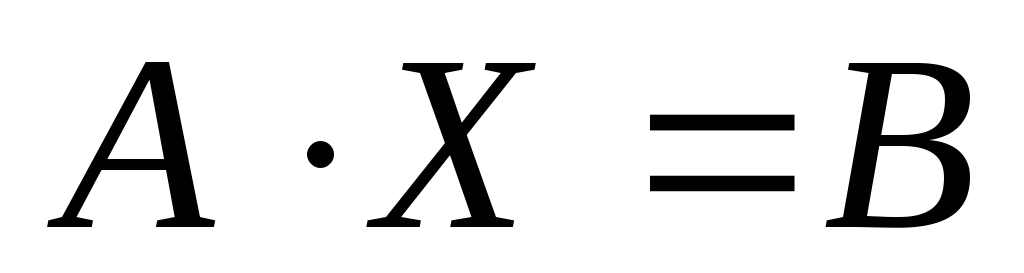 .
.
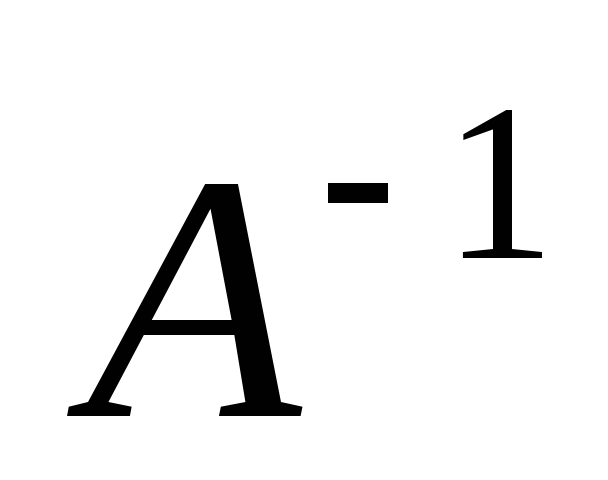 слева
слева 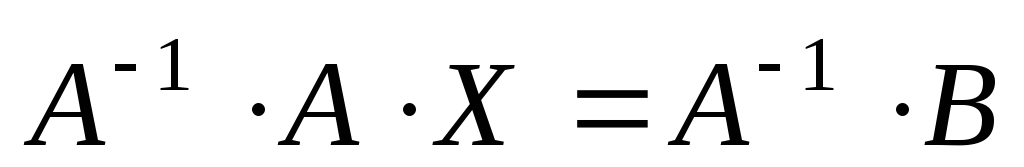 .
.
Так
как,  ,
то имеем
,
то имеем
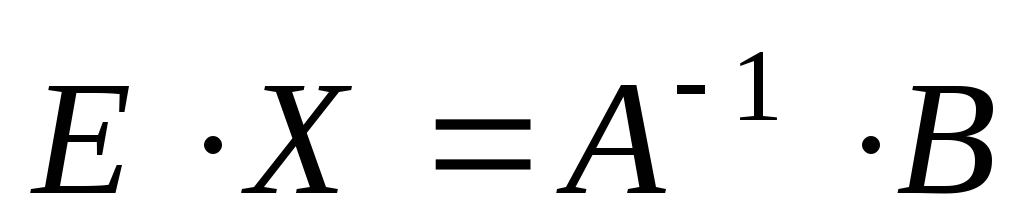
или
 .
(II.6)
.
(II.6)
3. Метод Гаусса
Метод Гаусса основан на алгоритме последовательного исключения неизвестных. Выпишем расширенную матрицу коэффициентов системы (II.5):

Задача состоит в том, чтобы привести ее к «треугольному» виду при помощи эквивалентных преобразований и получить единицы на главной диагонали и нули под ними.
Алгоритм состоит в том, что на каждом шаге выполняются следующие действия (количество шагов определяется количеством уравнений). Выбирается одна из ненулевых не рассмотренных ранее строк, ее номер считаем равным i. Все элементы этой строки делятся на элемент, стоящий на i-м месте (номер столбца этого элемента равен j). Если на i-м шаге какая-то из строк содержит уже на i—м месте единицу, то именно она переставляется и считается i—й строкой. Далее, добавляя к остальным, ранее не рассмотренным строкам i—ю строку умноженную на подходящее число, добиваемся того, что все элементы j-го столбца, расположенные ниже i—й строки, были равны нулю.
При решении систем алгебраических уравнений больших порядков требуется выполнять большой объем вычислений, в этом случае без техники не обойтись, следовательно, актуальной становится финансовая сторона вопроса.
Оценим число арифметических операций, необходимых для решения систем алгебраических уравнений порядка n методом Крамера. Будем учитывать только операции умножения и деления, поскольку времени на выполнение операций сложения и вычитания требуется на порядок меньше.
Для нахождения решения необходимо вычислить n+1 определитель порядка n, каждый из них содержит n! членов, пренебрегая операциями сложения и вычитания и учитывая, что для нахождения n неизвестных требуется n операций деления, окончательно получаем (n+1)! операций. Поскольку у быстродействующей вычислительной техники программное обеспечение ориентировано на параллельную обработку информации (содержит параллельные программы), то время на выполнение вычислений может быть существенно уменьшено, но не более чем до n!.
Оценим
число операций, необходимое для решения
той же системы методом Гаусса. В первом
уравнении этой системы n неизвестных, и для приведения к 1 всех
коэффициентов в каждом из n уравнений требуется 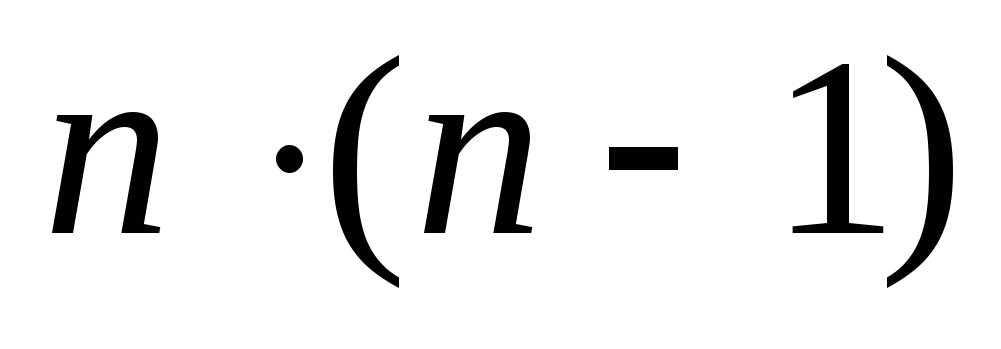 операций деления.
Для получения
системы изn-1
уравнения требуется выполнить
операций деления.
Для получения
системы изn-1
уравнения требуется выполнить 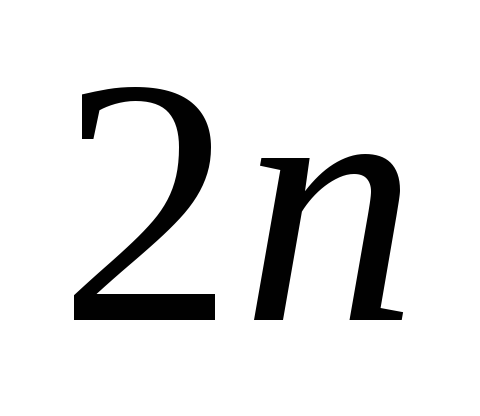 операций вычитания, пренебрегая которыми,
получаем после 1-го шага
операций вычитания, пренебрегая которыми,
получаем после 1-го шага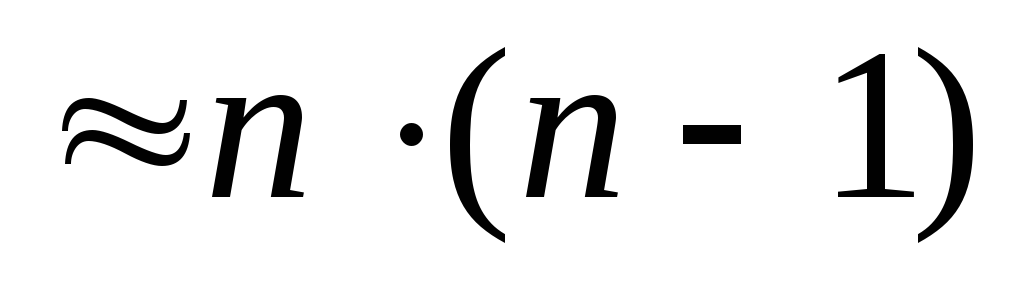 операций. Далее, по индукции, получаем
операций. Далее, по индукции, получаем и т.д. до 21
операций, то есть окончательно
получаем
и т.д. до 21
операций, то есть окончательно
получаем
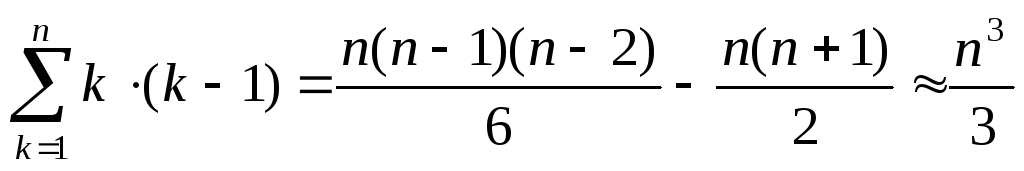
Таким образом, при больших n предпочтение, несомненно, должно быть отдано методу Гаусса. Часто по этой причине метод Гаусса называют машинным.
Плата за эффективность метода достаточно велика – это «неустойчивость» решения. Другими словами, правильность полученного решения системы методом Гаусса, вообще говоря, невозможно проверить.
При решении системы уравнений (II.5) методом Гаусса возможны следующие случаи.
Если матрица
 приведена к треугольному виду, то
система (II.3)
совместна и имеет единственное решение.
приведена к треугольному виду, то
система (II.3)
совместна и имеет единственное решение.Если матрица
 содержит хотя бы одну строку, все
элементы которой равны нулю, то система
(II.5)
совместна и имеет множество решений.
содержит хотя бы одну строку, все
элементы которой равны нулю, то система
(II.5)
совместна и имеет множество решений.Если матрица
 содержит строку, все элементы которой,
кроме свободного члена, равны нулю, то
система (II.5)
несовместна, то есть решения не имеет.
содержит строку, все элементы которой,
кроме свободного члена, равны нулю, то
система (II.5)
несовместна, то есть решения не имеет.
Пример II.8. Решить систему уравнений
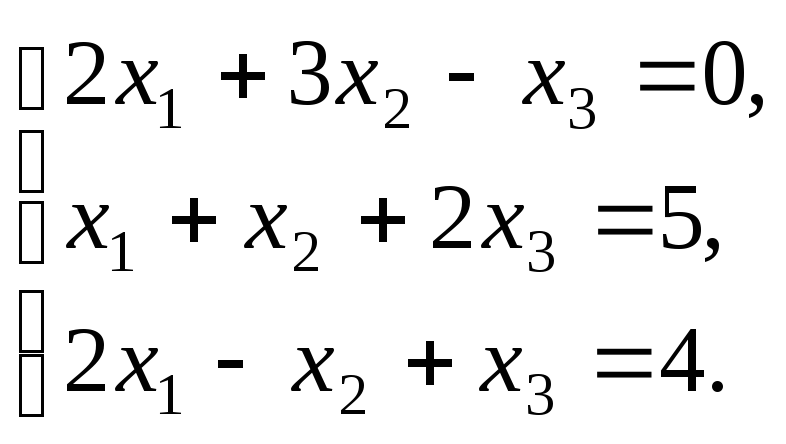
Решение. 1). Решим систему методом Крамера.
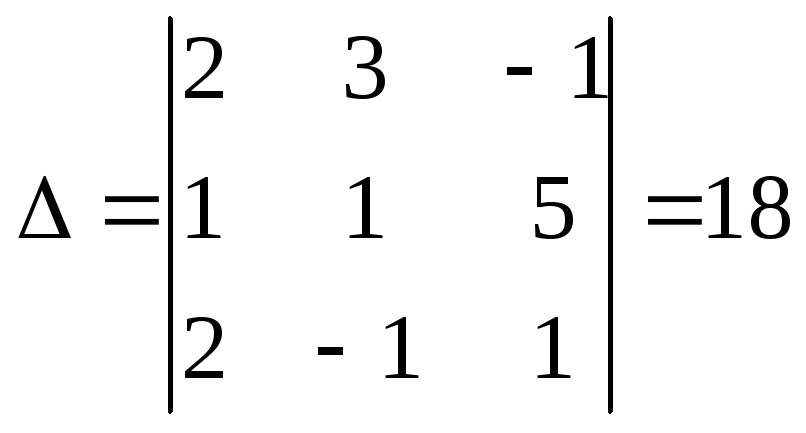 ,
, 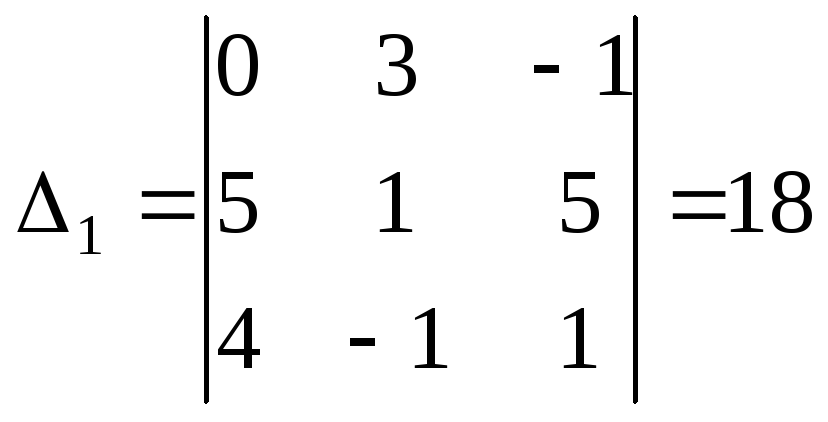 ,
,
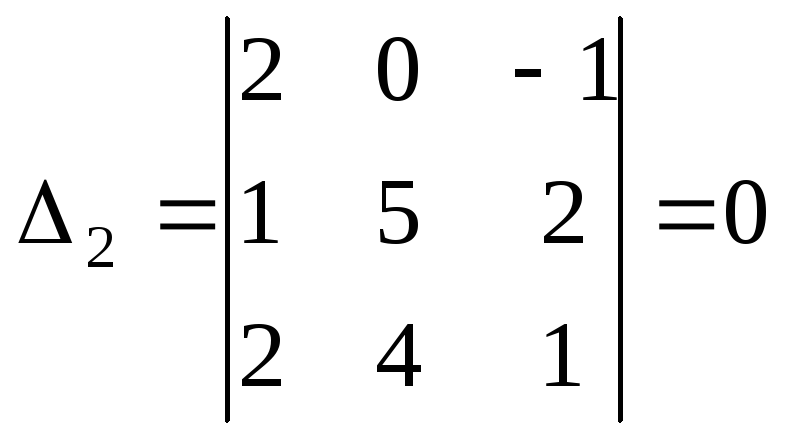 ,
, 
Так
как 0,
то система совместна и имеет единственное
решение: 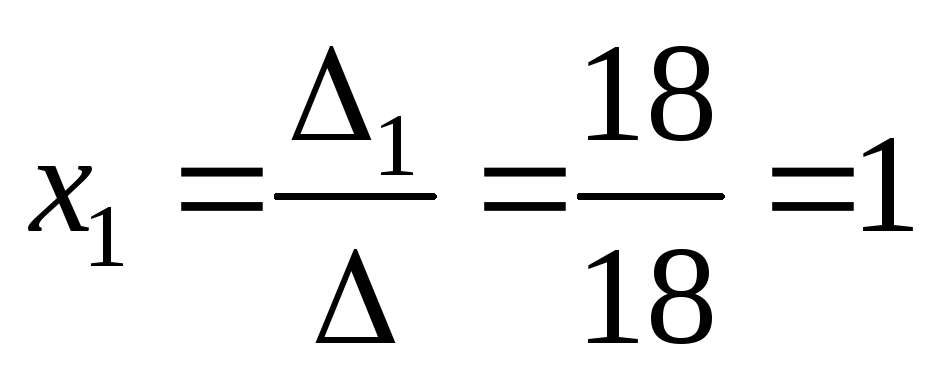 ,
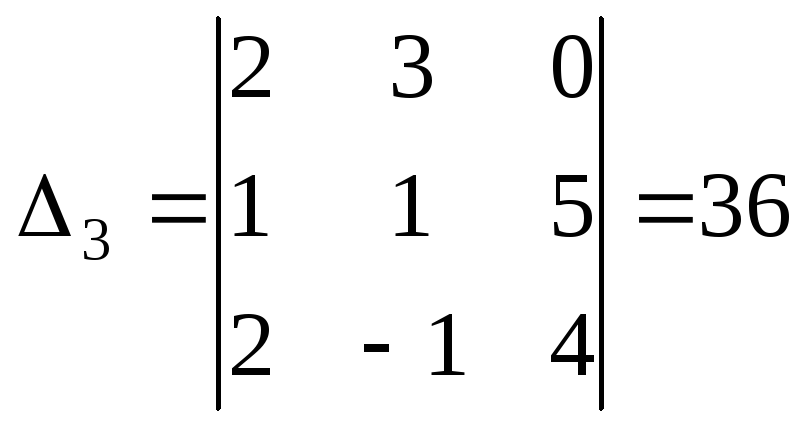
, ,
,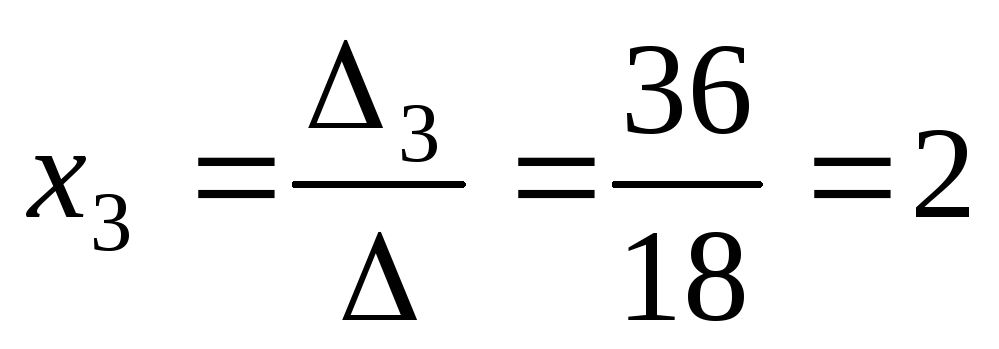 .
.
2). Решим систему матричным методом.
Так как 0, то обратная матрица к матрице A существует. Вычислим алгебраические дополнения, имеем:
тогда
обратная матрица 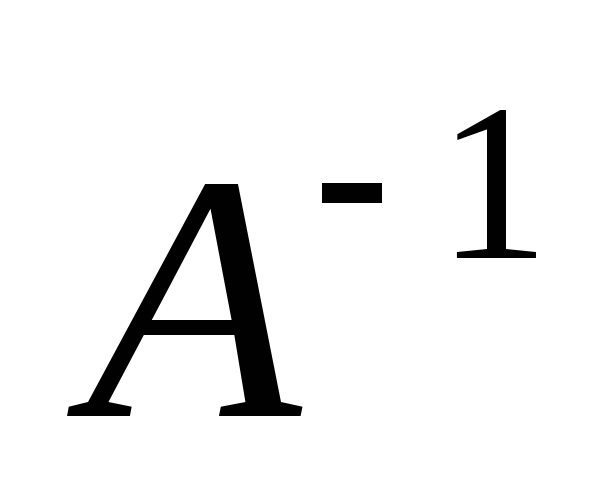 имеет следующий вид:
имеет следующий вид:
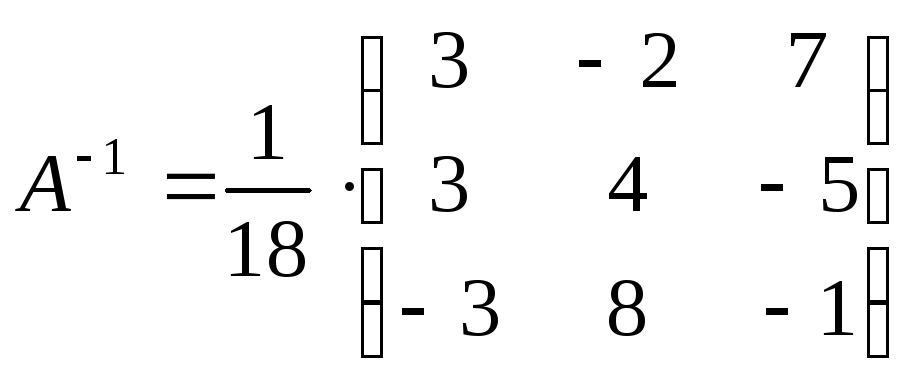 .
.
Найдем решение системы. Для этого запишем уравнение (II.6) в координатной форме:
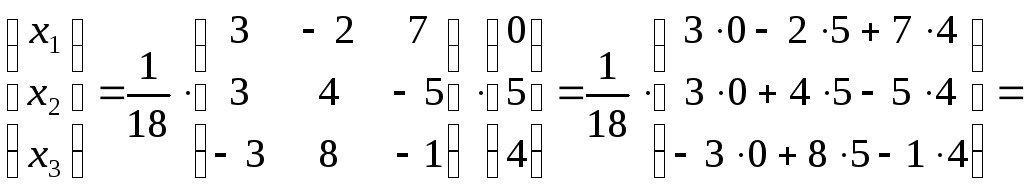
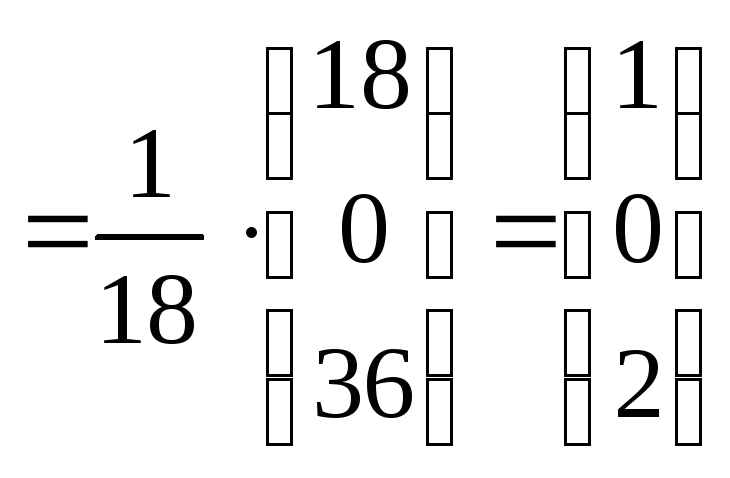 ,
,
следовательно, х1= 1, х2= 0, х3= 2.
3).
Решим систему методом Гаусса. Приведем
расширенную матрицу коэффициентов  к “треугольному виду”. Для этого
переставим 1-ю и 2-ю строки местами. Затем
домножим 1-ю строку на (-2) и прибавим ко
2-й и 3-й строкам. Полученную 2-ю строку
домножим на (3) и прибавим к полученной
3-й строке. В итоге последнюю строку
разделим на 18.
к “треугольному виду”. Для этого
переставим 1-ю и 2-ю строки местами. Затем
домножим 1-ю строку на (-2) и прибавим ко
2-й и 3-й строкам. Полученную 2-ю строку
домножим на (3) и прибавим к полученной
3-й строке. В итоге последнюю строку
разделим на 18.
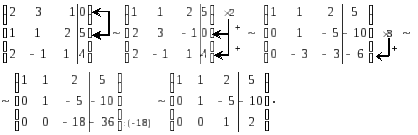 Матрица
приведена к треугольному виду,
следовательно, система совместна и
имеет единственное решение. Найдем его,
выписав систему уравнений, соответствующую
последней матрице.
Матрица
приведена к треугольному виду,
следовательно, система совместна и
имеет единственное решение. Найдем его,
выписав систему уравнений, соответствующую
последней матрице.
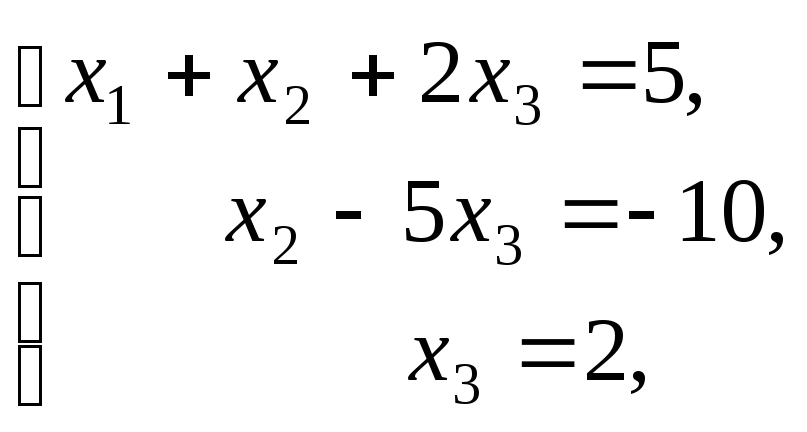
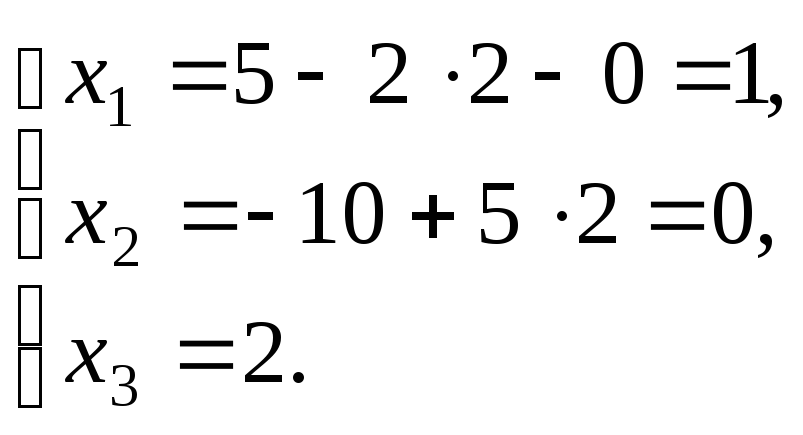
Ответ: х1=1, х2=0, х3=2.
Пример II.9.
Решить систему уравнений
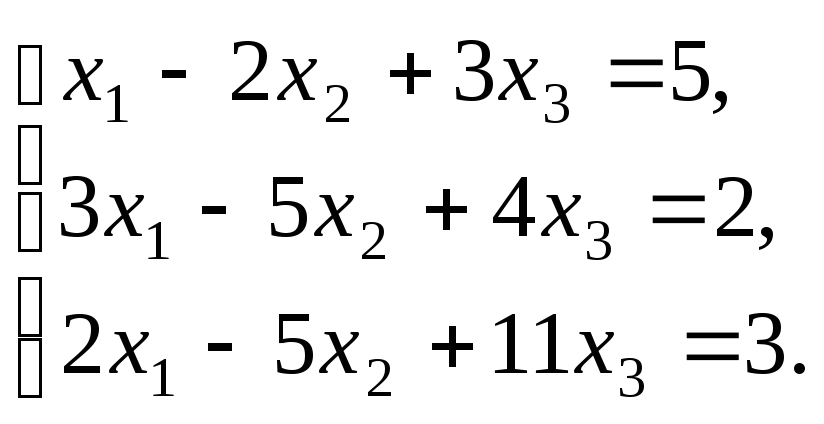
Решение.
Решим систему методом Крамера, имеем
 ,
,  .
.
Так как =0, 10, то система несовместна, решения не имеет.
Решим систему матричным методом. Так как =0, то обратная матрица к матрице A не существует, матричный метод неприменим.
Решим систему методом Гаусса. Приведем расширенную матрицу коэффициентов
 к треугольному виду. Для этого домножим
1-ю строку на (-3) и (-2) и прибавим ко 2-й и
3-й строкам соответственно. Полученную
2-ю строку прибавим к полученной 3-й
строке.
к треугольному виду. Для этого домножим
1-ю строку на (-3) и (-2) и прибавим ко 2-й и
3-й строкам соответственно. Полученную
2-ю строку прибавим к полученной 3-й
строке.
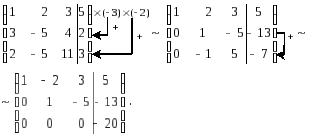
Так как у полученной матрицы, в последней строке, коэффициенты при неизвестных равны нулю, а свободный член не равен нулю, то решения нет, то есть система несовместна.
Ответ: система несовместна.
studfile.net
9.) Методы решения систем линейных алгебраических уравнений:
Прямые(конечные) методы решения СЛАУ: (позволяют найти решение за определенное число операций.) Метод Крамера Метод обратной матрицы Метод ГауссаИтерационные методы решения линейных алгебраических систем: (основанны на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений.)Метод простой итерации или метод Якоби Метод Гаусса – Зейделя
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
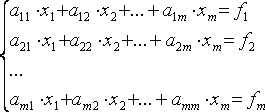 ,
,
Эту систему уравнений можно записать также в матричном виде:
 ,
,
где  ,
, 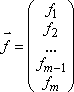 ,
, 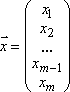 .
.
A –
матрица системы,  –
вектор правых частей,
–
вектор правых частей, 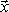 –
вектор неизвестных.
–
вектор неизвестных.
При
известных A и 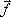 требуется
найти такие
требуется
найти такие 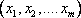 ,
при подстановке которых в систему
уравнений она превращается в тождество.
,
при подстановке которых в систему
уравнений она превращается в тождество.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
Система называется обусловленной (не вырожденной, не особенной), если определитель системы 0, и тогда система имеет единственное решение.
Система называется не обусловленной (вырожденной, особенной), если = 0, и тогда система не имеет решений или имеет бесконечное множество решений.
Система называется плохо обусловленной, если неустранимая погрешность оказывает сильное влияние на решение; у таких систем определитель близок, но не равен 0.
10.) Прямые методы решения слау Метод Крамера:
 число
уравнений равно числу неизвестных
переменных и определитель основной
матрицы системы отличен от нуля, то
есть,
число
уравнений равно числу неизвестных
переменных и определитель основной
матрицы системы отличен от нуля, то
есть, 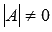 .
.
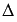 —
определитель основной матрицы системы,
а
—
определитель основной матрицы системы,
а  —
определители матриц, которые получаются
из А заменой 1-ого,
2-ого, …, n-ого столбца
соответственно на столбец свободных
членов:
—
определители матриц, которые получаются
из А заменой 1-ого,
2-ого, …, n-ого столбца
соответственно на столбец свободных
членов: 
При
таких обозначениях неизвестные переменные
вычисляются по формулам метода Крамера
как 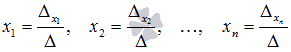 .
Так находится решение системы линейных
алгебраических уравнений методом
Крамера.
Основным
недостатком метода Крамера является
трудоемкость вычисления определителей,
когда число уравнений системы больше
трех.
.
Так находится решение системы линейных
алгебраических уравнений методом
Крамера.
Основным
недостатком метода Крамера является
трудоемкость вычисления определителей,
когда число уравнений системы больше
трех.
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Матричной
форма СЛАУ- 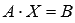 ,
где матрица A имеет
размерность n на n и
ее определитель отличен от нуля.
,
где матрица A имеет
размерность n на n и
ее определитель отличен от нуля.
Так
как  ,
то матрица А –
обратима, то есть, существует обратная
матрица
,
то матрица А –
обратима, то есть, существует обратная
матрица  .
Если умножить обе части равенства
.
Если умножить обе части равенства 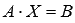 на
на 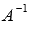 слева,
то получим формулу для нахождения
матрицы-столбца неизвестных
переменных
слева,
то получим формулу для нахождения
матрицы-столбца неизвестных
переменных  -решение
системы линейных алгебраических
уравнений матричным методом.
-решение
системы линейных алгебраических
уравнений матричным методом.
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Метод Гаусса- этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений
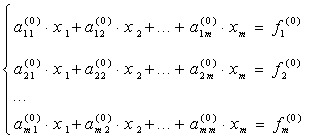
первый
элемент  .
Назовем его ведущим
элементом первой
строки. Поделим все элементы этой строки
на
.
Назовем его ведущим
элементом первой
строки. Поделим все элементы этой строки
на  и
исключим x1 из
всех последующих строк, начиная со
второй, путем вычитания первой
(преобразованной), умноженной на
коэффициент при
и
исключим x1 из
всех последующих строк, начиная со
второй, путем вычитания первой
(преобразованной), умноженной на
коэффициент при 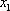 в
соответствующей строке. Получим
в
соответствующей строке. Получим
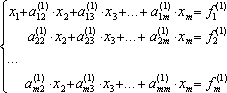 .
.
Если  ,
то, продолжая аналогичное исключение,
приходим к системе уравнений с верхней
треугольной матрицей
,
то, продолжая аналогичное исключение,
приходим к системе уравнений с верхней
треугольной матрицей
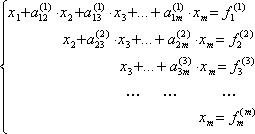 .
.
Из нее в обратном порядке находим все значения xi:
 .
.
Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:
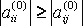 ,
j = i+1,i+ 2, …, m;
,
j = i+1,i+ 2, …, m;
т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a11 был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x1 из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.
studfile.net
Система линейных алгебраических уравнений
Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.
Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.
Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему
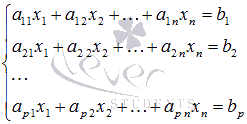
содержащую m уравнений и n неизвестных (x1,x2,…,xn). Прилагательное «линейных» означает, что все неизвестные (их еще называют переменными) входят только в первой степени.
Параметры aij называют коэффициентами, а bi – свободными членами СЛАУ. Иногда, чтобы подчеркнуть количество уравнений и неизвестных, говорят так «m×n система линейных уравнений», – тем самым указывая, что СЛАУ содержит m уравнений и n неизвестных.
Если все свободные члены bi=0 то СЛАУ называют однородной. Если среди свободных членов есть хотя бы один, отличный от нуля, СЛАУ называют неоднородной.
Решением СЛАУ (1) называют всякую упорядоченную совокупность чисел (α1,α2,…,αn), если элементы этой совокупности, подставленные в заданном порядке вместо неизвестных x1,x2,…,xn, обращают каждое уравнение СЛАУ в тождество.
Любая однородная СЛАУ имеет хотя бы одно решение: нулевое (в иной терминологии – тривиальное), т.е. x1=x2=…=xn=0.
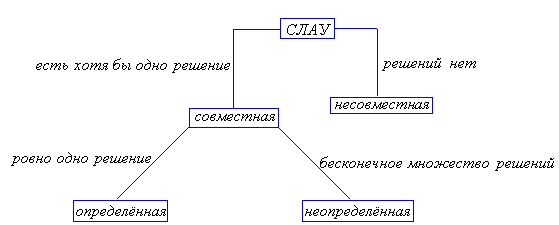
Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной, если же решений нет – несовместной. Если совместная СЛАУ имеет ровно одно решение, её именуют определённой, если бесконечное множество решений – неопределённой.
Матричная форма записи систем линейных алгебраических уравнений.
С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:

Матрица A называется матрицей системы. Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.
Матрица A˜ называется расширенной матрицей системы. Её получают добавлением к матрице системы столбца, содержащего свободные члены b1,b2,…,bm. Обычно этот столбец отделяют вертикальной чертой, – для наглядности.
Матрица-столбец B называется матрицей свободных членов, а матрица-столбец X – матрицей неизвестных.
Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: A⋅X=B.
Примечание
Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков
Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность.
Теорема Кронекера-Капелли
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. rangA=rangA˜.
Система называется совместной, если она имеет хоть одно решение. Теорема Кронекера-Капелли говорит вот о чём: если rangA=rangA˜, то решение есть; если rangA≠rangA˜, то данная СЛАУ не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы Кронекера-Капелли. В формулировке следствия использована буква n, которая равна количеству переменных заданной СЛАУ.
Следствие из теоремы Кронекера-Капелли
Если rangA≠rangA˜, то СЛАУ несовместна (не имеет решений).
Если rangA=rangA˜<n, то СЛАУ является неопределённой (имеет бесконечное количество решений).
Если rangA=rangA˜=n, то СЛАУ является определённой (имеет ровно одно решение).
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения нет, а если существуют – то сколько.
Методы решения СЛАУ
Метод Крамера
Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода Крамера можно выразить в трёх пунктах:
Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. Δ≠0.
Для каждой переменной xi необходимо составить определитель Δ Xi, полученный из определителя Δ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
Найти значения неизвестных по формуле xi= Δ Xi /Δ
Решение систем линейных алгебраических уравнений с помощью обратной матрицы.
Решение систем линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы (иногда этот способ именуют ещё матричным методом или методом обратной матрицы) требует предварительного ознакомления с таким понятием как матричная форма записи СЛАУ. Метод обратной матрицы предназначен для решения тех систем линейных алгебраических уравнений, у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода обратной матрицы можно выразить в трёх пунктах:
Записать три матрицы: матрицу системы A, матрицу неизвестных X, матрицу свободных членов B.
Найти обратную матрицу A-1.
Используя равенство X=A-1⋅B получить решение заданной СЛАУ.
Метод Гаусса. Примеры решения систем линейных алгебраических уравнений методом Гаусса.
Метод Гаусса является одним из самых наглядных и простых способов решения систем линейных алгебраических уравнений (СЛАУ): как однородных, так и неоднородных. Коротко говоря, суть данного метода состоит в последовательном исключении неизвестных.
Преобразования, допустимые в методе Гаусса:
Смена мест двух строк;
Умножение всех элементов строки на некоторое число, не равное нулю.
Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
Вычеркивание строки, все элементы которой равны нулю.
Вычеркивание повторяющихся строк.
Насчет последних двух пунктов: повторяющиеся строки можно вычёркивать на любом этапе решения методом Гаусса, – естественно, оставляя при этом одну из них. Например, если строки №2, №5, №6 повторяются, то можно оставить одну из них, – например, строку №5. При этом строки №2 и №6 будут удалены.
Нулевые строки убираются из расширенной матрицы системы по мере их появления.
studfile.net
Решение систем линейных алгебраических уравнений общего вида.
В
общем случае число уравнений системы pне совпадает с числом неизвестных
переменныхn:
Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.
Далее нам потребуется понятие минора матрицы и ранга матрицы, которые даны в статье ранг матрицы: определение, методы нахождения, примеры, решения.
Теорема Кронекера – Капелли.
Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает теорема Кронекера – Капелли: для того, чтобы система изpуравнений сnнеизвестными (pможет быть равноn) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть,Rank(A)=Rank(T).
Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений.
Пример.
Выясните,
имеет ли система линейных уравнений 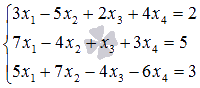 решения.
решения.
Решение.
Найдем
ранг основной матрицы системы 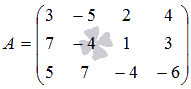 .
Воспользуемся методом окаймляющих
миноров. Минор второго порядка
.
Воспользуемся методом окаймляющих
миноров. Минор второго порядка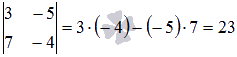 отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
Так как все окаймляющие миноры третьего порядка равны нулю, то ранг основной матрицы равен двум.
В
свою очередь ранг расширенной матрицы  равен
трем, так как минор третьего порядка
равен
трем, так как минор третьего порядка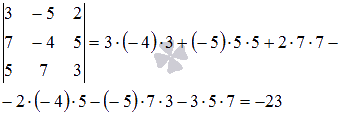 отличен
от нуля.
отличен
от нуля.
Таким образом, Rang(A) < Rang(T), следовательно, по теореме Кронекера – Капелли можно сделать вывод, что исходная система линейных уравнений несовместна.
Ответ:
система решений не имеет.
Итак, мы научились устанавливать несовместность системы с помощью теоремы Кронекера – Капелли.
А как же находить решение СЛАУ, если установлена ее совместность?
Для этого нам потребуется понятие базисного минора матрицы и теорема о ранге матрицы.
Минор наивысшего порядка матрицы А, отличный от нуля, называетсябазисным.
Из определения базисного минора следует, что его порядок равен рангу матрицы. Для ненулевой матрицы Абазисных миноров может быть несколько, один базисный минор есть всегда.
Для
примера рассмотрим матрицу 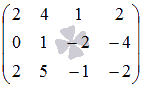 .
.
Все миноры третьего порядка этой матрицы равны нулю, так как элементы третьей строки этой матрицы представляют собой сумму соответствующих элементов первой и второй строк.
Базисными
являются следующие миноры второго
порядка, так как они отличны от нуля 
Миноры  базисными
не являются, так как равны нулю.
базисными
не являются, так как равны нулю.
Теорема о ранге матрицы.
Если ранг матрицы порядка pнаnравенr, то все элементы строк (и столбцов) матрицы, не образующие выбранный базисный минор, линейно выражаются через соответствующие элементы строк (и столбцов), образующих базисный минор.
Что нам дает теорема о ранге матрицы?
Если по теореме Кронекера – Капелли мы установили совместность системы, то выбираем любой базисный минор основной матрицы системы (его порядок равен r), и исключаем из системы все уравнения, которые не образуют выбранный базисный минор. Полученная таким образом СЛАУ будет эквивалентна исходной, так как отброшенные уравнения все равно излишни (они согласно теореме о ранге матрицы являются линейной комбинацией оставшихся уравнений).
В итоге, после отбрасывания излишних уравнений системы, возможны два случая.
Если число уравнений rв полученной системе будет равно числу неизвестных переменных, то она будет определенной и единственное решение можно будет найти методом Крамера, матричным методом или методом Гаусса.
Пример.
Решите
систему линейных алгебраических
уравнений 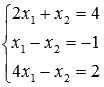 .
.
Решение.
Ранг
основной матрицы системы 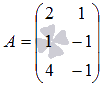 равен
двум, так как минор второго порядка
равен
двум, так как минор второго порядка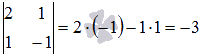 отличен
от нуля. Ранг расширенной матрицы
отличен
от нуля. Ранг расширенной матрицы также
равен двум, так как единственный минор
третьего порядка равен нулю
также
равен двум, так как единственный минор
третьего порядка равен нулю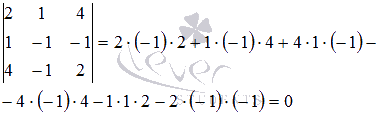 а
рассмотренный выше минор второго порядка
отличен от нуля. На основании теоремы
Кронекера – Капелли можно утверждать
совместность исходной системы линейных
уравнений, так какRank(A)=Rank(T)=2.
а
рассмотренный выше минор второго порядка
отличен от нуля. На основании теоремы
Кронекера – Капелли можно утверждать
совместность исходной системы линейных
уравнений, так какRank(A)=Rank(T)=2.
В
качестве базисного минора возьмем  .
Его образуют коэффициенты первого и
второго уравнений:
.
Его образуют коэффициенты первого и
второго уравнений: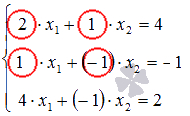
Третье
уравнение системы не участвует в
образовании базисного минора, поэтому
исключим его из системы на основании
теоремы о ранге матрицы: 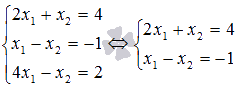
Так
мы получили элементарную систему
линейных алгебраических уравнений.
Решим ее методом Крамера: 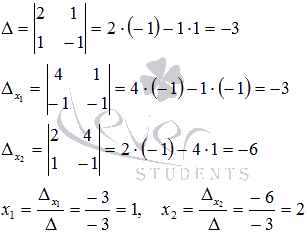
Ответ:
x1 = 1, x2 = 2.
Если число уравнений rв полученной СЛАУ меньше числа неизвестных переменныхn, то в левых частях уравнений оставляем слагаемые, образующие базисный минор, остальные слагаемые переносим в правые части уравнений системы с противоположным знаком.
Неизвестные переменные (их rштук), оставшиеся в левых частях уравнений, называютсяосновными.
Неизвестные переменные (их n — rштук), которые оказались в правых частях, называютсясвободными.
Теперь считаем, что свободные неизвестные переменные могут принимать произвольные значения, при этом rосновных неизвестных переменных будут выражаться через свободные неизвестные переменные единственным образом. Их выражение можно найти решая полученную СЛАУ методом Крамера, матричным методом или методом Гаусса.
Разберем на примере.
Пример.
Решите систему линейных алгебраических уравнений .
Решение.
Найдем
ранг основной матрицы системы 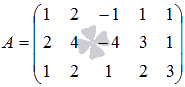 методом
окаймляющих миноров. В качестве ненулевого
минора первого порядка возьмемa1
1 = 1. Начнем поиск ненулевого
минора второго порядка, окаймляющего
данный минор:
методом
окаймляющих миноров. В качестве ненулевого
минора первого порядка возьмемa1
1 = 1. Начнем поиск ненулевого
минора второго порядка, окаймляющего
данный минор: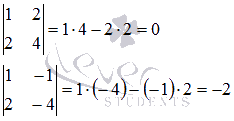
Так
мы нашли ненулевой минор второго порядка.
Начнем поиск ненулевого окаймляющего
минора третьего порядка: 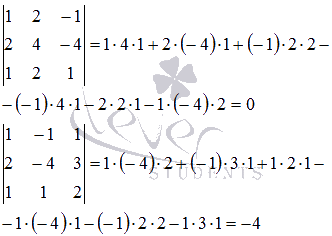
Таким образом, ранг основной матрицы равен трем. Ранг расширенной матрицы также равен трем, то есть, система совместна.
Найденный ненулевой минор третьего порядка возьмем в качестве базисного.
Для
наглядности покажем элементы, образующие
базисный минор: 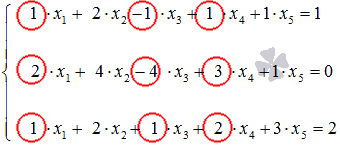
Оставляем
в левой части уравнений системы слагаемые,
участвующие в базисном миноре, остальные
переносим с противоположными знаками
в правые части: 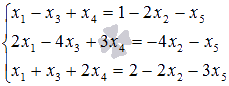
Придадим
свободным неизвестным переменным x2иx5произвольные значения,
то есть, примем ,
где
,
где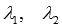 —
произвольные числа. При этом СЛАУ примет
вид
—
произвольные числа. При этом СЛАУ примет
вид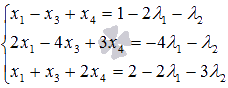
Полученную
элементарную систему линейных
алгебраических уравнений решим методом
Крамера: 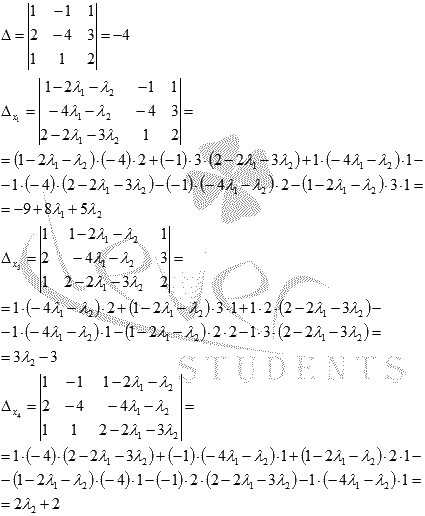
Следовательно, 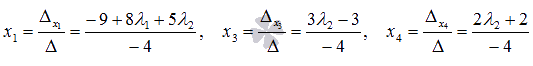 .
.
В ответе не забываем указать свободные неизвестные переменные.
Ответ:
 ,
где
,
где 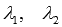 —
произвольные числа.
—
произвольные числа.
Подведем итог.
Чтобы решить систему линейных алгебраических уравнений общего вида, сначала выясняем ее совместность, используя теорему Кронекера – Капелли. Если ранг основной матрицы не равен рангу расширенной матрицы, то делаем вывод о несовместности системы.
Если ранг основной матрицы равен рангу расширенной матрицы, то выбираем базисный минор и отбрасываем уравнения системы, которые не участвуют в образовании выбранного базисного минора.
Если порядок базисного минора равен числу неизвестных переменных, то СЛАУ имеет единственное решение, которое находим любым известным нам методом.
Если порядок базисного минора меньше числа неизвестных переменных, то в левой части уравнений системы оставляем слагаемые с основными неизвестными переменными, остальные слагаемые переносим в правые части и придаем свободным неизвестным переменным произвольные значения. Из полученной системы линейных уравнений находим основные неизвестные переменные методом Крамера, матричным методом или методом Гаусса.
К началу страницы
studfile.net
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравненийЭтот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье
2. Методы решения систем линейных алгебраических уравнений
Прямые методы решения СЛАУ:
Метод Крамера
Метод обратной матрицы
Метод Гаусса
Итерационные методы решения линейных алгебраических систем:
Метод простой итерации или метод Якоби
Метод Гаусса – Зейделя
К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи ( по некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики.
Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
,
Эту систему уравнений можно записать также в матричном виде:
,
где , , .
A – матрица системы, – вектор правых частей, – вектор неизвестных.
При известных A и требуется найти такие , при подстановке которых в систему уравнений она превращается в тождество.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
В дальнейшем будем предполагать наличие единственного решения.
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).
Прямые методы решения СЛАУ
Метод Крамера
При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:
(i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц Ai, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Так А1 получается из матрицы А заменой первого столбца на столбец правых частей f.
Например, для системы двух линейных уравнений
Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10158 вычислительных операций (процесс займёт примерно 1019 лет), что не под силу даже самым мощным современным ЭВМ
Метод обратной матрицы
Если det A ≠ 0, то существует обратная матрица . Тогда решение СЛАУ записывается в виде: . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.
Метод Гаусса
Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений
первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим
.
Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей
.
Из нее в обратном порядке находим все значения xi:
.
Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:
, j = i+1,i+ 2, …, m;
т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a11 был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x1 из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.
Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:
В первом уравнении коэффициент при =0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:
Исключим из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:
Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при в третьем. Поэтому поместим его на место второго:
Исключим из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:
Обратный ход: .
Проверка: 0.5*8+0=4, -3+8-0=5, -2*(-3)+0=6.
Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.
Часто возникает необходимость в решении СЛАУ, матрицы которые являются слабо заполненными, т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Например, метод прогонки, который мы рассмотрим позже при решении краевой задачи для обыкновенного дифференциального уравнения второго порядка.
Итерационные методы решения линейных алгебраических систем
Метод простой итерации или метод Якоби
Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:
,
где , , .
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:
(1),
Теперь, задав нулевое приближение , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:
(2)Аналогично находятся следующие приближения , где в (2) вместо необходимо подставить .
Или в общем случае:
. (3)
или
Условие окончания итерационного процесса .
Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. , то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут или .
Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, а может и не сойтись.
Пример.
Решить систему линейных уравнений с точностью :
|
|
8 |
4 |
2 |
|
10 |
|
x1 |
|
|
= |
3 |
5 |
1 |
= |
5 |
= |
x2 |
|
|
|
3 |
–2 |
10 |
|
4 |
|
x3 |
|
Решение прямыми методами, например, обратной матрицей, даёт решение:
.
Найдем решение методом простой итерации. Проверяем условие диагонального преобладания: , , .
Приводим систему уравнений к виду (1):
.
Начальное приближение . Дальнейшие вычисления оформим в виде таблицы:
|
k |
x1 |
x2 |
x3 |
точность |
|
0 |
0 |
0 |
0 |
|
|
1 |
1.250 |
1.000 |
0.400 |
1.2500 |
|
2 |
0.650 |
0.170 |
0.225 |
0.8300 |
|
3 |
1.109 |
0.565 |
0.239 |
0.4588 |
|
……… |
||||
|
4 |
0.908 |
0.287 |
0.180 |
0.2781 |
|
5 |
1.061 |
0.419 |
0.185 |
0.1537 |
|
6 |
0.994 |
0.326 |
0.165 |
0.0931 |
|
7 |
1.046 |
0.370 |
0.167 |
0.0515 |
|
8 |
1.023 |
0.594 |
0.160 |
0.2235 |
|
9 |
0.913 |
0.582 |
0.212 |
0.1101 |
|
10 |
0.906 |
0.505 |
0.242 |
0.0764 |
|
11 |
0.937 |
0.495 |
0.229 |
0.0305 |
|
12 |
0.945 |
0.516 |
0.218 |
0.0210 |
|
…… |
||||
|
13 |
0.937 |
0.523 |
0.220 |
0.0077 |
Здесь
,
И т.д., пока не получим, в последнем столбце величину меньшую 0.01, что произойдет на 13 – ой итерации.
Следовательно, приближенное решение имеет вид:
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.
Подробные формулы имеют вид:
Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:
Начальное приближение:
Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.
Расчетные формулы:
|
k |
x1 |
x2 |
x3 |
точность |
|
0 |
0 |
0 |
0 |
|
|
1 |
1.250 |
0.250 |
0.075 |
1.2500 |
|
2 |
1.106 |
0.321 |
0.132 |
0.1438 |
|
3 |
1.056 |
0.340 |
0.151 |
0.0500 |
|
4 |
1.042 |
0.344 |
0.156 |
0.0139 |
|
5 |
1.039 |
0.346 |
0.157 |
0.0036 |
Из таблицы видно, что нужная точность достигнута уже на 5–ой итерации вместо 13–ой по методу простой итерации и значения корней более близки к значениям, полученным методом обратной матрицы.
pers.narod.ru
3 Решение систем линейных алгебраических уравнений итерационными методами
Тема 3. Решение систем линейных алгебраических уравнений итерационными методами.
Описанные выше прямые методы решения СЛАУ не очень эффективны при решении систем большой размерности (т.е. когдо значение n достаточно велико). Для решения СЛАУ в таких случаях больше подходят итерационные методы
Итерационные методы решения СЛАУ (их второе название — методы последовательного приближения к решению) не дают точного решения СЛАУ, а дают только приближение к решению, причем каждое следующее приближение получается из предыдущего и является более точным, чем предыдущее (при условии, что обеспечена сходимость итераций). Начальное (или, так называемое, нулевое) приближение выбирается вблизи предполагаемого решения или произвольно (в качестве его можно взять вектор правой части системы). Точное решение находится как предел таких приближений при стремлении их количества к бесконечности. Как правило, за конечное число шагов (т.е. итераций) этот предел не достигается. Поэтому, на практике, вводится понятие точности решения, а именно задается некоторое положительное и достаточно малое число e и процесс вычислений (итераций) проводят до тех пор, пока не будет выполнено соотношение 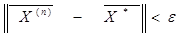 .
.
Здесь  — приближение к решению, полученное после итерации номер n, а
— приближение к решению, полученное после итерации номер n, а 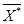 — точное решение СЛАУ (которое заранее неизвестно). Число итераций n=n(e), необходимое для достижения заданной точности для конкретных методов можно получить из теоретических рассмотрений (т. е. для этого имеются расчетные формулы). Качество различных итерационных методов можно сравнить по необходимому числу итераций для достижения одной и той же точности.
— точное решение СЛАУ (которое заранее неизвестно). Число итераций n=n(e), необходимое для достижения заданной точности для конкретных методов можно получить из теоретических рассмотрений (т. е. для этого имеются расчетные формулы). Качество различных итерационных методов можно сравнить по необходимому числу итераций для достижения одной и той же точности.
Для исследования итерационных методов на сходимость необходимо уметь вычислять нормы матриц. Норма матрицы — это некая числовая величина, характеризующая величину элементов матрицы по абсолютной величине. В высшей математике имеется несколько различных видов норм матриц, которые, как правило, являются эквивалентными. В нашем курсе мы будем пользоваться только одной из них. А именно, под нормой матрицы мы будем понимать максимальную величину среди сумм абсолютных величин элементов отдельных строк матрицы. Для обозначения нормы матрицы — ее название заключается в две пары вертикальных черточек. Так, для матрицы A под ее нормой будем понимать величину
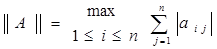 . (3.1)
. (3.1)
Так, к примеру, норма матрицы А из примера 1 находится следующим образом :

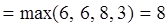 .
.
Наиболее широкое применение для решения СЛАУ получили три итерационных метода
— метод простой итерации
— метод Якоби
— метод Гуасса-Зейделя.
Метод простой итерации предполагает переход от записи СЛАУ в исходном виде (2.1) к записи ее в виде
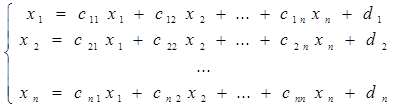 (3.2)
(3.2)
или, что тоже, в матричном виде,
x = С×x + D, (3.3)
где :
C — матрица коэффициентов преобразованной системы размерности n´n
x — вектор неизвестных, состоящий из n компонент
D — вектор правых частей преобразованной системы, состоящий из n компонент.
Система в виде (3.2) может быть представлена в сокращенном виде
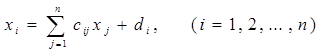
Исходя из этого представления формула простой итерации будет иметь вид
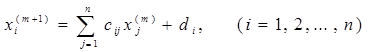 (3.4)
(3.4)
где m — номер итерации, а 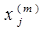 — значение xj на m-ом шаге итерации. Тогда, если процесс итераций сходится, с увеличением количества итераций будет наблюдаться
— значение xj на m-ом шаге итерации. Тогда, если процесс итераций сходится, с увеличением количества итераций будет наблюдаться
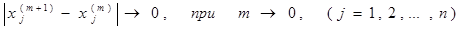
Доказано, что процесс итераций сходится, если норма матрицы D будет меньше единицы.
Если за начальное (нулевое) приближение взять вектор свободных членов, т.е. x(0) = D, то величина погрешности имеет вид
 (3.5)
(3.5)
здесь под x* понимается точное решение системы. Следовательно,
если 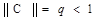 , то по заданной точности e можно заранее расчитать необходимое количество итераций. А именно, из соотношения
, то по заданной точности e можно заранее расчитать необходимое количество итераций. А именно, из соотношения
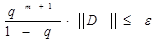
после небольших преобразований получим
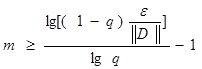 . (3.6)
. (3.6)
При выполнении такого количества итераций гарантировано будет обеспечена заданная точность нахождения решения системы. Эта теоретическая оценка необходимого количества шагов итерации несколько завышена. На практике необходимая точность может быть достигнута за меньшее количество итераций.
Поиск решений заданной СЛАУ методом простой итерации удобно производить с занесением полученных результатов в таблицу следующего вида :
Следует особо отметить, что в решении СЛАУ этим методом наиболее сложным и трудоемким является выполнение преобразования системы из вида (2.1) к виду (3.2). Эти преобразования должны быть эквивалентными, т.е. не меняющими решения исходной системы, и обеспечивающие величину нормы матрицы C (после выполнения их) меньшей единицы. Единого рецепта для выполнения таких преобразований не существует. Здесь в каждом конкретном случае необходимо проявлять творчество. Рассмотрим примеры, в которых будут приведены некоторые способы преобразования системы к необходимому виду.
Пример 1. Найдем решение системы линейных алгебраических уравнений методом простой итерации (с точностью e=0.001)
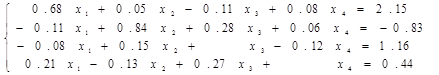
Эта система приводится к необходимому виду простейшим способом. Перенесем все слагаемые из левой части в правую, а затем к обоим частям каждого уравнения прибавим по xi (i=1, 2, 3, 4). Получим преобразованную систему следующего вида
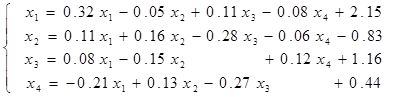 .
.
Матрица C и вектор D в этом случае будут следующими
C = 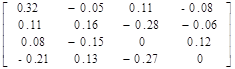 , D =
, D =  .
.
Вычислим норму матрицы C. Получим
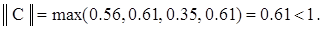
Так как норма оказалась меньшей единицы — сходимость метода простой итерации обеспечена. В качестве начального (нулевого) приближения примем компоненты вектора D. Получим
 ,
,  ,
, 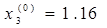 ,
, 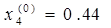 .
.
По формуле (3.6) вычислим необходимое число шагов итерации. Определим сначала норму вектора D. Получим

Тогда
 .
.
Следовательно, для достижения заданной точности необходимо выполнить не менее 17 итераций. Выполним первую итерацию. Получим

или
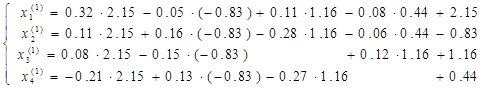
Выполнив все арифметические операции, получим
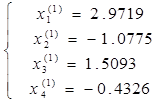 .
.
Продолжая аналогично, выполним дальнейшие шаги итераций. Результаты их сведем в следующую таблицу (D — наибольшая величина изменения компонент решения между текущим и предыдущим шагами)
M |
|
|
|
| D |
0 | 2.15 | -0.83 | 1.16 | 0.44 | — |
1 | 2.9719 | -1.0775 | 1.5093 | -0.4326 | 0.8215 |
2 | 3.3555 | -1.0721 | 1.5075 | -0.7317 | 0.3836 |
3 | 3.5017 | -1.0106 | 1.5015 | -0.8111 | 0.1462 |
4 | 3.5511 | -0.9277 | 1.4944 | -0.8321 | 0.0494 |
5 | 3.5637 | -0.9563 | 1.4834 | -0.8298 | 0.0286 |
6 | 3.5678 | -0.9566 | 1.4890 | -0.8332 | 0.0056 |
7 | 3.5700 | -0.9575 | 1.4889 | -0.8356 | 0.0024 |
8 | 3.5709 | -0.9573 | 1.4890 | -0.8362 | 0.0009 |
9 | 3.5712 | -0.9571 | 1.4889 | -0.8364 | 0.0003 |
10 | 3.5713 | -0.9570 | 1.4890 | -0.8364 | 0.0001 |
Так как уже после десятого шага разность между значениями на двух последних итерациях стала меньше заданной точности — процесс итераций прекратим. В качестве найденного решения примем значения, полученные на последнем шаге.
Пример 2. Преобразуем систему уравнений

к виду, который позволил бы использовать при ее решении метод простой итерации.
Поступим сначала аналогично предыдущему примеру. Получим
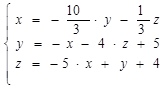
Матрица C такой системы будет
C =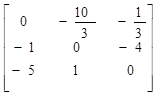 .
.
Вычислим ее норму. Получим
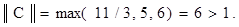
Очевидно, что итерационный процесс для такой матрицы сходящимся не будет. Необходимо найти иной способ преобразования заданной системы уравнений.
Переставим в исходной системе уравнений отдельные ее уравнения так, чтобы третья строка стала первой, первая — второй, вторая — третьей. Тогда, преобразуя ее тем же способом, получим
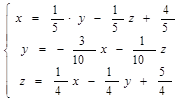
Матрица C такой системы будет
C =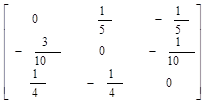 .
.
Вычислим ее норму. Получим
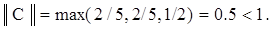
Так как норма матрицы C оказалась меньшей единицы, преобразованная таким образом система пригодна для решения методом простой итерации.
Пример 3. Преобразуем систему уравнений
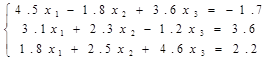
к виду, который позволил бы использовать при ее решении метод простой итерации.
Поступим сначала аналогично примеру 1. Получим

Матрица C такой системы будет
C =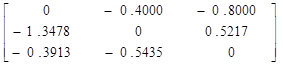 .
.
Вычислим ее норму. Получим
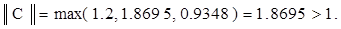
Очевидно, что итерационный процесс для такой матрицы сходящимся не будет.
Для преобразования исходной матрицы к виду, удобному для применения метода простой итерации поступим следующим образом. Сначала образуем “промежуточную” систему уравнений, в которой
— первое уравнение является суммой первого и второго уравнений исходной системы
— второе уравнение — суммой удвоенного третьего уравнения со вторым за вычетом первого
— третье уравнение — разность третьего и второго уравнений исходной системы.
В результате получим эквивалентную исходной “промежуточную” систему уравнений
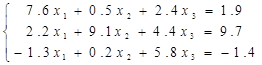
Из нее несложно получить еще одну систему “промежуточную” систему
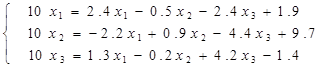 ,
,
а из нее преобразованную
 .
.
Матрица C такой системы будет
C =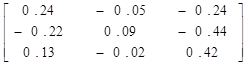 .
.
Вычислим ее норму. Получим

Итерационный процесс для такой матрицы будет сходящимся.
Метод Якоби предполагает, что все диагональные элементы матрицы A исходной системы (2.2) не равны нулю. Тогда исходную систему можно переписать в виде
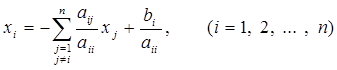 (3.7)
(3.7)
Из такой записи системы образована итерационная формула метода Якоби
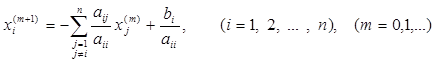 . (3.8)
. (3.8)
Условием сходимости итерационного процесса метода Якоби является так называемое условие доминирования диагонали в исходной системе (вида (2,1)). Аналитически это условие записывается в виде
 . (3.9)
. (3.9)
Следует отметить, что если в заданной системе уравнений условие сходимости метода Якоби (т.е. условие доминирования диагонали) не выполняется, во многих случаях можно путем эквивалентных преобразований исходной СЛАУ привести ее решение к решению эквивалентной СЛАУ, в которой это условие выполняется.
Пример 4. Преобразуем систему уравнений
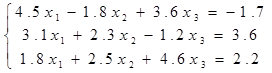
к виду, который позволил бы использовать при ее решении метод Якоби.
Эту систему мы уже рассматривали в примере 3, поэтому перейдем от нее к полученной там “промежуточной” системе уравнений. Легко установить, что у нее условие доминирования диагонали выполняется, поэтому преобразуем ее к виду, необходимому для применения метода Якоби. Получим
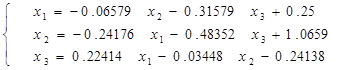
Из нее получаем формулу для выполнения вычислений по методу Якоби для заданной СЛАУ

Взяв за начальное, т.е. нулевое, приближение вектор свободных членов выполним все необходимые вычисления. Результаты сведем в таблицу
m |
|
|
| D | |
0 | 0.25000 | 1.06590 | -0.24138 | — | |
1 | 0.256100 | 1.122172 | -0.222097 | 0.056272 | |
2 | 0.246318 | 1.111374 | -0.222760 | 0.010798 | |
3 | 0.247200 | 1.114018 | -0.224493 | 0.002644 | |
4 | 0.247601 | 1.114684 | -0.224384 | 0.000666 | |
5 | 0.247523 | 1.114534 | -0.224317 | 0.000150 | |
6 | 0.247512 | 1.114521 | -0.224329 | 0.000013 | |
Довольно высокая точность полученного решения достигнута за шесть итераций.
Метод Гаусса-Зейделя является усовершенствованием метода Якоби и также предполагает, что все диагональные элементы матрицы A исходной системы (2.2) не равны нулю. Тогда исходную систему можно переписать в виде аналогичном методу Якоби, но несколько отличном от него
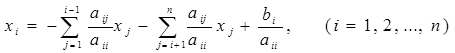 .
.
Здесь важно помнить, что если в знаке суммирования верхний индекс меньше нижнего, то никакого суммирования не производится.
Идея метода Гаусса-Зейделя заключается в том, что авторы метода усмотрели возможность ускорить процесс вычислений по отношению к методу Якоби за счет того, что в процессе очередной итерации найдя новое значение x1 можно сразу же использовать это новое значение в этой же итерации для вычисления остальных переменных. Аналогично этому, дальше, найдя новое значение x2 можно его также сразу использовать в этой же итерации и т.д.
Исходя из этого, формула итераций для метода Гаусса-Зейделя имеет следующий вид
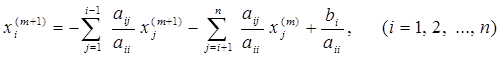 . (3.10)
. (3.10)
Достаточным условием сходимости итерационного процесса метода Гаусса-Зейделя является все то же условие доминирования диагонали (3.9). Скорость сходимости этого метода несколько выше, чем в метода Якоби.
Пример 5. Решим методом Гаусса-Зейделя систему уравнений
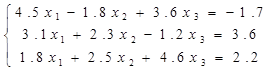
Эту систему мы уже рассматривали в примерах 3 и 4, поэтому сразу перейдем от нее к преобразованой системе уравнений (см. пример 4), в которой условие доминирования диагонали выполняется. Из нее получаем формулу для выполнения вычислений по методу Гаусса-Зейделя
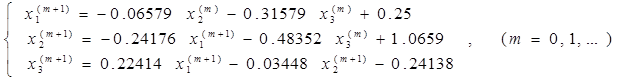
Взяв за начальное (т.е. нулевое) приближение вектор свободных членов, выполним все необходимые вычисления. Результаты сведем в таблицу
m |
|
|
| D |
0 | 0.25000 | 1.06590 | -0.24138 | — |
1 | 0.25610 | 1.12070 | -0.22262 | 0.0548 |
2 | 0.24657 | 1.11393 | -0.22452 | 0.00953 |
3 | 0.24762 | 1.11460 | -0.22431 | 0.00105 |
4 | 0.24751 | 1.11452 | -0.22433 | 0.00011 |
5 | 0.24750 | 1.11453 | -0.22433 | 0.00001 |
Довольно высокая точность полученного решения достигнута за пять итераций.
studizba.com
3.3. Общее, базисное и частное решение систем линейных алгебраических уравнений.
Пусть  переменных
переменных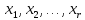 называются основными (или базисными),
если определитель матрицы из коэффициентов
при них (т.е. базисный минор) отличен от
нуля. Остальные
называются основными (или базисными),
если определитель матрицы из коэффициентов
при них (т.е. базисный минор) отличен от
нуля. Остальные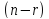 переменных
называются неосновными (или свободными).
Каждому разбиению переменных на основные
и неосновные соответствует одно базисное
решение, а число способов разбиения не
превосходит числа сочетаний
переменных
называются неосновными (или свободными).
Каждому разбиению переменных на основные
и неосновные соответствует одно базисное
решение, а число способов разбиения не
превосходит числа сочетаний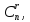 то
и базисных решений имеется не более
то
и базисных решений имеется не более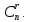
Совместная
система 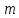 линейных уравнений с
линейных уравнений с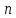 переменными
переменными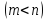 имеет
бесконечное множество решений, среди
которых базисных решений конечное
число, не превосходящее
имеет
бесконечное множество решений, среди
которых базисных решений конечное
число, не превосходящее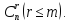
Достоинства метода Гаусса по сравнению с другими:
— менее трудоемкий метод;
— позволяет однозначно установить, совместна система или нет и в случае совместности найти ее решение;
— дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.
Рассмотрим пример. Найти решение системы линейных алгебраических уравнений
Составим расширенную матрицу по данной системе

поменяем местами первую и вторую строку
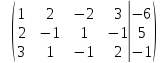
умножим
первую строку на  и сложим со второй строкой; умножим
первую строку на
и сложим со второй строкой; умножим
первую строку на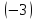 и сложим с третьей строкой
и сложим с третьей строкой
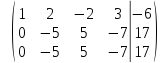
умножим
вторую строку на  и сложим с третьей строкой
и сложим с третьей строкой
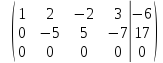
последняя строка вычеркивается, так как все ее элементы равны нулю

Ранг
основной матрицы 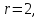 ранг
расширенной матрицы
ранг
расширенной матрицы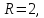 следовательно, система совместна. Число
строк в основной матрице
следовательно, система совместна. Число
строк в основной матрице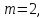 число
столбцов в основной матрице
число
столбцов в основной матрице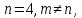 следовательно, система имеет множество
решений.
следовательно, система имеет множество
решений.
Выявим базисные переменные

следовательно,  базисные
переменные, тогда
базисные
переменные, тогда
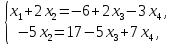
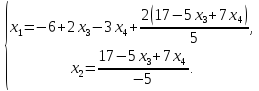
3.4. Однородные системы линейных алгебраических уравнений
Система 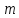 линейных уравнений с
линейных уравнений с переменными называетсясистемой
линейных однородных уравнений,
если все их свободные члены равны нулю.
переменными называетсясистемой
линейных однородных уравнений,
если все их свободные члены равны нулю.
Системы линейных однородных уравнений:
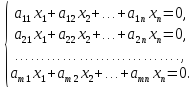
Система
линейных однородных уравнений всегда
совместна, так как имеет, по крайней
мере, нулевое решение 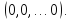
Если
в однородной системе  а
ее определитель отличен от нуля, то
такая система имеет только нулевое
решение.
а
ее определитель отличен от нуля, то
такая система имеет только нулевое
решение.
Система
линейных однородных уравнений имеет
ненулевое решение тогда и только тогда,
когда ранг ее матрицы коэффициентов
при переменных меньше числа переменных,
т.е. при 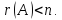
Рассмотрим пример. Найти решение системы линейных алгебраических уравнений
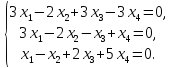
Составим по данной системе расширенную матрицу
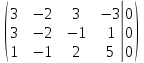
поменяем местами первую и третью строки
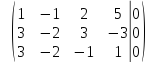
умножим
первую строку на  и сложим со второй строкой, а затем с
третьей строкой, получим
и сложим со второй строкой, а затем с
третьей строкой, получим
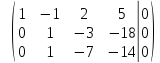
умножим
вторую строку на 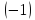 и сложим с третьей строкой
и сложим с третьей строкой
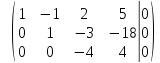
разделим
последнюю строку на 
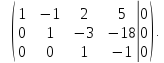
Таким
образом, ранг расширенной матрицы и
ранг основной матрицы равны  следовательно,
система совместна. Число строк в основной
матрице равно 3, а число столбцов равно
4, т.е. решений множество. Определим
базисные переменные
следовательно,
система совместна. Число строк в основной
матрице равно 3, а число столбцов равно
4, т.е. решений множество. Определим
базисные переменные
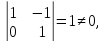
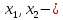 базисные
переменные.
базисные
переменные.
Перейдем
от матрицы к системе, выразим переменные  через другие переменные
через другие переменные
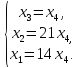
Контрольные вопросы
Сформулировать теорему Кронекера – Капелли.
Сформулировать Метод Гаусса решения систем m линейных уравнений с n неизвестными.
Дать определение базисному решению систем линейных алгебраических уравнений.
Какие системы линейных алгебраических уравнений называют однородными?
Лекция №4. Векторы
4.1. Векторы в науке и технике. Понятие вектора. Координаты вектора.
4.2. Линейные операции над векторами.
4.3. Декартова система координат. Базис векторного пространства.
4.4. Скалярное произведение векторов, основные свойства и выражение в координатной форме.
4.5. Векторное произведение векторов. Основные свойства векторного произведения векторов и выражение в координатной форме.
4.6. Применение векторного произведения векторов к решению задач.
4.7. Смешанное произведение векторов. Основные свойства смешанного произведения векторов и выражение в координатной форме.
4.8. Применение смешанного произведения векторов к решению задач.
Векторы в науке и технике. Понятие вектора. Координаты вектора
В физике и математике вектор – это величина, которая характеризуется численным значением и направлением. В физике встречается немало важных величин, которые характеризуются направлением. Например, сила, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким как масса, объем, давление, температура, плотность, которые можно описать обычным числом и называются они скалярными величинами.
Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, необходимо описать положение предмета, но полностью определить местоположение предмета невозможно, пока не будет известно направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.
При изучении и расчете цепей переменного тока удобно пользоваться векторными диаграммами, на которых синусоидальные напряжения и токи условно изображают с помощью векторов. Применение этих диаграмм упрощает изучение и расчет цепей и вносит наглядность в рассматриваемые соотношения.
Вектором
на плоскости называется
направленный отрезок  с начальной точкой
с начальной точкой  и конечной точкойкоторый
можно перемещать параллельно самому
себе.
и конечной точкойкоторый
можно перемещать параллельно самому
себе.

Рис. 1
Вектор на плоскости
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос. При параллельном переносе точки смещаются по параллельным или совпадающим прямым на одно и тоже расстояние.
Нулевой вектор – точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Абсолютной величиной или модулем вектора называется длина отрезка, изображающего вектор. Другими словами длина вектора есть расстояние между началом и концом вектора

Векторы
называются коллинеарными, если они
расположены на одной или на параллельных
прямых. Нулевой вектор коллинеарен
любому вектору. Если векторы  и
и коллинеарны и их лучи сонаправлены, то
векторы
коллинеарны и их лучи сонаправлены, то
векторы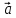 и
и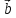 называютсонаправленными.
Обозначают
называютсонаправленными.
Обозначают  Если векторы
Если векторы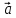 и
и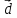 коллинеарны,
а их лучи не являются сонаправленными,
то векторы называютпротивоположно
направленными.
Обозначают
коллинеарны,
а их лучи не являются сонаправленными,
то векторы называютпротивоположно
направленными.
Обозначают 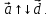 Нулевой вектор условились считать
сонаправленным с любым вектором.
Нулевой вектор условились считать
сонаправленным с любым вектором.

Рис.2
Коллинеарные вектора
Свойство коллинеарных векторов.
Если
векторы  и
и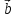 коллинеарны и
коллинеарны и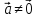 ,
то существует число
,
то существует число такое,
что
такое,
что .
Причем, если
.
Причем, если то векторы
то векторы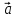 и
и сонаправленные, если
сонаправленные, если то
противоположно направленные.
то
противоположно направленные.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Признак компланарности трех векторов.
Если
вектор 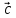 можно разложить по векторам
можно разложить по векторам и
и ,
т.е. представить в виде
,
т.е. представить в виде ,
где
,
где -некоторые
числа, то векторы
-некоторые
числа, то векторы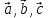 -компланарны.
-компланарны.

Рис.3
Компланарные вектора
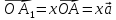 ,
где
,
где  ;
;
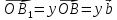 ,
где
,
где 
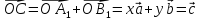 ,
где
,
где 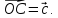
studfile.net
 приведена к треугольному виду, то
система (II.3)
совместна и имеет единственное решение.
приведена к треугольному виду, то
система (II.3)
совместна и имеет единственное решение. содержит хотя бы одну строку, все
элементы которой равны нулю, то система
(II.5)
совместна и имеет множество решений.
содержит хотя бы одну строку, все
элементы которой равны нулю, то система
(II.5)
совместна и имеет множество решений. содержит строку, все элементы которой,
кроме свободного члена, равны нулю, то
система (II.5)
несовместна, то есть решения не имеет.
содержит строку, все элементы которой,
кроме свободного члена, равны нулю, то
система (II.5)
несовместна, то есть решения не имеет. к треугольному виду. Для этого домножим
1-ю строку на (-3) и (-2) и прибавим ко 2-й и
3-й строкам соответственно. Полученную
2-ю строку прибавим к полученной 3-й
строке.
к треугольному виду. Для этого домножим
1-ю строку на (-3) и (-2) и прибавим ко 2-й и
3-й строкам соответственно. Полученную
2-ю строку прибавим к полученной 3-й
строке.