Формула силы тяжести

   

Здесь – сила тяжести, – масса, — ускорение свободного падения.

Единица измерения силы – Н (ньютон).

Для тела, находящегося на определённой высоте над Землёй сила тяжести может быть найдена по формуле:

   

Здесь – гравитационная постоянная, – масса тела, – масса Земли ( кг), – высота тела над Землёй, – радиус Земли ( м).

Из-за того, что Земля имеет сплюснутую форму, то есть её радиус не везде одинаков, ускорение свободного падения меняется в зависимости от географической широты, от на экваторе до на полюсах. – его среднее значение.

Сила тяжести действует на тело, имеющее опору или подвес. Если тело их не имеет, то есть находится в состоянии свободного падения, то говорят, что тело находится в невесомости. Сила тяжести всегда направлена к центру Земли.

Примеры решения задач по теме «Сила тяжести»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Закон всемирного тяготения. Вес тела — ЗФТШ, МФТИ

Анализируя законы Кеплера, описывающие движение планет, И. Ньютон в 1667 году пришёл к открытию закона всемирного тяготения:

\[\boxed{F = G \frac{mM}{r^2}},\]

где G -G\ — гравитационная постоянная.

Все тела во Вселенной взаимно притягиваются друг к другу с силами прямо пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними.

В такой форме закон справедлив только для двух тел, которые можно считать материальными точками. Однако можно доказать, что для двух однородных тел шарообразной формы эта форма записи закона тоже справедлива.

Измерить величину гравитационной постоянной удалось английскому физику Г. Кавендишу в 1798 году.

С помощью крутильных весов и свинцовых шаров ему удалось получить значение гравитационной постоянной:

\[\boxed{G = 6,67259 \cdot 10^{-11}\ \frac{\mathrm{Нм}^2}{\mathrm{кг}^2}}.\]

Второй закон Ньютона позволяет записать для силы, с которой тело притягивается к Земле: F=GMmR2=mgF = G\frac{Mm}{R^2} = mg, тогда g=GMR2 -\boxed{g = G\frac{M}{R^2}}\ — ускорение свободного падения на поверхности Земли (измерено Галилеем и Ньютоном), на расстоянии, большем радиуса на величину hh, ускорение свободного падения находится по формуле:

g=GM(R+h)2 -\boxed{g = G \frac M{(R+h)^2}}\ — ускорение свободного падения на высоте hh от поверхности Земли.

Силой тяжести называют силу, с которой тело притягивается к планете:

\[\boxed{F = mg} — \mathrm{сила}\ \mathrm{тяжести}\]

Рассмотрим твёрдое тело, расположенное на горизонтальной неподвижной опоре: под действием силы тяжести тело деформируется. Если тело находится на опоре, то на нижний слой действуют все верхние слои, и, как следствие, этот слой деформируется наибольшим образом. На предпоследний слой действует меньшее количество слоёв, и он деформируется меньше. Таким образом, тело, бывшее прямоугольным, примет вид трапеции. Нижний слой приблизился при такой деформации к центру тела, а значит, возникла сила упругости, направленная в сторону, противоположную направлению смещения частиц при деформации. Сила упругости, возникшая внутри данного тела, направлена перпендикулярно опоре. Эту силу, созданную деформированным телом и приложенную к опоре, называют весом тела. Опора под действием веса деформируется. Противоположная весу сила упругости действует на данное тело со стороны деформированной опоры и тоже направлена перпендикулярно опоре, но называется силой реакции опоры NN (от слова normal — перпендикуляр).










Рис. 9

На рисунке 9 тело не касается опоры для того, чтобы показать, что вес приложен к опоре, а сила реакции опоры к телу. В действительности площадь реального соприкосновения твёрдых тел невелика. Большей частью между телами находится тонкий слой воздуха.

Вполне очевидно, что если опоры нет, то и веса тело иметь не будет. Такое случится в том случае, если тело движется под действием только одной силы – силы тяготения.

Невесомостью называют состояние тела, когда оно движется под действием только силы тяготения.

Так же легко понять, что если на тело действует две силы (сила тяжести и сила реакции опоры), то эти силы не обязательно равны друг другу. Одна из них может быть больше другой.

Рассмотрим движение тела, помещённого в лифт. Пусть сам лифт движется с ускорением a→\vec a. Такое ускорение будет в двух случаях: 1) лифт поднимается равно ускорено, 2) лифт опускается равнозамедленно. Второй закон Ньютона для данного тела примет вид:








Рис. 10

N→+mg→=ma→.\vec N + m \vec g = m \vec a.

При рассмотрении данного движения из лабораторной неподвижной системы отсчёта OyOy увидим, что в проекции на вертикальную ось OyOy второй закон запишется следующим образом:

N-mg=ma,N — mg = ma,

откуда 

N=ma+mg=m(g+a).N = ma + mg = m(g+a).

Но по третьему закону Ньютона знаем, что сила реакции опоры и вес тела равны и противоположны, следовательно:

N=P,N = P,

тогда: P=m(g+a) -\boxed{P = m(g+a)}\ — вес тела, движущегося с ускорением, направленным вверх (рис. 10).

Не трудно проследить за тем, что мы получим, если ускорение тела будет направлено вниз.

В проекции на ось OyOy ускорение проецируется со знаком <<—>>, что даст окончательную формулу для веса:

P=m(g-a) -\boxed{P = m(g-a)}\ — вес тела, движущегося с ускорением, направленным вниз.

Или в общем случае: P=m(g±a) -\boxed{P = m(g \pm a)}\ — вес тела, движущегося с ускорением.







Рис. 11а

Подобным образом можно получить выражение для веса тела, движущегося равномерно по выпуклому участку дороги.

P=m(g-a)=m(g-v2R) -\boxed{P = m(g-a) = m(g — \frac{v^2}{R})}\ — вес тела, движущегося с ускорением, направленным вниз (выпуклая дорога).

P=m(g+a)=m(g+v2R) -\boxed{P = m(g+a) = m(g+ \frac{v^2}{R})}\ — вес тела, движущегося с ускорением, направленным вверх (вогнутая дорога).

Важное дополнение:

Для рассматриваемой силы, называемой весом, важно понимать и уметь правильно изображать точку приложения этой силы.








На рисунке 11а показан лифт, у которого нет ускорения. Тогда сила тяжести равна силе реакции опоры . А по третьему закону Ньютона, сила реакции опоры равна весу тела. Точка приложения силы тяжести расположена в геометрическом центре тела, если тело однородно и правильной формы. Точка приложения силы реакции опоры должна быть изображена внутри тела вблизи с нижней поверхностью тела на линии действия силы тяжести. Последнее свойство на рисунке не выдержано для удобства изображения (иначе силы на рисунке будут накладываться друг на друга). Точка приложения веса тела находится внутри опоры (пола лифта) вблизи поверхности на линии действия силы реакции опоры.










Рис. 11б                                    Рис. 11в

На рисунке 11б ускорение лифта направлено вниз. Тогда сила реакции опоры меньше силы тяжести . А вес снова равен силе реакции опоры.

На рисунке 11в ускорение лифта направлено верх. Тогда сила реакции опоры больше силы тяжести . А вес снова равен силе реакции опоры.

Пример 5. Определить среднюю плотность Солнца, если его масса равна 2·1030 кг2\cdot 10^{30}\ \text{кг}, а ускорение свободного падения на поверхности приблизительно составляет 273,1 м/с2273,1\ \text{м}/\text{с}^2.

Решение. Так как g=GMR2g = G\frac{M}{R^2}, то можем найти радиус Солнца: R=GMgR = \sqrt{\frac{GM}{g}}. Считая Солнце шаром найденного радиуса и известной массы, можем найти среднюю плотность.

\[\rho = \frac MV = \frac{M}{\frac 43 \pi R^3} = \frac{3M}{4\pi \left(\frac{GM}{g}\right)^{\frac 32}} = \frac{3}{4\pi \sqrt M}\left(\frac gG\right)^{\frac 32}.\]

Количественно ответ будет таким: ρ=1400 кг/м3\rho = 1400\ \text{кг}/\text{м}^3. Однако следует отметить, что этот ответ таков в данной модели. В действительности плотность Солнца не одинакова в недрах светила, и является функцией расстояния от центра. Мы же посчитали её везде одинаковой.








Рис. 12

Пример 6. На сколько изменится сила притяжения двух одинаковых шаров, изготовленных из одинакового вещества плотностью ρ\rho, если у одного из них создать полость сферической формы, расположенную внутри одного из них в его центре? Изначально шары касались друг друга и притягивались с силой 80 Н80\ \text{Н}. Радиус полости равен половине радиуса шара (рис. 12).

Решение. Сила взаимодействия определяется законом всемирного тяготения. Т. к. формы тел шарообразные, то мы можем применить известную формулу закона: F1=GMmR2F_1 = G\frac{Mm}{R^2}.

Массы тел равны, обозначим их mm, Масса извлечённой части m0=43π(R2)3ρ=18mm_0 = \frac 43 \pi (\frac{R}{2})^3 \rho = \frac 18 m. Новая сила будет меньше первоначальной на величину силы взаимодействия извлечённой части с первым шаром (принцип суперпозиции сил). Следовательно:

\[F_2 = G\frac{m_0 m}{(2R)^2} = G\frac{\frac 18 mm}{(2R)^2} = \frac 18 F\frac{mm}{(2R)^2} = \frac 18 F = 10\ \text{Н}.\]

Сила притяжения шаров станет меньше на 10 Н10\ \text{Н}, следовательно, станет равной 70 Н70\ \text{Н}.

zftsh.online

определение, формула, виды :: SYL.ru

На вопрос «Что такое сила?» физика отвечает так: «Сила есть мера взаимодействия вещественных тел между собой или между телами и другими материальными объектами – физическими полями». Все силы в природе могут быть отнесены к четырем фундаментальным видам взаимодействий: сильному, слабому, электромагнитному и гравитационному. Наша статья рассказывает о том, что представляют собой гравитационные силы – мера последнего и, пожалуй, наиболее широко распространенного в природе вида этих взаимодействий.

Начнем с притяжения земли

Всем живущим известно, что существует сила, которая притягивает объекты к земле. Она обычно именуется гравитацией, силой тяжести или земным притяжением. Благодаря ее наличию у человека возникли понятия «верх» и «низ», определяющие направление движения или расположения чего-либо относительно земной поверхности. Так в частном случае, на поверхности земли или вблизи нее, проявляют себя гравитационные силы, которые притягивают объекты, обладающие массой, друг к другу, проявляя свое действие на любых как самых малых, так и очень больших, даже по космическим меркам, расстояниях.

Сила тяжести и третий закон Ньютона

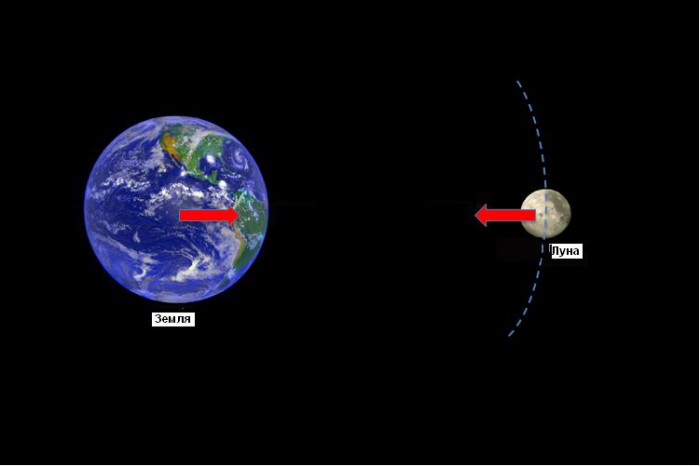
Как известно, любая сила, если она рассматривается как мера взаимодействия физических тел, всегда приложена к какому-нибудь из них. Так и в гравитационном взаимодействии тел друг с другом, каждое из них испытывает такие виды гравитационных сил, которые вызваны влиянием каждого из них. Если тел всего два (предполагается, что действием всех других можно пренебречь), то каждое из них по третьему закону Ньютона будет притягивать другое тело с одинаковой силой. Так Луна и Земля притягивают друг друга, следствием чего являются приливы и отливы земных морей.

Каждая планета в Солнечной системе испытывает сразу несколько сил притяжения со стороны Солнца и других планет. Конечно, определяет форму и размеры ее орбиты именно сила притяжения Солнца, но и влияние остальных небесных тел астрономы учитывают в своих расчетах траекторий их движения.

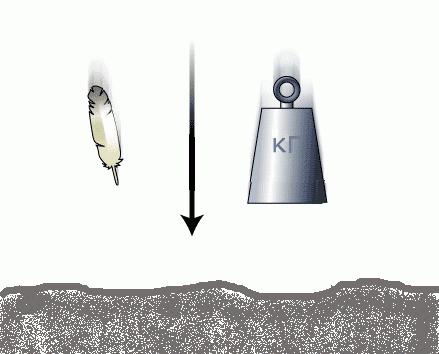
Что быстрее упадет на землю с высоты?

Главной особенностью этой силы является то, что все объекты падают на землю с одной скоростью, независимо от их массы. Когда-то, вплоть до 16-го ст., считалось, что все наоборот – более тяжелые тела должны падать быстрее, чем легкие. Чтобы развеять это заблуждение Галилео Галилею пришлось выполнить свой знаменитый опыт по одновременному сбрасыванию двух пушечных ядер разного веса с наклонной Пизанской башни. Вопреки ожиданиям свидетелей эксперимента оба ядра достигли поверхности одновременно. Сегодня каждый школьник знает, что это произошло благодаря тому, что сила тяжести сообщает любому телу одно и то же ускорение свободного падения g = 9,81 м/с² независимо от массы m этого тела, а величина ее по второму закону Ньютона равна F = mg.

Гравитационные силы на Луне и на других планетах имеют разные значения этого ускорения. Однако характер действия силы тяжести на них такой же.

Сила тяжести и вес тела

Если первая сила приложена непосредственно к самому телу, то вторая к его опоре или подвесу. В этой ситуации на тела со стороны опор и подвесов всегда действуют силы упругости. Гравитационные силы, приложенные к тем же телам, действуют им навстречу.

Представьте себе груз, подвешенный над землей на пружине. К нему приложены две силы: сила упругости растянутой пружины и сила тяжести. Согласно третьему закону Ньютона груз действует на пружину с силой, равной и противоположной силе упругости. Эта сила и будет его весом. У груза массой 1 кг вес равен Р = 1 кг ∙ 9,81 м/с² = 9,81 Н (ньютон).

Гравитационные силы: определение

Первая количественная теория гравитации, основанная на наблюдениях движения планет, была сформулирована Исааком Ньютоном в 1687 году в его знаменитых «Началах натуральной философии». Он писал, что силы притяжения, которые действуют на Солнце и планеты, зависят от количества вещества, которое они содержат. Они распространяются на большие расстояния и всегда уменьшаются как величины, обратные квадрату расстояния. Как же можно вычислить эти гравитационные силы? Формула для силы F между двумя объектами с массами m₁ и m₂, находящимися на расстоянии r, такова:

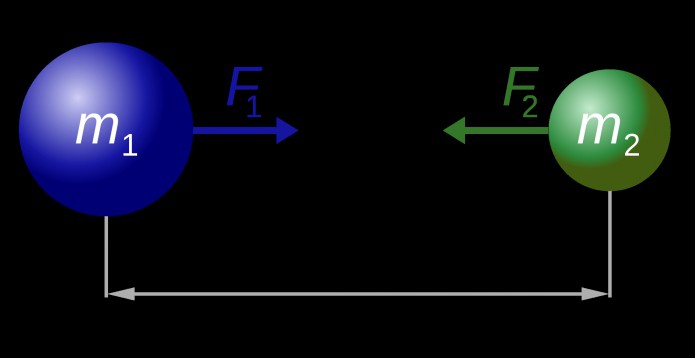
Физический механизм гравитации

Ньютон был не полностью удовлетворен своей теорией, поскольку она предполагала взаимодействие между притягивающимися телами на расстоянии. Сам великий англичанин был уверен, что должен существовать некий физический агент, ответственный за передачу действия одного тела на другое, о чем он вполне ясно высказался в одном из своих писем. Но время, когда было введено понятие гравитационного поля, которое пронизывает все пространство, наступило лишь через четыре столетия. Сегодня, говоря о гравитации, мы можем говорить о взаимодействии любого (космического) тела с гравитационным полем других тел, мерой которого и служат возникающие между каждой парой тел гравитационные силы. Закон всемирного тяготения, сформулированный Ньютоном в вышеприведенной форме, остается верным и подтверждается множеством фактов.

Теория гравитации и астрономия

Она была очень успешно применена к решению задач небесной механики во время XVIII и начале XIX века. К примеру, математики Д. Адамс и У. Леверье, анализируя нарушения орбиты Урана, предположили, что на него действуют гравитационные силы взаимодействия с еще неизвестной планетой. Ими было указано ее предполагаемое положение, и вскоре астрономом И. Галле там был обнаружен Нептун.

Хотя оставалась одна проблема. Леверье в 1845 году рассчитал, что орбита Меркурия прецессирует на 35» за столетие, в отличие от нулевого значения этой прецессии, получаемого по теории Ньютона. Последующие измерения дали более точное значение 43». (Наблюдаемая прецессия равна действительно 570»/век, но кропотливый расчет, позволяющий вычесть влияние от всех других планет, дает значение 43».)

Только в 1915 г. Альберт Эйнштейн смог объяснить это несоответствие в рамках созданной им теории гравитации. Оказалось, что массивное Солнце, как и любое другое массивное тело, искривляет пространство-время в своей окрестности. Эти эффекты вызывают отклонения в орбитах планет, но у Меркурия, как самой малой и ближайшей к нашей звезде планете, они проявляются сильнее всего.

Инерционная и гравитационная массы

Как уже отмечалось выше, Галилей был первым, кто наблюдал, что объекты падают на землю с одинаковой скоростью, независимо от их массы. В формулах Ньютона понятие массы происходит от двух разных уравнений. Второй его закон говорит, что сила F, приложенная к телу с массой m, дает ускорение по уравнению F = ma.

Однако сила тяжести F, приложенная к телу, удовлетворяет формуле F = mg, где g зависит от другого тела, взаимодействующего с рассматриваемым (земли обычно, когда мы говорим о силе тяжести). В обоих уравнений m есть коэффициент пропорциональности, но в первом случае это инерционная масса, а во втором – гравитационная, и нет никакой очевидной причины, что они должны быть одинаковыми для любого физического объекта.

Однако все эксперименты показывают, что это действительно так.

Теория гравитации Эйнштейна

Он взял факт равенства инерционной и гравитационной масс как отправную точку для своей теории. Ему удалось построить уравнения гравитационного поля, знаменитые уравнения Эйнштейна, и с их помощью вычислить правильное значение для прецессии орбиты Меркурия. Они также дают измеренное значение отклонения световых лучей, которые проходят вблизи Солнца, и нет никаких сомнений в том, что из них следуют правильные результаты для макроскопической гравитации. Теория гравитации Эйнштейна, или общая теория относительности (ОТО), как он сам ее назвал, является одним из величайших триумфов современной науки.

Гравитационные силы – это ускорение?

Если вы не можете отличить инерционную массу от гравитационной, то вы не можете отличить и гравитацию от ускорения. Эксперимент в гравитационном поле вместо этого может быть выполнен в ускоренно движущемся лифте в отсутствии гравитации. Когда космонавт в ракете ускоряется, удаляясь от земли, он испытывает силу тяжести, которая в несколько раз больше земной, причем подавляющая ее часть приходит от ускорения.

Если никто не может отличить гравитацию от ускорения, то первую всегда можно воспроизвести путем ускорения. Система, в которой ускорение заменяет силу тяжести, называется инерциальной. Поэтому Луну на околоземной орбите также можно рассматривать как инерциальную систему. Однако эта система будет отличаться от точки к точке, поскольку изменяется гравитационное поле. (В примере с Луной гравитационное поле изменяет направление из одной точки в другую.) Принцип, согласно которому всегда можно найти инерциальную систему в любой точке пространства и времени, в которой физика подчиняется законам в отсутствии гравитации, называется принципом эквивалентности.

Гравитация как проявление геометрических свойств пространства-времени

Тот факт, что гравитационные силы можно рассматривать как ускорения в инерциальных системах координат, которые отличаются от точки к точке, означает, что гравитация – это геометрическое понятие.

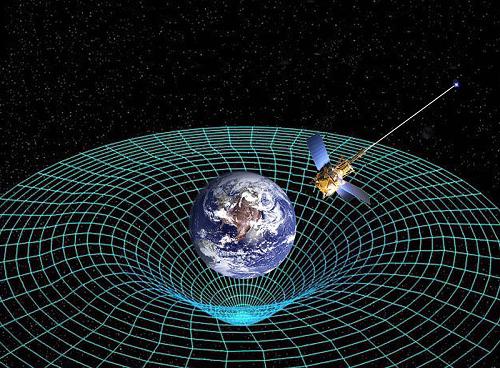
Мы говорим, что пространство-время искривляется. Рассмотрим мяч на плоской поверхности. Он будет покоиться или, если нет никакого трения, равномерно двигаться при отсутствии действия каких-либо сил на него. Если поверхность искривляется, мяч ускорится и будет двигаться до самой низкой точки, выбирая кратчайший путь. Аналогичным образом теория Эйнштейна утверждает, что четырехмерное пространство-время искривлено, и тело движется в этом искривленном пространстве по геодезической линии, которой соответствует кратчайший путь. Поэтому гравитационное поле и действующие в нем на физические тела гравитационные силы – это геометрические величины, зависящие от свойств пространства-времени, которые наиболее сильно изменяются вблизи массивных тел.

www.syl.ru

Движение в «лифте». Невесомость и перегрузки. Вращение в вертикальной плоскости | LAMPA

На самом деле сам вес мы найти не можем. Мы можем найти силу реакции опоры N⃗\vec{N}N⃗. О том, как это сделать, — чуть ниже. По 3-му закону Ньютона, с какой силой тело давит на опору (эта сила — вес тела P⃗\vec{P}P⃗) — с такой же силой опора давит на тело (это уже сила реакции опоры N⃗\vec{N}N⃗): P⃗=−N⃗\vec{P}=-\vec{N}P⃗=−N⃗. Поэтому нам достаточно найти именно силу реакции опоры N⃗\vec{N}N⃗. Итак, мы «целимся» именно в N⃗\vec{N}N⃗.

Двигаемся дальше.

Шаг 2. Запишем 2-й закон Ньютона в векторной форме. Вспомним, что на космонавта действуют только две силы: сила тяжести mg⃗m\vec{g}mg⃗​ и сила реакции опоры N⃗\vec{N}N⃗. Поэтому второй закон Ньютона будет выглядеть в нашем случае следующим образом:

N⃗+mg⃗=ma⃗\vec{N}+m\vec{g}=m\vec{a}N⃗+mg⃗​=ma⃗.

Запишем этот же закон, но уже в проекциях на ось OXOXOX:

N−mg=maN-mg=maN−mg=ma.

Вспомним: что нам нужно? Правильно — найти вес тела, который на самом деле равен силе реакции опоры NNN. Выражаем NNN:

N=ma+mgN=ma+mgN=ma+mg,

N=m⋅(g+a)N=m\cdot(g+a)N=m⋅(g+a).

Подставим численные значения:

N=m⋅(g+a)=80 кг⋅(10мс2+20мс2)=80⋅30 Н=2400 НN=m\cdot(g+a)=80\text{ кг}\cdot(10\frac{м}{с^2}+20\frac{м}{с^2})=80\cdot 30\text{ Н}=2400\text{ Н}N=m⋅(g+a)=80 кг⋅(10с2м​+20с2м​)=80⋅30 Н=2400 Н.

Ответ. Вес летчика-космонавта равен P=N=2400P=N=2400P=N=2400 Н.

Примечание. Можно заметить, что ускорение, с которым двигается ракета, равно двум ускорениям свободного падения: a=20мс2=2⋅10мс2=2ga=20\frac{м}{с^2}=2\cdot 10\frac{м}{с^2}=2ga=20с2м​=2⋅10с2м​=2g.

Поэтому можно увидеть, что вес тела (сила реакции опоры) равен P=N=m⋅(g+a)=m⋅(g+2g)=3mgP=N=m\cdot(g+a)=m\cdot(g+2g)=3mgP=N=m⋅(g+a)=m⋅(g+2g)=3mg.

Вспомним, что в спокойном состоянии, когда летчик-космонавт никуда не движется, его вес равен P=N=mgP=N=mgP=N=mg. То есть мы видим, что в условиях нашей задачи вес летчика увеличился в 333 раза (!). В этом случае говорят, что летчик испытывает трехкратные перегрузки. У него будут точно такие же ощущения, как если бы в спокойном состоянии его масса увеличилась в три раза. Или если бы на него сверху встали еще два таких же человека, как и он сам.

В только что разобранной задаче вес летчика-космонавта увеличился. Точно так же вес может уменьшиться или исчезнуть вовсе — наступит состояние невесомости. Рассмотрим похожую задачу.

Условие

С каким ускорением a1a_1a1​ надо поднимать гирю, чтобы ее вес увеличился вдвое? С каким ускорением a2a_2a2​ надо ее опускать, чтобы вес уменьшился вдвое?

(Источник: Рымкевич А.П. Задачник по физике)

Решение

Сначала займемся первым вопросом задачи.

Шаг 1. Делаем что? Правильно — рисунок. Гирю кто-то поднимает. То есть гиря должна стоять на какой-то опоре — например, на чьей-то ладони или же на полу в лифте, который ее поднимает.

Шаг 2. Запишем 2-й закон Ньютона:

N⃗+mg⃗=ma⃗1\vec{N}+m\vec{g}=m\vec{a}_1N⃗+mg⃗​=ma⃗1​.

В проекциях на ось OXOXOX:

N−mg=ma1N-mg=ma_1N−mg=ma1​.

По условию задачи вес гири должен увеличиться вдвое:

N=2mgN=2mgN=2mg.

Значит:

2mg−mg=ma12mg-mg=ma_12mg−mg=ma1​,

mg=ma1mg=ma_1mg=ma1​,

a1=ga_1=ga1​=g.

Нужно поднимать гирю с ускорением свободного падения: a1=ga_1=ga1​=g.

Теперь ответим на второй вопрос задачи: с каким ускорением надо опускать гирю, чтобы ее вес уменьшился вдвое?

Шаг 1. Что делаем? Конечно же, рисунок. Как и в первом случае, гиря стоит на какой-то опоре — на чьей-то ладони или же на полу в лифте.

Шаг 2. Записываем 2-й закон Ньютона в векторной форме:

N⃗+mg⃗=ma⃗2\vec{N}+m\vec{g}=m\vec{a}_2N⃗+mg⃗​=ma⃗2​.

В проекциях на ось OXOXOX:

N−mg=−ma2N-mg=-ma_2N−mg=−ma2​.

(В отличие от первого случая, ускорение направлено противоположно оси OXOXOX, поэтому у проекции ускорения появляется знак «минус».)

Вес гири должен быть вдвое меньше, чем в состоянии покоя:

N=mg2N=\frac{mg}{2}N=2mg​.

Подставляем в наше уравнение:

mg2−mg=−ma2\frac{mg}{2}-mg=-ma_22mg​−mg=−ma2​,

ma2=mg−mg2ma_2=mg-\frac{mg}{2}ma2​=mg−2mg​,

ma2=mg2ma_2=\frac{mg}{2}ma2​=2mg​,

a2=g2a_2=\frac{g}{2}a2​=2g​.

Ускорение, с которым опускается гиря, должно быть вдвое меньше ускорения свободного падения.

Ответ. a1=ga_1=ga1​=g; a2=g2a_2=\frac{g}{2}a2​=2g​.

Примечание. Заметим, что гирю можно опускать с таким ускорением, что сила реакции опоры NNN (а вместе с ней и вес PPP) станет равной нулю (!). Это произойдет в случае, если лифт (или рука, которая поддерживает гирю) будет «падать» с ускорением свободного падения ggg:

N=mg−ma2=mg−mg=0N=mg-ma_2=mg-mg=0N=mg−ma2​=mg−mg=0.

В этом случае нет силы реакции опоры NNN, нет и веса PPP: тело находится в состоянии невесомости.

lampa.io