Правила раскрытия скобок: сложение, вычитание, умножение, деление
В данной публикации мы рассмотрим основные правила раскрытия скобок, сопроводив их примерами для лучшего понимания теоретического материала.
Раскрытие скобок – замена выражения, содержащего скобки, на равное ему выражение, но без скобок.
Правила раскрытия скобок
Правило 1
Если перед скобками стоит “плюс”, то знаки всех чисел внутри скобок остаются без изменений.
a + (b – c – d + e) = a + b – c – d + e
Пояснение: Т.е. плюс на плюс дают плюс, а плюс на минус – минус.
Примеры:
- 6 + (21 – 18 – 37) = 6 + 21 – 18 – 37
- 20 + (-8 + 42 – 86 – 97) = 20 – 8 + 42 – 86 – 97
Правило 2
Если перед скобками стоит “минус”, то знаки всех чисел внутри скобок меняются на противоположные.
a – (b – c – d + e) = a – b + c + d – e
Пояснение: Т.
Примеры:
- 65 – (-20 + 16 – 3) = 65 + 20 – 16 + 3
- 116 – (49 + 37 – 18 – 21) = 116 – 49 – 37 + 18 + 21
Правило 3
Если перед или после скобок стоит знак “умножения”, все зависит от того, какие действие выполняются внутри них:
Сложение и/или вычитание
- a ⋅ (b – с + d) = a ⋅ b – a ⋅ c + a ⋅ d
- (b + с – d) ⋅ a = a ⋅ b + a ⋅ c – a ⋅ d
Умножение
- a ⋅ (b ⋅ с ⋅ d) = a ⋅ b ⋅ с ⋅ d
- (b ⋅ с ⋅ d) ⋅ a = b ⋅ с ⋅ d ⋅ a
Деление
- a ⋅ (b : с) = (a ⋅ b) : с = (a : c) ⋅ b
- (a : b) ⋅ c = (a ⋅ c) : b = (c : b) ⋅ a
Примеры:
- 18 ⋅ (11 + 5 – 3) = 18 ⋅ 11 + 18 ⋅ 5 – 18 ⋅ 3
- 4 ⋅ (9 ⋅ 13 ⋅ 27) = 4 ⋅ 9 ⋅ 13 ⋅ 27
- 100 ⋅ (36 : 12) = (100 ⋅ 36) : 12
Правило 4
Если перед или после скобок стоит знак “деления”, то как и в правиле выше, все зависит от того, какие действие выполняются внутри них:
Сложение и/или вычитание
- a : (b – с + d) = a : b – a : c + a : d
- (b + с – d) : a = b : a + c : a – d : a
Умножение
- a : (b ⋅ c) = a : b : c = a : c : b
- (b ⋅ c) : a = (b : a) ⋅ с = (с : a) ⋅ b
Деление
- a : (b : c) = (a : b) ⋅ с = (c : b) ⋅ a
- (b : c) : a = b : c : a = b : (a ⋅ c)
Примеры:
- 72 : (9 – 8) = 72 : 9 – 72 : 8
- 160 : (40 ⋅ 4) = 160 : 40 : 4
- 600 : (300 : 2) = (600 : 300) ⋅ 2
Как определить и проверить полярность с помощью мультиметра
Точное знание полярности электроприбора крайне важно.
Но иногда случается, что визуально определить полюса нет возможности. Для этого можно воспользоваться как обыкновенным тестером полярности, так и подручными средствами.
Определение полярности мультиметром
Иногда случается, что в новом электрическом аппарате, который необходимо подключить, отсутствует маркировка полярности или необходимо перепаять проводку поврежденного устройства, а все провода одного цвета. В такой ситуации важно правильно определить полюса проводов или контактов.
Но при наличии необходимых приборов возникает закономерный вопрос: как мультиметром определить плюс и минус электроприбора?
Для определения полярности мультиметр необходимо включить в режим замера постоянного напряжения до 20 В. Провод черного щупа подключается в гнездо с маркировкой СОМ (он соответствует отрицательному полюсу), а красный подключается в гнездо с маркером VΩmA (он, соответственно, является плюсом).
Провод черного щупа подключается в гнездо с маркировкой СОМ (он соответствует отрицательному полюсу), а красный подключается в гнездо с маркером VΩmA (он, соответственно, является плюсом).
После этого щупы подсоединяются к проводам или контактам и прибор, полярность которого необходимо узнать, включается.
Если на дисплее мультиметра отображается значение без дополнительных знаков, то полюса определены правильно, контакт к которому подключен красный щуп – это плюс, а к которому подключен черный щуп будет соответствовать минусу.
В том случае если мультиметр показал значение напряжения со знаком минус – это будет означать, что щупы подключены к устройству неверно и красный щуп будет минусом, а черный – плюсом.
Если мультиметр, которым производится замер, аналоговый (со стрелкой и табло с градациями значений), при правильном подключении полюсов стрелка покажет действительное значение напряжения, а сели полюса перепутаны то стрелка будет отклоняться в противоположную сторону относительно нуля, то есть показывает отрицательное значение напряжения тока.
Определение полярности альтернативными методами
Если случилось так, что мультиметра под рукой нет, а полярность необходимо найти, можно использовать альтернативные и «народные» средства.
К примеру, заряды проводки динамиков проверяются при помощи батарейки на 3 вольта. Для этого необходимо на короткий промежуток времени прикоснуться проводами, присоединенными к батарейке, к выводам динамика.
Если диффузор в динамике начинает двигаться наружу, это будет значить, что положительная клемма динамика присоединена к плюсу батарейки, а отрицательная к минусу. Если же диффузор движется внутрь – полярность перепутана: положительная клемма замкнута на минусе, а отрицательная на плюсе.
Если необходимо подключить блок питания постоянного напряжения или аккумулятор, но на них нет маркировки полярности, а под рукой нет мультиметра, плюс и минус можно определить «народными» методами при помощи подручных материалов.
Самый простой способ определения полярности, которым можно воспользоваться дома – это использовать картофель. Для этого необходимо взять один клубень сырого картофеля и разрезать пополам. После этого два провода (желательно разного цвета или с любым другим отличительным знаком) оголенными концами втыкаются в срез картофеля на расстоянии 1-2 сантиметра друг от друга.
Для этого необходимо взять один клубень сырого картофеля и разрезать пополам. После этого два провода (желательно разного цвета или с любым другим отличительным знаком) оголенными концами втыкаются в срез картофеля на расстоянии 1-2 сантиметра друг от друга.
Другие концы проводов подключаются к проверяемому источнику постоянно тока, и прибор включается в сеть (если это аккумулятор, то после подсоединения проводов больше ничего делать не нужно) на 15-20 минут. По истечении этого времени на срезе картофеля, вокруг одного из проводов образуется светло-зеленое пятно, которое будет признаком плюсового заряда провода.
Второй способ также не требует, каких либо, особых устройств или инструментов. Для определения полярности проводов источника постоянного тока понадобится емкость с теплой водой, в которую опускаются два подключенных к источнику питания провода.
После включения прибора в сеть вокруг одного из проводов начнут появляться пузыри газа (водород) – это процесс электролиза воды. Эти пузырьки образуются вокруг источника отрицательного заряда.
Эти пузырьки образуются вокруг источника отрицательного заряда.
Следующий способ подойдет в том случае, если есть не используемый, рабочий компьютерный кулер. Способ определения полярности данным методом заключается в том, что кулер необходимо запитать от проверяемого источника бесперебойного питания. Но зачастую в кулерах присутствует три провода:
- черный, отвечает за отрицательный заряд;
- красный, отвечает за положительный заряд;
- желтый, является датчиком оборотов.
В данном случае желтый провод игнорируется и никуда не подключается. Если после подключения кулера к источнику постоянного напряжения, кулер начал работать, то полярность определена правильно, плюс подключен к красному проводу, а минус – к черному. А если кулер не срабатывает – это будет означать что полярность неправильная.
Также, если мультиметр отсутствует, положительный и отрицательный контакты аккумулятора можно определить при помощи индикаторной отвертки.
Для этого необходимо дотронутся индикатором до одного из выводов аккумулятора, прижать палец к обратной стороне индикатора (к контакту на рукоятке), а ко второму выводу аккумулятора дотронуться рукой.
Если индикатор начал светиться, то заряд проверенного вывода, с которым он контактирует, имеет положительное значение, а если индикатор не засветился – вывод отрицательный. Но у этого способа определения полярности есть один недостаток.
Если аккумулятор разрядился или поврежден (пробит), индикатор будет загораться при контакте с обеими клеммами, из-за чего определить значения полюсов аккумуляторной батареи будет невозможно.
Отрицательные дроби. Действия с отрицательными дробями
Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
-2 : 7 и 2 : (-7),
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 | . |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус
можно ставить перед дробью, перед числителем или перед знаменателем:
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
Пример.
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 | 20 | 20 |
Таким образом:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = |
| 5 | 4 | 20 | 20 |
| = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
Пример.
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = |
| 12 | 12 | 12 | 12 |
| = | — | 5 | + | 11 | = | -5 + 11 | = | 6 | . |
| 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
Пример.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
Пример.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 | . |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 | . |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
Пример.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = |
| 3 | 5 | 3 | 5 |
| = | -2 · 5 | = | -10 | = | 10 | . |
| 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
положительных и отрицательных чисел | SkillsYouNeed
Стандартные числа, все, что больше нуля, описываются как «положительные» числа. Мы не ставим перед ними знак плюса (+), потому что в этом нет необходимости, поскольку, по общему мнению, числа без знака положительны.
Числа меньше нуля известны как «отрицательные» числа. Перед ними стоит знак минус (-), чтобы указать, что они меньше нуля (например, -10 или « минус 10 »).
Визуализация отрицательных и положительных чисел
Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую линию, инструмент, с которым вы, возможно, хорошо знакомы, особенно если у вас есть дети в начальной школе.
Это выглядит примерно так:
Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними делать.
Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).
Эта числовая линия является упрощенной версией, но вы можете нарисовать их с любым числом, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самостоятельно на обратной стороне конверта или клочка макулатуры, а также довольно сложно ошибиться в расчетах. Если вы внимательно подсчитываете количество мест, которые вы двигаетесь, вы получите правильный ответ.
Если вы внимательно подсчитываете количество мест, которые вы двигаетесь, вы получите правильный ответ.
Рабочие примеры
Что такое 10-25?
Начиная с 10, вы перемещаете 25 чисел влево и сразу видите, что ответ — -15.
Что такое −17 + 23?
На этот раз вы начинаете с -17 и перемещаетесь на 23 позиции вправо. Сразу видно, что ответ — 6.
Вычитание отрицательных чисел
Если вы вычесть отрицательное число, два отрицательных числа объединятся, чтобы получить положительное.
−10 — (- 10) не равно −20. Вместо этого вы можете думать об этом как о том, чтобы повернуть один из отрицательных знаков вертикально, пересечь другой и получить плюс.Тогда сумма будет -10 + 10 = 0.
Краткое примечание по скобкам
Для наглядности, никогда нельзя писать два знака минус рядом без скобок.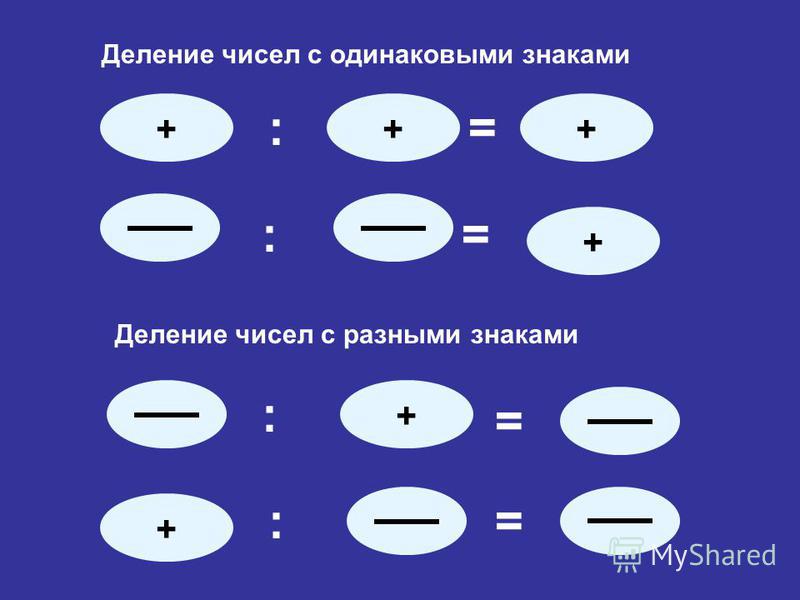
Итак, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли увидеть, что использование двух отрицательных знаков было намеренным.
-10-10 неверно (и сбивает с толку)
-10 — (- 10) правильно (и яснее)
Умножение и деление на положительные и отрицательные числа
При умножении или делении с комбинациями положительных и отрицательных чисел вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или деля числа, как если бы они оба были положительными.Получив числовой ответ, вы можете применить очень простое правило, чтобы определить знак ответа:
- Когда знаки двух чисел совпадают с , ответ будет положительным .
- Когда знаки двух чисел разные , ответ будет отрицательный .
Итак:
(положительное число) × (положительное число) = положительное число
(отрицательное число) × (отрицательное число) = положительное число
Но:
(положительное число) × (отрицательное число) = отрицательное число
В качестве побочного вопроса это каким-то образом объясняет, почему у вас не может быть квадратного корня из отрицательного числа (подробнее об этом читайте на нашей странице в Special Numbers and Concepts ). Квадратный корень — это число, которое умножается само на себя, чтобы получить число. Вы не можете умножить число на само по себе, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Квадратный корень — это число, которое умножается само на себя, чтобы получить число. Вы не можете умножить число на само по себе, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Правило работает так же, когда вам нужно умножить или разделить более двух чисел. Четное число отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.
Рабочих примеров
Что такое −5 × 25?
5 x 25 равно 125.Но здесь у вас есть одно отрицательное и одно положительное число, поэтому знак ответа будет отрицательным. Следовательно, ответ — −125 .
Что такое −40 ÷ 8?
40 ÷ 8 равно 5. Опять же, у вас есть одно положительное и одно отрицательное число, поэтому знак ответа будет отрицательным. Ответ: −5 .
Что такое −50 ÷ −5?
50 ÷ 5 равно 10. На этот раз у вас два отрицательных числа, поэтому знак ответа будет положительным.Ответ: 10 .
Что такое −100 × −2?
100 x 2 равно 200. Опять же, у вас два отрицательных числа, поэтому ответ положительный. Это 200 .
Что такое 10 x −2 × 3?
Для начала рассмотрим первую часть расчета. 10 x 2 = 20. У вас есть одно положительное и одно отрицательное число, поэтому знак ответа будет отрицательным, то есть −20.
Теперь возьмем вторую часть вычисления: −20 × 3.Итак, 20 × 3 = 60, но опять же, у вас есть отрицательное и положительное число, поэтому ответ будет отрицательным: −60 .
Почему умножение двух отрицаний дает положительный ответ?
Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто может сбивать с толку и казаться нелогичным.
Чтобы объяснить, почему это так, вспомните числовые линии, использованные ранее в этой статье, поскольку они помогают объяснить это визуально.
- Во-первых, представьте, что вы стоите на числовой прямой в нулевой точке и обращены в положительном направлении, то есть в направлении 1, 2 и так далее. Вы делаете два шага вперед, делаете паузу, затем делаете еще два шага. Вы переместились 2 × 2 шага = 4 шага.
Следовательно, положительный × положительный = положительный - Теперь вернитесь к нулю и посмотрите в отрицательном направлении, то есть в сторону −1, −2 и т. Д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × −2 шага = −4 шага.
Следовательно, отрицательный × положительный = отрицательный
В обоих этих примерах вы двигались вперед (т. Е. В том направлении, куда вы смотрели), что является положительным ходом.
- Вернитесь к нулю снова, но на этот раз вы собираетесь идти назад (отрицательное движение).
 Снова поверните голову в положительную сторону и сделайте два шага назад. Теперь вы стоите на -2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Снова поверните голову в положительную сторону и сделайте два шага назад. Теперь вы стоите на -2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Следовательно, положительный × отрицательный = отрицательный - Наконец, снова вернемся к нулю, повернемся в отрицательном направлении. Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись в отрицательном направлении и идя назад ( два отрицательных ), вы достигли положительного результата.
Следовательно, отрицательный × отрицательный = положительный
- Два негатива компенсируют друг друга. Это можно увидеть в речи:
- «Просто сделай это!» положительный стимул к чему-либо.
- «Не делай этого!» просит кого-то чего-то не делать. Это отрицательно.
- «Не делай этого» означает «пожалуйста».
 Два отрицания компенсируют и дают положительный результат как в математике, так и в речи.
Два отрицания компенсируют и дают положительный результат как в математике, так и в речи.
- Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются, чтобы получить положительный. Если у вас есть положительный и отрицательный ответ, останется один штрих, и ответ будет отрицательным. Это простая и наглядная памятная записка, хотя она не обязательно удовлетворит тех, кто хочет понять правило.
Заключение
Отрицательные знаки могут выглядеть немного устрашающе, но правила, регулирующие их использование, просты и понятны. Помните об этом, и у вас не будет проблем.
Правила использования положительных и отрицательных целых чисел
Целые числа, цифры, не имеющие дробей и десятичных знаков, также называются целыми числами. Они могут иметь одно из двух значений: положительное или отрицательное.
- Положительные целые числа имеют значения больше нуля.

- Отрицательные целые числа имеют значения меньше нуля.
- Ноль не является ни положительным, ни отрицательным.
Правила работы с положительными и отрицательными числами важны, потому что вы столкнетесь с ними в повседневной жизни, например, при балансировании банковского счета, вычислении веса или приготовлении рецептов.
Советы для успеха
Как и любой другой предмет, успех в математике требует практики и терпения. Некоторым людям легче работать с числами, чем другим.Вот несколько советов по работе с положительными и отрицательными целыми числами:
- Контекст может помочь вам разобраться в незнакомых концепциях. Попробуйте подумать о практическом приложении как о ведении счета, когда вы тренируетесь.
- Использование числовой линии , показывающей обе стороны нуля, очень полезно для понимания работы с положительными и отрицательными числами / целыми числами.

- Отрицательные числа легче отслеживать, если вы заключите их в скобки .
Дополнение
Независимо от того, добавляете ли вы положительные или отрицательные значения, это простейший расчет, который вы можете сделать с целыми числами. В обоих случаях вы просто вычисляете сумму чисел. Например, если вы складываете два положительных целых числа, это выглядит так:
Если вы вычисляете сумму двух отрицательных целых чисел, это выглядит так:
Чтобы получить сумму отрицательного и положительного числа, используйте знак большего числа и вычтите.Например:
- (–7) + 4 = –3
- 6 + (–9) = –3
- (–3) + 7 = 4
- 5 + (–3) = 2
Знак будет у большего числа. Помните, что добавление отрицательного числа — это то же самое, что вычитание положительного.
Вычитание
Правила вычитания аналогичны правилам сложения. Если у вас есть два положительных целых числа, вы вычитаете меньшее из большего. Результатом всегда будет положительное целое число:
Результатом всегда будет положительное целое число:
Точно так же, если вы вычтите положительное целое число из отрицательного, вычисление станет вопросом сложения (с добавлением отрицательного значения):
- (–5) — 3 = –5 + (–3) = –8
Если вы вычитаете отрицательные из положительных, эти два отрицания компенсируются, и это становится сложением:
- 5 — (–3) = 5 + 3 = 8
Если вы вычитаете отрицательное число из другого отрицательного целого числа, используйте знак большего числа и вычтите:
- (–5) — (–3) = (–5) + 3 = –2
- (–3) — (–5) = (–3) + 5 = 2
Если вы запутались, часто бывает полезно сначала написать положительное число в уравнении, а затем отрицательное.Это может упростить определение того, происходит ли смена знака.
Умножение
Умножение целых чисел довольно просто, если вы помните следующее правило: если оба целых числа либо положительные, либо отрицательные, сумма всегда будет положительным числом. Например:
Например:
- 3 х 2 = 6
- (–2) x (–8) = 16
Однако, если вы умножаете положительное целое число на отрицательное, результатом всегда будет отрицательное число:
- (–3) x 4 = –12
- 3 x (–4) = –12
Если вы умножаете большую серию положительных и отрицательных чисел, вы можете сложить, сколько положительных и отрицательных чисел.Последний знак будет лишним.
Отдел
Как и в случае с умножением, правила деления целых чисел следуют тому же положительному / отрицательному руководству. Разделение двух негативов или двух позитивов дает положительное число:
- 12/3 = 4
- (–12) / (–3) = 4
Деление одного отрицательного целого числа и одного положительного целого числа дает отрицательное число:
- (–12) / 3 = –4
- 12 / (–3) = –4
Как складывать, вычитать, умножать и делить положительные и отрицательные числа
Давайте посмотрим на следующую числовую строку и заметим, что каждая точка (точка) на числовой прямой соответствует одному числу:
В числовой строке выше мы видим три типа чисел или целых чисел: отрицательные числа, ноль и положительные числа.Отрицательные числа находятся слева от нуля, поэтому они меньше нуля. Положительные числа справа от нуля, поэтому они больше нуля. Ноль, разделительная точка, не является ни положительным, ни отрицательным.
Для числовой строки выше «1» соответствует или относится к красной точке, «2» относится к зеленой точке, «3» относится к синей точке и т. Д. Когда мы перемещаемся вправо по числовой строке, мы увеличиваем числа. Мы определили это как дополнение. Когда мы движемся влево, мы уменьшаемся.И мы определили это как вычитание. Обычно так работает числовая линия.
Когда мы складываем два положительных числа или умножаем два положительных числа, мы получаем положительное число. Однако мы можем вычесть положительное число из положительного, и вдруг мы не получим положительное число!
Например, если мы вычтем 7 из 4, мы начнем с 4 в числовой строке и переместимся влево на 7 позиций. Это подводит нас к -3. Поскольку -3 находится слева от 0, оно меньше нуля.
Глядя на обратную операцию, мы можем сказать, что если 4-7 = -3, то -3 + 7 = 4. И это правильно. Если мы начнем с -3 и переместим на 7 делений вправо, мы получим 4.
Положительные числа — это не только целые числа справа от нуля, но и все типы чисел, такие как дроби, десятичные дроби и радикалы. Отрицательные числа также включают различные формы и различные типы чисел, которые появляются слева от нуля.
У нас не всегда есть числовая строка, с которой можно работать, поэтому нам нужно изучить несколько правил работы с отрицательными числами.Во-первых, нам нужно определить абсолютное значение. Абсолютное значение числа — это количество единиц, отсчитываемых от нуля. Он всегда выражается положительно, но без знака «плюс».
Абсолютное значение 3 равно 3. Абсолютное значение -3 также равно 3. И 3, и -3 — три единицы от нуля. Абсолютное значение обозначается путем написания числа между двумя вертикальными полосами.
| 3 | = 3 и | -3 | = 3
| Добавление отрицательных чисел |
Если перед числом вы не видите отрицательный или положительный знак, это положительный знак.
При сложении чисел одного знака (положительного или отрицательного) сложите их абсолютные значения и дайте результату тот же знак.
6 + 5 = 11 (6 и 5 положительные; 6 + 5 равно 11, что положительно)
-7 + -8 = -15
(-7 и -8 оба отрицательны; сложите | 7 | + | 8 |, что равно 7 + 8, чтобы получить 15; ответ -15)
Если все числа в добавляемой группе отрицательные: -2 + -3 + -4 = -9, снова сложите абсолютные значения 2 + 3 + 4, чтобы получить 9 и поставить отрицательный знак.
| Добавление положительных и отрицательных чисел |
При сложении чисел противоположного знака возьмите их абсолютные значения, вычтите меньшее из большего и присвойте результату знак числа с большим абсолютным значением.
7 + -3 = | 7 | — | 3 | = 4
-8 + 6 = | 8 | что равно 8 и | 6 | что составляет 6. Вычтите меньшее из большего:
8-6, что дает результат 2 и дает ему знак большего числа, равного 8.
Ответ -2.
| Вычитание положительных и отрицательных чисел |
При вычитании положительного числа из отрицательного используйте то же правило, что и для сложения двух отрицательных чисел: сложите абсолютные значения и присвойте разнице отрицательный знак.
-5 — 4 = | 5 | + | 4 | = | 9 | = -9 (это как -5 + -4 = -9)
-2 — 12 = | 2 | + | 12 | = | 14 | = -14
При вычитании отрицательного числа из положительного числа двойной отрицательный результат вычитания отрицательного становится положительным, поэтому используйте то же правило, что и для сложения двух положительных чисел: сложите абсолютные значения и присвойте разнице положительный знак.
5 — -4 = | 5 | + | 4 | = 5 + 4 = 9
Если бы вы использовали числовую строку, вы бы пошли влево для вычитания, а затем перевернули (вправо) для отрицательного числа, так что окончательный ответ будет справа от исходного числа.
16 — -10 = | 16 | + | 10 | = 16 + 10 = 26
Аддитивное обратное число — это число с противоположным знаком, так что при сложении двух результат равен нулю.
а + (-а) = 0
Как видите, это положительные и отрицательные числа одного и того же абсолютного значения.
10 + -10 = 0
-24 + 24 = 0
| Умножение положительных и отрицательных чисел |
При умножении положительного числа и отрицательного числа (или отрицательного числа на положительное число) умножьте абсолютные значения и дайте ответу отрицательный знак.
8 х -5 = | 8 | х | 5 | = 8 x 5 = 40, но дайте ему отрицательный знак, и получится -40
-13 x 3 = -39
9 х -3 = -27
Чтобы умножить несколько чисел, посчитайте количество отрицательных знаков в числах, которые нужно умножить.Если это четное число, произведение будет положительным, а если нечетное, произведение будет отрицательным.
6 х -2 х -3 х 5 = | 6 | х | 2 | х | 3 | х | 5 |
6 x 2 = 12, 12 x 3 = 36 и 36 x 5 = 180
Имеется два отрицательных знака (четное число), поэтому ответ положительный.
Если бы было -6 x -2 x -3 x 5, ответ был бы -180
| Умножение двух отрицательных чисел |
При умножении двух отрицательных чисел два отрицательных числа компенсируют друг друга, поэтому умножьте абсолютные значения и дайте ответ положительный знак.
-21 х -3 = | 21 | х | 3 | = 63 (остается положительным)
-7 х -8 = | 7 | х | 8 | = 56
| Деление отрицательного числа на отрицательное |
Чтобы разделить два числа с одинаковым знаком (два положительных или два отрицательных), используйте абсолютные значения, и результат будет положительным.
16 ¸ 4 = | 16 | ¸ | 4 | = 4
-20 ¸ -10 = | 20 | ¸ | 10 | = 2
Деление положительного числа на отрицательное или отрицательного числа на положительное
Чтобы разделить пару чисел с разными знаками (отрицательное на положительное или положительное на отрицательное), используйте абсолютные значения двух чисел и присвойте результату отрицательный знак.
-12 ¸ 3 = | 12 | ¸ | 3 | = 4, но это -4
18 ¸ -3 = | 18 | ¸ | 3 | = 6, но это -6
| Использование отрицательных чисел |
Отрицательные числа используются для обозначения низких температур. Цифры ниже 0 ° C отрицательны и ниже точки замерзания. (Помните, что значения ниже 32 ° F ниже точки замерзания, но температура часто опускается ниже 0 ° F.)
Отрицательные числа используются для отображения измерений ниже уровня моря.Уровень моря равен 0.
.Отрицательные числа используются с деньгами, чтобы показать задолженность или денежную задолженность. Если человек или домохозяйство тратят больше денег, чем зарабатывают, мы говорим, что они «отрицательные на определенную сумму», или называем это «красным», потому что бухгалтеры используют красные чернила для отображения отрицательных чисел.
| Больше и меньше и наборы чисел |
Набор чисел — это группа чисел, которая соответствует заданному описанию.Например, набор целых чисел меньше 0 будет выражен как n <0. В этом предложении набор чисел, удовлетворяющий условиям, будет состоять из отрицательных целых чисел.
Все целые числа больше 0 будут выражены как n> 0. Набор чисел, удовлетворяющий этим условиям, будет набором всех положительных целых чисел. Каждое из этих целых чисел будет называться членом или элементом этого набора.
Какие целые числа от 3 до 8? Это будет 4, 5, 6 и 7.Другой способ выразить это — набор чисел больше 3, но меньше 8, которые можно представить в виде математического предложения, которое выглядит так:
3 Прочтите это: n такое, что n больше 3 и меньше 8 Так как 3 И n <8 или n меньше 8 или 8 больше n п = 4, 5, 6, 7 Мы могли бы сказать 3 n <8, и в этом случае в ответ было бы включено 3, поэтому n = 3, 4, 5, 6, 7.Знак означает «меньше или равно», а знак означает «больше или равно». Термин чисел со знаком относится к положительным и отрицательным числам. Если знак не отображается, число автоматически считается положительным. В числовой строке числа справа от 0 положительны.Числа слева от 0 отрицательны, как показано на рисунке 1. Рис. 1. Числовая строка с целыми числами. Для любых двух чисел в числовой строке число справа всегда больше, независимо от его знака (положительного или отрицательного). Обратите внимание, что дроби также могут быть помещены в числовую линию, как показано на рисунке 2. Рис. 2. Числовая прямая с использованием дробей. Когда складывает два числа с одинаковым знаком (как положительными, так и отрицательными), сложите абсолютные значения (число без знака) и сохраните тот же знак.Задачи сложения могут быть представлены как в вертикальной форме (вверх и вниз), так и в горизонтальной форме (поперек). Добавьте следующее. При сложении двух чисел с разными знаками (одно положительное и одно отрицательное) вычтите абсолютные значения и сохраните знак того числа с большим абсолютным значением. Добавьте следующее. Добавьте следующее. 15 3 3 5 Чтобы вычесть положительные и / или отрицательные числа, просто изменит знак вычитаемого числа и затем сложит. Вычтите следующее. Вычитание положительных и / или отрицательных чисел также может выполняться «по горизонтали». Вычтите следующее. +12 — (+4) = +12 + (–4) = 8 +16 — (–6) = +16 + (+6) = 22 –20 — (+3) = –20 + (–3) = –23 –5 — (–2) = –5 + (+2) = –3 Если перед круглой скобкой стоит минус, то это означает, что все, что находится в круглых скобках, должно быть вычтено.Поэтому, используя то же правило, что и при вычитании чисел со знаком, просто замените каждый знак в круглых скобках на противоположный, а затем сложите. Вычтите следующее. Чтобы умножать или делить числа со знаком, обрабатывает их как обычные числа, но помните следующее правило: нечетное количество отрицательных знаков дает отрицательный ответ.Четное количество отрицательных знаков даст положительный ответ. Умножьте или разделите следующее. (–3) (+ 8) (- 5) (- 1) (- 2) = +240 (–3) (+ 8) (- 1) (- 2) = –48 Цугер, Джоэл П. Средняя школа метро Чикаго Цели:
1.Это нацелено на 7 -х и 8 -х классов, а также студентов предалгебры и Необходимое оборудование:
1. Number Line Materials
1.1 Пронумеруйте строки для каждого студента, напечатанные на всем листе.
Линии должны быть расположены достаточно далеко друг от друга, чтобы маркеры бинго
покрывать только одну строку за раз.
1.2 Нужны полупрозрачные маркеры бинго, может быть, 5-10 на ученика.
1.3 Нужен один ацетатный лист с числовой линией для работы с накладными
проектор.
2. Функциональная машина
2.1 Вырезка из картона или дерева, представляющая машину с названием
«Функциональная машина» . Он может быть настолько сложным или простым, насколько вы Если вы умеете складывать целые числа, я уверен, что вы также можете вычитать целые числа.Ключевым шагом является преобразование задачи вычитания целых чисел в задачу сложения целых чисел. Процесс очень прост. Вот как это сделать: Шаг 1 : Преобразуйте задачу вычитания целых чисел в задачу сложения целых чисел. Вот как это сделать: Шаг 2 : Продолжайте обычное сложение целых чисел. ⊗ Обратите внимание, что в конечном итоге вы добавите целые числа. Итак, для вашего удобства, вот краткое изложение правил добавления целых чисел. Сложите их абсолютные значения и сохраните общий знак. Вычтите их абсолютные значения (большее абсолютное значение минус меньшее абсолютное значение), затем возьмите знак числа с большим абсолютным значением. Пример 1 : Вычтите указанные ниже целые числа. Решение: Нам нужно будет преобразовать задачу от вычитания к сложению. Для этого мы сохраняем первое число, равное –13, меняем операцию с вычитания на сложение, затем меняем знак + 4 на — 4. Последний шаг — продолжить регулярное добавление. Сложите их абсолютные значения.Затем определяем знак окончательного ответа. Поскольку мы добавляем целые числа с одинаковым знаком, мы сохраняем общий знак, который в данном случае отрицательный. Пример 2 : Вычтите целые числа, указанные ниже. Решение: Как и раньше, преобразуйте задачу вычитания в задачу сложения. Остается положительное 9, переключите операцию с «минус» на «плюс», затем получите противоположный знак вычитания (второе число) с отрицательного на положительный. А теперь добавим их.Мы складываем два положительных целых числа, поэтому ожидаем, что ответ также будет положительным, потому что общий знак положительный. Пример 3 : Найдите разность двух целых чисел. Решение: Надеюсь, вы уже разбираетесь в этом. Давайте сначала сделаем это задачей сложения целых чисел, а затем приступим к регулярному сложению целых чисел с разными знаками. Таким образом, мы сначала вычитаем их абсолютные значения, а затем получаем знак числа с большим абсолютным значением. Вычитая абсолютные значения, получаем 24 минус 19, что дает нам +5. Но окончательный ответ — — 5, потому что знак идет от — 24. Возможно, вас заинтересует: Целочисленное сложение Когда мы открываем отрицательные числа, мы, естественно, даже без сомнения, предполагаем, что они подчиняются тем же законам арифметики, что и обычные положительные счетные числа.То есть нам нравится верить, что основные законы, такие как \ (a \ times b = b \ times a \) и \ (a \ times 1 = a \) и \ (a \ times 0 = 0 \), выполняются для всех числа, как положительные, так и отрицательные, и что мы можем раскрывать скобки даже с отрицательными записями и т. д. Конечно, эти правила предполагают, что мы знаем, что априори умеют умножать на отрицательные числа. В начальной учебной программе умножение вводится в контексте целых счетных чисел и соответственно определяется как повторное сложение.Например, \ (4 \ times 5 \) читается как «четыре группы по пять» и вычисляется следующим образом: \ (4 \ times 5 = 5 + 5 + 5 + 5 = 20 \). На самом деле довольно удивительно, что \ (5 \ times 4 \), «пять групп по четыре», дает тот же числовой ответ, что и четыре группы по пять. Вычисление совершенно иное, когда числа 5 и 4 служат для смены ролей. Вопрос: Как бы вы убедили молодого студента в том, что 193 группы из 307 человек наверняка будут иметь такую же ценность, как 307 групп из 193 человек? Почему мы хотим, чтобы верили, что \ (a \ times b = b \ times a \) для подсчета чисел? (ПОДСКАЗКА: расставьте точки в прямоугольные массивы.) Повторное сложение позволяет нам умножить положительное число и отрицательное число. Например, \ (2 \ times \ left (-3 \ right) \) можно читать как «две группы отрицательных трех» и поэтому вычисляется как \ (2 \ times \ left (-3 \ right) = — 3 + \; — 3 = -6 \). По сваям и ямам это выглядит так: Однако интерпретация отрицательного числа, умноженного на положительное, и отрицательного, умноженного на отрицательное, путем повторного сложения проблематична. Что может означать \ (\ left (-2 \ right) \ times 3 \)? «Отрицательные две группы по три» не имеет смысла. И \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) одинаково странно: «две отрицательные группы из трех отрицательных». На самом деле умножение здесь не имеет значения в контексте повторяющегося сложения. Мы вступили на новую территорию, и если мы хотим открыть наш мир для новых типов чисел, неудивительно, что ранее конкретные, буквальные определения начинают ошибаться. Итак, мы должны провести сложный сдвиг мышления, отказавшись от вопроса Что такое умножение? вместо этого спросить: Как бы мы хотели, чтобы вело себя умножение? Комментарий: Позвольте мне подчеркнуть этот момент.На вопрос: «Что означает умножение отрицательных чисел?» Это вводящий в заблуждение вопрос, и это не тот вопрос, который следует задавать на данном этапе нашей работы: мы все еще пытаемся решить проблему того, каким может быть умножение в мире отрицательных чисел. Чтобы приблизиться к этому, мы сначала должны четко определить, какие особенности арифметики, по нашему мнению, должны оставаться верными. Положительные, умноженные на Отрицательные : Кажется убедительным придерживаться концепции «повторного сложения» для произведения отрицательного и положительного: \ (2 \ times \ left (-3 \ right) = \) две группы отрицательных трех \ (= — 3 + -3 = -6 \). Большинство людей согласны с тем, что мы должны придерживаться этой идеи. Отрицательное время Положительное : Это проблематично: \ (\ left (-2 \ right) \ times 3 =? \) Но кажется убедительным сказать, что закон коммутативности \ (a \ times b = b \ times a \) должен выполняться для всех типов чисел, включая отрицательные числа. В этом случае мы можем написать: \ (\ left (-2 \ right) \ times 3 = 3 \ times \ left (-2 \ right) \) три группы отрицательных двоек \ (= — 2 + -2 + -2 = -6 \). Отрицательное время Отрицательное : Как нам вычислить \ (\ left (-2 \ right) \ times \ left (-3 \ right) \)? Применение закона коммутативности и представление об этом как о \ (\ left (-3 \ right) \ times \ left (-2 \ right) \) в этом случае не помогает.Итак, какая математика может направлять нас в нашем мышлении? Мы действительно сказали, что нам нравится верить, что все обычные законы арифметики (\ (a \ times b = b \ times a \), \ (a \ times 1 = a \), \ (a \ times 0 = 0 \), раскрывающиеся скобки и т. д.) должны выполняться для всех типов чисел. Поскольку модель площади — это просто представление, которое мы верим в расширяющиеся скобки, модель площади должна работать и для отрицательных чисел! КЛЮЧЕВОЙ ПРИМЕР: Вот три способа вычислить \ (17 \ times 18 \), считая \ (17 \) либо \ (10 + 7 \), либо \ (20+ \ left (-3 \ right) \) и \ (18 \) как \ (10 + 8 \) или \ (20 + \ left (-2 \ right) \).Несмотря на то, что геометрически нет смысла иметь отрицательную длину стороны геометрической фигуры, мы видим, что математика, которую представляет каждая диаграмма, по-прежнему является правильной математикой. Но есть четвертая возможная картина! Математика раскрывающихся скобок предполагает, что правильное значение \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) равно \ (+ 6 \). (У продукта должен быть ответ \ (306 \).) УПРАЖНЕНИЕ: Нарисуйте четыре диаграммы, представляющие \ (26 \ times 35 \), и используйте последнюю, чтобы продемонстрировать, почему мы должны установить \ (\ left (-4 \ right) \ times \ left (-5 \ right) = +20 \). Как только мы договоримся, что \ (2 \ times \ left (-3 \ right) = — 6 \) (посредством повторного сложения) и \ (\ left (-3 \ right) \ times 2 = -6 \) (через a убежденность в коммутативности), что отрицательное умножение на отрицательное — положительное, является вынужденным логическим следствием следующих двух основных арифметических убеждений: \ (a \ times 0 = 0 \) и \ (a \ left (b + c \ right) = ab + ас \). Вот почему: Докажем \ (\ left (-2 \ right) \ times \ left (-3 \ right) = + 6 \). По первому правилу мы должны сказать: \ (\ left (-2 \ right) \ times 0 = 0 \). Переписывая первый ноль, мы должны договориться, что: \ (\ left (-2 \ right) \ times \ left (3+ \ left (-3 \ right) \ right) = 0 \). При распределении мы также должны согласиться с тем, что: \ (\ left (-2 \ right) \ times 3 + \ left (-2 \ right) \ times \ left (-3 \ right) = 0 \). Это читается так: \ (- 6 + \ left (-2 \ right) \ times \ left (-3 \ right) = 0 \). Отсюда следует, что \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) должно быть \ (+ 6 \). УПРАЖНЕНИЕ: Создайте аналогичный аргумент, чтобы установить, что \ (\ left (-4 \ right) \ times \ left (-5 \ right) = + 20 \). В контексте положительных целых чисел это повторное сложение. В контексте положительных и отрицательных целых чисел я лично не знаю, что это такое, кроме математически согласованной операции, установленной так, что если \ (a \) и \ (b \) являются положительными целыми числами, то \ ( a \ times \ left (-b \ right) = — ab \), и с логическими следствиями \ (\ left (-a \ right) \ times b = b \ times \ left (-a \ right) = — ab \) и \ (\ left (-a \ right) \ times \ left (-b \ right) = ab \). Люди пытаются придать всему этому конкретный смысл с помощью моделей солдат, идущих по числовым линиям, меняющих направление, систем прибыли и долга, работы с температурами выше и ниже нуля и т. Д. Каждая модель хороша для иллюстрации НЕКОТОРЫХ аспектов арифметики отрицательных чисел, но не всех. Например, идея «убрать пять градусов холода — это то же самое, что добавить пять градусов тепла» может сработать для некоторых, чтобы объяснить, почему \ (- \ left (-5 \ right) \) должно равняться \ (5 \) , но это не объясняет само по себе, почему отрицательное, умноженное на отрицательное, дублируется положительным. С педагогической точки зрения нам нужно отойти от начинающих учеников думать об умножении отрицательных чисел с помощью моделей, которые пытаются, но в какой-то момент должны потерпеть неудачу, «объяснить», что такое умножение отрицательных чисел. Вместо этого мы должны начать с обсуждения того, что, по нашему мнению, должно быть правдой в отношении умножения в целом и как оно ведет себя. Расширение скобок с помощью модели площади дает студентам убедительную иллюстрацию того, что математика «хочет», чтобы отрицательные значения, умноженные на отрицательные, были положительными. чисел со знаком (положительные и отрицательные числа)
чисел со знаком (положительные и отрицательные числа)
Номер строки
Сложение чисел со знаком
Пример 1
Пример 2
Пример 3
Вычитание чисел со знаком
Пример 4
Пример 5
Минус предшествующая скобка
Пример 6
Умножение и деление чисел со знаком
Пример 7
Правила смены знаков
Правила смены знаков Правила смены знаков
Вернуться к указателю математики
280-2020
1 -й -й курс алгебры.
2. Разберитесь со знаками плюс и минус во время
арифметических операций.
хотите его построить.
2.2 Полоски картона или другого материала, одна из которых входит в
машину сверху, а другая выходит сбоку.
2.3 Кривошип машины, который либо функционирует (протягивает верхнюю полосу
и выталкивает нижнюю полосу), либо повернут только на
для демонстрации
3. Keep It or Give It Game
3.1 Два кубика разного цвета.
3.2 Лист уравнений, вероятно, около 100 с положительными и
отрицательные числа с операциями сложения и умножения.
Рекомендуемая стратегия:
1. Стратегия числовой линии - показывает положительные и отрицательные числа как
направлений на линии, отрицательное слева, положительное справа.Объясните
разницу между отрицательными числами и вычитанием, т. Е. Счет
на 8,00 долларов - отрицательное число, это деньги в долгу, а у вас
нет; Получение 10 долларов США и оплата 8 долларов США для оплаты счета - это вычитание
, при переводе имеющихся у вас денег остается
долларов США.
Поэкспериментируйте с числовой прямой, используя накладные расходы (учащиеся
работают над своими листами с числовой прямой). Т.е. перемещение 10 (вправо) перемещение
-5 (влево) все должно быть на 5 (положительная сторона числовой прямой).
Продолжите с еще несколькими примерами, чтобы показать направление и как его использовать. Примечание: использует пару примеров вычитания отрицательных чисел,
использует обратное направление для вычитания, поэтому вычитаемые отрицательные числа
будут перемещаться в положительном направлении.
Поэкспериментируйте с умножением с использованием числовой прямой, также покажите на доске последовательный узор
, так что два метода подкрепляют правила знака
.
Пример: | 4 . 4 = 16 |,
Продукты показывают разницу в 4 при | 3 . 4 = 12 |, по
каждое последующее умножение. | 2 . 4 = 8 |,
| 1 . 4 = 4 |,
| 0 . 4 = 0 |,
| -1 . 4 = -4 |,
| -2 . 4 = -8 |;
Чтобы показать отрицательное время, отрицательное - положительное __________
шаблон использования: | 3 . (-4) = - 12 |,
используйте числовую прямую с указанием направления на | 2 . (-4) = -8 |,
показать результаты. Причина использования большего количества | 1 . (-4) = -4 |,
чем один маркер бинго показывает | 0 . (-4) = 0 |, шаблон
на числовой прямой. | -1 . (-4) = 4 |,
| -2 . (-4) = 8 |;
______________
Рекомендуется, чтобы число 1 st было кратным 2 числа nd
, т.е. 3x4 означает 4 + 4 + 4, а не 3 + 3 + 3 + 3. Несмотря на то, что умножение
коммутативно, в алгебре будет проще показать, что 5w равно 5 умножению на w, то есть w + w + w + w + w.
2. Функциональная машина - Используется в качестве подкрепления для вычисления с
как положительными, так и отрицательными числами. На картонной полосе
проставлена отметка ___________________________
| 1 | 2 | 3 | 4 | 5 | и т. д. | и это подается на вход
___________________________
машина (картонная, деревянная и т. д., окрашенная или
быть машиной), причем первой подается первая. Имеется 2 nd картон
, который является выходом, например: ____________________________
| 2 | 4 | 6 | 8 | 10 | и т.п.|
, которые есть у студентов ____________________________
угадайте, увидев один или два примера, на каком выходе будет
и какая функция делает этот вывод, этот случай - это ввод, умноженный на 2.
Сделайте разные полоски для ввода и вывода. Функция может быть как
сложный как (ввод - 3) умножить на -2.
3. Игра «Держи или отдай» - Используется в качестве подкрепления для операций
положительных и отрицательных чисел. Класс можно разделить на
на 6 групп.Каждая группа стартует с 50 очками. Команда
, первой набравшая 100 очков, побеждает. Работа с более чем 100 уравнениями на
, с первыми 6 уравнениями, пронумерованными 1-6. Команды идут по порядку, стартовая команда
№1. Использованы два кубика разного цвета. Один кубик
определяет, какая команда получит уравнение, если исходная команда
выдаст его. Другой определяет, какое уравнение решается. После
используется уравнение, следующее уравнение в списке (кроме исходного 6
) заменит используемое уравнение.У команды, бросающей кости
, есть 10 секунд, чтобы решить оставить уравнение или выдать его (команды
хотят положительных результатов и выдают отрицательные). У команды
есть 30 секунд, чтобы дать правильный ответ. В оценке участвуют
уравнения, то есть 8 . (6-3) . (-1), результат -24
баллов. Если в списке было 4 -го , следующее уравнение попадает в слот 4 -й ,
и т. Д. Если исходная команда выбрасывает 4 на кубиках, то команда 4 получает
уравнение, если исходная команда: 1) бежит вне времени, и результат
положительный 2) хочет отдать; или 3) хочет, но дает
неправильную оценку и результат положительный; иначе исходная команда получит
очков.Могут быть внесены любые другие правила или изменения. Подготовьте правила
и уравнения к уровню класса,
должно быть не только образовательным, но и увлекательным.
Примечание: - Учащиеся не должны спешить с мгновенными ответами.
Возможно, посчитайте 3 секунды, прежде чем дать возможность любому ученику ответить.
Вычитание целых чисел — ChiliMath
Шаги по вычитанию целых чисел
Примеры целочисленного вычитания
Практика с рабочими листами
Целочисленное умножение
Целочисленное деление 1.5 Почему ОТРИЦАТЕЛЬНО ВРЕМЯ ОТРИЦАТЕЛЬНО ПОЛОЖИТЕЛЬНО?
УМНОЖЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ НОМЕРОВ

 Снова поверните голову в положительную сторону и сделайте два шага назад. Теперь вы стоите на -2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Снова поверните голову в положительную сторону и сделайте два шага назад. Теперь вы стоите на -2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению. Два отрицания компенсируют и дают положительный результат как в математике, так и в речи.
Два отрицания компенсируют и дают положительный результат как в математике, так и в речи.
