РАЗЛОЖЕНИЕ ЧИСЛА на простые множители, таблица простых чисел
Разложение числа на простые множители – это часто встречающаяся задача, которую нужно уметь решать. Разложение на простые множители может потребоваться при нахождении НОД (наибольший общий делитель) и НОК (наименьшее общее кратное), а также при проверке, являются ли числа взаимно простыми.
Все числа можно разделить на два основных типа:
- Простое число – это число, которое делится только на само себя и на 1.
- Составное число – это число, которое имеет другие делители, кроме самого себя и 1.
Чтобы проверить, является ли число простым или составным, можно воспользоваться специальной таблицей простых чисел.
Таблица простых чисел
Для удобства вычислений все простые числа были собраны в таблицу. Ниже приведена таблица простых чисел из диапазона от 1 до 1000.
| 2 | 3 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | |
| 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 |
| 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 409 | 419 | 421 | 431 | 433 | |
| 439 | 443 | 449 | 457 | 461 | 463 | 467 | 479 | 487 | 491 | 499 | 503 |
| 509 | 521 | 523 | 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 | 739 | 743 |
| 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 | 887 | 907 | 911 |
| 919 | 929 | 937 | 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
Разложение на простые множители
Для разложения числа на простые множители можно использовать таблицу простых чисел и признаки делимости чисел. До тех пор, пока число не станет равно 1, нужно подбирать простое число, на которое делится текущее, и выполнять деление. Если не удалось подобрать ни одного множителя, не равного 1 и самому числу, то число простое. Рассмотрим, как это делается на примере.
Пример:
Разложить на простые множители число 63140.
Решение:
Чтобы не потерять множители, будем записывать их в столбик, как показано на картинке. Такое решение является достаточно компактным и удобным. Рассмотрим его подробнее.
Число 63140 четное, поэтому оно делится на 2:
Число 31570 четное, поэтому оно делится на 2:
Число 15785 нечетное, поэтому на 2 не делится. Сумма цифр числа
не делится на 3, поэтому число 15785 на 3 не делится. Зато оно заканчивается на 5, поэтому оно делится на 5:
Число 3157 заканчивается на 7, поэтому оно не делится на 5. Зато число 3157 делится на 7:
Число 451 больше на 7 не делится. Поэтому проверяем следующее простое число – 11: чтобы число 451 делилось на 11, нужно чтобы сумма цифр на нечетных местах была равна сумме цифр на четных местах:
Поэтому 451 делится на 11:
Число 41 является простым, поэтому следующий множитель равен 41.
Таким образом, число 63140 было разложено на множители:
63140 = 2 ⋅ 2 ⋅ 5 ⋅ 7 ⋅ 11 ⋅ 41
worksbase.ru
Простые множители — это… Что такое Простые множители?
Просто́е число́ — это натуральное число, которое имеет ровно 2 различных делителя (только 1 и самого себя). Все остальные числа, не равные единице, называются составными. Таким образом, все натуральные числа, за исключением единицы, разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел. В теории колец простым числам соответствуют неприводимые элементы.
Последовательность простых чисел начинается с
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, … (последовательность A000040 в OEIS, см. также список простых чисел)
Разложение натуральных чисел в произведение простых
Основная теорема арифметики утверждает, что каждое натуральное число, большее единицы (1), представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей. Таким образом, простые числа — элементарные «строительные блоки» натуральных чисел.
Представление натурального числа в виде произведения простых называется разложением на простые или факторизацией числа. На настоящий момент неизвестны полиномиальные алгоритмы факторизации чисел, хотя и не доказано, что таких алгоритмов не существует (здесь и далее речь идёт о полиномиальной зависимости времени работы алгоритма от логарифма проверяемого числа, то есть от количества его цифр). На предполагаемой вычислительной сложности задачи факторизации базируется криптосистема
Тесты простоты

Решето Эратосфена, решето Сундарама и решето Аткина дают простые способы нахождения начального списка простых чисел вплоть до некоторого значения.
Однако на практике вместо получения списка простых чисел зачастую требуется проверить, является ли данное число простым. Алгоритмы, решающие эту задачу, называются тестами простоты. Существует множество полиномиальных тестов простоты, но большинство их являются вероятностными (например, тест Миллера — Рабина) и используются для нужд криптографии. Только в 2002 году было доказано
Для некоторых классов чисел существуют специализированные эффективные тесты простоты. Например, для проверки на простоту чисел Мерсенна используется тест Люка — Лемера, а для проверки на простоту чисел Ферма — тест Пепина.
Сколько существует простых чисел?
Простых чисел бесконечно много. Самое старое известное доказательство этого факта было дано Евклидом в «Началах» (книга IX, утверждение 20). Его доказательство может быть кратко воспроизведено так:
- Представим, что количество простых чисел конечно. Перемножим их и прибавим единицу. Полученное число не делится ни на одно из конечного набора простых чисел, потому что остаток от деления на любое из них даёт единицу. Значит, число должно делиться на некоторое простое число, не включённое в этот набор.
Математики предлагали другие доказательства. Одно из них (приведённое Эйлером) показывает, что сумма всех чисел, обратных к простым, расходится.
Известная теорема о распределении простых чисел утверждает, что количество простых чисел меньших n, обозначаемое π(n), растёт как n / ln(n).
Наибольшее известное простое
Наибольшим известным простым числом по состоянию на сентябрь 2008 года является 243112609 − 1. Оно содержит 12 978 189 десятичных цифр и является простым числом Мерсенна (M43112609). Его нашли 23 августа 2008 года на математическом факультете университета UCLA в рамках проекта по распределённому поиску простых чисел Мерсенна 37156667, было найдено 6 сентября 2007 года участником проекта нем.
Числа Мерсенна выгодно отличаются от остальных наличием эффективного теста простоты: теста Люка — Лемера. Благодаря ему простые числа Мерсенна давно удерживают рекорд как самые большие известные простые.
За нахождение простого числа из более чем 108 десятичных цифр EFF назначила[2] награду в 150000 долларов США.
Некоторые свойства
- Если p — простое, и p делит ab, то p делит a или b. Доказательство этого факта было дано Евклидом и известно как лемма Евклида. Оно используется в доказательстве основной теоремы арифметики.
- Кольцо вычетов
 является полем тогда и только тогда, когда n — простое.
является полем тогда и только тогда, когда n — простое. - Характеристика каждого поля — это ноль или простое число.
- Если p — простое, а a — натуральное, то ap — a делится на p (малая теорема Ферма).
- Если G — конечная группа с pn элементов, то G содержит элемент порядка p.
- Если G — конечная группа, и pn — максимальная степень p, которая делит | G | , то G имеет подгруппу порядка pn, называемую силовской подгруппой, более того, количество силовских подгрупп равно pk + 1 для некоторого целого k (теоремы Силова).
- Натуральное p > 1 является простым тогда и только тогда, когда (p — 1)! + 1 делится на p (теорема Вильсона).
- Если n > 1 — натуральное, то существует простое p, такое, что n < p < 2n (постулат Бертрана).
- Ряд чисел, обратных к простым, расходится. Более того, при

- Любая арифметическая прогрессия вида a,a + q,a + 2q,a + 3q,…, где a,q > 1 — целые взаимно-простые числа, содержит бесконечно много простых чисел (Теорема Дирихле о простых числах в арифметической прогрессии).
- Всякое простое число, большее 3, представимо в виде 6k + 1, или в виде 6k − 1, где k — некоторое натуральное число.
- Если p > 3 — простое, то p2 − 1 кратно 24.
Открытые вопросы
До сих пор существует много открытых вопросов относительно простых чисел, наиболее известные из которых были перечислены Эдмундом Ландау на Пятом Международном математическом конгрессе[3]:
- Проблема Гольдбаха (первая проблема Ландау): доказать или опровергнуть, что каждое чётное число, большее двух, может быть представлено в виде суммы двух простых чисел, а каждое нечётное число, большее 5, может быть представлено в виде суммы трёх простых чисел.
- Вторая проблема Ландау: бесконечно ли множество «простых близнецов» — простых чисел, разность между которыми равна 2?
- Гипотеза Лежандра (третья проблема Ландау) верно ли, что между n2 и (n + 1)2 всегда найдётся простое число?
- Четвёртая проблема Ландау: бесконечно ли множество простых чисел вида n2 + 1?
Открытой проблемой является также существование бесконечного количества простых чисел во многих целочисленных последовательностях, включая числа Фибоначчи, числа Ферма и т. д.
Приложения
Большие простые числа (порядка 10300) используются в криптографии с открытым ключом. Простые числа также используются в хеш-таблицах и для генерации псевдослучайных чисел (в частности, в ГПСЧ Вихрь Мерсенна).
Вариации и обобщения
Литература
См. также
Примечания
Ссылки
Wikimedia Foundation. 2010.
dic.academic.ru
Разложение числа на простые множители
Простой множитель – это множитель, который представляет собой простое число.

Любое составное число можно представить в виде произведения простых чисел.
Пример. Представим в виде произведения простых множителей числа 4, 6 и 8:
4 = 2 · 2
6 = 2 · 3
8 = 2 · 2 · 2
Правые части полученных равенств называются разложением на простые множители.

Разложение на простые множители – это представление составного числа в виде произведения простых множителей.
Разложить составное число на простые множители – значит представить это число в виде произведения простых множителей.
Простые множители в разложении числа могут повторяться. Повторяющиеся простые множители можно записывать более компактно – в виде степени.
Пример.
24 = 2 · 2 · 2 · 3 = 23 · 3
Примечание. Простые множители обычно записывают в порядке их возрастания.
Как разложить число на простые множители
Последовательность действий при разложении числа на простые множители:
- Проверяем по таблице простых чисел, не является ли данное число простым.
- Если нет, то последовательно подбираем самое маленькое простое число из таблицы простых чисел, на которое данное число делится без остатка, и выполняем деление.
- Проверяем по таблице простых чисел, не является ли полученное частное простым числом.
- Если нет, то последовательно подбираем самое маленькое простое число из таблицы простых чисел, на которое полученное частное делится нацело, и выполняем деление.
- Повторяем пункты 3 и 4 до тех пор, пока в частном не получится единица.
Пример. Разложите число 102 на простые множители.
Решение:
Начинаем поиск наименьшего простого делителя числа 102. Для этого последовательно подбираем самое маленькое простое число из таблицы простых чисел, на которое 102 разделится без остатка. Берём число 2 и пробуем разделить на него 102, получаем:
102 : 2 = 51.
Число 102 разделилось на 2 без остатка, поэтому 2 – первый найденный простой множитель. Так как делимое равно делителю, умноженному на частное, то можно написать:
102 = 2 · 51
Переходим к следующему шагу. Проверяем по таблице простых чисел, не является ли полученное частное простым числом. Число 51 составное. Начиная с числа 2, подбираем из таблицы простых чисел наименьший простой делитель числа 51. Число 51 не делится нацело на 2. Переходим к следующему числу из таблицы простых чисел (к числу 3) и пробуем разделить на него 51, получаем:
51 : 3 = 17
Число 51 разделилось на 3, поэтому 3 – второй найденный простой множитель. Теперь мы можем и число 51 представить в виде произведения. Этот процесс можно записать так:
102 = 2 · 51 = 2 · 3 · 17
Проверяем по таблице простых чисел, не является ли полученное частное простым числом. Число 17 простое. Значит наименьшим простым числом, на которое делится 17, будет само это число:
17 : 17 = 1
Так как в частном у нас получилась единица, то разложение закончено. Таким образом, разложение числа 102 на простые множители имеет вид:
102 = 2 · 3 · 17
Ответ: 102 = 2 · 3 · 17.
В арифметике имеется ещё другая форма записи, облегчающая процесс разложения составных чисел. Она состоит в том, что весь процесс разложения записывают столбиком (в две колонки, разделённых вертикальной чертой). Слева от вертикальной черты, сверху вниз, записывают последовательно: данное составное число, затем получающиеся частные, а справа от черты – соответствующие наименьшие простые делители.
Пример. Разложить на простые множители число 120.
Решение:
Пишем число 120 и справа от него проводим вертикальную черту:

Справа от черты записываем самый маленький простой делитель числа 120:

Выполняем деление и получившееся частное (60) записываем под данным числом:

Подбираем наименьший простой делитель для 60, записываем его справа от вертикальной черты под предыдущим делителем и выполняем деление. Продолжаем процесс до тех пор, пока в частном не получится единица:

В частном у нас получилась единица, значит разложение закончено. После разложения в столбик множители следует выписать в строчку:
120 = 23 · 3 · 5.
Ответ: 120 = 23 · 3 · 5.
Составное число разлагается на простые множители единственным образом.
Это значит, что если, например, число 20 разложилось на две двойки и одну пятёрку, то оно и всегда будет так разлагаться независимо от того, начнём ли мы разложение с малых множителей или с больших. Принято начинать разложение с малых множителей, т. е. с двоек, троек и т. д.
| О сайте: | конспекты по математике, русскому языку и химии |
| Связь: | [email protected] |
| Новое на сайте | © 2018 – 2019 | |
izamorfix.ru
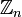 является полем тогда и только тогда, когда n — простое.
является полем тогда и только тогда, когда n — простое.