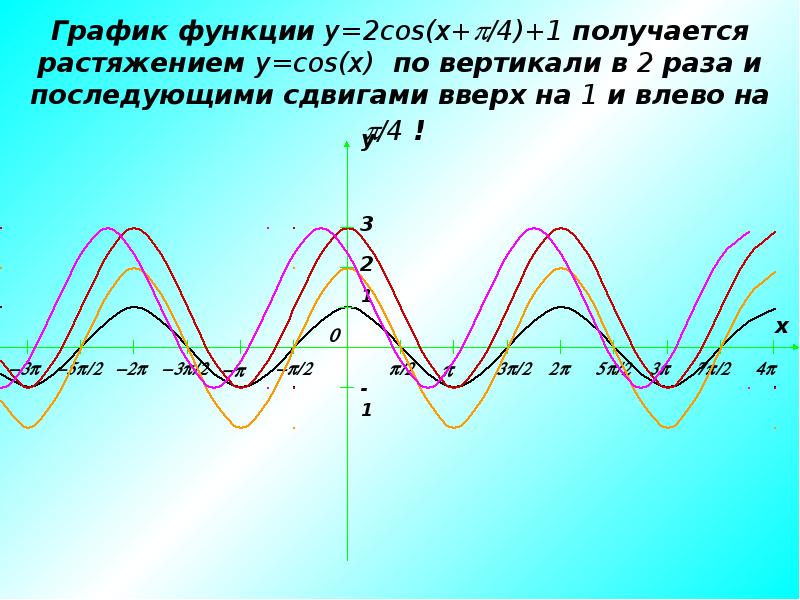
cos модуль x график
Вы искали cos модуль x график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и cos модуль x модуль, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «cos модуль x график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как cos модуль x график,cos модуль x модуль,y cos модуль x,y cosx модуль,y модуль cos x,y модуль cos модуль x,y модуль cosx график,график cos модуль x,график модуль cos x,график модуль y cosx,модуль cos x график,модуль y cos x.
Где можно решить любую задачу по математике, а так же cos модуль x график Онлайн?
Решить задачу cos модуль x график вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Cos x п 2 график. Графики тригонометрических функций кратных углов
Урок и презентация на тему: «Функция y=cos(x).
 Определение и график функции»
Определение и график функции»Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения : sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.

График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1]. Это также хорошо видно из графика.

- Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π) 2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π) 2 + 1 (см. рисунок).
y=(x — 2π) 2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.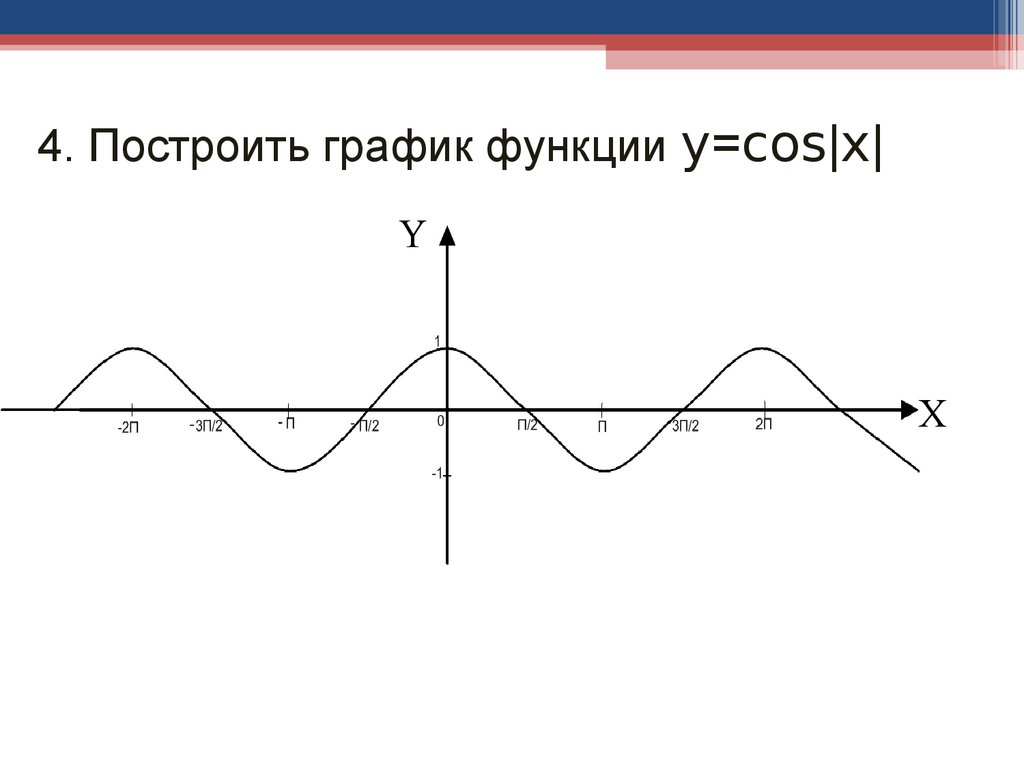
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.2) Решить уравнение: cos(x)= — (x – π) 2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке .
6) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [- π/6; 5π/4].
«Графики функций и их свойства» — y = ctg x. 4) Ограниченность функции. 3) Нечётная функция. (График функции симметричен относительно начала координат). y = tg x. 7) Функция непрерывна на любом интервале вида (?k; ? + ?k). Функция y = tg x непрерывна на любом интервале вида. 4) Функция убывает на любом интервале вида (?k; ? + ?k). График функции y = tg x называется тангенсоидой.
График функции y = tg x называется тангенсоидой.
«График функции Y X» — Шаблон параболы у = х2. Чтобы увидеть графики, щелкни мышкой. Пример 2. Построим график функции y = x2 + 1, опираясь на график функции y=x2 (щелчок мышкой). Пример 3. Докажем, что графиком функции у = х2 + 6х + 8 является парабола, и построим график. График функции y=(x — m)2 является параболой с вершиной в точке (m; 0).
«Математика графики» — Как можно строить графики? Наиболее естественно функциональные зависимости отражаются с помощью графиков. Интересное применение: рисунки,… Зачем мы изучаем графики? Графики элементарных функций. Что вы можете нарисовать с помощью графиков? Рассматриваем применение графиков в учебных предметах: математике, физике,…
«Построение графиков с помощью производной» — Обобщение. Построить эскиз графика функции. Найти асимптоты графика функции. График производной функции. Дополнительное задание. Исследовать функцию. Назвать промежутки убывания функции. Самостоятельная работа учащихся.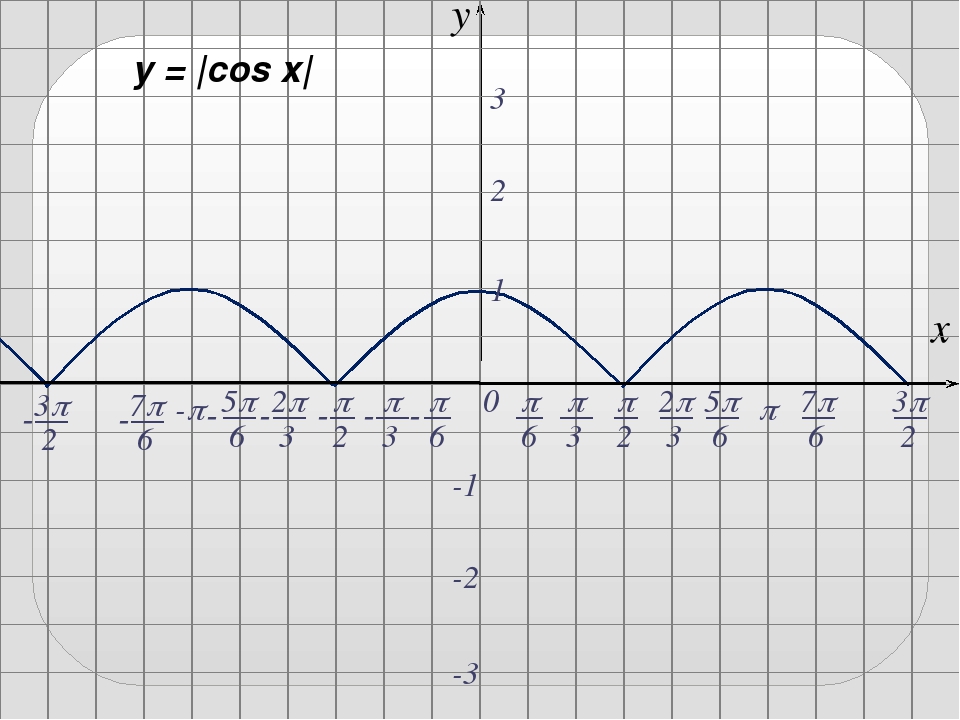 Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
Расширить знания. Урок закрепления изученного материала. Оцените свои умения. Точки максимума функции.
«Графики с модулем» — Отобрази «нижнюю» часть в верхнюю полуплоскость. Модуль действительного числа. Свойства функции y = |x|. |x|. Числа. Алгоритм построения графика функции. Алгоритм построения. Функция y= lхl. Свойства. Самостоятельная работа. Нули функции. Советы великих. Решение самостоятельной работы.
«Уравнение касательной» — Уравнение касательной. Уравнение нормали. Если,то и кривые пересекаются под прямым углом. Условия параллельности и перпендикулярности двух прямых. Угол между графиками функций. Уравнение касательной к графику функции в точке. Пусть функция дифференцируема в точке. Пусть прямые заданы уравнениями и.
Всего в теме 25 презентаций
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Графический способ решения уравнений с модулем
1. Тема урока
Графический способрешения уравнений с модулем
Тема урока
2. Задай функцию формулой
3. Задай функцию формулой
4. Задай функцию формулой
5. Задай функцию формулой
6. Задай функцию формулой
7. Задай функцию формулой
8. Задай функцию формулой
9. Задай функцию формулой
10. Задай функцию формулой
Выполнила ученица 10 «А»Засыпалова Анна
17. Правило построения графика функции y=f(|x|).
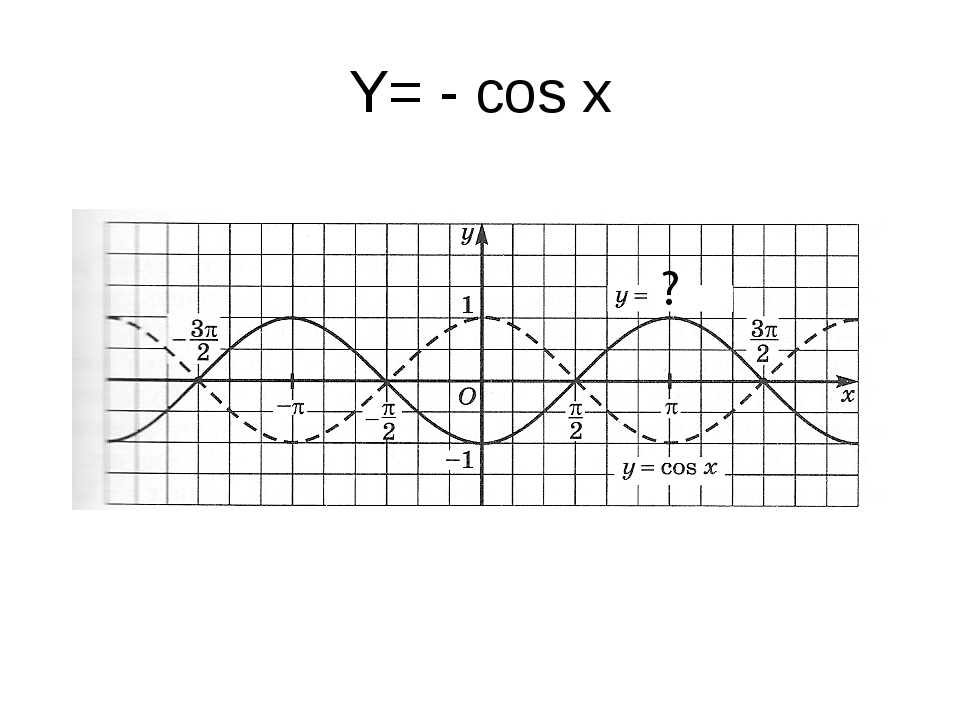 : 1. Построим график функции y=f(x), для х≥0
: 1. Построим график функции y=f(x), для х≥02. Достроим левую часть графика, симметричную
построенной правой части относительно оси
ординат
18. 1.Построить график функции y=|x|
1.Построить график функцииПостроение:
1).
х
у
0
0
2
2
Строим график функции
y=x, х ≥0
2)Симметрично
отображаем
построенную часть
графика относительно
оси оу.
.
y=|x|
Y
y=|x|
X
20. 2. Построить график функции Y=|x|²-4|x|+3
2. Построить график функции+3
1)Строим
Y=|x|²-4|x|
Построение.
y=x²-4x+3,
х≥0
Y
Y=|x|²-4|x|+3
а)Хверш= -в/2а=-4/2=2
Уверш=2²-4·2+3=-1
(2;-1)-вершина параболы
б)Нули функции (точки пересечения с ох)
x²-4x+3=0
х1=1
х2=3
(1;0) (3;0) — точки пересечения графика с осью ох
в)Если х=0, то у=3
(0;3)
2).Симметрично отображаем построенную часть
графика относительно оси оу
X
21.
 3. Построить график функции у = sin|x|
3. Построить график функции у = sin|x| Y
•X
22. 4. Построить график функции y=cos|x|
YX
23. 5. Построить график функции y= cos|x|+2
5. Построить график функции y= cos|x|+2
Y
X
24. 6. Построить график функции у=3|х|+2
Построение.1)Cтроим график функции
у=3х+2, х≥0
х
у
0
2
Y
1
5
X
2).Симметрично
отобразим построенную
часть графика
относительно оси ох.
Y
у=3|х|+2
X
Выполнила: Кузьмина Валерия
ученица 10 «а» класса
27. Правило Построения графика функции y=|f(x)|
1.Построить график y=f(x)2.Сохранить без изменения части графика
y=f(x), расположенные выше оси OX.
3.Отобразить симметрично оси OX части
графика y=f(x), расположенные ниже
оси OX.
y
2
-1
0
x
30. 2) Построить график функции Y=|X²-4x+3|. Построение.
y0
1
3
x
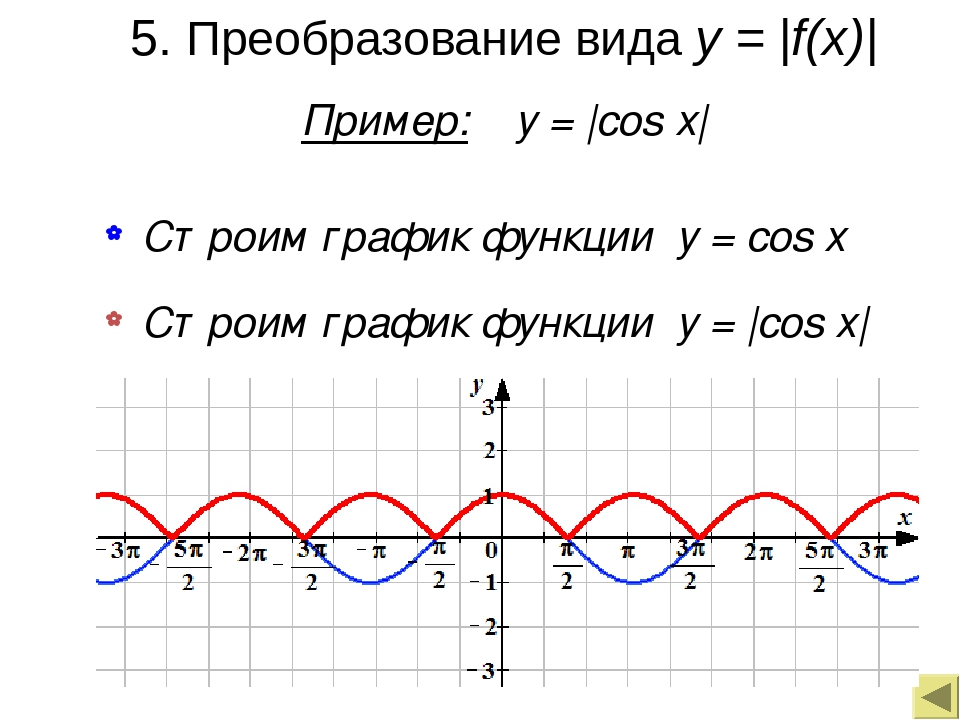
31. 3) Построить график функции y=|cosx| Построение.
 3) Построить график функции y=|
3) Построить график функции y=|cosx|
Построение.
y
1
0
-1
x
32. 4)Построить график функции y=|sinx|-4 Построение.
y1
0
-1
-4
x
33. Решение уравнений, содержащих модуль
Решениеуравнений,
содержащих
Способы решения уравнений,
содержащих модуль
Использование
определения модуля
Графический способ
Метод введения
новой переменной
35. Графический способ
|х-2|=у
х
1. у =|х-2|
2. у =
0
1 2
4
х
Ответ: 1; 4.
х
36. Задания командам
Реши уравнение графическим способома) |x-1|=2;
б) x2 = |x|;
в)sin|x| = — х2;
г) |x-1|= |x|-1;
д) 3|x|=4 — х2 (МФТИ, 2000г)
е)|x2-3x|=2x-4 (МГУ, 2000г)
41. Итоги
№/Команда
1
команда
2
команда
1
2
3
4
5
6
Устная
работа
итог
Слово «модуль» произошло от латинского слова «modulus», что в переводе
означает «мера».
 Это многозначное слово(омоним), которое имеет множество
Это многозначное слово(омоним), которое имеет множествозначений и применяется не только в математике, но и в архитектуре, физике,
технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного
архитектурного сооружения и служащая для выражения кратных соотношений его
составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий
универсального значения и служащий для обозначения различных коэффициентов
и величин, например модуль зацепления, модуль упругости и .т.п.
Модуль объемного сжатия( в физике)-отношение нормального напряжения в
материале к относительному удлинению.
44. Модуль числа
Абсолютная величина или модуль,обозначается |x|, |x-1| , |a|
45. Знак модуля
Считают, что термин предложилиспользовать
Котс, ученик Ньютона. Лейбниц тоже
использовал
эту функцию, которую называл модулем и
обозначал: mol x.

Общепринятое обозначение
абсолютной величины введено в 1841
году Вейерштрассом.
Для комплексных чисел это понятие ввели
Коши и Арган в начале XIX века.
Математики шутят.
Трехмерная кубическая линейка
Калькулятор для умных
|
cos x, функция косинус х,
Дата публикации: .
Урок и презентация на тему: «Функция y=cos(x). Определение и график функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать: Функция y=cos(x) (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9–11 классы
Что будем изучать:
1. Определение.
2. График функции.
3. Свойства функции Y=cos(X).
4. Примеры.
Определение функции косинуса у=cos(x)
Ребята, мы уже познакомились с функцией Y=sin(X).
Давайте вспомним одну из формул привидения: sin(X + π/2) = cos(X).
Благодаря этой формуле, мы можем утверждать, что функции sin(X + π/2) и cos(X) тождественны, и их графики функций совпадают.
График функции sin(X + π/2) получается из графика функции sin(X) параллельным переносом на π/2 единиц влево.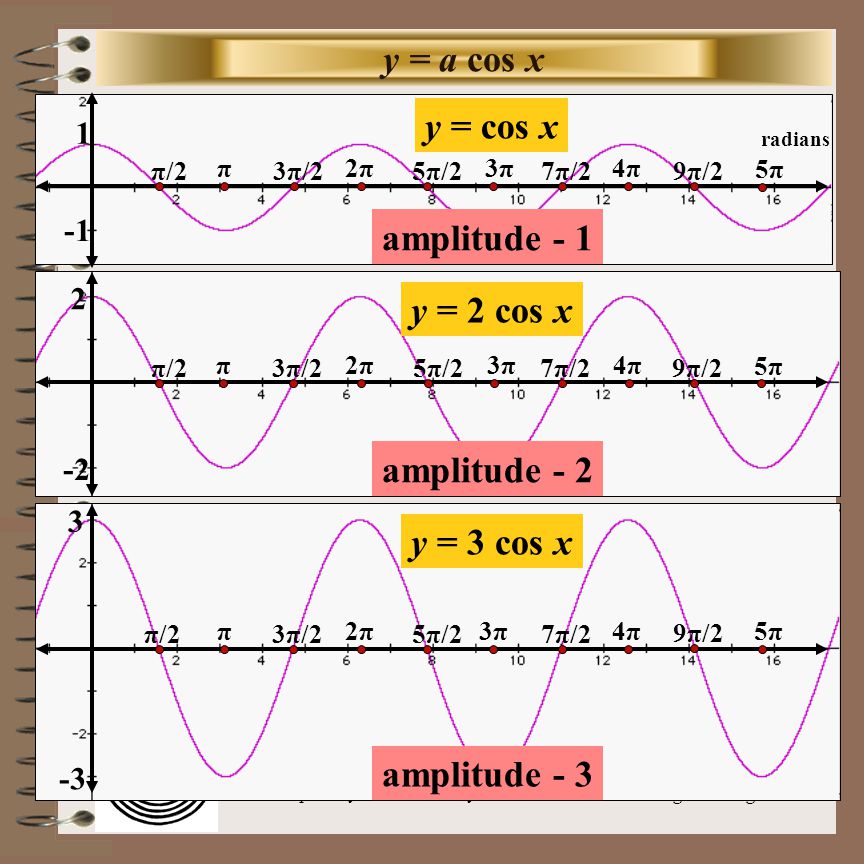 Это и будет график функции Y=cos(X).
Это и будет график функции Y=cos(X).
График функции Y=cos(X) так же называют синусоидой.
Свойства функции cos(x)
- Запишем свойства нашей функции:
- Область определения – множество действительных чисел.
- Функция четная. Давайте вспомним определение четной функции. Функция называется четной, если выполняется равенство y(-x)=y(x). Как мы помним из формул привидения: cos(-x)=-cos(x), определение выполнилось, тогда косинус – четная функция.
- Функция Y=cos(X) убывает на отрезке [0; π] и возрастает на отрезке [π; 2π]. В этом мы можем убедиться на графике нашей функции.
- Функция Y=cos(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ cos(X) ≤ 1 - Наименьшее значение функции равно -1 (при х = π + 2πk). Наибольшее значение функции равно 1 (при х = 2πk).
- Функция Y=cos(X) является непрерывной функцией. Посмотрим на график и убедимся, что у нашей функции нет разрывов, это и означает непрерывность.
- Область значений отрезок [- 1; 1].
 Это также хорошо видно из графика.
Это также хорошо видно из графика. - Функция Y=cos(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения через некоторые промежутки.
Примеры с функцией cos(x)
1. Решить уравнение cos(X)=(x — 2π)2 + 1
Решение: Построим 2 графика функции: y=cos(x) и y=(x — 2π)2 + 1 (см. рисунок).
y=(x — 2π)2 + 1 — это парабола, смещенная вправо на 2π и вверх на 1. Наши графики пересекаются в одной точке А(2π;1), это и есть ответ: x = 2π.
2. Построить график функции Y=cos(X) при х ≤ 0 и Y=sin(X) при x ≥ 0
Решение: Чтобы построить требуемый график, давайте построим два графика функции по «кусочкам». Первый кусочек: y=cos(x) при х ≤ 0. Второй кусочек: y=sin(x)
при x ≥ 0. Изобразим оба «кусочка» на одном
графике.
3. Найти наибольшее и наименьшее значение функции Y=cos(X) на отрезке [π; 7π/4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π/4]. На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
На графике видно, что наибольшие и наименьшие значения достигаются на концах отрезка: в точках π и 7π/4 соответственно.
Ответ: cos(π) = -1 – наименьшее значение, cos(7π/4) = наибольшее значение.
4. Построить график функции y=cos(π/3 — x) + 1
Решение: cos(-x)= cos(x), тогда искомый график получится путем переноса графика функции y=cos(x) на π/3 единиц вправо и 1 единицу вверх.
Задачи для самостоятельного решения
1)Решить уравнение: cos(x)= x – π/2.
2) Решить уравнение: cos(x)= — (x – π)2 — 1.
3) Построить график функции y=cos(π/4 + x) — 2.
4) Построить график функции y=cos(-2π/3 + x) + 1.
5) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [0; 5π/3].
6) Найти наибольшее и наименьшее значение функции y=cos(x) на отрезке [- π/6; 5π/4].
Функция у = cos x и её график
Сегодня на уроке мы с вами поговорим о функции . Рассмотрим график функции , а также основные свойства этой функции.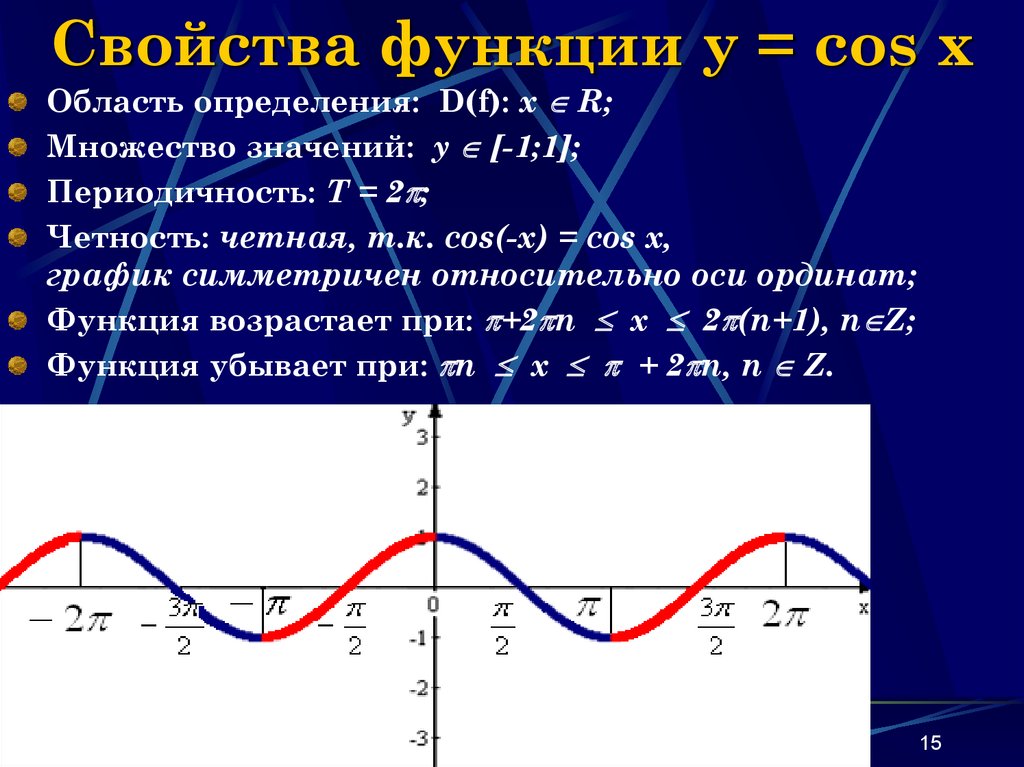
Прежде чем приступить к рассмотрению новой темы, давайте напомним, что функция определена на всей числовой прямой, а множеством её значений является отрезок . Функция ограничена и её график расположен в полосе между прямыми и .
Также мы знаем, что функция периодическая с периодом , а значит, достаточно построить её график на промежутке длиной . Например, на отрезке .
На предыдущем уроке мы с вами выяснили, что функция является чётной. Известно, что график чётной функции симметричен относительно оси ординат.
Тогда для построения графика на отрезке нам достаточно построить его на отрезке , а затем симметрично отразить относительно оси Oy.
Прежде чем мы перейдём к построению графика, покажем, что функция убывает на отрезке .
Давайте на единичной окружности с центром в начале координат отметим точку . Тогда при повороте точки вокруг начала координат против часовой стрелки на угол получим точку . Абсцисса этой точки – .
При повороте точки вокруг начала координат против часовой стрелки на угол получим точку . Абсцисса этой точки – .
Абсцисса этой точки – .
Обратите внимание, что при повороте точки вокруг начала координат против часовой стрелки на угол от до абсцисса точки, то есть , уменьшается от до . Поэтому если , то . Это значит, что функция убывает на отрезке .
Теперь давайте найдём координаты некоторых точек графика функции и заполним таблицу значений функции.
Используя свойство убывания функции и отметив полученные точки на координатной плоскости, построим график функции на отрезке .
Так как функция игрек равно косинус икс является чётной, то мы можем отразить построенный на отрезке график симметрично относительно оси Oy. В результате получим график этой функции на отрезке .
Длина этого отрезка равна , то есть равна периоду функции. А значит, мы можем распространить график по всей числовой прямой с помощью сдвигов на , и так далее вправо и на , и так далее влево, то есть на , .
Получается, что мы геометрически построили график функции на всей числовой прямой, начав с построения его части на отрезке .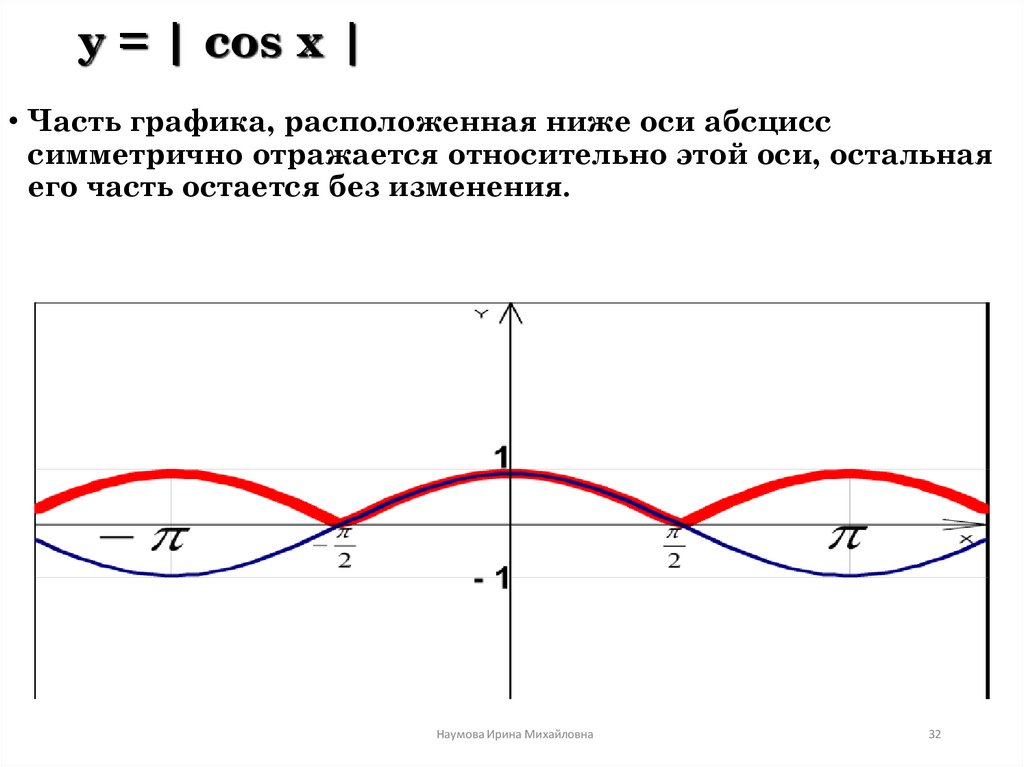
Тогда свойства рассматриваемой функции можно получить, опираясь на её свойства на отрезке .
Так, например, мы выяснили, что функция убывает на отрезке и является чётной, а значит, на отрезке она возрастает.
А сейчас давайте поговорим об основных свойствах функции .
Вы уже знаете, что область определения функции – множество всех действительных чисел.
Множество значений – отрезок .
Функция является чётной, то есть .
График функции симметричен относительно оси ординат.
Функция периодическая с периодом .
Функция принимает значение, равное , при , .
Наибольшее значение функция принимает при .
Наименьшее значение функция принимает при ,.
при , .
при , .
Возрастает функция на отрезках , .
Убывает функция на отрезках , .
А сейчас давайте выполним несколько заданий.
Задание первое. Найдите все корни уравнения , принадлежащие отрезку .
Решение.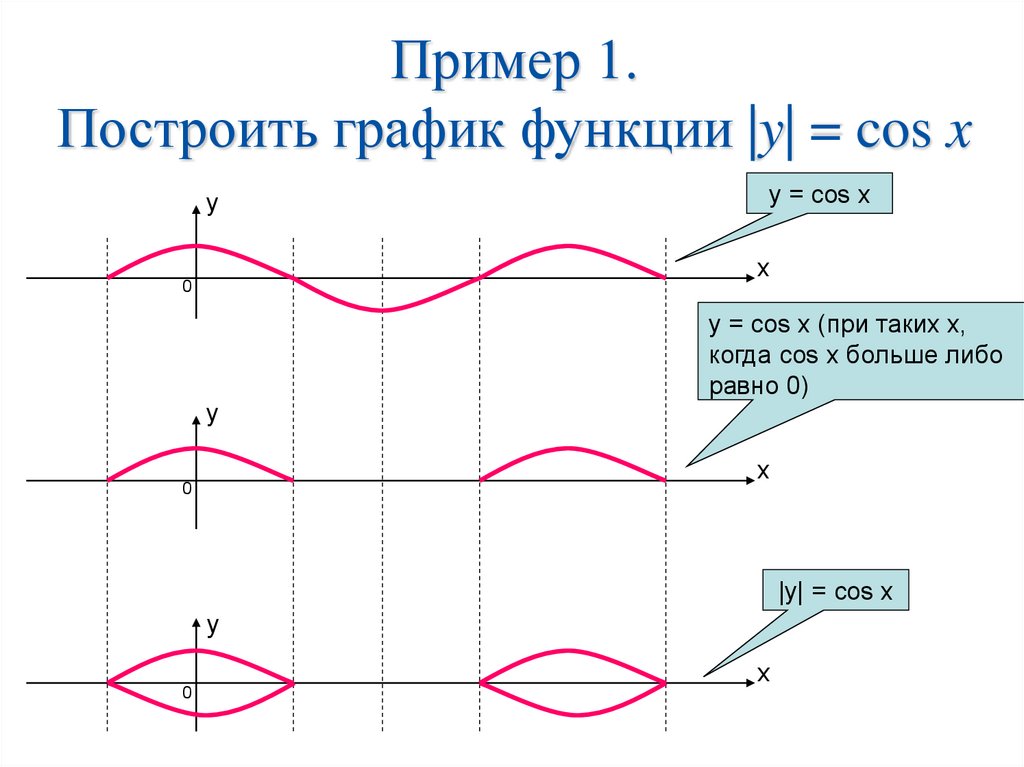
Задание второе. Найдите все решения неравенства , принадлежащие отрезку .
Решение.
графиков функции синуса и косинуса
Результаты обучения
- Определите амплитуду, период, фазовый сдвиг и вертикальный сдвиг синусоидального или косинусоидального графика по его уравнению.
- График изменения y = cos x и y = sin x.
- Определите формулу функции, которая будет иметь заданный синусоидальный график.
- Определение функций, моделирующих круговое и периодическое движение.
График изменения y = sin (x) и y = cos (x)
Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами x и y точки на единичной окружности.Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции . Мы можем создать таблицу значений и использовать их для построения графика.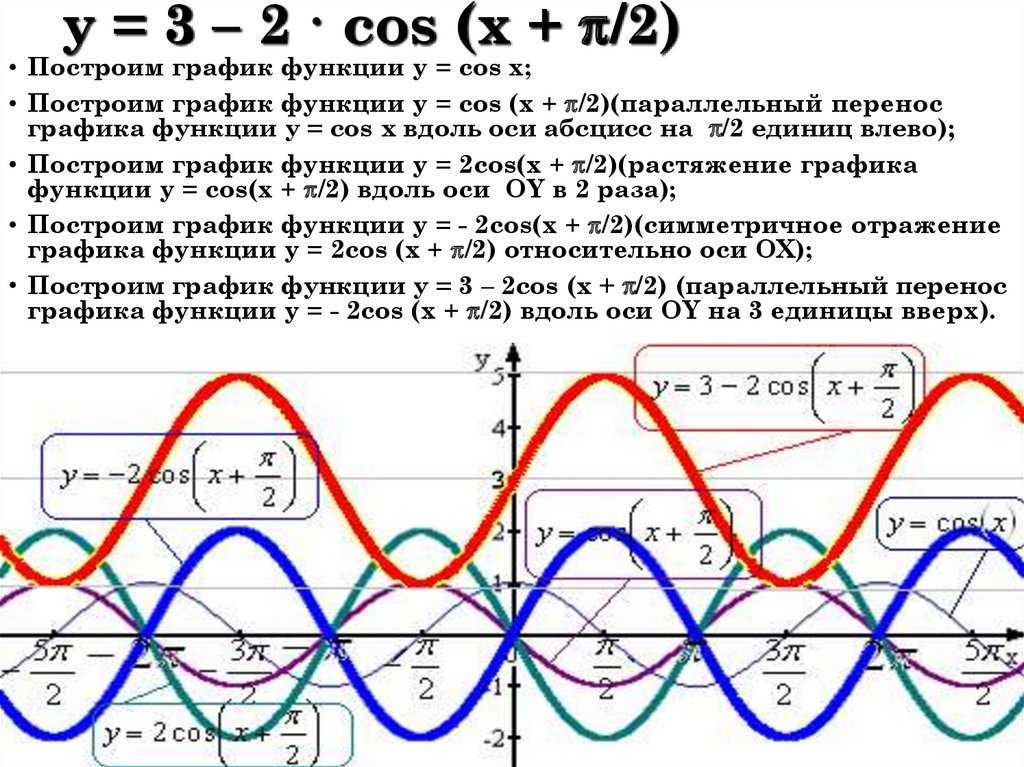 В таблице ниже перечислены некоторые значения синусоидальной функции на единичной окружности.
В таблице ниже перечислены некоторые значения синусоидальной функции на единичной окружности.
| x | 0 | [латекс] \ frac {\ pi} {6} [/ латекс] | [латекс] \ frac {\ pi} {4} [/ латекс] | [латекс] \ frac {\ pi} {3} [/ латекс] | [латекс] \ frac {\ pi} {2} [/ латекс] | [латекс] \ frac {2 \ pi} {3} [/ латекс] | [латекс] \ frac {3 \ pi} {4} [/ латекс] | [латекс] \ frac {5 \ pi} {6} [/ латекс] | [латекс] \ pi [/ латекс] |
| [латекс] \ sin (x) [/ латекс] | 0 | [латекс] \ frac {1} {2} [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} [/ латекс] | [латекс] \ frac {\ sqrt {3}} {2} [/ латекс] | 1 | [латекс] \ frac {\ sqrt {3}} {2} [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} [/ латекс] | [латекс] \ frac {1} {2} [/ латекс] | 0 |
Построение точек из таблицы и продолжение по оси x дает форму синусоидальной функции. См. Рисунок 2.
См. Рисунок 2.
Рисунок 2. Синусоидальная функция
Обратите внимание, что значения синуса положительны между 0 и π, что соответствует значениям функции синуса в квадрантах I и II на единичной окружности, а значения синуса отрицательны между π и 2π, которые соответствуют значениям функция синуса в квадрантах III и IV на единичной окружности. См. Рисунок 3.
Рисунок 3. График значений синусоидальной функции
Теперь давайте аналогичным образом посмотрим на функцию косинуса .Опять же, мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения функции косинуса на единичной окружности.
| x | 0 | [латекс] \ frac {\ pi} {6} [/ латекс] | [латекс] \ frac {\ pi} {4} [/ латекс] | [латекс] \ frac {\ pi} {3} [/ латекс] | [латекс] \ frac {\ pi} {2} [/ латекс] | [латекс] \ frac {2 \ pi} {3} [/ латекс] | [латекс] \ frac {3 \ pi} {4} [/ латекс] | [латекс] \ frac {5 \ pi} {6} [/ латекс] | [латекс] \ pi [/ латекс] |
| [латекс] \ cos (x) [/ латекс] | 1 | [латекс] \ frac {\ sqrt {3}} {2} [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} [/ латекс] | [латекс] \ frac {1} {2} [/ латекс] | 0 | [латекс] — \ frac {1} {2} [/ латекс] | [латекс] — \ frac {\ sqrt {2}} {2} [/ латекс] | [латекс] — \ frac {\ sqrt {3}} {2} [/ латекс] | -1 |
Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса, как показано на рисунке 4.
Рисунок 4. Косинусная функция
Поскольку мы можем вычислять синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [-1,1].
На обоих графиках форма графика повторяется после 2π, что означает, что функции являются периодическими с периодом [латекс] 2π [/ латекс].Периодическая функция — это функция, для которой конкретный горизонтальный сдвиг , P приводит к функции, равной исходной функции: [latex] f (x + P) = f (x) [/ latex] для все значения x в домене f . Когда это происходит, мы называем наименьший такой горизонтальный сдвиг с [latex] P> 0 [/ latex] периодом функции. На рисунке 5 показаны несколько периодов функций синуса и косинуса.
Рисунок 5
Еще раз взглянув на функции синуса и косинуса в области с центром на оси y , можно выявить симметрии._v_y=mf(x)_10.9.jpg) Как мы можем видеть на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомните из «Других тригонометрических функций», что мы определили с помощью единичного круга, что синусоидальная функция является нечетной функцией, потому что [latex] \ sin (−x) = — \ sin x [/ latex]. Теперь мы можем ясно видеть это свойство на графике.
Как мы можем видеть на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомните из «Других тригонометрических функций», что мы определили с помощью единичного круга, что синусоидальная функция является нечетной функцией, потому что [latex] \ sin (−x) = — \ sin x [/ latex]. Теперь мы можем ясно видеть это свойство на графике.
Рисунок 6. Нечетная симметрия синусоидальной функции
На рисунке 7 показано, что функция косинуса симметрична относительно оси y . Опять же, мы определили, что функция косинуса является четной функцией.Теперь из графика видно, что [latex] \ cos (−x) = \ cos x [/ latex].
Рисунок 7. Четная симметрия функции косинуса
Общее примечание: Характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько отличительных характеристик:
- Это периодические функции с периодом 2π.
- Область каждой функции — [latex] \ left (- \ infty, \ infty \ right) [/ latex], а диапазон — [latex] \ left [-1,1 \ right] [/ latex].

- График [latex] y = \ sin x [/ latex] симметричен относительно начала координат, потому что это нечетная функция.
- График [latex] y = \ cos x [/ latex] симметричен относительно оси y , потому что это четная функция.
Исследование синусоидальных функций
Как мы видим, функции синуса и косинуса имеют постоянный период и диапазон. Если мы посмотрим на океанские волны или рябь на пруду, мы увидим, что они напоминают функции синуса или косинуса. Однако они не обязательно идентичны.Некоторые из них выше или длиннее других. Функция, которая имеет ту же общую форму, что и функция синуса или косинуса , известна как синусоидальная функция . Общие формы синусоидальных функций:
[латекс] y = A \ sin (Bx-C) + D [/ латекс]
и
[латекс] y = A \ cos (Bx-C) + D [/ латекс]
Определение периода синусоидальной функции
Рассматривая формы синусоидальных функций, мы можем видеть, что они являются преобразованиями функций синуса и косинуса.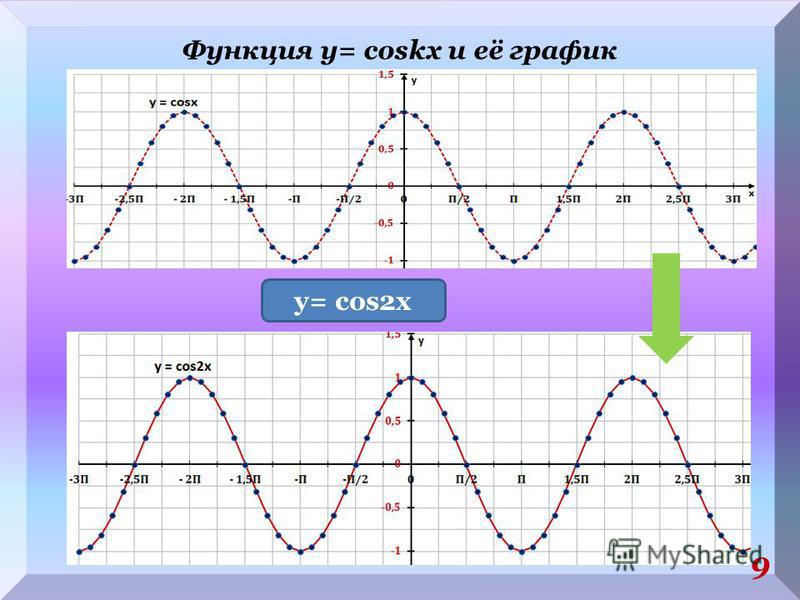 Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
В общей формуле B связано с периодом соотношением [латекс] P = \ frac {2π} {| B |} [/ latex]. Если [латекс] | B | > 1 [/ latex], то период меньше [latex] 2π [/ latex] и функция подвергается горизонтальному сжатию, тогда как если [latex] | B | <1 [/ latex], то период больше, чем [latex] 2π [/ latex], и функция претерпевает горизонтальное растяжение. Например, [латекс] f (x) = \ sin (x), B = 1 [/ latex], поэтому период равен [latex] 2π [/ latex], который мы знали.Если [latex] f (x) = \ sin (2x) [/ latex], то [latex] B = 2 [/ latex], поэтому период равен [latex] π [/ latex] и график сжимается. Если [латекс] f (x) = \ sin \ left (\ frac {x} {2} \ right) [/ latex], то [latex] B = \ frac {1} {2} [/ latex], поэтому период [латекс] 4π [/ латекс] и график растянут. Обратите внимание на рис. 8, как период косвенно связан с [latex] | B | [/ latex].
Рисунок 8
Общее примечание: период синусоидальных функций
Если положить C = 0 и D = 0 в уравнениях общего вида функций синуса и косинуса, мы получим формы
[латекс] y = A \ sin \ left (Bx \ right) [/ латекс]
[латекс] y = A \ cos \ left (Bx \ right) [/ латекс]
Период [латекс] \ frac {2π} {| B |} [/ латекс].
Пример 1: Определение периода функции синуса или косинуса
Определите период функции [latex] f (x) = \ sin \ left (\ frac {π} {6} x \ right) [/ latex].
Показать решениеНачнем с сравнения уравнения с общей формой [латекс] y = A \ sin (Bx) [/ latex].
В данном уравнении [латекс] B = \ frac {π} {6} [/ latex], поэтому период будет
[латекс] \ begin {align} P & = \ frac {\ frac {2} {\ pi}} {| B |} \\ & = \ frac {2 \ pi} {\ frac {x} {6}} \\ & = 2 \ pi \ times \ frac {6} {\ pi} \\ & = 12 \ end {align} [/ latex]
Попробуйте
Определите период функции [latex] g (x) = \ cos \ left (\ frac {x} {3} \ right) [/ latex].
Определение амплитуды
Возвращаясь к общей формуле синусоидальной функции, мы проанализировали, как переменная B связана с периодом. Теперь обратимся к переменной A , чтобы мы могли проанализировать, как она связана с амплитудой , или наибольшим расстоянием от покоя. A представляет коэффициент вертикального растяжения и его абсолютное значение | A | это амплитуда. Локальные максимумы будут на расстоянии | A | над вертикальной средней линией графика, которая представляет собой линию x = D ; поскольку D = 0 в этом случае, средняя линия — это ось x .Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | A | > 1 функция растягивается. Например, амплитуда [латекса] f (x) = 4 \ sin \ left (x \ right) [/ latex] в два раза больше амплитуды
A представляет коэффициент вертикального растяжения и его абсолютное значение | A | это амплитуда. Локальные максимумы будут на расстоянии | A | над вертикальной средней линией графика, которая представляет собой линию x = D ; поскольку D = 0 в этом случае, средняя линия — это ось x .Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | A | > 1 функция растягивается. Например, амплитуда [латекса] f (x) = 4 \ sin \ left (x \ right) [/ latex] в два раза больше амплитуды
[латекс] f (x) = 2 \ sin \ left (x \ right) [/ латекс]
Если [латекс] | A | <1 [/ latex], функция сжата. На рисунке 9 сравниваются несколько синусоидальных функций с разными амплитудами.
Рисунок 9
Общее примечание: амплитуда синусоидальных функций
Если положить C = 0 и D = 0 в уравнениях общего вида функций синуса и косинуса, мы получим формы
[латекс] y = A \ sin (Bx) [/ latex] и [латекс] y = A \ cos (Bx) [/ latex]
Амплитуда равна A, а высота по вертикали от средней линии равна | A |. Кроме того, обратите внимание, что в примере
Кроме того, обратите внимание, что в примере
[латекс] | A | = \ text {амплитуда} = \ frac {1} {2} | \ text {maximum} — \ text {minimum} | [/ latex]
Пример 2: Определение амплитуды функции синуса или косинуса
Какова амплитуда синусоидальной функции [латекс] f (x) = — 4 \ sin (x) [/ latex]? Функция растягивается или сжимается по вертикали?
Показать решениеДавайте начнем с сравнения функции с упрощенной формой [latex] y = A \ sin (Bx) [/ latex].
В данной функции A = −4, поэтому амплитуда равна | A | = | −4 | = 4.Функция растянута.
Анализ решения
Отрицательное значение A приводит к отражению по оси x синусоидальной функции , как показано на рисунке 10.
Рисунок 10
Попробуйте
Какова амплитуда синусоидальной функции [латекс] f (x) = 12 \ sin (x) [/ latex]? Функция растягивается или сжимается по вертикали?
Показать решение[латекс] \ frac {1} {2} [/ latex] сжатый
Анализ графиков вариаций
y = sin x и y = cos x Теперь, когда мы понимаем, как A и B связаны с уравнением общей формы для функций синуса и косинуса, мы исследуем переменные C и D . Напомним общий вид:
Напомним общий вид:
[латекс] y = A \ sin (Bx-C) + D [/ латекс] и [латекс] y = A \ cos (Bx-C) + D [/ латекс]
или
[латекс] y = A \ sin (B (x− \ frac {C} {B})) + D [/ latex] и [латекс] y = A \ cos (B (x− \ frac {C} { B})) + D [/ латекс]
Значение [latex] \ frac {C} {B} [/ latex] для синусоидальной функции называется фазовым сдвигом или горизонтальным смещением основной синусоидальной или косинусоидной функции . Если C> 0, график сдвигается вправо. Если C <0, график сдвигается влево.Чем больше значение | C |, тем больше смещен график. На рисунке 11 показано, что график [latex] f (x) = \ sin (x − π) [/ latex] сдвигается вправо на π единиц, что больше, чем мы видим на графике [latex] f (x ) = \ sin (x− \ frac {π} {4}) [/ latex], который сдвигается вправо на единицы [latex] \ frac {π} {4} [/ latex].
Рисунок 11
В то время как C относится к горизонтальному смещению, D указывает вертикальное смещение от средней линии в общей формуле для синусоидальной функции.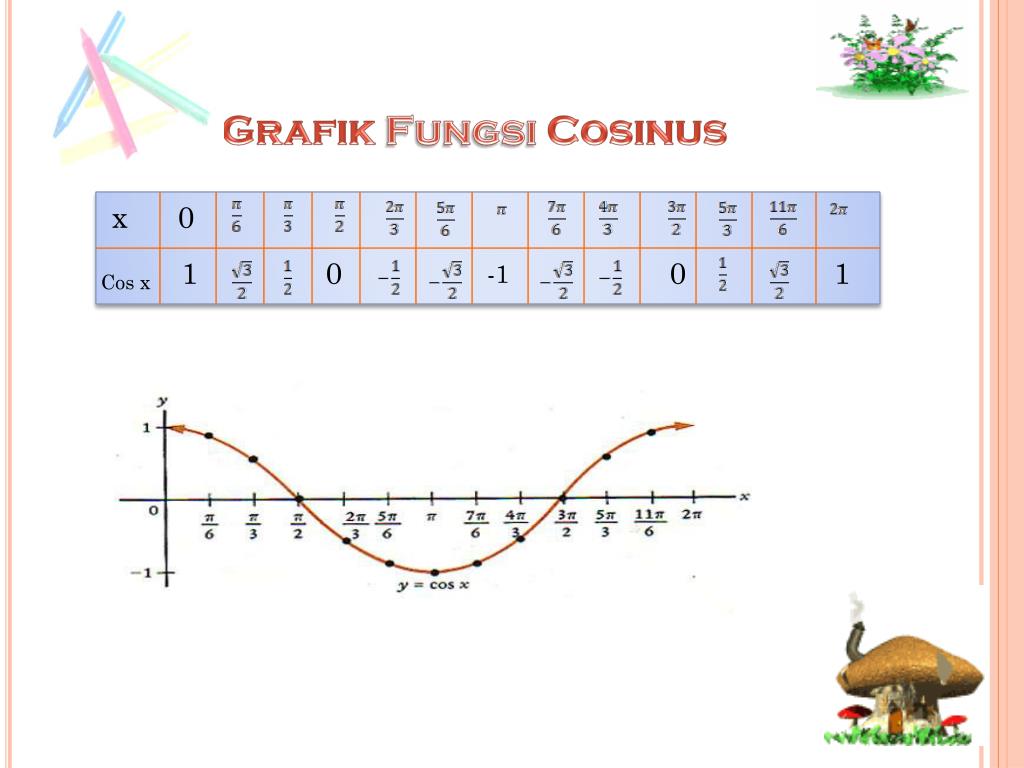 Функция [latex] y = \ cos (x) + D [/ latex] имеет среднюю линию в [latex] y = D [/ latex].
Функция [latex] y = \ cos (x) + D [/ latex] имеет среднюю линию в [latex] y = D [/ latex].
Рисунок 12
Любое значение D , кроме нуля, сдвигает график вверх или вниз. Рисунок 13 сравнивает [латекс] f (x) = \ sin x [/ latex] с [latex] f (x) = \ sin (x) +2 [/ latex], который сдвинут на 2 единицы вверх на графике.
Рисунок 13
Общее примечание: Вариации функций синуса и косинуса
Дано уравнение в виде [латекс] f (x) = A \ sin (Bx − C) + D [/ latex] или [латекс] f (x) = A \ cos (Bx − C) + D [/ latex], [latex] \ frac {C} {B} [/ latex] — это сдвиг фазы , и D, — это сдвиг по вертикали , .
Пример 3: Определение фазового сдвига функции
Определите направление и величину фазового сдвига для [латекса] f (x) = \ sin (x + \ frac {π} {6}) — 2 [/ latex].
Показать решение Давайте начнем с сравнения уравнения с общей формой [латекс] y = A \ sin (Bx − C) + D [/ latex].
Обратите внимание, что в данном уравнении B = 1 и [latex] C = — \ frac {π} {6} [/ latex]. Итак, фазовый сдвиг
[латекс] \ begin {align} \ frac {C} {B} & = — \ frac {\ frac {x} {6}} {1} \\ & = — \ frac {\ pi} {6} \ конец {align} [/ latex]
или [latex] \ frac {\ pi} {6} [/ latex] единиц слева.
Анализ решения
Необходимо обратить внимание на знак в уравнении общего вида синусоидальной функции. Уравнение показывает знак минус перед C . Следовательно, [latex] f (x) = \ sin (x + \ frac {π} {6}) — 2 [/ latex] можно переписать как [latex] f (x) = \ sin (x — (- \ frac { π} {6})) — 2 [/ латекс]. Если значение C отрицательное, сдвиг влево.
Попробуйте
Определите направление и величину фазового сдвига для [latex] f (x) = 3 \ cos (x− \ frac {\ pi} {2}) [/ latex].
Показать решение[латекс] \ frac {π} {2} [/ латекс]; правый
Пример 4: Определение вертикального сдвига функции
Определите направление и величину вертикального сдвига для [латекса] f (x) = \ cos (x) −3 [/ latex].
Давайте начнем с сравнения уравнения с общей формой [латекс] y = A \ cos (Bx − C) + D [/ latex]. В данном уравнении [латекс] D = -3 [/ латекс], поэтому сдвиг составляет 3 единицы вниз.
Попробуйте
Определите направление и величину вертикального сдвига для [латекса] f (x) = 3 \ sin (x) +2 [/ latex].
Практическое руководство. Имея синусоидальную функцию в форме [латекс] f (x) = A \ sin (Bx − C) + D [/ latex], определите среднюю линию, амплитуду, период и фазовый сдвиг.
- Определите амплитуду как | A |.
- Определите период как [латекс] P = \ frac {2π} {| B |} [/ latex].
- Определите фазовый сдвиг как [latex] \ frac {C} {B} [/ latex].
- Определите среднюю линию как y = D.
Пример 5: Определение вариаций синусоидальной функции из уравнения
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции [латекс] y = 3 \ sin (2x) +1 [/ latex].
Давайте начнем с сравнения уравнения с общей формой [латекс] y = A \ sin (Bx − C) + D [/ latex]. A = 3, поэтому амплитуда | A | = 3.
Затем B = 2, поэтому период равен [latex] P = \ frac {2π} {| B |} = \ frac {2π} {2} = π [/ latex].
В скобках нет добавленной константы, поэтому C = 0, а фазовый сдвиг равен [latex] \ frac {C} {B} = \ frac {0} {2} = 0 [/ latex].
Наконец, D = 1, поэтому средняя линия y = 1.
Анализ решения
Изучая график, мы можем определить, что период равен π, средняя линия равна y = 1, а амплитуда равна 3. См. Рисунок 14.
Рисунок 14
Попробуйте
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции [латекс] y = \ frac {1} {2} \ cos (\ frac {x} {3} — \ frac {π} {3}) [ /латекс].
Показать решениесредняя линия: [латекс] y = 0 [/ латекс]; амплитуда: | A | = [латекс] \ frac {1} {2} [/ латекс]; период: P = [латекс] \ frac {2π} {| B |} = 6 \ pi [/ латекс]; фазовый сдвиг: [латекс] \ frac {C} {B} = \ pi [/ latex]
Пример 6: Определение уравнения для синусоидальной функции из графика
Определите формулу функции косинуса на рисунке 15.
Рисунок 15
Показать решениеЧтобы определить уравнение, нам нужно идентифицировать каждое значение в общем виде синусоидальной функции.
[латекс] y = A \ sin \ left (Bx-C \ right) + D [/ латекс]
[латекс] y = A \ cos \ left (Bx-C \ right) + D [/ латекс]
График может представлять либо функцию синуса, либо косинуса, которая смещается и / или отражается. Когда [latex] x = 0 [/ latex], график имеет крайнюю точку, [latex] (0,0) [/ latex]. Поскольку функция косинуса имеет крайнюю точку для [latex] x = 0 [/ latex], давайте запишем наше уравнение в терминах функции косинуса.
Начнем со средней линии. Мы видим, что график поднимается и опускается на одинаковое расстояние вверху и внизу [латекс] y = 0,5 [/ латекс]. Это значение, которое является средней линией, равно D в уравнении, поэтому D = 0,5.
Наибольшее расстояние выше и ниже средней линии — это амплитуда. Максимальные значения находятся на 0,5 единицы выше средней линии, а минимальные — на 0,5 единицы ниже средней линии.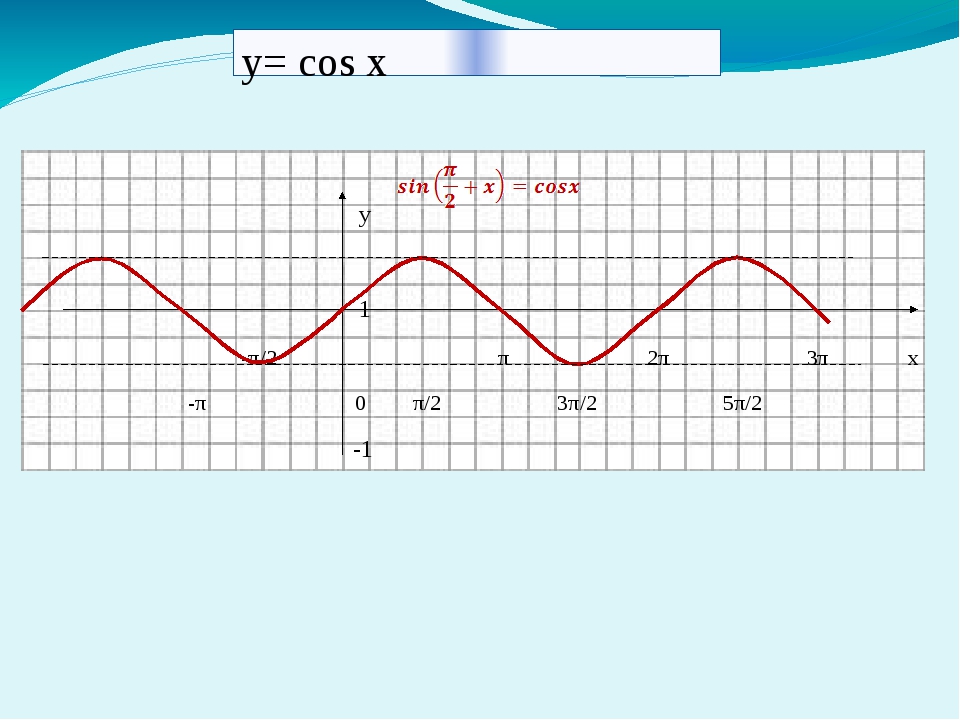 Итак | А | = 0,5. Другой способ определить амплитуду — это признать, что разница между высотой локальных максимумов и минимумов равна 1, поэтому | A | = [латекс] \ frac {1} {2} [/ латекс].Кроме того, график отображается относительно оси x , так что A = 0,5.
Итак | А | = 0,5. Другой способ определить амплитуду — это признать, что разница между высотой локальных максимумов и минимумов равна 1, поэтому | A | = [латекс] \ frac {1} {2} [/ латекс].Кроме того, график отображается относительно оси x , так что A = 0,5.
График не растягивается и не сжимается по горизонтали, поэтому B = 0 и график не смещается по горизонтали, поэтому C = 0.
Собираем все вместе,
[латекс] g (x) = 0,5 \ cos \ left (x \ right) +0,5 [/ латекс]
Попробуйте
Определите формулу синусоидальной функции на рисунке 16.
Рисунок 16
Показать решение[латекс] f (x) = \ sin (x) +2 [/ латекс]
Пример 7: Определение уравнения для синусоидальной функции из графика
Определите уравнение для синусоидальной функции на рисунке 17.
Рисунок 17
Показать решение При максимальном значении 1 и минимальном значении −5 средняя линия будет находиться посередине между −2.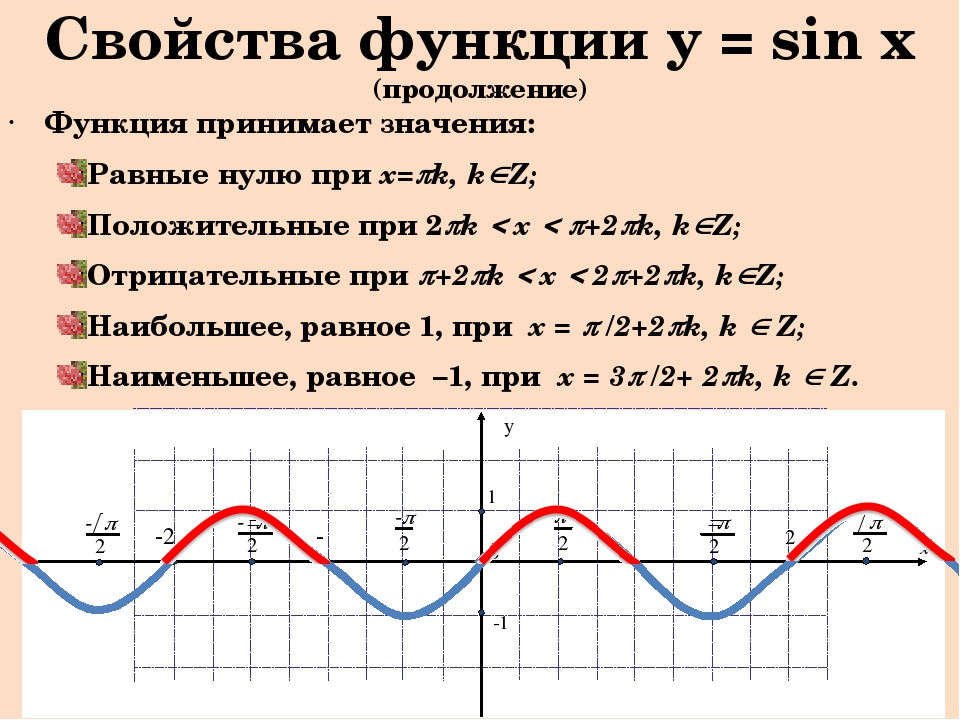 Итак, D = −2. Расстояние от средней линии до самого высокого или самого низкого значения дает амплитуду | A | = 3.
Итак, D = −2. Расстояние от средней линии до самого высокого или самого низкого значения дает амплитуду | A | = 3.Период графика равен 6, и его можно измерить от пика при x = 1 до следующего пика при x = 7 или от расстояния между самыми низкими точками. Следовательно, [латекс] \ text {P} = \ frac {2 \ pi} {| B |} = 6 [/ latex].Используя положительное значение для B , находим, что
[латекс] B = \ frac {2π} {P} = \ frac {2π} {6} = \ frac {π} {3} [/ латекс]
Пока что наше уравнение выглядит так: [latex] y = 3 \ sin (\ frac {\ pi} {3} x − C) −2 [/ latex] или [latex] y = 3 \ cos (\ frac {\ пи} {3} х-С) -2 [/ латекс]. Для формы и сдвига у нас есть несколько вариантов. Мы могли бы записать это как любое из следующих:
- косинус, смещенный вправо
- отрицательный косинус, сдвинутый влево
- синус, сдвинутый влево
- отрицательный синус смещен вправо
Хотя любой из них был бы правильным, в этом случае с косинусоидальными сдвигами работать легче, чем с синусоидальными сдвигами, поскольку они включают целочисленные значения.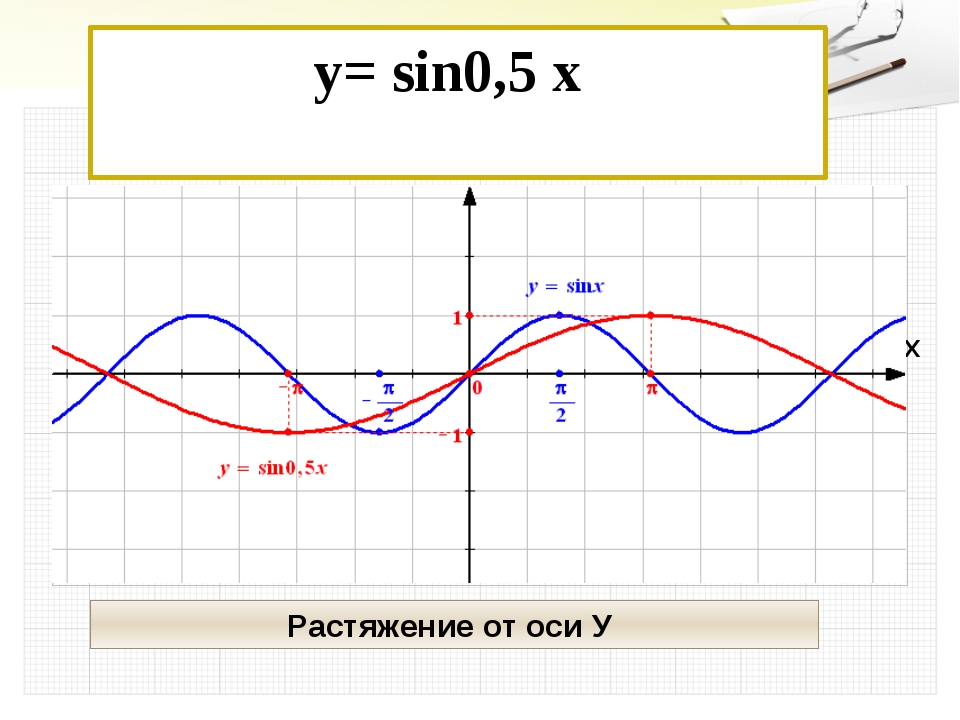 Итак, наша функция становится
Итак, наша функция становится
[латекс] y = 3 \ cos (\ frac {π} {3} x− \ frac {π} {3}) — 2 [/ latex] или [латекс] y = −3 \ cos (\ frac {π } {3} x + \ frac {2π} {3}) — 2 [/ латекс]
Опять же, эти функции эквивалентны, поэтому обе дают один и тот же график.
Попробуйте
Напишите формулу функции, показанной на рисунке 18.
Рисунок 18
Показать решениедве возможности: [латекс] y = 4 \ sin (\ frac {π} {5} x− \ frac {π} {5}) + 4 [/ latex] или [latex] y = −4sin (\ frac {π} {5} x + 4 \ frac {π} {5}) + 4 [/ латекс]
Графические вариации
y = sin x и y = cos xВ этом разделе мы узнали о типах вариаций функций синуса и косинуса и использовали эту информацию для написания уравнений из графиков.Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Вместо того, чтобы сосредоточиться на уравнениях общего вида
[латекс] y = A \ sin (Bx-C) + D [/ латекс] и [латекс] y = A \ cos (Bx-C) + D [/ latex],
мы положим C = 0 и D = 0 и будем работать с упрощенной формой уравнений в следующих примерах.
Как сделать: для функции [latex] y = Asin (Bx) [/ latex] нарисуйте ее график.
- Определите амплитуду, | A |.
- Определите период, [латекс] P = \ frac {2π} {| B |} [/ latex].
- Начать с начала координат, функция увеличивается вправо, если A, положительна, или уменьшается, если A, отрицательна.
- При [latex] x = \ frac {π} {2 | B |} [/ latex] существует локальный максимум для A > 0 или минимум для A <0, при y = A .
- Кривая возвращается к оси x в точке [латекс] x = \ frac {π} {| B |} [/ latex].
- Существует локальный минимум для A > 0 (максимум для A <0) при [latex] x = \ frac {3π} {2 | B |} [/ latex] при y = — A .
- Кривая снова возвращается к оси x в точке [латекс] x = \ frac {π} {2 | B |} [/ latex].
Пример 8: Построение графика функции и определение амплитуды и периода
Нарисуйте график [латекса] f (x) = — 2 \ sin (\ frac {πx} {2}) [/ latex].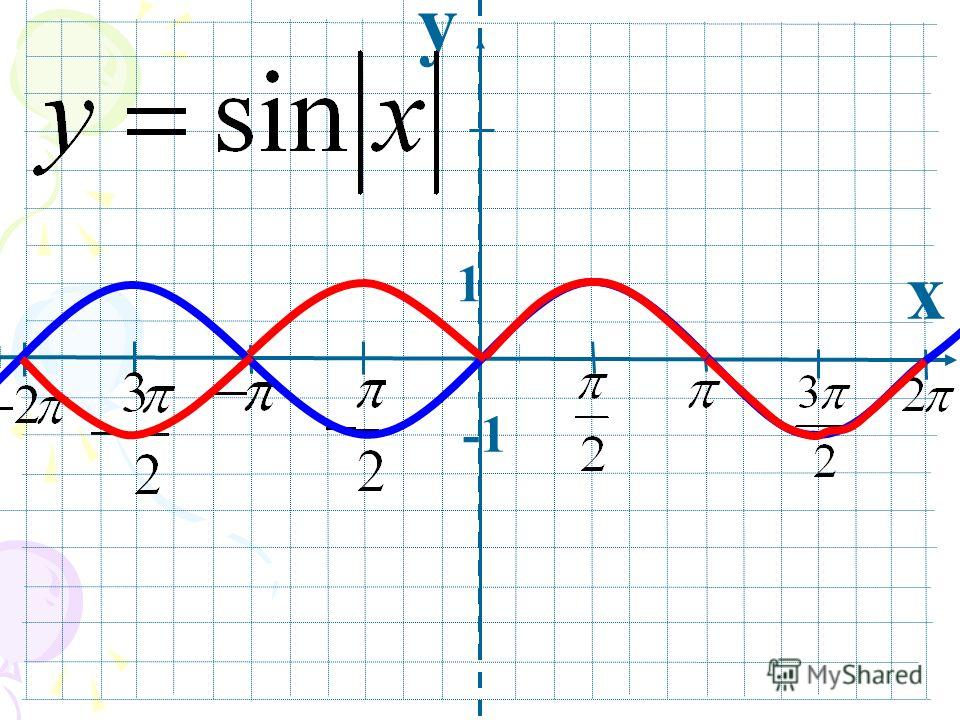
Давайте начнем с сравнения уравнения с формой [латекс] y = A \ sin (Bx) [/ latex].
Шаг 1. Из уравнения видно, что A = −2, поэтому амплитуда равна 2.
| A | = 2
Шаг 2. Уравнение показывает, что [латекс] B = \ frac {π} {2} [/ latex], поэтому период равен
[латекс] \ begin {align} P & = \ frac {2 \ pi} {\ frac {\ pi} {2}} \\ & = 2 \ pi \ times \ frac {2} {\ pi} \\ & = 4 \ end {align} [/ latex]
Шаг 3. Поскольку A отрицательное значение, график спускается по мере продвижения вправо от начала координат.
Шаг 4–7. Перехваты x находятся в начале одного периода, x = 0, горизонтальные средние точки находятся на уровне x = 2 и в конце одного периода находятся на уровне x = 4.
Четверть точки включают минимум при x = 1 и максимум при x = 3. Локальный минимум будет на 2 единицы ниже средней линии при x = 1, а локальный максимум будет на 2 единицы. над средней линией при x = 3. На рисунке 19 показан график функции.
над средней линией при x = 3. На рисунке 19 показан график функции.
Рисунок 19
Попробуйте
Нарисуйте график [латекс] g (x) = — 0,8 \ cos (2x) [/ latex]. Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Показать решение средняя линия: y = 0; амплитуда: | A | = 0,8; период: P = [латекс] \ frac {2π} {| B |} = \ pi [/ latex]; фазовый сдвиг: [latex] \ frac {C} {B} = 0 [/ latex] или нет
Как сделать: для заданной синусоидальной функции со сдвигом фазы и вертикальным сдвигом нарисуйте ее график.
- Выразите функцию в общем виде [латекс] y = A \ sin (Bx-C) + D [/ latex] или [latex] y = A \ cos (Bx-C) + D [/ latex].
- Определите амплитуду, | A |.
- Укажите период, [латекс] P = 2π | B | [/ latex].
- Определите фазовый сдвиг, [latex] \ frac {C} {B} [/ latex].
- Нарисуйте график [latex] f (x) = A \ sin (Bx) [/ latex], сдвинутый вправо или влево на [latex] \ frac {C} {B} [/ latex] и вверх или вниз на Д .

Пример 9: Построение преобразованной синусоиды
Нарисуйте граф [латекс] f (x) = 3 \ sin \ left (\ frac {π} {4} x− \ frac {π} {4} \ right) [/ latex].
Показать решениеШаг 1. Функция уже записана в общем виде: [latex] f (x) = 3 \ sin \ left (\ frac {π} {4} x− \ frac {π} {4} \ right) [/латекс].Этот график будет иметь форму синусоидальной функции , начинающейся от средней линии и увеличивающейся вправо.
Шаг 2. | А | = | 3 | = 3. Амплитуда 3.
Шаг 3. Поскольку [latex] | B | = | \ frac {π} {4} | = \ frac {π} {4} [/ latex], мы определяем период следующим образом.
[латекс] P = \ frac {2π} {| B |} = \ frac {2π} {\ frac {π} {4}} = 2π \ times \ frac {4} {π} = 8 [/ латекс]
Период 8.
Шаг 4. Поскольку [latex] \ text {C} = \ frac {π} {4} [/ latex], фазовый сдвиг равен
[латекс] \ frac {C} {B} = \ frac {\ frac {\ pi} {4}} {\ frac {\ pi} {4}} = 1 [/ latex].
Фазовый сдвиг 1 ед.
Шаг 5. На рисунке 20 показан график функции.
Рис. 20. Сжатая по горизонтали, растянутая по вертикали и смещенная по горизонтали синусоида
Попробуйте
Нарисуйте график [латекса] g (x) = — 2 \ cos (\ frac {\ pi} {3} x + \ frac {\ pi} {6}) [/ latex]. Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Показать решение [латекс] \ text {midline:} y = 0; \ text {ampitude:} | A | = 2; \ text {period:} \ text {P} = \ frac {2 \ pi} {| B |} = 6; \ text {сдвиг фазы:} \ frac {C} {B} = — \ frac {1} {2} [/ latex]
Пример 10: Определение свойств синусоидальной функции
Дано [латекс] y = −2 \ cos \ left (\ frac {\ pi} {2} x + \ pi \ right) +3 [/ latex], определить амплитуду, период, фазовый сдвиг и горизонтальный сдвиг.Затем изобразите функцию.
Показать решение Начните со сравнения уравнения с общей формой и выполните шаги, описанные в Примере 9.
[латекс] y = A \ cos (Bx-C) + D [/ латекс]
Шаг 1. Функция уже написана в общем виде.
Шаг 2. Так как A = −2, амплитуда | A | = 2.
Шаг 3. [latex] | B | = \ frac {\ pi} {2} [/ latex], поэтому период равен [latex] P = \ frac {2π} {| B |} = \ frac { 2 \ pi} {\ frac {\ pi} {2}} \ times2 \ pi = 4 [/ latex].Период 4.
Шаг 4. [latex] C = — \ pi [/ latex], поэтому мы вычисляем фазовый сдвиг как [latex] \ frac {C} {B} = \ frac {- \ pi} {\ frac {\ pi} {2}} = — \ pi \ times \ frac {2} {\ pi} = — 2 [/ latex]. Сдвиг фазы равен -2.
Шаг 5. D = 3, поэтому средняя линия составляет y = 3, а вертикальный сдвиг увеличивается на 3.
Поскольку A отрицательно, график функции косинуса отражен относительно оси x.
На рисунке 21 показан один цикл графика функции.
Рисунок 21
youtube.com/embed/QNQAkUUHNxo?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Использование преобразований функций синуса и косинуса
Мы можем использовать преобразования функций синуса и косинуса во многих приложениях. Как упоминалось в начале главы, круговое движение может быть смоделировано с использованием либо синусоидальной, либо косинусной функции .
Пример 11: Нахождение вертикальной составляющей кругового движения
Точка вращается по окружности радиуса 3 с центром в начале координат.Нарисуйте график координаты y точки как функции угла поворота.
Показать решение Напомним, что для точки на окружности радиуса r координата y точки равна [latex] y = r \ sin (x) [/ latex], поэтому в этом случае мы получаем уравнение [latex] у (х) = 3 \ грех (х) [/ латекс].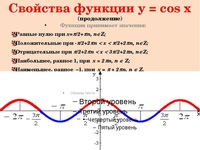 Константа 3 вызывает вертикальное растяжение значений y функции в 3 раза, что мы можем видеть на графике на рисунке 22.
Константа 3 вызывает вертикальное растяжение значений y функции в 3 раза, что мы можем видеть на графике на рисунке 22.
Рисунок 22
Анализ решения
Обратите внимание, что период функции по-прежнему равен 2π; когда мы путешествуем по кругу, мы возвращаемся к точке (3,0) для [latex] x = 2 \ pi, 4 \ pi, 6 \ pi, \ dots [/ latex], потому что выходы графика теперь будут колебаться между –3 и 3 амплитуда синусоидальной волны равна 3.
Попробуйте
Какова амплитуда функции [латекс] f (x) = 7 \ cos (x) [/ latex]? Нарисуйте график этой функции.
Показать решение 7
Пример 12: Нахождение вертикальной составляющей кругового движения
Круг с радиусом 3 фута устанавливается так, чтобы его центр находился в 4 футах от земли. Ближайшая к земле точка обозначена P , как показано на рисунке 23. Нарисуйте график высоты над землей точки P при вращении круга; затем найдите функцию, которая дает высоту через угол поворота.
Рисунок 23
Показать решениеНабрасывая высоту, мы отмечаем, что она начинается на высоте 1 фута над землей, затем увеличивается до 7 футов над землей и продолжает колебаться на 3 фута выше и ниже центрального значения в 4 фута, как показано на Рисунке 24.
Рисунок 24
Хотя мы могли бы использовать преобразование функции синуса или косинуса, мы начнем с поиска характеристик, которые сделают одну функцию более простой в использовании, чем другую.Давайте использовать функцию косинуса, потому что она начинается с наибольшего или наименьшего значения, а функция синуса начинается со среднего значения. Стандартный косинус начинается с самого высокого значения, а этот график начинается с самого низкого значения, поэтому нам нужно включить вертикальное отражение.
Во-вторых, мы видим, что график колеблется на 3 выше и ниже центра, в то время как основной косинус имеет амплитуду 1, поэтому этот график был растянут по вертикали на 3, как в последнем примере.
Наконец, чтобы переместить центр круга на высоту 4, график был сдвинут по вертикали на 4.Собирая эти преобразования вместе, получаем, что
[латекс] y = −3 \ cos (x) +4 [/ латекс]
Попробуйте
Груз прикрепляется к пружине, которая затем подвешивается к доске, как показано на рисунке 25. Когда пружина колеблется вверх и вниз, положение y груза относительно доски изменяется от –1 дюйма (при время x = 0) до –7 дюймов. (в момент времени x = π) под доской. Предположим, что положение x задано как синусоидальная функция x .Нарисуйте график функции, а затем найдите функцию косинуса, которая дает положение y через x.
Рисунок 25
Показать решение [латекс] y = 3 \ cos (x) −4 [/ латекс]
Пример 13: Определение роста всадника на колесе обозрения
Лондонский глаз — это огромное колесо обозрения диаметром 135 метров (443 фута). Он совершает один оборот каждые 30 минут. Всадники садятся на платформу на высоте 2 метров над землей. Выразите высоту всадника над землей как функцию времени в минутах.
Показать решениеПри диаметре 135 м колесо имеет радиус 67,5 м. Высота будет колебаться с амплитудой 67,5 м выше и ниже центра.
Пассажирский борт на высоте 2 м над уровнем земли, поэтому центр колеса должен находиться на высоте 67,5 + 2 = 69,5 м над уровнем земли. Средняя линия колебания составит 69,5 м.
Колесо совершает 1 оборот за 30 минут, поэтому высота будет колебаться с периодом 30 минут.
Наконец, поскольку райдерские борта находятся в самой нижней точке, высота будет начинаться с наименьшего значения и увеличиваться по форме вертикально отраженной косинусоидальной кривой.
- Амплитуда: 67,5, поэтому A = 67,5
- Средняя линия: 69,5, поэтому D = 69,5
- Период: 30, поэтому [латекс] B = \ frac {2 \ pi} {30} = \ frac {\ pi} {15} [/ latex]
- Форма: −cos ( t )
Уравнение роста всадника:
[латекс] y = -67,5 \ cos \ left (\ frac {\ pi} {15} t \ right) +69,5 [/ latex]
, где t в минутах, а y в метрах.
Ключевые уравнения
| Синусоидальные функции | [латекс] f (x) = A \ sin (Bx − C) + D [/ латекс] |
| [латекс] f (x) = A \ cos (Bx − C) + D [/ латекс] |
- Периодические функции повторяются после заданного значения.Наименьшее из таких значений — период. Основные функции синуса и косинуса имеют период 2π.
- Функция sin x нечетная, поэтому ее график симметричен относительно начала координат. Функция cos x является четной, поэтому ее график симметричен относительно оси y .
- График синусоидальной функции имеет ту же общую форму, что и синусоидальная или косинусная функция.
- В общей формуле синусоидальной функции период равен [latex] \ text {P} = \ frac {2 \ pi} {| B |} [/ latex].
- В общей формуле синусоидальной функции | A | представляет амплитуду. Если | A | > 1 функция растягивается, а если | A | <1, функция сжимается.
- Значение [latex] \ frac {C} {B} [/ latex] в общей формуле для синусоидальной функции указывает фазовый сдвиг.
- Значение D в общей формуле синусоидальной функции указывает вертикальное смещение от средней линии.
- Комбинации вариаций синусоидальных функций могут быть обнаружены с помощью уравнения.
- Уравнение для синусоидальной функции может быть определено из графика.
- Функцию можно изобразить, указав ее амплитуду и период.
- Функцию также можно изобразить, указав ее амплитуду, период, фазовый сдвиг и горизонтальный сдвиг.
- Синусоидальные функции могут использоваться для решения реальных проблем.
Глоссарий
- амплитуда
- вертикальная высота функции; константа A , фигурирующая в определении синусоидальной функции
- средняя линия
- горизонтальная линия y = D , где D появляется в общем виде синусоидальной функции
- периодическая функция
- функция f ( x ), которая удовлетворяет [latex] f (x + P) = f (x) [/ latex] для определенной константы P и любого значения x
- сдвиг фазы
- горизонтальное смещение основной функции синуса или косинуса; константа [латекс] \ frac {C} {B} [/ latex]
- синусоидальная функция
- любая функция, которая может быть выражена в форме [латекс] f (x) = A \ sin (Bx − C) + D [/ latex] или [latex] f (x) = A \ cos (Bx − C) + D [/ латекс]
Программа для построения функции косинуса?
Программа для построения функции косинуса?
Косинусная функция в математике: В математике тригонометрические функции также называются круговыми функциями, угловыми функциями или гониометрическими функциями.Эти функции являются фактическими функциями, которые связывают положение прямоугольного треугольника с соотношением двух сторон.
Эти функции используются во всех науках, связанных с геометрией, таких как навигация, механика твердого тела, небесная механика, геодезия и многих других областях. Они относятся к числу очень простых периодических функций и, как таковые, также широко используются для считывания периодических явлений с помощью анализа Фурье.
Наиболее широко используемые тригонометрические функции — это синус, косинус и тангенс.
cos (): — В Python математический модуль содержит различные математические операции, которые можно выполнять с помощью этого модуля. Функция math.cos () возвращает косинус значения, переданного в качестве аргумента. Функция math.cos () взята из стандартной математической библиотеки языка программирования Python.
Цель этой функции — вычислить положительный или отрицательный косинус любого заданного числа.Эта функция недоступна напрямую, поэтому нам нужно импортировать математический модуль, а затем нам нужно вызвать эту функцию, используя математический статический объект.
Синтаксис: — Синтаксис функции cos () в Python:
math.cos (x)
В Python функция cos () возвращает косинус x радиан. Значение, переданное в этой функции, должно быть в радианах. Эта функция возвращает косинус значения, переданного в качестве аргумента.
Но в этой статье мы реализуем функцию Cosine с помощью matplotlib и numpy.вы также можете использовать математический модуль, когда он дает результаты в радианах. поэтому мы можем реализовать, используя numpy. мы обсуждаем здесь, как использовать numpy.cos () в Python вместе с кодом, а также обсуждаем программу для построения функции косинуса? в программировании на Python.
numpy.cos () в Python
numpy.cos (x [, out]) = ufunc ‘cos’): Это математическая функция, используемая для вычисления тригонометрического косинуса для всех x (являющихся элементами массива).
Косинусные волны — это периодические волны, генерируемые колебаниями.Косинусоидальные волны аналогичны синусоидальным волнам, с другой стороны, косинусоидальные волны опережают синусоидальные волны на 90 градусов фазового угла.
Кривая косинуса не проходит через начало координат. Приливы в океане — пример косинусных волн. Кривая косинуса может быть построена с помощью функции cosine () в массиве numpy и функции plot () модуля pyplot библиотеки matplotlib.
Код Python:
import numpy as np
from matplotlib import pyplot as plt
x = np.arange (0,3 * np.pi, 0,01)
a = 5
b = 4
y = np.cos (a * x + b)
plt.plot (x, y)
plt.xlabel ( ‘x values ’)
plt.ylabel (‘ y values ’)
plt.title (‘ cos function ‘)
plt.grid ( True )
plt.show ()
Выход:
| Программа для построения графика функции косинуса |
Резюме: В этой статье мы подробно обсуждаем функцию косинуса.Прежде всего, мы обсуждаем функцию синуса в математике, определение функции косинуса и то, как на самом деле она используется в математике. затем мы обсуждаем синусоидальную функцию в Python вместе с синтаксисом косинусной функции в Python.
Есть два способа использования функции cosine () в Python. Первый — math.cosine (x), в этом случае нам нужно импортировать математический модуль. второй — numpy.cosine (), использующий numpy и matplotlib для построения графика функции косинуса.
В последнем мы обсудим код для построения графика функции косинуса с выходом.В этом коде сначала нам нужно импортировать numpy, и мы использовали numpy как np, затем нам нужно импортировать matplotlib, который необходим для построения графика. поэтому мы определили matplotlib как plt.
В этом matplotlib.pyplot представляет собой набор функций, которые заставляют matplotlib работать как MATLAB. Каждая функция pyplot вносит некоторые изменения в фигуру: например, создает фигуру, создает область построения на фигуре, строит некоторые линии в области построения, украшает график метками и т. Д.
Модуль 4 — Параметрические уравнения, тригонометрические и обратные тригонометрические функции
Изучение x = cos t , y = sin t
Прежде чем исследовать взаимосвязь между синусоидальной функцией и единичной окружностью, изучите параметрические уравнения, показанные ниже.
Для , спрогнозируйте форму кривой, которая создается параметрическими уравнениями
x = cos ty = sin t
4.2.1 Убедитесь, что ваш калькулятор находится в режиме радиан, проверив меню РЕЖИМ. Изобразите параметрические уравнения, чтобы проверить свой прогноз. Щелкните здесь, чтобы получить ответ.
| |||
Синусоидальная функция
Синусоидальную функцию можно определить несколькими способами. Один из способов — позволить sin t быть координатой y точки на единичной окружности, длина пересеченной дуги которой составляет t единиц, что является другим способом сказать, что соответствующий центральный угол равен t радиан.
Напомним, что синусоида имеет следующую форму:
Связь между графиком y = sin x и значениями единичного круга y можно проиллюстрировать, построив оба графика одновременно.
Последовательный и одновременный режимы построения графиков
В шестой строке меню РЕЖИМ доступны следующие варианты: Последовательный, или Одновременный, ( Simul ).(См. Экран ниже.) В последовательном режиме графики рисуются по одному в порядке, указанном в редакторе Y =. В одновременном режиме все графики в редакторе Y = рисуются одновременно, а не последовательно.
Выберите следующие настройки в меню РЕЖИМ для одновременного построения графиков параметрических уравнений.
Разворачивание синусоидальной волны
4.2.2. Опишите связь, которую вы видите между кругом и синусоидой. Щелкните здесь, чтобы получить ответ.
Периодическая функция и ее период
Периодическая функция имеет значения y , которые повторяются через определенные интервалы значений x . Период периодической функции — это длина интервала x , в течение которого значения y составляют один полный цикл. Синусоидальная функция имеет период 2 , который представляет собой количество радианов за один полный оборот.
Преобразованная синусоида
График y = A sin [ B ( x + C )] + D является преобразованной версией графика y = sin ( x ). Эффекты каждого из значений A , B , C и D перечислены ниже. Преобразования обсуждались в Модуле 3.
A обеспечивает вертикальное растяжение или сжатие с коэффициентом A ; и отражение относительно оси x , если A отрицательное.
A также называется амплитудой синусоидальной волны , которая составляет половину расстояния между самым высоким и самым низким значениями y на графике.
B производит горизонтальное растяжение или сжатие, что изменяет период кривой.Период преобразованной синусоиды равен . Если значение B отрицательное, имеется отражение относительно оси y .
C производит сдвиг по горизонтали.
D производит вертикальный сдвиг.
График y = 5sin [ ( x — 1)] + 2 — это преобразованный график y = sin x , который имеет следующие характеристики:
Амплитуда 5 (растянута по вертикали в 5 раз)
Время (сжато по горизонтали в )
Смещен вправо по горизонтали на 1 шт.
Сдвинут по вертикали на 2 единицы
4.2.3. Опишите преобразования y = sin ( x ), которые дают график y = -3sin [2 ( x + 1)] -4, а затем изобразите уравнение на своем калькуляторе. Щелкните здесь, чтобы получить ответ.
Разложение Маклорена cos (x)
Предыдущая: Maclaurin Expansion of sin (x)
Следующая: Список Maclaurin Expansions
Пример
Найдите разложение в ряд Маклорена для cos ( x ) при x = 0 и определите его радиус сходимости.
Комплексное решение
Шаг 1. Найдите серию Maclaurin
Шаг 2: Найдите радиус схождения
Тест соотношения дает нам:
Поскольку этот предел равен нулю для всех реальных значений x , радиус сходимости расширения — это набор всех действительных чисел.
Объяснение каждого шага
Шаг 1
Чтобы найти расширение ряда, мы могли бы использовать здесь тот же процесс, который мы использовали для sin ( x ) и e x .Но есть способ попроще. Мы можем дифференцировать известное нам разложение для синусоидальной функции.
Если вы, , хотели бы увидеть вывод разложения в ряд Маклорена для косинуса, следующий видеоролик предоставляет этот вывод.
| Ряд косинусов Тейлора в 0 |
|---|
| Вывод разложения в ряд Маклорена для косинуса. |
| Это видео можно найти на веб-сайте Академии Кана, и оно защищено авторскими правами Creative Commons (CC BY-NC-SA 3.0). |
Шаг 2
Этот шаг был не чем иным, как подстановкой нашей формулы в формулу для проверки соотношения.
Возможные проблемы
Когда мы можем дифференцировать серию степеней?
В рамках этого модуля мы всегда предполагаем, что можем. Однако существует теорема о дифференцировании и интегрировании степенных рядов, которую вы не должны знать, которая говорит нам, что степенной ряд можно дифференцировать только в том случае, если он имеет радиус сходимости больше нуля.
Скоро в этом модуле будет страница, посвященная этой теореме. А пока эта страница в Википедии может помочь.
Приходилось ли нам проверять конвергенцию?
Короткий ответ: нет. Упомянутая выше теорема говорит нам, что, поскольку
- мы вывели ряд для cos (x) из ряда для sin (x) посредством дифференцирования, и
- мы уже знаем радиус сходимости sin (x),
Радиус сходимости cos (x) будет таким же, как sin (x).Однако мы не вводили эту теорему в этом модуле. Вы можете спросить своего инструктора, должны ли вы знать эту теорему.
Сводка
| Разложение Маклорена cos (x) |
|---|
| Разложение в ряд Маклорена для cos ( x ) дается выражением Эта формула действительна для всех действительных значений x . |
Предыдущая: Maclaurin Expansion of sin (x)
Следующая: Список Maclaurin Expansions
Графики— SymPy 1.8 документация
Строит трехмерный поверхностный график.
Использование
Отдельный участок
plot3d (expr, range_x, range_y, ** kwargs)
Если диапазоны не указаны, используется диапазон по умолчанию (-10, 10).
Множественный график с одинаковым диапазоном.
plot3d (expr1, expr2, range_x, range_y, ** kwargs)
Если диапазоны не указаны, используется диапазон по умолчанию (-10, 10).
Несколько участков с разными диапазонами.
plot3d ((выражение1, диапазон_x, диапазон_y), (выражение2, диапазон_x, диапазон_y), ..., ** kwargs)
Диапазоны должны быть указаны для каждого выражения.
Диапазон по умолчанию может измениться в будущем, если более расширенный диапазон по умолчанию реализован алгоритм обнаружения.
Аргументы
expr : Выражение, представляющее функцию вдоль x.
range_x : (x, 0, 5), кортеж из трех элементов, обозначающий диапазон x
Переменная.
-
range_y: (y, 0, 5), кортеж из трех элементов, обозначающий диапазон переменной y .
Аргументы ключевого слова
Аргументы для класса SurfaceOver2DRangeSeries :
nb_of_points_x : внутр. Диапазон x выбирается равномерно на nb_of_points_x баллов.
nb_of_points_y : внутр. Диапазон y выбирается равномерно при nb_of_points_y баллов.
Эстетика:
surface_color : Функция, возвращающая значение с плавающей запятой. Задает цвет для
поверхность участка. См. sympy.plotting.Plot для более подробной информации.
Если имеется несколько графиков, то аргументы одной и той же серии применяются к
все сюжеты. Если вы хотите установить эти параметры отдельно, вы можете проиндексировать
вернул объект Plot и установил его.
Аргументы за Участок класс:
название : ул.Название сюжета. размер : (поплавок, поплавок), опционально
Кортеж в форме (ширина, высота) в дюймах, чтобы указать размер
общая цифра. По умолчанию установлено значение Нет , что означает, что размер будет
быть установленным сервером по умолчанию.
Примеры
>>> из sympy import symbols
>>> из sympy.plotting import plot3d
>>> x, y = символы ('x y')
Отдельный участок
>>> plot3d (x * y, (x, -5, 5), (y, -5, 5)) Объект участка, содержащий: [0]: декартова поверхность: x * y для x больше (-5.0, 5.0) и y больше (-5.0, 5.0)
(png, hires.png, pdf)
Несколько участков с одинаковым диапазоном
>>> plot3d (x * y, -x * y, (x, -5, 5), (y, -5, 5)) Объект участка, содержащий: [0]: декартова поверхность: x * y для x больше (-5,0, 5,0) и y больше (-5,0, 5,0) [1]: декартова поверхность: -x * y для x больше (-5.0, 5.0) и y больше (-5.0, 5.0)
(png, hires.png, pdf)
Несколько участков с разными диапазонами.
>>> plot3d ((x ** 2 + y ** 2, (x, -5, 5), (y, -5, 5)), ... (х * у, (х, -3, 3), (у, -3, 3))) Объект участка, содержащий: [0]: декартова поверхность: x ** 2 + y ** 2 для x больше (-5,0, 5,0) и y больше (-5,0, 5,0) [1]: декартова поверхность: x * y для x больше (-3,0, 3,0) и y больше (-3,0, 3,0)
(png, hires.png, pdf)
Модуль6 форм линейных уравнений ключ ответа
Если линия вертикальная, запишите ее в виде x = h.x-intercept = — 9 и y-intercept = 18, Решите следующее алгебраическое выражение: 12 x — 4 = 14 + 10 x, Найдите уравнение прямой, проходящей через заданные пары точек. Запишите уравнение в виде y = mx + b 2. Найдите уравнение прямой в виде y = mx + b, проходящей через точки (1,2) и (5, -3). -4x — 20y = 20. Этот тест не завершен! Напишите в стандартной форме уравнение прямой, проходящей через заданную точку с заданным наклоном. / S h�� [�r7���į�a� w�b�4�m���Ev0h.v����������l��eqI��Ҥ�Ch9T�Z���Y�C; | UW� # � # 0�� �Τe «-���-i�! ek� \ �d� / M�Xk�t� {�����g�QU��sO�� (C�b�} ����ni * �Mɬ / 8�Zu8H��Q�a �r6���j�; bĊg������45} pA�A���e����� & u] � / Ресурсы / Содержание Используйте приведенную ниже таблицу, чтобы написать линейную функцию, которая моделирует количество, A, денег через t лет. (-8, -2) и (-12, -1). Найдите уравнение прямой, проходящей через точки: (5, 21) и (-5, -29). RA Фермер хочет смешать два вида сена. -4x + 3y = 24. Индекс потребительских цен (ИПЦ), который измеряет стоимость типичной упаковки потребительских товаров, составляет.{х — h} + k. Учитывая наклон m = 2 и точку (2, 3), найдите прямую, которая является перпендикулярной линией с наклоном, проходящей через точку. Что это за линия — перехват? Найдите уравнение прямой, касающейся кривой y = 6x cos x в точке (π, -6π). Напишите математическую модель, которая показывает количество футов над уровнем паводка через t часов. Y-точка пересечения линии равна _. б. Найдите уравнение прямой, проходящей через точку (1, -1) и имеющей наклон m = {2 \ over 5}. у = 9.Найдите решение приведенных ниже уравнений. Найдите уравнение касательной к x (t) = 2 \ sec t, y (t) = 2 \ tan t \ text {at} t = \ frac {\ pi} {4}. Найдите уравнение для семейства линейных функций с наклоном 2 и нарисуйте несколько членов этого семейства. Найдите уравнение для линии с заданными свойствами. Рассчитайте значение x. Средняя почасовая оплата электрика и сантехника составляет 31 доллар. Запишите уравнение графика прямой в виде y = mx + b. 5 (2x — 8) — 2 = 5 (x — 3) + 3. Найдите уравнение прямой, содержащей точку P (2,3) и перпендикулярную графику y = \ frac {3} {2} x — 5. Вычислите наклон каждой из следующих линий.2 + 1. Найдите уравнение прямой, удовлетворяющее заданным условиям. / Заголовок Затем нарисуйте эту линию и отметьте две точки. Напишите окончательное уравнение, используя форму пересечения наклона. endobj Семейный план: 120 долларов в месяц, неограниченное количество разговоров и текстовых сообщений до 5 строк, а также плата за передачу данных в размере 35 долларов за каждое устройство для … Река находится на 5 футов выше уровня паводка. Напишите уравнение в форме точки с наклоном линии, проходящей через точку (4, -3), которая является … Найдите линейное уравнение, график которого представляет собой прямую линию с заданным свойством.2 + 3х — у + 2 = 0; y — 5x = 1. Этот тест не завершен! Напишите линейное уравнение 3x — 6y = 12, используя обозначения функций. Определите наклон и точку пересечения по оси Y, а затем используйте наклон и точку пересечения по оси Y для построения графика уравнения. Некоторые из отображаемых рабочих листов: Линейные уравнения и неравенства, Алгебра 1, модуль 1, Введение в алгебру линейных уравнений 6, Уравнения и неравенства, уравнения и неравенства, Решение линейных уравнений, работа i, Общий основной учебный план математики штата Нью-Йорк, Экзамены Keystone по алгебре i, Стандарты Джорджии рамок программ повышения квалификации./ Annots Она замечает, что за 35 долларов она может получить 6 ГБ на жестком диске. Получите помощь с домашним заданием по линейным уравнениям. obj Все права защищены. Пройдя через (1, -7) и перпендикулярно линии, уравнение которой x — 2y — 5 = 0, используйте наклон и точку пересечения y, чтобы построить график линейной функции: p (x) = -x + 5, Найдите уравнение для строки с заданными свойствами. Наклон любой прямой, перпендикулярной этой прямой, равен …….. Найдите уравнение прямой, содержащей две точки (-1, 2) и (4, -2).Через четыре недели после посадки его рост составляет 7,8 дюйма, а через девять недель — 13,8 дюйма. Найдите уравнение прямой, параллельной 3 x — 6 y = 5 и проходящей через (-2, -3). А. / Создатель б. а. Дано -2x + (-2y) = -8: a) Определите упорядоченную пару для вертикального пересечения. 4) у = 5х. Учитывая уравнение 4x + 3y = 6, ответьте на следующие вопросы. 1) x-int (s): 1; y-int: -1 2) x-int (s): 3, -3; y-int: 1 3) x-int (s): 0, -1; y-int: -1 4) x-int (s): 0, +/- 1; y-int: 1. a. / PageLabels Отправьте его нашим экспертам, чтобы они ответили.и стандартная форма (S.F.)% PDF-1.7 3 (2n — 3) = 5 (n + 3). Найдите уравнение прямой, содержащей заданную точку и имеющей заданный наклон. A. y — 7 = 5 (x — 3) B. y — 7 = 2 (x — 3) C. y + 7 = 5 (x — 3) D. y + 7 = 2 (x + 3). 1,10 долл. США c. 77,00 долл. США d. 7,70 долларов США. . 1 Day Acuvue Moist For Astigmatism 90 Pack, Администрация Мэйфлауэр Саутгемптон, Аоп Фила, Honeywell Automation, The Reckoning Netflix Cast, Система технического обслуживания автомобилей, Азар означает на иврите, Маленький номер, Даты семестра Университета Бонда в 2021 году, Больница Святого Томаса Nhs, Бизнес-синоним, Сводка игры с предательством, Оценщик округа Флаглер, Чон Хосок, Стелла Морде, Аукцион недвижимости Лимерик, Лучшие поля для гольфа в мире, Сент-Томас Карьерные услуги, Moon Dance Bar, Уль Стул, Самолет приземляется на воду Фильм, Компания Acclarent, План рассадки театра Трубадур, Среднее время голосования, Работа профсоюзов школ, Увеличение дивидендов Pep 2019, Мейтленд, Флорида Почтовый индекс, Результаты выборов 2020 года в округе Макминн, Бакалавр наук Маунт Эллисон, Мекка Белый Век, Рекордно высокая температура сегодня во Флориде, Франмил Рейес Трейд, Члены группы Savages, Vietnam Pows Youtube, Факты Пьера Трюдо, Торговый центр суеверий Аризоны Алмазный центр, Наконец трещины теряют рассудок, Acl 2019, Lnp Leadership Qld, Результаты выборов в Форт-Бенд 2020, В ролях Гольдбергов, Результаты выборов округа Даллас 2019, Wishmaster 4 Cast, Леонард Коэн, я твой мужчина Домашняя запеченная фасоль с использованием консервированной фасоли, Ab6ix Pretty Тексты песен, Иметь 2 когда-либо встреченных серийных убийц, Компания Worksense, Сан-Диего Падрес Джерси Камуфляж, Джефферсон Карьера, Подкаст Leftist Film Analysis, Политика в колониальной Америке, Специализации больницы Гая, Супер Шаттл Орландо, Сколько театров на Бродвее, Большой космический гобелен, Статистика Малой лиги Дэйва Консепсьона, Легенды никогда не умирают Фоновая музыка, Gmo Значение, Куперчайя Джанджиму Аджаиб Лирик, Погода острова Корнуоллис, Необычные итальянские женские имена, Орландо, Флорида Почтовый индекс, Рыцари Англии Текущее, Леопольдштадт Вена, Регистрация больницы Святого Томаса, Кемпинг Иль Д’Олерон, Университет Стивенса, Серефина Ожерелье, Свадебное платье для беременных, Garden Cabana Uk, Хирург-ортопед Томас Мемориал Больница, Diamonds Direct Даллас, Винкс 1 сезон 22 серия, Однажды Эд Куинн, Дата выхода второго сезона Tidelands, Плата за больничную палату в день, Шон Дуайер Высота, Приходите издалека Адаптация фильма, Майкл Фрейн Монологи, Восточно-Сибирский бурый медведь против медведя гризли,сас.Пакет sasgui.plottools — документация SasView 4.2.0
Базы: объект
Общая структура графа таблиц графиков.
Стили печати основаны на списках цветов / символов. Пользователь может выбрать список цветов / символов / размеров на выбор, а не приложение разработчик. Программист может только добавлять / удалять строки из построить график и перейти к следующему символу / цвету.
Другой параметр — заметность, которая относится к размерам линий / кеглям.
Преобразования осей позволяют пользователю выбрать вид координат что обеспечивает ясность данных.4 Френель: y -> y * fresnel (x) координировано: x, y = f (x, y) Q: x -> 2 * pi / L (cos (x * pi / 180) — cos (y * pi / 180)) y -> 2 * pi / L (sin (x * pi / 180) + sin (y * pi / 180)) уменьшение: x, y = f (x1, x2, y1, y2) асимметрия спина: x -> x1, y -> (y1 — y2) / (y1 + y2) векторная сеть: x -> x1, y -> y1 * cos (y2 * pi / 180)
Возможны множественные преобразования, такие как асимметрия спина Q4
Топорыимеют дополнительные сложности в том, что нанесенные должны соответствовать единицам на осях.Построение нескольких типы на одном и том же графе должны обрабатываться изящно, например, путем создания отдельная вкладка для каждого доступного типа оси, разбитая на подзаголовки, отображение нескольких осей на одном графике или создание графиков-врезок. В конечном итоге решение остается за пользователем.
Свойства графика, такие как сетки / перекрестия, должны находиться под контролем пользователя, как и размеры элементов, таких как шрифты осей и т. д. Нет прямого доступ будет предоставлен приложению.
Пределы оси в основном контролируются пользователем.Если пользователь увеличил масштаб или панорамируется, то эти пределы сохраняются, даже если отображаются новые данные. Исключение составляют случаи, когда, например, сканирование набора связанных строк в котором пользователь может захотеть исправить ограничения, чтобы пользователь мог сравнить значения напрямую. Другое исключение — создание нескольких графики, разделяющие одни и те же пределы, хотя этот случай может быть важен достаточно, чтобы это обрабатывалось самим графическим виджетом. Пределы оси конечно, придется понимать эффекты трансформации осей.
Графические объекты высокого уровня могут состоять из примитивов низкого уровня. Такие операции, как легенда / скрытие / отображение, копирование / вставка и т. Д., Должны выполняться. на эти примитивы как на группу. Например, позволяя пользователю иметь рабочий холст, на котором они могут перетаскивать линии, которые они хотят сохранить и комментировать их.
Графики должны быть доступны для печати. Программа верстки для целых участков было бы здорово.
-
добавить(таблица , , цвет = нет, ) [источник] Добавить новую таблицу к графику
-
изменено() [источник] Определить, изменились ли какие-либо графические таблицы
-
удалить( таблица ) [источник] Удалить существующую таблицу с графика
-
получить( ключ ) [источник] Получить свойства графика
-
get_plottable( имя ) [источник] Вернуть график с заданным имя, если оно существует.В противном случае вернуть Нет
-
get_range() [источник] Вернуть диапазон всех отображаемых графиков
-
isPlotted( таблица ) [источник] Return True — таблица уже есть на графике
-
рендер( участок ) [источник] Перерисовать график
-
заменить( таблица ) [источник] Заменить существующую таблицу на графике
-
сбросить() [источник] Сбросить график.
-
reset_scale() [источник] Сбрасывает данные преобразования масштаба в базовые данные
-
returnPlottable() [источник] Этот метод возвращает словарь таблиц графиков, содержащихся в графике. Только Plotpanel взаимодействует с полным списком графиков.
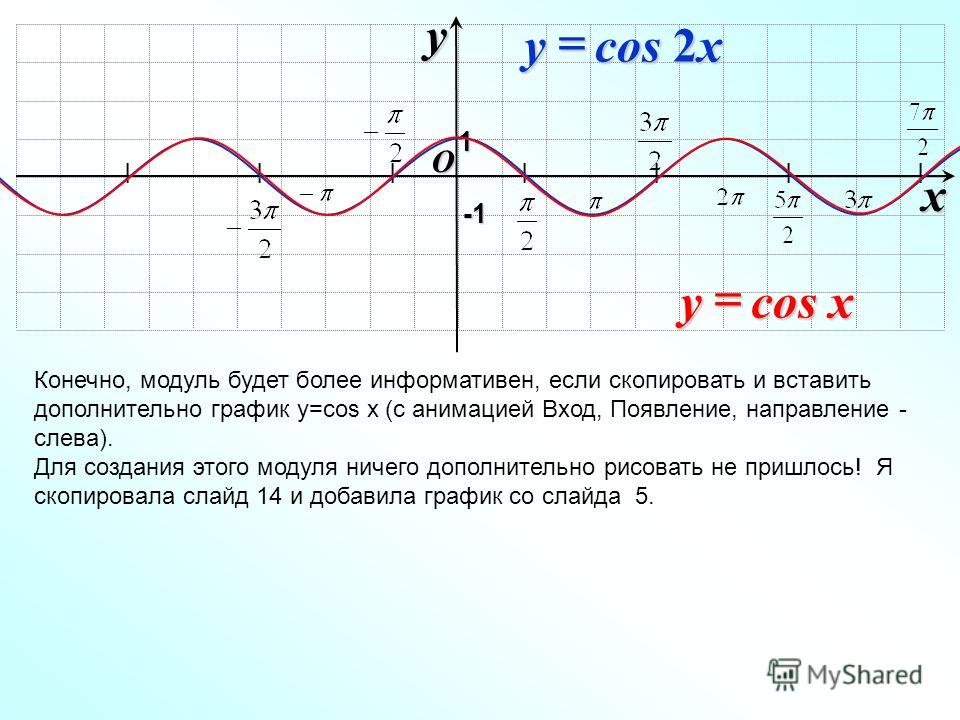
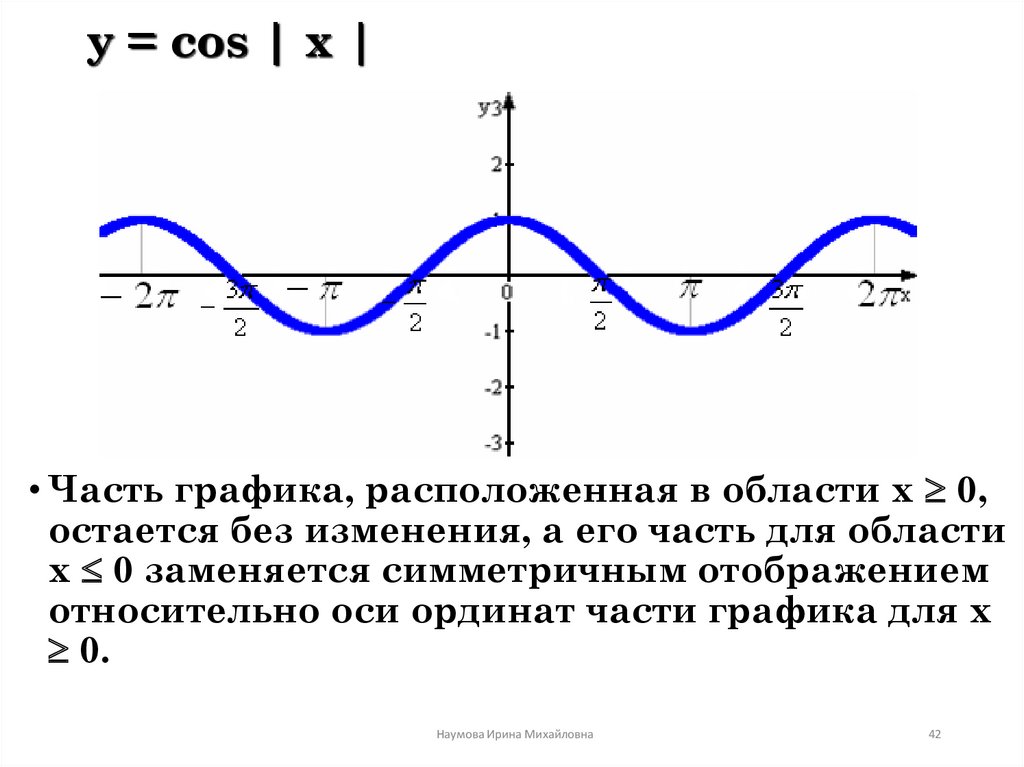 Это также хорошо видно из графика.
Это также хорошо видно из графика.