Уравнения и неравенства с модулями

здравствуйте тема данного видеоурока уравнения и неравенства с моделями напомню что модулем числа а называется само число а если она не отрицательно то есть а больше равно 0 и называется ему противоположное то есть минус а если число отрицательный это определение мы можем использовать для решения уравнений и не раз давайте начнем с уравнение пусть у нас есть вот такой пример x квадрат плюс 2 модуль x минус 1 минус 6 давно нулю чтобы решить это уравнение мы должны расписать вот этот модуль по определению а именно мы должны рассмотреть два случая первый случай когда выражение внутри модуля то есть x минус 1 не отрицательно больше равно 0 если выражение внутри модуля больше равна 0 то модуль раскрывается следующим образом просто убирается таким образом таком случае мы получим x квадрат плюс два модуля убираем x минус 1 минус 6 равно нулю получили обычное квадратное уравнение давайте его решим получим x квадрат плюс 2x минус 2 минус 6 минус 8 равно нулю решая это уравнение мы получим сумма корней -2 произведение минус восемь это минус 4 и 2 то есть у нас x либо минус 4 либо 2 но учитываем что в таком смотрит так раскрывается в только при случае x минус 1 больше о на 0 или x больше равно 1 тогда смотрим x равна минус 4 не удовлетворяет этому условию значит это ложный корень таким образом здесь корень только икс равное 2 рассмотрим второй случай а именно когда выражение внутри модуля x минус 1 отрицательное если выражение внутри модуля отрицательное то модуль раскрывать со знаком минус мы получим x квадрат здесь тогда уже будет минус 2x минус 1 минус 6 равно 0 опять получили квадратные уравнения решаем его x квадрат минус 2 x минус 4 равно 0 мы можем воспользоваться формулой дискриминанта и получим x равно 1 плюс минус корень из 5 если решим это уравнение получим такие корни но учитываем что эти корни нужно проверить с условием x минус 1 меньше 0 или x меньше 1 очевидно вариант с плюсом будет больше одного не удовлетворяет а варят с минусом как раз таки подходит таким образом здесь будет x равна 1 минус корень из 5 тогда числа икс равное 2 и x равна 1 минус корень из 5 является корнями этого уравнения теперь рассмотрим уравнение вот такого вида когда у нас есть некоторое выражение в модуле модели форекс и равняется не которому выражению jetix как мы можем решить такое уравнение мы можем решить его точно также как предыдущем случае а именно рассмотреть два случая первый случай когда выражение внутри модуля неотрицательного больше она 0 если она не отрицательно это модуль раскрывается со своим знаком той же останется f от x равно jetix это в системе и второй случай когда f от x меньше 0 тогда модуль расковать со знаком минус будет минус f от x равно же от x останется нам решить две системы это у нас они выполняются и либо это либо это значит совокупность мы можем решить и вот таким способом однако в данном случае может удобнее использовать следующую схему обратите внимание если же от x у нас равняется модулю то сама же от x обязательно больше равно 0 потому что оно равняется модулю некоторые выражения тогда f от x чтобы равнялась модуль f от x равнялось же должно быть что f от x равняется либо же либо минус же эти вы 2 условие выполняется или одно или другое значит совокупности но оба этих уравнений должны быть одновременно с нижним условиям тогда это будет система для вот такого уравнения часто можно удобно использовать такую схему но в некоторых случаях когда выражение же довольно-таки сложная вот эту роль неравенство сложное в таких случаях лучше использовать вот эту схему давайте рассмотрим такой пример мы можем рассмотреть два случая то есть вот это выражение больше нуля либо меньше нуля и расписать по такой схеме но как видим что правая часть у нас значительно легче чем выражение под модулем тогда нам лучше пользоваться вот этой схемой согласно этой схеме вот это уравнение будет равносильно системе выражение справа же от x больше модуля то есть x минус 1 должно быть больше равно 0 а вот это выражение внутри модуля x квадрат минус 2 x минус 1 равняется либо же либо минус же то есть равно либо просто x минус 1 либо со правил противоположным знаком минус x + 1 и вот эти два выражения у нас в совокупности то есть либо одно либо другое останется решить два уравнения и проверить условия давайте это проделаем сверху мы получим x квадрат минус 3x равно нулю потому что минус они взаимно уничтожатся снизу x квадрат минус x минус 2 равно 0 и x больше равно 1 решаем эти уровни здесь корни легкие это икс равное 0 икс равное 3 решаем это уравнение потерями вето сумма корней один произведение минус 2 это 2 и минус 1 то есть x равен 2 x равен -1 и у нас есть условии что их больше равно 1 если их больше равно 1 то корень 0 не подходит корень -1 не подходит останется только икс равное 2 икс равное трем это будет корнями исходного уравнения теперь рассмотрим случай когда у нас есть два отдельно стоящих модуля метод решения таких уравнений схож с первым методом то есть мы раскрываем модули по определению единственный то что у нас теперь два модуля обычно делает так приравнивает к нулю каждый модуль x минус 1 равен нулю получаем x равна 1 отмечает эту точку на оси x минус 2 равна нулю получаем 2 отмечает от . на сидит и того числовая прямая у нас разбилась на 3 промежутка и нам нужно рассмотреть данное уравнение на всех этих трех промежутках давайте начнем с первой промежутка а именно x меньше 1 я могу сделать меньше 1 или меньше равно 1 давайте возьмем строго меньше если x меньше 1 то этот модуль раскрывается со знаком минус потому что внутри выражения будет отрицательным как я могу это проверить беру любое число меньше 1 допустим 0 0 минус 1 отрицательная значит этот модуль раскрывается с минусом то есть будет минус x + 1 аналогично здесь будет минус x плюс 2 равно 1 решаем это уравнение получим икс равное одному x равна одному этом условии не удовлетворяет значит здесь корней на самом деле нет проверяем теперь на промежутке от 1 до 2 если я здесь один не включил то есть не поставил равно то здесь я уже должны его включить x больше равно 1 и давайте сделаем так меньше равно 2 если их больше равно 1 и меньше равно 2 то вот этот модуль будет раскрываться со знаком плюс возьмем любое число которое в этом промежутке например полтора полтора -1 положительное это с плюсов этот аналогично будет уже с минус а минус x плюс 2 равно 1 если мы здесь упростим заметим что у нас иксы взаимно уничтожатся слева останется один из справа останется один то есть получили истинное выражение 1 10 равно 1 это означает что любой x из этого промежутка является корнем тогда говорят что здесь решение будет x принадлежит от одного до двух обратить внимание у нас было уравнение но решение получилось виде промежутка такое тоже возможно и третий случай когда x строго больше двух тогда оба модуля раскрывается с плюсом решаем данное уравнение получим x равно 2x равно дом опять не удовлетворяет этому условию значит здесь тоже корней нет тогда нашем случае решением будет вот этот промежуток любой x из этого промежутка является решением этого уравнения перейдем к неравенства с моделями первый вид не раньше-то не равенство вида модуль f от x меньше чем некоторые же от x меньше или меньше равно такие неравенства равносильной системе системе когда f от x меньше же от x и f от x больше чем минус же от x таким образом неравенства с модулем у нас преобразуется систему обычных уравнений решаем каждое неравенство и находим пересечении ответов давайте рассмотрим такой пример x квадрат минус 2 x меньше равно чем x минус 1 тогда согласно этой схеме это будет равносильно f от x меньше же от x то есть x квадрат минус 2 x меньше равно чем x минус 1 f от x больше чем мин уже от x то есть x квадрат минус 2 x больше равно чем это выражение только с минус а минус x + 1 останется решить такую систему сверху получим x квадрат минус 3x + 1 меньше равно 0 снизу получим x квадрат минус x минус 1 больше равно 0 решаем вот эти уравнение здесь находим в корне x будет равняться 3 плюс минус корень из дискриминанта дискриминант здесь будет 9 минус 45 пополам а во втором будут корни следующий x равняется 1 плюс минус корень из дискриминанта тоже 5 пополам отмечаем эти корни на числовой прямой даже на двух прямых в первом случае отмечаем 3 плюс корень из 5 пополам и отмечаем 3 минус корень из 5 пополам отмечаем корень один плюс корень из 5 пополам и корень один минус корень из 5 пополам главное чтобы они шли в правильном порядке теперь остается расставить знаки плюс минус плюс нам нужно из первого нужно меньше равна 0 то есть минус во втором также плюс минус плюс но нам уже нужно больше равно 0 то есть вот этот промежуток и того мы видим что пересекается данное решение вот здесь тогда x принадлежит один плюс корень из 5 пополам до 3 плюс корень из 5 пополам следующая неравенства с модулем это неравенство вида модуль f от x больше чем gtx такое неравенство решается следующим образом это не нравится равносильно уже совокупности f от x больше же от x f от x меньше чем минус же от x давайте рассмотрим пример модуль x больше чем x квадрат минус 6 тогда вот это 7 и такой невеста будет равносильно f от x больше чем же от x то есть x больше чем x квадрат минус 6 f от x меньше чем минусы от x то есть x меньше чем минус x квадрат плюс 6 получили совокупность из двух не нравится остался и решить преобразуем первое неравенство в виде x квадрат минус x минус 6 меньше нуля здесь будет икс-квадрат плюс x минус 6 тоже меньше нуля решаем находим в корне в первом случае в первом случае корни будут следующие сумма у нас один произведение минус 6 это 3 и минус 2 во втором случае корни будет наоборот сумма минус 1 произведение минус 6 это минус 3i 2 отмечаем это все на числовой прямой 3 и минус 2 во втором случае 2 и минус 3 в обоих случаю нас меньше нуля если мы растянем знаке будет плюс минус плюс то есть нам нужен промежуток посередине и здесь и здесь но так как у нас это стоит совокупности то мы должны объединить все решения все решение мы можем объединить следующем от -3 до трех таким образом x принадлежит от -3 до трех теперь рассмотрим неравенство когда у нас есть два разных модулях решается на аналогичное такому уравнению то есть мы приравниваем каждый модуль к нулю здесь получим 2 здесь получим минус 4 и рассматриваем это неравенства на 3 промежутках первый промежуток x меньше -4 если x меньше -4 то тогда оба модуля раскроется со знаком минус будет минус x плюс 2 минус x минус 4 меньше десяти решаем это неравенство получим x больше чем минус 6 x больше минус 6 но это должно выполняться одновременно с условием x меньше чем -4 тогда здесь мы можем сказать что x принадлежит от -6 до -4 рассмотрим второй случай когда x принадлежит от минус 4 до 2 я здесь -4 не включил тогда включаю его здесь x больше равно минус 4 меньше равно 2 если их больше равно -4 и меньше равно 2 то вот этот модуль раскрывать со знаком минус а этот модуль со знаком плюс плюс x плюс 4 меньше десяти мы получаем минус x уничтожается сэкс получаем 2 + 4 6 меньше 10 6 меньше десяти это истинный значит любой x из этого промежутка является решением тогда здесь мы получаем что x принадлежит от минус 4 до 2 и осталось рассмотреть последний промежуток а именно x больше двух если их больше двух то оба модуля раскрывать со знаком плюс x минус 2 плюс x плюс 4 меньше десяти решаем это не раса получим что x меньше здесь у нас -2 плюс 42 переносим сюда будет 10 минут за 8 2 x меньше 8 и x меньше 4 x меньше четырех и x больше двух значит здесь у нас решение будет x принадлежит от 2 до 4 нам осталось объединить все вот эти 3 ответа эти ответы объединяться следующим образом x принадлежит от -6 до -4 и здесь сразу от -4 причем здесь включительно до двух значит вот эти два промежутка мы можем записать как от -6 до двух потом u2 и здесь от 2 до 4 значит мы все это можно записать как от -6 до четырех это будет решением исходного неравенства на этом данный видео урок окончен [музыка]

Как извлечь из модуля

Модуль – это абсолютная величина числа или выражения. Если требуется раскрыть модуль, то, согласно его свойствам, результат этой операции всегда должен быть неотрицательным.

Если под знаком модуля находится число, значение которого вам известно, то раскрыть его очень просто. Модуль числа a, или |a|, будет равен самому этому числу, если a больше либо равно 0. Если a меньше нуля, то есть является отрицательным, то его модуль будет равен противоположному ему, то есть |-a|=a. Согласно этому свойству, модули противоположных чисел равны, то есть |-a|=|a|.

В том случае, если подмодульное выражение возведено в квадрат или в другую четную степень, то можно просто опустить скобки модуля, так как любое число, возведенное в четную степень, является неотрицательным. Если нужно извлечь квадратный корень из квадрата числа, то это также будет модуль этого числа, поэтому модульные скобки можно опустить и в этом случае.

Если в подмодульном выражении имеются неотрицательные числа, то их можно вынести за пределы модуля. |c*x|=c*|x|, где с – неотрицательное число.

Когда имеет место уравнение вида |x|=|c|, где x является искомой переменной, а c действительным числом, то раскрыто оно должно быть следующим образом: x=+-|c|.

Если нужно решить уравнение, содержащее модуль выражения, результатом которого должно быть вещественное число, то знак модуля раскрывают, исходя из свойств этой неопределенности. К примеру, если имеется выражение |x-12|, то, если (x-12) – неотрицательное, оно останется неизменным, то есть модуль раскроется как (x-12). Но |x-12| превратится в (12-x), если (x-12) меньше нуля. То есть, модуль раскрывается в зависимости от значения переменной или выражения в скобках. Когда знак результата выражения неизвестен, то задача превращается в систему уравнений, первое из которых рассматривает возможность отрицательного значения подмодульного выражения, а второе – положительного.

Иногда модуль можно однозначно раскрыть, даже если его значение неизвестно по условиям задачи. Например, если под модулем находится квадрат переменной, то результат будет положительным. 2$.
5. $|a|=|-a|$.

Геометрический смысл модуля действительного числа

Числовая прямая служит хорошим примером множества действительных чисел. Давайте отметим на числовой прямой две точки a и b и постараемся найти расстояние $ρ(a; b)$ между этими точками. Очевидно, что это расстояние равно $b-a$, если $b>a$.
Если $a>b$, то расстояние будет равно $a-b$.
Если $a=b$, то расстояние равно нулю, так как получается единая точка.
Все три случая мы можем описать единообразно: $ρ(a;b)=|a-b|$.

Пример.
Решите уравнение:
а) $|x-3|=6$;
б) $|x+5|=3$;
в) $|x|=2,8$;
г) $|x-\sqrt{3}|=2$.

Решение.
а) Надо найти на координатной прямой такие точки, которые удалены от точки 3 на расстояние равное 6.
$ρ(x;3)=6$.
Это точки – 9 и -3 (прибавили и отняли шестерку от тройки).
Ответ: $х=9$ и $х=-3$.

б) $|x+5|=3$, перепишем уравнение в виде $|x-(-5)|=3$.
$ρ(x;-5)=3$.
Найдем расстояние от точки -5, удаленное на 3. Такое расстояние, получается от двух точек: $х=2$ и $х=-8$.

Ответ: $х=2$ и $х=-8$.

в) $|x|=2,8$ можно представить в виде $|х-0|=2,8$ или $ρ(x;0)=2,8$.
Очевидно, что $х=-2,8$ или $х=2,8$.
Ответ: $х=-2,8$ и $х=2,8$.

г) $|x-√3|=2$ эквивалентно $ρ(x; \sqrt{3})=2$.
Очевидно, что $х=\sqrt{3}-2$ или $х=\sqrt{3}+2$.
Ответ: $x=\sqrt{3}-2$ или $x=\sqrt{3}+2$.

Пример.
Решить уравнения:
а) $|2x-8|=4$;
б) $|3-3x|=6$;
в) $|10x+5|=-2$.

Решение.
а) Преобразуем левую часть уравнения: $|2x-8|=|2(x-4)|=|2||x-4|=2|x-4|$.
Тогда уравнение можно переписать в виде: $|x-4|=2$.
Или $ρ(x;4)=2$.
Ответ: $х=6$ или $х=2$.

б) Опять же преобразуем левую часть: $|3-3x|=|-3(x-1)|=|-3||(x-1)|=3|x-1|$.
Тогда уравнение можно переписать в виде: $|x-1|=2$.
Или $ρ(x;1)=2$.
Ответ: $х=3$ или $х=-1$.

в)$|10x+5|=-2 $.
Модуль не может быть отрицательным числом, тогда, очевидно, что корней нет.

Ответ: нет корней.

График функции $y=|x|$.

Вычислить модуль мы можем из любого числа. 2}$.

Может ли значение модуля быть отрицательным. Модуль числа (абсолютная величина числа), определения, примеры, свойства

Модуль числа вводится новое понятие в математике. Разберем подробно, что такое модуль числа и как с ним работать?

Рассмотрим пример:

Мы вышли из дома в магазин. Прошли 300 м, математически это выражение можно записать как +300, смысл числа 300 от знака “+” не поменяется. Расстояние или модуль числа в математике это одно и тоже можно записать так: |300|=300. Знак модуля числа обозначается двумя вертикальными линиями.

А потом в обратном направлении прошли 200м. Математически обратный путь мы можем записать как -200. Но мы не говорим так “мы прошли минус двести метров”, хотя мы вернулись, потому что расстояние как величина остается положительной. Для этого в математике ввели понятие модуля. Записать расстояние или модуль числа -200 можно так: |-200|=200.

Свойства модуля.

Определение:
Модуль числа или абсолютная величина числа – это расстояние от отправной точки до точки назначения.

Модуль целого числа не равного нулю, всегда положительное число.

Записывается модуль так:

1. Модуль положительного числа равно самому числу.
| a|= a

2. Модуль отрицательного числа равно противоположному числу.
|- a|= a

3. Модуль нуля, равен нулю.
|0|=0

4. Модули противоположных чисел равны.
| a|=|- a|= a

Вопросы по теме:
Что такое модуль числа?
Ответ: модуль — это расстояние от отправной точки до точки назначения.

Если перед целым числом поставить знак “+” , что произойдет?
Ответ: число не поменяет свой смысл, например, 4=+4.

Если перед целым числом поставить знак “-” , что произойдет?
Ответ: число изменится на , например, 4 и -4.

У каких чисел одинаковый модуль?
Ответ: у положительных чисел и нуля модуль будет тот же. Например, 15=|15|.

У каких чисел модуль – противоположное число?
Ответ: у отрицательных чисел, модуль будет равен противоположному числу. Например, |-6|=6.

Пример №1:
Найдите модуль чисел: а) 0 б) 5 в) -7?

Решение:
а) |0|=0
б) |5|=5
в)|-7|=7

Пример №2:
Существуют ли два различных числа, модули которых равны?

Решение:
|10|=10
|-10|=10

Модули противоположных чисел равны.

Пример №3:
Какие два противоположных числа, имеют модуль 9?

Решение:
|9|=9
|-9|=9

Ответ: 9 и -9.

Пример №4:
Выполните действия: а) |+5|+|-3| б) |-3|+|-8| в)|+4|-|+1|

Решение:
а) |+5|+|-3|=5+3=8
б) |-3|+|-8|=3+8=11
в)|+4|-|+1|=4-1=3

Пример №5:
Найдите: а) модуль числа 2 б) модуль числа 6 в) модуль числа 8 г) модуль числа 1 д) модуль числа 0.
Решение:

а) модуль числа 2 обозначается как |2| или |+2| это одно и тоже.
|2|=2

б) модуль числа 6 обозначается как |6| или |+6| это одно и тоже.
|6|=6

в) модуль числа 8 обозначается как |8| или |+8| это одно и тоже.
|8|=8

г) модуль числа 1 обозначается как |1| или |+1| это одно и тоже.
|1|=1

д) модуль числа 0 обозначается как |0|, |+0| или |-0| это одно и тоже.
|0|=0

Противоположные числа – это числа, которые отличаются друг от друга только знаком. Выражение –а обозначает, что это число противоположное числу а .

Например, 7 и – 7;

41 и – 41 и т.д.

Число 0 противоположно самому себе!

То есть, для того, чтобы показать противоположность чисел в математике используют знак « – ».

Приписав знак « – » перед положительным числом 5 , мы получим отрицательное число – 5 .

Приписав знак « – » перед отрицательным числом – 5 , мы получим противоположное ему положительное число 5 , то есть – (–5) = 5.

– (–а) = а

На координатной прямой точки, у которых противоположные координаты, расположены на одинаковом расстоянии от начала отсчёта.

AO = OC

BO = OD

Модуль числа

Модуль числа – это расстояние (в единичных отрезках) от начала отсчёта до точки, которая изображает это число на координатной прямой.

Точки А(– 4) и В (4) отдалены от начала отсчёта на 4 единичных отрезков, а числа – 4 и 4 имеют одинаковые модули, равные 4.

Модуль числа а обозначают | а |

Так как модуль – это расстояние, а расстояние не может быть отрицательным, то

модуль числа не может быть отрицательным числом !!!

Модулем положительного числа и нуля является тоже самое число, а модулем отрицательного числа – противоположное ему число:

| а | = а, если а ≥ 0 (если а – неотрицательное число)

| а | = – а, если а

Выводы

Свойства модуля числа:

1. Модуль числа не может быть отрицательным. Модуль числа всегда или положительное число или равен 0.

1. Противоположные числа имеют равные модули.

| – а | = | а | = а

Пример, | – 12 | = | 12 | = 12

Решение уравнений (примеры)

1. – x = 7

вместо – x и 7 напишем противоположные им числа, используя знак «–»
–(– x) = – 7
воспользуемся правилом, что – (–а) = а получим
x = – 7

2. – x = – 10

–(– x) = –(– 10)
x = 10

3. x = –(– 32)

x = 32

4. | x | = 4

x = 4 или x = – 4
Ответ: 4; – 4

5. | x | = 0

x = 0
Ответ: 0

6. | y | = – 8

модуль не может быть отрицательным числом, а значит данное уравнение не имеет решения
Ответ: нет корней

7. | – x | = 12

вспомним второе свойство модуля, что | – а | = | а | = а, тогда
| x | = 12
x = 12 или x = – 12
Ответ: 12; – 12

8. | y | – 2 = 12

подобные уравнения решаются как простые уравнения, только с учётом модуля
| y | = 12 + 2
| y | = 14
y = 14 или y = – 14
Ответ: 14; – 14

9.

10 – 2| x | = 4
2| x | = 10 – 4
2| x | = 6
| x | = 6: 2
| x | = 3
x = 3 или x = – 3
Ответ: 3; – 3

То есть при решении уравнений, содержащих модуль мы получим три вида ответа :

два корня (если под знаком модуля положительное число) , один корень (если под знаком модуля 0)
нет корней (если под знаком модуля отрицательное число) .

Решение простейших неравенств, содержащих модуль

В 5 классе мы решали примеры с простейшими неравенствами. Линейные неравенства бывают строгие и нестрогие.
Строгие неравенства – это неравенства со знаками больше (>) или меньше ( x > a; x

Нестрогие неравенства – это неравенства со знаками больше либо равно (≥) или меньше либо равно (≤).
x ≥ a; x ≤ a.

Примеры

1. Найдите все натуральные значения x, при которых является правильным неравенство x

Решение.
Данное неравенство будет правильным при таких значениях x: 1; 2; 3; 4; 5; 6; 7; 8.
Ответ : х = {1; 2; 3; 4; 5; 6; 7; 8} – натуральные решения данного неравенства.

Примечание:
Число 0 не является решением этого неравества, так как 0 не является натуральным числом;
Число 9 не является решением этого неравества, так как данное неравенство строгое, то есть х строго меньше 9 и не может быть равным 9.

2. а удовлетворяет неравенство а > 12?

Решение.
Поскольку неравенство строгое, то число 13 является наименьшим натуральным значением а, которое удовлетворяет данному неравенству.

Ответ: 13

3. Какое наименьшее натуральное значение а удовлетворяет неравенство а ≥ 12?

Решение.
Поскольку неравенство нестрогое, то число 12 является наименьшим натуральным значением а, которое удовлетворяет данному неравенству.
Ответ: 12.

4.

Решение.
Неравенство двойное (читают как «х больше от 2, но меньше от 9»), строгое, поэтому 3; 4; 5; 6; 7; 8 – натуральные решения данного двойного неравенства.
Ответ : х = {3; 4; 5; 6; 7; 8}

5. Найдите все натуральные значения x, при которых является правильным неравенство 2

Решение.
3; 4; 5; 6; 7; 8; 9 – натуральные решения данного двойного неравенства.
Ответ: х = {3; 4; 5; 6; 7; 8; 9}

6. Найти все целые числа, которые удовлетворяют неравенству| x |

Решение.
| x | Неравенство | x | может быть также записано ) –5 Ответ: х = {–4; –3; –2; –1; 0; 1; 2; 3; 4}

7. Найти все целые числа, которые удовлетворяют неравенству| x | ≤ 5.

Решение.
Неравенство | x | ≤ 5 эквивалентно –5 ≤ x ≤ 5. Неравенство двойное, нестрогое, поэтому числа –5 и 5 войдут в множество чисел, при которых данное неравенство будет правильным. Таким образом, данное неравенство будет правильным при таких значениях x: –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5.
Ответ : х = {–5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5}

8. Найти все целые числа, которые удовлетворяют неравенству | x | > 2 и обозначте их на координатной прямой.

Решение.
Неравенство | x | > 2 эквивалентно x 2. Обозначим на координатной прямой точки, координаты которых удовлетворяют данному неравенству

Поскольку неравенство строгое, то числа – 2 и 2 не входят в множество целых чисел, при которых данное неравенство будет правильным. А на координатной прямой эти точки обозначаем в виде незакрашенной точки.

Ответ : х = {…–5; –4; –3; 3; 4; 5…}

9. Найти все целые числа, которые удовлетворяют неравенству | x | ≥ 2 и обозначте их на координатной прямой.

Решение.
Неравенство | x | ≥ 2 эквивалентно x ≤ – 2 или x ≥ 2. Обозначим на координатной прямой точки, координаты которых удовлетворяют данному неравенству

Поскольку неравенство нестрогое, то числа – 2 и 2 входят в множество целых чисел, при которых данное неравенство будет правильным. А на координатной прямой эти точки обозначаем в виде закрашенной точки.

Ответ : х = {…–5; –4; –3; –2; 2; 3; 4; 5…}

10. Найти все целые числа, которые удовлетворяют неравенству 1

Решение.
Рассмотрим сначала левую часть неравенства. Она означает, что расстояние от начала отсчёта до точек меньше 1. Рассмотрим правую часть неравенства: расстояние от начала отсчёта до этих же точек меньше или равно 3.
Построим эти точки на координатной прямой:

1 и – 1 не входят в множество целых чисел, которые удовлетворяют неравенству, потому что неравенство строгое.
3 и – 3 входят в множество целых чисел, которые удовлетворяют неравенству, потому что неравенство нестрогое.

Ответ: х = {–3; –2; 2; 3}

Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?

На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.

Но для начала вспомним определение модуля . Итак, модулем числа a называется само это число, если a неотрицательно и -a , если число a меньше нуля. Записать это можно так:

|a| = a, если a ≥ 0 и |a| = -a, если a

Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.

Теперь перейдем непосредственно к решению уравнений.

1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.

Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:

{±c, если с > 0

Если |x| = c, то x = {0, если с = 0

{нет корней, если с

1) |x| = 5, т.к. 5 > 0, то x = ±5;

2) |x| = -5, т.к. -5

3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b

1) |x + 2| = 4, т. к. 4 > 0, то

x + 2 = 4 или x + 2 = -4

2) |x 2 – 5| = 11, т.к. 11 > 0, то

x 2 – 5 = 11 или x 2 – 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 нет корней

3) |x 2 – 5x| = -8 , т.к. -8

3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:

f(x) = g(x) или f(x) = -g(x) .

1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.

1. О.Д.З. 5x – 10 ≥ 0

2. Решение:

2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)

3. Объединяем О.Д.З. и решение, получаем:

Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.

Ответ: x = 3

2) |x – 1| = 1 – x 2 .

1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:

(1 – x)(1 + x) ≥ 0

2. Решение:

x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)

x 2 + x – 2 = 0 x 2 – x = 0

x = -2 или x = 1 x = 0 или x = 1

3. Объединяем решение и О.Д.З.:

Подходят только корни x = 1 и x = 0.

Ответ: x = 0, x = 1.

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).

1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:

x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5

x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0

x = 3 или x = 4 x = 2 или x = 1

Ответ: x = 1, x = 2, x = 3, x = 4.

5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:

x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:

|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:

t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:

|x| = 1 или |x| = 5

x = ±1 x = ± 5

Ответ: x = -5, x = -1, x = 1, x = 5.

Рассмотрим еще один пример:

x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому

|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:

t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:

|x| = -2 или |x| = 1

Нет корней x = ± 1

Ответ: x = -1, x = 1.

6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.

1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:

3 – |x| = 4 или 3 – |x| = -4.

Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.

Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1

Ответ x = -7, x = 7.

2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:

3 + |x + 1| = 5 или 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 или x + 1 = -2. Нет корней.

Ответ: x = -3, x = 1.

Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Модуль числа — это расстояние от этого числа до нуля на координатной прямой.

Модуль обозначается с помощью символа: | |.

• Запись |6| читается как «модуль числа 6», или «модуль шести».
• Запись |8| читается как «модуль 8-ми».

Модуль положительного числа равен самому числу. Например, |2| = 2. Модуль отрицательного числа равен противоположному числу |-3| = 3. Модуль нуля равен нулю, то есть |0| = 0. Модули противоположных чисел равны, то есть |-a| = |a|.

Для лучшего понимания темы: «модуль числа» предлагаем воспользоваться методом ассоциаций.

Представим, что модуль числа — это баня , а знак «минус» — грязь .

Оказываясь под знаком модуля (то есть в «бане») отрицательное число «моется» , и выходит без знака «минус» — чистым .

В бане могут «мыться» (то есть стоять под знаком модуля) и отрицательные , и положительные числа , и число ноль . Однако будучи «чистым» положительные числа , и ноль свой знак при выходе из «бани» (то есть из под знака модуля) не меняют !

История модуля числа или 6 интересных фактов о модуле числа

1. Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
2. Ввел в обращение этот термин ученик Исаака Ньютона — английский математик и философ Роджер Котс (1682 – 1716).
3. Великий немецкий физик, изобретатель, математик и философ Готфрид Лейбниц в своих работах и трудах использовал функцию модуля, которую он обозначил mod x .
4. Обозначение модуля было введено в 1841 году немецким математиком
Карлом Вейерштрассом (1815 — 1897).
5. При написании модуль обозначается с помощью символа: | |.
6. Еще одной версии термин «модуль» был введен в 1806 году французским
математиком по имени Жан Робер Аргáн (1768 — 1822). Но это не совсем так.
В начале девятнадцатого века математики Жан Робер Аргáн (1768 — 1822)
и Огюстен Луи Коши (1789 — 1857) ввели понятие «модуль комплексного числа»,
который изучается в курсе высшей математики.

Решение задач на тему «Модуль числа»

Задача №1. Расположи выражения: -|12|, 0, 54, |-(-2)|, -17 в порядке возрастания.

— | 12 | = — 12
| — (— 2) | = 2

17 -17

Ответ: -17

Задача№2. Нужно расположить выражения: -|-14|, -|30|, |-16|, -21, | -(-9) |
в порядке убывания.

Для начала раскроем скобки и модули:

— | — 14| = — 14
— |30| = -30
|-16| = 16
| -(-9) | = 9

16 > 9 > -14 > — 21 > — 30 что будет равносильно:
|-16| > | -(-9) | > — | — 14| > — 21 > — |30|.

Ответ: |-16| > | -(-9) | > — | — 14| > — 21 > — |30|

Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.

Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.

Графически абсолютное значение а обозначается как |a| .

Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.

Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.

Геометрическое значение

Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.

Графически это можно выразить следующим образом: |a| = OA.

Свойства абсолютной величины

Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:

Особенности решения уравнений с модулем

Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.

К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.

|А + 5| = А + 5 , если, А больше или равняется нулю.

5-А , если, А значение меньше нуля.

В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.

Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.

Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.

Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.

Поделитесь статьей с друзьями:

Похожие статьи

Абсолютное значение в алгебре

Абсолютное значение означает …

… насколько далеко число от нуля:

«6» — это 6 от нуля,
и «-6» — это , а также 6 от нуля.

Таким образом, абсолютное значение 6 равно 6 ,
, а абсолютное значение -6 также равно 6

.

 

Символ абсолютного значения

Чтобы показать, что нам нужно абсолютное значение, мы поместили «|» метки с обеих сторон (называемые «полосами»), как в этих примерах:

«|» можно найти над клавишей ввода на большинстве клавиатур.

Более формальный

Более формально имеем:

Что говорит о том, что абсолютное значение x равно:

• x, когда x больше нуля
• 0, когда x равно 0
• −x, когда x меньше нуля (это «переворачивает» число обратно в положительное)

Итак, когда число положительное или нулевое, мы оставляем его в покое, когда оно отрицательное, мы меняем его на положительное с помощью -x.

Пример: что такое |−17| ?

Ну, это меньше нуля, поэтому нам нужно вычислить «−x»:

— ( -17 ) = + 17

(Потому что два минуса дают плюс)

Полезные свойства

Вот некоторые полезные свойства абсолютных значений:

• |а| ≥ 0 всегда!

  В этом есть смысл… |а| никогда не может быть меньше нуля.

• |а| = √(а ² )

  Возведение в квадрат делает его положительным или нулевым (для действительного числа). Тогда взятие квадратного корня «отменит» возведение в квадрат, но оставит его положительным или нулевым.

• |а × б| = |а| × |б|

  Означает, что это одно и то же:

  • абсолютное значение (a умноженное на b) и
  • (абсолютное значение a) умножить на (абсолютное значение b)

  Что также может быть полезно при решении

• |у| = a совпадает с u = ±a и наоборот

  Что часто является ключом к решению большинства вопросов об абсолютном значении.

Пример: Решите |x+2| = 5

Использование «|u| = a совпадает с u = ±a «:

это:|x+2| = 5

то же самое, что и это: x+2 = ±5

 

Имеет два решения:

х+2 = -5	х+2 = +5
х = -7	х = 3

Графически

Построим график этого примера:

|х+2| = 5

Легче построить график, когда у нас есть уравнение «=0», поэтому вычтите 5 с обеих сторон:

|х+2| − 5 = 0

Итак, теперь мы можем построить y=|x+2|−5 и найти, где оно равно нулю.

Вот график y=|x+2|−5, но просто для развлечения построим график, сдвинув его примерно на :

Начните с y=|x|	, затем сдвиньте его влево, чтобы превратилось в y=|x+2|	, затем сдвиньте его вниз, чтобы стало y=|x+2|−5

И два решения (обведены) это -7 и +3.

Неравенства абсолютного значения

Смешивание абсолютных значений и неравенств требует осторожности!

Есть 4 неравенства:

<	≤		>	≥
менее	меньше чем или равно		больше	больше, чем или равно

Меньше, меньше или равно

С «<" и "≤" мы получаем один интервал с центром на нуле:

Пример: Решите |x|

< 3

Это означает, что расстояние от x до нуля должно быть меньше 3:

Все между (но не включая) -3 и 3

Можно переписать как:

−3 < х < 3

 

В качестве интервала можно записать так:

(−3, 3)

То же самое работает для «Меньше или равно»:

Пример: Решите |x| ≤ 3

Все между и включая -3 и 3

Можно переписать как:

−3 ≤ х ≤ 3

В качестве интервала можно записать так:

[−3, 3]

Как насчет большего примера?

Пример: Решите |3x-6| ≤ 12

Перепишите как:

−12 ≤ 3x−6 ≤ 12

Добавить 6:

−6 ≤ 3x ≤ 18

Наконец, умножьте на (1/3). Поскольку мы умножаем на положительное число, неравенства не изменятся:

−2 ≤ х ≤ 6

Готово!

В качестве интервала можно записать так:

[−2, 6]

Больше, больше или равно

Это другое… мы получаем два отдельных интервала :

Пример: Решите |x| > 3

Выглядит так:

До -3 или от 3 и далее

Можно переписать как

.

х < −3   или   х > 3

 

В качестве интервала можно записать так:

(-∞, -3) U (3, +∞)

Осторожно! Не писать как

−3 > х > 3    

«x» не может быть меньше -3 и больше 3 одновременно

Это действительно:

х < −3   или   х > 3    

«x» меньше -3 или больше 3

 

То же самое работает для «Больше или равно»:

Пример: Решите |x| ≥ 3

Можно переписать как

х ≤ −3 или х ≥ 3

 

В качестве интервала можно записать так:

(-∞, -3] U [3, +∞)

 

Функции абсолютного значения

Функция абсолютного значения — это функция, которая содержит алгебраическое выражение в символах абсолютного значения. Напомним, что абсолютное значение числа — это его расстояние от 0 на числовой прямой.

Родительская функция абсолютного значения, записанная как f(x)=| х |, определяется как

f(x)={x      если  x>00      если  x=0−x   если  x<0

Чтобы построить график функции абсолютного значения, выберите несколько значений x и найдите несколько упорядоченных пар.

х	г=| х |
−2	2
−1	1
0	0
1	1
2	2

Нанесите точки на координатную плоскость и соедините их.

Обратите внимание, что график имеет V-образную форму.

(1) Вершина графа (0,0).

(2) Ось симметрии (x=0 или ось y) — это линия, которая делит график на две конгруэнтные половины.

(3) Домен — это множество всех действительных чисел.

(4) Диапазон — это набор всех действительных чисел, больших или равных 0. То есть y≥0.

(5) Точки пересечения по оси X и Y равны 0.

Вертикальное смещение

Для перевода функции абсолютного значения f(x)=| х | по вертикали можно использовать функцию

г(х)=f(х)+к.

Когда k>0, график g(x) смещается на k единиц вверх.

Когда k<0, график g(x) переводит k единиц вниз.

Горизонтальное смещение

Для перевода функции абсолютного значения f(x)=| х | по горизонтали можно использовать функцию

г (х) = f (х-ч).

Когда h>0, график f(x) смещается на h единиц вправо, чтобы получить g(x).

Когда h<0, график f(x) сдвигается на h единиц влево, чтобы получить g(x).

Растяжение и сжатие

Растяжение или сжатие функции абсолютного значения y=| х | определяется функцией y=a| х | где а — константа. График открывается, если a>0 и открывается вниз, когда a<0.

Для уравнений абсолютного значения, умноженных на константу (например, y=a| x |), если 01 — растягивается. Кроме того, если a отрицательно, то график открывается вниз, а не вверх, как обычно.

В более общем виде уравнение для функции абсолютного значения имеет вид y=a| х−h |+k. Также:

• Вершина графа (h,k).
• Домен графа состоит из всех действительных чисел, а диапазон равен y≥k, когда a>0.
• Домен графа состоит из всех действительных чисел, а диапазон равен y≤k, когда a<0.
• Ось симметрии x=h.
• Он открывается вверх, если a>0, и открывается вниз, если a<0.
• Граф y=| х | можно перевести h единиц по горизонтали и k единиц по вертикали, чтобы получить график у = а | х−h |+k.
• График y=a| х | шире, чем график y=| х | если | a |<1 и уже, если |a|>1.

Решение уравнений абсолютного значения — ChiliMath

Решение уравнений с абсолютными значениями так же просто, как работа с обычными линейными уравнениями. Единственный дополнительный ключевой шаг, который вам нужно запомнить, — это разделить исходное уравнение абсолютного значения на две части: положительную и отрицательную ( ± ) составляющие.

Ниже приведен общий подход к тому, как разбить их на два уравнения:

---

Кроме того, нам также необходимо помнить о следующих ключевых моментах относительно описанной выше настройки:

Ключевые моменты, которые следует помнить при решении уравнений абсолютного значения

Ключевой момент №1: Знак \left| х \ справа | должен быть положительным.Для акцента \left| х \ справа | \к + \влево| х \право|.

Ключевой момент № 2: X внутри символа абсолютного значения, \left| {\,\,\,\,\,} \right|, могут быть любыми выражениями.

Ключевой момент № 3. А в правой части уравнения должно быть либо 90 466 положительным числом 90 467, либо 90 466 нулем 90 467, чтобы было решение.

Ключевой момент № 4: Если буква a в правой части является отрицательным числом , то оно не имеет решения.

---

Примеры решения уравнений абсолютного значения

Пример 1: Решите уравнение абсолютного значения \left| х \ справа | =\, — 5 .

Абсолютное значение любого числа либо положительное, либо нулевое. Но это уравнение предполагает, что существует число, абсолютное значение которого отрицательно. Можете ли вы придумать какие-либо числа, которые могут сделать уравнение верным? Нет его.

Поскольку не существует значения x, удовлетворяющего уравнению, мы говорим, что оно не имеет решения .

Фактически, следующие уравнения абсолютного значения также не имеют решений.

---

Пример 2: Решить уравнение абсолютного значения — \left| х \ справа | =\, — 5 .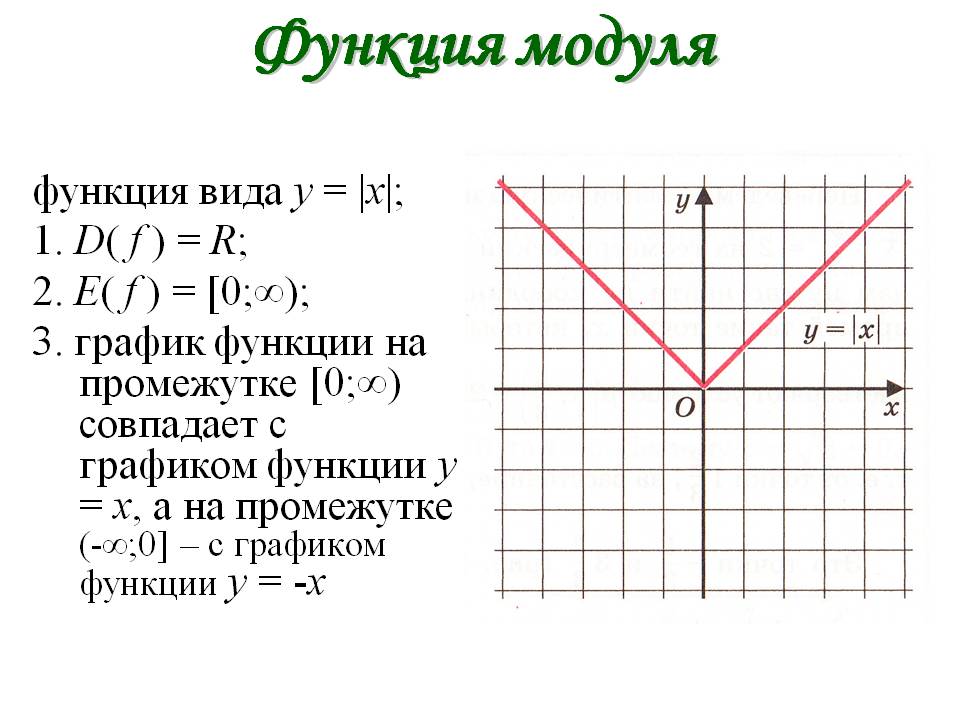

Не спешите делать вывод, что это уравнение не имеет решения. Хотя правая часть уравнения отрицательна, само выражение абсолютного значения должно быть положительным. Но это не так, верно?

Ключевой момент № 1 : Знак \left| х \ справа | должен быть положительным. Для акцента \left| х \ справа | \к + \влево| х \право|.

Прежде чем мы сможем продолжить, нам нужно исключить отрицательный знак символа абсолютного значения.

Заметьте, что данное уравнение имеет коэффициент -1.Разделите обе части уравнения на это значение, чтобы избавиться от отрицательного знака.

Поскольку выражение абсолютного значения и число оба положительны, теперь мы можем применить процедуру, чтобы разбить его на два уравнения.

Следовательно, решение задачи становится

Вы можете проверить наши ответы, подставив их обратно в исходное уравнение. Я оставлю это вам.

---

Пример 3: Решите уравнение абсолютного значения \left| {х — 5} \право| = 3 .

Эта проблема становится интересной, поскольку выражение внутри символа абсолютного значения больше не является просто одной переменной. Не волнуйтесь; установка остается прежней. Просто будьте осторожны, когда вы разбиваете заданное уравнение абсолютного значения на два более простых линейных уравнения, а затем действуйте, как вы обычно решаете уравнения.

Вы можете сверить ответы с исходным уравнением.

---

Пример 4: Решите уравнение абсолютного значения \left| { — 2x + 7} \право| = 25 .

Вы можете подумать, что эта задача сложная из-за -2 рядом с переменной x. Однако это не должно вас пугать, потому что ключевая идея остается прежней. У нас есть символ абсолютного значения, изолированный с одной стороны, и положительное число с другой. Решение этой проблемы похоже на еще один день в парке!

Разбейте его на компоненты + и -, затем решите каждое уравнение.

---

Пример 5 : Решите уравнение абсолютного значения \left| { — 6x + 3} \право| — 7 = 20.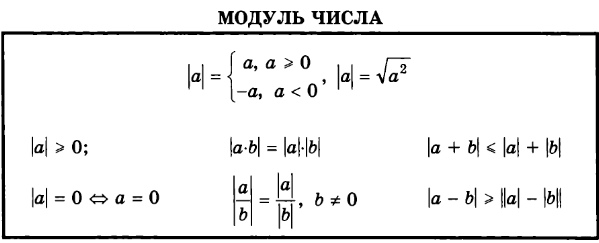

Этот не готов  еще не разделен на два компонента. Почему? Это потому, что символ абсолютного значения сам по себе не находится на одной стороне уравнения. Если вы посмотрите на это, слева будет -7 , которую нужно устранить в первую очередь. Как только мы избавимся от этого, мы сможем продолжать как обычно.

Удалите -7 с левой стороны, добавив с обеих сторон \color{blue}7.

Теперь у нас есть уравнение абсолютного значения, которое можно разбить на две части.2} + 2x — 4} \право| = 4.

Это интересная задача, потому что у нас есть квадратное выражение внутри символа абсолютного значения. Надеюсь, вас не отвлекает то, как это выглядит! Если вы столкнулись с ситуацией, в которой не знаете, как поступить, придерживайтесь основ и вещей, которые вы уже знаете.

Нам все равно, что внутри символа абсолютного значения. Пока оно изолировано, а другая сторона является положительным числом, мы определенно можем применить правило, чтобы разделить уравнение на два случая.

На самом деле, единственное отличие этой задачи от того, что вы делали до сих пор, заключается в том, что вы будете решать квадратные уравнения, а не линейные уравнения.

Мы можем проверить, что наши четыре ответа или решения равны x = -1,4,-2, 0 и 2, построив графики двух функций и посмотрев на их точки пересечения.

---

Решение уравнений с абсолютными значениями Рабочие листы

---

Вас также может заинтересовать:

Графики функций абсолютного значения
Решение неравенств абсолютного значения

Абсолютное значение – свойства и примеры

Что такое абсолютное значение?

Абсолютное значение относится к расстоянию точки от нуля или начала координат на числовой прямой, независимо от направления.Абсолютное значение числа всегда положительно.

Абсолютное значение числа обозначается двумя вертикальными чертами, заключающими число или выражение. Например, абсолютное значение числа 5 записывается как |5| = 5. Это означает, что расстояние от 0 равно 5 единицам:

Точно так же абсолютное значение отрицательного числа 5 обозначается как |-5| = 5. Это означает, что расстояние от 0 составляет 5 единиц:

Число не только показывает расстояние от начала координат, но также важно для построения графика абсолютного значения.

Рассмотрим выражение | х | > 5. Чтобы представить это на числовой прямой, вам нужны все числа, абсолютное значение которых больше 5. Это делается графически, помещая открытую точку на числовой строке.

Рассмотрим другой случай, когда | х | = 5. Сюда входят все абсолютные значения, которые меньше или равны 5. Это выражение изображается на графике путем помещения закрытой точки на числовую прямую. Знак равенства указывает, что все сравниваемые значения включены в график.

Простой способ представления выражений с помощью неравенств заключается в следовании следующим правилам.

• Для | х | < 5, -5 < x  < 5
• Для | х | = 5, -5 = x  = 5
• Для |x + 6| < 5, -5 < 90 605 x 90 606 + 6 < 5

Свойства абсолютного значения

Абсолютное значение обладает следующими фундаментальными свойствами:

1. Неотрицательность |a| ≥ 0
2. Положительная определенность |a| = 0a = 0
3. Мультипликативность         |ab| = |а| |б|
4. Субаддитивность |a + b| ≤ |а| + |б|
5. Идемпотентность ||a|| = |а|
6. Симметрия |−a| = |а|
7. Тождество неразличимого |a − b| = 0 ⇔ a = b
8. Неравенство треугольника |a − b| ≤ |а — с| + |с — б|
9. Сохранение деления |a/b|=|a|/|b| если  b ≠ 0

Пример 1

Упростить -|-6|

Решение

• Преобразование символов абсолютного значения в круглые скобки

–| –6 | = – (6)

• Теперь я могу взять минус через скобки:

– (6) = – 6

Пример 2

Найдите возможные значения x.

|4x| = 16

Решение

В этом уравнении 4x может быть как положительным, так и отрицательным. Итак, мы можем написать его как:

4x = 16 или -4x = 16

разделить обе стороны на 4.

x = 4 или x = -4

, следовательно, два возможных значения x ны -4 и 4.

Пример 3

Решите следующие задачи:

a)        Решите | –9|

Ответить

| –9| = 9

б)        Упростить | 0 – 8 |.

Ответить

| 0 – 8 | = | –8 | = 8

c)        Решить | 9 – 3 |.

Ответить

| 9 – 3 | = | 6| = 6

d)        Упростить | 3 – 7 |.

Ответить

| 3 – 7 | = | –4 | = 4

e)        Тренировка | 0 (–12) |.

Ответить

| 0(–12) | = | 0 | = 0

f)         Упростить | 6 + 2(–2) |.

Ответить

| 6 + 2(–2) | = | 6 – 4 | = | 2| = 2

g)        Решить –| –6 |.

Ответить

–| –6| = – (6) = –6

ч)        Упростить –| (–7) ²  |.

Ответить

–| (–7) ²  | = –| 49 | = –49

i)         Вычислить –| –9 | ²

Ответить

–| –9 | ²  = – (9) ²  = –(4) = –81

j)         Упростить (–| –3|) ² .

Ответ

(- | -3 |) ² = (- (3)) ² = (-3) ² = 9

Пример 4

-|-7 + 4|

Решение

• Прежде всего, начните с вычисления выражений в символах абсолютного значения:
  -|-7 + 4| = -|-3|
• Ввести круглые скобки
  -|-3| = -(3) = -3
• Итак, ответ равен -3.

Пример 5

Водолаз находится на -20 футов ниже поверхности воды. Какое расстояние ему нужно проплыть, чтобы выбраться на поверхность?

Решение

Ему нужно поплавать |-20| = 20 футов.

Пример 6

Вычислите абсолютное значение 19 – 36(3) + 2(4 – 87)?

Решение

19 — 36 (3) + 2 (4 — 87)

= 19 — 108 + 2 (-83)

= 19 — 108 — 166

= -255

Пример 7

Решите уравнение, определив абсолютные значения,

2 |-2 × – 2| – 3 = 13

Решение

Перепишите выражение со знаком абсолютного значения с одной стороны.

• Добавьте 3 к обеим частям выражения

2 | – 2 × – 2| – 3 + 3 = 13 + 3

2 | – 2 × – 2| = 16

|- 2 × – 2| = 8

• Оставшееся уравнение такое же, как и при записи выражения в виде:

– 2 × – 2 = 8 или – 8

1. a) -2 x – 2 = 8

Теперь найдите x
х = – 5

1. б) – 2 х – 2 = – 8

х = 3

• Правильный ответ: (-5, 3).

Пример 8

Вычислить действительные значения выражения с абсолютным значением.

|х – 1| = 2x + 1

Решение

Один из методов решения этого уравнения заключается в рассмотрении двух случаев:
a) Предположим, что x – 1 ≥ 0, и перепишем выражение в следующем виде:

x – 1 = 2x + 1

Вычислить значение x
x = -2
b) Предположим, что x – 1 ≤ 0, и перепишем это выражение как
-(x – 1) = 2x + 1
– x + 1 = 2x + 1
найти x как
x = 0

Важно проверить правильность решений уравнения, потому что все значения x были приняты.
Замена x на – 2 в обеих частях выражения дает.

| (-2) – 1| = |-2 + 1| = 1 в левой части и 2(-2) + 1 = – 3 в правой части

Поскольку два уравнения не равны, следовательно, x = -2 не является ответом на это уравнение.
Проверка x = 0

Замена x на 0 в обеих частях уравнения дает:

|(0) – 1| = 1 слева и 2(0) + 1 = 1 справа.

Два выражения равны, поэтому x = 0 является решением этого уравнения.

 

Обучение абсолютному значению числа в математике

Урок 2: Развитие понятия

Материалы: Каталожные карточки или цифровые «карточки», которые можно раздать учащимся

Стандарты:

• Под абсолютным значением рационального числа понимается его расстояние от 0 на числовой прямой. (6.NS.C.7.C)

Подготовка: Сделайте карточки для У меня есть… У кого есть?

Итоговая и оценочная игра

• Попросите учащихся написать и поделиться своими определениями и примерами из жизни ситуаций с абсолютными значениями.
• Играть У меня есть… У кого есть? Составьте набор из 15 карточек с уравнениями абсолютного значения и 15 карточек со значениями переменной. Если каталожные карточки недоступны или вы адаптируете это для дистанционного обучения, создайте способ, чтобы приведенные ниже 30 уравнений были максимально равномерно распределены между вашими учащимися.

Карты с абсолютной стоимостью	Карты с переменной стоимостью
| х + 5| = 20	x = 15
|5 – x | = 30	x = –25
| х + 6| = 41	x = 35
|–27 – x | = 20	x = –47
–7 + | х | = 0	x = –7
|25 – x | = 18	x = 7
| х + –5| = 38	x = 43
|37 – x | = 70	x = –33
114 – | х | = 7	х = 107
|– х + 100| = 21	х = 121
–|1 + х | = -80	x = 79
| х | = 81	x = –81
| х + 3| = 84	x = 81
|25 + x | = 62	x = –87
| х – 26| = 11	x = 37

Каждая указанная карта абсолютных значений имеет два значения для x Эти значения перекрываются, так что каждая карта значений переменных удовлетворяет двум заданным уравнениям абсолютного значения (первое и второе значения удовлетворяют первому уравнению, второе и третье значения удовлетворяют второму уравнению и так далее, пока последнее и первое значения не удовлетворяют заданному уравнению). последнее уравнение).

Раздайте карточки или уравнения поровну. Убедитесь, что все они были распределены. Выберите учащегося, который скажет «У меня есть», а затем прочитайте значение или уравнение на его карточке. Затем попросите студента сказать: «У кого есть совпадение с моей карточкой?» Любой ученик, у которого есть совпадение, должен сказать «У меня есть… У кого есть…», и игра продолжается до тех пор, пока не будут прочитаны все карточки.Вы можете предложить учащимся встать, когда игра начнется, и сидеть, когда они предлагают ответ. Чтобы все были вовлечены, предложите вознаграждение за успешное завершение игры, поощряя вызовы на подозрительные ответы.

***

Ищете учебную программу по математике, которая повысит уверенность учащихся в математике и предоставит вам насыщенные уроки и задания для учащихся средних классов? Изучите HMH Into Math , наше основное математическое решение для классов K–8.

Решение абсолютных уравнений и неравенств (Алгебра 1, Линейные неравенства) – Mathplanet

Абсолютное число числа а записывается как

$$\слева | а \право |$$

И представляет собой расстояние между а и 0 на числовой прямой.

Уравнение абсолютного значения — это уравнение, содержащее выражение абсолютного значения. Уравнение

$$\слева | х \справа |=а$$

Имеет два решения x = a и x = -a, так как оба числа находятся на расстоянии a от 0.

Чтобы решить уравнение абсолютного значения как

$$\слева | х+7 \справа |=14$$

Вы начинаете с того, что составляете два отдельных уравнения, а затем решаете их по отдельности.

$$x+7 =14$$

$$x+7\, {\color{green} {-\, 7}}\, =14\, {\color{green} {-\, 7}}$$

$$x=7$$

или

$$x+7 =-14$$

$$x+7\, {\color{green} {-\, 7}}\, =-14\, {\color{green} {-\, 7}}$$

$$x=-21$$

Уравнение абсолютного значения не имеет решения, если выражение абсолютного значения равно отрицательному числу, поскольку абсолютное значение никогда не может быть отрицательным.

Неравенство

$$\слева | х \справа |<2$$

Представляет расстояние между x и 0, которое меньше 2

Тогда как неравенство

$$\слева | х \справа |>2$$

Представляет расстояние между x и 0, которое больше 2

Вы можете записать абсолютное неравенство как сложное неравенство.

$$\слева | х \справа |<2\: или

$$-2

Это верно для всех абсолютных значений неравенства.

$$\слева | ax+b \right |0$$

$$=-c

$$\слева | ax+b \right |>c,\: где\: c>0$$

$$=ax+b<-c\: or\: ax+b>c$$

Вы можете заменить > выше на ≥ и < на ≤.

При решении абсолютного неравенства необходимо сначала выделить выражение абсолютного значения на одной стороне неравенства, прежде чем решать неравенство.

---

Пример

Решите абсолютное неравенство

$$2\влево |3x+9 \вправо |<36$$

$$\frac{2\left |3x+9 \right |}{2}<\frac{36}{2}$$

$$\слева | 3x+9 \справа |<18$$

$$-18<3x+9<18$$

$$-18\, {\color{green} {-\, 9}}<3x+9\, {\color{green} {-\, 9}}<18\, {\color{green} { -\, 9}}$$

$$-27<3x<9$$

$$\frac{-27}{{\color{green} 3}}<\frac{3x}{{\color{green} 3}}<\frac{9}{{\color{green} 3} }$$

$$-9

---

Видеоурок

Решите уравнение абсолютного значения

$$4 \влево |2x -1 \вправо | -2 = 10$$

Решение уравнений, содержащих абсолютное значение

Решение уравнений, содержащих абсолютное значение

Чтобы решить уравнение, содержащее абсолютное значение, изолировать абсолютное значение в одной части уравнения.Затем установите его содержимое равным как положительному, так и отрицательному значению числа на другой стороне уравнения и решите оба уравнения.

Пример 1

Решить | х | + 2 = 5.

Изолировать абсолютное значение.

Установите содержимое части абсолютного значения равным +3 и –3.

Ответ: 3, –3

Пример 2

Решить 3| х – 1| – 1 = 11.

Изолировать абсолютное значение.

Установите содержимое части абсолютного значения равным +4 и –4.

Решение для х,

Ответ: 5, –3

Решение неравенств, содержащих абсолютное значение, и построение графика

Чтобы решить неравенство, содержащее абсолютное значение , начните с тех же шагов, что и для решения уравнений с абсолютным значением. Создавая сравнения как с +, так и с другой стороной неравенства, измените направление неравенства при сравнении с отрицательным знаком.

Пример 3

Решите и нарисуйте ответ: | х – 1| > 2.

Обратите внимание, что выражение абсолютного значения уже изолировано.

| х – 1| > 2

Сравните содержимое части абсолютного значения как с 2, так и с –2. Обязательно измените направление неравенства при сравнении его с –2.

Решить для x .

Нарисуйте ответ (см. рисунок 1).

Рис. 1.Графическое решение | х – 1| > 2.

Пример 4

Решите и нарисуйте ответ: 3| х | – 2 ≤ 1,

Изолировать абсолютное значение.

Сравните содержимое части абсолютного значения как с 1, так и с –1. Обязательно измените направление неравенства на обратное, сравнивая его с –1.

Нарисуйте ответ (см. рис. 2).

Рис. 2. График решения задачи 3| х | – 2 ≤ 1.

Пример 5

Решите и нарисуйте ответ: 2|1 – x | + 1 ≥ 3,

Изолировать абсолютное значение.

Сравните содержимое части абсолютного значения как с 1, так и с –1. Обязательно измените направление неравенства на обратное, сравнивая его с –1.

Решить для x .

(Не забудьте переключить направление неравенства при делении на минус)

Нарисуйте ответ (см. рис. 3).

Рисунок 3. График решения 2|1 – x | + 1 ≥ 3,

.