Можно ли извлечь из нуля корень: Квадратный корень из нуля — МАТВОКС — Детская игровая комната «Волшебный лес»

Posted on 03.07.197318.01.2022 by alexxlab

Содержание

Как найти корень из числа. Извлечение корней: способы, примеры, решения

Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.

Ниже мы по очереди рассмотрим основные способы извлечения корней.

Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.

Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.

Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.

Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.

Приступим.

Использование таблицы квадратов, таблицы кубов и т.д.

В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т. д. Что же представляют собой эти таблицы?

Таблица квадратов целых чисел от 0 до 99 включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0 до 99 . Для примера выберем строку 8 десятков и столбец 3 единицы, этим мы зафиксировали число 83 . Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0 до 99 . На пересечении выбранной нами строки 8 десятков и столбца 3 единицы находится ячейка с числом 6 889 , которое является квадратом числа 83 .

Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.

Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.

д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.

Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.

В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .

Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.

Разложение подкоренного числа на простые множители

Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.

Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .

Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.

Разберемся с этим при решении примеров.

Пример.

Извлеките квадратный корень из 144 .

Решение.

Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .

Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.

Разложим 144 на простые множители:

То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .

Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .

Ответ:

Для закрепления материала рассмотрим решения еще двух примеров.

Пример.

Вычислите значение корня .

Решение.

Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .

Ответ:

Пример.

Является ли значение корня целым числом?

Решение.

Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.

Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.

Ответ:

Нет.

Извлечение корней из дробных чисел

Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.

Разберем пример извлечения корня из дроби.

Пример.

Чему равен квадратный корень из обыкновенной дроби 25/169 .

Решение.

По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5 , а квадратный корень из знаменателя равен 13 . Тогда . На этом извлечение корня из обыкновенной дроби 25/169 завершено.

Ответ:

Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.

Пример.

Извлеките кубический корень из десятичной дроби 474,552 .

Решение.

Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .

Ответ:

Извлечение корня из отрицательного числа

Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a и нечетного показателя корня 2·n−1 справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.

Рассмотрим решение примера.

Пример.

Найдите значение корня .

Решение.

Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .

Приведем краткую запись решения: .

Ответ:

Порязрядное нахождение значения корня

В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n -ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.

На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.

Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.

К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.

Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .

Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.

Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9 , вычисляя соответственно 0 2 , 1 2 , …, 9 2 до того момента, пока не получим значение, большее подкоренного числа 5 . Все эти вычисления удобно представлять в виде таблицы:

Так значение разряда единиц равно 2 (так как 2 2 5 ). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9 , сравнивая полученные значения с подкоренным числом 5 :

Так как 2,2 2 5 , то значение разряда десятых равно 2 . Можно переходить к нахождению значения разряда сотых:

Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .

Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.

Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =02 151,186 , таким образом, старшим разрядом является разряд десятков.

Определим его значение.

Так как 10 3 2 151,186 , то значение разряда десятков равно 1 . Переходим к единицам.

Таким образом, значение разряда единиц равно 2 . Переходим к десятым.

Так как даже 12,9 3 меньше подкоренного числа 2 151,186 , то значение разряда десятых равно 9 . Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.

На этом этапе найдено значение корня с точностью до сотых: .

В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.

Список литературы.

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Формулы корней. Свойства квадратных корней.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. ..»
И для тех, кто «очень даже…»)

В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.

Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…

Начнём с самой простой. Вот она:

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Для вычисления квадратного корня без калькулятора существует несколько методов.

Как найти корень из числа – 1 способ

Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.

Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя. Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
√5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18.
Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.

Как найти корень из числа – 2 способ

Другой способ заключается в делении в столбик. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.

На первый взгляд может показаться, что процедура разложения квадратного корня на множители сложная и неприступная. Но это не так. В этой статье мы расскажем вам, как подступиться к квадратному корню и множителям, а также легко и просто разложить квадратный корень, воспользовавшись двумя проверенными методами.

Yandex.RTB R-A-339285-1

Разложение корня на множители

Для начала определим цель процедуры разложения квадратного корня на множители. Цель — упростить квадратный корень и записать его в удобном для вычислений виде.

Определение 1

Разложение квадратного корня на множители — нахождение двух или нескольких чисел, которые, при условии перемножения их друг на друга, дадут число равное исходному. Например: 4×4 = 16.

Если вы найдете множители, то сможете легко упростить выражение с квадратным корнем или вовсе его упразднить:

Пример 1

Разделите подкоренное число на 2, если оно четное.

Подкоренное число всегда следует делить на простые числа, поскольку любое значение простого числа можно разложить на простые множители. Если у вас нечетное число, то попробуйте разделить его на 3. Не делится на 3? Делите дальше на 5, 7, 9 и т.д.

Запишите выражение в виде корня произведения двух чисел.

Например, можно упростить таким способом 98: = 98 ÷ 2 = 49 . Из этого следует, что 2 × 49 = 98 , поэтому можно переписать задачу следующим образом: 98 = (2 × 49) .

Продолжите раскладывать числа, пока под корнем не останется произведение двух одинаковых чисел и других чисел.

Возьмем наш пример (2 × 49) :

Поскольку 2 уже и так максимально упрощено, необходимо упростить 49 . Ищем простое число, на которое можно разделить 49 . Очевидно, что ни 3 , ни 5 не подходят. Остается 7: 49 ÷ 7 = 7 , поэтому 7 × 7 = 49 .

Записываем пример в следующем виде: (2 × 49) = (2 × 7 × 7) .

Упростите выражение с квадратным корнем.

Поскольку в скобках у нас произведение 2 и двух одинаковых чисел (7) , то мы можем вынести за знак корня число 7 .

Пример 2

(2 × 7 × 7) = (2) × (7 × 7) = (2) × 7 = 7 (2) .

В тот момент, когда под корнем оказалось два одинаковых числа, останавливайтесь с разложением чисел на множители. Конечно, если вы использовали все возможности по максимуму.

Запомните: существуют корни, которые можно упрощать многократно.

В таком случае, числа, которые мы выносим из-под корня, и числа, которые стоят перед ним, перемножаются.

Пример 3

180 = (2 × 90) 180 = (2 × 2 × 45) 180 = 2 45

но 45 можно разложить на множители и еще раз упростить корень.

180 = 2 (3 × 15) 180 = 2 (3 × 3 × 5) 180 = 2 × 3 5 180 = 6 5

Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.

Если после разложения подкоренного выражения на произведение простых чисел, у вас не получилось получить два одинаковых числа, то такой корень упростить нельзя.

Пример 4

70 = 35 × 2 , поэтому 70 = (35 × 2)

35 = 7 × 5 , поэтому (35 × 2) = (7 × 5 × 2)

Как видим, все три множителя — простые числа, которые нельзя разложить на множители. Среди них нет одинаковых чисел, поэтому не представляется возможным вынести целое число из-под корня. Упростить 70 нельзя.

Полный квадрат

Запомните несколько квадратов простых чисел.

Квадрат числа получается, если умножить его на самого себя, т.е. при возведении в квадрат. Если вы запомните десяток квадратов простых чисел, то это очень упростить вам жизнь в дальнейшем упрощении корней.

Пример 5

1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81 10 2 = 100

В случае если под знаком корня квадратного корня находится полный квадрат, то стоит убрать знак корня и записать квадратный корень данного полного квадрата.

Сложно? Нет:

Пример 6

1 = 1 4 = 2 9 = 3 16 = 4 25 = 5 36 = 6 49 = 7 64 = 8 81 = 9 100 = 10

Попробуйте разложить число под знаком корня на произведения полного квадрата и другого числа.

Если вы видите, что подкоренное выражение раскладывается на произведение полного квадрата и какого-либо числа, то, запомнив несколько примеров, вы существенно сэкономите время и нервы:

Пример 7

50 = (25 × 2) = 5 2 . Если подкоренное число оканчивается на 25, 50 или 75, вы всегда можете разложить его на произведение 25 и какого-то числа.

1700 = (100 × 17) = 10 17 . Если подкоренное число оканчивается на 00, вы всегда можете разложить его на произведение 100 и какого-то числа.

72 = (9 × 8) = 3 8 . Если сумма цифр подкоренного числа равна 9, вы всегда можете разложить его на произведение 9 и какого-то числа.

Попробуйте разложить подкоренное число на произведение нескольких полных квадратов: вынесите их из-под знака корня и перемножьте.

Пример 8

72 = (9 × 8) 72 = (9 × 4 × 2) 72 = 9 × 4 × 2 72 = 3 × 2 × 2 72 = 6 2

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Цель упрощения квадратного корня – это переписать его в такой форме, которую проще использовать в вычислениях. Разложение числа на множители – это нахождение двух или нескольких чисел, которые при перемножении дадут исходное число, например, 3 х 3 = 9. Найдя множители, вы сможете упростить квадратный корень или вообще избавиться от него. Например, √9 = √(3×3) = 3.

Если подкоренное число четное, разделите его на 2. Если подкоренное число нечетное, попробуйте разделить его на 3 (если число на 3 не делится, делите его на 5, 7 и так далее по списку простых чисел). Делите подкоренное число исключительно на простые числа, так как любое число можно разложить на простые множители. Например, вам не нужно делить подкоренное число на 4, так как 4 делится на 2, а вы уже разделили подкоренное число на 2.

Перепишите задачу как корень из произведения двух чисел. Например, упростим √98: 98 ÷ 2 = 49, поэтому 98 = 2 x 49. Перепишите задачу так: √98 = √(2 x 49).

Продолжите разложение чисел до тех пор, пока под корнем не останется произведение двух одинаковых чисел и других чисел. Это имеет смысл, если задуматься о смысле квадратного корня: √(2 х 2) равен числу, которое, будучи умноженным само на себя, будет равно 2 х 2. Очевидно, что это число 2! Повторите описанные выше действия для нашего примера: √(2 х 49).

2 уже максимально упрощено, так как это простое число (см. список простых чисел выше). Поэтому разложите на множители число 49.
49 на 2, 3, 5 не делится. Поэтому переходите к следующему простому числу – 7.
49 ÷ 7 = 7, поэтому 49 = 7 x 7.
Перепишите задачу так: √(2 x 49) = √(2 x 7 x 7).

Упростите квадратный корень. Так как под корнем находится произведение 2 и двух одинаковых чисел (7), вы можете вынести такое число за знак корня. В нашем примере: √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).

Как только под корнем вы получили два одинаковых числа, вы можете остановиться с разложением чисел на множители (если их все еще можно разложить). Например, √(16) = √(4 х 4) = 4. Если вы продолжите разложение чисел на множители, вы получите тот же ответ, но проделаете больше вычислений: √(16) = √(4 х 4) = √(2 х 2 х 2 х 2) = √(2 х 2) √(2 х 2) = 2 х 2 = 4.

Некоторые корни можно упрощать многократно. В этом случае числа, выносимые из-под знака корня, и числа, стоящие перед корнем, перемножаются. Например:

√180 = √(2 x 90)
√180 = √(2 x 2 x 45)
√180 = 2√45, но 45 можно разложить на множители и еще раз упростить корень.
√180 = 2√(3 x 15)
√180 = 2√(3 x 3 x 5)
√180 = (2)(3√5)
√180 = 6√5

Если вы не можете получить два одинаковых числа под знаком корня, то такой корень упростить нельзя. Если вы разложили подкоренное выражение на произведение простых множителей, и среди них нет двух одинаковых чисел, то такой корень упростить нельзя. Например, попробуем упростить √70:

70 = 35 x 2, поэтому √70 = √(35 x 2)
35 = 7 x 5, поэтому √(35 x 2) = √(7 x 5 x 2)
Все три множителя являются простыми, поэтому их больше нельзя разложить на множители. Все три множителя разные, поэтому вы не сможете вынести целое число из-под знака корня. Следовательно, √70 упростить нельзя.

Извлечение квадратного корня в математике с примерами решения и образцами выполнения

Квадратный корень легко извлекается с помощью калькулятора. Для этого достаточно набрать на нём исходное число и нажать клавишу корня √ .

Если калькулятора под рукой нет, то квадратный корень извлекают пользуясь алгоритмом извлечения квадратного корня.

Определение действия извлечения корня

Корнем n-й степени из числа а называется число х, n-я степень которого равна а. Например, число 2 есть корень пятой степени из 32, ибо Корень второй степени иначе называется квадратным корнем, корень третьей степени — кубическим корнем.

Действие, посредством которого по данному числу а и показателю n находится корень n-й степени из а, называется извлечением корня. Показатель n называется показателем корня. Извлечение корня есть
действие, обратное действию возведения в степень. Корень n-й степени из числа а обозначается следующим образом:

В случае квадратного корня показатель не указывается, так что квадратный корень из числа а обозначается

Из определения корня следует, что в частности

Арифметическое значение квадратного корня

Допустим, что нам дано положительное число а такое, что для него существует квадратный корень, например а = 4. Мы видим, что не одно, а целых два числа удовлетворяют определению квадратного корня из 4, именно числа 2 и —2. Действительно, Таким же образом обстоит дело и для всякого другого положительного числа а: если х удовлетворяет условию то и число —х удовлетворяет этому условию, именно Поэтому каждое из двух противоположных чисел х и —х с одинаковым основанием может быть названо квадратным корнем из числа а. Из этих двух чисел одно положительно, другое отрицательно. Однако положительное значение квадратного корня из положительного числа может существовать только одно.

Действительно, допустим, что

причем х и у оба положительны. Тогда

Разлагая на множители левую часть, мы придем к равенству

Произведение двух чисел х—у и х + у равно нулю. Следовательно, равен нулю один из сомножителей. Однако х + у есть положительное число, как сумма двух положительных чисел.

Следовательно,

Положительное значение квадратного корня из положительного числа называется арифметическим значением квадратного корня.

Условимся знаком обозначать именно арифметическое значение квадратного корня. Это условие вносит определенность при пользовании знаком корня. Так, согласно этому условию,

Однако приняв это условие, о нем необходимо помнить, чтобы не делать ошибок при пользовании знаком квадратного корня.

Так, а не —2, что, казалось бы, более естественно. Равенство есть верное равенство только при

При мы должны считать В то же время равенство будет верно всегда.

Постановка вопроса о приближенном вычислении корня

Извлечение квадратного корня из данного числа выполнимо далеко не всегда, если ограничиться рассмотрением рациональных чисел. Так, извлечение квадратного корня из отрицательного числа есть действие невыполнимое, ибо квадрат любого рационального числа не может быть отрицательным.

Более того, далеко не из каждого рационального положительного числа можно извлечь рациональный квадратный корень. Действительно, рассмотрим таблицу квадратов целых чисел:

Мы видим, что квадраты целых чисел очень быстро возрастают, так что промежутки между квадратами соседних целых чисел тоже довольно быстро растут. Целые числа, находящиеся внутри таких промежутков, не являются квадратами целых чисел. Докажем, что они не являются и квадратами дробных чисел.

Для этого достаточно установить, что квадрат дробного числа не может быть числом целым.

Действительно, каждое дробное число а может быть представлено в виде несократимой дроби т. е. в виде частного от деления двух целых чисел р и q, не имеющих общих простых множителей, причем q > 1.

Если Очевидно, что тоже есть
несократимая дробь, ибо содержит только те простые множители, которые входят в — только те простые множители, которые входят в q а р и q общих множителей не имеют. Таким образом, не может быть целым числом.

Итак, числа 2, 3, 5, 6, 7, 8, 10, 11, 12… не являются ни квадратами целых чисел, ни квадратами чисел дробных. Следовательно, извлечение квадратного корня из этих чисел есть действие невыполнимое, если оставаться в области рациональных чисел.

Рассмотрим теперь более подробную таблицу квадратов, придавая числу а значения через Ограничимся при этом рассмотрением промежутка от а = 1 до а = 2:

Промежуток между двумя соседними квадратами в этой таблице в среднем в 10 раз меньше, чем промежуток между соседними квадратами 1 и 4 в предшествующей таблице.

Рассмотрим теперь таблицу квадратов, придавая числу а значения через , ограничившись промежутком от а = 1,4 до а =1,5:

По сравнению с предыдущей таблицей, промежутки между соседними квадратами еще уменьшились, в среднем в 10 раз.

Таким образом, если брать значения а все более «густо», т. е. делая промежутки между соседними значениями для а все меньше и меньше, то и промежутки между соседними значениями будут становиться все меньше и меньше. Поэтому, если взять промежутки
между соседними значениями для а достаточно малыми, мы можем приблизиться посредством значений к любому положительному числу b с любой степенью точности.

Проследим, например, за приближениями к числу 2 посредством квадратов на протяжении составленных таблиц. Из первой таблицы мы находим, что наиболее близкие к числу 2 квадраты имеют числа 1 и 2; Во второй таблице числами, дающими наиболее близкие к числу 2 квадраты, являются 1,4 и 1,5, причем Третья таблица дает еще лучшие приближения:

Если мы пожелаем еще улучшить приближения, мы можем рассмотреть квадраты чисел между 1,41 и 1,42, взяв их через 0,001. Это рассмотрение нам даст

Таким образом, среди рациональных чисел не существует числа, квадрат которого равен 2, но существуют числа, квадраты которых сколь угодно близко подходят к 2.

То же самое можно сказать о любом другом положительном числе, для которого точное извлечение корня в области рациональных чисел невозможно. Поэтому имеет смысл ставить вопрос о приближенном
вычислении квадратного корня с некоторой наперед заданной точностью. Так, числа 1 и 2 являются приближенными значениями для с точностью до 1; числа 1,4 и 1,5 являются приближенными значениями для с точностью до 0,1; 1,41 и 1,42 — приближенные значения с точностью до 0,01; 1,414 и 1,415 — приближенные значения с точностью до 0,001 и т. д.

Дадим теперь строгое определение приближенных значений квадратного корня из данного положительного числа.

Приближенным значением с недостатком для квадратного корня из данного положительного числа bс точностью до а называется такое положительное число а, что

В свою очередь, число а + а называется приближенным значением с избытком для с точностью до а.

Для практических целей в качестве меры точности а принимаются числа 0,1, 0,01, 0,001 и т. д. В этих случаях за приближенное значение корня принимаются десятичные дроби с соответствующим числом цифр после запятой.

Приближенные значения корня можно находить посредством испытаний, постепенно увеличивая точность до той, которая требуется в задаче. Рассмотрим еще один пример.

Пример:

Вычислить с точностью до 0,01.

Решение:

Приближения с точностью до 0,1. мы находим из приведенной выше таблицы. Приближение с недостатком есть 1,7 ибо Для вычисления приближения с точностью до 0,01 испытываем Таким образом, с точностью до 0,01 (с
недостатком)

Способом испытаний мы можем приближенно вычислять корень из любого положительного числа с любой степенью точности. Однако этот способ требует хотя и простых, но утомительных вычислений. В следующих параграфах мы познакомимся с более удобными способами вычисления квадратного корня.

Отметим, что ставить вопрос о приближенном вычислении квадратного корня из отрицательного числа бессмысленно, так как приближаться к данному отрицательному числу посредством квадратов рациональных чисел невозможно.

Извлечение квадратного корня при помощи графика

Выведенные в предшествующих параграфах свойства и особенности действия извлечения квадратного корня становятся особенно наглядными, если перейти от рассмотрения таблицы квадратов к графику зависимости Этот график нами уже рассматривался в § 17 гл. II

Приводим снова этот график (рис. 26). Он имеет вид кривой линии, состоящей из двух бесконечных ветвей, симметричных относительно оси ординат. Эти ветви сходятся в начале координат, плавно переходя одна в другую. Как уже было сказано, эта кривая называется параболой.

Задача извлечения
квадратного корня заключается в
определении числа х из зависимости
при данном у. Для решения этой задачи при помощи
графика нужно на параболе
найти точки, имеющие данную ординату у, и определить абсциссы этих точек.

Очевидно, что при у < 0 таких точек нет, ибо весь график расположен выше оси абсцисс, касаясь ее лишь в начале координат. При у = 0 такая точка единственна, это начало координат. Абсцисса ее равна тоже нулю. При у > 0 таких точек оказывается две, расположенных симметрично относительно оси ординат. Это соответствует тому, что квадратный корень из положительного числа имеет два значения, имеющие одинаковую абсолютную величину, но отличающиеся знаками. Выбор арифметического значения квадратного корня соответствует тому, что из двух ветвей параболы мы рассматриваем только одну, именно правую ветвь. На этой ветви точка с заданной ординатой оказывается уже единственной. Измерив абсциссу этой точки, мы получим приближенное значение с той точностью, которую допускает график.

Таким образом, из графика зависимости мы видим, что корень из отрицательного числа не существует и что корень из любого положительного числа существует и имеет два значения.

Увеличивая масштаб, мы можем построить график с любой заданной степенью точности. Следовательно, и само извлечение корня из данного положительного числа можно осуществить с любой точностью.

График зависимости может служить для фактического вычисления квадратных корней с небольшой точностью.

С этой целью следует тщательно построить график на
миллиметровой бумаге, приняв за единицу масштаба 10 см и придавая переменной х значения от 0 до 1 через каждые 0,1 (рис. 27). Тогда непосредственно по графику находятся квадратные корни чисел, заключенных между 0 и 1.

При помощи этого графика можно также находить значения корня из любого положительного числа b. Для этого нужно найти какое либо число а, удовлетворяющее условию Затем, найдя частное , которое будет меньше единицы, извлечь из него корень при помощи графика и умножить этот корень на а. Результат даст Действительно,

Следовательно,

Если подобрать а так, то точность при применении этого способа достигает 1 — 2% величины искомого корня.

Пусть, например, требуется найти Возьмем По графику, и следовательно, Ручаться за точность второго знака после запятой здесь нельзя,
возможна ошибка на 0,02 — 0,03 в ту или другую сторону. В действительности с точностью до 0,001

Извлечение квадратного корня из числа, заключенного между 1 и 100, с точностью до 0,1

Приступим к объяснению одной удобной арифметической схемы для приближенного извлечения квадратного корня с заданной точностью.

Допустим, что нам уже известно, что число 7,236 есть
приближенное значение квадратного корня из числа A= 52,365, взятое с недостатком, с точностью до 0,001. Тогда числа 7; 7,2; 7,23 и 7,236 представляют собой приближенные значения с недостатком, и каждое последующее из этих приближений является более точным, чем предыдущее. Мы можем считать, что каждое последующее получается из предыдущего прибавлением некоторой поправки. Именно, 7,2 = 7 + 0,2; 7,23 = 7,2 + 0,03; 7,236 = 7,23 + 0,006.

Мы сможем вычислять квадратные корни с любой степенью точности, если нам удастся указать способ вычисления поправки к уже известному приближению с недостатком так, чтобы после прибавления этой поправки получалось бы снова приближение с недостатком, но значительно более точное.

Для вывода удобного способа вычисления таких поправок рассмотрим задачу в общем виде.

Пусть а есть приближенное значение с недостатком для
квадратного корня из положительного числа A, и пусть b есть поправка, которую нужно добавить к числу а, чтобы получить более точное приближение к корню, тоже с недостатком. Предположим, что эта поправка мала по сравнению с самим числом а.

Примем сначала, что a + b есть точное значение . Тогда имеет место равенство Раскрывая скобки, получим

откуда

Вспомним теперь, что поправку b мы ищем только приближенно. Ввиду сделанного предположения, что искомая поправка мала по сравнению с числом а мы можем отбросить в знаменателе слагаемое b, и тогда получим для b приближенное равенство

В знаменателе мы отбросили положительное слагаемое, тем самым мы уменьшили знаменатель, а всю дробь увеличили. Следовательно, число больше истинной поправки. Поэтому если мы хотим получить значение корня снова с недостатком, то мы должны взять в качестве поправки число, несколько меньшее, чем , например округлить это частное, приняв во внимание только первую значащую цифру.

Для того чтобы проверить, что вычисленная таким способом поправка дает после прибавления к а снова приближение с недостатком, надо проверить, что разность положительна. Эту разность удобно представить в виде

Действительно, число уже вычислялось при вычислении поправки, а вычисление произведения выполняется без труда. Если исследуемая разность все же окажется отрицательной, то это обозначает, что вычисленная поправка велика и ее следует еще уменьшить.

Рассмотрим пример на применение этих соображений. Пример. Вычислить с точностью до 0,1.

Решение. В качестве первого приближения возьмем а = 9. В качестве поправки следует взять число, немного меньшее, чем

Берем поправку b = 0,6. Эта поправка дает значение с недостатком, ибо

Таким образом, число a + b = 9,6 есть приближение к с недостатком. Число 9,7 является приближением с избытком, ибо поправка , в силу сказанного выше, уже больше
истинной, а поправка 0,7 и подавно. Итак, с точностью до (с недостатком).

Все вычисления очень удобно производить по следующей схеме:

Порядок действий следующий:

1) пишем данное число под знаком корня;
2) определяем целую часть корня 9, возводим ее в квадрат и вычитаем из подкоренного выражения;
3) слева от полученной разности проводим вертикальную черту и слева от нее запишем4) приближенно делим разность 11,43 на 18 с точностью до 0,1 с недостатком. Получаем 0,6;
5) к числу 18 добавляем 0,6 и сумму умножаем на 0,6. Произведение записываем под ранее вычисленной разностью 11,43 и вычитаем из нее. Так как последняя разность 0,27 оказалась положительной, то вычисление заканчивается. Число 0,6 присоединяется к числу 9 в качестве поправки. Напоминаем, что последняя разность 0,27 есть разность чисел 92,43 и

Пример:

Вычислить с точностью до 0,1.

Решение:

Решаем этот пример, пользуясь той же схемой:

При делении числа 15 на 6 мы получим, после округления, 0,8. Однако такая поправка слишком велика, так как 6,8 • 0,8 = 5,44 > 5. Примем в качестве поправки 0,7.

Поправка 0,7 оказалась подходящей.

Последняя разность 0,31 есть К числу 5 мы приписали нули после запятой, чтобы было удобнее производить вычитание.

Пример:

Вычислить с точностью до 0,l. Решение.

При делении числа 2,41 на 2 получается с точностью до 0,1 число 1,2, которое явно велико в качестве поправки. Такой плохой результат получается потому, что здесь поправка совсем немала по сравнению с первым приближением, и поэтому приближенное равенство
оказывается очень грубым.

Даже 0,9 велико в качестве поправки, ибо 2,9 • 0,9 = 2,61 >2,41. Берем 0,8.

Извлечение квадратного корня из числа, заключенного между 1 и 100, с точностью до 0,01

Пример:

Извлечь квадратный корень из числа 92,4317 с
точностью до 0,01.

Решение:

Сначала извлекаем корень с точностью до 0,1,
пользуясь уже рассмотренным способом:

Легко сообразить, что следует делать дальше. Примем а = 9,6 за исходное приближение и ищем для него поправку по прежнему правилу. Вычислять снова разность нам не нужно, ибо эта разность уже вычислена, ©на равна последней разности 0,2717. Мы должны поделить эту разность на 2-9,6 = 19,2 с точностью до 0,01. Получившуюся поправку b = 0,01 добавить к 2а =19,2, полученное число 2а -}-&= 19,21 умножить на 6 = 0,01 и сравнить с разностью 0,2717. Все эти действия удобно провести по прежней схеме. Полная запись будет выглядеть так:

Последняя разность 0,0796 есть

Заметим, что мы могли бы не записывать в третьей строчке две последние цифры, так как их роль сказывается только в пятой строчке. Далее, для упрощения записи можно было бы не писать запятых и
нулей перед значащими цифрами, имея при этом в виду, что тогда при делении последнюю цифру делимого нужно отбрасывать, выполняя деление с точностью до целого.

Принимая все это во внимание, запись можно провести так:

Продолжая вычисления, мы можем извлечь корень с точностью до 0,001; 0,0001 и т. д.

Извлечение квадратного корня из любого данного числа с любым заданным числом десятичных знаков

Способ извлечения квадратного корня, изложенный в § 5 и 6, применялся там только к числам, заключенным между 1 и 100, т. е. к числам с однозначной или двузначной целой частью. Однако этот способ легко распространяется на любые положительные числа, целые или заданные десятичной дробью. Это следует из того, что при умножении подкоренного числа на 100 корень увеличивается в 10 раз, а при делении подкоренного числа на 100 корень уменьшается в 10 раз.

Действительно, если то

так как а

ибо

Умножение или деление на 100 равносильно перенесению запятой на два разряда вправо или влево. Умножение или деление на 10 равносильно перенесению запятой на один разряд. Повторное умножение или деление на 100 равносильно перенесению запятой на четное число урядов. Очевидно, что за счет такого перенесения запятой в подкоренном числе можно добиться того, чтобы целая часть нового подкоренного числа оказалась однозначным или двузначным числом.

К этому числу можно применить указанный прием для извлечения квадратного корня. Чтобы получить корень из исходного числа, нужно в полученном корне перенести запятую в обратном направлении на вдвое меньшее число разрядов.

Например, чтобы извлечь корень мы сначала перенесем запятую на два разряда вправо. мы вычислили; он равен 9,61 (с точностью до 0,01). Следовательно, (с точностью до 0,001).

Сформулируем теперь общее правило для извлечения корня из данного числа с данным числом десятичных знаков, обобщив в этом правиле все высказанные выше соображения.

Правило. Чтобы извлечь квадратный корень из данного положительного целого или записанного в виде десятичной дроби числа с, данной точностью, нужно:

Целая часть, вычисляемая в п. 5 правила, может оказаться больше 9 только на первом шагу вычислений, т. е. при вычислении второй цифры.

Записать это число под знаком квадратного корня и разбить его цифры на «грани» по две цифры в каждой, начиная от запятой, вправо и влево. Если требуется вычислить корень с точностью до 1, то грани, расположенные направо от запятой, можно отбросить. Если требуется вычислить корень с точностью до 0,1, следует справа от запятой сохранить одну грань, при вычислении с точностью до 0,01 оставить две грани и т. д. Если при этом окажется, что цифр для заполнения нужного числа граней не хватает, приписать надлежащее количество нулей.
Извлечь корень из старшей грани с точностью до 1, с недостатком (или точно, если это возможно). Полученное число принять за первую цифру искомого корня.
Из старшей грани вычесть квадрат первой цифры и к полученной разности приписать вторую грань. Слева от полуденного результата провести вертикальную черту.
Слева от черты записать удвоенную первую цифру.
Найти целую часть частного от деления числа десятков первой разности на число, записанное слева. Если полученное число окажется больше 10, заменить числом 9.
Полученное однозначное число подвергнуть следующему испытанию: приписать его в качестве цифры к числу, записанному слева, получившееся число умножить на испытуемое однозначное число и сравнить произведение с разностью, записанной справа от черты. Если это произведение больше указанной разности, уменьшить испытуемое число на одну единицу и вновь подвергнуть испытанию.
Если после испытания произведение окажется меньше указанной разности, подписать его под ней и вычесть. Испытанное однозначное число принять за вторую цифру корня.
К вновь полученной разности приписать следующую грань и определить третью цифру тем же приемом, каким била определена вторая цифра.
Продолжать аналогичные вычисления до тех пор, пока не будет достигнута требуемая точность.
Запятую в результате нужно поставить после того, как будут исчерпаны грани, предшествующие запятой в подкоренном числе.

Отрицательный результат испытания в п. 6 правила довольно часто имеет место на первом шагу вычислений, когда поправка еще не очень мала, по
сравнению с первым приближением. На дальнейших шагах вычислений отрицательный результат испытания получается крайне редко.

Если подкоренное число имеет 0 целых и вслед затем следует нуль, корень имеет тоже 0 целых и затем столько нулей, сколько граней из нулей следует за запятой в подкоренном числе. Первая значащая цифра корня есть целая часть корня из первой значащей грани подкоренного числа.

Применение графиков для приближенного решения уравнений и систем двух уравнений с двумя неизвестными

Мы уже не раз пользовались графиками для приближенных вычислений. Графический способ решения задач является очень полезным для приложений вследствие большой простоты и наглядности. Конечно, им следует пользоваться только в тех случаях, когда не требуется очень большой точности результата. Достоинством графического
способа является также его большая общность. В частности, с помощью графиков можно решать приближенно даже довольно сложные уравнения и системы уравнений. Не вдаваясь в общую теорию построения графиков и их применений* ограничимся рассмотрением двух примеров.

Пример:

Решить приближенно уравнение

Решение:

Построим сначала график зависимости

а затем найдем на этом графике точки, для которых у = 0. Абсциссы этих точек и дадут решения уравнения. Прежде всего вычислим таблицу значений:

По этой таблице строим график (рис. 28), соединяя точки возможно более плавной линией. Из этого графика мы видим, что интересующих нас точек имеется три. Их абсциссы приближенно равны —1,8; 0,3 и 1,5. Следовательно, уравнение

имеет три решения

Чтобы найти более точные значения для корней уравнения, нужно построить с большей точностью и в большем масштабе участки графика, примыкающие к интересующим нас точкам.

Пример:

Решить приближенно систему уравнений

Для решения задачи строим на одном чертеже графики зависимостей и Нас интересуют точки, координаты которых связаны обеими зависимостями, т.е. точки, принадлежащие обоим графикам. Такими точками, являются точки пересечения графиков. Вычислим таблицы значений.

При вычислении второй таблицы мы придавали конкретные значения величине у и вычисляли соответствующие значения для х. Здесь это удобно, так как уравнение, определяющее зависимость, решено относительно х.

Графики по этим таблицам изображены на рис. 29. Мы видим, что графики пересекаются в четырех точках. Следовательно, система имеет четыре решения.

Приближенные решения системы даются следующими значениями для х и у:

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Тождественные преобразования алгебраических выражений
Функции и графики
Преобразования графиков функций
Квадратная функция и её графики
Алгебраические неравенства
Неравенства
Неравенства с переменными
Прогрессии в математике
Арифметическая прогрессия
Геометрическая прогрессия
Показатели в математике
Логарифмы в математике
Исследование уравнений
Уравнения высших степеней
Уравнения высших степеней с одним неизвестным
Комплексные числа
Непрерывная дробь (цепная дробь)
Алгебраические уравнения
Неопределенные уравнения
Соединения
Бином Ньютона
Число е
Непрерывные дроби
Функция
Исследование функций
Предел
Интеграл
Двойной интеграл
Тройной интеграл
Интегрирование
Неопределённый интеграл
Определенный интеграл
Криволинейные интегралы
Поверхностные интегралы
Несобственные интегралы
Кратные интегралы
Интегралы, зависящие от параметра
Квадратный трехчлен
Производная
Применение производной к исследованию функций
Приложения производной
Дифференциал функции
Дифференцирование в математике
Формулы и правила дифференцирования
Дифференциальное исчисление
Дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Дифференциальные уравнения в частных производных
Тригонометрические функции
Тригонометрические уравнения и неравенства
Показательная функция
Показательные уравнения
Обобщенная степень
Взаимно обратные функции
Логарифмическая функция
Уравнения и неравенства
Положительные и отрицательные числа
Алгебраические выражения
Иррациональные алгебраические выражения
Преобразование алгебраических выражений
Преобразование дробных алгебраических выражений
Разложение многочленов на множители
Многочлены от одного переменного
Алгебраические дроби
Пропорции
Уравнения
Системы уравнений
Системы уравнений высших степеней
Системы алгебраических уравнений
Системы линейных уравнений
Системы дифференциальных уравнений
Арифметический квадратный корень
Квадратные и кубические корни
Рациональные числа
Иррациональные числа
Арифметический корень
Квадратные уравнения
Иррациональные уравнения
Последовательность
Ряды сходящиеся и расходящиеся
Тригонометрические функции произвольного угла
Тригонометрические формулы
Обратные тригонометрические функции
Теорема Безу
Математическая индукция
Показатель степени
Показательные функции и логарифмы
Множество
Множество действительных чисел
Числовые множества
Преобразование рациональных выражений
Преобразование иррациональных выражений
Геометрия
Действительные числа
Степени и корни
Степень с рациональным показателем
Тригонометрические функции угла
Тригонометрические функции числового аргумента
Тригонометрические выражения и их преобразования
Преобразование тригонометрических выражений
Комбинаторика
Вычислительная математика
Прямая линия на плоскости и ее уравнения
Прямая и плоскость
Линии и уравнения
Прямая линия
Уравнения прямой и плоскости в пространстве
Кривые второго порядка
Кривые и поверхности второго порядка
Числовые ряды
Степенные ряды
Ряды Фурье
Преобразование Фурье
Функциональные ряды
Функции многих переменных
Метод координат
Гармонический анализ
Вещественные числа
Предел последовательности
Аналитическая геометрия
Аналитическая геометрия на плоскости
Аналитическая геометрия в пространстве
Функции одной переменной
Высшая алгебра
Векторная алгебра
Векторный анализ
Векторы
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Операции над векторами
Непрерывность функций
Предел и непрерывность функций нескольких переменных
Предел и непрерывность функции одной переменной
Производные и дифференциалы функции одной переменной
Частные производные и дифференцируемость функций нескольких переменных
Дифференциальное исчисление функции одной переменной
Матрицы
Линейные и евклидовы пространства
Линейные отображения
Дифференциальные теоремы о среднем
Теория устойчивости дифференциальных уравнений
Функции комплексного переменного
Преобразование Лапласа
Теории поля
Операционное исчисление
Системы координат
Рациональная функция
Интегральное исчисление
Интегральное исчисление функций одной переменной
Дифференциальное исчисление функций нескольких переменных
Отношение в математике
Математическая логика
Графы в математике
Линейные пространства
Первообразная и неопределенный интеграл
Линейная функция
Выпуклые множества точек
Система координат

Урок 41.

извлечение корня из комплексного числа — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №41. Извлечение корня из комплексного числа.

Перечень вопросов, рассматриваемых в теме

1) понятие корня из комплексного числа;

2) алгоритмы извлечения корня из комплексного числа;

3) пример извлечения корня из комплексного числа в тригонометрической форме.

Глоссарий по теме

Определение. Корнем n-ой степени из комплексного числа ω называется комплексное число z такое, что zn=ω. Множество всех корней n-ой степени из ω обозначается через .

Теорема. Уравнение zⁿ=ω, где ω- комплексное число, n- натуральное, имеет ровно n различных комплексных корней.

Все n корней z_k лежат на оркужности радиусом с центом в начале кооринат; они делят окружность на n дуг величиной каждая и являются вершинами вписанного в нее правильного n-угольника.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Теорема. Уравнение zⁿ=ω, где ω- комплексное число, n- натуральное, имеет ровно n различных комплексных корней.

Доказательство. Пусть ω=|ω|∙(cosφ+isinφ), число z будем искать в виде

z=|z|∙(cosα+isinα).

Преобразуем уравнение zⁿ=ω, используя формулу Муавра:

|z|n(cosnζ+isinnζ)=|ω|∙(cosθ+isinθ).

Отсюда вытекают равенства:

|z|ⁿ=|ω|, nζ= θ+2πk, k- целое,

Из которых для модуля искомого корня получается определенное значение , тогда как его аргумент , k- целое, может принимать различные значения при разных k. При этом значениям k= 0, 1, 2, …, n-1 соответствуют различные значения корня, а при k= n значение корня совпадает с его значением при k=0. При k=n+1 получим значение корня, что и при k=1, и т.д.

Таким образом, число различных значений корня равно n- это

, где k=0, 1, 2,…, n-1 что и требовалось доказать.

Пример 1. Найдите все корни n-ой степени из действительного числа x>0.

Решение. Если х- положительное действительное число, то |x|=x, θ=arg x=0. Формула корней в этом случае дает ответ:

, где k=0, 1, 2,…, n-1.

При k=0 получим – это арифметический корень. При четном n=2m имеется еще один дейсвтиельный корень., получающийся при k=m. (ζ= arg z_m=π):

Корни n-ой степени из 1 часто обозначают через ε_k,k= 0, 1, 2, …, n-1. Согласно предыдущему примеру:

Пример 2. Вычислите корни третьей степени из комплексного числа 2+2i.

Решение: Найдем тригонометрическую форму данного числа:

По формуле корней из комплексного числа имеем:

, где k пробегает значения 0, 1, 2. Запишем полученные корни:

Используя формулы для косинуса и синуса разности углов, получаем:

Ответ: ; -1+i; .

Немного иначе извлекаются корни из комплексных чисел, аргумент которых не приводится к виду , где m, n – целые числа.

Пример 3. Найдите

Решение. Пусть ω=3+4i. Положим φ=arg ω.

, тогда ω=5(cosφ+isinφ), где , .

Следовательно, , где k=0, 1.

Запишем подробнее:

Найдем и , используя формулу двойного угла:

, откуда , ; тогда , Угол φ лежит в первой четверти, а следовательно, и угол тоже, поэтому Тогда

Ответ:

Пример 4. Выполнить операцию извлечения корня z³ для заданных комплексных чисел в алгебраической форме представления: .

Решение: Тригонометрическая форма записи некоторого комплексного числа имеет вид z=r(cosφ+i⋅sinφ). По условию . Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа, используя формулу (*):. Подставим полученные значения и получим:

Для k=0 получаем:

Для k=1 получим:

Для k=2 получим:

Разбор решения заданий тренировочного модуля

№1. Тип задания: множественный выбор

Найдите

Выберите верные ответы из предложенных:

2+i
-2+i
-2-i
2-i

Решение. Пусть ω=3-4i. Положим φ=arg ω.

, тогда ω=5(cosφ+isinφ), где , .

Следовательно, , где k=0, 1.

Запишем подробнее:

Найдем и , используя формулу двойного угла:

, откуда , ; тогда , Угол φ лежит в первой четверти, а следовательно, и угол тоже, поэтому Тогда

Ответ: 2+i; -2-i

Верные ответы: 1, 3

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Чему будет равно произведение: (5 + 3i)∙(1 — 2i)=______

Решение:

((5 + 3i) · (1 — 2i) = 5·1 — 5·2i + 3·1i — 3·2i² = 5 — 10i + 3i + 6 =11 — 7i

Ответ: 11-7i

Как найти квадратный корень числа вручную. Извлечение корней: способы, примеры, решения

Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.

Шаги

Часть 1

Извлечение кубического корня на простом примере

Запишите задачу. 2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.

Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток).
Подумайте, является ли полученный ответ достаточно точным. Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1.
- Чтобы проверить точность ответа, возведите его в куб: 2,1*2,1*2,1 = 9,261.
- Если вы считаете, что ответ достаточно точный, вычисления можно не продолжать; в противном случае проделайте еще одно вычитание.
Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше. {3}=729} , то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.
Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа.
- В нашем примере число 600 находится между числами 512 и 729. Например, к первому найденному числу (8) припишите цифру 5. Получится число 8,5.
- В нашем примере: 8 , 5 ∗ 8 , 5 ∗ 8 , 5 = 614 , 1. {\displaystyle 8,5*8,5*8,5=614,1.}
Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число. {3}=614,1} . Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.
Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа.
- В нашем примере 8 , 44 ∗ 8 , 44 ∗ 8 , 44 = 601 , 2 {\displaystyle 8,44*8,44*8,44=601,2} . Это чуть больше исходного числа, поэтому оцените другое (меньшее) число, например, 8,43: 8 , 43 ∗ 8 , 43 ∗ 8 , 43 = 599 , 07 {\displaystyle 8,43*8,43*8,43=599,07} . Таким образом, значение кубического корня из 600 лежит между 8,43 и 8,44.
Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее. {3}=599,93} , то есть результат меньше исходного числа менее чем на 0,1.

Из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:

Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.

*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.

Мы знаем, что:

Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):

Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?

1. Это кубы чисел кратных десяти:

Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.

2. Это свойство чисел при произведении.

Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?

Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.

1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …

То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.

При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.

Покажем соответствие в табличке для всех чисел:

Знания представленных двух моментов вполне достаточно.

Рассмотрим примеры:

Извлечь кубический корень из 21952.

Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.

Извлечь кубический корень из 54852.

Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.

Извлечь кубический корень из 571787.

Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.

Извлечь кубический корень из 614125.

Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.

Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.

Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.

После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉

На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.

Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную.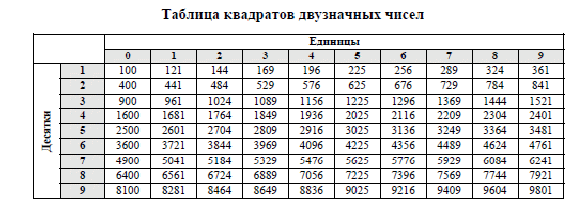 Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.

Шаги

Разложение на простые множители

Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.

Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Записать это можно следующим образом: √400 = √(25 х 16).

Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.

В нашем примере извлеките корень из 25 и из 16.
√(25 х 16)
√25 х √16
5 х 4 = 20

Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.

Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
= √(49 х 3)
= √49 х √3
= 7√3

Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.

Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.

Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.

Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
Рассмотрим другой пример: √88.
= √(2 х 44)
= √ (2 х 4 х 11)
= √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
= 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.

Вычисление квадратного корня вручную

При помощи деления в столбик

Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).

Понимание процесса

Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.

Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.

Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.

Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).

Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12. (10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.

Ниже мы по очереди рассмотрим основные способы извлечения корней.

Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.

Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.

Приступим.

Использование таблицы квадратов, таблицы кубов и т.д.

В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?

Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.

Разложение подкоренного числа на простые множители

Разберемся с этим при решении примеров.

Пример.

Извлеките квадратный корень из 144 .

Решение.

Разложим 144 на простые множители:

Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .

Ответ:

Для закрепления материала рассмотрим решения еще двух примеров.

Пример.

Вычислите значение корня .

Решение.

Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .

Ответ:

Пример.

Является ли значение корня целым числом?

Решение.

Ответ:

Нет.

Извлечение корней из дробных чисел

Разберем пример извлечения корня из дроби.

Пример.

Чему равен квадратный корень из обыкновенной дроби 25/169 .

Решение.

Ответ:

Пример.

Извлеките кубический корень из десятичной дроби 474,552 .

Решение.

Ответ:

Извлечение корня из отрицательного числа

Рассмотрим решение примера.

Пример.

Найдите значение корня .

Решение.

Приведем краткую запись решения: .

Ответ:

Порязрядное нахождение значения корня

Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.

Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.

Так как 2,2 2 5 , то значение разряда десятых равно 2 . Можно переходить к нахождению значения разряда сотых:

Определим его значение.

Так как 10 3 2 151,186 , то значение разряда десятков равно 1 . Переходим к единицам.

Таким образом, значение разряда единиц равно 2 . Переходим к десятым.

На этом этапе найдено значение корня с точностью до сотых: .

Список литературы.

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Инструкция

Чтобы возвести число в степень 1/3, введите это число, затем нажмите на кнопку возведения в степень и наберите приблизительное значение числа 1/3 — 0,333. y».

Корень третьей степени можно вычислить и в программе MS Excel. Для этого введите в любую клетку «=» и выберите значок «вставка » (fx). Выберите в появившемся окошке функцию «СТЕПЕНЬ» и нажмите кнопку «Ок». В появившемся окошке введите значение числа, для которого необходимо вычислить корень третьей степени. В «Степень» введите число «1/3». Число 1/3 набирайте именно в таком виде – как обыкновенную . После этого нажмите кнопку «Ок». В той клетке таблицы, где создавалась , появится кубический корень из заданного числа.

Если корень третьей степени приходится вычислять постоянно, то немного усовершенствуйте описанный выше метод. В качестве числа, из которого требуется извлечь корень, укажите не само число, а клетку таблицы. После этого, просто каждый раз вводите в эту клетку исходное число – в клетке с формулой будет появляться его кубический корень.

Видео по теме

Обратите внимание

Заключение. В данной работе были рассмотрены различные методы вычисления значений кубического корня. Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.

Полезный совет

Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия. Квадратный корень: В этом случае показатель степени обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень. Практическое вычисление корней Алгоритм нахождения корня n-ной степени. Квадратные и кубические корни обычно предусмотрены во всех калькуляторах.

Источники:

корень третий степени
Как извлечь квадратный корень в N степени в Excel

Операцию нахождения корня третьей степени обычно называют извлечением «кубического» корня, а заключается она в нахождении такого вещественного числа, возведение которого в куб даст значение равное подкоренному числу. Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов.

Квадратный корень из 0 (√0)

Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 0. Мы начнем с определения, а затем ответим на некоторые общие вопросы. вопросы о квадратном корне из 0. Затем мы покажем вам различные способы вычисления квадратного корня из 0 с и без компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!

Квадратный корень из 0 определение
Квадратный корень из 0 в математической форме записывается с таким знаком радикала √0.Мы называем это квадратным корнем из 0 в радикальной форме. Квадратный корень из 0 — это величина (q), которая при умножении сама на себя будет равна 0.
√0 = q × q = q ²

Является ли 0 полным квадратом?
0 является полным квадратом, если квадратный корень из 0 равен целому числу. Как мы рассчитали дальше внизу на этой странице квадратный корень из 0 — это целое число.
0 — идеальный квадрат.

Является ли квадратный корень из 0 рациональным или иррациональным?
Квадратный корень из 0 является рациональным числом, если 0 является полным квадратом.Это иррациональное число, если оно не является полным квадратом. Поскольку 0 — совершенный квадрат, это рациональное число. Это означает, что ответ на вопрос «квадратный корень из 0?» не будет иметь десятичных знаков.
√0 является рациональным числом

Можно ли упростить квадратный корень из 0?
Квадратный корень из полного квадрата можно упростить, потому что квадратный корень из полного квадрата будет равен целому числу:
√0 = 0

Как вычислить квадратный корень из 0 с помощью калькулятора
Самый простой и скучный способ вычислить квадратный корень из 0 — воспользоваться калькулятором! Просто введите 0, а затем √x, чтобы получить ответ. Мы сделали это с помощью нашего калькулятора и получили следующий ответ:
√0 = 0

Как вычислить квадратный корень из 0 с помощью компьютера
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT (0) в ячейку, чтобы получить квадратный корень из 0. Ниже приведен результат, который мы получили:
SQRT(0) = 0

Чему равен квадратный корень из 0, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (основание) с дробной степенью.Квадратный корень из 0 не является исключением. Вот правило и ответ в «квадратный корень из 0, преобразованный в основание с показателем степени?»:
√b = b ^½
√0 = 0 ^½

Как найти квадратный корень из 0 методом деления в длину
Здесь мы покажем вам, как вычислить квадратный корень из 0, используя метод деления в большую сторону. это потерянный искусство того, как они вычисляли квадратный корень из 0 вручную до того, как были изобретены современные технологии.
Шаг 1)
Наберите 0 в парах из двух цифр справа налево:

Шаг 2)
Начиная с первого набора: самый большой совершенный квадрат, меньший или равный 0, равен 0, а квадратный корень из 0 равен 0. Поэтому поместите 0 сверху и 0 снизу следующим образом:
Разница между двумя нижними числами равна нулю, поэтому все готово! Ответ — зеленая цифра сверху. Еще раз, квадратный корень из 0 равно 0.

Квадратный корень из числа
Пожалуйста, введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 0 на этой странице.

Примечания
Помните, что отрицательное значение, умноженное на отрицательное, равно положительному. Таким образом, квадратный корень из 0 имеет не только положительный ответ что мы объяснили выше, но и отрицательный аналог.
На этой странице мы часто ссылаемся на совершенные квадратные корни. Вы можете использовать список идеальных квадратов для справки.

Квадратный корень из 1
Вот следующее число в нашем списке, о котором у нас есть такая же подробная информация о квадратном корне.
Авторское право  | Политика конфиденциальности  | Отказ от ответственности  | Контакт
Нахождение квадратного корня из отрицательного 1
Решение
Конечно, точно так же, как квадратный корень из 25 имеет два корня (+5 и -5), квадратный корень из минус 1 также имеет два корня:
Квадратный корень из -1
Итак, наш ответ на задачу квадратного корня из минус 1 — это два числа: + i и — i .5 и
Схема повторяется.
Любой квадратный корень из отрицательного числа будет иметь компонент i ; например, квадратный корень из -4 будет равен +2 i или -2 i . Комплексные числа имеют вид a + bi , где a и b — оба действительные числа, а i — мнимая часть. Например, наше решение для квадратного корня из минус 1 можно рассматривать как два комплексных числа: 0 + i и 0 — i .Действительные числа — это подмножество комплексных чисел, где b = 0, а a может быть любым действительным числом.
Хотя концепция квадратного корня из отрицательной единицы начиналась как просто теоретическое математическое упражнение, она нашла широкое применение в современной жизни. Одним из таких применений является электротехника. Разработчики компьютерных печатных плат, сотовых телефонов и планшетов используют мнимые числа, чтобы проектировать все более сложные, компактные и эффективные системы, которые помогают нам питать современный мир.Другие области, в которых используется эта концепция, включают квантовую механику, диффузию тепла, оптику и гидродинамику — и это лишь некоторые из них.
Вычислить квадратный корень, квадратный корень со знаком или обратную величину квадрата root
HDL Coder™ предоставляет дополнительные параметры конфигурации, влияющие на HDL. реализация и синтезированная логика.
Режимы функции Sqrt
Для блока Sqrt с функцией , установленной на sqrt , генератор кода поддерживает различные архитектуры и типы данных.
Архитектура sqrtfunction поддерживает код генерация для типов с фиксированной точкой и типов с плавающей запятой. Когда вы используете типы с плавающей запятой, установите IP-библиотеку с плавающей запятой (HDL Coder) на Native Floating Пункт. Вы можете указать LatencyStrategy и CustomLatency Свойства HDL для выбора из диапазона частотных значений при нацеливании на ваш дизайн на аппаратной платформе.
Использование свойства блока UseMultiplier HDL в комбинации с LatencyStrategy и Свойства CustomLatency , чтобы указать, следует ли вычислять квадратный корень с помощью конвейерного сдвига и сложения или умножения алгоритм
Собственные настройки операций с плавающей запятой для различных режимов
Для этой архитектуры можно указать HandleDenormals и Настройки LatencyStrategy из Native Вкладка Floating Point в диалоговом окне HDL Block Properties.
— —
Архитектура с фиксированной точкой Native с плавающей точкой HandleDenormals LatencyStrategy
sqrtfunction ✓ ✓ ✓ ✓
sqrtnewton ✓ — — —
sqrtnewtonsinglerate ✓ — — —
recipsqrtnewton ✓ — — — —
Recipsqrtnewtonsinglerate ✓ — — —
HDL Архитектура
Этот блок имеет многолетние реализации, которые вводят дополнительные задержка в сгенерированном коде.Чтобы увидеть добавленную задержку, просмотрите сгенерированная модель или модель проверки. См. Сгенерированная модель и Модель проверки (HDL Coder).
Архитектура Параметр Дополнительные циклы Задержки Описание
SQRTFunction (по умолчанию)
USEMULTIPLIER
Запуседника
CustomLatence
Зависит от вариантов параметра, длина вывода, и входной и выходной фракции длины.
Чтобы указать эту архитектуру, установите Функция на кв или rSqrt .
Вычисления квадратный корень с помощью конвейерного сдвига/сложения алгоритм или алгоритм на основе умножения.
Архитектура SqrtFunction имеет максимальная задержка, определяемая выходным словом длина, а также входные и выходные дробные длины, для данные с фиксированной точкой. Например, максимальная задержка 11 для длины выходного слова 17 .
Чтобы увидеть задержку расчет в командной строке MATLAB, введите:
Улучшить проектной частоты и сократить использование ресурсов, установив UseMultiplier для от и LatencyStrategy для наследует .
SqrtNewton Итерации Итерации + 3
Чтобы указать эту архитектуру кв .
Использовать итерационный метод Ньютона. Выберите этот параметр, чтобы оптимизировать площадь.
Значение по умолчанию для Итерации — 3.
рекомендуемое значение для итераций равно от 2 до 10. Если Итерации вне рекомендуемого диапазона, HDL Coder генерирует сообщение.
sqrtnewtonsinglerate итераций ( итерации * 4) + 6
Для указания этой архитектуры набор функция кв .
Использовать односкоростной конвейерный метод Ньютона. Выберите этот параметр, чтобы оптимизировать скорость, или, если вы хотите, чтобы единая скорость выполнение.
Значение по умолчанию для Итерации — 3.
рекомендуемое значение для итераций равно от 2 до 10. Если Итерации вне рекомендуемого диапазона, кодер генерирует сообщение.
RecipSqrtNewton Итерации Итерации + 2
rSqrt .
Использовать итерационный метод Ньютона. Выберите этот параметр, чтобы оптимизировать площадь.
ReciPSQRTNEWTONSINGERATE ITERATION ( итераций * 4) + 5
Для указания этой архитектуры набор функция rSqrt .
Использовать односкоростной конвейерный метод Ньютона. Выберите этот параметр, чтобы оптимизировать скорость, или, если вы хотите, чтобы единая скорость выполнение.
Итерационный метод Ньютона-Рафсона:
ReciprocalRsqrtBasedNewton и ReciprocalRsqrtBasedNewtonSingleRate реализовать Метод Ньютона-Рафсон с:
HDL Block Properties
General
Constrice Outputpipipeline
Количество реестров на место в выходные данные, перемещая существующие задержки в вашем дизайне.Распределенный конвейерная обработка не перераспределяет эти регистры. По умолчанию 0 . Дополнительные сведения см. в разделе ConstrainedOutputPipeline (HDL Coder).
Итерации
Количество итераций для SqrtNewton или SqrtNewtonSingleRate выполнение.
InputPipeline
Количество ступеней входного конвейера для вставки в сгенерированный код.Распределенная конвейерная обработка и ограниченная конвейерная обработка вывода может перемещать эти регистры. По умолчанию 0 . Дополнительные сведения см. в разделе InputPipeline (HDL Coder).
OutputPipeline
Количество этапов выходного конвейера для вставки в сгенерированный код. Распределенная конвейерная обработка и ограниченная конвейерная обработка вывода может перемещать эти регистры.По умолчанию 0 . Дополнительные сведения см. в разделе OutputPipeline (HDL Coder).
UseMultiplier
Выберите алгоритм для реализации SqrtFunction . От по умолчанию для этого свойства установлено значение вместо и блок вычисляет квадратный корень с помощью Shift-Add алгоритм. Когда свойство установлено в на квадратный корень вычисляется с помощью множители.
Увеличить расчетную частоту и уменьшить использование ресурсов, установив Использовать множитель для от и LatencyStrategy для наследует .
LatencyStrategy
Укажите, следует ли отображать блоки в вашем проекте на MAX , МИН. , ПОЛЬЗОВАТЕЛЬСКИЙ или ZERO задержка для фиксированной точки и типы с плавающей запятой.По умолчанию МАКС . Настройки блока для типы с плавающей запятой переопределяют настройки уровня модели. За типы с фиксированной точкой, настройка уровня блока определяет латентная стратегия. См. также LatencyStrategy (HDL Coder).
Увеличить расчетную частоту и уменьшить использование ресурсов, установив Использовать множитель для от и LatencyStrategy для наследует .
CustomLatency
Когда для LatencyStrategy установлено значение CUSTOM и если вы используете типы с фиксированной точкой, используйте это свойство для указать пользовательское значение задержки между ZERO и MAX для типы с фиксированной точкой. Для типов с плавающей запятой это значение становится пользовательской задержкой оператора. См. также NFPCustomLatency (HDL Coder).
Нативное плавающее точка
Обработываются
Укажите, хотите ли вы контроллер HDL вставить дополнительную логику для обработки номеров даномера в вашем дизайне.Денормализованные числа — это числа, величина которых меньше наименьшего числа с плавающей запятой. число, которое может быть представлено без лидирующих нулей в мантиссе. По умолчанию наследует . См. также HandleDenormals (HDL Coder).
Корни или нули многочлена
7
Полиномиальное уравнение
Корни или нули многочлена
x - и y - пересекает
В ЭТОЙ ТЕМЕ мы представим основы рисования графика.
1. Что такое полиномиальное уравнение?
Это набор полиномов, равный 0. P ( x ) = 0,
P ( х ) = 5 х ³ - 4 х ² + 7 х - 8 = 0
2. Что мы понимаем под корнем или нулем многочлена?
Это решение полиномиального уравнения, P ( x ) = 0.
Именно значение x делает полином равным 0.
Другими словами, число r является корнем многочлена P ( x )
тогда и только тогда, когда P ( r ) = 0,
Пример 1. Пусть P ( x ) = 5 x ³ - 4 x ² + 7 x - 80111 x - 8. Тогда корень этого полинома составляет 1, потому что, согласно к определению:
   Р (1) = 5 · 1 ³ − 4 · 1 ² + 7 · 1 − 8

= 5 - 4 + 7 - 8

= 0.
Традиционно говорят о корне многочлена. О функции вообще говорят о нуле.
Пример 2. Корни этого квадратного числа
х ² - х - 6 = ( х + 2)( х - 3)
равно −2 и 3. Это значения x , при которых полином будет равен 0,
.
3. Что такое пересечение 90 111 x 90 112 и 90 111 y 90 112 на графике?
Точка пересечения x - это значение x , при котором график пересекает или касается оси x . На точке пересечения x -- на оси x -- y = 0,
Точка пересечения y - это значение y , при котором график пересекает ось y . На пересечении y- x = 0,
4. Какая связь между корнем многочлена
4.   и x -перехваты его графика?
Корни - это x - пересечения!
Корни x ² − x − 6 равны −2 и 3.Таким образом, график
у = х ² - х - 6
будет иметь значение 0 -- он будет пересекать ось x -- в точках -2 и 3.
5. Как найти x -пересечения графика любой функции
5.    y = f ( x )?
Решите уравнение, f ( x ) = 0,
Проблема 1.
а) Найдите корень многочлена 2 x + 10.
Мы должны решить уравнение
2 x + 10 = 0. Решение: x = −5.
б) Где находится x -пересечение графика y = 2 x + 10?
В х = -5. x -перехват - это корень.
Проблема 2.
а) Если произведение факторов равно 0 -- если ab = 0 -- то какой вывод мы можем сделать
а) о факторах а , б ?
Либо a = 0, либо b = 0.
б) Назовите корни этого многочлена:
е ( х ) = ( х + 4)( х + 2)( х - 1)
−4, −2, 1.
c) Нарисуйте график f ( x ). То есть нарисуйте непрерывную кривую и покажите 90 003 c) ее точки пересечения 90 111 x 90 112.
Точки пересечения x являются корнями.
Что касается точки пересечения y , то это значение y , когда x = 0. Таким образом, точка пересечения y полинома представляет собой просто постоянный член, который является произведением постоянных членов из всех факторов. (См. раздел 6, пример 9.)
Что касается нахождения поворотных точек, холма и долины, то здесь придется подождать вычислений.
О корнях многочленов степени больше 2 см. Тему 13.
Следующая тема: Наклон прямой линии
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: teacher@themathpage.ком

Степени и корни: другие корни в математике
Как вы знаете, если вы просматриваете эту серию математических видео по порядку — в последнем видео мы рассмотрели квадратные корни. Теперь в этом видео мы рассмотрим другие корни в математике — например, кубические корни и т. д.
<noscript><img src='/800/600/https/mypresentation.ru/documents_6/d58f6ef51b8c49a002ed4f1c8a92a87e/img7.jpg' /></noscript> youtube.com/embed/dtOw4Ajq_bc?feature=oembed&autoplay=1" src="data:text/html;https://www.youtube.com/embed/dtOw4Ajq_bc?feature=oembed&autoplay=1;base64,PGJvZHkgc3R5bGU9J3dpZHRoOjEwMCU7aGVpZ2h0OjEwMCU7bWFyZ2luOjA7cGFkZGluZzowO2JhY2tncm91bmQ6dXJsKGh0dHBzOi8vaW1nLnlvdXR1YmUuY29tL3ZpL2R0T3c0QWpxX2JjLzAuanBnKSBjZW50ZXIvMTAwJSBuby1yZXBlYXQnPjxzdHlsZT5ib2R5ey0tYnRuQmFja2dyb3VuZDpyZ2JhKDAsMCwwLC42NSk7fWJvZHk6aG92ZXJ7LS1idG5CYWNrZ3JvdW5kOnJnYmEoMCwwLDApO2N1cnNvcjpwb2ludGVyO30jcGxheUJ0bntkaXNwbGF5OmZsZXg7YWxpZ24taXRlbXM6Y2VudGVyO2p1c3RpZnktY29udGVudDpjZW50ZXI7Y2xlYXI6Ym90aDt3aWR0aDoxMDBweDtoZWlnaHQ6NzBweDtsaW5lLWhlaWdodDo3MHB4O2ZvbnQtc2l6ZTo0NXB4O2JhY2tncm91bmQ6dmFyKC0tYnRuQmFja2dyb3VuZCk7dGV4dC1hbGlnbjpjZW50ZXI7Y29sb3I6I2ZmZjtib3JkZXItcmFkaXVzOjE4cHg7dmVydGljYWwtYWxpZ246bWlkZGxlO3Bvc2l0aW9uOmFic29sdXRlO3RvcDo1MCU7bGVmdDo1MCU7bWFyZ2luLWxlZnQ6LTUwcHg7bWFyZ2luLXRvcDotMzVweH0jcGxheUFycm93e3dpZHRoOjA7aGVpZ2h0OjA7Ym9yZGVyLXRvcDoxNXB4IHNvbGlkIHRyYW5zcGFyZW50O2JvcmRlci1ib3R0b206MTVweCBzb2xpZCB0cmFuc3BhcmVudDtib3JkZXItbGVmdDoyNXB4IHNvbGlkICNmZmY7fTwvc3R5bGU+PGRpdiBpZD0ncGxheUJ0bic+PGRpdiBpZD0ncGxheUFycm93Jz48L2Rpdj48L2Rpdj48c2NyaXB0PmRvY3VtZW50LmJvZHkuYWRkRXZlbnRMaXN0ZW5lcignY2xpY2snLCBmdW5jdGlvbigpe3dpbmRvdy5wYXJlbnQucG9zdE1lc3NhZ2Uoe2FjdGlvbjogJ3BsYXlCdG5DbGlja2VkJ30sICcqJyk7fSk7PC9zY3JpcHQ+PC9ib2R5Pg=="/>
В этом уроке мы поговорим о других корнях. Кубические корни, корни четвертой степени и тому подобное. Точно так же, как квадратный корень более или менее «отменяет действие возведения в квадрат.«Конечно, мы узнали, что это не совсем так, есть корни более высокого порядка, которые аналогичным образом уничтожают другие силы. Например, кубические корни отменяют действие кубирования чего-либо.
Так же, как мы можем возвести что-то в третью степень, мы можем найти, какое число, возведенное в третью степень, будет соответствовать определенному результату. Прежде всего, поговорим об обозначениях. Квадратный корень из k, радикал k, обозначает квадратный корень из k. Обозначения для всех остальных корней аналогичны, мы используем тот же подкоренной символ.Но для всех остальных корней мы ставим небольшое число перед корнем, чтобы обозначить порядок корня.
Другими словами, берем ли мы кубический корень, корень четвертой степени, корень пятой степени и т. д. Итак, для кубического корня мы должны поставить небольшую цифру 3 перед знаком корня, и это будет означать кубический корень из k. Мы также должны думать о положительных и отрицательных числах, потому что положительные и отрицательные числа здесь довольно сложны. Помните, что, прежде всего, мы возводим в квадрат.
Положительный в квадрате положительный, отрицательный в квадрате тоже положительный, понятно? Так что это верно для возведения в квадрат.Поэтому верно, что если у нас есть x2 = положительное, то это имеет два решения, одно положительное и одно отрицательное. Например, х в квадрате равно 9, это может быть плюс 3 или минус 3. Напротив, х2 = отрицательное не имеет возможного решения, х в квадрате равно отрицательному 9, не существует действительного числа, удовлетворяющего этому уравнению.
Другие корни в математике: кубические корни
Положительные и отрицательные корни для кубов немного отличаются. Помните, что если мы возьмем в куб положительное, то получим положительное, а если возьмем в куб отрицательное, то получим отрицательное.Следовательно, x3 = положительное имеет одно положительное решение, а x3 = отрицательное имеет одно отрицательное решение. Таким образом, вы не получаете проблему двойных корней в одном случае и никакого решения в другом случае, как мы получили для возведения в квадрат.
С квадратными корнями мы можем найти квадратный корень только из положительных чисел. Конечно, мы могли бы также найти квадратный корень из 0, но мы не можем извлечь квадратный корень из минуса, ясно? Таким образом, почти по той же причине, как мы не можем возвести что-то в квадрат и получить отрицательное значение, мы не можем извлечь квадратный корень из отрицательного значения.Но для кубических корней правила совсем другие.
Мы можем извлечь кубический корень из любого числа на числовой прямой, положительного, нулевого или отрицательного. Итак, мы можем возвести каждое число в отрицательной строке в третью степень и найти из него кубический корень. Например, кубический корень из 8 равен 2, кубический корень из 0 равен 0, а кубический корень из -8 равен -2.
Таким образом, в отличие от квадратного корня, кубический корень может иметь отрицательный результат. Когда мы вкладываем негатив, мы получаем негатив. Для быстрых вычислений полезно запомнить кубы до 10.Конечно, первые шесть очень важно запомнить, и действительно, если вы знаете все 10, это сэкономит время. И пару вещей отмечу.
Обратите внимание, что 8 в кубе, конечно же, будет 2 в 9-м. Обратите внимание, что 4 в кубе — это 2 в квадрате в кубе. Так что это будет 2 к 6-му. Это также будет 2 в 3-м квадрате или 8 в квадрате. И, конечно, 8 в квадрате тоже 64. Итак, здесь есть некоторые закономерности, которые мы можем наблюдать, применяя наши законы показателей.
Итак, если мы запоминаем эти кубы автоматически, мы запоминаем кучу кубических корней.А так может быть очень удобно. Кубические корни относительно редко встречаются в тестах. Корни более высокого порядка, четвертый корень, пятый корень, шестой корень встречаются еще реже. Так что это не очень вероятные темы, поэтому сразу предупрежу.
Общие закономерности корней в математике
Но я скажу несколько слов в общем обо всех корнях. Так что это верно для всех возможных корней в математике: квадратного корня, кубического корня и т. д. Здесь мы поговорим обо всех закономерностях.
Прежде всего, квадратный корень из а, корень 4-й степени из а, корень 6-й степени из а и т. д.— эти называются четными корнями . Поэтому, когда у нас там записано четное число, это четный корень.
_{Изображение от dizain}
И, конечно, с квадратным корнем подразумевается два, так что это тоже четный корень. Кубический корень, корень 5-й степени, корень 7-й степени называются нечетными корнями. Итак, мы отличаем все четные корни от всех нечетных. И причина, по которой мы это делаем, заключается в том, что те же положительные и отрицательные явления, о которых мы говорили с квадратами и кубами, распространяются на все четные и нечетные числа.
Как и в случае с квадратными корнями, мы можем взять любой четный корень из положительного числа, что приведет к положительному результату. Но мы не можем извлечь четный корень из отрицательного числа. Мы пытались взять четный корень из отрицательного числа, он не определен. Оно ничему не равно на числовой прямой. Напротив, как и в случае с кубическими корнями, любой нечетный корень из положительного числа положителен. И любой нечетный корень отрицательного является отрицательным.
Таким образом, это следует той же схеме плюс-минус. Для других свойств я буду использовать обозначение с буквой n перед знаком радикала.Итак, у нас есть корень n-й степени из a. И здесь я говорю об общем корне. Конечно, подразумевается, что n — целое число, большее или равное 2. Для всех корней мы можем взять корень n-й степени из 0, и он будет равен 0. А корень n-й степени из 1 равен 1, так что это верно для всех корней. значения н.
Дополнительные общие черты для всех корней в математике
Все корни сохраняют порядок неравенства. Итак, если у нас есть три числа подряд — если они положительные числа — мы берем из них корни.Пока это один и тот же корень, который мы извлекаем из каждого числа, они остаются в том же порядке неравенства.
Например, предположим, что нам нужно вычислить корень четвертой степени из 50. Ну, мы хотели бы найти его между двумя четвертыми степенями.
Итак, мы знаем, что 2 в 4-м равно 16, 3 в 4-м равно 81. Итак, поскольку 50 находится между 16 и 81, мы можем извлечь из них корень 4-го порядка. И мы видим, что 4-й корень из 50 должен быть десятичным числом где-то между 2 и 3. Тест не предполагает, что вы сделаете что-то более причудливое с поиском 4-го корня из 50, но до тех пор, пока вы можете выяснить, какой между двумя целыми числами, это нормально.
Сравните размеры корней разных порядков
Мы также можем сравнить размеры корней разных порядков. Таким образом, для числа больше 1 — чем выше корень, тем меньше фактическое число. Таким образом, корень n-го порядка является корнем более высокого порядка, чем корень m-го порядка. И корень mth меньше. Итак, давайте подумаем об этом, предположим, что мы извлекаем разные корни из 19. Ну, конечно, квадратный корень из 19 должен быть меньше, чем 19.
Теперь кубический корень из 19 должен быть еще меньше, потому что он занимает всего два квадратного корня.Если мы умножим два квадратных корня вместе, мы получим 19. Мы должны умножить три кубических корня вместе, чтобы получить 19. И тогда мы можем расширить эту логику. Ну, 4-й корень должен быть еще меньше, потому что мне нужно умножить четыре из них, чтобы получить 19. Я должен умножить пять из них или шесть из них и так далее.
Наблюдение за появлением закономерностей
Итак, это означает, что по мере того, как мы получаем корни все более и более высокого порядка, все эти числа становятся меньше. Но они всегда больше 1. Теперь, даже если мы не можем понять, что такое десятичные дроби, должно быть верно, что корень 30-й степени из 19 меньше, чем корень 20-й степени из 19.Другими словами, мы должны быть в состоянии сделать это сравнение, даже если мы не можем определить точные значения этих десятичных знаков.
_{Изображение New Africa}

Теперь, когда мы попадаем в область между 0 и 1, все становится немного иначе. И вы, возможно, помните, здесь все было по-другому. Прежде всего, если мы возьмем корень, корни больше, чем b, если предположить, что b — это дробь между 0 и 1. И чем выше порядок корня, тем выше он становится.
Итак, n — корень более высокого порядка, он выше. Корень n-й степени b больше, чем корень m-й степени b. Итак, предположим, что мы берем разные корни, скажем, из двух пятых. Ну, две пятых меньше, чем квадратный корень из двух пятых. Это будет меньше, чем кубический корень, который меньше корня в четвертой степени, и так далее.
Продолжаем эту схему. Оказывается, все эти корни остаются меньше 1. Таким образом, они становятся все больше, больше и больше, но никогда не становятся больше 1. И эта закономерность продолжается со всеми корнями более высокого порядка.Таким образом, даже если бы нам пришлось сравнить два очень больших корня, мы могли бы сказать, например, что мы знаем, что корень в 50-й степени из двух пятых, который должен быть больше, чем корень в две пятых, но он должен быть меньше, чем корень в 75-й степени из две пятых.
И 75-й корень из двух пятых по-прежнему должен быть меньше 1. Таким образом, мы должны быть в состоянии выяснить, где эти четыре члена попадают в неравенство, даже если мы можем вычислить точные десятичные значения этих корней. Подводя итог, можно сказать, что чем выше порядок корня, тем ближе результат к 1.То есть, если числа больше 1, извлечение корней более высокого порядка делает их все меньше и меньше, приближая их к 1.
Извлечение корней из чисел от 0 до 1 делает их больше, и они приближаются все ближе и ближе к 1. Итак, это это закономерность, все приближается к 1. И одна из причин этого, конечно же, в том, что мы можем взять любой корень из 1 и он будет равен 1. Эти свойства редко проверяются, и только на самых сложных задачах теста .
Итак, еще раз, это не то, что вы будете видеть каждый раз, когда садитесь за тест.Это очень редкие проблемы.
Резюме
В общем, в отличие от квадратных корней, мы можем извлекать кубические корни как из положительных, так и из отрицательных, это отличная идея. На самом деле мы можем взять любой четный корень из положительных, но не из отрицательных, но мы можем взять любой нечетный корень из любого числа на числовой прямой.
Это тоже отличная идея. Любой корень из 1 равен 1, а любой корень из 0 равен 0. Все корни сохраняют порядок неравенств, предполагая, что все числа положительные.И чем выше порядок корня, тем ближе результат к 1. Итак, опять же, числа больше 1, когда мы извлекаем корни, становятся меньше и приближаются к 1.
Когда мы извлекаем корни из чисел, находящихся между 0 и 1, они становятся больше и приближаются к 1.
Майк работал экспертом по GMAT в Magoosh, помогая создавать сотни видео уроков и практические вопросы, чтобы помочь студентам GMAT добиться успеха. Он также был признан «участником месяца» более двух лет в GMAT Club.Майк имеет A.B. по физике (окончание с отличием ) и степень МТС. в религиях мира, оба из Гарварда. Помимо стандартного тестирования, Майк имеет более чем 20-летний опыт преподавания как в частных, так и в государственных средних школах, специализируясь на математике и физике. В свободное время Майк любит разбивать настольные мячи на орбите, и, несмотря на то, что у него нет явных дефектов черепа, он настаивает на том, чтобы болеть за нью-йоркский Метс. Узнайте больше о GMAT из видеороликов Майка на Youtube и ресурсов, таких как What is a Good GMAT Score? и диагностический тест GMAT.
Посмотреть все сообщения
Почему "±" с другой стороны?
Пурпурная математика
В разделе "Решение квадратного корня" урока "Решение квадратичных уравнений" у нас была следующая задача и решение:
Мои шаги были:
х ² – 4 = 0
х ² = 4
х = ± 2
Тогда мое решение было:
Справка по математике.
ком
... и я объяснил форму решения, сказав:
Почему знак "±" ("плюс-минус")? Потому что это могли быть положительные 2 или отрицательные 2, которые были возведены в квадрат, чтобы получить 4.
Хотя это и правильное объяснение, мы можем быть более точны с математической точки зрения относительно источника этого «плюс-минус».Объяснение может выглядеть следующим образом:
Предположим, нам дано уравнение " x ² = 4" и нам предлагается решить его. Когда мы «извлекаем квадратный корень» из любой части, мы делаем более короткий путь от обычного решения. Если вместо этого мы применим обычные методы факторизации к этому квадрату, мы сначала переместим все в одну сторону от знака «равно», сомножим и решим:
х ² = 4
х ² – 4 = 0
( х – 2)( х + 2) = 0
х = 2, –2
Поскольку мы факторизовали разность квадратов, мы пришли к двум решениям, равным во всем, кроме знаков. «Извлекая квадратный корень» из любой стороны первой вычислительной строки выше и ставя знак «плюс-минус» перед числовой частью уравнения, мы нашли бы два одинаковых значения решения, включая их разные знаки. , на один или два шага меньше. Но используемые рассуждения более ясны в факторизованной форме.
В приведенном выше примере мы извлекали квадратный корень из точного квадрата (а именно, 4), но этот процесс работает так же хорошо, когда строго числовая часть уравнения такого рода не является точным квадратом.Например:
Это можно преобразовать в разность квадратов, если мы допускаем, что квадратный корень из семи является одним из возводимых в квадрат значений:
Затем мы можем разложить как обычно:
x ² – (sqrt[7]) ² = 0
( х – кв[7])( х + кв[7]) = 0
x = ± кв. кв.[7]
Это тот же результат, который мы получили бы, «извлекая квадратный корень» из любой части исходного уравнения, а затем добавляя «±» перед числовой частью:
x ² = (sqrt[7]) ²
sqrt[ x ² ] = ± sqrt[7]
x = ± кв.кв.[7]
Другое объяснение наличия «±» с одной стороны уравнения гораздо более техническое, основанное на математических определениях:
Предположим, нам дано уравнение " x ² = 4" и нам предлагается решить его.Когда мы возьмем квадратный корень из любой стороны, мы получим следующее:
То есть, с технической точки зрения, у нас нет "±" в знаке квадратного корня справа. Однако —
Техническое определение "квадратный корень из x в квадрате" является "абсолютным значением x ". То есть:
Из-за этого весьма технического соображения уравнение на самом деле упрощается следующим образом:
х ² = 4
| х | = 2
Но x может быть как положительным, так и отрицательным (хотя, очевидно, не нулем).Чтобы решить это абсолютное уравнение, мы должны рассмотреть каждый из двух случаев. Если x положительно, то мы можем удалить столбцы абсолютного значения, ничего не изменяя:
Если x > 0, то | х | = х , поэтому | х | = х = 2
С другой стороны, если x отрицательно, то мы должны изменить знак на x , когда мы удалим столбцы абсолютного значения, так что мы получим:
Если х < 0, то| х | = – x , значит | х | = – х = 2
Решая это, мы получаем, что x = –2.
То есть пока мы ставим знак «±» со стороны числа, «плюс-минус» на самом деле (технически) идет со стороны с переменной, потому что квадратный корень из квадрата переменной возвращает абсолютное значение эта переменная. «Извлекая квадратный корень» из любой части и помещая «±» перед числовым значением, мы избавляем себя от необходимости решать уравнение абсолютного значения, которое (технически) было создано путем извлечения квадратного корня.
Большинству учащихся проще всего запомнить, что всякий раз, когда вы извлекаете квадратный корень из обеих частей уравнения, вы должны не забывать ставить «±» на стороне, противоположной переменной. Вы должны использовать то, что лучше всего подходит для вас.
URL-адрес: https://www. Purplemath.com/modules/why_plus.htm
scipy.optimize.root — Руководство по SciPy v1.7.1
Найти корень векторной функции.
Параметры
fun callable
Векторная функция для нахождения корня.
x0 ndarray
Начальное предположение.
args кортеж, необязательный
Дополнительные аргументы, переданные целевой функции и ее якобиану.
метод стр, опционально
Тип решателя. Должен быть один из
jac bool или callable, необязательно значение якобиана вместе с целевой функцией. Если Ложь, Якобиан будет оцениваться численно. jac также может быть вызываемым, возвращающим якобиан fun . В в этом случае он должен принимать те же аргументы, что и fun .
tol с плавающей запятой, опционально
Допуск на заделку. Для детального контроля используйте специфичный для решателя опции.
функция обратного вызова , дополнительная функция
Дополнительная функция обратного вызова. Он вызывается на каждой итерации как callback(x, f) , где x — текущее решение, а f соответствующий остаток. Для всех методов, кроме «hybr» и «lm».
options dict, необязательный
Словарь опций решателя.Например, xtol или maxiter , см. show_options() для подробностей.
Возвращает
sol OptimizeResult
Решение, представленное как объект OptimizeResult . Важные атрибуты: x массив решений, успех a Логический флаг, указывающий, успешно ли завершен алгоритм и сообщение , в котором описывается причина завершения. Видеть OptimizeResult для описания других атрибутов.
См. также
show_options
Дополнительные опции, принимаемые решателями
Примечания
В этом разделе описываются доступные решатели, которые могут быть выбраны параметр «метод». Метод по умолчанию — hybr .
Метод
hybr использует модификацию гибридного метода Пауэлла как реализован в MINPACK [1].
Метод lm решает систему нелинейных уравнений методом наименьших квадратов смысле, используя модификацию алгоритма Левенберга-Марквардта как реализован в MINPACK [1].
Метод df-sane — это спектральный метод без производных. [3]
Методы broyden1 , broyden2 , anderson , linearmixing , диагбройден , возбуждающий смешивание , крылов являются неточными методами Ньютона, с возвратом или полным поиском строки [2]. Каждый метод соответствует конкретным приближениям Якоби. Подробности см. в nonlin .
Метод broyden1 использует первое приближение Якоби Бройдена, это известный как хороший метод Бройдена.
В методе broyden2 используется второе приближение Якоби Бройдена. известен как плохой метод Бройдена.
В методе anderson используется (расширенное) перемешивание по Андерсону.
Метод Крылова использует аппроксимацию Крылова для обратного якобиана.Это подходит для масштабной проблемы.
Метод diagbroyden использует диагональное приближение Бройдена-Якоби.
В методе linearmixing используется скалярная аппроксимация Якоби.
Метод excitingmixing использует настроенный диагональный якобиан приближение.
Предупреждение
Алгоритмы реализованы для методов диагбройден , linearmixing и excitingmixing могут быть полезны для определенных проблем, но будут ли они работать, может сильно зависеть от проблема.
Ссылки
1(1,2)
Мор, Хорхе Дж., Бертон С. Гарбоу и Кеннет Э. Хиллстром. 1980. Руководство пользователя для MINPACK-1.
2
К. Т. Келли. 1995. Итерационные методы для линейных и нелинейных Уравнения. Общество промышленной и прикладной математики.
3
Ла Круз, Дж. М. Мартинес, М. Райдан. Мат. Комп. 75, 1429 (2006).
Примеры
Следующие функции определяют систему нелинейных уравнений и ее якобиан.
>>> забава по определению (x): ... вернуть [x[0] + 0,5 * (x[0] - x[1])**3 - 1,0, ... 0,5 * (x[1] - x[0])**3 + x[1]]
>>> определение jac(x): ... вернуть np.array([[1 + 1,5 * (x[0] - x[1])**2, ... -1,5 * (х[0] - х[1])**2], ... [-1,5 * (x[1] - x[0])**2, ... 1 + 1.5 * (х[1] - х[0])**2]])
Решение можно получить следующим образом.

>>> из Scipy Import Optimize >>> sol = optimise.