Начертательная геометрия | Лекция 6. Многогранники

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра.
Ребра, пересекаясь, образуют вершины.
Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

Дана пирамида, основание которой  параллельно π₁. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).

Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

Решение

1.  

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции  необходимо выполнять при помощи пропорционального деления отрезка.

3. В сечении находим точки M и N принадлежащие прямой m.
4. Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки \overline{1},\overline{2},\overline{3}, проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны плоскости проекций π₁.

Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы

Порядок построения:

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
3. В сечении находим точки K и L принадлежащие прямой m.
4. Определяем видимость прямой m. Если грань АВ на π₂ видна, то точка К на π₂ видима, грань ВС невидима, следовательно, точка Lневидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

Рисунок 6.4 – Построение развёртки призмы
Порядок построения:

1.  

1. Найдем истинную величину сечения – (1
   02₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
2. Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
   /1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

3. Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней

.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Упражнение

Построить линии пересечения призмы с пирамидой (Рисунок 6.6).

Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение

1.  

1. Находим на π₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
2. Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость τ⊥π₂.
3. Полученные на π₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Упражнение

остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

1. По двум проекциям построить третью;
2. На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
3. Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
4. Построить развёртку пирамиды с нанесением линии пересечения.

Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение:

1. Проводим линии рёбер призмы на всех проекциях.
2. Введём плоскость σ⊥π₂, σ//π₁:

• σ//АВС – основанию пирамиды;
• σ пересекает пирамиду ’ сечение подобно ΔА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Грань D₂E₂∩S

2B₂ =6₂.

Ребро F₂∩S₂B₂ =7₂.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

6.4. Задачи для самостоятельной работы

1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

Рисунок 6.8

Рисунок 6.9

Рисунок 6.10

Рисунок 6.11

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.

Пересечение ПОВЕРХНОСТИ МНОГОГРАННИКОВ плоскостью общего положения (варианты заданий)

   Задание:
1) построить две проекции линии пересечения поверхностей заданных тел (3-х, 4-х, 5-ти и 6-ти угольных призм и пирамид) плоскостью;
2) определить видимость фигур сечения и поверхностей;
3) построить развертки боковых поверхностей тел.

   Для многогранников построение фигуры сечения сводится к нахождению точек пересечения ребер пирамиды или призмы с плоскостью общего положения. Для этого следует каждое ребро заключить во вспомогательную плоскость.

Примечание: боковые развертки выполнены не для всех заданий. При необходимости обратитесь к администрации сайта для выполнения.

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ МНОГОГРАННИКОВ С ПЛОСКОСТЬЮ ОБЩЕГО ПОЛОЖЕНИЯ Задания взяты из: «Задачи и контрольные задания по начертательной геометрии: учеб. пособие / А. М. Асташов, Л. А. Мартынова.
Описание: Пересечение 4-х угольной призмы плоскостью общего положения.	Описание: Пересечение 4-х угольной призмы плоскостью общего положения.
Описание: Пересечение 4-х угольной пирамиды плоскостью общего положения.	Описание: Пересечение 3-х угольной пирамиды плоскостью общего положения.
Описание: Пересечение 6-ти угольной призмы плоскостью общего положения.	Описание: Пересечение 5-ти угольной призмы плоскостью общего положения.
Описание: Пересечение 3-х угольной пирамиды плоскостью общего положения.	Описание: Пересечение 4-х угольной призмы плоскостью общего положения.
Описание: Пересечение 3-х угольной пирамиды плоскостью общего положения.	Описание: Пересечение 3-х угольной призмы плоскостью общего положения.
Описание: Пересечение 3-х угольной призмы плоскостью общего положения.	Описание: Пересечение 3-х угольной призмы плоскостью общего положения.
Описание: Пересечение 4-х угольной пирамиды плоскостью общего положения.	Описание: Пересечение 4-х угольной призмы плоскостью общего положения.
Описание: Пересечение 4-х угольной призмы плоскостью общего положения.	Описание: Пересечение 4-х угольной призмы плоскостью общего положения.

Развертка поверхности усеченной пирамиды | Начертательная геометрия

Сечение пирамиды SABCDE плоскостью α(αH, αV) выполнено ранее. Развертка боковой поверхности пирамиды будет представлять собой плоскую фигуру, состоящую из треугольников, являющихся гранями пирамиды. Развертка поверхности усеченной пирамиды 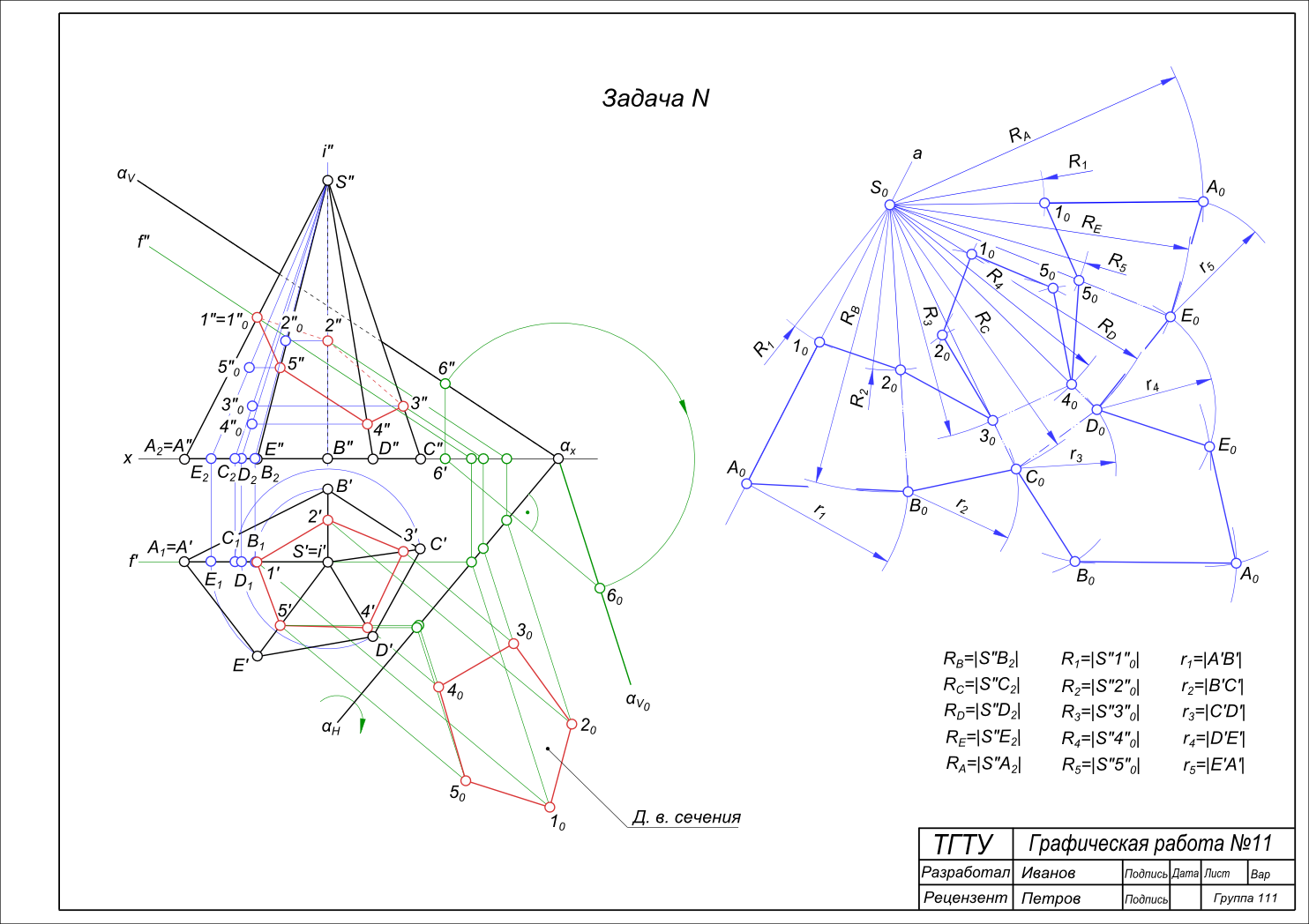строится в два этапа. Развертка поверхности усеченной пирамиды Этап первый — построение действительной величины сечения. Выполняется способом вращения вокруг следа плоскости αH: — взяв на следе плоскости αV произвольную точку 6(6″, 6`), строим ее совмещенное положение с плоскостью H — 60; — строим совмещенное положение с плоскостью H фронтального следа плоскости αV — αV0 по точкам αx и 60; — строим совмещенное положение с плоскостью H точки сечения 1 — 10 находим на пересечении соответствующей фронтали плоскости α с проекцией линии вращения; — аналогично строим совмещенное положение с плоскостью H остальных точек сечения 2, 3, 4, 5 — 20, 30, 40, 50. Данные построения выделены зеленым цветом. Развертка поверхности усеченной пирамиды — этап второй. Построение выделено синим цветом. Построение развертки выполняем способом треугольников: — Определяем действительную величину ребер пирамиды способом вращения их вокруг оси i ∋ S также i ⊥ H, в том же ключе строим действительную величину ребер усеченной пирамиды: A1, B2, C3, D4, E5; — на прямой a произвольного положения откладываем величину |S0A0| ≅ |S»A2|; — из точки A0 проводим дугу радиусом r1 = |A`B`|; — из точки S0 проводим дугу радиусом RB = |S»B2|; — пересечение дуг r1 и RB определяет положение вершины B0 треугольника ΔS0B0A0. ΔS0B0A0 ≅ ΔSBA — грани пирамиды; — из точки S0 проводим дугу радиусом R1 = |S»1″0|, из точки S0 проводим дугу радиусом R2 = |S»2″0|; — пересечение дуги R1 и S0A0 а также R2 и S0B0 определяет положение вершин 10 и 20. 1020B0A0 ≅ 12BA — грани усеченной пирамиды; Развертка поверхности усеченной пирамиды продолжается таким же образом и для остальных ее граней. К построенной развертке боковой поверхности усеченной пирамиды присоединяем основание A0B0C0b>D0E0 и сечение 1020304050, которые строим способом триангуляции. +

Построение проекций пирамиды

Построение проекций пирамиды

1. Строим проекции треугольника АВС.

 

2. Строим фронталь в плоскости треугольника АВС.

  

3. Строим горизонтаь в плоскости треугольника АВС.

 

 

4. Через точку А проводим перпендикуляр к плоскости АВС

 

 

5. На перпендикуляре h строим отрезок произвольной длины АК и определяем его натуральную величину.

 

6. Строим высоту AS.

 

 

8. Строим ребра пирамиды.

 

 

9. С помощью конкурирующих точек 3 и 4 определяем видимость ребер пирамиды на фронтальной плоскости проекций.

 

 

10. С помощью конкурирующих точек 5 и 6 определяем видимость ребер пирамиды на горизонтальной плоскости проекций.

 

 

 9. Оформление задачи.

 

 

Начертательная геометрия решение задач

 

• < Назад
• Вперёд >

Добавить комментарий

[Начертательная геометрия 1 курс] Построение проекции пирамиды

[Начертательная геометрия 1 курс] Построение проекции пирамиды

Дано:
Таблица значения координат основания ABC прямоугольной пирамиды. Значение высоты h прямоугольной пирамиды SABC

Вариант	XA	YA	ZA	XB	YB	ZB	XC	YC	ZC	h
1	117	90	9	52	25	79	0	83	48	85

Необходимо: Построить проекции пирамиды

Решение задачи на построение проекции пирамиды схоже с решением задачи на построение плоскости параллельной заданной.

Алгоритм решение задачи по начертательной геометрии на построение проекции пирамиды:

Подробнее в видеоуроке по начертательной геометрии в Автокад.

Построение проекции пирамиды

Построить две проекции сечения пирамиды плоскостью. | Интерактивное сообщество — Решение задач по инженерной графике

Наклонная пирамида SABC пересекается плоскостью общего положения а, заданной параметрами Xa, Ya, Za. Требуется: 1) Построить две проекции сечения пирамиды плоскостью. 2) Найти способом вращения вокруг фронтального следа плоскости foa» истинную величину сечения. 3) Построить развёртку боковой поверхности нижней усечённой части пирамиды.

Условия задачи: смотреть эпюр 6

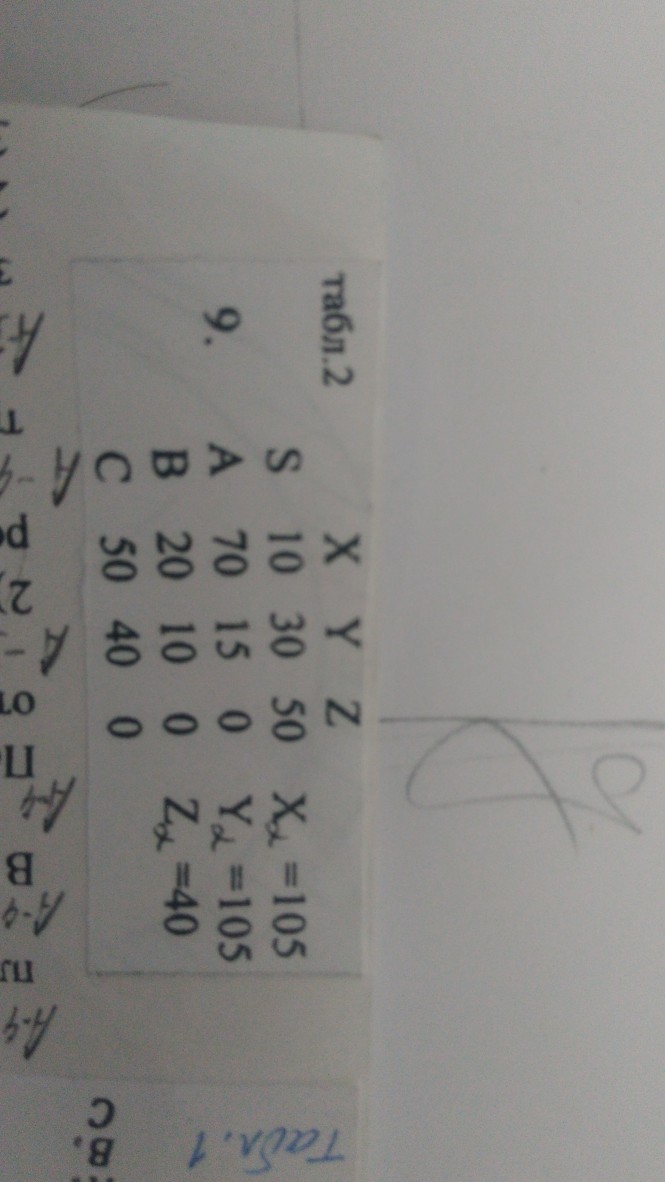
Данные необходимые для решения задачи ЭПЮР 6

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

Наклонная пирамида SABC пересекается плоскостью общего положения а, заданной параметрами Xa, Ya, Za. Требуется: 1) Построить две проекции сечения пирамиды плоскостью. 2) Найти способом вращения вокруг фронтального следа плоскости foa» истинную величину сечения. 3) Построить развёртку боковой поверхности нижней усечённой части пирамиды

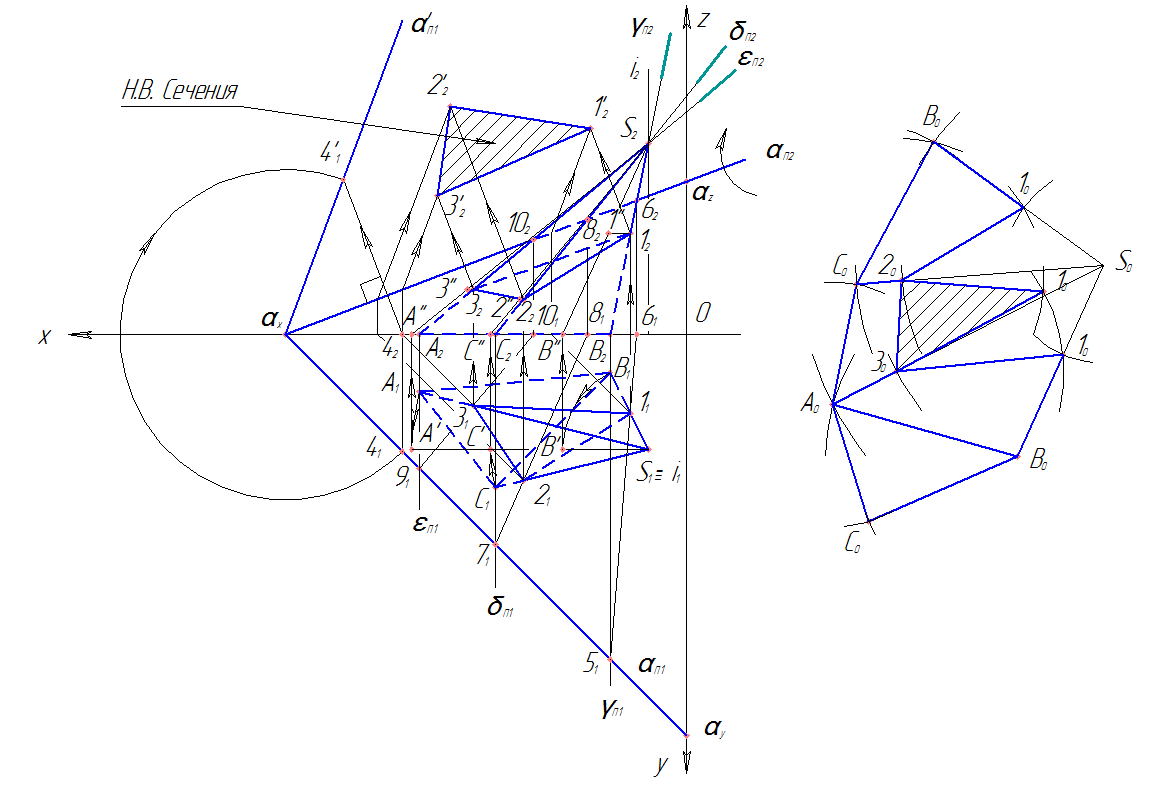
Построение эпюра

План решения задачи:

1	Построение сечения пирамиды SABC плоскостью α:
	— проводим вспомогательные плоскости γ,δ и ε через ребра SB, SC и SA соответственно;
	— находим линии пересечения плоскостей γ,δ и ε с заданной плоскостью α это 5_6, 7-8 и 9-10 соответственно;
	— находим точки пересечения линий 5_6, 7-8 и 9-10  с ребрами SB, SC и SA пирамиды α это 1, 2 и 3 соответственно;
2	Построение натуральной величины сечения способом совмещения(вращение вокруг фронтального следа плоскости αП2):
	— находим новое положение горизонтального следа αП1 это α’П1:- отмечаем произвольную точку на αП1 это точка 4;- строим траекторию движения точки 4 при вращении и находим ее новое положение 4’1;- через точку 4’1 проводим след  α’П1;
	— строим траекторию движения точек 1, 2 и 3 при вращении и находим их новое положение это 1’2, 2’2 и  3’2;
	— соединяем найденные точки 1’2, 2’2 и  3’2 прямыми линиями и получаем натуральную величину сечения;
3	Построение развертки усеченной поверхности пирамиды:
	— вращением ребер SB, SC и SA пирамиды вокруг горизонтально проецирующей оси i находим их натуральные величины это SB», SC» и SA»
	— на свободном месте чертежа выполняем построение развертки.

Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь