Наименьшее значение функции онлайн · Как пользоваться Контрольная Работа РУ
Чтобы найти наименьшее значение заданной функции, то стоит воспользоваться сервисом на сайте «Контрольная работа РУ».
На примере функции 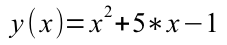
как можно найти наименьшее значение онлайн.
Итак:
1. Вам нужно перейти на страницу сервиса по исследованию функций онлайн и построения графиков.
2. Для указанного примера вбиваем функцию x^2 + 5*x — 1 в форму:

3. После того как вбили функцию, для которой надо найти наименьшее значение, то нажимаем кнопку «Найти наименьшее значение!»
4. Ждём, когда сервер произведёт исследование функции (1-2 сек) и вы увидите результат данного исследования. В том числе там будет подробное решение по нахождению наименьшего значения функции. Я скопировал часть результата исследования для моего примера, которая связана с вычислением минимального значения функции:
- Экстремумы функции:
- Для того, чтобы найти экстремумы, нужно решить уравнение y’=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y'=2*x + 5=0
Решаем это уравнение и его корни будут экстремумами:- x=-5/2. Точка: (-5/2, -29/4)
- Интервалы возрастания и убывания функции:
- Найдем интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим на ведет себя функция в экстремумах при малейшем отклонении от экстремума:
- Минимумы функции в точках:
- Максимумов у функции нету
- Возрастает на промежутках: [-5/2, oo)
- Убывает на промежутках: (-oo, -5/2]
Видим, что наименьшее значение функции для моего примера найдено и равно y min = -5/2 = — 2.5
www.kontrolnaya-rabota.ru
13. Схема нахождения наибольшего и наименьшего значений функции на отрезке. (Пример из т.Р.II, задача №13)
Пусть функция y=f(x)непрерывна на
отрезке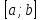
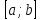 ,
либо на границе отрезка, т. е. приx0=a илиx0=b.
Еслиx0
,
либо на границе отрезка, т. е. приx0=a илиx0=b.
Еслиx0 ,
то точкуx0следует искать среди критических точек
данной функции.
,
то точкуx0следует искать среди критических точек
данной функции. Правило нахождения наибольшего и
наименьшего значений функции на отрезке 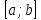 :
:
Найти критические точки функции на интервале
 ;
;Вычислить значения функции в найденных критических точках;
Вычислить значения функции на концах отрезка, т. е. в точках x=a иx=b;
Среди всех вычисленных значений функции выбрать наибольшее и наименьшее.
Замечания: 1. Если функция y=f(x)на
отрезке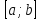 имеет лишь одну критическую точку и она
является точкой максимума (минимума),
то в этой точке функция принимает
наибольшее (наименьшее) значение.
имеет лишь одну критическую точку и она
является точкой максимума (минимума),
то в этой точке функция принимает
наибольшее (наименьшее) значение.
2. Если функция y=f(x)на отрезке не имеет критических точек, то это
означает, что на нем функция монотонно
возрастает или убывает. Следовательно,
свое наибольшее значение функция
принимает на одном конце отрезка, а
наименьшее – на другом.
не имеет критических точек, то это
означает, что на нем функция монотонно
возрастает или убывает. Следовательно,
свое наибольшее значение функция
принимает на одном конце отрезка, а
наименьшее – на другом.
Пример нахождения наибольшего и наименьшего значений функции на отрезке – задача №13 из тип. Расчета
II (Вариант 6). Найти наибольшее и наименьшее значения
функции 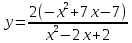 на отрезке
на отрезке .
.
Находим критические точки. Для этого находим производную от данной функции, приравниваем её к нулю и находим корни полученного уравнения:


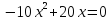
x1=0, x2=2
x1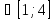 , x2
, x2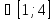
Вычисляем значение функции в найденной критической точке:
 .
.Вычисляем значение функции на концах отрезка:
 ,
,
Ответ: yнаиб=-2приx=1,yнаим=3приx=2.
14. Понятия периодической, четной, нечетной, монотонной, ограниченной функций. Графики элементарных функций. Привести примеры.
Функция y=f(x), определенная на множествеD, называетсяпериодической на этом множестве, если существует такое число
значение ,
что при каждом
,
что при каждом
 и
и .
При этом число
.
При этом число называетсяпериодом функции.
Если
называетсяпериодом функции.
Если — период функции, то ее периодами будут
также числа
— период функции, то ее периодами будут
также числа ,
где
,
где Так
например, для
Так
например, для периодами будут числа
периодами будут числа Основной
период (наименьший положительный) –
это период
Основной
период (наименьший положительный) –
это период
 ,
удовлетворяющее равенству
,
удовлетворяющее равенству .
.Функция y=f(x), определенная на множествеD, называетсячетной, если
выполняются условия выполняются условия
выполняются условия и
и .
Функцияy=f(x), определенная на множествеD,
называетсянечетной, если
.
Функцияy=f(x), определенная на множествеD,
называетсянечетной, если
 и
и .
График
четной функции симметричен относительно
оси
.
График
четной функции симметричен относительно
оси ,
а нечетной – относительно начала
координат.
Например,
,
а нечетной – относительно начала
координат.
Например, ,
, ,
, — четные функции;
— четные функции; ,
, — нечетные функции.
— нечетные функции.Пусть функция y=f(x)определена на множествеDи пусть

 аргументов из неравенстваx1
аргументов из неравенстваx1 x2вытекает
неравенство:
x2вытекает
неравенство: ,
то функция называетсявозрастающейна множестве
,
то функция называетсявозрастающейна множестве ;
; ,
то функция называетсянеубывающейна множестве
,
то функция называетсянеубывающейна множестве ;
; ,
то функция называетсяубывающейна множестве
,
то функция называетсяубывающейна множестве ;
; ,
то то функция называетсяневозрастающейна множестве
,
то то функция называетсяневозрастающейна множестве .
Возрастающие,
невозрастающие, убывающие и неубывающие
функции на множественазываютсямонотоннымина этом
множестве, а возрастающие и убывающие
–строго монотонными. Интервалы,
в которых функция монотонна, называютсяинтервалами монотонности.
.
Возрастающие,
невозрастающие, убывающие и неубывающие
функции на множественазываютсямонотоннымина этом
множестве, а возрастающие и убывающие
–строго монотонными. Интервалы,
в которых функция монотонна, называютсяинтервалами монотонности.Функция y=f(x), определенная на множествеD, называетсяограниченнойна этом множестве, если существует такое число
 ,
что для всех
,
что для всех
 (короткая запись:
(короткая запись: ,
называется ограниченной на
,
называется ограниченной на ,
если
,
если ).
Отсюда следует, что график ограниченной
функции лежит между прямыми
).
Отсюда следует, что график ограниченной
функции лежит между прямыми .
.
Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия от функции, называется элементарной функцией.
Графики элементарных функций:
Показательнаяфункция
 .
. 

Степеннаяфункция
 .
.






Логарифмическаяфункция
 .
.

Тригонометрические функции
 .
.



Обратные тригонометрические функции
 .
. 



Примерами элементарных функций могут
служить функции: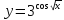 ;
;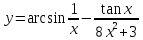 ;
;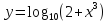 .
.
studfile.net
Как найти наименьшее значение функции??? Если поможите-ответ признаю лучшим!!!
Когда нужно найти наименьшее (или наибольшее) значение функции на заданном отрезке, нужно определить значения этой функции на границах отрезка. Кроме того, на заданном отрезке функция может иметь минимум (или максимум, в общем случае — экстремум). Поэтому нужно определить, имеет ли функция экстремум на заданном отрезке. Для этого нужно найти ПЕРВУЮ производную заданной функции, приравнять ее нулю и найти значения аргумента (х), при которых ПЕРВАЯ производная равна нулю. При этих значениях функция имеет экстремум. Значение его вычисляется подстановкой найденного значения аргумента в выражение функции. Чтобы узнать, какой именно, т.е минимум или максимум, есть два способа. 1) Нужно вычислить значение ВТОРОЙ производной в этих точках. В принципе важно не само значение, а только его знак. Если в заданной точке ВТОРАЯ производная положительна, то в этой точке минимум, если ВТОРАЯ производная отрицательна, то в этой точке максимум. 2) Нужно определить знаки ПЕРВОЙ производной чуть левее проверяемой точки, и чуть правее. Если ПЕРВАЯ производная в данной точке меняет знак с минуса на плюс, то в этой точке — минимум, если наоборот, с плюса на минус, то в этой точке максимум. Но при этом нужно помнить, что функция может иметь несколько экстремумов, поэтому, при выборе проверочных точек, нужно следить, чтобы не выйти за значение другого экстремума. Каким именно способом определять, зависит от вида функции (и ее ПЕРВОЙ и ВТОРОЙ производных). Иногда удобнее оказывается первый способ, иногда второй. После того, как найдены экстремумы в пределах заданного отрезка и значения функции на границах отрезка, из полученных значений выбирается то, что требуется найти, т.е наименьшее или наибольшее значение. ПЕРВАЯ ЗАДАЧА: у=х^5/15-х^3 на отрезке [0;4]. Находим значения функции при х=0 и х=4, записывается так: у(0), у(4). у(0)=0, у(4)=4^5/15-4^3=4^3*(16/15-1)=4^3/15=(4 + 4/15). Находим первую производную: y’=5*x^4/15-3*x^2=x^4/3-3*x^2. Решаем уравнение: x^4/3-3*x^2=0, x^2*(x^2/3-3)=0. Получаем 3 решения: х=0, х=3 и х=-3. В заданные отрезок [0;4] входят две точки: х=0 и х=3. у(0) у нас уже известно. у(3)=3^5/15-3^3=3^3*(9/15-1)=-27*6/15=-54/5=-10,8. Из трех значений у(0)=0, у(3)=-10,8 и у(4)=(4 + 4/15) минимальное равно -10,8, и задача уже решена. Но здесь есть один интересный момент, поэтому продолжу. Чтобы определить, минимум или максимум при х=0 и х=3 применим первый способ. Найдем ВТОРУЮ производную: y»=4*x^3/3-6*x. у»(3)=36-18=18, знак (+), значит при х=3 функция имеет минимум. y»(0)=0. Здесь знак не определен, поэтому придется применить второй способ. Выберем проверочные значения х=-1 и х=1. y'(-1)=1/3-3=-(2+2/3), y'(1)=1/3-3=-(2+2/3). Опять «неудача». Знак первой производной и левее и правее точки х=0 отрицательный. Это значит, что в точке х=0 НЕТ НИ МИНИМУМА, НИ МАКСИМУМА. Так тоже бывает, например как при прохождении через точку х=0 функции у=-x^3. Эта функция на всей числовой оси только убывает, но в точке х=0 касательная к ней горизонтальна. Вторая задача: f(x)=3(5x-4)^2-(5x-4)^3 при |2х-3| < = 1. Здесь выражением |2х-3|<=1 заданы границы отрезка. Нужно просто решить это неравенство. При 2*x-3 >= 0, т.е. при х >= 1,5 получаем неравенство 2*х-3 <= 1, откуда х <= 2, с учетом х >= 1,5 получаем: 1,5 <= х <= 2. При 2*x-3 < 0, т.е. при х < 1,5 получаем неравенство 3-2*х <= 1, откуда 2 <= 2*х, и х >= 1, с учетом х < 1,5 получаем: 1 <= х < 1,5. Объединяя, получаем 1 <= х <= 2, т.е. отрезок [1; 2]. Для удобства, можно сделать замену 5x-4=t, только надо пересчитать границы: Нижняя 5*1-4=1, верхняя 5*2-4=6. Получаем более простое выражение: f(t)=3*t^2-t^3, на отрезке [1; 6]. f(1)=3*1^2-1^3=2, f(6)=3*6^2-6^3=-108. Находим ПЕРВУЮ производную: f'(t)=6*t-3*t^2, решаем уравнение 6*t-3*t^2=0, получаем t=0 и t=2. Значение t=2 попадает в исследуемый интервал. Находим ВТОРУЮ производную при t-2: f»(2)=6-6*2=-6, знак (-), значит при t=2 максимум, равный f(2)=3*2^2-2^3=12-8=4. Ответ
Через производную… Удачи!!!
touch.otvet.mail.ru
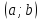 ;
;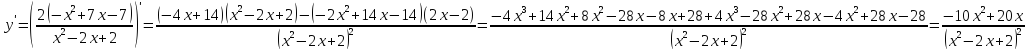
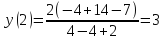 .
.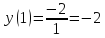 ,
,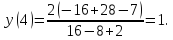
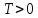 ,
что при каждом
,
что при каждом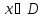
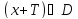 и
и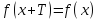 .
При этом число
.
При этом число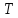 называетсяпериодом функции.
Если
называетсяпериодом функции.
Если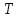 — период функции, то ее периодами будут
также числа
— период функции, то ее периодами будут
также числа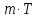 ,
где
,
где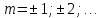 Так
например, для
Так
например, для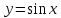 периодами будут числа
периодами будут числа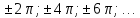 Основной
период (наименьший положительный) –
это период
Основной
период (наименьший положительный) –
это период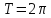
 ,
удовлетворяющее равенству
,
удовлетворяющее равенству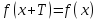 .
.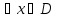 выполняются условия
выполняются условия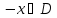 и
и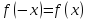 .
Функцияy=f(x), определенная на множествеD,
называетсянечетной, если
.
Функцияy=f(x), определенная на множествеD,
называетсянечетной, если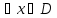
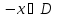 и
и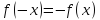 .
График
четной функции симметричен относительно
оси
.
График
четной функции симметричен относительно
оси ,
а нечетной – относительно начала
координат.
Например,
,
а нечетной – относительно начала
координат.
Например,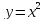 ,
,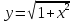 ,
, — четные функции;
— четные функции; ,
,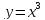 — нечетные функции.
— нечетные функции.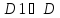
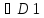 аргументов из неравенстваx1
аргументов из неравенстваx1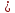 x2вытекает
неравенство:
x2вытекает
неравенство: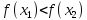 ,
то функция называетсявозрастающейна множестве
,
то функция называетсявозрастающейна множестве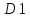 ;
;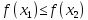 ,
то функция называетсянеубывающейна множестве
,
то функция называетсянеубывающейна множестве ;
;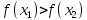 ,
то функция называетсяубывающейна множестве
,
то функция называетсяубывающейна множестве ;
; ,
то то функция называетсяневозрастающейна множестве
,
то то функция называетсяневозрастающейна множестве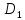 .
Возрастающие,
невозрастающие, убывающие и неубывающие
функции на множественазываютсямонотоннымина этом
множестве, а возрастающие и убывающие
–строго монотонными. Интервалы,
в которых функция монотонна, называютсяинтервалами монотонности.
.
Возрастающие,
невозрастающие, убывающие и неубывающие
функции на множественазываютсямонотоннымина этом
множестве, а возрастающие и убывающие
–строго монотонными. Интервалы,
в которых функция монотонна, называютсяинтервалами монотонности.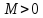 ,
что для всех
,
что для всех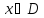
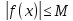 (короткая запись:
(короткая запись: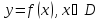 ,
называется ограниченной на
,
называется ограниченной на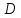 ,
если
,
если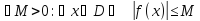 ).
Отсюда следует, что график ограниченной
функции лежит между прямыми
).
Отсюда следует, что график ограниченной
функции лежит между прямыми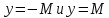 .
.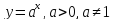 .
. 

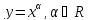 .
.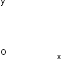






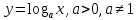 .
.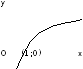
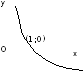
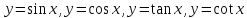 .
.



 .
.