Нахождение координат вектора через координаты точек. Как найти вектор по двум точкам

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i→ должно совпадать с осью Ox, а направление вектора j→ с осью Oy.

Определение 1

Векторы i→ и j→ называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p→ можно разложить по векторам p→=xi→+yj→. Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p→ по координатным векторам называются координатами вектора p→ в данной системе координат.

Координаты вектора записываются в фигурных скобках p→x; y. На рисунке вектор OA→ имеет координаты 2; 1, а вектор b→ имеет координаты 3;-2. Нулевой вектор представляется в виде 0→0; 0.

Если векторы a→ и b→ равны, то и y1=y2. Запишем это так: a→=x1i→+y1j→=b→=x2i→+y2j→, значит x1=x2, y1=y2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на Oxy заданы координаты точек начала и конца AB→: Axa, ya, Bxb, yb. Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем OA→+AB→=OB→, где O – начало координат. Отсюда следует, что AB→=OB→-OA→.

OA→ и OB→ – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения OA→=xa, ya, OB→=xb, yb.

Слишком сложно?

Не парься, мы поможем разобраться и подарим скидку 10% на любую работу

Опиши задание

По правилу операций над векторами найдем AB→=OB→-OA→=xb-xa, yb-ya.

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Пример 1

Найти координаты OA→ и AB→ при значении координат точек A(2,-3), B(-4,-1).

Решение

Для начала определяется радиус-вектор точки A. OA→=(2,-3). Чтобы найти AB→, нужно вычесть значение координат точек начала из координат точек конца.

Получаем: AB→=(-4-2,-1-(-3))=(-6, 2).

Ответ: OA→=(2,-3), AB→=(-6,-2).

Пример 2

Задано трехмерное пространство с точкой A=(3, 5, 7), AB→=(2, 0,-2). Найти координаты конца AB→.

Решение

Подставляем координаты точки A: AB→=(xb-3, yb-5, zb-7).

По условию известно, что AB→=(2, 0,-2).

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: xb-3=2yb-5=0zb-7=-2

Отсюда следует, что координаты точки B AB→равны: xb=5yb=5zb=5 

Ответ:  B(5, 5, 5).

Координаты и векторы. Исчерпывающий гид (ЕГЭ — 2021)

Нам нужно найти угол между прямыми \( \displaystyle SB\) и \( \displaystyle CD\).

Таким образом, наша задача сводится к поиску координат точек: \( \displaystyle S,B,C,D\).

Координаты последних трех мы найдем по маленькому рисунку, а коодинату вершины \( \displaystyle S\) найдем через координату точки \( \displaystyle O\).

Работы навалом, но надо к ней приступать!

a) Координата \( \displaystyle D\): ясно, что ее аппликата и ордината равны нулю.

Найдем абсциссу. Для этого рассмотрим прямоугольный треугольник \( \displaystyle EDP\). Увы, в нем нам известна только гипотенуза, которая равна \( \displaystyle 1\). Катет \( \displaystyle DP\) мы будем стараться отыскать (ибо ясно, что удвоенная длина катета \( \displaystyle DP\) даст нам абсциссу точки \( \displaystyle D\)).

Как же нам ее искать?

Давай вспомним, что за фигура у нас лежит в основании пирамиды? Это правильный шестиугольник.

А что это значит? Это значит, что у него все стороны и все углы равны. \circ \)

Опять-таки, при решении этой задачи я не использовал никаких изошренных приемов, кроме формулы суммы углов правильного n-угольника, а также определения косинуса и синуса прямоугольного треугольника.

3. Поскольку нам опять не даны длины ребер в пирамиде, то я буду считать их равными единице.

Таким образом, поскольку ВСЕ ребра, а не только боковые, равны между собой, то в основании пирамиды и меня лежит квадрат, а боковые грани – правильные треугольники.

Изобразим такую пирамиду, а также ее основание на плоскости, отметив все данные, приведенные в тексте задачи:

Как найти координаты вектора в трехмерном пространстве

Еще из школьного курса алгебры и геометрии мы знаем о понятии трехмерного пространства. Если разобраться, сам термин «трехмерное пространство» определяется как система координат с тремя измерениями (это знают все). По сути, описать любой объемный объект можно при помощи длины, ширины и высоты в классическом понимании. Однако давайте, как говорится, копнем несколько глубже.

Что такое трехмерное пространство

Как уже стало ясно, понимание трехмерного пространства и объектов, способных существовать внутри него, определяется тремя основными понятиями. Правда, в случае с точкой это именно три значения, а в случае с прямыми, кривыми, ломаными линиями или объемными объектами соответствующих координат может быть больше.

В данном случае все зависит именно от типа объекта и применяемой системы координат. Сегодня наиболее распространенной (классической) считается Декартова система, которую иногда еще называют прямоугольной. Она и некоторые другие разновидности будут рассмотрены несколько позже.

Кроме всего прочего, здесь нужно разграничивать абстрактные понятия (если можно так сказать, бесформенные) вроде точек, прямых или плоскостей и фигуры, обладающие конечными размерами или даже объемом. Для каждого из таких определений существуют и свои уравнения, описывающие их возможное положение в трехмерном пространстве. Но сейчас не об этом.

Понятие точки в трехмерном пространстве

Для начала определимся, что представляет собой точка в трехмерном пространстве. В общем-то, ее можно назвать некой основной единицей, определяющей любую плоскую или объемную фигуру, прямую, отрезок, вектор, плоскость и т. д.

Сама же точка характеризуется тремя основными координатами. Для них в прямоугольной системе применяются специальные направляющие, называемые осями X, Y и Z, причем первые две оси служат для выражения горизонтального положения объекта, а третья относится к вертикальному заданию координат. Естественно, для удобства выражения положения объекта относительно нулевых координат в системе приняты положительные и отрицательные значения. Однако же сегодня можно найти и другие системы.

Разновидности систем координат

Как уже говорилось, прямоугольная система координат, созданная Декартом, сегодня является основной. Тем не менее в некоторых методиках задания местоположения объекта в трехмерном пространстве применяются и некоторые другие разновидности.

Наиболее известными считаются цилиндрическая и сферическая системы. Отличие от классической состоит в том, что при задании тех же трех величин, определяющих местоположение точки в трехмерном пространстве, одно из значений является угловым. Иными словами, в таких системах используется окружность, соответствующая углу в 360 градусов. Отсюда и специфичное задание координат, включающее такие элементы, как радиус, угол и образующая. Координаты в трехмерном пространстве (системе) такого типа подчиняются несколько другим закономерностям. Их задание в данном случае контролируется правилом правой руки: если совместить большой и указательный палец с осями X и Y, соответственно, остальные пальцы в изогнутом положении укажут на направление оси Z.

Понятие прямой в трехмерном пространстве

Теперь несколько слов о том, что представляет собой прямая в трехмерном пространстве. Исходя из основного понятия прямой, это некая бесконечная линия, проведенная через точку или две, не считая множества точек, расположенных в последовательности, не изменяющей прямое прохождение линии через них.

Если посмотреть на прямую, проведенную через две точки в трехмерном пространстве, придется учитывать по три координаты обеих точек. То же самое относится к отрезкам и векторам. Последние определяют базис трехмерного пространства и его размерность.

Определение векторов и базиса трехмерного пространства

Как принято считать, в трехмерной системе координат может существовать три основных вектора, которые определяют базис. При этом базисов с соответствующими независимыми тремя векторами может быть бесчисленное множество.

Заметьте, это могут быть только три вектора, но вот троек векторов можно определить сколько угодно. Размерность пространства определяется количеством линейно-независимых векторов (в нашем случае – три). И пространство, в котором имеется конечное число таких векторов, называется конечномерным.

Зависимые и независимые векторы

Что касается определения зависимых и независимых векторов, линейно-независимыми принято считать векторы, являющиеся проекциями (например, векторы оси X, спроецированные на ось Y).

Как уже понятно, любой четвертый вектор является зависимым (теория линейных пространств). А вот три независимых вектора в трехмерном пространстве в обязательном порядке не должны лежать в одной плоскости. Кроме того, если определять независимые векторы в трехмерном пространстве, они не могут являться, так сказать, один продолжением другого. Как уже понятно, в рассматриваемом нами случае с тремя измерениями, согласно общей теории, можно построить исключительно только тройки линейно-независимых векторов в определенной системе координат (без разницы, какого типа).

Плоскость в трехмерном пространстве

Если рассматривать понятие плоскости, не вдаваясь в математические определения, для более простого понимания этого термина, такой объект можно рассматривать исключительно как двумерный. Иными словами, это бесконечная совокупность точек, у которых одна из координат является постоянной (константой).

К примеру, плоскостью можно назвать любое количество точек с разными координатами по осям X и Y, но одинаковыми координатами по оси Z. В любом случае одна из трехмерных координат остается неизменной. Однако это, так сказать, общий случай. В некоторых ситуациях трехмерное пространство может пересекаться плоскостью по всем осям.

Существует ли более трех измерений

Вопрос о том, сколько может существовать измерений, достаточно интересен. Как считается, мы живем не в трехмерном с классической точки зрения пространстве, а в четырехмерном. Кроме известных всем длины, ширины и высоты, такое пространство включает в себя еще и время существования объекта, причем время и пространство между собой взаимосвязаны достаточно сильно. Это доказал еще Эйнштейн в своей теории относительности, хотя это больше относится к физике, нежели к алгебре и геометрии.

Интересен и тот факт, что сегодня ученые уже доказали существование как минимум двенадцати измерений. Конечно, понять, что они собой представляют, сможет далеко не каждый, поскольку это относится скорее к некой абстрактной области, которая находится вне человеческого восприятия мира. Тем не менее факт остается фактом. И не зря же многие антропологи и историки утверждают, что наши пращуры могли иметь некие специфичные развитые органы чувств вроде третьего глаза, которые помогали воспринимать многомерную действительность, а не исключительно трехмерное пространство.

Кстати сказать, сегодня существует достаточно много мнений по поводу того, что экстрасенсорика тоже является одним из проявлений восприятия многомерного мира, и тому можно найти достаточно много подтверждений.

Заметьте, что современными базовыми уравнениями и теоремами описать многомерные пространства, отличающиеся от нашего четырехмерного мира, тоже не всегда представляется возможным. Да и наука в этой области относится скорее к области теорий и предположений, нежели к тому, что можно явно ощутить или, так сказать, потрогать или увидеть воочию. Тем не менее косвенные доказательства существования многомерных миров, в которых может существовать четыре и более измерений, сегодня ни у кого не вызывают сомнений.

Заключение

В целом же, мы очень кратко рассмотрели основные понятия, относящиеся к трехмерному пространству и базовым определениям. Естественно, существует множество частных случаев, связанных с разными системами координат. К тому же мы постарались особо не лезть в математические дебри для объяснения основных терминов только для того, чтобы вопрос, связанный с ними, был понятен любому школьнику (так сказать, объяснение «на пальцах»).

Тем не менее, думается, даже из таких простых трактовок можно сделать вывод о математическом аспекте всех составляющих, входящих в базовый школьный курс алгебры и геометрии.

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.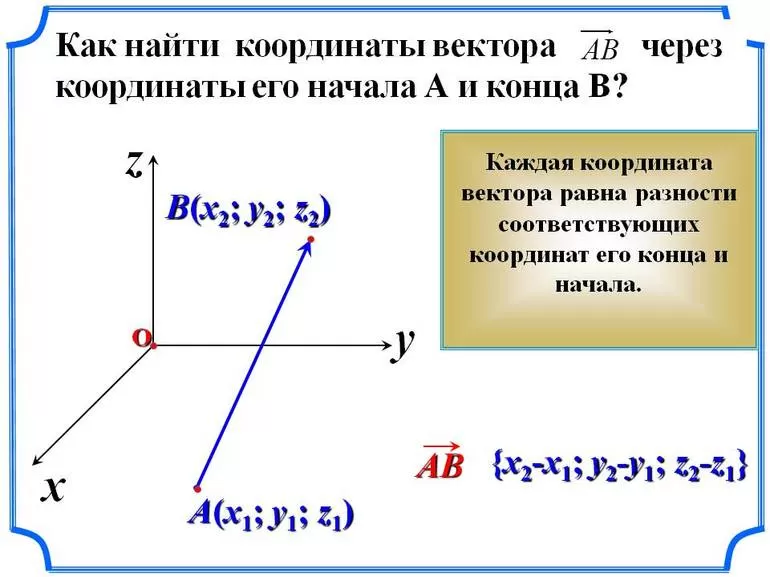

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением A_x + B_y + C_z + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Калькулятор служит для вычисления длины вектора в трехмерном пространстве.

Длиной или модулем вектора мы называем длину отрезка, изображающего данный вектор.

Формула для определения длины вектора a в трехмерном пространстве через его координаты представлена ниже.

Чтобы произвести вычисление длины вектора в трехмерном пространстве, введите в соответствующих полях значение координаты x и координаты y и координаты z, после чего нажмите кнопку » ВЫЧИСЛИТЬ «.

Результатом работы программы будет значение длины вектора в трехмерном пространстве.

как вычислить координаты вектора

Вы искали как вычислить координаты вектора? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как найти вектор ab если известно координаты этих точек, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как вычислить координаты вектора».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как вычислить координаты вектора,как найти вектор ab если известно координаты этих точек,как найти координаты вектора,как найти координаты вектора в пространстве,как найти координаты вектора зная координаты его начала и конца,как найти координаты вектора зная координаты начала и конца,как находить координаты векторов,как определить координаты вектора,как узнать координаты вектора,координат вектора формула,координата вектора формула,координати вектора,координаты вектора в пространстве как найти,координаты вектора координаты точки,координаты вектора формула,координаты вектора формулы,координаты векторов как найти,найдите координаты вектора,найдите координаты векторов,найти координаты вектора,найти координаты вектора ав,найти координаты векторов,определение координат вектора по координатам его начала и конца,определить по рисунку 276 координаты вектора,формула координат вектора,формула координата вектора,формула координаты вектора,формула нахождения координат вектора,формулы координаты вектора. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как вычислить координаты вектора. Просто введите задачу в окошко и нажмите «решить» здесь (например, как найти координаты вектора).

Где можно решить любую задачу по математике, а так же как вычислить координаты вектора Онлайн?

Решить задачу как вычислить координаты вектора вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Задачи с векторами

    Задачи с векторами на ЕГЭ. Дорогие друзья! Вы знаете, что в состав экзамена по математике входят такие задания. Не факт, что такая задача попадёт именно вам, но готовиться к этому и понимать тему в любом случае нужно. На блоге мы уже рассмотрели несколько задач на сумму (разность) векторов, длину вектора, в этой же статье есть необходимая теория. Посмотрите её, прежде чем рассматривать задачи представленные ниже.

Также загляните в справочник на блоге. Если нужно вспомнить, что такое абсцисса и ордината точки, тогда посмотрите эту статью. Кратко повторим:

Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты начала:

Формула для определения длины вектора, если известны координаты его начала и конца:

Формула для определения длины вектора, если известны его координаты:

27725. Вектор АВ с началом в точке A(2;4) имеет координаты (6;2). Найдите ординату точки B.

Как уже сказано координаты вектора находятся следующим образом: из соответствующих координат конца вычитаются координаты начала вектора. То есть:

Координаты вектора нам даны, координаты его начала тоже, значит:

Следовательно можем найти координаты точки В:

х₂ – 2 = 6         у₂ – 4 = 2

х₂  = 8             у₂  = 6

Таким образом, ордината точки В равна 6.

Ответ: 6

27726. Вектор АВ с началом в точке A(3;6) имеет координаты (9;3). Найдите сумму координат точки B. 

Задача по процессу решения такая же как и предыдущая, но иначе поставлен вопрос. Вычисления так же находятся в пределах устного счёта. Ещё раз запишем координаты вектора, когда известны координаты его начала и конца:

Координаты вектора и координаты его начала даны, значит:

Можем найти координаты точки В:

х₂ – 3 = 9         у₂ – 6 = 3

х₂  = 12             у₂  = 9

Таким образом, сумма координат точки В равна 21.

Ответ: 21

27727. Вектор АВ с концом в точке B (5;3) имеет координаты (3;1). Найдите абсциссу и ординату точки A, также сумму её координат. 

Нам известны  координаты вектора и координаты его конца, значит:

Можем найти координаты точки А:

5 – х₁  = 3        3 – у₁  = 1

х₁  = 2             у₁  = 2

Таким образом, абсцисса точки А равна двум,  ордината тоже равна двум, а сумма координат равна  2+2 = 4.

Ответ: 4

27731 Найдите квадрат длинны вектора a+b.

В данной задаче необходимо найти координаты вектора, который является суммой указанных векторов, затем найти его длину и возвести её в квадрат. Запишем формулу длины вектора, если известны его координаты:

Или в другой форме:

Найдём координаты вектора, который является суммой данных векторов. Для этого сначала найдём координаты данных векторов. 

Рассмотрим вектор:

Рассмотрим вектор:

*Можно было глядя на эскиз сразу их записать, так как точки их начал совпадают с началом координат.

Теперь найдём координаты вектора являющегося их суммой:

(2 + 8; 6 + 4) = (10;10)

Таким образом, длина  вектора являющегося суммой векторов a и b равна:

Следовательно квадрат длины будет равен 200.

*Имея опыт в решении подобных задач, можно сразу записывать:

Как видите, вычисления можно осуществить устно. Здесь для вас умышленно представлено подробное решение.

Ответ: 200

27733. Найдите квадрат длины вектора a – b.

Задача аналогична предыдущей. Необходимо найти координаты вектора, который является разностью представленных векторов, затем найти его длину и результат возвести в квадрат.

Координаты данных векторов нам уже известны (из предыдущей задачи):

Теперь найдём координаты вектора, который является их разностью: 

(2 – 8; 6 – 4) = (–6;2)

Таким образом, длина  вектора, который является разностью векторов

Следовательно квадрат её длины будет равен 40.

*Можно сразу записывать и вычислять:

Ответ: 40

27723. Найдите сумму координат вектора АВ.

Посмотреть решение

27724.Вектор АВ с началом А(2;4) имеет координаты (6;2) Найдите абсциссу точки В.

Посмотреть решение

27730. Найдите сумму координат вектора а + b.

Посмотреть решение

27732. Найдите сумму координат вектора а–b.

Посмотреть решение

27736. Найдите сумму координат вектора а + b

Посмотреть решение

27739. Найдите квадрат длины вектора а–b.

Посмотреть решение

Вы убедились, что задачи с векторами на ЕГЭ это одни из самых простых заданий. Есть, конечно, задания со скалярным произведением векторов, но о они сложности не представляют, нужно лишь знать формулу скалярного произведения. Такие задачи мы также рассмотрим, не пропустите!

На этом всё. Если что-то непонятно, пишите. Успеха Вам!

С уважением, Александр Крутицких

Уроки сделаны… Мама охрипла… Сын оглох … Соседи выучили всё наизусть, собака пересказала!!!. .

P.S: Делитесь  этой статьёй в сетях.

Координаты вектора. Как найти? | Калькулятор

Вектором называется направленный отрезок AB; точка A — начало, точка B — конец вектора
Чтобы найти координаты вектора AB, зная координаты его начальной точки А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Формула определения координат вектора для плоских задач

В случае плоской задачи вектор AB заданный координатами точек A(A_x ; A_y) и B(B_x ; B_y) можно найти воспользовавшись следующей формулой

AB = {B_x-A_x; B_y-A_y}

Формула определения координат вектора для пространственных задач

В случае пространственной задачи вектор AB заданный координатами точек A(A_x; A_y; A_z) и B(B_x; B_y; B_z) можно найти воспользовавшись следующей формулой

AB = {B_x-A_x ; B_y-A_y ; B_z-A_z}

Формула определения координат вектора для n -мерного пространства

В случае n-мерного пространства вектор AB заданный координатами точек A(A₁ ; A₂ ; … ; A_n) и B(B₁ ; B₂ ; … ; B_n) можно найти воспользовавшись следующей формулой

AB = {B₁-A₁ ; B₂-A₂ ; … ; B_n-A_n}

Примеры задач

Рассмотрим несколько задач связанных с определением координат вектора по двум точкам

Пример 1.

Найти координаты вектора AB, если A(1; 4), B(3; 1).

Решение: AB = {3-1; 1-4} = {2; -3}.

Пример 2.

Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).

Решение:

AB _x = B _x-A _x => B _x = AB _x + A _x => B _x = 5 + 3 = 8
AB _y = B _y-A _y => B _y = AB _y + A _y => B _y = 1 + (-4) = -3

Ответ: B(8;-3).

Пример 3.

Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).

Решение: AB = {3-1; 1-4; 1-5} = {2; -3; -4}.

Пример 4.

Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).

Решение: AB = {3-1; 0-4; 1-5; -2-5; 5-(-3)} = {2; -4; -4; -7; 8}.

Полезен ли материал?

#Калькуляторы

Координаты вектора. Разложение вектора по двум неколлинеарным векторам 9 класс онлайн-подготовка на Ростелеком Лицей |

 

Координаты вектора. Разложение вектора по двум неколлинеарным векторам.

Если векторы a⃗ и b⃗ коллинеарны и a⃗≠0⃗, то существует такое число k, что b⃗=ka⃗.

Пусть a⃗ и b⃗ – два данных вектора. Если вектор p представлен в виде p⃗=xa⃗+yb⃗, где x и y – некоторые числа, то говорят, что вектор p⃗ разложен по векторам a⃗ и b⃗. Числа x и y называются коэффициентами разложения.

Теорема

На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Напомню, что для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.

В дальнейшем под длиной отрезка мы будем понимать это число.

 

 

Отложим от начала координат O единичные векторы (т.е. векторы, длины которых равны единице) i⃗ и j⃗ так, чтобы направление вектора i⃗совпало с напралением оси Ox, а направление вектора j⃗ – с направлением оси Oy. Векторы i⃗ и j⃗ назовем координатными векторами.

Координатные векторы не коллинеарны, поэтому любой вектор p⃗ можно разложить по координатным векторам, т.е. представить в виде p⃗=xi⃗+yj⃗, причем коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора p⃗ по координатным векторамназываются координатными векторамиp⃗ в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: p⃗{x;y}.

Так как нулевой вектор можно представить в виде 0⃗=0.i⃗+0^.j⃗, то его координаты равны нулю: 0⃗{0;0}. Если векторы a⃗=x1i⃗+y1j⃗ и b⃗=x₂i⃗+y₂j⃗ равны, то x₁ = x₂ и y₁ = y₃. Таким образом, координаты равных векторов соответственно равны.

Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.

1. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

   Докажем это утверждение для двух векторов. Рассмотрим векторы a{x1;y1} и b{x2;y2}. Так как a⃗=x1i⃗+y1j⃗ и b ⃗=x2i⃗ +y2j⃗ ,то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:

   a⃗+b⃗=x₁i⃗+y₁j⃗+x₂i⃗+y₂j⃗=(x₁+x₂)i⃗+(y₁+y₂)j⃗ .

   Следовательно, что координаты вектора a⃗+b⃗ равны {x1+x2;y1+y2}.

   Аналогично доказывается следующее утверждение:

2. Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов.

   Иными словами, если a⃗{x₁;y₁} и b⃗{x₂;y₂} – данные векторы, то вектор a⃗–b⃗ имеет координаты {x1-x2;y1-y2}.

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

   В самом деле, пусть вектор a⃗ имеет координаты {x;y}. Найдем координаты вектора ka⃗, гдеk – произвольное число. Так как a⃗=xi⃗+yj⃗, то kxi⃗+kyj⃗. Отсюда следует, что координаты вектора ka⃗ равны {kx;ky}.

   Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

   Найти координаты вектора a⃗+b⃗,если a⃗{3;2},b⃗{2;5}

   Чтобы найти координаты вектора суммы, надо сложить соответствующие координаты данных векторов, получим:

   a⃗+b⃗ имеет координаты {3 + 2; 2 + 5}, то есть {5; 7}

   Найти координаты вектора 2a⃗, если a⃗{3;2}

   Значит, вектор 2a⃗ имеет координаты {2 ⋅ 3; 2 ⋅ 2}, то есть {6;4}

Итак, сегодня мы узнали, что любой вектор можно разложить по двум неколлинеарным векторам, ввели понятие координат вектора и рассмотрели правила, позволяющие находить координаты суммы, разности векторов, и произведения вектора на число. А в следующий раз мы найдем связь между координатами вектора и координатами его начала и конца.

Найти вектор направления по двум точкам

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы вуза предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как так как ChillingEffects. org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушают ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Нахождение координат точек с помощью векторов? (См. Рисунок)

Чтобы найти координаты A B C , нам нужно найти пересечение векторных линий. Это можно сделать, приравняв каждую пару векторных линий.

Чтобы найти точку A , воспользуемся векторными линиями AB и AC . См. Диаграмму.

#AB = AC #

# ((0), (2)) + r ((2), (1)) = ((0), (5)) + t ((1), (- 1)) #

# цвет (белый) (->) 2r = t #
# 2 + r = 5-t #

Решение для # r # и # t #:

# г = 3-т #

# 2 (3-t) = t => t = 2 #

# 2r = 2 => r = 1 #

Использование их в #AB = AC #

# ((0), (2)) + 1 ((2), (1)) = ((0), (5)) + 2 ((1), (- 1)) #

# ((2), (3)) = ((2), (3)) #

Координата A : # цвет (белый) (8) (2 цвета (белый) (1), 3) #

Для поиска точки B воспользуемся векторными линиями AB и BC .

#AB = BC #

# ((0), (2)) + r ((2), (1)) = ((8), (6)) + s ((- 1), (- 2)) #

# цвет (белый) (888) 2r = 8-s #
# 2 + r = 6-2s #

# r = 4-2s #

# 2 (4-2s) = 8-s => s = 0 #
# 2 + r = 6-2 (0) => r = 4 #

Используя их в #AB = BC #

# ((0), (2)) + 4 ((2), (1)) = ((8), (6)) + 0 ((- 1), (- 2)) #

# ((8), (6)) = ((8), (6)) #

Координата B : # цвет (белый) (8) (8 цвет (белый) (1), 6) #

Для поиска точки C воспользуемся векторными линиями AC и BC .

# AC = BC #

# ((0), (5)) + t ((1), (- 1)) = ((8), (6)) + s ((- 1), (- 2)) #

# цвет (белый) (8888) t = 8-s #
# 5-t = 6-2s #

# 5- (8-s) = 6-2s => s = 3 #
# t = 8-3 => t = 5 #

Использование их в #AC = BC #

# ((0), (5)) + 5 ((1), (- 1)) = ((8), (6)) + 3 ((- 1), (- 2)) #

# ((5), (0)) = ((5), (0)) #

Координата C : # цвет (белый) (8) (5 цвет (белый) (1), 0) #

Чтобы вычислить длины сторон, мы могли бы использовать формулу расстояния или найти векторы #vec (AB), vec (AC) и vec (CB) # и найти их величину.2)) = sqrt (45) = 3sqrt (5) #

Стороны AB и BC имеют одинаковую длину.

Координаты:

# A = (2, 3) #
# B = (8, 6) #
# C = (5, 0) #

Длина сторон:

# AB = 3sqrt (5) #
# BC = 3sqrt (5) #
# AC = 3sqrt (2) #

Координаты точки, компоненты вектора и середина отрезка

Координаты точки на плоскости

Давайте посмотрим, как векторы используются для присвоения координат точкам на плоскости.

Мы рассматриваем фиксированную точку на плоскости $$ O $$ (известную как начало координат) и базис $$ B = \ {\ overrightarrow {u}, \ overrightarrow {v} \} $$ из $$ V_2 $$. (Космический вектор размерности $$ 2 $$).

Напомним, что в основе $$ V_2 $$ лежат два линейно независимых вектора. Набор, образованный $$ O $$ и $$ B = \ {\ overrightarrow {u}, \ overrightarrow {v} \} $$, составляет систему отсчета на плоскости, поскольку позволяет нам определять положение любой другой точки на плоскости.

Это происходит потому, что любые другие точки $$ P $$ на плоскости определяют вместе с точкой $$ O $$ вектор $$ \ overrightarrow {OP} $$.Пусть $$ (p_1, p_2) $$ — компоненты вектора в базисе $$ B $$. Тогда $$ (p_1, p_2) $$ — координаты точки $$ P $$ в системе отсчета $$ R = \ {O; \ overrightarrow {u}, \ overrightarrow {v} \} $$ и запишем $$ P = (p_1, p_2) $$.

Процедура определения координат точки $$ P $$ в данной системе отсчета следующая:

1. Из точек $$ O $$ и $$ P $$ определяем вектор $$ \ overrightarrow {OP} $$

2. Мы выражаем вектор $$ \ overrightarrow {OP} $$ как линейную комбинацию векторов базиса $$ B = \ {\ overrightarrow {u}, \ overrightarrow {v} \} $$, то есть , $$ \ overrightarrow {OP} = p_1 \ cdot \ overrightarrow {u} + p_2 \ cdot \ overrightarrow {v} $$

3. $$ P = (p_1, p_2) $$

Экспресс-точка $$ P $$ чертежа в системе отсчета $$ R = \ {O; \ overrightarrow {u}, \ overrightarrow {v} \} $$.

• Рисуем вектор $$ \ overrightarrow {OP} $$:

• Выразим вектор $$ \ overrightarrow {OP} $$ как линейную комбинацию векторов базиса $$ B = \ {\ overrightarrow {u}, \ overrightarrow {v} \} $$:

• Получаем $$ \ overrightarrow {OP} = \ overrightarrow {u} +2 \ overrightarrow {v} $$ и поэтому координаты точки $$ P $$ равны $$ P = (1, 2) $$

С этого момента мы будем рассматривать в качестве системы отсчета $$ R $$ систему, образованную началом координат $$ O = (0, 0) $$ и каноническим базисом $$ V_2 $$ $$ B = \ {\ overrightarrow {i}, \ overrightarrow {j} \} $$.

Составляющие вектора, определяемые двумя точками

Давайте теперь посмотрим, как определить компоненты вектора, если мы знаем координаты его конечных точек:

Пусть $$ P = (p_1, p_2) $$ и $$ Q = (q_1, q_2) $$ — две точки плоскости, а $$ \ overrightarrow {PQ} $$ вектор, идущий от $$ P От $$ до $$ Q $$. Тогда компоненты вектора $$ \ overrightarrow {PQ} $$ равны $$ \ overrightarrow {PQ} = (q_1-p_1, q_2-p_2) $$.

Дано $$ P = (2, 6) $$ и $$ Q = (-3, 9) $$. Компоненты вектора $$ \ overrightarrow {PQ} $$: $$ \ overrightarrow {PQ} = (-3 — 2, 9 — 6) = (-5, 3) $$

Применение вектора к точке

Для данной точки $$ P $$ и вектора $$ \ overrightarrow {v} $$ результатом применения вектора к точке будет новая точка $$ Q $$, помещенная в направлении $$ \ overrightarrow { v} $$ и на расстоянии $$ | \ overrightarrow {v} | $$.(модуль вектора $$ \ overrightarrow {v} $$)

Координаты этой новой точки $$ Q $$ вычисляются на основе координат $$ P = (p_1, p_2) $$ и $$ \ overrightarrow {v} = (v_1, v_2) $$, таким образом, $$$ Q = P + \ overrightarrow {v} = (p_1 + v_1, p_2 + v_2) $$$

ПРИМЕЧАНИЕ. Очень важно помнить, что эта операция сложения имеет смысл только между точкой и вектором. Мы никогда не должны складывать две точки, и результатом сложения двух векторов будет другой вектор, а не точка!

Рассматривая следующий рисунок, определите координаты точки $$ P $$ фигуры, результат применения вектора $$ \ overrightarrow {v} $$ к точке $$ A $$.

Начнем с вычисления компонентов вектора $$ \ overrightarrow {v} $$: $$$ \ overrightarrow {v} = (2 — (-1), 4-2) = (3, 2) $$$ Поскольку $$ P $$ является результатом применения вектора $$ \ overrightarrow {v} $$ к имеющейся у нас точке $$ A $$, $$$ P = A + \ overrightarrow {v} = (0,4) + (3,2) = (3,6) $$$

Середина отрезка

Рассмотрим теперь сегмент с конечными точками $$ A = (a_1, a_2) $$ и $$ B = (b_1, b_2) $$. Пусть $$ M = (m_1, m_2) $$ — середина указанного выше отрезка.Очевидно, что вышеупомянутый пункт удовлетворяет тому, что $$ \ overrightarrow {AB} = 2 \ cdot \ overrightarrow {AM} $$ или что $$ (b_1-a_1, b_2-a_2) = 2 \ cdot (m_1-a_1, m_2- а_2) $$

Разделив компонент на компонент, получим: $$$ \ begin {array} {rcl} b_1-a_1 & = & 2 \ cdot (m_1-a_1) \\ b_2-a_2 & = & 2 \ cdot (m_2-a_2) \ end {array} $$$ и изолируя мы имеем: $$$ \ begin {array} {rcl} m_1 & = & \ displaystyle \ frac {a_1 + b_1} {2} \\ m_2 & = & \ displaystyle \ frac {a_2 + b_2} {2} \ end {array} $$$ Таким образом, мы можем вычислить координаты средней точки отрезка по координатам его конечных точек.

Рассматривая точки $$ A = (-3, 7) $$ и $$ B = (1, 2) $$, найдите среднюю точку отрезка, который они определяют.

Применяя предыдущие формулы, получаем: $$$ \ begin {array} {rcl} m_1 & = & \ displaystyle \ frac {a_1 + b_1} {2} = \ frac {-3 + 2} {2} = — 1 \\ m_2 & = & \ displaystyle \ frac {a_2 + b_2} {2} = \ frac {7 + 2} {2} = \ frac {9} {2} \ end {array} $$$ Следовательно, середина сегмента $$ AB $$ равна $$ M = (-1, \ displaystyle \ frac {9} {2}) $$

Векторов

Это вектор:

Вектор имеет величину , (размер) и направление :

Длина линии показывает ее величину, а стрелка указывает направление.

Мы можем сложить два вектора, соединив их голова к хвосту:

И неважно, в каком порядке мы их добавляем, результат будет тот же:

Пример: самолет летит на север, но дует ветер с северо-запада.

Два вектора (скорость, создаваемая воздушным винтом, и скорость ветра) приводят к несколько более низкой путевой скорости при движении немного к востоку от севера.

Если бы вы смотрели на самолет с земли, казалось бы, он немного поскользнулся.

Вы когда-нибудь видели это? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают это объяснить.

Скорость, ускорение, сила и многое другое — векторы.

Вычитание

Мы также можем вычесть один вектор из другого:

• сначала мы меняем направление вектора, который мы хотим вычесть,
• , затем добавьте их как обычно:

а — б

Обозначение

Вектор часто пишется жирным шрифтом , например a или b .

Вектор также может быть записан как буквы его головы и хвоста со стрелкой над ним, например:

Расчеты

А теперь … как нам делать расчеты?

Самый распространенный способ — сначала разбить векторы на части x и y, например:

Вектор a разбит на
два вектора a _x и a _y

(Позже мы увидим, как это сделать. )

Добавление векторов

Затем мы можем сложить векторы на , добавив части x и , добавив части y :

Сумма вектора (8, 13) и вектора (26, 7) дает вектор (34, 20)

Пример: складываем векторы a = (8, 13) и b = (26, 7)

c = a + b

с = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)

Когда мы разбиваем такой вектор, каждая часть называется компонентом :

Вычитание векторов

Для вычитания сначала переверните вектор, который мы хотим вычесть, а затем сложите.

Пример: вычесть k = (4, 5) из v = (12, 2)

a = v + — k

a = (12, 2) + — (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)

Величина вектора

Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:

| a |

ИЛИ можно написать с двойной вертикальной чертой (чтобы не путать с абсолютным значением):

|| a ||

Мы используем теорему Пифагора для его вычисления:

| a | = √ (х ² + y ² )

Пример: какова величина вектора b = (6, 8)?

| b | = √ (6 ² + 8 ² ) = √ (36 + 64) = √100 = 10

Вектор с величиной 1 называется единичным вектором.

Вектор против Скалярного

Скаляр имеет величину (размер) только .

Скаляр: просто число (например, 7 или -0,32) … определенно не вектор.

Вектор имеет величину и направление и часто выделяется полужирным шрифтом , поэтому мы знаем, что это не скаляр:

• , поэтому c — вектор, он имеет величину и направление
• , но c — это просто значение, например 3 или 12.4

Пример: k b на самом деле является скаляром, умноженным на k, вектор b .

Умножение вектора на скаляр

Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы изменяем размер вектора.

Пример: умножить вектор m = (7, 3) на скаляр 3

a = 3 м = (3 × 7, 3 × 3) = (21, 9)

По-прежнему указывает в том же направлении, но в 3 раза длиннее

(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз. )

Умножение вектора на вектор (скалярное произведение и кросс-произведение)

Как мы, , умножим два вектора вместе? Есть несколько способов! (Подробности см. На этих страницах.)

Более двух размеров

Векторы также отлично работают в трех и более измерениях:

Вектор (1, 4, 5)

Пример: складываем векторы a = (3, 7, 4) и b = (2, 9, 11)

c = a + b

с = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)

Пример: какова величина вектора w = (1, −2, 3)?

| w | = √ (1 ² + (−2) ² + 3 ² ) = √ (1 + 4 + 9) = √14

Вот пример с 4-мя измерениями (но его сложно нарисовать!):

Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)

(3, 3, 3, 3) + — (1, 2, 3, 4)
= (3, 3, 3, 3) + (−1, −2, −3, −4)
= (3 −1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)

Величина и направление

Мы можем знать величину и направление вектора, но нам нужны его длины x и y (или наоборот):

	<=>
Вектор a в полярных координатах		Вектор a в декартовых координатах

Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткое описание:

От полярных координат (r, θ ) до декартовых координат (x, y)		От декартовых координат (x, y) до полярных координат (r, θ)
x = r × cos ( θ ) y = r × sin ( θ )		r = √ (x 2 + y 2 ) θ = tan -1 (y / x)

Пример

Сэм и Алекс тянут ящик.

• Сэм тянет с силой 200 Ньютонов при 60 °
• Алекс тянет с усилием 120 Ньютонов под углом 45 °, как показано на рисунке

Что такое объединенная сила и ее направление?

Давайте сложим два вектора голова к хвосту:

Первое преобразование из полярной в декартову (до 2 десятичных знаков):

Вектор Сэма:

• x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
• y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21

Вектор Алекса:

• x = r × cos ( θ ) = 120 × cos (-45 °) = 120 × 0,7071 = 84,85
• y = r × sin ( θ ) = 120 × sin (-45 °) = 120 × -0,7071 = -84,85

Теперь у нас:

Добавьте их:

(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)

Этот ответ верен, но давайте вернемся к полярному, поскольку вопрос был в полярном:

• r = √ (x ² + y ² ) = √ (184. 85 ² + 88,36 ² ) = 204,88
• θ = загар ^-1 (y / x) = загар ^-1 (88,36 / 184,85) = 25,5 °

И у нас есть (округленный) результат:

А для Сэма и Алекса это выглядит так:

Они могли бы получить лучший результат, если бы стояли плечом к плечу!

7. Векторы в трехмерном пространстве

Ранее мы видели, как представить двумерные векторы на плоскости x — y .

Теперь мы расширяем идею представления трехмерных векторов с помощью осей x — y — z . (См. «Трехмерную систему координат» для справки по этому поводу).

Пример

Вектор OP имеет начальную точку в начале координат O (0, 0, 0) и конечную точку в P (2, 3, 5). Мы можем нарисовать вектор OP следующим образом:

Величина трехмерного вектора

Ранее мы видели, что расстояние между двумя точками в трехмерном пространстве равно

. 2) = 6.16 \ «единиц» `

Добавление трехмерных векторов

Ранее мы видели, как складывать двумерные векторы. Теперь мы расширим идею для трехмерных векторов.

Мы просто складываем компоненты i вместе, затем компоненты j и, наконец, компоненты k .

Пример 1

Два якоря удерживают судно на месте, и их силы, действующие на судно, представлены векторами A, и B следующим образом:

A = 2 i + 5 j — 4 k и B = — 2 i — 3 j — 5 k

Если бы мы заменили 2 якоря на 1 якорь, какой вектор представляет этот единственный вектор?

Ответ

Задача просто требует, чтобы мы сложили векторы, чтобы получить единственный результирующий вектор.

A + B

= (2 + −2) i + (5 — 3) j + (−4 — 5) k = 0 i + 2 j — 9 k = 2 j — 9 k

Точечное произведение трехмерных векторов

Чтобы найти скалярное произведение (или скалярное произведение) трехмерных векторов, мы просто расширяем идеи скалярного произведения в двух измерениях, с которыми мы встречались ранее.

Пример 2 — Точечное произведение с использованием величины и угла

Найдите скалярное произведение векторов P и Q , учитывая, что угол между двумя векторами составляет 35 ° и

.

| P | = 25 ед. с и | Q | = 4 шт.

Ответ

Используя нашу формулу для скалярного произведения:

P • Q = | P | | Q | cos θ

имеем:

P • Q

= | P | | Q | cos θ = 25 × 4 × cos 35 ° = 81.92

Пример 3 — Точечное произведение, если векторы являются кратными единичным векторам

Найдите скалярное произведение векторов A и B (они взяты из нашего примера привязки выше):

A = 2 i + 5 j — 4 k и B = — 2 i — 3 j — 5 k

Ответ

A • B

= (2 i + 5 j — 4 k ) • (−2 i — 3 j — 5 k ) = (2 × −2) + (5 × −3) + (−4 × −5) = −4 + ​​−15 + 20 = 1

Направляющие косинусы

Предположим, у нас есть вектор OA с начальной точкой в ​​начале координат и конечной точкой в ​​A.

Предположим также, что у нас есть единичный вектор в том же направлении, что и OA . (См. Напоминание об единичных векторах).

Пусть наш единичный вектор будет:

u = u ₁ i + u ₂ j + u ₃ k

На графике u — это единичный вектор (черный), указывающий в том же направлении, что и вектор OA , и i , j и k (единичные векторы в x-, y- и z- соответственно) отмечены зеленым.

Теперь мы увеличиваем вектор и и немного меняем ориентацию, как показано ниже:

Теперь, если на диаграмме выше,

α — угол между u и осью x (темно-красным),
β — угол между u и осью y (зеленый) и
γ — угол между u и z — ось (розового цвета),

, то мы можем использовать скалярное произведение и записать:

u 1	= u • i = 1 × 1 × cos α = cos α

u 2	= u • j = 1 × 1 × cos β = cos β

u 3	= u • k = 1 × 1 × cos γ = cos γ

Итак, мы можем записать единичный вектор и как:

u = cos α i + cos β j + cos γ k

Эти 3 косинуса называются направляющими косинусами .

Угол между трехмерными векторами

Ранее мы видели, как найти угол между двумерными векторами. Мы используем ту же формулу для трехмерных векторов:

`theta = arccos ((P * Q) / (| P || Q |))`

Пример 4

Найдите угол между векторами P = 4 i + 0 j + 7 k и Q = -2 i + j + 3 k .

Ответ

Векторы P и Q следующие.Вектор P находится на плоскости x — z (обратите внимание, что значение y для вектора P равно «0»), а Q находится «позади» y — z самолет.

По формуле

`theta = arccos ((P * Q) / (| P || Q |))`

имеем:

P • Q

= (4 i + 0 j + 7 j ) • (−2 i + j + 3 k) = (4 × −2) + (0 × 1) + (7 × 3) = 13

А теперь знаменатель:

`| P || Q | = sqrt (4 ^ 2 + (0) ^ 2 + 7 ^ 2)` `xxsqrt ((- 2) ^ 2 + 1 ^ 2 + 3 ^ 2)`

`= sqrt (65) sqrt (14)`

`= 30. 166 \ «единиц» `

Так

θ = arccos (13 ÷ 30,166)

Следовательно, угол между векторами P и Q равен

.

θ = 64,47 °

Упражнение

Найдите угол между векторами P = 3 i + 4 j -7 k и Q = -2 i + j + 3 k .

Ответ

По формуле

`theta = arccos ((P * Q) / (| P || Q |))`

сначала находим скалярное произведение:

P • Q

= (3 i + 4 j — 7 j ) • (−2 i + j + 3 k) = (3 × −2) + (4 × 1) + (−7 × 3) = −23

А теперь знаменатель:

| P | | Q |

= √ (3 2 + 4 2 + (−7) 2 ) × √ ((- 2) 2 + 1 2 + 3 2 ) = 32. 187

Так

θ = arccos (−23 ÷ 32,187)

Следовательно, угол между векторами P и Q равен

.

θ = 135,6 °

Приложение

У нас есть куб ABCO PQRS, у которого есть нить, идущая вдоль диагонали куба от B до S, а другая — по другой диагонали от C до P

Какой угол между двумя струнами?

Ответ

Для удобства предположим, что у нас есть куб единиц (каждая сторона имеет длину 1 единицу), и разместим его так, чтобы один угол куба находился в начале координат.

Единичные векторы i , j и k действуют в направлениях x -, y — и z — соответственно. Итак, на нашей диаграмме, поскольку у нас есть единичный куб,

OA = i
OC = j
OS = k

Из диаграммы мы видим, что для перехода от B к S нам нужно пройти −1 единицу в направлении x , −1 единицу в направлении y и вверх на 1 единицу в направлении z .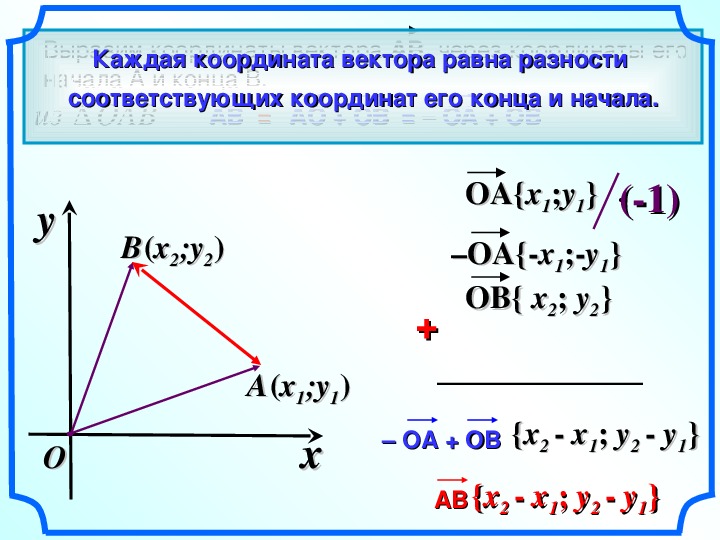 .Поскольку у нас есть единичный куб, мы можем написать:

BS = −i — j + k

и аналогично:

CP = i — j + k

Скалярное произведение векторов BS и CP :

BS • CP = | BS | | CP | cos θ

, где θ — угол между BS и CP .

Таким образом, угол θ равен

θ = arccos [( BS • CP ) ÷ ( | BS | | CP | )]

Сейчас,

BS • CP

= ( −i — j + k ) • ( i — j + k )

= – 1 + 1 + 1

= 1

и

| BS | | CP |

`= sqrt ((- 1) ^ 2 + (-1) ^ 2 + 1 ^ 2)` `× sqrt (1 ^ 2 + (-1) ^ 2 + 1 ^ 2)`

`= (sqrt3) (sqrt3)`

= 3

Так

`θ = arccos (1/3)`

θ = 70. 5 °

Итак, угол между струнами равен «70,5 °». (В этой ситуации мы предполагаем, что «угол» относится к острому углу между струнами.)

Использование векторов для нахождения координат вершины в квадрате и ее площади

Стенограмма видео

𝐴𝐵𝐶𝐷 — квадрат, в котором координаты точек 𝐴, 𝐵 и 𝐶 равны единице, минус восемь; три, отрицательные 10; и пять, минус восемь. Используйте векторы, чтобы определить координаты точки 𝐷 и площадь квадрата.

Во-первых, важно помнить, что здесь мы имеем дело с квадратом. Мы знаем, что в квадрате противоположные стороны параллельны и равны по длине. Мы также знаем, что смежные стороны расположены под прямым углом друг к другу, хотя это может оказаться полезным, а может и не оказаться полезным при рассмотрении этого вопроса. Нам также говорят, что 𝐴, 𝐵 и 𝐶 — это единицы, отрицательные восемь; три, отрицательные 10; и пять — минус восемь соответственно. И поэтому мы можем нанести эти точки на координатную сетку, как показано.

Отсюда следует, что 𝐷, четвертая вершина квадрата, будет где-то здесь вверху. На самом деле, есть несколько способов использовать векторы для определения точных координат этой точки. Возможно, это не похоже на мою диаграмму, но мы знаем, что векторы, соединяющие 𝐴 с 𝐷 и 𝐵 с, должны быть параллельны и равны по длине.

Итак, давайте начнем с поиска вектора. Один из способов сделать это — вычесть вектор 𝑂𝐵 из вектора. Как вектор-столбец, — пять отрицательных, восемь и 𝑂𝐵 — три, отрицательные 10.Чтобы вычесть векторы, мы просто вычитаем их отдельные компоненты. Пять минус три — два. И минус восемь минус минус 10 тоже два. Итак, мы видим, что вектор 𝐵𝐶 равен два, два.

Это, в свою очередь, означает, что вектор 𝐴𝐷 тоже должен быть два, два. И один из способов, которым мы могли бы путешествовать из точки 𝑂 в 𝐷, чтобы помочь нам найти вектор 𝑂𝐷, — это переместиться из в 𝐴 — это вектор 𝑂𝐴 — а затем пройти от 𝐴 к 𝐷. Итак, мы добавили вектор 𝐴𝐷. 𝑂𝐴 имеет вектор один, отрицательный восемь. И мы только что обнаружили, что вектор 𝐴𝐷 равен два, два.В сумме это три, отрицательные шесть. И мы обнаруживаем, что вектор 𝑂𝐷 равен трем, отрицательным шести. Следовательно, координата 𝐷 должна быть равна трем, отрицательным шести.

Вторая часть этого вопроса просит нас найти площадь квадрата. Итак, мы напоминаем, что, чтобы найти площадь квадрата, мы просто возводим в квадрат его ширину или высоту. Итак, как нам найти ширину или высоту нашего квадрата? Ну, это длина линии, соединяющей любые две соседние вершины. Мы рассмотрим вершины 𝐵 и.Мы знаем, что вектор 𝐵𝐶 равен два, два. Это означает, что длина отрезка, соединяющего 𝐵 и, является величиной этого вектора. И мы находим величину вектора, находя квадратный корень из суммы квадратов каждого из его компонентов.

Итак, это квадратный корень из двух в квадрате плюс два в квадрате, то есть квадратный корень из восьми. И мы видим, что каждая сторона нашего квадрата должна быть квадратным корнем из восьми единиц. Площадь — это квадрат этого значения. Это квадратный корень из восьми в квадрате, который, конечно же, равен восьми.Площадь квадрата — восемь квадратных единиц.

Что это такое и как рассчитать их составные части и модуль

Теперь я объясню вам, что такое векторы, и концепции, связанные с векторами, которые вам понадобятся для вычисления и работы с ними, например, компоненты вектора, модуль вектора, его направление и смысл.

Мы также рассмотрим типы существующих векторов и типы векторов, с которыми удобно работать в математике.

Что такое векторы?

Векторы — это ориентированные сегменты, которые начинаются в точке, соответствующей началу вектора, и заканчиваются в другой точке, которая является концом вектора:

Они определяются двумя компонентами: компонентом x и компонентом y, также называемыми векторными координатами. Это двумерные величины.

Чтобы выразить их аналитически, они обычно выражаются строчной буквой со стрелкой вверху с двумя ее компонентами в круглых скобках (например, координатами):

Буквы u, v, w и z обычно используются, но не являются обязательными и могут использоваться в любой букве.

Вот несколько примеров векторов:

Это также можно выразить двумя заглавными буквами со стрелкой вверху, где первая буква — это точка отсчета, а вторая буква — точка, где находится конец:

Таким образом, вектор AB будет иметь начало в точке A и конец в точке B:

В дополнение к компонентам вектора другими характеристиками, которые определяют векторы, являются модуль, направление и направление.

Мы собираемся увидеть каждого из них.

Компоненты вектора

Каковы компоненты вектора?

Это элементы, которые определяют вектор, поскольку, зная его координаты, мы знаем о нем все: модуль (который нужно будет вычислить), направление и смысл.

Говорить о компонентах вектора и координатах вектора — это одно и то же.

Как вычислить компоненты вектора?

Чтобы вычислить компоненты вектора, нам нужно заранее знать координаты его начала и координаты его конца, так как они будут вычисляться по ним.

Если координаты начальной точки вектора:

И координаты конечной точки вектора:

Вычисляем координаты вектора, вычитая координаты конца минус координаты начала:

Чтобы вычислить компонент x вектора, мы вычитаем координату x конца за вычетом координаты x начала координат. Таким же образом, чтобы вычислить компонент «y» вектора, мы вычитаем координату «y» конца минус координату «y» начала координат.

Помните, всегда крайнее меньшее происхождение, и каждый компонент вычитается со своим собственным: x с x и y с 0 и.

Рассмотрим пример:

У нас есть пункт отправления:

И точка, соответствующая концу вектора:

Координаты вектора AB будут соответствовать x-координатам конца минус x-координата начала координат с одной стороны и y-координаты конца минус y-координату начала координат с другой стороны:

Теперь мы работаем в рамках каждого компонента, и он у нас есть:

Модуль вектора

Что такое векторный модуль?

Модуль вектора — это расстояние от начала до конца, поэтому он соответствует длине вектора.

Буква вектора (или букв) представлена ​​заключенной между двумя полосами:

Модуль вектора, будучи длиной, всегда положителен.

Как рассчитывается модуль?

Модуль вектора вычисляется из координат вектора по следующей формуле:

Модуль вектора — это квадратный корень из квадрата координаты x плюс квадрат координаты y.

Звонит ли эта формула в колокол?

Это то же самое, что и для вычисления гипотенузы прямоугольного треугольника, поскольку для ее получения применяется теорема Пифагора в треугольнике, образованном между вектором и его компонентами, где вектор будет гипотенузой:

Вам не нужно знать, откуда вы взяли формулу, но это важно знать.

Давайте посмотрим на примере, как вычислить векторный модуль. У нас есть следующий вектор:

Какой у вас модуль?

Применяем формулу и она подходит:

Теперь действуем и решаем, получив значение модуля:

Оставляем в виде корня, так как корень 13 не точный.

Как вычислить модуль вектора с координатами его начала и конца

Как мы видели ранее, компоненты вектора вычисляются по координатам точек его начала и конца.

Следовательно, мы можем вычислить модуль вектора напрямую, если нам известны координаты точек его начала и конца, просто заменив в предыдущей расчетной формуле модуля компоненты x и «y» вычитанием координат конца минус координаты начала:

Давайте посмотрим на это на примере.

У нас есть вектор, начало которого находится в точке A, а его конец — в точке B:

Мы собираемся вычислить модуль вектора AB, который будет корнем из квадрата вычитания координат x, минус квадрат вычитания координат «y», всегда вычитая крайнее минус начало координат:

Будьте осторожны с отрицательными координатами.Убираем скобку -4 во втором члене внутренней части корня:

Теперь мы работаем внутри каждой скобки:

Возводим в квадрат и решаем:

Также можно проделать операцию в обратном порядке, то есть, зная модуль вектора, вычислить его компоненты.

Направление и направление вектора

Как мы говорили ранее, вектор — это сегмент, ориентированный, поэтому направление вектора — это линия, которой принадлежит этот вектор.

Все параллельные векторы имеют одинаковое направление.

Направление вектора — это то место, куда направляется этот вектор, куда указывает стрелка.

Направление вектора AB будет идти от точки A к точке B, а направление вектора BA будет идти от точки B к точке A:

Оба вектора имеют одинаковое направление, но противоположные направления

Давайте сравним вектор с прямой дорогой. Сама дорога будет направлением вектора, и внутри дороги вы можете двигаться в обоих направлениях, которые будут соответствовать направлениям вектора.

Типы векторов

Векторов можно фиксировать, когда их точка начала и конец не может перемещаться, и когда их исходная точка может находиться где угодно в пространстве.

Фиксированный вектор

Чтобы определить фиксированный вектор, вам необходимо знать координаты его начала и координаты его конца. Поскольку он зафиксирован, его никак нельзя перемещать.

Два параллельных вектора одного и того же модуля, но из разных исходных точек, являются разными векторами.

Векторы, которые имеют одинаковый модуль, направление и направление, но начинаются в разных точках, называются равноправными векторами.

Бесплатный вектор

Свободные векторы — это те векторы, начало которых может быть расположено в любой точке, и с которыми мы работаем в математике, поскольку они имеют особенность, которая делает их особенными.

А что делает бесплатный вектор таким особенным?

Поскольку мы можем переместить начало свободного вектора в нужную точку, мы всегда можем предположить, что его начало находится в начале координат (0.0), и поэтому вектор будет определяться только зная координаты конца.

Вам больше не нужно вычитать координаты начала координат из координат конечной точки для вычисления компонентов вектора.

Итак, когда мы говорим, что вектор:

Мы пытаемся сказать, что его происхождение (0,0), а крайнее значение (1.