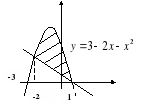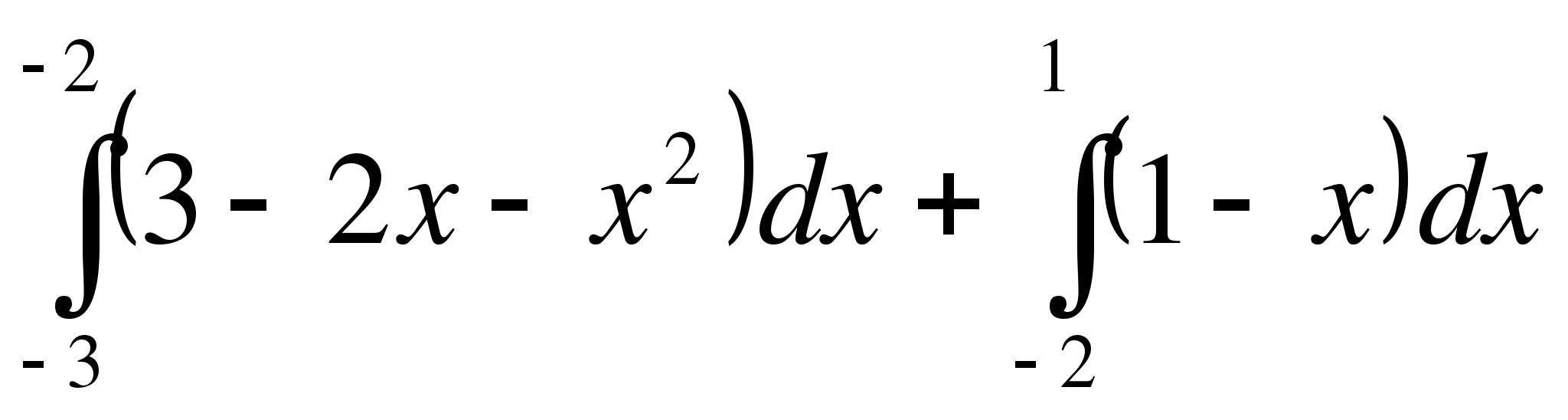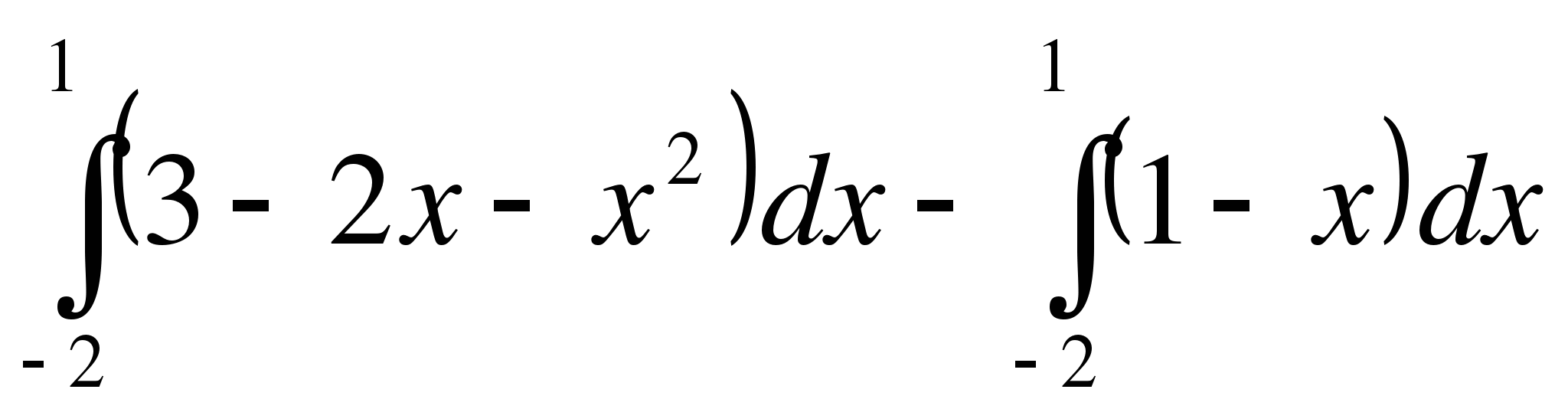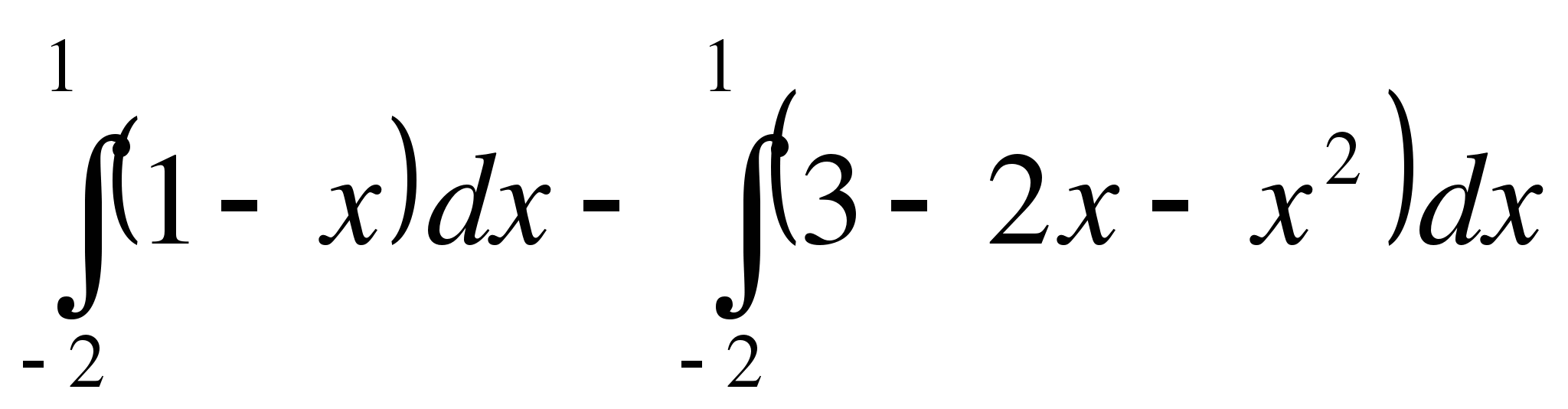Вычисление площадей плоских фигур | matematicus.ru

Площадь плоских фигур определяется через определённый интеграл от неотрицательной функции и равна площади криволинейной трапеции. В этом также заключается и геометрический смысл определённого интеграла.

Криволинейной трапецией называется фигура, которая ограничена графиком непрерывной функции f(x)≥0, прямыми x=a, y=b  и осью OX.

---

I. Площадь криволинейной трапеции на оси OX вычисляется по формуле:

---

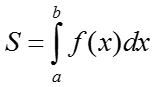
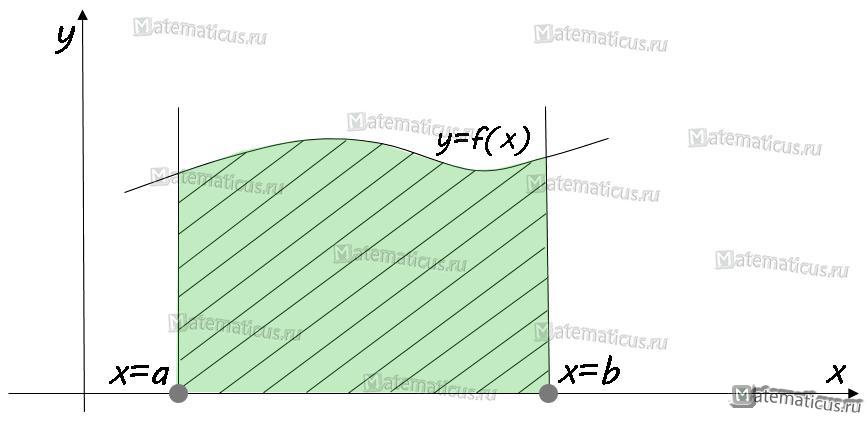
II. Если функция f(x)<0, то криволинейная трапеция находится ниже оси OX и тогда её площадь определяется по формуле:

---

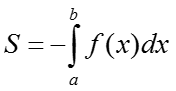
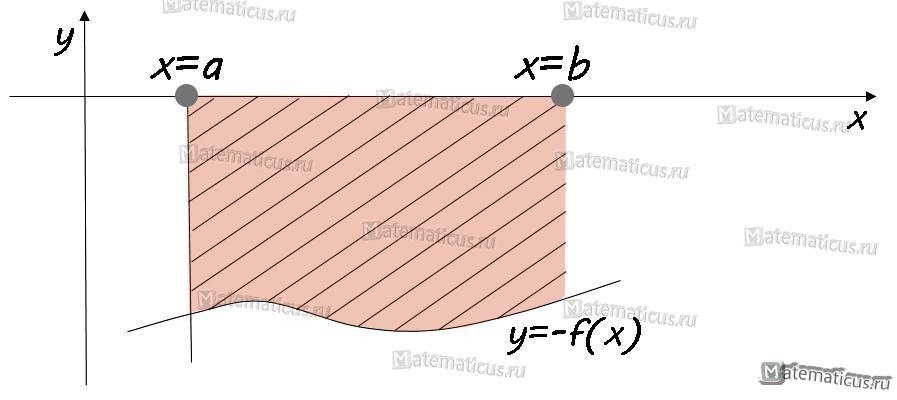
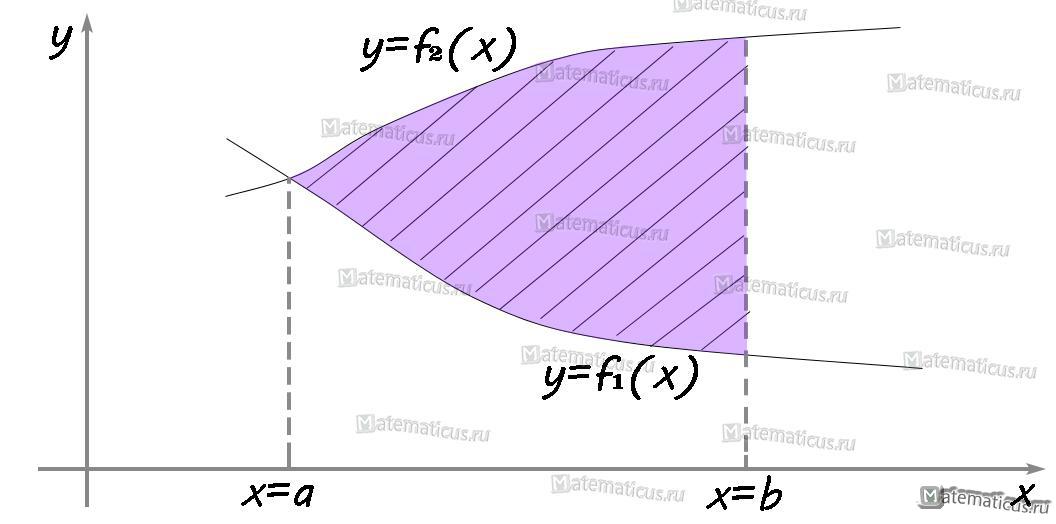
III. Если функция f₂(x)≥f₁(x), f₂(x)-f₁(x)≥0 то площадь фигуры находится по формуле:

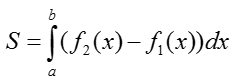
Читается так: из верхней функции вычитаем нижнюю.

---

IV. Площадь криволинейной трапеции на оси OY определяется по формуле: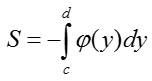

---

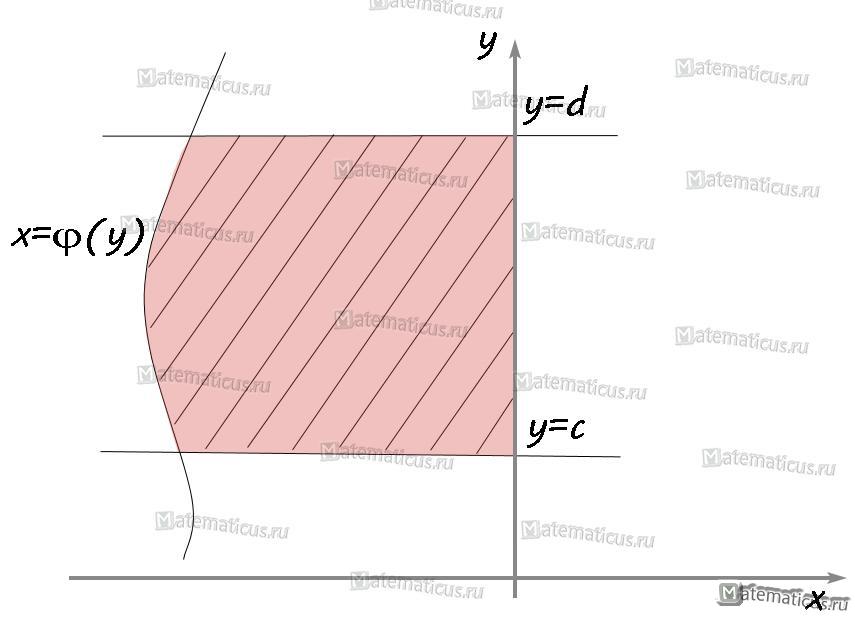
V. Если криволинейная трапеция расположена левее оси OY, то её площадь находится по формуле: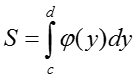

---

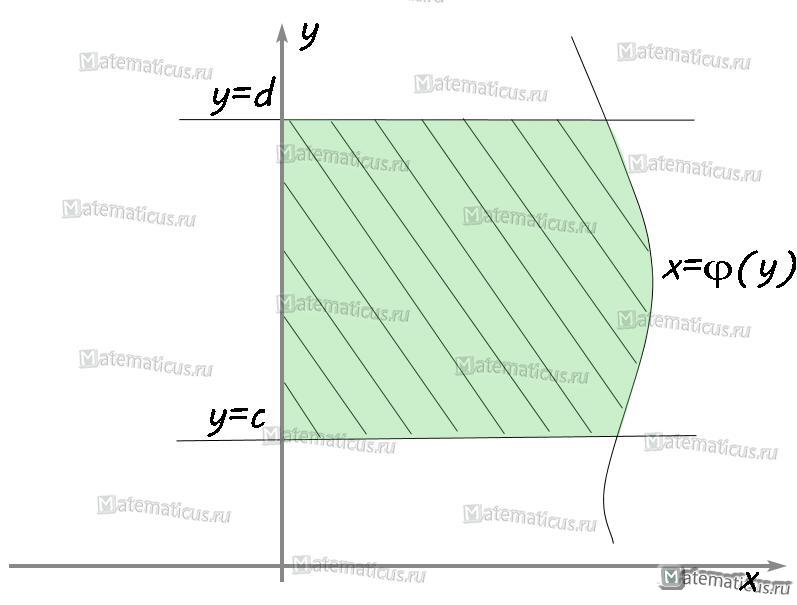
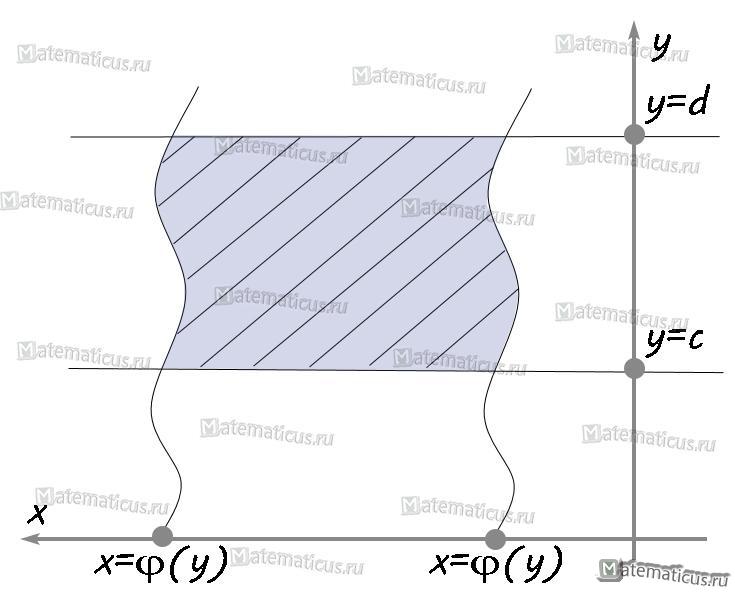
VI. Если функция φ₂(x)≥φ₁(x), φ₂(x)-φ₁(x)≥0, то площадь криволинейной трапеции ограниченна графиками x=φ₁(x), x=φ₂(x) и прямыми y=d, y=c и определяется по формуле:

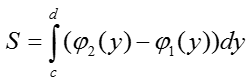
Если плоская фигура не относится к криволинейной трапеции вышеперечисленных видов, то её разбивают прямыми на криволинейные трапеции, которые параллельны оси OX или OY. Затем используют приведённые формулы выше.

---

Пример 1

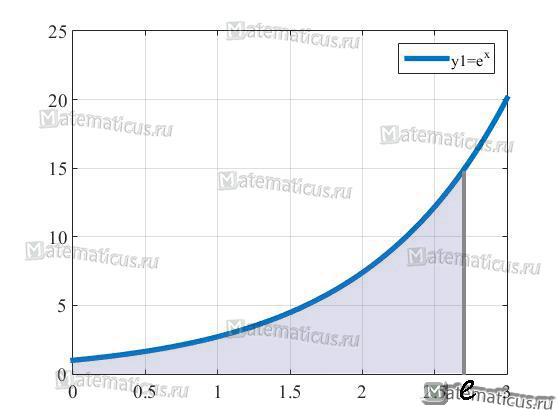
Найти площадь S фигуры, ограниченной функцией f(x)=e^x и линиями x=0 и x=e

Решение

Построим график функции f(x)=e^x

---

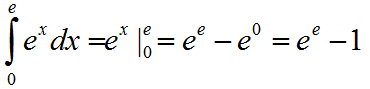
Пример 2

Найти площадь S фигуры, ограниченной линиями y=x² и y=3x

Решение

Пределами интегрирования являются точки абсциссы пересечения этих функций.

Графически можно представить следующем образом.

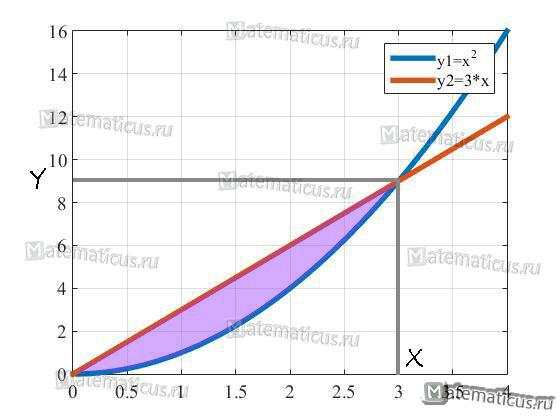
Найдем их через решения системы уравнений.

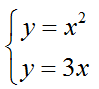
Решая систему находим корни x₁=0 и x₂=3

$$\eqalign{& \int\limits_0^3 {3x — {x^2}dx = } \cr & = \left( {\frac{3}{2}{x^2} — \frac{1}{3}{x^3}} \right)|_0^3 = \cr & = \frac{{27}}{2} — \frac{{27}}{3} = \frac{{27}}{6} = 4,5 \cr} $$

www.matematicus.ru

Вычисление площадей и объемов с помощью определенного интеграла

Площадь криволинейной трапеции

Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на отрезке функции, осью и прямыми и равен

Пример.Вычислить площадь фигуры, ограниченной линиями

Изображая эти линии, получаем криволинейную трапецию

Площадь фигуры ограниченной графиками двух функций и прямыми и

Если на заданном отрезке непрерывные функции и имеют то свойство, что для всех то

Пример.Вычислить площадь фигуры, ограниченной линиями

Изобразим заданные линии и абсциссы их точек пересечения.

Абсциссы точек пересечения:

Тогда по формуле

Объемы тел

В общем случае

Если тело заключено между двумя перпендикулярными к оси плоскостями, проходящими через точки и то

где

— площадь сечения тела плоскостью, которая проходит через точку и перпендикулярна к оси

Для тела вращения

Если тело получено в результате вращения вокруг оси криволинейной трапеции, которая ограничена графиком непрерывной и невідємної функции

на отрезке и прямыми и то

cubens.com

26. Вычисление площадей плоских фигур с помощью определенного интеграла

Определение 1. 

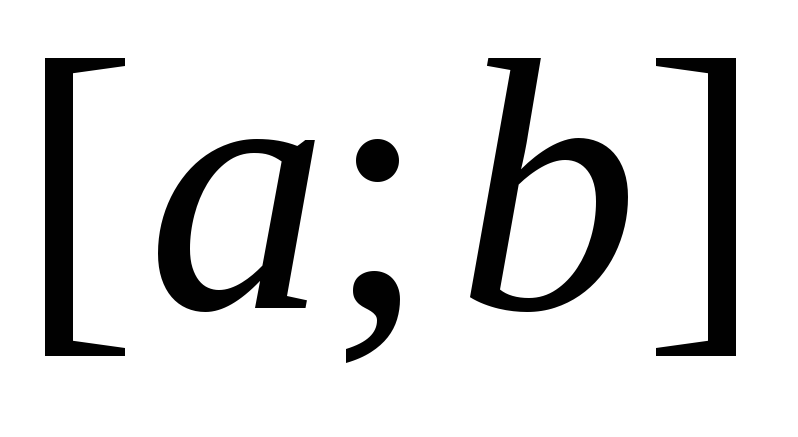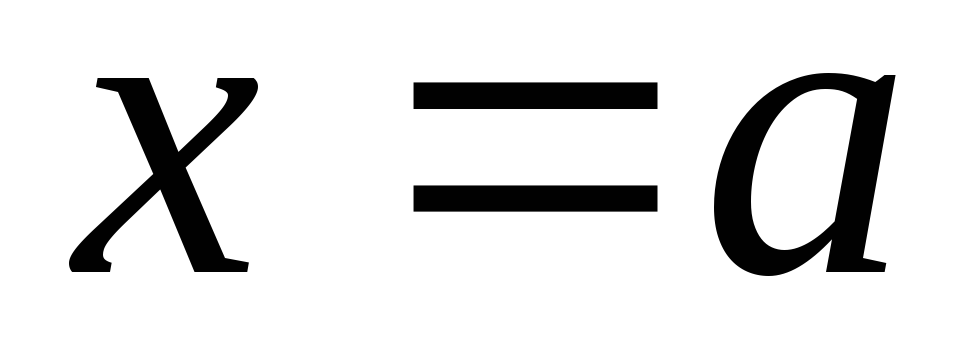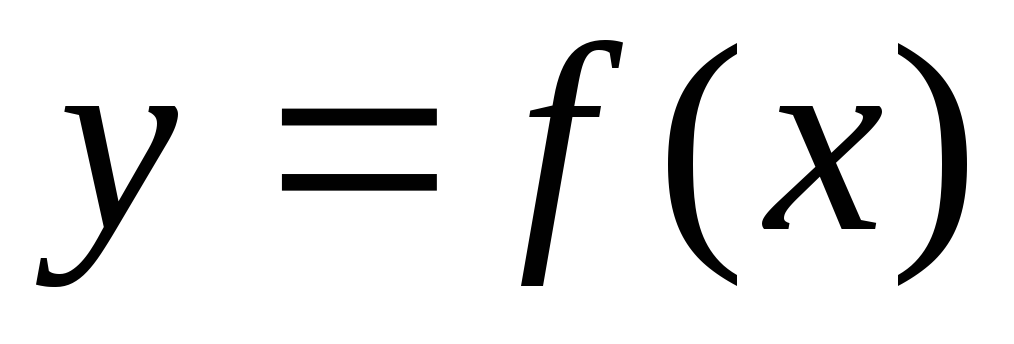Криволинейной трапецией, порожденной графиком неотрицательной функцииfна отрезке, называется фигура, ограниченная отрезкомоси абсцисс, отрезками прямых,и графиком функциина.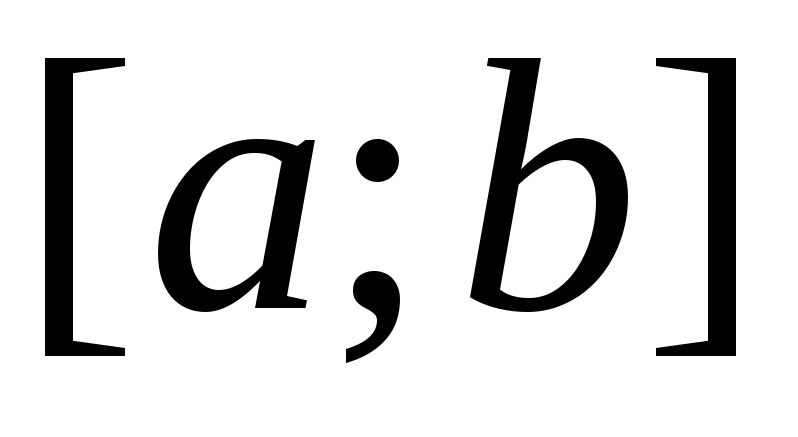

Введем далее понятие площади такой фигуры и одновременно правило ее вычисления.

1. Разобьем отрезок 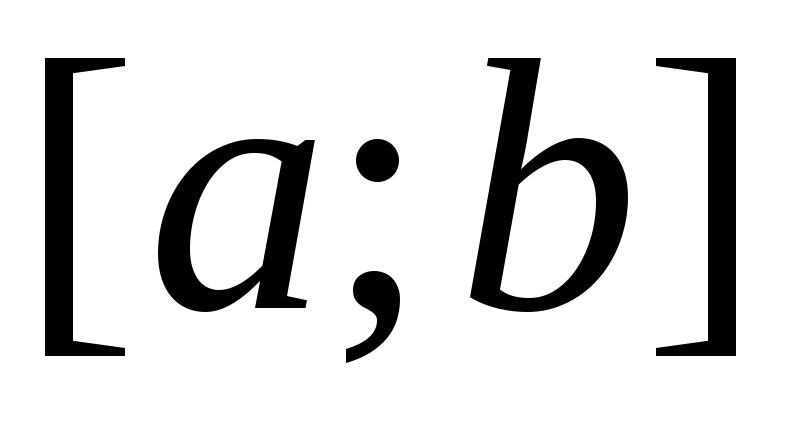точками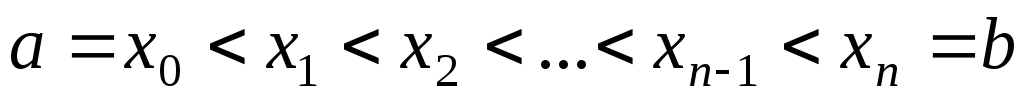

на частичные отрезки.

2. В каждом отрезке 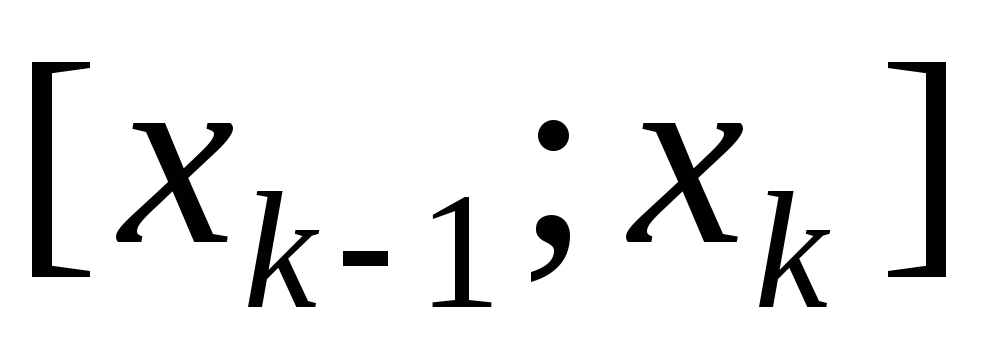(гдеk=1,2,…,n) выберем произвольную точку .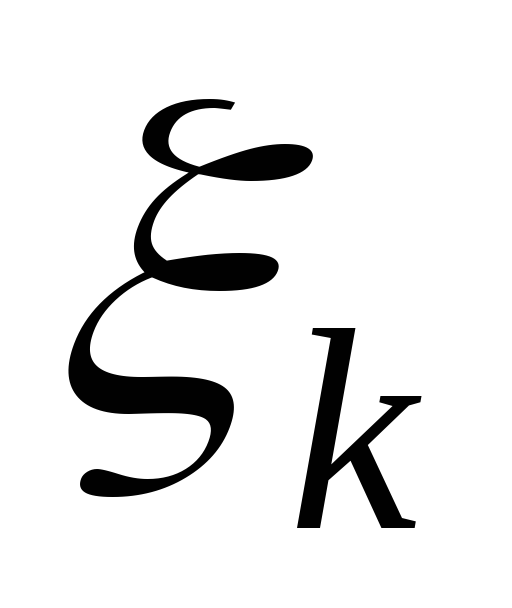

3. Вычислим площади прямоугольников, у которых основания есть отрезки оси абсцисс, а высоты имеют длины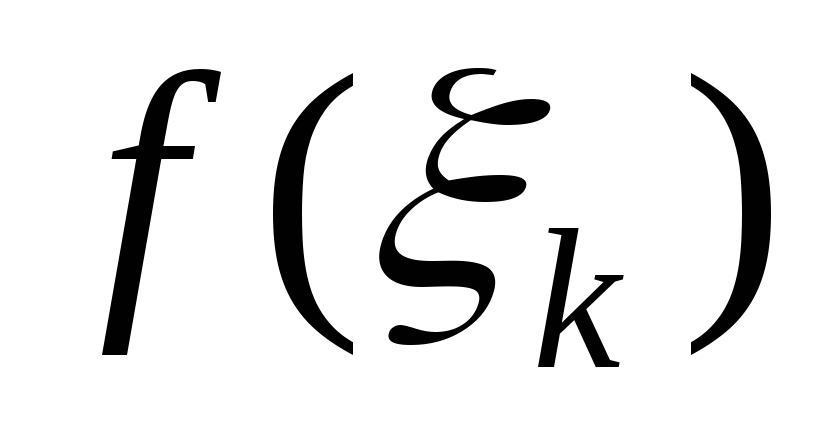. Тогда площадь ступенчатой фигуры, образованной этими прямоугольниками, равна.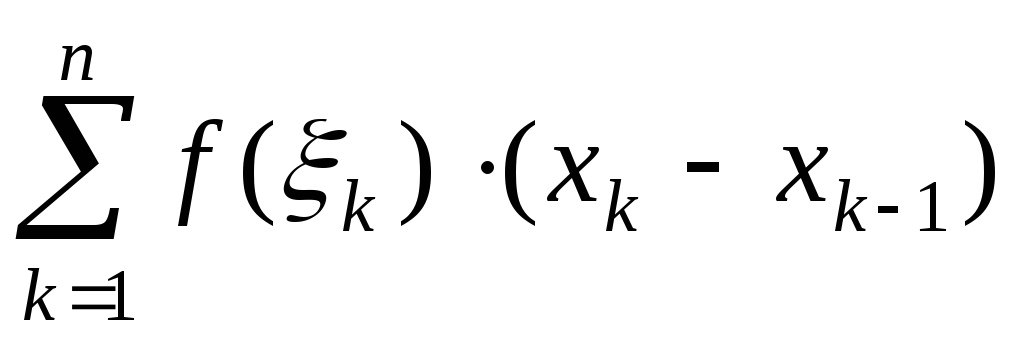

Заметим, что чем меньше длины частичных отрезков, тем более ступенчатая фигура по расположению близка к данной криволинейной трапеции. Поэтому естественно дать следующее определение.

Определение 2. Площадью криволинейной трапеции, порожденной графиком неотрицательной функции f на отрезке 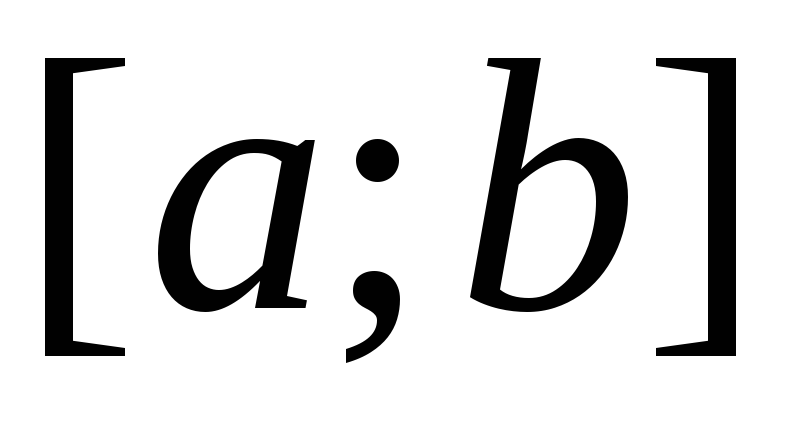, называется предел (при стремлении к 0 длин всех частичных отрезков) площадей ступенчатых фигур, если:

1) этот предел существует и конечен;

2) не зависит от способа разбиения отрезка 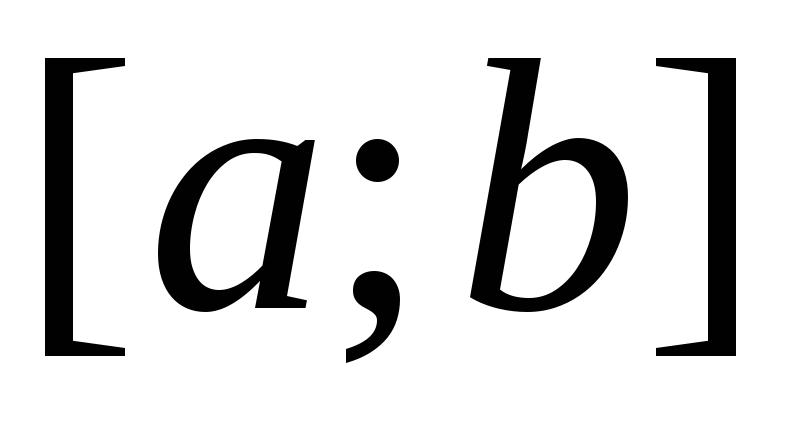на частичные отрезки;

3) не зависит от выбора точек .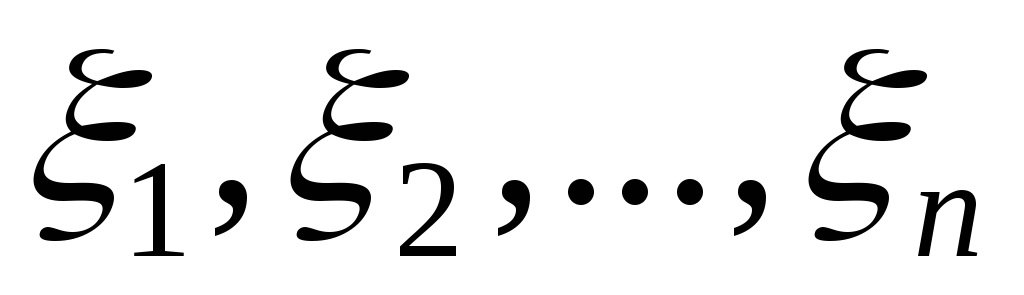

Теорема 1. Если функция 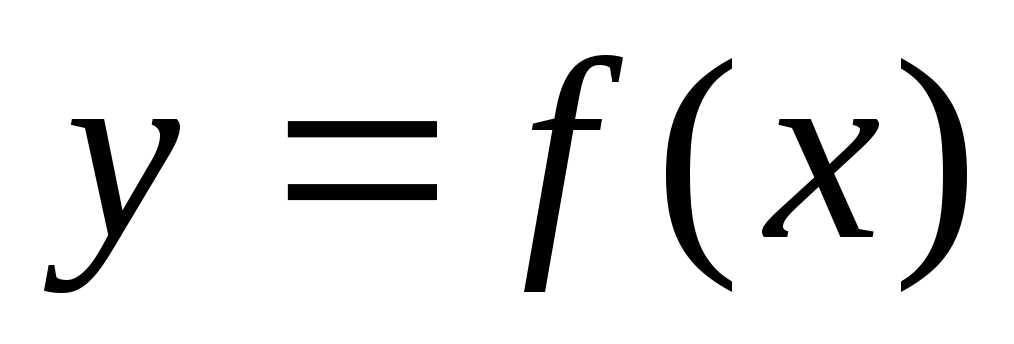непрерывна и неотрицательна на отрезке

, то криволинейная трапецияF, порожденная графиком функции f на 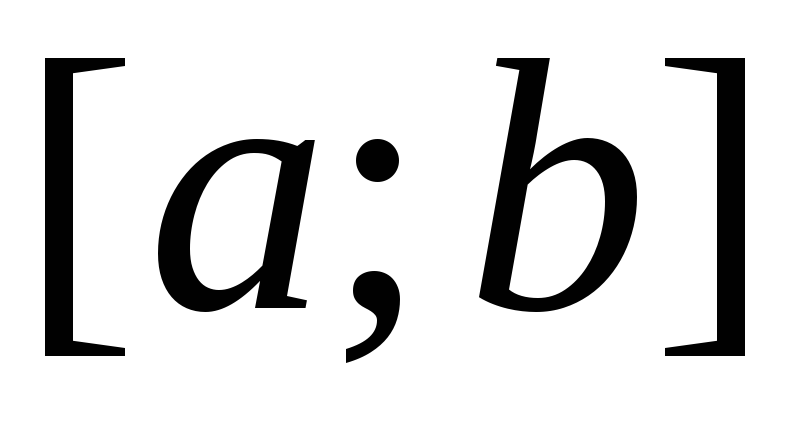, имеет площадь, которая вычисляется по формуле.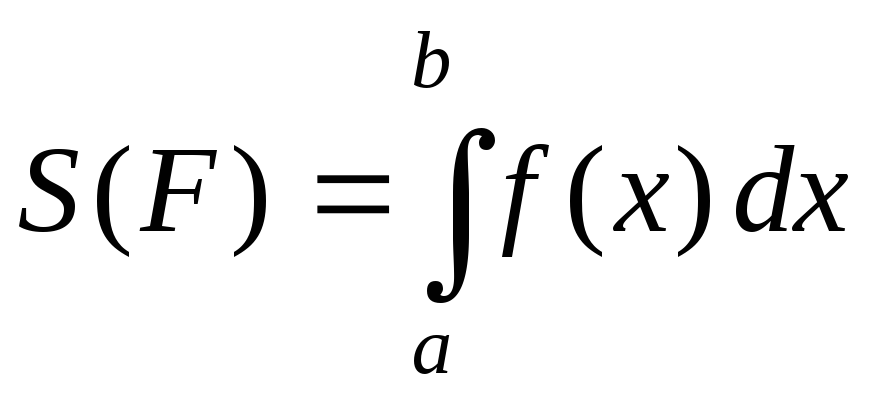

С помощью определенного интеграла можно вычислять площади плоских фигур и более сложного вида.

Если fиg— непрерывные и неотрицательные на отрезке 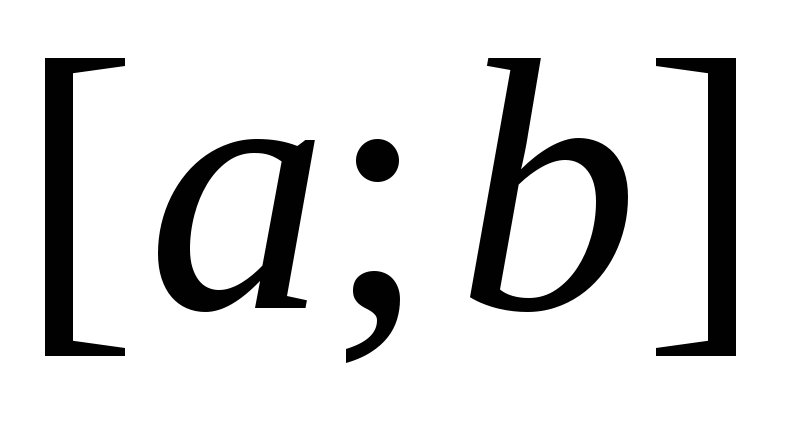функции, причем для всехxиз отрезка выполняется неравенство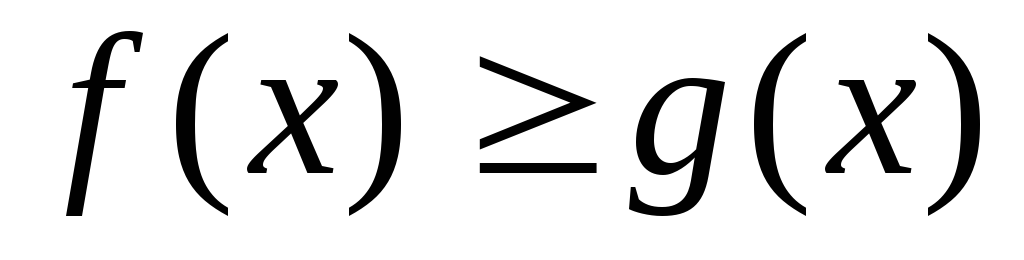, то площадь фигуры

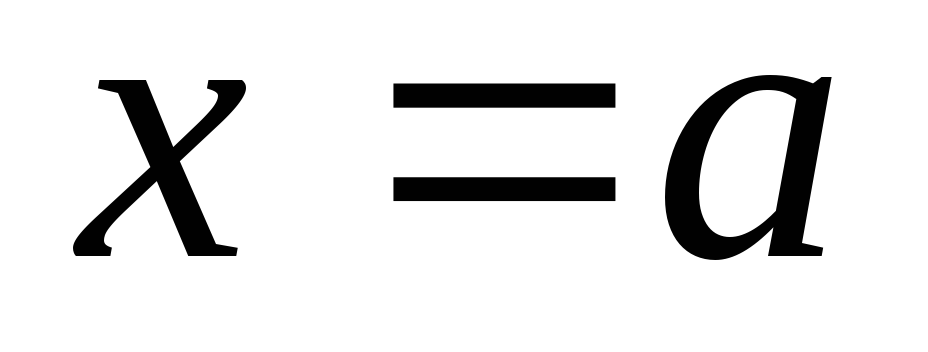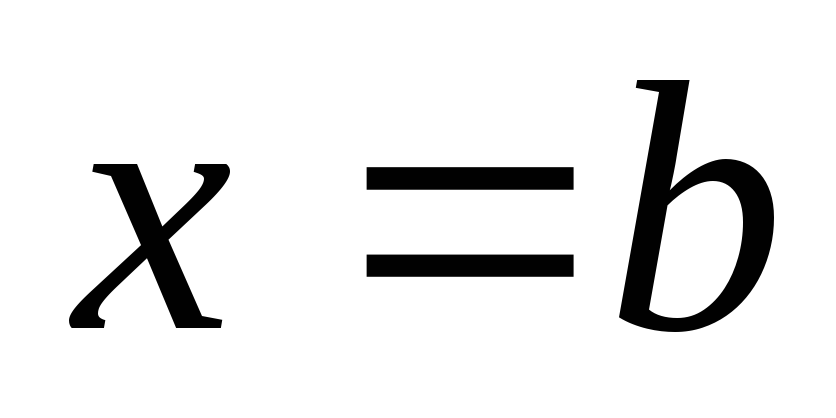F,ограниченной прямыми,и графиками функций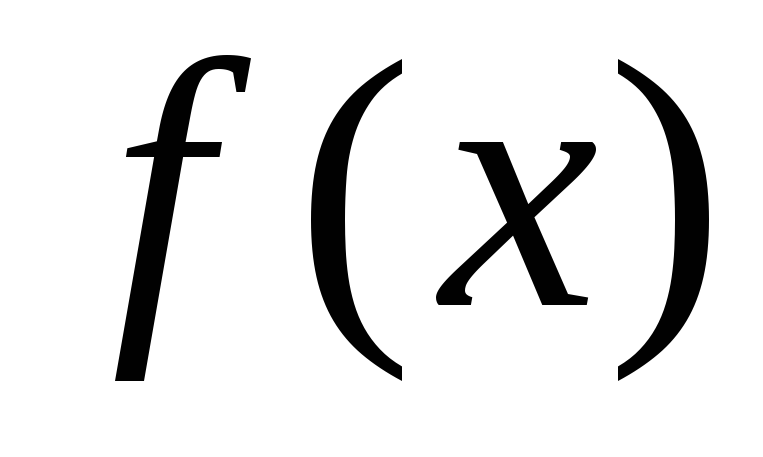,,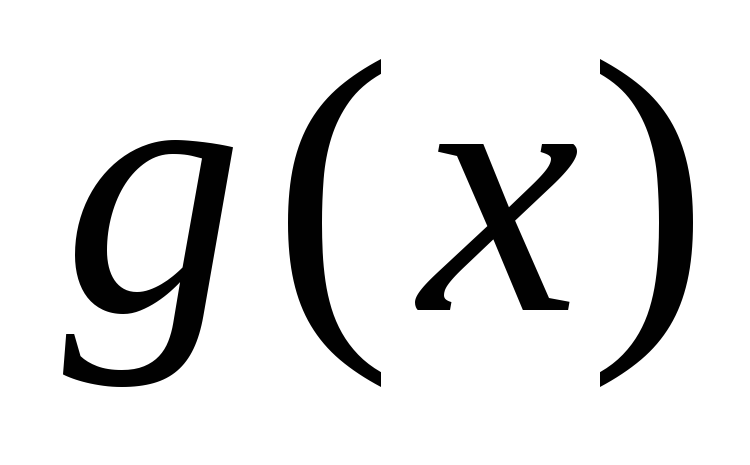 вычисляется по формуле .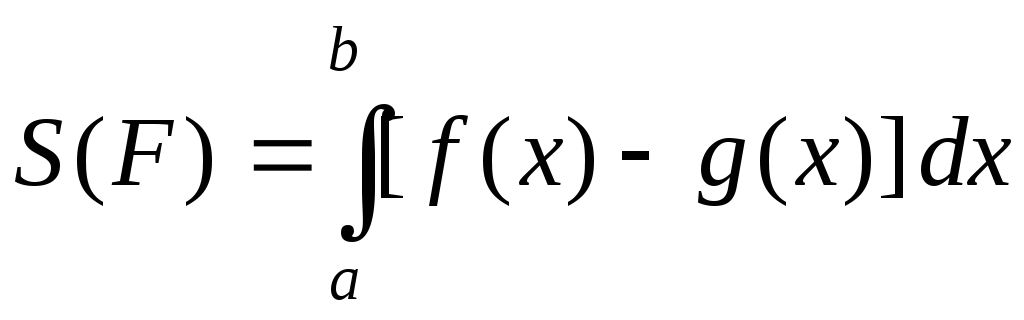

Замечание. Если отбросить условие неотрицательности функцийfиg, последняя формула остается верной.

Тема 9. Дифференциальные уравнения

27. Понятие о дифференциальном уравнении. Общее и частное решение. Задача Коши. Задача о построении математической модели демографического процесса

Теория дифференциальных уравнений возникла в конце 17 века под влиянием потребностей механики и других естественнонаучных дисциплин, по существу одновременно с интегральным и дифференциальным исчислением.

Определение 1. Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида, в котором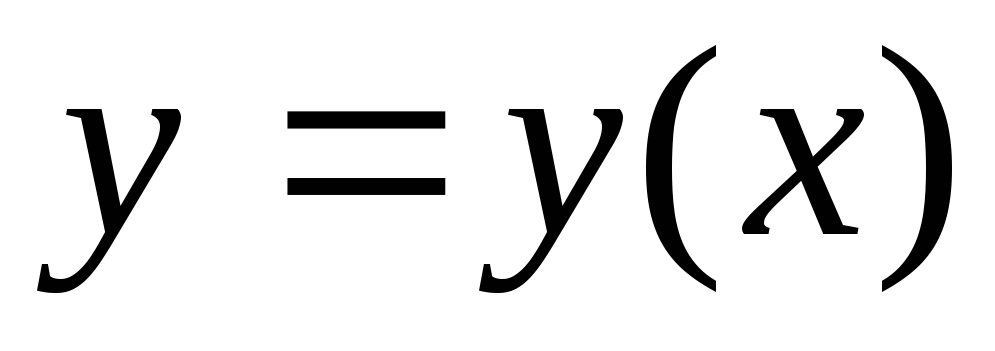— неизвестная функция.

Определение 2. Функция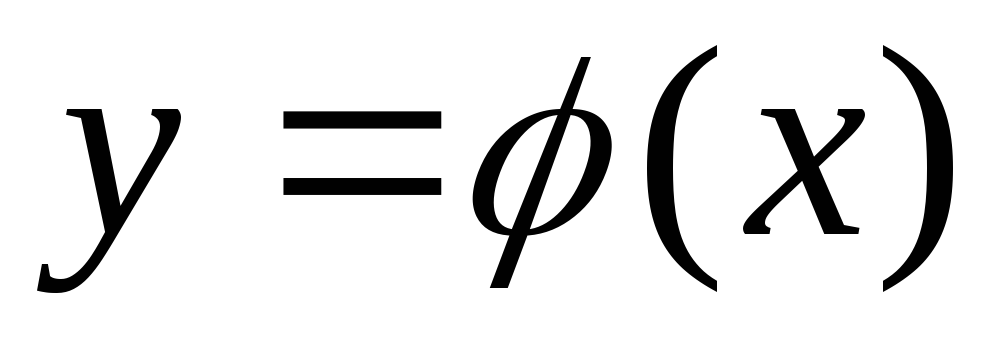называется решениям дифференциального уравнения на промежуткеI, если при подстановке этой функции и ее производных дифференциальное уравнение обращается в тождество.

Решить дифференциальное уравнение— это найти все его решения.

Определение 3. График решения дифференциального уравнения называетсяинтегральной кривойдифференциального уравнения.

Определение 4. Обыкновенным дифференциальным уравнением 1-го порядка называется уравнение вида.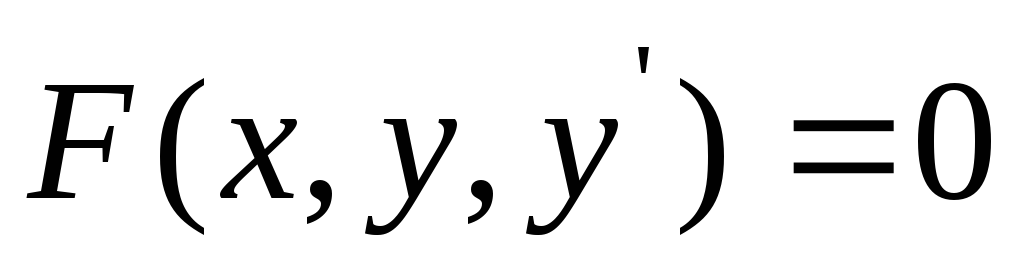

Определение 5. Уравнение вида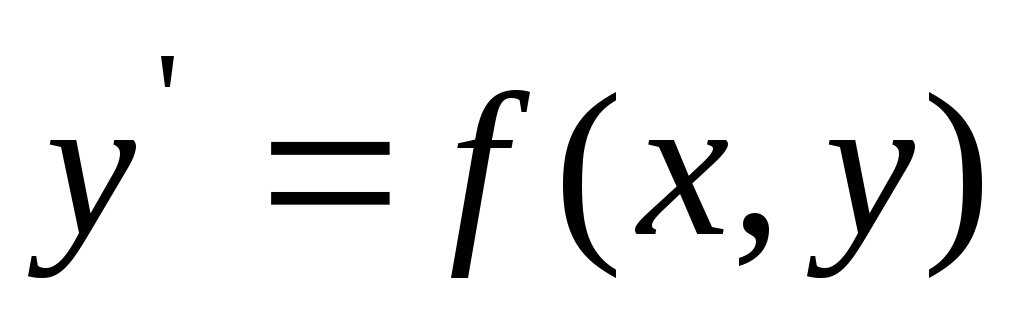называется дифференциальным уравнением 1-го порядка,разрешенным относительно производной.

Как правило, любое дифференциальное уравнение имеет бесконечно много решений. Чтобы выделить из совокупности всех решений какое-либо одно, надо наложить дополнительные условия.

Определение 6. Условие вида, накладываемое на решение дифференциального уравнения 1-го порядка, называетсяначальным условием, илиусловием Коши.

Геометрически это означает, что соответствующая интегральная кривая проходит через точку .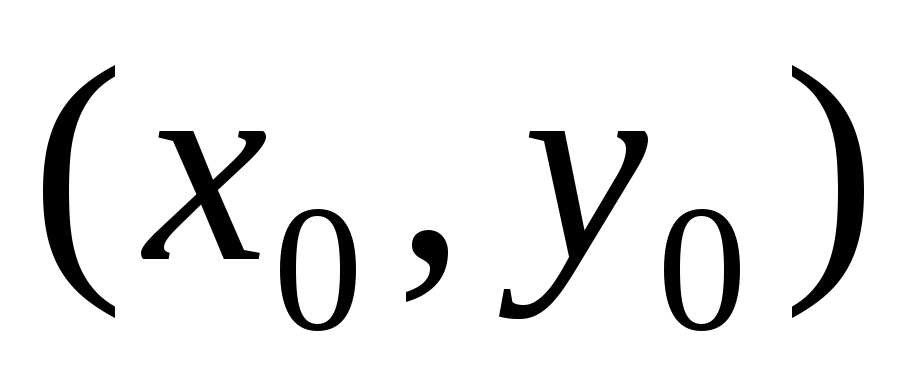

Определение 7. Общим решением дифференциального уравнения 1-го порядкана плоской областиDназывается однопараметрическое семейство функций, удовлетворяющее условиям:

1) для любого 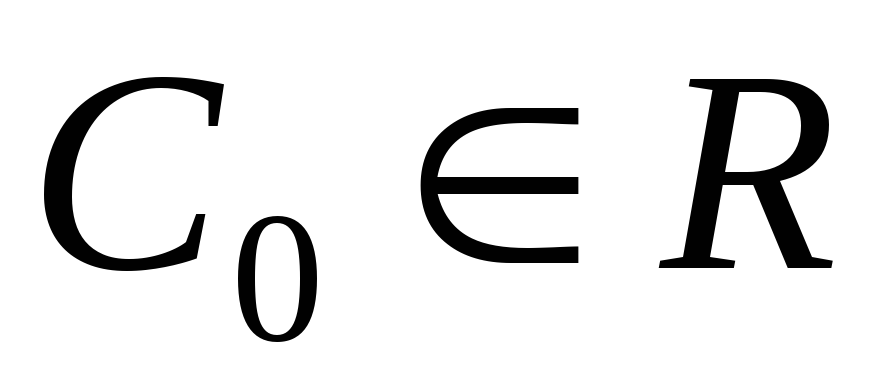функцияявляется решением уравнения;

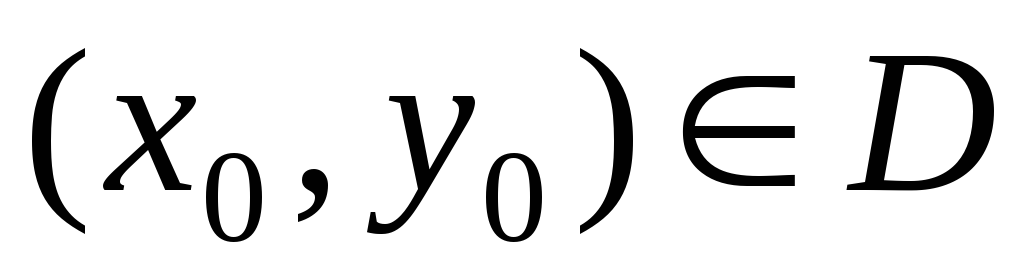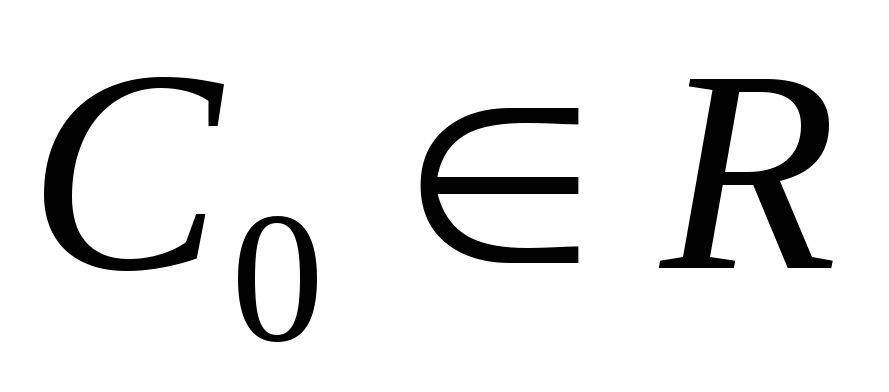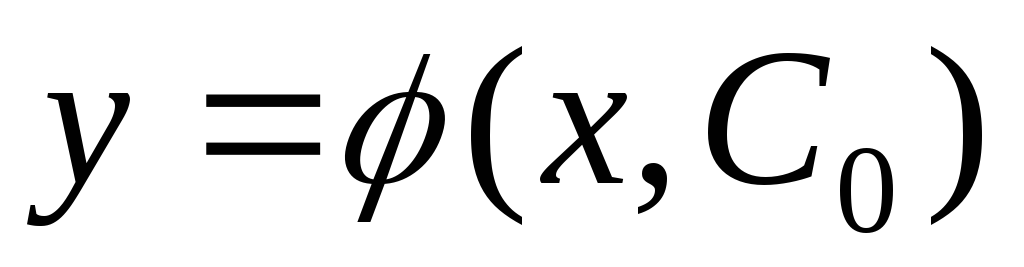2) для каждой точки существует такое значение параметра, что соответствующая функцияявляется решением уравнения, удовлетворяющим начальному условию.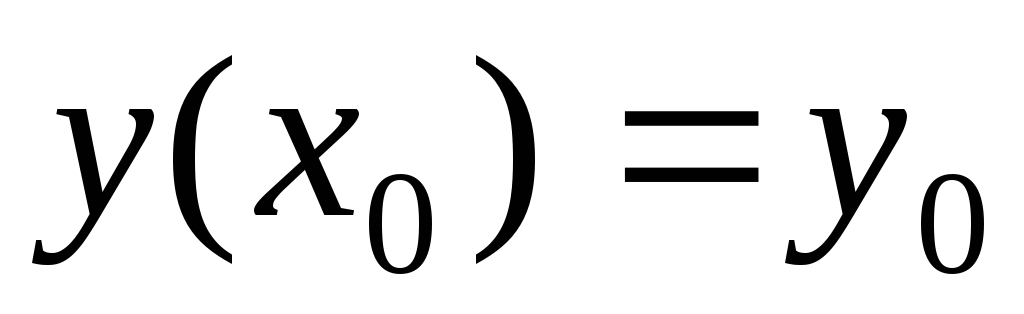

Определение 8. Решение, получаемое из общего решения при некотором значении параметра, называетсячастным решениемдифференциального уравнения.

Определение 9. Особым решением дифференциального уравнения называется всякое решение, которое не может быть получено из общего решения ни при каком значении параметра.

Решение дифференциальных уравнений — очень сложная задача, и, вообще говоря, чем выше порядок уравнения, тем труднее указать способы решения уравнения. Даже для дифференциальных уравнений первого порядка удается лишь в небольшом числе частных случаев указать приемы нахождения общего решения. Более того, и в этих случаях искомое решение не всегда является элементарной функцией.

Одна из основных задач теории дифференциальных уравнений, впервые изучавшаяся О. Коши, состоит в отыскании решения дифференциального уравнения, удовлетворяющего заданным начальным условиям.

Например, всегда ли существует решение дифференциального уравнения 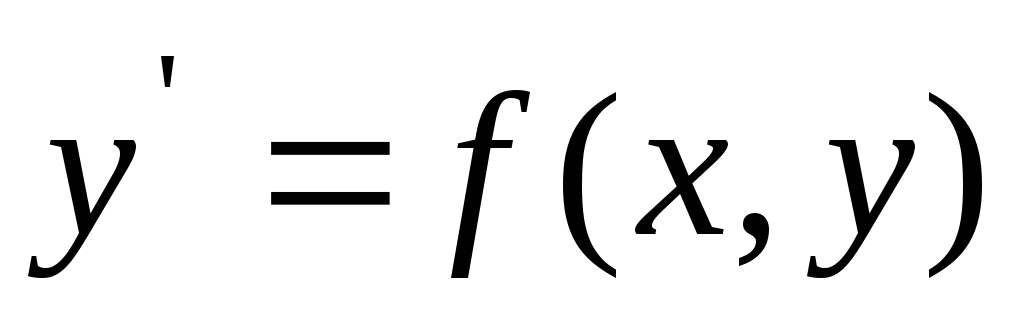, удовлетворяющее начальному условию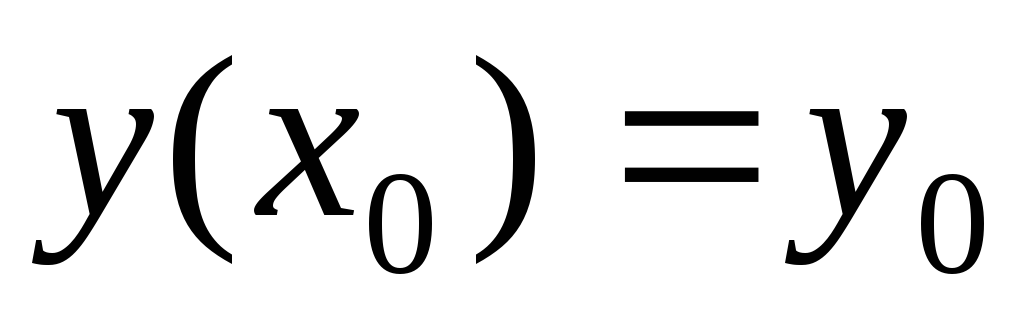, и будет ли оно единственным? Вообще говоря, ответ отрицательный. В самом деле, уравнение, правая часть которого непрерывна на всей плоскости, имеет решенияy=0 иy=(x+C)³,CR. Следовательно, через любую точку оси Охпроходит две интегральные кривые.

Таким образом, функция должна удовлетворять некоторым требованиям. В следующей теореме содержится один из вариантов достаточных условий для существования и единственности решения дифференциального уравнения 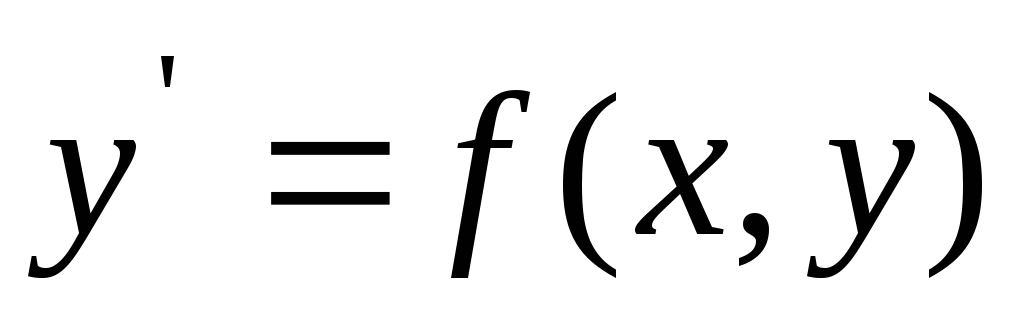, удовлетворяющего начальному условию.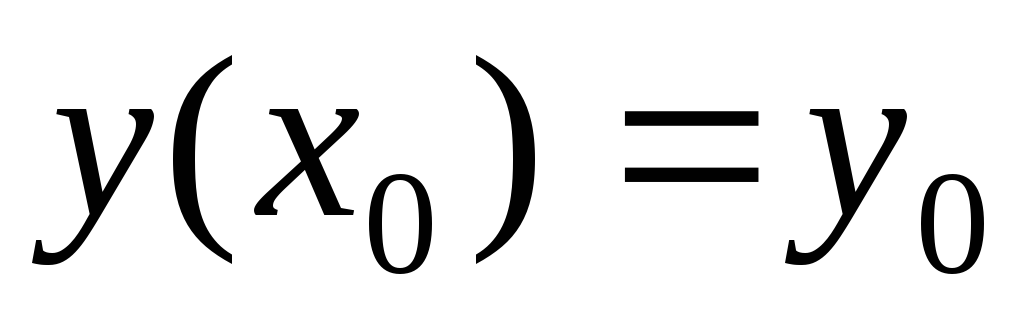

Теорема 1. Пусть функция 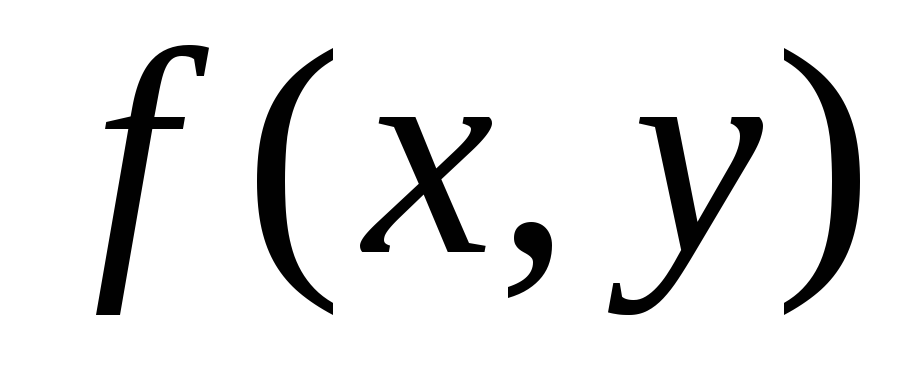и ее частная производная 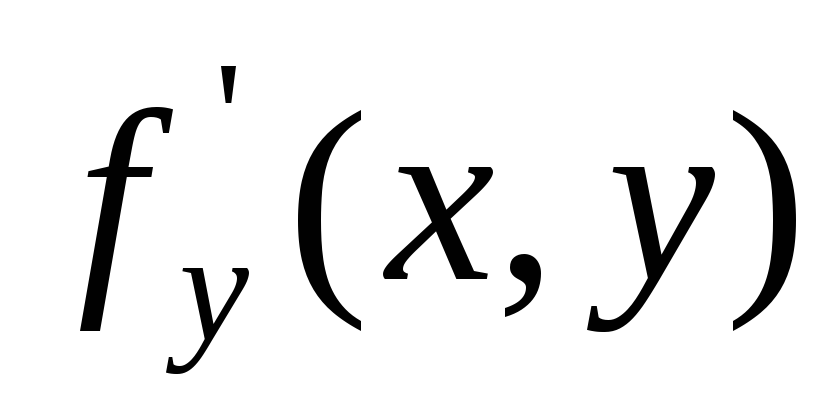непрерывны в некоторой области D на плоскости хОу, точка .

Тогда в некотором интервале, содержащем х₀ , существует, и притом единственное, решение 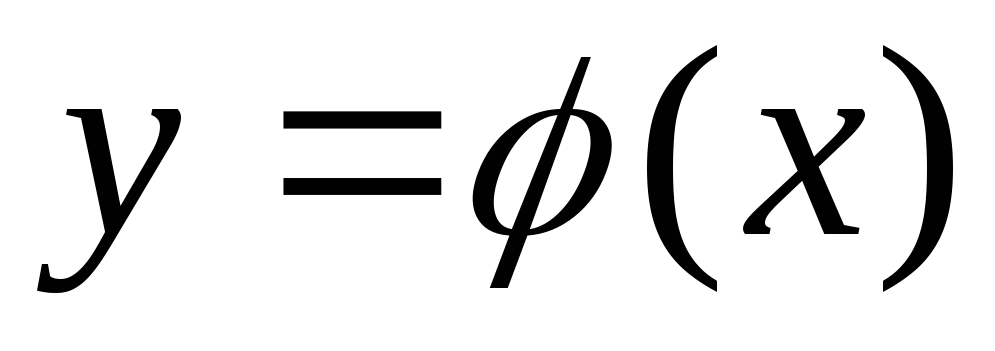дифференциального уравнения, удовлетворяющее начальному условию.

studfile.net

Геометрический и экономический смысл определенного интеграла

Из определения следует, что для неотрицательной функции f(x) определенный интегралравен площади криволинейной трапеции, ограниченной кривой у =f(x), прямыми х = а, х =bи осью абсциссy= 0 (рисунок 4.1).

Если функция – f(x) неположительна, то определенный интегралравен площади соответствующей криволинейной трапеции, взятой со знаком минус (рисунок 4.7).

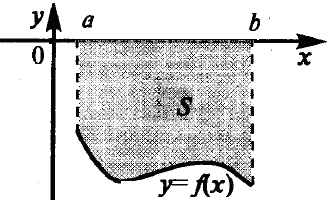
Рисунок 4.7 – Геометрический смысл определенного интеграла для неположительной функции

Для произвольной непрерывной функции f(x) определенный интегралравен сумме площадей криволинейных трапеций, лежащих под графиком функцииf(x) и выше оси абсцисс, за вычетом суммы площадей криволинейных трапеций, лежащих над графиком функцииf(x) и ниже оси абсцисс (рисунок 4.8).

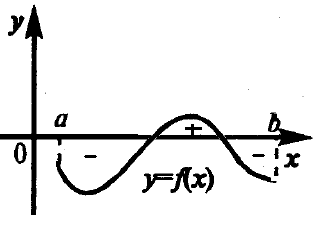
Рисунок 4.8 – Геометрический смысл определенного интеграла для произвольной непрерывной функции f(x) (знаком «плюс» помечена площадь, которую прибавляют, а «минусом» — та, которую вычитают).

При вычислении на практике площадей криволинейных фигур часто используется следующая формула: 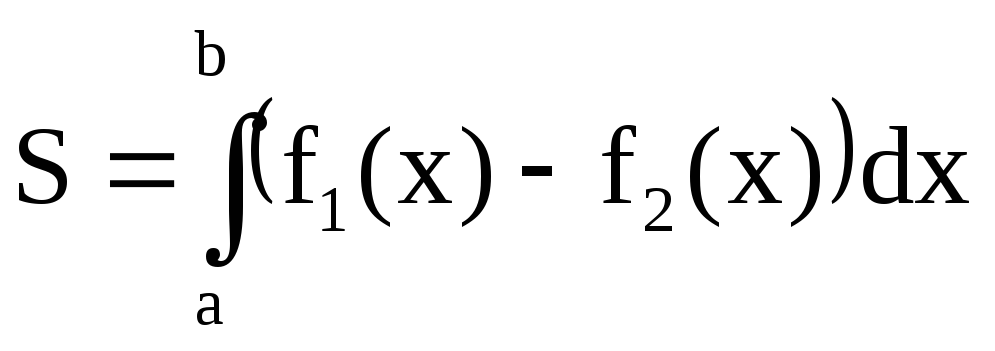, гдеS– площадь фигуры, заключенной между кривыми y = f₁(x) и y = f₂(x) на отрезке [а,b], а f₁(x) и f₂(x) — непрерывные функции, заданные на этом отрезке, такие, что f₁(x) ≥ f₂(x) (см. рисунки 4.9, 4.10).

При изучении экономического смысла производной было выяснено, что производная выступает как скорость изменения некоторого экономического объекта или процесса во времени или относительного другого исследуемого фактора. Чтобы установить экономический смысл определенного интеграла, необходимо саму эту скорость рассмотреть в виде функции от времени или другого фактора. Тогда, так как определенный интеграл представляет собой изменение первообразной, мы получим, что в экономике он оценивает изменение этого объекта (процесса) за определенный период времени (или при определенном изменении другого фактора).

Например, если функция q=q(t) описывает производительность труда в зависимости от времени, то определенный интеграл от этой функциипредставляет собой объем выпущенной продукцииQза промежуток времени отt₀доt₁.

Методы вычисления определенных интеграловоснованы на рассмотренных ранее методах интегрирования (доказательств проводить не будем).

При нахождении неопределенного интеграла мы пользовались методом замены переменной, основанным на формуле: f(x)dx= =f((t))`(t)dt, где x =(t) — функция, дифференцируемая на рассматриваемом промежутке. Для определенного интеграла формула замены переменной примет вид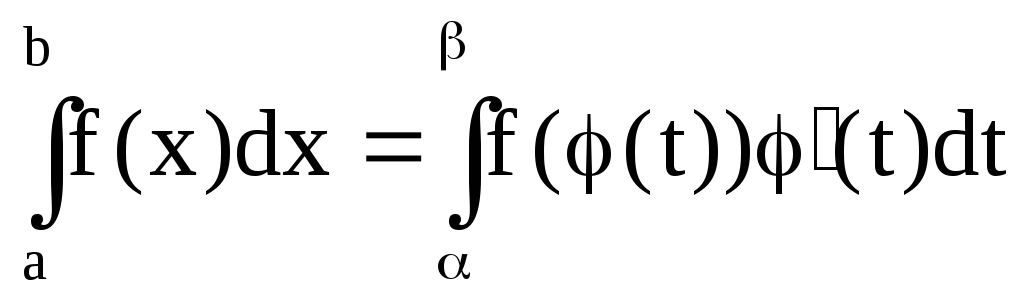, где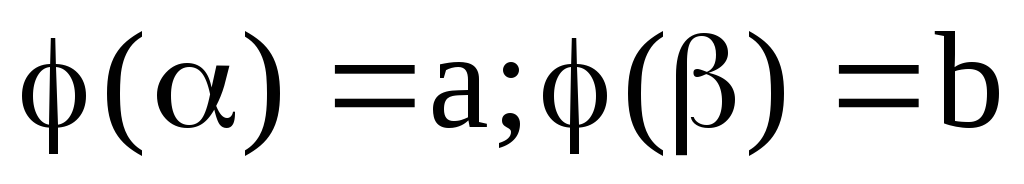и для всех.

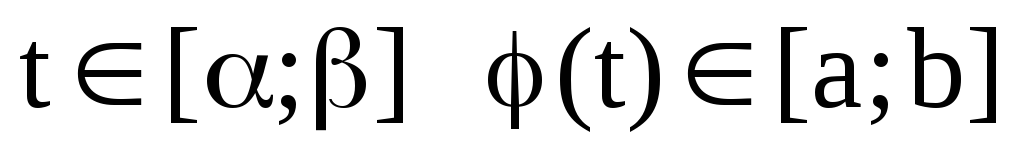Пример 1. Найти

Пусть t= 2 –x². Тогдаdt= -2xdxиxdx= — ½dt.

При х = 0 t= 2 – 0²= 2. При х = 1t= 2 – 1²= 1. Тогда

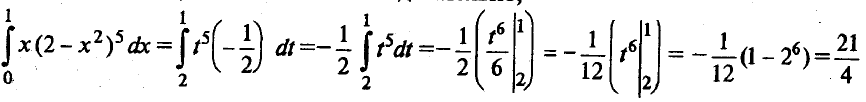
Пример 2. Найти

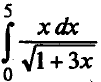
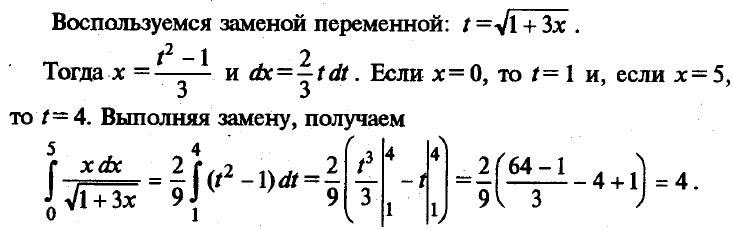
Пример 3. Найти

Формула интегрирования по частям для определенного интеграла примет вид: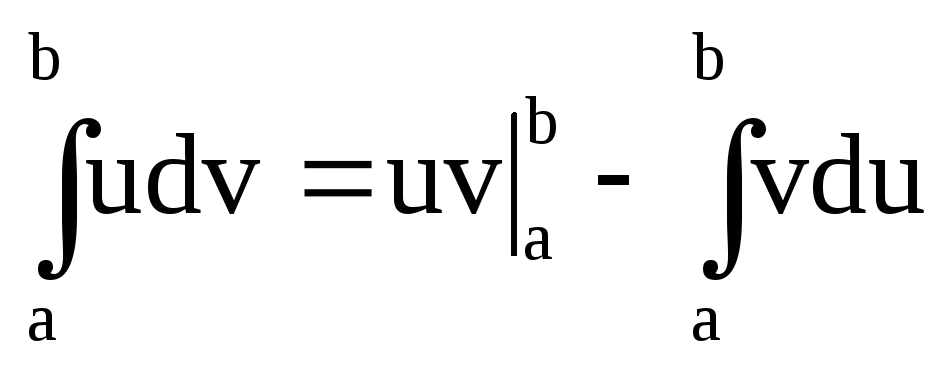, где.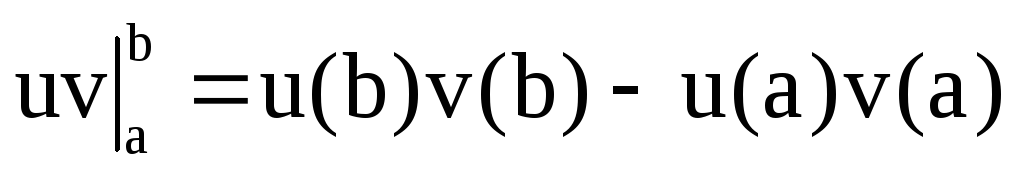

Пример 1. Найти

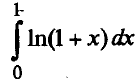
Пусть u=ln(1 +x),dv=dx. Тогда

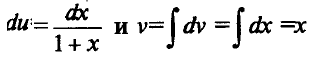
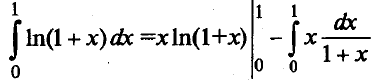
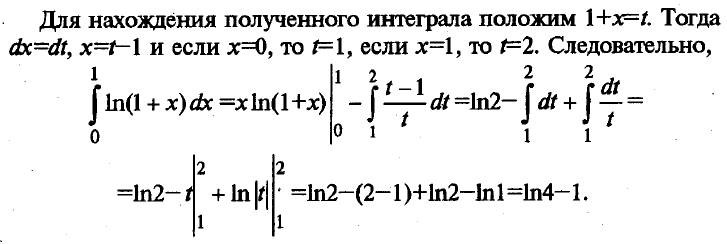
Пример 2. Найти

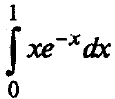
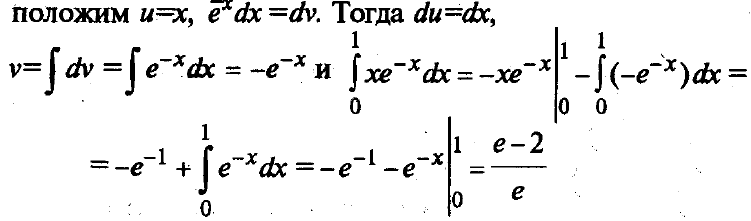
Вычисление площадей плоских фигур с помощью определенного интеграла

Пример 1.Найти площадь фигуры, ограниченной линиями у = х²– 2 иy=x.

График функции y= х²– 2 представляет собой параболу с точкой минимума приx= 0,y= -2; ось абсцисс пересекается в точках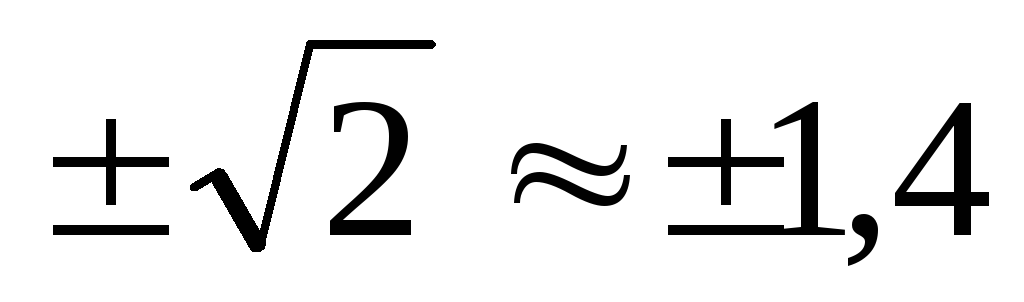. График функции у = х– прямая, биссектриса неотрицательной координатной четверти.

Найдем координаты точек пересечения параболы у = х²– 2 и прямой у = х, решив систему этих уравнений:

х²– 2 = х

х²– х — 2 = 0

Д = 1 + 8 = 9

х = 2; y= 2 или х = -1;y= -1

Таким образом, фигуру, площадь которой необходимо найти, можно представить на рисунке 4.9.

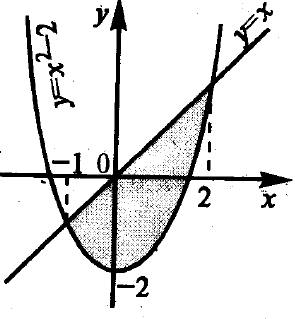
Рисунок 4.9 – Фигура, ограниченная линиями у = х²– 2 иy=x

На отрезке [-1, 2] х ≥ х²– 2 .

Воспользуемся формулой , полагая f₁(х) = х; f₂(х) = х²– 2;a= -1;b= 2.

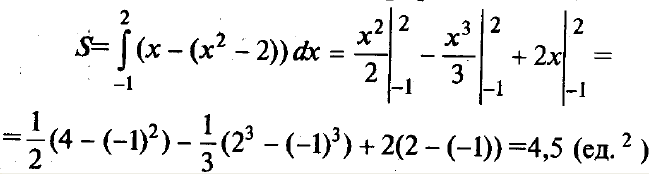
Пример 2.Найти площадь фигуры, ограниченной линиями у = 4 — х²иy= х²– 2x.

График функции y = 4 — х²представляет собой параболу с точкой максимума приx= 0,y= 4; ось абсцисс пересекается в точках 2 и -2. График функции у = х²– 2x– парабола с точкой минимума при 2x- 2 = 0, х = 1;y= -1; ось абсцисс пересекается в точках 0 и 2.

Найдем координаты точек пересечения кривых:

4 — х²= х²– 2х

2х²– 2х — 4 = 0

х²– х — 2 = 0

Д = 1 + 8 = 9

х = 2; y= 0 или х = -1;y= 3

Таким образом, фигуру, площадь которой необходимо найти, можно предствить на рисунке 4.10.

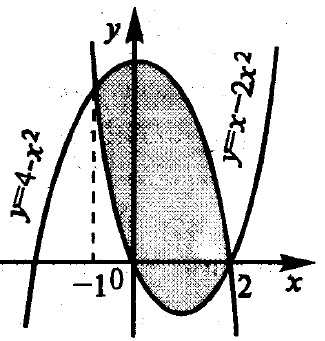
Рисунок 4.10 — Фигура, ограниченная линиями у = 4 — х²иy= х²– 2x

На отрезке [-1, 2] 4 — х²≥ х²– 2x.

Воспользуемся формулой 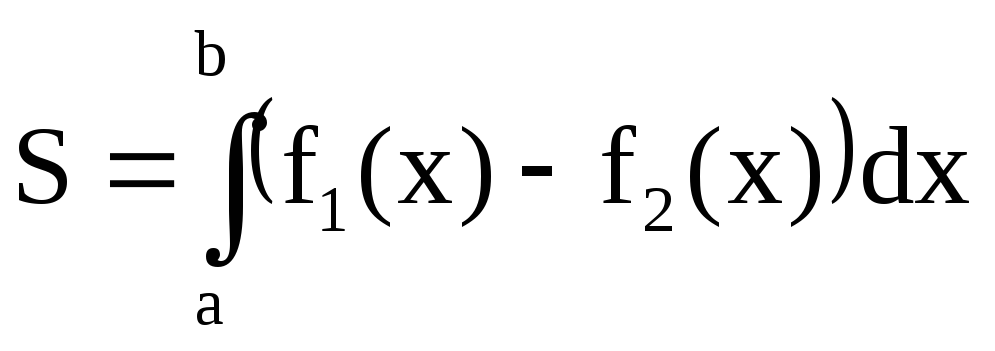, полагая f₁(х) = 4 — — х²; f₂(х) = х²– 2х;a= -1;b= 2.

Пример 3.Найти площадь фигуры, ограниченной линиями у = 1/х;y= х²иy= 4 в неотрицательной координатной четверти.

График функции у = 1/х представляет собой гиперболу, при положительных х она выпукла вниз; оси координат являются асимптотами. График функции у = х²в неотрицательной координатной четверти – ветвь параболы с точкой минимума в начале координат. Эти графики пересекаются при 1/х = х²; х³= 1; х = 1; у = 1.

Прямую y= 4 график функции у = 1/х пересекает при х =1/4, а график функции у = х²при х = 2 (или -2).

Таким образом, фигуру, площадь которой необходимо найти, можно представить на рисунке 4.11.

Рисунок 4.11 — Фигура, ограниченная линиями у = 1/х; y= х²иy= 4 в неотрицательной координатной четверти

Искомая площадь фигуры ABCравна разности между площадью прямоугольника АВНЕ, которая равна 4*(2 – ¼) = 7, и суммой площадей двух криволинейных трапеций АСFЕ и СВНF. Вычислим площадь АСFЕ:

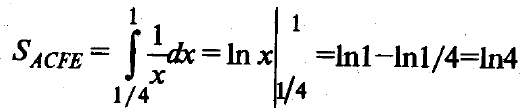
Вычислим площадь СВНF:

.

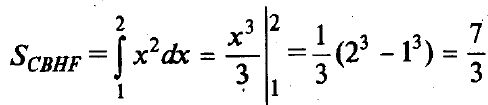Итак, искомая площадь равна 7 – (ln4 + 7/3) = 14/3 –ln43,28 (ед.²).

studfile.net

«Вычисление площадей фигур с помощью интеграла»

Практическая работа

по теме: «Вычисление площадей фигур с помощью интеграла»

Цель работы: закрепить навык вычисления площади криволинейной трапеции.

Необходимо знать: определение криволинейной трапеции, формулу Ньютона-Лейбница для расчёта определённого интеграла.

Необходимо уметь: по готовому чертежу составлять формулу площади и находить её значение.

1. Теоретическая часть

Определение. Криволинейной трапецией (рис. 1) называют фигуру, которая ограничена:

• сверху — графиком непрерывной функции y=y(x)

• снизу – осью OX (y=0)

• слева – прямой x=a

• справа – прямой x=b

Утверждение. Геометрический смысл определённого интеграла в том, что его значение равно площади соответствующей криволинейной трапеции:

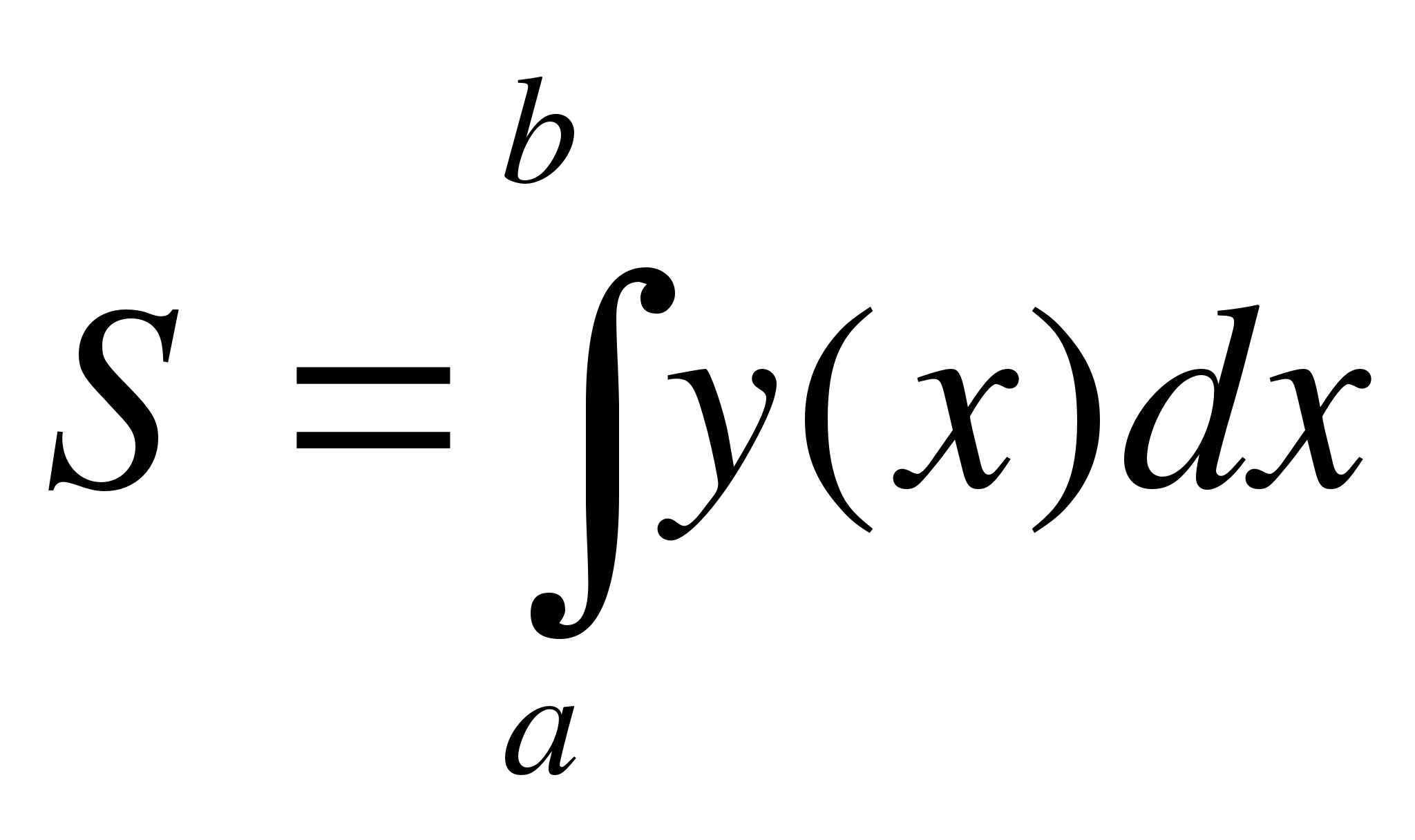(1)

Рассмотрим различные методы вычисления площадей плоских фигур.

Пример 1. Вычислить площадь плоской фигуры, ограниченной линиями: 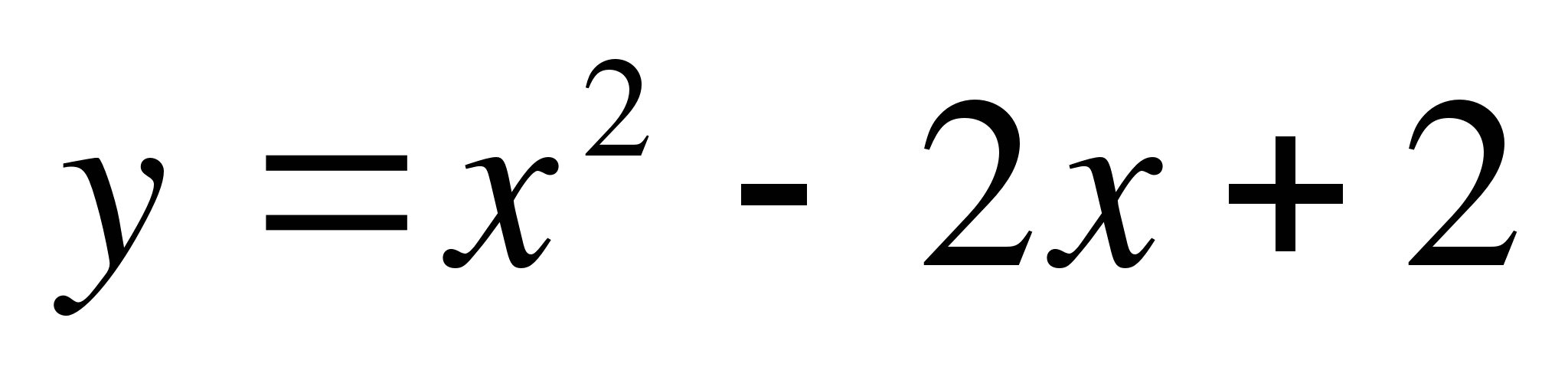, x=-1, x=2 и осью OX.

Решение: данная фигура (рис. 2) представляет собой криволинейную трапецию, поэтому её площадь вычисляется по формуле (1).

X

-1

2

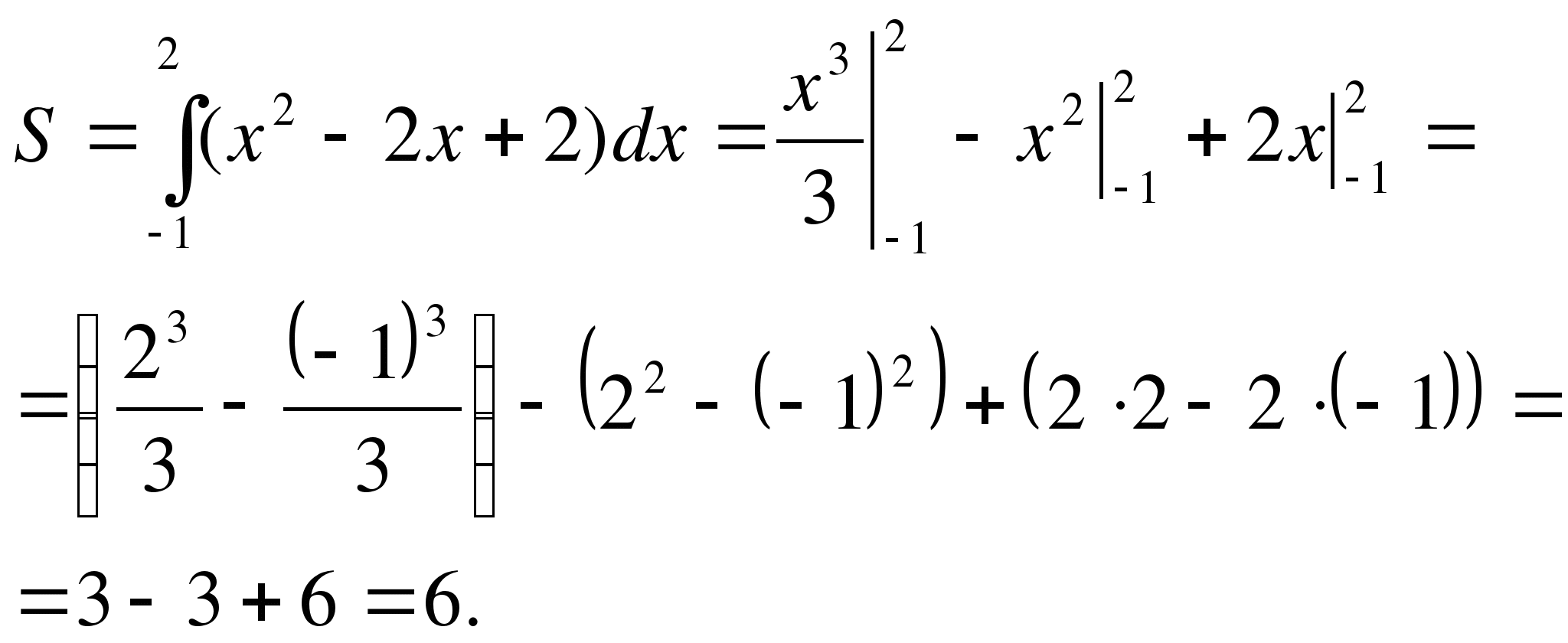
Ответ: 6 кв.ед.

Пусть y=f(x) – непрерывная функция при x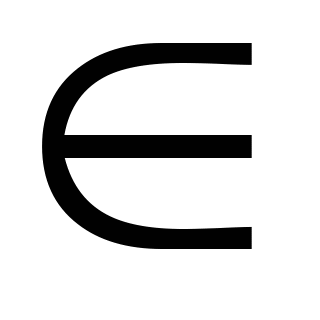[a, b], график которой расположен ниже оси OX (рис. 3). Значение определённого интеграла будет отрицательным, поэтому для расчёта площади берём значение интеграла по модулю.

Рис. 3

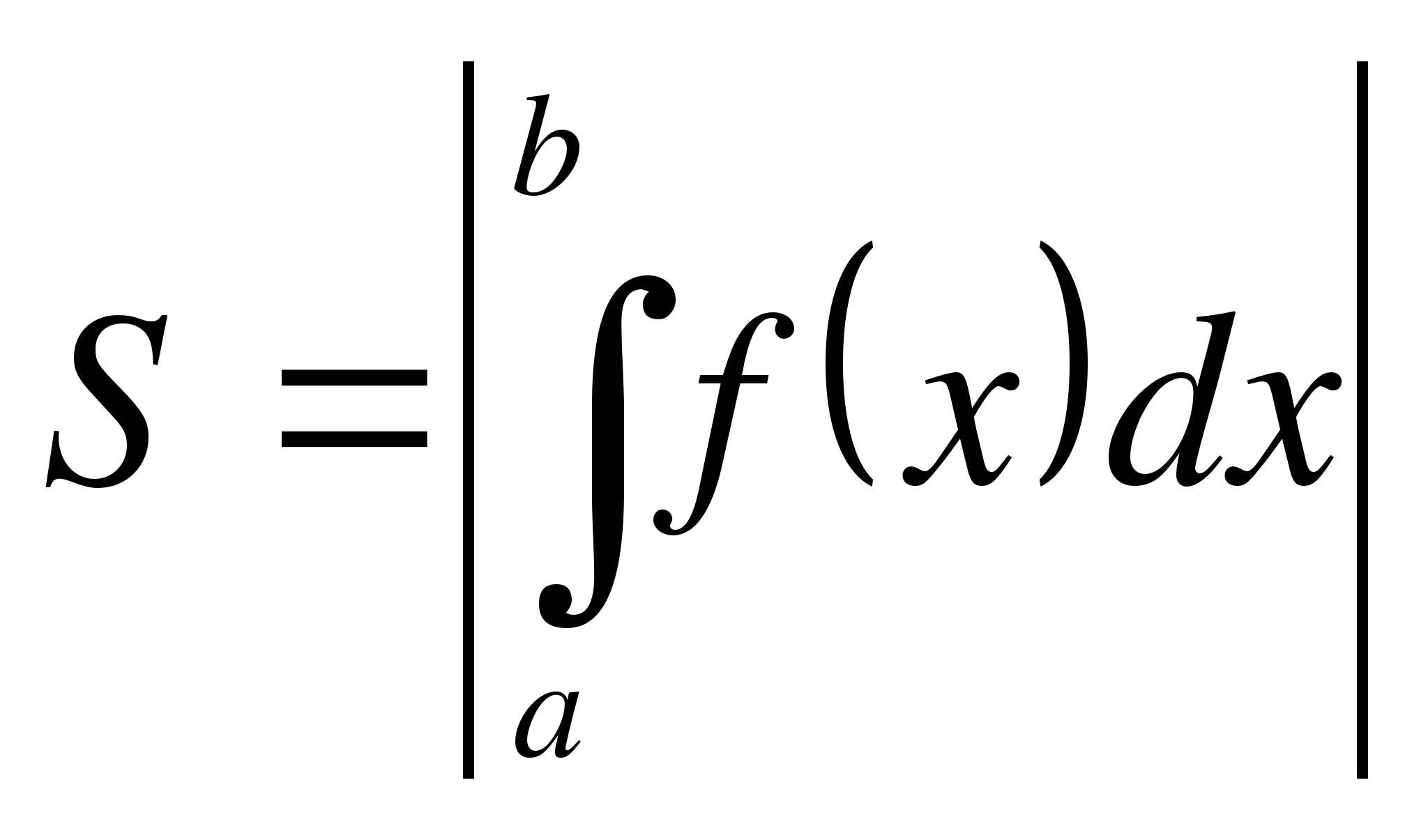(2)

Пример 2. Вычислить площадь плоской фигуры, ограниченной графиком функции 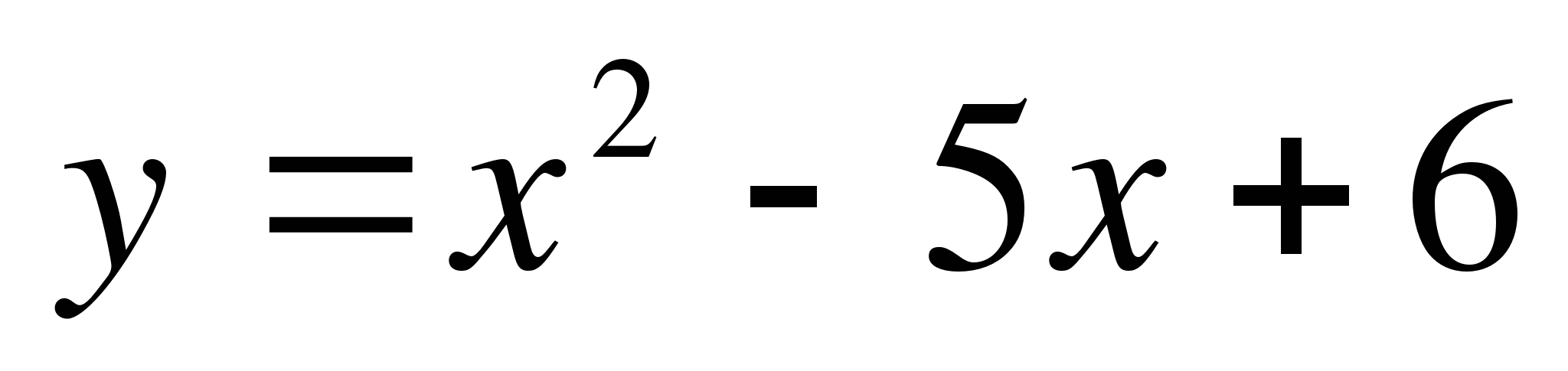и осью OX.

Решение: данная фигура (рис. 4) расположена ниже оси OX, поэтому применим формулу (2).

Рис. 4

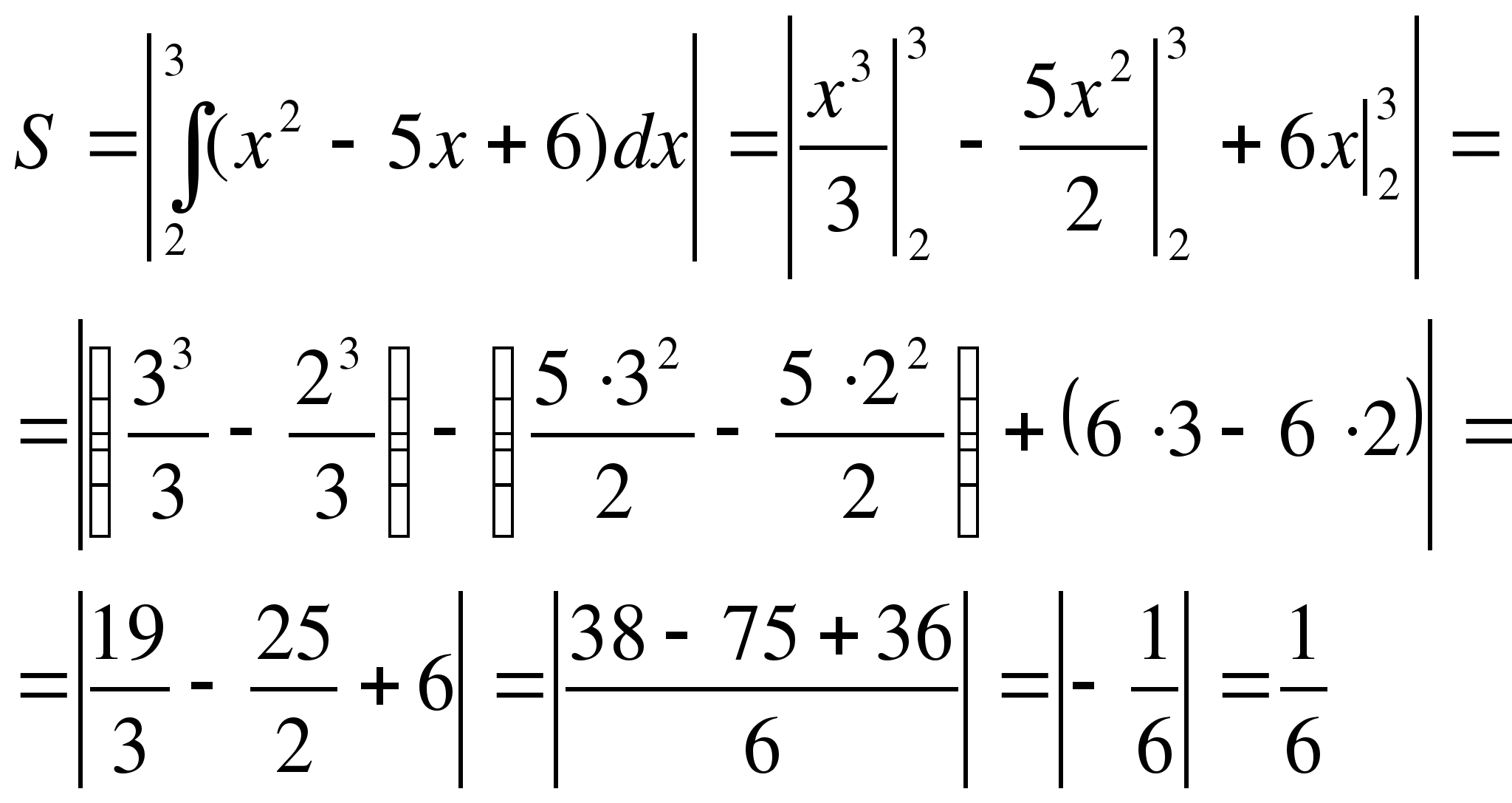
Ответ: 1/6 кв.ед.

Пример 3. Вычислить площадь плоской фигуры, ограниченной графиками функци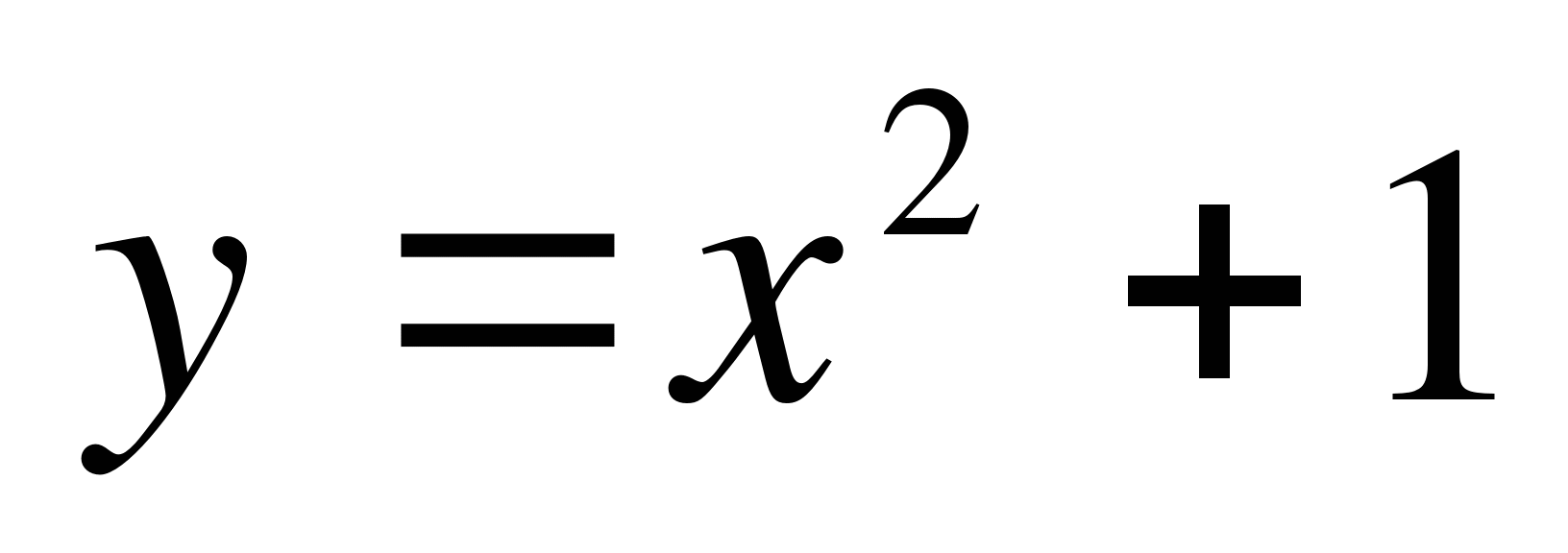й и .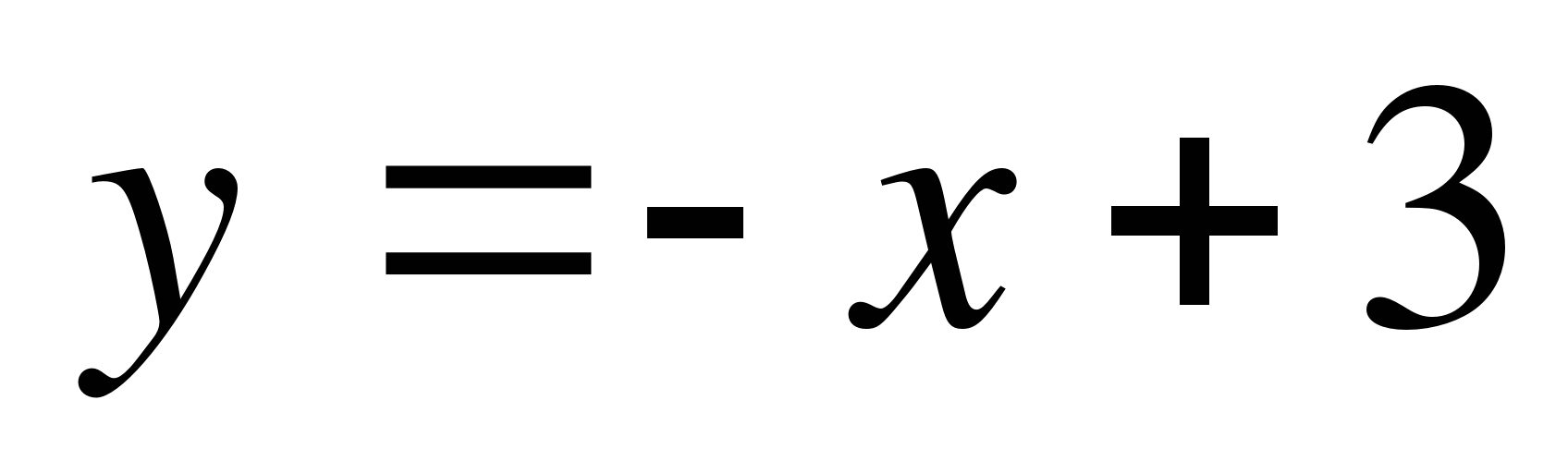

Решение: данная фигура (рис. 5)представляет собой разность криволинейных трапеций

Абсциссы точек пересечения находим по чертежу: x₁=-2 и x₂=1.

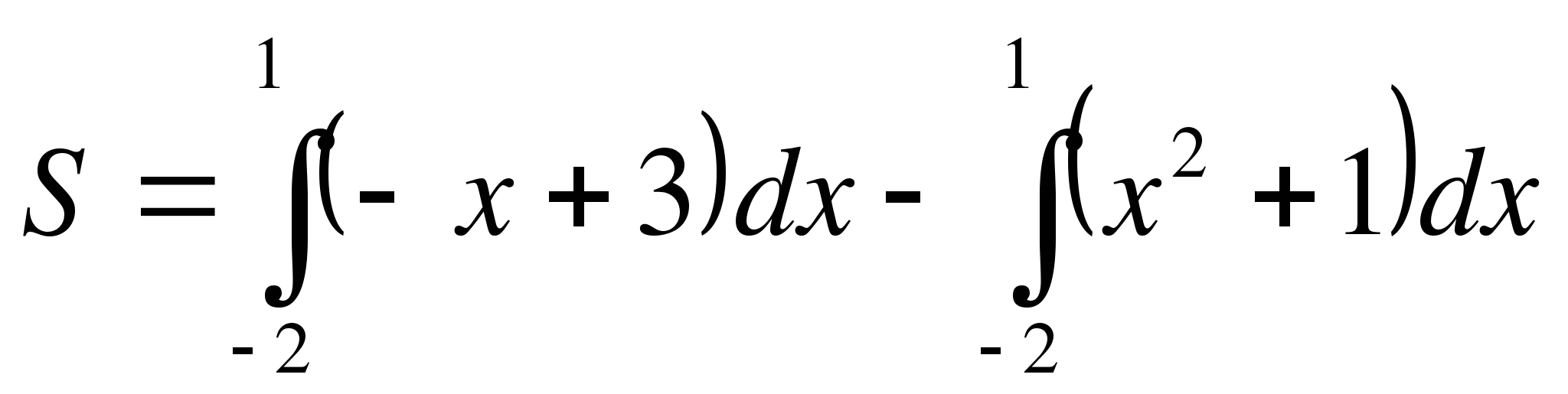. Можно записать под один интеграл:

Рис. 5

Y

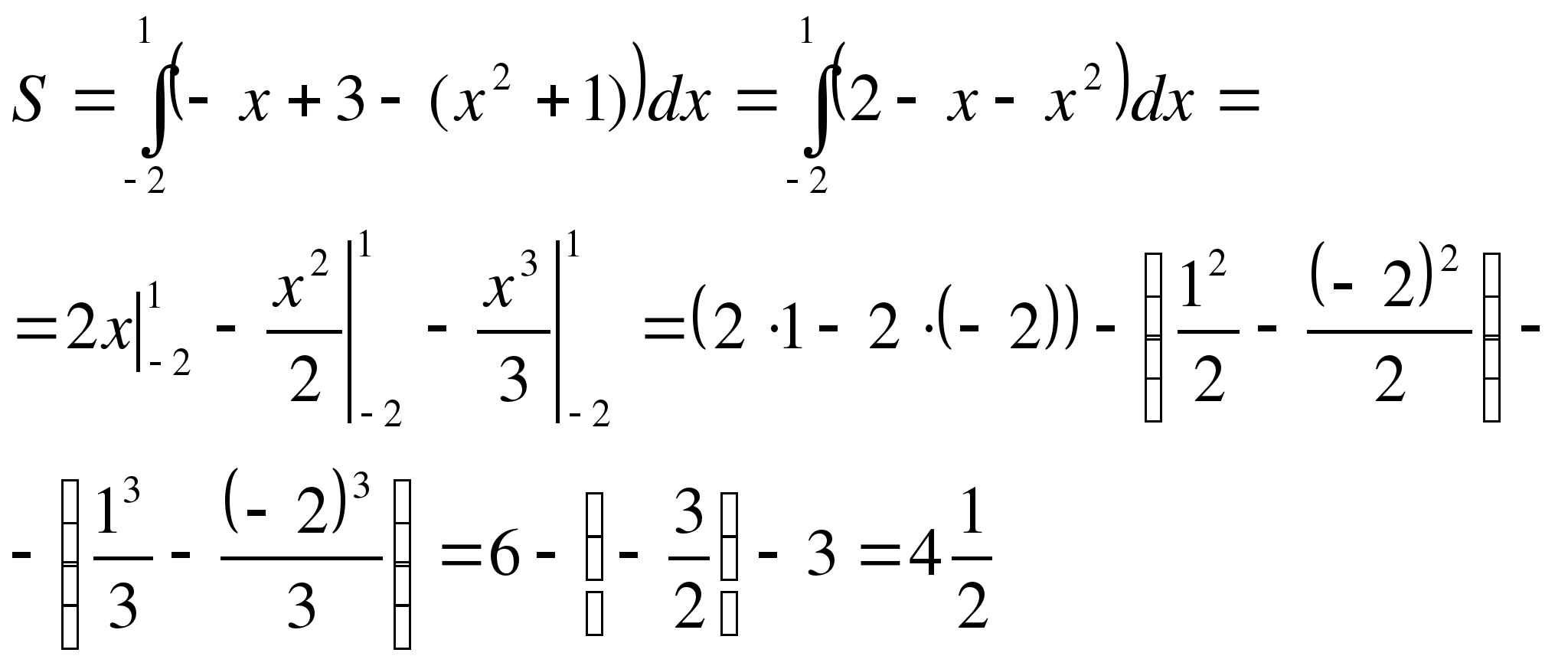
Ответ: 4,5 кв.ед.

Пример 4. Вычислить площадь плоской фигуры, ограниченной графиками функци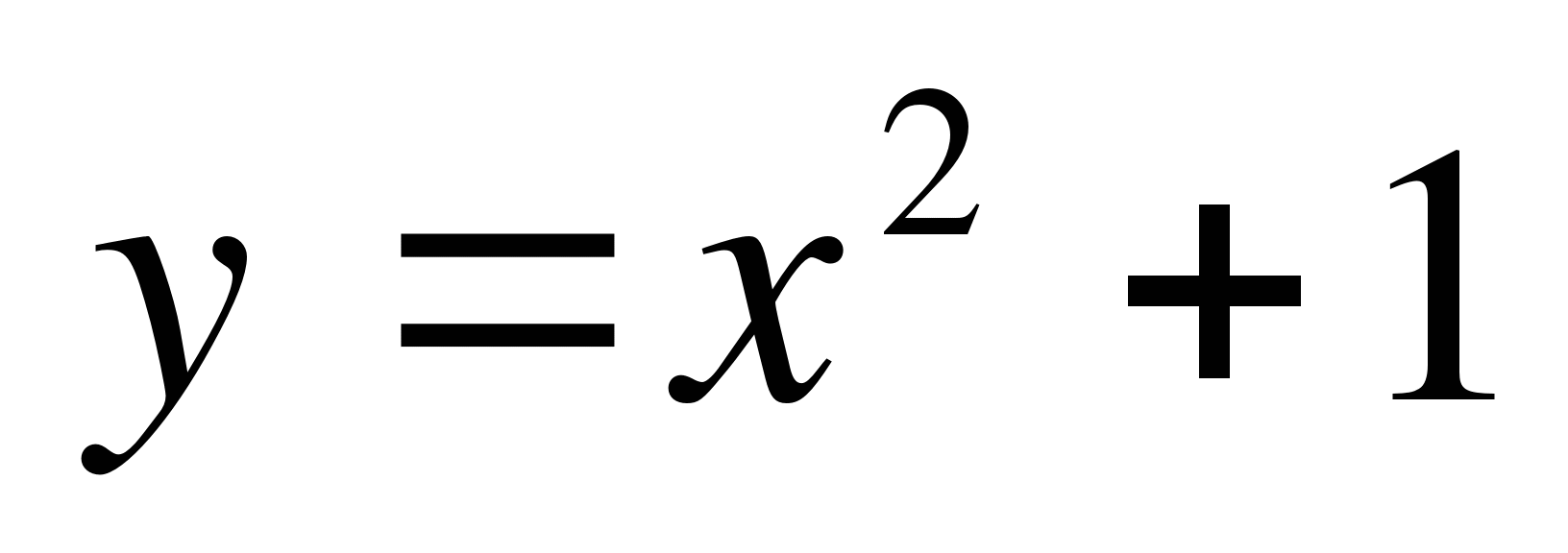й и 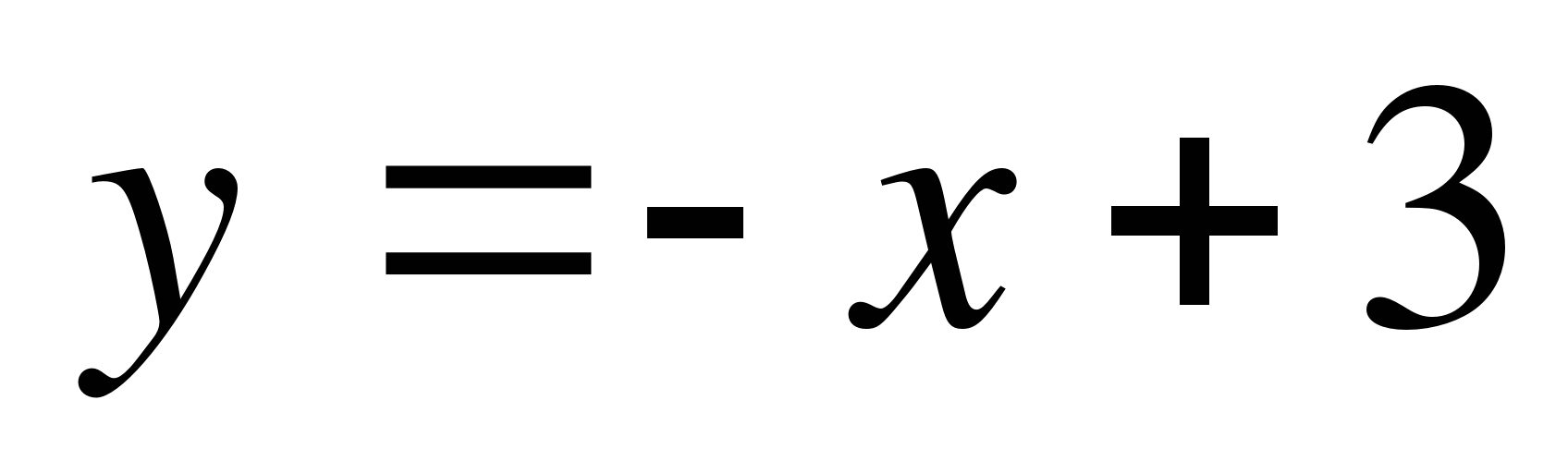, и координатными осями.

Решение: данная фигура (рис. 6) представляет собой сумму криволинейных трапеций S=S₁+S₂, где 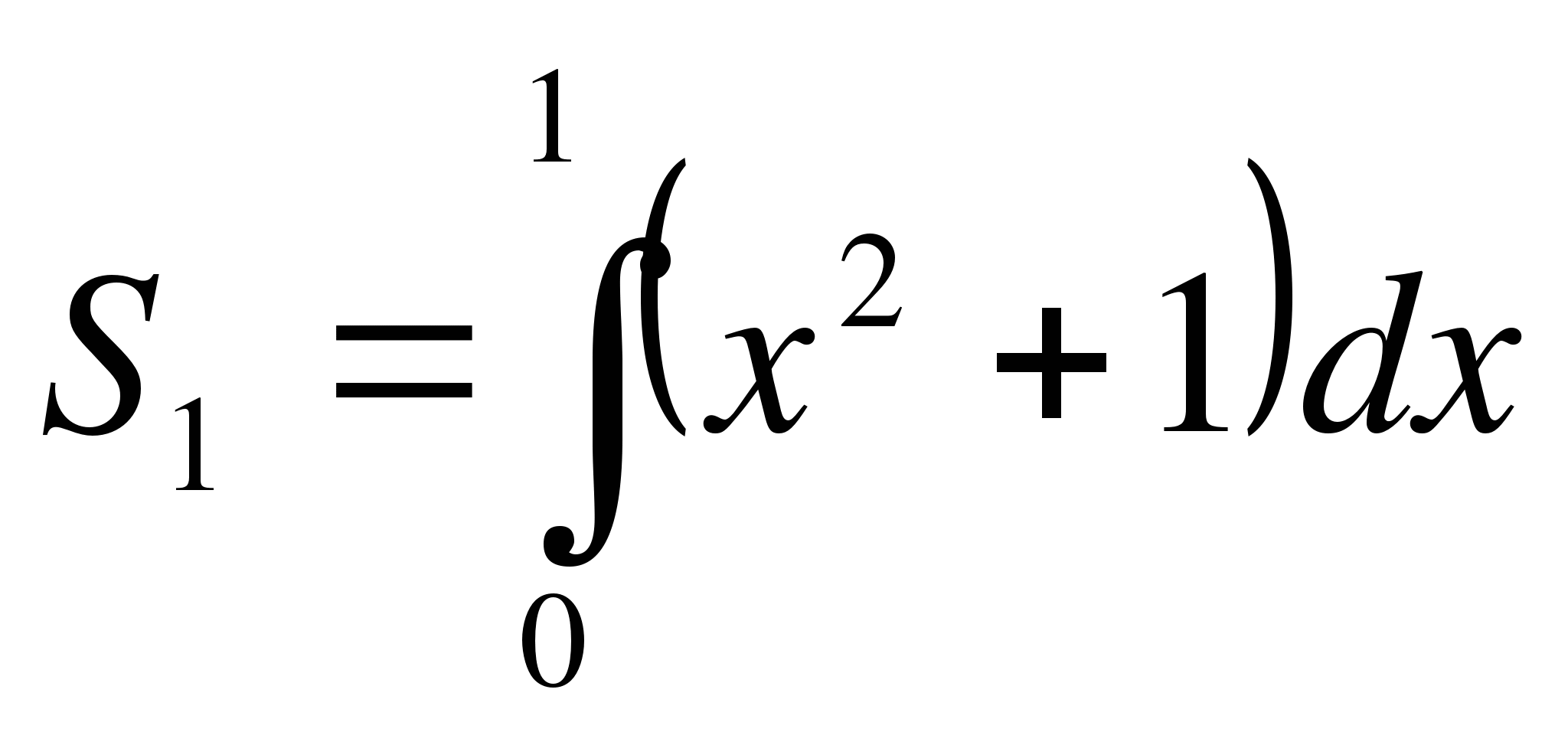и 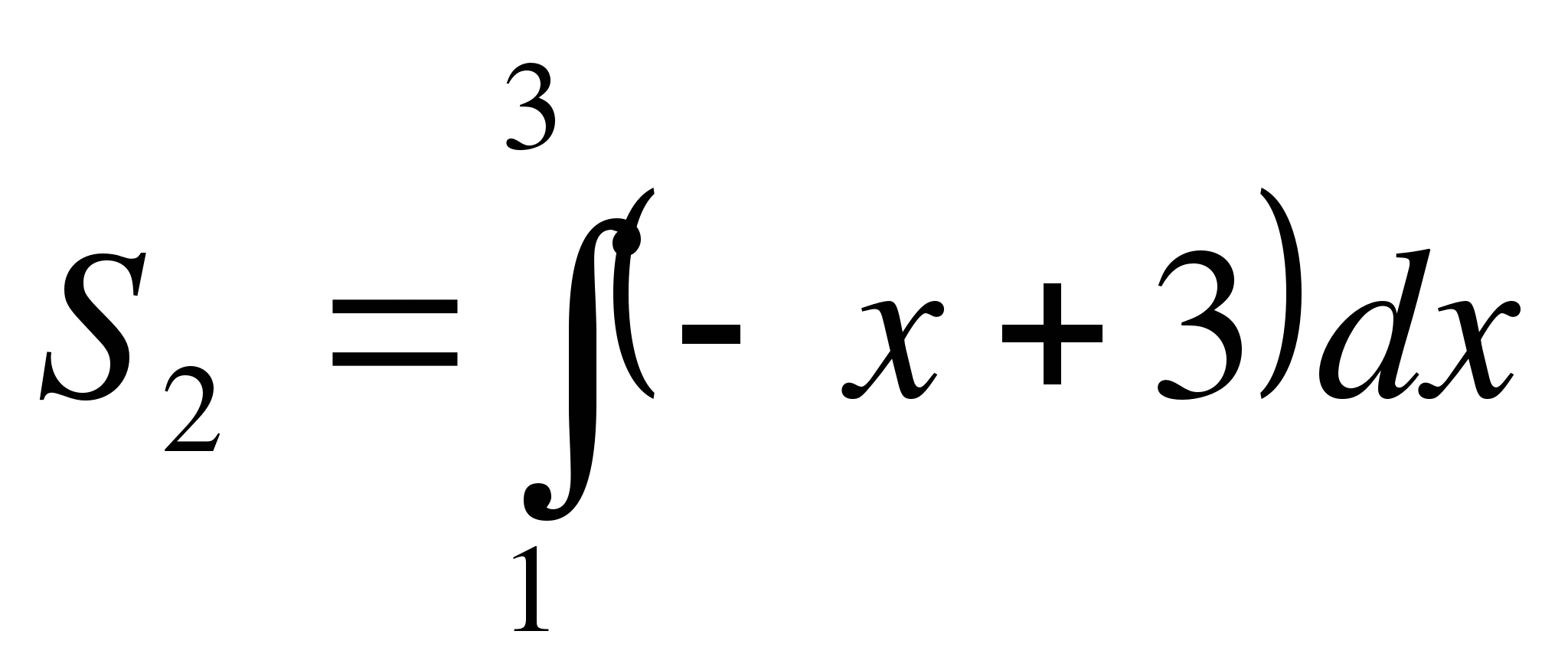. Получим формулу:

Рис. 6

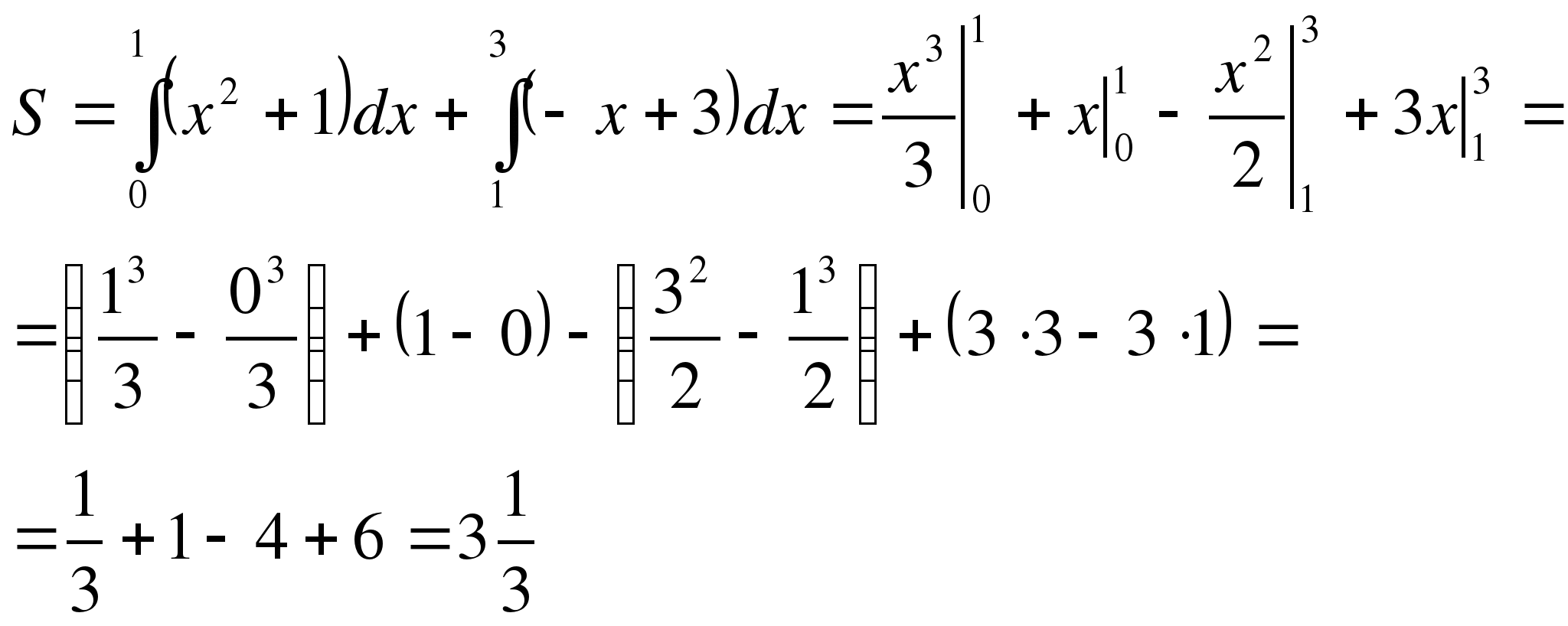
Ответ: 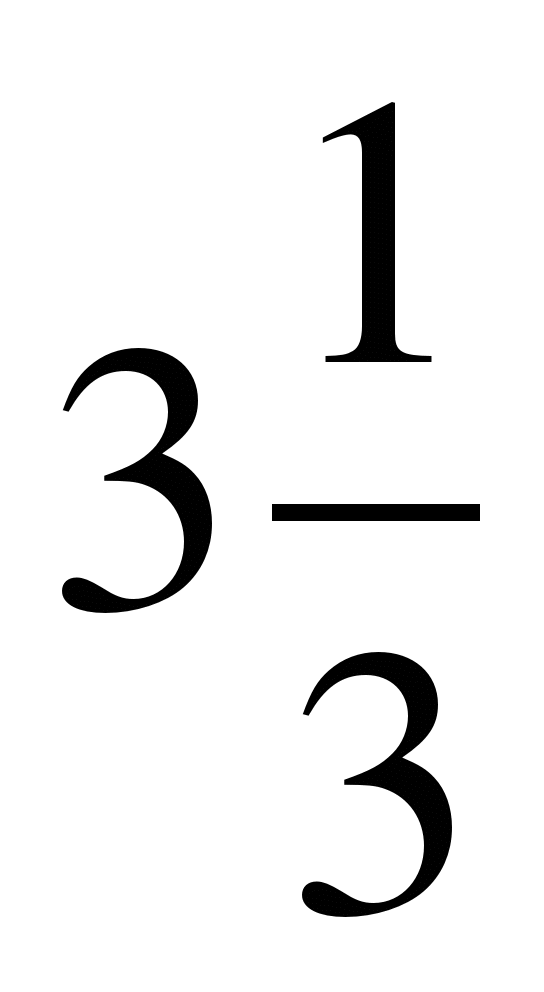кв.ед.

2. Проверьте себя

1

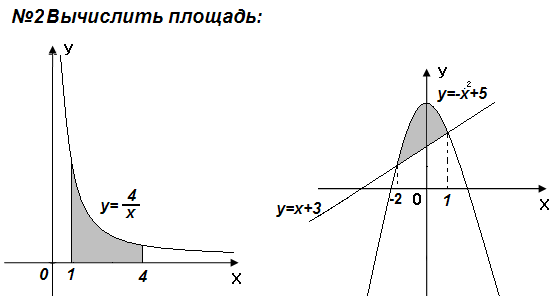
№2

№3

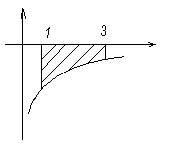
y=-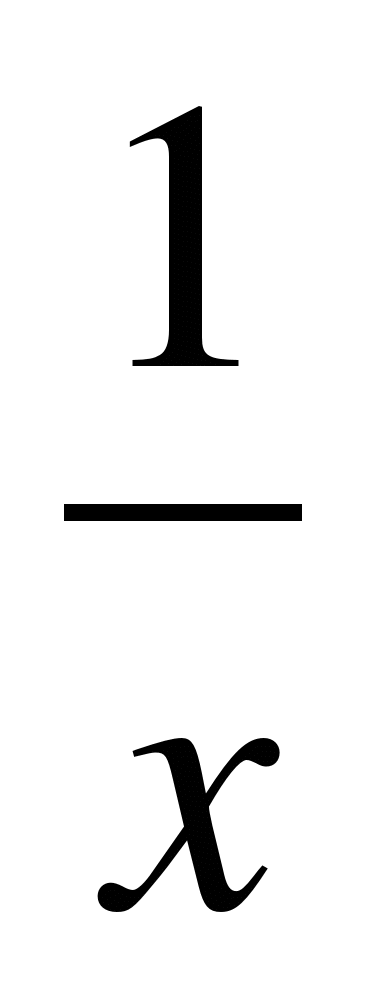

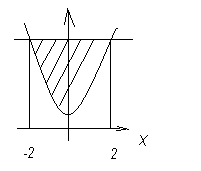
y=5

y=x²+1

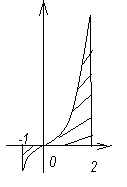
y=x³

Ответы: №1 ln3 кв.ед., №2 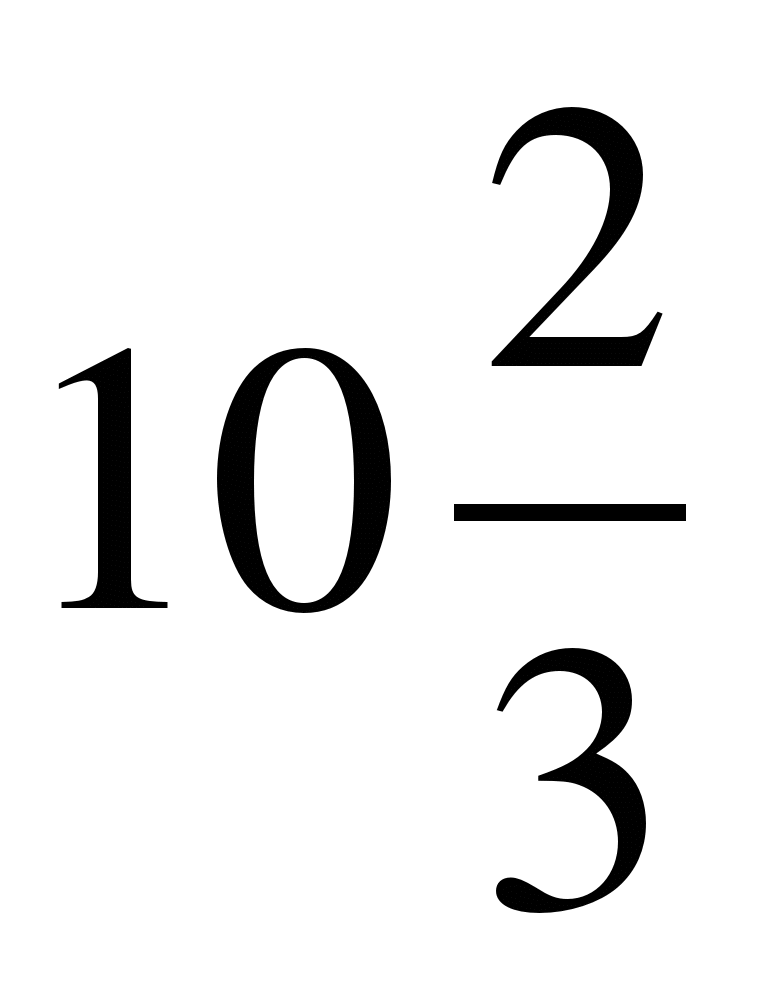кв.ед., №3 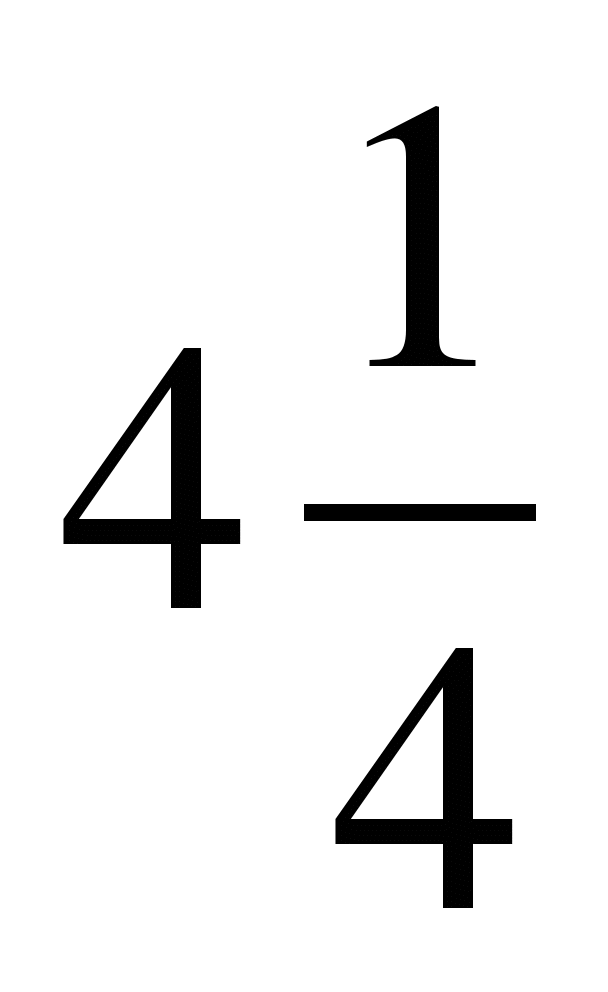кв.ед.

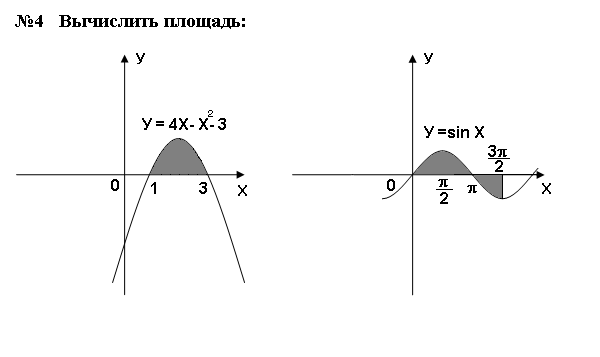
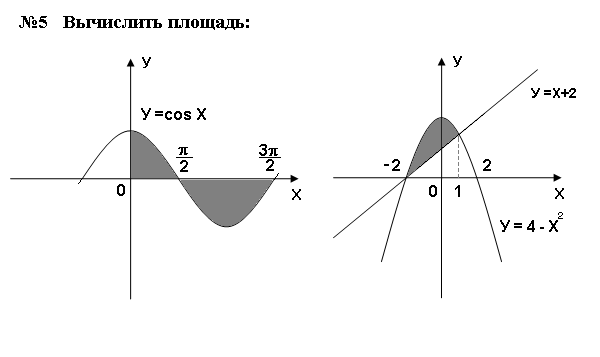
3. Самостоятельная работа

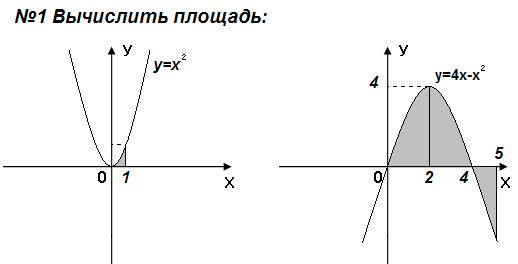
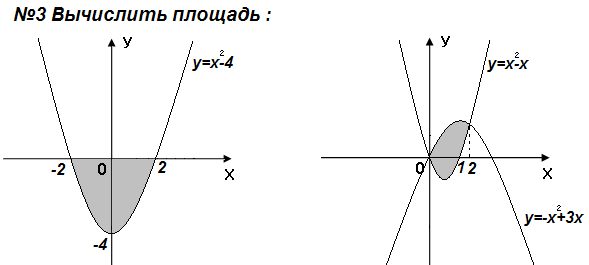
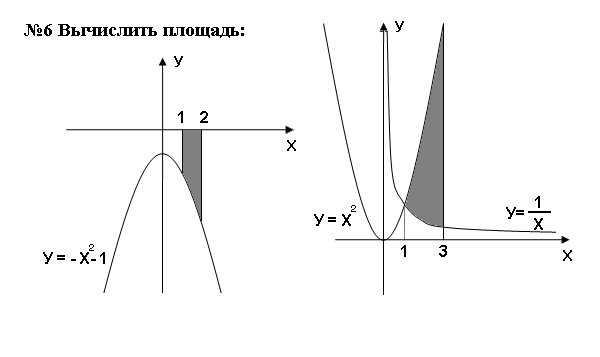
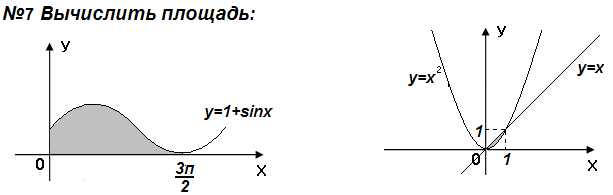
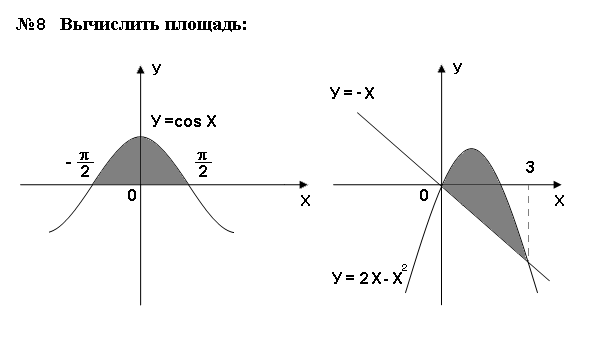
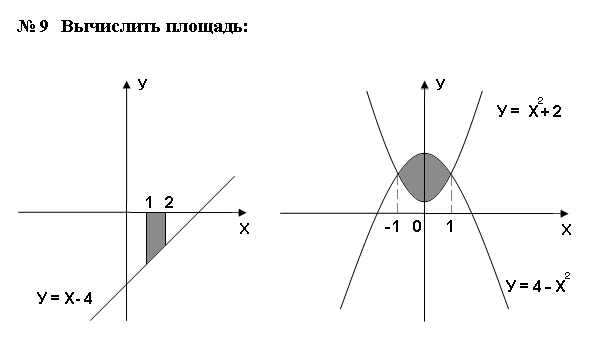
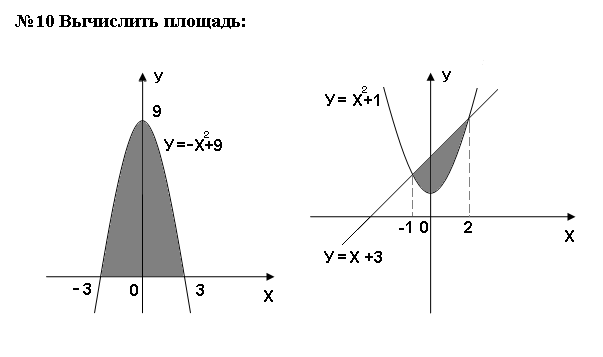
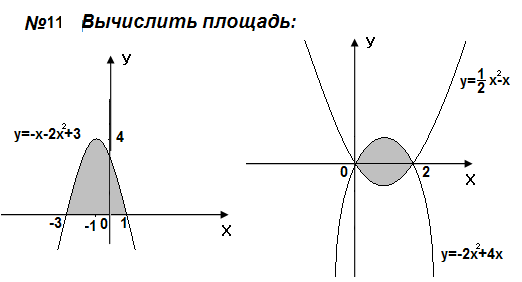
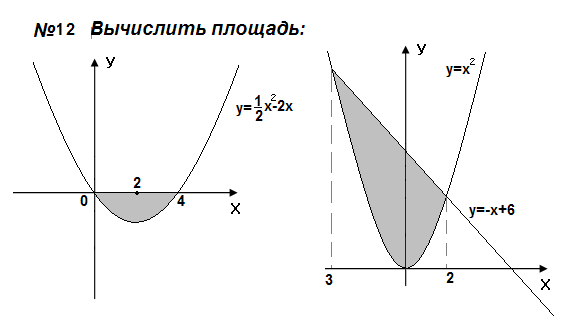
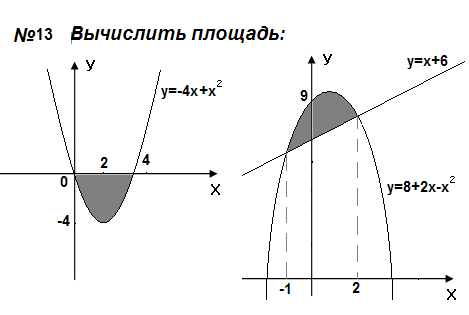
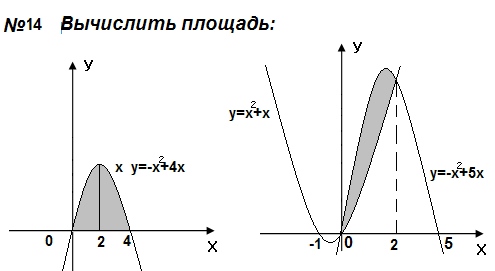
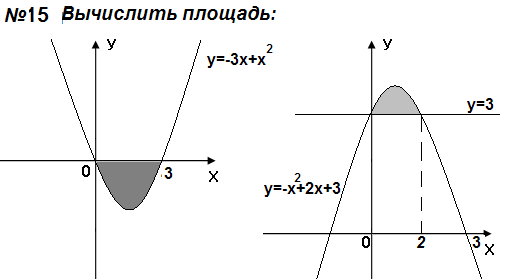
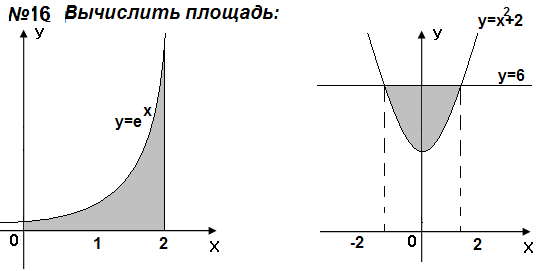
4. Контрольные вопросы

1. Приведите определение криволинейной трапеции.

2. В чём геометрический смысл определённого интеграла?

3. Выберите формулу площади заштрихованной фигуры:

y=1-x

А.

Б.

В.

4. Составьте формулу для вычисления площади изображённой фигуры

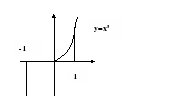
Критерии оценки

«Отлично» — даны ответы на все контрольные вопросы, задания самостоятельной работы выполнено полностью.

«Хорошо» — даны ответы на все контрольные вопросы; при выполнении заданий самостоятельной работы допущены 1-2 арифметические ошибки.

«Удовлетворительно» — выполнено 60%-70% заданий самостоятельной работы, даны ответы не на все контрольные вопросы;.

«Неудовлетворительно» — выполнено менее 60% заданий для самостоятельной работы

infourok.ru

Приложения определенного интеграла Геометрические приложения определенного интеграла Вычисление площадей плоских фигур

Пусть функция y=f(x) неотрицательна и непрерывна на отрезке [a, b]. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой y=f(x) на [ a, b] численно равна определенному интегралу 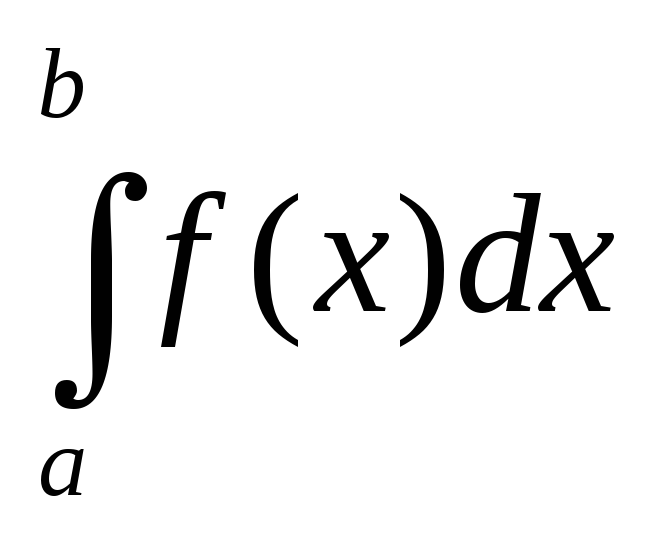, т.е.

S=.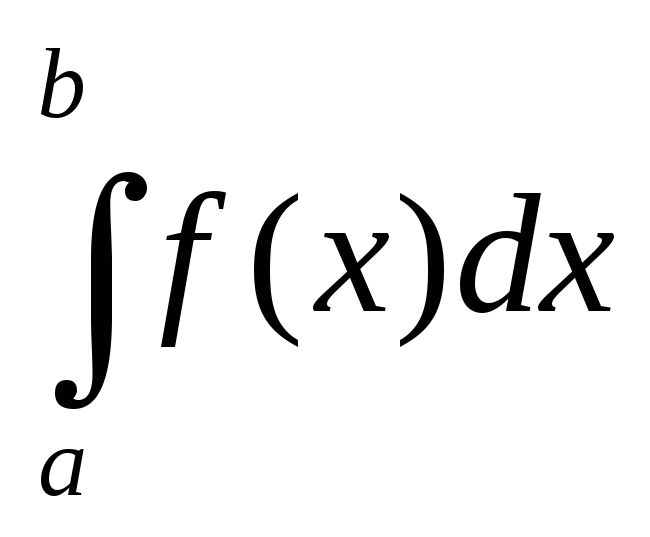

Пример. Найти площадь фигуры, ограниченной линиями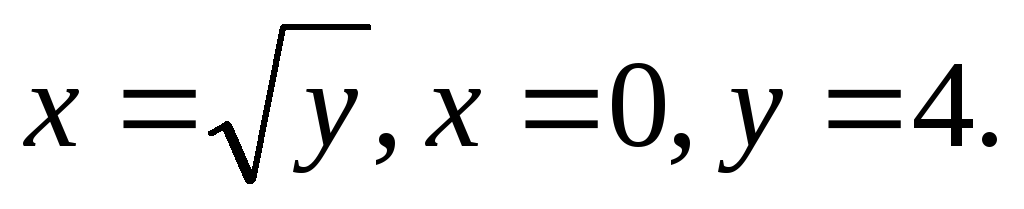

S = 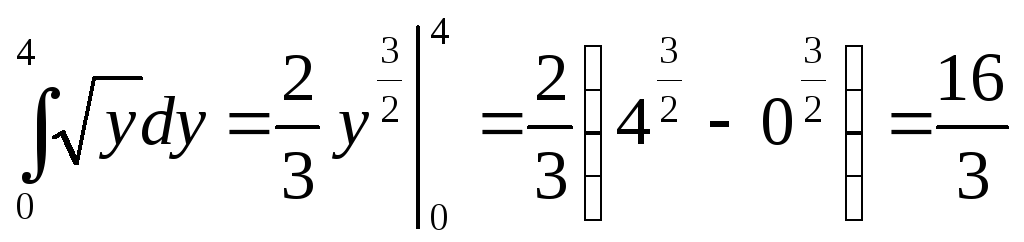(кв. ед.)

Пусть функция y=f(x) неположительна и непрерывна на отрезке [a, b]. Площадь S над кривой y=f(x) на [ a, b] отличается знаком от определенного интеграла , т.е.

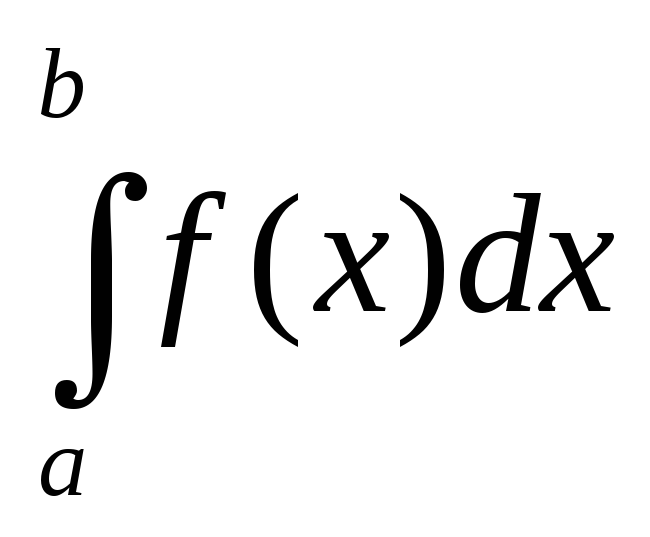S= —. (17)

Приведем формулу, применение которой упрощает решение задач на вычисление площадей плоских фигур.

Теорема. Пусть на отрезке [a, b] заданы непрерывные функции y=f₁(x) и y=f₂(x) такие, что 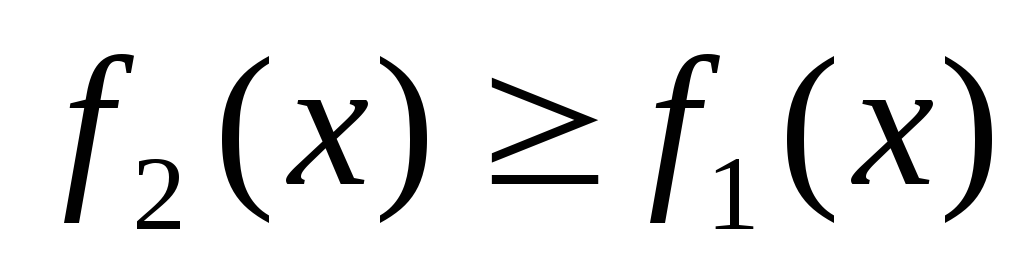. Тогда площадьS фигуры, заключенной между кривыми y=f₁(x) и y=f₂(x) на отрезке [ a, b] вычисляется по формуле

S=. (18)

Пример. Вычислить площадь фигуры, ограниченной линиями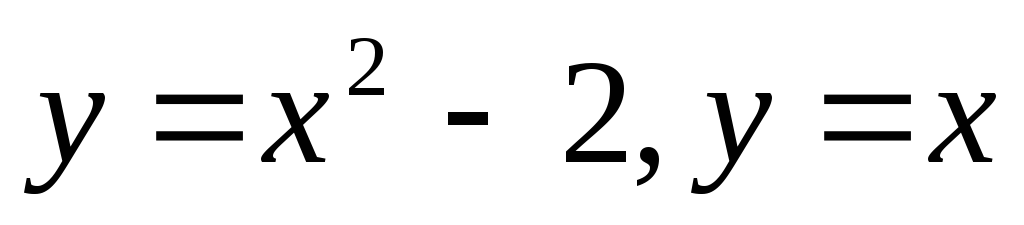

Найдем координаты точек пересечения параболы 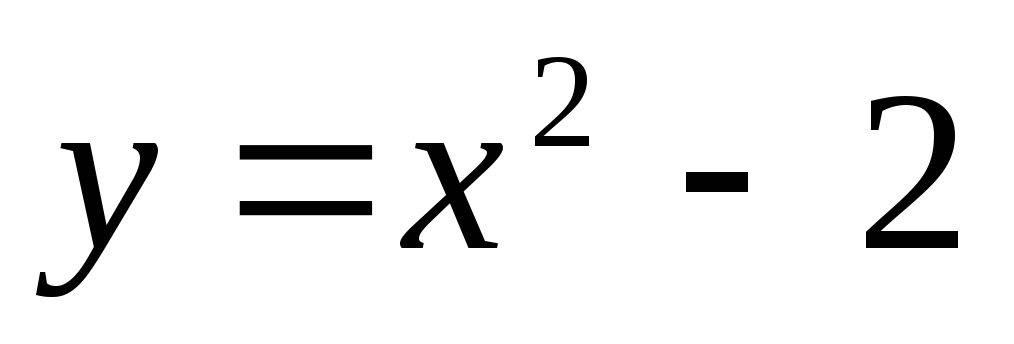и прямой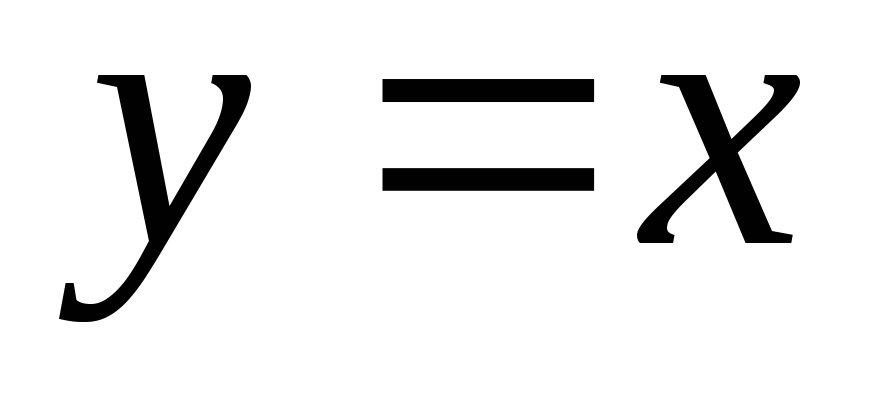, решив систему этих уравнений: (-1; -1) и (2; 2). На отрезке [-1; 2] . Воспользуемся формулой (18), полагая f₂(x)=x, f₁(x)=x² – 2. Абсциссы точек пересечения линий зададут пределы интегрирования:

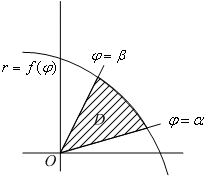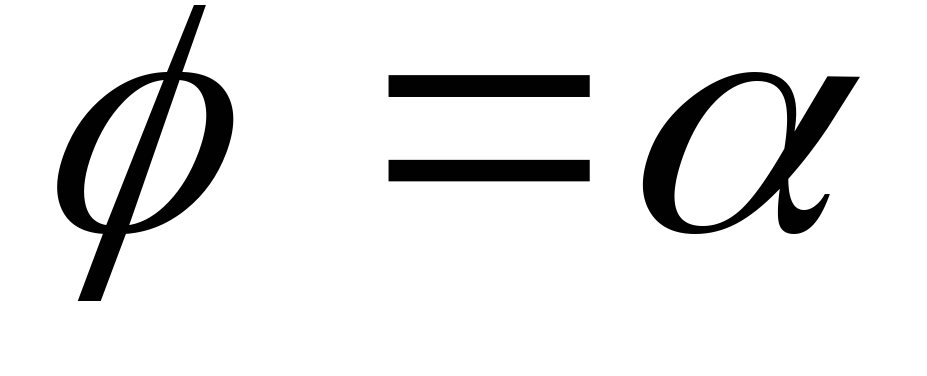Площадькриволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением r=f() и двумя лучамии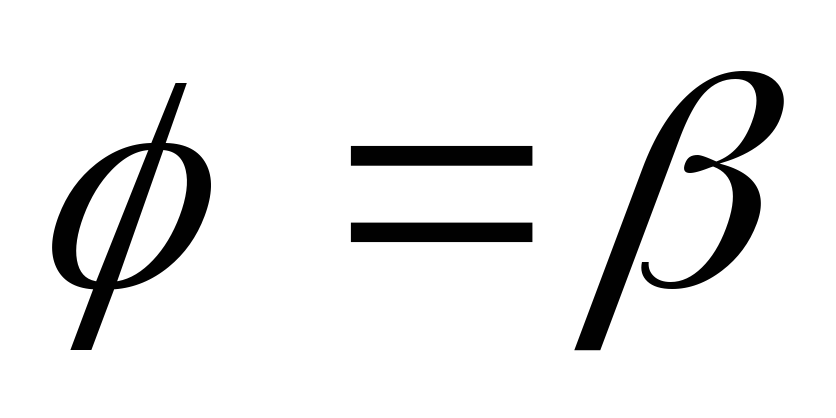вычисляется по формуле:

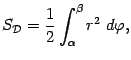
Пример. Найдём площадь 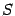области, ограниченной частью спиралиr=a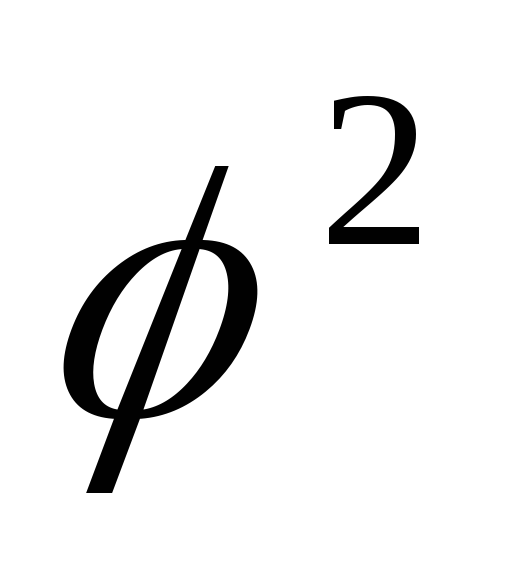 (a>0) при ;и отрезком;оси(см. рис.).

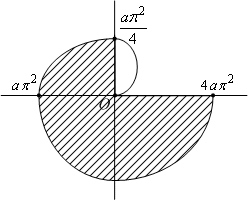
Применяя формулу, получаем:

Если область 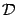имеет границу, состоящую из двух отрезков лучейи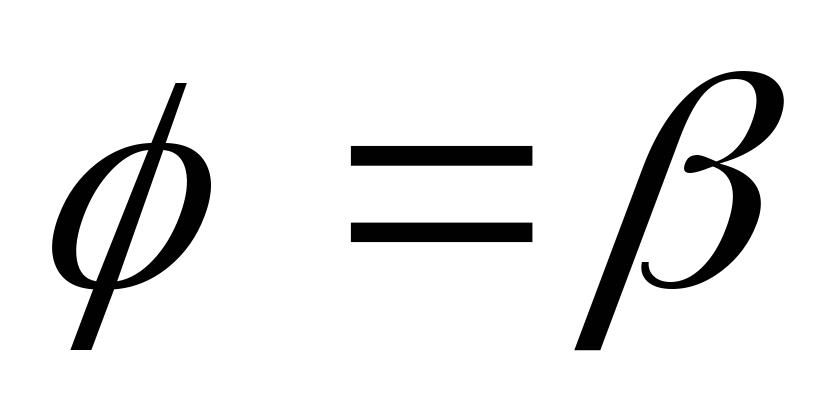(эти отрезки могут вырождаться в одну точку) и двумя линиями, заданными уравнениями в полярных координатах:r=f₁() иr=f₂(), причёмf₁(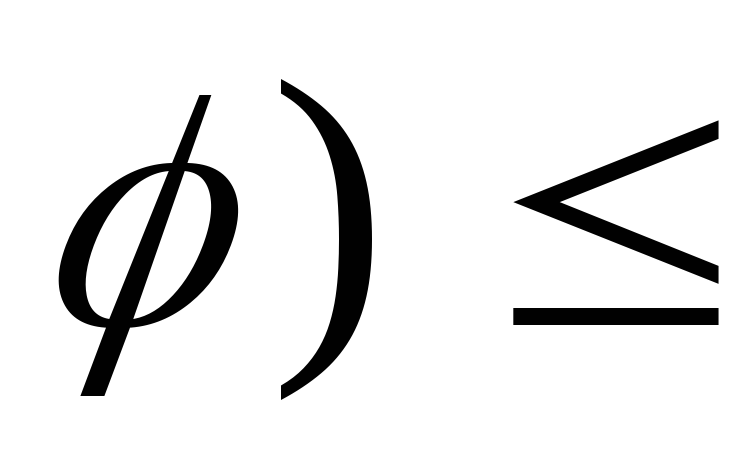f₂(), при всех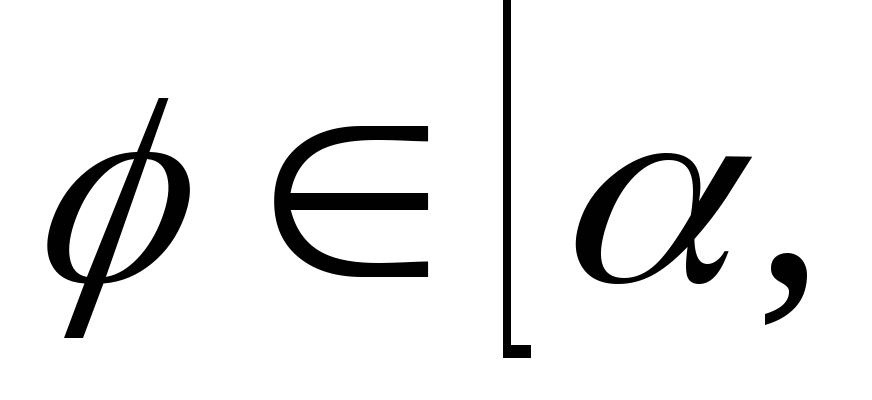(см.рис.)

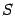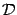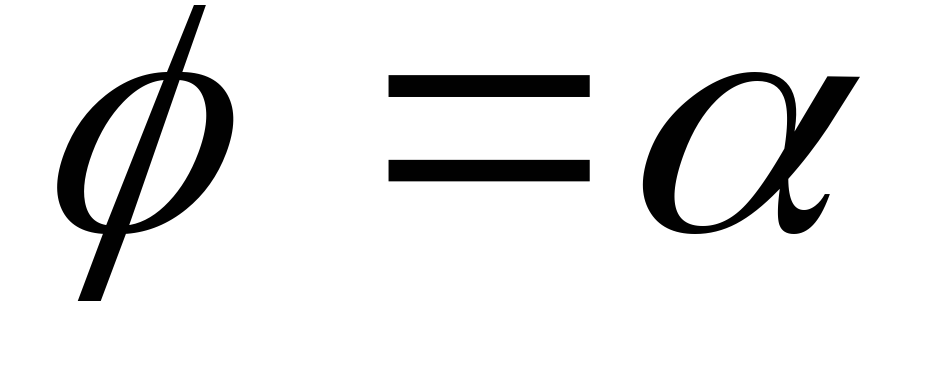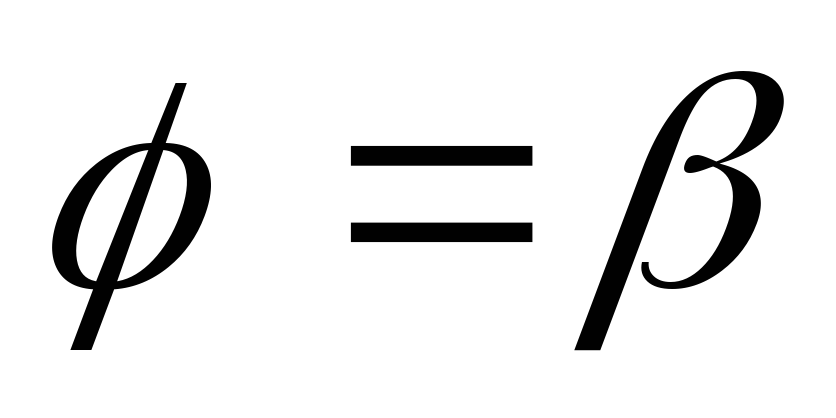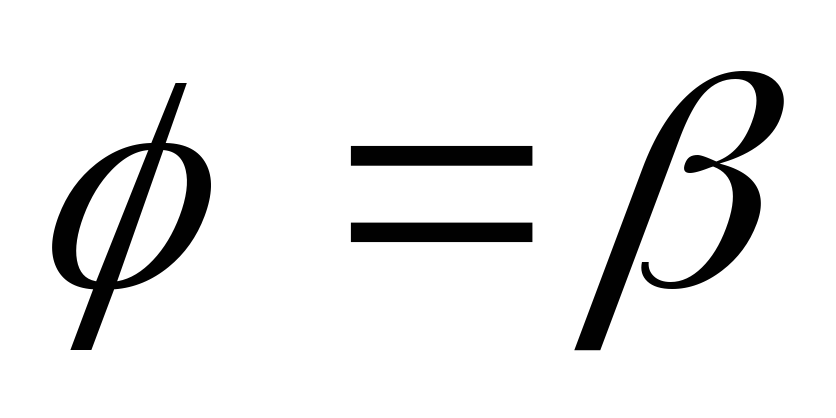то площадьобластиможно представить как разность двух площадей:S₂— площади области, лежащей между лучами и, и линиейr=f₂(), иS₁— площади области, лежащей между лучами и, линиейr=f₁().

Каждую из площадей S₁ и S₂ можно подсчитать по формуле, так что получаем в итоге

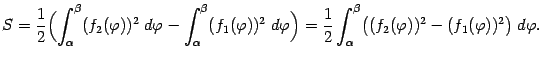
Если кривая задана параметрическими уравнениями x=x=(t) и y=y(t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и отрезком [a,b] оси Ox выражается формулой

.

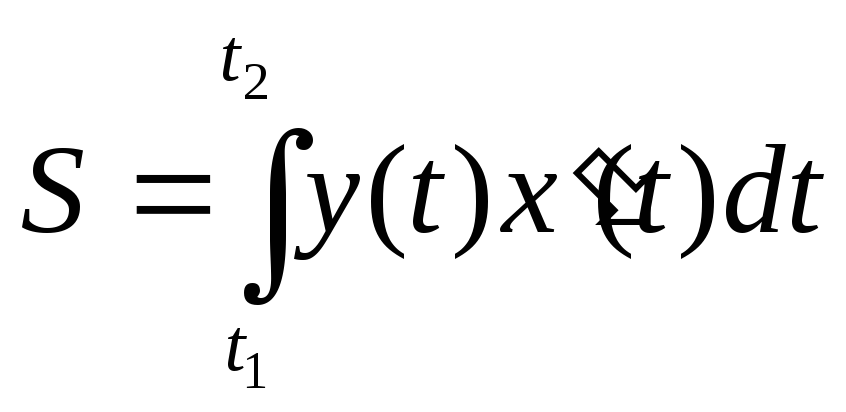Вычисление длины дуги

1. Явное задание кривой. В этом случае кривая задается в виде 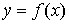,, и длина ее дуги равна L=.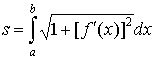

2. Кривая в полярных координатах. Уравнение кривой имеет в этом случае вид и длина ее дуги равнаL=_.

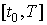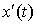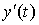3. Параметрическое задании кривой. Пусть функции x(t) и y(t) имеют на отрезке непрерывные производные и. Тогда длина дуги кривой

_L=.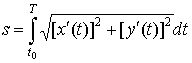

Пример. Найдём длину дуги кривой (циклоиды), заданной на плоскости параметрическими уравнениями

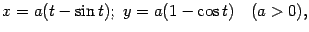
л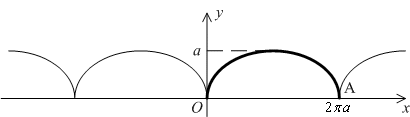ежащей между точкамиO(0;0) (соответствует ) иA(2a;0) (соответствует ).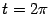

Для функций f₁(t)=a(t-sint) и f₂(t)=a(1-cost) вычислим производные: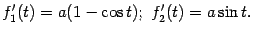

Тогда искомая длина дуги равна

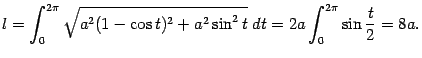
П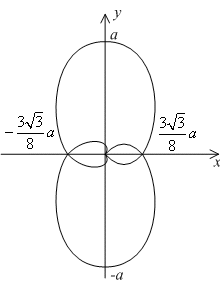ример. Пусть линия на плоскости с полярными координатами (r;) задана уравнениемr=a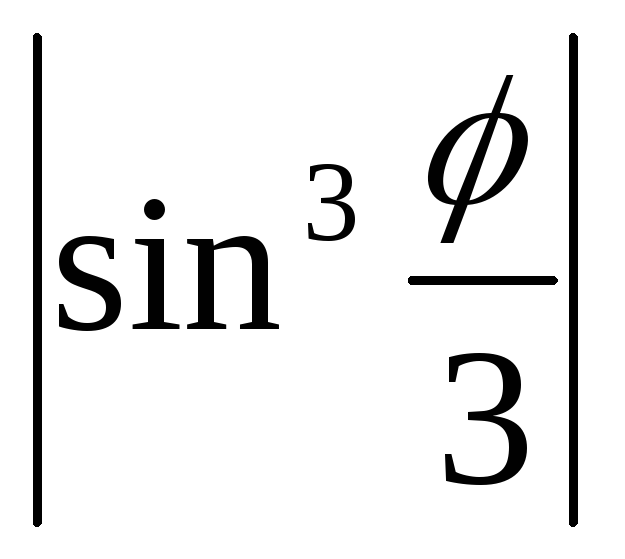 (a>0). Поскольку функция f()=a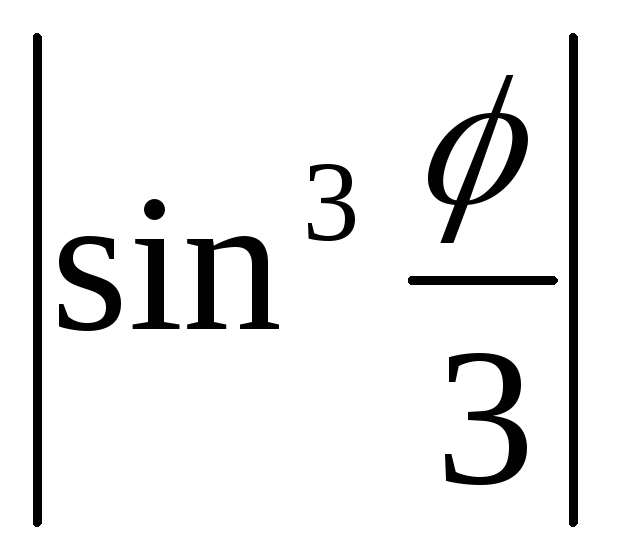периодична с периодом , достаточно рассматривать только значения аргумента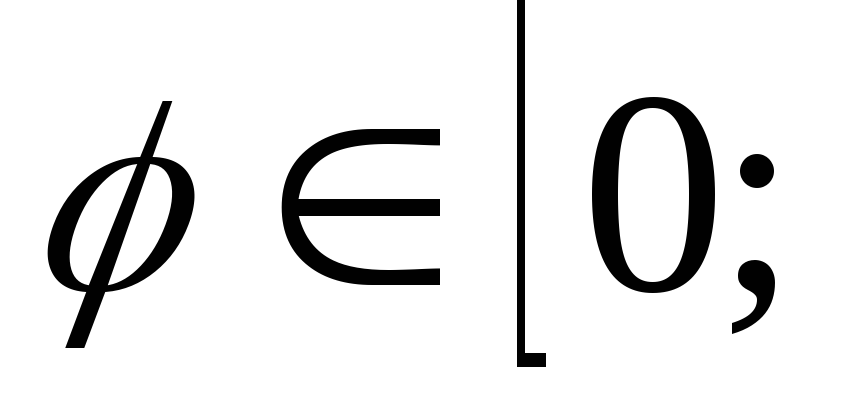, при которых выражение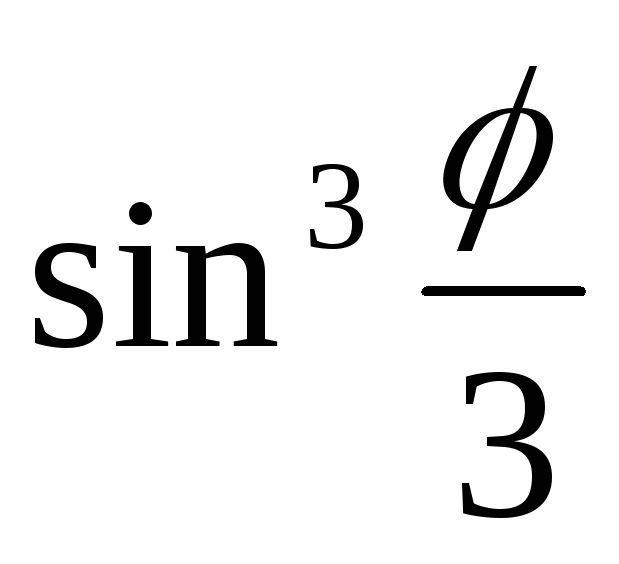неотрицательно. Кривая имеет вид, изображённый на следующем рисунке.

Найдём длину этой линии.

Имеем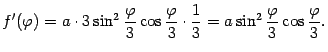

Поэтому искомая дли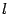на равна

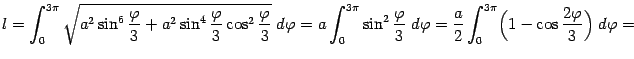
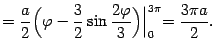
studfile.net

«Вычисление площадей плоских фигур с помощью определенного интеграла». 11-й класс

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока: вывести формулу для вычисления площадей плоских фигур с помощью определенного интеграла; сформировать навык вычисления площадей плоских фигур с помощью определенного интеграла; повторить известные и сообщить новые сведения из истории интегрального исчисления; подготовка к экзамену; продолжить работу по развитию внимания, речи, логического мышления, аккуратности в записи; совершенствовать графическую культуру; продолжить работу по развитию творческих способностей учащихся; повысить интерес к изучению математики;

Оборудование: мультимедийный проектор, экран, презентация по теме, разработанная в среде Power Point.

Ход урока

I. Организационный момент, сообщение темы и цели урока.

(Слайд 1)

II. Проверка домашнего задания.

(Слайд 2)

Проверка дополнительного домашнего задания (учитель показывает решение на заранее подготовленном рисунке, решение с обратной стороны доски):

Вычислите площадь фигуры, ограниченной графиками функций y = 1+ 3cos(x/2), x = -π/2, x = 3π/2, y = 0

Решение:

III. Актуализация опорных знаний.

1. Устная работа (Слайды 3-4)

1. Выразите с помощью интеграла площади фигур, изображенных на рисунках:   
2. Вычислите интегралы:

2. Немного истории. (Слайды 5-9)

Фрагмент компьютерного проекта учащихся на тему «Из истории интегрального исчисления».

1 учащийся

Интеграл – одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны отыскивать функции по их производным, а с другой – измерять площади, объемы, длины дуг, работу сил за определенный промежуток времени и т. п.

Само слово интеграл придумал Я. Бернулли (1690 г.). Оно происходит от латинского integero, переводится как приводить в прежнее состояние, восстанавливать.

Другие известные вам термины, относящиеся к интегральному исчислению, появились значительно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее «примитивная функция», которое ввел Жозеф Луи Лагранж (1797 г.). Латинское слово primitivus переводится как «начальный».

Возникновение задач интегрального исчисления связано с нахождением площадей и объемов. Ряд задач такого рода был решен математиками древней Греции. Первым известным методом для расчёта интегралов является метод исчерпания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известен. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга.

Однако Архимед не выделил общего содержания интеграционных приемов и понятий об интеграле, а тем более не создал алгоритма интегрального исчисления.

Труды Архимеда, впервые созданные в 1544 году, явились одним из важнейших отправных пунктов развития интегрального исчисления.

2 учащийся

Понятие интеграл непосредственно связано с интегральным исчислением – разделом математики, занимающимся изучением интегралов, их свойств и методов вычисления.

Более близко и точно к понятию интеграл подошел Исаак Ньютон. Он первый построил дифференциаль­ное и интегральное исчисления и назвал его «Методом флюксий…» (1670-1671 гг., опубл. 1736 г.). Переменные величины Ньютон назвал флюентами (текущими величинами, от лат. fluo – теку). Скорости изменения флюент Ньютон – флюксиями, а необходимые для вычисления флюксий бесконечно малые изменения флюент – «моментами» (у Лейбница они назывались дифференциалами). Таким образом, Ньютон положил в основу понятия флюксий (производной) и флюенты (первообразной, или неопределённого интеграла).

Это сразу позволило решать самые разнообразные, математические и физические, задачи.

Одновременно с Ньютоном к аналогичным идеям пришёл другой выдающийся учёный – Готфрид Вильгельм Лейбниц.

Размышляя над философ­скими и математическими вопросами, Лейб­ниц убедился, что самым надежным средством искать и находить истину в науке может стать математика. Знак интеграла (∫), был впервые использован Лейбницем в конце XVII века. Этот символ образовался из буквы S — сокращения слова лат. summa (сумма).

Ньютон и Лейбниц разработали две трактовки понятия обычного определенного интеграла.

Ньютон трактовал определенный интеграл как разность соответствующих значений первообразной функции:

,
где F`(x)=f(x).

Для Лейбница определенный интеграл был суммой всех бесконечно малых дифференциалов.

.

Формулу, которую открыли независимо друг от друга Ньютон и Лейбниц назвали формула Ньютона – Лейбница.

Таким образом, понятие интеграл было связано с именами знаменитых ученых: Ньютон, Лейбниц, Бернулли, положивших основу современного математического анализа.

IV. Объяснение нового материала.

(Слайд 10)

С помощью интеграла можно вычислять площади не только криволинейных трапеций, но и плоских фигур более сложного вида.

Пусть фигура P ограничена прямыми х = a, x = b и графиками функций y = f(x) и y = g(x), причем на отрезке [a;b] выполняется неравенство g(x)f(x).

Для вычисления площади фигуры будем рассуждать следующим образом. Выполним параллельный перенос фигуры P на m единиц вверх так, чтобы фигура P оказалась расположенной в координатной плоскости выше оси абсцисс.

Теперь она ограничена сверху и снизу графиками функций y = f(x)+m и

y = g(x)+m, причем обе функции непрерывны и неотрицательны на отрезке [a;b].

Полученную фигуру обозначим ABCD. Ее площадь можно найти как разность площадей фигур:

S_ABCD = S_aDCb – S_aABb =  =
=

Таким образом, площадь фигуры S, ограниченной прямыми х = a, x = b и графиками функций y = f(x) и y = g(x), непрерывных на отрезке [a;b] и таких, что для всех х из отрезка [a;b] выполняется неравенство g(x)f(x), вычисляется по формуле

Пример. (Слайд 11) Вычислите площадь фигуры, ограниченной линиями y = x, y = 5 – x, x = 1, x = 2.

V. Закрепление изученного материала.

Задание 1. (Слайд 12) Вычислите площадь фигуры, ограниченной линиями y = 3 – х² , y = 1+ | x |

Решение.

1. Найдем точки пересечения графиков функций:

	3 – х2 = 1 + |x| –х2 – |x| + 2 = 0 х2 + |x| – 2 = 0
x > 0 х2 + x – 2 = 0 x = – 2 – не подходит x = 1		x  0 х2 – x – 2 = 0 x = 2 – не подходит x = – 1

2. S₁ = S₂ S = 2∙S₁

3.

Задание 2. (Слайд 13)

С помощью определенного интеграла записывают формулы для вычисления площадей фигур, заштрихованных на рисунках.

Подберите из данных формул для вычисления площади фигуры ту, которая подходит к одному из шести чертежей. (Слайд 14)

Задание 3. (Слайд 15) Вычислите площадь фигуры, ограниченной графиком функции y = 0,5х² + 2, касательной к этому графику в точке с абсциссой х = -2 и прямой х = 0.

Решение.

1. Составим уравнение касательной к графику функции y = 0,5х² + 2 в точке с абсциссой х = -2:

y = f (x₀) + f ‘(x₀)(x – x₀)
f (-2) = 0,5∙(-2)² + 2 = 4
f ‘(x) = (0,5х² + 2)’= x
f ‘(-2) = -2
y = 4 – 2(x + 2)
y = -2x

2. Построим графики функций.

3. Найдем площадь фигуры АВС.

S_ABC =

VI. Подведение итогов.

(Слайд 16)

• формула для вычисления площадей плоских фигур;
• запись формул площадей плоских фигур с помощью определенного интеграла;
• повторение уравнения касательной к графику функции и решения уравнения с модулем;
• выставление оценок учащимся.

VII. Домашнее задание.

(Слайд 17)

1. п. 4 стр. 228-230;
2. №1025(в, г), №1037(в, г), №1038(в, г)

учебник: А. Г. Мордкович «Алгебра и начала анализа 10–11»

urok.1sept.ru