Уравнение касательной к графику функции
Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f (x0). Тогда прямая, проходящая через точку (x0; f (x0)), имеющая угловой коэффициент f ’(x0), называется касательной.
А что будет, если производная в точке x0 не существует? Возможны два варианта:
- Касательная к графику тоже не существует. Классический пример — функция y = |x| в точке (0; 0).
- Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π/2).
Уравнение касательной
Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент.
Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.
Задача. Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 2.
Уравнение касательной: y = f ’(x0) · (x − x0) + f(x0). Точка x0 = 2 нам дана, а вот значения f (x 0) и f ’(x0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f (x0) = f (2) = 23 = 8;
Теперь найдем производную: f ’(x) = (x3)’ = 3x2;
Подставляем в производную x0 = 2: f ’(x0) = f ’(2) = 3 · 22 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.
Задача. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x0 = π/2.
В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:
f (x0) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x0) = f ’(π/2) = 2cos (π/2) = 0;
Уравнение касательной:
y = 0 · (x − π/2) + 7 ⇒ y = 7
В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.
Смотрите также:
- Правила вычисления производных
- Вводный урок по вычислению производных степенной функции
- Что такое логарифм
- Тест к уроку «Площади многоугольников без координатной сетки» (легкий)
- Текстовые задачи про рельсы
- Задача B4: Семья из трех человек ведет из Москвы в Нижний Новгород
Уравнение касательной
В этой статье мы разберем все типы задач на нахождение уравнения касательной.
Вспомним геометрический смысл производной: если к графику функции в точке проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси ) равен производной функции в точке .
Возьмем на касательной произвольную точку с координатами :
И рассмотрим прямоугольный треугольник :
В этом треугольнике
Отсюда
Или
Это и есть уравнение касательной, проведенной к графику функции в точке .
Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти и .
Есть три основных типа задач на составление уравнения касательной.
1. Дана точка касания
2. Дан коэффициент наклона касательной, то есть значение производной функции в точке .
3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.
Рассмотрим каждый тип задач.
1. Написать уравнение касательной к графику функции в точке .
а) Найдем значение функции в точке .
.
б) Найдем значение производной в точке . Сначала найдем производную функции
Подставим найденные значения в уравнение касательной:
Раскроем скобки в правой части уравнения. Получим:
Ответ: .
2. Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.
Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции в точках касания равно нулю.
а) Найдем производную функции .
б) Приравняем производную к нулю и найдем значения , в которых касательная параллельна оси :
Приравняем каждый множитель к нулю, получим:
Ответ: 0;3;5
3. Написать уравнения касательных к графику функции , параллельных прямой .
Написать уравнения касательных к графику функции , параллельных прямой .
Касательная параллельна прямой . Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.
Это второй тип задач на нахождение уравнения касательной.
Итак, у нас дана функция и значение производной в точке касания.
а) Найдем точки, в которых производная функции равна -1.
Сначала найдем уравнение производной.
Нам нужно найти производную дроби.
Приравняем производную к числу -1.
или
или
б) Найдем уравнение касательной к графику функции в точке .
Найдем значение функции в точке .
(по условию)
Подставим эти значения в уравнение касательной:
.
б) Найдем уравнение касательной к графику функции в точке .
Найдем значение функции в точке .
(по условию).
Подставим эти значения в уравнение касательной:
.
Ответ:
4. Написать уравнение касательной к кривой , проходящей через точку
Сначала проверим, не является ли точка точкой касания. Если точка является точкой касания, то она принадлежит графику функции, и её координаты должны удовлетворять уравнению функции. Подставим координаты точки в уравнение функции.
. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и не является точкой касания.
Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания
.Найдем значение .
Пусть — точка касания. Точка принадлежит касательной к графику функции . Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:
Если мы подставим координаты этой точки в уравнение касательной, то получим верное равенство:
.
Значение функции в точке равно .
Найдем значение производной функции в точке .
Сначала найдем производную функции . Это сложная функция.
Производная в точке равна .
Подставим выражения для и в уравнение касательной. Получим уравнение относительно :
Решим это уравнение.
Сократим числитель и знаменатель дроби на 2:
Приведем правую часть уравнения к общему знаменателю. Получим:
Упростим числитель дроби и умножим обе части на — это выражение строго больше нуля.
Получим уравнение
Это иррациональное уравнение.
Решим его. Для этого возведем обе части в квадрат и перейдем к системе.
Решим первое уравнение.
Решим квадратное уравнение, получим
или
Второй корень не удовлетворяет условию , следовательно, у нас только одна точка касания и её абсцисса равна .
Напишем уравнение касательной к кривой в точке . Для этого подставим значение в уравнение — мы его уже записывали.
Получим:
Ответ:
И.В. Фельдман, репетитор по математике.
Итоговый урок по теме «Уравнение касательной» – Документ 1 – УчМет
Ковалева Елена Ивановна
Учитель 1 категории
МБОУ СОШ№5 г.Рославль, Смоленская область
Учебник Алгебра и начала анализа. 10кл. В 2 ч. (профильный уровень) Мордкович А.Г., Семенов П.В.
ПЛАН-КОНСПЕК УРОКА
Итоговый урок
по теме «Уравнение касательной»
10 класс
Цель урока:
систематизировать и обобщить сведения, полученные учащимися на предыдущем уроке;
расширить представления учащихся о теме;
дополнить и обобщить представления учащихся о применении данной темы в жизни;
познакомить с историей данного вопроса.

9. Задачи:
— обучающие: научиться распознавать сложные функции, знать правила дифференцирования, уметь применять формулу производной сложной функции при решении задач; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером.
-развивающие развивать познавательные интересы через применение информационных технологий.
-воспитательные воспитывать адаптивность к современным условиям обучения.
Тип урока урок закрепления изучаемого материала и выработки практических умений и навыков
Формы работы учащихся самостоятельная, индивидуальная, фронтальная работа.
Необходимое техническое
оборудование компьютер, проектор,
экран, презентация для сопровождения
занятия, раздаточный материал для
учащихся.
I. Организационный момент (0.5 мин.).
II. Постановка целей урока. Мотивация учащихся ( 2 мин). (слайд 1)
III. Обобщение знаний учащихся по теме «Производная. Уравнение касательной»(15 мин)(слайд 2)
Учитель приветствует учащихся и объявляет цель урока и план, используя презентационное сопровождение. Зачитывается эпиграф к уроку.
Учитель. Сегодня на уроке мы обобщим и закрепим идею геометрического смысла производной, сформируем начальное представление о приложениях производной в математике и истории их развития, «откроем» зависимость между свойствами монотонности функции, экстремумами и значениями производной; эпиграфом к уроку служат слова французского философа-материалиста Дени Дидро (1713 – 1784) – современника Декарта, Лейбница, личного библиотекаря Екатерины Великой.
«Начинать исследования можно
по-разному… Все равно начало почти
всегда оказывается весьма несовершенной,
нередко безуспешной попыткой. Есть
истины, как страны, наиболее удобный
путь, к которым становится известным
лишь после того, как мы испробуем все
пути. Кому-то приходится, рискуя собой,
сходить с проторенной дороги, чтобы
указать другим правильный путь… На
пути к истине мы почти всегда обречены,
совершать ошибки» (Дени Дидро)
Есть
истины, как страны, наиболее удобный
путь, к которым становится известным
лишь после того, как мы испробуем все
пути. Кому-то приходится, рискуя собой,
сходить с проторенной дороги, чтобы
указать другим правильный путь… На
пути к истине мы почти всегда обречены,
совершать ошибки» (Дени Дидро)
Сегодня мы закрепим материал на тему «Уравнение касательной» решением ключевых или опорных задач, проверим усвоение техники нахождения производной и исследуем связь уравнения касательной с исследованием свойств графика функции , что в дальнейшем нам даст аппарат для построения практически графика любой функции и нахождения ее свойств. Приведет к решению задач на оптимизацию, те нахождения наибольшего и наименьшего значения некоторого конкретного тела, …
Итак, для проверки техники вычисления производной приглашаются учащиеся к компьютерам ( тесты на два варианта)
На местах ребята обсуждают предложенные незавершенные предложения ( слайды 3-4)
1. В чем состоит геометрический
смысл производной?
В чем состоит геометрический
смысл производной?
2.В любой ли точке можно построить касательную?
3.Какая функция называется дифференцируемой в точке?
4.Касательная наклонена к под тупым углом к положительному направлению оси Ох ….
5.Кастельная наклонена под острым углом к оси ох…
6.Касательная наклонена под прямым углом к положительному направлению оси Ох…
7.Касательная параллельна оси Ох, следовательно…
8. Что называется секущей для графика функции y=f(x)?
9. Какая прямая называется касательной к графику функции?
10. Какая из отмеченных точек является точкой касания?
11. Записать уравнение касательной к графику функции в заданной точке в общем виде. 12. Чему равен угол наклона касательной к графику функции в заданной точке? 6. Как найти угловой коэффициент касательной?
13. Известно, что угловой коэффициент
касательной к графику функции в точке
с абсциссой хо, равен 0,6. Чему равно
значение производной в этой точке?
Известно, что угловой коэффициент
касательной к графику функции в точке
с абсциссой хо, равен 0,6. Чему равно
значение производной в этой точке?
14. Касательная к графику функции f(x) в точке с абсциссой хо образует с положительным направлением оси ох угол 45о. Найти f/(xo).
Затем обсуждаем решение ключевых задач. (слайд 5)
Задание из предложенных ключевых задач составить свою задачу.
после обсуждения, решенных у доски задач , учащимся предлагается составить алгоритм решения из ключевых задач.
Учитель. Математический анализ,
ядро которого составляют дифференциальное
и интегральное исчисления, — самая тонкая
область всей математики. Раздел
математики, в котором изучаются
производные и их применения к исследованию
функций, называется дифференциальным
исчислением, а раздел математики, в
котором изучается операция интегрирования
функции, то есть восстановления функции
по её производной, называется интегральным
исчислением.
Немного истории ( небольшое сообщение ученицы) (слайды 6-10)
Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце XVII столетия.
Большой вклад в развитие дифференциального исчисления внесли:
Архимед, который задолго до этого решил задачу на построение касательной к спирали, сумел найти максимум функции f(x) = х2 (а — х),
Пьер Ферма (1601 -1665), математическое определение производной, которого было принято всеми математиками, успешно применявшими в своём методе нахождения экстремумов многочленов задачи о построениях касательных к кривым,
Готфрид Вильгельм Лейбниц
(1646 -1716), который установил геометрический
смысл производной, как тангенс угла
наклона касательной. «Штрихи к портрету»
Готфрида Лейбница : в своей работе
«Новый метод максимумов и минимумов»,
используя геометрическое истолкование,
он кратко разъясняет признаки возрастания
и убывания, максимума
и минимума, выпуклости
и вогнутости (следовательно, и
достаточные условия экстремума
для простейшего случая), а также точки
перегиба. Его знаменитая фраза: «Без
настоящих единиц не может быть и
множества». С ним связаны имена
выдающихся личностей, термины и понятия:
Эпоха Просвещения, Петр I,
Россия, Ньютон, рококо, арифмометр,
кратер на Луне, подводная лодка,
«Философский век». Подумайте над этим
дома.
Его знаменитая фраза: «Без
настоящих единиц не может быть и
множества». С ним связаны имена
выдающихся личностей, термины и понятия:
Эпоха Просвещения, Петр I,
Россия, Ньютон, рококо, арифмометр,
кратер на Луне, подводная лодка,
«Философский век». Подумайте над этим
дома.
V I. Решение задач с практическим содержанием ( слайд 11)
Учитель . Обсуждая успехи своего ученика, учитель математики так отозвался о нем: «Он очень мало знает, но у него положительная производная». Все поняли, что хотел сказать учитель: скорость приращения знаний у ученика положительна, а это есть залог того, что его знания возрастут. Подумайте, как вы могли бы охарактеризовать три кривые роста знаний.
Ответ:I -ого знания не растут т.к.
производная в каждой точке прямой равна
нулю, знания II-го растут быстрее, чем
III-го т.к. угол наклона касательных будет
больше, а следовательно и больше
производная, потому что тангенс функция
возрастающая. (слайд 10-анимированный ,
в музыкальном сопровождении)
(слайд 10-анимированный ,
в музыкальном сопровождении)
У вас на столах график некоторой функции, проведите в указанных точках схематично касательные и охарактеризуйте данную функцию у учетом изученного в 10 и 9-ом классах.
А теперь послушайте музыку, которая сейчас помогала исследованию В чем связь? ( слайд12) Почему именно музыку и график функции мы сегодня связываем?
Не всякую музыку можно слушать легко, для восприятия необходимо произвести усилия, вслушаться , представить действие , проникнуться настроением, поймать мысль композитора.
«Здесь мало увидеть,
Здесь нужно всмотреться,
Здесь мало услышать,
Здесь вслушаться нужно,» Н.Рыленков «Все в тающей дымке»
А может быть и с графиком , его надо не только увидеть, но в него надо всмотреться, почувствовать всю гармонию мелодии графика.
Такую мелодию нам предложит
Семченкова Настя( на гитаре попыталась
проиграть мелодию, повторяющую
предложенный график).
А теперь попробуйте сами. Звучит вальс из балета «Лебединое озеро»
П.И.Чайковского.
Учитель. Ребята, а зачем нужно изучать данную тему.
Выберем ответы из левого столбца:
|
|
Нужна ли производная для будущей профессии?
Российский математик 19века
Панфутий Львович Чебышев говорил, что
«особенную важность имеют те методы
науки, которые позволяют решать задачу,
общую для всей практической деятельности
человека, например, как располагать
своими средствами для достижения
наибольшей выгоды».
С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:
Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.
Вам предложены задачи из жизни, необходимо применить для решения свойства касательной.
1.Профиль моста имеет форму параболы с высотой центральной части 10 м и длиной основания 120м. Какой должен быть наклон насыпи на концах моста? (слайд13-анимированный –этапы рассуждений)
2.Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м. Из точки Р, расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е(илиА). Какую
высоту h нужно придать
центральной части теплицы , если
желательно, чтобы струя воды( она имеет
форму параболы с вершиной в точке
Р) не достигла крыши теплицы?
Из точки Р, расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е(илиА). Какую
высоту h нужно придать
центральной части теплицы , если
желательно, чтобы струя воды( она имеет
форму параболы с вершиной в точке
Р) не достигла крыши теплицы?
Во многих приложениях встречается
понятие касания кривых между собой.
Кривые называются касающимися ,если
они имеют в этой точке общую касательную.
3.Каково необходимое и достаточное условие двух функций у =f(x) и y=g(x) касаются друг друга в точке х0
4.Покажите, что кривые у=4х2+2х-8 и у=-х3-х+10 касаются в точке А(3;34). Будут ли они касаться в точке В(2;-4)
5. При каких соотношениях парабола ах2+вх+с-0 касается оси Ох?
6. Найдите те значения х, при которых касательные в соответствующих точках параллельны между собой. При каком значении а кривые будут касаться друг друга?
Вам было предложено дома решить не менее творческую задачу: составления алгоритма решения нестандартной задачи , по теме «Уравнение касательной»
Обсуждаем данные алгоритмы.
Как вы уже заметили, что в данных алгоритмах повторяющиеся блоки, перечислите их: составление уравнения касательной в точке; нахождения точки касания по углу наклона касательной к положительному направлению оси Ох, по известному угловому коэффициенту, который может быть известен по условию параллельности прямых ,описанию условия нахождения точек касания
А теперь перейдем к выполнению
практической работы , при выполнении
которой вы должны применить все на
практике. (Приложение1)
(Приложение1)
V. Постановка дифференцированного домашнего задания
Учитель раздает карточки с вариантами заданий (4 варианта) , которые содержат обязательную и необязательную части домашнего задания, делает соответствующие пояснения о том, что результаты будут необходимы на следующем уроке.
VI. Итог урока.
Учитель предлагает обобщить учащимся свои исследования, демонстрирует на слайдах результаты подведения итогов и дальнейший план изучения темы. На экране непрерывно идут титрами новые математические понятия: необходимое условие, достаточное условие, необходимое и достаточное условие.
Учащиеся высказывают свое мнение, подводят общий итог исследованию
Список используемой литературы
Алгебра и начала анализа. 10 класс. В 2 ч. Ч.1. Учебник (профильный уровень) / А.
 Г. Мордкович, П. В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.
Г. Мордкович, П. В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений
/А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.; Под ред. А.Н.Колмогорова-
10-е изд.- М..: Просвещение,2000. – стр. 160-166Единый государственный экзамен: Математика: Контрол. измерит. материалы
/Л.О.Денищева, Е.М.Бойченко, Ю.А.Глазков и.др.; М-во образования Рос.
Федерации.- М.: Просвещение, 2003.Производная и её применение: Дидакт. матер, по курсу алгебры и начал анализа
для 10-11 кл.ср.шк./Под ред. М.И.Башмакова — СПб, Свет, 1995.Клайн М. Математика. Утрата определённости: Пер. с англ./ Под ред. С предисл. И
примеч. И.М.Яглома.- М.: Мир, 1984.Степанова М.В. Учебно-исследовательская деятельность школьников в профильном обучении: учебно-методическое пособие для учителя/ Под ред.
 А.П.Тряпининой. –
СПб.: КАРО, 2005.
А.П.Тряпининой. –
СПб.: КАРО, 2005.Маркова В. Что такое исследовательская деятельность школьников / Математика (приложение к 1 сентября), №12, 2007.
Интернет – источники
Музыка «Балет «Лебединое озеро» — Вальс A-dur, акт 1» — (Пётр Ильич Чайковский)http://www.rusmusic.su/instrumental.php
Дени Дидро
http://books.atheism.ru/gallery/Diderot/
Екатерина Великая
http://mail.spb.fio.ru/archive/group15/c3wu3/pagehistory1.htm
Лейбниц
http://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86%2C_%D0%93%D0%BE%D1%82%D1%84%D1%80%D0%B8%D0%B4_%D0%92%D0%B8%D0%BB%D1%8C%D0%B3%D0%B5%D0%BB%D1%8C%D0%BC
Ньютон
http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%2C_%D0%98%D1%81%D0%B0%D0%B0%D0%BA
Архимед
http://ru. wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4
wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4
Лагранж
http://ru.wikipedia.org/wiki/%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6%2C_%D0%96%D0%BE%D0%B7%D0%B5%D1%84_%D0%9B%D1%83%D0%B8
Ферма
http://ru.wikipedia.org/wiki/%D0%A4%D0%B5%D1%80%D0%BC%D0%B0%2C_%D0%9F%D1%8C%D0%B5%D1%80
Ньютон
http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%2C_%D0%98%D1%81%D0%B0%D0%B0%D0%BA
Приложения к плану-конспекту урока
Итоговый урок по теме «Уравнение касательной»
Приложение 1
Геометрическое приложение производной
1.Профиль моста имеет форму параболы с высотой центральной части 10 м и длиной основания 120м. Какой должен быть наклон насыпи на концах моста?
2. Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м.
Из точки Р , расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е (или А ). Какую
высоту h нужно придать
центральной части теплицы, если
желательно, чтобы струя воды ( она имеет
форму параболы с вершиной в точке Р) не
достигла крыши теплицы?
Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м.
Из точки Р , расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е (или А ). Какую
высоту h нужно придать
центральной части теплицы, если
желательно, чтобы струя воды ( она имеет
форму параболы с вершиной в точке Р) не
достигла крыши теплицы?
C
Р
В D
А Е
Во многих приложениях встречается понятие касания кривых между собой. Кривые называются касающимися , если они имеют в этой точке общую касательную.
3.Каково необходимое и достаточное условие двух функций у =f(x) и y=g(x) касаются друг друга в точке х0
4. Покажите, что кривые у=4х2+2х-8
и у=-х3-х+10 касаются в точке А
(3;34). Будут ли они касаться в точке В
(2;-4)
Покажите, что кривые у=4х2+2х-8
и у=-х3-х+10 касаются в точке А
(3;34). Будут ли они касаться в точке В
(2;-4)
5. При каких соотношениях парабола ах2+вх+с-0 касается оси О х?
Приложение 2
Вариант 2 |
А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0 |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5.3Угловой
коэффициент касательной, проведенной
к параболе A) y = 4x — 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x — 5 E) y = 4x — 9 |
А5.4 В какой точке касательная, проведенная к графику функции y = x — 2x + 1, параллельна
прямой y = -4(x + 1)? |
А5.5.В каких точках касательная к графику функции образует с осью Ох угол в 450? |
А5.6. Найти длину отрезка касательной, заключенного между осями координат к кривой , проведенной в точке с абсциссой х=108 |
А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
А5. |
Вариант 3 |
А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0 |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5.3 Угловой коэффициент касательной,
проведенной к графику функции y =
,в точке (x0, y0) равен
.
Найдите x0, y0. |
А5.4.В каких точках касательная к графику функции образует с осью Ох угол в 450? |
А5. параллельна прямой y = 6x + 1 ? A) -2 и 3 B) 1 и 3 C) -2 и 1 D) 2 и -1 E) -1 и 3 |
А5.6.В точке А(5;0) проведена касательная к графику функции .Найти длину отрезка касательной, заключенного между осями координат. |
А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
А5.8. В какой точке нужно провести касательную к графику функции , чтобы она пересекла ось ординат в точке (0;6) ? |
Вариант 4 |
А5. |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5.3. Угловой коэффициент
касательной, проведенной к параболе A) y = 4x — 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x — 5 E) y = 4x — 9 |
А5.4. Какая из прямых параллельна касательной
к кривой y = 4 – x
в точке x0 = 2? |
А5. |
А5.6. Найти длину отрезка касательной, заключенного между осями координат к кривой , проведенной в точке с абсциссой х=108 |
А5.7.Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
А5.8.Касательные, проведенные к графику функции в точках с абсциссами х1 и х2 параллельны. Известно, что х1 =. Найдите отношение |
Приложение 3
Практическая тетрадь по теме «Касательная к графику функции»
ПРАКТИЧЕСКАЯ ТЕТРАДЬ
по теме «Касательная к графику функции»
Пояснительная записка:
Практическая тетрадь «Касательная к графику функции» предназначена в первую очередь для самоконтроля учащихся усвоения ЗУН по вышеуказанной теме. Учителя могут использовать данный материал при подготовке учащихся средней школы к итоговой аттестации по алгебре и началам анализа.
Учителя могут использовать данный материал при подготовке учащихся средней школы к итоговой аттестации по алгебре и началам анализа.
Тема: КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
СПРАВОЧНЫЙ МАТЕРИАЛ
Пусть функция f дифференцируема в точке х0.Тогда существует касательная к графику функции f в точке (х0,у0),где у0= f(x0),уравнение которой имеет вид:
у=f(x0)+f ‘(x0)(x-x0).
Геометрический смысл производной
Значение производной состоит в том,что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.
f‘((x)== tgα
Механический смысл производной скорости движения.
Пусть точка движется по закону .
Тогда ; ,
где s — путь, пройденный точкой; V — скорость точки; а — ускорение точки.
УПРАЖНЕНИЯ С РЕШЕНИЯМИ
Пример 1. Составьте уравнение касательной к графику функции в точке
Решение:
1) — уравнение искомой касательной;
2) ;
3) ;
4) ;
5) Подставляем значения , и в уравнение касательной: или ,
Пример 2. Составьте уравнение касательной к гиперболе в точке с абциссой
Решение:
1) ;
2) ;
3) ;
4) ;
5) ;
Пример 3. Тело движется прямолинейно по закону , где измеряется в метрах, время — в секундах. Найдите скорость движения тела в момент времени
Найдите скорость движения тела в момент времени
Решение:
,
Пример 4. Тело движется прямолинейно по закону , где измеряется в метрах, время — в секундах. Найдите ускорение движения тела в момент времени
Решение:
Функция есть закон прямолинейного движения. Мгновенная скорость этого движения равна производной Мгновенная скорость есть функция от времени. Ускорение движения есть скорость изменения скорости, поэтому ускорение движения в момент времени равно производной . Таким образом, ускорение движения в момент времени равно: , т.е. равно производной от производной. Эту производную называют второй производной от функции и обозначают Поэтому ускорение движения равно второй производной
Итак, = ; ; ;
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
1. Составьте уравнение касательной к графику данной функции f(x) в указанной точке М:
; ,, .
Ответ:.
2. Точка движется по закону . Найдите зависимость скорости движения от времени. Определите мгновенную скорость в момент времени .
Ответ:.
3. Найдите угол между касательной к графику функции в точке и осью . Ответ: .
4. Найдите уравнение касательной к графику функции в точке с абсциссой .
Ответ:.
5. Найдите угол, образованный касательной к кривой в точке с положительным направлением оси абсцисс.
Ответ: 1350.
6. Точка движется прямолинейно по закону
Найдите зависимость ускорения движения от времени, если .
Ответ: .
7. Найдите уравнение касательной к графику функции в точке с абсциссой 2.
Ответ: .
8. Тело массой 10 кг движется прямолинейно по закону . Найдите кинетическую энергию тела через 4с после начала движения.
Ответ: 3125 Дж.
ТЕСТ №1
1. Составьте уравнение касательной к графику функции у=3х2+6х+1 в
точке пересечения этого графика с осью ординат.
А) у=-6х+1; В) у=х+6; С) у=6х+1; D) у=6х; Е) у=6х-1.
2. Найти тангенс угла наклона касательной к графику функции
f(x)=2х3-5х в точке М(2;6)
А) tg α=13; В) tgα=19; С) tgα=17; D) tgα=29; Е) tgα=8.
3. Скорость движения материальной точки по прямой изменяется по закону
V(t)=4t+1/t. Наибольшее значение скорости за время 0,25 ≤ t ≤1 равно
А) 5; В) 4; С) 3; D) 7; Е) 0.
4. Какой угол образует с направлением оси Ох касательная к графику
Какой угол образует с направлением оси Ох касательная к графику
функции f(x)=(1-х)3, проведенная в точке х=3?
А) острый; В) 300; С) прямой; D) тупой; Е) 00.
5. Точка движется прямолинейно по закону .Найти значения скорости в момент времени .
А) 202; В) 198; С) 98; D) 104; Е) 128.
6. К графику функции f(x)=5х3+9х-27в точке с абсциссой х=0 проведена
касательная. Найдите абсциссу точки пересечения касательной с осью Ох.
А) 3; В) 1; С) 4; D) 2; Е) -2.
7. Точка движется прямолинейно по закону .В какой момент времени скорость точки окажется равной нулю.
А) 9 В) 4 С) 3 D) 8 Е) 6.
8.Дана функция .Составьте уравнение касательной к графику функции в точке
А) ; В) ; С);
D) Е)
9. Точка движется по координатной прямой по закону S(t)=-t2+10t-7. Найдите S(3).
Точка движется по координатной прямой по закону S(t)=-t2+10t-7. Найдите S(3).
А) 19; В) 14; С) 4; D) 46; Е) -5.
10. Найти угловой коэффициент прямой, проходящей через точки А(1;-1) и В(2;3).
А) ; В) -; С) -4; D) 1; Е) 4.
ТЕСТ №2
1. Какой угол с осью Ох образует касательная к графику функции в точке с абсциссой ?
А) ; В); С); D); Е).
2. Какой угол с осью Ох образует касательная к графику функции в точке с абсциссой ?
А); В) ; С) ; D) ; Е).
3. Напишите уравнение касательной к графику функции в точке .
А); В) ; С) ; D) ; Е) .
4. Материальная точка движется по прямой линии по закону . Найдите скорость материальной точки в момент времени .
А) В) С) D) Е)
5. Прямолинейное движение точки задано уравнением .Найти скорость движения точки в момент времени .
Прямолинейное движение точки задано уравнением .Найти скорость движения точки в момент времени .
А)28 В)34 С)25 D)45 Е)18.
6. Точка движется прямолинейно по закону .Найти значения ускорения в момент времени .
А) 48 В) 50 С)32 D)58 Е)74
7. Напишите уравнение касательной к графику функции в точке пересечения графика с осью ординат.
А) В) С) D) Е)
8. Написать уравнение касательной к графику функции в точке с абсциссой .
А) В) С) D) Е)
9. Найдите уравнение касательной к графику функции , которая параллельна прямой, заданной уравнением .
А) В) С) D) Е)
10. При каком значении прямая является касательной к графику функции
А) В) С) D) Е)
ОТВЕТЫ
Тема: КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Тест№1 | С | В | А | D | D | А | С | В | С | Е |
Тест№2 | D | Е | А | С | А | В | В | В | Е | D |
Внеклассный урок — Касательная к графику функции
Касательная к графику функции
Касательная – это прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка (рис. 1).
1).
Другое определение: это предельное положение секущей при Δx→0.
Пояснение: Возьмем прямую, пересекающую кривую в двух точках: А и b (см.рисунок). Это секущая. Будем поворачивать ее по часовой стрелке до тех пор, пока она не обретет только одну общую точку с кривой. Так мы получим касательную.
Строгое определение касательной:
Касательная к графику функции f, дифференцируемой в точке xо, — это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
Угловой коэффициент имеет прямая вида y = kx + b. Коэффициент k и является угловым коэффициентом этой прямой.
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:
Здесь угол α – это угол между прямой y = kx + b и положительным (то есть против часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой (рис.1 и 2).
Он называется углом наклона прямой (рис.1 и 2).
Если угол наклона прямой y = kx + b острый, то угловой коэффициент является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4).
Уравнение касательной к графику функции y = f(x) в точке xо:
|
Алгоритм решения уравнения касательной к графику функции y = f(x):
1. 2. Вычислить производные f ′(x) и f ′(xо). 3. Внести найденные числа xо, f(xо), f ′(xо) в уравнение касательной и решить его. |
Пример: Найдем уравнение касательной к графику функции f(x) = x3 – 2x2 + 1 в точке с абсциссой 2.
Решение.
Следуем алгоритму.
1) Точка касания xо равна 2. Вычислим f(xо):
f(xо) = f(2) = 23 – 2 ∙ 22 + 1 = 8 – 8 + 1 = 1
2) Находим f ′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х2 = 2х, а х3 = 3х2. Значит:
Значит:
f ′(x) = 3х2 – 2 ∙ 2х = 3х2 – 4х.
Теперь, используя полученное значение f ′(x), вычислим f ′(xо):
f ′(xо) = f ′(2) = 3 ∙ 22 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: xо = 2, f(xо) = 1, f ′(xо) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f(xо) + f ′(xо) (x – xо) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ: у = 4х – 7.
6.4 Уравнение касательной к кривой | Дифференциальное исчисление
Нарисуйте график \ (f \) с указанием всех перехватов. {2} — 4x + 3 = 0 \\
(х-3) (х-1) = 0 \\
х = 3 \ текст {или} х = 1 \\
\ text {Форма: «хмуриться»} (a
Найдите уравнения касательных к \ (f \) в точке:
{2} — 4x + 3 = 0 \\
(х-3) (х-1) = 0 \\
х = 3 \ текст {или} х = 1 \\
\ text {Форма: «хмуриться»} (a
Найдите уравнения касательных к \ (f \) в точке:
- \ (y \) — точка пересечения \ (f \).
- поворотный момент \ (f \).
- точка, где \ (x = \ text {4,25} \).
- \ begin {align *} y _ {\ text {int}}: (0; -3) \\ m _ {\ text {касательная}} = f ‘(x) & = -2x + 4 \\ f ‘(0) & = — 2 (0) + 4 \\ \ поэтому m & = 4 \\ \ text {Касательная} y & = 4x + c \\ \ text {Through} (0; -3) \ поэтому y & = 4x-3 \ end {align *}
- \ begin {align *} \ text {Поворотный момент:} (2; 1) \\ m _ {\ text {касательная}} = f ‘(2) & = -2 (2) + 4 \\ & = 0 \\ \ text {Касательное уравнение} y & = 1 \ end {align *}
- \ begin {align *} \ text {If} x & = \ text {4,25} \\ f (\ text {4,25}) & = — \ text {4,25} ^ {2} +4 (\ text {4,25}) — 3 \\ & = — \ text {4,0625} \\ m _ {\ text {касательная}} \ text {at} x & = \ text {4,25} \\ m & = — 2 (\ text {4,25}) + 4 \\ & = — \ текст {4,5} \\ \ text {Касательная} y & = — \ text {4,5} x + c \\ \ text {Сквозь} (\ text {4,25}; — \ text {4,0625}) \\ — \ text {4,0625} & = — \ text {4,5} (\ text {4,25}) + c \\ \ поэтому c & = \ text {15,0625} \\ y & = — \ text {4,5} x + \ text {15,0625} \ end {align *}
Нарисуйте три касательных выше на вашем графике
\ (е \).
Запишите все наблюдения о трех касательные к \ (f \).
Касательная в точке \ (y _ {\ text {int}} \) (синяя линия): градиент положительный, функция возрастает в этой точке.
Касательная в точке поворота (зеленая линия): градиент равен нулю, касательная — горизонтальная линия, параллельная оси \ (x \).
Касательная в точке \ (x = \ text {4,25} \) (фиолетовая линия): градиент
отрицательный, функция в этой точке убывает.
Как найти наклон линии, касательной к кривой — Magoosh Blog
Многие общие вопросы, которые задают на экзаменах по математическому анализу AP, связаны с нахождением уравнения прямой, касательной к кривой в точке. Если мы умеем быстро брать производные от функций, то 90 процентов работы для такого рода задач выполняется. Все остальное сводится к быстрой алгебре.
Первое, что нам нужно сделать, это вернуться к тому, что мы изучили в нашей алгебре: уравнение прямой или y = mx + b , где m — наш наклон, а b — наш y- перехватить.Это должно быть у нас под рукой. Теперь у нас не всегда есть точка пересечения оси y, поэтому часто бывает полезна немного другая форма нашего уравнения линии: y-y1 = m (x-x1), где м, — наш наклон, а x 1 и y 1 — координаты точки. Вопросы, связанные с нахождением уравнения касательной к точке, сводятся к двум частям: нахождение наклона и нахождение точки на прямой.
Давайте возьмем пример
Найдите уравнения касательной прямой к y = x 3 -2x 2 + x-3 в точке x = 1.
Во-первых, какой будет наклон этой линии? Каждый раз, когда нас спрашивают о наклоне, немедленно найдите производную функции. У нас должно получиться y ‘= 3x 2 — 4x + 1. Вычислим эту производную при x = 1, и мы получим 3 (1) 2 -4 (1) +1 = 3-4 + 1 = 0. Наклон м этой функции при x = 1 равен 0 . м = 0 . (Обратите внимание, что для экзамена AP вы также должны иметь возможность использовать производную этой функции аналогичным образом для поиска локальных минимумов и максимумов — мы должны быть в состоянии увидеть, что, поскольку наш наклон равен 0, мы смотрим на линию существующий на локальном минимуме или максимуме).
Во-вторых, давайте найдем набор точек ( x 1 , y 1 ) , которые существуют на линии. На этом этапе мы можем использовать только одно значение x, и это заданное значение x = 1. Чтобы найти значение y, мы подставляем его в исходное уравнение: y = (1) 3 -2 (1) 2 + 1-3 = 1-2 + 1-3 = -3. Следовательно ( x 1 , y 1 ) = (1, -3). Теперь у нас есть точка и угол наклона линии.Это все, что нам нужно, чтобы найти наше уравнение.
На этом этапе мы можем использовать только одно значение x, и это заданное значение x = 1. Чтобы найти значение y, мы подставляем его в исходное уравнение: y = (1) 3 -2 (1) 2 + 1-3 = 1-2 + 1-3 = -3. Следовательно ( x 1 , y 1 ) = (1, -3). Теперь у нас есть точка и угол наклона линии.Это все, что нам нужно, чтобы найти наше уравнение.
Уравнение нашей линии:
y-y1 = m (x-x1)
y — (- 3) = 0 (x-1)
y +3 = 0
y = -3
Здесь у нас есть уравнение с проведенной касательной:
(Вы можете найти локальный максимум этой функции?)
Другой пример уравнения касательной линии
Давайте задайте тот же вопрос, что и выше, но в новой точке: Найдите уравнения касательной прямой к y = x 3 -2x 2 + x-3 в точке x = 2.
Опять же, каков будет наклон этой линии? Во-первых, производная: y ‘= 3x 2 — 4x + 1. Вычислить при x = 2.
Вычислить при x = 2.
3 (2) 2 -4 (2) +1 = 12-8 + 1 = 5. Наклон , m , этой функции при x = 2 составляет 5 ( m = 5) .
Набор точек ( x 1 , y 1 ). Мы можем использовать только x = 2. Подключаем его к нашему исходному уравнению.
y = 2 3 -2 (2) 2 + 2-3 = 8-8 + 2-3 = -1.
( x 1 , y 1 ) = (2, -1).
Уравнение нашей линии:
y-y1 = m (x-x1)
y — (- 1) = 5 (x-2)
y +1 = 5x-10
y = 5x-11
Нахождение наклона касательной линии: обзор
Нахождение уравнения касательной линии к кривой в точке всегда сводится к следующим трем этапам:
- Найдите производную и используйте ее для определения нашего наклона м в заданной точке
- Определите значение y функции при заданном нам значении x.

- Подставьте то, что мы обнаружили, в уравнение прямой.
Освойте эти шаги, и мы сможем найти касательную к любой кривой в любой точке.
Гарантированно улучшите свой результат SAT или ACT. Начните 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep уже сегодня!
Захари — бывший инженер-механик, учитель физики, математики и информатики в средней школе.Он окончил Университет Макгилла в 2011 году и работал в автомобильной промышленности в Детройте, прежде чем перейти к образованию. Он преподает и занимается репетиторством в течение последних пяти лет, но вы также можете найти его за приключениями, чтением, скалолазанием и путешествиями, когда появляется такая возможность.
Просмотреть все сообщения
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
РЕШЕНО: Касательная к графику функции y = f (x) в точке с абсциссой x = a образует с осью x угол \ pi / 3, а в точке с абсциссой x = b угол \ pi / 4, затем значение интеграла \ int_ {a} ^ {b} f ^ {\ prime} (x).
 {\ prime \ prime} (x) будет непрерывным] (a) 0 (b) 1 (c) -1 (d) Ни один из этих
{\ prime \ prime} (x) будет непрерывным] (a) 0 (b) 1 (c) -1 (d) Ни один из этихСтенограмма видео
найти производную от нашей жены. Итак, здесь нам придется использовать наше правило частного. Я когда-нибудь dx. Итак, это первое выражение. Умножение верхнего выражения на производную нижнего выражения. Итак, мы назовем это: «О, понятно. Это будешь ты. Итак, наша прямая производная от верхнего выражения или? Да, производная верхнего выражения — единица.Вы умножаете это на все свое нижнее выражение лица. А затем вы вычитаете это из смещения по нижнему выражению, умноженного на все верхнее выражение по всему нижнему выражению в квадрате. Чтобы упростить, вы получите один минус X в квадрате над его словом. Последний. Правильно? Итак, это ваша производная функция. Затем мы хотим найти касательную для каждого из значений X 012 и 3. Итак, мы собираемся подключить X. И в вашу жизненную функцию, и в вашу производную функцию здесь. Итак, у нас будет почему? Здесь? И я слышал, что я вроде как создал небольшую диаграмму. Итак, как только вы подключитесь и начнете глотать, вы должны понять, что вы умны, равны нулю, от половины до пятой и 3/10. И затем ваши производные, которые вы напрямую подключаете к своим яйцам в эту функцию прямо здесь, фактически дают вам наклон уравнений. Итак, вы получите ноль. Хорошо, один мм один ноль -3 25 И отрицательный — 1000 с. Таким образом, используя это, вы можете фактически вставить свои значения для Y, равного mx плюс B. Чтобы вычислить значение B, потому что у вас есть X. Который является каждым из них, а затем у вас есть свой M, который является каждым из них, и у вас есть Y .Который является каждым из них. Итак, я напишу ваши уравнения прямо здесь. Таким образом, если X равно единице или 012 и трем, вы должны получить свои уравнения, поскольку Y равно X для нуля или половины. А затем 0,12 X плюс 0,6 навсегда и отрицательно. Это должно быть отрицательным и отрицательным 0,08 x плюс 0,54. Так что я знаю, что это немного мелковато. Дай мне посмотреть, смогу ли я в этом боксировать немного лучше.
Итак, как только вы подключитесь и начнете глотать, вы должны понять, что вы умны, равны нулю, от половины до пятой и 3/10. И затем ваши производные, которые вы напрямую подключаете к своим яйцам в эту функцию прямо здесь, фактически дают вам наклон уравнений. Итак, вы получите ноль. Хорошо, один мм один ноль -3 25 И отрицательный — 1000 с. Таким образом, используя это, вы можете фактически вставить свои значения для Y, равного mx плюс B. Чтобы вычислить значение B, потому что у вас есть X. Который является каждым из них, а затем у вас есть свой M, который является каждым из них, и у вас есть Y .Который является каждым из них. Итак, я напишу ваши уравнения прямо здесь. Таким образом, если X равно единице или 012 и трем, вы должны получить свои уравнения, поскольку Y равно X для нуля или половины. А затем 0,12 X плюс 0,6 навсегда и отрицательно. Это должно быть отрицательным и отрицательным 0,08 x плюс 0,54. Так что я знаю, что это немного мелковато. Дай мне посмотреть, смогу ли я в этом боксировать немного лучше. Это ваше Y равно mx плюс B уравнений для всех этих значений X. Я сотру это прямо здесь, чтобы показать вам, как будет выглядеть график. И поскольку это выражение over или X.Выражение в квадрате дает возможность предвосхитить сам график. И на самом деле это будет что-то вроде этой закорючки, потому что позвольте мне показать вам здесь ноль 123, 4. Итак, наш первый — почему равен X. Ноль. Итак, мы знаем, что это прямая линия, верно? И тогда наша единица равна половине, так что мы знаем, что она постоянна. Так что мы поместим это прямо здесь, и тогда у нас будет отрицательный момент: Позвольте мне сделать 1/2 немного выше. И тогда у нас есть — .2. А тут собственно перехват вроде.64. Итак, мы знаем, что это похоже на спуск по этой дороге. А затем у нас есть отрицательное значение 0,8, что означает более пологий уклон. Таким образом, мы можем видеть, как мы пишем что-то в этом роде, а также уходим в негатив.
Это ваше Y равно mx плюс B уравнений для всех этих значений X. Я сотру это прямо здесь, чтобы показать вам, как будет выглядеть график. И поскольку это выражение over или X.Выражение в квадрате дает возможность предвосхитить сам график. И на самом деле это будет что-то вроде этой закорючки, потому что позвольте мне показать вам здесь ноль 123, 4. Итак, наш первый — почему равен X. Ноль. Итак, мы знаем, что это прямая линия, верно? И тогда наша единица равна половине, так что мы знаем, что она постоянна. Так что мы поместим это прямо здесь, и тогда у нас будет отрицательный момент: Позвольте мне сделать 1/2 немного выше. И тогда у нас есть — .2. А тут собственно перехват вроде.64. Итак, мы знаем, что это похоже на спуск по этой дороге. А затем у нас есть отрицательное значение 0,8, что означает более пологий уклон. Таким образом, мы можем видеть, как мы пишем что-то в этом роде, а также уходим в негатив.
4.5 Производные и форма графика — Объем исчисления 1
Цели обучения
- Объясните, как знак первой производной влияет на форму графика функции.

- Укажите первую производную проверку для критических точек.
- Используйте точки вогнутости и перегиба, чтобы объяснить, как знак второй производной влияет на форму графика функции.
- Объясните тест на вогнутость функции на открытом интервале.
- Объясните взаимосвязь между функцией и ее первой и второй производными.
- Укажите критерий второй производной для локальных экстремумов.
Ранее в этой главе мы заявляли, что если функция имеет локальный экстремум в точке, то она должна быть критической точкой. Однако не гарантируется, что функция имеет локальный экстремум в критической точке.Например, имеет критическую точку в, поскольку в точке равен нулю, но в точке нет локального экстремума. Используя результаты из предыдущего раздела, теперь мы можем определить, действительно ли критическая точка функции соответствует локальному экстремальному значению. В этом разделе мы также увидим, как вторая производная предоставляет информацию о форме графика, описывая, изгибается ли график функции вверх или вниз.
Следствие 3 теоремы о среднем значении показало, что если производная функции положительна на интервале, то функция возрастает на протяжении С другой стороны, если производная функции отрицательна на интервале, то функция убывает на протяжении как показано на следующем рисунке.
0. Другими словами, f увеличивается. На рисунке b показана функция, вогнутая, возрастающая от (a, f (a)) до (b, f (b)). В двух точках берется производная, и отмечается, что в обеих точках f ’> 0. Другими словами, f увеличивается. На рисунке c показана функция, вогнутая, убывающая от (a, f (a)) до (b, f (b)). В двух точках берется производная, и отмечается, что в обеих точках f ’<0. Другими словами, f уменьшается. На рисунке d показана функция, выпукло убывающая от (a, f (a)) до (b, f (b)). В двух точках берется производная, и отмечается, что в обеих точках f ’<0.Другими словами, f уменьшается. "> Рисунок 1. Обе функции увеличиваются в интервале В каждой точке производная Обе функции убывают в интервале В каждой точке производная Непрерывная функция имеет локальный максимум в точке тогда и только тогда, когда она переключается с увеличения на уменьшение в точке Аналогично, имеет локальный минимум в том и только в том случае, если переключается с уменьшения на увеличение в точке If является непрерывной функцией на интервале, содержащем и дифференцируемым по за исключением, возможно, единственного способа переключения с увеличения на уменьшение (или наоборот) в точке, если меняет знак при увеличении через If, дифференцируемо единственным способом, который может изменять знак при увеличении через, если, следовательно, для функции, которая является непрерывной в течение интервала, содержащего и дифференцируемого, за исключением, возможно, единственного способа переключения с увеличения на уменьшение (или наоборот) — это if или undefined. Следовательно, чтобы найти локальные экстремумы для функции, мы ищем точки в области определения таких, что или не определено. Напомним, такие точки называются критическими точками
Следовательно, чтобы найти локальные экстремумы для функции, мы ищем точки в области определения таких, что или не определено. Напомним, такие точки называются критическими точками
Обратите внимание, что не обязательно иметь локальные экстремумы в критической точке. Критические точки являются кандидатами только в локальные экстремумы. На (Рисунок) мы показываем, что если непрерывная функция имеет локальный экстремум, он должен возникать в критической точке, но функция может не иметь локального экстремума в критической точке. Мы показываем, что если в критической точке имеется локальный экстремум, то знак переключается как увеличивается через эту точку.
Используя (рисунок), мы суммируем основные результаты, касающиеся локальных экстремумов.
Этот результат известен как тест первой производной .
Мы можем резюмировать тест первой производной как стратегию поиска локальных экстремумов.
Теперь давайте посмотрим, как использовать эту стратегию для поиска всех локальных экстремумов для определенных функций.
Использование теста первой производной для поиска локальных экстремумов
Используйте тест первой производной, чтобы найти расположение всех локальных экстремумов. Используйте графическую утилиту для подтверждения результатов.
Используйте тест первой производной, чтобы найти все локальные экстремумы для
Решение
имеет местный минимум -2 и местный максимум 3.
Использование теста первой производной
Используйте тест первой производной, чтобы найти расположение всех локальных экстремумов. Используйте графическую утилиту для подтверждения результатов.
Используйте тест первой производной, чтобы найти все локальные экстремумы для
Решение
не имеет локальных экстремумов, потому что не меняет знак на
Теперь мы знаем, как определить, где функция увеличивается или уменьшается.Однако есть еще одна проблема, которую следует учитывать в отношении формы графика функции. Если график изгибается, изгибается ли он вверх или вниз? Это понятие называется вогнутостью функции.
Если график изгибается, изгибается ли он вверх или вниз? Это понятие называется вогнутостью функции.
(рисунок) (a) показывает функцию с графиком, который изгибается вверх. По мере увеличения наклон касательной увеличивается. Таким образом, поскольку производная увеличивается с увеличением, является возрастающей функцией. Мы говорим, что эта функция вогнута вверх . (Рисунок) (b) показывает функцию, которая изгибается вниз.По мере увеличения наклон касательной уменьшается. Поскольку производная убывает при увеличении, является убывающей функцией. Мы говорим, что эта функция вогнута вниз на .
В общем, не имея графика функции, как мы можем определить ее вогнутость? По определению функция вогнута вверх, если возрастает. Из следствия 3 мы знаем, что if — дифференцируемая функция, то возрастает, если ее производная. Следовательно, дважды дифференцируемая функция вогнута вверх, когда Аналогично, функция вогнута вниз, если убывает. Мы знаем, что дифференцируемая функция убывает, если ее производная. Следовательно, дважды дифференцируемая функция вогнута вниз, когда Применение этой логики известно как тест на вогнутость .
Мы знаем, что дифференцируемая функция убывает, если ее производная. Следовательно, дважды дифференцируемая функция вогнута вниз, когда Применение этой логики известно как тест на вогнутость .
Мы пришли к выводу, что мы можем определить вогнутость функции, посмотрев на вторую производную от. Кроме того, мы замечаем, что функция может переключать вогнутость ((рисунок)). Однако непрерывная функция может переключать вогнутость только в точке, если или не определено. Следовательно, чтобы определить интервалы, в которых функция вогнута вверх и вогнута вниз, мы ищем те значения, где или не определено.Когда мы определили эти точки, мы разделим область на меньшие интервалы и определим знак для каждого из этих меньших интервалов. Если меняет знак, когда мы проходим через точку, то меняется и вогнутость. Важно помнить, что функция не может изменять вогнутость в какой-то точке, даже если или не определено. Если, однако, вогнутость в какой-то точке меняется и остается непрерывной в точке, мы говорим, что это точка перегиба , из
.
Испытание на вогнутость
Для функции определите все интервалы, где находится вогнутый вверх, и все интервалы, где вогнутый вниз.Перечислите все точки перегиба для использования графической утилиты, чтобы подтвердить свои результаты.
Теперь мы суммируем на (рис.) Информацию, которую первая и вторая производные функции предоставляют о графике, и проиллюстрируем эту информацию на (рис.).
| Знак | Знак | Увеличивается или уменьшается? | Вогнутость |
|---|---|---|---|
| Положительный | Положительно | Увеличение | Вогнутый вверх |
| Положительный | Отрицательный | Увеличение | Вогнутая вниз |
| Отрицательный | Положительно | По убыванию | Вогнутый вверх |
| Отрицательный | Отрицательный | По убыванию | Вогнутая вниз |
Тест первой производной предоставляет аналитический инструмент для поиска локальных экстремумов, но вторая производная также может использоваться для определения экстремальных значений. Иногда использование второй производной может быть более простым методом, чем использование первой производной.
Иногда использование второй производной может быть более простым методом, чем использование первой производной.
Мы знаем, что если у непрерывной функции есть локальные экстремумы, они должны возникать в критической точке. Однако функция не обязательно должна иметь локальные экстремумы в критической точке. Здесь мы исследуем, как можно использовать тест второй производной , чтобы определить, имеет ли функция локальный экстремум в критической точке. Пусть — дважды дифференцируемая функция такая, что и непрерывна на открытом интервале, содержащем Предположим, что поскольку она непрерывна для всех ((рисунок)).Тогда, согласно следствию 3, является убывающей функцией над Поскольку мы заключаем, что для всех, если и если Следовательно, по первому критерию производной, имеет локальный максимум в С другой стороны, предположим, что существует точка такая, что, но С непрерывно над открытый интервал, содержащий затем для всех ((Рисунок)). Тогда по следствию есть возрастающая функция над. Так как мы заключаем, что для всех, если и если Следовательно, по первому критерию производной, имеет локальный минимум на
Так как мы заключаем, что для всех, если и если Следовательно, по первому критерию производной, имеет локальный минимум на
Обратите внимание, что для случая iii.когда тогда может быть локальный максимум, локальный минимум или ни один из них, например, функции и все имеют критические точки в В каждом случае вторая производная равна нулю в точке Однако функция имеет локальный минимум в, тогда как функция имеет локальный минимум максимум при и функция не имеет локального экстремума при
Давайте теперь посмотрим, как использовать второй тест производной, чтобы определить, есть ли локальный максимум или локальный минимум в критической точке, где
Использование теста второй производной
Используйте вторую производную, чтобы найти местоположение всех локальных экстремумов для
Теперь мы разработали инструменты, необходимые для определения того, где функция увеличивается и уменьшается, а также получили понимание основной формы графика.В следующем разделе мы обсудим, что происходит с функцией. На этом этапе у нас есть достаточно инструментов для создания точных графиков большого количества функций.
На этом этапе у нас есть достаточно инструментов для создания точных графиков большого количества функций.
1. If — критическая точка, когда нет локального максимума или минимума в Объяснении.
2. Для функции одновременно точка перегиба и локальный максимум / минимум?
Решение
Это не локальный максимум / минимум, потому что не меняет знак
3. Для функции есть точка перегиба?
4. Может ли точка быть одновременно точкой перегиба и локальным экстремумом дважды дифференцируемой функции?
5. Зачем вам нужна непрерывность для первого производного теста? Придумайте пример.
6. Объясните, должна ли функция вогнутого вниз пересекаться для некоторого значения
.Решение
Ложь; например,
7. Объясните, может ли многочлен степени 2 иметь точку перегиба.
Для следующих упражнений проанализируйте графики и перечислите все интервалы, в которых увеличивается или уменьшается.
9. 10.Решение
Уменьшение для увеличения на
11. 12.Для следующих упражнений проанализируйте графики, затем перечислите все интервалы, где
- увеличивается и уменьшается и
- расположены минимумы и максимумы.
Решение
а. Увеличивается по уменьшению в течение b. Минимум
17.Для следующих упражнений проанализируйте графики и перечислите все точки перегиба и интервалы, которые являются вогнутыми вверх и вогнутыми вниз.
18,Решение
Вогнутость во всех точках без перегиба
19. 20.
Решение
Вогнутость во всех точках без перегиба
21. 22.Для следующих упражнений нарисуйте график, который удовлетворяет заданным спецификациям для области. Функция не обязательно должна быть непрерывной или дифференцируемой.
Решение
Ответы будут отличаться
25. выше локального максимума в локальных минимумах на
26. Существует локальный максимум в локальном минимуме в, и график не вогнутый вверх и не вогнутый вниз.
Решение
Ответы будут отличаться
27. Имеются локальные максимумы на функции — вогнутая для всех, и функция остается положительной для всех
.Для следующих упражнений определите
- интервалов увеличения или уменьшения и
- локальных минимумов и максимумов
29.
Для следующих упражнений определите a. интервалы, где вогнутый вверх или вогнутый вниз, и b. точки перегиба
интервалы, где вогнутый вверх или вогнутый вниз, и b. точки перегиба
30.
Решение
а.Вогнутая вверх для вогнутой вниз для b. Точка перегиба на
Для следующих упражнений определите
- интервалов увеличения или уменьшения,
- локальных минимумов и максимумов
- интервалов, где вогнутая вверх и вогнутая вниз, и
- точки перегиба
31.
32.
33.
34.
35.
37.
Для следующих упражнений определите
- интервалов увеличения или уменьшения,
- локальных минимумов и максимумов
- интервалов, где вогнутая вверх и вогнутая вниз, и
- точек перегиба нарисуйте кривую, затем с помощью калькулятора сравните свой ответ. Если вы не можете определить точный ответ аналитически, воспользуйтесь калькулятором.

38. [Т] свыше
39.[T] более
41. [Т]
42. [Т]
Решение
а. Увеличение для всех, где это определено b. Нет локальных минимумов или максимумов c. Вогнутая вверх для вогнутой вниз на d. В домене
нет точек перегиба44. более
45.
46.
47.
Для следующих упражнений интерпретируйте предложения в терминах
.48. Население растет медленнее. Вот население.
Решение
49. Велосипед ускоряется быстрее, но автомобиль едет быстрее. Здесь позиция велосипеда минус позиция автомобиля.
50. Самолет плавно приземляется. Вот высота самолета.
Решение
51. Цены на акции достигли пика. Вот цена акции.
Цены на акции достигли пика. Вот цена акции.
52. Экономика набирает обороты.Вот такой показатель экономики, как ВВП.
Решение
Для следующих упражнений рассмотрите многочлен третьей степени, который имеет свойства Определить, являются ли следующие утверждения истинными или ложными . Обосновать ответ.
53. для некоторых
54. для некоторых
Решение
Верно, по теореме о среднем значении
55. Абсолютного максимума на
не существует.56. Если имеет три корня, то имеет 1 точку перегиба.
Решение
Верно, изучите производную
57. Если имеет одну точку перегиба, то имеет три действительных корня.
Кривизна и радиус кривизны
Рассмотрим плоскую кривую, заданную уравнением \ (y = f \ left (x \ right). \) Предположим, что касательная линия проведена к кривой в точке \ (M \ left ({x, y} \ right ). \) Касательная образует угол \ (\ alpha \) с горизонтальной осью (Рисунок \ (1 \ text {).} \)
\) Предположим, что касательная линия проведена к кривой в точке \ (M \ left ({x, y} \ right ). \) Касательная образует угол \ (\ alpha \) с горизонтальной осью (Рисунок \ (1 \ text {).} \)
При смещении \ (\ Delta s \) по дуге кривой точка \ (M \) перемещается в точку \ ({M_1}. \) Положение касательной также изменяется: угол наклона касательной к положительному \ (x- \ text {axis} \) в точке \ ({M_1} \) будет \ (\ alpha + \ Delta \ alpha. \) Таким образом, по мере движения точки на расстояние \ (\ Delta s, \) касательная поворачивается на угол \ (\ Delta \ alpha. \) (Предполагается, что угол \ (\ alpha \) увеличивается при вращении против часовой стрелки.)
Абсолютное значение отношения \ (\ frac {{\ Delta \ alpha}} {{\ Delta s}} \) называется средней кривизной дуги \ (M {M_1}. \) В пределе как \ (\ Delta s \ to 0, \) получаем кривизну кривой в точке \ (M: \)
\ [K = \ lim \ limits _ {\ Delta s \ to 0} \ left | {\ frac {{\ Delta \ alpha}} {{\ Delta s}}} \ right |. \]
\]
Из этого определения следует, что кривизна в точке кривой характеризует скорость вращения касательной к кривой в этой точке.2}}} = 1 \] в его вершинах.
Решение.
Очевидно, достаточно найти кривизну эллипса в точках \ (A \ left ({a, 0} \ right) \) и \ (B \ left ({0, b} \ right) \) (Рисунок \ (2 \)), потому что из-за симметрии кривой кривизна в двух противоположных вершинах эллипса будет одинаковой.
Рисунок 2.Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме:
\ [x = a \ cos t, \; \; \; y = b \ sin t, \]
где \ (t \) — параметр.{\ frac {3} {2}}}}} = 2, \; \; R = \ frac {1} {K} = \ frac {1} {2}. \]
Пример 3.
Найдите кривизну и радиус кривизны кривой \ [y = \ cos mx \] в точке максимума.
Решение.
Эта функция достигает максимума в точках \ (x = {\ frac {{2 \ pi n}} {m}}, \; n \ in Z. \) По периодичности кривизна во всех точках максимума равна то же самое, поэтому достаточно рассмотреть только точку \ (x = 0. 2} \ cos mx.{\ frac {3} {2}}}}} = \ frac {2} {{5 \ sqrt 5}}, \; \; \; R \ left ({x = 1} \ right) = \ frac { 1} {K} = \ frac {{5 \ sqrt 5}} {2}. \]
2} \ cos mx.{\ frac {3} {2}}}}} = \ frac {2} {{5 \ sqrt 5}}, \; \; \; R \ left ({x = 1} \ right) = \ frac { 1} {K} = \ frac {{5 \ sqrt 5}} {2}. \]
См. Другие проблемы на странице 2.
Круговые функции
График уравнения x 2 + y 2 = 1 — это круг в прямоугольной системе координат. Этот график называется единичной окружностью , имеет центр в начале координат и радиус 1 единицу. Тригонометрические функции определены так, что их области представляют собой наборы углов , а их диапазоны являются наборами действительных чисел. Круговые функции определены так, что их области представляют собой наборы чисел , которые соответствуют размерам (в радианах) углов аналогичных тригонометрических функций. Диапазоны этих круговых функций, как и их аналогичные тригонометрические функции, представляют собой наборы действительных чисел. Эти функции называются круговыми функциями, потому что меры углов в радианах определяются длинами дуг окружностей. В частности, тригонометрические функции, определенные с помощью единичного круга, ведут непосредственно к этим круговым функциям.
В частности, тригонометрические функции, определенные с помощью единичного круга, ведут непосредственно к этим круговым функциям.
Начните с единичной окружности x 2 + y 2 = 1, показанной на рисунке. Точка A (1,0) расположена на пересечении единичной окружности и оси x . Пусть q — любое действительное число. Начните с точки A и измерьте | q | единиц по единичной окружности против часовой стрелки, если q > 0, и по часовой стрелке, если q <0, заканчиваясь в точке P ( x, y ).Определите синус и косинус q как координаты точки P . Другие круговые функции (тангенс, котангенс, секанс и косеканс) могут быть определены в терминах синуса и косинуса.
Рисунок 1
Обозначение единичной окружности.
Sin q и cos q существуют для каждого действительного числа q , потому что (cos q , sin q ) — это координаты точки P , расположенной на единичной окружности, что соответствует длине дуги из | кв |. Поскольку эта длина дуги может быть положительной (против часовой стрелки) или отрицательной (по часовой стрелке), область каждой из этих круговых функций является набором действительных чисел. Диапазон более ограничен. Косинус и синус — это абсцисса и ордината точки, которая движется по единичной окружности, и они варьируются от -1 до 1. Следовательно, диапазон каждой из этих функций представляет собой набор действительных чисел z , таких что -1 ⩽ z ⩽ 1 (см. Рисунок 2).
Поскольку эта длина дуги может быть положительной (против часовой стрелки) или отрицательной (по часовой стрелке), область каждой из этих круговых функций является набором действительных чисел. Диапазон более ограничен. Косинус и синус — это абсцисса и ордината точки, которая движется по единичной окружности, и они варьируются от -1 до 1. Следовательно, диапазон каждой из этих функций представляет собой набор действительных чисел z , таких что -1 ⩽ z ⩽ 1 (см. Рисунок 2).
Рисунок 2
Диапазон значений триггерных функций.
Пример 1: Какие значения x в области синусоидальной функции между −2π и 2π имеют значение диапазона 1 (рисунок 3)?
Рисунок 3
Чертеж для примера 1.
Диапазон значений sin x равен 1, когда точка P имеет координаты (0, 1). Это происходит, когда x = π / 2 и x = −3π / 2.
Пример 2: Какие значения x в области функции косинуса между −2π и 2π имеют значение диапазона — 1 (рисунок 4)?
Рисунок 4
Рисунок для примера 2.
Диапазон значений cos x равен -1, когда точка P (cos x , sin x ) имеет координаты (-1, 0). Это происходит, когда x = π и x = −π.
Пример 3: Точка P находится на единичной окружности. Длина дуги от точки A (1,0) до точки P составляет q единиц. Каковы значения шести круговых функций q ?
Значения синуса и косинуса следуют из определений и являются координатами точки P .Остальные четыре функции выводятся с помощью синуса и косинуса.
Знак каждой из шести круговых функций (см. Таблицу 1) зависит от длины дуги q . Обратите внимание, что четыре интервала для q непосредственно соответствуют четырем квадрантам для тригонометрических функций.
8.4: Парабола — математика LibreTexts
Знаете ли вы, что олимпийский факел зажигается за несколько месяцев до начала игр? Обрядовый метод зажигания пламени такой же, как и в древности.Церемония проходит в Храме Геры в Олимпии, Греция, и уходит своими корнями в греческую мифологию, отдавая дань уважения Прометею, который украл огонь у Зевса, чтобы раздать его всем людям. Одна из одиннадцати действующих жриц помещает факел в фокус параболического зеркала (рис. \ (\ PageIndex {1} \)), которое фокусирует световые лучи от солнца, чтобы зажечь пламя.
Параболические зеркала (или отражатели) могут улавливать энергию и фокусировать ее в одной точке. О преимуществах этого свойства свидетельствует обширный список параболических объектов, которые мы используем каждый день: спутниковые антенны, подвесные мосты, телескопы, микрофоны, прожекторы и автомобильные фары и многие другие.Параболические отражатели также используются в устройствах альтернативной энергетики, таких как солнечные плиты и водонагреватели, поскольку они недорогие в производстве и не требуют значительного обслуживания.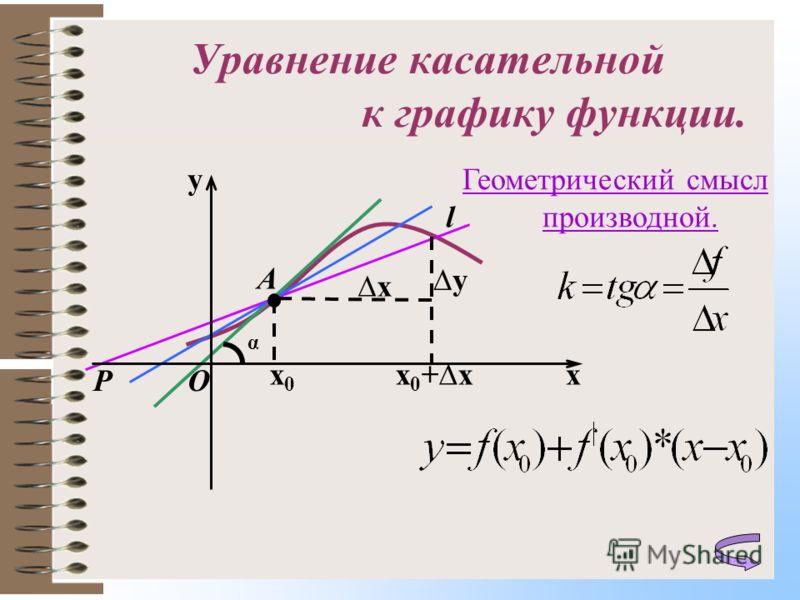 В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
Графические параболы с вершинами в начале координат
Ранее мы видели, что эллипс образуется, когда плоскость пересекает правый круговой конус. Если плоскость параллельна краю конуса, образуется неограниченная кривая.Эта кривая представляет собой параболу (рисунок \ (\ PageIndex {2} \)).
Рисунок \ (\ PageIndex {2} \): ParabolaПодобно эллипсу и гиперболе, парабола также может быть определена набором точек на координатной плоскости. Парабола — это набор всех точек \ ((x, y) \) в плоскости, которые находятся на одинаковом расстоянии от фиксированной линии, называемой направляющей , и фиксированной точкой (фокус ) не на направляющей. .
Ранее мы узнали о вершине параболы и оси симметрии.Теперь мы расширяем обсуждение, чтобы включить другие ключевые особенности параболы (Рисунок \ (\ PageIndex {3} \)). Обратите внимание, что ось симметрии проходит через фокус и вершину и перпендикулярна направляющей. Вершина — это середина между направляющей и фокусом. Отрезок прямой, проходящий через фокус и параллельный направляющей, называется latus rectum . Концы прямой кишки лежат на изгибе. По определению расстояние d от фокуса до любой точки \ (P \) на параболе равно расстоянию от \ (P \) до директрисы.
Обратите внимание, что ось симметрии проходит через фокус и вершину и перпендикулярна направляющей. Вершина — это середина между направляющей и фокусом. Отрезок прямой, проходящий через фокус и параллельный направляющей, называется latus rectum . Концы прямой кишки лежат на изгибе. По определению расстояние d от фокуса до любой точки \ (P \) на параболе равно расстоянию от \ (P \) до директрисы.
Для работы с параболами в координатной плоскости мы рассматриваем два случая: с вершиной в начале координат и с вершиной в точке. кроме происхождения. Начнем с первого.
Рисунок \ (\ PageIndex {4} \) Пусть \ ((x, y) \) будет точкой параболы с вершиной \ ((0,0) \), фокусом \ ((0, p) \), и директрису \ (y = −p \), как показано на рисунке \ (\ PageIndex {4} \). Расстояние d от точки \ ((x, y) \) до точки \ ((x, −p) \) на направляющей — это разность значений y : \ (d = y + p \).2 = 4py \), когда ось y является осью симметрии. 2 = 4py \)
2 = 4py \)
Ключевыми особенностями параболы являются ее вершина, ось симметрии, фокус, директриса и прямая кишка , прямая кишка (рисунок \ (\ PageIndex {5} \)). Получив стандартное уравнение для параболы с центром в начале координат, мы можем легко определить ключевые особенности для построения графика параболы.2 = 4px \), то
- ось симметрии — ось \ (x \), \ (y = 0 \)
- установите \ (4p \) равным коэффициенту \ (x \) в данном уравнении, чтобы найти \ (p \).
 Если \ (p> 0 \), парабола открывается вправо. Если \ (p <0 \), парабола открывается влево.
Если \ (p> 0 \), парабола открывается вправо. Если \ (p <0 \), парабола открывается влево. - используйте \ (p \), чтобы найти координаты фокуса, \ ((p, 0) \)
- используйте \ (p \), чтобы найти уравнение директрисы, \ (x = −p \)
- используйте \ (p \), чтобы найти конечные точки прямой кишки, \ ((p, \ pm 2p) \).2 = 4py \), то
- ось симметрии — ось \ (y \), \ (x = 0 \)
- установите \ (4p \) равным коэффициенту при \ (y \) в данном уравнении, чтобы найти \ (p \). Если \ (p> 0 \), парабола раскрывается. Если \ (p <0 \), парабола открывается вниз.
- используйте \ (p \), чтобы найти координаты фокуса, \ ((0, p) \)
- используйте \ (p \), чтобы найти уравнение директрисы, \ (y = −p \)
- используйте \ (p \), чтобы найти конечные точки прямой кишки, \ ((\ pm 2p, p) \)
 2 = 4 пикселя \). Таким образом, осью симметрии является ось x . Отсюда следует, что:
2 = 4 пикселя \). Таким образом, осью симметрии является ось x . Отсюда следует, что:- \ (24 = 4p \), поэтому \ (p = 6 \). Поскольку \ (p> 0 \), парабола открывается вправо
- координаты фокуса \ ((p, 0) = (6,0) \)
- уравнение директрисы: \ (x = −p = −6 \)
- конечные точки прямой кишки имеют одинаковую координату x в фокусе. Чтобы найти конечные точки, подставьте \ (x = 6 \) в исходное уравнение: \ ((6, \ pm 12) \)
Затем мы рисуем фокус, директрису и широту прямой кишки и рисуем плавную кривую, чтобы сформировать параболу (рисунок \ (\ PageIndex {7} \)).2 = 4py \). Таким образом, ось симметрии — это ось \ (y \). Отсюда следует, что:
- \ (- 6 = 4p \), поэтому \ (p = — \ dfrac {3} {2} \). Поскольку \ (p <0 \), парабола открывается вниз.
- координаты фокуса: \ ((0, p) = (0, — \ dfrac {3} {2}) \)
- уравнение директрисы: \ (y = −p = \ dfrac {3} {2} \)
- конечные точки прямой кишки можно найти, подставив \ (y = \ dfrac {3} {2} \) в исходное уравнение, \ ((\ pm 3, — \ dfrac {3} {2}) \)
Затем мы рисуем фокус, директрису и latus rectum и рисуем плавную кривую, чтобы сформировать параболу. 2 = 8л \). Определите и обозначьте фокус, направляющую и конечные точки прямой кишки latus .
2 = 8л \). Определите и обозначьте фокус, направляющую и конечные точки прямой кишки latus .
- Ответ
- Фокус: \ ((0,2) \)
- Направляющая: \ (y = −2 \)
- Конечные точки прямой кишки: \ ((\ pm 4,2) \).
Графические параболы с вершинами не в начале координат
Как и другие графики, с которыми мы работали, график параболы можно преобразовать.2 = 4p (y − k) \) для парабол, ось симметрии которых параллельна оси \ (y \). Эти стандартные формы представлены ниже вместе с их общими графиками и ключевыми характеристиками.
СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРТЕКСОМ \ ((H, K) \)
Таблица \ (\ PageIndex {2} \) и рисунок \ (\ PageIndex {11} \) суммируют стандартные характеристики парабол с вершиной в точке \ ((h, k) \).
| Ось симметрии | Уравнение | Фокус | Директрикс | Конечные точки прямой мышцы живота |
|---|---|---|---|---|
| \ (y = k \) | \ ({(y − k)} ^ 2 = 4p (x − h) \) | \ ((h + p, k) \) | \ (х = h − p \) | \ ((h + p, k \ pm 2p) \) |
| \ (x = h \) | \ ({(x − h)} ^ 2 = 4p (y − k) \) | \ ((з, к + р) \) | \ (у = k − p \) | \ ((h \ pm 2p, k + p) \) |
 2 = 4p (y − k) \), то:
2 = 4p (y − k) \), то:- используйте данное уравнение для определения \ (h \) и \ (k \) для вершины, \ ((h, k) \)
- используйте значение \ (h \) для определения оси симметрии, \ (x = h \)
- установите \ (4p \) равным коэффициенту при \ ((y − k) \) в данном уравнении, чтобы найти \ (p \).Если \ (p> 0 \), парабола раскрывается. Если \ (p <0 \), парабола открывается вниз.
- используйте \ (h \), \ (k \) и \ (p \), чтобы найти координаты фокуса, \ ((h, k + p) \)
- используйте \ (k \) и \ (p \), чтобы найти уравнение директрисы, \ (y = k − p \)
- используйте \ (h \), \ (k \) и \ (p \), чтобы найти конечные точки прямой кишки, \ ((h \ pm 2p, k + p) \)
 Отсюда следует, что:
Отсюда следует, что:- вершина равна \ ((h, k) = (- 3,1) \)
- ось симметрии \ (y = k = 1 \)
- \ (- 16 = 4p \), поэтому \ (p = −4 \). Поскольку \ (p <0 \), парабола открывается влево.
- координаты фокуса: \ ((h + p, k) = (- 3 + (- 4), 1) = (- 7,1) \)
- уравнение директрисы: \ (x = h − p = −3 — (- 4) = 1 \)
- конечными точками прямой кишки являются \ ((h + p, k \ pm 2p) = (- 3 + (- 4), 1 \ pm 2 (−4)) \) или \ ((- 7, — 7) \) и \ ((- 7,9) \)
Затем мы строим вершину, ось симметрии, фокус, директрису и широту прямой кишки и рисуем плавную кривую, чтобы сформировать параболу (рисунок \ (\ PageIndex {10} \)).2 = 4 (x − 8) \). Определите и обозначьте вершину, ось симметрии, фокус, директрису и конечные точки прямой кишки latus .
- Ответ
- Вершина: \ ((8, −1) \)
- Ось симметрии: \ (y = −1 \)
- Фокус: \ ((9, −1) \)
- Направляющая: \ (x = 7 \)
- Конечные точки прямой кишки latus : \ ((9, −3) \) и \ ((9,1) \).
 2−8x − 28y − 208 = 0 \).2 & = 4⋅7⋅ (y + 8) \ end {align *} \]
2−8x − 28y − 208 = 0 \).2 & = 4⋅7⋅ (y + 8) \ end {align *} \]Отсюда следует, что:
- вершина равна \ ((h, k) = (4, −8) \)
- ось симметрии \ (x = h = 4 \)
- , поскольку \ (p = 7 \), \ (p> 0 \), поэтому парабола открывается
- координаты фокуса: \ ((h, k + p) = (4, −8 + 7) = (4, −1) \)
- уравнение директрисы: \ (y = k − p = −8−7 = −15 \)
- конечными точками прямой кишки являются \ ((h \ pm 2p, k + p) = (4 \ pm 2 (7), — 8 + 7) \) или \ ((- 10, −1) \) и \ ((18, −1) \)
Затем мы строим вершину, ось симметрии, фокус, директрису и широту прямой кишки и рисуем плавную кривую, чтобы сформировать параболу (рисунок \ (\ PageIndex {14} \)).2 = −20 (y − 3) \). Определите и обозначьте вершину, ось симметрии, фокус, директрису и конечные точки прямой кишки latus .
- Ответ
- Вершина: \ ((- 2,3) \)
- Ось симметрии: \ (x = −2 \)
- Фокус: \ ((- 2, −2) \)
- Директриса: \ (y = 8 \)
- Конечные точки прямой кишки latus : \ ((- 12, −2) \) и \ ((8, −2) \).

Решение прикладных задач с использованием парабол
Как мы упоминали в начале раздела, параболы используются для проектирования многих объектов, которые мы используем каждый день, таких как телескопы, подвесные мосты, микрофоны и радарное оборудование.Параболические зеркала, такие как то, что используется для освещения олимпийского факела, обладают уникальным отражающим свойством. Когда лучи света, параллельные оси симметрии параболы, направляются к любой поверхности зеркала, свет отражается прямо в фокус (рисунок \ (\ PageIndex {16} \)). Вот почему олимпийский факел зажигается, когда он находится в фокусе параболического зеркала.
Рисунок \ (\ PageIndex {16} \): Отражающее свойство парабол.Параболические зеркала обладают способностью фокусировать солнечную энергию в одной точке, повышая температуру на сотни градусов за считанные секунды.Таким образом, параболические зеркала используются во многих недорогих, энергоэффективных солнечных изделиях, таких как солнечные плиты, солнечные обогреватели и даже разжигатели огня для путешествий.
 2 = 4py \), где \ (p> 0 \).2 & = 6,8y \ qquad \ text {Substitute} 2,25 \ text {for} x \\ y & \ приблизительно 0,74 \ qquad \ text {Решить для} y \ end {align *} \]
2 = 4py \), где \ (p> 0 \).2 & = 6,8y \ qquad \ text {Substitute} 2,25 \ text {for} x \\ y & \ приблизительно 0,74 \ qquad \ text {Решить для} y \ end {align *} \]Блюдо имеет глубину около 0,74 дюйма.
Упражнение \ (\ PageIndex {6} \)
Солнечные плиты размером с балкон были разработаны для семей, живущих в Индии. Верх тарелки имеет диаметр \ (1600 \) мм. Солнечные лучи отражаются от параболического зеркала в сторону «плиты», которая расположена на расстоянии \ (320 \) мм от основания.
- Найдите уравнение, моделирующее поперечное сечение солнечной плиты.2 = 1280x \)
- Ответ б
Глубина плиты \ (500 \) мм


 Г. Мордкович, П. В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.
Г. Мордкович, П. В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007. А.П.Тряпининой. –
СПб.: КАРО, 2005.
А.П.Тряпининой. –
СПб.: КАРО, 2005. Напишите
уравнение этой касательной.
Напишите
уравнение этой касательной. 8.
8. 5. При каких значениях x касательная
к графику функции y = 2x
+ 3x
— 6x
5. При каких значениях x касательная
к графику функции y = 2x
+ 3x
— 6x  1.Написать
уравнение касательной к графику
функции в точке с абсциссой х0
1.Написать
уравнение касательной к графику
функции в точке с абсциссой х0  5.В каких
точках касательная к графику функции
образует с осью Ох угол в 1350?
5.В каких
точках касательная к графику функции
образует с осью Ох угол в 1350?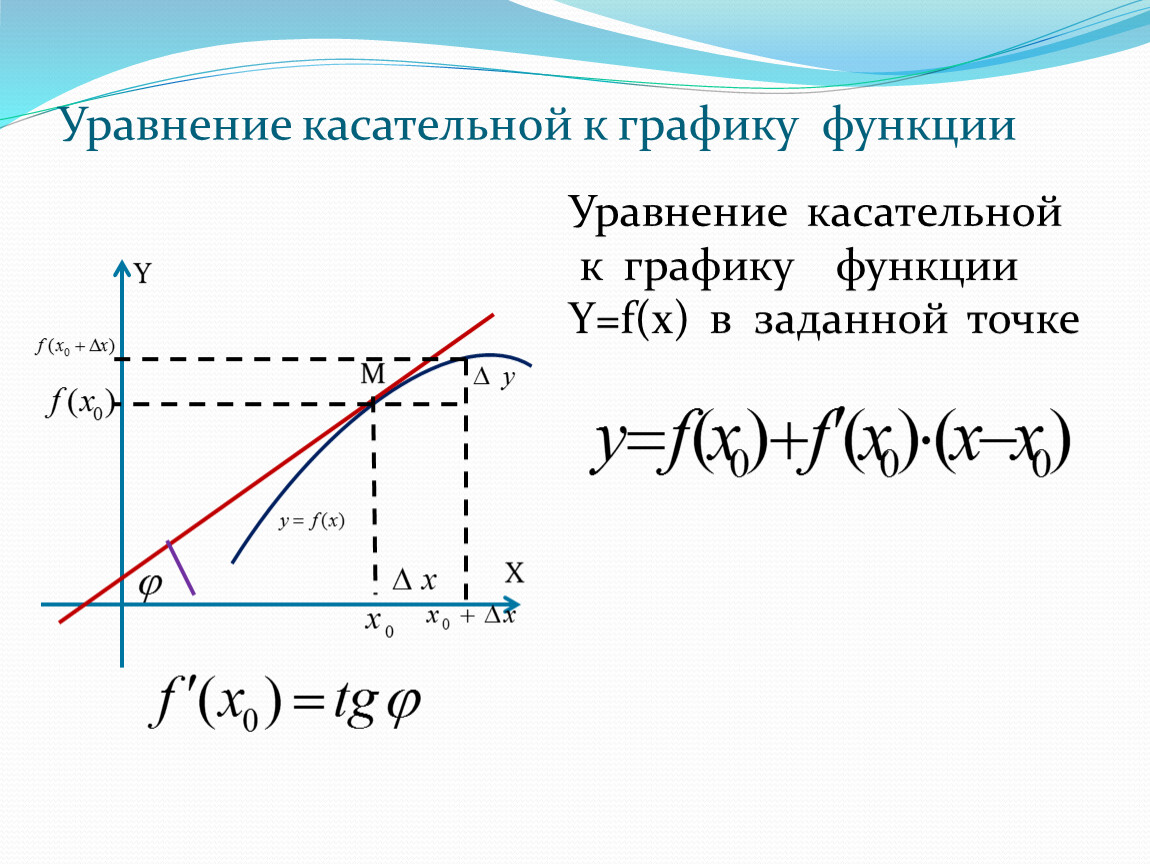 Вычислить f(xо).
Вычислить f(xо).


 Если \ (p> 0 \), парабола открывается вправо. Если \ (p <0 \), парабола открывается влево.
Если \ (p> 0 \), парабола открывается вправо. Если \ (p <0 \), парабола открывается влево. 2−8x − 28y − 208 = 0 \).2 & = 4⋅7⋅ (y + 8) \ end {align *} \]
2−8x − 28y − 208 = 0 \).2 & = 4⋅7⋅ (y + 8) \ end {align *} \]
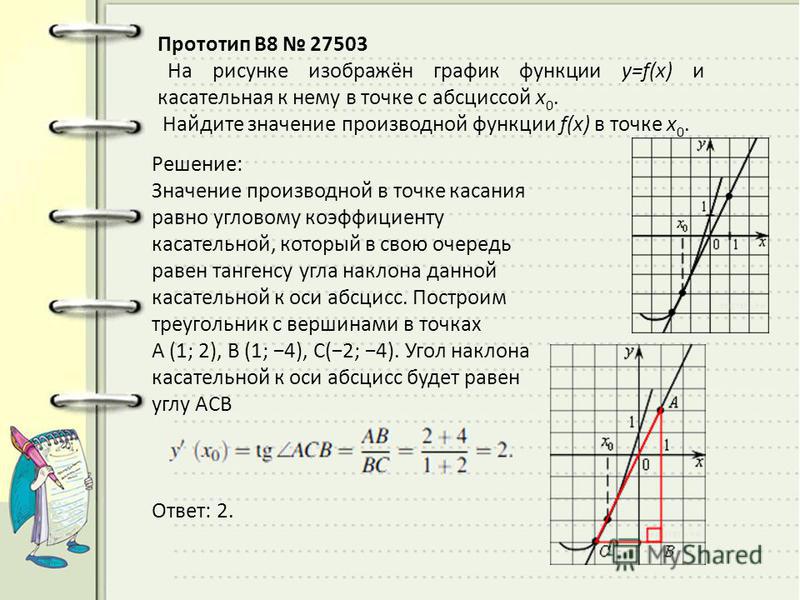 2 = 4py \), где \ (p> 0 \).2 & = 6,8y \ qquad \ text {Substitute} 2,25 \ text {for} x \\ y & \ приблизительно 0,74 \ qquad \ text {Решить для} y \ end {align *} \]
2 = 4py \), где \ (p> 0 \).2 & = 6,8y \ qquad \ text {Substitute} 2,25 \ text {for} x \\ y & \ приблизительно 0,74 \ qquad \ text {Решить для} y \ end {align *} \]