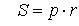Формулы геометрии. Площади фигур. — материалы для подготовки к ЕГЭ по Математике

Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

---

Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.

Ты нашел то, что искал? Поделись с друзьями!

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.

1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в  раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в  раз меньше, чем площадь всего круга.

Ответ: .

Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.

Как найти площадь треугольника — Лайфхакер

Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника

Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.

Зная сторону и высоту

1. Умножьте сторону треугольника на высоту, проведённую к этой стороне.
2. Поделите результат на два.

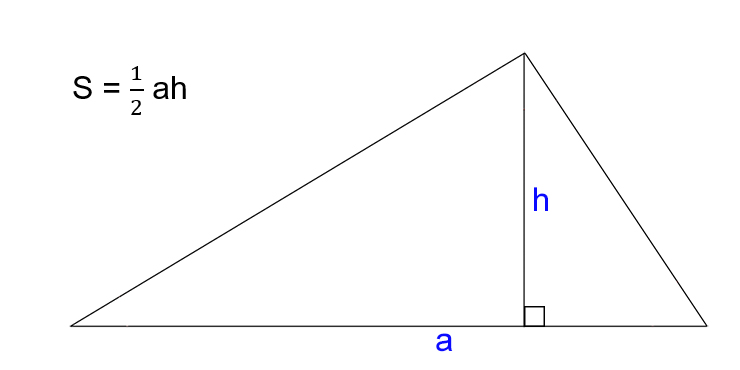
• S — искомая площадь треугольника.
• a — сторона треугольника.
• h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.

Зная две стороны и угол между ними

1. Посчитайте произведение двух известных сторон треугольника.
2. Найдите синус угла между выбранными сторонами.
3. Перемножьте полученные числа.
4. Поделите результат на два.

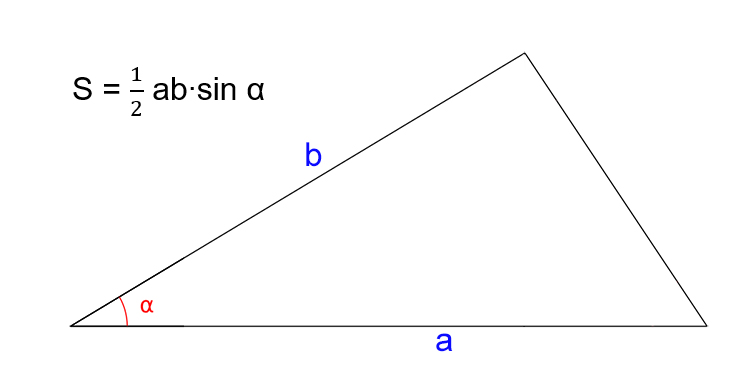
• S — искомая площадь треугольника.
• a и b — стороны треугольника.
• α — угол между сторонами a и b.

Сейчас читают 🔥

Зная три стороны (формула Герона)

1. Посчитайте разности полупериметра треугольника и каждой из его сторон.
2. Найдите произведение полученных чисел.
3. Умножьте результат на полупериметр.
4. Найдите корень из полученного числа.

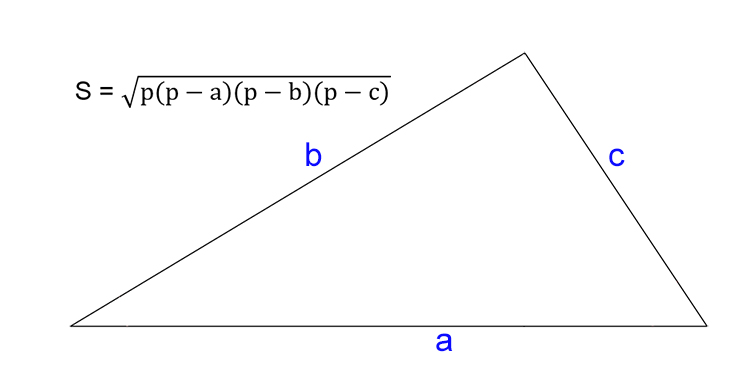
• S — искомая площадь треугольника.
• a, b, c — стороны треугольника.
• p — полупериметр (равен половине от суммы всех сторон треугольника).

Зная три стороны и радиус описанной окружности

1. Найдите произведение всех сторон треугольника.
2. Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.

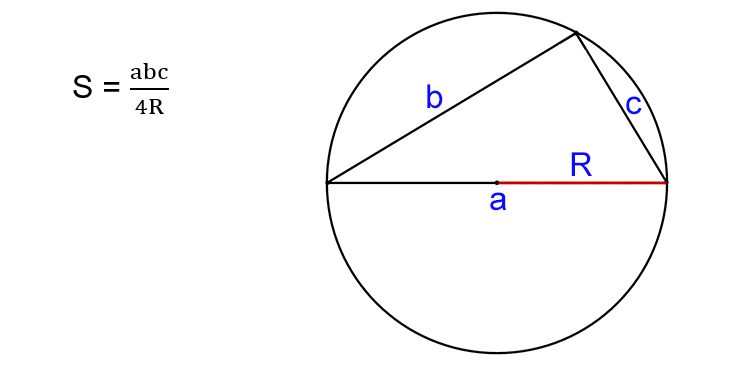
• S — искомая площадь треугольника.
• R — радиус описанной окружности.
• a, b, c — стороны треугольника.

Зная радиус вписанной окружности и полупериметр

Умножьте радиус окружности, вписанной в треугольник, на полупериметр.

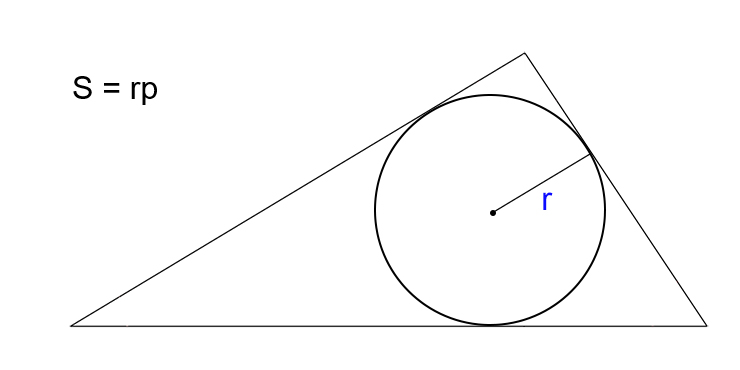
• S — искомая площадь треугольника.
• r — радиус вписанной окружности.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Как найти площадь прямоугольного треугольника

1. Посчитайте произведение катетов треугольника.
2. Поделите результат на два.

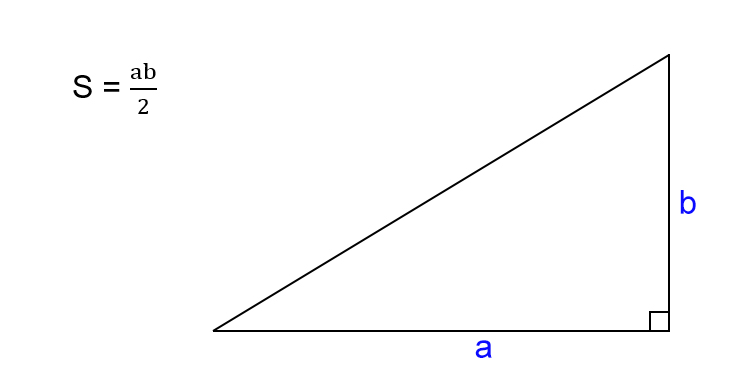
• S — искомая площадь треугольника.
• a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.

Как найти площадь равнобедренного треугольника

1. Умножьте основание на высоту треугольника.
2. Поделите результат на два.

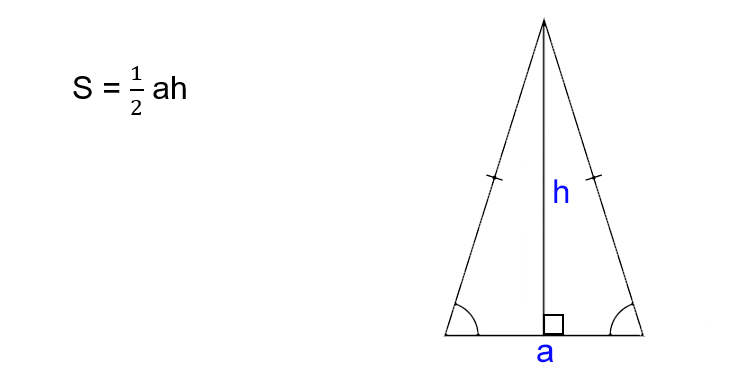
• S — искомая площадь треугольника.
• a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
• h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

Как найти площадь равностороннего треугольника

1. Умножьте квадрат стороны треугольника на корень из трёх.
2. Поделите результат на четыре.

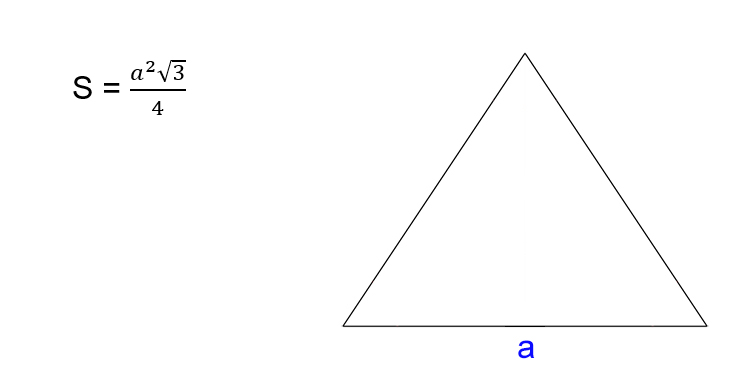
• S — искомая площадь треугольника.
• a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻‍🎓✍🏻

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Формулы для площади треугольника

      Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.

Фигура	Рисунок	Формула площади	Обозначения
Произвольный треугольник		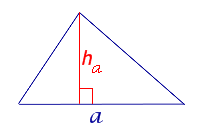Посмотреть вывод формулы	a – любая сторона, ha – высота, опущенная на эту сторону
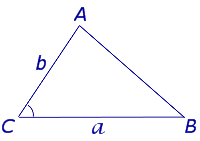		Посмотреть вывод формулы	a и b – две любые стороны, С – угол между ними
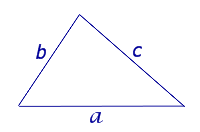		. Посмотреть вывод формулы Герона	a, b, c – стороны, p – полупериметр Формулу называют «Формула Герона»
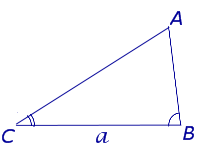		Посмотреть вывод формулы	a – любая сторона, B, С – прилежащие к ней углы
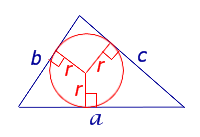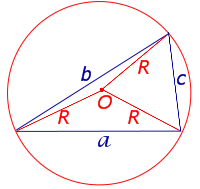		Посмотреть вывод формулы	a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр
		Посмотреть вывод формулы	a, b, c  – стороны, R – радиус описанной окружности
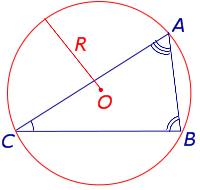		S = 2R2 sin A sin B sin C Посмотреть вывод формулы	A, B, С – углы, R – радиус описанной окружности
Равносторонний (правильный) треугольник		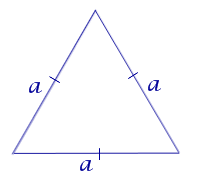Посмотреть вывод формулы	a – сторона
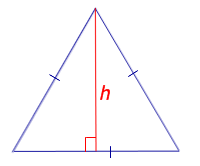		Посмотреть вывод формулы	h – высота
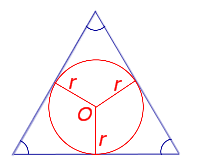		Посмотреть вывод формулы	r – радиус вписанной окружности
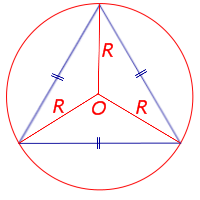		Посмотреть вывод формулы	R – радиус описанной окружности
Прямоугольный треугольник		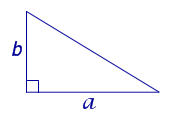Посмотреть вывод формулы	a и b – катеты
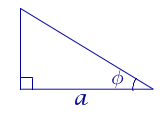		Посмотреть вывод формулы	a – катет, φ – прилежащий острый угол
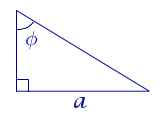		Посмотреть вывод формулы	a – катет, φ – противолежащий острый угол
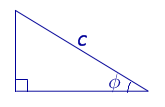		Посмотреть вывод формулы	c – гипотенуза, φ – любой из острых углов

Произвольный треугольник
	где a – любая сторона, ha – высота, опущенная на эту сторону Посмотреть вывод формулы
	где a и b – две любые стороны, С – угол между ними Посмотреть вывод формулы
	. где a, b, c – стороны, p – полупериметр Формулу называют «Формула Герона» Посмотреть вывод формулы Герона
	где a – любая сторона, B, С – прилежащие к ней углы Посмотреть вывод формулы
	где a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр Посмотреть вывод формулы
	где a, b, c  – стороны, R – радиус описанной окружности Посмотреть вывод формулы
	S = 2R2 sin A sin B sin C где A, B, С – углы, R – радиус описанной окружности Посмотреть вывод формулы
Равносторонний (правильный) треугольник
	где a – сторона Посмотреть вывод формулы
	где h – высота Посмотреть вывод формулы
	где r – радиус вписанной окружности Посмотреть вывод формулы
	где R – радиус описанной окружности Посмотреть вывод формулы
Прямоугольный треугольник
	где a и b – катеты Посмотреть вывод формулы
	где a – катет, φ – прилежащий острый угол Посмотреть вывод формулы
	где a – катет, φ – противолежащий острый угол Посмотреть вывод формулы
	где c – гипотенуза, φ – любой из острых углов Посмотреть вывод формулы

Произвольный треугольник

где a – любая сторона, ha – высота, опущенная на эту сторону Посмотреть вывод формулы

где a и b – две любые стороны, С – угол между ними Посмотреть вывод формулы

. где a, b, c – стороны, p – полупериметр Формулу называют «Формула Герона» Посмотреть вывод формулы Герона

где a – любая сторона, B, С – прилежащие к ней углы Посмотреть вывод формулы

где a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр Посмотреть вывод формулы

где a, b, c  – стороны, R – радиус описанной окружности Посмотреть вывод формулы

S = 2R2 sin A sin B sin C где A, B, С – углы, R – радиус описанной окружности Посмотреть вывод формулы

Равносторонний (правильный) треугольник

где a – сторона Посмотреть вывод формулы

где h – высота Посмотреть вывод формулы

где r – радиус вписанной окружности Посмотреть вывод формулы

где R – радиус описанной окружности Посмотреть вывод формулы

Прямоугольный треугольник

где a и b – катеты Посмотреть вывод формулы

где a – катет, φ – прилежащий острый угол Посмотреть вывод формулы

где a – катет, φ – противолежащий острый угол Посмотреть вывод формулы

где c – гипотенуза, φ – любой из острых углов Посмотреть вывод формулы

Вывод формул для площади произвольного треугольника

      Утверждение 1. Площадь треугольника можно найти по формуле

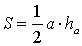
где a – любая сторона треугольника, а h_a – высота, опущенная на эту сторону.

      Доказательство.

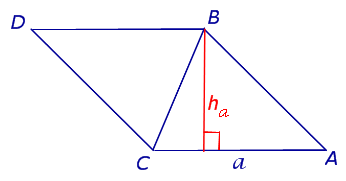
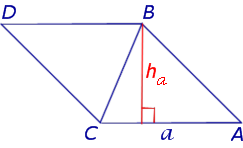
Рис. 1

Достроив треугольник ABC до параллелограммапараллелограмма ABDC (рис. 1), получим

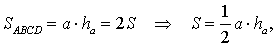
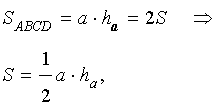
что и требовалось доказать.

      Утверждение 2. Площадь треугольника можно найти по формуле

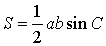
где a и b – две любые стороны треугольника, а С – угол между ними.

      Доказательство.

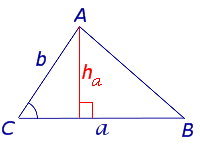
Рис. 2

Поскольку

h_a = b sin C ,

то, в силу утверждения 1, справедлива формула

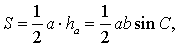
что и требовалось доказать.

      Утверждение 3. Площадь треугольника можно найти по формуле

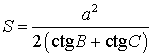
где a – любая сторона треугольника, а B, С – прилежащие к ней углы.

      Замечание. Докажем утверждение 3 в случае остроугольного треугольника. Доказательство в случаях прямоугольного и тупоугольного треугольников требует лишь незначительных изменений, совершить которые мы предоставляем читателю в качестве самостоятельного упражнения.

      Доказательство.

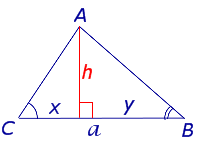
Рис. 3

Поскольку (рис.3)

x = h_actg C ,       y = h_actg B ,

то

a = x + y =
= h_actg C + h_actg B =
= h_a( ctg C + ctg B) .

      Следовательно,

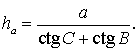
      Поэтому

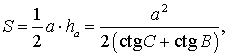
что и требовалось доказать.

      Утверждение 4. Площадь треугольника можно найти по формуле

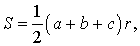
где a, b, c – стороны треугольника, а r – радиус вписанной окружности.

      Доказательство.

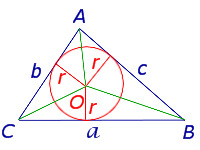
Рис. 4

Соединив центр O вписанной окружности с вершинами треугольника (рис.4), получим

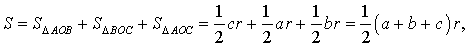
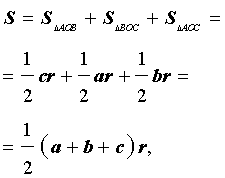
что и требовалось доказать.

      Утверждение 5. Площадь треугольника можно найти по формуле

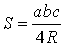
где a, b, c – стороны треугольника, а R – радиус описанной окружности.

      Доказательство.

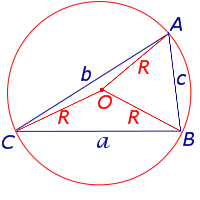
Рис. 5

В силу теоремы синусов справедливо равенство

.

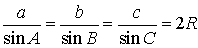      Следовательно,

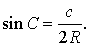
      Поэтому

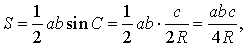
что и требовалось доказать.

      Утверждение 6. Площадь треугольника можно найти по формуле:

S = 2R² sin A sin B sin C ,

где A, B, С – углы треугольника, а R – радиус описанной окружности.

      Доказательство.

Рис. 6

В силу теоремы синусов справедливо равенство

.

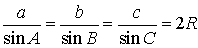      Поэтому

a = 2R sin A ,    
b = 2R sin B ,    
c = 2R  sin C ,

      В силу утверждения 5

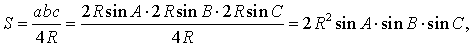
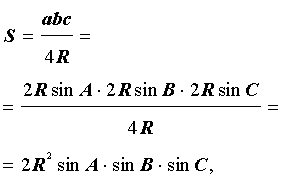
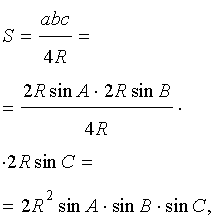
что и требовалось доказать.

Вывод формул для площади равностороннего треугольника

      Утверждение 7.

2. Если h – высота равностороннего треугольника, то его площадь

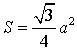
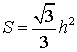
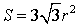
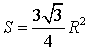
      Доказательство.

1. Рассмотрим рисунок 7.



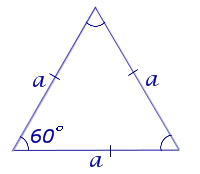
Рис. 7

В силу утверждения 2



2. Рассмотрим рисунок 8.



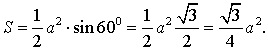
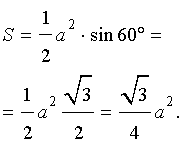
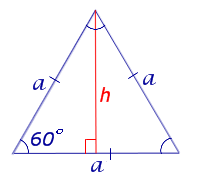
Рис. 8

Поскольку



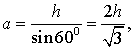
то



3. Рассмотрим рисунок 9.



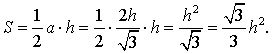
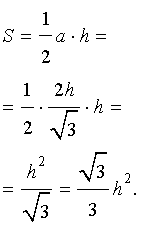
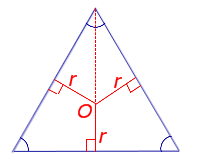
Рис. 9

Поскольку у равностороннего треугольника центр вписанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство   h = 3r.  Следовательно,



4. Рассмотрим рисунок 10.



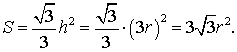
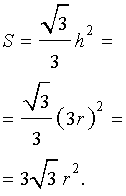
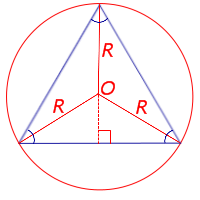
Рис. 10

Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство 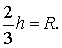Следовательно,



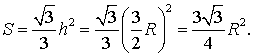
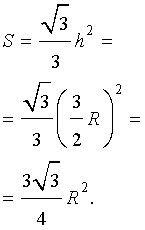
      Доказательство утверждения 7 завершено.

Вывод формул для площади прямоугольного треугольника

      Утверждение 8.

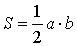
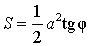
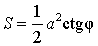
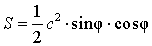
      Доказательство.

1. Рассмотрим рисунок 11.



Рис. 11

В силу утверждения 2



2. Рассмотрим рисунок 12.



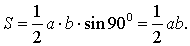
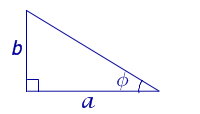
Рис. 12

Поскольку

b = a tg φ ,

то



3. Рассмотрим рисунок 13.



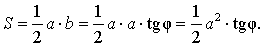
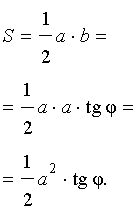
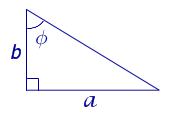
Рис. 13

Поскольку

b = a ctg φ ,

то



4. Рассмотрим рисунок 14.



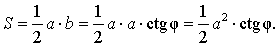
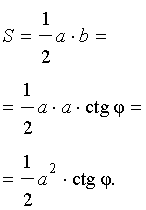
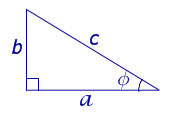
Рис. 14

Поскольку

a = c cos φ ,    
b = c sin φ ,

то



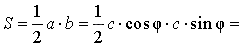
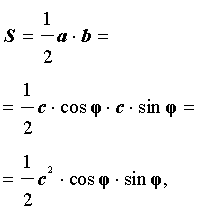
      Доказательство утверждения 8 завершено.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Площадь прямоугольника

Площадь прямоугольника, формулы для вычисления площади прямоугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и сводная таблица с формулами площадей прямоугольника.

Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь прямоугольника с помощью различных формул или проверить уже выполненные вычисления.

Таблица с формулами площади прямоугольника ((в конце страницы))

1

Площадь прямоугольника через две стороны

… подготовка …

a — сторона

b — сторона

---

2

Площадь прямоугольника через периметр и одну из сторон

В указанной формуле, площадь периметра прямоугольника вычисляется: 

… подготовка …

a (или b) — сторона

P — периметр

---

3

Площадь прямоугольника по диагонали и стороне

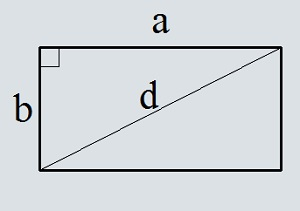
… подготовка …

a (или b) — сторона

d — диагональ

---

4

Площадь прямоугольника по диагоналям и углу между ними

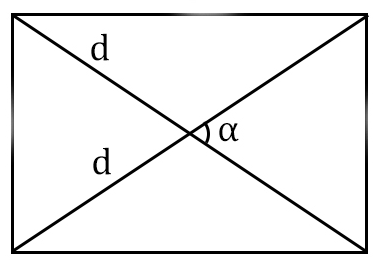
… подготовка …

d — диагональ

α° — угол между диагоналями

---

5

Площадь прямоугольника через сторону и радиус описанной окружности

… подготовка …

a (или b) — сторона

R — радиус описанной окружности

---

6

Площадь прямоугольника через сторону и диаметр описанной окружности

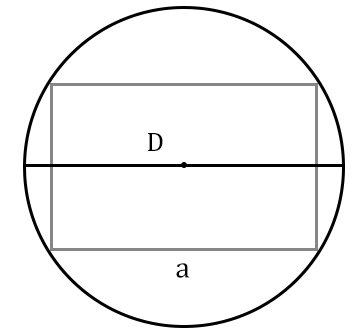
… подготовка …

a (или b) — сторона

D — диаметр описанной окружности

---

Примечание:

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться нашим «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

---

Таблица с формулами площади прямоугольника

---

Определения

Прямоугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.
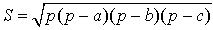
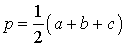