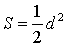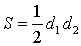Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | 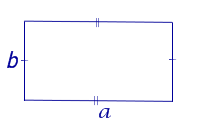 | S = ab | a и b – смежные стороны |
 |
Посмотреть вывод формулы | d – диагональ, | |
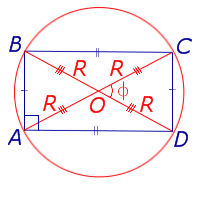 | S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R | R – радиус описанной окружности, | |
| Параллелограмм | 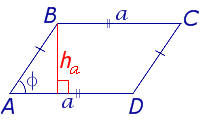 | S = a ha Посмотреть вывод формулы | a – сторона, |
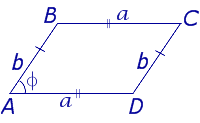 | S = absin φ Посмотреть вывод формулы | a и b – смежные стороны, | |
 |
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
| Квадрат | 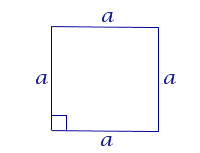 | S = a2 | a – сторона квадрата |
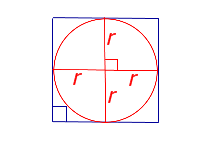 | S = 4r2 | r – радиус вписанной окружности | |
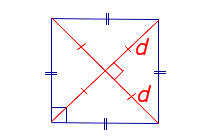 |
Посмотреть вывод формулы | d – диагональ квадрата | |
 | S = 2R2 Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | |
| Ромб |  | S = a ha Посмотреть вывод формулы | a – сторона, |
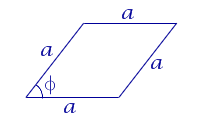 | S = a2 sin φ Посмотреть вывод формулы | a – сторона, | |
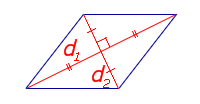 |
Посмотреть вывод формулы | d1, d2 – диагонали | |
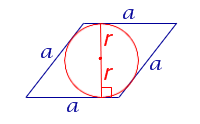 | S = 2ar Посмотреть вывод формулы | a – сторона, | |
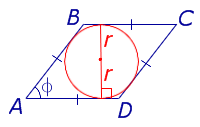 |
Посмотреть вывод формулы | r – радиус вписанной окружности, | |
| Трапеция | 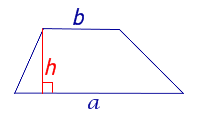 |
Посмотреть вывод формулы | a и b – основания, |
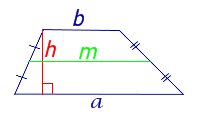 | S = m h | m – средняя линия, | |
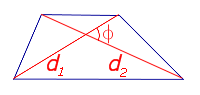 |
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
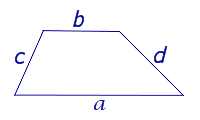 |
Посмотреть вывод формулы | a и b – основания, | |
| Дельтоид | 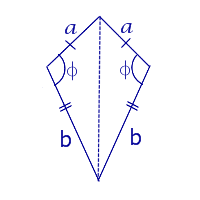 | S = ab sin φ | a и b – неравные стороны, |
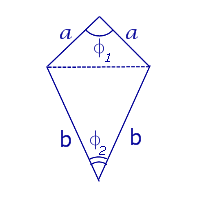 | 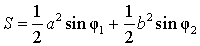 | a и b – неравные стороны, | |
 | S = (a + b) r Посмотреть вывод формулы | a и b – неравные стороны, | |
 |
Посмотреть вывод формулы | d1, d2 – диагонали | |
| Произвольный выпуклый четырёхугольник | 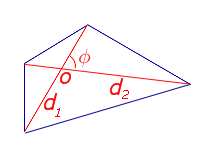 |
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними |
| Вписанный четырёхугольник | 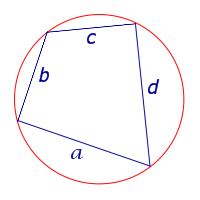 |
Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
 | S = ab где |
 |
где Посмотреть вывод формулы |
 | S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм | |
 | S = a ha где Посмотреть вывод формулы |
 | S = absin φ где Посмотреть вывод формулы |
 |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат | |
 | S = a2 где |
 | S = 4r2 где |
 |
где Посмотреть вывод формулы |
 | S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб | |
 | S = a ha где Посмотреть вывод формулы |
 | S = a2 sin φ где Посмотреть вывод формулы |
 |
где Посмотреть вывод формулы |
 | S = 2ar где Посмотреть вывод формулы |
 |
где Посмотреть вывод формулы |
| Трапеция | |
 |
где Посмотреть вывод формулы |
 | S = m h где |
 |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
 |
где Посмотреть вывод формулы |
| Дельтоид | |
 | S = ab sin φ где |
 | 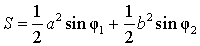 где |
 | S = (a + b) r где Посмотреть вывод формулы |
 |
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник | |
 |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник | |
 |
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
| Прямоугольник |
 S = ab где |

где Посмотреть вывод формулы |
 S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
 S = a ha где Посмотреть вывод формулы |
 S = absin φ где Посмотреть вывод формулы |

где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
 S = a2 где |
 S = 4r2 где |

где Посмотреть вывод формулы |
 S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
 S = a ha где Посмотреть вывод формулы |
 S = a2 sin φ где Посмотреть вывод формулы |

где Посмотреть вывод формулы |
 S = 2ar где Посмотреть вывод формулы |

где Посмотреть вывод формулы |
| Трапеция |

где Посмотреть вывод формулы |
 S = m h где |

где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
 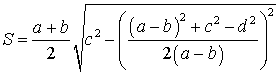 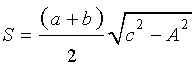 где Посмотреть вывод формулы |
| Дельтоид |
 S = ab sin φ где |

где |
 S = (a + b) r где Посмотреть вывод формулы |

где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |

где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
 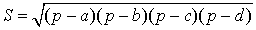 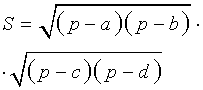 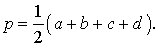 где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
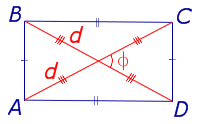
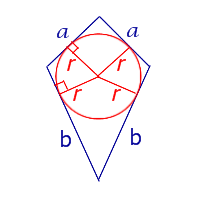
Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле
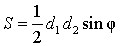
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
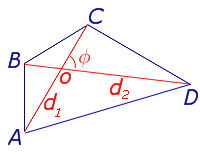
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
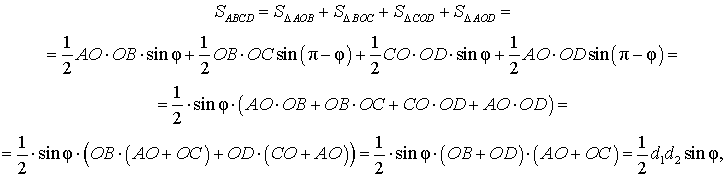
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
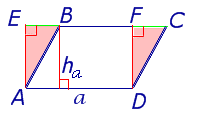
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
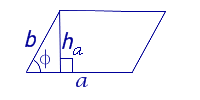
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
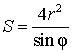 ,
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
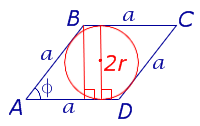
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
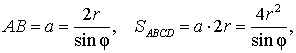
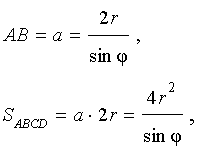
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
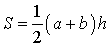 ,
,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
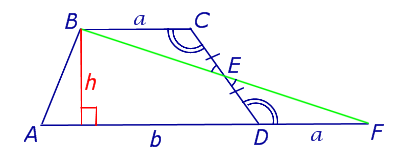
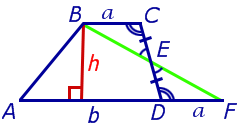
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
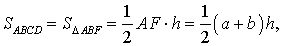
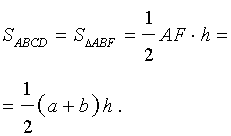
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
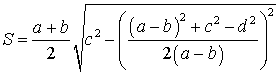 ,
,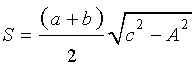
где a и b – основания, а c и d – боковые стороны трапеции,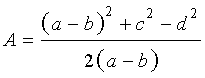
(рис.6).
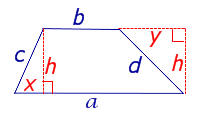
Рис. 6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
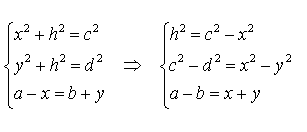
Следовательно,
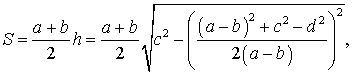
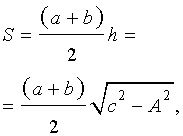
где
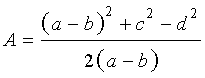 ,
,что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
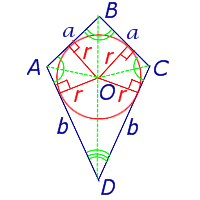
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
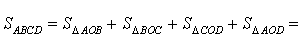
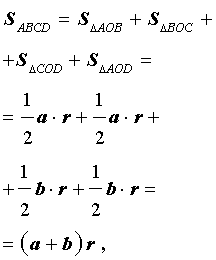
что и требовалось доказать.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
www.resolventa.ru
Формула Пика
Как определить площадь сложной фигуры? Если она нарисована на клетчатой бумаге, и невырождена -площадь ее ненулевая, все вершины имеют целые координаты, а стороны не пересекают друг друга – то удобно воспользоваться формулой Пика.
Если обозначить: В – количество целочисленных точек внутри этой фигуры, Г – количество целочисленных точек на ее границе, S – площадь фигуры, то
S=В+Г/2-1
Рассмотрим следующую фигуру:

Формула Пика – определение числа узлов внутри и на границе фигуры.
Обозначим все внутренние целочисленные точки красными кружками, а те, что на границах – синими. Целочисленные – это те, что лежат на пересечениях сетки (в ее узлах). Считаем те и другие:
Давайте проверим правильность наших расчетов, тем более, что здесь это просто: рассчитаем площадь квадрата, обведенного красным, и вычтем площади цветных треугольников:

Вычисление площади при помощи отрезания “лишнего”
Тогда площадь квадрата Sкв=36, площадь голубого треугольника 6, площадь зеленого – 2, площадь фиолетового 15.
Площадь белого треугольника тогда: S=36-6-15-2=13.
Рассмотрим такую фигуру:

Еще один пример определения площади сложной фигуры с помощью формулы Пика
Для нее S=В+Г/2-1=4+3-1=6.
Проверим:

Отрежем лишнее
Тогда площадь прямоугольника Sпр=20, площадь голубого треугольника 5, площадь зеленого – 4, площадь фиолетового 5.
Площадь искомой фигуры тогда: S=20-5-4-5=6.
Третья фигура:

Еще один пример работы с формулой Пика
Для нее S=В+Г/2-1=4+4-1=7.
Проверим: площадь треугольников, составляющих нашу фигуру: голубого – 4, зеленого – 1, оранжевого – 2. Сумма их площадей S=4+1+2=7.

Расчет площади с помощью разрезания фигуры
Еще две фигуры:

Узлы решетки внутри и на границе фигуры
Площадь первой: S=10+2-1=11,

Узлы решетки внутри и на границе
второй – S=10+5-1=14.
Проверить правильность расчета их площадей вы можете самостоятельно.
easy-physic.ru
Площадь фигуры — это… Что такое Площадь фигуры?
Пло́щадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Об определении
Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.
Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости, такая что:
- (положительность) площадь неотрицательна;
- (нормировка) квадрат со стороной единица имеет площадь 1;
- конгруэнтные фигуры имеют равную площадь;
- (аддитивность) площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
Определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
- Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:
Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура называется квадрируемой, если для любого существует пара многоугольников и , такие что и , где обозначает площадь .
Связанные определения
- Две фигуры называются равновеликими, если они имеют равную площадь.
Комментарии
На самом деле, есть довольно неестественный и неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. На множестве всех ограниченных подмножеств плоскости существуют различные функции площади, т. е. не равные функции, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур, на которых функционал площади определяется однозначно.
То же самое можно сделать для длины на прямой, но нельзя для объёма в евклидовом пространстве и также нельзя для площади на единичной сфере в евклидовом пространстве, (смотри соответственно парадокс Банаха — Тарского и парадокс Хаусдорфа).
Площади некоторых фигур
Формулы для нахождения площадей различных фигур
| Фигура | Формула | Комментарий |
|---|---|---|
| Правильный треугольник | — длина стороны треугольника. | |
| Треугольник | Формула Герона. — полупериметр, , и — длины сторон треугольника. | |
| Треугольник | и — две стороны треугольника, а — угол между ними. | |
| Треугольник | и — сторона треугольника и высота, проведённая к этой стороне. | |
| Квадрат | — длина стороны квадрата. | |
| Прямоугольник | и — длины сторон прямоугольника. | |
| Ромб | и — длины диагоналей ромба. | |
| Параллелограмм | — длина одной из сторон параллелограмма, а — высота, проведённая к этой стороне. | |
| Трапеция | и — длины параллельных сторон, а — расстояние между ними (высота). | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — длина стороны многоугольника, а — количество сторон многоугольника. | |
| — апофема (или радиус вписанной в многоугольник окружности), а — периметр многоугольника. | ||
| Круг | или | — радиус окружности, а — её диаметр. |
| Сектор круга | и — соответственно радиус и угол сектора (в радианах). | |
| Эллипс | и — большая и малая полуоси эллипса. | |
| Поверхность Цилиндра | и — радиус и высота цилиндра соответственно. | |
| Боковая поверхность цилиндра | и — радиус и высота цилиндра соответственно. | |
| Поверхность конуса | и — радиус и длина образующей соответственно. | |
| Боковая поверхность конуса | и — радиус и длина образующей соответственно. | |
| Поверхность сферы | и — радиус и диаметр соответственно. | |
| Поверхность эллипсоида | См. статью. |
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне:
- Площадь прямоугольника равна произведению его смежных сторон:
- Площадь произвольного четырехугольника ABCD равна половине произведения диагоналей и синуса угла между ними:
- ,
- где — угол между диагоналями.
- Площадь ромба ABCD равна половине произведения диагоналей:
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:
- Площадь трапеции равна произведению полусуммы оснований на высоту:
См. также
Ссылки
- В.Болтянский, О понятиях площади и объёма. Квант, № 5, 1977
- Б. П. Гейдман, Площади многоугольников, Библиотека «Математическое просвещение», выпуск 16, (2002).
- В. А. Рохлин, Площадь и объём, Энциклопедия элементарной математики, Книга 5, Геометрия, под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина.
dic.academic.ru
Площади плоских фигур
Площадь простой фигуры – это положительная величина, численное значение которой обладает следующими свойствами:
- равные фигуры имеют равные площади;
- если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей;
- площадь квадрата со стороной, равной единице измерения, равна единице.
 Площадь прямоугольника можно найти следующим образом:
Площадь прямоугольника можно найти следующим образом:
S = ab,
Где a и b – стороны прямоугольника.
Квадрат – это прямоугольник, у которого стороны равны, а, значит, площадь квадрата со стороной a равна a2, то есть
S = a2,
где а – его сторона.
Площадь квадрата можно также вычислить по формуле
S = d2/2,
где d – диагональ квадрата.
Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне, то есть вычисляется по формуле
S = ah,
где а – его сторона, h – высота, проведённая к этой стороне.
Площадь параллелограмма можно вычислить и по формуле
S = ab sin α,
где а и b – стороны, α – угол параллелограмма.
Ромб – «частный случай» параллелограмма, значит, его площадь можно находить так же, как и площадь параллелограмма. Кроме того, имеются и другие формулы площади ромба:
S = a2 sin α,
где а – сторона ромба, α – угол ромба;
S = 1/2 d1 d2,
где d1и d2 – диагонали ромба.
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне, то есть её можно найти по формуле
S = 1/2 ah.
Есть и другие формулы для нахождения площади треугольника:
S = 1/2 ab sin γ,
где а и b – стороны, γ – угол между этими сторонами.
При необходимости для нахождения площади треугольника можно использовать формулу Герона, древнегреческого учёного, который жил в Александрии в I веке нашей эры:
 ,
,
где а, b, с – стороны треугольника, p – его полупериметр p = (а + b + с)/2 .
Площадь трапеции равна произведению полусуммы её оснований на высоту:
S = (а + b) / 2 · h,
где а и b – основания трапеции, h – высота.
Также советуем вам посмотреть наш новый видеоурок по теме нахождения площади плоских фигур:
Данные формулы позволяют нам решать многие геометрические задачи, рассмотрим некоторые из них.
Задача 1.
В параллелограмме ABCD сторона AB = 12 см и диагональ AC = 16 см. Вершина D удалена от диагонали AC на 4 см. Найдите расстояние от точки D до прямой AB.
Решение.
S ABCD = 2S ADC = AC · DM = 64 см2,
а так как S ABCD = AB · DK,
то DK = 64/12,
то есть DK = около 5,33 см.
Ответ. ≈ 5,33 см.
Задача 2.
Через центр О квадрата ABCD со стороной а проведена прямая k, пересекающая сторону AB, но не проходящая через точки A и B. Выразить сумму расстояния от вершин B и C до прямой k через a и b, если b – длина отрезка прямой k, заключённого внутри квадрата.
Решение.
Обозначим искомую сумму через с, тогда в силу центральной симметрии фигуры с = 2 (h1 + h2).
S AOB = 0,25a2, S AOB = 0,25 b (h1 + h2),
откуда 0,25a2, S AOB = 0,25 b (h1 + h2) и с = 2a2/b.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Площадь фигуры — это… Что такое Площадь фигуры?
Пло́щадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Об определении
Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.
Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости, такая что:
- (положительность) площадь неотрицательна;
- (нормировка) квадрат со стороной единица имеет площадь 1;
- конгруэнтные фигуры имеют равную площадь;
- (аддитивность) площадь объединения двух фигур без общих внутренних точек равна сумме площадей.
Определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть
- Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:
Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура называется квадрируемой, если для любого существует пара многоугольников и , такие что и , где обозначает площадь .
Связанные определения
- Две фигуры называются равновеликими, если они имеют равную площадь.
Комментарии
На самом деле, есть довольно неестественный и неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. На множестве всех ограниченных подмножеств плоскости существуют различные функции площади, т. е. не равные функции, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур, на которых функционал площади определяется однозначно.
То же самое можно сделать для длины на прямой, но нельзя для объёма в евклидовом пространстве и также нельзя для площади на единичной сфере в евклидовом пространстве, (смотри соответственно парадокс Банаха — Тарского и парадокс Хаусдорфа).
Площади некоторых фигур
Формулы для нахождения площадей различных фигур
| Фигура | Формула | Комментарий |
|---|---|---|
| Правильный треугольник | — длина стороны треугольника. | |
| Треугольник | Формула Герона. — полупериметр, , и — длины сторон треугольника. | |
| Треугольник | и — две стороны треугольника, а — угол между ними. | |
| Треугольник | и — сторона треугольника и высота, проведённая к этой стороне. | |
| Квадрат | — длина стороны квадрата. | |
| Прямоугольник | и — длины сторон прямоугольника. | |
| Ромб | и — длины диагоналей ромба. | |
| Параллелограмм | — длина одной из сторон параллелограмма, а — высота, проведённая к этой стороне. | |
| Трапеция | и — длины параллельных сторон, а — расстояние между ними (высота). | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — длина стороны многоугольника, а — количество сторон многоугольника. | |
| — апофема (или радиус вписанной в многоугольник окружности), а — периметр многоугольника. | ||
| Круг | или | — радиус окружности, а — её диаметр. |
| Сектор круга | и — соответственно радиус и угол сектора (в радианах). | |
| Эллипс | и — большая и малая полуоси эллипса. | |
| Поверхность Цилиндра | и — радиус и высота цилиндра соответственно. | |
| Боковая поверхность цилиндра | и — радиус и высота цилиндра соответственно. | |
| Поверхность конуса | и — радиус и длина образующей соответственно. | |
| Боковая поверхность конуса | и — радиус и длина образующей соответственно. | |
| Поверхность сферы | и — радиус и диаметр соответственно. | |
| Поверхность эллипсоида | См. статью. |
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне:
- Площадь прямоугольника равна произведению его смежных сторон:
- Площадь произвольного четырехугольника ABCD равна половине произведения диагоналей и синуса угла между ними:
- ,
- где — угол между диагоналями.
- Площадь ромба ABCD равна половине произведения диагоналей:
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:
- Площадь трапеции равна произведению полусуммы оснований на высоту:
См. также
Ссылки
- В.Болтянский, О понятиях площади и объёма. Квант, № 5, 1977
- Б. П. Гейдман, Площади многоугольников, Библиотека «Математическое просвещение», выпуск 16, (2002).
- В. А. Рохлин, Площадь и объём, Энциклопедия элементарной математики, Книга 5, Геометрия, под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина.
dis.academic.ru
| Слайд 1 Орг. момент Учитель читает стихи про карандаш. |
|
| Слайды 2-6
Устный счёт «Собери букет», «Испеки пирог». (таблица умножения на 8, 9) |
|
| Слайд 7 – Ребята, какая я невнимательная, забыла написать тему сегодняшнего урока. Как быть? Слайд 8 |
|
| – Прочитайте задание на слайде. – Открываем тетрадь. Прочитайте внимательно задания теста. – Выполните все задания теста. Время – 5минут! – Так какая тема сегодняшнего урока? |
|
| Слайд 9 – Совершенно верно, тема сегодняшнего урока: «Площадь прямоугольника». – Перед нами стоят такие задачи: 1) Выяснить значения слова площадь; 2) Повторить способы сравнения площади фигур и познакомиться с новым способом; 3) Сформулировать правило нахождения площади прямоугольника и вывести формулу; 4) Уметь решать задачи на нахождение площади прямоугольника. |
|
| Слайд 10 – Какие ассоциации у вас возникают при слове «площадь»? Что сразу приходит на ум? – Пожалуйста, поделитесь своими мыслями. Учитель заслушивает все варианты ответа. (площадь в центре города, строительная площадка, площадка во дворе для игр, спортивная площадка, лестничная площадка, площадь обоев, площадь стола, площадь футбольного поля, площадь поля, засеянного какими-либо культурами и др.) |
|
| Слайд 11
– Посмотрите, что изображено на слайде? – Да, это Красная площадь – центральная площадь Москвы. Возникновение Красной площади относится к концу 15 века, когда по приказу царя Ивана III были снесены деревянные постройки вокруг Кремля, угрожавшие постоянными пожарами. На их месте была организована площадь для мелкой торговли. Первоначально она так и называлась – Торговая. Красной площадь стали называть только в 17 веке. – А это что за площадь? Это одна из центральных площадей города Санкт-Петербурга. Она называется Сенатская площадь. Сенатская площадь была названа так после размещения на ней правительственного учреждения Сената. Сенатская площадь является одной из самых старых площадей Санкт-Петербурга. – Все узнали центральную площадь нашего города. Кто знает, как она называется? Совершенно верно, это площадь Ленинского комсомола. – Почему её так назвали? В каком году была построена площадь? Какие важные здания находятся на этой площади? – Обратитесь за помощью к родителям, бабушкам и дедушкам, справочной литературе, сети Интернет, чтобы найти ответы на эти вопросы. А на ближайшем уроке окружающего мира мы вернёмся к этой теме. |
|
| Слайд 12 – Давайте прочитаем значения слова «площадь». Два ученика по слайду зачитывают по просьбе учителя. |
|
| Слайд 13 – Заглянем в толковый словарь русского языка В.И. Даля. – Внимательно прочитайте значение слова «площадь». Вдумайтесь в смысл! |
|
| Слайд 14
– Какие способы измерения площади фигур вам известны? Учитель заслушивает все варианты ответа. |
|
| Слайд 15
– Действительно, существует несколько способов: визуально, т.е. на глаз, способ наложения фигур и с использованием мерок. |
|
| Слайд 16
– Сравните на глаз площади треугольников. Что вы можете о них сказать? – Какова площадь круга: больше или меньше? |
|
| Слайд 17
– Что можете сказать о площади квадратов? – Почему площадь зелёного квадрата меньше? (полностью помещается в розовом квадрате) – Можно ли утверждать, что площадь треугольника больше площади самого маленького квадрата? – Почему? |
|
| Слайд 18 – Ещё один способ: подсчёт количества мерок, уложившихся в той или иной фигуре. – Сколько мерок уложилось в жёлтом прямоугольнике? – Площадь какого прямоугольника больше? – Что получится, если я буду использовать разные мерки для сравнения площадей этих прямоугольников: квадраты, круги, треугольники, овалы и т.д.? |
|
| Слайд 19 – Прочитаем вывод хором! Учитель говорит о том, что пришло время отдохнуть, напоминает о взаимной вежливости. |
|
| Слайд 20
Физ.минутка |
|
| Слайд 21 Учитель зачитывает по слайду. Гиперссылка = нажать на слово «единицы». – Если данная мерка – это один квадратный сантиметр, то чему тогда равна площадь каждого прямоугольника? (ответы детей)Гиперссылка = нажать на слово «мерка». |
|
| Слайд 22 – Есть ли такие единицы измерения площади, как квадратный дециметр, квадратный метр?Учитель заслушивает все варианты ответов. – Об этом мы узнаем на ближайших уроках математики. |
|
| Слайд 23 лежат конверты. Откройте их, достаньте геометрические фигуры. – Прочитайте задание на слайде. – Работа в парах: нужно сравнить площади этих фигур. – Как это сделать? Время для работы – одна минута! |
|
| – Ребята, вы молодцы! – Есть такое приспособление в математике!Слайд 24 Учитель зачитывает по слайду, раздаёт всем палетки. – Измерьте при помощи палетки площади данных фигур. – Что вы заметили? |
|
| Слайд 25 Дети сравнивают свои ответы с данным. – Молодцы! |
|
| Слайд 26 – Прочитайте вывод. |
|
| Слайд 27
– Как найти площадь прямоугольника? |
|
| Слайд 28 – Сначала нужно измерить стороны прямоугольника, т.е. узнать длину и ширину. – Потом перемножить полученные числа. |
|
| Слайд 29 – Прочитайте «про себя» правило нахождения площади прямоугольника. – Постарайтесь запомнить его, а дома выучить наизусть. |
|
urok.1sept.ru