Неравенство бернулли метод математической индукции: Неравенство Бернулли — Википедия – Неравенства и лемма Бернулли (с доказательствами)

Posted on by alexxlab

Неравенство Бернулли — Википедия

Материал из Википедии — свободной энциклопедии

Нера́венство Берну́лли утверждает: если x≥−1{\displaystyle x\geq -1}, то

(1+x)n≥1+nx{\displaystyle (1+x)^{n}\geq 1+nx} для всех n∈N0.{\displaystyle n\in \mathbb {N} _{0}.}

Доказательство неравенства проводится методом математической индукции по n. При n = 1 неравенство, очевидно, верно. Допустим, что оно верно для n, докажем его верность для n+1:

(1+x)n+1=(1+x)(1+x)n≥(1+x)(1+nx)≥(1+nx)+x=1+(n+1)x{\displaystyle (1+x)^{n+1}=(1+x)(1+x)^{n}\geq (1+x)(1+nx)\geq (1+nx)+x=1+(n+1)x},

ч.т.д.

Обобщенное неравенство Бернулли утверждает, что при x>−1 {\displaystyle x>-1\!\ } и n∈R{\displaystyle n\in \mathbb {R} }:

Доказательство

Рассмотрим f(x)=(1+x)n−nx {\displaystyle f(x)=(1+x)^{n}-nx\!\ }, причем x>−1,n≠0,n≠1 {\displaystyle x>-1,n\neq 0,n\neq 1\!\ }.
Производная f′(x)=n(1+x)n−1−n=0 {\displaystyle f'(x)=n(1+x)^{n-1}-n=0\!\ } при x=x0=0 {\displaystyle x=x_{0}=0\!\ }, поскольку n≠0 {\displaystyle n\neq 0\!\ }.
Функция f {\displaystyle f\!\ } дважды дифференцируема в проколотой окрестности точки x0 {\displaystyle x_{0}\!\ }. Поэтому f″(x)=n(n−1)(1+x)n−2 {\displaystyle f»(x)=n(n-1)(1+x)^{n-2}\!\ }. Получаем:

Значение функции f(x0)=1 {\displaystyle f(x_{0})=1\!\ }, следовательно, справедливы следующие утверждения:

  • если n∈(−∞;0)∪[1;+∞){\displaystyle n\in (-\infty ;0)\cup [1;+\infty )}, то (1+x)n≥1+nx{\displaystyle (1+x)^{n}\geq 1+nx}
  • если n∈(0;1] {\displaystyle n\in (0;1]\!\ }, то (1+x)n≤1+nx{\displaystyle (1+x)^{n}\leq 1+nx}

Несложно заметить, что при соответствующих значениях x0=0 {\displaystyle x_{0}=0\!\ } или n=0,n=1 {\displaystyle n=0,n=1\!\ } функция f(x)=f(x0) {\displaystyle f(x)=f(x_{0})\!\ }. При этом в конечном неравенстве исчезают ограничения на n {\displaystyle n\!\ }, заданные в начале доказательства, поскольку для них исполняется равенство. ■

  • Неравенство также справедливо для x≥−2{\displaystyle x\geq -2} (при n∈N0{\displaystyle n\in \mathbb {N} _{0}}). Доказательство для случая x∈[−2,−1){\displaystyle x\in \left[-2,-1\right)} можно провести так же методом математической индукции.

(1+x)n+1+(1+x)n=(1+x)n(1+x+1)≥(1+nx)(1+x+1)=1+(n+1)x+1+nx(1+x){\displaystyle (1+x)^{n+1}+(1+x)^{n}=(1+x)^{n}(1+x+1)\geq (1+nx)(1+x+1)=1+(n+1)x+1+nx(1+x)}

Так как при x∈[−2,−1){\displaystyle x\in \left[-2,-1\right)} (1+x)n≤1≤1+nx(1+x){\displaystyle (1+x)^{n}\leq 1\leq 1+nx(1+x)}, то (1+x)n+1≥1+(n+1)x{\displaystyle (1+x)^{n+1}\geq 1+(n+1)x}

Калькулятор неравенства Бернулли онлайн | BBF.RU

Неравенства представляют собой два числа или математических выражения, которые соединены одним из следующих знаков: больше, меньше, больше или равно, меньше или равно. Неравенства широко применяются в прикладной математике, а некоторые из них считаются классическими и используются для решения задач определенного спектра. 

Классические неравенства

С точки зрения математической логики каждое неравенство считается высказыванием, которое требуется доказать или опровергнуть. Среди множества неравенств выделяют ряд особенных выражений, которые были сформулированы и доказаны выдающимися математиками. Первым классическим неравенством было безымянное выражение вида:

(1 + x)α ≥ 1 + αx.

Это своего рода фундаментальное математическое выражение, которое положило начало ряду классических неравенств. Доказательством этого высказывания занимались многие ученые, но лучше всех с задачей справился Якоб Бернулли. Он доказал данное неравенство для случая, когда α принадлежит натуральному множеству. 

Работа великих математиков кажется нам чем-то магическим и непостижим, а их результаты всегда поражают. Однако главное очарование математики состоит в том, что простые методы и идеи, примененные в определенном порядке, зачастую приводят к неожиданным результатам. Так работал и Бернулли. Неравенство его имени легко в основу других классических неравенств, таких как неравенства Коши, Гельдера, Юнга и Минковского.

Доказательство неравенств

Фундаментальное неравенство (1 + x)α ≥ 1 + αx легко доказать при помощи производных. Дифференцируя обе части уравнения можно показать, что при значениях аргумента x в диапазоне от 0 до 1 функция убывает, а для всех других значений — возрастает. Бернулли отсек отрицательные значения аргумента и принял, что α – любое натуральное число n. В итоге он получил знаменитое математическое высказывание:

(1 + x)n ≥ 1 + nx

Как же доказать это выражение? Для неравенств с натуральным аргументом математики используют метод математической индукции. Рассмотрим подробнее. 

Метод математической индукции

Математическая индукция — это метод доказательства высказываний с натуральным аргументом. Его суть состоит в доказательстве неравенства для значений аргумента, равных 1, n и n + 1. Если выражение тождественно для этих трех случаев, то оно тождественно для любого натурального числа n. Давайте попробуем доказать неравенство Бернулли (1 + x)n ≤ 1 + nx методом математической индукции. 

Итак, примем n = 1. В этом случае выражение принимает вид:

  • (1 + x)1 ≥ 1 + 1x;
  • (1 + x) ≥ 1 + x.

Очевидно, что это тождественное неравенство, так как справа и слева стоят одинаковые выражения, следовательно, они равны. Теперь посмотрим, как ведет себя высказывание при аргументах, которые равны n и n + 1. 

Если справедливо высказывание:

(1 + x)n ≥ 1 + nx,

то справедливо и

(1 + x)(n + 1) ≥ 1 + (n+1)x

Мы помним, что Якоб Бернулли рассматривал неравенство при значениях x > -1, следовательно, выражение 1 + x > 0. Используя правила тождественного преобразования неравенств, умножим обе части исходного неравенства на 1 + x. Получим:

(1 + x) × (1 + x)n ≥ (1 + nx) × (1 + x).

Очевидно, что если умножить (1 + x)n на (1 + x), то мы получим (1 + x) в степени (n + 1), так как возведение в степень — это повторяющееся умножение, а мы умножили выражение вn-ной степени еще один раз на себя же. Правило сложения степеней гласит, что в этом случае счетчик степени просто увеличится на единицу. Итак, мы получили, что в левой части неравенства у нас стоит (1 + x)(n + 1), то есть значение выражения для аргумента n + 1. Раскроем скобки в правой части и увидим:

(1 + x)(n + 1) ≥ 1 + (n + 1)x + nx2.

Мы знаем, что nx2 больше нуля, поэтому 1 + (n + 1)x + nx2 ≥ 1 + (n + 1)x. Получаем переходное неравенство, что:

(1 + x)(n + 1) ≥ 1 + (n + 1)x + nx2 ≥ 1 + (n+1)x,

следовательно,

(1 + x)(n + 1) ≥ 1 + (n+1)x

Мы показали, что неравенства для значений 1, n и n + 1 тождественны, а это значит, что неравенство Бернулли истинно для любых натуральных чисел. На первый взгляд это чистая, высокая математика, которая не выходит за пределы теории, но классические неравенства широко применяются на практике.

Использование неравенства Бернулли 

Данное математическое высказывание находит применение при сравнении иррациональных чисел. Допустим, у нас есть иррациональное число в виде корня 200-ой степени из 2. Также у нас есть рациональное число 1,005. Давайте подумаем, какое из двух чисел больше? Вручную подсчитать такой корень невозможно, но на помощь приходит классическое неравенство Бернулли. 

Воспользуемся первым тождественным преобразованием: возведем оба числа в 200 степень и получим 2 и 1,005200. Выражение вида 1,005200

мы можем подсчитать вручную как раз при помощи классического неравенства. Выразим, что 1,005 — это 1 + 0,005. Тогда согласно неравенству:

(1 + 0,005)200 ≥ 1 + 200 × 0,005

Легко подсчитать, что 200 × 0,005 = 1. Следовательно, выражение приобретает вид:

(1 + 0,005)200 ≥ 2 или 1,005200 ≥ 2.

Таким образом, 1,005 больше, чем корень 200-ой степени из 2. 

Наш калькулятор представляет собой программу, которая реализует выражение Бернулли и представляет его в замкнутом виде. Для использования калькулятора требуется ввести значения x и n, после чего нажать кнопку «Рассчитать». Программа вычислит значения выражений (1 + x)n и 1 + nx, после чего вы наглядно убедитесь, что полученные числа полностью удовлетворяют неравенству Бернулли. Например, используем x = 4 и n = 3. Получим, что:

  • (1 + x)n = (1 + 4)3 = 125;
  • 1 + nx = 1 + 3 × 4 = 13.

Очевидно, что 125 больше 13. 

Заключение

Математическое выражение Бернулли — это классическое неравенство, которое широко используется специалистами, работающими с неравными объектами. Наш каталог калькуляторов пригодится как профессионалам, так и студентам, которые только открывают для себя увлекательный мир математики.

§8. Метод математической индукции. Неравенство я. Бернулли.

Напомним известную забаву. Кости домино выставляются таким образом, что каждая из них падая, опрокинет следующую. Если толкнуть первую, то одна за другой упадут все кости. Принцип математической индукции формулируется сходным образом. Рассмотрим применение метода математической индукции (ММИ) на примере.

Пример 1. Сумма членов арифметической прогрессииравна. Рассмотрим похожую сумму. Доказать равенство(утверждение).

Решение. Утверждениеистинно, т.к. приЛ.ч.=П.ч.=1.

Докажем, что . Если, то.=, т.е.

Таким образом, .

Формулировка принципа математической индукции:

Пусть 1) − база индукции;

2) − шаг индукции.

Тогда .

Упражнение. Доказать, что.

Пример 2. Доказатьнеравенство Бернулли:если, то(утверждение).

Доказательство. 1), т.к. приЛ.ч.=Пр.ч.=1

2) Пусть , т.е.при. Домножим обе части этого неравенства на величину. Т.к., то мы получим.

Таким образом, , т.е.истинно.

Мы доказали, что 1) и 2). В соответствии с принципом математической индукции. Ч. и т.д.

Замечание. Из приведенного доказательства следует также, что, если, в неравенстве Бернулли знак “” можно заменить знаком “”.

§9. Существование предела . Число. Натуральные логарифмы.

Теорема. Существует конечный предел последовательности .

Доказательство. Обозначим,. Докажем, чтообразуют последовательность вложенных стягивающихся отрезков.

1). Очевидно, что .

2). означает, чтоили. Носогласно неравенству Бернулли.

3). означает, что, т.е.или. Носогласно неравенству Бернулли.

4). при.

Поэтому из теоремы о вложенных отрезках следует, что существует . Ч. и т.д.

Принято этот предел обозначать . Вычисления показывают, что. Отметим, что логарифмы при основанииeназываютнатуральнымилогарифмами. Для них обычно используют обозначениевместо того, чтобы писать.

Следствие. Из приведенного рассуждения следует также, что при натуральных значенияхсправедливы неравенства:

и, следовательно, неравенства

.

§10. Первый замечательный предел. Следствия.

Теорема. (Первый замечательный предел.) При радианном измерении углов

.

Доказательство. Пусть сначала. Сравним площади треугольниковOCB,OCDи

кругового сектора OCMB(см. Рис.). Мы видим, что

.

Заменяя площади их значениями, получим

.

Отсюда легко вывести, что

,

а так как , то.

Из теоремы о двусторонней оценке следует, что . Так как− четная функция, то. В итоге получаем требуемое утверждение:.

Следствие 1. Первый замечательный предел можно записать в форме эквивалентности:. (Это − табличная эквивалентность 1.)

Следствие 2. Из следствия 1. легко выводятся табличные эквивалентности 2. − 5.

§11. Второй замечательный предел. Следствия.

Теорема. (Второй замечательный предел.)

.

(Напомним, “” мы обозначили чуть раньше предел.)

Доказательство.Мы предположим сначала, что. Если обозначим(обозначает целую часть числа), то будетили.

Это приводит к двусторонней оценке:

.

Т.к. крайние члены последнего неравенства при стремящемся к нулю справа стремятся к числу, то.

Пусть теперь и пусть. В таком случаеи=

при, т.к. при этом условии. Следовательно,.

Мы видим, что оба односторонних предела равны , то

.

Следствие 1.Имеет место эквивалентность, когда,.

Доказательство.Логарифмируя доказанное только что соотношение по основанию, получим. Позже будет доказана возможность поменять местами операциии(свойство непрерывности логарифмической функции). Воспользовавшись этой возможностью, получим, т.е..

Следствие 2.. Имеет место эквивалентность.

Доказательство.Если, то. Поэтомуи.

Следствие 3.. Имеет место эквивалентность..

Доказательство. Можно считать, что. Поэтомубудети.

Помогите решить / разобраться (М)

ewert, хорошее доказательство, я его раньше не встречал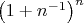 :shock: при доказательстве монотонности $\left( 1+{n}^{-1} \right) ^{n}$. У Фихтенгольца (еще один камень в его огород) это доказывается через бином. Но такое доказательство толком не применимо когда 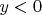$y<0$ или когда надо доказать убывание: $\left( 1+{n}^{-1} \right) ^{n+1}$.
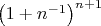Примерно то же самое предлагал и DeBill только он говорил про индукцию, хотя на самом деле это даже не индуктивное доказательство.
Вот такая запись может даже проще:
$$\left( 1+{\frac {y}{n+1}} \right) ^{n+1} \left( 1+{\frac {y}{ n}} \right) ^{-n}>1 \Leftrightarrow \left( 1+{\frac {y}{n+1}} \right) ^{{ \frac {n+1}{n}}} \left( 1+{\frac {y}{n}} \right) ^{-1}\ge $$$$\ge \left( 1+{\frac {y}{n+1}} \right) \left( 1+{\frac {y}{n \left( n+1 \right) }} \right) \left( 1+{\frac {y}{n}} \right) ^{-1}= \left( 1+{ \frac {y}{n}}+{\frac {{y}^{2}}{n \left( n+1 \right) ^{2}}} \right) \left( 1+{\frac {y}{n}} \right) ^{-1} >1$$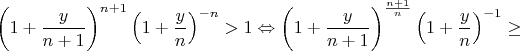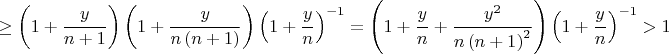ewert в сообщении #1137983 писал(а):deep blue в сообщении #1137883 писал(а):

Наверное это как-то можно обойти.


Можно. Просто не надо возводить второе неравенство в степень при 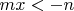$mx<-n$, т.к. в этом случае уже исходное неравенство тривиально.То есть неравенства равносильны при дополнительном условии на второе неравенство: 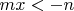$mx<-n$. В других случаях второе неравенство тривиально само по себе.

Неравенство Бернулли — Википедия

Материал из Википедии — свободной энциклопедии

Нера́венство Берну́лли утверждает: если x≥−1{\displaystyle x\geq -1}, то

(1+x)n≥1+nx{\displaystyle (1+x)^{n}\geq 1+nx} для всех n∈N0.{\displaystyle n\in \mathbb {N} _{0}.}

Доказательство

Доказательство неравенства проводится методом математической индукции по n. При n = 1 неравенство, очевидно, верно. Допустим, что оно верно для n, докажем его верность для n+1:

(1+x)n+1=(1+x)(1+x)n≥(1+x)(1+nx)≥(1+nx)+x=1+(n+1)x{\displaystyle (1+x)^{n+1}=(1+x)(1+x)^{n}\geq (1+x)(1+nx)\geq (1+nx)+x=1+(n+1)x},

ч.т.д.

Обобщенное неравенство Бернулли

Обобщенное неравенство Бернулли утверждает, что при x>−1 {\displaystyle x>-1\!\ } и n∈R{\displaystyle n\in \mathbb {R} }:

Доказательство

Рассмотрим f(x)=(1+x)n−nx {\displaystyle f(x)=(1+x)^{n}-nx\!\ }, причем x>−1,n≠0,n≠1 {\displaystyle x>-1,n\neq 0,n\neq 1\!\ }.
Производная f′(x)=n(1+x)n−1−n=0 {\displaystyle f'(x)=n(1+x)^{n-1}-n=0\!\ } при x=x0=0 {\displaystyle x=x_{0}=0\!\ }, поскольку n≠0 {\displaystyle n\neq 0\!\ }.
Функция f {\displaystyle f\!\ } дважды дифференцируема в проколотой окрестности точки x0 {\displaystyle x_{0}\!\ }. Поэтому f″(x)=n(n−1)(1+x)n−2 {\displaystyle f»(x)=n(n-1)(1+x)^{n-2}\!\ }. Получаем:

Значение функции f(x0)=1 {\displaystyle f(x_{0})=1\!\ }, следовательно, справедливы следующие утверждения:

  • если n∈(−∞;0)∪[1;+∞){\displaystyle n\in (-\infty ;0)\cup [1;+\infty )}, то (1+x)n≥1+nx{\displaystyle (1+x)^{n}\geq 1+nx}
  • если n∈(0;1] {\displaystyle n\in (0;1]\!\ }, то (1+x)n≤1+nx{\displaystyle (1+x)^{n}\leq 1+nx}

Несложно заметить, что при соответствующих значениях x0=0 {\displaystyle x_{0}=0\!\ } или n=0,n=1 {\displaystyle n=0,n=1\!\ } функция f(x)=f(x0) {\displaystyle f(x)=f(x_{0})\!\ }. При этом в конечном неравенстве исчезают ограничения на n {\displaystyle n\!\ }, заданные в начале доказательства, поскольку для них исполняется равенство. ■

Примечания

  • Неравенство также справедливо для x≥−2{\displaystyle x\geq -2} (при n∈N0{\displaystyle n\in \mathbb {N} _{0}}). Доказательство для случая x∈[−2,−1){\displaystyle x\in \left[-2,-1\right)} можно провести так же методом математической индукции.

(1+x)n+1+(1+x)n=(1+x)n(1+x+1)≥(1+nx)(1+x+1)=1+(n+1)x+1+nx(1+x){\displaystyle (1+x)^{n+1}+(1+x)^{n}=(1+x)^{n}(1+x+1)\geq (1+nx)(1+x+1)=1+(n+1)x+1+nx(1+x)}

Так как при x∈[−2,−1){\displaystyle x\in \left[-2,-1\right)} (1+x)n≤1≤1+nx(1+x){\displaystyle (1+x)^{n}\leq 1\leq 1+nx(1+x)}, то (1+x)n+1≥1+(n+1)x{\displaystyle (1+x)^{n+1}\geq 1+(n+1)x}

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *