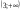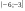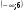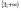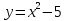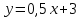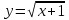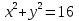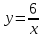Урок 43. нелинейные уравнения и неравенства с двумя переменными — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №43.Нелинейные уравнения и неравенства с двумя переменными.
Перечень вопросов, рассматриваемых в теме:
- уравнение и неравенство, способы их решения;
- система уравнений, система неравенств;
- изображение в координатной плоскости множество решений уравнений, неравенств, систем уравнений, систем неравенств и нахождение площади получившейся фигуры;
Глоссарий по теме
Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.
Все уравнения, которые не являются линейными называются нелинейными.
Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с<0 или ах + bу + с >0, где х и у – переменные, а, b, c – некоторые числа.
Все неравенства, которые не являются линейными называются нелинейными
Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Все системы неравенств, которые не являются линейными называются нелинейными.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Учебник: Алгебра 9 кл с углубленным изучением математики Мнемозина, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Сегодня на уроке мы вспомним нелинейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое нелинейным уравнением и неравенством.
1.Линейные уравнения с двумя переменными.
Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.
Все уравнения, которые не являются линейными называются нелинейными.
Например,  нелинейные уравнения с двумя переменными. Уравнение с двумя переменными можно заменить равносильным уравнением, в котором правая часть будет нулем, а левая многочленом стандартного вида:
нелинейные уравнения с двумя переменными. Уравнение с двумя переменными можно заменить равносильным уравнением, в котором правая часть будет нулем, а левая многочленом стандартного вида: 
Нелинейные уравнения с двумя переменными изображаются на координатной плоскости различными фигурами, каждое уравнение нужно рассматривать индивидуально.
Пример.
Найти множество точек координатной плоскости, удовлетворяющих уравнению:
Уравнение запишем в виде (х-у)(х+у) = 0, значит либо х-у=0, либо х
+у=0. Поэтому множество точек удовлетворяющих уравнению – пара пересекающихся прямых.
Преобразуем левую часть уравнения, используя метод выделения полного квадрата:


Сумма неотрицательных слагаемых равна 0 только в одном случае, когда оба слагаемых одновременно равны 0.
Это уравнение имеет единственное решение: х=2; у=-3. Поэтому множество точек удовлетворяющих уравнению – точка (2;-3).
Пусть на координатной плоскости Оху выбрана точка А(а;b), М(х;у) – произвольная точка этой плоскости, R- расстояние от точки М до точки А. Тогда  , где R>0. Уравнение окружности с радиусом R и с центром в точке А(а;b).
, где R>0. Уравнение окружности с радиусом R и с центром в точке А(а;b).
Запишем уравнение в виде  Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка.
Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка.
Рассмотрим примеры уравнений с двумя переменными, содержащих знак модуля:
Если  то х+у=2 Множество решений этого уравнения часть прямой (отрезок АВ), где А(2;0), В(0;2)
то х+у=2 Множество решений этого уравнения часть прямой (отрезок АВ), где А(2;0), В(0;2)
Аналогично строятся отрезки в трех оставшихся координатных углах. (рисунок 1)

Рисунок 1 – графика 
2.Нелинейные неравенства с двумя переменными.
Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с<0 или ах + bу + с >0, где х и у – переменные, а, b, c – некоторые числа.
Все неравенства, которые не являются линейными называются нелинейными.
Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное равенство.
Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.
- Некоторые из таких неравенств можно привести к виду у<f(x), где f(x) многочлен степени выше первой, те f(x)=0 нелинейное уравнение с одной переменной.
Неравенству у<f(x), соответствует уравнение у = f(x), график которого делит множество не принадлежащих ему точек плоскости на две области: верхнюю и нижнюю. Верхняя область является графиком неравенства у>f(x), а нижняя – графиком неравенства у <f(x).
- Пусть на координатной плоскости Оху выбрана точка А(а;b), М(х;у) – произвольная точка этой плоскости, тогда неравенству
 , где R>0 удовлетворяют все те точки, которые находятся от точки А на расстоянии меньшем R, те все точки и только они, расположенные внутри окружности с радиусом R и центром в точке А(а;b). Аналогично, множество решений неравенства
, где R>0 удовлетворяют все те точки, которые находятся от точки А на расстоянии меньшем R, те все точки и только они, расположенные внутри окружности с радиусом R и центром в точке А(а;b). Аналогично, множество решений неравенства  есть множество точек , лежащих вне окружности.
есть множество точек , лежащих вне окружности.
Пример.
Изобразите в координатной плоскости множества решений неравенства  .
.
- Начертим график уравнения
 . Запишем уравнение в виде
. Запишем уравнение в виде  Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка.
Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка. - Искомое множество решения неравенства – множество точек, лежащих на окружности и внутри окружности с центром в точке (-1;4) и радиусом 3 единичных отрезка.
3. Системы нелинейных уравнений с двумя переменными.
 , где а,b,с,d,e,f – некоторые числа, называется линейной системой с двумя переменными х и у.
, где а,b,с,d,e,f – некоторые числа, называется линейной системой с двумя переменными х и у.Все системы уравнений, которые не являются линейными называются нелинейными.
Пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство называют решением системы.
Решить систему – значит найти множество ее решений.
Каждое решение уравнения с двумя переменными представляет координаты некоторой его точки его графика. Каждое решение системы есть координаты общих точек графиков уравнений системы. Построим графики этих уравнений и найдем координаты точек пересечения.
Например.
Решить систему уравнений 

Первое уравнение системы задает параболу, второе – окружность с центром (-1;3) и радиусом  . Окружность и парабола имеют две общие точки (0;1) (-1,3;5,3). Координаты второй точки приближенные (рисунок 2).
. Окружность и парабола имеют две общие точки (0;1) (-1,3;5,3). Координаты второй точки приближенные (рисунок 2).

Рисунок 2 – решение системы
4. Системы нелинейных неравенств с двумя переменными.
Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Все системы неравенств, которые не являются линейными называются нелинейными.
Рассмотрим систему нелинейных неравенств с двумя переменными на примере:
Изобразить на координатной плоскости Оху фигуру Ф, заданную системой неравенств, и найти площадь фигуры:

Неравенство  заменим равносильной системой
заменим равносильной системой  которая задает множество точек, лежащих на полуокружности и вне ее. А неравенство
которая задает множество точек, лежащих на полуокружности и вне ее. А неравенство  заменим равносильной совокупностью систем
заменим равносильной совокупностью систем  или
или  (рисунок 3)
(рисунок 3)

Рисунок 3 – решение системы
Дополнительный материал
- Найти множество точек координатной плоскости, удовлетворяющих уравнению
 .(рисунок 4)
.(рисунок 4)
График уравнения х^2 можно получить из окружности
можно получить из окружности  сжатием к оси х в 2 раза.
сжатием к оси х в 2 раза.

Рисунок 4 – график уравнения 
Заметим, что фигуру, которая получается сжатием окружности к одному из ее диаметров, называют эллипсом.
- Уравнение вида
 — уравнение ромба , где точка (a;b) точка пересечения диагоналей; диагонали ромба соответственно равны
— уравнение ромба , где точка (a;b) точка пересечения диагоналей; диагонали ромба соответственно равны  .
.
Рассмотрим частный случай:
Если k=m, то диагонали ромба будут равны, значит заданная фигура – квадрат.
Примеры и разборы решений заданий тренировочного модуля
Пример 1.

Графиком данного уравнения является парабола, показанная на рисунке.(рисунок 5)

Рисунок 5 – график 
Пример 2.
Изобразите в координатной плоскости множества решений неравенства  (рисунок 6)
(рисунок 6)
Начертим график уравнения  . Графиком данного уравнения является парабола. Нижняя из образовавшихся областей является графиком неравенства
. Графиком данного уравнения является парабола. Нижняя из образовавшихся областей является графиком неравенства 
Проверим себя: Например, пара (0;0) является решением неравенства  , и принадлежит нижней из образовавшихся областей, значит графиком неравенства 2х+3у<6 является нижняя область.
, и принадлежит нижней из образовавшихся областей, значит графиком неравенства 2х+3у<6 является нижняя область.

Рисунок 6 – решение
Конспект и презентация Неравенства с двумя переменными
Дата проведения _________ УРОК № 48 9 класс, алгебра
Тема Неравенства с двумя переменными
Цели: ввести понятие неравенства с двумя переменными и его решения; формировать умение решать линейные неравенства с двумя переменными.
Образовательные: рассмотреть, как могут решаться неравенства с двумя переменными
Развивающие: Развитие познавательной активности и самостоятельности, умения анализировать, выделять главное, сравнивать, обобщать, обосновывать свое решение
Воспитательные: Привитие интереса к изучаемому предмету.
Основные формы и методы работы: фронтальный опрос, работа в парах
Ход урока
Организационный момент.
5-минутка подготовки к ОГЭ
Устная работа
1. Какие из следующих чисел: –2; –1; 0; 2; 3 – являются решением неравенства х3 – 2х ≥ 1?
2. Подберите два каких-нибудь числа разных знаков, чтобы их сумма была больше 5.
III. Объяснение нового материала.
Объяснение нового материала проводить согласно пункту учебника. Сначала ввести понятие неравенства с двумя переменными и его решения, а затем разобрать, как решается линейное неравенство с двумя переменными.
Вопрос о решении неравенств второй степени с двумя переменными целесообразно рассмотреть на следующем уроке.
Формирование умений и навыков.
1. № 482, № 483 (а, в).
2. № 484 (а, г), № 485.
3. Изобразите на координатной плоскости множество точек, задаваемое неравенством:
а) х < 2; в) –1 ≤ х ≤ 4;
б) у ≥ –3; г) –2 < у < 2.
4. № 492 (а).
Р е ш е н и е
ху ≥ 0.
Произведение двух чисел является неотрицательным в том случае, если эти числа имеют одинаковые знаки. Значит, когда

Первой системе соответствует первая координатная четверть, а другой системе – третья координатная четверть.
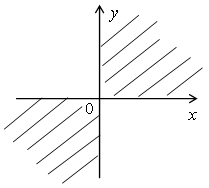
Сильным в учебе учащимся можно предложить дополнительно выполнить № 556.
Р е ш е н и е
| х | + | у | ≤ 1;
| у | ≤ 1 – | х |.
Построим график уравнения | у | = 1 – | х |. Для этого нужно раскрыть знаки модуля.
Получим четыре случая:
1) х ≥ 0, у ≥ 0;у = 1 – х.
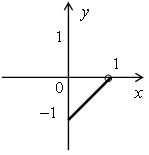
2) х ≥ 0, у < 0;
–у = 1 – х;
у = х – 1.
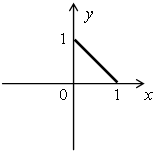
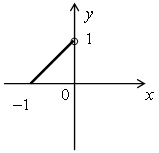
3) х < 0, у ≥ 0;
у = 1 + x.
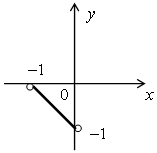
4) x < 0, y < 0;
–у = 1 + х;
у = –х – 1.
Объединяя все эти случаи, получим фигуру:
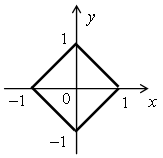
Данному неравенству удовлетворяет множество точек внутренней области этой фигуры.
Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется решением неравенства с двумя переменными?
– Сколько решений может иметь неравенство с двумя переменными?
– Как найти множество решений линейного неравенства с двумя переменными?
Домашнее задание: № 483 (б, г), № 484 (б, в), № 486.
Приложение ОГЭ
Неравенства
1. О числах 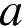 и
и 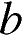 известно, что
известно, что 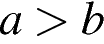 . Среди приведенных ниже неравенств выберите верные:
. Среди приведенных ниже неравенств выберите верные:
В ответе укажите номер правильного варианта.
1) 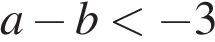 2)
2) 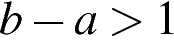 3)
3) 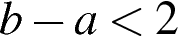 4) Верно 1, 2 и 3
4) Верно 1, 2 и 3
2. На координатной прямой изображены числа 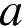 и
и 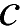 . Какое из следующих неравенств неверно?
. Какое из следующих неравенств неверно?

1) 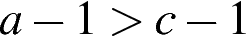 2)
2)  3)
3) 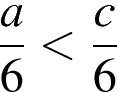 4)
4) 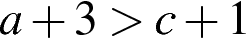
3. Какое из следующих неравенств не следует из неравенства 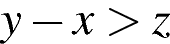 ?
?
В ответе укажите номер правильного варианта.
1) 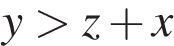 2)
2) 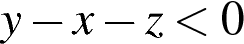 3)
3) 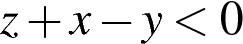 4)
4) 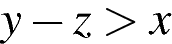
4. Известно, что 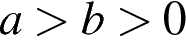 . Какое из указанных утверждений верно?
. Какое из указанных утверждений верно?
В ответе укажите номер правильного варианта.
1) 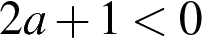 2)
2) 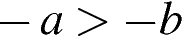 3)
3) 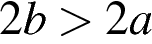 4)
4) 
5. На координатной прямой отмечено число 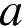 . Какое из утверждений относительно этого числа является верным?
. Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.

1)  2)
2) 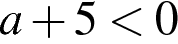 3)
3) 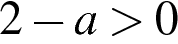 4)
4) 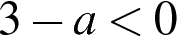
6. На координатной прямой изображены числа 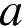 и
и 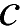 . Какое из следующих неравенств неверно?
. Какое из следующих неравенств неверно?
В ответе укажите номер правильного варианта.

1) 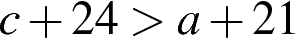 2)
2) 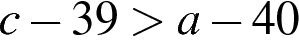 3)
3) 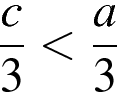 4)
4) 
7. На координатной прямой отмечено число а.
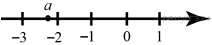
Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
1) 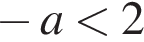 2)
2) 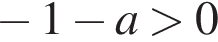 3)
3) 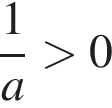 4)
4) 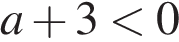
8. На координатной прямой отмечено число а.
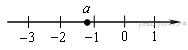
Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
1) 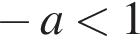 2)
2) 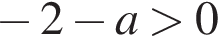 3)
3) 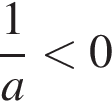 4)
4) 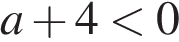
9. На координатной прямой отмечено число а.
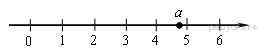
Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
1) 
2) 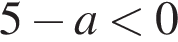
3) 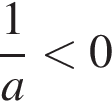
4) 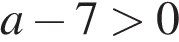
10. На координатной прямой отмечено число а.
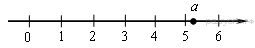
Какое из утверждений относительно этого числа является верным?
В ответе укажите номер правильного варианта.
1) 
2) 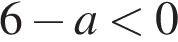
3) 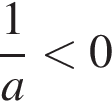
4) 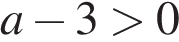
| 1. | Выбор неравенства по рисунку | 1 вид — рецептивный | лёгкое | 1 Б. | По данному рисунку нужно выбрать неравенство из предложенных вариантов. |
| 2. | Выбор линейного неравенства по рисунку | 1 вид — рецептивный | лёгкое | 1 Б. | По данному рисунку выбирается линейное неравенство из предложенных вариантов. Для выбора необходимо проанализировать также построение прямой. |
| 3. | Выбор рисунка по данному уравнению | 1 вид — рецептивный | лёгкое | 1 Б. | Анализируя рисунки и данное уравнение, ставим в соответствие уравнению определённый рисунок. |
| 4. | Выбор и решение уравнения, если известна пара чисел | 1 вид — рецептивный | лёгкое | 1 Б. | Из предложенных уравнений выбирается уравнение, решением которого является данная пара чисел. |
| 5. | Уравнение в целых числах | 2 вид — интерпретация | среднее | 3 Б. | Предлагается решить линейное уравнение с двумя переменными в целых числах. |
| 6. | Площадь фигуры | 2 вид — интерпретация | среднее | 3 Б. | Определяется площадь фигуры, являющейся решением системы неравенств. В шагах решения предлагается схематичный график, точность которого может проверить учитель. |
| 7. | Назови уравнение по рисунку | 3 вид — анализ | среднее | 3 Б. | Требуется выбрать уравнение, которому соответствует данный рисунок. |
| 8. | Реши уравнение второй степени в целых числах | 3 вид — анализ | сложное | 4 Б. | Предлагается решить уравнение второй степени в целых числах с двумя переменными. В ходе решения применяется разложение на множители способом группировки. |
| 9. | Текстовая задача | 3 вид — анализ | сложное | 4 Б. | Предлагается решить текстовую задачу путём составления диофантова уравнения. |
| 10. | Построй график и найди площадь | 3 вид — анализ | сложное | 4 Б. | Требуется построить график уравнения и найти площадь полученной фигуры. |
| 11. | Линейное уравнение с двумя неизвестными | 2 вид — интерпретация | сложное | 2 Б. | Решение линейного уравнения с двумя неизвестными в натуральных числах. |
Неравенства с двумя переменными
2. Изучение нового материала:
1) Слайд 1.
Выполните устно следующее упражнение:
Учащиеся находят отличия в записанных неравенствах (в 2-х неравенствах- по 1 переменной, в остальных – по две)
2) Слайд 2.
Определение неравенства с двумя переменными (заучивание определения и тут же опрос по цепочке).
3) Рассмотрим неравенство
2х2 – у < 6.
При х = 2, у = 5 это неравенство обращается в верное числовое неравенство
2 • 22 — 5 < 6.
Говорят, что пара (2; 5) является решением этого неравенства.
Слайд 3.Определение решения неравенства с двумя переменными (заучивание определения и тут же опрос по цепочке).
4) Рассмотрим на примерах, как изображается на координатной плоскости множество решений неравенства с двумя переменными.
Слайды 4 — 7. Задание 1. Изучить алгоритм нахождения множества решений неравенства
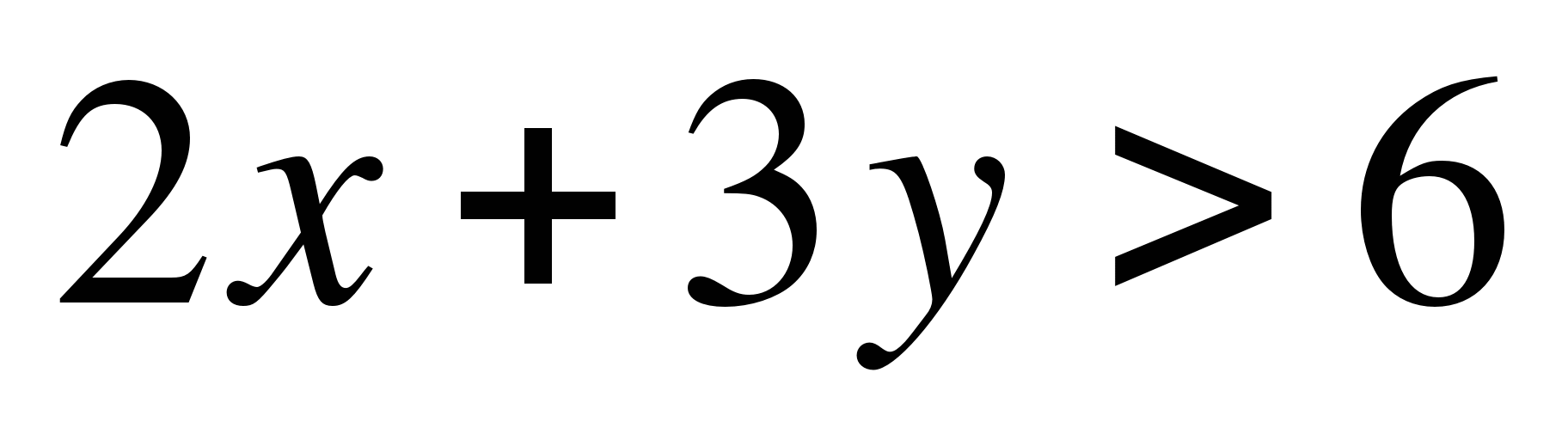 (объяснение учителем по слайдам)
(объяснение учителем по слайдам)
(Алгоритм (есть запись на слайде 9), заготовленный заранее учителем, приклеивается в тетрадях учащимися). Так получается быстрее!!!
5) Повторение алгоритма учащимися.
3. Закрепление изученного материала
Слайды 8 – 11. (Открыть только 8 слайд, когда учащиеся перепишут задание, открыть алгоритм выполнения задания на 9 слайде)
Задание 2. Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству
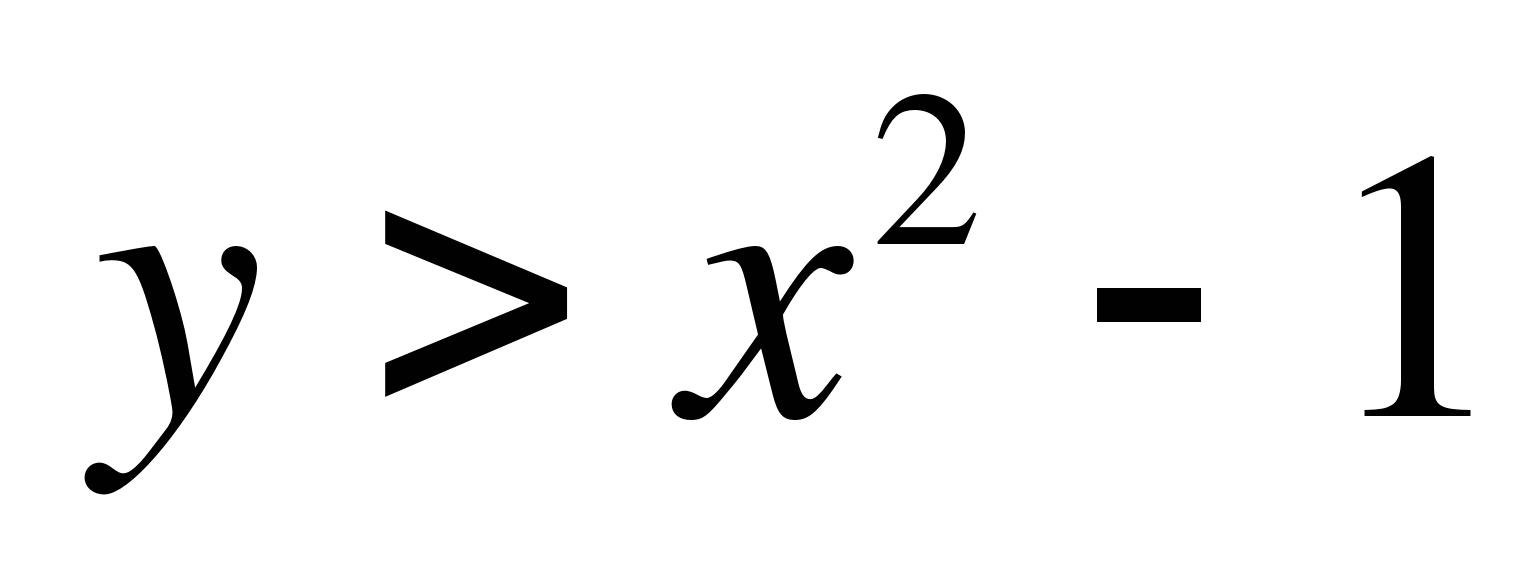 (К доске вызывается 1 ученик)
(К доске вызывается 1 ученик)
Проверка – на 10,11 слайдах.
4.Заключительная часть урока
1) Фронтальный опрос учащихся
— Что называется решением неравенства с двумя переменными?
— Как найти множество решений неравенства с двумя переменными? (повторить 4 пункта алгоритма, если хватает времени, то поспрашивать учащихся)
— Всегда ли решением будет полуплоскость? (нет) Доказательство посмотреть на слайдах.
Слайды12-14. Решение неравенства
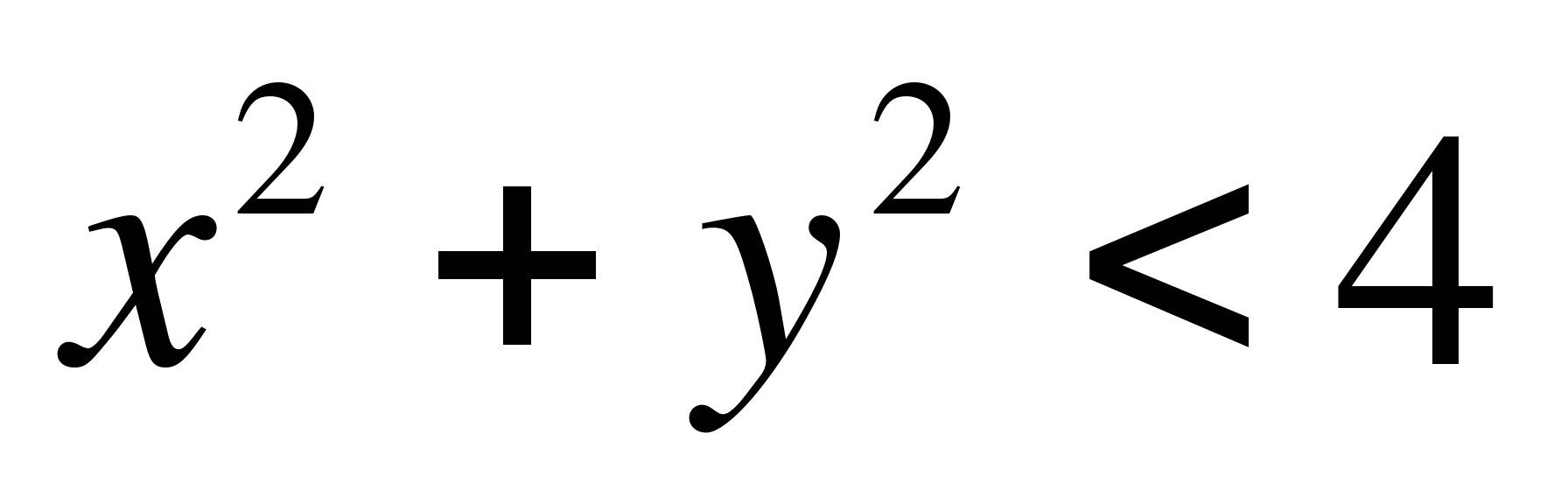 (Ответом является часть плоскости – круг)
(Ответом является часть плоскости – круг)
2) Итог урока. Выставление оценок.
3) Задание на дом:
п.21, выучить правила, №482, №484
Конспект уроков на тему «Неравенства с двумя переменными»














 Предмет: алгебра Класс: 9
Предмет: алгебра Класс: 9
Составитель: Курова Валентина Вениаминовна
Название ОУ: ГУ Затобольская средняя школа № 2 отдела образования акимата Костанайского района
Источники материалов:
1.Алгебра и начала анализа 10-11 класс, Абылкасымова А.Е.
2.Алгебра и начала анализа, Задачник для 10-11 классов Мордюкович А Г.
3. Сборники тестовых заданий ЕНТ, 2012 г
Урок № 1.
Тема урока: Неравенства с двумя переменными
Цель урока: ввести понятие неравенства с двумя переменными, научить решать неравенства с двумя переменными, повторить изученные функции и их графики, развивать умения строить графики, находить решение неравенство с двумя переменными, развивать вычислительные навыки, развивать внимание, математическую речь, умения работать в паре, воспитание самостоятельности, аккуратности, трудолюбия.
Ход урока
Орг момент Тема, цель урока. (2 мин)
Заполняем таблицу.Знаю — Хочу знать — Узнал.
Проверка домашнего задания. Мини-тест( 5 мин)
1 ВАРИАНТ
1. Определите верное решение неравенства: 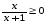
(- ∞; — 1]
 [0; + ∞)
[0; + ∞)(- ∞; 0)
 [1; + ∞)
[1; + ∞)(- ∞; 0]
 (1; + ∞)
(1; + ∞)(- ∞; — 1)
 [0; + ∞)
[0; + ∞)(- ∞; 0]
 [1; + ∞)
[1; + ∞)
2.Решите систему неравенств: 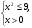
(0; 3)
( — 3; 3)
[0; 3)
(0; 3]
[- 3; 3]
3. Решите систему неравенств 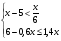
2 ВАРИАНТ
1. Решите систему неравенств: 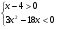
(4; 6)
( — ∞; 4)
[4; 6)
(- ∞; + ∞)
нет решения.
2.Решите неравенство: 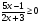
A) 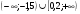
B) 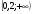
C) 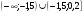
D) 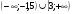 E)
E) 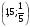
3. Решите систему неравенств: 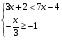
A) 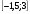 B)
B) 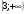
C) 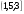 D)
D) 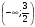 Е) 0
Е) 0
Взаимопроверка.(2 мин). Оценивание. «5» — 3 задания
«4»- 2 задания
«3» — 1 задание
1 ВАРИАНТ 1 Д 2 Д 3 Е 2 ВАРИАНТ 1А 2 А 3С
Повторение изученного материала.(7 мин)
Заполнить таблицу. Коллективная работа.
Формула, задающая функцию
Линия, являющаяся графиком этой функции





5. Изучение нового материала (10 мин)
Найдите отличие в записанных неравенствах
у-9 < 2у + 11, 2х + 3y> 16,
x + 5 > 10, х + 4 <y + 12,
6y> 21y + 3. x + 2 >y,
Определение неравенства с двумя переменными
Выражения, составленные с помощью чисел, двух переменных, знаков действий и знаков сравнения : больше (больше или равно), меньше (меньше или равно), называются неравенствами с двумя переменными.
Неравенства вида f(х, у) > 0 или f(х, у) < 0, где f(х; у) — алгебраическое выражение, называется неравенством с двумя переменными.
Например .х – 5у < 0, у² — 0,5х +16 ≥ 0, х³+(х — у)² -1>0
Решением неравенства с двумя переменными называется пара значений переменных, обращающее данное неравенство в верное неравенство.
Неравенство с двумя переменными чаще всего имеет бесконечное множество решений.
Решить неравенство с двумя переменными, значит найти все его решения или доказать, что решений нет.
Для решения неравенств с двумя переменными используется графический метод.
Рассмотрим неравенство 2х2 – у <6.
При х = 2, у = 5 это неравенство обращается в верное числовое неравенство
2 • 22 — 5 < 6. пара (2; 5) является решением этого неравенства.
Как решить неравенство с двумя переменными?
Алгоритм решения.
Заменить знак неравенства на равно.
Выразить переменную у через переменную х.
Построить график полученного уравнения, линия графика зависит от типа неравенства
(строгое-пунктир, нестрогое- сплошная линия)
Выделить часть плоскости, соответствующую знаку неравенства.
Коллективная работа. Решить неравенство.2x + 3y> 6
Закрепление изученного материала (12 мин)
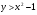 (1 ученик работает у доски, комментируя свои действия)
(1 ученик работает у доски, комментируя свои действия)
х2 + y2< 4 (самостоятельно с последующей проверкой)
7. Итог урока. Оценивание. Дом задание.( 5 мин)
Решить неравенство у ≥ х² — 4х + 4 х² + у² -100 < 0;
— Что называется решением неравенства с двумя переменными?
— Как найти множество решений неравенства с двумя переменными? (повторить алгоритм) Всегда ли решением будет полуплоскость? (нет).
8. Рефлексия (2 мин).
Урок № 2.
Тема урока: Неравенства с двумя переменными
Цель урока: закрепить понятие неравенства с двумя переменными, функции и их графики развивать умения и навыки решать неравенства с двумя переменными, развивать вычислительные навыки, развивать внимание, математическую речь, воспитывать добросовестное отношение к учебе.
Ход урока
Орг момент Тема, цель урока. (2 мин)
Проверка домашнего задания. Проверить наличие домашнего задания. Ответить на вопросы учащихся. (3 мин)
Актуализация знаний учащихся.(5 мин)
а)Назвать графики функций.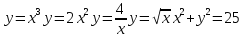
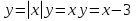
б) Алгоритм решения неравенств с двумя переменными
Заменить знак неравенства на равно.
Выразить переменную у через переменную х.
Построить график полученного уравнения , линия графика зависит от типа неравенства
( строгое-пунктир, нестрогое- сплошная линия)
Выделить часть плоскости, соответствующую знаку неравенства.
Закрепление изученного материала (15 мин).
Работа учащихся у доски и в тетрадях.
-Решить неравенство: x · y ≤ 4
Решение.
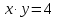 разлелим обе части уравнения на х
разлелим обе части уравнения на х
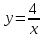 построим график функции, гиперболу
построим график функции, гиперболу
у
х
Контрольные точки (3;2) 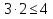 неверно (1;2)
неверно (1;2) 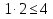 верно
верно
Решить неравенство:у ≥ х² — 4х + 1
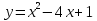
координаты вершины параболы (вопрос из ВОУД)
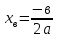 ;
; 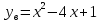
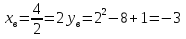 (2;-3)
(2;-3)
При х=0, у=1; (0; 1) симметричная ей точка (4;1)
у
х контрольные точки (3; 1) 1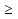 9-12+1 верно
9-12+1 верно
0 2 (-3;-3) -3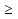 9+12+1 неверно
9+12+1 неверно
Самостоятельная работа проверочного характера.(15 мин)
Решите неравенство: 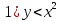 2) 2у + 3х ≤0 3)
2) 2у + 3х ≤0 3) 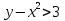
Тетради учащихся собрать на проверку.
6. Итог урока. Оценивание. Дом задание.( 5 мин)
Изобразите на координатной плоскости множество решений неравенства: а)0,5х2 -2у+l<0;
б)4х — 5у > 20 в) | х | + | у | ≤ 1 дополнительно для подготовленных учащихся.
7. Рефлексия (2 мин).
Критерии успеха
Ученик А
Ученик В
Ученик С
Знает виды, типы неравенств, алгоритм решения.
Умеет выражать одну переменную через другую.
Может изобразить решение на координатной плоскости.
Умеет решать неравенства любого вида.
Объясняет ход решения с применением свойств неравенств и видов функции.
Может анализировать материал, выделять главное, второстепенное, находить правильное решение.
Может самостоятельно принимать решения, брать ответственность за работу других учащихся.
Способен аргументировать, отстаивать свою точку зрения
Выполняет задания повышенной сложности.
Неравенства с двумя переменными. Метод областей — Мегаобучалка
Неравенство с двумя переменными в общем случае выглядит так:
f(x,y) V g(x,y), где V — знак ≤, ≥, <, >. (2).
Его ОДЗ — это общая часть областей определения функций f(x,y) и g(x,y), т. е. ОДЗ(2) = D(f) ∩ D(g). Решением неравенства (2) называется такая упорядоченная пара (х0, у0), что f(х0, у0) V g(х0, у0). Что для нахождения множества решений неравенства (2) удобно использовать аналог метода интервалов, который называется методом областей и представляет собой следующий алгоритм.
Для решения неравенства (2) достаточно сделать следующее.
| Найти ОДЗ неравенства (2). Линии, не входящие в ОДЗ следует изобразить пунктирными. Изобразить на плоскости линии, являющиеся графиком уравнения . В случае нестрогого знака (т. е. ≥ или ≤) неравенства (2) эти линии следует изобразить сплошными, если же знак неравенства (2) строгий (т. е. > или <), то пунктирными. Линии из предыдущих двух пунктов разбивают плоскость на области. Из каждой области следует выбрать по точке и подставить ее координаты в исходное неравенство (2) чтобы проверить: выполнено это неравенство в выбранной области, или нет. Заштриховать области, в которых неравенство (2) выполняется. |
Замечание. Поскольку никакая из точек, лежащих на пунктирной линии, не может быть решением неравенства, точки пресечения сплошных и пунктирных линий на координатной плоскости следует изображать светлыми (или, что то же самое выколотыми).
Рассмотрим пример использования метода областей.
Пример 4. Решить методом областей неравенство .
Решение.
ОДЗ этого неравенства состоит из всех точек координатной плоскости, удовлетворяющих неравенству или , т.е. . Пунктирной линией изображаем окружность с центром в точке (-2,0) радиуса 2 (рис. 6).
Решая уравнение, соответствующее данному неравенству, получим на ОДЗ или . Графиком последнего уравнения является ось Ох и парабола . Точки пересечения этих линий с пунктирной окружностью изображаем светлыми (рис. 6).
Нарисованные линии разбивают плоскость на восемь областей. Из каждой области выбираем по точке и подставляем их координаты в данное неравенство.
(1,1) , т. е. неравенство выполняется.
(1,-1) , т. е. неравенство выполняется.
(1,10) , т. е. неравенство не выполняется.
(1,-10) , т. е. неравенство выполняется.
, т. е. неравенство не выполняется.
, т. е. неравенство выполняется.
(-2,1) , т. е. неравенство выполняется.
Замечание. При решении нестрогих неравенств с двумя переменными, также как и в случае одной переменной, могут получиться изолированные решения. Примером может служить неравенство . Дело в том, что график уравнения является только одна точка — (0,-1) (поскольку это уравнение может выполняться только в случае, когда одновременно и ). Поэтому решением неравенства будет верхняя полуплоскость и одна точка нижней полуплоскости — (0,-1).
Задачи с параметром
Уравнения с параметрами. В общем случае уравнение с переменной х и параметром а имеет вид
F(x, a) = 0, (3)
где F(x, a) — некоторое алгебраическое выражение от х и а. Решением такого уравнения называется функция x = f(a), определенная на некотором множеств , при подстановке которой уравнение (3) превращается в тождество
F(f(a), a) = 0 на всем множестве А. Решить уравнение (3) — это означает разбить всю действительную прямую R (область изменения параметра ) на множества А, В, С, …, на каждом из которых необходимо найти все решения этого уравнения, либо доказать, что решений не существует. Граничные точки множеств А, В, С, … принято называть критическими значениями параметра. Рассмотрим несколько примеров.
Пример 1. Решить уравнение .
Решение. или . В этом примере мы получили два решения и (где и ), причем . Критических значений параметра нет.
Ответ: или
Пример 2. Решить уравнение .
Решение. Для нахождения зависимости х от а необходимо разделить обе части этого уравнения на коэффициент при переменной х. Сначала рассмотрим случай, когда этот коэффициент обращается в ноль. При а = 1 получается уравнение , справедливое при всех . При а = — 1 получается уравнение без корней. При всех остальных значениях параметра получаем или . В этом примере на множестве А = (- ∞; -1) U (- 1; 1) U (1; ∞) найдено решение . На одноточечном множестве В = { — 1 } доказано,что нет решений, а на множестве С = { 1 } уравнение справедливо при всех . Критическими значениями параметра являются .
Ответ: при уравнение справедливо при всех х;
при нет решений;
при решением является .
Пример 3. Решить уравнение .
Решение. При а = 0 это уравнение превращается в линейное — 2х + 1 = 0 с корнем . Во всех остальных случаях уравнение будет квадратным, его дискриминант равен D = 4a + 4. Условию D ≥ 0 удовлетворяют все а ≥ — 1. Таким образом, при а < — 1 данное уравнение не имеет решений, а при используя формулу корней квадратного уравнения, получаем . В этом примере на множестве А = [- 1; 0) U (0; ∞) было найдено два решения и (где и ), на одноточечном множестве В = {0} решение уравнения единственно — и, наконец, при всех значений параметра из множества С = (-∞; — 1) уравнение не имеет решений. Критическими значениями параметра являются а = -1 и а = 0.
Ответ: при а = 0 ;
при а < — 1 нет решений;
при остальных значениях параметра решениями являются
Метод, с помощью которого были решены три предыдущих задачи, можно назвать алгебраическим. В этих примерах с помощью простых алгебраических преобразований от исходного уравнения по цепочке равносильных уравнений мы приходим к уравнению (или совокупности уравнений), которое является решением уравнения с параметром. В дальнейшем мы будем использовать графический способ решения уравнений с параметром, который заключается в следующем.
| 1. От уравнения F(x, a) = 0 перейти к системе F(x, y) = 0, y = a. 2. На плоскости хОу построить график уравнения F(x, y) = 0. 3. Пересечь прямую у = а с графиком уравнения F(x, y) = 0 и спроецировать это пересечение на ось Ох (т.е., фактически, найти первые координаты точек пересечения прямой у = а с графиком уравнений F(x, y) = 0). |
Решим графическим способом следующую задачу
Пример 4. Решить уравнение |2x — 1| + |x — 3 | = x + a.
Решение. 1. Перейдем к системе |2x — 1| + |x — 3 | = x + у,
у = а.
2. Необходимо построить график уравнения |2x — 1| + |x — 3 | = x + у или
у = |2x — 1| + |x — 3 | — x . Нулями подмодульных выражений будут и
х = 3. Знаки подмодульных выражений на каждом из трех промежутков определяются без труда.
| 2х — 1 | - | + | + |
| х — 3 | - | - | + |
Раскрывая модули на каждом из трех промежутков, получим
График этой функции изображен на рисунке.
3. Пересекая прямую у = а с графиком уравнения, замечаем, что возможны три различных случая.
При а < 2 пересечение пусто и данное уравнение решений не имеет. При а = 2 пересечением является отрезок и его проекция на ось Ох являются . Наконец, при а > 2 будут две точки пересечения. Первая точка определяется из системы у = 4 — 4х и
у = а, ее первая координата находится из уравнения 4 — 4х = а и . Вторая точка определяется из системы у = 2х — 4 и у = а, ее первая координата находится из уравнения 2х — 4 = а и равна .
Ответ: при а < 2 нет решений;
при а = 2 ;
при а > 2 или .
Замечание. Плоскость хОу предпочтительнее плоскости хОа в графическом способе решения по следующим двум причинам. Во-первых, прямая у = а в плоскости хОу обозначает горизонтальную прямую, в плоскости хОа уравнение а = а задает всю плоскость и формально преодолеть это затруднение непросто. Во-вторых, в уравнение с параметром F(x, a) = 0 переменные х и а входят не равнозначно. Связано это с необходимостью выразить х через а, а не наоборот. В плоскости хОа разный «статус» переменных х и а теряется, в то же время переход к системе F(x, a) = 0 и у = а сохраняет информацию о том, что а является параметром.
Заключение.
В результате выполненной работы мы выяснили, что метод интервалов не только широко используется для решения многих неравенств, но для и исследования многих задач повышенной трудности. Метод областей позволяет эффективно строить множества точек на координатной плоскости.
Также было показано, что метод областей может быть более эффективен, чем метод интервалов при решении уравнений и неравенств с параметром, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра.
В процессе исследования был систематизирован теоретический материал по проблемам неравенств с двумя неизвестными и системам неравенств с двумя неизвестными. Практически выработаны методики решения задач на нахождение: множества точек плоскости, координаты, которых удовлетворяют данному неравенству; площади фигуры ограниченной неравенством; значений параметра.
Результаты данной работы могут быть использованы для приобретения опыта решения задач с использованием метода областей, для повышения уровня логической культуры и для более глубокой подготовки к ЕГЭ.
Список использованной литературы:
1)Математика для поступающих в серьезные вузы. О.Ю.Черкасов , А.Г.Якушев . – M.: Московский лицей, 2009.
2)ЕГЭ 2010 математика .Федеральный институт педагогических измерений. Официальный разработчик контрольных измерительных материалов для ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА. Общая редакция: А.Л.Семенов, И.В.Ященко.
3) http://ege-study.ru/materialy-ege/metod-intervalov/
4) http://school-collection.edu.ru/catalog/rubr/49e3d8f3-baf8-4599-b6e3-b9fe79594e71/82292/




 , где R>0 удовлетворяют все те точки, которые находятся от точки А на расстоянии меньшем R, те все точки и только они, расположенные внутри окружности с радиусом R и центром в точке А(а;b). Аналогично, множество решений неравенства
, где R>0 удовлетворяют все те точки, которые находятся от точки А на расстоянии меньшем R, те все точки и только они, расположенные внутри окружности с радиусом R и центром в точке А(а;b). Аналогично, множество решений неравенства  есть множество точек , лежащих вне окружности.
есть множество точек , лежащих вне окружности. . Запишем уравнение в виде
. Запишем уравнение в виде  Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка.
Множеством решения данного уравнения является окружность центром в точке (-1;4) и радиусом 3 единичных отрезка. .(рисунок 4)
.(рисунок 4) — уравнение ромба , где точка (a;b) точка пересечения диагоналей; диагонали ромба соответственно равны
— уравнение ромба , где точка (a;b) точка пересечения диагоналей; диагонали ромба соответственно равны  .
.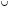 [0; + ∞)
[0; + ∞)