несобственные интегралы 1 и 2 рода — Высшая математика
Несобственные интегралы 1 и 2 рода.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
Область интегрирования является бесконечной. Например, является бесконечным интервалом
.
Функция является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал конечный, и функция интегрируема по Риману, то значение несобственного интеграла совпадает с значением определённого интеграла.
Несобственные интегралы I рода
Пусть определена и непрерывна на интервале и. Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае
называется сходящимся.
- Если не существует конечного ( или ), то интеграл
называется расходящимся к , или просто расходящимся.
Пусть определена и непрерывна на множестве от и
. Тогда:
- Если , то используется обозначение и интеграл называется несобственным интегралом Римана первого рода. В этом случае
называется сходящимся.
- Если не существует конечного ( или ), то интеграл
называется расходящимся к , или просто расходящимся.
Если функция определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
, где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
Несобственные интегралы II рода
Пусть определена на , терпит бесконечный разрыв в точке x=a и
. Тогда:
Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если или , то обозначение сохраняется, а
называется расходящимся к , или просто расходящимся.
Пусть определена на , терпит бесконечный разрыв при x=b и
. Тогда:
Если , то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если или , то обозначение сохраняется, а
называется расходящимся к , или просто расходящимся.
Абсолютная сходимость
Интеграл называется абсолютно сходящимся, если
сходится. Если интеграл сходится абсолютно, то он сходится.
Условная сходимость
Интеграл называется условно сходящимся, если сходится, а
расходится.
Пример 1. Вычислить интеграл:
Положим z = e ix, тогда cos x = (z + z — 1)/2. Вычислим dz = d(e ix), откуда dx = (dz)/(iz), а исходный интеграл запишется в виде:
Так как при |a|<1, подинтегральная функция внутри круга
имеет один полюс первого порядка в точке z = a.
Поскольку будем иметь
Пример 2.1. Вычислить интеграл:
Рассмотрим функцию
Она является аналитической функцией, имеющей полюсы второго порядка в точках и в бесконечности имеет нуль второго порядка.
Согласно формуле (1.1) имеем
Пример 2.2. Вычислить интеграл:
Используя результаты вычисления интеграла в примере 2.1 (обозначив его
как I 1 ), вычислим данный интеграл:
Источники использованной информации:
https://ru.wikipedia.org/wiki/Несобственный_интеграл
http://www.mathprofi.ru/nesobstvennye_integraly.html
http://www.exponenta.ru/educat/class/courses/tfkp/theme11/example.asp
Электронный учебник по математическому анализу
был построен в предположении, что числа $a,\,b$ конечны и $f(x)$ — непрерывная функция. Если одно из этих предположений нарушается, говорят о несобственных интегралах.
Несобственный интеграл 1 рода возникает, когда по крайней мере одно из чисел $a,\,b$ бесконечно.
10.1.1 Определение и основные свойства
Рассмотрим сначала ситуацию, когда нижний предел интегрирования конечен, а верхний равен $+\infty$, другие варианты обсудим несколько позднее. Для $f(x)$, непрерывной при всех интересующих нас $x$, рассмотрим интеграл
\begin{equation} I=\int _a^{+\infty}f(x)dx. \quad(19) \label{inf1} \end{equation}Прежде всего надо установить смысл этого выражения. Для этого введем функцию
\[ I(N)=\int _a^{N}f(x)dx \]и рассмотрим ее поведение при $N\rightarrow +\infty$.
Определение. Пусть существует конечный предел
\[ A=\lim_{N \rightarrow +\infty}I(N)=\lim_{N \rightarrow +\infty}\int _a^{N}f(x)dx. \]Тогда говорят, что несобственный интеграл 1 рода (19) является сходящимся и ему приписывают значение $A$, саму функцию называют интегрируемой на интервале $\left[ a, \, +\infty \right )$. Если же указанного предела не существует или он равен $\pm \infty$, то говорят, что интеграл (19) расходится.
Пример.
Рассмотрим интеграл
\[ I=\int _0^{+\infty} \frac{dx}{1+x^2}. \]Положим
\[ I(N)=\int _0^{N} \frac{dx}{1+x^2}. \]В данном случае известна первообразная подинтегральной функции, так что
\[ I(N)=\int _0^{N} \frac{dx}{1+x^2}=arctgx|_0^{N}=arctgN. \]Известно, что $arctg N \rightarrow \pi /2 $ при $N \rightarrow +\infty$. Таким образом, $I(N)$ имеет конечный предел, наш несобственный интеграл сходится и равен $\pi /2$.
Сходящиеся несобственные интегралы 1 рода обладают всеми стандартными свойствами обычных определенных интегралов.
1. Если $f(x)$, $g(x)$ интегрируемы на интервале $\left[ a, \, +\infty \right )$, то их сумма $f(x)+g(x)$ также интегрируема на этом интервале, причем \[ \int _a^{+\infty}\left(f(x)+g(x)\right )dx=\int _a^{+\infty}f(x)dx+\int _a^{+\infty}g(x)dx. \] 2. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right )$, то для любой константы $C$ функция $C\cdot f(x)$ также интегрируема на этом интервале, причем \[ \int _a^{+\infty}C\cdot f(x)dx=C \cdot \int _a^{+\infty}f(x)dx. \] 3. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right )$, причем на этом интервале $f(x)>0$, то \[ \int _a^{+\infty} f(x)dx\,>\,0. \] 4. Если $f(x)$ интегрируема на интервале $\left[ a, \, +\infty \right )$, то для любого $b>a$ интеграл \[ \int _b^{+\infty} f(x)dx \] сходится, причем \[ \int _a^{+\infty}f(x)dx=\int _a^{b} f(x)dx+\int _b^{+\infty} f(x)dx \] (аддитивность интеграла по интервалу).Справедливы также формулы замены переменной, интегрирования по частям и т.д. (с естественными оговорками).
Пример.
Рассмотрим интеграл
\begin{equation} I=\int _1^{+\infty}\frac{1}{x^k}\,dx. \quad (20) \label{mod} \end{equation}Введем функцию
\[ I(N)=\int _1^{N}\frac{1}{x^k}\,dx. \]В данном случае первообразная известна, так что
\[ I(N)=\int _1^{N}\frac{1}{x^k}\,dx\,=\frac{x^{1-k}}{1-k}|_1^N= \frac{N^{1-k}}{1-k}-\frac{1}{1-k} \]при $k \neq 1$,
\[ I(N)=\int _1^{N}\frac{1}{x}\,dx\,=lnx|_1^N= lnN \]при $k = 1$. Рассматривая поведение при $N \rightarrow +\infty$, приходим к выводу, что интеграл (20) сходится при $k>1$, а при $k \leq 1$ — расходится.
Рассмотрим теперь вариант, когда нижний предел интегрирования равен $-\infty$, а верхний конечен, т.е. рассмотрим интегралы
\[ I=\int _{-\infty}^af(x)dx. \]Однако этот вариант можно свести к предыдущему, если сделать замену переменных $x=-s$ и поменять затем пределы интегрирования местами, так что
\[ I=\int _{-a}^{+\infty}g(s)ds, \]$g(s)=f(-s)$. Рассмотрим теперь случай, когда имеется два бесконечных предела, т.е. интеграл
\begin{equation} I=\int _{-\infty}^{+\infty}f(x)dx, \quad (21) \label{intr} \end{equation}причем $f(x)$ непрерывна при всех $x \in \mathbb{R}$. Разобъем интервал на две части: возьмем $c \in \mathbb{R}$, и рассмотрим два интеграла,
\[ I_1=\int _{-\infty}^{c}f(x)dx, \quad I_2=\int _{c}^{+\infty}f(x)dx. \]Определение. Если оба интеграла $I_1$, $I_2$ сходятся, то интеграл (21) называется сходящимся, ему приписывают значение $I=I_1+I_2$ ( в соответствии с аддитивностью по интервалу). Если хотя бы один из интегралов $I_1$, $I_2$ расходится, интеграл (21) называется расходящимся.
Можно доказать, что сходимость интеграла (21) не зависит от выбора точки $c$.
Несобственные интегралы 1 рода с интервалами интегирования $\left(-\infty, \, c \right]$ или $(-\infty, \, +\infty )$ также обладают всеми стандартными свойствами определенных интегралов (с соответствующей переформулировкой, учитывающей выбор интервал интегрирования).
10.1.2 Признаки сходимости несобственных интегралов 1 рода
Теорема(первый признак сравнения). Пусть $f(x)$, $g(x)$ — непрерывны при $x>a$, причем $0a$. Тогда
1. Если интеграл \[ \int _a^{+\infty}g(x)dx \] сходится, то сходится и интеграл \[ \int _a^{+\infty}f(x)dx. \] 2. Если интеграл \[ \int _a^{+\infty}f(x)dx \] расходится, то расходится и интеграл \[ \int _a^{+\infty}g(x)dx. \]Теорема(второй признак сравнения). Пусть $f(x)$, $g(x)$ — непрерывны и положительны при $x>a$, причем существует конечный предел
\[ \theta = \lim_{x \rightarrow +\infty} \frac{f(x)}{g(x)}, \quad \theta \neq 0, \, +\infty. \]Тогда интегралы
\[ \int _a^{+\infty}f(x)dx, \quad \int _a^{+\infty}g(x)dx \]сходятся или расходятся одновременно.
Пример.
Рассмотрим интеграл
\[ I=\int _1^{+\infty}\frac{1}{x+\sin x}\,dx. \]Подинтегральное выражение — положительная функция на интервале интегрирования. Далее, при $x \rightarrow +\infty$ имеем:
$\sin x$ является «малой» поправкой в знаменателе. Точнее, если взять $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$, то
\[ \lim _{x \rightarrow +\infty}\frac{f(x)}{g(x)}=\lim _{x \rightarrow +\infty}\frac{x}{x+\sin x}=1. \]Применяя второй признак сравнения, приходим к выводу, что наш интеграл сходится или расходится одновременно с интегралом
\[ \int _1^{+\infty}\frac{1}{x}\,dx . \]Как было показано в предыдущем примере, этот интеграл расходится ($k=1$). Следовательно, исходный интеграл расходится.
Задачи.
Вычислить несобственный интеграл или установить его сходимость (расходимость).
1. \[ \int _{0}^{+\infty}e^{-ax}\,dx. \] 2. \[ \int _{0}^{+\infty}xe^{-x^2}\,dx. \] 3. \[ \int _{-\infty}^{+\infty}\frac{2xdx}{x^2+1}. \] 4. \[ \int _{0}^{+\infty}\frac{xdx}{(x+2)^3}. \] 5. \[ \int _{-\infty}^{+\infty}\frac{dx}{x^2+2x+2}. \] 6. \[ \int _{1}^{+\infty}\frac{lnx}{x^2}\,dx. \] 7. \[ \int _{1}^{+\infty}\frac{dx}{(1+x)\sqrt{x}}. \] 8. \[ \int _{0}^{+\infty}e^{-\sqrt{x}}\,dx. \] 9. \[ \int _{0}^{+\infty}e^{-ax}\cos x\,dx. \] 10. \[ \int _{0}^{+\infty}\frac{xdx}{x^3+1}. \]15. Несобственные интегралы. Несобственные интегралы первого рода
Выше был определён интеграл для ограниченных и заданных на ограниченном отрезке функций. Распространим понятие интеграла на случаи, когда одно или оба этих условия нарушаются.
Определение. Пусть задана на бесконечном промежутке и для всякого существует интеграл Предел называется несобственным интегралом первого рода (интегралом по неограниченному промежутку) и обозначается Если существует и конечен, то несобственный интеграл первого рода называется сходящимся, если же он не существует или равен Бесконечности, то несобственный интеграл первого рода называется расходящимся.
Примеры.
1. Рассмотрим . Пусть Тогда Таким образом, рассмотренный интеграл при расходится. Пусть теперь Тогда
И мы окончательно получили, что рассматриваемый интеграл при расходится и при сходится. Этот интеграл часто используется в признаке сравнения в качестве эталонного.
2. Выясним сходимость интеграла .
Имеем
. Следовательно, интеграл сходится и его значение равно .
3. Выяснить сходимость интеграла . По определению получаем
.
Следовательно, интеграл сходится и его значение равно .
4. Для интеграла имеем
.
Следовательно, интеграл расходится.
5. Для интеграла по определению имеем
.
Следовательно, интеграл сходится и его значение равно 1.
6. Выяснить сходимость интеграла , .
По определению
Следовательно, интеграл сходится и его значение равно .
Задание 2.4
Вычислить несобственные интегралы первого рода или доказать их расходимость.
1. ; 2.; 3. ; 4. ;
5. ; 6. .
Ответы: 1. ; 2. расходится; 3. ; 4. расходится; 5. расходится; 6. .
Нам в дальнейшем понадобится следующий важный результат.
Теорема 2.8. (Критерий Коши). Несобственный интеграл первого рода сходится тогда и только тогда, когда для всякого существует Такое, что для всех выполнено неравенство
Доказательство этого результата опустим.
Определение. Несобственный интеграл первого рода называется абсолютно сходящимся, если сходится интеграл
Отметим, что если несобственный интеграл первого рода сходится абсолютно, то он сходится. Действительно, тогда для интеграла выполнен критерий Коши, а в силу справедливости неравенства , критерий Коши выполнен и для интеграла
Обратное утверждение неверно.
Сходимость несобственного интеграла определяется аналогично. Предлагается проделать это самостоятельно.
Для несобственного интеграла можем записать и назвать этот интеграл сходящимся, если сходятся оба слагаемых. Если хотя бы один из этих интегралов расходится, то будем считать интеграл расходящимся. В качестве точки выбирают обычно 0.
Пример. Рассмотрим интеграл По определению сходимости этого интеграла получаем
Так как оба слагаемых расходятся, то исходный интеграл расходится. Получаемая при этом неопределённость при разных скоростях стремления к и к даёт разные результаты. В частности, если , , то
.
Если , , то абсолютно аналогично показывается, что этот предел равен . Подобрав скорости стремления к и к можно получить в пределе любое заранее заданное число от до .
С другой стороны, при согласованном стремлении верхнего и нижнего пределов к можем записать
Это дает возможность ввести новое понятие.
Определение. Говорят, что несобственный интеграл первого рода сходится в смысле главного значения Коши, если существует и конечен предел .
Рассмотренный выше пример показывает, что несобственный интеграл первого рода может сходиться в смысле главного значения Коши и расходиться в обычном смысле.
Отметим несколько свойств несобственных интегралов первого рода
1. Если интеграл сходится, то для всякого интеграл сходится и
2. Если интеграл сходится, то сходится интеграл и имеет место равенство
3. Если интегралы и сходятся, то сходятся интегралы и имеет место равенство
Обратное утверждение неверно, то есть, если интеграл от алгебраической суммы функций сходится, то интегралы от слагаемых сходиться не обязаны. Например, интегралы и расходятся, а интеграл , как будет показано позднее, сходится.
Для других типов несобственных интегралов первого рода свойства аналогичны.
Сходимость не всех несобственных интегралов первого рода просто выяснить по определению. Поэтому часто используют так называемые признаки сравнения в непредельной и предельной формах.
Теорема 2.9. Пусть для всякого Выполнено неравенство . Тогда, если интеграл абсолютно сходится, то интеграл абсолютно сходится, а если интеграл абсолютно расходится, то интеграл абсолютно расходится.
Доказательство. Действительно, в условиях теоремы для всех имеем . Тогда, если интеграл сходится, то есть монотонно возрастающая ограниченная сверху функция от и поэтому имеет предел при . Если интеграл расходится, то и поэтому .
Теорема 2.10. Если и — бесконечно малые в одного порядка малости, то есть , то интегралы И либо оба абсолютно сходятся, либо оба абсолютно расходятся.
Доказательство. Так как , то . Возьмем . По определению предела существует такое, что для всех выполнено неравенство а, следовательно, и неравенство Из последнего неравенства и теоремы 2.9 получаем утверждение теоремы.
Замечание. После изучения теоремы 2.10 может сложиться впечатление, что для сходимости несобственного интеграла первого рода, в том числе и абсолютной, необходимо, чтобы подынтегральная функция была бесконечно малой при . То, что это не так, показывает следующий пример [15].
Возьмем функцию, график которой состоит из отрезков прямых, соединяющих точки , , , . Ее аналитическое выражение имеет вид
Площадь, заключенная между графиком этой функции и осью , равна сумме площадей треугольников с вершинами в точках , , , . Так как площадь каждого такого треугольника равна , , то . Заметим, что условие ограниченности функции несущественно, так как вершины треугольников можно взять, например, в точках , , , ..
Примеры
1. Выяснить сходимость интеграла
Так как для всех а интеграл сходится, то и исходный интеграл тоже сходится.
2. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 2 и так как сходится, то исходный интеграл сходится.
3. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 1,5 и так как сходится, то исходный интеграл сходится.
4. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен И, следовательно, интеграл сходится.
5. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 1,5 и, следовательно, интеграл сходится.
6. Выяснить сходимость интеграла
Находя порядок малости подынтегральной функции относительно функции, получаем
Таким образом, порядок малости подынтегральной функции относительно равен 0,5 и, следовательно, интеграл расходится.
7. Интеграл сходится, так как имеет место оценка для всех , а интеграл , как было показано ранее, сходящийся.8. Интеграл расходится, так как имеет место оценка для всех , а интеграл, как было показано ранее, расходится.
Задание 2.5
Используя признак сравнения выяснить сходимость несобственных интегралов. В ответе указана сходимость и порядок малости подынтегральной функции относительно .
1. ; 2. ; 3. ; 4. ; 5. ; 6. .
Ответы: 1. сходится, ; 2. сходится, ;
3. расходится, ; 4. сходится, ; 5. сходится, ;
6. сходится, ;
| < Предыдущая | Следующая > |
|---|
§1. Несобственные интегралы 1-го рода
– 68–
Тема НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
 для случая конечного промежутка
для случая конечного промежутка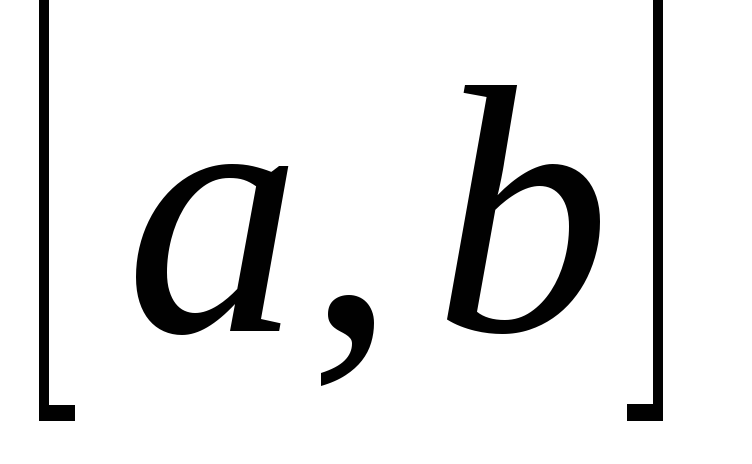 и ограниченной функции
и ограниченной функции (см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации.
(см. теорему 1 из §3). Теперь займемся
обобщением этого понятия для случаев
бесконечного промежутка и неограниченной
функции. Необходимость такого обобщения
показывают, например, такие ситуации. 1.
Если, используя формулу для длины дуги,
попытаться вычислить длину четверти
окружности 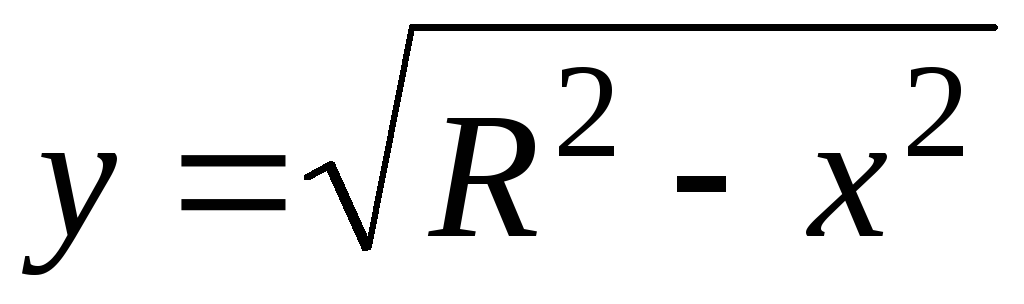 ,
, ,
то придем к интегралу от неограниченной
функции:
,
то придем к интегралу от неограниченной
функции:

 .
. 2.
Пусть тело массой  движется
по инерции в среде с силой сопротивления
движется
по инерции в среде с силой сопротивления  ,
где
,
где — скорость тела. Используя второй закон
Ньютона (
— скорость тела. Используя второй закон
Ньютона ( ,
где
,
где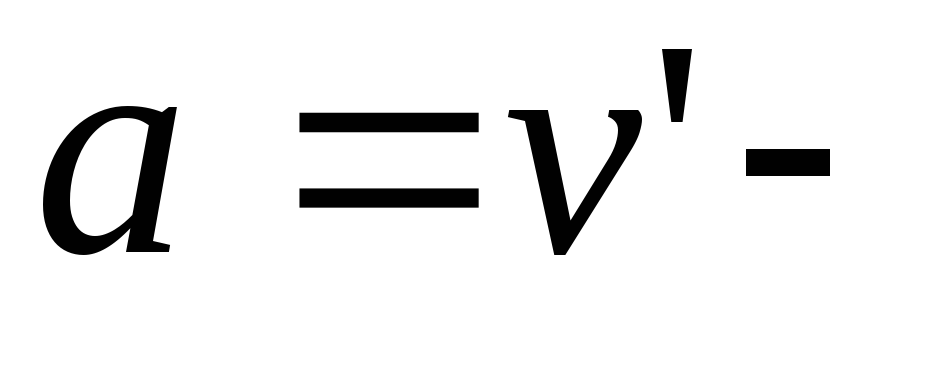 ускорение),
получим уравнение:
ускорение),
получим уравнение: ,
где
,
где
 Если
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда
Если
нам потребуется вычислить путь, пройденный
телом до полной остановки, т.е. до момента,
когда  ,
то придем к интегралу по бесконечному
промежутку:
,
то придем к интегралу по бесконечному
промежутку: 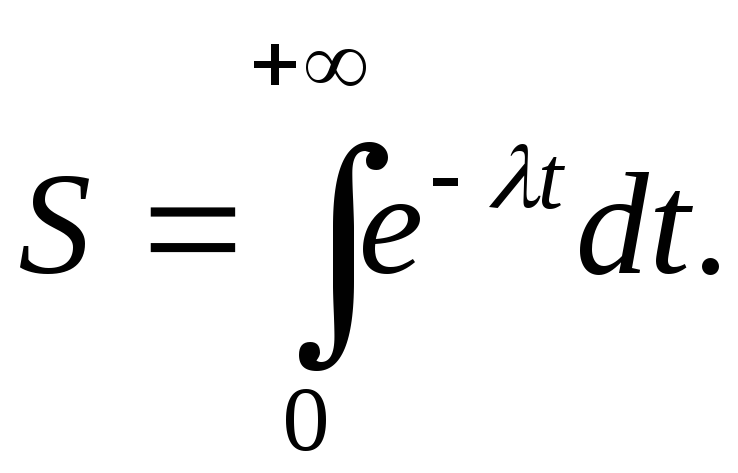
I Определение
Пусть
функция 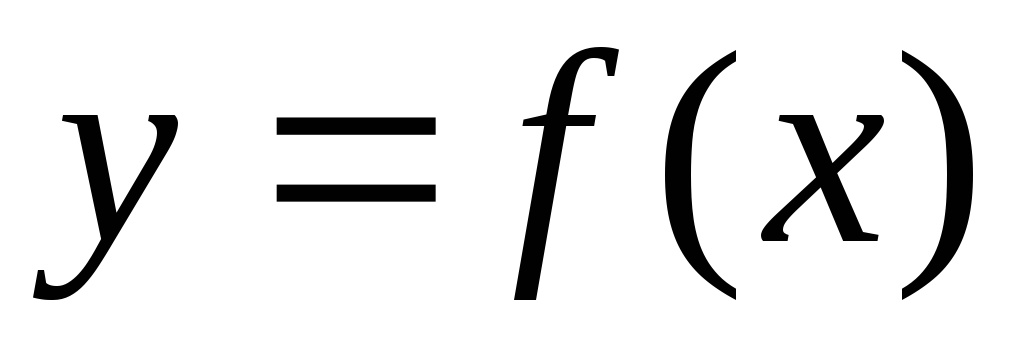 определена и непрерывна на промежутке
определена и непрерывна на промежутке .
Тогда для любого
.
Тогда для любого она интегрируема на промежутке
она интегрируема на промежутке ,
то есть существует интеграл
,
то есть существует интеграл .
.
Определение
1.
Конечный или бесконечный предел этого
интеграла при  называют несобственным интегралом 1-го
рода от функции
называют несобственным интегралом 1-го
рода от функции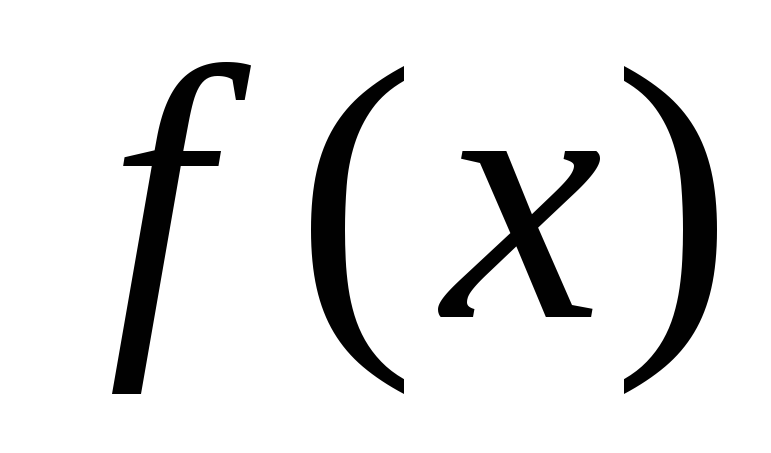 по промежутку
по промежутку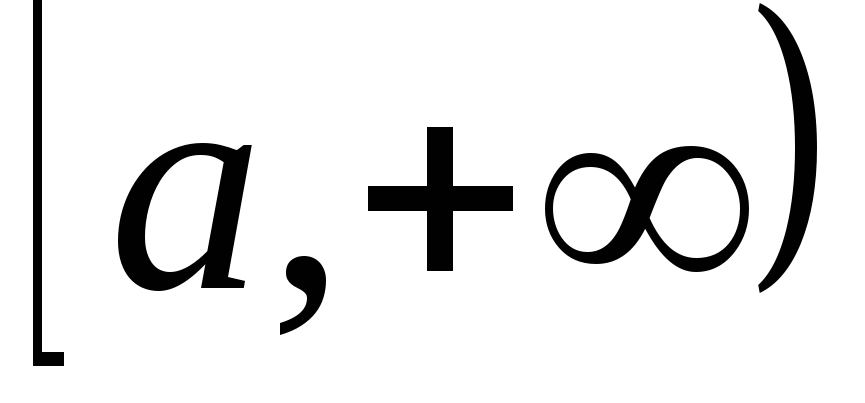 и обозначают символом
и обозначают символом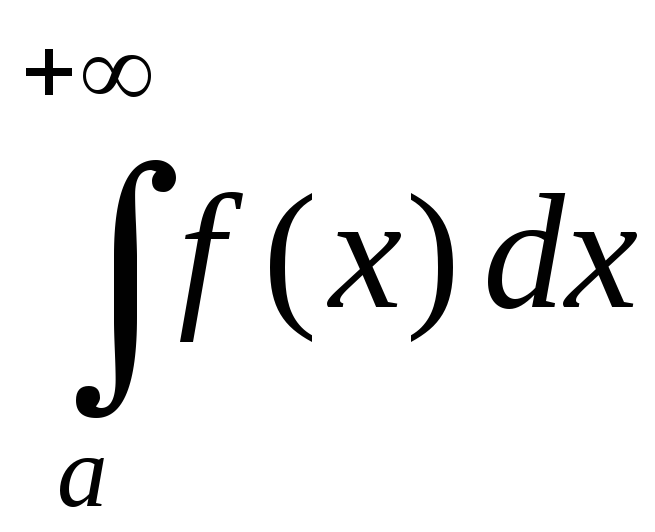 .
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (
.
При этом, если указанный предел конечен,
то несобственный интеграл называют
сходящимся, в противном случае (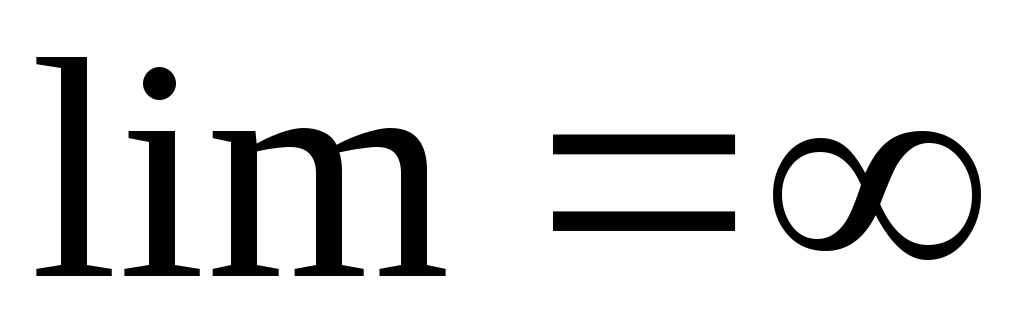 или не существует ) – расходящимся.
или не существует ) – расходящимся.
Итак, по определению
| (1) |
Примеры
1..
2.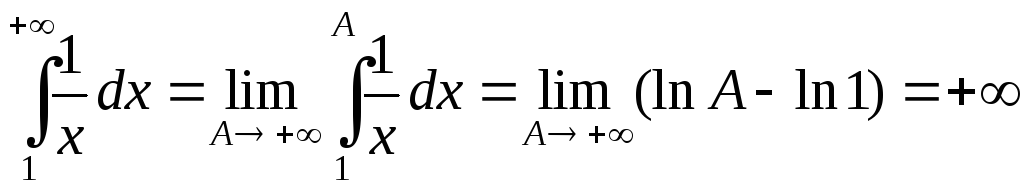 .
.
3.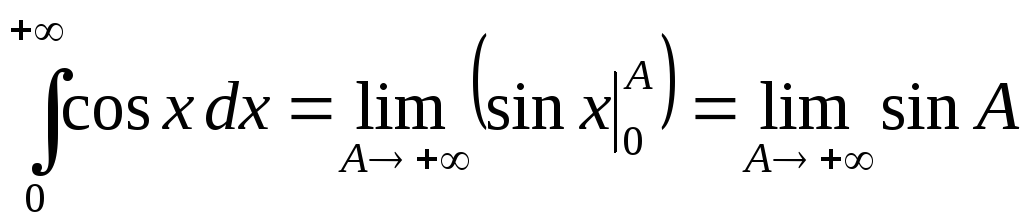 – не существует.
– не существует.
Несобственный интеграл из примера 1 сходится, в примерах 2 и 3 интегралы расходятся.
II Формула Ньютона – Лейбница для несобственного интеграла первого рода
Пусть 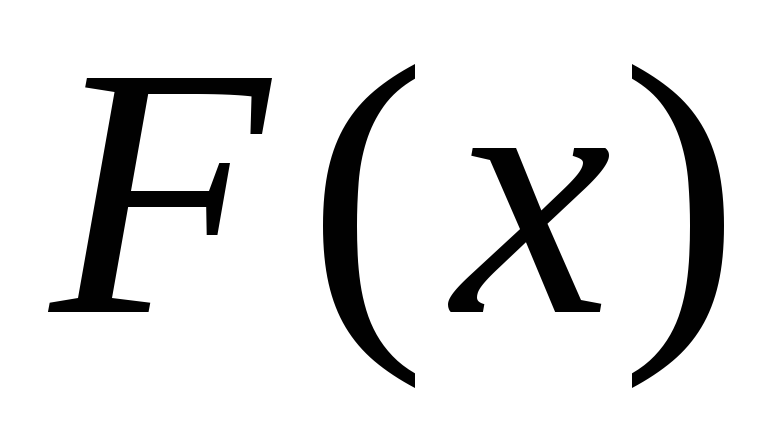 — некоторая первообразная для функции
— некоторая первообразная для функции (сущест-вует на
(сущест-вует на ,
т.к.
,
т.к. — непрерывна). Тогда
— непрерывна). Тогда
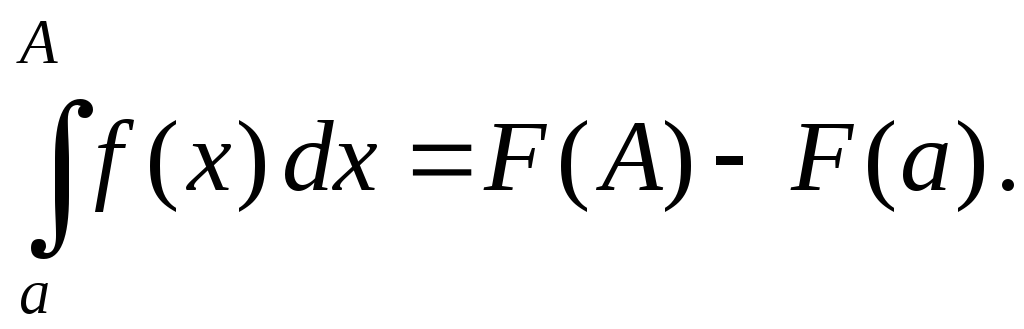
Отсюда
ясно, что сходимость несобственного
интеграла (1) равносильна существованию
конечного предела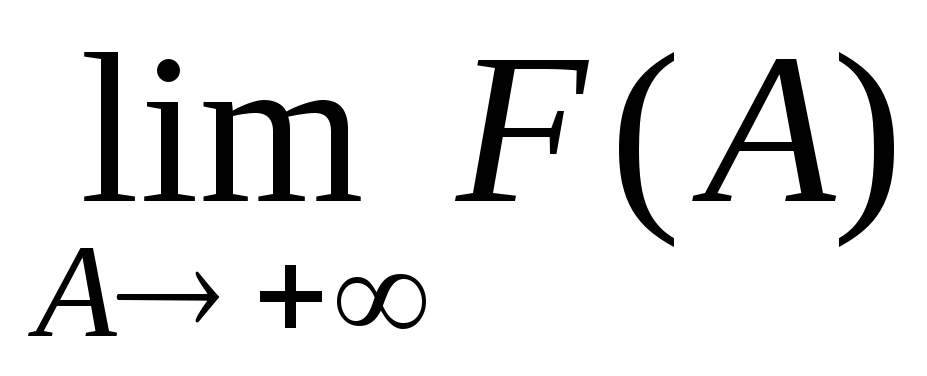 .
Если этот предел обозначить
.
Если этот предел обозначить ,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
,
то можно написать для интеграла (1)
формулу Ньютона-Лейбница:
 ,
где
,
где  .
.
Примеры.
4.  .
.
5.  .
.
6.
Более сложный пример: 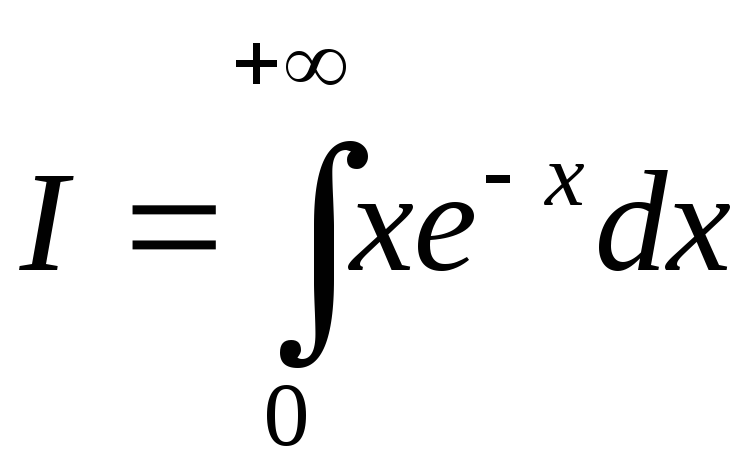 .
Сначала найдем первообразную:
.
Сначала найдем первообразную:

Теперь
можем найти интеграл  , учитывая,
что
, учитывая,
что
 :
:
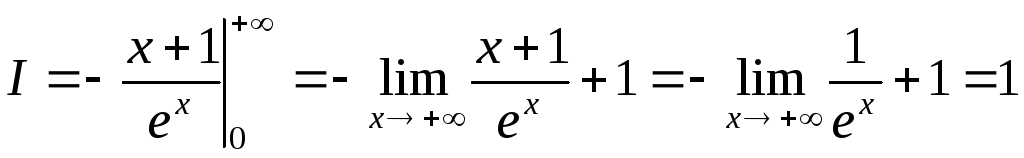 .
.
III Свойства
Приведем ряд свойств несобственного интеграла (1), которые вытекают из общих свойств пределов и определенного интеграла:
интегралы
 и
и
 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;если
 ,
то интегралы
,
то интегралы и
и сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно;если интеграл
 сходится, то
сходится, то .
.
IV Другие определения
Определение
2.
Если  непрерывна
на
непрерывна
на  ,
то
,
то
 .
.
Определение
3.
Если 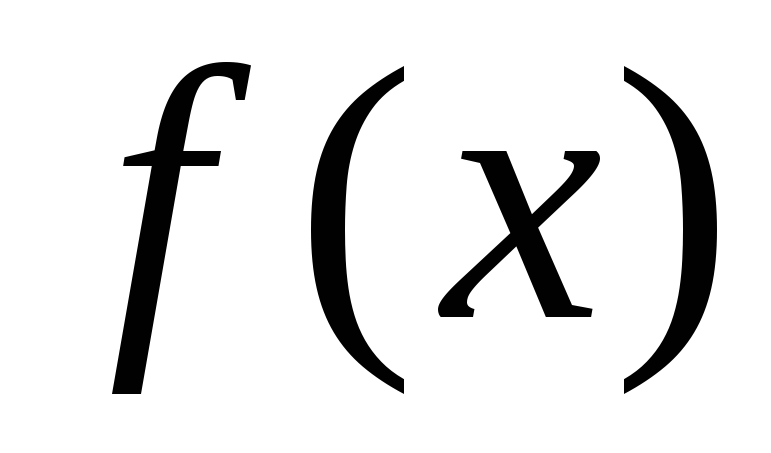 непрерывна
на
непрерывна
на ,
то принимают по определению
,
то принимают по определению
 (
( –
произвольное),
–
произвольное),
причем несобственный интеграл в левой части сходится, если только оба ин-теграла в правой части сходятся.
Для этих интегралов, как и для интеграла (1) можно написать соответствующие формулы Ньютона – Лейбница.
Пример
7. 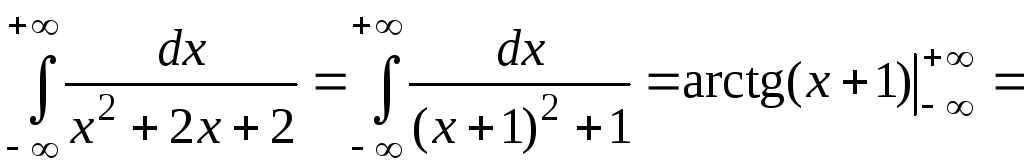

§2. Признаки сходимости несобственного интеграла 1-го рода
Чаще всего несобственный интеграл вычислить по определению не-возможно, поэтому используют приближенное равенство
 (для
больших
(для
больших  ).
).
Однако, это соотношение имеет смысл лишь для сходящихся интегралов. Необходимо иметь методы выяснения поведения интеграла минуя определение.
I Интегралы от положительных функций
Пусть  на
на  . Тогда определенный интеграл
. Тогда определенный интеграл  как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
как функция верхнего предела есть
функция возрастаю-щая (это следует из
общих свойств определенного интеграла).
Теорема
1.
Несобственный интеграл 1го рода от неотрицательной функ-ции сходится
тогда и только тогда, когда функция 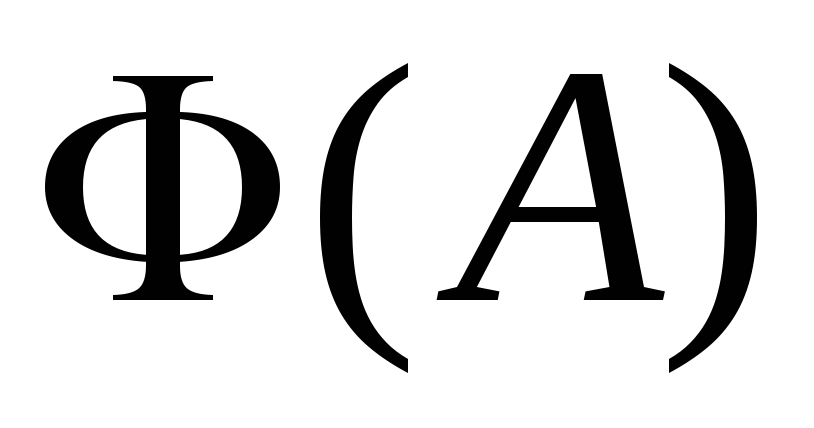 остается
ограниченной при увеличении
остается
ограниченной при увеличении .
.
Эта теорема – следствие общих свойств монотонных функций. Практического смысла теорема почти не имеет, но позволяет получить т.н. признаки сходимости.
Теорема
2 (1-й признак сравнения). Пусть функции 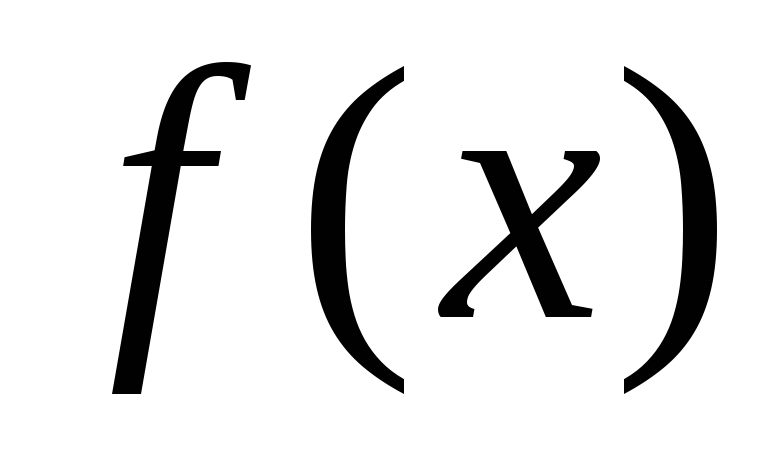 и
и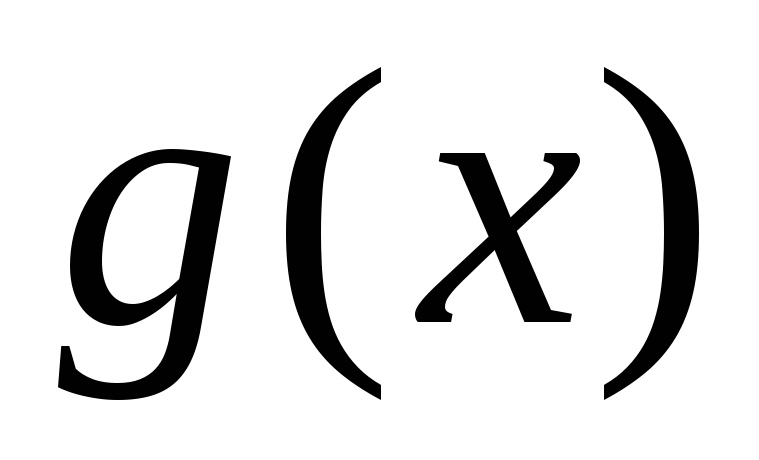 непре-рывны на
непре-рывны на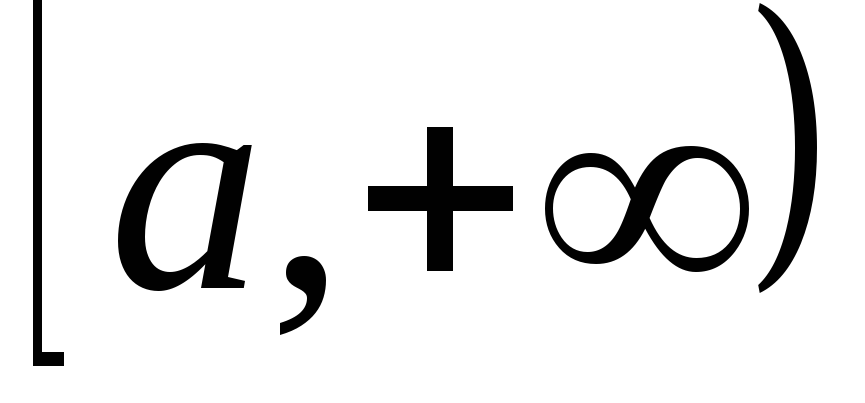 и удовлетворяют неравенству
и удовлетворяют неравенству .
Тогда:
.
Тогда:
1)
если интеграл  сходится, то и
сходится, то и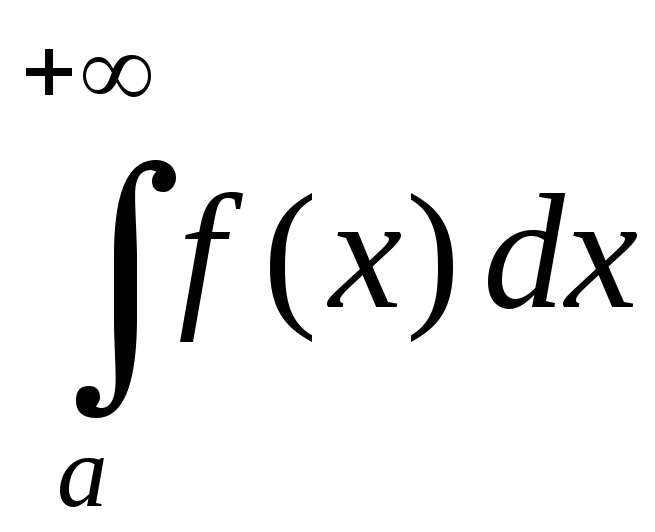 сходится;
сходится;
2)
если интеграл  расходится, то и
расходится, то и расходится.
расходится.
Доказательство.
Обозначим:  и
и .
Так как
.
Так как ,
то
,
то
 .
Пусть интеграл
.
Пусть интеграл сходится, тогда (в силу теоремы 1) функция
сходится, тогда (в силу теоремы 1) функция ‒ ограничена. Но тогда и
‒ ограничена. Но тогда и ограничена,
а значит, интеграл
ограничена,
а значит, интеграл тоже сходится. Аналогично доказывается
и вторая часть теоремы.
тоже сходится. Аналогично доказывается
и вторая часть теоремы.
Этот
признак не применим в случае расходимости
интеграла от  или сходимости интеграла от
или сходимости интеграла от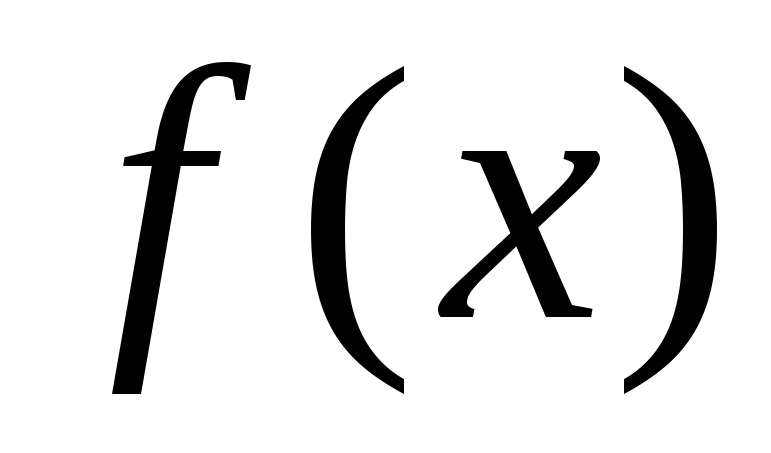 .
Этот недостаток отсутствует у 2-го
признака сравнения.
.
Этот недостаток отсутствует у 2-го
признака сравнения.
Теорема
3 (2-й признак сравнения). Пусть функции 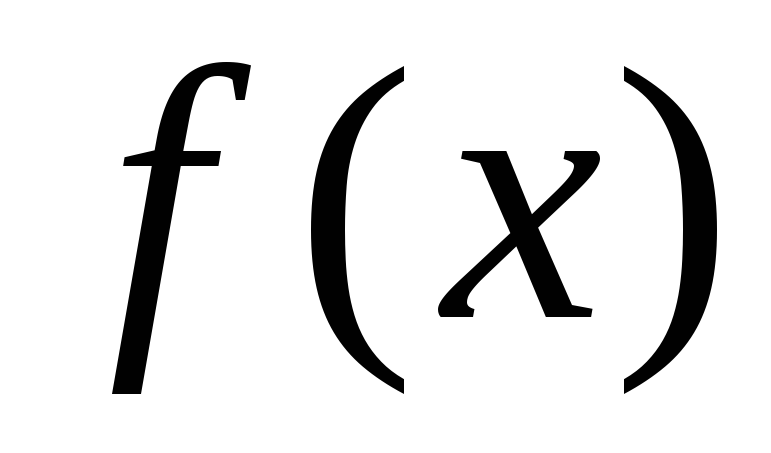 и
и непрерывны и неотрицательны на
непрерывны и неотрицательны на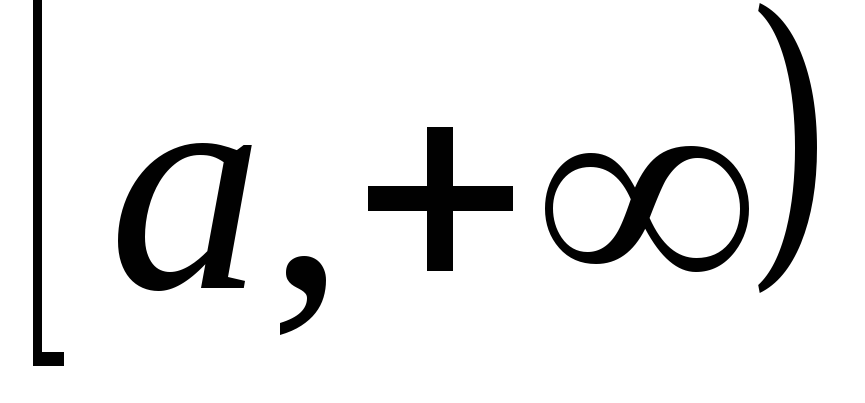 .
Тогда, если
.
Тогда, если при
при ,
то несобственные интегралы
,
то несобственные интегралы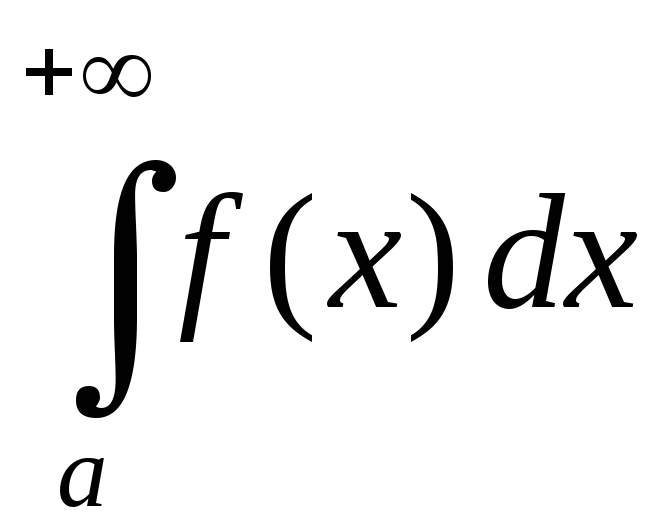 и
и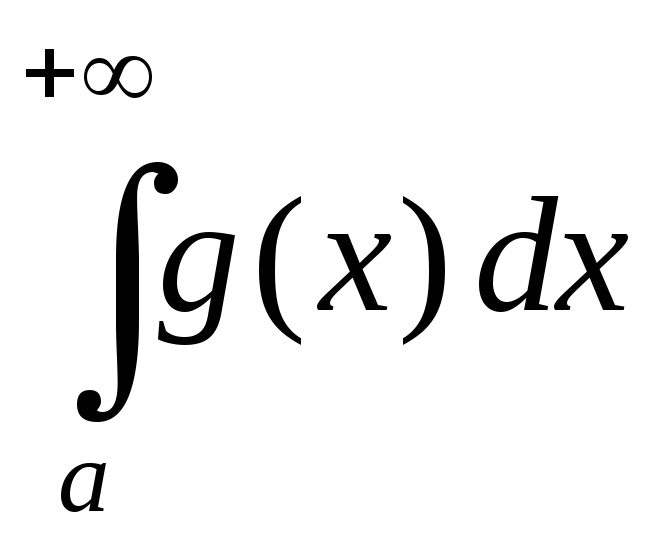 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Из условия теоремы получим такую цепочку равно-сильных утверждений:
 ,
, 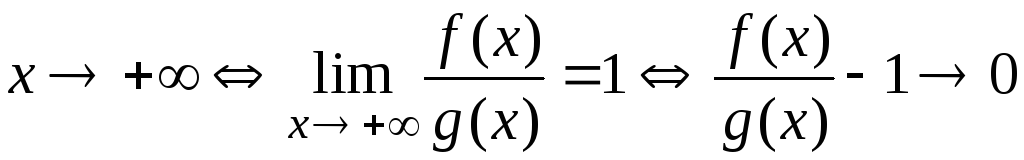 ,
,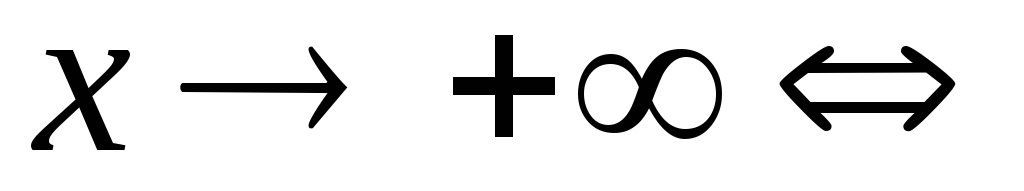
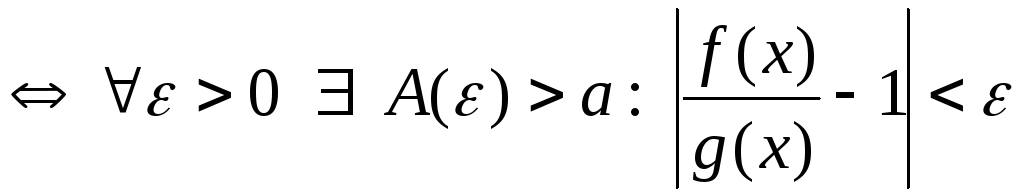
 .
.
Пусть,
например,  .
Тогда:
.
Тогда:
 .
.
Применим теорему 2 и свойство 1) из §1 и получим утверждение теоремы 3.
В
качестве эталонной функции, с которой
сравнивают данную, высту-пает степенная
функция  ,
, .
Предлагаем студентам самим доказать,
что интеграл
.
Предлагаем студентам самим доказать,
что интеграл
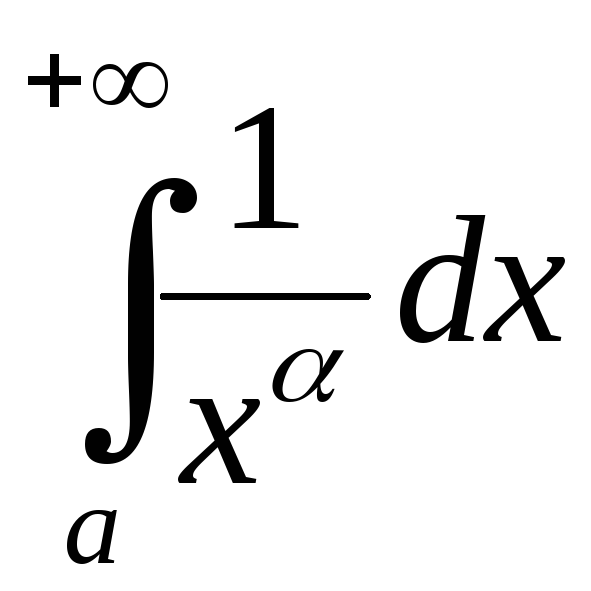
сходится
при  и расходится при
и расходится при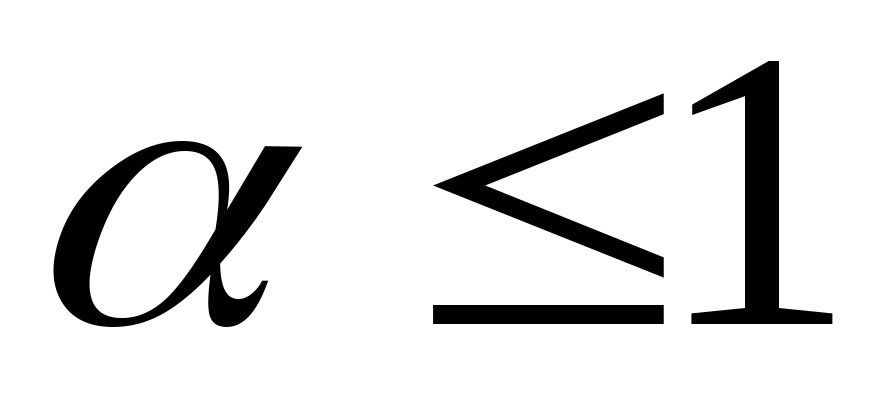 .
.
Примеры.
1.  .
.
Рассмотрим
подынтегральную функцию на промежутке  :
:
 ,
, 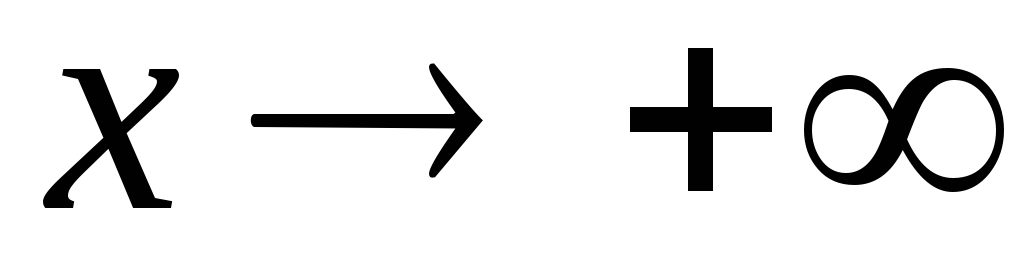 .
.
Интеграл  сходится, ибо
сходится, ибо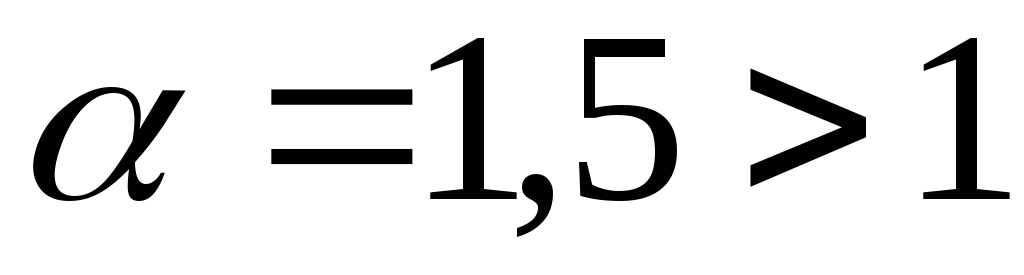 .
По 2-му признаку сравнения сходится и
интеграл
.
По 2-му признаку сравнения сходится и
интеграл ,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
,
а в силу свойства 2) из §1 сходится и
исход-ный интеграл.
2. .
.
Так
как  ,
тоcуществует
,
тоcуществует  такое, что при
такое, что при
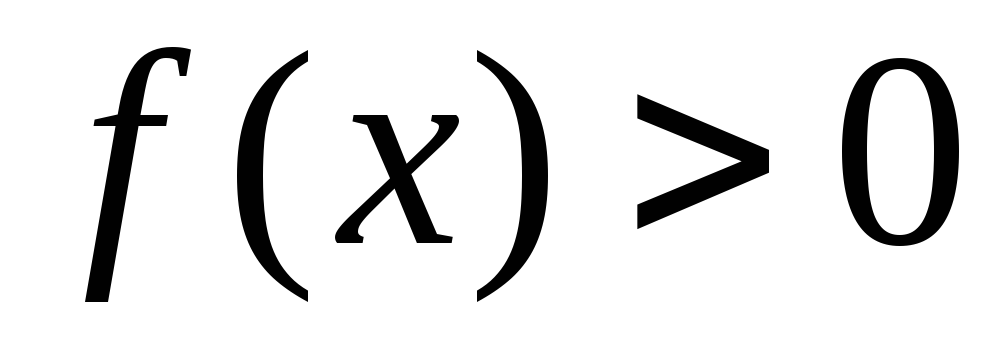 .
Для таких значений переменной:
.
Для таких значений переменной:
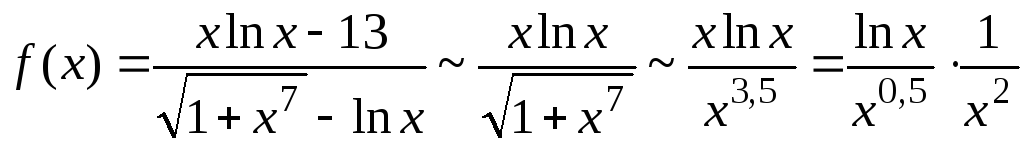 .
.
Известно, что логарифмическая функция растет медленнее степенной, т.е.
 ,
,
а значит, начиная с некоторого значения переменной, эта дробь меньше 1. Поэтому
 .
.
Интеграл  сходится как эталонный. В силу 1-го
признака сравнения сходится и
сходится как эталонный. В силу 1-го
признака сравнения сходится и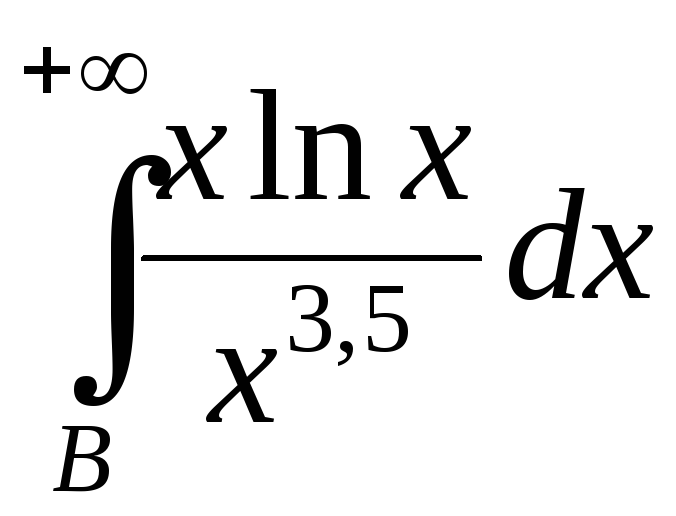 .
Применяя 2-й признак, получим, что и
интеграл
.
Применяя 2-й признак, получим, что и
интеграл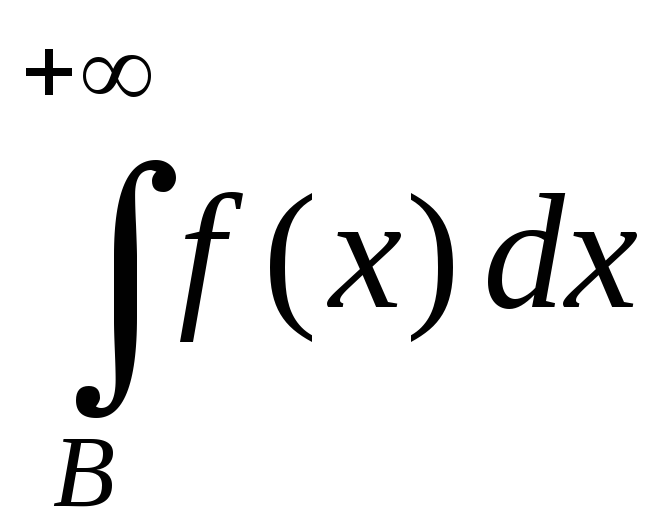 сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
сходится. И снова свойство 2) из §1
доказывает сходимость исходного
интеграла.
несобственный интеграл второго рода — ПриМат
В противном случае несобственный интеграл называют расходящимся.
Аналогично, если существует конечный , то несобственный интеграл $II$ рода называют сходящимся и полагают
$$\int\limits_a^b{f(x)dx}=\lim_{\xi \to a+0}\int\limits_{\xi}^{b}{f(x)dx}$$
В противном случае, если такого предела нет, расходящимся.
Тест по теме: Несобственные интегралы от неограниченных функций
Лимит времени: 0
Информация
Этот тест покажет насколько хорошо вы усвоили данную тему.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 5
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Нет рубрики 0%
- Математический анализ 0%
- С ответом
- С отметкой о просмотре
Таблица лучших: Тест по теме: Несобственные интегралы от неограниченных функций
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Поделиться ссылкой:
15. Несобственные интегралы по неограниченному промежутку (первого рода)
Определение
несобственного интеграла по бесконечному
промежутку. Пусть функция f(x)
определена на полуоси и
интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла
и
интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла при
при называется
несобственным интегралом функции f(x)
от a
до
называется
несобственным интегралом функции f(x)
от a
до  и
обозначается
и
обозначается Итак,
по определению,
Итак,
по определению, 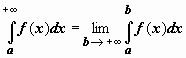 Если
этот предел существует и конечен,
интеграл
Если
этот предел существует и конечен,
интеграл называется
сходящимся; если предел не существует
или бесконечен, интеграл называется
расходящимся.
называется
сходящимся; если предел не существует
или бесконечен, интеграл называется
расходящимся.
Несобственные интегралы от неограниченных функций (второго рода)
Особенность
на левом конце промежутка интегрирования.
Пусть функция f(x)
определена на полуинтервале (a,
b],
интегрируема по любому отрезку  ,
и имеет бесконечный предел при
,
и имеет бесконечный предел при 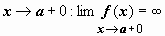 Несобственным
интегралом от f(x) по отрезку [a, b] называется
предел
Несобственным
интегралом от f(x) по отрезку [a, b] называется
предел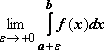 Если
этот предел конечен, говорят, что интеграл
сходится; если предел не существует или
бесконечен, говорят, что интеграл
расходится.
Если
этот предел конечен, говорят, что интеграл
сходится; если предел не существует или
бесконечен, говорят, что интеграл
расходится.
16.Правила оценки сходимости несобственных интегралов
Для
исследования сходимости и расходимости
несобственных интегралов применяется
признак сравнения: Пусть функция f(x) и
g(x) удовлетворяют неравенству:  и
несобственный интеграл
и
несобственный интеграл сходится.
Тогда сходится и несобственный
интеграл
сходится.
Тогда сходится и несобственный
интеграл Доказательство:
В силу сходимости
Доказательство:
В силу сходимости по критерию Коши для функции
по критерию Коши для функции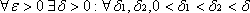 выполняется
неравенство
выполняется
неравенство .
Но тогда, ввиду неравенств:
.
Но тогда, ввиду неравенств: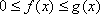 аналогично
неравенство будет справедливо и для
функции f(x), т.е.
аналогично
неравенство будет справедливо и для
функции f(x), т.е. Следовательно,
по критерию Коши существует предел:
Следовательно,
по критерию Коши существует предел: т.е.
этот интеграл сходится.
т.е.
этот интеграл сходится.
Замечание1:
Аналогичный признак сравнения справедлив
и для несобственных интегралов 2 рода.
Замечание2: Отрицанием признака сравнения
будет следующее утверждение: если
несобственный интеграл 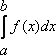 расходится,
то расходится и несобственный интеграл
расходится,
то расходится и несобственный интеграл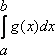
Интегральный
признак сходимости. Сходимость ряда 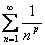 Теорема. Пусть
Теорема. Пусть  — непрерывная, неотрицательная, монотонно
убывающая функция, определенная при
— непрерывная, неотрицательная, монотонно
убывающая функция, определенная при  .
Тогда ряд
.
Тогда ряд  и
интеграл
и
интеграл  либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся.
Доказательство. Ввиду монотонности при всех  выполняются
неравенства
выполняются
неравенства 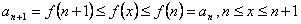 .
Интегрируя, получаем
.
Интегрируя, получаем 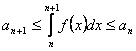 .
Тогда
.
Тогда  ,
или
,
или 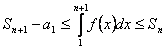 .
Поэтому если
.
Поэтому если  сходится,
то
сходится,
то  .
Тогда
.
Тогда 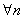
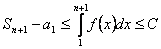 и
и  ,
,  ряд сходится. Пусть теперь наоборот,
известно, что ряд сходится. Тогда
ряд сходится. Пусть теперь наоборот,
известно, что ряд сходится. Тогда  .
Взяв произвольное
.
Взяв произвольное  выберем
выберем 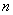 так,
чтобы
так,
чтобы  .
Тогда
.
Тогда  .
Значит,
.
Значит,  сходится.
сходится.
17.Площадь плоской фигуры.
(Площадь плоской фигуры) Заключим фигуру Р в прямоугольник со сторонами параллельными осм Ох и Оу прямоуг обозн R; Разабьём прам R на мн-во мелких прямоуг.; Обозначим А фигуру полученную объединением прямоуг , целиком лежащих в плоскости R, а через В фигуру полученную объедин прямоугольников лежащих в Р. A-òA B-òB ; Пусть d- наибольшая диагональ прямоугольников разбиения, если при d®0 òA и òB ® к одному и томуже пределу, то фигура Р-наз квадрируемой, а её площадь считается равной ò; Пусть ф-ция f(x) –непрерывна на [a,b] и f(x)³0 «xÎ [a;b] и ограничена снизу осью Ох а по бокам x=a, x=b. Пусть t={xi}i=0i=it-произвольное разбиение отр [a,b]; git={(x,y), xÎ[xi-1,xi], 0£y£mi=inff(x)} Git={(x,y), xÎ [xi-1,xi], 0£y£Mi=supf(x)}; Sgt=åi=1itmiDxi; SGt=åi=1itMiDxi {T} Для того, чтобы ф-ция f(x) огр на [a,b] была интегрируема на этом отр. необходимо и достаточно : lim|t|®0(Sgt-SGt)=0 {Д} т.к. ф-ция f(x) –нерерывна на отр[a,b] то она интегрируема на этом отр. Þ по критерию итегрируемости lim|t|®0SGt= lim|t|®0Sgt=S=aòbf(x)dx {сектор} Сектор ограничен кривой r=f(j), где f(j) – непрерывна на [a,b] и f(j)³0 «jÎ[a,b] {} Пусь t-произвольное разбиение git={(j,r), jÎ[ji-1,ji], 0£r£mi=inff(j)} Git={(j,r), jÎ[ji-1,ji], 0£r£Mi=supf(j)} Т.к. ф-ция f(x)-непрерывна на отр[a,b] то она интегрируема на этом отрезкеÞ Площадь сектора git=m²iDj/2 и Git=M²iDj/2; Sgt=1/2×åi=1itm²iDj SGt=1/2×åi=1itM²iDj по критерии итегрируемости Þ lim|t|®0SGt= lim|t|®0Sgt=S=1/2×aòtf²(j)djÞ P-квадрируема и Sp=1/2×aòbf²(j)dj.
37. Несобственные интегралы первого и второго рода.
1)
Пусть f(x) опред на [a;+∞) и интегрируема в любой конечной его части [a;R] так, что существует определенный интеграл
∃
Если при R→+∞ для этого интеграла существует определенный конечный предел, то его называют несобственным интегралом ф-ии f(x) в промежутке [a;+∞).
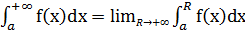 (1)- несобственный интеграл 1ого порядка
(1)- несобственный интеграл 1ого порядка
При интегрировании говорят, что интеграл существует, те сходится, если lim бесконечен или не существует, то про интеграл говорят, что он не существует или расходится

 —
при условии, что оба интеграла сходятся
—
при условии, что оба интеграла сходятся
2)
Несобственный интеграл от неограниченной ф-ии
f (x) опр.
[a,b)
(x) опр.
[a,b)
(∙)x=b-особ. (∙), если ф-я неограниченна в любой окрестности этой (∙), но ограничена на любом отрезке [a,b—𝜇], заключенном в [a,b).
Пусть на любом отрезке[a,b—𝜇] ф-я интегрируема, те существуетопределенный интеграл
∃ , ∀𝜇>0, b—𝜇>a
, ∀𝜇>0, b—𝜇>a
Если
для интеграла  при 𝜇→0
существует конечный lim, то его называют
интегралом 2ого порядка.
при 𝜇→0
существует конечный lim, то его называют
интегралом 2ого порядка.
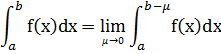
Если  есть, то интеграл существует (сходится),
если нет, то расходится.
есть, то интеграл существует (сходится),
если нет, то расходится.
38. Признаки сходимости для несобственных интегралов первого и второго родов.
1)признак сравнения несобственных инт.
a)f(x)g(x)- неопред. [a,+∞)
0≤ f(x)≤ g(x)
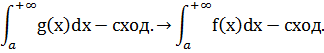
2)если f(x)g(x)—неотрицательные
ф-ии и существует конечный предел их
отношения при x→+∞,то
несобственные интегралы  сходятся и расходятся одновременно
сходятся и расходятся одновременно
3)частный признак сравнения.
Если x→+∞
неопр. ф-я f(x)
является б.малой порядка 𝛾(𝛾>0),
то 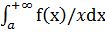 сходится при 𝛾>1 и расходится при
𝛾≤1.
сходится при 𝛾>1 и расходится при
𝛾≤1.
2.Если
ф-я определена для всех x≥a и 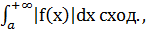 то
то  сходится абсолютно. Если сходится
условно, то
сходится абсолютно. Если сходится
условно, то
39. Дифференциальное уравнение и его решение. Примеры. Формулировка теоремы о существовании и единственности решения дифференциального уоавнения первого порядка с геометрической интерпретацией.
ДУ- ур-е, в котором неизвестная ф-я или вектор-ф-я входит под знаком производной или дифференциала.
1)Обыкновенные ДУ, в котором неизвестные являются ф-ей 1ой переменной
2)ДУ в частных производных, в которых неизвестные ф-ии являются ф-ями 2х и более переменных.
Порядок ДУ- порядок старшей входящей в ДУ неизвестной ф-ии.
Решением обыкновенного ДУ n-ого порядка , те ур-я вида
F(x, y(x),y’(x), y»(x),…, y(n)(x))=0
называется ф-я y=𝜑(x),которая при подстановке в ДУ обращает его в тождество.
График решения ДУ называется интегральной кривой.
Решение ДУ- интегрирование ДУ. Задача интегрирование- нахождение всех решении этого ур-я и изучении их св-в.
ДУ 1ого порядка- ур-е вида F(x, y, y’)=0, где x— независимая переменная, y- искомая ф-я, y’- ее производная.
Если его можно разрешить относительно y’, то y’= dy/dx =f(x,y)- ур-е 1ого порядка, разрешенное относительно производной.
P(x,y)dx+Q(x,y)dy=0.
Теорема Коши(Теорема о существованиии единственности решения ДУ 1ого порядка)
Если ф-я f(x,y) и ее частная приизводня f’y(x,y) определены и непрерывны в некоторой области G плоскости oxy, то какова бы не была внутренняя точка (x0, y0) области G, в некоторой окрестности этой точки существует единственное решение ур-я y’= f(x,y), удовлетворяющее условиям y=y0, x=x0
Геометрически теорема утверждает, что через каждую внутреннюю точку (y0, x0) области G проходит единственная интегральная кривая.

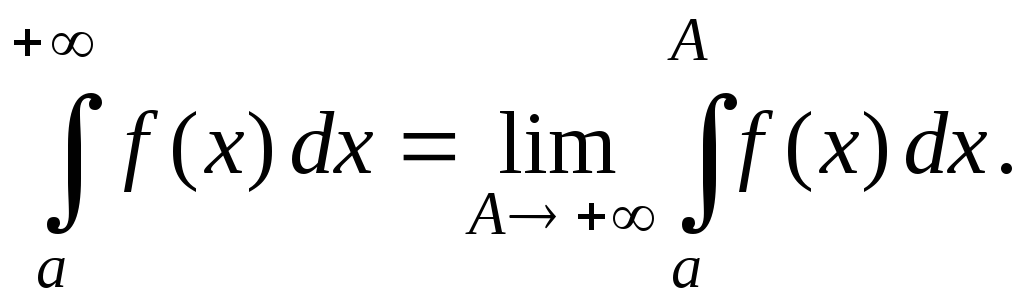
 и
и
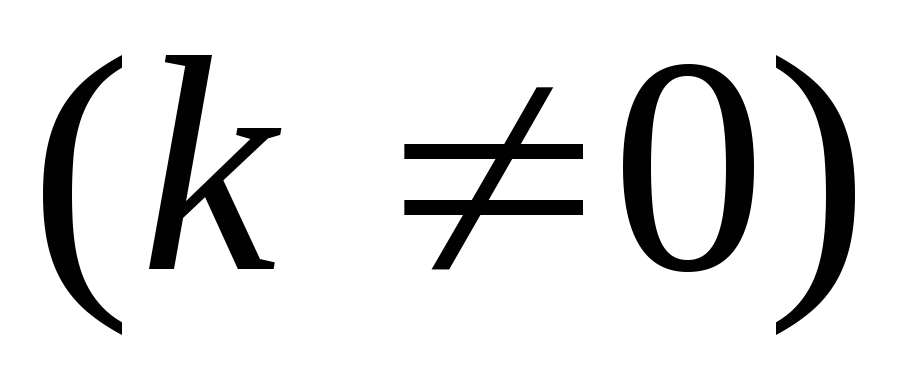 сходятся или расходятся одновременно;
сходятся или расходятся одновременно;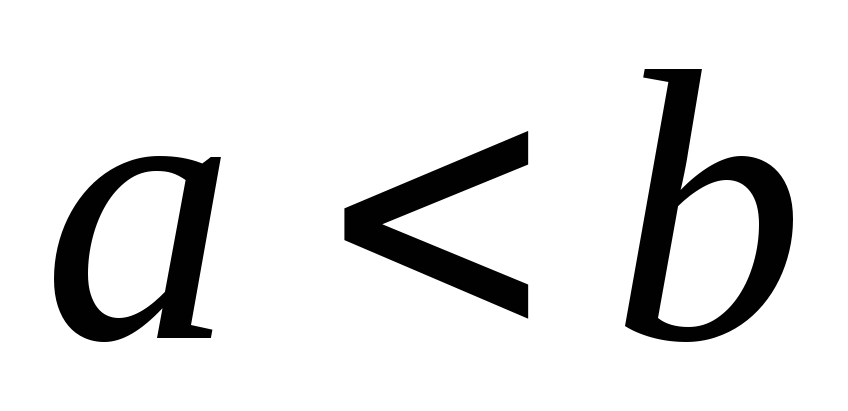 ,
то интегралы
,
то интегралы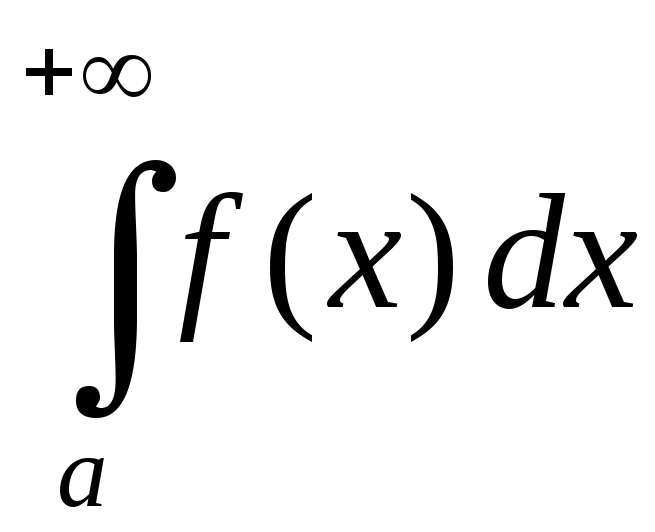 и
и сходятся или рас-ходятся одновременно;
сходятся или рас-ходятся одновременно;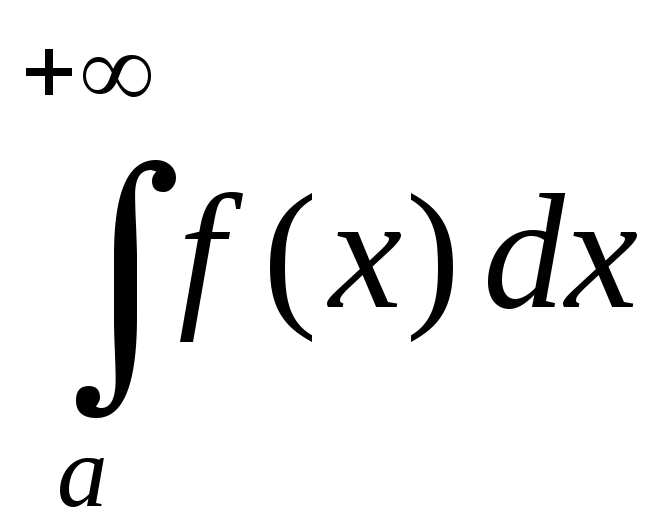 сходится, то
сходится, то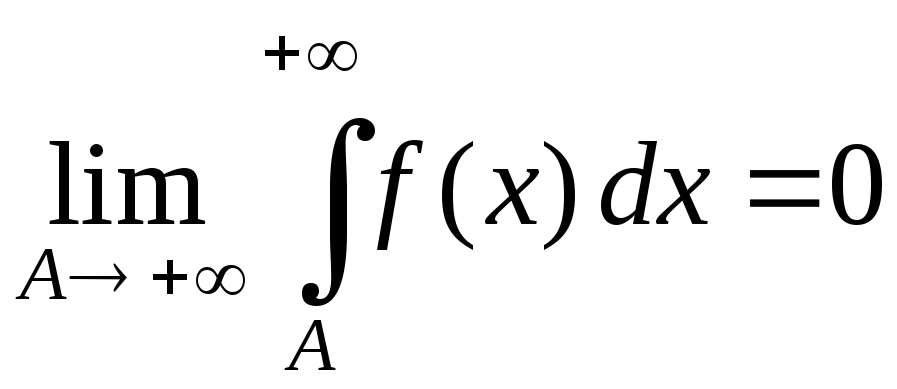 .
.