Учебный проект «Нестандартные приемы решения квадратных уравнений»

Введение

Тема «Квадратные уравнения» является одной из самых актуальных. Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение в разных разделах математики.

В школьном курсе изучаются формулы корней квадратного уравнения, с помощью которых можно решать любые квадратные уравнения. Однако, имеются и другие приемы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать квадратные уравнения?

Гипотеза: установление связи между коэффициентами и корнями квадратного уравнения позволит найти эффективные приемы быстрого решения квадратного уравнения.

Цель: установив связь между коэффициентами и корнями квадратного уравнения, найти новые рациональные приемы решения уравнений

Задачи:

• Изучить литературу по истории приемов решения квадратных уравнений
• Обобщить накопленные знания о квадратных уравнениях и способах их решения.
• Установить зависимость корней квадратного уравнения от его коэффициентов и найти эффективные приемы быстрого решения квадратного уравнения, в том числе с большими коэффициентами.
• Сделать выводы.
• Разработать дидактический материал для проведения практикума по решению квадратных уравнений с использованием новых приемов в помощь ученикам, увлеченным математикой и учителям, ведущим факультативные занятия.

Объект исследования: квадратные уравнения

Предмет изучения: методы и приемы решения квадратных уравнений, в том числе с большими коэффициентами

Глава 1.
Изучение литературы

Основной материал, связанный с изучением темы «Квадратные уравнения» находится в УМК под ред.С.А.Теляковского. В учебнике разобраны все основные вопросы по теме:

1. Определение и виды квадратных уравнений

2. Основные методы решения квадратных уравнений

Однако, дополнительный материал, связанный с историей вопроса о возникновении квадратных уравнений можно найти в «Энциклопедия по математике» «Занимательная математика», М., 2007. Способы решения задач на квадратные уравнения в полном объёме раскрыты в изданиях «Сборник элективных курсов» Волгоград, 2006 г.

Изученная литература позволила приобрести новые интересные знания по истории возникновения квадратного уравнения, приобрести опыт по решению различных квадратных уравнений и перейти к следующему этапу в исследовании – перенести полученные знания в нестандартную ситуацию.

Глава 2.
Изучение истории вопроса о квадратных уравнениях

Глава 3.
Обобщение имеющихся знаний о квадратных уравнениях и способах их решения

Глава 4.
Нестандартные приемы решения квадратных уравнений

Дидактический материал по применению нестандартных приемов решения квадратных уравнений.

1. Найди наиболее рациональным способом корни уравнения:

4х² – 13х + 9 =0
(1; 2,25)

1978х² – 1984х + 6=0
(1; 6/1978)

4х² + 11х + 7 = 0
(-1; -7/4)

319х² + 1988х +1669=0
(-1; -1669/319)

1999х² + 2000х+1=0
(-1; -1/1999)

2. Решить квадратные уравнения с большими коэффициентами

313х² +326х+13=0
(-1; -13/313)

839х

2– 448х -391=0
(1; -391/839)

345х² – 137х – 208=0
(1;.-208/345)

939х²+978х+39=0
(-1; -39/939)

3. Используя полученные знания, установи соответствие:

1) х2+5х+6=0 2) 6х2-5х+1=0 3) 2х2-5х+3=0 4) 3х2-5х+2=0 5) х2-5х+6=0 6) 6х2+5х+1=0 7) 2х2+5х+2=0 8) 3х2+5х+2=0

1) 1/6;1/2 2) 1; 3/2 3) 1; 2/3 4) -2; -3 5) -1/3 ; -1/2 6) -1; -3/2 7) -1; -2/3 8) 2;3

Глава 5.
Анализ работы учащихся по решению квадратных уравнений нестандартными способами

Разработаны критерии оценки проведенного практикума:

1. За каждое верно выполненное задание ставится 1 балл;
2. Наиболее возможное количество набранных баллов-17
3. Если ученик набирает менее

7 баллов, то выставляется оценка «2»
от 7 до 11 баллов «3»
от 12 до 15 баллов «4»
от 16-17 баллов «5»

Результаты практикума.

Выполняли работу – 11человек

Набрали баллов

от 16-17 – 5человек (45%)
от 12-15– 6человек (55%)
Менее 12 – 0 человек

Средний балл – 4,45

Процент качества – 100%

Типичные ошибки, допущенные в работе связаны с невнимательностью учащихся.

Выводы по результатам проведения практикума

Успешно выполненная работа учащимися 8 класса, позволяет сделать следующие выводы:

• нестандартные приемы решения квадратных уравнений заслуживают внимания;
• позволяют экономить время решения, что обусловлено применением тестовой системы экзаменов.

Глава 6.
Выводы

В процессе работы над проектом, была создана система нестандартных приемов решения квадратных уравнений и разработан банк заданий, на основе которого проведена успешная апробация этих приемов.

Данный материал можно рекомендовать для внеклассных и факультативных занятий по математике. Учителя могут использовать его как методическое пособие при изучении темы «Решение квадратных уравнений», а также, для контроля за знаниями учащихся.

Материалом этого проекта могут воспользоваться и те, кто любит математику и хочет знать о математике больше.

Литература

1. Выгодский М.Я

. Справочник по элементарной математике. – М. государственное издательство физико-математической литературы, 1970.

Галицкий М.Л., Гольдман М., Звавич Л.И

. Сборник задач по алгебре для 8-9 классов: учебное пособие для учащихся школ и классов с углубленным изучением математики:4-е изд.-М.: Просвещение, 1997.

Макарычев Ю.Н., Миндюк Н.Г

. Алгебра. Учебник для 8 класса. М., Просвещение, 2001.

Макарычев Ю.Н., Миндюк Н.Г

. Дополнительные главы к школьному учебнику. 8 класс М., Просвещение, 1996.

Штейнгауз В.Г

. Математический калейдоскоп. – М.: Бюро «Квантум», 2005.

Энциклопедический словарь юного математика. – М.: Педагогика, 1985.

Нестандартные способы решения квадратных уравнений

Муниципальное казенное общеобразовательное учреждение

«Богучарская средняя общеобразовательная школа №1»

Научно-исследовательская работа по теме: «Нестандартные способы решения квадратных уравнений»

Автор: ученица 9«А» класса

Прядкова Екатерина Сергеевна

Руководитель: Алабина Галина Юрьевна

Выявить способы решения квадратных уравнений

Узнать можно ли решить любое квадратное уравнение данными способами и выделить особенности и недостатки этих способов

• Анализировать источники литературы для выявления способов решения квадратных уравнений
• Показать различные способы решения квадратных уравнений
• Выявить наиболее удобные способы решения квадратных уравнений
• Научиться решать квадратные уравнения различными способами

Существуют другие способы решения квадратного уравнения кроме тех, которые мы изучили в школе

Способы решения квадратных уравнений

Разложение левой части на множители

Метод выделения полного квадрата

По формуле

Основные

С использованием теоремы Виета (прямой и обратной)

Графический способ

По свойствам коэффициентов

Способом «переброски»

Дополнительные

С помощью циркуля и линейки

С помощью номограммы

Геометрический способ

Социологический опрос

Свойства коэффициентов

Свойства:

Способ «переброски»

Умножив обе части уравнения на а, получим

Пусть

, откуда

Тогда получим уравнение с новой переменной

Его корни у 1 и у 2 . Окончательно

С помощью циркуля и линейки

Радиус окружности больше ординаты центра

, окружность пересекает ось Ох в двух точках , где корни исходного уравнения.

Радиус окружности равен ординате центра

, окружность пересекает ось Ох в одной точке где корень исходного уравнения.

Радиус окружности меньше ординаты центра

, окружность не имеет общих точек с осью Ох. В этом случае исходное уравнение не имеет корней.

С помощью номограммы

х 2 -9х+8=0

Х 1 =8; х 2 =1

Геометрический способ

Рассмотрим, как древние греки решали уравнение

Решение представлено на рисунке, где

или

Выражения

и 16 + 9

геометрически представляют собой один и тот же квадрат со стороной 5.

Поэтому

Обработка данных

Метод выделения

полного квадрата

Разложение левой части

уравнения на множители

Ответ: -4,5; 1.

Обработка данных

С использованием

формул Виета

По формуле

имеет два разных

по знаку корня

больший по модулю

корень отрицательный

Ответ: -4,5; 1.

Обработка данных

По свойству коэффициентов

Способом «переброски»

Перебросим коэффициент а = 2 к свободному члену и получим уравнение:

Так как

то

из которого по формулам Виета

Корнями исходного уравнения будут

Ответ: -4,5; 1.

Обработка данных

Графический метод

С помощью циркуля и линейки

Запишем уравнение в виде

Определим координаты центра окружности по формулам:

Построим в одной системе координат графики функций

Проведем окружность радиуса SA, где А (0;1).

Ответ: -4,5; 1.

Обработка данных

Геометрический способ

С помощью номограммы

Представим уравнение в виде:

Представим уравнение в виде:

Площадь полученного квадрата:

Так как

Номограмма дает положительный корень

то:

Таким образом, получили уравнение:

отрицательный корень

Ответ: -4,5; 1.

Положительные стороны и недостатки

Название способа решения квадратных уравнений

Положительные стороны

Разложение левой части уравнения на множители

Недостатки

Дает возможность сразу увидеть корни уравнения.

Метод выделения полного квадрата

Нужно правильно расчленить слагаемые для

группировки.

По формуле

За минимальное количество действий можно найти корни уравнений

Нужно правильно найти все слагаемые для выделения полного квадрата.

Можно применить ко всем квадратным уравнениям.

С использованием формул Виета

Нужно выучить формулы.

Достаточно легкий способ, дает возможность сразу увидеть корни уравнения.

Легко находятся только целые корни.

Название способа решения квадратных уравнений

Положительные стороны

Недостатки

Способом «переброски»

За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета.

По свойствам коэффициентов

Графический способ

Легко найти только целые корни.

Не требует особых усилий

Наглядный способ

Подходит только к некоторым уравнениям

С помощью циркуля и линейки

Могут быть неточности при составлении графиков

Наглядный способ

С помощью номограммы

Наглядный способ, прост в применении.

Могут быть неточности

Геометрический способ

Наглядный способ.

Не всегда под рукой имеется номограмма.

Похож на способ выделения полного квадрата

Для того, чтобы хорошо решать любое квадратные уравнения необходимо

знать:

    формулу нахождения дискриминанта;

    формулу нахождения корней квадратного уравнения;

    алгоритмы решения уравнений данного вида.

уметь:

    решать неполные квадратные уравнения;

    решать полные квадратные уравнения;

   решать приведенные квадратные уравнения;

  находить ошибки в решенных уравнениях и исправлять их;

    делать проверку.

Думаю, что моя работа будет интересна учащимся 8-9 классов, а также тем, которые хотят научиться рационально решать квадратные уравнения и хорошо подготовиться к выпускным экзаменам. На уроках математики я рассказала своим одноклассникам методы решения квадратных уравнений и ребятам они понравились. Также она будет интересна и учителям математики, так как в своей работе я не только рассмотрела методы решения квадратных уравнений, но и историю их развития.

Нестандартные способы решения квадратных уравнений

Слайд 1

Нестандартные способы решения квадратных уравнений Выполнила: Нестерова Дарья , 10 класс МКОУ « Новоникольская СОШ»

Слайд 2

История развития квадратных уравнений

Слайд 3

Квадратные уравнения в Древнем Вавилоне Необходимость решать уравнения не только первой, но и второй степени ёщё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера , а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения: Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводя только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилонии , в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Слайд 4

Как составлял и решал Диофант квадратные уравнения «Найти два числа, зная, что их сумма равна 20, а произведение 96» Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, т.к. если бы они равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы , т.е. 10+ X , другое же меньше, т.е. 10- X . Разность между ними 2 Х Отсюда Х=2 . Одно из искомых чисел равно 12, другое 8. Решение Х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа. УРАВНЕНИЕ: или же:

Слайд 5

Квадратные уравнения в Индии Задачи на квадратные уравнения встречаются и в астрономическом трактате « Ариабхаттиам », составленном в 499 г. индийским математиком и астрономом Ариабхаттой . Другой индийский ученый, Брахмагупта , изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ax ² +bx=c , a>0 Одна из задач знаменитого индийского математика XІІ века Бхаскары Обезьянок резвых стая Всласть поевши, развлекалась. Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам… Стали прыгать повисая… Сколько было обезьянок Ты скажи мне, в этой стае?. Соответствующее задачи уравнение: Баскара пишет под видом: Дополнил левую часть до квадрата,

Слайд 6

Квадратные уравнения в Древней Азии Вот как решал это уравнение среднеазиатский ученый ал-Хорезми : Он писал : «Правило таково: раздвои число корней, х=2х · 5 получите в этой задаче пять, 5 умножь на это равное ему, будет двадцать пять, 5 · 5=25 прибавь это к тридцати девяти, 25+39 будет шестьдесят четыре, 64 извлеки из этого корень, будет восемь, 8 и вычти из этого половину числа корней, т.е.пять, 8-5 останется 3 это будет корень квадрата , который ты искал.» А второй корень ? Второй корень не находили, так как отрицательные числа не были известны. х 2 +10 х = 39

Слайд 7

Квадратные уравнения в Европе XIII-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х2+вх+с=0 , было сформулировано в Европе лишь в 1544 г. Штифелем. . Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. итальянским математиком Леонардом Фибоначчи. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Лишь в 17 в. благодаря трудам Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид

Слайд 8

О теореме Виета Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. Следующим образом: «Если B+D, умноженное на А-А , равно BD , то А равно В и равно D » . Чтобы понять Виета, следует помнить, что А, как и всякая гласная буква , означало у него неизвестное (наше х ), гласные же B,D- кэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает : Если приведенное квадратное уравнение x 2 +px+q=0 имеет действительные корни, то их сумма равна — p , а произведение равно q , то есть x 1 + x 2 = — p , x 1 x 2 = q (сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).

Слайд 9

Метод разложения на множители привести квадратное уравнение общего вида к виду: А( х ) · В( х )=0, где А( х ) и В( х ) – многочлены относительно х. Цель: Вынесение общего множителя за скобки; Использование формул сокращенного умножения; Способ группировки. Способы: Пример:

Слайд 10

Решим уравнение: х 2 + 6х — 7 = 0. х 2 + 6х -7 = 0. ( х +3) 2 – 16 = 0. ( х +3) 2 = 16. х + 3 = 4; х + 3 = -4. х = 1, х =-7. Ответ: 1; -7. Метод выделения полного квадрата (a + b) 2 = a 2 + 2ab + b 2 , (a — b) 2 = a 2 — 2ab + b 2 .

Слайд 11

Корни квадратного уравнения: ax 2 +bx+c=0 Если D>0 , Если D

Слайд 12

x 1 и х 2 – корни уравнения Решение уравнений с помощью теоремы Виета Х 2 + 3Х – 10 = 0 Х 1 · Х 2 = – 10, значит корни имеют разные знаки Х 1 + Х 2 = – 3, значит больший по модулю корень — отрицательный Подбором находим корни: Х 1 = – 5, Х 2 = 2 Например :

Слайд 13

Решите уравнение: 2х 2 — 11х +15 = 0. Перебросим коэффициент 2 к свободному члену у 2 — 11у +30= 0. D>0, по теореме, обратной теореме Виета, получаем корни: 5;6, далее возвращаемся к корням исходного уравнения: 2,5; 3. Ответ: 2,5; 3. Решение уравнений способом «переброски»

Слайд 14

Если в квадратном уравнении a+b+c =0 , то один из корней равен 1, а второй по теореме Виета равен Если в квадратном уравнении a+c =b , то один из корней равен (-1), а второй по теореме Виета равен Пример : Свойства коэффициентов квадратного уравнения 137 х 2 + 20 х – 157 = 0. a = 137, b = 20, c = -157. a + b+ c = 137 + 20 – 157 =0. x 1 = 1, Ответ : 1;

Слайд 15

Второй коэффициент — четный

Слайд 16

Графический способ решения квадратного уравнения Не используя формул квадратное уравнение можно решить графическим способом. Решим уравнение Для этого построим два графика : X -3 -2 -1 0 1 2 3 Y 9 4 1 0 1 4 9 X -1 0 1 Y 0 1 2 Ответ: Абсциссы точек пересечения графиков и будет корнями уравнения. Если графики пересекаются в двух точках, то уравнение имеет два корня. Если графики пересекаются в одной точке, то уравнение имеет один корень. Если графики не пересекаются, то уравнение корней не имеет. 1) y = x 2 2) y = x +1

Слайд 17

Решение квадратных уравнений с помощью циркуля и линейки Корни квадратного уравнения ах 2 + b х + с = 0 ( а ≠ 0) можно рассматривать как абсциссы точек пересечения окружности с центром Q (- ; ), проходящей через точку A (О; 1), и оси Ох .

Слайд 18

Решение квадратных уравнений с помощью номограммы Это старый и незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83 «Четырехзначные математические таблицы» Брадис В.М. Таблица XXII. Номограмма для решения уравнения Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения. Для уравнения номограмма дает корни

Слайд 19

Геометрический способ решения квадратных уравнений В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. А вот, например, как древние греки решали уравнение: или Выражения и геометрически предоставляют собой один и тот же квадрат, а исходное уравнение одно и тоже уравнение. Откуда и получаем что , или

Слайд 20

Заключение данные приёмы решения заслуживают внимания, поскольку они не все отражены в школьных учебниках математики; овладение данными приёмами поможет учащимся экономить время и эффективно решать уравнения; потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов;

РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ

Альдебенева А.Н. 1

---

1ГБОУ СОШ ж.-д.ст. Погрузная Самарской области

Степанова Г.А. 1

---

1ГБОУ СОЩ ж.-д.ст. Погрузная

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека так или иначе связано с математикой. Поэтому решение многих практических задач сводится к решению различных видов квадратных уравнений, которые необходимо научиться решать.

В данной работе я попыталась обобщить и систематизировать изученный материал по выше указанной теме. Я расположила материал по степени его сложности, начиная с самого простого. В него вошли как известные мне способы решения квадратных уравнений из школьного курса алгебры, так и нестандартные нетрадиционные способы решения, которые не изучаются в школьном курсе, но знание которых сокращает процесс решения квадратных уравнений. Квадратные уравнения – это фундамент, на котором покоится величественной здание алгебры.

Для выявления актуальности темы моей работы я провела исследование среди учащихся 8-11 классов нашей школы. Им было предложено решить полное квадратное уравнение любым известным способом. В исследовании приняло участие 72 учащихся из 86 (84 %) .

Метод решение квадратного уравнения	Кол-во учащихся
1.Метод выделения квадрата двучлена	0 чел	0%
2.Метод разложения левой части уравнения на множители способом группировки	0 чел	0%
3.Решение уравнений по формулам дискриминанта и корней квадратного уравнения	40 чел	56%
4.Решение уравнений, используя теорему Виета	4 чел	15%
5.Решение уравнений графическим способом	0 чел	0%
6.Неверно решили уравнения	8 чел	30%
7.Решение уравнений с использованием свойств коэффициентов	20 чел	27%

Таким образом, ясно, что при решении квадратных уравнений учащиеся нашей школы используют традиционно формулы дискриминанта и корней уравнения, что требует громоздких вычислений и как следствие больших затрат времени, что непозволительно в процессе сдачи экзаменов.

Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать квадратные уравнения? Какие существуют рациональные способы решения квадратных уравнений?

Гипотеза: установление связи между коэффициентами и корнями квадратного уравнения позволит найти эффективные приемы быстрого решения квадратного уравнения.

Цель: установив связь между коэффициентами и корнями квадратного уравнения, найти новые рациональные приемы решения уравнений.

Задачи:

1.Изучить литературу по истории приемов решения квадратных уравнений

2. Обобщить накопленные знания о квадратных уравнениях и способах их решения.

3. Установить зависимость корней квадратного уравнения от его коэффициентов и найти эффективные приемы быстрого решения квадратного уравнения, в том числе с большими коэффициентами.

4.Изложить наиболее известные способы решения квадратных уравнений.

3.Показать нестандартные способы решения квадратных уравнений. Сделать выводы.

5. Разработать дидактический материал для проведения практикума по решению квадратных уравнений с использованием новых приемов в помощь ученикам, увлеченным математикой.

Объект исследования: квадратные уравнения

Предмет исследования: методы и приемы решения квадратных уравнений, в том числе с большими коэффициентами

Актуальность темы: тема «Квадратные уравнения» является одной из самых актуальных. Она находит широкое применение в разных разделах математики, имеет теоретическую и практическую значимость. Ведь почти все, что окружает человека так или иначе связано с математикой. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.

Тема исследования:

Нетрадиционные способы решения квадратных уравнений.

Методы исследования: анкетирование, сбор статистических данных, обработка собранных сведений и информации, оформление результатов исследования.

Итог работы.

Каждый ученик должен прийти к выводу «Мой способ решения квадратного уравнения – понятный, но я хочу найти для себя самый рациональный»

Глава 1. Историческая справка.

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах, содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37…», — поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами. Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

Основной материал, связанный с изучением темы «Квадратные уравнения» находится в УМК под редакцией С. А. Теляковского за 8 класс. В учебнике разобраны все основные вопросы по теме:

1. Определение и виды квадратных уравнений

2. Основные методы решения квадратных уравнений

Однако, дополнительный материал, связанный с историей вопроса о возникновении квадратных уравнений можно найти в «Энциклопедия по математике» «Занимательная математика», М., 2007. Способы решения задач на квадратные уравнения в полном объёме раскрыты в изданиях «Сборник элективных курсов» Волгоград, 2006 г. Рациональные приемы решения квадратных уравнений в полном объеме освещены на сайтах интернет.

Таким образом, изученная литература позволила приобрести новые интересные знания по истории возникновения квадратного уравнения, приобрести опыт по решению различных квадратных уравнений и перейти к следующему этапу в исследовании – перенести полученные знания в нестандартную ситуацию.

Глава 2.Обобщение имеющихся знаний о квадратных уравнениях и способах их решения

2.1. Определение квадратного уравнения

Определение: Квадратным уравнением называется уравнение вида

аx ² + bx + c = 0, где х – переменная, а, b и с– некоторые числа, причем, а ≠ 0.

Числа а, b и с — коэффициенты квадратного уравнения. Число а называют первым коэффициентом, число b– вторым коэффициентом и число c – свободным членом.

● Пример. 8x² – 7x + 3 = 0

В каждом из уравнений вида ax ² + bx + c = 0, где а ≠ 0, наибольшая степень переменной x – квадрат. Отсюда и название: квадратное уравнение.

Квадратное уравнение, в котором коэффициент при х ² равен 1, называют приведенным квадратным уравнением.

● Пример. х ² – 11х+30=0, х² – 8х= 0.

2.2. Решение квадратных уравнений с помощью выделения квадрата двучлена

Рассмотрим на примере решение квадратного уравнения, в котором оба коэффициента при неизвестных и свободный член отличны от нуля. Такой способ решения квадратного уравнения называют выделением квадрата двучлена.

Пример. Рассмотрим уравнение 7х ² – 6х – 1= 0.

Разделив обе части этого уравнения на 7, получим равносильное ему приведенное квадратное уравнение

Х² – х – = 0.

Выделим из трехчлена х² – x- –квадрат двучлена. Для этого разность

х² – х представим в виде х ² – 2· х, прибавим к ней выражение и вычтем его. Получим

х² – 2· х + – – = 0.

Отсюда х ² – 2· х + = + ,

= .

Следовательно, х — = – или х — = , ,

х – = — или х — = ,

х = – или х = 1.

Уравнение имеет два корня: – и 1.

2.3. Решение квадратных уравнений по формуле

Решение квадратных уравнений выделением квадрата двучлена часто приводит к громоздким преобразованиям. Поэтому поступают иначе. Решают уравнение в общем виде и в результате получают формулу корней. Затем эту формулу применяют при решении любого квадратного уравнения. Решим квадратное уравнение

аx ² + bx + c = 0.

Разделив его обе части на а, получим равносильное ему приведенное квадратное уравнение

х ² + х + = 0.

Выделим из трехчлена х ² + х + квадрат двучлена. Для этого сумму

х ² + х представим в виде х ² +2х∙ ,прибавим к ней выражение

и вычтем его. Получим

х² +2х∙ + – + = 0,

х ²+2х∙ + = – ,

= – ,

= ,

Уравнение = равносильно уравнению ax ² + bx + c = 0.

Число его корней зависит от знака дроби . Так как а ≠ 0, то 4a–положительное число, поэтому знак этой дроби определяется знаком его числителя, т. е. выражения b² – 4ас. Это выражение называют дискриминантом квадратного уравнения ax ² + bx + c = 0. Его обозначают буквой D, т.е.

D = b – 4ас. Дискриминант квадратного уравнения ax ² + bx + c = 0

– выражение b² – 4ас= D – по знаку которого судят о наличии у этого уравнения действительных корней.

Различные возможные случаи в зависимости от значения D.

1.Если D>0, то уравнение имеет два корня:

X₁ =и x₂ =

Пример. Рассмотрим уравнение 2x ² –3x + 1= 0.

а=2; b= –3; с=1,

D= b – 4ас =(–3) – 4ас= 9–8= 1; 2 корня.

X₁= = = = 0,5

X₂ = = = =1

Ответ: 0,5;1

2.Если D= 0, то уравнение имеет один корень:

х = – .

Пример. Рассмотрим уравнение 9х² +6х+1= 0.

а=9; b= 6; с=1,

D= b – 4ас=6 – 4ас=36–36= 0; 1 корень.

X= = = -0,3

Ответ: -0,3

3. Если D 0. тогда это уравнение имеет два корня:

x₁ =и x₂ =

Найдем сумму и произведение корней:

x₁ + x ₂= + = = –p;

x₁ . x ₂ = . = = = =q.

Следовательно,

x₁ + x ₂ =-p, x₁ . x ₂ =q .

Пример. Рассмотрим уравнение х ² – 3х + 2 = 0.

D =1, уравнение имеет два корня. х₁ = 2 и х₂ = 1, p= –3; q= 2.

По теореме Виета x₁ + x ₂ =-p , значит 2 + 1= 3;

x₁ . x ₂ =q , значит 2 ∙ 1 =2.

Следовательно, х ₁ = 2 и х₂ = 1 являются корнями уравнения х² – 3х + 2 = 0.

При D = 0 корни уравнения можно вычислить по формуле

х = и x= .

Квадратное уравнение ax ² + bx + c = 0 имеет корни х₁ и х ₂ равносильное ему приведенное квадратное уравнение имеет вид

х + х = – , х ∙ х = .

Справедливо утверждение, обратное теореме Виета:

Теорема: Если числа m и n таковы, что их сумма равна –p, а произведение

равно q, то эти числа являются корнями уравнения х ² + px + q = 0.

Пример. Рассмотрим уравнение х ² +3х – 40=0.

D= 32+4 ∙40= 169.

По формуле корней квадратного уравнения получаем

х = ; х = .

Отсюда х ₁ =-8 ; х ₂ =5.

Покажем, что корни уравнения найдены правильно. В уравнении

х² +3х – 40=0 коэффициент р равен 3, а свободный член q равен –40. Сумма найденных чисел –8 и 5 равна –3, а их произведение равно –40. Значит, по теореме, обратной теореме Виета, эти числа являются корнями уравнения

х² +3х – 40=0.

Итак, квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала некоторые из них, которые сама очень активно применяю.

Глава 3. Рациональные способы решения квадратного уравнения.

3.1.Свойства коэффициентов квадратного уравнения.

1) Если а+ b+c= 0, х₁ = 1 , х ₂ =

Пример. Рассмотрим уравнение х² +4х – 5= 0.

a+ b+c= 0, х ₁ =1 , х ₂ = . 1+4+ (-5) =0 .

Значит, корнями этого уравнения являются 1 и –5. Проверим это с помощью нахождения дискриминанта:

D= b – 4ас= 4 – 4∙1∙(–5)= 36.

х = = = – 5.

х = = =1.

Отсюда следует, что если а+b+c= 0 , то х ₁ =1 , х ₂ =

2) Если b= а+c, то х₁ =-1, х ₂ = -

Пример. Рассмотрим уравнение 2х² +8х +6 = 0.

2) Если b= а+c, то х₁ =-1, х ₂ = — . 8= 2+6

Значит корнями этого уравнения являются –1 и –3. Проверим это с помощью нахождения дискриминанта:

D= b – 4ас=8 – 4∙2∙6= 16.

х = = = –3.

х = = = –1.

Отсюда следует, что если b= а+c , то х₁ = -1 , х ₂ =

Пример 345х² – 137х – 208 = 0.

Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то

х₁ = 1, х₂ = c/a = -208/345.

Ответ: 1; -208/345.

Пример 132х2 – 247х + 115 = 0.

Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то

х₁ = 1, х₂ = c/a = 115/132.

Ответ: 1; 115/132

3). Если второй коэффициент b = 2k – четное число, то формулу корней

Пример. Решим уравнение 3х² — 14х + 16 = 0.

Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;

D = k² – ac = (- 7)² – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;

Ответ: 2; 8/3

3.2. Способ «переброски».

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а±b+c≠0, то используется прием переброски:

1. 2х² – 11х+5=0 х² – 11х+10= 0

х = 10; х =1. Корни уравнения необходимо поделить на 2.

Ответ: 5; 0,5.

1. 4х² -37 х +9 =0 Ответ: ¼, 9

3.3.Закономерность коэффициентов

1) Если в уравнении ax ²+ bx + c = 0 коэффициент b равен (а² +1), а коэффициент с численно равен коэффициенту а, то его корни равны

х = –а; х = – .

ах ² + (а² +1)∙ х+ а= 0

Пример. Рассмотрим уравнение 6х² +37х +6 = 0.

х = –6; х = – .

2) Если в уравнении ax² – bx + c = 0 коэффициент b равен (а² +1),а коэффициент с численно равен коэффициенту а, то его корни равны

х = а; х = .

ax ²– (а² +1)∙ х+ а= 0

Пример. Рассмотрим уравнение 15х ²–226х +15 = 0.

х = 15; х = – .

3) Если в уравнении ax² + bx – c = 0 коэффициент b равен (а² –1), а коэффициент с численно равен коэффициенту а, то его корни равны

х = –а; х = .

ax² + (а² –1)∙ х– а= 0

Пример. Рассмотрим уравнение 17х² +288х – 17 = 0.

х = –17; х = .

4) Если в уравнении ax ²– bx – c = 0 коэффициент b равен (а² –1), а коэффициент с численно равен коэффициенту а, то его корни равны

х = а; х = – .

ax ²+ (а²–1)∙ х– а= 0

Пример. Рассмотрим уравнение 10х²–99х – 10 = 0.

х = 10; х = – .

3.4.Графическое решение квадратного уравнения.

Если в уравнении

х² + px + q = 0

перенести второй и третий члены в правую часть, то получим

х² = — px — q.

Построим графики зависимости у = х² и у = — px — q.

График первой зависимости — парабола, проходящая через начало координат. График второй зависимости —

прямая (рис.1). Возможны следующие случаи:

— прямая и парабола могут пересекаться в двух точках,

абсциссы точек пересечения являются корнями квад- ратного уравнения;

— прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;

— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

Примеры.

1) Решим графически уравнение х² — 3х — 4 = 0 (рис. 2).

Решение. Запишем уравнение в виде х² = 3х + 4.

Построим параболу у = х² и прямую у = 3х + 4. Прямую

у = 3х + 4 можно построить по двум точкам М (0; 4) и

N (3; 13). Прямая и парабола пересекаются в двух точках

А и В с абсциссами х1 = — 1 и х² = 4. Ответ: х1 = — 1;

х² = 4.

2) Решим графически уравнение (рис. 3) х² — 2х + 1 = 0.

Решение. Запишем уравнение в виде х² = 2х — 1.

Построим параболу у = х² и прямую у = 2х — 1.

Прямую у = 2х — 1 построим по двум точкам М (0; — 1)

и N(1/2; 0). Прямая и парабола пересекаются в точке А с

абсциссой х = 1. Ответ: х = 1.

3) Решим графически уравнение х² — 2х + 5 = 0 (рис. 4).

Решение. Запишем уравнение в виде х² = 5х — 5. Построим параболу у = х² и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.

Ответ. Уравнение х² — 2х + 5 = 0 корней не имеет.

Итак, квадратным уравнением называется уравнение вида ax² + bx + c = 0. Квадратные уравнения бывают полными, неполными и приведенными. Способы решений полных уравнений различны: выделение квадрата двучлена, по формуле, по теореме Виета, способ переброски, способы, основанные на свойствах и закономерностях коэффициентов квадратного уравнения. В данной работе я изложила и показала на примерах все эти способы. Проанализировав дополнительный материал, я пришла к выводу, что с помощью рациональных способов решения квадратных уравнений , решать уравнения стало намного намного проще и быстрее.

Предложенные методы решения квадратных уравнений просты в применении, и они, безусловно, должно заинтересовать увлекающихся математикой учеников. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.

Заключение.

Таким образом, я считаю, что тема данного исследования полностью раскрыта. При работе над темой я узнала много нового из истории квадратных уравнений, а также научилась их решать более удобным способом. Полученные знания пригодятся мне в будущем.

В процессе работы мною создана система нестандартных приемов решения квадратных уравнений и разработан банк заданий, на основе которого мною проведена успешная апробация этих приемов. Хочется отметить и то, что излагаемая тема в этой работе еще полностью не изучена, она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.

Данный материал можно рекомендовать для внеклассных занятий по математике. Материалом могут воспользоваться те, кто любит математику и хочет знать о математике больше.

Список литературы:

1.Алгебра 8 класс: учебник для общеобразовательных учреждений. Авторы: Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Издательство «Просвещение», Москва 2009 г.

2.Брадис В.М. Четырехзначные математические таблицы: для сред.шк.-57-е изд. – М.: Просвещение, 1990.

3. Штейнгауз В.Г. Математический калейдоскоп. – М.: Бюро «Квантум», 2005.

Просмотров работы: 4210

Нестандартные приёмы решения квадратных уравнений

Нестандартные приёмы решения квадратных уравнений

Малахаева  А.О. 1

---

1МБОУ города Астрахани «Гимназия №3»

Лебедева  С.В. 1

---

1МБОУ города Астрахани «Гимназия №3»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Уравнение — одно из важнейших понятий математики. В большинстве практических и научных задач, где какую-то величину нельзя непосредственно измерить или вычислить по готовой формуле, удается составить соотношение (или несколько соотношений), которым оно удовлетворяет. Так получают уравнение (или систему уравнений) для определения неизвестной величины. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры.

 

В школьном курсе математики решение уравнений начинается практически с первого класса и сопровождает нас всю школьную жизнь. Квадратным уравнениям посвящён большой раздел алгебры 8 класса. Мы изучаем, что такое квадратное уравнение, как решить уравнение с помощью определенной формулы, знакомимся с теоремой Виета и ей обратной. Но, существуют и другие способы решения уравнений такого вида, которые могли расширить наши знания об уравнениях и методах нахождения их корней. Поэтому,

цель работы:

Научится решать квадратные уравнения способами, которыми в школьной программе практически не рассматриваются или им уделяется недостаточной внимание.

В ходе исследования решаются следующие задачи:

• познакомиться с историей развития решения квадратных уравнений;
• изучить методы решения квадратных уравнений, изложенные в школьных учебниках;
• выявить нестандартные способы решения квадратных уравнений;
• рассмотреть на конкретных примерах эти методы решения.

 

Исторические сведения о квадратных уравнениях

4000 лет тому назад в двуречье Тигра и Евфрата возникло могучее государство Вавилон. Многочисленные документы той эпохи(глиняные плитки с нанесенным на них клинописными знаками, расшифрованные только в начале XX века) свидетельствуют о том, что вавилоняне умели решать квадратные уравнения. На одной из клинописных табличек записана такая задача: «Множимое и множитель 2;30». Речь в ней идет о двух взаимообратных величинах x и y(xy=1), сумма которых равна 2;30, т.е. 2+30/60+2,5. Таким образом, ученику для решения предлагается система, которую в современной символике можно записать так

Где a=2,5, b=1. Далее в тексте таблички указывается, какие операции нужно проделать, чтобы получить ответ. Практически дается рецепт для решения квадратного уравнения z2-az+b=0, к которому сводится эта система.

Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел».

В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в)-собрание задач на составление уравнений с систематическим изложением их решений. Вот одна из задач Диофанта: «найти два числа, зная, что их сумма равна 20, а произведение 96». Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, т.к. если бы они равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10+Х, другое же меньше, т.е. 10-Х. Разность между ними 2Х. Отсюда Х=2. Одно из искомых чисел равно 12, другое 8. Решение Х+-2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Задачи на квадратные уравнения встречаются и в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта, изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:   ax²+bx=c, a>0. Одна из задач знаменитого индийского математика XІІ века Бхаскары сформулирована в виде стихотворения:

Обезьянок резвых стая

Всласть поевши, развлекалась.

Их в квадрате часть восьмая

На поляне забавлялась.

А двенадцать по лианам…

Стали прыгать повисая…

Сколько было обезьянок

Ты скажи мне, в этой стае?

Однако первым руководством по решению задач,

Получившим широкую известность, стал труд багдадского учёногоIXв. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия трактата- «Китаб аль-джеберваль-мукабала»(«Книга о восстановлении и противопоставлении»)- со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений. Вот как решал квадратное уравнение среднеазиатский ученый ал-Хорезми:

Х²+10Х=39

Он писал: «Правило таково:

Раздвои число корней,                                                               Х=2Х*5

Получите в этой задаче пять,                                                          5

Умножь на это равное ему, будет двадцать пять,                  5*5+25

Прибавь это к тридцати девяти,                                                    25+39

Будет шестьдесят четыре                                                                    64

Извлеки из этого корень, будет восемь                                          8

И вычти из этого половину числа корней, т.е пять                8-5

Останется                                                                                          3

Это будет корень квадрата, который ты искал.»

А второй корень? Второй корень не находили, так как отрицательные числа не известны.

Общее правило решения квадратных уравнений, приведенных у единому каноническому виду  x2+bx+c=0, было сформулировано в Европе лишь в 1554 г. Штифелем.

 

Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. Итальянским математиком

Леонардом Фибоначчи

 

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Лишь в 17 веке благодаря трудам Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

 

Что такое квадратное уравнение

Квадратное уравнение — это алгебраическое уравнение общего вида

Просмотров работы: 73

«Нестандартные способы решения квадратных уравнений»

Урок открытия нового знания.

Технологии:

1) Технология адаптивного обучения;

2) Групповая технология;

3) Проектная технология;

4) ИКТ

5) Игровая технология.

Тема: Нестандартные методы решения квадратных уравнений.

Цель: Рассмотреть методы решение квадратных уравнений, выходящие за пределы курса основной школы. Отработать новые методы на практике обобщить и систематизировать методы решения квадратных уравнений.

Задачи:

1. Образовательная: рассмотреть нестандартные методы решения квадратных уравнений, отработать на практике, обобщить и систематизировать способы решения квадратных уравнений.

2. Развивающая: развить умения работать в группе; способность учащихся к самооценке своих знаний, самоконтролю; способность к самостоятельному поиску информации и ее

3. Воспитательная: привить учащимся интерес к математике, к поиску новой информации.

ХОД УРОКА

Учащиеся рассажены по 4 группам, в каждой группе есть наставник, учащийся 10 класса.

1. Организационные моменты. (2мин)

Здравствуйте ребята, присаживайтесь. откройте тетради, число, классная работа. На своих столах вы видите рабочие карты урока, проставьте на них число, напишите свою фамилию, имя. Также на столах вы видите критерии урока, ознакомьтесь с ними. Сегодня мы работаем в командах, в ваших командах есть наставник, назовите свою группу и пусть наставник передаст мне название.

Какую большой блок алгебры мы проходили свами на последних уроках. (Квадратные уравнения и способы их решения).

2. Актуализация опорных знаний.(2-3мин)

Какие способы решения квадратных уравнений мы свами изучили?

• По формуле (Д,Д1)

• По обратной теореме Виета

• С помощью коэффициентов.

3. Практическая работа на повторение( 5мин)

Давайте повторим решение квадратных уравнений данными способами:

К доске вызываются четыре учащихся из четырех групп. Каждая группа получает свое задание (группа решает свое задание) (сл.4)

Задание 1 группы:

Решить квадратное уравнений, с помощью дискриминанта:

Задание 2 группы:

Решить квадратное уравнение, с помощью дискриминанта, с четным коэффициентом b :

Задание 3 группы:

Решить квадратное уравнение с помощью обратной т. Виета.

Задание 4 группы:

Решить квадратные уравнение по формулам коэффициентов:

Каждый представить рассказывает, как он решал свое уравнение:

Учитель: Ребята мы повторили основные способы решения квадратных уравнений. Возьмите в руки карты урока и критерии, в графе «повторение» поставьте себе оценку, согласно приложенным критериям.

4. Изучение нового материала (25мин)

4.1. Создание проектов (10мин).

Данные способы решения, изучают в школьном курсе математики, как вы думаете за столь большое время, которое люди решают квадратные уравнения они не придумали другие способы решения квадратных уравнений? (Ответ учащихся)

Цель нашего сегодняшнего урока познакомится с нестандартными способами решения квадратных уравнений, которые выходят за рамки школьного курса, выяснить удобны ли они и попробовать применить их на практике.

Запишите пожалуйста тему сегоднешнего урока: «Нестандартные методы решения квадратных уравнений»

И изучать, мы их будем нестандартно, каждая группа станет учителем и наставником для других, а ребята из 10 класса в этом вам помогут.

Учитель: наставники подойдите и возьмите конверт с заданием для своей команды.

Каждая команда получает свое задание в конверте. Ваша задача создать проект, объяснить новый материал остальным командам, и показать примеры решения. Время выполнения проекта 10мин. А я сегодня буду в роли Вашего помощника и организатора. В рабочей карте урока внесите название способа, который вы будете разбирать.

Задание команды 1.

Создать проект (на листе ватмана) решения квадратных уравнений способом переброски коэффициентов, показать примеры решения квадратных уравнений данным способом. (Материал для проекта прилагается)

Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение

ах² + bх + с = 0, где а ≠ 0.

Умножая обе его части на а, получаем уравнение а²х² + аbх + ас = 0.

Пусть ах = у, откуда х = ; тогда приходим к уравнению у² + by + ас = 0,

равносильно данному. Его корни у₁ и у₂ найдем с помощью теоремы Виета и окончательно:

х₁ = и х₁ =

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример.

Решим уравнение 2х² – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у² – 11у + 30 = 0.

Согласно теореме Виета

у₁ = 5 , х₁ = 5/2 , x₁ = 2,5

у₂ = 6; x₂ = 6/2; x₂ = 3.

Ответ: 2,5; 3.

Задание команде 2.

Создать проект (на листе ватмана) решения квадратных уравнений с помощью циркуля и линейки, показать примеры решения квадратных уравнений данным способом. (Материал для проекта прилагается)

Решение квадратных уравнений с помощью циркуля и линейки.

Предлагаю следующий способ нахождения корней квадратного уравнения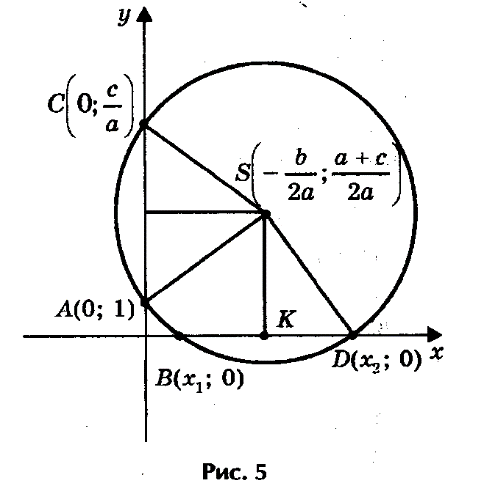

ах² + bх + с = 0 с помощью циркуля и линейки (рис.1 ).

Допустим, что искомая окружность пересекает ось

абсцисс в точках В(х₁; 0 ) и D (х₂; 0), где х₁ и х₂ — корни уравнения ах² + bх + с = 0, и проходит через точки

А(0; 1) и С(0; ) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = == .

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому

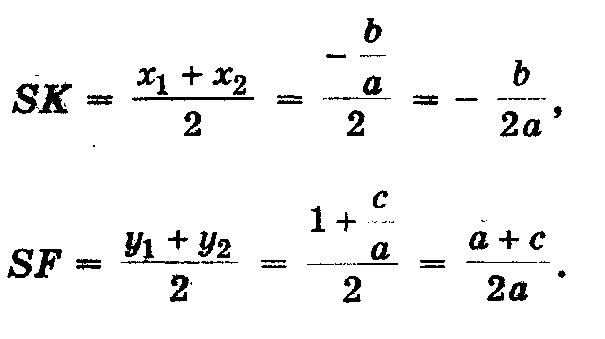
Итак: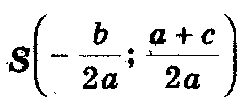

1) построим точки (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

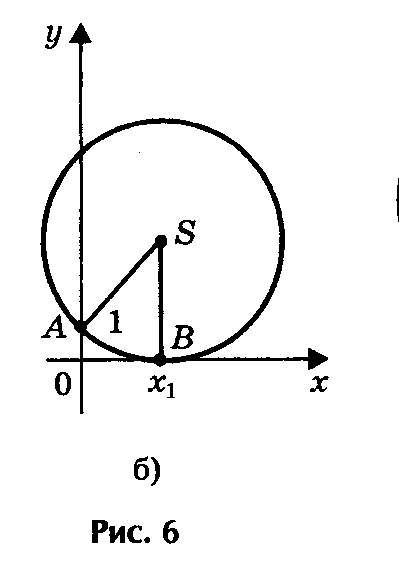
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 2а) В(х₁; 0) и D(х₂; 0),

где х₁ и х₂ — корни квадратного уравнения ах² + bх + с = 0.

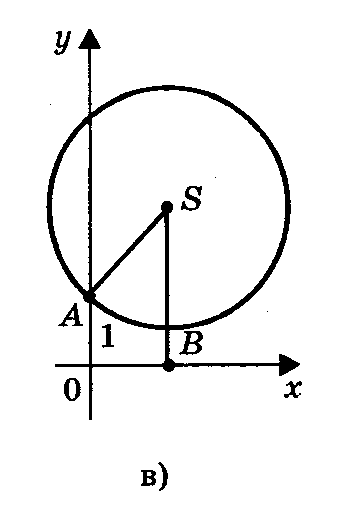
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис.2б) в точке В(х₁; 0), где х₁ — корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис 2в), в этом случае уравнение не имеет решения.

Рис.2

а) б) в)

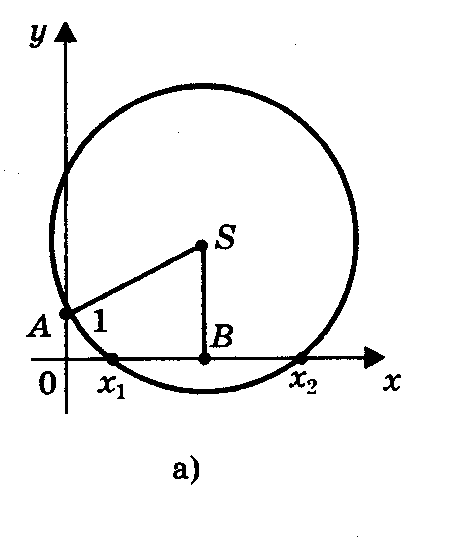
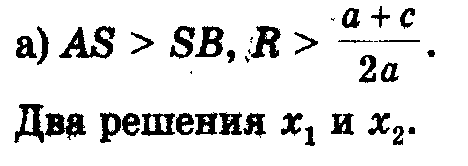
Пример.

Решим уравнение х² — 2х — 3 = 0 (рис.3).

Решение. Определим координаты точки центра окружности по формулам:

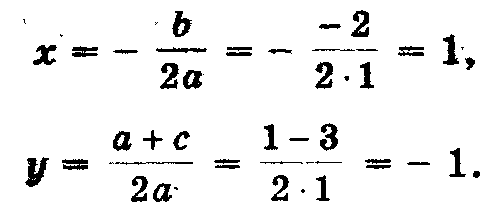
Проведем окружность радиуса SA, где А (0; 1).

Ответ: х₁ = — 1; х₂ = 3.

Задание команде 3.

Создать проект (на листе ватмана) решения квадратных уравнений способом коэффициентов. (не проходят в школе), показать примеры решения (Материалы для проекта прилагаются)

Пример:

1 формула:

b=10=3²+1, а=3=с, x₁= -3, x₂=-1/3

2,3,4 формулы ребята составляют сами.

Задание команде 4.

Создать проект (на листе ватмана) решения квадратных уравнений геометрическим способом, показать примеры решения. квадратных уравнений (Материалы для проекта прилагаются).

Геометрический способ решения.

Древние греки решали уравнение у² + 6у — 16 = 0.

Решение представлено на рис 1. где

у² + 6у = 16, или у² + 6у + 9 = 16 + 9.

Решение. Выражения у² + 6у + 9 и 16 + 9 геометрически представляют собой

один и тот же квадрат, а исходное уравнение у² + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у₁ = 2, у₂ = — 8 (рис.1) .

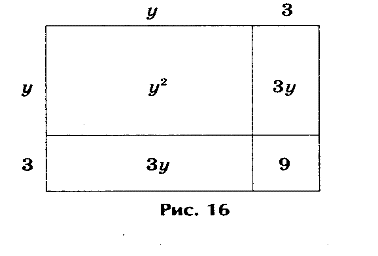
рис.1

3) Решить геометрически уравнение у² — 6у — 16 = 0.

Преобразуя уравнение, получаем

у² — 6у = 16.

На рис 2. находим «изображения» выражения у² — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у² — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у² — 6у равным ему числом 16,

получаем: (у — 3)² = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у₁ = 8 и у₂ = — 2.

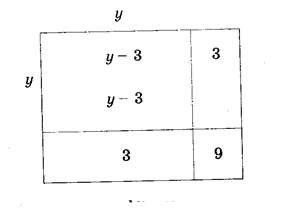рис2.

Каждой команде отводится время 10мин. для подготовки проекта, выдается ватман и маркеры, для оформления проекта.

****Разминка – эстафета «Лесенка»

Найти дискриминант каждого уравнения, подняться по ступенькам. Выполняется задание по очереди, участвует вся команда, если дискриминант найден не верно, то команда теряет время, следующий исправляет и только потом решает свое задание. Получившиеся значения дискриминанта заносится в лесенку, поднимаясь по ступенькам. Первая команда закончившая задание получает дополнительную пятерку!

После окончания эстафеты физкультминутка :

Если уравнение имеет два корня, то руки вверх.

Ели уравнение не имеет корней, то руки в стороны.

Если уравнение имеет один корень, то закрываем глаза руками.

Идем по ступенькам вверх.

Команда №1

1)

2)

3)

4)

5)

6)

7)

Команда №2.

1)

2)

3)

4)

5)

6)

7)

Команда №3.

1)

2)

3)

4)

5)

6)

7)

Команда №4.

1)

2)

3)

4)

5)

6)

7)

4.2 Защита проектов. 15мин

Представители команды объясняют новый материал, показывают примеры решения. Остальные команды записывают суть способа, примеры решения в тетрадь. Учитель помогает и направляет защитников проекта.

После защиты каждой команды, учитель просит учащихся выставить оценки в рабочую карту урока, согласно критериям изучения новой темы.

5. Первичное закрепление новой темы (5-8мин)

Команды защитники проектов, получают задание учителя и номер команды, которая должна решить квадратное уравнение способом, который представляли учащиеся. Они совместно решают и представляю решение на проекторе (гусёнок).

Задание учителя: решить квадратное уравнение:

1. Методом переброски коэффициентов

2. Методом коэффициентов:

3. Геометрическим методом:

4. С помощью циркуля и линейки:

Каждая команда ставит оценку в рабочую карту урока, согласно критерием первичного закрепления материала по предложенной ей теме.

6. Подведение итогов урока. 2мин

Все проекты вывешены на доске.

Ребята на сегодняшнем уроке мы рассмотрели 4 новых способа решения квадратных уравнений, изучение которых выходит за курс школьной программы математики.

• Какие способы мы прошли?

• Какой способ Вас заинтересовал?

• Какой способ, вы считаете пригодится вам?

Поставьте пожалуйста итоговую оценку в рабочую карту, согласно критерию работы на уроке.

А также поставьте, оценку в графе интересен вам был урок, по пятибалльной шкале. Наставники соберите рабочие карты урока у своих команд, сдайте их учителю.

Я же могу в свою очередь сказать, что вы сегодня очень хорошо потрудились!

Результаты вашей работы мы повесим в кабинете, что бы другие учащиеся могли тоже посмотреть «Нестандартные способы решения квадратных уравнений»

7. Домашнее задание

Карточка

№ 1. Решить уравнение:

1. Способом «переброски» №33.4(6, 7)

2. Способом «циркуль и линейка» №33.5 (7,8)

3. Геометрическим способом № 33.16(1,2)

№2. Составить 4 уравнения которые можно решить способом «коэффициентов»

Спасибо Вам за урок!

Проект » Квадратные уравнения»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №13

Учебный проект

Нестандартные приемы решения квадратных уравнений.

Автор: ученик 8»а» класса

Комарков Дмитрий

Руководитель:

учитель математики

высшей категории

Смирнова

Надежда Александровна

2012 год

Оглавление.

Введение

Глава 1. Изучение литературы

Глава 2. Обобщение имеющихся знаний о квадратных уравнениях и приемах их решения

Глава 3. Нестандартные приемы решения квадратных уравнений

Глава 4. Материал для проведения практикума по решению квадратных уравнений нестандартными способами

Глава 5. Анализ работы учащихся по решению квадратных уравнений нестандартными способами.

Глава 6. Выводы

Список литературы

Введение.

Тема «Квадратные уравнения » является одной из самых актуальных. Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение в разных разделах математики.

В школьном курсе изучаются формулы корней квадратного уравнения, с помощью которых можно решать любые квадратные уравнения. Однако, имеются и другие приемы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Цель: создание системы нестандартных приемов решения квадратных уравнений и банка задач

Проблемный вопрос: как решить квадратное уравнение, если забыл формулы?

Гипотеза: Предполагаем, что существуют методы решения квадратных уравнений без использования формул, изучаемых в школьном курсе алгебры

Задачи:

1. Обобщить и систематизировать имеющийся материал о квадратных уравнениях и способах их решения

2. Установить связь между коэффициентами и корнями квадратного уравнения и найти нестандартные приемы решения некоторых квадратных уравнений

3. Изучить дополнительные литературу и источники информации

4. Систематизировать нестандартные приемы решения некоторых квадратных уравнений

5. Разработать дидактический материал и провести его апробацию на факультативе в 8 классе

6. Ход работы над проектом:

1. Изучение литературы по истории вопроса

2.Обобщение накопленных знаний о квадратных уравнениях и способах их решения из школьной программы

3. Изучение дополнительной литературы и других источников информации

4. Систематизация приемов решения квадратных уравнений.

5. Разработка дидактического материала

6. Проведение практической работы

7.Анализ практической работы

Объект исследования: квадратные уравнения

Предмет изучения: приемы решения квадратных уравнений

Глава 1

Изучение литературы

Основной материал, связанный с изучением темы «Решение квадратных уравнений» находится в УМК под ред.С.А.Теляковского. В учебнике Ю.Н.Макарычев, Н.Г.Миндюк Алгебра-8 класс разобраны основные вопросы по теме:

1. Определение и виды квадратных уравнений

2.Основные методы решения квадратных уравнений

Однако, дополнительный материал, связанный с историей вопроса о возникновении квадратных уравнений, о нестандартных приемах их решения, в школьных учебниках отсутствуют. Поэтому в ходе работы над проектом изучалась дополнительная научная литература и другие источники информации.

Изученная литература позволила приобрести новые интересные знания по истории возникновения квадратного уравнения, приобрести опыт по решению различных квадратных уравнений нестандартными приемами и перейти к следующему этапу в исследовании- научиться применять полученные знания на практике.

Глава 2.

Обобщение накопленных знаний о квадратных уравнениях и способах их решения.

1. Немного истории.

Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения  не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их  клинописных текстах  встречаются, кроме неполных, и полные квадратные уравнения.

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила.. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

В III в. н. э. квадратное уравнение
х² – 20х + 96 = 0
без обращения к геометрии
решил великий древнегреческий математик Диофант (3век).

В 1591 г. Ф. Виет вывел формулы, выражающие зависимость корней квадратного уравнения от его коэффициентов и сформулировал свою знаменитую теорему.

Именно с 1591 г. мы пользуемся формулами при решении квадратных уравнений.

2. Обобщение накопленных знаний о квадратных уравнениях и способах их решения.

А) Общий вид квадратного уравнения

Б) Известные способы решения

квадратных уравнений

полные

Известные способы решения

квадратных уравнений

полные (особые случаи)

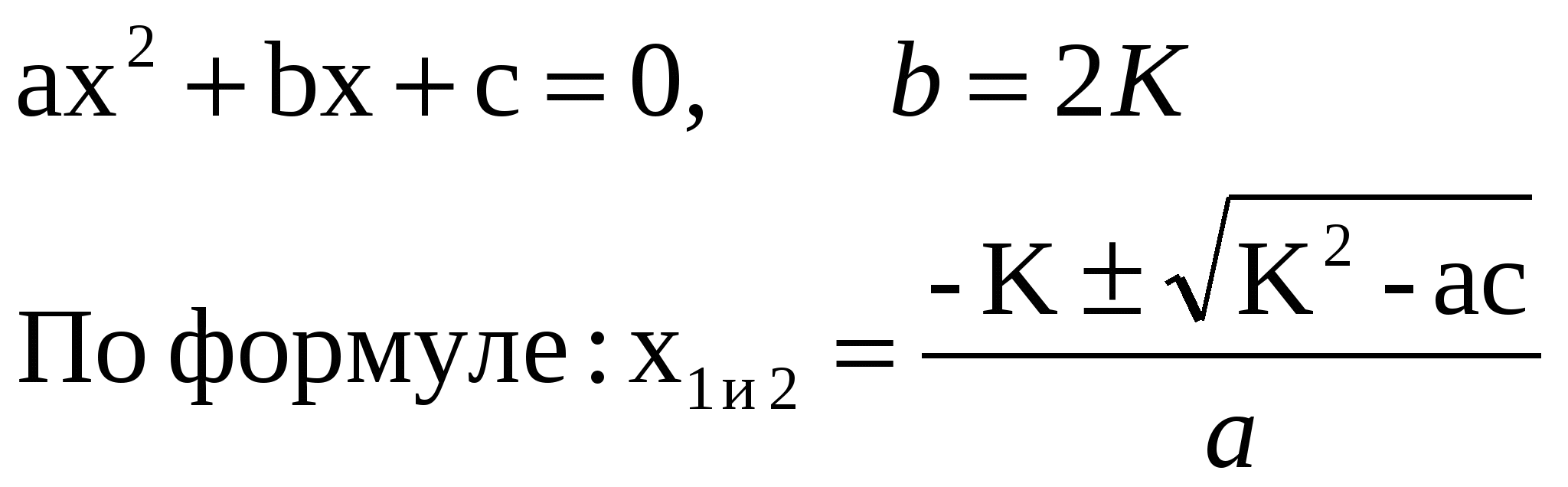
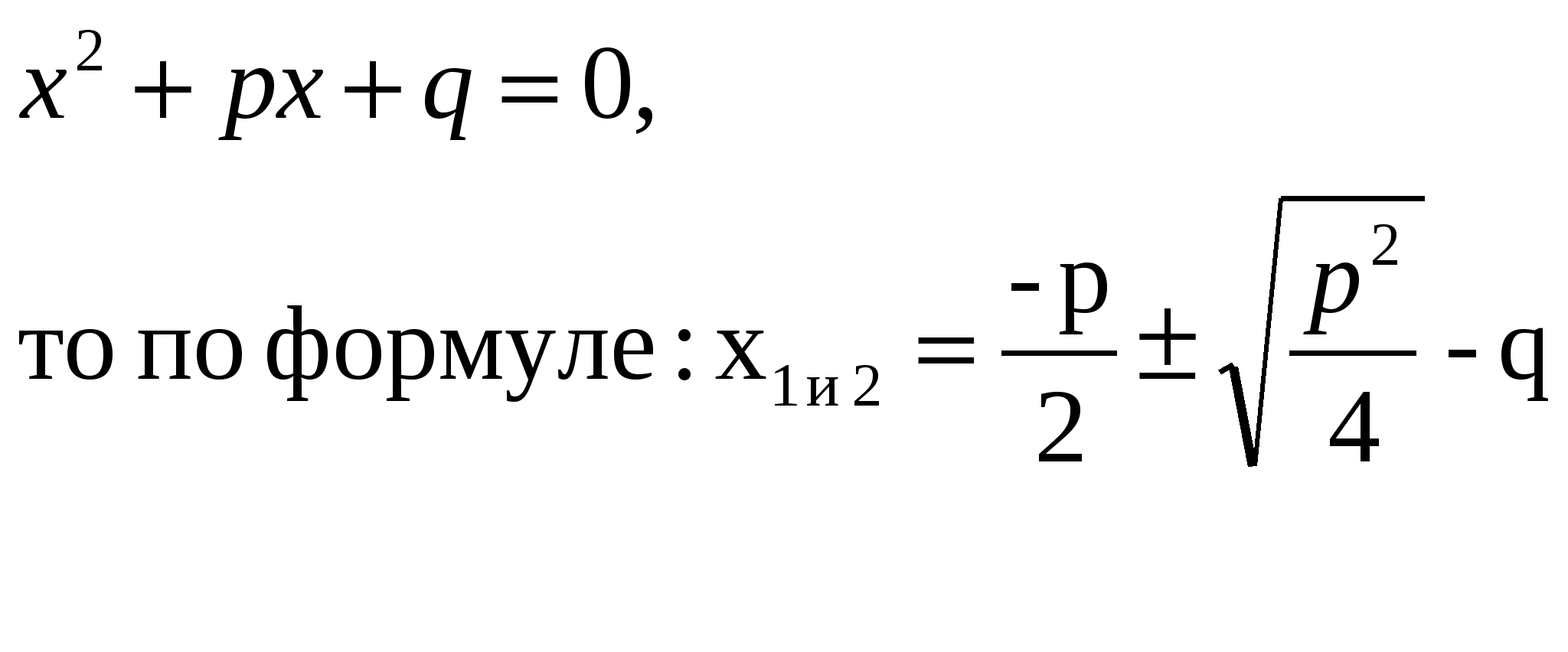
полные приведённые квадратные уравнения

Теорема, обратная теореме Виета

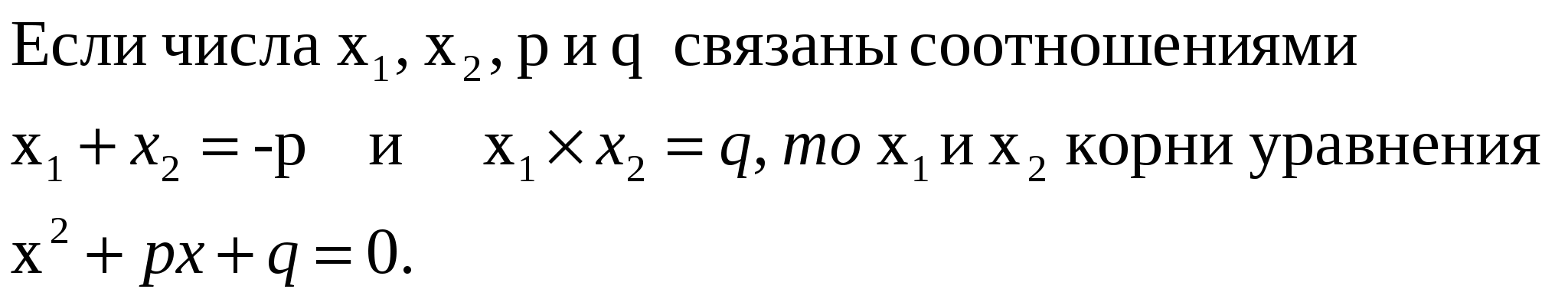
Неполные квадратные уравнения

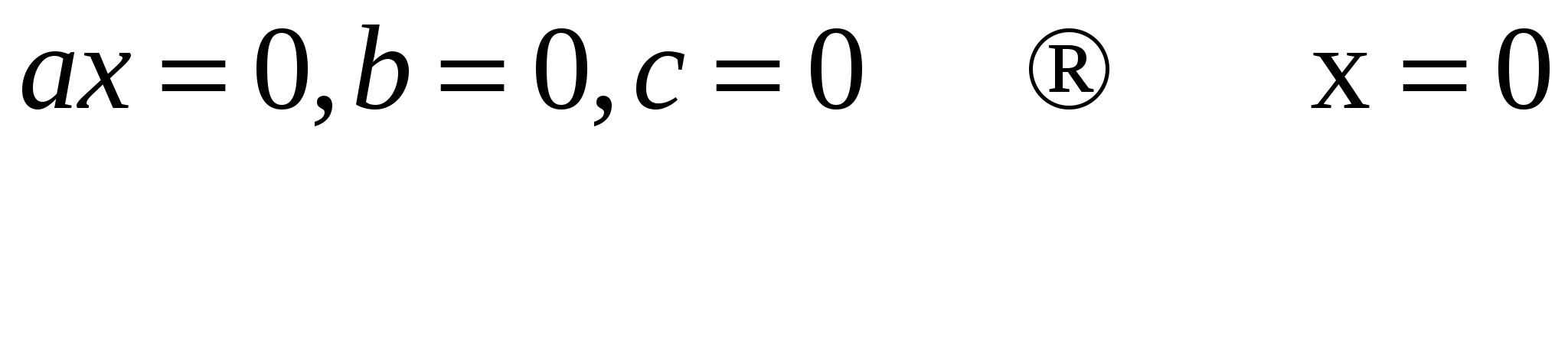
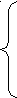
— Нет корней, если –с/a <0

+ √-с/a ,если –c|a>0

—

Решение квадратных уравнений с применением циркуля и линейки

Корни квадратного уравнения ах² + bx + с = 0 (а ≠ 0)

можно рассматривать как абсциссы точек пересечения

окружности с центром Q (- в/2a ; (a+c)/2a ), проходящей через точку

A(О; 1), и оси Ох .

1) если QA > (a+c)/2a , то
окружность пересекает ось Ох в двух точках
М(х₁; 0) и N(х₂; 0) , уравнение имеет
корни х₁ ; х₂

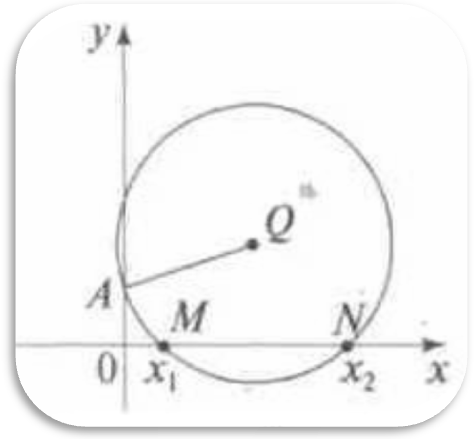
2) если QA = (a+c)/2a , то

окружность касается оси Ох в точке М(х₁; 0),
уравнение имеет корень х_1.

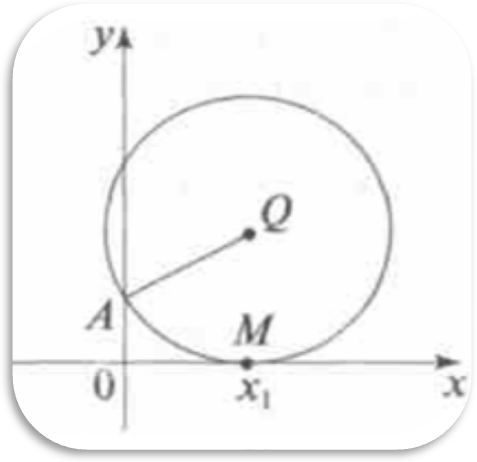
3) если QA<(a+c)/2a , то окружность не имеет общих точек с осью Ох,
и уравнение
не имеет корней.

Проведя анализ, я заметил, что значения корней квадратного уравнения зависят от его коэффициентов. Следовательно, искать нестандартные приемы решения квадратных уравнений необходимо учитывая эти связи.

Глава 3

Нестандартные приемы решения квадратных уравнений

метод коэффициентов

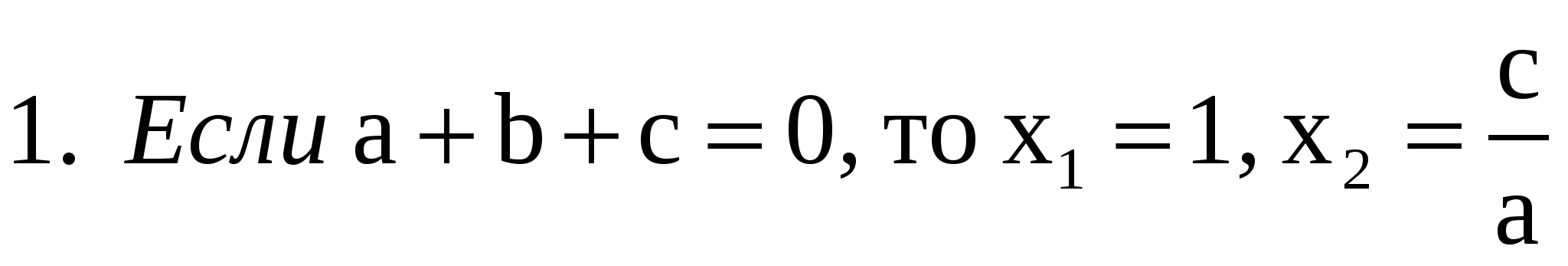
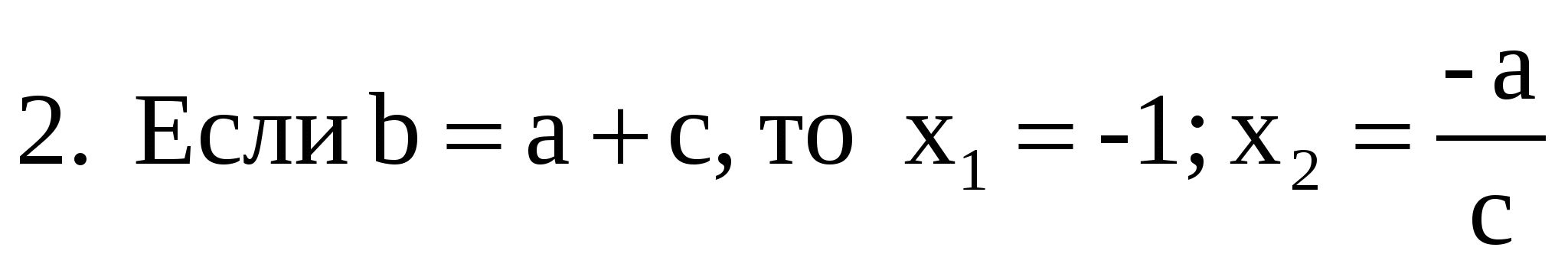
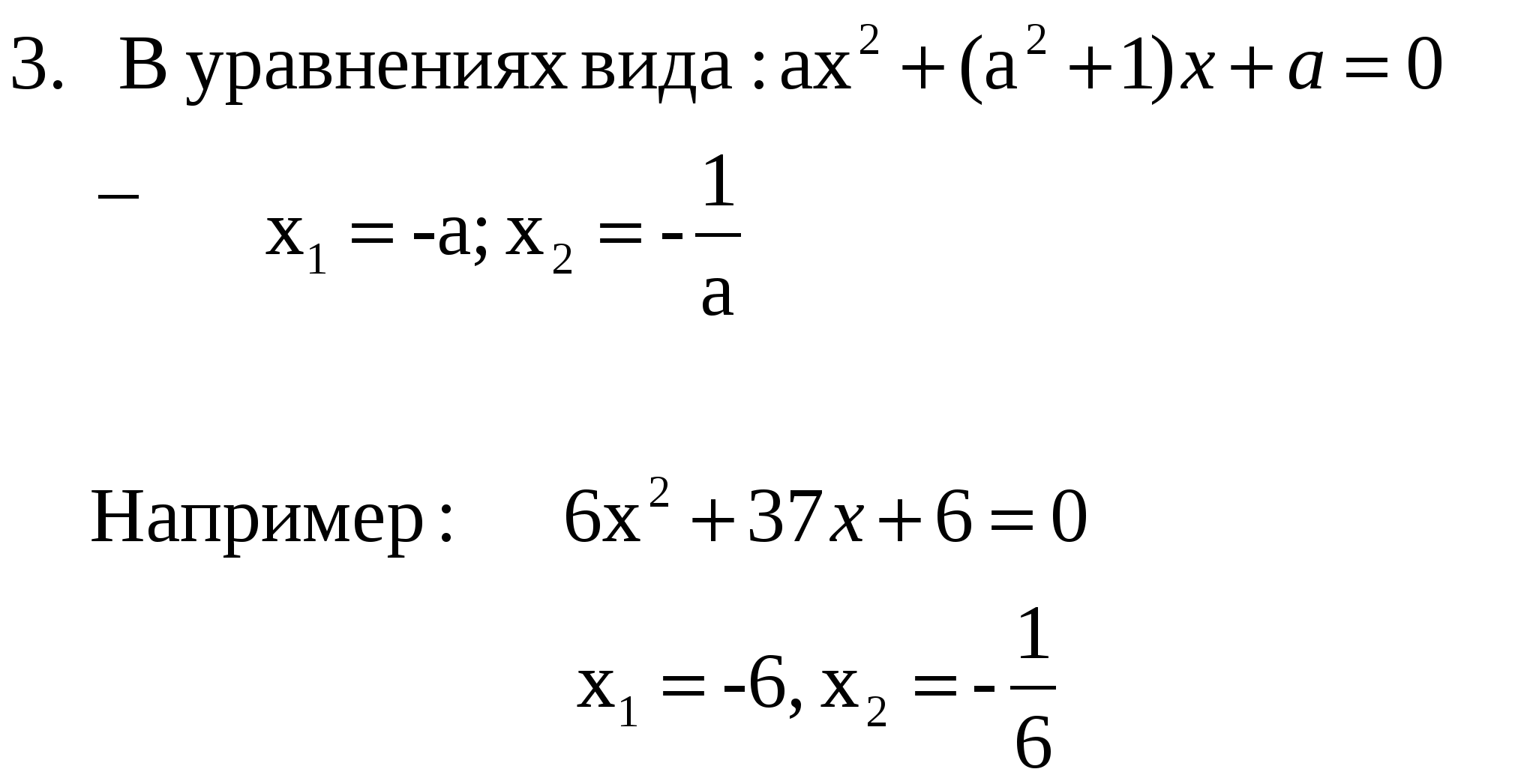
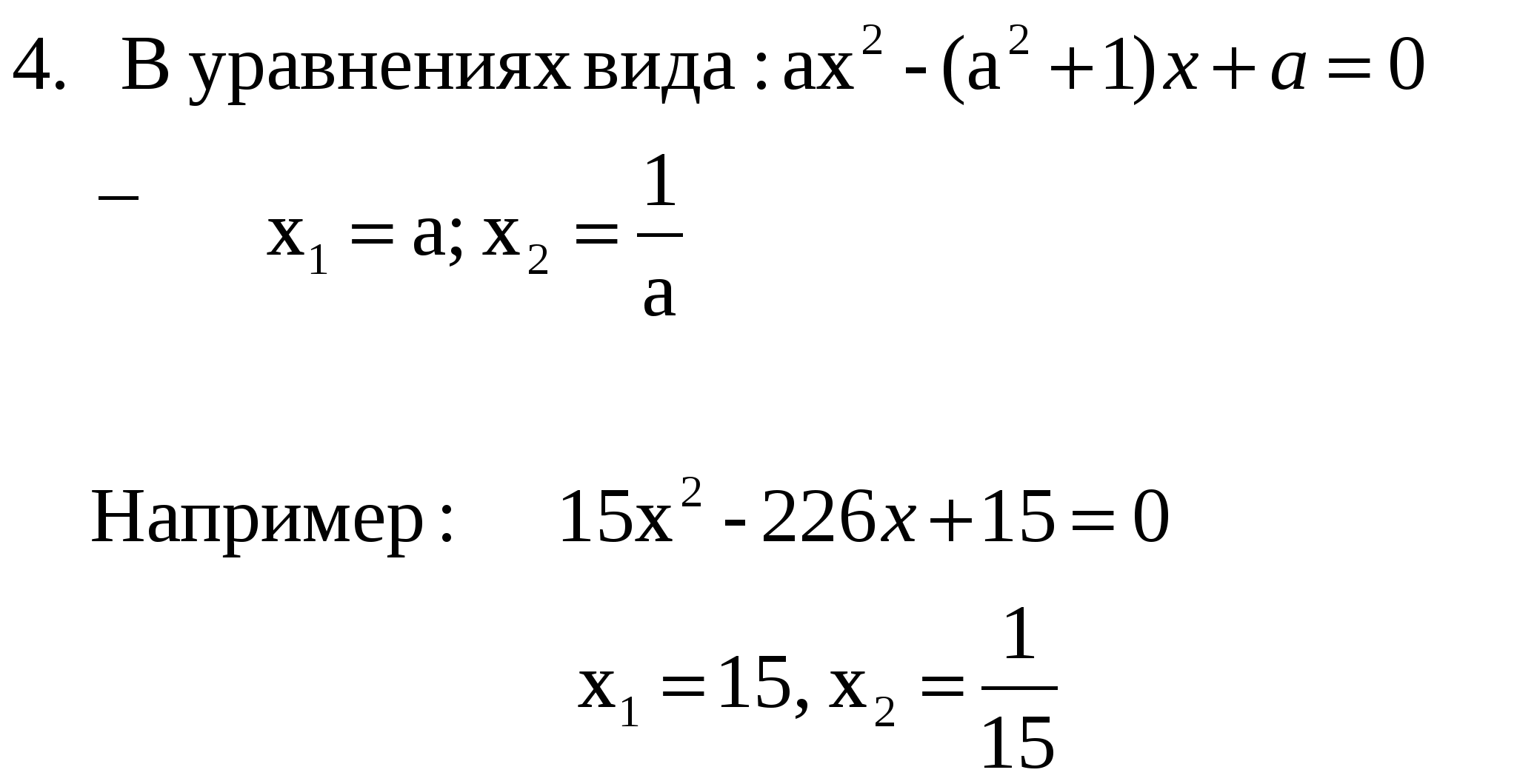
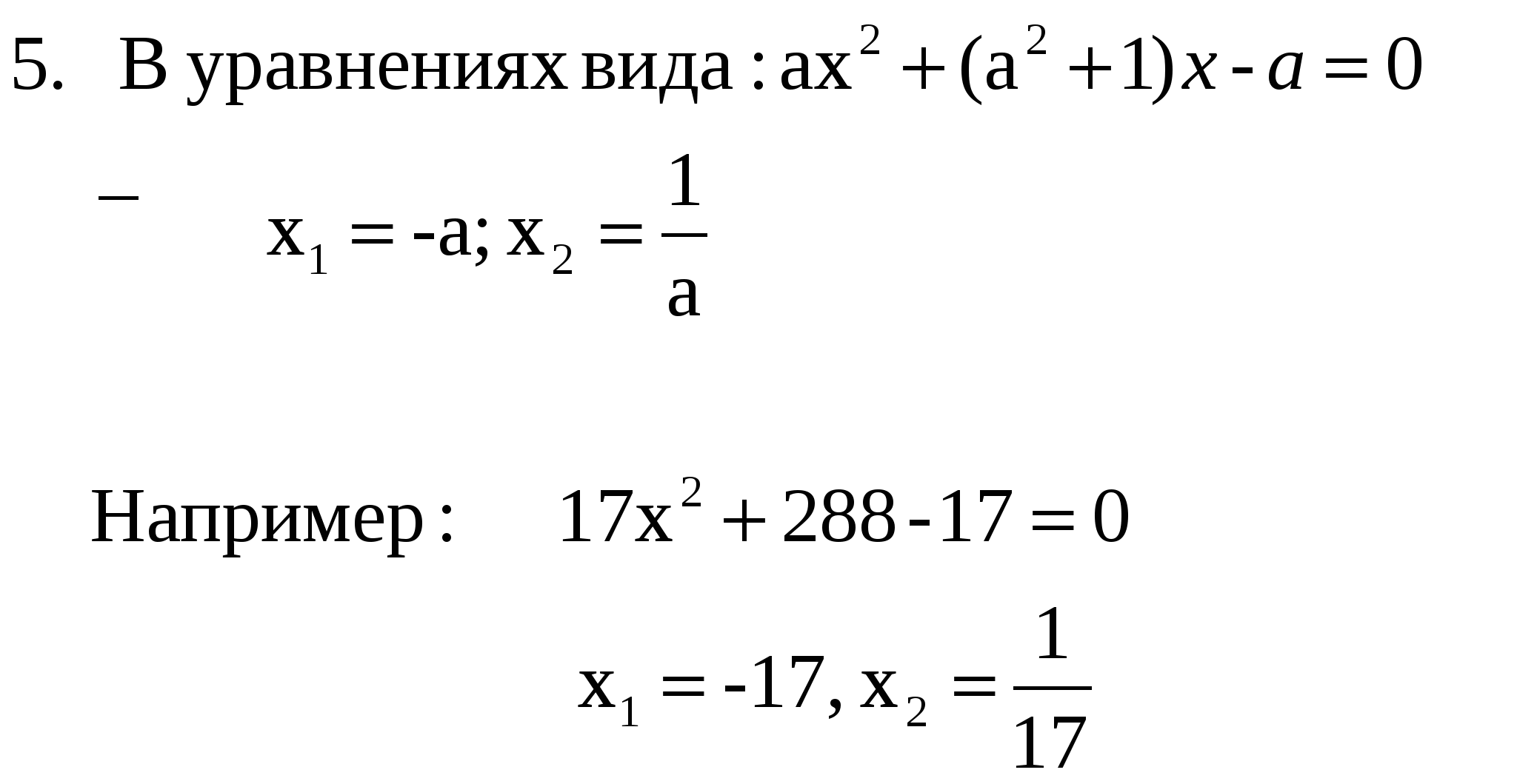
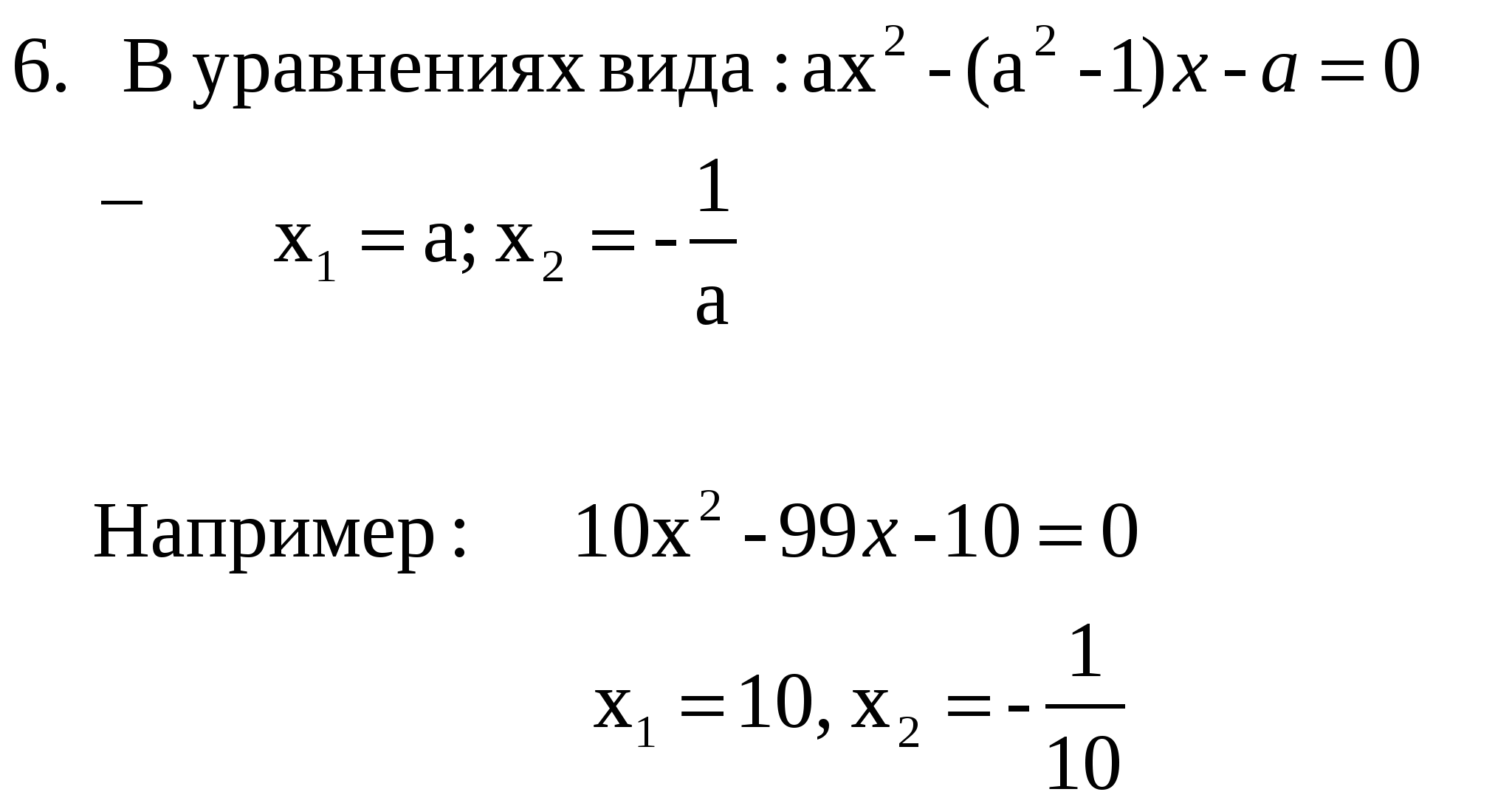
Прием « переброски» старшего коэффициента

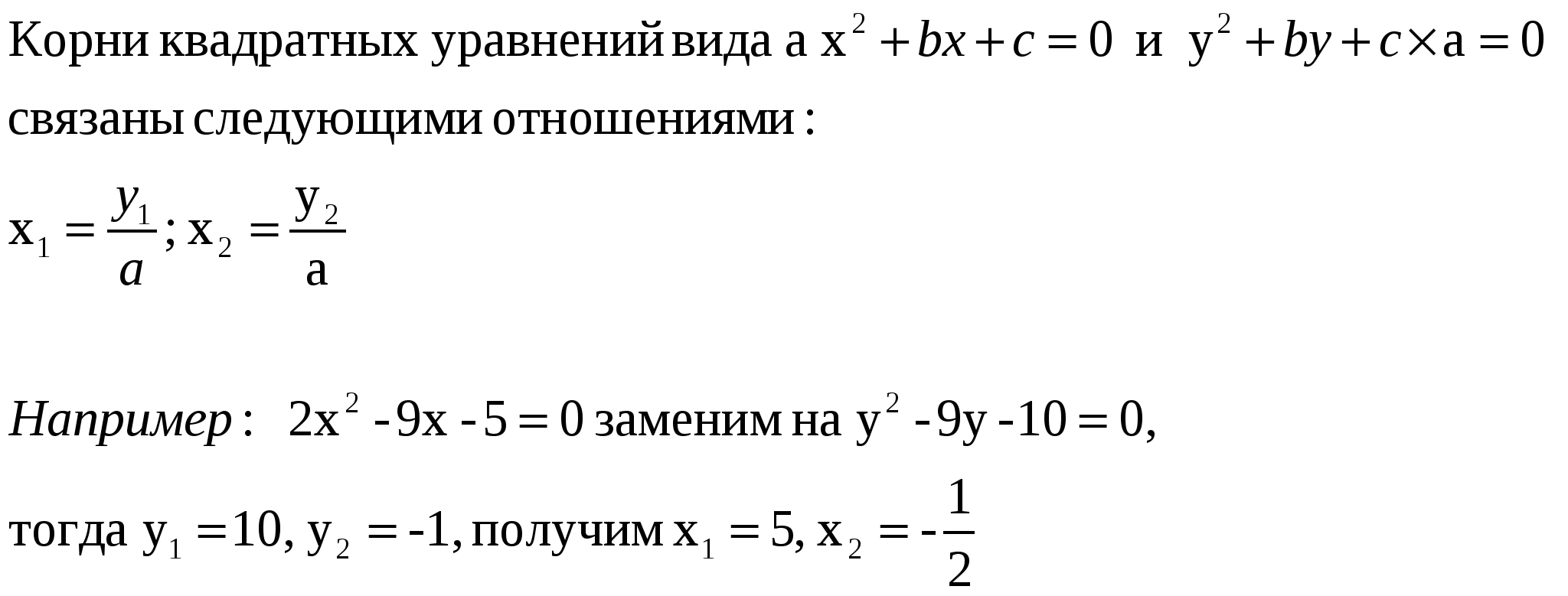
Глава 4

Материал для проведения проверочной работы по решению квадратных уравнений с помощью нестандартных приемов

Найденные нестандартные приемы было решение апробировать на факультативном занятии в 8 классе.

Цель данной работы: проверить на практике использование нестандартных приемов вычисления корней квадратного уравнения.

Данная работа проведена в 2 этапа:

1. Изучение теории

2. Практическая работа

Были подобраны задачи для проведения работы.

1. Найди наиболее рациональным способом корни уравнения:

А) 4х² – 13х + 9 =0

(1; 2,25)

Б) 1978х² – 1984х + 6=0

(1; 6/1978)

В) 4х² + 11х + 7 = 0

(-1; -7/4)

Г) 319х² + 1988х +1669=0

(-1; -1669/319)

Д) 1999х² + 2000х+1=0

(-1; -1/1999)

2. Решить квадратные уравнения с большими коэффициентами

А) 313х² +326х+13=0

(-1; -13/313)

Б) 839х²— 448х -391=0

(1; -391/839)

В) 345х² – 137х – 208=0

(1;.-208/345)

Г) 939х²+978х+39=0

(-1; -39/939)

3. Используя полученные знания, установи соответствие:

1. х²+5х+6=0 1. 1/6;1/2

2. 6х²-5х+1=0 2. 1; 3/2

3. 2х²-5х+3=0 3. 1; 2/3

4. 3х²-5х+2=0 4. -2; -3

5. х²-5х+6=0 5. -1/3 ; -1/2

6. 6х²+5х+1=0 6. -1; -3/2

7. 2х²+5х+2=0 7. -1; -2/3

8. 3х²+5х+2=0 8. 2; 3

Глава 5

Анализ работы учащихся по решению квадратных уравнений нестандартными способами

Разработаны критерии оценки проведенного практикума:

1. За каждое верно выполненное задание ставится 1 балл;

2. Наиболее возможное количество набранных баллов-17

3. Если ученик набирает менее 7 баллов, то выставляется оценка «2»

от 7 до 11 баллов «3»

от 12 до 15 баллов «4»

от 16-17 баллов «5»

Результаты практикума.

Выполняли работу- 11человек

Набрали баллов от 16-17 — 5человек (45%)

От 12-15- 6человек (55%)

Менее 12 – 0 человек

Средний балл -4,45

Процент качества- 100%

Типичные ошибки, допущенные в работе связаны с невнимательностью учащихся.

Выводы по результатам проведения практикума

Успешно выполненная работа учащимися 8 класса, позволяет сделать следующие выводы:

нестандартные приемы решения квадратных уравнений заслуживают внимания;

позволяют экономить время решения, что обусловлено применением тестовой системы экзаменов.

Глава 6

Выводы

В процессе работы над проектом, была создана система нестандартных приемов решения квадратных уравнений и разработан банк заданий, на основе которого проведена успешная апробация этих приемов.

Данный материал можно рекомендовать для внеклассных и факультативных занятий по математике. Учителя могут использовать его как методическое пособие при изучении темы «Решение квадратных уравнений», а также, для контроля за знаниями учащихся.

Материалом этого проекта могут воспользоваться и те, кто любит математику и хочет знать о математике больше.

Литература

1.Выгодский М.Я. Справочник по элементарной математике: — М. государственное издательство физико-математической литературы, 1970

2 А М.Л.Галицкий,.М.Гольдман, Л.И.Звавич. Сборник задач по алгебре для 8-9 классов: учебное пособие для учащихся школ и классов с углубленным изучением математики:4-е изд.-М.: Просвещение, 1997

3. Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Учебник для 8 класса. М., Просвещение. 2001

4. Макарычев Ю.Н., Миндюк Н.Г.Дополнительные главы к школьному учебнику. 8 класс М., Просвещение, 1996

5. Штейнгауз В.Г.:Математический калейдоскоп.- М.: Бюро «Квантум»,2005

6.Знциклопедический словарь юного математика. – М.: Педагогика,1985

Защита проекта «Нестандартные приемы решения квадратных уравнений»

В этом учебном году на уроках алгебры мы изучили тему «Квадратные уравнения и способы их решения».

Тема «Квадратные уравнения » является одной из самых актуальных. Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение в разных разделах математики.

В школьном курсе изучаются формулы корней квадратного уравнения, с помощью которых можно решать любые квадратные уравнения.

Недавно ко мне обратился мой знакомый -ученик 11 класса, который забыл общие формулы решения квадратного уравнения. Я сначала удивился, но потом задумался над тем, как помочь таким ребятам найти другие, ранее не изученные приемы решения квадратных уравнений, без применения основных формул решения квадратного уравнения.

Так появился учебный проект «Нестандартные приемы решения квадратных уравнений»(Слайд1)_

Эпиграфом к проекту могут служить слова Сойера:(2слайд)

«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».

У. Сойер.

Цель проекта;(3 слайд)

создание системы нестандартных приемов решения квадратных уравнений и банка задач

Проблемный вопрос (3 Слайд)

как решить квадратное уравнение, если забыл формулы?

Я преположил(3слайд — гипотеза)

что существуют методы решения квадратных уравнений без использования формул, изучаемых в школьном курсе алгебры

План исследования (4слайд)

1. Изучение литературы по истории вопроса

2.Обобщение накопленных знаний о квадратных уравнениях и способах их решения из школьной программы

3. Изучение дополнительной литературы и других источников информации

4. Систематизация приемов решения квадратных уравнений.

5. Разработка дидактического материала

6. Проведение практической работы

7.Анализ практической работы

Немного истории вопроса(5 слайд)

Необходимость решать уравнения  не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Однако, почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

В 1591 г. Ф. Виет вывел формулы, выражающие зависимость корней квадратного уравнения от его коэффициентов и сформулировал свою знаменитую теорему.

Именно с 1591 г. мы пользуемся формулами при решении квадратных уравнений.

В результате обобщения знаний о способах решения квадратных уравнений, анализа дополнительной литературы и других источников информации, найдены нестандартные приемы решения квадратных уравнений.

(слайд6)Метод коэффициентов

Рассказать

(слайд7) метод переброски

Рассказать

Для проверки эффективности использования этих приемов я разработал дидактический материал и предложил провести занятие факультатива в 8 классе поданной теме. Цель занятия: проверить на практике использование нестандартных приемов вычисления корней квадратного уравнения.

Проведен анализ работы учащихся по решению квадратных уравнений нестандартными способами (слайд 8)

Разработаны критерии оценки проведенного практикума:

Всего предложено 17 заданий.

1. За каждое верно выполненное задание ставится 1 балл; наибольшее количество набранных баллов-17

2. Если ученик набирает менее 7 баллов, то выставляется оценка «2»

от 7 до 11 баллов «3»

от 12 до 15 баллов «4»

от 16-17 баллов «5»

Результаты практикума.

Выполняли работу- 11человек

Набрали баллов от 16-17 — 5человек (45%)

От 12-15- 6человек (55%)

Менее 12 – 0 человек

Средний балл -4,45

Процент качества- 100%

Типичные ошибки, допущенные в работе связаны с невнимательностью учащихся.

Выводы по результатам проведения практикума

Успешно выполненная работа учащимися 8 класса, позволяет сделать следующие выводы:

нестандартные приемы решения квадратных уравнений: заслуживают внимания;

позволяют экономить время решения, что обусловлено применением тестовой системы экзаменов.

Слайд 9

Выводы

В процессе работы над проектом, была создана система нестандартных приемов решения квадратных уравнений и разработан банк заданий, на основе которого проведена апробация этих приемов.

Данный материал можно рекомендовать для внеклассных и факультативных занятий по математике. Учителя могут использовать его как методическое пособие при изучении темы «Решение квадратных уравнений», а так же, для контроля за знаниями учащихся.

Материалом этого проекта могут воспользоваться и те, кто любит математику и хочет знать о математике больше.

Слайд 10 Спасибо за внимание

история

первое тысячелетие н.э. – Римские завоевательные войны. К этому периоду относится творчество Диофанта. Его трактат “Арифметика” содержит ряд задач, решаемых при помощи квадратных уравнений. В IX веке узбекский математик Аль-Хорезми в Трактате “Алгебра” классифицирует квадратные уравнения. Для нас это время знаковое тем, что приблизительно в это время образуется древнерусское государство Киевская Русь.

Все это время отличные по записи уравнения считались различными. Не было единого подхода к их решению.

И только в XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым заложил основы буквенной алгебры.

Глава 2

Классификация задач на проценты

В ходе проведения исследовательской работы в УМК под ред. Г.В.Дорофеева была проведена классификация всех задач по их основным типам.

Глава 3

Описание средств, методов

организации деятельности

В работе использовался общественный опрос и проведена обработка собранных данных по следующим вопросам:

1. Количественный состав

2. Внешний вид

3. Темперамент

4. Данные гороскопа

5 .Увлечения

6. Распределение времени суток

7. Успеваемость

Заключение

Проводя исследование мы решили много практических задач на проценты, применяя умения решать опорные задачи .

Это помогло нам не только дать полное и яркое представление о нашем классе, но и закрепить умение решать задачи на проценты.

Данный проект был апробирован на общем собрании учащихся и родителей. Материалы проекта будут использованы при подготовке других внеклассных дел в классе и в школе, а в дальнейшем планируется разработать подобный проект для использования их при подготовке выпускных вечеров класса.

Глава 2

Изучение истории вопроса о квадратных уравнениях

Список литературы

1. Г.В. Дорофеев «Математика-6» Издательство Просвещение, 2008г

2. А.В. Шевкин «Обучение решению текстовых задач», Русское слово, 2001

3. «Энциклопедия по математике» «Занимательная математика»,М.,2007

4. «Сборник элективных курсов» Волгоград, 2006

Глава 2

Изучение истории вопроса о квадратных уравнениях

Глава 3

Обобщение имеющихся знаний о квадратных уравнениях и способах их решения

Глава 4

Нестандартные приемы решения квадратных уравнений

Глава5

Выводы

В ходе исследования я изучил литературу, решил множество различных квадратных уравнений и пришел к выводу, что существует связь между коэффициентами квадратного уравнения и приемами его решения. Учитывая этот факт были найдены и отработаны нестандартные приемы решения квадратных уравнений.

Данные приемы решения заслуживают внимания, так как они не отражены в школьных учебниках.

Овладение данными приемами поможет учащимся экономить время и эффективно решать уравнения.

Потребность в быстром решении обусловлена применением тестовой системы экзаменов.

Дидактический материал по применению нестандартных приемов решения квадратных уравнений.

4. Найди наиболее рациональным способом корни уравнения:

4х² – 13х + 9 =0

(1; 2,25)

1978х² – 1984х + 6=0

(1; 6/1978)

4х² + 11х + 7 = 0

(-1; -7/4)

319х² + 1988х +1669=0

(-1; -1669/319)

1999х² + 2000х+1=0

(-1; -1/1999)

5. Решить квадратные уравнения с большими коэффициентами

313х² +326х+13=0

(-1; -13/313)

839х²— 448х -391=0

(1; -391/839)

345х² – 137х – 208=0

(1;.-208/345)

939х²+978х+39=0

(-1; -39/939)

3. Используя полученные знания, установи соответствие:

1. х²+5х+6=0 1. 1/6;1/2

2. 6х²-5х+1=0 2. 1; 3/2

3. 2х²-5х+3=0 3. 1; 2/3

4. 3х²-5х+2=0 4. -2; -3

5. х²-5х+6=0 5. -1/3 ; -1/2

6. 6х²+5х+1=0 6. -1; -3/2

7. 2х²+5х+2=0 7. -1; -2/3

8. 3х²+5х+2=0 8. 2;3