Почему нельзя делить на ноль ℹ️ что будет если поделить на ноль в высшей математике, правило с примером, объяснение аксиомы и принцип неопределенности

Учителя многое недоговаривали

Сразу же стоит отметить, что эта аксиома является не совсем правдивой. На самом деле на ноль делить можно, и конец света от этого не настанет. Просто уравнение будет иметь бесконечное количество решений. Чем-то напоминает число «Пи», которое можно высчитывать в течение всей жизни и так и не получить конечного результата. Однако когда человек учится в школе, у него даже не возникает вопроса о том, что будет, если поделить на ноль. Слова преподавателя он воспринимает на веру.

Но может ли учитель объяснить маленькому ребенку, что такое принцип неопределенности или натуральный предел? Куда проще будет сказать, что на 0 делить нельзя. Правило не является совсем правдивым, зато школьник не будет пытаться решить уравнение, которое имеет несколько миллиардов решений. Если же в процессе разбора задачи выходит так, что все-таки приходится поделить на ноль, значит, где-то была допущена ошибка.

На самом деле у такой задачи может быть и иное решение — бесконечность (при условии, что при расчетах не было допущено ошибок). Чтобы это доказать, не придется использовать формулу массы или закон сохранения энергии из физики. В

большинстве случаев алгебраическое доказательство сводится к решению одного простого уравнения или функции, которая в итоге имеет бесконечное количество решений.

Четыре действия в арифметике

Сложение, умножение, деление и вычитание — эти принципы известны каждому школьнику, учащемуся в средних классах. Однако далеко не все знают, что равноправными действиями обладают лишь первые два из них.

Деление и вычитание — это операции, которые являются обратными сложению и умножению. Любые действия в математике могут быть легко построены лишь с помощью этих двух основ. Нужно лишь знать, как правильно выражать деление с помощью умножения или вычитание с помощью сложения. Здесь на помощь приходят уравнения, а также положительные и отрицательные числа. Иногда также приходится возводить число в какую-нибудь степень.

Чтобы было более понятно, следует немного попрактиковаться в арифметике. Что значит пример: «4−2»? Большинство школьников ответит на него достаточно просто: «Нужно взять 4 предмета, после чего провести удаление — отнять два из них, а затем взглянуть, сколько осталось». Вот только профессиональные математики представляют эту задачу совершенно иначе. Ее решение будет представлено уравнением: «x+2=4», корень которого представлен заменой арифметического действия. Нетрудно догадаться, что число «x» будет равно двум. Стоит отметить, что пример был решен без единого минуса.

Теперь немного о том, почему деление не считается полноправным действием в арифметике. В качестве примера возьмем следующее уравнение: «8:4=x». Всем и так понятно, что число «x» будет равно двум. Однако как получить это значение, не используя при этом деление? Правильно, нужно заменить его умножением. В результате математик получит уравнение: «x*4=8». Все очень просто и логично. Однако именно благодаря тому, что мы можем разделить, просто умножив, появляется первое определение того, что деление на ноль не имеет никакого смысла.

Попробуем решить простой пример: «6:0». Пятиклассник сразу скажет, что оно не имеет решения. Однако мы ведь знаем, что можно записать это же выражение другой фразой: «0*x=6». То есть математик получает задание отыскать число, которое бы при умножении на 0 дало ему 6. Вот только каждому известно, что при умножении на 0 в итоге все равно получится 0. Это свойство числа является неотъемлемым и любой шанс опровергнуть аксиому лишен всякого смысла. Именно поэтому учителя и будут продолжать запрещать ученикам делить на ноль, ведь решить уравнение с умножением на это число попросту невозможно.

Принцип бесконечности

Однако деление на ноль в высшей математике все-таки имеет решение. И оно даже не одно, их огромное множество. Этот прием называется принципом бесконечности и доказывает, что все-таки существует одно единственное число, которое можно разделить на ноль. Какое именно? Ну конечно же, сам ноль! Ведь если мы возьмем уравнение: «0*x=0», то оно будет успешно решаться — x будет равен нулю или любому другому числу, например, 512.

В этом и заключается принцип бесконечности. Ведь если вместо неизвестного показателя можно поставить любое число, то это значит, что уравнение с делением имеет огромное количество решений. Самое главное, чтобы один из множителей в обратном уравнении был также равен нулю. Другими словами, этот математический феномен также называется «принципом неопределенности» — какое бы число вы ни подставили вместо «x» (с плюсом или минусом, целое или дробное — неважно) — операция будет иметь неопределенное количество решений.

Работает ли этот факт с вычитанием? Не совсем! Если вы возьмете 5 яблок и вычтете из них ноль, то в итоге получится число, равное пяти. Но что если мы заменим одно из слагаемых числом «x»? Получится уравнение «5+x=5» Нетрудно догадаться, что уравнение имеет только одно решение, которое равно нулю. Однако можно ли подставить еще какое-то число, которое при сложении с другим отразит его зеркально? Разумеется, нет.

В этом и заключается одна из главных особенностей нуля. Если вы видите уравнение, в котором присутствует два слагаемых, а сумма равняется 5, то можете смело писать в решении «0», даже если вместо x там написана сложная система или логарифм.

Арифметическая шутка с нулем

Правило «делить на ноль нельзя» (пример в предыдущем разделе) лежит в основе многих арифметических шуток, которые могут доказывать, что 2+2 равняется не 4, а 7. Однако если математик уяснит его, то никогда не будет введен в заблуждение. Возьмем в качестве примера уравнение «4*x+2-=7*x-35.» Подробный алгоритм решения выглядит следующим образом:

• Выносим за скобки знаменатели, дабы упростить решение. В правой части это будет четверка, а в левой — семерка. Получим уравнение: «4*(x — 5)=7*(x-5)».
• Теперь необходимо умножить каждую часть уравнения на дробное число, которое равняется «1/(x-5)». Пример принимает следующий вид: «4*(х-5)/(х-5)=7*(х-5)/(х-5)».
• Сокращаем дроби на «(x-5)», после чего получаем, что «4=7». Разбиваем левую часть на множители и узнаем, что «2+2» равняется не четырем, а семи.

Однако весь подвох заключается в том, что корень уравнения был равен пяти, а сокращать его с помощью дроби было нельзя, поскольку в итоге это привело к тому, что все уравнение было поделено на ноль. Поэтому при решении таких задач следует помнить важное правило: нельзя допускать, чтобы в знаменателе дроби оказался ноль. В противном случае это приведет вот к такому забавному решению, которое натолкнет математика на «открытие» ранее неизведанных «теорем».

Философия, да и только

Многие люди используют пример с делением на ноль для того, чтобы объяснить некоторые закономерности, которые попросту не поддаются объяснению. Ведь что представляет собой само понятие «бесконечность», которую мы иногда можем получить в процессе решения некоторых уравнений? Никто не сможет ответить на этот вопрос, поскольку он находится за пределами нашего понимания. Это как объяснять гусенице, что такое закон притяжения. Безусловно, он на нее действует, однако столь примитивный организм никогда не сможет понять те законы, которые нас окружают, ведь ей движут всего лишь инстинкты.

То же самое и с делением на бесконечность. Да, мы можем записать огромное количество решений для функций и уравнений, в которых приходится делить на ноль. Но что в итоге это даст?

Бесконечность — число или понятие, которое находится за гранью нашего восприятия. Решение подобного уравнения сравнимо с путешествием в кроличью нору. Даже если конечный результат не будет достигнут — есть над чем задуматься. К примеру, насколько же все-таки многогранным и удивительным является это число — ноль. Оно одновременно ничего не значит и значит слишком много.

График функции с нулем

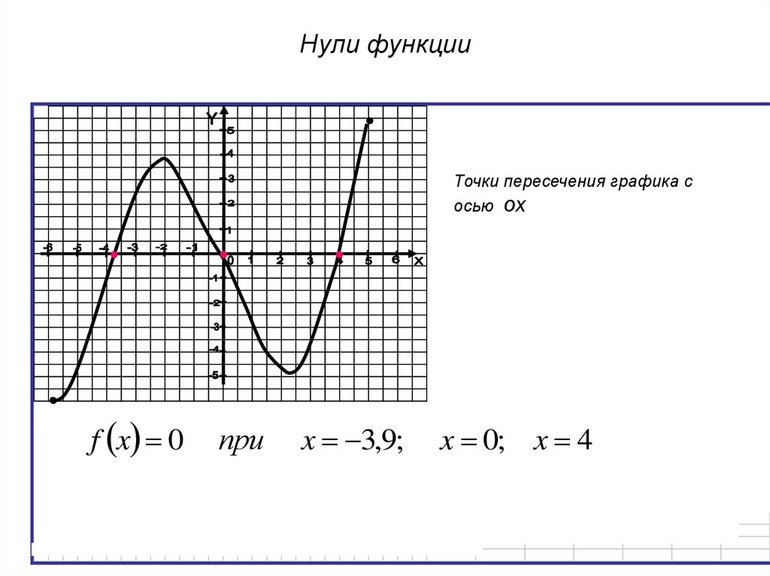
Лучше всего понять, что тип уравнения, в котором приходится делить на ноль, имеет бесконечное количество решений, помогает обычный график функции, который доводилось изучать каждому школьнику. Если говорить точнее, то потребуется гипербола, которая имеет обратную зависимость от функции. Выглядит рисунок в виде кривой с асимптотами — прямыми линиями, к которым симметрично стремится гипербола. Однако всем известно, что она никогда их не достигнет. Да, она пересекается возле точки, которая максимально близка к нулю, однако все-таки не достигает ее.

Вот такая получается математическая драма. Чем ближе функция приближается к своему значению, тем больше становится показатель «игрек», а «икс» — уменьшается. То есть если «y» будет стремиться к нулю, то «x» станет стремиться к бесконечности (или минус бесконечности). Так что такая функция не будет иметь решений, как бы математик не старался. Но ведь, по сути, в процессе решения никто не делит число на ноль. В роли делителя выступает число, которое имеет ничтожно малую величину. Вот так.

Именно поэтому многие опытные математики говорят, что при делении на ноль мы получаем бесконечность со знаком плюс или минус (в зависимости от знаменателя). Само собой, можно расписать на бумаге огромное множество решений до тех пор, пока известные числа просто не закончатся. Но стоит ли тратить свою жизнь на то, чтобы делать это? Ведь даже в школе учеников держат подальше от того, чтобы связываться с делением на ноль. Решить такое уравнение попросту невозможно, поскольку существуют миллиарды и даже триллионы возможных решений. Вот такой забавный парадокс с этим нулем.

Несколько умных ответов математикам

Поскольку решить уравнение с делением на ноль невозможно, стоит рассмотреть вариант ответов на случай, если на экзамене или где-нибудь на собеседовании будет задан вопрос от математика: «Почему на ноль делить нельзя?» Вот лишь несколько вариантов ответов, которые можно использовать и не ошибиться:

• деление на ноль провоцирует принцип неопределённости;
• ответов на такое уравнение существует бесконечное множество;
• решение функции с гиперболой будет стремиться к нулю, но не достигнет его.

Ну а в качестве примера или «доказательства» аксиомы можно использовать уравнения, которые являются обратными общепринятым арифметическим действиям. Вот лишь несколько из них:

• 0*x=0 — где вместо «x» можно подставить любое число, которое только вздумается;
• 5-x=5 — таких «зеркальных» уравнений также существует бесконечное множество;
• график функции, на котором «x» стремится к нулю, а «y» — к бесконечности.

Многие работодатели и авторитетные личности, которые хотят проверить человека с математическим образованием на его знания, попросят доказать принцип бесконечности, на что можно привести эти простые примеры. Ведь каждый высший математик должен не просто знать правило, что на ноль делить нельзя, а уметь объяснить, почему именно решение таких уравнений является бессмысленным.

Надеемся, теперь вы понимаете, что решение задач, в которых в качестве делителя выступает ноль, неприлично много. Это значит, что пытаться разобрать их будет бессмысленно, поскольку принцип неопределенности попросту не даст довести пример до логического завершения.

Возможно, именно поэтому индейцы племени Майя и называли это число «началом и бесконечностью», ведь даже график функции никогда его не достигнет.

Можно ли делить на ноль? Отвечает математик | Наука | Общество

Евгений Ширяев, преподаватель и руководитель Лаборатории математики Политехнического музея, рассказал АиФ.ru о делении на ноль:

1. Юрисдикция вопроса

Согласитесь, особенную провокационность правилу придает запрет. Как это нельзя? Кто запретил? А как же наши гражданские права?

Ни конституция РФ, ни Уголовный кодекс, ни даже устав вашей школы не возражают против интересующего нас интеллектуального действия. А значит, запрет не имеет юридической силы, и ничто не мешает прямо тут, на страницах АиФ.ru, попробовать что-нибудь разделить на ноль. Например, тысячу.

2. Разделим, как учили

Вспомните, когда вы только узнали, как делить, первые примеры решали спроверкой умножением: результат, умноженный на делитель должен был совпасть сделимым. Не совпал — не решили.

Пример 1. 1000 : 0 =…

Забудем на минуту про запретное правило и сделаем несколько попыток угадать ответ.

Неправильные отсечёт проверка. Перебирайте варианты: 100, 1, −23, 17, 0, 10 000. Для каждого из них проверка даст один и тот же результат:

100 · 0 = 1 · 0 = − 23 · 0 = 17 · 0 = 0 · 0 = 10 000 · 0 = 0

Ноль умножением все превращает в себя и никогда в тысячу. Вывод сформулировать несложно: никакое число не пройдет проверку. Т. е. ни одно число не может быть результатом деления ненулевого числа на ноль. Такое деление не запрещено, а просто не имеет результата.

3. Нюанс

Чуть не упустили одну возможность опровергнуть запрет. Да, мы признаем, что ненулевое число не разделится на 0. Но может быть, сам 0 сможет?

Пример 2. 0 : 0 = …

Ваши предложения для частного? 100? Пожалуйста: частное 100, умноженное на делитель 0, равно делимому 0.

Еще варианты! 1? Тоже подходит. И −23, и 17, и все-все-все. В этом примере проверка на результат будет положительной для любого числа. И по-честному, решением в этом примере надо называть не число, а множество чисел. Всех. А так недолго договориться и до того, что Алиса это не Алиса, а Мэри-Энн, а обе они — сон кролика.

4. Что там про высшую математику?

Проблема разрешена, нюансы учтены, точки расставлены, все прояснилось — ответом для примера с делением на ноль не может быть ни одно число. Такие задачки решать — дело безнадежное и невозможное. А значит… интересное! Дубль два.

Пример 3. Придумать, как разделить 1000 на 0.

А никак. Зато 1000 можно без трудностей делить на другие числа. Ну, давайте хотя бы делать, что получается, пусть даже изменив поставленную задачу. А там, глядишь, увлечемся, и ответ сам собой объявится. Забываем на минуту про ноль и делим на сто:

1000 : 100 = 10.

Сотня далека от нуля. Сделаем шаг к нему, уменьшив делитель:

1000 : 50 = 20.

Еще один:

1000 : 40 = 25.

И потопали дальше:

1000 : 25 = 40,
1000 : 20 = 50,
  1000 : 10 = 100,
    1000 : 8 = 125,
    1000 : 5 = 200,
    1000 : 4 = 250,
    1000 : 2 = 500,
      1000 : 1 = 1000.

Очевидная динамика: чем ближе делитель к нулю, тем больше частное. Тенденцию можно наблюдать и дальше, переходя к дробям и продолжая уменьшать числитель:

 

Осталось заметить, что к нулю мы можем подойти как угодно близко, делая частное сколь угодно большим.

В этом процессе нет нуля и нет последнего частного. Мы обозначили движение к ним, заменив число на последовательность, сходящуюся к интересующему нас числу:

 

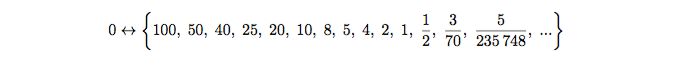
При этом подразумевается аналогичная замена и для делимого:

1000 ↔ { 1000, 1000, 1000,… }

Стрелки не зря поставлены двусторонними: некоторые последовательности могут сходиться к числам. Тогда мы можем поставить в соответствие последовательности ее числовой предел.

 

Посмотрим на последовательность частных:

 

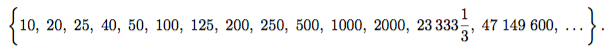
Она растет неограниченно, не стремясь ни к какому числу и превосходя любое. Математики добавляют к числам символ ∞, чтобы иметь возможность рядом с такой последовательностью поставить двустороннюю стрелку:

 

Сопоставление числам последовательностей, имеющих предел, позволяет предложить решение к третьему примеру:

При поэлементном делении последовательности, сходящейся к 1000, на последовательность из положительных чисел, сходящуюся к 0, получим последовательность, сходящуюся к ∞.

5. И здесь нюанс с двумя нулями

Что будет результатом деления двух последовательностей положительных чисел, сходящихся к нулю? Если они одинаковые, то тождественная единица. Если к нулю быстрее сходится последовательность-делимое, то в частном последовательность снулевым пределом. А когда элементы делителя убывают гораздо быстрее, чем у делимого, последовательность частного будет сильно расти:

 

 

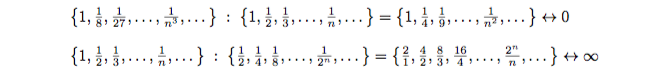
Неопределенная ситуация. И так и называется: неопределенность вида 0/0. Когда математики видят последовательности, подходящие под такую неопределенность, они не бросаются делить два одинаковых числа друг на друга, а разбираются, какая из последовательностей быстрее бежит к нулю и как именно. И в каждом примере будет свой конкретный ответ!

6. В жизни

Закон Ома связывает силу тока, напряжение и сопротивление в цепи. Часто его записывают в такой форме:

 

Позволим себе пренебречь аккуратным физическим пониманием и формально посмотрим на правую часть как на частное двух чисел. Вообразим, что решаем школьную задачу по электричеству. В условии дано напряжение в вольтах и сопротивление в омах. Вопрос очевиден, решение в одно действие.

А теперь заглянем в определение сверхпроводимости: это свойство некоторых металлов обладать нулевым электрическим сопротивлением.

Ну что, решим задачку для сверхпроводящей цепи? Просто так подставить R = 0 не выйдет, физика подкидывает интересную задачу, за которой, очевидно, стоит научное открытие. И люди, сумевшие поделить на ноль в этой ситуации, получили Нобелевскую премию. Любые запреты полезно уметь обходить!

Почему нельзя делить на ноль? Ответ поражает!

Ноль является одной из наиболее интересных математических цифр. Сам по себе он ничего не означает, но, когда эта цифра стоит возле пятерки, шестерки или семерки, чисто автоматически увеличивается десятикратно. Что же касается деления на эту цифру, учителя в школе однозначно ответят, что такое действие невозможно. Рассмотрим подробнее, почему нельзя делить на ноль.

Почему нельзя делить на 0?

Изначально следует заметить, что данная истина в некотором смысле неправильная. В действительности делить на 0 возможно, но у такого примера будет бесконечное число ответов. В чём-то подобное уравнение схоже с числом «Пи», у которого отсутствует конечный результат. Вот почему нельзя делить на ноль, по утверждению школьных учителей, а ученики безоговорочно верят этому.

Школьные учителя вряд ли смогут детям пояснить, в чём суть принципа бесконечности. Легче просто сказать, чтобы ученики взяли за аксиому правило, что делить на это число нельзя. Пусть это не совсем так, но дети не будут стараться решать пример, у которого бесконечное количество ответов. В случае, когда, разбирая задачу, школьник вынужден в решении проводить деление на 0, это означает, что он допустил ошибку.

Как происходит деление?

В действительности при решении такого уравнения можно получить и другой ответ – бесконечность (если расчеты были проведены правильно). В качестве доказательства не придётся прибегать к помощи физических формул. Чаще всего математические доказательства подразумевают решение одной простой задачи, у которой есть бесконечное число ответов.

В качестве примера постараемся разделить 5 на ноль. Любой ученик пятого класса ответит, что у этого примера решение отсутствует. Но нам известно, что это действие можно представить в виде такого уравнения: «0*х=5».

Другими словами, перед нами стоит задача найти число, при умножении которого на ноль получится 5. Но общеизвестно, что, если любое число умножить на ноль, результатом будет 0. Такие свойства цифры являются неотъемлемыми, а любая попытка опровержения аксиомы попросту бессмысленна. Вот почему нельзя делить на ноль, по утверждению школьных учителей. И такой запрет будет существовать и впредь, так как решение примера, где нужно число умножить на 0 и получить что-то, отличающееся от нуля, просто нереально, по крайней мере для школьника.

Но высшая математика позволяет решать примеры с делением на 0. Причем такое уравнение дает большое количество ответов. Такой приём имеет название «принцип бесконечности». Он позволяет доказать существование одного единственного числа, которое делится на 0. Этим числом является сам 0. Попробуем решить такой пример: 0*х=0. Результат получаем такой:

• х=0;
• также ответом может быть любое другое число, к примеру, 379.

Когда х можно заменить каким угодно числом, это означает, что у задачи на деление есть много ответов. Главное условие – один множитель в обратном уравнении должен равняться 0.

Почему на ноль делить нельзя?

Так политики делят бюджетные деньги. народу ноль, но всё таки делятся же!

Не дели, денег не будет!

Если говорят нельзя делить то и не СТОИТ!

«Делить на ноль нельзя! » — большинство школьников заучивает это правило наизусть, не задаваясь вопросами. Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему? » А ведь на самом деле очень интересно и важно знать, почему же нельзя. Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух. Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись 5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания. Есть только задача — найти подходящее число. Точно так же обстоит дело с умножением и делением. Запись 8 : 4 можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8. Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения. Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение. ) А значит, записи 5 : 0 не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя. Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0=0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д. Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности» , но в арифметике таких случаев не встречается. ) Вот такая особенность есть у операции деления. А точнее — у операции умножения и связанного с ней числа ноль. Ну, а самые дотошные, дочитав до этого места, могут спросить: почему так получается, что делить на ноль нельзя, а вычитать ноль можно? В некотором смысле, именно с этого вопроса и начинается настоящая математика. Ответить на него можно только познакомившись с формальными математическими определениями числовых множеств и операций над ними. Это не так уж сложно, но почему-то не изучается в школе. Зато на лекциях по математике в университете вас в первую очередь будут учить именно этому

Строго говоря, никто не запрещает пытаться делать это. Вопрос всего лишь в том, получите ли вы какой-либо результат, который можно было бы с уверенностью использовать практичеки.

ааааа, ээээээ, ыыы, гыыы если с юмором и под стук (как делают монтаж немонтируемых кадров в кино) , то можно !

на дырку не поделишь, все в нее и уйдет…

Стрянно, если хошь чтоб осталось целое яблоко, зачем делить???

Ну и жадина ты

Какой смысл делить, если все равно остается. Сами себе и ответили. Вот поэтому и нельзя. Не делать лишних операций. Это-аксиома.

На нОль делить можно! Но останешься на нУле!

«Делить на ноль нельзя! » — старая математическая истина, аксиома, если хотите. Доказывать это не надо, это общепринято. Фраза «делить на ноль нельзя» имеет, прежде всего, моральную подоплеку и читается в данном случае как «не делить нельзя» , то есть нельзя оставаться собственником, единственным обладателем чего бы то ни было.

Дели — не бойся, уходи — не плачь

ну вот смотри по своим яблокам если делить 1 яблоко на ноль то кто его получит ответ никто

делить-то можно, просто бессмысленно

Ну почему же! ? Можно! Бублик делится и не плохо!

Если стукнуть по голове пустым мешком, то ничего не будет. Положи, что нибудь потяжелее-будет деление. Грубо, но доходчиво. После этого я не спрашивала- Почему?

Энто ладно, Ирочка дала исчерпывающий и полный ответ. А вот можешь ли ты доказать, что 2+2=5?

наверно потому что если даже что нибудь разделишь на ноль все равно получаетсяч ноль

Нельзя, вот у тебя два яблока, а рядом никого не с кем поделиться…

что будет если разделить на ноль?

на ноль делить можно, но если начать то это никогда ни кончится, поэтому нет смысла даже начинать :))) А если подробнее, что такое делить на какое то число? Поделить яблоко на 4 части, но тоесть поделить 1 на 4. А если делить на 0. То после каждого отрезания от яблака 0(дургими словами ничего) яблоко останется таким же и поэтому такая процедура займёт бесконечное количество времени. Ещё говорят что получится бесконечность что тоже верно, так как у вас получитса бесконечное количество несуществующих ломтиков яблока. Точнее неполучится, так как деление никогда незакончится, поэтому говорят что нельзя делить на 0 :))

На ноль делить нельзя!!!!

полнейший ноль

бесконечность

ничего не будет

На ноль делить нельзя.

правило есть такое — на ноль делить НЕЛЬЗЯ!! !

нельзя на ноль делить!

получится пустое множество, зеро, ноль. » Из ничего и выйдет — ничего»…

На ноль делить нельзя, но если всетаки попробывать, то получиться нуль.

на ноль делить нельзя) правило из первого класса

вообще то делить на ноль нельзя. Ну это если по правилам

на 0 делить НЕЛЬЗЯ!!!!

На ноль не льзя делить

бесконечность

Будет «двойка» — это однозначно 😉

Никому ничего не достанется))) ) Можно на двоих поделить, там на троих.. . А как ни накого не делить непонятно)))

по правилам высшей математики получится бесконечность

если 1 разделить, то будет е, а другие надо считать

1 делить на 0 ?

неопределённость, хотя если заметил что когда делишь число на другое чесло меньше единицы, но больше нуля — то оно увеличивается, причём чем больше к нулю, тем сильнее оно увеличивается, поэтому я думаю, что сделали допущение, что всё таки существуют такие маленькие величины, на которые можно делить, но которые очень близки к нулю, деление которыми очень сильно увеличивают число

на ноль делить нельзя)

Бесконечность. Или иногда говорят, что результат «стремится к бесконечности». А бесконечность — это то, что никогда не достигается. И выполнять с ней никаких действий нельзя (в том числе умножать на 0)

НА 0 делить НЕЛЬЗЯ!!!!

Существует теория обратного числа относительно 1 то-есть обратное число 2 это 1/2(одна вторая) обратное 3 это 1/3(одна третья) , это правило работает в обе стороны то-есть обратное число 1/2(одной второй) это 2 и т. д. тут есть некая закономерность чем больше число тем меньше число ему обратное то-есть чем дальше число на числовой прямой тем ближе к нулю обратное ему число например берем 2 обатное ему-1/2(одна вторая) теперь берем 4 обратное ему 1/4(одна четвертая) 1/4 ближе к нулю чем 1/2, а 4 дальше на числовой прямой чем 2 . А теперь берём 0(ноль) — он меньше любого числа то-есть обратное ему число (1/0) БОЛЬШЕ ЛЮБОГО ПОЛОЖИТЕЛЬНОГО ЧИСЛА, а это и есть ∞(бесконечность).

1 поделить на 0 равно бесканечно

1 делить на ноль нельзя

те, кто говорят, что делить на ноль — нельзя, руководствуются лишь школьными знаниями, а следуя из них — глупо говорить так, лишь потому, что им это в голову вбивали с первого класса.

На сколько я помню, до делится не сам ноль, а переменная стремящаяся к нему, т. е. число максимально стремящееся к нулю, но не являющееся им: 0,1 0,01 0,001 и сколько угодно нулей перед единицей. Так как числовой ряд не имеет ограничений, то и результат деления будет стремиться к бесконечности и являться ею

Чем ближе делитель к нолю, тем больше число приближается к бесконечности. Тут работают уже не вычисления, а простая логика. Но так как числа тоже бесконечные, то 0 это ничего. По сути, получится не бесконечность, а ничего. Делишь на 0 — опустошаешь бытие.

1/0=бесконечность, так как 1/бесконечность=0, а 1 является одним из вариантов неопределённости бесконечность/0

Чем больше делитель тем меньше будет результат, но чем менше делитель тем больше будет результат! Если мы поделим на самое маленькое положительное число, то есть 0, то мы получим самое большое положительное число. Так как ряд натуральных чисел бесконечный, то мы не можем вычислить это число, по этому что бы не заморачиваться мы говорим что нельзя делить на 0.

Будет бесконечность. В математике не принято делить на ноль, потому что всегда ответ бекоченность и смысл решать выражение не имеет смысла, из-за этого может быть бесконечное число ответов, а это не допустимо. Поэтому деление на ноль разрешено только в пределах и там этот ответ и будет как раз бесконечность, поскольку там это значение допустимо, в отличие от других выражений и функций

Говоря проще если палку колбасы поделить на 0.1 часть то в результате получеться 10 таких кусков, а если ее поделить на 0 ю часть, то ответ предполагает бесконечное число кусков, потому что ничем можно делить бесконечно

ответ существует, уважаемые, не забывайте о применении комплексных чисел, где квадрат «мнимой единицы» равен -1, значит и существует такое число, которое получается при делении на 0, отличное от бесконечности и, скорее всего, иррациональное.

Бесконечность будет

Я нашел решение: делить на ноль можно! Ответ: любое число с вероятностью 0%. Следовательно — решение есть, но с нулевой вероятностью, или не имеет смысла. Отсюда и запрет (лучше бы объяснили детям: почему нельзя?). Я так думаю…