Шаровой слой. Шаровой сектор. Шаровой сегмент.

\({\color{red}{{\small{\textbf{Факт 1. Про шаровой сегмент}}}}}\)
\(\bullet\) Шаровой сегмент – шасть шара, отсекаемая от него плоскостью (\(\alpha\)).

\(\bullet\) Если \(O\) – центр шара, \(OB=R\) – радиус шара, перпендикулярный плоскости \(\alpha\), \(A\) – центр круга (основания шарового сегмента), а также точка пересечения радиуса \(OB\) c этим кругом, то
\(H=AB\) – высота шарового сегмента.
\(\bullet\) Площадь сферического сегмента (часть сферы, отсекаемая от нее плоскостью \(\alpha\)) вычисляется по формуле \[S=2\pi \cdot RH\] \(\bullet\) Объем шарового сегмента вычисляется по формуле \[V=\pi H^2\cdot \left(R-\frac13H\right)\]

 

\({\color{red}{{\small{\textbf{Факт 2. Про шаровой слой}}}}}\)
\(\bullet\) Шаровой слой – часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар.

\(\bullet\) Основания шарового слоя – это сечения шара плоскостями.
\(\bullet\) Высота \(H=AB\) шарового слоя – это расстояние между основаниями.
\(\bullet\) Площадь сферической части шарового слоя равна \[S=2\pi RH\] где \(R\) – радиус шара.
\(\bullet\) Объем шарового слоя равен разности объемов двух шаровых сегментов: \[V=V_{A}-V_{B}\]

 

\({\color{red}{{\small{\textbf{Факт 3. Про шаровой сектор}}}}}\)
\(\bullet\) Шаровой сектор – часть шара, ограниченная сферической частью шарового сегмента и боковой поверхностью конуса, имеющего то же основание, что и шаровой сегмент.

\(\bullet\) Если \(H=AB\), то объем шарового сектора равен \[V=\dfrac23\pi R^2\cdot H\]

Объем шара и его частей

Просмотр содержимого документа
«Объем шара и его частей»

Объем шара и его частей

• Какое геометрическое тело называется шаром ?
• Что называется шаровым сегментом?
• Что называется шаровым слоем ?
• Что называется шаровым сектором ?

Тело, полученное при вращении полукруга вокруг диаметра, называется шаром , а поверхность, образуемая при этом окружностью, называется шаровой или сферической поверхностью .

Шаровым сегментом называется часть шара, отсекаемая от него какой-либо плоскостью

Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями

Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 90 градусов, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов .

Объем шарового сегмента?

V = π h²(R – 1 / 3 h)

Объем шарового слоя можно вычислить как разность объемов двух шаровых сегментов.

V шар.сект. = 2 / 3 π R²h

Объем шара равен произведению его поверхности на треть радиуса V = 4 / 3 π R³

Вычислить объем купола, имеющего форму полушара, у которого диаметр равен 12 м, а высота – 6 м.

V = 144 π м ³

В цилиндрический сосуд, у которого диаметр основания 6 см, а высота 36 см, налита вода до половины высоты сосуда. На сколько поднимется уровень воды в сосуде, если в нее погрузить шар диаметром 5 см ?

Сколько дождевых капель нужно, чтобы из них составился 1 м ³ воды, если капли имеют форму шара с диаметром 2 мм ?

100 см ³ масла, вылитые на поверхность воды, образовали пленку в форме круга диаметром 18 м. Определить толщину пленки.

V конуса = 1/3 π R² V цилиндра = π R²H S сферы = 4 π R² V шара = 4/3 π R³ V шар.сегм. = π h²(R – 1 / 3 h) V шар.сект. = 2 / 3 π R²h

Объём шара и его частей

План урока геометрии в 11 классе

Тема: Объём шара и его частей.

Учитель: Капанский Ю.М.-учитель математики КГУ «Ушановская СШ»

Эпиграф урока: Считай несчастным тот день или тот час, в котором ты не усвоил ничего нового и ничего не прибавил к своему образованию. Коменский Я.А.

Цели:

1.Образовательные:

-сформировать умения применять формулы объёма шара, шарового сегмента и шарового сектора при решении задач.

2. Развивающие:

-создание условия для развития на уроке психологических качеств учащихся: интеллекта, мышления, памяти, внимания;

-обеспечить условия для развития познавательных процессов, для формирования общеучебных и специальных умений, совершенствованию мыслительных операций;

-создание условий для развития коммуникативной культуры.

3. Воспитательные:

-обеспечить условия для формирования положительного отношения к знаниям, к процессу учения.

Задачи урока:

1.Образовательные:

-повторить известные формулы для вычисления объёма шара и его частей, площади поверхности шара, площади круга и длины окружности;

-научить применять данные формулы при решении задач;

-совершенствовать вычислительные навыки.

2.Развивающие:

-выработать умение правильно применять известные и новые формулы при вычислении объёмов фигур вращения;

-развивать внимание, умение сравнивать, делать выводы и обобщения.

3.Воспитательные:

-создать условия для раскрытия коммуникативных способностей учащихся;

-побудить учащихся к активной мыслительной деятельности;

-прививать и укреплять умение давать полный и обоснованный ответ на поставленный вопрос.

Оборудование: 1.Слайды: «Шар и его части». 2.Видеомодуль «Сфера, шар, шаровой сегмент и шаровой сектор». 3. Компьютер (с видеопроектором).

Ход урока:

I.Организационный момент.

II.Актуализация знаний:

-Просмотр Видеомодуля «Сфера, шар».

-Слайд 1:

-Слайд 2:

-Пояснения по слайдам.

III.Решение задач. Формирование умения применять формулы при решении задач.

Работа в парах по карточкам.

Учащиеся решают задачи карточки в паре или самостоятельно. Готовят объяснение для другого ученика. В случае затруднения в решении могут обратиться за помощью к учителю или любому другому ученику. После того как первые задачи решены, ученик ищет себе партнера и объясняет ему решение, в ответ он сам получает объяснение от своего партнера. После этого решает вторую задачу карточки, показывает решение учителю, или ученику, уже сдавшему решение. Заполняет лист оценок и далее ищет нового партнера. Если партнера не находится, то может самостоятельно решать другие задачи по теме. Продолжается до тех пор, пока не будут решены все задачи. Если не остается времени, то можно продолжить на следующем уроке или взять задание на дом.

Карточка № 1 (уровень А):

11. Объем шара равен 36π. Найдите площадь сферы, ограничивающей данный шар.

12. Площадь поверхности шара равна 144π. Найдите объем данного шара.

Карточка № 2 (уровень А):

21.В шаре радиуса 15 см проведено сечение, площадь которого равна 81π см. Найдите объем меньшего шарового сегмента, отсекаемого плоскостью сечения.

22.На расстоянии 9 м от центра шара проведено сечение, длина окружности которого равна 24π. Найдите объем меньшего шарового сегмента, отсекаемого плоскостью сечения.

Карточка № 3 (уровень А):

31. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота соответствующего сегмента составляет шестую часть диаметра шара.

32. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара

Карточка № 4 (уровень В):

41. Внешний диаметр полого шара равен 18 см, а толщина стенок – 3 см. Найдите объем материала из которого сделан шар.

42. Внутренний диаметр полого шара равен 12 см, а толщина стенок – 3 см. Найдите объем материала из которого сделан шар.

Карточка № 5 (уровень В):

51. Сечение, перпендикулярное диаметру шара, делит этот диаметр в отношении 1 : 3. Найдите объем меньшего шарового сегмента, отсекаемого от шара, если площадь поверхности шара равна 144 π.

52. Сечение, перпендикулярное диаметру шара, делит этот радиус пополам. Площадь поверхности шара равна 64 π. Найдите объем большего шарового сегмента, отсекаемого от шара.

Карточка № 6 (уровень В):

61. Радиус шарового сектора равен R, а угол между радиусами в осевом сечении сектора равен 120º. Найдите объем сектора.

62.Круговой сектор радиуса R c центральным углом 60º вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения.

ответы:

11	12	21	22	31	32	41	42	51	52	61	62
36 π	288 π	126 π	468 π	48 π	48 π	684 π	684 π	72 π

IV. Дополнительные задания. Тест. Тела вращения. Объёмы.

№ 2, 4, 6, 10, 12, 16.

V. Домашнее задание. Стр.85. № 61, 63, 65.

V. Рефлексия. Подведение итогов. Выставление оценок.

Лист оценок ученика 11 класса:______________________________________________________

Объём шара и его частей. 21 февраля 2013 года.

№	11	12	21	22	31	32	41	42	51	52	61	62
Само- оценка
Оценка партнера (за объяснение)
Оценка за сам. решение

При выставлении оценок руководствоваться следующими принципами:

• Самооценка- ученик сам ставит себе оценку за решение первой задачи карточки; «5»- если решил правильно и самостоятельно, «4» — если решил правильно, но обращался за помощью к другим ученикам или учителю за незначительными разъяснениями, «3» в другом случае, кроме «2» когда задача не решена.

• Другие оценки в разделе «Самооценка» выставляются учеником за решение вторых задач карточки, в случае если никто не объяснял ему решение первой задачи из этой карточки;

• Оценка партнера- ставится учеником, которому данный ученик объяснял первую задачу карточки в зависимости от уровня объяснения.

• Оценка за самостоятельное решение ставится учителем или учеником, ранее решившим эту задачу правильно. «5»- задача решена правильно и без ошибок. «4»- задача решена, но допущена незначительная ошибка или недочеты. «3»- задача решена с ошибками.

Итоговая оценка за урок выставляется с учетом всех оценок при этом преимуществом пользуются оценки полученные в плане самооценки.

На следующем уроке дается самостоятельная работа по задачам карточки, по которой ученику объясняли задачу другие ученики. Если ученик правильно решает эти задачи, то тому ученику, кто объяснял ему эти задачи на предыдущем уроке, выставляется дополнительная оценка, полученная им как оценка парнера(если ученик согласен с этой оценкой).

В итоге все ученики активно работают на уроке, решают свои задачи, объясняют решение партнерам, и вновь решают. Затем алгоритм повторяется: решаю-объясняю-слушаю парнера-решаю. Реализуется принцип: уча других — учусь сам.

Тест по геометрии (11 класс) на тему: Объём шара и его частей

Геометрия 11 класс

Самостоятельная работа на тему:

Поверхность шара и объем шара

Вариант 1

1. Найти диаметр шара, если площадь его поверхности равна 289π.

2. В куб вписан шар. Найти площадь поверхности шара, если площадь полной поверхности куба равна .

3. Площадь поверхности шара равна 330. Найти площадь полной поверхности цилиндра, описанного около шара.

4. Объем шара равен 135. Найти объем другого шара, диаметр которого в 3 раза больше, чем у данного.

5. Площадь сечения шара плоскостью равна 15. Секущая плоскость отстоит от центра шара на . Найти площадь поверхности шара.

6. Через конец радиуса шара под углом 60° к нему проведена плоскость. Найти объем шара, если площадь полученного сечения равна .

Вариант 2

1. В куб вписан шар. Найти объем шара, если объем куба равен .

2. Площадь поверхности шара равна 43. Найти площадь поверхности другого шара, объем которого в 27 раз больше объема данного шара.

3. Около шара описан цилиндр. Найти объем цилиндра, если объем шара равен 168.

4. Объем шара равен 12. Найти объем другого шара, у которого площадь поверхности в 9 раз больше, чем у данного шара.

5. Площадь сечения шара плоскостью равна 16π. Найти расстояние от плоскости сечения до центра шара, если объем шара равен .

6. Через конец радиуса шара проведена плоскость под углом 60° к нему. Площадь полученного сечения равна 11.  Найти площадь поверхности шара.

Ответы:

	1	2	3	4	5	6
Вариант 1	17	195	495	3645	180	64
Вариант 2	26	387	252	324	3	176

М-11 Контрольная работа по теме 1 вариант

«Объём шара и его частей».

1. Высота конуса равна 15 см , а радиус основания равен 8 см. Найти объём и площадь полной поверхности конуса.

2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найти отношение объёмов шара и цилиндра.

3. В шаре радиуса 15 см проведено сечение, площадь которого равна 81 см2. Найти объём меньшего шарового сегмента, отсекаемого плоскостью сечения.

4. Площадь поверхности шара равна 144π см2. Найти объём данного шара.

5. Найти объём шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.

М-11 Контрольная работа по теме 2 вариант

«Объём шара и его частей».

1. Свинцовый шар, диаметр которого 20 см, переплавлен в шарики с диаметром в 10 раз меньше. Сколько таких шариков получилось?

2. Радиус шара равен R. Определить объём шарового сектора, если дуга в осевом сечении сектор равна 60°.

3. Найти радиус шара, вписанного в правильную треугольную пирамиду с высотой , равной 8, и апофемой, равной 10.

4. В конус, осевое сечение которого правильный треугольник, вписан шар. Найти отношение площади сферы к площади боковой поверхности конуса.

5. Диаметр шара равен высоте цилиндра, осевое сечение которого – квадрат. Найти отношение объёмов цилиндра и шара.

М-11 Контрольная работа по теме 3 вариант

«Объём шара и его частей».

1. Медный куб, ребро которого 10 см, переплавлен в шар. Найти радиус шара.

2. Радиус шара равен R. Определить объём шарового сектора, если дуга в осевом сечении сектор равна 90°.

3. Внешний диаметр полого шара 18 см, толщина стенок 3 см. Найти объём стенок.

4. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60°. Найти отношение объёмов конуса и шара.

5. Объём цилиндра равен 96π см3. Площадь его осевого сечения 48 см2. Найти площадь сферы, описанной около цилиндра.

Урок геометрии в 11 классе «Решение задач по теме «Объем шара, площадь сферы»

План – конспект урока геометрии в 11 классе

Тема: «Решение задач по темам «Объем шара и его частей», «Площадь сферы».

Тип урока: Урок закрепления изученного материала

Цели урока: 

1.Образовательные:

-сформировать умения применять формулы объёма шара, площади шара при решении задач.

2. Развивающие:

-создать условия для развития на уроке психологических качеств учащихся: интеллекта, мышления, памяти, внимания;

-обеспечить условия для развития познавательных процессов,  для формирования общеучебных и специальных умений, совершенствованию мыслительных операций;

-создать условия для развития коммуникативной культуры.

3. Воспитательные:

-обеспечить условия для формирования положительного отношения к знаниям, к процессу учения.

Задачи урока:

1.Образовательные (формирование познавательных УУД):

Совершенствовать умения:

• применять формулы объёма шара, площади шара при решении задач.

• Анализировать полученные результаты

• Моделировать решение задачи с помощью плана

2. Воспитательные (формирование коммуникативных и личностных УДД):

Воспитывать:

• Познавательный интерес и навыки взаимоконтроля, взаимопроверки

• Коммуникативные способности во время работы в парах, группах

• Понимание ответственности за индивидуальную деятельность и деятельность работы в паре

• Положительный эффект настойчивости для достижения цели

3.Развивающие (формирование регулятивных УУД:

Развивать умения:

• Анализировать, сравнивать, обобщать, делать выводы

• Участвовать во взаимоконтроле, самоконтроле, вносить предложения.

• Осуществлять рефлексию своей деятельности

Оборудование: 1. Компьютер (с видеопроектором).

2.Раздаточный материал

Ход урока

1. Организационный момент

У : Посмотрите на эти механические часы (висят в классе). Что будет, если мы уберем 1 деталь? Так же и знания человека состоят из маленьких «деталей». И только, когда эти «детали» собраны вместе и не упущена ни одна, тогда знания начинают действовать и их можно применить в жизни. То, что мы узнаем на уроке сегодня и являются такими «деталями» наших знаний. Девиз нашего урока

«Мудрым никто не родился, а научился» Cлайд №1

— Как понимаете эти слова?

— Сегодня продолжим путь к мудрости

— С чего начнем?

У : С проверки домашнего задания и с повторения того, что мы уже с вами знаем.

2. Проверка домашнего задания

Задача № 723. Сколько кожи пойдет на пошивку футбольного мяча радиуса 10 см? (На швы добавить 8% от площади поверхности мяча).

Решение: S_сферы =4ПR²; S = 4П* 10²=400П(см²)

1% S составляют 0,01* 400П=4П (см²).

8% S составляют 8*4П = 32П(см²).

S= 400П+32П=432П=1357 (см²)

Ответ: 1357 (см²) Слайд №2

Формулируем тему урока: « Решение задач по темам «Объем шара и его частей», «Площадь сферы». Слайд №3

Поставьте каждый для себя цель урока. Слайд №4

Целеполагание:

Учащиеся сообщают, какие цели они для себя выбирают. Приходим к общему мнению. Записывают дату, тему в тетрадь, определяют цель урока

III. Актуализация знаний учащихся

1. Теоретический диктант (с последующей взаимопроверкой).(Работа в паре)

Вписать в текст недостающие по смыслу слова.

Вариант I

1) Всякое сечение шара плоскостью есть круг. Центр этого круга есть … перпендикуляра, опущенного из центра шара на секущую плоскость.

2) Центр шара является его … симметрии.

3) Осевое сечение шара есть ….

4) Линия пересечения двух сфер есть ….

5) Плоскости, равноудаленные от центра, пересекают шар по… кругам.

6) Около любой правильной пирамиды можно описать сферу, причем ее центр лежит на … пирамиды.

(высоте, основание, плоскостью, центром, круг, равным, перпендикулярен, окружность, касания)

Вариант II

1) Любая диаметральная плоскость шара является его … симметрии.

2) Осевое сечение сферы есть ….

3) Центр шара, описанного около правильной пирамиды, лежит на …пирамиды.

4) Радиус сферы, проведенной в точку касания сферы и плоскости … к касательной плоскости.

5) Касательная плоскость имеет с шаром только одну общую точку — точку….

6) В любую правильную пирамиду можно вписать сферу, причем ее центр лежит на … пирамиды.

(высоте, основание, плоскостью, центром, круг, равным, перпендикулярен, окружность, касания)

Взаимопроверка Слайд №5

Ответы (на экране):

Вариант I                  Вариант II

1) основание,           1) плоскостью,

2) центром,             2) окружность,

3) круг,                 3) высоте,

4) окружность,          4) перпендикулярен,

5) равным,               5) касания,

6) высоте.               6) высоте.

2. Опрос теоретический

Что такое сфера, шар, шаровой сегмент, шаровой слой, шаровой сектор.

IV.Закрепление теоретического материала

1. Индивидуальная работа по карточкам.

Карточка№ 1

Плоскость, перпендикулярная диаметру шара, делит его на части 3 см и 9 см. Найдите объем шара.

Карточка №2.

Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объем общей части шаров к объему целого шара?

Карточка №3

Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара, равного 20 см?

Демонстрация решений по карточкам с последующим обсуждением. Выставление оценок.

2.Решение задач.

1.Объем шара радиуса R равен V.

Найдите: объем шара радиуса: а)2R; б) 0,5 R.

(Ответ: а) 32/3ПR; б) 1/6 ПR³)

2. Чему равен объем шарового сектора, если радиус окружности основания равен 60 см, а радиус шара – 75 см?

(Ответ: 112,5П см³, или 450П см³).

3. Самостоятельная работа с последующей проверкой ответов.

1. На расстоянии 12 см от центра шара проведено сечение, радиус которого равен 9 см. Найдите объем шара и площадь его поверхности.

2. Сфера радиуса 3 имеет центр в точке О (4;-2;1). Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости ОXY. Найдите объем шара, ограниченного данной сферой.

(Ответы: 1) 4500 П см³, 900П см²; 2) (x-4)²+(y+2)²+(z+1)²=9; 36П)

Взаимооценка труда учащихся:

Кто из ребят, по вашему мнению, работал лучше всех на уроке?

Почему?

Что вам понравилось на уроке? Можно ли сказать, что вы стали чуть мудрее?

Сегодня на уроке вы работали активно, старательно, участвовали в обсуждении плана решения задач, высказывали своё мнение.

Рефлексия

Проанализируйте все этапы урока, цели которые вы ставил перед собой. Оцените свое эмоциональное состояние от участия в работе на уроке. Поднимите карточку красного цвета, если вы не поняли тему урока, желтую- если вы не совсем уверены, зеленую – если вы хорошо усвоили новый материал.

VI. Домашнее задание. Слайд №6

1. Повторить п. 82-84, формулы п. 82-84.

2. Просмотреть решения задач предыдущих уроков.

3. Решить задачи.

№1 Объем шара равен 36п см³. Найдите его радиус.

№2 Объемы двух шаров относятся как 8:1. Найдите отношения их радиусов.

№3 В шар вписан куб со стороной а. Найдите объем шара.

Спасибо за урок!! До свидания.

Вариант I

1) Всякое сечение шара плоскостью есть круг. Центр этого круга есть … ……………..перпендикуляра, опущенного из центра шара на секущую плоскость.

2) Центр шара является его … симметрии.

3) Осевое сечение шара есть ….

4) Линия пересечения двух сфер есть ….

5) Плоскости, равноудаленные от центра, пересекают шар по… кругам.

6) Около любой правильной пирамиды можно описать сферу, причем ее центр лежит на … ……………….пирамиды.

Вариант II

1) Любая диаметральная плоскость шара является его …………… симметрии.

2) Осевое сечение сферы есть ….

3) Центр шара, описанного около правильной пирамиды, лежит на …………….пирамиды.

4) Радиус сферы, проведенной в точку касания сферы и плоскости ………….. к касательной плоскости.

5) Касательная плоскость имеет с шаром только одну общую точку — точку….

6) В любую правильную пирамиду можно вписать сферу, причем ее центр лежит на … пирамиды.

Карточка№ 1

Плоскость, перпендикулярная диаметру шара, делит его на части 3 см и 9 см. Найдите объем шара.

Карточка №2.

Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объем общей части шаров к объему целого шара?

Карточка №3

Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара, равного 20 см?

Самостоятельная работа с последующей проверкой ответов.

1. На расстоянии 12 см от центра шара проведено сечение, радиус которого равен 9 см. Найдите объем шара и площадь его поверхности.

2. Сфера радиуса 3 имеет центр в точке О (4;-2;1). Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости ОXY. Найдите объем шара, ограниченного данной сферой.

3. Решить задачи.

№1 Объем шара равен 36п см³. Найдите его радиус.

№2 Объемы двух шаров относятся как 8:1. Найдите отношения их радиусов.

№3 В шар вписан куб со стороной а. Найдите объем шара.

«ОБЪЕМ ШАРА И ЕГО ЧАСТЕЙ» (11 класс)

Урок на тему:
ОБЪЕМ ШАРА И ЕГО ЧАСТЕЙ

Цель: вывести формулу объема шара и его частей.

Ход урока

I. Объяснение нового материала.

1. Объем шара радиуса R равен πR³.

Доказательство см. п. 82–83.

2. Шаровым сегментом называется часть шара, отсекаемая от него плоскостью (рис. а, в).

а)

б)

в)

Объем шарового сегмента определяется формулой V = πH² , где H – высота шарового сегмента.

3. Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар (рис. б).

4. Шаровым сектором называется тело, которое получается из шарового сегмента и конуса.

а)

б)

Объем шарового сектора определяется формулой V = πR²H, где H – высота соответствующего шарового сегмента.

II. Решение задач.

См.: Крамор В. С. Повторяем и систематизируем школьный курс геометрии. – М.: Просвещение, 1992.

Задача 1. Чему равен объем шарового сектора, если радиус окружности его основания равен 60 см, а радиус шара равен 75 см?

Решение

1. Под основанием сектора в задаче понимается основание соответствующего сектору сегмента. Пусть R – радиус шара, r – радиус основания сегмента.

2. Наша задача сводится к отысканию высоты этого сегмента: H = PO₁. OP – радиус шара, перпендикулярный основанию сегмента.

3. Из прямоугольного треугольника OO₁M (MO₁O = 90°) найдем:

OO₁ == 45, поэтому H = PO₁ =
= OP – OO₁ = R – OO₁ = 75 – 45 = 30.

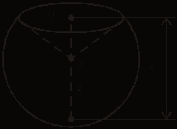
а) б)

4. Объем шарового сектора.

V =πR²H =π 75² ∙ 30 = 112 500π см^3.

5. Примечание. Поставленная задача имеет два решения:

1) Шаровой сектор, который мы рассматривали, называется выпуклым, и его высота равна R – OO, называется невыпуклым. Найдем его объем.

6. Рассмотрим второй случай, где высота сектора H = R – OO₁ = 120, так что полученный объем будет в 4 раза больше, чем вычисленный: V = π 45 ∙ 10⁴ см^3.

7. Таким образом, искомый объем равен либо 112 500π см³, либо 450 000π см³.

Задача 2. В шаре радиуса R выделен шаровой сектор с углом α в осевом сечении. Найдите его объем.

Решение

1. Объем сектора V =πR²H.

2. Так как R – известная величина, то остается нам найти H = AO₁.

3. Из условия C₁OC = α, значит, AOC = и соответственно
AC =, тогда ACO₁ =ABC =.

4. Из прямоугольного треугольника AO₁C получаем AO₁ = AC sin.

5. Из прямоугольного треугольника ABC находим AC = AB sin, или AC = 2R sin, следовательно, H = 2R sin².

6. Таким образом, .

Задача 3. В полусфере радиуса R через середину высоты проведено сечение, параллельное основанию полушара. Найдите объем полученного шарового пояса.

Решение

1. A₁O₁B₁ || AOB, AO = OC = R, OO₁ = O₁C =.

2. Объем шарового слоя найдем из равенства V = V_{полушара} – V_сегм.

3. V_{полушара} =.

4. У сегмента H =, V_сегм = πH².

5. Следовательно, V =πR³ –.

Задача 4. Круговой сектор радиуса R с дугой 120° вращается около прямой, проходящей через центр и составляющей с сектором угол 30°. Найдите объем тела вращения.

Решение

1. Дано: AO = R, AB = 120°, BOD = 30°.

2. AB = 120°, AOB = 120°, тогда AOO₁ = 180° – (120° + 30°) =
= 30°. Следовательно, объемы двух полученных секторов будут равны. Тогда

V_{т. в.} = V_шара – 2V_сект.

3. Из прямоугольного треугольника OO₂B найдем:

OO₂ = R cos 30° =.

4. V_{т. в.} ==
=, V_{т. в.} =.

Задача 5. Круговой сектор с углом 30° и радиусом R вращается около одного из боковых радиусов. Найдите объем полученного тела (рис.).

Решение

1. По условию BOA = 30°, значит, BOC = 60°, OB = OC = R, поэтому треугольник BOC правильный, причем его сторона BC отсекает от радиуса OA отрезок DA, равный высоте H соответствующего шаровому сектору сегмента.

2. H = AD = AO – OD = R – R= R.

3. Объем сектора .

Задача 6. Плоскость, перпендикулярная диаметру шара, делит диаметр на части 3 и 9 см. На какие части делится объем шара?

Решение

1. Радиус шара = 6.

2. Высота меньшего сегмента H = 3, объем его

V₁ = πH²= 45π см³.

3. Объем всего шара V₃ = πR³ = 288π см³.

4. Объем второго сегмента V₁ = V₃ – V₁ = 288π – 45π = 243π см³.

Задача 7. Из деревянного равностороннего цилиндра выточен наибольший возможный шар. Сколько процентов материала сточено?

Решение

1. Из условия вытекает, что высота цилиндра H = 2R, подставим значение H в формулу объема цилиндра: V₄ = πR²H = 2πR³.

2. Объем шара V_ш =πR³.

3. Найдем, сколько сточено материала: V₄ – V_ш = 2πR³ – πR³.

4. Найдем, сколько процентов составляет сточенный материал: .

Домашнее задание: теория (п. 82–83), №№ 710, 711, 717.

Контрольная работа по теме «Объём шара и его частей»

М-11 Контрольная работа по теме 3 вариант

«Объём шара и его частей».

1Медный куб, ребро которого 10 см, переплавлен в шар. Найти радиус шара.

2. Радиус шара равен R. Определить объём шарового сектора, если дуга в осевом сечении сектор равна 90°.

3. Внешний диаметр полого шара 18 см, толщина стенок 3 см. Найти объём стенок.

4. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60°. Найти отношение объёмов конуса и шара.

5. Объём цилиндра равен 96π см³. Площадь его осевого сечения 48 см². Найти площадь сферы, описанной около цилиндра.

М-11 Контрольная работа по теме 3 вариант

«Объём шара и его частей».

1Медный куб, ребро которого 10 см, переплавлен в шар. Найти радиус шара.

2. Радиус шара равен R. Определить объём шарового сектора, если дуга в осевом сечении сектор равна 90°.

3. Внешний диаметр полого шара 18 см, толщина стенок 3 см. Найти объём стенок.

4. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60°. Найти отношение объёмов конуса и шара.

5. Объём цилиндра равен 96π см³. Площадь его осевого сечения 48 см². Найти площадь сферы, описанной около цилиндра.

М-11 Контрольная работа по теме 2 вариант

«Объём шара и его частей».

1. Свинцовый шар, диаметр которого 20 см, переплавлен в шарики с диаметром в 10 раз меньше. Сколько таких шариков получилось?

2. Радиус шара равен R. Определить объём шарового сектора, если дуга в осевом сечении сектор равна 60°.

3. Найти радиус шара, вписанного в правильную треугольную пирамиду с высотой , равной 8, и апофемой, равной 10.

4. В конус, осевое сечение которого правильный треугольник, вписан шар. Найти отношение площади сферы к площади боковой поверхности конуса.

5. Диаметр шара равен высоте цилиндра, осевое сечение которого – квадрат. Найти отношение объёмов цилиндра и шара.

М-11 Контрольная работа по теме 1 вариант

«Объём шара и его частей».

1. Высота конуса равна 15 см , а радиус основания равен 8 см. Найти объём и площадь полной поверхности конуса.

2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найти отношение объёмов шара и цилиндра.

3. В шаре радиуса 15 см проведено сечение, площадь которого равна 81 см². Найти объём меньшего шарового сегмента, отсекаемого плоскостью сечения.

4. Площадь поверхности шара равна 144π см². Найти объём данного шара.

5. Найти объём шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.