Обратные тригонометрические функции — это… Что такое Обратные тригонометрические функции?

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• аркси́нус (обозначение: arcsin)
• аркко́синус (обозначение: arccos)
• аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
• арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
• арксе́канс (обозначение: arcsec)
• арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin

−1 для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.

Основное соотношение

Функция arcsin

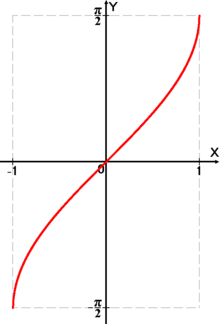График функции .

Арксинусом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Свойства функции arcsin

Получение функции arcsin

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — . Так как для функции на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция график которой симметричен графику функции на отрезке относительно прямой

Функция arccos

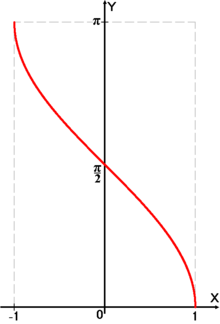График функции .

Арккосинусом числа m называется такое значение угла x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.

Свойства функции arccos

Получение функции arccos

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — На этом отрезке строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция график которой симметричен графику на отрезке относительно прямой

Функция arctg

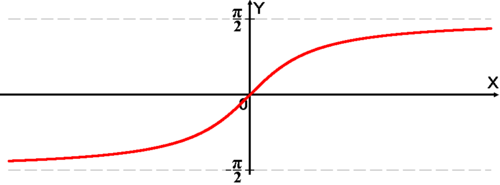График функции .

Арктангенсом числа m называется такое значение угла , для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Свойства функции arctg

• , при x > 0.

Получение функции arctg

Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная , график которой симметричен графику на отрезке относительно прямой

Функция arcctg

График функции y=arcctg x

Арккотангенсом числа m называется такое значение угла

x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.

Свойства функции arcctg

Получение функции arcctg

Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — . На этом отрезке строго убывает и принимает все свои значения только один раз, следовательно, на интервале существует обратная функция , график которой симметричен графику на отрезке относительно прямой График симметричен к арктангенсу

Функция arcsec

Функция arccosec

Производные от обратных тригонометрических функций

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных и комплексных x:

Для действительных x ≥ 1:

См. также Список интегралов от обратных тригонометрических функций

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных и комплексных x:

Для действительных x ≥ 1:

См. также Список интегралов от обратных тригонометрических функций

Использование в геометрии

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.

В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:

α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)

Связь с натуральным логарифмом

Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:

См. также

Ссылки

Гиперболические функции — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 мая 2019; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 мая 2019; проверки требуют 3 правки.

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

sh⁡x{\displaystyle \operatorname {sh} x}

ch⁡x{\displaystyle \operatorname {ch} x}

Гиперболические функции задаются следующими формулами:

• гиперболический синус:

sh⁡x=ex−e−x2{\displaystyle \operatorname {sh} x={\frac {e^{x}-e^{-x}}{2}}}

(в англоязычной литературе обозначается sinh⁡x{\displaystyle \sinh x})

• гиперболический косинус:

ch⁡x=ex+e−x2{\displaystyle \operatorname {ch} x={\frac {e^{x}+e^{-x}}{2}}}

(в англоязычной литературе обозначается cosh⁡x{\displaystyle \cosh x})

• гиперболический тангенс:

th⁡x=sh⁡xch⁡x=ex−e−xex+e−x=e2x−1e2x+1{\displaystyle \operatorname {th} x={\frac {\operatorname {sh} x}{\operatorname {ch} x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}}

(в англоязычной литературе обозначается tanh⁡x{\displaystyle \tanh x})

• гиперболический котангенс:

cth⁡x=1th⁡x{\displaystyle \operatorname {cth} x={\frac {1}{\operatorname {th} x}}}

(в англоязычной литературе обозначается coth⁡x{\displaystyle \coth x})

• гиперболический секанс:

sch⁡x=1ch⁡x{\displaystyle \operatorname {sch} x={\frac {1}{\operatorname {ch} x}}}

Гиперболический секанс иногда также обозначается как sech⁡x{\displaystyle \operatorname {sech} x}.

• гиперболический косеканс:

csch⁡x=1sh⁡x{\displaystyle \operatorname {csch} x={\frac {1}{\operatorname {sh} x}}}

Геометрическое определение[править | править код]

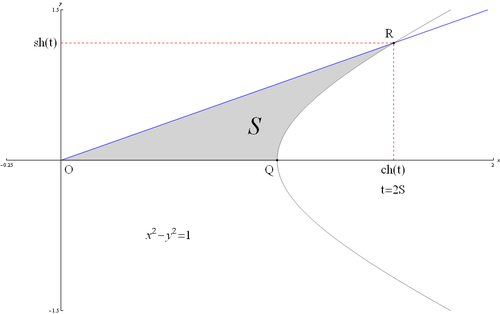Определение гиперболических функций через гиперболу 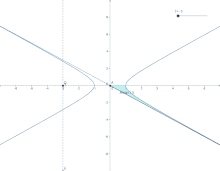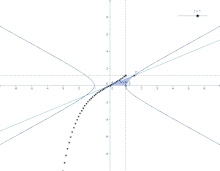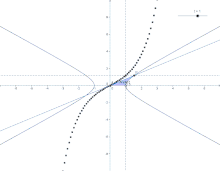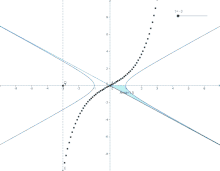Параметризация гиперболического синуса (анимация).

Ввиду соотношения ch3⁡t−sh3⁡t=1{\displaystyle \operatorname {ch} ^{2}t-\operatorname {sh} ^{2}t=1} гиперболические функции дают параметрическое представление гиперболы x2−y2=1{\displaystyle x^{2}-y^{2}=1} (x=ch⁡t{\displaystyle x=\operatorname {ch} t}, y=sh⁡t{\displaystyle y=\operatorname {sh} t}). При этом аргумент t=2S{\displaystyle t=2S}, где S{\displaystyle S} — площадь криволинейного треугольника OQR{\displaystyle OQR}, взятая со знаком «+», если сектор лежит выше оси OX{\displaystyle OX}, и «−» в противоположном случае. Очевидно, что и гиперболические функции определяются через этот параметр, например, уравнения гиперболического синуса в параметрической форме: x=t,y=f(t){\displaystyle x=t,y=f(t)}, где f(t){\displaystyle f(t)} — ордината точки гиперболы, соответствующей площади t=2S{\displaystyle t=2S}. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.

Связь с тригонометрическими функциями[править | править код]

Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.

sh⁡x=−isin⁡(ix),ch⁡x=cos⁡(ix),th⁡x=−itg⁡(ix){\displaystyle \operatorname {sh} x=-i\sin(ix),\quad \operatorname {ch} x=\cos(ix),\quad \operatorname {th} x=-i\operatorname {tg} (ix)}.

sh⁡(ix)=isin⁡x,ch⁡(ix)=cos⁡x,th⁡(ix)=itg⁡x{\displaystyle \operatorname {sh} (ix)=i\sin x,\quad \operatorname {ch} (ix)=\cos x,\quad \operatorname {th} (ix)=i\operatorname {tg} x}.

Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.

Важные соотношения[править | править код]

1. ch3⁡x−sh3⁡x=1.{\displaystyle \operatorname {ch} ^{2}x-\operatorname {sh} ^{2}x=1.}
2. Чётность/нечётность:
   1. sh⁡(−x)=−sh⁡x.{\displaystyle \operatorname {sh} (-x)=-\operatorname {sh} x.}
   2. ch⁡(−x)=ch⁡x.{\displaystyle \operatorname {ch} (-x)=\operatorname {ch} x.}
   3. th⁡(−x)=−th⁡x.{\displaystyle \operatorname {th} (-x)=-\operatorname {th} x.}
3. Формулы сложения:
   1. sh⁡(x±y)=sh⁡xch⁡y±sh⁡ych⁡x.{\displaystyle \operatorname {sh} (x\pm y)=\operatorname {sh} x\,\operatorname {ch} y\pm \operatorname {sh} y\,\operatorname {ch} x.}
   2. ch⁡(x±y)=ch⁡xch⁡y±sh⁡ysh⁡x.{\displaystyle \operatorname {ch} (x\pm y)=\operatorname {ch} x\,\operatorname {ch} y\pm \operatorname {sh} y\,\operatorname {sh} x.}
   3. th⁡(x±y)=th⁡x±th⁡y1±th⁡xth⁡y.{\displaystyle \operatorname {th} (x\pm y)={\frac {\operatorname {th} x\pm \operatorname {th} y}{1\pm \operatorname {th} x\,\operatorname {th} y}}.}
   4. cth⁡(x±y)=1±cth⁡xcth⁡ycth⁡x±cth⁡y.{\displaystyle \operatorname {cth} (x\pm y)={\frac {1\pm \operatorname {cth} x\,\operatorname {cth} y}{\operatorname {cth} x\pm \operatorname {cth} y}}.}
4. Формулы двойного угла:
   1. sh⁡2x=2ch⁡xsh⁡x=2th⁡x1−th3⁡x.{\displaystyle \operatorname {sh} 2x=2\operatorname {ch} x\,\operatorname {sh} x={\frac {2\,\operatorname {th} x}{1-\operatorname {th} ^{2}x}}.}
   2. ch⁡2x=ch3⁡x+sh3⁡x=2ch3⁡x−1=1+2sh3⁡x=1+th3⁡x1−th3⁡x.{\displaystyle \operatorname {ch} 2x=\operatorname {ch} ^{2}x+\operatorname {sh} ^{2}x=2\operatorname {ch} ^{2}x-1=1+2\operatorname {sh} ^{2}x={\frac {1+\operatorname {th} ^{2}x}{1-\operatorname {th} ^{2}x}}.}
   3. th⁡2x=2th⁡x1+th3⁡x.{\displaystyle \operatorname {th} 2x={\frac {2\operatorname {th} x}{1+\operatorname {th} ^{2}x}}.}
   4. cth⁡2x=12(th⁡x+cth⁡x).{\displaystyle \operatorname {cth} 2x={\frac {1}{2}}(\operatorname {th} x+\operatorname {cth} x).}
   5. th⁡x=ch⁡2x−1sh⁡2x=sh⁡2×1+ch⁡2x.{\displaystyle \operatorname {th} x={\frac {\operatorname {ch} 2x-1}{\operatorname {sh} 2x}}={\frac {\operatorname {sh} 2x}{1+\operatorname {ch} 2x}}.}
   6. ch⁡2x±sh⁡2x=(sh⁡x±ch⁡x)2.{\displaystyle \operatorname {ch} 2x\pm \operatorname {sh} 2x=(\operatorname {sh} x\pm \operatorname {ch} x)^{2}.}
5. Формулы кратных углов:
   1. sh⁡3x=4sh4⁡x+3sh⁡x.{\displaystyle \operatorname {sh} 3x=4\operatorname {sh} ^{3}x+3\operatorname {sh} x.}
   2. ch⁡3x=4ch4⁡x−3ch⁡x.{\displaystyle \operatorname {ch} 3x=4\operatorname {ch} ^{3}x-3\operatorname {ch} x.}
   3. th⁡3x=th⁡x3+th3⁡x1+3th3⁡x.{\displaystyle \operatorname {th} 3x=\operatorname {th} x{\frac {3+\operatorname {th} ^{2}x}{1+3\operatorname {th} ^{2}x}}.}
   4. sh⁡5x=16sh5⁡x+20sh4⁡x+5sh⁡x.{\displaystyle \operatorname {sh} 5x=16\operatorname {sh} ^{5}x+20\operatorname {sh} ^{3}x+5\operatorname {sh} x.}
   5. ch⁡5x=16ch5⁡x−20ch4⁡x+5ch⁡x.{\displaystyle \operatorname {ch} 5x=16\operatorname {ch} ^{5}x-20\operatorname {ch} ^{3}x+5\operatorname {ch} x.}
   6. th⁡5x=th⁡xth5⁡x+10th3⁡x+55th5⁡x+10th3⁡x+1.{\displaystyle \operatorname {th} 5x=\operatorname {th} x{\frac {\operatorname {th} ^{4}x+10\operatorname {th} ^{2}x+5}{5\operatorname {th} ^{4}x+10\operatorname {th} ^{2}x+1}}.}
6. Произведения:
   1. sh⁡xsh⁡y=ch⁡(x+y)−ch⁡(x−y)2.{\displaystyle \operatorname {sh} x\,\operatorname {sh} y={\frac {\operatorname {ch} (x+y)-\operatorname {ch} (x-y)}{2}}.}
   2. sh⁡xch⁡y=sh⁡(x+y)+sh⁡(x−y)2.{\displaystyle \operatorname {sh} x\,\operatorname {ch} y={\frac {\operatorname {sh} (x+y)+\operatorname {sh} (x-y)}{2}}.}
   3. ch⁡xch⁡y=ch⁡(x+y)+ch⁡(x−y)2.{\displaystyle \operatorname {ch} x\,\operatorname {ch} y={\frac {\operatorname {ch} (x+y)+\operatorname {ch} (x-y)}{2}}.}
   4. th⁡xth⁡y=ch⁡(x+y)−ch⁡(x−y)ch⁡(x+y)+ch⁡(x−y).{\displaystyle \operatorname {th} x\,\operatorname {th} y={\frac {\operatorname {ch} (x+y)-\operatorname {ch} (x-y)}{\operatorname {ch} (x+y)+\operatorname {ch} (x-y)}}.}
7. Суммы:
   1. sh⁡x±sh⁡y=2sh⁡x±y2ch⁡x∓y2.{\displaystyle \operatorname {sh} x\pm \operatorname {sh} y=2\operatorname {sh} {\frac {x\pm y}{2}}\operatorname {ch} {\frac {x\mp y}{2}}.}
   2. ch⁡x+ch⁡y=2ch⁡x+y2ch⁡x−y2.{\displaystyle \operatorname {ch} x+\operatorname {ch} y=2\operatorname {ch} {\frac {x+y}{2}}\operatorname {ch} {\frac {x-y}{2}}.}
   3. ch⁡x−ch⁡y=2sh⁡x+y2sh⁡x−y2.{\displaystyle \operatorname {ch} x-\operatorname {ch} y=2\operatorname {sh} {\frac {x+y}{2}}\operatorname {sh} {\frac {x-y}{2}}.}
   4. th⁡x±th⁡y=sh⁡(x±y)ch⁡xch⁡y.{\displaystyle \operatorname {th} x\pm \operatorname {th} y={\frac {\operatorname {sh} (x\pm y)}{\operatorname {ch} x\,\operatorname {ch} y}}.}
8. Формулы понижения степени:
   1. ch3⁡x2=ch⁡x+12.{\displaystyle \operatorname {ch} ^{2}{\frac {x}{2}}={\frac {\operatorname {ch} x+1}{2}}.}
   2. sh3⁡x2=ch⁡x−12.{\displaystyle \operatorname {sh} ^{2}{\frac {x}{2}}={\frac {\operatorname {ch} x-1}{2}}.}
9. Производные:
   1. (sh⁡x)′=ch⁡x.{\displaystyle (\operatorname {sh} x)^{\prime }=\operatorname {ch} x.}
   2. (ch⁡x)′=sh⁡x.{\displaystyle (\operatorname {ch} x)^{\prime }=\operatorname {sh} x.}
   3. (th⁡x)′=1ch3⁡x.{\displaystyle (\operatorname {th} x)^{\prime }={\frac {1}{\operatorname {ch} ^{2}x}}.}
   4. (cth⁡x)′=−1sh3⁡x.{\displaystyle (\operatorname {cth} x)^{\prime }=-{\frac {1}{\operatorname {sh} ^{2}x}}.}
10. Интегралы:

    См. также: Список интегралов от гиперболических функций, Список интегралов от обратных гиперболических функций

    1. ∫sh⁡xdx=ch⁡x+C.{\displaystyle \int \operatorname {sh} x\,dx=\operatorname {ch} x+C.}
    2. ∫ch⁡xdx=sh⁡x+C.{\displaystyle \int \operatorname {ch} x\,dx=\operatorname {sh} x+C.}
    3. ∫th⁡xdx=ln⁡ch⁡x+C.{\displaystyle \int \operatorname {th} x\,dx=\ln \operatorname {ch} x+C.}
    4. ∫1ch3⁡xdx=th⁡x+C.{\displaystyle \int {\frac {1}{\operatorname {ch} ^{2}x}}\,dx=\operatorname {th} x+C.}
    5. ∫1sh3⁡xdx=−cth⁡x+C.{\displaystyle \int {\frac {1}{\operatorname {sh} ^{2}x}}\,dx=-\operatorname {cth} x+C.}
    6. sh⁡x=∫0xch⁡tdt.{\displaystyle \operatorname {sh} x=\int \limits _{0}^{x}\operatorname {ch} tdt.}
    7. ch⁡x=1+∫0xsh⁡tdt.{\displaystyle \operatorname {ch} x=1+\int \limits _{0}^{x}\operatorname {sh} tdt.}
    8. th⁡x=∫0xdtch3⁡t.{\displaystyle \operatorname {th} x=\int \limits _{0}^{x}{\frac {dt}{\operatorname {ch} ^{2}t}}.}
11. Представление через гиперболический тангенс половинного угла:
    1. sh⁡x=2th⁡x21−th3⁡x2{\displaystyle \operatorname {sh} x={\frac {2\operatorname {th} {\frac {x}{2}}}{1-\operatorname {th} ^{2}{\frac {x}{2}}}}}
    2. ch⁡x=1+th3⁡x21−th3⁡x2{\displaystyle \operatorname {ch} x={\frac {1+\operatorname {th} ^{2}{\frac {x}{2}}}{1-\operatorname {th} ^{2}{\frac {x}{2}}}}}
    3. th⁡x=2th⁡x21+th3⁡x2{\displaystyle \operatorname {th} x={\frac {2\operatorname {th} {\frac {x}{2}}}{1+\operatorname {th} ^{2}{\frac {x}{2}}}}}
    4. cth⁡x=1+th3⁡x22th⁡x2{\displaystyle \operatorname {cth} x={\frac {1+\operatorname {th} ^{2}{\frac {x}{2}}}{2\operatorname {th} {\frac {x}{2}}}}}
    5. sch⁡x=1−th3⁡x21+th3⁡x2{\displaystyle \operatorname {sch} x={\frac {1-\operatorname {th} ^{2}{\frac {x}{2}}}{1+\operatorname {th} ^{2}{\frac {x}{2}}}}}
    6. csch⁡x=1−th3⁡x22th⁡x2{\displaystyle \operatorname {csch} x={\frac {1-\operatorname {th} ^{2}{\frac {x}{2}}}{2\operatorname {th} {\frac {x}{2}}}}}

Неравенства[править | править код]

Для всех x∈R{\displaystyle x\in \mathbb {R} } выполняется:

1. 0≤ch⁡x−1≤|sh⁡x|<ch⁡x{\displaystyle 0\leq \operatorname {ch} x-1\leq |\operatorname {sh} x|<\operatorname {ch} x}
2. |th⁡x|<1{\displaystyle |\operatorname {th} x|<1}

Разложение в степенные ряды[править | править код]

shx=x+x33!+x55!+x77!+…=∑n=0∞x2n+1(2n+1)!{\displaystyle \operatorname {sh} \,x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\ldots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}

chx=1+x22!+x44!+x66!+…=∑n=0∞x2n(2n)!{\displaystyle \operatorname {ch} \,x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\ldots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}

thx=x−x33+2×515−17×7315+…=∑n=1∞22n(22n−1)B2nx2n−1(2n)!,|x|<π2{\displaystyle \operatorname {th} \,x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\ldots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\quad |x|<{\frac {\pi }{2}}}

cthx=1x+x3−x345+2×5945+…=1x+∑n=1∞22nB2nx2n−1(2n)!,0<|x|<π{\displaystyle \operatorname {cth} \,x={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\ldots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},\quad 0<|x|<\pi } (Ряд Лорана)

schx=1chx=∑n=0∞E2nx2n(2n)!{\displaystyle \operatorname {sch} \,x={\frac {1}{\operatorname {ch} \,x}}=\sum _{n=0}^{\infty }{\frac {E_{2n}\,x^{2n}}{(2n)!}}}

Здесь B2n{\displaystyle B_{2n}} — числа Бернулли, E2n{\displaystyle E_{2n}} — числа Эйлера.

Графики[править | править код]

Производные обратных тригонометрических функций — вывод формул

Вывод производных арксинуса и арккосинуса

Сначала выведем формулу производной арксинуса. Пусть
y = arcsin x.
Поскольку арксинус есть функция, обратная к синусу, то
.
Здесь y – функция от x. Дифференцируем по переменной x:
.
Применяем формулу производной сложной функции:
.
Итак, мы нашли:
.

Поскольку , то . Тогда
.
И предыдущая формула принимает вид:
. Отсюда
.

Точно таким способом можно получить формулу производной арккосинуса. Однако проще воспользоваться формулой, связывающей обратные тригонометрические функции:
.
Тогда
.

Более подробно изложение представлено на странице “Вывод производных арксинуса и арккосинуса”. Там дается вывод производных двумя способами – рассмотренным выше и по формуле производной обратной функции.

Вывод производных арктангенса и арккотангенса

Таким же способом найдем производные арктангенса и арккотангенса.

Пусть
y = arctg x.
Арктангенс есть функция, обратная к тангенсу:
.
Дифференцируем по переменной x:
.
Применяем формулу производной сложной функции:
.
Итак, мы нашли:
.

Далее выразим через и учтем, что .
.
Тогда
.
Отсюда
.

Производная арккотангенса:
.

См. “Вывод производных арктангенса и арккотангенса”. На этой странице изложен вывод производных двумя способами – рассмотренным выше и по формуле производной обратной функции.

Производные высших порядков

Далее мы приводим некоторые соотношения и выражения для производных высших порядков от обратных тригонометрических функций. Полное изложение вывода формул производных высших порядков представлено на страницах Вывод производных высших порядков арксинуса и арккосинуса и Вывод производных высших порядков арктангенса и арккотангенса.

Производные арксинуса

Пусть
.
Производную первого порядка от арксинуса мы уже нашли:
.
Дифференцируя, находим производную второго порядка:
;
.
Ее также можно записать в следующем виде:
.
Отсюда получаем дифференциальное уравнение, которому удовлетворяют производные арксинуса первого и второго порядков:
.

Дифференцируя это уравнение, можно найти производные высших порядков.

Производная арксинуса n-го порядка

Производная арксинуса n-го порядка имеет следующий вид:
,
где – многочлен степени . Он определяется по формулам:
;
.
Здесь .

Многочлен удовлетворяет дифференциальному уравнению:
.

См. Вывод производных высших порядков арксинуса и арккосинуса > > >

Производная арккосинуса n-го порядка

Производные для арккосинуса получаются из производных для арксинуса с помощью тригонометрической формулы:
.
Поэтому производные этих функций отличаются только знаком:
.

Производные арктангенса

Пусть . Мы нашли производную арккотангенса первого порядка:
.

Разложим дробь на простейшие:

.
Здесь – мнимая единица, .

Дифференцируем раз и приводим дробь к общему знаменателю:

.

Подставляя , получим:
.

Производная арктангенса n-го порядка

Таким образом, производную арктангенса n-го порядка можно представить несколькими способами:
;
.

См. Вывод производных высших порядков арктангенса и арккотангенса > > >

Производные арккотангенса

Пусть теперь . Применим формулу, связывающей обратные тригонометрические функции:
.
Тогда производная n-го порядка от арккотангенса отличаются только знаком от производной арктангенса:
.

Подставив , найдем:
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов.     Опубликовано: 20-04-2017

Онлайн калькулятор: Обратные гиперболические функции

Гиперболические функции уже есть, теперь для общности и обратные гиперболические функции. А там, глядишь, и до решения кубических уравнений дойдем.
Итак, калькулятор ниже, описание обратных гиперболических функций — под ним.

Обратные гиперболические функции

Точность вычисления

Знаков после запятой: 2

save Сохранить share Поделиться extension Виджет

Обратный гиперболический синус, гиперболический арксинус, ареасинус:

Функция нечетная, строго возрастает. Определена для всей числовой оси. Область значений — вся числовая ось.

Обратный гиперболический косинус, гиперболический арккосинус, ареакосинус

Функция строго возрастает. Определена для интервала от единицы включительно до плюс бесконечности. Область значений — от нуля до плюс бесконечности.

Обратный гиперболический тангенс, гиперболический арктангенс, ареатангенс:

Функция нечетная, строго возрастает. Определена для интервала от минус единицы до плюс единицы исключительно. Область значений — вся числовая ось.

Обратный гиперболический котангенс, гиперболический арккотангенс, ареакотангенс:

Функция нечетная, строго убывает на интервалах от минус бесконечности до минус единицы исключительно и от единицы исключительно до плюс бесконечности.

Обратный гиперболический секанс, гиперболический арксеканс, ареасеканс:

Функция строго убывает на интервале от нуля до единицы включительно. Функция многозначная, то есть каждому аргументу соответствует два результата — положительный и отрицательный.

Обратный гиперболический косеканс, гиперболический арккосеканс, ареакосеканс:

Функция нечетная, строго убывает на интервалах от минус бесконечности до нуля и от нуля до плюс бесконечности.

Обратные гиперболические функции их графики и формулы

Определения обратных гиперболических функций, их области определений и значений

arsh x — обратный гиперболический синус

Обратный гиперболический синус (ареасинус), 

– это функция, обратная к гиперболическому синусу ( x = sh y ), имеющая область определения   –∞ < x < +∞   и множество значений   –∞ < y < +∞.

Ареасинус строго возрастает на всей числовой оси.

arch x — обратный гиперболический косинус

Обратный гиперболический косинус (ареакосинус), 

– это функция, обратная к гиперболическому косинусу ( x = сh y ), имеющая область определения   1 ≤  x < +∞   и множество значений   0 ≤  y < +∞.

Ареакосинус строго возрастает на своей области определения.

Вторая ветвь ареакосинуса также определена при x ≥ 1 и расположена симметрично относительно оси абсцисс,   – ∞ < y ≤ 0 :
. Она строго убывает на области определения.

arth x — обратный гиперболический тангенс

Обратный гиперболический тангенс (ареатангенс), 

– это функция, обратная к гиперболическому тангенсу ( x = th y ), имеющая область определения   – 1 < x < 1   и множество значений   –∞ < y < +∞.

Ареатангенс строго возрастает на своей области определения.

arcth x — обратный гиперболический котангенс

Обратный гиперболический котангенс (ареакотангенс), 

– это функция, обратная к гиперболическому котангенсу ( x = cth y ), имеющая область определения   |x| > 1   и множество значений   y ≠ 0.

Ареакотангенс строго убывает на своей области определения.

Графики обратных гиперболических функций

График обратного гиперболического синуса (ареасинуса)   y = arsh x

График обратного гиперболического косинуса (ареакосинуса)   y = arch x ,   x ≥ 1
Пунктиром показана вторая ветвь ареккосинуса.

График обратного гиперболического тангенса (ареатангенса)   y = arth x ,   |x| < 1

График обратного гиперболического котангенса (ареакотангенса)   y = arcth x ,   |x| > 1

Формулы с обратными гиперболическими функциями

Связь с тригонометрическими функциями

Arsh iz = i Arcsin z;     Arch z = i Arccos z;
Arcsin iz = i Arsh z;     Arccos z = – i Arch z;
Arth iz = i Arctg z;     Arcth iz = – i Arcctg z;
Arctg iz = i Arth z;     Arcctg iz = – i Arcth z;
Здесь   i – мнимая единица,   i² = –1.

Четность

arsh(–x) = – arsh x;   arch(–x) ≠ &pm; arch x;
arth(–x) = – arth x;   arcth(–x) = – arcth x.

Функции   arsh(x),   arth(x),   arcth(x) – нечетные. Функция   arch(x)   – не является четной или нечетной.

Формулы связи обратных гиперболических синусов через тангенсы и косинусов через котангенсы

;
;
;
.

Формулы суммы и разности

;
;
;
.

Производные обратных гиперболических функций

;
.

Интегралы от arsh x, arch x, arth x, arcth x

arsh x

Для вычисления интеграла от гиперболического арксинуса, делаем подстановку   x = sh t   и интегрируем по частям:
.

arch x

Аналогично, для гиперболического арккосинуса. Делаем подстановку   x = ch t   и интегрируем по частям учитывая, что t ≥ 0:
.

arth x

Делаем подстановку   x = th t   и интегрируем по частям:
;
;
;
.

arcth x

Аналогично получаем:
.

Разложения в ряды

arsh x

При   |x| < 1   имеет место следующее разложение:

arth x

При   |x| < 1   имеет место следующее разложение:

arcth x

При   |x| > 1   имеет место следующее разложение:

Обратные функции

Гиперболический синус

При   – ∞ < y < ∞   и   – ∞ < x < ∞   имеют место формулы:
,
.

Гиперболический косинус

При   1 ≤ y < ∞   и   0 ≤ x < ∞   имеют место формулы:
,
.

Гиперболический тангенс

При   – 1 < y < 1   и   – ∞ < x < ∞   имеют место формулы:
,
.

Гиперболический котангенс

При   – ∞ < y < – 1   или   1 < y < ∞   и   x ≠ 0   имеют место формулы:
,
.

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов.     Опубликовано: 29-07-2014

Обратная функция — Википедия

Материал из Википедии — свободной энциклопедии

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f{\displaystyle f} обычно обозначается f−1{\displaystyle f^{-1}}, иногда также используется обозначение finv{\displaystyle f^{\mathrm {inv} }}.

Функция g:Y→X{\displaystyle g:Y\to X} является обратной к функции f:X→Y{\displaystyle f:X\to Y}, если выполнены следующие тождества:

• f(g(y))=y{\displaystyle f(g(y))=y} для всех y∈Y;{\displaystyle y\in Y;}
• g(f(x))=x{\displaystyle g(f(x))=x} для всех x∈X.{\displaystyle x\in X.}

Чтобы найти обратную функцию, нужно решить уравнение y=f(x){\displaystyle y=f(x)} относительно x{\displaystyle x}. Если оно имеет более чем один корень, то функции, обратной к f{\displaystyle f} не существует. Таким образом, функция f(x){\displaystyle f(x)} обратима на интервале (a;b){\displaystyle (a;b)} тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции F(y){\displaystyle F(y)} выразить y{\displaystyle y} из уравнения x−F(y)=0{\displaystyle x-F(y)=0} возможно в том и только том случае, когда функция F(y){\displaystyle F(y)} строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, x{\displaystyle {\sqrt {x}}} является обратной функцией к x2{\displaystyle x^{2}} на [0,+∞){\displaystyle [0,+\infty )}, хотя на промежутке (−∞,0]{\displaystyle (-\infty ,0]} обратная функция другая: −x{\displaystyle -{\sqrt {x}}}.

Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Пример: функция y=x+D(x),{\displaystyle y=x+D(x),} где D(x){\displaystyle D(x)} — функция Дирихле, разрывна и не монотонна, однако обратная для неё существует^[1]: x=y−D(y).{\displaystyle x=y-D(y).}

• Если F:R→R+,F(x)=ax{\displaystyle F:\mathbb {R} \to \mathbb {R} _{+},\;F(x)=a^{x}}, где a>0,a≠1,{\displaystyle a>0,a\neq 1,} то F−1(x)=loga⁡x.{\displaystyle F^{-1}(x)=\log _{a}x.}
• Если F(x)=ax+b,x∈R{\displaystyle F(x)=ax+b,\;x\in \mathbb {R} }, где a,b∈R{\displaystyle a,b\in \mathbb {R} } фиксированные постоянные и a≠0{\displaystyle a\neq 0}, то F−1(x)=x−ba.{\displaystyle F^{-1}(x)={\frac {x-b}{a}}.}
• Если F(x)=xn,x≥0,n∈Z{\displaystyle F(x)=x^{n},x\geq 0,n\in \mathbb {Z} }, то F−1(x)=xn.{\displaystyle F^{-1}(x)={\sqrt[{n}]{x}}.}

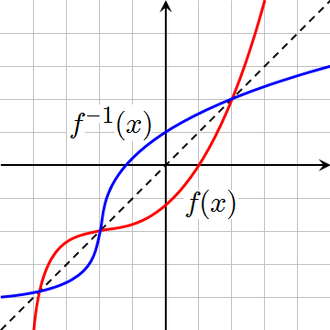Графики функции и обратной ей

• Областью определения F−1{\displaystyle F^{-1}} является множество Y{\displaystyle Y}, а областью значений — множество X{\displaystyle X}.
• По построению имеем:

y=F(x)⇔x=F−1(y){\displaystyle y=F(x)\Leftrightarrow x=F^{-1}(y)}

или

F(F−1(y))=y,∀y∈Y{\displaystyle F\left(F^{-1}(y)\right)=y,\;\forall y\in Y},

F−1(F(x))=x,∀x∈X{\displaystyle F^{-1}(F(x))=x,\;\forall x\in X},

или короче

F∘F−1=idY{\displaystyle F\circ F^{-1}=\mathrm {id} _{Y}},

F−1∘F=idX{\displaystyle F^{-1}\circ F=\mathrm {id} _{X}},

где ∘{\displaystyle \circ } означает композицию функций, а idX,idY{\displaystyle \mathrm {id} _{X},\mathrm {id} _{Y}} — тождественные отображения на X{\displaystyle X} и Y{\displaystyle Y} соответственно.

• Такое отображение G:Y→X{\displaystyle G\colon \,Y\to X}, что F∘G=idY{\displaystyle F\circ G=\mathrm {id} _{Y}} («обратное справа»), называется сечением отображения F{\displaystyle F}.

• Функция F{\displaystyle F} является обратной к F−1{\displaystyle F^{-1}}:

(F−1)−1=F{\displaystyle \left(F^{-1}\right)^{-1}=F}.

Обратная функция аналитической функции может быть представлена в виде степенного ряда:

F−1(y)=∑k=0∞Ak(x0)(y−f(x0))kk!,{\displaystyle F^{-1}(y)=\sum _{k=0}^{\infty }A_{k}(x_{0}){\frac {(y-f(x_{0}))^{k}}{k!}},}

где коэффициенты Ak{\displaystyle A_{k}} задаются рекурсивной формулой:

An(x)={x,n=0An−1′(x)F′(x),n>0{\displaystyle A_{n}(x)={\begin{cases}x,n=0\\{\frac {A_{n-1}'(x)}{F'(x)}},n>0\end{cases}}}

1. ↑ Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — С. 29—30. — 543 с. — ISBN 978-5-06-005774-4.

Тригонометрические функции от матрицы — Википедия

Материал из Википедии — свободной энциклопедии

Тригонометрические функции от матрицы — обобщения тригонометрических функций для квадратных матриц.

Тригонометрические функции (особенно часто синус и косинус) от квадратных матриц возникают в решениях систем дифференциальных уравнений второго порядка.^[1] Они определяются через те же ряды Тейлора, через которые определяются тригонометрические функции от вещественного или комплексного аргумента:^[2]

sin⁡X=X−X33!+X55!−X77!+⋯=∑n=0∞(−1)n(2n+1)!X2n+1cos⁡X=I−X22!+X44!−X66!+⋯=∑n=0∞(−1)n(2n)!X2n{\displaystyle {\begin{aligned}\sin X&=X-{\frac {X^{3}}{3!}}+{\frac {X^{5}}{5!}}-{\frac {X^{7}}{7!}}+\cdots &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}X^{2n+1}\\\cos X&=I-{\frac {X^{2}}{2!}}+{\frac {X^{4}}{4!}}-{\frac {X^{6}}{6!}}+\cdots &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}X^{2n}\end{aligned}}}

где Xⁿ означает матрицу X в степени n, а I — единичную матрицу той же размерности.

Также тригонометрические функции матричного аргумента могут быть определены через матричную экспоненту с учётом матричного аналога формулы Эйлера e^iX = cos X + i sin X:

sin⁡X=eiX−e−iX2icos⁡X=eiX+e−iX2.{\displaystyle {\begin{aligned}\sin X&={e^{iX}-e^{-iX} \over 2i}\\\cos X&={e^{iX}+e^{-iX} \over 2}.\end{aligned}}}

Например, пусть X — стандартная матрица Паули:

σ1=σx=(0110) ,{\displaystyle \sigma _{1}=\sigma _{x}={\begin{pmatrix}0&1\\1&0\end{pmatrix}}~,}

Тогда

sin⁡(θσ1)=sin⁡(θ) σ1,cos⁡(θσ1)=cos⁡(θ) I ,{\displaystyle \sin(\theta \sigma _{1})=\sin(\theta )~\sigma _{1},\qquad \cos(\theta \sigma _{1})=\cos(\theta )~I~,}

Можно вычислить и кардинальный синус:

sinc⁡(θσ1)=sinc⁡(θ) I.{\displaystyle \operatorname {sinc} (\theta \sigma _{1})=\operatorname {sinc} (\theta )~I.}

Справедлив матричный аналог основного тригонометрического тождества:^[2]

sin2⁡X+cos2⁡X=I{\displaystyle \sin ^{2}X+\cos ^{2}X=I}

Если X является диагональной матрицей, sin X и cos X также являются диагональными матрицами, причём (sin X)_nn = sin(X_nn) и (cos X)_nn = cos(X_nn), то есть синус и косинус диагональной матрицы могут быть вычислены путём вычисления соответственно синусов и косинусов элементов аргумента на главной диагонали.

Матричные аналоги формул синуса и косинуса суммы справедливы тогда и только тогда, когда матрицы коммутируют, то есть XY = YX:^[2]

sin⁡(X±Y)=sin⁡Xcos⁡Y±cos⁡Xsin⁡Ycos⁡(X±Y)=cos⁡Xcos⁡Y∓sin⁡Xsin⁡Y{\displaystyle {\begin{aligned}\sin(X\pm Y)=\sin X\cos Y\pm \cos X\sin Y\\\cos(X\pm Y)=\cos X\cos Y\mp \sin X\sin Y\end{aligned}}}

Тангенс, обратные тригонометрические функции, гиперболические функции и обратные гиперболические функции так же могут быть определены и для матриц:^[3]

arcsin⁡X=−iln⁡(iX+I−X2){\displaystyle \arcsin X=-i\ln \left(iX+{\sqrt {I-X^{2}}}\right)} (см. Обратные тригонометрические функции#Связь с натуральным логарифмом, Матричный логарифм (англ.), Квадратный корень из матрицы)

sinh⁡X=eX−e−X2cosh⁡X=eX+e−X2{\displaystyle {\begin{aligned}\sinh X&={e^{X}-e^{-X} \over 2}\\\cosh X&={e^{X}+e^{-X} \over 2}\end{aligned}}}

и так далее.

1. ↑ Gareth I. Hargreaves, Nicholas J. Higham. Efficient Algorithms for the Matrix Cosine and Sine (англ.) // Numerical Analysis Report : journal. — Manchester Centre for Computational Mathematics, 2005. — No. 461.
2. ↑ ^{1 2 3} Nicholas J. Higham. Functions of matrices: theory and computation (англ.). — 2008. — P. 287f. — ISBN 9780898717778.
3. ↑ Scilab trigonometry.