Линейная функция. Часть 1. Определение линейной функции и ее свойства
Движение с постоянной скоростью (или равномерное движение) по определению – это движение, при котором с изменением времени на одну и ту же величину, пройденный путь также изменяется одинаково (Рис. 1).
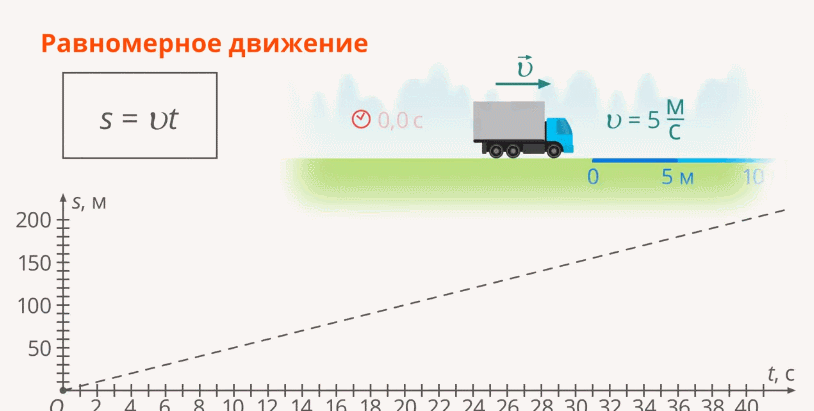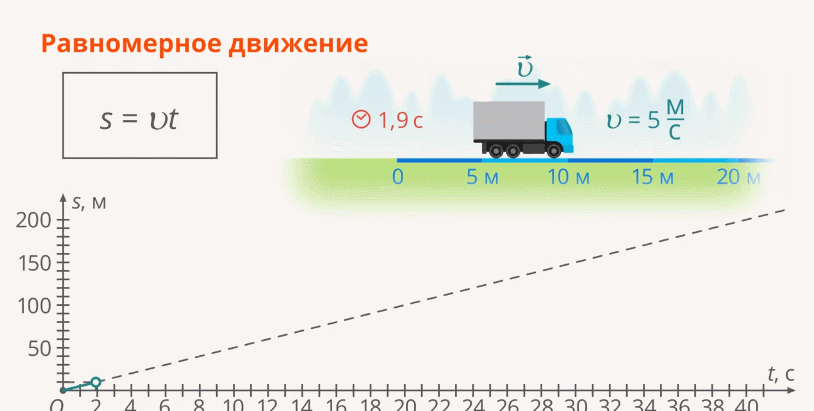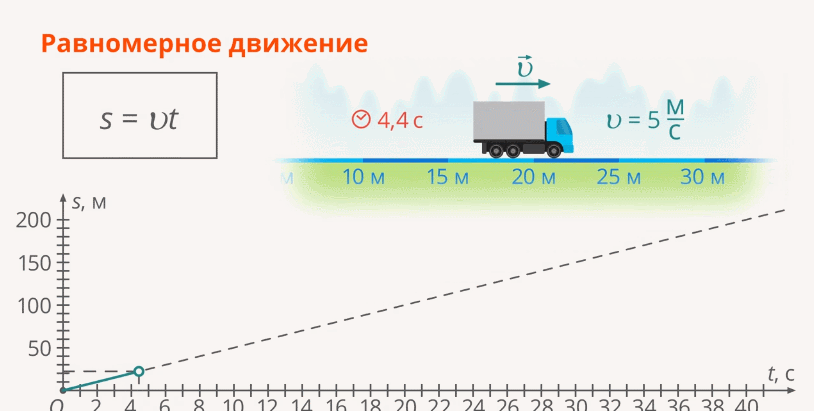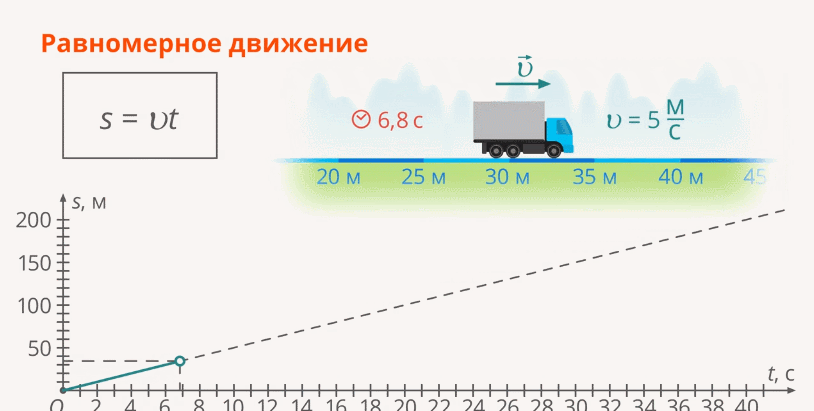
Рис. 1. График изменения пути при равномерном движении
Такие функции, как  , у которых одинаковые изменения аргумента приводят к одинаковым изменениям значения функции (Рис. 2), называются линейными функциями.
, у которых одинаковые изменения аргумента приводят к одинаковым изменениям значения функции (Рис. 2), называются линейными функциями.

Рис. 2. Одинаковые изменения аргумента приводят к одинаковым изменениям значениям функции
Правильнее было бы называть их прямолинейными (потому что их графиками являются прямые, о чём мы поговорим чуть позже), но прижилось именно такое сокращенное название.
Линейную функцию (или линейную зависимость) мы часто используем в жизни. Например, если из книги, в которой 50 страниц, мы за день прочитали 10 страниц, то можно сделать предположение, что всю книгу мы прочитаем за 5 дней (Рис. 3).

Рис. 3. Пример линейной зависимости в жизни
Или если мы идем в школу и прошли третью часть пути за 5 минут, то предполагаем, что на оставшийся путь потратим 10 минут.
Конечно, вряд ли мы будем успевать читать каждый день одно и то же количество страниц или будем идти в школу, не меняя свою среднюю скорость движения. Но для оценки значения некоторых величин, как видим, линейная функция является удобным инструментом.
Чтобы изучать какие-то объекты, их часто разбивают на группы, которые чем-то похожи. Например, разных живых организмов очень много, поэтому, чтобы их изучать, их делят на царства (животные, растения и т.д.), которые в свою очередь также делятся на более мелкие группы.
Различных функций очень много, поэтому для изучения их разбивают на разные классы. Как в жизни, мы объединяем объекты в одну группу по некоторым общим признакам (например, в супермаркете – хлебобулочные изделия, бакалея, соки-воды и т.д.), так и классы функций объединяют функции одного вида.
Линейные функции – один из этих классов (Рис. 4). Все остальные функции – нелинейные и их гораздо больше: реальные процессы описываются, в основном нелинейными функциями (Рис. 5).

Рис. 4. Линейные функции
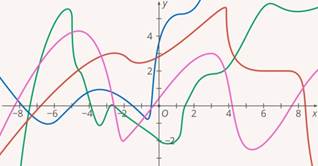
Рис. 5. Нелинейные функции
Но, во-первых, линейные функции мы умеем изучать и описывать, а во-вторых, многие нелинейные функции в малых областях можно рассматривать как линейные (Рис. 6).

Рис. 6. Приближение нелинейных функций линейными
Значит, линейные функции можно использовать как удобный инструмент для изучения других функций.
Конечно, линейные функции – не единственный класс функций, который мы умеем и будем изучать. Ещё будут квадратичные функции, показательные, обратная пропорциональность и т.д. Но о них поговорим позже.
Итак, линейные функции часто встречаются и их можно изучать. Поэтому на этом уроке мы и займемся этим классом функций.
Аналитически линейная функция задается формулой 
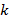 и
и 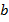 – произвольные заданные числа,
– произвольные заданные числа, 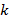 – угловой коэффициент,
– угловой коэффициент, 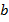 – свободный коэффициент (свободен от
– свободный коэффициент (свободен от  ).
).Ее характеристическое свойство (т.е. свойство, которым обладают только линейные функции, ее эквивалентное определение) состоит в том, что при изменении аргумента на одну и ту же величину значение функции так же изменяется на одну и ту же величину.
Только для линейных функций совершенно неважно, изменился  на
на  от
от 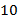 до
до  или от
или от 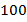 до
до 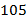 и т.д. –
и т.д. – 

Рис. 7. Эквивалентное определение линейной функции
Например, растём мы нелинейно (с  до
до  лет и с
лет и с  до
до  изменение роста сильно отличается), бегаем – тоже (бежать первый километр значительно легче, чем, например, пятый) и т.д.
изменение роста сильно отличается), бегаем – тоже (бежать первый километр значительно легче, чем, например, пятый) и т.д.
Линейное уравнение с двумя переменными
Рассмотрим линейное уравнение 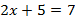 .
.
Мы уже умеем его решать – для этого перенесем число из левой части в правую, затем разделим на коэффициент при переменной:


Рассмотрим похожее уравнение 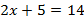 . Его решение будет практически таким же:
. Его решение будет практически таким же:

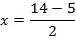
Аналогично:
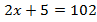
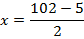
Обобщим рассмотренные уравнения и напишем в правой части число  , решение от этого не изменится:
, решение от этого не изменится:


Когда меняется значение  , меняется и значение
, меняется и значение  . Если мы не знаем значение
. Если мы не знаем значение  , то тогда в уравнении
, то тогда в уравнении  две неизвестных:
две неизвестных:  и
и  .
.
Уравнение вида 
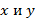 – переменные,
– переменные,  – произвольные числа.
– произвольные числа.Перепишем уравнение  следующим образом:
следующим образом: 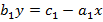 .
.
Если  , то на него мы можем разделить обе части уравнения:
, то на него мы можем разделить обе части уравнения: 
Перепишем так, чтобы один член был с переменной  , а второй – без:
, а второй – без:

Переобозначим коэффициенты:


Тогда  .
.
Т.е. линейное уравнение с двумя переменными задает линейную функцию.
Рассмотрим отдельно случай, когда 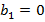 :
:

При  мы получим
мы получим  . Или просто
. Или просто 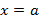 .
.
Такое уравнение тоже задает прямую (только вертикальную), но 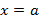 линейной функцией не является, т.к. одному значению
линейной функцией не является, т.к. одному значению  (
(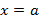 ) соответствует бесконечное множество значений
) соответствует бесконечное множество значений  (Рис. 1).
(Рис. 1).
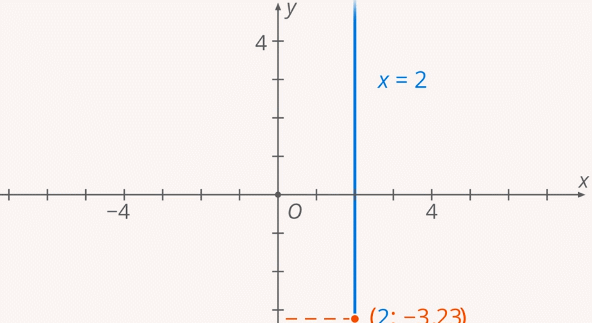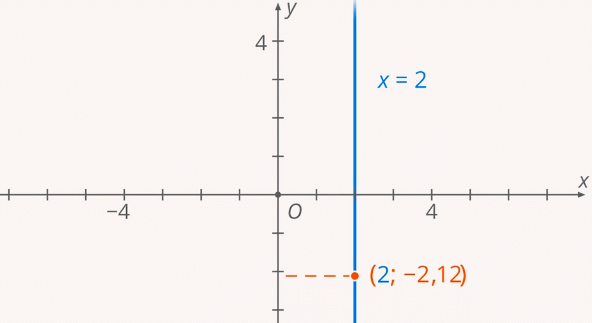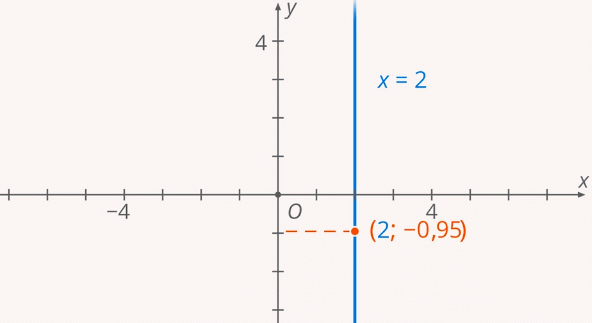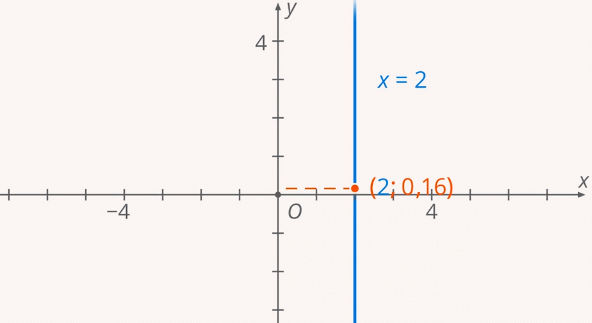
Рис. 1. Одному значению  соответствует бесконечное множество значений
соответствует бесконечное множество значений 
Онлайн урок обратная функция.
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

Функция — зависимость, по которой каждому элементу х из области определения ставится в соответствие единственное значение у из области значений функции.

Областью определения функции f(x) называется множество всех допустимых значений переменной x функции f.

Областью значений функции f(x) называют множество значений, которые может принимать функция f.
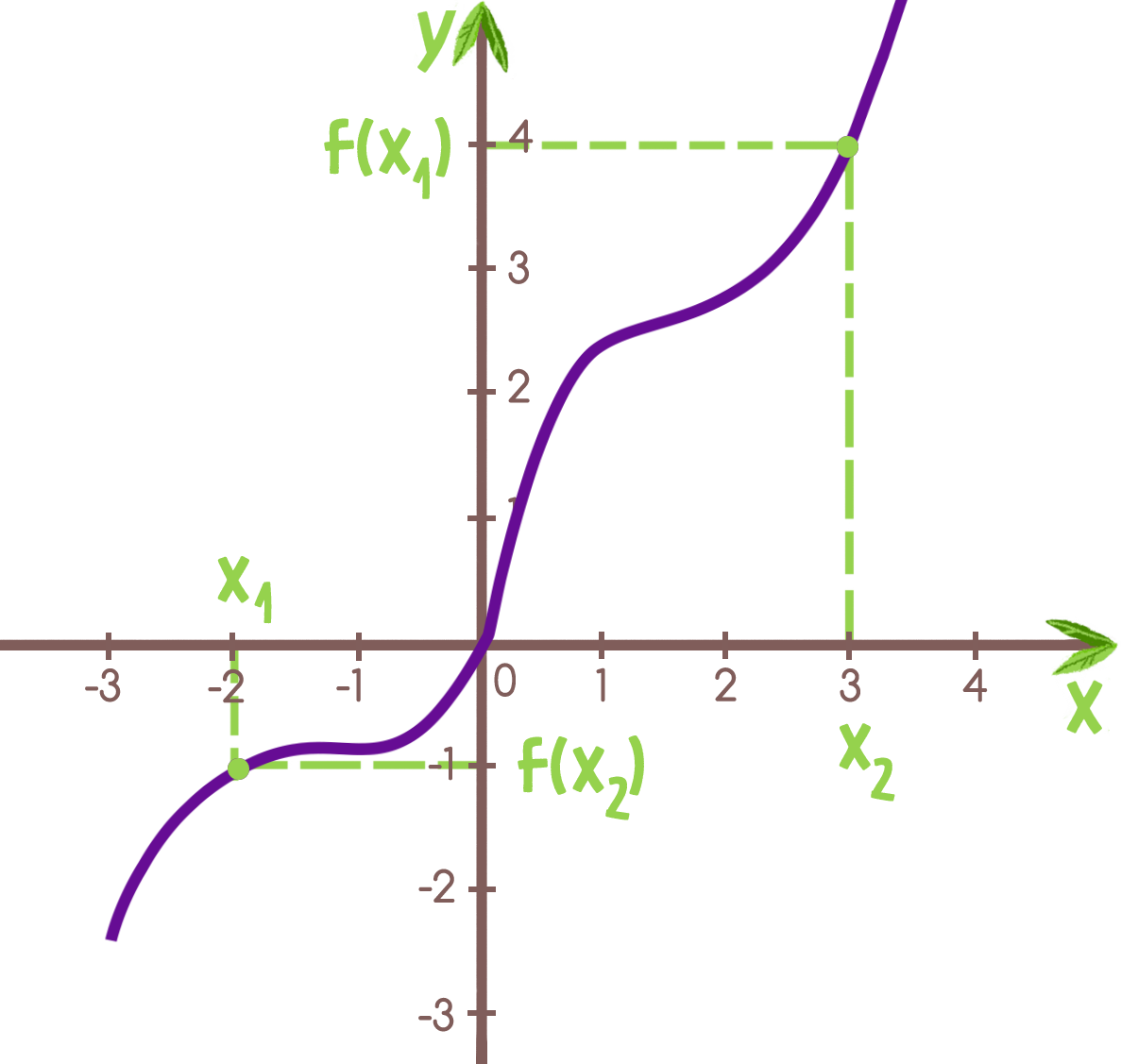
Функция y = f(x) называется возрастающей на промежутке Х, если для любых х1, х2 из Х таких, что х2 > x1, выполняется неравенство f(x2) ≥ f(x1).
Теперь установи соответствие между определениями, которые мы только что повторили, и картинками.
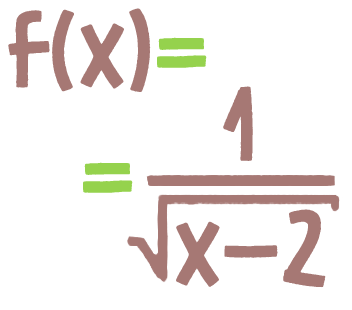
D(f) — [2; +∞)E(f) — [2; +∞)E(f) — (2; +∞)D(f) — (2; +∞)

f — является функциейf — не является функциейx — является функциейy — является функцией

E(f) — [-4; +∞)E(f) — [0; +∞)E(f) — любое числоE(f) — любое число, кроме {-4}
Прежде чем начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
1. Обратная функция.
2. Условие обратимости функции.
3. Графики обратных функций.
Онлайн урок линейная функция.
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

Точка — это абстрактный объект в геометрии, который не имеет никаких измерительных характеристик. Прямая — это геометрическая фигура, которая не имеет ни начала, ни конца, она бесконечна.
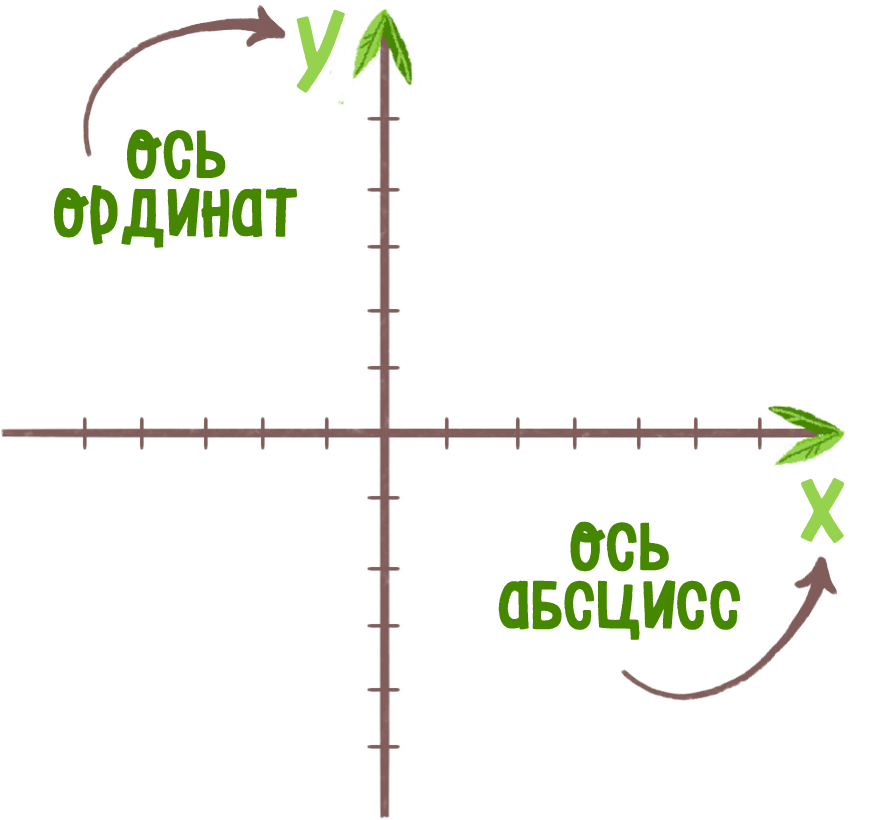
Вертикальную координатную прямую называют осью ординат или Oy. Горизонтальную координатную прямую называют осью абсцисс или Ox.

Тангенс острого угла — это отношение противолежащего катета к прилежащему в прямоугольном треугольнике. Тангенс тупого угла имеет отрицательное значение.

Функция называется нечетной, если для любого х из области определения функции выполняется равенство f(-x) = — f(x). Ее график симметричен относительно начала координат.
Теперь установи соответствие между картинками и определениями, которые мы только что повторили.

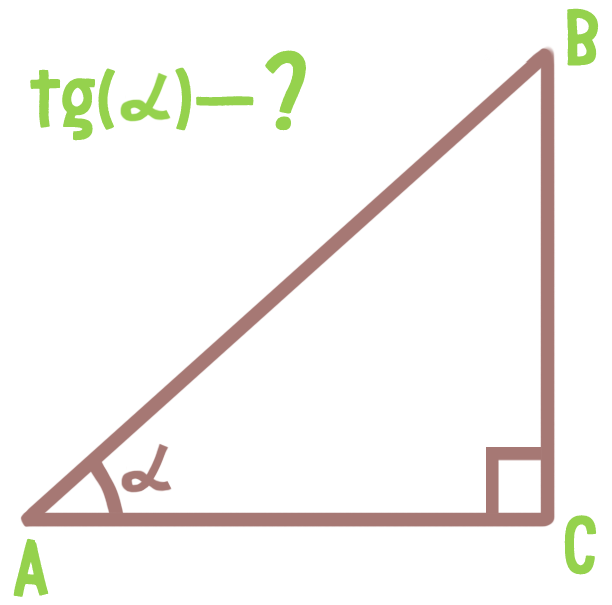
tg(α) = AC/BCtg(α) = AC/ABtg(α) = BC/ABtg(α) = BC/AC

E(f) = {все числа}D(f) = {все числа, кроме -1}D(f) = {все числа}E(f) = {все числа, кроме -1}
Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
1. Линейная функция.
2. Прямая пропорциональность.
3. Свойства линейной функции.
4. График линейной функции.
Обратный оператор — Википедия
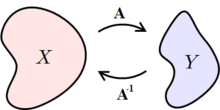 Если A отображает X на Y, то A−1 отображает Y на X
Если A отображает X на Y, то A−1 отображает Y на XОбратный оператор к оператору A{\displaystyle A} — оператор, который каждому y{\displaystyle y} из множества значений ImA{\displaystyle {\mbox{Im}}\,A} оператора A{\displaystyle A} ставит в соответствие единственный элемент x{\displaystyle x} из области определения D(A){\displaystyle {\mathcal {D}}(A)} оператора A{\displaystyle A}, являющийся решением уравнения Ax=y{\displaystyle Ax=y}. Если оператор A{\displaystyle A} имеет обратный, то есть уравнение Ax=y{\displaystyle Ax=y} имеет единственное решение при любом y{\displaystyle y} из ImA{\displaystyle {\mbox{Im}}\,A}, то A{\displaystyle A} называется обратимым. Обратный оператор обозначается A−1{\displaystyle A^{-1}}[1].
Определение и условия существования[править | править код]
Другое определение: оператор B{\displaystyle B} называется обратным к оператору A{\displaystyle A}, если BA=I,AB=I{\displaystyle BA=I,\,AB=I}, где I{\displaystyle I} — единичный оператор. Если выполняется только соотношение BA=I{\displaystyle BA=I} или только AB=I,{\displaystyle AB=I,} то оператор B{\displaystyle B} называется левым обратным или правым обратным соответственно. Если оператор A{\displaystyle A} имеет левый обратный и правый обратный, то они равны между собой, а оператор A{\displaystyle A} является обратимым[2]. Если обратный оператор существует, он определяется единственным образом[3].
Оператор A{\displaystyle A} обратим, если он отображает D(A){\displaystyle {\mathcal {D}}(A)} на ImA{\displaystyle {\mbox{Im}}\,A} взаимно однозначно, то есть при различных x∈D(A){\displaystyle x\in {\mathcal {D}}(A)} принимает различные значения y{\displaystyle y}.[4] Если оператор A{\displaystyle A} — линейный, то для существования обратного оператора достаточно, чтобы Ax=0{\displaystyle Ax=0} выполнялось только при x=0{\displaystyle x=0}[5].
Линейный оператор (даже ограниченный) может иметь обратный, определённый не на всём пространстве. Например, в пространстве ℓ2{\displaystyle \ell _{2}} линейный оператор
- A(x1,x2,x3,…)=(0,x1,x2,…){\displaystyle A(x_{1},x_{2},x_{3},\dots )=(0,x_{1},x_{2},\dots )}
имеет обратный, который определен для векторов с первой координатой равной нулю: x1=0{\displaystyle x_{1}=0}[5].
Теорема Банаха[править | править код]
Теорема Банаха является одним из основных принципов линейного анализа[8]. Из неё следует теорема об открытом отображении: линейное непрерывное отображение A{\displaystyle A} банахова пространства E{\displaystyle E} на (всё) банахово пространство E1{\displaystyle E_{1}} открыто[9].
Достаточные условия существования обратного оператора[править | править код]
- ‖Ax‖≥m‖x‖,{\displaystyle \|Ax\|\geq m\|x\|,}
где m>0{\displaystyle m>0} — некоторая константа. Тогда существует обратный ограниченный линейный оператор A−1{\displaystyle A^{-1}}[10].
- ‖B−1−A−1‖≤‖ΔA‖1−‖A−1‖‖ΔA‖‖A−1‖2{\displaystyle \|B^{-1}-A^{-1}\|\leq {\frac {\|\Delta A\|}{1-\|A^{-1}\|\|\Delta A\|}}\|A^{-1}\|^{2}}[11][12].
- (I−A)−1=∑k=1∞Ak{\displaystyle (I-A)^{-1}=\sum \limits _{k=1}^{\infty }A^{k}}[13].
Преобразование Фурье[править | править код]
- g(λ)=∫−∞∞f(t)e−iλtdt{\displaystyle g(\lambda )=\int \limits _{-\infty }^{\infty }f(t)e^{-i\lambda t}dt}
можно рассматривать как линейный ограниченный оператор, действующим из пространства L2(−∞,∞){\displaystyle L_{2}(-\infty ,\infty )} в себя. Обратным оператором для него является обратное преобразование Фурье
- f(t)=12π∫−∞∞g(λ)eiλtdλ{\displaystyle f(t)={\frac {1}{2\pi }}\int \limits _{-\infty }^{\infty }g(\lambda )e^{i\lambda t}d\lambda }[14].
Операторы интегрирования и дифференцирования[править | править код]
Для оператора интегрирования
- Ax=∫0tx(τ)dτ,{\displaystyle Ax=\int \limits _{0}^{t}x(\tau )\,d\tau ,}
действующего в пространстве непрерывных функций C[0,1]{\displaystyle C[0,1]}, обратным будет оператор дифференцирования:
- A−1y=ddty(t),{\displaystyle A^{-1}y={\frac {d}{dt}}y(t),}
определённый на линейном многообразии непрерывно дифференцируемых функций, таких что y(0)=0{\displaystyle y(0)=0}[15].
Оператор Штурма-Лиувилля[править | править код]
Для дифференциального оператора Штурма-Лиувилля Ax=ddt{p(t)dxdt}+q(t)x,{\displaystyle Ax={\frac {d}{dt}}\left\{p(t){\frac {dx}{dt}}\right\}+q(t)x,} определённого на линейном многообразии дважды непрерывно дифференцируемых функций таких, что x(0)=x(1)=0{\displaystyle x(0)=x(1)=0}, обратным оператором является интегральный оператор
- A−1y=∫01G(t,τ)y(τ)dτ,{\displaystyle A^{-1}y=\int \limits _{0}^{1}G(t,\tau )y(\tau )\,d\tau ,}
где G(t,τ){\displaystyle G(t,\tau )} — функция Грина. A−1{\displaystyle A^{-1}} — линейный ограниченный оператор в C[0,1]{\displaystyle C[0,1]}[15].
Интегральный оператор[править | править код]
Пусть
- Ax=∫01K(t,s)x(s)ds{\displaystyle Ax=\int \limits _{0}^{1}K(t,s)x(s)\,ds}
— интегральный оператор в пространстве непрерывных функций C[0,1]{\displaystyle C[0,1]}. При достаточно малых значениях параметра λ{\displaystyle \lambda } оператор (I−λA){\displaystyle (I-\lambda A)} (где I{\displaystyle I} — единичный оператор) имеет ограниченный обратный
- (I−λA)−1y=y(t)+λ∫01R(t,s,λ)y(s)ds{\displaystyle (I-\lambda A)^{-1}y=y(t)+\lambda \int \limits _{0}^{1}R(t,s,\lambda )y(s)\,ds},
где R(t,s,λ){\displaystyle R(t,s,\lambda )} — резольвента ядра K(t,s){\displaystyle K(t,s)}. Зная резольвенту, можно найти решение интегрального уравнения
- x(t)=y(t)+λ∫01K(t,s)x(s)ds{\displaystyle x(t)=y(t)+\lambda \int \limits _{0}^{1}K(t,s)x(s)\,ds}
при любом свободном члене y(t){\displaystyle y(t)}[16].
Обратный оператор в конечномерном пространстве[править | править код]
Оператор в конечномерном пространстве обратим тогда и только тогда, когда его ранг совпадает с размерностью пространства. Иначе говоря, определитель его матрицы отличен от нуля. Обратному оператору отвечает обратная матрица[17].
- ↑ 1 2 Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 225.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 128.
- ↑ 1 2 Рисс Ф., Сёкефальви-Надь Б. Лекции по функциональному анализу, 1979, с. 168.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 351.
- ↑ 1 2 Рисс Ф., Сёкефальви-Надь Б. Лекции по функциональному анализу, 1979, с. 319.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 154.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 207.
- ↑ Хелемский А. Я. Линейный оператор // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1982. — Т. 3. — 592 с. — 150 000 экз.
- ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, глава IV, §5, п. 4.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 155.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 157.
- ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 229.
- ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, с. 230.
- ↑ Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, 1976, глава VIII.
- ↑ 1 2 Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 161.
- ↑ Люстерник Л. А., Соболев В. И. Элементы функционального анализа, 1965, с. 163.
- ↑ Ильин В. А., Позняк Э. Г. Линейная алгебра. Учеб. для вузов. — 5-e изд.. — М.: Физматлит, 2002. — 320 с. — ISBN 5-9221-0129-3.
Линейная функция — это… Что такое Линейная функция?
Примеры линейных функций.Линейная функция — функция вида
- (для функций одной переменной).
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.
График линейной функции является прямой линией, с чем и связано ее название. Это касается вещественной функции одной вещественной переменной.
- Частный случай линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности), в отличие от — неоднородных линейных функций.
Свойства
Линейная функция нескольких переменных
Линейная функция переменных — функция вида
где — некоторые фиксированные числа. Областью определения линейной функции является всё -мерное пространство переменных вещественных или комплексных. При линейная функция называется однородной, или линейной формой.
Если все переменные и коэффициенты — вещественные числа, то графиком линейной функции в -мерном пространстве переменных является -мерная гиперплоскость
в частности при — прямая линия на плоскости.
Абстрактная алгебра
Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства над некоторым полем в это поле, то есть для такого отображения , что для любых элементов и любых справедливо равенство
причём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.
Алгебра логики
Булева функция называется линейной, если существуют такие , где , что для любых имеет место равенство:
- .
Нелинейные функции
Для функций, не являющихся линейными (то есть достаточно произвольных), когда хотят подчеркнуть некие свойства, употребляют термин нелинейные функции. Обычно это происходит, когда функциональную зависимость вначале приближают линейной, а потом переходят к изучению более общего случая, часто начиная с младших степеней, например рассматривая квадратичные поправки.
То же относится и к употреблению слова нелинейные в отношении других объектов, не обладающих свойством линейности, например — нелинейные дифференциальные уравнения.
В ряде случаев этот термин может применяться и к зависимостям , где , то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае и . Например, нелинейной зависимостью считают для материала с упрочнением (см. теория пластичности).
См. также
Ссылки
- Справочник по математике для инженеров и учащихся втузов. Бронштейн И. Н., Семендяев К. А.- М.: Наука, 1981.- 720с., ил.