Свойства обратных тригонометрических функций
- Главная
- Справочник
- Тригонометрия
- Свойства обратных тригонометрических функций
Так как геометрически значение обратной тригонометрической функции связано с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку, то названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.
Арксинус
Арксинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \sin \alpha=a,\;|a|\leqslant 1,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Областью определения функции арксинус является отрезок \( [-1;1]. \)
- Областью значений функции арксинус является отрезок \( [-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Арксинус строго возрастающая функция.

- \( \sin \left (\arcsin a \right )=a,\;|a|\leqslant 1. \)
- \( \arcsin\left (\sin \alpha \right )=\alpha,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Арксинус является нечетной функцией: \( \arcsin(-a)=-\arcsin a,\;|a| \leqslant 1. \)
- \( \arcsin a>0,\;a\in(0;1]. \)
- \( \arcsin a=0,\;a=0. \)
- \( \arcsin a<0,\;a\in[-1;0). \)
Арккосинус
Арккосинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \cos \alpha=a,\;|a|\leqslant 1,\;\alpha\in[0;\pi]. \)
- Областью определения функции арккосинус является отрезок \( [-1;1]. \)
- Областью значений функции арккосинус является отрезок \( [0;\pi]. \)
- Арккосинус строго убывающая функция.
- \( \cos \left (\arccos a \right )=a,\;|a|\leqslant 1. \)
- \( \arccos\left (\cos \alpha\right )=\alpha,\;\alpha\in[0;\pi]. \)
- Арккосинус является индифферентной функцией: \( \arccos (-a)=\pi-\arccos a,\;|a|\leqslant 1.
 \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
\) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \) - \( \arccos a>0,\;a\in[-1;1). \)
- \( \arccos a=0,\;a=1. \)
Арктангенс
Арктангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{tg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Областью определения функции арктангенс является вся числовая прямая: \( \mathbb{R}. \)
- Областью значений функции арктангенс является интервал \( \left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Арктангенс строго возрастающая функция.
- \( \text{tg}\left (\text{arctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
- \( \text{arctg}\left (\text{tg}\,\alpha \right ) =\alpha,\;\alpha\in\left ( -\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Арктангенс является нечетной функцией: \( \text{arctg}\left (-a \right ) =-\text{arctg}\,a,\;a\in\mathbb{R}.
 \)
\) - \( \text{arctg}\,a>0,\;a\in(0;\infty ). \)
- \( \text{arctg}\,a=0,\;a=0. \)
- \( \text{arctg}\,a<0,\;a\in(-\infty;0). \)
Арккотангенс
Арккотангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{ctg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (0;\pi \right ). \)
- Областью определения функции арккотангенс является вся числовая прямая: \( \mathbb{R}. \)
- Областью значений функции арккотангенс является интервал \( \left (0;\pi \right ). \)
- Арккотангенс строго убывающая функция.
- \( \text{ctg}\left (\text{arcctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
- \( \text{arcctg}\left (\text{ctg}\,\alpha \right ) =\alpha,\;\alpha\in\left (0;\pi \right ). \)
- Арккотангенс является индифферентной функцией: \( \text{arcctg}\left (-a \right ) =\pi-\text{arcctg}\,a,\;a\in\mathbb{R}. \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ).
 k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)
k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)
или \( \left[\begin{matrix} x&=&\arcsin\,a+2\pi k,&\;k\in\mathbb{Z}\\ x&=&\pi-\arcsin\,a+2\pi l,&\;l\in\mathbb{Z} \end{matrix}\right. \)
\( \cos x=a,\;|a|\leqslant 1\Rightarrow x=\pm\arccos\,a+2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arctg}\,a+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arcctg}\,a+\pi k,\;k\in\mathbb{Z} \)
Частные случаи
\( \cos x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)
\( \sin x=1\Rightarrow x=\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)
\( \cos x=1\Rightarrow x=2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \sin x=-1\Rightarrow x=-\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)
\( \cos x=-1\Rightarrow x=\pi+2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=-1\Rightarrow x=-\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=-1\Rightarrow x=\frac{3\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsboxОбратные тригонометрические функции — Документ
Обратные тригонометрические функции
Определения. Многозначность и главные значения
обратных тригонометрических функций.
Соотношение x = sin y позволяет найти как x по заданному y, так и y по заданному x ( при | x | 1 ). Таким образом, можно рассматривать не только синус как функцию угла, но и угол – как функцию синуса. Этот факт может быть записан как: y = arcsin x ( “arcsin” читается “арксинус” ). Например, вместо 1/2 = sin 30 можно записать: 30arcsin 1/2. При второй форме записи угол обычно представляется в радианах: 6 = arcsin 1/2.
Определения. arcsin x – это угол, синус которого равен x.
 Аналогично определяются функции arccos x, arctan x, arccot x, arcsec x, arccosec x. Эти
функции являются обратными по отношению
к функциям sin x,
cos x, tan x,
cot x, sec x,
cosec x, поэтому
они называются обратными
тригонометрическими функциями. Все
обратные тригонометрические функции
являются многозначными
функциями, то есть каждому
значению аргумента соответствует
бесчисленное множество значений функции.
Так, например, углы 30,
150,
390
510750имеют
один и тот же синус.
Аналогично определяются функции arccos x, arctan x, arccot x, arcsec x, arccosec x. Эти
функции являются обратными по отношению
к функциям sin x,
cos x, tan x,
cot x, sec x,
cosec x, поэтому
они называются обратными
тригонометрическими функциями. Все
обратные тригонометрические функции
являются многозначными
функциями, то есть каждому
значению аргумента соответствует
бесчисленное множество значений функции.
Так, например, углы 30,
150,
390
510750имеют
один и тот же синус.Главное значение arcsin x – это его значение, которое находится между 2 и + 2 ( 90 и + 90 ), включая границы:
– / 2 arcsin x + / 2 .
Главное значение arccos x – это его значение, которое находится между 0 и ( 0 и + 180 ), включая границы:
0 arccos x .

Главное значение arctan x – это его значение, которое находится между 2 и + 2 ( 90 и + 90 ) без границ:
– / 2 < arctan x < + / 2 .
Главное значение arccot x – это его значение, которое находится между 0 и ( 0 и + 180 ) без границ:
0 < arccot x < .
Если обозначить любое из значений обратных тригонометрических функций через Arcsin x, Arccos
где k – любое целое число. При k = 0 мы имеем главные значения.
Таблица «Свойства обратных тригонометрических функций»
Обратные тригонометрические функции.

арксинус
арккосинус
арктангенс
арккотангенс
[-1;1] → [-π/2;π/2]
x → arcsinx
1) D (arcsinx) = [-1;1].
2) E (arcsinx) = [π/2;π/2].
3) arcsinx = 0 при х = 0.
4) arcsinx > 0 при 0 < x ≤ 1.
аrcsinx < 0 при -1 ≤ x < 0.
5) Нечетная, так как
arcsin(-x) = — arcsinx.
6) Непрерывна на всей области определения.
7) Возрастает на всей области определения.
8) yнаиб = π/2 при х = 1.
yнаим = -π/2 при х = -1.
9) Асимптот нет.
[-1;1] → [0;π]
x → arccosx
1) D (arccosx) =[-1;1].
2) E (arccosx) = [0;π].
3) arccosx = 0 при х = 1.
4) arccosx > 0 при -1 ≤ x ≤ 1.
5) Функция общего вида.
6) Непрерывна на всей области определения.
7) Убывает на всей области определения.

8) yнаиб = π при х = -1.
yнаим = 0 при х = 0.
9) Асимптот нет.
R → (-π/2;π/2)
x → arctgx
1) D (arctgx) = R.
2) E (arctgx) = (-π/2;π/2).
3) arctgx = 0 при х = 0.
4) arctgx > 0 при x >0
arctgx < 0 при x < 0.
5) Нечетная, так как arctg(-x)
= -arctgx.
6) Непрерывна на всей области определения.
7) Возрастает на всей области определения.
8) Нет
9) y = π/2.
y = -π/2.
R → (0;π)
x → arcctgx
1) D (arcctgx) = [-1;1].
2) E (arcctgx) = (0;π).
3) arcctgx 0 при любом х R.
4) arcctgx > 0 при любом х R.
5) Функция общего вида.
6) Непрерывна на всей области определения.
7) Убывает на всей области определения.
8) Нет.
9) y=π.
y=0.
Обратные тригонометрические функции _ Онлайн обучение
Обратные тригонометрические функциипросто определяются как функции, обратные основным тригонометрическим функциям, которые являются функциями синуса, косинуса, тангенса, котангенса, секанса и косеканса.
 Их также называют функциями дуги, антитригонометрическими функциями или циклометрическими функциями. Эти обратные функции в тригонометрии используются для получения угла с любым из тригонометрических соотношений. Функции обратной тригонометрии широко применяются в области инженерии, физики, геометрии и навигации.
Их также называют функциями дуги, антитригонометрическими функциями или циклометрическими функциями. Эти обратные функции в тригонометрии используются для получения угла с любым из тригонометрических соотношений. Функции обратной тригонометрии широко применяются в области инженерии, физики, геометрии и навигации.Оглавление:
Что такое обратные тригонометрические функции?
Обратные тригонометрические функции также называют «Функции дуги”Поскольку для данного значения тригонометрических функций они производят длину дуги, необходимую для получения этого конкретного значения. Обратные тригонометрические функции выполняют операции, противоположные тригонометрическим функциям, таким как синус, косинус, тангенс, косеканс, секанс и котангенс. Мы знаем, что тригонометрические функции особенно применимы к прямоугольному треугольнику. Эти шесть важных функций используются для нахождения меры угла в прямоугольном треугольнике, когда известны две стороны этого треугольника.

Формулы
Основные обратные тригонометрические формулы следующие:
Обратные триггерные функции Формулы Арксинус sin (-x) = -sin (x), x ∈ [-1, 1] Арккосин cos (-x) = π -cos (x), x ∈ [-1, 1] Арктангенс tan (-x) = -tan (x), x ∈ R Арккотангенс cot (-x) = π — cot (x), x ∈ R Arcsecant sec (-x) = π -sec (x), | x | ≥ 1 Арккосеканс cosec (-x) = -cosec (x), | x | ≥ 1 Графы обратных тригонометрических функций
В частности, есть шесть обратных тригонометрических функций для каждого тригонометрического соотношения. Обратными к шести важным тригонометрическим функциям являются:
- Арксинус
- Арккосин
- Арктангенс
- Арккотангенс
- Arcsecant
- Арккосеканс
Давайте обсудим все шесть важных типов обратных тригонометрических функций вместе с их определением, формулами, графиками, свойствами и решенными примерами.

Функция арксинуса
Функция арксинуса является обратной функцией синуса, обозначаемой sinИкс. Это представлено на графике, как показано ниже:
Домен -1 ≤ х ≤ 1 Диапазон -π / 2 ≤ y ≤ π / 2 Функция арккосинуса
Функция арккосинуса — это функция, обратная функции косинуса, обозначаемой cosИкс. Это представлено на графике, как показано ниже:
Следовательно, функция, обратная cos, может быть выражена как; у = cosx (арккозин Икс)
Домен и диапазон функции арксинуса:
Домен -1≤x≤1 Диапазон 0 ≤ у ≤ π Функция арктангенса
Функция арктангенса — это обратная функция касательной, обозначенная tanИкс. Это представлено на графике, как показано ниже:
Следовательно, функция, обратная касательной, может быть выражена как; y = tanx (арктангенс Икс)
Домен и диапазон арктангенса:
Домен -∞ <х <∞ Диапазон -π / 2 <у <π / 2 Арккотангенс (Арккот) Функция
Функция арккотангенса является обратной функцией котангенса и обозначается cot.
 Икс. Это представлено на графике, как показано ниже:
Икс. Это представлено на графике, как показано ниже:Следовательно, функция, обратная котангенсу, может быть выражена как; y = cotx (арккотангенс Икс)
Область и диапазон аркотангенса:
Домен -∞ <х <∞ Диапазон 0 <у <π Функция Arcsecant
Что такое функция arcsecant (arcsec)? Функция Arcsecant является обратной функцией секущей, обозначенной сек.Икс. Это представлено на графике, как показано ниже:
Следовательно, функция, обратная секущей, может быть выражена как; y = secx (арксеканс Икс)
Домен и диапазон Arcsecant:
Домен -∞ ≤ x ≤ -1 или 1 ≤ x ≤ ∞ Диапазон 0 ≤ y ≤ π, y ≠ π / 2 Функция Arccosecant
Что такое арккосеканс (arccsc Икс) функция? Функция арккосеканса является обратной функцией косеканса, обозначаемой cosecИкс.
 Это представлено на графике, как показано ниже:
Это представлено на графике, как показано ниже:Следовательно, функция, обратная косекансу, может быть выражена как; y = cosecx (арккосеканс Икс)
Область и диапазон арккосеканса:
Домен -∞ ≤ x ≤ -1 или 1 ≤ x ≤ ∞ Диапазон -π / 2 ≤ y ≤ π / 2, y ≠ 0 Таблица обратных тригонометрических функций
Давайте перепишем здесь все обратные тригонометрические функции с их обозначениями, определением, областью определения и диапазоном.
Название функции Обозначение Определение Домен x Диапазон Арксинус или обратный синус у = грех(Икс) х = грех у -1 ≤ х ≤ 1 - — π / 2 ≤ y ≤ π / 2
- -90°≤ у ≤ 90°
Арккосинус или обратный косинус y = cos(Икс) х = соз у -1 ≤ х ≤ 1 - 0 ≤ у ≤ π
- 0 ° ≤ y ≤ 180 °
Арктангенс или Обратная касательная
y = загар(Икс) х = загар у Для всех реальных чисел - — π / 2 <y <π / 2
- -90°<у <90°
Арккотангенс или Обратная кроватка
y = детская кроватка(Икс) x = детская кроватка y Для всех реальных чисел - 0 <у <π
- 0 ° <у <180 °
Arcsecant или Обратный секанс
y = сек(Икс) х = сек у x ≤ −1 или 1 ≤ x - 0≤y <π / 2 или π / 2 <y≤π
- 0 ° ≤y <90 ° или 90 ° <y≤180 °
Арккосеканс y = csc(Икс) x = csc y x ≤ −1 или 1 ≤ x - −π / 2≤y <0 или 0 <y≤π / 2
- −90 ° ≤y <0 ° или 0 ° <y≤90 °
Производные обратных тригонометрических функций
Производные обратных тригонометрических функций являются производными первого порядка.
 Давайте проверим здесь производные всех шести обратных функций.
Давайте проверим здесь производные всех шести обратных функций.Функция обратного запуска dy / dx у = грех(Икс) 1 / √ (1-х) y = cos(Икс) -1 / √ (1-х) y = загар(Икс) 1 / (1 + х) y = детская кроватка(Икс) -1 / (1 + х) y = сек(Икс) 1 / [| x | √ (x-1)] y = csc(Икс) -1 / [| х | √ (х-1)] Узнайте подробно о выводе этих функций здесь: Производные обратные тригонометрические функции
Читайте также:
Свойства обратных тригонометрических функций
Обратные тригонометрические функции также известны как функции дуги. Обратные тригонометрические функции определены в определенном интервале (в ограниченных областях). Подробнее об обратных тригонометрических свойствах читайте здесь.
Основы тригонометрии
Основы тригонометрии включают базовую тригонометрию и тригонометрические соотношения, такие как sin x, cos x, tan x, cosec x, sec x и cot x.
 {- 1} x} \ \ x = \ frac {1} {5}
{- 1} x} \ \ x = \ frac {1} {5}Проблемы с практикой
Проблема 1: Решить: загар (arcsin 12/13)
Проблема 2: Найдите значение x, cos (arccos 1) = cos x
Узнайте больше об обратных тригонометрических функциях с BYJU’S. Загрузите приложение BYJU’S — Learning для других статей, связанных с математикой, и получите доступ к различным интерактивным видео, которые упрощают математику.
Тригонометрические функции sin arcsin x2. Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α.
 Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности.
 Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).

- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис.
 1 – 1, рис. 2 – 4.
1 – 1, рис. 2 – 4.Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой.
 Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.
Определение обратных тригонометрических функций
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны.
 Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn (где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.
Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn (где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Арксинус (y = arcsin x ) — это функция, обратная к синусу (x = sin y
Арккосинус (y = arccos x ) — это функция, обратная к косинусу (x = cos y ), имеющая область определения и множество значений .
Арктангенс (y = arctg x ) — это функция, обратная к тангенсу (x = tg y ), имеющая область определения и множество значений .

Арккотангенс (y = arcctg x ) — это функция, обратная к котангенсу (x = ctg y ), имеющая область определения и множество значений .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус , Тангенс, котангенс .
y = arcsin x
y = arccos x
y = arctg x
y = arcctg xОсновные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = xarctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = xФормулы, связывающие обратные тригонометрические функции
Формулы суммы и разности
при илипри и
при и
при илипри и
при и
припри
припри
Урок и презентация на темы: «Арксинус.
 Таблица арксинусов. Формула y=arcsin(x)»
Таблица арксинусов. Формула y=arcsin(x)»Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Программная среда «1С: Математический конструктор 6.1»
Решаем задачи по геометрии. Интерактивные задания на построение в пространствеЧто будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.6. Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения.
 Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos.
 Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πkПерепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).
Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.

С учётом этого, запишем общую формула решения для уравнения sin(x)=a:Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.4. Решить уравнение: sin(x) = -√2/2.
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.7. Решить неравенство sin(x) Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках.
 Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.
 ) Прямо здесь и сейчас вы в этом убедитесь.
) Прямо здесь и сейчас вы в этом убедитесь.Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4Как пишется, так и слышится.
 ) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.
 ) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов .
 Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1.
 Это будет 2.) Что и является правильным ответом.
Это будет 2.) Что и является правильным ответом.Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.

С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов.

Основные формулы
Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций. Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых. Свойства обратных функций можно разбить на две группы.
В первую группу входят формулы, справедливые на всей области определения обратных функций:
sin(arcsin x) = x
cos(arccos x) = x
tg(arctg x) = x (-∞ ctg(arcctg x) = x (-∞Во вторую группу входят формулы, справедливые только на множестве значений обратных функций.

arcsin(sin x) = x при
arccos(cos x) = x при
arctg(tg x) = x при
arcctg(ctg x) = x приЕсли переменная x не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n — целое):
sin x = sin(- x-π) ; sin x = sin(π-x) ; sin x = sin(x+2 πn) ;
cos x = cos(-x) ; cos x = cos(2 π-x) ; cos x = cos(x+2 πn) ;
tg x = tg(x+πn) ; ctg x = ctg(x+πn)Например, если известно, что то
arcsin(sin x) = arcsin(sin( π — x )) = π — x .Легко убедиться, что при π — x попадает в нужный интервал. Для этого умножим на -1 : и прибавим π : или Все правильно.
Обратные функции отрицательного аргумента
Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.
arcsin(- x) = arcsin(-sin arcsin x) = arcsin(sin(-arcsin x)) = — arcsin x
Поскольку то умножив на -1 , имеем: или
Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.
Поэтому формула верна.Аналогично для остальных функций.
arccos(- x) = arccos(-cos arccos x) = arccos(cos(π-arccos x)) = π — arccos xarctg(- x) = arctg(-tg arctg x) = arctg(tg(-arctg x)) = — arctg x
arcctg(- x) = arcctg(-ctg arcctg x) = arcctg(ctg(π-arcctg x)) = π — arcctg x
Выражение арксинуса через арккосинус и арктангенса через арккотангенс
Выразим арксинус через арккосинус.
Формула справедлива при Эти неравенства выполняются, поскольку
Чтобы убедиться в этом, умножим неравенства на -1 : и прибавим π/2 : или Все правильно.
Аналогично выражаем арктангенс через арккотангенс.
Выражение арксинуса через арктангенс, арккосинуса через арккотангенс и наоборот
Поступаем аналогичным способом.
Формулы суммы и разности
Аналогичным способом, получим формулу суммы арксинусов.
Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin x , Y = arcsin y .
 Формула применима при
Формула применима при
. Далее замечаем, что, поскольку arcsin(- x) = — arcsin x, arcsin(- y) = — arcsin y, то при разных знаках у x и y , X и Y также разного знака и поэтому неравенства выполняются. Условие различных знаков у x и y можно написать одним неравенством: . То есть при формула справедлива.Теперь рассмотрим случай x > 0 и y > 0 , или X > 0 и Y > 0 . Тогда условие применимости формулы заключается в выполнении неравенства: . Поскольку косинус монотонно убывает при значениях аргумента в интервале от 0 , до π , то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение:
;
;
;
.
Поскольку и ; то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:
;
.
Подставляем sin X = sin arcsin x = x :
;
;
;
.Итак, полученная формула справедлива при или .
Теперь рассмотрим случай x > 0, y > 0 и x 2 + y 2 > 1 .
 Здесь аргумент синуса принимает значения: .
Его нужно привести к интервалу области значения арксинуса :
Здесь аргумент синуса принимает значения: .
Его нужно привести к интервалу области значения арксинуса :Итак,
при и.
Заменив x и y на — x и — y , имеем
при и.
Выполняем преобразования:при и.
Илипри и.
Итак, мы получили следующие выражения для суммы арксинусов:
при или ;
при и ;
при и .
Математические и тригонометрические функции (справочник)
ABS
Возвращает модуль (абсолютную величину) числа.
ACOS
Возвращает арккосинус числа.
ACOSH
Возвращает гиперболический арккосинус числа.

ACOT
Возвращает арккотангенс числа.
ACOTH
Возвращает гиперболический арккотангенс числа.
АГРЕГАТ
Возвращает агрегат для списка или базы данных.
АРАБСКОЕ
Преобразует римские числа в арабские в виде числа.

ASIN
Возвращает арксинус числа.
ASINH
Возвращает гиперболический арксинус числа.
ATAN
Возвращает арктангенс числа.
ATAN2
Возвращает арктангенс для заданных координат x и y.

ATANH
Возвращает гиперболический арктангенс числа.
ОСНОВАНИЕ
Преобразует число в текстовое представление с данным основанием (базой).
ОКРВВЕРХ
Округляет число до ближайшего целого или кратного.
ОКРВВЕРХ.МАТ
Округляет число в большую сторону до ближайшего целого или кратного.

ОКРВВЕРХ.ТОЧН
Округляет число до ближайшего целого или кратного. Число округляется до большего значения вне зависимости от его знака.
ЧИСЛКОМБ
Возвращает количество комбинаций для заданного числа объектов.
ЧИСЛКОМБА
Возвращает количество комбинаций с повторами для заданного числа элементов.
COS
Возвращает косинус числа.

COSH
Возвращает гиперболический косинус числа.
COT
Возвращает котангенс угла.
COTH
Возвращает гиперболический котангенс числа.
CSC
Возвращает косеканс угла.

CSCH
Возвращает гиперболический косеканс угла.
ДЕС
Преобразует текстовое представление числа в заданном основании в десятичное число.
ГРАДУСЫ
Преобразует радианы в градусы.
ЧЁТН
Округляет число до ближайшего четного целого.

EXP
Возвращает число e, возведенное в указанную степень.
ФАКТР
Возвращает факториал числа.
ДВФАКТР
Возвращает двойной факториал числа.
ОКРВНИЗ
Округляет число до ближайшего меньшего по модулю значения.

ОКРВНИЗ.МАТ
Округляет число в меньшую сторону до ближайшего целого или кратного.
ОКРВНИЗ.ТОЧН
Округляет число в меньшую сторону до ближайшего целого или кратного. Число округляется в меньшую сторону независимо от знака.
НОД
Возвращает наибольший общий делитель.
ЦЕЛОЕ
Округляет число до ближайшего меньшего целого.

ISO.ОКРВВЕРХ
Округляет число в большую сторону до ближайшего целого или кратного.
НОК
Возвращает наименьшее общее кратное.
LN
Возвращает натуральный логарифм числа.
LOG
Возвращает логарифм числа по заданному основанию.

LOG10
Возвращает десятичный логарифм числа.
МОПРЕД
Возвращает определитель матрицы массива.
МОБР
Возвращает обратную матрицу массива.
МУМНОЖ
Возвращает матричное произведение двух массивов.

ОСТАТ
Возвращает остаток от деления.
ОКРУГЛТ
Возвращает число, округленное с требуемой точностью.
МУЛЬТИНОМ
Возвращает мультиномиальный коэффициент множества чисел.
МЕДИН
Возвращает матрицу единицы или заданный размер.

НЕЧЁТ
Округляет число до ближайшего нечетного целого.
ПИ
Возвращает число пи.
СТЕПЕНЬ
Возвращает результат возведения числа в степень.
ПРОИЗВЕД
Возвращает произведение аргументов.

ЧАСТНОЕ
Возвращает целую часть частного при делении.
РАДИАНЫ
Преобразует градусы в радианы.
СЛЧИС
Возвращает случайное число в интервале от 0 до 1.
Функция СЛУЧМАССИВ
Возвращает массив случайных чисел в интервале от 0 до 1.
 Но вы можете указать количество заполняемых строк и столбцов, минимальное и максимальное значения, а также какие значения необходимо возвращать: целые или десятичные.
Но вы можете указать количество заполняемых строк и столбцов, минимальное и максимальное значения, а также какие значения необходимо возвращать: целые или десятичные.Функция СЛУЧМЕЖДУ
Возвращает случайное число в интервале между двумя заданными числами.
РИМСКОЕ
Преобразует арабские числа в римские в виде текста.
ОКРУГЛ
Округляет число до указанного количества десятичных разрядов.

ОКРУГЛВНИЗ
Округляет число до ближайшего меньшего по модулю значения.
ОКРУГЛВВЕРХ
Округляет число до ближайшего большего по модулю значения.
SEC
Возвращает секанс угла.
SECH
Возвращает гиперболический секанс угла.

РЯД.СУММ
Возвращает сумму степенного ряда, вычисленную по формуле.
ЗНАК
Возвращает знак числа.
SIN
Возвращает синус заданного угла.
SINH
Возвращает гиперболический синус числа.

КОРЕНЬ
Возвращает положительное значение квадратного корня.
КОРЕНЬПИ
Возвращает квадратный корень из значения выражения (число * пи).
ПРОМЕЖУТОЧНЫЕ.ИТОГИ
Возвращает промежуточный итог в списке или базе данных.
СУММ
Суммирует аргументы.

СУММЕСЛИ
Суммирует ячейки, удовлетворяющие заданному условию.
СУММЕСЛИМН
Суммирует ячейки в диапазоне, удовлетворяющие нескольким условиям.
СУММПРОИЗВ
Возвращает сумму произведений соответствующих элементов массивов.
СУММКВ
Возвращает сумму квадратов аргументов.

СУММРАЗНКВ
Возвращает сумму разностей квадратов соответствующих значений в двух массивах.
СУММСУММКВ
Возвращает сумму сумм квадратов соответствующих элементов двух массивов.
СУММКВРАЗН
Возвращает сумму квадратов разностей соответствующих значений в двух массивах.
TAN
Возвращает тангенс числа.

TANH
Возвращает гиперболический тангенс числа.
ОТБР
Отбрасывает дробную часть числа.
7. Обратные тригонометрические функции
М. Борна
В разделе Тригонометрические функции любого угла мы решали вопросы типа
«Найдите 2 угла, косинус которых равен 0,7.»
Этот вопрос связан с использованием кнопки cos -1 на наших калькуляторах. Мы нашли cos -1 0,7, а затем рассмотрели квадранты, в которых косинус был положительным. Помните, что число, которое мы получаем при нахождении функции арккосинуса, cos -1 , представляет собой угол .
 -1`, когда речь идет о функции арккосинуса.]
-1`, когда речь идет о функции арккосинуса.]Давайте сначала вспомним график `y = cos\ x` (который мы встречали в графе y = a cos x), чтобы мы могли видеть, откуда берется график `y = arccos\ x`.
0,5ππ-0,5π0,511,522,5-0,5-1xyГрафик y = cos x .
Теперь мы выбираем часть этого графика от x = 0 до x = π , показанную здесь заштрихованной частью:
0,5ππ-0,5π0,511,522,53-0,5-1xyГрафик y = cos x с заштрихованной частью `0
График обратного косинуса x находится путем отражения выбранной части графика `cos x` через прямую `y = x`.
0,5ππ-0,5π0,511,522,53-0,5-1xyy = xГрафик y = cos x и линия `y=x`.
Теперь мы отразим каждую точку на этой части кривой `cos x` через линию y = x (я показал лишь несколько типичных отраженных точек.)
0,5ππ-0,5π123-1xy(π,−1)(−1,π)0,5πОтражение точек на кривой через прямую `y=x`.

Результатом является график `y = arccos x`:
См. анимацию этого процесса здесь: Анимация графика обратной тригонометрической функции.
Это все для графика — он не выходит за рамки того, что вы видите здесь. (Если бы это было так, то для каждого значения x было бы несколько значений и , и тогда у нас больше не было бы функции.) Я указал точки «начало» и «конец», `(-1 , pi)` и `(1,0)` с точками.
ПРИМЕЧАНИЕ 1: Метки осей также были отражены. То есть теперь по оси x идут обычные числа, а по оси y — кратные `0,5pi`.
ПРИМЕЧАНИЕ 2: Вы также можете встретить «arccos» в записи «acos», особенно в компьютерном программировании.
Домен (возможные значения x ) для arccos x равен
-1 ≤ x ≤ 1
Диапазон (из значений и для графика) для arccos x равен
0 ≤ arccos x ≤ π
Функция обратного синуса (арксинус)
Мы определяем функцию обратного синуса как
`y=arcsin\ x` для `-pi/2<=y<=pi/2`
, где y — это угол, синус которого равен x .
 Это означает, что
Это означает, что`х = грех у`
График
y = arcsin xДавайте сначала посмотрим на график y = sin x , а затем получим кривую y = arcsin x .
График y = sin x , с выделенной частью от `-pi/2` до `pi/2`.
Как и раньше, если отразить указанную часть y = sin x (часть между `x=-pi/2` и `x=pi/2`) через линию y = x получаем график y = arcsin x :
Еще раз: что видишь, то и получаешь.График не выходит за указанные границы x и y . Я указал точки «начало» и «конец» точками.
Домен (возможные значения x ) arcsin x равен
-1 ≤ x ≤ 1
Диапазон (из и значений для графика) для arcsin x равен
`-π/2 ≤ arcsin\ x ≤ π/2`
См.
 анимацию этого процесса здесь:
анимацию этого процесса здесь:Анимация графика обратной тригонометрической функции.
Функция арктангенса (arctan)
Напомню, вот график y = tan x , который мы встречали ранее в Графиках tan, cot, sec и csc.
Отразив заштрихованную часть графика (от `x=-pi/2` до `pi/2`) в строке y = x , мы получим график y = arctan x :
График `y=»arctan»\ x`.
На этот раз график выходит за пределы того, что вы видите, как в отрицательном, так и в положительном направлениях x , и он не пересекает пунктирные линии (асимптоты при `y=-pi/2` и `y=pi /2`).
Домен (возможные значения x ) arctan x равен
Все значения x
Диапазон (из значений и для графика) для arctan x равен
`-π/2
Числовые примеры arcsin, arccos и arctan
С помощью калькулятора в радианном режиме получаем следующее:
arcsin 0,6294 = sin -1 (0.
 6294) = 0,6808
6294) = 0,6808arcsin (-0,1568) = sin -1 (-0,1568) = -0,1574
arccos (-0,8026) = cos -1 (-0,8026) = 2,5024
арктангенс (-1,9268) = тангенс -1 (-1,9268) = -1,0921
Обратите внимание, что калькулятор выдаст значения которые находятся в пределах определенного диапазона для каждой функции.
Ответы в каждом случае углов (в радианах).
Функция обратной секущей (угловые секунды)
График y = sec x , который мы встречали ранее в Графиках tan, cot, sec и csc:
График y = arcsec x получается путем отражения заштрихованной части приведенной выше кривой в линии y = x :
:График `y=»arcsec»\ x`.
Кривая определена за пределами участка между −1 и 1. Я указал «начальные» точки `(-1,pi)` и `(1,0)` точками.
Домен `»дуги»сек\х` равен
Все значения x , кроме −1 < x < 1
Диапазон угловых секунд x равен
0 ≤ угловых секунд x ≤ π , `»угловых» секунд\ x ≠ π/2`
Функция обратного косеканса (arccsc)
График y = csc x , который мы встречали ранее в Графиках tan, cot, sec и csc, выглядит так:
Обратите внимание, что нет значений y между −1 и 1.

Теперь для графика y = arccsc x , который мы получаем, отражая заштрихованную часть приведенной выше кривой в линии y = x :
График `y=»arccsc»\x`.
График не определен между -1 и 1, но простирается в отрицательном и положительном x -направлениях оттуда.
Домен arccsc x равен
Все значения x , кроме −1 < x < 1
Диапазон arccsc x равен
`-π/2 ≤ «дуга»csc\ x ≤ π/2,` arccsc x ≠ 0
Функция арккотангенса (arccot)
График y = cot x , который мы встречали ранее в Графиках tan, cot, sec и csc, выглядит следующим образом:
Взяв выделенную часть, как указано выше, и отразив ее в строке y = x , мы получим график y = arccot x :
График `y=»arccot»\x`.

График простирается в отрицательном и положительном направлениях x (он не останавливается на -8 и 8, как показано на графике).
Итак, домен для arccot x :
Все значения x
Диапазон для arccot x равен
0 < arccot x < π
Альтернативный вид
Некоторые учебники по математике (и некоторое уважаемое математическое программное обеспечение, напр.г. Mathematica) рассматривают следующее как область y = кроватка x , которую следует использовать:
Это даст следующее при отражении в строке y = x :
График `y=»arccot»\ x`; альтернативный взгляд.
Опять же, график расширяется в отрицательном и положительном x -направлениях.
Домен arccot x также будет:
Все значения x
В этой версии диапазон для arccot x будет следующим:
`-π/2 arccot x ≠ 0)
См.
. обсуждение этого вопроса по адресу:
обсуждение этого вопроса по адресу:Какой правильный график arccot x?.(-1)(-1)=-pi/4`
`cos(-pi/4)=1/2sqrt(2)`
Математика формул, таблиц и производных
Определение обратных тригонометрических функций
Обратные тригонометрические функции известны как антитригонометрические функции, поскольку они являются обратными тригонометрическим функциям. Они также известны как «функции дуги». Обратные тригонометрические функции выполняют функции, противоположные тригонометрическим функциям. Эти функции полезны для нахождения углов, когда заданы любые две стороны прямоугольного треугольника.Обратные тригонометрические функции пишутся с префиксом «дуга».
Читайте также: Проверьте важные вопросы тригонометрии
Формулы обратных тригонометрических функций
Обратные тригонометрические формулы необходимы для решения вопросов. Вот некоторые основные тригонометрические формулы: x), x ∈ [-1, 1]
- tan-1(-x) = -tan-1(x), x ∈ R
- cot-1(-x) = π – cot-1(x) , x ∈ R
- сек-1(-x) = π -сек-1(x), |x| ≥ 1
- cosec-1(-x) = -cosec-1(x), |x| ≥ 1
- sin -1 x + cos -1 x = π/2, x ∈ [-1,1]
- tan -1 x+ cot -1 x = π/2, x ∈ R
- с -1 x + cosec -1 x = π/2, x ∈ R — [-1,1]
- sin -1 x = cosec -1 1/x, x ∈ R — (-1,1)
- cos -1 x = sec -1 1/x, x ∈ R — (-1,1)
- tan -1 x = cot — 1 1/x, x > 0
- tan -1 x = — π + cot -1 x, x < 0
- sin -1 x + sin -1 y = sin 1 (х.
 √ (1 — у 2 ) + у√(1 — х 2 ))
√ (1 — у 2 ) + у√(1 — х 2 )) - sin -1 x — sin -1 y = sin -1 x .2 (1 — y 2 ) — y√(1 — x 2 ))
- cos -1 x + cos -1 y = cos -1 (xy — 90 90 17 √ х 2 ).√(1 — у 2 ))
- cos -1 x — cos -1 y = cos -1 (xy + √ 1 -1 х 20 (0 1 -1 х 20 (0 1 -1 х 20) ).√(1 — y 2 ))
- тангенс -1 x + тангенс -1 y = тангенс -1 (x + y)/(1 — xy), если xy < 1
- tan -1 x + tan -1 y = tan -1 (x — y)/(1 + xy), если xy > — 1
Графики обратных тригонометрических функций
- 1 -1 x График
sin -1 x является обратной функцией синуса. Это обозначено графом, как показано ниже:
Это обозначено графом, как показано ниже:
- Домен = -1 ≤ x ≤ 1
- Диапазон = -π/≤ π/2 2
- cos -1 (x) График
косинус, обратный -2x 900 Это обозначено на графике, как показано ниже:
cos -1 (x) График- Домен = -1≤ x ≤1
- Диапазон = 0 ≤ y ≤ 9 2 π2 tan -1 (x) График
- Домен = -∞ < x < ∞
- Диапазон = -π/2 < y < π/ 2
- Домен = -∞ ≤ x ≤ -1 или 1 ≤ x ≤ ∞
- Диапазон = -π /2 ≤ y ≤ π/2, y ≠ 0
- сек -1 (x) График
- Домен = -∞ ≤ x ≤ -1 или 1 ≤ x ≤ ∞
- Диапазон 0 ≤ y ≤ π , y ≠ π/2
- кроватка -1 (x) Graph
- Домен = -∞ < x < ∞
- Диапазон = 0 < y < π
- Обратные тригонометрические функции являются обратными по отношению к основным тригонометрическим функциям, таким как sin x, cosx, tanx, cosec x, secx и коткс.
- Обратная тригонометрия используется для нахождения угла прямоугольного треугольника, если известны две стороны.
- Обратные тригонометрические функции также известны как функции дуги, антитригонометрические функции или циклометрические функции.

- Некоторые из основных обратных тригонометрических формул-:
- sin-1(-x) = -sin-1(x), x ∈ [-1, 1]
- cos-1(-x) = π -cos -1(x), x ∈ [-1, 1]
- tan-1(-x) = -tan-1(x), x ∈ R
- cot-1(-x) = π – cot-1 (x), x ∈ R
- сек-1(-x) = π -сек-1(x), |x| ≥ 1
- cosec-1(-x) = -cosec-1(x), |x| ≥ 1
- tan -1 x + tan -1 y = tan -1 (x + y)/(1 — xy), если xy < 1
- tan -1 x + 1 tan 9001 -1 y = tan -1 (x — y)/(1 + xy), если xy > — 1
- Область определения функции представлена по оси x, а диапазон функции представлен по ось Y.
- Производные обратных тригонометрических функций также являются важной частью исчисления. Они используются при решении многих задач.
- длина противоположной стороны угол θ
- разделить на длину гипотенузы
- Угол, который кабель образует с морским дном, составляет 39°
- Длина кабеля 30 м.

- Расстояние вниз 18,88 м.
- Длина кабеля 30 м.
- sin принимает угол и дает нам отношение «противоположное/гипотенуза»
- sin -1 берет отношение «противоположное/гипотенуза» и дает нам угол .
- arcsin(y) совпадает с sin -1 (y)
- atan(θ) то же, что и tan -1 (θ)
- и т.
 д.
д. - Чем-то они похожи, правда?
- Но арксинус и арккосинус не «продолжаются вечно», как синус и косинус…
sin-1x, cos-1x, tan-1x и т. д. обозначают углы или вещественные числа, у которых синус равен x, косинус равен x, а тангенс равен x, при условии, что даны наименьшие численные ответы.Их также называют арксинус х, арккосинус х и т. д.
Если есть два угла, один положительный, а другой отрицательный, имеющие одинаковое числовое значение, то следует взять положительный угол.
Главные значения, домены обратных круговых функций и диапазона функций обратного триггата:
Арксинус
Арккосинус
Арктангенс
Арккотангенс
Arcsecant
Arccosecant
sin-1x ограничен в [-π/2, π/2].

sin-1x — возрастающая функция.
В своей области sin-1x достигает своего максимального значения π/2 при x = 1, а его минимальное значение равно -π/2, которое происходит при x = -1.
cos-1x ограничен в [0, π].
cos-1x — убывающая функция.
В своей области cos-1x достигает своего максимального значения π при x = -1, а его минимальное значение равно 0, что происходит при x = 1. ,где x ∈ R, y ∈ (- \[\frac{π}{2}\], \[\frac{π}{2}\])
Изображение скоро будет загружено
tan-1x ограничен в (-π/2, π/2).

tan-1x — возрастающая функция.
4.Арккотангенс
y = cot-1x, где x ∈ R, y ∈ (0, π)
Изображение скоро будет загружено
cot-1x ограничен (0, π).
кроватка-1x — убывающая функция.
5.Arccosecant
y = cosec-1x, |x| ≥ 1, y ∈ [-π/2, 0) ∪ (0, π/2].
Изображение скоро будет загружено
cosec-1x ограничен в [-π/2, π/2].
cosec-1x — убывающая функция.
В своей области cosec-1x достигает своего максимального значения π/2 при x = 1, а минимальное значение равно -π/2, которое происходит при x = -1.

6. Аркссеканс
y = sec-1x, |x| ≥ 1, y ∈ [0, π/2) ∪ (π/2, π].
Изображение скоро будет загружено
сек-1x ограничено в [0, π]. 1x является возрастающей функцией
В своей области sec-1x достигает своего максимального значения π при x = -1, в то время как его минимальное значение равно 0, которое происходит при x = 1.
Вот список всех обратных трех функций Trig с их обозначением, определение, домен и диапазон обратных тригоносных функций
обратные тригонометрические функции таблицы
170003
9
Arcsine или Inverse Sine
Y = SIN-1 (X)
X = sin y
-1 ≤ x ≤ 1
— π / 2 ≤ y ≤ π / 2
-90 ≤ y ≤ 90 °
Arccosine или обратный Cosine
y = cos-1 (x)
x = cos y
-1 ≤ x ≤ 1
0 ≤ y ≤ π
0 ° ≤ y ≤ 180 °
92 177 Arctengent или обратного тангенса
y = Tan-1 (x)
X = Tan Y
для всех действительных номеров
— π / 2
-90 °
Arccotangent или
Обратная COT
y = COT-1 (x)
x = COT Y
для всех действительных чисел
0
0 °
Arcsecant или
Обратная секунда
y = Sec-1 (x)
x = sec y
x ≤ −1 или 1 ≤ x
0≤y<π/2 или π/2
0°≤y<90° или 90°
Arccosecant
y = Cosec-1 (x)
x = COSEC Y
x ≤ -1 или 1 ≤ x
-π / 2≤y <0 или 0
−90°≤y<0°или 0°
Производные обратных триггерных функций являются производными первого порядка.

tan -1 (x) является обратной функцией Тангенс.Это обозначено графом, как показано ниже:
tan -1 (x) ГрафикЧитайте также: SIN 180 DEALESS Значение и деривация
- 2 -1 -1 (x) (x) График 2
3
COSEC -1 (X) является обратным функция косинуса. Это обозначено графом, как показано ниже:
Это обозначено графом, как показано ниже:
сек -1Это обозначено графом, как показано ниже:
сек -1 (x) Графиккроватка -1 Это обозначается следующим графиком:
кроватка -1 (x) ГрафикТригонометрические функции
Графики помогают понять и сравнить различные функции. Область определения функции показана по оси x графика, а диапазон функции обозначен по оси y графика. Домен и диапазон дают нам основное значение обратной тригонометрической функции. Домен и диапазон различных функций следующие:
Область определения функции показана по оси x графика, а диапазон функции обозначен по оси y графика. Домен и диапазон дают нам основное значение обратной тригонометрической функции. Домен и диапазон различных функций следующие:
| Функция | Домен | Диапазон | |
|---|---|---|---|
| y = sin-1(x) | −1 ≤ x ≤ 1 9088 ≤ y ≤ π/2 | ||
| y=cos-1(x) | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π | |
| y=tan-1(x) | 6 Все действительные числа | − π/2 < y < π/2 | |
| y=cosec-1(x) | x ≤ −1 или 1 ≤ x y = sec-1(x) | x ≤ −1 или 1 ≤ x | 0≤y<π/2 или π/2 |
| y=cot-1(x) | Все действительные числа | 0 < y < π |
Производная обратной тригонометрической функции
Обратные тригонометрические функции являются целыми числами в исчислении.Производные обратных тригонометрических функций используются для решения многих вопросов. Производные этих функций являются производными первого порядка. Производные функций следующие:
Производные этих функций являются производными первого порядка. Производные функций следующие:
| обратная тригонометрическая функция | dy/dx | |
|---|---|---|
| y = sin-1(x) | 1/√(1-x2) | = cos-1(x)-1/√(1-x2) |
| y = tan-1(x) | 1/(1+x2) | |
| y = cot-1(x ) | -1/(1+x2) | |
| y = sec-1(x) | 1/[|x|√(x2-1)] | |
| y = cosec-1(x) | -1/[|x|√(x2-1)] |
Что следует помнить
Примеры вопросов
Вопросы. Докажите, что Tan -1 2/11 + Tan -1 7/24 = Tan -1 -1 1/2 (4 марка)
Докажите, что Tan -1 2/11 + Tan -1 7/24 = Tan -1 -1 1/2 (4 марка)
ANS. Используя формулу tan -1 x + tan -1 y = tan -1 (x + y) / (1 — xy)
Получаем, LHS = tan -1 2/11 + загар -1 7/24
= загар -1 [(2/11 + 7/24) / (1 — (2/11).(7/24)]
= тангенс -1 [((48 + 77) / 264) / ((264 — 14) / 264)]
Упрощая термины,
= тангенс -1 (125 / 250)
= тан -1 (1 / 2)
= RHS
Вопросы. Найдите значение tan (sin -1 3/5 + cot -1 3/2) (5 баллов)
. Ans Здесь основная тригонометрическая функция sinx = y может быть изменена на x = sin -1 y
Пусть sin -1 3/5 = x
⇒ sin x = 3/5
Тогда cos x = √ 1 — sin 2 x
= 4/5
⇒ сек x = 5/4
Следовательно, тангенс x = √ сек 2 x — 1
= √1 ( 2) -5 . …(1)
…(1)
Теперь кроватка -1 3 / 2 = загар -1 2 / 3 ….(2)
Используя уравнение (1) и (2)
загар ( sin -1 3/5 + cot -1 2/3) = tan (tan -1 3/4 + tan -1 2/3)
= tan [tan -1 ( 3/4 + 2/3) / (1 — (3/4).(2/3)]
= тангенс (тангенс -1 17/6)
= 17/6
Вопросы. Найти значения загара -1 √3 — кроватка -1 (- √3) (4 балла)
Ответ. Здесь основная тригонометрическая функция sinx = y может быть изменена на x = sin -1 y
Пусть tan -1 √3 = x
Итак, tan x = √3
= tan π / 3
где π / 3 ∈ (- π/2, π/2)
Итак, tan -1 √3 = π/3
Предположим, что ctg -1 (- √3) = y
Следовательно, кроватка у = (- √3)
= — кроватка (π / 6)
= кроватка (π — π / 6)
= кроватка (5π / 6)
Так как, Диапазон основного значения раскладушка -1 x = (0, π)
Следовательно, раскладушка -1 (- √3) = (5π / 6)
Тогда тангенс -1 √3 — раскладушка -1 (- √3)
= π / 3 — 5π / 6
= — π / 2
Вопрос. Докажите, что 3 sin -1 x = sin -1 (3x — 4x 3 90), [2, 1-18 90], (2, 1-18 90) марки)
Докажите, что 3 sin -1 x = sin -1 (3x — 4x 3 90), [2, 1-18 90], (2, 1-18 90) марки)
Отв. Базовую тригонометрическую функцию Sin θ = y можно заменить на θ = sin -1 y
Пусть x = sin θ
Следовательно, sin -1 (x) = θ
Теперь
RHS = sin -1 (3x — 4×3)
Используя тригонометрическую функцию
sin 3 θ = 3 sin θ — 4 sin 3 θ
= sin -1 3 (3sin θ9) 1 0 0 4s
= sin -1 (sin 3θ)
= 3 θ
= 3 sin -1 x
= LHS
Запрос.Решите: 2 tan -1 (cos x) = tan -1 (2cosec x) (4 балла)
Ответ. Базовую тригонометрическую функцию sin θ = y можно изменить на θ = sin -1 y
Дано, что 2 tan -1 (cos x)
= tan -1 (2 cosec x) .
Поскольку 2 тангенс -1 (x) = тангенс -1 2x/(1 + x 2 )
Следовательно,
⇒ тангенс -1 ) [(1 cos x — cos 2 x)]
= tan -1 (2 cosec x)
⇒ (2 cos x) / (sin 2 x)
= 2/sin x
⇒ 9000s sin x
⇒ tanx = 1
⇒ tan x
= tan π/4
Следовательно,
x = nπ + π/4, где n ∈ Z
Обратный синус, косинус 900, тангенс
Быстрый ответ:
Для прямоугольного треугольника:
функция синуса sin принимает угол θ и дает отношение против гипотенузы
Функция обратного синуса sin -1 принимает отношение против гипотенузы и дает угол θ
Косинус и тангенс следуют той же идее.
Пример (длина только до одного десятичного знака):
sin(35°) = Противоположный / Гипотенуза
= 2,8/4,9
= 0,57. ..
..
sin -1 (Противоположная / гипотенуза) = sin -1 (0,57…)
= 35°
А теперь подробности:
Синус, косинус и тангенс основаны на прямоугольном треугольнике
Очень похожие функции… поэтому мы рассмотрим функцию синуса , а затем обратную синусоиду , чтобы узнать, что это такое.
Синусоидальная функция
Синус угла θ равен:
Или проще:
sin( θ ) = Противоположность / Гипотенуза
Пример: чему равен синус 35°?
Используя этот треугольник (длина только до одного десятичного знака): sin(35°) = противоположность / гипотенуза |
Функция синуса может помочь нам решить такие задачи:
Пример: Используйте синусоидальную функцию
, чтобы найти «d»Мы знаем
И мы хотим знать «d» (расстояние вниз).
Начните с:sin 39° = противоположность/гипотенуза
sin 39° = d/30
Поменять местами стороны:d/30 = sin 39°
Используйте калькулятор, чтобы найти sin 39°: d/30 = 0.6293…
Умножить обе стороны на 30:d = 0,6293… x 30
d = 18,88 до 2 знаков после запятой
Глубина «d» 18,88 м
Функция обратного синуса
Но иногда нам нужно найти угол .
Здесь на помощь приходит «обратный синус».
Отвечает на вопрос «какой угол имеет синус, равный противолежащему/гипотенузе?»
Символ обратного синуса: sin -1 , или иногда arcsin .
Пример: Найдите угол
«а»Мы знаем
И мы хотим знать угол «а»
Начните с:sin a° = противоположность/гипотенуза
sin а° = 18,88/30
Вычислить 18,88/30:sin a° = 0,6293. ..
..
Синус какого угла равен 0.6293…?
Обратный синус расскажет нам.
Обратный синус: a° = sin −1 (0,6293…)
Используйте калькулятор, чтобы найти sin −1 (0,6293…):a° = 39,0° (с точностью до 1 знака после запятой)
Угол «а» равен 39,0°
Они как вперед и назад!
Пример:
Функция синуса: sin( 30° ) = 0,5
Обратный синус:sin −1 ( 0,5 ) = 30°
Калькулятор
На калькуляторе вы нажимаете одну из следующих клавиш (в зависимости от марки вашего калькулятора):
либо «2ndF sin», либо «shift sin». |
Попробуйте использовать на калькуляторе sin, а затем sin -1 , чтобы посмотреть, что получится
Больше, чем один ракурс!
Обратный синус показывает только один угол … но есть и другие углы, которые могли бы сработать.
Пример: Вот два угла, где противолежащие/гипотенуза = 0,5
На самом деле существует бесконечно много углов , потому что вы можете продолжать прибавлять (или вычитать) 360°:
Помните об этом, потому что бывают случаи, когда вам действительно нужен один из других ракурсов!
Резюме
Синус угла θ равен:
sin( θ ) = Противоположность / Гипотенуза
И обратный синус:
sin -1 (Противоположная / Гипотенуза) = θ
Как насчет «cos» и «tan» .
 .. ?
.. ?Точно такая же идея, но разные соотношения сторон.
Косинус
Косинус угла θ равен:
cos( θ ) = Смежный / Гипотенуза
и арккосинус:
cos -1 (прилегающая / гипотенуза) = θ
Пример: Найдите величину угла a°
cos a° = Смежный / Гипотенуза
cos а° = 6750/8100 = 0.8333…
a° = cos -1 (0,8333…) = 33,6° (до 1 знака после запятой)
Касательная
Тангенс угла θ равен:
tan( θ ) = Противоположный / Смежный
Итак, арктангенс:
tan -1 (Противоположный/Смежный) = θ
Пример: Найдите величину угла x°
тангенс x° = напротив/смежно
тангенс x° = 300/400 = 0.75
x° = тангенс -1 (0,75) = 36,9° (с точностью до 1 знака после запятой)
Другие названия
Иногда SIN -1 называется ASIN или Arcsin или Arcsin
аналогично COS -1 называется ACOS или Arccos и Tan -1 называется ATAN или Arctan
Примеры:
Графики
И, наконец, вот графики синуса, арксинуса, косинуса и арккосинуса:
Синус
Обратный синус
Косинус
Обратный косинус
Вы что-нибудь заметили на графиках?
Рассмотрим на примере косинуса.
Вот косинус и арккосинус , нанесенные на один и тот же график:
Косинус и арккосинус
Они зеркальные (по диагонали)
Но почему арккосинус обрезается сверху и снизу (точки на самом деле не являются частью функции) … ?
Поскольку, чтобы быть функцией, она может дать только один ответ
, когда мы спрашиваем «что такое cos -1 (x)?»
Один ответ или бесконечно много ответов
Но мы видели ранее, что существует бесконечно много ответов , и пунктирная линия на графике показывает это.
Так что да там есть бесконечно много ответов…
… но представьте, что вы вводите 0,5 в свой калькулятор, нажимаете cos -1 , и он дает вам бесконечный список возможных ответов …
Итак, у нас есть правило, что функция может дать только один ответ .
Итак, отрубив его таким образом, мы получим только один ответ, но мы должны помнить, что могут быть и другие ответы .
Тангенс и арктангенс
А вот функция тангенса и арктангенса.Вы видите, насколько они зеркальны (о диагонали)…?
Тангенс
Арктангенс
Таблицы тригонометрических функций
Таблицы тригонометрических функций
Калькуляторы и таблицы используются для определения значений тригонометрических функций. Большинство научных калькуляторов имеют функциональные кнопки для нахождения синуса, косинуса и тангенса углов.Величина угла вводится в градусах или радианах, в зависимости от настройки калькулятора. Здесь будет использоваться градусная мера, если специально не указано иное. При решении задач с использованием тригонометрических функций либо известен угол и необходимо найти значение тригонометрической функции, либо известно значение тригонометрической функции и необходимо найти угол. Эти два процесса обратны друг другу. Обратные обозначения используются для выражения угла через значение тригонометрической функции.Выражение sin θ = 0,4295 можно записать как θ = Sin −1 0,4295 или θ = Arcsin0,4295, и оба эти уравнения читаются как «тета равно Arcsin 0,4295». Иногда используется выражение «обратный синус 0,4295». Некоторые калькуляторы имеют кнопку с пометкой «дуга», которая нажимается перед функциональной клавишей, чтобы выразить функции «дуги». Дуговые функции используются для нахождения меры угла, если известно значение тригонометрической функции. Если таблицы используются вместо калькулятора, одна и та же таблица используется для любого процесса.Примечание. Использование калькуляторов или таблиц дает только приблизительные ответы.
Здесь будет использоваться градусная мера, если специально не указано иное. При решении задач с использованием тригонометрических функций либо известен угол и необходимо найти значение тригонометрической функции, либо известно значение тригонометрической функции и необходимо найти угол. Эти два процесса обратны друг другу. Обратные обозначения используются для выражения угла через значение тригонометрической функции.Выражение sin θ = 0,4295 можно записать как θ = Sin −1 0,4295 или θ = Arcsin0,4295, и оба эти уравнения читаются как «тета равно Arcsin 0,4295». Иногда используется выражение «обратный синус 0,4295». Некоторые калькуляторы имеют кнопку с пометкой «дуга», которая нажимается перед функциональной клавишей, чтобы выразить функции «дуги». Дуговые функции используются для нахождения меры угла, если известно значение тригонометрической функции. Если таблицы используются вместо калькулятора, одна и та же таблица используется для любого процесса.Примечание. Использование калькуляторов или таблиц дает только приблизительные ответы. Тем не менее, вместо приблизительного знака (≈ или ≅) иногда используется знак равенства (=).
Тем не менее, вместо приблизительного знака (≈ или ≅) иногда используется знак равенства (=).Пример 1: Чему равен синус 48°?
Пример 2: Косинус какого угла равен 0,3912?
Хотя калькулятор может легко найти тригонометрические функции дробной меры угла, это может быть неверно, если для поиска значений необходимо использовать таблицу.Таблицы не могут перечислить всех углов. Поэтому для нахождения значений между значениями, перечисленными в таблице, необходимо использовать аппроксимацию. Этот метод известен как линейная интерполяция . Сделано предположение, что различия в значениях функций прямо пропорциональны различиям мер углов на малых интервалах . На самом деле это не так, но дает лучший ответ, чем простое использование ближайшего значения в таблице. Этот метод иллюстрируется следующими примерами.
Пример 3 : Используя линейную интерполяцию, найдите тангенс 28,43°, учитывая, что тангенс 28,40° = 0,5407 и тангенс 28,50° = 0,5430.
Установите пропорцию, используя переменную x .
Поскольку x — это разница между тангенсом 28,40° и тангенсом 28,43°,
Пример 4: Найдите первый квадрант угла α, где cos α ≈ 0,2622, учитывая, что cos 74° ≈ 0,275 и стоимость 75° ≈ 0,2588.
Установите пропорцию, используя переменную x .
Следовательно, α ≈ 74,0° + 0,8° ≈ 74,8°
Существует интересный метод аппроксимации для нахождения синуса и тангенса углов, меньших 0,4 радиана (приблизительно 23°). Синус и тангенс углов менее 0,4 радиана примерно равны угловой мере. Например, в радианах sin0,15 ≈ 0,149 и tan 0,15 ≈ 0,151.
Пример 5: Найдите θ на рисунке без использования таблиц тригонометрии или калькулятора, чтобы найти значение какой-либо тригонометрической функции.
Рисунок 1 Поскольку sin θ = 5/23 ≈ 0,21739, размер угла может быть приблизительно равен 0,217 радианам, что примерно равно 12,46°. На самом деле ответ ближе к 0,219 радианам, или 12,56° — довольно близко для приближения. Если для нахождения третьей стороны треугольника используется теорема Пифагора, этот процесс можно использовать и для касательной.
На самом деле ответ ближе к 0,219 радианам, или 12,56° — довольно близко для приближения. Если для нахождения третьей стороны треугольника используется теорема Пифагора, этот процесс можно использовать и для касательной.
Пример 6: Найдите величину острого угла α с точностью до минуты, если tan α = 0,8884.
Использование калькулятора
Калькулятор обратных тригонометрических функций
Использование калькулятора
Этот калькулятор найдет обратные тригонометрические значения для главных значений в диапазонах, указанных в таблице. Вы можете просмотреть диапазоны в Графики обратной тригонометрической функции.
Диапазоны функции обратного запуска
Арксинус
≤Arcsin x или sin -1 x
-1 ≤ х ≤ 1
-π/2 ≤ у ≤
π/2
Арккосинус
Arccos x или cos -1 x
-1 ≤ х ≤ 1
0 ≤ у ≤ π
Арктангенс
Arctan x или tan -1 x
х, все действительные числа
-π/2 < y < π/2
Арккотангенс
Arccot x или детская кроватка -1 x
х, все действительные числа
кроме 0 = π/2
-π/2 < y < π/2
Арксеканс
угловых секунд x или секунд -1 x
х ≤ -1 и х ≥ 1
0 ≤ y < π/2 или
π/2 < у ≤ π
Арккосеканс
Arccsc x или csc -1 x
х ≤ -1 и х ≥ 1
-π/2 ≤ y < 0 или 0 < y ≤
π/2
Производные обратных тригонометрических функций
Введение в обратные тригонометрические функции
В предыдущей теме мы изучили производные шести основных тригонометрических функций:
\[\color{blue}{\sin x,\;} \color{red}{\cos x,\;} \color{darkgreen}{\tan x,\;} \color{magenta}{\cot x,\;} \color{chocolate}{\sec x,\;} \color{maroon}{\csc x.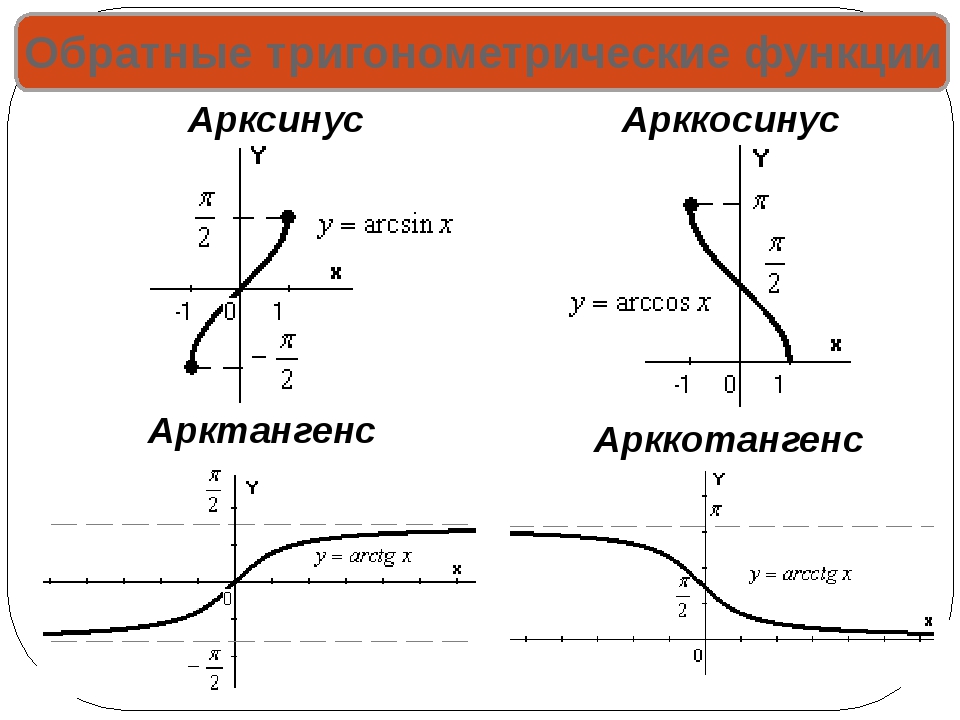 \;}\]
\;}\]
В этом разделе мы рассмотрим производные обратных тригонометрических функций, которые соответственно обозначаются как
.\[\color{blue}{\arcsin x,\;} \color{red}{\arccos x,\;} \color{darkgreen}{\arctan x,\;} \color{magenta}{\text {arccot}x,\;} \color{chocolate}{\text{arcsec}x,\;} \color{maroon}{\text{arccsc}x.\;}\]
Обратные функции существуют, если на область определения исходных функций наложены соответствующие ограничения.
Например, домен для \(\arcsin x\) находится в диапазоне от \(-1\) до \(1.\) Диапазон или вывод для \(\arcsin x\) — это все углы от \( — \frac{\pi }{2}\) до \(\frac{\pi }{2}\) радиан.
Области определения других тригонометрических функций ограничены соответствующим образом, так что они становятся взаимно однозначными функциями и могут быть определены их обратные функции.
Производные обратных тригонометрических функций
Производные обратных тригонометрических функций можно получить с помощью теоремы об обратных функциях. 2}}}}\]
2}}}}\]
Пример 1.4}}}.\]
Дополнительные проблемы см. на стр. 2.
Обратные тригонометрические функции. Введение, графики, производные и примеры
Мы уже знаем об обратных операциях. Как известно, сложение и вычитание — обратные операции, а умножение и деление — обратные операции. Каждая операция имеет противоположность обратной. Точно так же обратные функции основных тригонометрических функций называются обратными тригонометрическими функциями.Его также называют функциями дуги, антитригонометрическими функциями или циклометрическими функциями.
Обратное значение g обозначается как «g -1».
Пусть y = f(y) = sin x, тогда его обратное выражение равно y = sin-1x.
В этой статье давайте изучим обратные тригонометрические функции, такие как синус, косинус, тангенс, котангенс, секанс и косеканс.
Изображение будет загружено в ближайшее время
Введение в функцию обратного триггера
Обратные тригонометрические функции фактически выполняют операции, противоположные тригонометрическим функциям, таким как синус, косинус, тангенс, косеканс, секанс и котангенс. Мы знаем, что триггерные функции особенно применимы к прямоугольному треугольнику. Эти шесть важных функций используются для нахождения меры угла в прямоугольном треугольнике, когда известны две стороны треугольника.
Мы знаем, что триггерные функции особенно применимы к прямоугольному треугольнику. Эти шесть важных функций используются для нахождения меры угла в прямоугольном треугольнике, когда известны две стороны треугольника.
Условный символ для представления обратной тригонометрической функции с использованием префикса дуги, такого как arcsin(x), arccos(x), arctan(x), arccsc(x), arcsec(x), arccot(x).
| 9 | S. | Функция | Домен | Диапазон | |
|---|---|---|---|---|---|
1. | y = sin-1x | -1 ≤ x ≤ 1 | -π / 2 ≤ Y ≤ π / 2 | ||
2. | y = cos-1x | -1 ≤ x ≤ 1 | 0 ≤ Y ≤ π | ||
3. | y = tan-1x | x ∈ R -π | -π | -π | -π 2 |
4 | y = COT-1X | x ∈ R | 0 | ||
5. | y = cosec-1x | x ≤ -1 или x ≥ 1 | -π / 2 ≤ Y ≤ π / 2, Y ≠ 0 | ||
6. | y = sec-1x | x ≤ -1 или x ≥ 1 | 0 ≤ y ≤ π, y ≠ π / 2 |
обратные тригонометрические функции графики
обратные тригонометрические функции для каждого тригонометрического отношения. Обратным шесть важных тригонометрических функций:
Графики всех функций Обратные Круговые
1.Арксинус
y = sin-1x, |x| ≤ 1, y ∈ [-π/2, π/2]
Изображение скоро будет загружено
2.Арккосинус
y = cos-1x, |x| ≤ 1, y ∈ [0, π]
Изображение скоро будет загружено

 \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
\) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \) \)
\) k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)
k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)

 Аналогично определяются функции arccos x, arctan x, arccot x, arcsec x, arccosec x. Эти
функции являются обратными по отношению
к функциям sin x,
cos x, tan x,
cot x, sec x,
cosec x, поэтому
они называются обратными
тригонометрическими функциями. Все
обратные тригонометрические функции
являются многозначными
функциями, то есть каждому
значению аргумента соответствует
бесчисленное множество значений функции.
Так, например, углы 30,
150,
390
510750имеют
один и тот же синус.
Аналогично определяются функции arccos x, arctan x, arccot x, arcsec x, arccosec x. Эти
функции являются обратными по отношению
к функциям sin x,
cos x, tan x,
cot x, sec x,
cosec x, поэтому
они называются обратными
тригонометрическими функциями. Все
обратные тригонометрические функции
являются многозначными
функциями, то есть каждому
значению аргумента соответствует
бесчисленное множество значений функции.
Так, например, углы 30,
150,
390
510750имеют
один и тот же синус.


 Их также называют функциями дуги, антитригонометрическими функциями или циклометрическими функциями. Эти обратные функции в тригонометрии используются для получения угла с любым из тригонометрических соотношений. Функции обратной тригонометрии широко применяются в области инженерии, физики, геометрии и навигации.
Их также называют функциями дуги, антитригонометрическими функциями или циклометрическими функциями. Эти обратные функции в тригонометрии используются для получения угла с любым из тригонометрических соотношений. Функции обратной тригонометрии широко применяются в области инженерии, физики, геометрии и навигации.

 Икс. Это представлено на графике, как показано ниже:
Икс. Это представлено на графике, как показано ниже: Это представлено на графике, как показано ниже:
Это представлено на графике, как показано ниже: Давайте проверим здесь производные всех шести обратных функций.
Давайте проверим здесь производные всех шести обратных функций. {- 1} x} \ \ x = \ frac {1} {5}
{- 1} x} \ \ x = \ frac {1} {5} Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
 1 – 1, рис. 2 – 4.
1 – 1, рис. 2 – 4. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания. Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn (где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.
Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn (где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.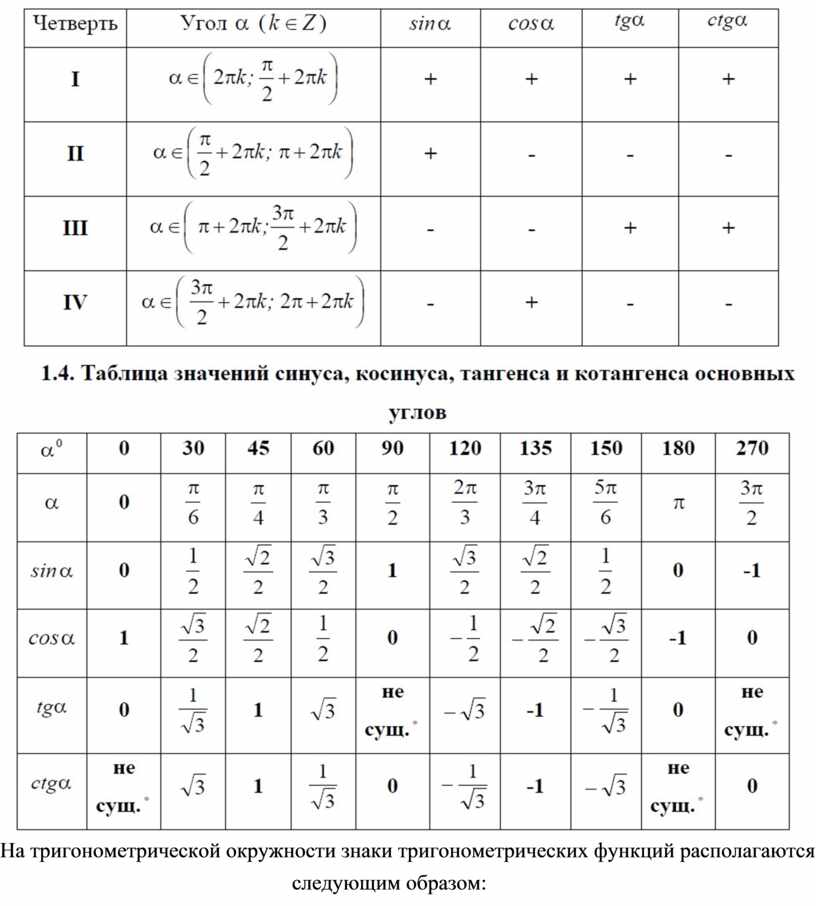
 Таблица арксинусов. Формула y=arcsin(x)»
Таблица арксинусов. Формула y=arcsin(x)» Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,  Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.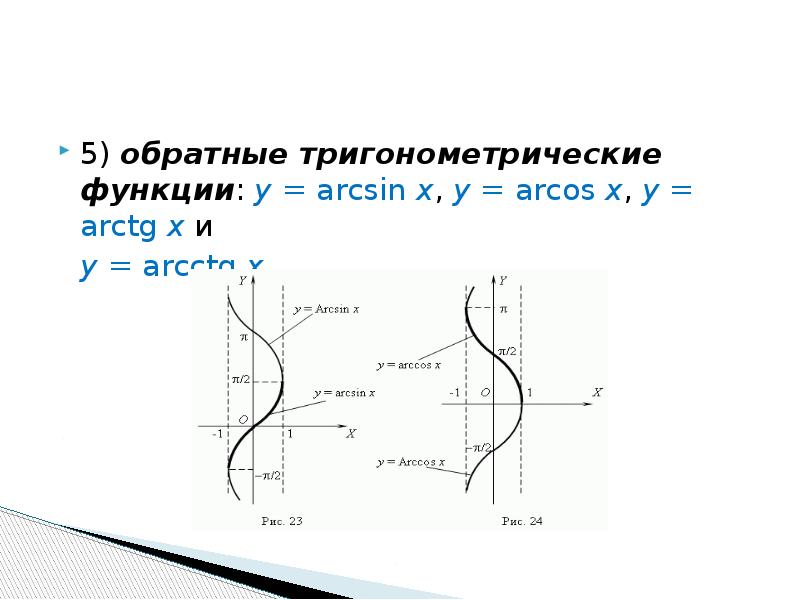
 По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk  ) Прямо здесь и сейчас вы в этом убедитесь.
) Прямо здесь и сейчас вы в этом убедитесь. ) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции. ) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.) Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать: Это будет 2.) Что и является правильным ответом.
Это будет 2.) Что и является правильным ответом.


 Поэтому формула верна.
Поэтому формула верна. Формула применима при
Формула применима при Здесь аргумент синуса принимает значения: .
Его нужно привести к интервалу области значения арксинуса :
Здесь аргумент синуса принимает значения: .
Его нужно привести к интервалу области значения арксинуса :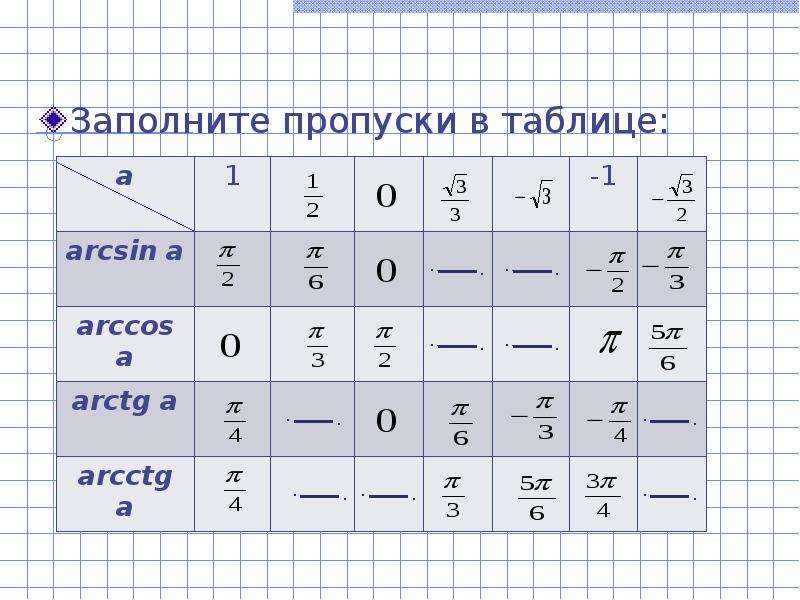

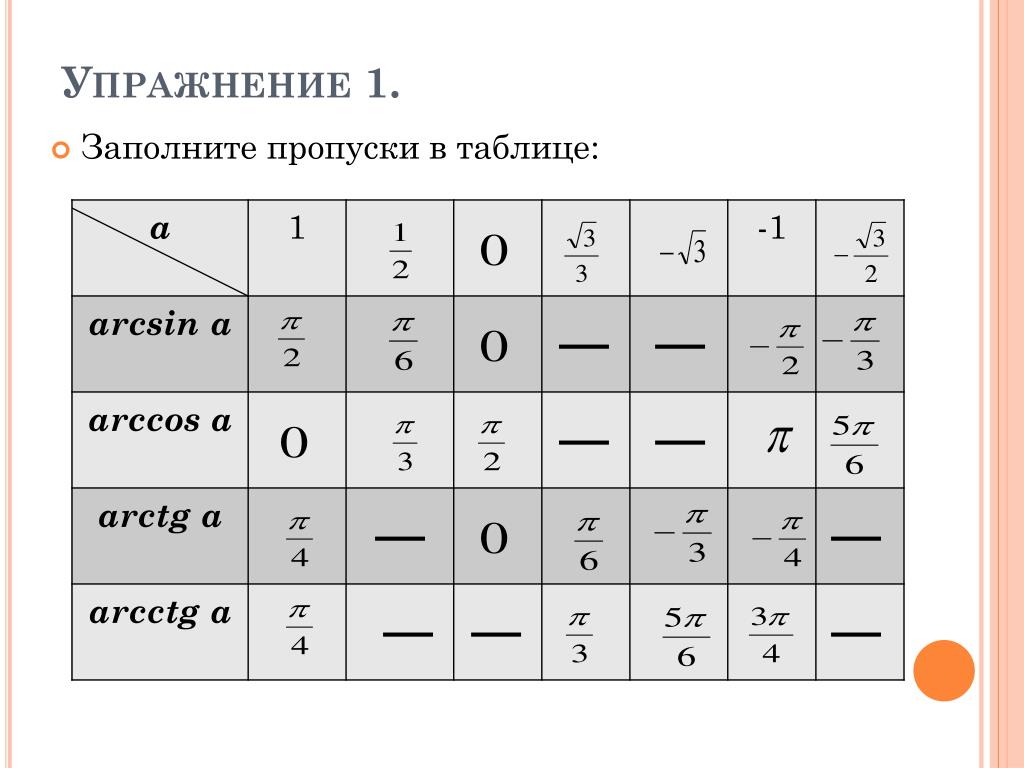










 Но вы можете указать количество заполняемых строк и столбцов, минимальное и максимальное значения, а также какие значения необходимо возвращать: целые или десятичные.
Но вы можете указать количество заполняемых строк и столбцов, минимальное и максимальное значения, а также какие значения необходимо возвращать: целые или десятичные.



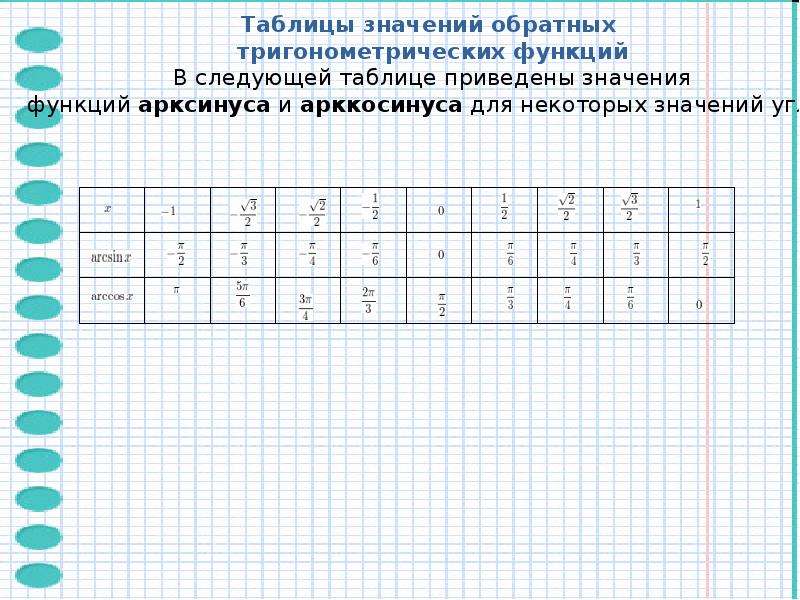
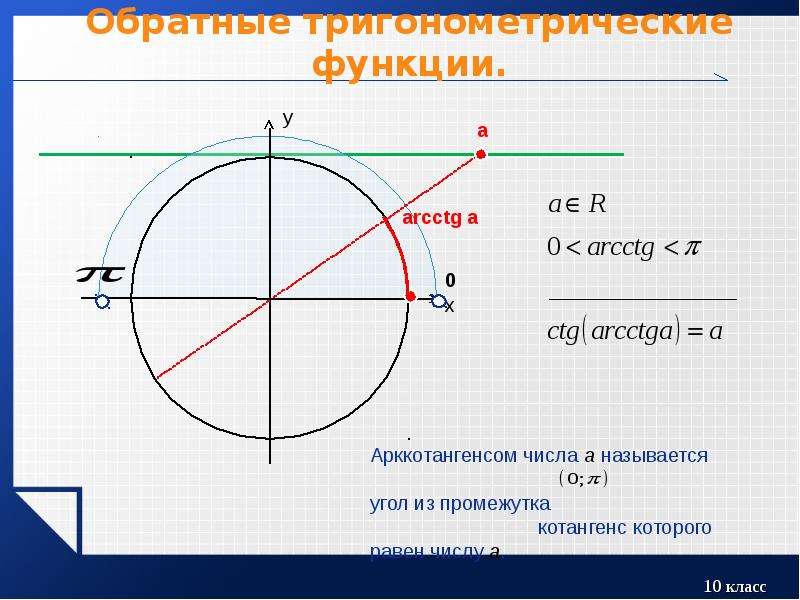
 -1`, когда речь идет о функции арккосинуса.]
-1`, когда речь идет о функции арккосинуса.]
 Это означает, что
Это означает, что анимацию этого процесса здесь:
анимацию этого процесса здесь: 6294) = 0,6808
6294) = 0,6808

 обсуждение этого вопроса по адресу:
обсуждение этого вопроса по адресу: √ (1 — у 2 ) + у√(1 — х 2 ))
√ (1 — у 2 ) + у√(1 — х 2 ))

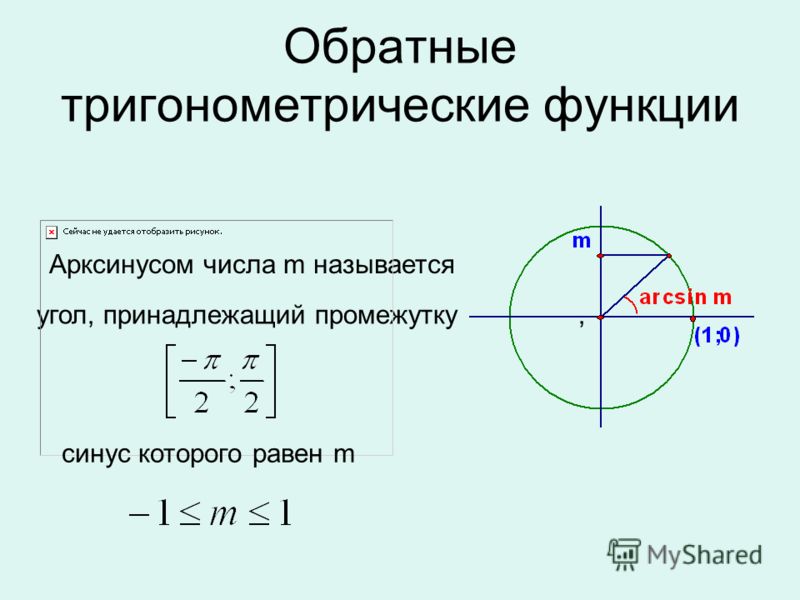 д.
д. №
№