ln 0 5
Вы искали ln 0 5? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и ln калькулятор, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «ln 0 5».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как ln 0 5,ln калькулятор,ln калькулятор онлайн,ln онлайн,ln онлайн калькулятор,вычисление логарифма натурального онлайн,вычисление натурального логарифма онлайн,вычислить логарифм натуральный,вычислить логарифм натуральный онлайн,вычислить логарифм натуральный онлайн калькулятор,вычислить натуральный логарифм онлайн,вычислить натуральный логарифм онлайн калькулятор,как посчитать логарифм натуральный,как считать логарифм натуральный,калькулятор ln,калькулятор ln онлайн,калькулятор логарифма натурального,калькулятор логарифмов натуральных,калькулятор натурального логарифма,калькулятор натуральный логарифм,калькулятор натуральных логарифмов,калькулятор натуральных логарифмов онлайн,калькулятор онлайн натуральные логарифмы,логарифм ln онлайн калькулятор,логарифм натуральный онлайн,логарифм натуральный онлайн калькулятор,логарифм онлайн калькулятор ln,найти логарифм натуральный онлайн,найти натуральный логарифм онлайн,натуральные логарифмы калькулятор онлайн,натуральные логарифмы онлайн калькулятор,натуральный логарифм вычислить онлайн,натуральный логарифм калькулятор,натуральный логарифм калькулятор онлайн,натуральный логарифм найти онлайн,натуральный логарифм онлайн,натуральный логарифм онлайн калькулятор,натуральный логарифм посчитать,натуральный логарифм посчитать онлайн,онлайн ln,онлайн вычисление натурального логарифма,онлайн калькулятор ln,онлайн калькулятор натуральный логарифм,онлайн калькулятор натуральных логарифмов,посчитать логарифм натуральный,посчитать натуральный логарифм,посчитать натуральный логарифм онлайн,расчет логарифма натурального онлайн,расчет натурального логарифма онлайн,решение логарифмов натуральных онлайн,решение натуральных логарифмов онлайн,решение онлайн натуральных логарифмов.
Где можно решить любую задачу по математике, а так же ln 0 5 Онлайн?
Решить задачу ln 0 5 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Добро пожаловать в калькулятор логарифмов онлайн. Для чего нужен этот калькулятор. Ну, в первую очередь для того, что бы свериться со своими письменными или умственными расчетами. С логарифмами (в российских школах) столкнуться можно уже в 10-том классе. И эта тема считается достаточно сложной. Решение логарифмов, особенно с большими или дробными числами, знаете ли, дело не легкое. Уж лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте основание с числом. Калькулятор логарифмов чем то, схож с калькулятором факториалов, который автоматически выдает несколько решений.  Далее калькулятор логарифмов логарифмирует заданное выражение и выводит на ваши экраны такой результат. Далее калькулятор логарифмов логарифмирует заданное выражение и выводит на ваши экраны такой результат.Калькулятор логарифмов (вещественных) – этот калькулятор находит логарифм по заданному основанию онлайн.
Понятие вещественного логарифма: Существует множество разных определений логарифма. Сперва, неплохо было бы узнать, что логарифм — это некая алгебраическая запись, обозначенная как log a b, где а – основание, b – число. А читается эта запись так: Логарифм по основанию a числа b. Иногда используется обозначение log b . А теперь собственно, определение самого логарифма: Логарифмом положительного числа b по основанию a (где a>0, a≠1)называется степень, в которую нужно возвести число а, чтобы получить число b. Кстати, не только основание должно быть в положительной форме. Число(аргумент), так же должно быть положительным. В противном случае калькулятор логарифмов включит неприятную тревогу. Логарифмирование – это операция нахождения логарифма, по заданному основанию. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните:
А операция обратная логарифмированию это – Потенцирование. |
Как найти натуральный логарифм
Термин «логарифм» произошел от двух греческих слов, одно из которых обозначает «число», а другое — «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую надо возвести постоянное значение (основание), чтобы получить число, указанное под знаком логарифма. Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».Вам понадобится
Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую надо возвести постоянное значение (основание), чтобы получить число, указанное под знаком логарифма. Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».Вам понадобитсяВоспользуйтесь во множестве представленными в интернете онлайн-калькуляторами — это, пожалуй, самый быстрый и простой способ вычисления натурального а. Поиском соответствующего сервиса вам заниматься не придется, так как многие поисковые системы и сами имеют встроенные калькуляторы, вполне пригодные для работы с логарифмами. Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления логарифма числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил правильный ответ с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.
Используйте соответствующую встроенную функцию, если необходимость вычисления значения натурального логарифма возникает при работе с данными в популярном табличном редакторе Microsoft Office Excel. Эта функция здесь вызывается с использованием общепринятого обозначения такого логарифма в верхнем регистре — LN. Выделите ячейку, в которой должен быть отображен результат вычисления, и введите знак равенства — так в этом табличном редакторе должны начинаться записи в ячейках, содержащих формулы. Затем наберите название функции (LN) и в скобках укажите числовое значение, логарифм которого требуется вычислить — например, =LN(457). После того, как вы нажмете Enter, в этой ячейке таблицы отобразится результат вычисления натурального логарифма.
Откройте программу-калькулятор, которая устанавливается вместе с операционной системой, если оба приведенных выше способа вам не подходят. Найти соответствующую ссылку в ОС Windows 7 можно, если раскрыть главное меню щелчком по кнопке «Пуск», а затем ввести «каль» в поле «Найти программы и файлы». Ссылка с названием «Калькулятор» будет первой строкой в результате поиска. В других версиях ОС ее надо искать в подразделе «Стандартные» раздела «Все программы» главного меню. Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.
Ссылка с названием «Калькулятор» будет первой строкой в результате поиска. В других версиях ОС ее надо искать в подразделе «Стандартные» раздела «Все программы» главного меню. Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.
Элементарные функции
Пользователи также искали:
антилогарифм, логарифмов, логарифма, логарифм, обратный, Антилогарифм, excel, степенями, антилогарифм таблица, обратный натуральный логарифм, как найти основание логарифма, обратное логарифмирование, обратный логарифм в excel, калькулятор логарифмов со степенями, таблица, антилогарифм примеры, натуральный, найти, основание, обратное, логарифмирование, калькулятор, примеры, антилогарифм в excel, гауссова функция, гаусса, функция, гауссова, онлайн, Гауссова,
Свойства логарифмов и примеры их решений (ЕГЭ — 2021)
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться \( 1\). {\frac{1}{2}}}=\sqrt{4}=2\)), а вот \( \displaystyle {{\log }_{-4}}2\) не существует.
{\frac{1}{2}}}=\sqrt{4}=2\)), а вот \( \displaystyle {{\log }_{-4}}2\) не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное.
Значит, аргумент должен быть положительным.
Например, \( \displaystyle {{\log }_{2}}\left( -4 \right)\) не существует, так как \( 2\) ни в какой степени не будет отрицательным числом (и даже нулем, поэтому \( \displaystyle {{\log }_{2}}0\) тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ.
Приведу пример:
Решим уравнение \( \displaystyle {{\log }_{x}}\left( x+2 \right)=2\).
Вспомним определение: логарифм \( \displaystyle {{\log }_{x}}\left( x+2 \right)\) – это степень, в которую надо возвести основание \( x\), чтобы получить аргумент \( \displaystyle \left( x+2 \right)\).
И по условию, эта степень равна \( 2\): \( \displaystyle {{x}^{2}}=x+2\). {2}}-x-2=0\).
{2}}-x-2=0\).
Решим его с помощью теоремы Виета: сумма корней равна \( 1\), а произведение \( -2\). Легко подобрать, это числа \( 2\) и \( -1\).
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу на ЕГЭ.
Почему?
Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
\( \displaystyle x=2\text{: }{{\log }_{2}}\left( 2+2 \right)={{\log }_{2}}4=2\) – верно.
\( \displaystyle x=-1\text{: }{{\log }_{-1}}\left( -1+2 \right)=2\) – это явно неверно, так как основание не может быть отрицательным, то есть корень \( x=-1\) – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
\( \displaystyle \left\{ \begin{array}{l}x>0\\x\ne 1\\x+2>0\end{array} \right.\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}x>0\\x\ne 1.\end{array} \right.\)
Тогда, получив корни \( x=2\) и \( x=-1\), сразу отбросим корень \( -1\), и напишем правильный ответ. {2}}-4=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=2\\x=-2.\end{array} \right.\)
{2}}-4=0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}x=2\\x=-2.\end{array} \right.\)
Казалось бы, меньший корень равен \( \displaystyle -2\). Но это не так: согласно ОДЗ корень \( \displaystyle x=-2\) – сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: \( \displaystyle x=2\).
Ответ: \( \displaystyle x=2\).
Преобразование выражений с использованием свойств логарифмов: примеры, решения
Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.
Свойства логарифмов
Чтобы преобразовывать выражения с логарифмами, обычно используют выражение, называемое основным логарифмическим тождеством: alogab=b, a>0, a≠1, b>0. Также нужно помнить следующие свойства:
Определение 1- loga1=0 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaa=1logaa=1 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaap=p, при этом a>0, a≠1 и p может быть любым действительным числом.
- loga(x·y)=logax+logay, a>0, a≠1, x>0, y>0. В обобщенном виде это свойство можно представить как loga(x1·x2·…·xn)=logax1+logax2+…+logaxn, a>0, a≠1, x1>0, x2>0, …, xn>0
- ) logaxy=logax-logay.
- logaxy=logax-logay , при этом a>0, a≠1, x>0, y>0.
- logaxy=logax-logay , a>0, a≠1, x>0, y>0.
- logabp=p·logab, при этом a>0, a≠1, b>0, а p может быть любым действительным числом.
- это свойство является следствием предыдущего: logabn=1n·logab , a>0, a≠1, n может быть любым натуральным числом больше 1, b>0.

- logab=logcblogca , при этом a>0, a≠1, b>0, c>0, c≠1.
- свойство, также являющееся следствием: logab=1logba , где a>0, a≠1, b>0, b≠1.
- logaqbp=pq·logab , a>0, a≠1, b>0, p и q могут быть любыми действительными числами, q≠0
- logaqbp=pq , a>0, a≠1, p и q – любые действительные числа, q≠0.
- logaq ap=pq, blogac=clogab , при этом a>0, a≠1, b>0, c>0.
Преобразовывая выражения, мы можем использовать данные равенства как справа налево, так и наоборот. Учить их все наизусть нет необходимости, достаточно знать основные свойства логарифмов и несколько других свойств, например, что bn=b1n , если b≥0. Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия logaqbp=pq·logab и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:
logaq bp=logabploga aq=p·logabq=pq·logab
То же относится и к последнему свойству из списка, выраженному формулой blogac=Clogac=clogab : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Как преобразовать числовое выражение с логарифмом
После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Как выбрать свойство логарифма для преобразования
Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.
В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.
Для начала преобразуем выражение, используя определение логарифма, выраженное формулой alogab=b, a>0, a≠1, b>0.
Пример 1Условие: преобразуйте и вычислите значение следующих выражений: 1) 5log54 ; 2) 10lg(1+2·π), 3) 2+3log2+3 ln15 ; 4) 2log2(−7); 5) (-5)log-5 e3
Решение
В первом примере прослеживается формула alogab. У нас есть a=5, b=4, что соответствует необходимому условию a>0, a≠1, b>0. Используем нужное равенство alogab=b и получим 5log54=4.
Во втором случае a будет равно 10, b – 1+2·π. Необходимое условие выполнено, значит, мы можем записать это в виде равенства: 10lg(1+2·π) =1+2·π.
В третьем выражении у нас есть степень вида alogab, причем a=2+3 и b=ln15. Запишем: 2+3log2+3 ln15=ln15 . Хотя равенство также соответствует формуле alogab, где a равно 2, а b=-7, мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, -7 не соответствует условию b>0, что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2log2(−7) =−7 будет ошибочна.
Хотя равенство также соответствует формуле alogab, где a равно 2, а b=-7, мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, -7 не соответствует условию b>0, что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2log2(−7) =−7 будет ошибочна.
То же самое относится и к четвертому примеру. Мы не можем записать, что -5log-5·e3=e3 , поскольку такое выражение смысла не имеет.
Ответ:1) 5log54=4; 2) 10lg(1+2·π)=1+2·π; 3) 2+3log2+3ln 15=ln 15 ; 4 и 5 — не имеют смысла.
Довольно часто в задачах встречается такой вид преобразования, когда некоторое положительно число представляют в виде степени другого числа, также положительного и не равного 1, имеющего в показателе логарифм. Основной такого преобразования также является основное определение логарифма alogab=b, a>0, a≠1, b>0, но в перевернутом виде, т. е. прочитанное справа налево, например, 3=eln3 или 5=5log55.
е. прочитанное справа налево, например, 3=eln3 или 5=5log55.
Далее возьмем примеры с другими свойствами логарифмов.
Пример 2Условие: вычислите, если возможно: 1) log−21, 2) log11,3) log01, 4) log71, 5) ln1, 6) lg 1,7) log3,751, 8) log5·π71.
Решение
В первых трех примерах мы видим не имеющие смысла выражения log−21, log11, log01. Основанием логарифма не может быть число меньше 1, в т.ч. 0 и отрицательные значения, т.к. для них логарифм не определен. Значит, значение этих выражений вычислить нельзя.
В других случаях логарифмы имеют подходящие основания: 7, e, 10, 3,75 и 5·π7, а под знаками логарифма везде 1. Зная соответствующее свойство логарифма (loga1=0 при любом a>0, a≠1., мы можем сделать вывод, что значения этих выражений равны 0.
Ответ: 1, 2, 3 смысла не имеют; 4) log71=0, 5) ln1=0, 6) lg1=0, 7) log3,751=0, 8) log5·e71=0.
Пример 3Условие: вычислите значения: 1) log1313 , 2) ln e, 3) lg 10,4) log5·π3−2(5·π3−2), 5) log−3(−3), 6) log11.
Решение
Нам потребуется свойство логарифма, выраженное формулой logaa=1 при a>0, a≠1. Исходные логарифмы схожи между собой в том, что их основания и числа под знаком логарифма являются одинаковыми. Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1, 2, 3, 4 действительно ответом будет 1, а вот в 5 и 6 исходные выражения смысла не имеют.
Ответ: 1) log13=13=1, 2) ln e=1, 3) lg10=1, 4) log5·π3−2(5·π3−2)=1; 5,6 не имеют смысла.
Пример 4Условие: вычислите: 1) log3311, 2) log1+22(1+22)723 , 3) logπ5(π5)-2 , 4) log−10(−10)6.
Решение
Видим, что под логарифмами находятся некоторые степени основания, значит, нам нужно использовать соответствующее свойство logaap=p, где a>0, a≠1 и p будет любым действительным числом. С учетом этого можно записать следующее:
- log3311=11
- log1+22(1+2·2)723=723
- logπ5(π5)-2=-2
- для этого примера мы не можем написать такое же равенство, как и в предыдущем примере, поскольку log−10(−10)6=6 не имеет смысла.

Ответ: 1) log3311=11, 2) log1+22(1+2·2)723=723 , 3) logπ5(π5)-2=-2 , 4) не имеет смысла.
Пример 5Условие: даны выражения log2,64·127, ln2+1π и lg((−5)·(−12)). Нужно представить их как суммы или разности логарифмов по тому же основанию.
Решение
Смотрим, что находится под знаком логарифма. Там произведение, значит, берем свойство логарифма произведения: loga(x·y) = logax+logay, a>0, a≠1, x>0, y>0. В исходных примерах основания и числа в произведениях положительны, т.е. условие данного свойства соблюдено. Применим его для первого выражения:
log2,64·127=log2,6 4+log2,6127
Чтобы вычислить значение второго выражения, нам нужно свойство логарифма частного: logaxy=logax-logay, a>0, a≠1, x>0, y>0. Здесь в основании стоит положительное число e, также у нас есть положительный числитель 2+1 и знаменатель π, т.е. условия свойства соблюдены. Применяем свойство и записываем, что ln2+1π=ln2+1-ln π .
Разберем третий пример. Начнем с того, что выражение lg((−5)·(−12)) будет иметь смысл, однако формула логарифма произведения для него не подойдет, поскольку оба числа -5 и -12 отрицательны. Значит, преобразование lg((−5) ·(−12))=lg(−5)+lg(−12) не подходит. Какое же свойство тогда использовать?
Проведем предварительное преобразование, чтобы избавиться от отрицательных чисел. Далее мы подробно поговорим, когда нужно выполнять такое действие, а пока ограничимся записью самого решения, которое и так понятно: lg((−5) ·(−12))=lg(5·12)=lg5+lg12.
Ответ: 1) log2,64·127=log2,64+log2,6127 , 2) ln2+1π=ln2+1-ln π , 3) lg((−5)·(−12))=lg5+lg12.
Пример 6Условие: упростите выражения log30,25+log316+log30,5 и ln23-ln13 .
Решение
Здесь мы тоже можем использовать свойства логарифма частного и произведения по аналогии с предыдущим примером, только нам потребуется их обратная запись. Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, а во втором ln23-ln13=ln23:13=ln 2.
В итоге у нас получается в первом примере log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, а во втором ln23-ln13=ln23:13=ln 2.
Ответ: 1) log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, 2) ln23-ln13=ln 2 .
Пример 7Условие: есть выражения log0,7511, log3-1(3-2+5·673)5+1 и log3(−5)6. Нужно избавиться от степени в выражении под знаком логарифма.
Решение
Очевидно, что у нас здесь есть выражения вида logabp. Берем свойство, которое выражается формулой вида
logabp=p·logab, где a>0, a≠1, b>0, p — любое действительное число. Поскольку условия a>0, a≠1, b>0 выполнены, то мы можем преобразовать logabpв произведение p·logab.
- в случае с первым выражением a равно 7, b – пяти и p– 11. Тогда log0,7511=11·log0,75.
- тут a=3-1, b=3-2+5·673, p=5+1 . Нужные условия выполнены, значит, мы можем записать, что:
log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) - у нас есть выражение той же структуры: logabp, a=3, b=−5, p=6, однако одно из условий не выполняется, а именно b у нас меньше 0.
 Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log3(−5)6=log356=6·log35.
Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log3(−5)6=log356=6·log35.
Ответ: 1) log0,7511=11·log0,75, 2) log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) 3) log3(−5)6=6·log35.
Применение формулы в обратном порядке в виде p·logab=logabp требуется довольно часто. При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3·ln 5=ln 53 и lg 2·log23=log23lg2.
Пример 8Условие: согласно таблице логарифмов, lg2≈0,3010 и lg5≈0,6990. Вычислите, сколько будет log25. Здесь же: запишите ln 11ln 3 в виде логарифма, основание которого равно 3.
Решение
Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.
log25=lg 5lg 2
Вычисляем и находим ответ: lg 5lg 2≈0,69900,3010≈2,3223 .
Во втором примере также будет достаточно формулы перехода к новому основанию, только в обратном порядке, т.е. logcblogca=logab .
Считаем: ln 11ln 3=log311
Ответ: 1) log25≈2,3223, 2) ln 11ln 3=log311 .
Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Пример 9Условие: 1) дан логарифм ln1+π7 . Необходимо избавиться от корня под знаком логарифма; 2) выполните преобразование дроби 1log25 в логарифм с основанием 4; 3) преобразуйте логарифм loge2345 так, чтобы избавиться от степени в основании; 4) вычислите, сколько будет log2-13216 ; 5) осуществите замену 2,3log73 на степень с основанием 3.
Решение
- Вспоминаем следствие из свойства логарифма степени, которое выражается формулой logabn=1n·logab .В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) .
- во втором случае нам понадобится формула logab=1logba , примененная в обратном порядке. Получим 1log25=log52.
- здесь нам потребуется свойство logaqbp=pq·logab . Применяем его и получаем loge2345=452·ln 3=25·ln 3.
- в этом случае нам нужно будет следствие, выраженное формулой logaqap=pq: log(2)-13216=16-13=-12
- используем формулу свойства blogac=clogab и вычисляем ответ:
2,3log7·3=3log72,3
Ответ: 1) ln1+π7=17·ln(1+π) ; 2) 1log25=log52 ; 3) loge2345=25·ln 3; 4) log(2)-13216=-12 . 5) 2,3log7·3=3log72,3 .
Задачи с применением нескольких свойств логарифмов
В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Условие: вычислите, сколько будет (log315−log35) ·7log75.
Решение
Мы можем заменить выражение в скобках логарифмом log3(15:5), используя свойство частного. Вычисляем его значение и получаем log3(15:5) =log33=1.
Согласно основному определению логарифма, значением 7log75 будет 5. Подставим в исходное выражение получившиеся результаты и найдем, что (log315−log35) ·7log75=1·5=5.
Вот все решение без комментариев:
(log315−log35)·7log75=log3 (15:5)·5==log33·5=1·5=5
Ответ: (log315−log35) ·7log75=5.
Пример 11Условие: вычислите, чему равен log3log223−1.
Решение
Начнем с преобразования логарифма, который, в свою очередь, сам находится под знаком логарифма. Используем для этого формулу логарифма степени log223=3. Получим, что log3log223=log33, а дальше log33=1. Следовательно, log3log223−1=1−1=0.
Используем для этого формулу логарифма степени log223=3. Получим, что log3log223=log33, а дальше log33=1. Следовательно, log3log223−1=1−1=0.
Ответ: log3log223−1=0.
Пример 12Условие: выполните упрощение выражения 3ln 5ln 3log52 .
Решение
Берем формулу перехода к новому основанию. С ее помощью можно представить отношение логарифмов ln 5ln 3 как log35. У нас получилось 3log35log52 . Теперь применяем формулу основного определения логарифма 3log35=5 и получаем, что 3log35log52 . Нам осталось лишь вычислить значение этого выражения. Оно будет равно 2.
Ответ: 3ln 5ln 3log52=2 .
Перейдем к дальнейшему пункту обсуждения логарифмических преобразований. У нас есть выражения log334, 52+log53, lg 0,01. Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 52+log53=52·5log53=25·3=75, log334=log31234=412=8 и lg 0,01=lg 10−2=−2. Разберем подробнее, как именно это делается.
Разберем подробнее, как именно это делается.
Предварительное преобразование перед применением основных свойств логарифмов
На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.
Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.
- Довольно часто приходится получать степени под знаком и в основании, чтобы потом использовать формулу логарифма степени и последствия данного свойства. Мы выполняем такое преобразование, если в видим в условии логарифмы следующего вида: ln2532332 , log381.
- Также нужно уметь выполнять преобразование, связанное со свойствами степени. Оно нужно нам для последующего использования формулы, которая отвечает определению логарифма. Мы применяем его, когда у нас есть выражения, подобные 2log223, 32·log35, 71+log74, 25(log35)-3 и др.
- Обязательно нужно преобразовывать выражения с десятичными дробями под знаком логарифма или в его основании. Иногда после этого мы обнаруживаем, что основание под знаком степени и основание логарифма будут равны, как, например, здесь: log15(0,2)7
- Также нужно знать правила преобразования выражений, где под знаком логарифма стоит отрицательное число. Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.

Разберем подробно каждый вид преобразования.
Как выделить степень в основании логарифма и под его знаком
Сразу возьмем конкретный пример. У нас есть выражение log1981 , структура которого не подсказывает нам ни одного возможного свойства логарифмов, которое можно было бы использовать. Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 19. Их легко представить в виде степени с основанием 3 : 81=34 и 19=3−2. Значит, все выражение можно переписать как log3-234 , а здесь уже видна возможность использования свойства logaqbp=pq·logab . Таким образом, log1981=log3-2=4-2=-2 .
Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.
В некоторых случаях число можно преобразовать в целую степень, как в примере выше. В задачах то и дело встречаются степени чисел 2 и 3, которые легко узнать с первого взгляда: 243=35, 81=34, 8=23, 64=26 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10, чтобы сразу видеть возможности преобразования выражений. Также легко работать с выражениями, включающими целые степени 10, 100 и др.
В задачах то и дело встречаются степени чисел 2 и 3, которые легко узнать с первого взгляда: 243=35, 81=34, 8=23, 64=26 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10, чтобы сразу видеть возможности преобразования выражений. Также легко работать с выражениями, включающими целые степени 10, 100 и др.
Условие: вычислите или упростите выражения log6216, log3431243, log0,0000010,001.
Решение
- В первом случае мы сразу видим, что 216 можно представить в виде 63. Значит, log6216=log663=3.
- у нас есть числа 343 и 1243. Обратимся к таблице степеней и увидим, что их можно представить в виде 73 и 3−4. Выполняем дальнейшие преобразования и получаем:
log3431243=log733-4==-43·log73=-113·log73 - Поскольку 0,000001=10−6 и 0,001=10−3, тогда log0,0000010,001=log10−610−3= -3-6=12
Ответ: 1) log6216=3, 2) log3431243=-113·log73 ; 3) log0,0000010,001=12.
Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.
Пример 14Условие: упростите выражение log3648·log23.
Решение
Выполняем разложение 648 на простые множители.
64832416281931222333
Значит, это число можно представить в виде 648=23·34. Следовательно, log3648·log23=log3(23·34)·log23
Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.
log3(23·34)·log23=(log323+log334)·log23= =(3·log32+4)·log23.
Упрощаем выражение через раскрытие скобок:
(3·log32+4)·log23=3·log32·log23+4·log23.
В полученном выражении log32·log23 является произведением взаимно обратных чисел, которое равно 1. Следовательно, формулируем ответ как 3·log32·log23+4·log23=3·1+4·log23=3+4·log23.
Ответ: log3648·log23=3+4·log23.
Зачастую под логарифмом записываются выражения, представляющие собой отношения или произведения корней: 323·3-2, 2·2273 и т. д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.
д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.
Слишком сложно?
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Опиши задание Пример 15Условие: найдите значение выражений log52·5-0.5·5-153454 и log372919.
Решение
В первом случае у нас есть произведение степеней, имеющих одинаковые основания. Используя нужное свойство, получим: 52·5−0,5·5−1=52−0,5−1=50,5. Для преобразования дроби сначала выполним переход от корня к степени, затем используем свойство отношения степеней с одинаковыми основаниями:
53454=5344=534-4=5-314
Полученное выражение подставим в исходный логарифм, применив формулу logaqaq=pq, и получим ответ:
log52·5-0.5·5-153454=log50.55-314=-3140. 5==-13412=-132=-612
5==-13412=-132=-612
Во втором случае представим число 729 как 36 , а 19 как 3−2. Исходный логарифм приобретет вид log3363-2. Используя свойство корня из степени, преобразуем основание логарифма и получим:
336=333=31-3=3-2
Заканчиваем преобразование: log3363-2=log3-23-2=1 .
Ответ: 1) log52·5-0.5·5-153454=-612 ; 2) log372919=1
Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.
Пример 16Условие: вычислите значения log13-1132·3+1-5 и log2·cos1(1+cos2)3 .
Решение
Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:
13-1=3+13-1·3+1=3+132-12=3+12
Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:
132·3+1-5=3+1532=3+1525=3+125
В результате преобразований у нас получился логарифм степени основания log3+123+135 . Значение данного выражения будет равно 5.
Значение данного выражения будет равно 5.
Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos2a=1+cos2a2 :
log2·cos1(1+cos2)3=log2·cos1(2·cos21)3
Преобразуем второй логарифм, записав его как степень 2·cos2112 или же 2·cos123=2·cos16. Оба выражения будут иметь одно и то же значение, равное шести.
Ответ: 1) log13-1132·3+1-5=5 ; 2) log2·cos1(1+cos2)3=6 .
Как применять свойства степени при преобразовании выражений с логарифмами
Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.
Для начала возьмем задачи на применение свойства степеней с одинаковыми основаниями ap·aq=ap+q. Чаще всего его применяют в обратном порядке, т.е. справа налево.
Пример 17Условие: вычислите значения 3−2+log37 и 0,72−log0,70,1.
Решение
В первом примере нужно представить исходную степень как произведение двух степеней, т.е. 3−2+log37=3−2·3log37. Теперь найдем, чему равен первый множитель. Возведем его в степень, потом вычислим значение второго множителя, используя определение логарифма, и подсчитаем их произведение:
3−2·3log37= (19) ·7=79
Во втором примере нам надо подготовить выражение к преобразованию, выполнив переход к произведению степеней: 0,72−log0,70,1=0,72·0,7−log0,70,1. После этого нам нужно представить показатель −log0,70,1 в виде llog0,7(0,1)−1=log0,710. Теперь все, что нам осталось, – это закончить вычисления:
0,72·0,7−log0,70,1=0,49·0,7log0,710=0,49·10=4,9
Ответ: 1) 3−2+log37=79; 2) 0,72−log0,70,1=4,9.
Также для предварительных преобразований нужно обязательно знать свойство степени в степени, которое выражается формулой (ap)q=ap·q, например, если у нас есть выражение (eln2)3, то мы можем заключить, что значение части в скобках будет равно 2. Значит, (eln2)3=23=8. А если в условии указано (e3)ln2 или (e3)ln2, то мы сначала приводим их к виду (eln2)3:
Значит, (eln2)3=23=8. А если в условии указано (e3)ln2 или (e3)ln2, то мы сначала приводим их к виду (eln2)3:
e3·ln2=eln2·3=(eln2)3 и (e3)ln2=e3·ln2=eln2·3=(eln2)3.
Посмотрим пример решения такой задачи.
Пример 18Условие: выполните упрощение выражений 2log223−3log23 и 5(log85) −1.
Решение
Отметим, что выражения 2log223и 2log223 не являются равными друг другу. Мы можем представить 2log223 как 2log23·log23. Используя свойство степени, представим его как (2log23)log23, что будет тождественно равным 3log23. В итоге мы имеем, что 2log223−3log23=3log23−3log23=0.
Вот запись всего решения:
2log223−3log23=2log23·log23−3log23==(2log23)log23−3log23=3log23−3log23=0
Перейдем ко второму примеру. Запись 25(log85)-1 не будет равна (25log85)−1. Мы можем представить степень (log85)−1 как дробь 1log85 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле logab=1logba, чтобы получить log58.
Так, 25(log85)-1=25log58. Поскольку 25 – это 52, имеем 5log58= (52)log58. То, что у нас получилось, представляем в виде (5log58). Нам осталось только вычислить значение: (5log58)2=82=64.
Ответ: 1) 2log223−3log23=0, 2) 25(log85)−1=64.
Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,
4−0,5+2·log43=4−0,5·42·log43==12·(4log43)2=12·32=12·9=4,5
Преобразование логарифмов с десятичными дробями
Применить свойства логарифмов можно и тогда, когда под знаком логарифма у нас стоит десятичная дробь. Что можно сделать с выражением log0,4253? Отметим, что 25 и 0,4 равны между собой 0,4=410=25, то есть это разные формы записи для одного и то же числа.
В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.
Это поможет увидеть возможности использования свойств логарифмов.
Разберем подобную задачу.
Пример 19Условие: вычислите значение выражения log0,46,25.
Решение
Начнем с перехода от десятичных дробей к обыкновенным.
log0,46,25=log410625100=log25254
Теперь видно, что мы можем преобразовать 254 в виде (25)−2 и воспользоваться формулой логарифма степени. Вычисляем значение:
log25254=log2525-2=-2
Ответ: -2.
Преобразование выражений с отрицательными числами под знаком логарифма
Еще один случай, который мы хотели бы рассмотреть – это преобразование выражений, в которых под знаком логарифма стоит отрицательное число, например, log3-93-27 или log3((−2)·(−5)).
Мы не можем сразу воспользоваться формулами свойств логарифмов в том виде, в каком приводили их в последнем пункте, например, сразу перейти от log3((−2)·(−5)) к log3(−2)+log3(−5), применить свойство логарифма степени к log2(−2)6 или логарифма частного к log3-93-27 , поскольку отрицательные числа не могут находиться под знаком логарифма и в его основании.
Что это значит на практике? Вернемся к нашему примеру log3((−2)·(−5)). Структура выражения соответствует формуле loga(x·y), где a равно 3, x-3 и y-5. Поскольку условия a>0, a≠1, x>0, y>0 не выполнены, формулу loga(x·y)=logax+logay мы применить не можем, и равенство log3((−2)·(−5)) =log3(−2) +log3(−5) записать нельзя. Преобразования вида log3-93-27=log3-93-log3(-27) также будут неправильными.
Это не значит, что выражения с отрицательными числами не могут быть преобразованы с использованием свойств логарифмов. Это допускается при условии предварительных преобразований, позволяющих избавиться от минуса. Они базируются на хорошо известных нам правилах работы с числами, меньшими 0.
Вернемся опять к нашему примеру. Согласно правилам умножения, (−2)·(−5) =2·5, значит, log3((−2)·(−5))=log3(2·5). К выражению в таком виде мы уже можем применить формулу log3(2·5) =log32+log35. А вот для примера log2(−2)6 нужно будет выполнить следующие действия:
(−2)6= ((−1)·2)6=(−1)6·26=1·26=26
Значит, log2(−2)6=log226=6.
Условие: найдите значение выражения log2-163-2-23.
Решение
Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.
Определив корень нечетной степени из отрицательного числа, выполним переход от -163-2-23 к -163-2-23 . Согласно правилам деления, получим -163-2-23=1632-23 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.
1632-23=2432-23=2432-23=243—23=22log2-163-2-23=log222=2
Ответ: log2-163-2-23=2 .
Некоторые свойства, например, логарифма частного, степени с четным показателем и произведения, можно распространить и на отрицательные числа с помощью модулей. Как это делается, мы покажем далее. Так, поскольку свойство логарифма произведения выглядит как loga(x·y)=loga|x|+loga|y|, где a>0, a≠1, x≠0, y≠0, то после преобразования мы получим log3((−2)·(−5)) =log3|−2|+log3|−5|=log32+log35.
Как преобразовать логарифмическое выражение с переменными
В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
Особенности преобразований выражений с переменными
Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.
У нас есть логарифмическое выражение log2(x+1)4. При преобразовании нужно обязательно учитывать область допустимых значений, поэтому первым шагом должно стать ее нахождение. Здесь она определена неравенством (x+1)4>0, значение которого является числовым множеством (−∞, −1) ∪ (−1, +∞). Решить его можно с помощью метода интервалов.
Здесь она определена неравенством (x+1)4>0, значение которого является числовым множеством (−∞, −1) ∪ (−1, +∞). Решить его можно с помощью метода интервалов.
Исходное выражение соответствует формуле logABp, где A равно 2, B – x+1, а p – четырем.
Мы видим, что заданное выражение соответствует виду logABp, где A=2, B=x+1 и p=4. Такие выражения преобразовываются по свойству логарифма степени logabp=p·logab. Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x=−2. В итоге: log2(−2+1)4=log21=0, а 4·log2(−2+1) =4·log2(−1) –выражение, не имеющее смысла. Значит, мы ошиблись.
Причина ошибки в том, что мы взяли формулу logabp=p·logab, но это допустимо лишь при условии a>0, a≠1, b>0, p — любое действительное число. Иными словами, проделанное нами преобразование возможно, если x+1>0, что аналогично x>−1 (для A и p – условия выполнены). Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x>−1, но и из промежутка x <−1. Но для x <−1 мы не имели права осуществлять преобразование по выбранной формуле.
Но для x <−1 мы не имели права осуществлять преобразование по выбранной формуле.
Почему надо учитывать область допустимых значений
Продолжая работу с выражением log2(x+1)4, проанализируем, как изменится область значений, когда мы выполним переход к виду 4·log2(x+1). Ранее мы уже определили эту область как множество (−∞, −1) ∪ (−1, +∞). Теперь вычислим, какова будет область допустимых значений для 4·log2(x+1). Она определяется условием x+1>0, а ему, в свою очередь, будет отвечать множество (−1, +∞). Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.
Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.
Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:
Определение 3- когда мы переходим от логарифма произведения к сумме, например, ln(x·(x+3)) =lnx+ln(x+3) сузит нужную область.
- Когда мы переходим от логарифма частного к разности. Пример такого преобразования – замена log2xsin x на log2x−log2sinx .
- Когда мы выносим четный показатель степени, используя формулу логарифма степени logabp=p·logab и формулу logabp=pq·logab . Примеры таких преобразований – logx3(x-8)2=23·logx(x-8) , ln(x+3)−4=−4·ln(x+3).
Иногда в результате преобразования область допустимых значений может не сужаться, а расширяться, например, при переходе от 4·log2(x+1) к log2(x+1)4. В этом случае область расширяется от (−1, +∞) до (−∞, −1) ∪ (−1, +∞). Такие преобразования имеют место, если оставаться в рамках ОДЗ для исходного выражения. Так, преобразование 4·log2(x+1) =log2(x+1)4 имеет место на области значений переменной x для исходного выражения 4·log2(x+1), то есть, при x+1>0, что аналогично (−1, +∞).
Так, преобразование 4·log2(x+1) =log2(x+1)4 имеет место на области значений переменной x для исходного выражения 4·log2(x+1), то есть, при x+1>0, что аналогично (−1, +∞).
Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.
Правила проведения преобразований
Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.
Пример 21Условие: упростите 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4.
Решение
На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.
Чтобы перейти от lg(x+2)7 к 7·lg(x+2) и от lg(x+2)4к 4·lg(x+2), нам нужно, чтобы x+2>0. Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств (x+2)7>0,x+2>0,(x+2)4>0 , которая будет равносильной условию x+2>0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:
Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств (x+2)7>0,x+2>0,(x+2)4>0 , которая будет равносильной условию x+2>0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:
3·lg(x+2)7−lg(x+2)−5·lg(x+2)4==3·7·lg(x+2)−lg(x+2)−5·4·lg(x+2)==21·lg(x+2)−lg(x+2)−20·lg(x+2)==(21−1−20)·lg(x+2)=0
Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:
3·lg(x+2)7-lg(x+2)-5·lg(x+2)4==lg((x+2)7)3-lg(x+2)-lg((x+2)4)5==lg(x+2)21-lg(x+2)-lg(x+2)20==lg(x+2)21(x+2)·(x+2)20=lg1=0
Ответ: 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4=0.
А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.
Пример 22Условие: выполнить упрощение выражения lg(x+2)4−lg(x+2)2.
Решение
Здесь свободно использовать свойство логарифма степени мы не можем. Область допустимых значений x можно представить в виде объединения промежутков x>−2 и x<−2. Если x>−2, то применяем нужное свойство и действуем по аналогии с тем, как мы решали задачу выше: lg(x+2)4−lg(x+2)2=4·lg(x+2) −2·lg(x+2) =2·lg(x+2). Однако в области значений есть и промежуток x+2<0, и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?
Применим знаки модуля. Вспомним определение данного понятия и представим x+2 при x+2<0 как −|x+2|. В таком случае мы можем выполнить переход от lg(x+2)4−lg(x+2)2 к lg(−|x+2|)4−lg(−|x+2|)2, и далее к lg|x+2|4−lg|x+2|2 .То, что у нас получилось в итоге, может быть преобразовано с использованием свойства логарифма степени, ведь |x+2|>0 при любом x.
Модуль нам больше не нужен, значит, избавляемся от него. С учетом того, что мы преобразовывали при |x+2|<0, имеем 2·lg|x+2|=2·lg(−(x+2)). Это и будет ответом на поставленный вопрос.
Это и будет ответом на поставленный вопрос.
Ответ: lg(x+2)4-lg(x+2)2=2·lg(x+2), x+2>02·lg(-(x+2)), x+2<0 . Можно записать ответ компактнее, используя знаки модуля: lg(x+2)4-lg(x+2)2=2·lgx+2 .
Возьмем еще один пример, чтобы закрепить навыки работы с модулями.
Пример 23Условие: представьте выражение lnx-1·x-2x-3 как сумму и разность логарифмов линейных двучленов x−1, x−2 и x−3.
Решение
Вычисляем область допустимых значений данного выражения:
x-1·x-2x-2>0,(1, 2)∪3, +∞
Поскольку значения x−1, x−2 и x−3 будут положительны на промежутке от трех до плюс бесконечности, то мы можем использовать формулы свойств логарифма суммы и разности:
lnx-1·x-2x-3==ln(x-1)+ln(x-2)-ln(x-3)
А на интервале от одного до двух значение x−1 будет положительным, а x−2 и x−3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
lnx-1·x-2x-3=lnx-1·-x-2-x-3==ln(x-1)·x-2x-3
После этого можно спокойно применять формулу логарифма произведений и частного, поскольку на интервале от одного до двух значения всех трех выражений x−1, |x−2| и |x−3| будут положительными. В итоге имеем:
В итоге имеем:
lnx-1·x-2x-3=ln(x-1)+lnx-2-lnx-3==lnx-1+ln(-(x-2))-ln(-(x-3))
Теперь объединяем получившиеся результаты.
Ответ: lnx-1·x-2x-3=lnx-1+ln(-(x-2))-ln(-(x-3))
С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:
Определение 4- сумма логарифмов loga|X|+loga|Y|, a>0, a≠1 может быть использована вместо логарифма произведения loga(X·Y).
- Разность логарифмов loga|X|−loga|Y|, где a>0, a≠1, X и Y являются произвольными выражениями, может быть использована вместо логарифма частного.
- Выражение p·loga|B|, где a>0, a≠1, p является четным числом, а B – произвольным выражением, может быть использована вместо логарифма B в четной степени p.
Условие: выполните упрощение выражения 13·log8((x+4)·(x-2))-log8x+413x-2 .
Решение
На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
(x+4)·(x-2)>0,(x+4)13x-2>0-∞, -4∪2, +∞
У нас получилось, что значения выражений x+4, x−2 и (x+4)13 в данной области могут быть как положительными, так и отрицательными. Значит, нам нужно использовать модули.
13·log8((x+4)·(x-2))-log8(x+4)13x-2==13·log8x+4+13·log8x-2—log8x+413-log8x-2==13·log8x+4+13·log8x-2—log8(x+14)13+log8x-2==13·log8x+4-log8(x+4)13+14·log8x-2
Зная свойства модуля, перепишем x+413 в виде x+413 . Значит, что:
13·log8x+4-log8(x+4)13+14·log8x-2==13·log8x+4-log8x+413+14·log8x-2
Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:
13·log8x+4-log8x+413+14·log8x-2==13·log8x+4-13·log8x+4+14·log8x-2==14·log8x-2
Возможны и другие преобразования, которые дают тот же результат:
13·log8((x+4)·(x-2))-log8x+413x-2==log8((x+4)·(x-2))13-log8x+413x-2==log8((x+4)13·(x-2))13-log8x+413x-2==log8(x+4)13·(x-2)13x+413x-2=log8(x-2)14
Поскольку на области допустимых значений x−2 может быть и положительным, и отрицательным, необходимо заключить это выражение под знак модуля во время вынесения четного показателя степени. У нас получится, что log8(x-2)14=14·log8x-2
У нас получится, что log8(x-2)14=14·log8x-2
А что было бы, если бы мы не стали использовать модуль, а сразу начали применять свойства логарифмов? У нас получился бы результат 14·log8(x−2), который был бы верен при x∈ (2, +∞), однако ошибочен на всей остальной области допустимых значений.
Ответ: 13·log8((x+4)·(x-2))-log8x+413x-2=14·log8x-2 .
Инженерный калькулятор онлайн
Инструкция инженерного калькулятора
Данный инженерный калькулятор позволяет производить инженерные вычисления с применением переменных (a:=, f:=, a1:= и т.д.), арифметических операций (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, факториал), тригонометрических функций (синус, косинус, тангенс, котангенс), обратных тригонометрических функций (арксинус, арккосинус, арктангенс, арккотангенс), гиперболических функций (гиперболический синус, гиперболический косинус, гиперболический тангенс, гиперболический котангенс) натурального логарифма (ln) и логарифма с основанием 10 (log). 3+R/3
3+R/3
Здесь переменной R присвоили значение некоторого выражения. Переменной U присвоили значение выражения, в котором присутствует переменная R. Далее, командой U= можно посмотреть результат. Если переменная в выражении не существует, то она будет выводится ошибка «—?».
Вставка, удаление и изменение выражения.
Для удаления формулы нужно выбирать левой кнопкой мыши нужную формулу и в открывающем окне (Рис.2) нажимать на надпись ‘Удалить’. Нужно учитывать, что все формулы нужно пересчитать, т.к. при удалении переменной значение этой переменной могут быть использованы в дальнейших выражениях. Для пересчитывания нужно использовать кнопку на калькуляторе которая станет зеленым. Каждый раз, когда эта кнопка становится зеленым, нужно его нажимать для пересчитывания формул.
Рис.2
Для изменения формулы нужно выбирать левой кнопкой мыши нужную формулу и в открывающем окне (Рис.2) выбирать надпись ‘Изменить’. В окне калькулятора появится формула, которая можно редактировать а в конце нажимать на ‘=’ или . Нужно учитывать, что все формулы будут пересчитаны, т.к. при изменении переменной значение этой переменной могут быть использованы в дальнейших выражениях.
Нужно учитывать, что все формулы будут пересчитаны, т.к. при изменении переменной значение этой переменной могут быть использованы в дальнейших выражениях.
Для вставки формулы нужно выбирать левой кнопкой мыши ту формулу, перед которой нужно вставить формулу и в открывающем окне (Рис.2) нажимать на надпись ‘Вставить’. В окне калькулятора нужно набирать формулу и в конце нажимать на ‘=’ или .Нужно учитывать, что все формулы будут пересчитаны, т.к. при вставки переменной значение этой переменной могут быть использованы в дальнейших выражениях.
Работа с дробями
Дроби набираются так: «числитель» / «знаменатель» или «числитель» : «знаменатель» (примеры 89/8, -6.87/8, 1.9:8.67 и т. д.). Если дробь имеет целую часть, то дробь набирается так : «целая часть»_ «числитель» / «знаменатель» (примеры: 5_7/8, -8_87/342 и т.д.)
Особенности работы с тригонометрическими функциями
По умолчанию углы в тригонометрических функциях берутся в градусах. Для перехода от градусов к радианам используйте кнопку на калькуляторе. (1/2)
(1/2)
| Команда | Действие |
|---|---|
| sin( ) | вычислить синус |
| cos( ) | вычислить косинус |
| tg( ) | вычислить тангенс |
| ctg( ) | вычислить котангенс |
| arcsin( ) | вычислить арксинус |
| arccos( ) | вычислить арккосинус |
| arctg( ) | вычислить арктангенс |
| arcctg( ) | вычислить арккотангенс |
| sinh( ) | вычислить гиперболический синус |
| cosh( ) | вычислить гиперболический косинус |
| tanh( ) | вычислить гиперболический тангенс |
| ctanh( ) | вычислить гиперболический котангенс |
Онлайн логарифмов двоичного калькулятора десятичного, по заданному основанию
- Подробности
Калькулятор натурального расчета: ln (b) ; двоичный логарифм LG 2 (b) ; деcятичный логарифм LG (b) ; логарифм по заданному основанию log a (b) .
Помощь на развитии проекта premierdevelopment.ru
Отправить письмо и мы будем знать, что движемся в правильном направлении.Спасибо, что не прошели мимо!
I. Для справки:
- натуральный логарифм
- — это логарифм по основанию e, где e — иррациональная константа, равная 2,718.
Натуральный логарифм обозначается как ln (b), log e (b) или иногда просто log (b), если основание e подразумевается.
Натуральный логарифм числа b — это показатель степени, в котором нужно возвести число e, чтобы получить b. - двоичный логарифм
- — логарифм по основанию 2.
 Двойной логарифм обозначается как lg 2 (b). Двоичный логарифм числа b есть решение уравнения 2 x = b.
Двойной логарифм обозначается как lg 2 (b). Двоичный логарифм числа b есть решение уравнения 2 x = b. - десятичный логарифм
- — логарифм по основанию 10. Десятичный логарифм обозначается как lg (b). Десятичный логарифм числа b есть решение уравнения 10 x = b.
- логарифм числа b по основанию a
- — показатель степени, в которую надо возвести основание a, чтобы получить число b. Он обозначается как log a (b). Логари́фм числа b по основанию a есть решение уравнения a x = b.
II. Примечание:
- Округление результатов расчета выполняется до количества знаков после запятой (по умолачанию — округление до сотых).
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Калькулятор логарифмов. Решение логарифмов онлайн
Данная страница рассматривает калькулятор логарифмов — ещё одну функцию в богатом арсенале, предоставляет соответствующий бесплатный калькулятор на нашем сайте. Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представлять суть логарифма.
Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представлять суть логарифма.
Буквально 20-30 лет назад решение логарифмов требований серьезных знаний в математике и как минимум умения пользоваться таблицами логарифмов или логарифмической линейкой. Чтобы привести к табличному виду исходное выражение, часто приходилось преобразовывать, учитывая свойства логарифмов и их функций.
Сегодня же достаточно иметь доступ в интернет, чтобы без труда вычислять всевозможные логарифмические уравнения и неравенства любой сложности. Размещенный на нашем сайте калькулятор онлайн может любой логарифм вычислить за одно мгновение! Используйте этот простой способ решения — вычисление логарифмов онлайн! Лучше добавить калькулятор в социальных сетях, наверняка найдётся открыть его ещё раз.
Решение логарифма log y x сводится к нахождению ответа на вопрос, в какую степень требуется возвести основание логарифма y, чтобы получилось значение равное x. Онлайн калькулятор логарифмов рассчитать все виды логарифмов: двоичные, десятичные и натуральные логарифмы, а также логарифм комплексного числа и логарифм отрицательного числа и др.
Онлайн калькулятор логарифмов рассчитать все виды логарифмов: двоичные, десятичные и натуральные логарифмы, а также логарифм комплексного числа и логарифм отрицательного числа и др.
Вычисление логарифмов в онлайн-калькуляторе записывается как log и выполняется с помощью четырёх кнопок: нахождение двоичного логарифма, решение десятичных логарифмов, с произвольным основанием и вычисление натурального логарифма.
Кнопки, позволяющие вычислить логарифм онлайн
И десятичный логарифм калькулятор посчитает, и натуральный логарифм калькулятор найдёт!
Некоторые кнопки одна для записи одного и того же действия. Возьмём, к примеру, расчёт логарифмов с произвольным основанием. Понятно что, если указать основание 10, то рассчитывается десятичный логарифм, а если 2, то двоичный. Учитывая, что математическое выражение можно и вручную набрать, тот же самый десятичный логарифм посчитать можно тремя способами (точнее записать эту операцию в калькуляторе):
- 1.
 используя кнопку log , тогда нужно указать только число
используя кнопку log , тогда нужно указать только число - 2. с помощью кнопки log y x , через запятую указываются число и основание логарифма
- 3. Внести обозначение логарифма вручную
Подробная информация о том, как работать с клавиатурой калькулятора, а также обзор всех его возможностей, можно найти на странице Функции калькулятора.
Логарифмы примеры решения в калькуляторе
Логарифм по основанию 2
Используйте эту кнопку, чтобы рассчитать логарифм, основание которого дво двое.
В строке ввода отображается запись log2 (x), соответственно, вам остаётся ввести число, без указания, и расчет расчёт. В примере найден ответ, чему равенство логарифм 8 по основанию 2.
Логарифм по основанию 2
Десятичный логарифм 10
Эта кнопка поможет найти логарифм числа по основанию 10.
Логарифм десятичный онлайн калькулятор обозначает записью log (x x, y). На графикано, чему равен десятичный логарифм числа 10000.
На графикано, чему равен десятичный логарифм числа 10000.
Логарифм по основанию 10
Натуральный логарифм
Клавишей ln выполняется решение натуральных логарифмов, основанием которого является число е. Основание натурального логарифма е — число Эйлера — равно 2.71828182845905.
Онлайн калькулятор можно определить, чему равен натуральный логарифм любого числа. На рисунках в качестве логарифма найдены значения натурального логарифма: слева — ln логарифм числа 8, справа — натуральный логарифм от числа 50.
Натуральные логарифмы примеры решения
Как решать логарифмы с произвольным основанием
Конечно, калькулятор позволяет решить не только по определенному, но и по любому основанию. Чтобы найти значение логарифмов с произвольным основанием для любого числа, используйте эту кнопочку log y x, она подставляет в строку ввода запись log (x x, y).
Определение логарифма числа
Калькулятор Инструкция — обзор основных и дополнительных функций калькулятора и общая информация о том, как пользоваться калькулятором.
пер 0 5
Вы искали ln 0 5? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной и ln калькулятором, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.Например, «ln 0 5».
Применение различных математических задач, калькуляторов, функций и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве и даже спорте. Математику человек
использует еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
Таким образом, мы можем наслаждаться плодами своей деятельности, например, как онлайн-калькулятор, который
может решить задачи, такие, как ln 0 5, ln калькулятор, ln калькулятор онлайн, ln онлайн, ln онлайн калькулятор, вычислить логарифма натуральный онлайн, вычислить логарифм натуральный онлайн, вычислить логарифм натуральный онлайн калькулятор, вычислить натуральный логарифм онлайн, вычислить натуральный логарифм онлайн калькулятор, как посчитать логарифм натуральный, как считать логарифм натуральный, калькулятор ln, калькулятор ln онлайн, калькулятор логарифма натуральный, калькулятор логарифм натуральный, калькулятор натуральный логарифма, калькулятор натуральный логарифм, калькулятор натуральный логарифма, калькулятор натуральный логарифм, калькулятор натуральный логарифм логарифмов онлайн, калькулятор онлайн натуральные логарифмы, логарифм ln онлайн калькулятор, логарифм натуральный онлайн, логарифм натуральный онлайн калькулятор, логарифм онлайн калькулятор, найти логарифм натуральный онлайн, найти натуральный логарифм онлайн, натуральные логарифмы калькулятор онлайн, натурный уральные логарифмы онлайн калькулятор, натуральный логарифм вычислить онлайн, натуральный логарифм калькулятор, натуральный логарифм калькулятор онлайн, натуральный логарифм онлайн, натуральный логарифм онлайн, натуральный логарифм онлайн калькулятор, натуральный логарифм посчитать, натуральный логарифм посчитать онлайн, онлайн перевод, онлайн вычислить, натуральный логарифм онлайн калькулятор ln, онлайн калькулятор натуральный логарифм, онлайн калькулятор натуральный логарифм, посчитать логарифм натуральный, посчитать натуральный логарифм, посчитать натуральный логарифм онлайн, расчет логарифма натуральный онлайн, расчет натуральный логарифма онлайн, решение онлайн логарифма натуральный, решение натуральный логарифм логарифмов. На этой странице вы найдёте калькулятор,
который поможет решить вопрос, в том числе и ln 0 5. Просто введите любую задачу в окошко и нажмите
«Решить» здесь (например, ln калькулятор онлайн).
На этой странице вы найдёте калькулятор,
который поможет решить вопрос, в том числе и ln 0 5. Просто введите любую задачу в окошко и нажмите
«Решить» здесь (например, ln калькулятор онлайн).
Где можно решить любую задачу по математике, а так же ln 0 5 Онлайн?
Решить задачу ln 0 5 вы на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель решить онлайн задачу любой сложности за считанные секунды.Все, что вам необходимо сделать — это просто привести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно достичь вашу задачу на нашем сайте. Если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Натуральный логарифм, формулы и онлайн калькуляторы
Содержание:
Для различного теоретических и практических исследований наиболее часто
основанием логарифма
является иррациональное число $ e $. {c} $.
Логарифм имеет смысл, если $ a> 0, a \ neq 1, b> 0 $.
{c} $.
Логарифм имеет смысл, если $ a> 0, a \ neq 1, b> 0 $.
Натуральным логарифмом называется логарифм по основанию $ e $. Такие логарифмы обозначаются символом ln. Запись $ \ ln x $ означает тоже самое, что и $ \ log _ {e} x $.
Основание натурального логарифма — число е.
Свойства и основные формулы натурального логарифма
1 $ \ ln 1 = 0 $
Натуральный логарифм единицы равенства нулю (Заметим, что логарифм по любому основанию от 1 равенства 0).{n} = n \ cdot \ ln x
долларов6 График функции $ y = \ ln x $:
Примеры решения задач
Пример
Задание. Вычислить $ \ frac {2 \ ln 3 e- \ ln 9} {3 \ ln 5 e- \ frac {3} {2} \ ln 25} $
Решение. Преобразуем данное выражение, применяя к первым логарифмам в числителе и знаменателя свойства логарифмов, а ко вторым свойство логарифма степени.
$ \ frac {2 \ ln 3 e- \ ln 9} {3 \ ln 5 e- \ frac {3} {2} \ ln 25} = \ frac {2 (\ ln 3+ \ ln e) — \ ln 3 ^ {2}} {3 (\ ln 5+ \ ln e) — \ frac {3} {2} \ ln 5 ^ {2}} =
долларов США$ = \ frac {2 \ ln 3 + 2 \ ln e-2 \ ln 3} {3 \ ln 5 + 3 \ ln e-3 \ ln 5} = \ frac {2 \ ln e} {3 \ ln e} = \ frac {2 \ cdot 1} {3 \ cdot 1} = \ frac {2} {3}
долларов Ответ. {2 n}} {n} + \ ldots, | x | \ lt 1
{2 n}} {n} + \ ldots, | x | \ lt 1
Читать дальше: десятичный логарифм.
Как набирать функции и константы
В отличие от форума и материалов, где для ввода формул используется язык LaTex, в онлайн сервисе существуют свои правила ввода функций — более простые и наглядные.
Как ввести функции и некоторые константы:
| Простейшие математические операции | |
| Сумма: +; Вычитание: -; Умножение: * или пробел; Деление и дроби: / | |
| Некоторые константы | |
| e — основание натурального логарифма с приближенным числовым значением 2.x — экспонента значения x, | log (a, x) — логарифм с основанием a, log (x) = ln (x) — натуральный логарифм, dilog (x) — дилогарифм значений x, |
| Тригонометрические функции | |
| sin (x) — синус значения x cos (x) — косинус значения x tan (x) — тангенс значения x | cot (x) = ctg (x) — котангенс значения x sec (x) — секанс значения x, sec (x) = 1 / cos (x) csc (x) — косеканс значения x , csc (x) = 1 / sin (x) |
| Обратные тригонометрические функции | |
| arcsin (x) — арксинус значения x, arccos (x) — арккосинус значения x, arctan (x) — арктангенс значения x, | arccot (x) — арккотангенс значения x, arcsec (x) — арксеканс значения x, arccsc (x) — арккосеканс значения x, |
| Примеры: | |
| sqrt (1-pi x ^ 2) — cos (x) x-e ^ x + log (4, x) — | сек (EulerGamma x) / 5 — |
Что делать, если вместо решения пустой экран
Если вы ввели функцию, нажали на кнопку «решить», открылось поле с решением, но оно пустое, как, например, изображено:
или
значит, имеется конфликт с заголовками сервера. Исправить ситуацию можно отключить в браузере CSP (Content Security Policy). Для Chrome это реализуется установкой расширения, которое скачать можно здесь: Disable Content-Security-Policy. Для остальных браузеров можно найти аналогичные решения.
Исправить ситуацию можно отключить в браузере CSP (Content Security Policy). Для Chrome это реализуется установкой расширения, которое скачать можно здесь: Disable Content-Security-Policy. Для остальных браузеров можно найти аналогичные решения.
Однако крайне рекомендуем после окончания работы с сайтом matematikam.ru снова включить CSP. Это повысит безопасность при работе в интернете.
Расчет логарифмов
Простой математический калькулятор для вычислений логарифмов чисел с указанным основанием.Данный калькулятор посчитать как десятичный логарифм, так и натуральный.
Теперь вы можете без всяких формул быстро зайти на наш сайт и узнать его логарифм.
Также на нашем сайте вы посчитать и обратный логарифм числа, антилогарифм, просто нужно зайти на службу:
Поле не заполнено.
«% 1» не является допустимым адресом электронной почты.
Пожалуйста, заполните это поле.
Поле должно содержать не менее% 1 символов.
Значение не должно быть длиннее% 1 символов.
Значение поля не совпадает с полем «% 1»
Недопустимый символ. Допустимые символы: «% 1».
Ожидаемое число.
Ожидается положительное число.
Ожидаемое целое число.
Ожидается положительное целое число.
Значение должно быть в диапазоне [% 1 ..% 2]
«% 1» уже присутствует в наборе допустимых символов.
Поле должно быть меньше 1%.
Первый символ должен быть буквой латинского алфавита.
Su
Пн
Ту
ср
Чт
Fr
Sa
января
Февраль
марта
Апрель
мая
июнь
июля
августа
Сентябрь
Октябрь
Ноябрь
Декабрь
век
Б.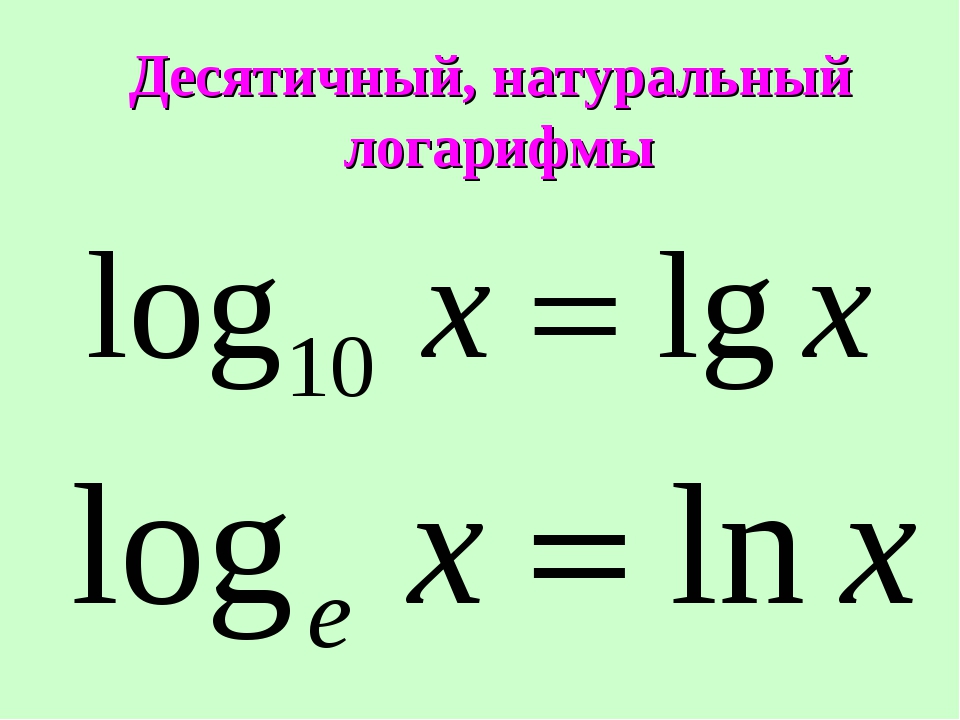 С.
С.
% 1 век
Ошибка при импорте данных в строке% 1. Значение: «% 2». Ошибка: % 3
Не удалось определить разделитель полей. Для разделения полей можно использовать следующие символы: табуляция, точка с запятой (;) или запятая (,).
% 3.% 2.% 1% 4
% 3.% 2.% 1% 4% 6:% 7
с.ш.
грн.
v.d.
z.d.
да
нет
Неверный формат файла.Только следующие форматы:% 1
Пожалуйста, оставьте свой номер телефона и / или электронную почту.
Свойства логарифмов и примеры их решений (ЕГЭ — 2021)
То есть и аргумент, и основание должно быть больше нуля, а основание еще и не может равняться \ (1 \).
Почему так?
Начнем с простого: допустим, что \ (a = 1 \). Тогда, например, число не существует, так как в какую степень бы мы не возводили \ (1 \), всегда получается \ (1 \).
Более того, \ (\ displaystyle {{\ log} _ {1}} b \) не существует ни для какого \ (\ displaystyle b \ ne 1 \). {\ frac {1} {2}}} = \ sqrt {4} = 2 \)), а вот \ (\ displaystyle {{\ log} _ {- 4}} 2 \) не существует.
{\ frac {1} {2}}} = \ sqrt {4} = 2 \)), а вот \ (\ displaystyle {{\ log} _ {- 4}} 2 \) не существует.
Поэтому и отрицательные основания выбросить, чем возиться с ними.
Ну а поскольку у нас бывает только положительное, то в какой бы степени мы его ни возводили, всегда получим число строго положительное.
Значит, аргумент должен быть положительным.
Например, \ (\ displaystyle {{\ log} _ {2}} \ left (-4 \ right) \) не существует, так как \ (2 \) ни в какой степени не будет отрицательным числом (и даже нулем , поэтому \ (\ displaystyle {{\ log} _ {2}} 0 \) тоже не существует).
Задача с логарифмами первым делом нужно записать ОДЗ .
Приведу пример:
Решим уравнение \ (\ displaystyle {{\ log} _ {x}} \ left (x + 2 \ right) = 2 \).
Вспомним определение: логарифм \ (\ displaystyle {{\ log} _ {x}} \ left (x + 2 \ right) \) — это степень, в которую надо возвести основание \ (x \), чтобы получить аргумент \ (\ Displaystyle \ влево (х + 2 \ вправо) \).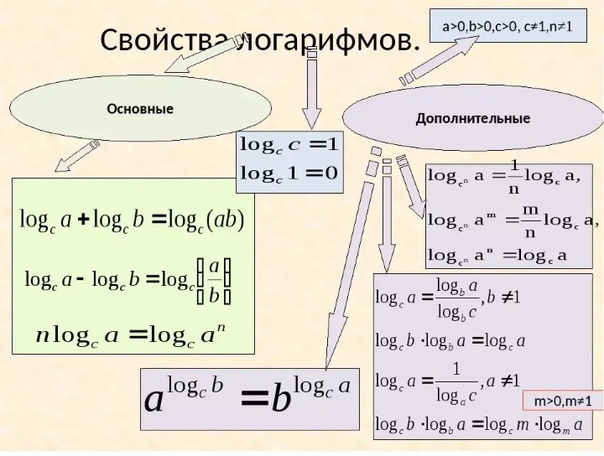 {2}} = x + 2 \).{2}} — х-2 = 0 \).
{2}} = x + 2 \).{2}} — х-2 = 0 \).
Решим его с помощью теоремы Виета: сумма корней равна \ (1 \), произведение \ (-2 \). Легко подобрать, это числа \ (2 \) и \ (-1 \).
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу на ЕГЭ.
Почему?
Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
\ (\ Displaystyle x = 2 \ text {:} {{\ log} _ {2}} \ left (2 + 2 \ right) = {{\ log} _ {2}} 4 = 2 \) — верно.
\ (\ displaystyle x = -1 \ text {:} {{\ log} _ {- 1}} \ left (-1 + 2 \ right) = 2 \) — это явно неверно, так как основание не может быть отрицательным, то есть корень \ (x = -1 \) — «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
\ (\ displaystyle \ left \ {\ begin {array} {l} x> 0 \ x \ ne 1 \\ x + 2> 0 \ end {array} \ right. \ Text {} \ Leftrightarrow \ text {} \ left \ {\ begin {array} {l} x> 0 \\ x \ ne 1. \ end {array} \ right. \ )
\ end {array} \ right. \ )
Тогда, получив корни \ (x = 2 \) и \ (x = -1 \), сразу отбросим корень \ (-1 \), и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно)
Найдите корень уравнения \ (\ displaystyle {{\ log} _ {x + 1}} \ left (2x + 5 \ right) = 2 \).Если корней несколько, в ответе укажите меньший из них.
Решение:
\ (\ displaystyle {{\ log} _ {x + 1}} \ left (2x + 5 \ right) = 2 \).
В первую очередь напишем ОДЗ:
\ (\ displaystyle \ left \ {\ begin {array} {l} x + 1> 0 \\ x + 1 \ ne 1 \\ 2x + 5> 0 \ end {array } \ right. \ text {} \ Leftrightarrow \ text {} \ left \ {\ begin {array} {l} x> -1 \\ x \ ne 0 \\ x> — \ frac {5} {2} \ end {array} \ right. \ text {} \ Leftrightarrow \ text {} \ left \ {\ begin {array} {l} x> -1 \\ x \ ne 0. \ end {array} \ right.{2}} — 4 = 0 \ text {} \ Leftrightarrow \ text {} \ left [\ begin {array} {l} x = 2 \\ x = -2. \ End {array} \ right.


 Например, десятичный логарифм.
Например, десятичный логарифм. 95424251.
95424251. Продавцы понимают, что скидки не являются средством повышения дохода. Наибольшую эффективность имеет не 1-2 скидки на конкретный товар, а система скидок, которая должна быть проста и понятна сотрудникам фирмы и ее покупателям.
Продавцы понимают, что скидки не являются средством повышения дохода. Наибольшую эффективность имеет не 1-2 скидки на конкретный товар, а система скидок, которая должна быть проста и понятна сотрудникам фирмы и ее покупателям. Затем рассчитайте ожидаемый объем прибыли, который вы хотели бы получить на продаваемый товар. Ее верхний предел будет органичен покупательной способностью товара и его конкурентными свойствами. Максимальную
Затем рассчитайте ожидаемый объем прибыли, который вы хотели бы получить на продаваемый товар. Ее верхний предел будет органичен покупательной способностью товара и его конкурентными свойствами. Максимальную  Подобными скидками пользуются супермаркеты для того, чтобы разгрузить работу магазина в вечерние часы и выходные дни. В данном случае размер скидки определяется размером упущенной выгоды при неудовлетворении покупательского спроса в часы пик.
Подобными скидками пользуются супермаркеты для того, чтобы разгрузить работу магазина в вечерние часы и выходные дни. В данном случае размер скидки определяется размером упущенной выгоды при неудовлетворении покупательского спроса в часы пик.
 Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4.
Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4. Например, для уравнений:
Например, для уравнений: Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов.
Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов. Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.
Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде. Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.
Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.

 Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.
Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции. Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.
Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.
 72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x.
72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x. Такой вариант подсчета создан на основе двух математических фактов:
Такой вариант подсчета создан на основе двух математических фактов:
 Позже диалог возобновился, но уже между Эйлером и Даламбером.
Позже диалог возобновился, но уже между Эйлером и Даламбером. Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .
Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .
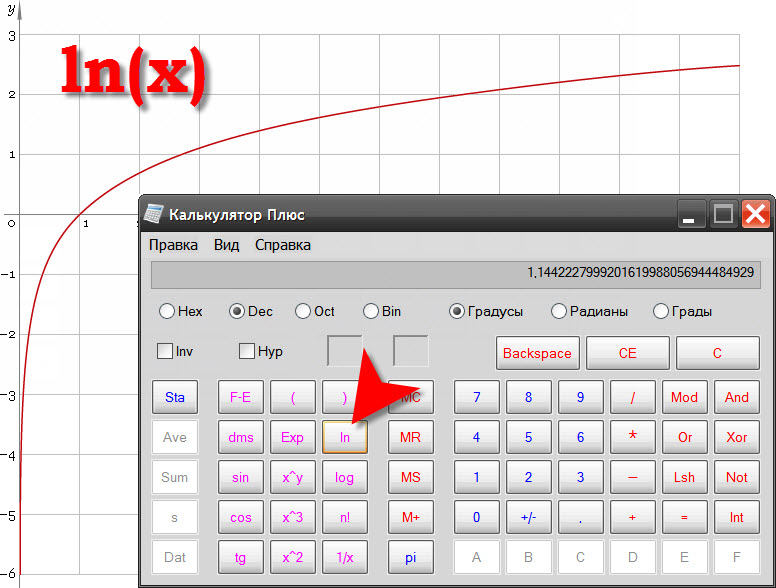


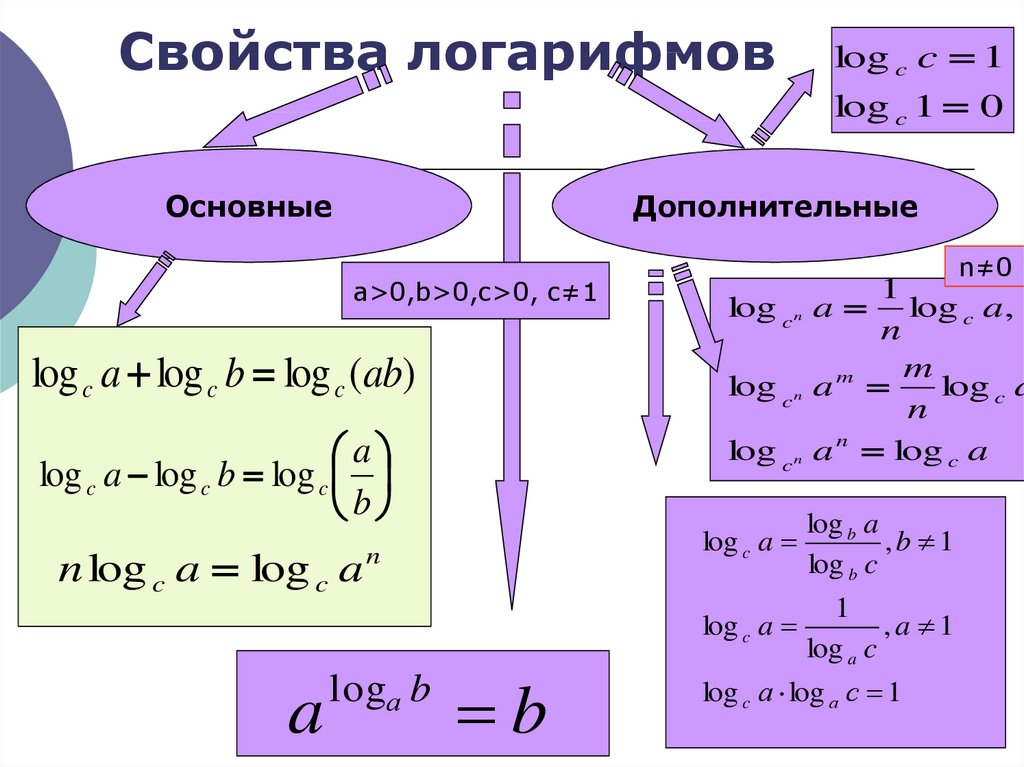 Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log3(−5)6=log356=6·log35.
Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log3(−5)6=log356=6·log35.
 Двойной логарифм обозначается как lg 2 (b). Двоичный логарифм числа b есть решение уравнения 2 x = b.
Двойной логарифм обозначается как lg 2 (b). Двоичный логарифм числа b есть решение уравнения 2 x = b. используя кнопку log , тогда нужно указать только число
используя кнопку log , тогда нужно указать только число