Конус ℹ️ определение, основные свойства и элементы геометрической фигуры, формулы нахождения площадей и объема, построение сечений, виды уравнений

Из огромного перечня математических заданий часто встречаются задачи, связанные с темой «Конус». На уроках геометрии школьники должны усвоить основные понятия и названия всех элементов этой фигуры и понять, как и по каким формулам производится расчет нужных параметров. 

О данной геометрической фигуре пойдёт речь в сегодняшней статье.

Определение и элементы конуса

Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние. 

При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.

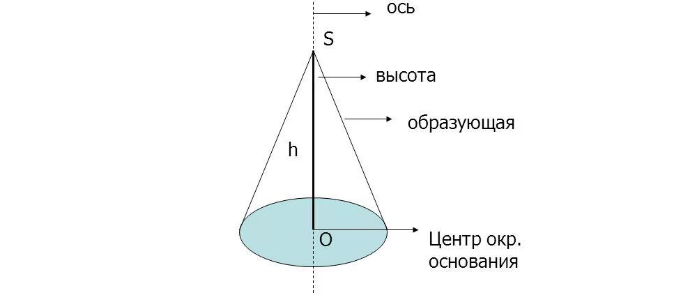
Обратите внимание! Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.

Хотелось бы рассмотреть ещё несколько понятий по этой теме:

1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:

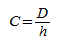
Важно! Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.

2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:

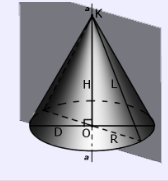
3. Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.

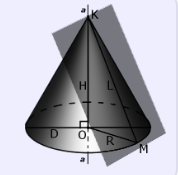
Свойства кругового конуса

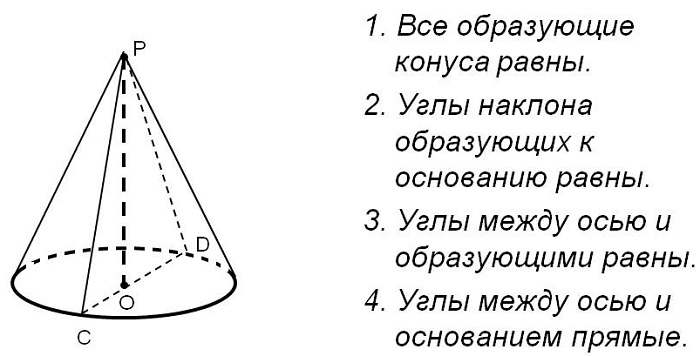
Выделяют несколько особенностей, которыми обладает фигура данного типа:

1. Образующие кругового конуса равны друг другу.

2. Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.

3. Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.

Интересный факт! Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.

Общая формула объёма фигуры

Чтобы найти объём кругового конуса, необходимо умножить число Пи на его высоту, на радиус в квадрате и всё это произведение поделить на три:

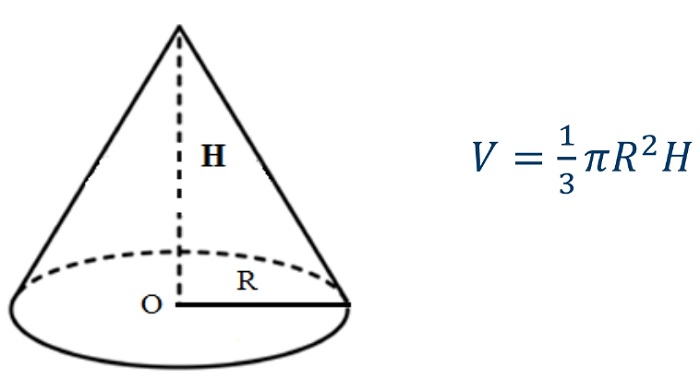
Дополнительная информация! Чтобы узнать объём фигуры, нужно умножить площадь её основы на высоту и поделить на три:

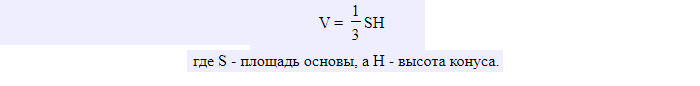
Объём усечённого конуса

Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:

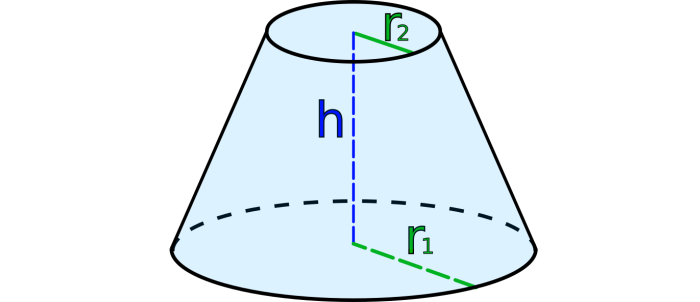
Объём данного тела можно вычислить по формуле:

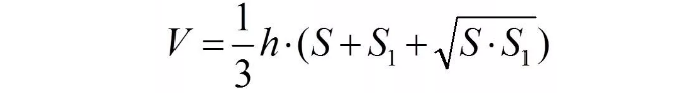
Важно! S и S₁ это площади соответствующих основ, которые равняются ПR² и ПR₁² При нахождении этих значений поможет онлайн калькулятор.

Площадь поверхности фигуры

Для вычисления данного параметра потребуется знать площадь боковой поверхности. Она равняется произведению числа π, радиуса и длины образующей.

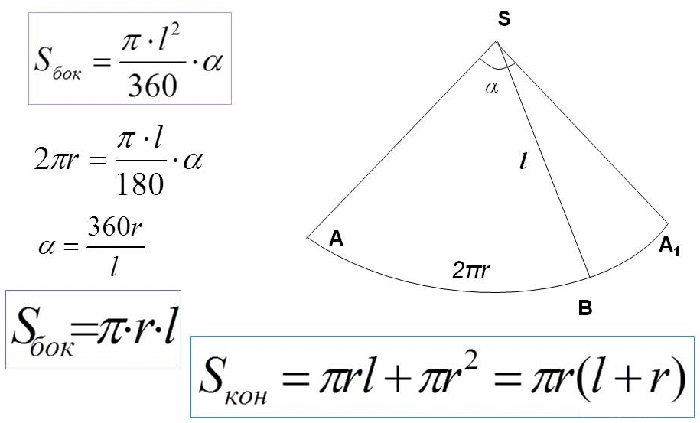
Чтобы рассчитать площадь всей поверхности, нужно сложить площади его основы и боковой поверхности.

Площадь усечённого конуса

Для нахождения данного параметра нужно воспользоваться формулами:

• площади боковой поверхности усечённого конуса S

  бок;

• полной площади усечённой фигуры S_пол, которая равна сумме площадей двух оснований и площади боковой поверхности:

Здесь l — длина образующей, а R и r — радиусы большего и меньшего оснований соответственно.

Уравнение конуса

Часто требуется при решении математических задач. Записывается в следующем виде:

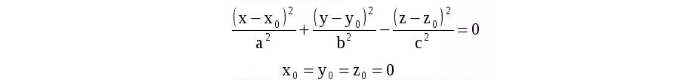
где x₀, y_0,z₀— координаты по соответствующим осям.

Таким образом, в данной статье были представлены основные сведения, которые могут понадобиться при решении задач на тему «Конус».

Конусность — Википедия

Материал из Википедии — свободной энциклопедии

а — полный конус.
б — усеченный конус.
В качестве примера приведено условное обозначение конусности по ГОСТ 2.307-68.

Конусность (C) — отношение диаметра окружности (D) основания конуса к его высоте (H) для полных конусов или отношение разности диаметров двух торцевых поперечных сечений конуса (

D и d) к расстоянию между ними (L) для усеченных конусов. Конусность, как правило, выражается в отношении двух чисел например конусность 1:10 означает что высота полного конуса в 10 раз больше диаметра основания.

C=DH=D−dL{\displaystyle C={\frac {D}{H}}={\frac {D-d}{L}}}

Также конусность может задаваться углом вершины конуса (α). Половина угла вершины конуса называется уклоном конуса (α/2).

C=2tg(α/2){\displaystyle C=2tg(\alpha /2)}

В некоторых странах (в основном это страны с распространенной имперской системой длины) конусность задают в виде диаметра основания конуса единичной высоты. Например 0,6 дюйма на фут или 0,05 дюйма на дюйм, что соответствует конусности 1:20.

Конусность может задаваться в процентах и промилле.

ГОСТ Р 53440-2009 (ГОСТ 8593-81 утратил силу на территории РФ с 01.01.2012) предусматривает следующие конусности:

1:500, 1:200, 1:100, 1:50, 1:30, 1:20, 1:15, 1:12, 1:10, 1:8, 1:7, 1:6, 1:5, 1:4, 1:3, 30°, 45°, 60°, 75°, 90°, 120°

Конусность	Угловая конусность	Уклон конуса
1:200	0° 17’ 12”	0° 8’ 36”
1:100	0° 34’ 23”	0° 17’ 11”
1:50	1° 8’ 45”	0° 34’ 23”
1:30	1° 54’ 35”	0° 57’ 17”
1:20	2° 51’ 51”	1° 25’ 56”
1:15	3° 49’ 6”	1° 54’ 33”
1:12	4° 46’ 19”	2° 23’ 9”
1:10	5° 43’ 29”	2° 51’ 45”
1:8	7° 9’ 10”	3° 34’ 35”
1:7	8° 10’ 16”	4° 5’ 8”
1:5	11° 25’ 16”	5° 42’ 38”
1:4	14° 15’ 0”	7° 7’ 30”
1:3	18° 55’ 29”	9° 27’ 44”
1:1,866	30°	15°
1:1,207	45°	22° 30’
1:0,866	60°	30°
1:0,652	75°	37° 30’
1:0,500	90°	45°
1:0,289	120°	60°

Конус — это… Что такое Конус?

Прямой круговой конус. Прямой и косой круговой конусы с равным основанием и высотой. Эти тела обладают одинаковым объёмом. Усечённый прямой круговой конус.

Ко́нус (от др.-греч. κώνος «шишка») — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют

основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Связанные определения

• Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
• Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.
• Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
• Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
• Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
• Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
• Круговой конус — конус, основание которого является кругом.
• Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
• Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
• Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.

Свойства

• Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
• Телесный угол при вершине прямого кругового конуса равен

где  — угол раствора конуса.

• Площадь боковой поверхности такого конуса равна

• Площадь поверхности такого конуса равна

где  — радиус основания,  — длина образующей.

• Объём кругового конуса равен

• Для усечённого конуса (не обязательно прямого и кругового) объём равен:

где S₁ и S₂ — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

Уравнение конуса

Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:

или

Это уравнение в каноническом виде записывается как

где константы a, с определяются пропорцией Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид

причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением где функция  является однородной, то есть удовлетворяющей условию для любого действительного числа α.

Развёртка

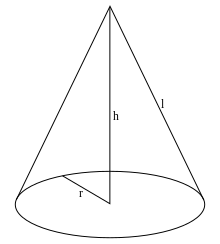
Развёртка прямого кругового конуса

Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора в развёртке боковой поверхности конуса определяется по формуле:

φ = 360°·(r/l).

С имеющимися и полученными значениями можно нарисовать развёртку конуса на бумаге или другом материале, чтобы из развёртки получить конус как наглядное пособие или промышленное изделие.

Вариации и обобщения

См. также

Литература

Конус (значения) — Википедия

Материал из Википедии — свободной энциклопедии

Перейти к навигации Перейти к поиску

Ко́нус.

• Конус — геометрическая фигура.
• Конус — топологическое пространство CX{\displaystyle \mathrm {C} X}, получающееся из произведения X×[0,1]{\displaystyle X\times [0,\;1]} стягиванием подпространства X×{0}{\displaystyle X\times \{0\}} в одну точку.
• Световой конус — гиперповерхность в пространстве-времени, ограничивающая области будущего и прошлого относительно заданного события.
• Конус^[en] — понятие, используемое для определения предела в теории категорий.

• Конус (остров) — остров.
• Конус выноса — отложения рыхлого материала при выходе рек из гор на равнину.
• Конусы (лат. Conidae) — семейство хищных морских брюхоногих моллюсков. Своё название получили из-за характерной формы раковины.
• Конусы (лат. Conus) — самый многочисленный род брюхоногих моллюсков из семейства конусов.
• «Конус» — 120-мм управляемая ракета ГККБ «Луч»^[1].

Скрытая категория:

Конус — Википедия. Что такое Конус

Материал из Википедии — свободной энциклопедии прямой круговой конус прямой и косой круговые конусы с равным основанием и высотой: они обладают одинаковым объёмом усечённый прямой круговой конус

Ко́нус (от др.-греч. κώνος «сосновая шишка»^[1]) — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Связанные определения

• образующая конуса — отрезок, соединяющий вершину и границу основания.
• образующая (или боковая) поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
• высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
• угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
• конусность — соотношение высоты и диаметра основания конуса.
• прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
• косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
• круговой конус — конус, основание которого является кругом.
• прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
• конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.
• усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.

Свойства

• Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

V=13SH,{\displaystyle V={1 \over 3}SH,}

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
• Телесный угол при вершине прямого кругового конуса равен

2π(1−cos⁡α2),{\displaystyle 2\pi \left(1-\cos {\alpha \over 2}\right),}

где α — угол раствора конуса.

• Площадь боковой поверхности такого конуса равна

S=πRl,{\displaystyle S=\pi Rl,}

а полная площадь поверхности (то есть сумма площадей боковой поверхности и основания)

S=πR(l+R),{\displaystyle S=\pi R(l+R),}

где R — радиус основания, l=R2+h3{\displaystyle l={\sqrt {R^{2}+H^{2}}}} — длина образующей.

• Объём кругового (не обязательно прямого) конуса равен

V=13πR2H.{\displaystyle V={1 \over 3}\pi R^{2}H.}

• Для усечённого кругового конуса (не обязательно прямого) объём равен:

V=13πH(R2+Rr+r2),{\displaystyle V={1 \over 3}\pi H(R^{2}+Rr+r^{2}),}

где R{\displaystyle R} и r{\displaystyle r}  — радиусы соответственно нижнего и верхнего оснований, H{\displaystyle H} — высота от плоскости нижнего основания,до верхнего основания.

• Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:

V=13(h3S2−h2S1),{\displaystyle V={1 \over 3}(H_{2}S_{2}-H_{1}S_{1}),}

где S1{\displaystyle S_{1}} и S2{\displaystyle S_{2}}  — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h2{\displaystyle H_{1}} и h3{\displaystyle H_{2}}  — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

Уравнение прямого кругового конуса

Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:

θ=Θ.{\displaystyle \theta =\Theta .}

z=r⋅ctg⁡Θ{\displaystyle z=r\cdot \operatorname {ctg} \Theta } или r=z⋅tg⁡Θ.{\displaystyle r=z\cdot \operatorname {tg} \Theta .}

z=±x2+y2⋅ctg⁡Θ.{\displaystyle z=\pm {\sqrt {x^{2}+y^{2}}}\cdot \operatorname {ctg} \Theta .}

Это уравнение в каноническом виде записывается как

x2a2+y2a2−z2c2=0,{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{a^{2}}}-{\frac {z^{2}}{c^{2}}}=0,}

где константы a, с определяются пропорцией c/a=cos⁡Θ/sin⁡Θ.{\displaystyle c/a=\cos \Theta /\sin \Theta .} Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид

x2a2+y2b2−z2c2=0,{\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0,}

причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением f(x,y,z)=0,{\displaystyle f(x,y,z)=0,} где функция f(x,y,z){\displaystyle f(x,y,z)} является однородной, то есть удовлетворяющей условию f(αx,αy,αz)=αnf(x,y,z){\displaystyle f(\alpha x,\alpha y,\alpha z)=\alpha ^{n}f(x,y,z)} для любого действительного числа α.

Развёртка

Развёртка прямого кругового конуса

Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора φ{\displaystyle \varphi } в развёртке боковой поверхности конуса определяется по формуле:

φ = 360°·(r/l).

Вариации и обобщения

См. также

Примечания

Литература

Конус — Вікіпедія

Прямий і похилий конуси

Ко́нус (геометрія) (лат. conus від дав.-гр. κώνος — «шпичак шолома», «шишка»)^[1] — геометричне тіло, отримане шляхом об’єднання всіх променів, що виходять з однієї точки — вершини конуса, і таких що проходять через довільну плоску криву. Іноді конусом називають частину такого тіла, отриману об’єднанням усіх відрізків, що з’єднують вершину і точки пласкої поверхні (яку в такому випадку називають основою конуса, а конус називають таким, що спирається на дану поверхню). Надалі буде розглядатися саме цей випадок, якщо не сказано про інше.

За ДСТУ: конус — узагальнений термін, під яким залежно від конкретних умов розуміють конічну поверхню, конічну деталь чи конічний елемент^[2].

Відрізок, опущений перпендикулярно з вершини на площину основи (а також його довжина), називається висотою конуса. Якщо площа основи має скінченне значення, то об’єм конуса також має скінченне значення і дорівнює третині добутку висоти на площу основи. Таким чином всі конуси, що спираються на дану основу, і мають вершину в площині, паралельній цій основі, мають рівний об’єм, оскільки їх висоти рівні. Якщо основою конуса є многокутник, тоді конус стає пірамідою. Таким чином піраміди є підмножиною конусів.

Відрізок, що сполучає вершину конуса з точкою границі його основи називається твірною конуса. Множина всіх твірних конуса називається бічною поверхнею конуса.

Якщо основа конуса має центр симетрії (наприклад, є еліпсом) і ортогональна проекція вершини конуса на його основу збігається з цим центром, то конус називається прямим. При цьому пряма, що сполучає вершину конуса з центром його основи називається віссю конуса. Якщо ж ортогональна проекція вершини не збігається з центром основи, то такий конус називається косим.

Означення кругового конуса[ред. | ред. код]

У курсі шкільної геометрії розглядають конус (точніше, прямий круговий конус). Конусом (точніше, круговим конусом) називається тіло, яке складається із круга — основи конуса, точки, що не лежить в площині цього круга, — вершини конуса і всіх відрізків, які з’єднують вершину конуса з точками основи.

Конус обертання[ред. | ред. код]

Прямий круговий конус (часто його називають просто конусом) можна отримати обертанням прямокутного трикутника навколо одного з катетів, який таким чином стане віссю конуса. Конус обертання в прямокутній системі координат описується системою нерівностей:

{x2+y2≤(zrh)20≤z≤h{\displaystyle \left\{{{x^{2}+y^{2}\leq \left({\frac {zr}{h}}\right)^{2}} \atop {0\leq z\leq h}}\right.}

де r>0, h>0{\displaystyle r>0,\ h>0}

З усіх конусів тільки прямий круговий є тілом обертання.

Перетин площини з прямим круговим конусом є одним з конічних перерізів (в невироджених випадках — еліпсом, параболою чи гіперболою, в залежності від розміщення січної площини).

Частина конуса, що лежить між основою і площиною, паралельною до основи і знаходиться між вершиною і основою, називається зрізаним конусом.

Конус, що спирається на еліпс, гіперболу чи параболу називається відповідно еліптичним, гіперболічним чи параболічним конусом (останні два мають нескінченний об’єм).

Площа поверхні конуса[ред. | ред. код]

Прямий круговий конус

Повна площа прямого кругового конуса

S=πrl+πr2{\displaystyle S=\pi rl+\pi r^{2}} ,

де r та l — радіус кола основи та довжина твірної бічної поверхні відповідно.

Площа бічної поверхні прямого кругового конуса

Sb=πrl{\displaystyle S_{b}=\pi rl},

де r та l — радіус кола основи та довжина твірної бічної поверхні відповідно.

Об’єм конуса[ред. | ред. код]

У загальному випадку:

V=13Sh{\displaystyle V={\frac {1}{3}}Sh},

де S — площа основи, h — висота конуса.

Об’єм кругового конуса, відповідно:

V=13πr2h{\displaystyle V={\frac {1}{3}}\pi r^{2}h},

Формулу об’єму конуса легко отримати із використанням інтегрального числення. Ми знаємо, що об’єм твердого тіла дорівнює інтегралу площі його перерізу вздовж певної осі. Отже, з точністю до сталої, це інтеграл ∫x2dx=13×3.{\displaystyle \int x^{2}dx={\tfrac {1}{3}}x^{3}.}

Кут конуса[ред. | ред. код]

Цей термін означає кут α{\displaystyle \alpha } при вершині в осьовому перерізі конуса.

α=2arctg⁡rh{\displaystyle \alpha =2\operatorname {arctg} {\frac {r}{h}}}

Вписані та описані тіла[ред. | ред. код]

Конус, описаний навколо піраміди[ред. | ред. код]

Конус можна описати навколо піраміди, якщо її основа — многокутник, навколо якого можна описати коло, а вершина піраміди проектується в центр цього кола. Радіус конуса дорівнює радіусу цього кола; висоти конуса і піраміди співпадають.

Конус, вписаний у піраміду[ред. | ред. код]

Конус можна вписати в піраміду, якщо її основа — многокутник, у який можна вписати коло, а вершина піраміди проектується в центр цього кола. Радіус конуса дорівнює радіусу цього кола; висота конуса і піраміди співпадають.

Куля, описана навколо конуса[ред. | ред. код]

Куля, описана навколо конуса

Кулю можна описати навколо довільного конуса. Коло основи конуса і вершина конуса лежать на поверхні кулі. Центр кулі лежить на осі конуса і співпадає з центром кола, описаного навколо трикутника, який є осьовим перерізом конуса. Переріз площиною, що проходить через вісь конуса (осьовий переріз). Об’єм кулі, описаної навколо прямого кругового конуса:

Vk=16πl6(l2−r2)l2−r2{\displaystyle V_{k}={1 \over 6}\pi {\frac {l^{6}}{(l^{2}-r^{2}){\sqrt {l^{2}-r^{2}}}}}}, де l{\displaystyle l} — твірна конуса; r{\displaystyle r} — радіус основи конуса.

Радіус кулі R, радіус основи конуса r і висота конуса H пов’язані співвідношенням: Куля, вписана в конусR2=(H−R)2+r2{\displaystyle R^{2}={\bigl (}H-R{\bigr )}^{2}+r^{2}}

Це співвідношення справедливе зокрема для випадку, коли H≤R{\displaystyle H\leq R}.

Куля, вписана в конус[ред. | ред. код]

Кулю можна вписати в довільний конус. Куля дотикається основи конуса в його центрі і бічної поверхні конуса по колу, що лежить в площині, яка паралельна основі конуса. Центр кулі лежить на осі конуса і співпадає з центром кола, вписаного в трикутник, що є осьовим перерізом конуса. Радіус кулі R, радіус основи конуса r і висота конуса H пов’язані співвідношенням: RH−R=rh3+r2{\displaystyle {\frac {R}{H-R}}={\frac {r}{\sqrt {H^{2}+r^{2}}}}}

Земляний конус

Форму конусів мають насипані на горизонтальній поверхні купи піску, зерна, вугілля, породи, щебеню тощо. Кожному такому матеріалу відповідає кут природного укосу^[3]— кут нахилу твірної до площини основи конуса. Для піску він дорівнює приблизно 30°, для вугілля — 42°, для породи — 46°.

1. Геометрія. 10-11 класи [Текст]: пробний підручник / Афанасьєва О. М. [та ін.]. — Тернопіль: Навчальна книга- Богдан, 2003. — 264 с. — ISBN 966-692-161-8

2. Геометрія. 11 клас [Текст]: підручник для загальноосвітніх навчальних закладів: академічний рівень, профіл.рівень / Бевз Г. П. [та ін.]. — Київ: Генеза, 2011. — 336 с.

3. Геометрія: Стереометрія: 10-11 класи [Текст]: підручник / Погорєлов О. В.  — Київ: Освіта, 2001. — 128 с.

4. Наочний довідник з геометрії [Текст] / Генденштейн Л. Е., Єршова А. П.  — Харків — Тернопіль: Гімназія — Підручники і посібники, 1997. — 96 с.

Конус. Формули, ознаки та властивості

Елементи конуса

Означення. Вершина конуса — це точка (K), з якої виходять промені.

Означення. Основа конуса — це площина, що утворена внаслідок перетину плоскої поверхні та всіх променів, що виходять з вершини конуса. У конуса можуть бути такі основи, як круг, еліпс, гіпербола та парабола.

Означення. Твірною конуса (L) називається будь-який відрізок, які сполучає вершину конуса з межею основи конуса. Твірна є відрізком променя, що виходить з вершини конуса.

Формула. Довжина твірної (L) прямого кругового конуса через радіус R та висоту H (через теорему Піфагора):

L² = R² + H²

Означення. Напрямна конуса — це крива, яка описує контур основи конуса.

Означення. Бічна поверхня конуса — це сукупність усіх твірних конуса. Тобто, поверхня, яка утворюється рухом твірної по напрямній конуса.

Означення. Поверхня конуса складається з бічної поверхні та основи конуса.

Означення.Висота конуса (H) — це відрізок, який виходить з вершини конуса та перпендикулярний до його основи.

Означення. Вісь конуса (a) — це пряма, яка проходить через вершину конуса та центр основи конуса.

Означення. Конусність (С) конуса — це відношення діаметра основи конуса до його висоти. У випадку зрізаного конуса — це відношення різниці діамерів поперечних перерізів D та d зрізаного конуса до відстані між ними:

C =	D	та      C =	D — d
	H		d

де C — конусність, D — діаметр основи, d — діаметр меншої основи та h — відстань між основами.

Конусність характеризує гостроту конуса, тобто, кут нахилу твірної до основи конуса. Чим більша конусність, тим гостріший кут нахилу. Кут конуса α буде:

де R — радіус основи, а H — висота конуса. Означення. Осьовий переріз конуса — це переріз конуса площиною, яка проходить через вісь конуса. Такий переріз утворює рівнобедрений трикутник, у якого сторони утворені твірними, а основа трикутника — це діаметр основи конуса. Означення. Дотична площина до конуса — це площина, яка проходить через твірну конуса і перепендикулярна до осьового перерізу конуса.

Означення. Конус, що спирається на круг, еліпс, гіперболу чи параболу називається відповідно круговим, еліптичним, гіперболічним чи параболічним конусом (останні два мають нескінченний об’єм).

Основні властивості кругового конуса

1. Всі твірні прямого кругового конуса рівні між собою.

2. При обертанні прямокутного трикутника навколо свого катета на 360° утворюється прямий коловий конус.

3. При обертанні рівнобедреного трикутника навколо своєї вісі на 180° утворюється прямий коловий конус.

4. В місці перетину конуса площиною, яка паралельна основі конуса, утворюється коло. (див. Зрізаний конус)

5. Якщо при перетині площина не паралельна основі конуса і не перетинається з основою, то в місці перетину утвориться еліпс (мал. 3).

6. Якщо площина перерізу проходить через основу, то в місці перетину утвориться парабола (мал. 4).

7. Якщо площина перерізу проходить через вершину, то в місці перетину утвориться рівнобедрений трикутник (див. Осьовий переріз).

8. Центр ваги будь-якого конуса знаходиться на одній четвертій висоти від центра основи.

Будь-які нецензурні коментарі будуть видалені, а їх автори занесені в чорний список!