Определение степени свойства: Свойства степеней, действия со степенями

Posted on by alexxlab

Содержание

Степень и ее свойства. Определение степени

После того как определена степень числа , логично поговорить про свойства степени . В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров.

Навигация по странице.

Свойства степеней с натуральными показателями

По определению степени с натуральным показателем степень a n представляет собой произведение n множителей, каждый из которых равен a . Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел , можно получить и обосновать следующие свойства степени с натуральным показателем :

  1. основное свойство степени a m ·a n =a m+n , его обобщение ;
  2. свойство частного степеней с одинаковыми основаниями a m:a n =a m−n ;
  3. свойство степени произведения (a·b) n =a n ·b n , его расширение ;
  4. свойство частного в натуральной степени (a:b) n =a n:b n ;
  5. возведение степени в степень (a m) n =a m·n , его обобщение (((a n 1) n 2) …) n k =a n 1 ·n 2 ·…·n k ;
  6. сравнение степени с нулем:
    • если a>0 , то a n >0 для любого натурального n ;
    • если a=0 , то a n =0 ;
    • если a0 , если aнечетное число 2·m−1 , то a 2·m−1
  7. если a и b – положительные числа и a
  8. если m и n такие натуральные числа, что m>n , то при 00 справедливо неравенство a m >a n .

Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби a m ·a n =a m+n при упрощении выражений часто применяется в виде a m+n =a m ·a n .

Теперь рассмотрим каждое из них подробно.

    Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называют

    основным свойством степени : для любого действительного числа a и любых натуральных чисел m и n справедливо равенство a m ·a n =a m+n .

    Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a m ·a n можно записать как произведение . В силу свойств умножения полученное выражение можно записать как , а это произведение есть степень числа a с натуральным показателем m+n , то есть, a m+n . На этом доказательство завершено.

    Приведем пример, подтверждающий основное свойство степени. Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3 , по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень , имеем 2 2 ·2 3 =(2·2)·(2·2·2)=4·8=32 и 2 5 =2·2·2·2·2=32 , так как получаются равные значения, то равенство 2 2 ·2 3 =2 5 — верное, и оно подтверждает основное свойство степени.

    Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями. Так для любого количества k натуральных чисел n 1 , n 2 , …, n k справедливо равенство a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k .

    Например, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .

    Можно переходить к следующему свойству степеней с натуральным показателем – свойству частного степеней с одинаковыми основаниями : для любого отличного от нуля действительного числа a и произвольных натуральных чисел m и n , удовлетворяющих условию m>n , справедливо равенство a m:a n =a m−n .

    Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0 n =0 , а при знакомстве с делением мы условились, что на нуль делить нельзя. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n ), либо отрицательным числом (что происходит при m

    Доказательство. Основное свойство дроби позволяет записать равенство a m−n ·a n =a (m−n)+n =a m . Из полученного равенства a m−n ·a n =a m и из следует, что a m−n является частным степеней a m и a n . Этим доказано свойство частного степеней с одинаковыми основаниями.

    Приведем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2 , рассмотренному свойству степени отвечает равенство π 5:π 2 =π 5−3 =π 3 .

    Теперь рассмотрим свойство степени произведения : натуральная степень n произведения двух любых действительных чисел a и b равна произведению степеней a n и b n , то есть, (a·b) n =a n ·b n .

    Действительно, по определению степени с натуральным показателем имеем . Последнее произведение на основании свойств умножения можно переписать как , что равно a n ·b n .

    Приведем пример: .

    Данное свойство распространяется на степень произведения трех и большего количества множителей. То есть, свойство натуральной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .

    Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .

    Следующее свойство представляет собой свойство частного в натуральной степени : частное действительных чисел a и b , b≠0 в натуральной степени n равно частному степеней a n и b n , то есть, (a:b) n =a n:b n .

    Доказательство можно провести, используя предыдущее свойство. Так (a:b) n ·b n =((a:b)·b) n =a n , а из равенства (a:b) n ·b n =a n следует, что (a:b) n является частным от деления a n на b n .

    Запишем это свойство на примере конкретных чисел: .

    Теперь озвучим свойство возведения степени в степень : для любого действительного числа a и любых натуральных чисел m и n степень a m в степени n равна степени числа a с показателем m·n , то есть, (a m) n =a m·n .

    Например, (5 2) 3 =5 2·3 =5 6 .

    Доказательством свойства степени в степени является следующая цепочка равенств: .

    Рассмотренное свойство можно распространить на степень в степени в степени и т.д. Например, для любых натуральных чисел p , q , r и s справедливо равенство . Для большей ясности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .

    Осталось остановиться на свойствах сравнения степеней с натуральным показателем.

    Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.

    Для начала обоснуем, что a n >0 при любом a>0 .

    Произведение двух положительных чисел является положительным числом, что следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .

    Достаточно очевидно, что для любого натурального n при a=0 степень a n есть нуль. Действительно, 0 n =0·0·…·0=0 . К примеру, 0 3 =0 и 0 762 =0 .

    Переходим к отрицательным основаниям степени.

    Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m , где m — натуральное. Тогда . По каждое из произведений вида a·a равно произведению модулей чисел a и a , значит, является положительным числом. Следовательно, положительным будет и произведение и степень a 2·m . Приведем примеры: (−6) 4 >0 , (−2,2) 12 >0 и .

    Наконец, когда основание степени a является отрицательным числом, а показатель степени есть нечетное число 2·m−1 , то . Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 .

    Переходим к свойству сравнения степеней с одинаковыми натуральными показателями, которое имеет следующую формулировку: из двух степеней с одинаковыми натуральными показателями n меньше та, основание которой меньше, а больше та, основание которой больше. Докажем его.

    Неравенство a n свойств неравенств справедливо и доказываемое неравенство вида a n .

    Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем его. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями, меньшими единицы, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше. Переходим к доказательству этого свойства.

    Докажем, что при m>n и 00 в силу исходного условия m>n , откуда следует, что при 0

    Осталось доказать вторую часть свойства. Докажем, что при m>n и a>1 справедливо a m >a n . Разность a m −a n после вынесения a n за скобки принимает вид a n ·(a m−n −1) . Это произведение положительно, так как при a>1 степень a n есть положительное число, и разность a m−n −1 есть положительное число, так как m−n>0 в силу начального условия, и при a>1 степень a m−n больше единицы. Следовательно, a m −a n >0 и a m >a n , что и требовалось доказать. Иллюстрацией этого свойства служит неравенство 3 7 >3 2 .

Свойства степеней с целыми показателями

Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.

Степень с целым отрицательным показателем , а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.

Итак, для любых действительных и отличных от нуля чисел a и b , а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями :

  1. a m ·a n =a m+n ;
  2. a m:a n =a m−n ;
  3. (a·b) n =a n ·b n ;
  4. (a:b) n =a n:b n ;
  5. (a m) n =a m·n ;
  6. если n – целое положительное число, a и b – положительные числа, причем ab −n ;
  7. если m и n – целые числа, причем m>n , то при 01 выполняется неравенство a m >a n .

При a=0 степени a m и a n имеют смысл лишь когда и m , и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.

Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (a p) q =a p·q , (a −p) q =a (−p)·q , (a p) −q =a p·(−q) и (a −p) −q =a (−p)·(−q) . Сделаем это.

Для положительных p и q равенство (a p) q =a p·q доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0·q =a 0 =1 , откуда (a 0) q =a 0·q . Аналогично, если q=0 , то (a p) 0 =1 и a p·0 =a 0 =1 , откуда (a p) 0 =a p·0 . Если же и p=0 и q=0 , то (a 0) 0 =1 0 =1 и a 0·0 =a 0 =1 , откуда (a 0) 0 =a 0·0 .

Теперь докажем, что (a −p) q =a (−p)·q . По определению степени с целым отрицательным показателем , тогда . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению является степенью вида a −(p·q) , которую в силу правил умножения можно записать как a (−p)·q .

Аналогично .

И .

По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.

В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a −n >b −n , которое справедливо для любого целого отрицательного −n и любых положительных a и b , для которых выполняется условие a. Так как по условию a0 . Произведение a n ·b n тоже положительно как произведение положительных чисел a n и b n . Тогда полученная дробь положительна как частное положительных чисел b n −a n и a n ·b n . Следовательно, откуда a −n >b −n , что и требовалось доказать.

Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.

Свойства степеней с рациональными показателями

Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:

Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на и на свойствах степени с целым показателем. Приведем доказательства.

По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено.

Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:

По схожим принципам доказываются и остальные равенства:

Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b , a b p . Запишем рациональное число p как m/n , где m – целое число, а n – натуральное. Условиям p0 в этом случае будут эквивалентны условия m0 соответственно. При m>0 и a

Аналогично, при mb m , откуда , то есть, и a p >b p .

Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q , p>q при 00 – неравенство a p >a q . Мы всегда можем привести к общему знаменателю рациональные числа p и q , пусть при этом мы получим обыкновенные дроби и , где m 1 и m 2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m 1 >m 2 , что следует из . Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 01 – неравенство a m 1 >a m 2 . Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 00 – неравенство a p >a q .

Свойства степеней с иррациональными показателями

Из того, как определяется степень с иррациональным показателем , можно заключить, что она обладает всеми свойствами степеней с рациональными показателями. Так для любых a>0 , b>0 и иррациональных чисел p и q справедливы следующие свойства степеней с иррациональными показателями :

  1. a p ·a q =a p+q ;
  2. a p:a q =a p−q ;
  3. (a·b) p =a p ·b p ;
  4. (a:b) p =a p:b p ;
  5. (a p) q =a p·q ;
  6. для любых положительных чисел a и b , a0 справедливо неравенство a p b p ;
  7. для иррациональных чисел p и q , p>q при 00 – неравенство a p >a q .

Отсюда можно сделать вывод, что степени с любыми действительными показателями p и q при a>0 обладают этими же свойствами.

Список литературы.

  • Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. МатематикаЖ учебник для 5 кл. общеобразовательных учреждений.
  • Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 кл. общеобразовательных учреждений.
  • Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
  • Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 9 кл. общеобразовательных учреждений.
  • Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
  • Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Основная цель

Ознакомить учащихся со свойствами степеней с натуральными показателями и научить выполнять действия со степенями.

Тема “ Степень и её свойства ” включает три вопроса:

  • Определение степени с натуральным показателем.
  • Умножение и деление степеней.
  • Возведение в степень произведения и степени.

Контрольные вопросы

  1. Сформулируйте определение степени с натуральным показателем, большим 1. Приведите пример.
  2. Сформулируйте определение степени с показателем 1. Приведите пример.
  3. Каков порядок выполнения действий при вычислении значения выражения, содержащего степени?
  4. Сформулируйте основное свойство степени. Приведите пример.
  5. Сформулируйте правило умножения степеней с одинаковыми основаниями. Приведите пример.
  6. Сформулируйте правило деления степеней с одинаковыми основаниями. Приведите пример.
  7. Сформулируйте правило возведения в степень произведения. Приведите пример. Докажите тождество (ab) n = a n b n .
  8. Сформулируйте правило возведения степени в степень. Приведите пример. Докажите тождество (а m) n = а m n .

Определение степени.

Степенью числа a с натуральным показателем n , большим 1, называется произведение n множителей, каждый из которых равен а . Степенью числа а с показателем 1 называется само число а .

Степень с основанием а и показателем n записывается так: а n . Читается “ а в степени n ”; “ n- я степень числа а ”.

По определению степени:

а 4 = а а а а

. . . . . . . . . . . .

Нахождение значения степени называют возведением в степень .

1. Примеры возведения в степень:

3 3 = 3 3 3 = 27

0 4 = 0 0 0 0 = 0

(-5) 3 = (-5) (-5) (-5) = -125

25 ; 0,09 ;

25 = 5 2 ; 0,09 = (0,3) 2 ; .

27 ; 0,001 ; 8 .

27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .

4. Найти значения выражений:

а) 3 10 3 = 3 10 10 10 = 3 1000 = 3000

б) -2 4 + (-3) 2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7

Вариант 1

а) 0,3 0,3 0,3

в) b b b b b b b

г) (-х) (-х) (-х) (-х)

д) (ab) (ab) (ab)

2. Представьте в виде квадрата числа:

3. Представьте в виде куба числа:

4. Найти значения выражений:

в) -1 4 + (-2) 3

г) -4 3 + (-3) 2

д) 100 — 5 2 4

Умножение степеней.

Для любого числа а и произвольных чисел m и n выполняется:

a m a n = a m + n .

Доказательство:

Правило : При умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают.

a m a n a k = a m + n a k = a (m + n) + k = a m + n + k

а) х 5 х 4 = х 5 + 4 = х 9

б) y y 6 = y 1 y 6 = y 1 + 6 = y 7

в) b 2 b 5 b 4 = b 2 + 5 + 4 = b 11

г) 3 4 9 = 3 4 3 2 = 3 6

д) 0,01 0,1 3 = 0,1 2 0,1 3 = 0,1 5

а) 2 3 2 = 2 4 = 16

б) 3 2 3 5 = 3 7 = 2187

Вариант 1

1. Представить в виде степени:

а) х 3 х 4 е) х 2 х 3 х 4

б) а 6 а 2 ж) 3 3 9

в) у 4 у з) 7 4 49

г) а а 8 и) 16 2 7

д) 2 3 2 4 к) 0,3 3 0,09

2. Представить в виде степени и найти значение по таблице:

а) 2 2 2 3 в) 8 2 5

б) 3 4 3 2 г) 27 243

Деление степеней.

Для любого числа а0 и произвольных натуральных чисел m и n, таких, что m>n выполняется:

a m: a n = a m — n

Доказательство:

a m — n a n = a (m — n) + n = a m — n + n = a m

по определению частного:

a m: a n = a m — n .

Правило : При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Определение: Степень числа а, не равного нулю, с нулевым показателем равна единице :

т.к. а n: a n = 1 при а0 .

а) х 4:х 2 = х 4 — 2 = х 2

б) у 8:у 3 = у 8 — 3 = у 5

в) а 7:а = а 7:а 1 = а 7 — 1 = а 6

г) с 5:с 0 = с 5:1 = с 5

а) 5 7:5 5 = 5 2 = 25

б) 10 20:10 17 = 10 3 = 1000

в)

г)

д)

Вариант 1

1. Представьте в виде степени частное:

2. Найдите значения выражений:

Возведение в степень произведения.

Для любых а и b и произвольного натурального числа n:

(ab) n = a n b n

Доказательство:

По определению степени

(ab) n =

Сгруппировав отдельно множители а и множители b, получим:

=

Доказанное свойство степени произведения распространяется на степень произведения трех и более множителей.

Например:

(a b c) n = a n b n c n ;

(a b c d) n = a n b n c n d n .

Правило : При возведении в степень произведения возводят в эту степень каждый множитель и результат перемножают.

1. Возвести в степень:

а) (a b) 4 = a 4 b 4

б) (2 х у) 3 =2 3 х 3 у 3 = 8 х 3 у 3

в) (3 а) 4 = 3 4 а 4 = 81 а 4

г) (-5 у) 3 = (-5) 3 у 3 = -125 у 3

д) (-0,2 х у) 2 = (-0,2) 2 х 2 у 2 = 0,04 х 2 у 2

е) (-3 a b c) 4 = (-3) 4 a 4 b 4 c 4 = 81 a 4 b 4 c 4

2. Найти значение выражения:

а) (2 10) 4 = 2 4 10 4 = 16 1000 = 16000

б) (3 5 20) 2 = 3 2 100 2 = 9 10000= 90000

в) 2 4 5 4 = (2 5) 4 = 10 4 = 10000

г) 0,25 11 4 11 = (0,25 4) 11 = 1 11 = 1

д)

Вариант 1

1. Возвести в степень:

б) (2 а с) 4

д) (-0,1 х у) 3

2. Найти значение выражения:

б) (5 7 20) 2

Возведение в степень степени.

Для любого числа а и произвольных натуральных чисел m и n:

(а m) n = а m n

Доказательство:

По определению степени

(а m) n =

Правило: При возведении степени в степень основание оставляют тем же, а показатели перемножают .

1. Возвести в степень:

(а 3) 2 = а 6 (х 5) 4 = х 20

(у 5) 2 = у 10 (b 3) 3 = b 9

2. Упростите выражения:

а) а 3 (а 2) 5 = а 3 а 10 = а 13

б) (b 3) 2 b 7 = b 6 b 7 = b 13

в) (х 3) 2 (х 2) 4 = х 6 х 8 = х 14

г) (у у 7) 3 = (у 8) 3 = у 24

а)

б)

Вариант 1

1. Возвести в степень:

а) (а 4) 2 б) (х 4) 5

в) (у 3) 2 г) (b 4) 4

2. Упростите выражения:

а) а 4 (а 3) 2

б) (b 4) 3 b 5+

в) (х 2) 4 (х 4) 3

г) (у у 9) 2

3. Найдите значение выражений:

Приложение

Определение степени.

Вариант 2

1ю Запишите произведение в виде степени:

а) 0,4 0,4 0,4

в) а а а а а а а а

г) (-у) (-у) (-у) (-у)

д) (bс) (bс) (bс)

2. Представьте в виде квадрата числа:

3. Представьте в виде куба числа:

4. Найти значения выражений:

в) -1 3 + (-2) 4

г) -6 2 + (-3) 2

д) 4 5 2 – 100

Вариант 3

1. Запишите произведение в виде степени:

а) 0,5 0,5 0,5

в) с с с с с с с с с

г) (-х) (-х) (-х) (-х)

д) (ab) (ab) (ab)

2. Представьте в виде квадрата числа: 100 ; 0,49 ; .

3. Представьте в виде куба числа:

4. Найти значения выражений:

в) -1 5 + (-3) 2

г) -5 3 + (-4) 2

д) 5 4 2 — 100

Вариант 4

1. Запишите произведение в виде степени:

а) 0,7 0,7 0,7

в) х х х х х х

г) (-а) (-а) (-а)

д) (bс) (bс) (bс) (bc)

2. Представьте в виде квадрата числа:

3. Представьте в виде куба числа:

4. Найти значения выражений:

в) -1 4 + (-3) 3

г) -3 4 + (-5) 2

д) 100 — 3 2 5

Умножение степеней.

Вариант 2

1. Представить в виде степени:

а) х 4 x 5 е) х 3 х 4 х 5

б) а 7 а 3 ж) 2 3 4

в) у 5 у з) 4 3 16

г) а а 7 и) 4 2 5

д) 2 2 2 5 к) 0,2 3 0,04

2. Представить в виде степени и найти значение по таблице:

а) 3 2 3 3 в) 16 2 3

б) 2 4 2 5 г) 9 81

Вариант 3

1. Представить в виде степени:

а) а 3 а 5 е) у 2 у 4 у 6

б) х 4 х 7 ж) 3 5 9

в) b 6 b з) 5 3 25

г) у у 8 и) 49 7 4

д) 2 3 2 6 к) 0,3 4 0,27

2. Представить в виде степени и найти значение по таблице:

а) 3 3 3 4 в) 27 3 4

б) 2 4 2 6 г) 16 64

Вариант 4

1. Представить в виде степени:

а) а 6 а 2 е) х 4 х х 6

б) х 7 х 8 ж) 3 4 27

в) у 6 у з) 4 3 16

г) х х 10 и) 36 6 3

д) 2 4 2 5 к) 0,2 2 0,008

2. Представить в виде степени и найти значение по таблице:

а) 2 6 2 3 в) 64 2 4

б) 3 5 3 2 г) 81 27

Деление степеней.

Вариант 2

1. Представьте в виде степени частное:

2. Найдите значения выражений.

Урок на тему: «Правила умножения и деления степеней с одинаковыми и разными показателями. Примеры»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. 3}=\frac{8}{125}

Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.

Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .

Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n . a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные .

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов. 5}$. Ответ: $\frac{2x}{1}$ или 2x.

3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .

4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.

Что такое степень числа? Ответ на webmath.ru

Содержание:

Определение степени числа

Натуральной $n$-й степенью действительного числа $a$ называется действительное число $b$, получаемое в результате умножения числа $a$ самого на себя $n$ раз:

$n$-ю степень числа $a$ обозначают $a_n$ и пишут $b=a_n$ . 2 = -16$  

Решение. 1) Степень $x$ четная, поэтому возможны два значения:

$$x_{1}=\sqrt[1]{81}=3, x_{2}=-\sqrt[1]{81}=-3$$

2) Степень $y$ нечетная, поэтому данное уравнение имеет единственный корень:

$$y=\sqrt[3]{-125}=-\sqrt[3]{125}=-5$$

3) Это уравнение можно преобразовать к виду: $z = \sqrt{-16}$ . Нельзя извлечь корень четной степени из отрицательного числа. Поэтому действительных корней данное уравнение не имеет.

Ответ.  1) $x_1 = 3, x_2 = -3$

             2) $y = -5$

             3) решений нет.

Для любого $x$

Корень второй степени из числа называют квадратным корнем, а показатель 2 корня при записи опускают.

Например. Корень квадратный из 7 обозначают просто $\sqrt{7}$ .

Корень третей степени называют кубичным корнем: $\sqrt[3]{a}$ .

Алгебраические свойства корней

Для любых натуральных $n$ и $k$, больших единицы, и любых неотрицательных $a$ и $b$ верны равенства:

Степенью числа $a \gt 0$ с рациональным показателем $r = \frac{m}{n}$, где $m$ — целое число, а $n$ — натуральное ($n \gt 1$), называется число $a^{\frac{m}{n}}=\sqrt[n]{a^{m}}$. При $a \lt 0$ , рациональная степень числа $a$ не определена. Все свойства степеней с натуральным показателем справедливы так же и для степеней с рациональным показателем.

Читать дальше: что такое модуль числа.

Определение степени с целым отрицательным показателем

В курсе математики 7 класса вы научились вычислять значение степени с любым натуральным показателем.

Напомним, что степенью числа а с натуральным показателем  (), называется выражение , которое равно произведению  множителей, каждый из которых равен .

Степенью числа а с показателем единица является само число а. А вот при возведении в степень нуля всегда получаем нуль.

Также вам уже известны свойства степеней с натуральными показателями.

При умножении степеней с одинаковыми основаниями основание остаётся прежним, а показатели степеней складываются. Т.е. для любого числа  и натуральных чисел  и  верно равенство:

При делении степеней с одинаковыми основаниями основание остаётся прежним, а из показателя степени делимого вычитается показатель степени делителя. Т.е. для любого числа  и натуральных чисел  и , таких, что , справедливо равенство:

Чтобы возвести в степень произведение, нужно каждый множитель возвести в эту степень и результаты перемножить. Аналогично и для частного. Т.е. для любых чисел  и  и натурального числа  верно равенство:

При возведении степени в степень основание оставляют прежним, а показатели степеней перемножают. Т.е. для любого числа  и произвольных натуральных чисел  и верно равенство:

Заметим, что

Рассмотрим случай, когда показатель степени делимого меньше показателя степени делителя.

Такое соглашение принимается для степеней с любыми основаниями, отличными от нуля.

Определение:

Если  и  – целое отрицательное число, то верно равенство:

Задание: заменить степень с целым отрицательным показателем дробью.

Решение:

Замечание: поскольку деление на нуль невозможно, такие выражения, как , не имеют смысла.

Напомним, что при натуральном  выражение .

Задание: представьте числа в виде степени с основанием 3.

Решение:

Задание: найдите значения выражений.

Решение:

Итоги:

Свойства степени с натуральным показателем

1. Разгадайте ребусы

Степень
Повторение
Обобщение
Урок повторения и
обобщения по теме
«Свойства степени
с натуральным
показателем»

3. Цели:

1. Повторить и обобщить наши знания по
данной теме.
2. Ликвидировать имеющиеся пробелы.
3. Подготовиться к изучению следующей темы.

4. «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь.» М.В.Ломоносов

5. Повторим!

Сформулируйте определение
степени числа с натуральным
показателем.
Степенью числа a с натуральным
показателем n, большим 1, называется
произведение n множителей, каждый из
которых равен а:
аⁿ = а·а·а·…·а
n
Степенью числа а с показателем 1
называется само число а:
а¹ = а
Определение степени
5
Основание
7
Показатель
Умножение степеней с одинаковыми
основаниями
a a a
m
n
m n
При умножении степеней с
одинаковыми основаниями основание
оставляют прежним, а показатели
складывают.
Деление степеней с одинаковыми
основаниями
a a a
m
n
При делении степеней с
одинаковыми основаниями
основание оставляют прежним, а
из показателя делимого
вычитают показатель делителя.
m n
Возведение в степень степени
a
m
n
a
mn
При возведении степени в степень
основание оставляют прежним, а
показатели перемножают.
Возведение в степень дроби
a
b
n
an
bn
При возведении в степень дроби возводят в эту
степень числитель и знаменатель дроби.
Возведение в степень произведения
ab
n
a b
n
n
При возведении в степень произведения возводят в эту
степень каждый множитель и результаты
перемножают.
Задание 1.Найдите с помощью стрелок верные высказывания.
Слева указаны начала определений, справа — окончания определений.
Соедините линиями верные высказывания.
а) При умножении степеней с
одинаковыми основаниями …
1)основанием степени
б) При делении степеней с
одинаковыми основаниями ….
2) Показатель степени
в) Число а называют
3) произведение n множителей,
каждый из которых равен а.
г) При возведении степени в степень
…
4)… основание остается прежним , а
показатели складываются.
д)Степенью числа а с натуральным
показателем n, большим 1,
называется
е) Число n называют
5)… основание остается прежним, а
показатели перемножаются.
ж) Выражение а n называют
7)…основание остается прежним , а
показатели вычитаются.
6) Степенью
Ответы: а – 4, б – 7, в – 1, г – 5, д – 3, е – 2, ж – 6.
7 баллов – молодец!
6 баллов – очень хорошо!
5 баллов – хорошо!
4 балла – не очень хорошо!
3 балла – плохо!
0-2 балла – очень плохо!
Задание 2 (устно). Записать в виде степени
4
3
у у уу
=
9
у
2
3
4
((х ) ) =
24
х
=
= 64
6
8
4
8
2
8
Задание 3. Записать в виде степени с основанием с.
Вариант 1.
Вариант 2.
1. С5 • С3
1. С7 : С5
2. С8 : С6
2. (С4)3 • С
3. (С4)3
3. С4 • С5 • С0
4. С5 • С3 : С6
4. С16 : С8
5. С14 • С8
5. (С3)5
Р
Ш
М
Ю
К
Н
А
Т
Е
Д
С8
С5
С1 С40 С13 С12 С9 С15 С2 С22
Особо следует отметить переработанную им математическую
символику, близкую к современной. Коэффициенты он
обозначал a, b, c…, а неизвестные — x, y, z.
Натуральный показатель степени принял современный вид.
Задание 4. Определите, какие ответы правильные, а какие
ложные.
• истинному ответу поставьте в соответствие 1, ложному – 0.
• получив упорядоченный набор из единиц и нулей, вы узнаете
имя еще одного известного математика.
а) x2 x3 = x5
б) s3 s5 s8 = s16
в) x7 : x4 = x28
г) (c+d)8 :(c+d) 7 = c+d
д) (x5 )6 = x 30
• Ада Августа Лавлейс
• Софи Жермен
• Исаак Ньютон
• Готфрид Вильгельм Лейбниц
11001
10101
11101
11011
Задание 4. Определите, какие ответы правильные, а какие
ложные.
• истинному ответу поставьте в соответствие 1, ложному – 0.
• получив упорядоченный набор из единиц и нулей, вы узнаете
имя еще одного известного математика.
а) x2 x3 = x5
б) s3 s5 s8 = s16
в) x7 : x4 = x28
г) (c+d)8 :(c+d) 7 = c+d
д) (x5 )6 = x 30
• Ада Августа Лавлейс
• Софи Жермен
• Исаак Ньютон
• Готфрид Вильгельм Лейбниц
11001
10101
11101
11011
В период работы над арифметической машиной Лейбниц занимался
двоичной системой счисления. В рукописи на латинском языке, подписанной
15 марта 1679 года, Лейбниц разъяснил, как выполнить вычисления в
двоичной системе счисления, в частности умножение, а позже разработал в
общих чертах проект вычислительной машины, работающей в двоичной
системе счисления.
Подробнее о трудах Лейбница, а также о том, кто из ученых стал развивать
его идеи, можно прочитать здесь:
https://ru.wikipedia.org/wiki/Лейбниц_Готфрид_Вильгельм
https://ru.wikipedia.org/wiki/Двоичная_система_счисления
Задание 5. Решение задач.
1. т · т4 · (т2)2 · т0
2. (23)7 : (25)3
3. (р2)4 : р5
4. (34)2 · (32)3 : 311

23. «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь.» М.В.Ломоносов

Спасибо за работу на уроке!

Определение и свойства степени | Математика, которая мне нравится

Определение. Пусть . Пусть — показательная функция с основанием . Тогда ; ; если , то .

Если , то ; если , то .

Теорема. Пусть . Тогда

1) ;

2) ;

3) ;

4) ;

5) .

Доказательство. 1) Если , это очевидно; если , то пусть — показательная функция с основанием .

Тогда левая часть равенства — это , а правая — . Равенство следует из определения показательной функции.

2) >.

3) 1. > — равенство очевидно;

2. — равенство очевидно;

3. . Рассмотрим функцию . Докажем, что — показательная функция. строго монотонна как композиция строго монотонных функций:

   

   

   

Основание : .

Следовательно,

.

4. 1) или

Рассмотрим функцию . Она строго монотонна, так как является произведением двух положительных функций, которые обе возрастают или обе убывают.

   

Следовательно, — показательная функция. Ее основание .

, т.е. .

2) или — равенство очевидно.

3)

   

4)

(т.к.

   

   

5)

, , дальнейшее аналогично пункту 4).

6) . Аналогично пункту 4) или 5).

5.

Задачи.

1) Решите уравнения

1.

2.

3.

4.

5.

6.

7.

3) Решите неравенства

1.

2.

3.

Степени Понятие степени Возведение в степень Чтение степеней

Степени Понятие степени Возведение в степень Чтение степеней Свойства степеней

Понятие степени Определение Компоненты Чётная и нечётная степень

Прочитайте слова Степень Чётная степень Нечётная степень Основание основание степени Показатель показатель степени

Прочитайте

Вставьте слова

Назовите компоненты степени основание степени показатель степени

Подберите антонимы Разные показатели Разные основания

Расскажите об этих степенях Эти степени имеют одинаковые основания и разные показатели. Эти степени с одинаковыми основаниями и разными показателями. Эти степени имеют одинаковые показатели и разные основания. Эти степени с одинаковыми показателями и разными основаниями что имеет что (4) что с чем (5)

что (1) есть что (1) Чётная степень всякого числа есть произведение чётного числа сомножителей. Нечётная степень всякого числа… есть произведение нечётного числа сомножителей.

Прочитайте

Расскажите о степени В данном случае степень нечётная, поскольку мы видим произведение нечётного числа сомножителей.

Вставьте слово Нечётная степень положительного числа положительное есть ________ число. Чётная степень отрицательного числа есть положительное ________ число. Нечётная степень отрицательного числа отрицательное есть ________ число.

Возведение в степень Представление о действии. Чтение степеней

Прочитайте Возводить/возвести в степень (4) Возводить в квадрат (4) Возводить в куб (4) Возведение в степень (4) В виде (6) + чего (2) Представлять/представить число в виде степени

Прочитайте

Образуйте форму предложного падежа 1 6 квадрат в квадрате куб в кубе нулевая степень в нулевой степени третья степень пятая степень в третьей степени в пятой степени

Чтение степеней а + в какой степени а в степени + сколько

Запомните! а квадрат а в квадрате а куб а в кубе

Домашнее задание Задание 4. 1. Прочитать и перевести текст. 2. Написать ответы на вопросы в тетради Подготовка к тесту по аудированию.

Прочитайте представлять/представить что (4) в виде чего (2)

Представьте числа в виде квадрата или куба 8= 81= 25 = 64 = 0, 001=

Свойства степеней Умножение степеней Деление степеней Возведение степени в степень

Образуйте по модели умножение при + умножении (6) деление при делении (6) возведение степени в степень при возведении (6) степени (2) в степень (4)

Свойства степеней произведение степеней частное степеней степень степени степень произведения степень частного

Свойства степеней основное свойство степени свойство частного степеней свойство степени произведения свойство возведения степени в степень свойство частного в натуральной степени

Назовите свойство степени

Домашнее задание

Прочитайте образец а в шестой степени умножить на а в минус третьей степени, умножить на а в минус третьей степени. Чтобы выполнить действие, используем основное свойство степени. Складываем показатели. Получаем а в нулевой степени, то есть единицу.

Выполните действия по образцу (2, 3, 4, 6)

Выучите Презентация «Степени» : Ø свойства степени (названия, ситуации употребления)

Презентация к уроку алгебры «Свойства степени с натуральным показателем»

библиотека
материалов

Содержание слайдов

Номер слайда 1

Свойства степени

Номер слайда 2

«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь» М. В. Ломоносов

Номер слайда 3

Найдем произведение a2 и a3a2 = a · a2 разаa3 = a · a · a 3 разаa2 a3 = 5 разa2 a3 = a2+3 = a5 2+3a·a·a·a·a=a5

Номер слайда 4

Основное свойство степени. Для любого числа a и произвольных натуральных чисел m и nam an = am+n

Номер слайда 5

Правило умножения степеней При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складываютam · an· ak = a (m+n) ·ak = am+n+k. Примеры:

Номер слайда 6

Выбираем правильный ответ. Молодцы!

Номер слайда 7

Решаем в параха17· а23 =d4 · d6 =b4 · b11 =c12 · c13 =k3 · k34 =h42 · h31 =g24 · g13 =а40 d10 b15 c25 k37 h53 g37

Номер слайда 8

Найдем частное двух степеней a7 и a3 a ≠ 0a4 𝑎∙𝑎∙𝑎∙𝑎∙𝑎∙𝑎∙𝑎 =a7 : a3 a7 : a3 = a 7-3 = a4 𝑎∙𝑎∙𝑎 = 𝑎∙𝑎∙𝑎∙𝑎= 

Номер слайда 9

свойство степени Для любого числа a ≠ 0 и произвольных натуральных чисел m и n, таких, что m > n,am : an = am-nam : an = am-n

Номер слайда 10

Правило деления степеней При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. Примеры:

Номер слайда 11

Выбираем правильный ответ. Молодцы!rrrr

Номер слайда 12

Определение степени с нулевым показателем. При a ≠ 0 Степень числа a, не равного нулю, с нулевым показателем равна единице.

Номер слайда 13

Задание 3(а3)4=а3∙а3∙а3∙а3=а3+3+3+3=а12 4 множителя(а𝑚)𝑛=а𝑚∙а𝑚…∙а𝑚=а𝑚+𝑚…+𝑚=а𝑚∙𝑛 n множителей

Номер слайда 14

Задание 4(𝑎𝑏)3=𝑎𝑏∙𝑎𝑏∙𝑎𝑏=(𝑎𝑎𝑎)∙(𝑏𝑏𝑏)=а3𝑏3 3 множителя(𝑎𝑏)𝑛=𝑎𝑏∙𝑎𝑏∙. .∙𝑎𝑏=𝑎𝑎..𝑎∙𝑏𝑏..𝑏 =а𝑛𝑏𝑛 n множителейn мн.n мн.

Номер слайда 15

Пример 1 Упростите выражениеа) (а5)2 ∙ (а6)7=б) (−𝑏4)9=в) (−с3)8= 

Номер слайда 16

Пример 2 Представьте в виде степени 216а3𝑏6216 а3𝑏6= 63∙𝑎3∙(𝑏2)3 = (6𝑎𝑏2)3 

Номер слайда 17

Работа с учебником№ 204, 208, 211, 213

Номер слайда 18

Домашнее задание§6 формулы№ 205, 210, 212, 214 

Номер слайда 19

Спасибо за урок!style. colorfillcolorfill.typestyle.font. Sizestyle.colorfillcolorfill.typestyle.font. Size

Какова степень развития микрорайона?

Степень развития и скорость роста

Степень развития микрорайона, который упоминается как «застроенный» в формах отчета об оценке, представляет собой процент доступной земли в микрорайоне, который был улучшен. Степень развития района может указывать на то, является ли конкретное имущество жилым по своей природе.

При рассмотрении оценки недвижимости, расположенной в сельской или относительно неосвоенной местности, кредитор должен сосредоточиться на характеристиках собственности, зонировании и текущем использовании земли, чтобы определить, следует ли считать недвижимость жилой по своему характеру.Например, если типичная строительная площадка с одной единицей в определенной области (исходя из зонирования, наиболее эффективного и наилучшего использования земли и текущего землепользования) составляет два акра, ипотека будет иметь право на покупку или секьюритизации независимо от процента от общей оценочной стоимости имущества, которое представляет участок, при условии, что оценщик демонстрирует посредством использования сопоставимых продаж, что имущество является типичным жилым помещением для данного конкретного района.

Поскольку Fannie Mae не покупает и не секьюритизирует ипотечные кредиты, обеспеченные недвижимостью сельскохозяйственного типа, незастроенной землей или недвижимостью типа застройки, кредитор должен просмотреть отчет об оценке недвижимости, площадь участка которой больше, чем типичная для жилой недвижимости по соседству. . Особое внимание должно быть уделено описанию оценщиком района, зонированию, определению наилучшего и наилучшего использования, а также степени сопоставимости между оцениваемым имуществом и сопоставимыми продажами.Если объект недвижимости имеет значительно больший участок, чем сопоставимые объекты, использованные в анализе оценщика, объект недвижимости может не быть типичным жилым объектом для района.

 

Для получения дополнительной информации см. B4-1.3-03, раздел «Соседство» отчета об оценке.

Урок 2. Основные экономические принципы оценки недвижимого имущества (доходный подход к оценке)

Оценочное обучение: самостоятельное онлайн-обучение

Открыть все Закрыть все

На стоимость недвижимости могут влиять многие факторы, такие как местоположение и тип использования; однако, когда оценщики составляют/представляют мнение о рыночной стоимости, они также должны принимать во внимание то, как типичные покупатели и продавцы реагируют на рынке. Оценщики подражают тому, что информированные покупатели и продавцы будут делать на открытом рынке. Поэтому мы начнем этот урок с рассмотрения некоторых основных концепций экономики недвижимости, которые влияют на то, как обычно информированные покупатели и продавцы реагируют на открытом рынке, а затем рассмотрим некоторые концепции и принципы, применимые к доходному подходу.

Основываясь на наблюдениях и анализе рынков недвижимости, оценщики разработали принципы описания того, как работают рынки недвижимости.Эти основополагающие принципы оценки важны для понимания основ доходного подхода к стоимости и действий типичных покупателей и продавцов на рынке недвижимости. Хотя эти принципы перечислены по отдельности, многие из них взаимосвязаны или влияют друг на друга при определении стоимости недвижимого имущества. В этом уроке обсуждается следующее:

  • Концепция наилучшего и наилучшего использования
  • Принцип предвидения
  • Принцип замещения
  • Принцип спроса и предложения
  • Принцип изменения
  • Принцип соответствия
  • Принцип вклада
  • Принцип возрастающей и убывающей отдачи
  • Принцип равновесия

Концепция наилучшего и наилучшего использования

Концепция наилучшего и наилучшего использования требует, чтобы каждое имущество оценивалось так, как если бы оно использовалось с максимальной выгодой (максимально возможная чистая стоимость в настоящее время) с учетом возможных юридических, физических и финансовых ограничений. Это влечет за собой определение наиболее подходящего рынка и наиболее прибыльного использования на этом рынке.

Наилучшее и наиболее эффективное использование имущества — это разумное и вероятное использование, которое будет поддерживать наибольшую текущую стоимость на дату оценки. Использование должно быть:

  1. Разрешено законом:

    Наилучшее и лучшее использование должно быть разрешено правительством. Оценщик налога на имущество должен учитывать влияние любых обязательных государственных ограничений, таких как правила зонирования, на стоимость имущества.* Тем не менее, улучшенный участок с землепользованием, не разрешенным в соответствии с действующими правилами, мог быть построен до действующих правил. Эти усовершенствования признаются юридически (устаревшими) несоответствующими видами использования.

  2. Физически возможно:

    Максимальное и наилучшее использование зависит от физических факторов. Предлагаемое или существующее использование должно соответствовать размеру, форме, топографии и другим конкретным характеристикам, связанным с участком или местоположением.Например, использование, которое требует участка большего размера, чем оцениваемый объект, или требует использования коммунальных услуг, недоступных для рассматриваемого объекта, следует исключить из рассмотрения.

  3. Финансовая возможность:

    Высшее и лучшее использование не должно быть слишком спекулятивным. Должен существовать спрос на использование на рынке, который будет генерировать и поддерживать достаточный доход для покрытия затрат на строительство, иметь достаточно денег для обслуживания в течение экономической жизни собственности и обеспечивать как доход из , так и возврат на инвестиции.Это может включать затраты на поддержание или улучшение оставшегося срока экономической службы. Все виды использования, приносящие положительный доход, рассматриваются как финансово осуществимые.

  4. Максимально производительный:

    Наилучшее и лучшее использование должно быть наиболее продуктивным. Из всех финансово осуществимых видов использования тот, который обеспечивает наибольшую остаточную стоимость земли (приносит наибольшую чистую прибыль инвестору), является наиболее эффективным и наилучшим способом использования.Например, если физически возможно, юридически допустимо и финансово целесообразно построить жилой комплекс, офисное здание и ресторан на конкретном участке, но офисное здание принесет наибольшую ценность недвижимому имуществу, то офис строительство считается максимально продуктивным использованием.

Как правило, предлагаемое использование, которое, по мнению оценщика, может дать наиболее эффективное и оптимальное использование определенного объекта недвижимости, должно соответствовать всем четырем критериям, в противном случае предлагаемое использование (будь то текущее использование или альтернативное использование) не может считаться наилучшим и наилучшее использование недвижимого имущества. Из этого общего правила есть исключения. Например, если участок в настоящее время благоустроен с помощью химчистки, но зонирование позволяет построить офисное здание с более высокой стоимостью, затраты, связанные с очисткой имущества (восстановление имущества от любых потенциальных загрязнений), будут непомерно высокими или стоит столько, чтобы оставить текущее или существующее использование как самое лучшее и лучшее использование.

Если иное не оговорено в объеме работ, при оценке улучшенного имущества оценщик будет рассматривать наилучшее и наилучшее использование по мере его улучшения и наилучшее и наилучшее использование, как если бы оно было пустым. Наилучшее и лучшее использование как улучшенное указывает, как следует использовать уже улучшенное свойство. Наилучшее и наилучшее использование как свободное рассматривает, среди всех разумных альтернативных видов использования, использование, которое дает наибольшую текущую стоимость земли. Любые существующие улучшения могут быть снесены. На самом деле снос экономически целесообразен, когда рыночная стоимость земли, как бы свободной, превышает рыночную стоимость земли, как бы улучшенной.

Следствием концепции наилучшего и наилучшего использования является Принцип последовательного использования , согласно которому для улучшенного объекта и участок, и улучшения должны оцениваться как одно и то же использование.Этот принцип нарушается, когда оценщик пытается определить стоимость земли на основе одного наиболее эффективного и наилучшего использования, а стоимость улучшений — на основе другого наиболее эффективного и наилучшего использования. Однако допустимо рассматривать наиболее и наилучшее использование с поправкой на время, когда районы переходят от одного использования к другому, обычно «более высокому», с признанием промежуточного и конечного наилучшего и наилучшего использования.

Принцип прогнозирования будущих выгод

Имущество является ценным из-за ожидаемых (предполагаемых) будущих выгод, которые оно может обеспечить. Стоимость имущества может быть определена как текущая стоимость прав на все предполагаемые будущие выгоды, материальные и нематериальные, связанные с владением недвижимым имуществом. Таким образом, инвесторы покупают приносящую доход недвижимость сегодня, чтобы получить будущие выгоды или доход, который, как ожидается, они получат в будущем.

Одной из обязанностей оценщика является интерпретация взглядов лиц, торгующих на рынке недвижимости. Таким образом, оценщик обязан учитывать как вероятность будущих тенденций, так и влияние, которое такие тенденции окажут на покупателей, продавцов и арендаторов, выраженное в текущих рыночных сделках.Например, изменения в ожидаемом спросе, вызванные внешними улучшениями в виде автомагистралей, автострад, мостов, школ и бульваров, оказывают существенное влияние на стоимость, даже если такие улучшения могут быть на стадии планирования и не видны во время строительства. оценка. Поскольку текущая стоимость недвижимости зависит от ожидаемых будущих выгод, принцип предвосхищения требует, чтобы оценщик был полностью информирован о делах общества и экономических изменениях, ожидаемых на рынке, в котором находится оцениваемое имущество.

Именно будущее, а не прошлое, должно интересовать оценщика. История эксплуатации предмета или аналогичного имущества на рынке важна только для установления тенденции ожидаемых доходов в течение оставшегося срока экономической службы или периода владения оцениваемым имуществом. Прошлые операции и другие нетипичные методы управления могут препятствовать или, в случае накопленной деловой репутации, ускорять (по крайней мере, на время) получение дохода. Такие активы или обязательства собственности должны рассматриваться в меру приведенной стоимости.Для целей налога на имущество мы обязаны измерять полную стоимость имущества; это включает в себя хорошее управление, обслуживание и типичное взаимодействие с рынком.

Принцип замещения

Принцип замещения гласит, что верхний предел стоимости, как правило, определяется стоимостью приобретения столь же желательного заменителя, при условии отсутствия несвоевременных задержек. Благоразумный инвестор не будет платить за приносящую доход недвижимость не больше, чем будет стоить строительство или покупка аналогичной недвижимости.Точно так же благоразумный арендатор не стал бы платить больше, чем он заплатил бы за аренду столь же желательного имущества.

Когда доступно несколько товаров или услуг с практически одинаковой полезностью или выгодой, товар с самой низкой ценой привлекает наибольший спрос и самое широкое распространение. При доходном подходе стоимость, как правило, определяется затратами, необходимыми для покупки собственности, предлагающей столь же желательный поток дохода. Эта теория обеспечивает основу для использования сопоставимых свойств в доходном подходе к стоимости.

Из Оценка недвижимости цены, арендная плата и нормы прибыли на имущество, как правило, устанавливаются преобладающими ценами, арендной платой и нормами прибыли на столь же желательные замещающие объекты. Принцип замещения присутствует в каждом из трех подходов к оценке стоимости (доходный, сравнительный и затратный).

Все объекты недвижимости, независимо от того, насколько разнообразны их физические характеристики или географическое расположение, могут быть экономически взаимозаменяемы с точки зрения полезности услуг или доходной производительности при условии, что они могут быть созданы без неоправданной (затратной) задержки.При значительной задержке в приобретении заменителя необходимо учитывать стоимость задержки; значительная задержка, по сути, увеличивает стоимость. Принцип замещения тесно связан с экономической концепцией альтернативных издержек, согласно которой истинная стоимость экономического выбора измеряется возможностью, упущенной из-за выбора.

Принцип спроса и предложения

Взаимодействие между предложением товаров и спросом на товары устанавливает как цену, так и количество требуемых товаров.Спрос, количество товара или услуги, которые можно было бы приобрести по разным ценам в течение определенного периода времени, создается полезностью продукта, а также способностью и желанием людей покупать его. Покупатели и продавцы, как правило, устанавливают цену или стоимость товара на основе предложения товара и спроса на этот товар. Если предложение товара стабильно, а спрос на него увеличивается, продавцы этого товара склонны повышать цену. Предложение на рынке недвижимости создается долго; следовательно, если спрос на недвижимость увеличится, цена на недвижимость также будет расти, потому что предложение недвижимости будет регулироваться медленно.

Принцип изменения социально-экономических моделей

Ничто не статично; изменения происходят постоянно. Принцип изменения признает динамичный характер рынков недвижимости. В сфере недвижимости изменения затрагивают не только отдельные объекты, но и районы, сообщества и регионы. Эффекты предполагаемых изменений отражаются на рынке. Изменение — это, по сути, закон причины и следствия. Отдельные владения, районы, районы и целые сообщества часто имеют четыре фазы жизни: 90 007

  1. Рост: период, в течение которого район приобретает общественную пользу или признание.
  2. Стабильность: период равновесия без значительных прибылей или убытков.
  3. Упадок: период снижения спроса и признания.
  4. Обновление: период омоложения и возрождения рыночного спроса.

Принцип изменения тесно связан с принципом ожидания. Прошлый опыт доходов может указывать на определенную тенденцию, а текущий поток доходов может подтверждать эту тенденцию; тем не менее ожидаемый ожидаемый доход в будущем может радикально отличаться из-за важных изменений в национальной, региональной и местной деловой активности, частью которой является рынок недвижимости.

Принцип соответствия

Принцип соответствия гласит, что максимальная ценность реализуется, когда существует разумная степень архитектурной однородности и совместимо землепользование. Этот принцип подразумевает разумное сходство, а не монотонное единообразие, имеет тенденцию создавать и поддерживать ценность. Наилучшее и наилучшее землепользование обычно реализуется в условиях соответствия или гармонии. Основная цель правил зонирования и ограничений на частные сделки — поддерживать соответствие.

Принцип вклада, также известный как Принцип предельной производительности

Принцип вклада, также известный как принцип предельной производительности, применяет принцип увеличения и уменьшения отдачи от компонентов собственности. Этот принцип гласит, что стоимость компонента собственности измеряется с точки зрения его вклада в стоимость всего имущества, а не как отдельного компонента. Обратите внимание, что стоимость предмета не обязательно равна его вкладной стоимости.Например, строительство бассейна в жилом комплексе из 20 квартир может стоить 30 000 долларов; однако это может добавить только 20 000 долларов к общей стоимости комплекса.

Принцип возрастающей и убывающей отдачи

Принцип возрастающей и убывающей отдачи признает, что приращения агентов производства производят больший чистый доход (возрастающая отдача) до определенного момента (прибавочная производительность). Точка максимального вклада агентов в производство (точка убывающей отдачи) свидетельствует о правильной комбинации агентов, приводящей к максимальному и лучшему использованию.Любое дальнейшее увеличение количества агентов производства уменьшит разницу между стоимостью агентов и валовым доходом, который они будут производить, что приведет к уменьшению пропорциональной чистой прибыли.

Возрастающая и убывающая доходность применяется к многоквартирному дому максимального размера, который должен быть размещен на земельном участке. Добавление этажей к многоквартирному дому может привести к тому, что стоимость имущества превысит затраты, пока не будет достигнута точка, при которой конструкции должны быть обрамлены сталью поверх фундаментных свай, вбитых в скальную породу.В этот момент добавленная стоимость по сравнению с деревянным каркасом поверх бетонного подиума может не привести к добавленной стоимости, соизмеримой с затратами — это будет точкой снижения отдачи.

Падающая или убывающая отдача — это пропорциональное уменьшение суммы отдачи по мере увеличения одного элемента производства при неизменности всех других факторов. Этот Закон убывающей отдачи также известен как Закон переменных пропорций .

Принцип баланса в землепользовании и развитии

Принцип баланса тесно связан с принципом возрастающей и убывающей отдачи; он утверждает, что максимальная стоимость достигается и поддерживается, когда все элементы агентов производства находятся в экономическом равновесии. Стоимость недвижимости зависит от баланса:

  1. Земля
  2. Труд
  3. Капитал
  4. Предпринимательство

Земля включает землю, воздушное пространство и природные ресурсы, находящиеся на поверхности или в недрах земли.Труд включает человеческую работу, направленную на производство, то есть всю заработную плату и другие операционные расходы, связанные с человеческим трудом. Капитал состоит из товаров (например, оборудования и зданий) и нематериальных активов и прав (например, оборотного капитала и франшиз), используемых в производственном процессе. В отличие от других факторов производства, капитал должен быть произведен, прежде чем его можно будет использовать в производственном процессе. Человеческий капитал – это производительная сила людей, развитая посредством образования и обучения. Предпринимательство — это акт визуализации потребностей и принятие необходимых мер и рисков для производства продуктов, которые удовлетворяют эти потребности.В девелопменте недвижимости предпринимательство является синонимом функции развития.

Элементы, как внутренние, так и внешние по отношению к свойству, должны быть сбалансированы для достижения максимальной ценности. Внутри страны правильное сочетание земли и здания имеет решающее значение для экономического баланса. Внешне недвижимость должна быть в балансе с окружающими объектами. Например, дорогой дом, построенный на дешевом участке в скромном районе, может не продаваться по полной стоимости производства.

Резюме

В уроке, который вы только что прочитали, объяснялись принципы оценки, которые должен учитывать оценщик при определении стоимости имущества с использованием доходного подхода к оценке стоимости. В следующем уроке вы узнаете о предположениях, которые покупатели учитывают при покупке приносящей доход недвижимости. Прежде чем перейти к следующему уроку, пожалуйста, выполните упражнения для проверки знаний к этому уроку.

Примечание. Прежде чем перейти к следующему уроку, обязательно выполните упражнения этого урока.

Степень бакалавра и учебная программа: сертификат недвижимости

Обзор
Выпускник
Бакалавриат
Факультет
Требуется для получения Сертификата на недвижимость

Узнайте больше о Real Estate Track (PDF)

FINA 4380 – Финансы и инвестиции в недвижимость (3 CH)
Курс предоставляет обзор финансирования для всех основных классов активов недвижимого имущества.Он включает в себя принципы и методы финансирования и инвестиций в недвижимость с упором на основы коммерческой недвижимости, финансовые инструменты, необходимые для анализа и принятия решений, связанных с финансированием недвижимости, а также переменные, которые необходимо определить и количественно оценить как часть процесса. . Изучение левериджа, его влияние на проекты и способы расчета различных форм долговых структур, используемых в финансировании коммерческой недвижимости. Тематические исследования будут использоваться для иллюстрации общих практик в бизнесе.
Предварительное или необходимое условие: FINA 4330 Корпоративные финансы

FINA 4381 – Essentials of Real Estate (3 CH)
Вводный, обзорный курс, охватывающий все основные аспекты недвижимости и операций с недвижимостью, включая право собственности на землю и права собственности, право собственности, обременения и полисы страхования титула, обследования, законы и правила, контролирующие недвижимость, развитие и строительство, финансирование недвижимости, роли и обязанности участников девелопмента недвижимости и смежные темы.

FINA 4382 – Разработка проекта недвижимости (3 CH)
Знакомство с индустрией девелопмента, включая прикладные процессы и лучшие практики, используемые в реальных девелоперских проектах. Курс следует за процессом разработки с точки зрения предпринимательства и «заключения сделок». Темы курса включают анализ рынка, выбор участка, составление бюджета проекта/финансовый анализ, приобретение земли, маркетинг и аренду, совместные предприятия, финансирование, проектирование и управление строительством, а также распоряжение.Кроме того, в этом курсе будут использованы тематические исследования, чтобы проиллюстрировать эти методы и проиллюстрировать междисциплинарный характер команд по развитию недвижимости.

FINA 4383 – Анализ и оценка рынка недвижимости (3 CH)
Этот вводный курс охватывает основы исследования рынка недвижимости и определения осуществимости девелоперского проекта. Темы включают в себя экономику земли, анализ доли сдвига, прогнозы рыночного спроса и оценку условий конкуренции, определение рыночного риска, а также прогнозы вакансий и поглощения проектов для жилых, коммерческих и многофункциональных проектов.

Курсы по выбору

FINA 4397 – Многоквартирная недвижимость (3 CH)
Обзор основных разделов жилой недвижимости, многоквартирных домов, одной семьи, развития сообщества и жилищного строительства, в которых студенты получают знания и навыки во всех профессиональных аспектах жилого бизнеса, финансового анализа, анализа рынка, финансирования, развития, продажи или аренды. и операций. Это «предпринимательский курс», означающий, как многопрофильная компания, занимающаяся недвижимостью, организована и работает на корпоративном уровне.

 

 

Магистр экономики и финансов недвижимости

Обзор

В дополнение к нашей передовой академической программе, магистр экономики и финансов недвижимости предлагает ведущую в отрасли программу профессионального развития. Мы организуем многочисленные сетевые мероприятия с участием видных деятелей индустрии недвижимости, в том числе управляющих активами, инвестиционных фондов, девелоперов и консультантов инвестиционных и кредитных банков.Наш преданный консультант по вопросам карьеры предлагает семинары по резюме и собеседованиям, а наша активная сеть выпускников активно поддерживает нынешних студентов через схему наставничества.

События

Это ваш шанс встретиться с профессионалами, работающими в сфере недвижимости на разных этапах своей карьеры. Будет возможность встретиться и поговорить со специалистами по финансам в сфере недвижимости, финансовыми аналитиками, сюрвейерами, коммерческими аналитиками, специалистами в области частного капитала и другими.

Мероприятия для выпускников

Обычно летом и зимой.У нас есть активная сеть выпускников, которые регулярно встречаются и поддерживают нынешних студентов в их профессиональном развитии.

Карьерное мероприятие Лондонской фондовой биржи

Многие глобальные игроки в сфере недвижимости приезжают в LSE, чтобы встретиться с нашими студентами REEF во время осеннего сезона приема на работу.

Последние организации, участвовавшие в наших мероприятиях по трудоустройству, включают: Goldman Sachs, BNP Paribas, Eastdil, Deutsche Finance, Optimum Asset Management и Landlease.

Карьерное мероприятие Консультативного совета REEF

В дополнение к мероприятию по карьере в сфере недвижимости LSE мы также предлагаем эксклюзивное мероприятие, организованное консультативным советом нашей программы.

Это возможность пообщаться со старшими специалистами, которые приезжают в LSE, чтобы встретиться с нашими студентами по приглашению членов консультативного совета.

Мероприятия клуба недвижимости

Этот студенческий клуб работает при поддержке преподавателей и организует мероприятия, соответствующие профессиональным интересам его членов. К ним относятся мастер-классы и семинары по темам, определенным комитетом клуба.

Профессиональное наставничество

студентов REEF имеют доступ к специализированной сети высококлассных специалистов.Мы подбираем студентов, которые хотят участвовать в этой программе, с профессионалом, работающим в их области интересов. У нас есть сеть выпускников и друзей программы, охватывающая множество стран и специализаций в рамках широко определенной области недвижимости. Наставники консультируют по вопросам выбора карьеры, профессионального развития и помогают с рынком труда.

Коучинг

Специализированный сотрудник отдела по трудоустройству LSE оказывает индивидуальную поддержку карьере, связанной с недвижимостью. Офис также работает с группами и имеет очень полезные ресурсы для улучшения навыков интервьюирования и налаживания контактов.

LSE ЖИЗНЬ

LSE LIFE – это место, куда вы можете прийти, чтобы узнать больше о себе, своей учебе и своих целях. Студенты MSc REEF могут прийти в LSE LIFE, чтобы развить академические, коммуникативные, математические и исследовательские навыки, получить советы по личной эффективности и сделать жизненный выбор, а также получить представление о наборе выпускников и карьерных путях, и все это размещено в специально построенном пространстве на Первый этаж библиотеки LSE.

LSE LIFE предлагает широкий выбор мастерских. Некоторые семинары, которые могут оказаться полезными, включают:  Делайте четкие, краткие и критические заметки о прочитанном, Как читать для академической работы и Планируйте семестр на Михайлов день. Другие доклады и мастер-классы смотрите здесь.

Программное обеспечение и методы обучения

Карьера в области экономики и финансов недвижимости требует различных аналитических навыков, обучения методам и владения программным обеспечением. В дополнение к обязательному обучению мы предлагаем дополнительное обучение по:

—          Excel / анализ денежных потоков

—          ГИС (что это такое и для чего ее можно использовать)

—          Стата (что это такое и как ее можно использовать)

—          Сеанс данных (Обучение библиотек работе с данными о недвижимости и почему это важно)

Профессиональное партнерство

Форум инвестиционной собственности признает степень магистра Лондонской фондовой биржи REEF

Форум по инвестиционной собственности, IPF, включает программу магистра экономики и финансов в сфере недвижимости в выбранный список курсов последипломного образования, которые, по мнению Форума, обеспечивают соответствующие навыки, необходимые для тех, кто работает на рынке инвестиций в недвижимость.Это признание дает ряд преимуществ нашим выпускникам магистратуры, которым будет предложено ускоренное членство в Форуме.

Партнерство между MSc REEF и RICS

MSc REEF заключил партнерское соглашение с Королевским институтом дипломированных оценщиков в 2002 году. Выпускники, начиная с 2002 года, получают признание RICS; бывшие выпускники могут подать заявку на личное членство в RICS.

Признание успехов учащихся профессионалами

Наши студенты и их работа высоко ценятся различными профессиональными организациями, что нашло отражение в нескольких наградах, спонсируемых различными отраслевыми организациями.В настоящее время мы присуждаем две премии: премию HSBC Global Asset Management Dissertation Prize и премию IPF за диссертацию последипломного образования (Форум инвестиционной собственности).

Руководство Комиссии по недвижимости

Брокеры по недвижимости могут получить лицензию по стандартному методу после того, как они завершили и сдали обе части Брокерского экзамена. Брокеры по недвижимости, имевшие активную брокерскую лицензию в другом штате в течение последних пяти лет, не должны сдавать общую/национальную часть экзамена, чтобы иметь право на получение лицензии в Пенсильвании. Тем не менее, все кандидаты по стандартному методу должны быть одобрены Комиссией по недвижимости до регистрации для сдачи экзаменов брокера.

Чтобы иметь право сдавать экзамены, заявители должны пройти 240 часов (16 кредитов) обучения в области профессионального образования в сфере недвижимости, как это определено Комиссией в соответствии с разделом 35.271(b), в аккредитованном колледже или утвержденном учебном заведении в сфере недвижимости. в этом Содружестве. Курсы должны быть пройдены в течение 10 лет после даты сдачи обеих частей экзамена.Вы также можете соответствовать требованиям, если вы получили степень бакалавра по специальности «Недвижимость» в аккредитованном колледже, степень доктора юридических наук в аккредитованной юридической школе или прошли 240 часов курсовой работы перед получением лицензии брокера в другой юрисдикции, которая была одобрена для удовлетворения требования для получения лицензии в этой юрисдикции. Два кредита также будут предоставлены за каждый год активной практики, которую заявитель имел в качестве лицензированного брокера в другом штате в течение 10 лет, непосредственно предшествующих подаче заявки на экзамен.

Кандидат также должен документально подтвердить не менее 3 лет опыта работы в качестве лицензированного продавца, с квалификацией опыта, которую Комиссия считает достаточной для работы в качестве брокера, или иметь не менее 3 лет другого опыта, образования или и того, и другого, которые Комиссия считается эквивалентным 3-летнему опыту работы в качестве лицензированного продавца. Пожалуйста, прочитайте раздел 35.271 правил Комиссии по недвижимости, чтобы получить всю информацию о требованиях к образованию и опыту работы.

Чтобы получить разрешение на сдачу экзамена, вы должны зарегистрировать учетную запись или войти в свою зарегистрированную учетную запись на сайте www.pals.pa.gov и подать заявку на тип брокерской лицензии, которую вы хотите получить после сдачи экзамена. экзамены. Существует четыре основных типа брокерских лицензий:

Ассоциированный брокер – Индивидуальный брокер, нанятый другим брокером

Брокер Мультилицензиат – зарегистрированный брокер , ассоциация или корпорация, имеющая лицензию брокера

Брокерская корпорация, ООО или Товарищество — Брокерская организация, зарегистрированная как корпорация, ООО или товарищество в Бюро корпораций штата Пенсильвания

Брокер-индивидуальный владелец — Анкета индивидуальный брокер, не зарегистрированный в качестве корпорации, ООО или товарищества и не нанятый другим брокером

и квалификация экспертизы брокера. Затем вы предоставите документацию, подтверждающую, что вы соответствуете требованиям к образованию и опыту; вас не попросят предоставить оставшуюся документацию, указанную в заявлении, до тех пор, пока вы не сдадите экзамены. Как только ваша квалификация будет определена, вы будете уведомлены о том, что вам разрешено сдавать экзамены брокера. Затем вы можете перейти на веб-сайт PSI Exams, чтобы зарегистрироваться на экзамен. После того, как вы сдали экзамен, вы вернетесь к заявке на получение лицензии, чтобы загрузить листы проходных баллов и оставшуюся документацию, необходимую для лицензии.


Чтобы сократить время обработки, обратите внимание на следующие предложения и информацию:  

Комиссия по недвижимости не может предварительно рассматривать материалы заявки или квалификационные требования. Пожалуйста, не обращайтесь в Комиссию с вопросами о том, соответствуете ли вы требованиям или будет ли вам предоставлена ​​лицензия при каких-либо конкретных обстоятельствах, включая прошлые судимости. Вы должны соответствовать требованиям к образованию и экзаменам и подать заявку на лицензию, а затем подать заявку со всей необходимой документацией, чтобы получить определение относительно вашей квалификации и права на получение лицензии.

Официальная государственная проверка судимостей (CHRC) требуется от вашего текущего места жительства. Для заявителей, проживающих, работающих или проходящих обучение в Пенсильвании, ваш CHRC будет создан автоматически как часть вашего заявления, а необходимая плата будет включена при оформлении заказа.

В дополнение к проверке биографических данных из вашего текущего штата проживания, вам необходимо будет представить официальные государственные CHRC из каждого штата, где вы жили, работали или прошли обучение в течение последних 5 лет.Проверка данных ФБР может быть представлена ​​вместо государственных проверок, где вы ранее жили, работали или обучались. Никакие проверки записей не могут быть датированы более чем за 90 дней до даты подачи заявления.

Процесс подачи заявки на получение лицензии брокера по недвижимости начинается, когда вы регистрируетесь и входите в систему на сайте www.pals.pa.gov. После того, как вы вошли в систему, вы должны прокрутить до нижней части панели инструментов и нажать «Подать заявку на новую лицензию», затем выбрать «Комиссия по недвижимости», а затем выбрать тип брокерской лицензии, которую вы хотите иметь, как описано выше.Если вы никогда ранее не имели лицензии брокера в Содружестве, вы должны заполнить заявку и оплатить сборы как за лицензию, так и за квалификационный экзамен брокера. Затем вы предоставите документацию, подтверждающую, что вы соответствуете требованиям к образованию и опыту; вас не попросят предоставить оставшуюся документацию, указанную в заявлении, до тех пор, пока вы не сдадите экзамены. Как только ваша квалификация будет определена, вы будете уведомлены о том, что вам разрешено сдавать экзамены брокера.Затем вы можете перейти на веб-сайт PSI Exams, чтобы зарегистрироваться на экзамен. После того, как вы сдали экзамен, вы вернетесь к заявке на получение лицензии, чтобы загрузить листы проходных баллов и оставшуюся документацию, необходимую для лицензии.

Если вы хотите лицензировать корпорацию, ООО или товарищество в качестве брокера, вы должны сначала подать заявку на получение брокерской лицензии с несколькими лицензиями и (если вы никогда раньше не имели лицензии брокера) выполнить шаги, необходимые для прохождения экзамена. После того, как вы сдали экзамен, вы можете возобновить работу с приложением брокера с несколькими лицензиями и начать работу с брокерской корпорацией для компании, используя номер заявки из приложения брокера с несколькими лицензиями.

Чтобы загрузить дополнительные документы в свое приложение, вы должны вернуться в свою панель инструментов, а затем найти приложение в разделе «Действия». Нажмите на синий знак «плюс» рядом со справочным номером приложения, а затем нажмите на элемент контрольного списка, в который вы хотите загрузить документ. Система не покажет, что документ был загружен, однако, если вы увидите «галочку» после процесса загрузки, он был успешно загружен. Имейте в виду, что статус пунктов контрольного списка не изменится до тех пор, пока ваша заявка не будет рассмотрена проверяющим сотрудником в указанные сроки.Если отсутствуют документы или информация, которую необходимо исправить, вы получите электронное письмо на зарегистрированный адрес электронной почты с подробной информацией о том, как устранить недостающую или неправильную информацию.

Брокерские корпорации, ООО или товарищества и брокеры-индивидуальные предприниматели должны пройти проверку до выдачи лицензии. После того, как ваше заявление будет заполнено, оно будет передано инспектору, который свяжется с вами напрямую, чтобы запланировать осмотр офиса.

После того, как ваша лицензия будет выдана, вы сразу же увидите ее под баннером «Сведения о профессиональной лицензии» на панели инструментов.Вы получите лицензию в главном офисе брокера через 7-10 рабочих дней после даты выдачи.

Полезные ссылки:

Для регистрации на экзамены: www.psiexams.com или по телефону 855-746-8175

Чтобы ознакомиться с Законом и правилами Комиссии по недвижимости: www.dos.pa.gov/estate, нажмите » Закон и правила комиссии»

Чтобы найти утвержденного поставщика образовательных услуг в сфере недвижимости: www.pals.pa.gov/verify, нажмите «Поиск объекта», затем выберите Совет/комиссию как «Комиссия по недвижимости» и тип лицензии как » Провайдер образования в сфере недвижимости».В раскрывающемся меню есть три подтипа: тип RE предназначен для школ штата, тип RU — для школ за пределами штата, а тип RUC — для аккредитованных колледжей/университетов. Вы должны связаться с каждой школой в отдельности, чтобы определить, предлагают ли они курсы, отвечающие вашим потребностям.


Степень управления онлайн-бизнесом — бакалавр наук

Учебная программа, которая гарантирует, что вы освоите то, что работодатели хотят, чтобы вы знали.

В WGU мы разрабатываем нашу учебную программу так, чтобы она была своевременной, актуальной и практичной — и все это для того, чтобы ваша степень была доказательством того, что вы действительно знаете свое дело.

Каждый курс фокусируется на наборе четко определенных компетенций, которые вы должны доказать, что научились — с помощью тестов, работ, проектов или других оценок.

Демонстрация мастерства — это то, как вы проходите курс, поэтому степень бакалавра делового администрирования и менеджмента WGU является доказательством того, что вы продемонстрировали превосходство в том, что нужно для успеха в вашей карьере.

То, что вы узнаете в рамках этой программы, часто будет непосредственно применяться на следующий день на работе, а то, что вы делаете на работе, часто влияет на работу, которую вы выполняете на своих курсах. Все дело в применимости в реальном мире, поэтому каждый момент, проведенный за учебой, — это потраченное с пользой время.

Курсы, выполненные по степени младшего специалиста.

Это неофициальная оценка ваших переводных кредитов. Вы можете получить больше или меньше кредитов в зависимости от конкретных курсов, пройденных для получения степени, и других кредитов, которые у вас могут быть.

Ниже приведены ожидаемые курсы, которые будут проходить в зависимости от вашего заявления о том, что вы получили степень младшего специалиста. В процессе регистрации эта информация будет проверена.

Введение в гуманитарные науки Этика в технологиях Прикладная вероятность и статистика Английская композиция I Введение в общение Критическое мышление и логика Английская композиция II Прикладная алгебра Введение в социологию Интегрированные физические науки Обзор истории Соединенных Штатов

Курсы по этой программе.

Онлайн-программа получения степени по менеджменту состоит из следующих курсов. От некоторых из них можно отказаться путем перевода из вашего предыдущего опыта колледжа. Остальные вы, как правило, выполняете по одному, продвигаясь по своей программе, работая с вашим наставником программы каждый семестр над созданием вашего индивидуального плана получения степени. Вы будете работать над каждым курсом так быстро, как сможете изучать и усваивать материал.Как только вы будете готовы, вы пройдете оценку, закончите курс и двинетесь дальше. Это означает, что вы можете пройти столько курсов, сколько сможете, за семестр без каких-либо дополнительных затрат.

Программа на получение степени «Управление бизнесом» позволяет учащимся получать ценные сертификаты на пути к получению степени, включая стратегическое мышление и инновации, лидерство и управленческие сертификаты.

Введение в гуманитарные науки Прикладная вероятность и статистика Введение в общение Критическое мышление и логика Введение в социологию Интегрированные физические науки Обзор истории Соединенных Штатов Количественный анализ для бизнеса Управление операциями и цепочками поставок Задачи управления бизнесом Основы успеха в бизнесе Принципы финансового и управленческого учета Финансовые навыки для менеджеров Концепции в маркетинге, продажах и контактах с клиентами Приложения бизнес-среды I: бизнес-структуры и правовая среда Приложения бизнес-среды II: процессы, логистика и операции Управление в глобальной бизнес-среде Инновационное и стратегическое мышление Эмоциональный и культурный интеллект Введение в управление человеческими ресурсами Планирование рабочей силы: набор и отбор Компенсации и льготы Письменный проект Capstone по управлению бизнесом

Планируйте усердно работать: требования и ожидания программы.

Программа бакалавриата по бизнес-администрированию и менеджменту — это онлайн-программа на получение степени, которую вы пройдете, изучая и работая самостоятельно, под руководством и при поддержке преподавателей WGU. Ожидается, что вы пройдете не менее 12 модулей компетенции (эквивалент кредит-часа WGU) каждый 6-месячный срок.(Каждый курс обычно состоит из 3 или 4 единиц).

Первым человеком, с которым вы поговорите в WGU, будет ваш консультант по регистрации, который может более подробно объяснить требования и ожидания. Вы также можете прочитать больше о каждом курсе в Руководстве по программе.

Запрос информации у консультанта по регистрации

Загрузить руководство по программе

Специальные требования для этой программы:

Проект Capstone: В конце вашей программы вы завершите проект Capstone, который представляет собой кульминацию всей вашей тяжелой работы — проект, который позволит вам взять то, что вы узнали, и применить это к реальной ситуации. , предлагая решение актуальной проблемы, с которой вы сталкиваетесь на своем рабочем месте.

Мы предлагаем степени для востребованных профессий, которые дают знания и навыки, необходимые для достижения успеха. Придайте своему резюме импульс, в котором оно нуждается!

ЗАПРОСИТЬ ИНФОРМАЦИЮ

Качество, которому можно доверять: учебная программа разработана под руководством бизнес-лидеров и экспертов.

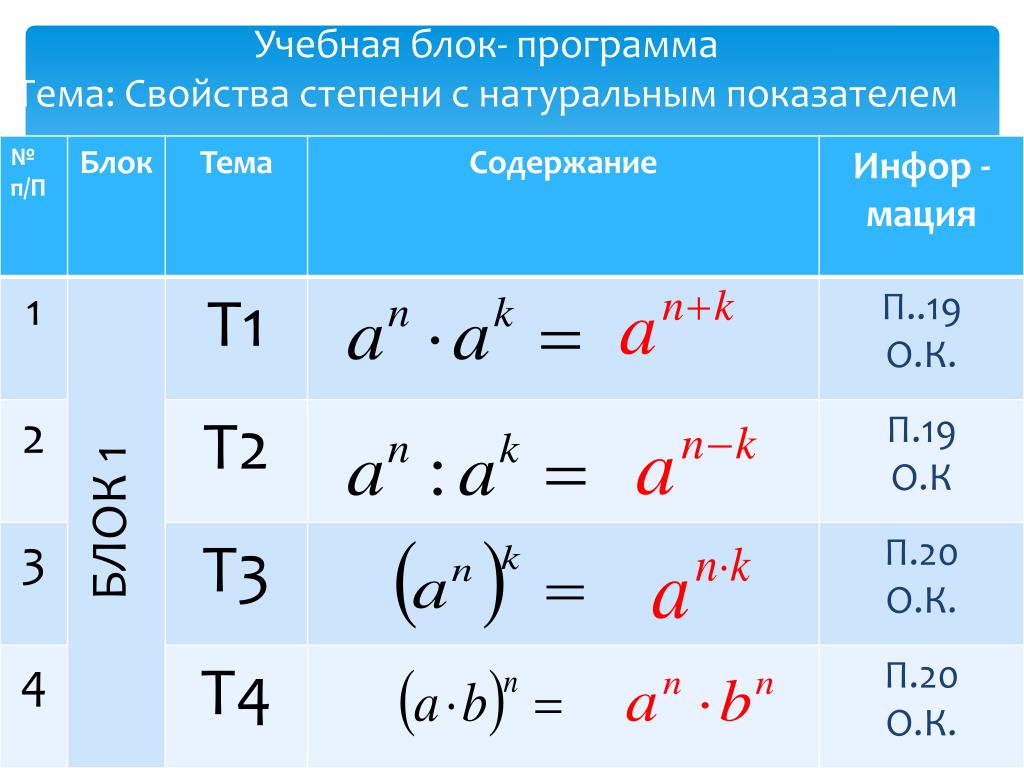
Советы по программам — группы отраслевых и академических экспертов — сотрудничают в создании наших программ, внося свой вклад в то, что должен освоить успешный выпускник.

Комиссия по недвижимости Как получить лицензию

Закон штата Теннесси о брокерах по недвижимости 1973 года, правила и положения, а также Закон штата Теннесси о таймшерах определяют, будет ли кандидату выдана лицензия.Успешная сдача экзамена не гарантирует выдачу какой-либо лицензии.
В день экзамена кандидаты должны ответить на ряд квалификационных вопросов, перечисленных ниже.
Ответ «да» на любой из вопросов с 1 по 5 может снизить шанс кандидата на получение лицензии в штате Теннесси.
После того, как кандидаты выполнили предварительные лицензионные требования, комиссия рассмотрит предоставленную информацию и примет решение об их квалификации.

Комиссия по недвижимости штата Теннесси не разрешает назначать экзамены лицам, условно-досрочно освобожденным или испытательным, если не прошло два (2) года с даты истечения срока испытательного срока, осуждения или освобождения из-под стражи, в зависимости от того, что наступит позднее.

КВАЛИФИКАЦИОННЫЕ ВОПРОСЫ

  1. Обладаете ли вы сейчас или когда-либо владели лицензией на недвижимость или таймшер в Теннесси или любом другом штате? Если у вас есть или была лицензия в другом штате (штатах), вы должны получить лицензионное свидетельство в каждом штате, в котором у вас есть или была лицензия. Эта заявка не будет обработана до тех пор, пока не будут получены сертификаты.
  2. Получали ли вы когда-либо отказ в выдаче лицензии или ее действие отзывалось, приостанавливалось, объявлялось выговор или оштрафовывалось каким-либо федеральным правительством, правительством штата или местным правительством? (Не включая водительские права.) Если вы добровольно отказались от лицензии в то время, когда против вас ожидалось дисциплинарное взыскание или в отношении вас проводилось расследование со стороны лицензирующего органа, государственного учреждения или профессиональной организации, вы должны предоставить информацию об отказе от лицензии.
  3. Вам когда-либо отказывали или отзывали, приостанавливали действие, объявляли выговор или штрафовали лицензию продавца недвижимости или таймшеров?
  4. Подавали ли вы когда-либо жалобу на вас в какой-либо регулирующий орган или в какой-либо суд?
  5. Были ли вы осуждены или признаны nolo contendere или виновны в каком-либо уголовном преступлении или правонарушении, связанном с кражей услуг, денег или имущества в течение последних десяти (10) лет? должны быть раскрыты.
  6. Если вы ответите «да» на вопрос 5, Комиссия потребует от вас предоставить заверенную копию вашей судимости в дополнение к письменным показаниям с подробной информацией о каждом обвинении.
  7. Вы можете подать заявление в Комиссию до прохождения или завершения предлицензионного обучения и/или экзамена на получение лицензии, подав «Заявление о принятии решения относительно предыдущих судимостей и/или дисциплинарных взысканий», которое можно загрузить. Затем эта форма вместе со всей запрошенной документацией будет рассмотрена Комиссией, и вы будете уведомлены об их решении.
  8. Вам исполнилось 18 лет?

Документация, описанная в каждом из вышеперечисленных случаев, будет затребована Комиссией по недвижимости штата Теннесси, когда кандидат сдает экзамен и желает подать заявку на получение лицензии. Информация не должна отправляться в PSI и не должна доставляться в экзаменационный центр.

Правило Комиссии не позволяет назначать экзамены лицам, условно-досрочно освобожденным или испытательным. Кандидаты должны быть освобождены от условно-досрочного освобождения или испытательного срока минимум на два (2) года.Кандидаты, нарушающие эту политику, не будут получать лицензию и не будут иметь права на возврат платы за экзамен.

С 1 января 2014 года все лицензиаты должны сдавать отпечатки пальцев. Нажмите здесь, чтобы получить инструкции [pdf].

Все лицензиаты должны предоставить форму подтверждения права на подтверждение прав. нажмите здесь для получения инструкций [pdf].

Хотя эта информация считается верной, законы, политики и правила меняются, и такие изменения могут не отражаться на этом веб-сайте.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *