Теорема Фалеса. Средняя линия треугольника [wiki.eduVdom.com]
Теорема 1. Теорема Фалеса1). Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство. Пусть А1, А2, А3 — точки пересечения параллельных прямых с одной из сторон угла и А2 лежит между А1 и А3 (рис.1).
Рис.1
Пусть B1 В2, В3 — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если А1А2 = A2A3, то В1В2 = В2В3.
Проведем через точку В2 прямую EF, параллельную прямой А1А3. По свойству параллелограмма А1А2 = FB2
И так как А1А2 = A2A3, то FB2 = В2Е.
Треугольники B2B1F и В2В3Е равны по второму признаку. У них B2F = В2Е по доказанному. Углы при вершине В2 равны как вертикальные, а углы B2FB1 и B2EB3 равны как внутренние накрест лежащие при параллельных А1В1 и A3B3 и секущей EF. Из равенства треугольников следует равенство сторон: В1В2 = В2В3 . Теорема доказана.
С использованием теоремы Фалеса устанавливается следующая теорема.
Теорема 2. Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке 2 отрезок ED — средняя линия треугольника ABC.
ED — средняя линия треугольника ABC
Рис.2
Пример 1. Разделить данный отрезок на четыре равные части.
Решение. Пусть АВ — данный отрезок (рис.3), который надо разделить на 4 равные части.
Деление отрезка на четыре равные части
Рис.3
Для этого через точку А проведем произвольную полупрямую а и отложим на ней последовательно четыре равных между собой отрезка AC, CD, DE, ЕК.
Соединим точки В и К отрезком. Проведем через оставшиеся точки С, D, Е прямые, параллельные прямой ВК, так, чтобы они пересекли отрезок АВ.
Согласно теореме Фалеса отрезок АВ разделится на четыре равные части.
Пример 2. Диагональ прямоугольника равна а. Чему равен периметр четырехугольника, вершины которого являются серединами сторон прямоугольника?
Решение. Пусть условию задачи отвечает рисунок 4.
Рис.4
Тогда EF — средняя линия треугольника ABC и, значит, по теореме 2. $$ EF = \frac{1}{2}AC = \frac{a}{2} $$
Аналогично $$ HG = \frac{1}{2}AC = \frac{a}{2} , EH = \frac{1}{2}BD = \frac{a}{2} , FG = \frac{1}{2}BD = \frac{a}{2} $$ и, следовательно, периметр четырехугольника EFGH равен 2a.
Пример 3. Стороны треугольника равны 2 см, 3 см и 4 см, а вершины его — середины сторон другого треугольника. Найти периметр большого треугольника.
Решение. Пусть условию задачи отвечает рисунок 5.
Рис.5
Отрезки АВ, ВС, АС — средние линии треугольника DEF. Следовательно, согласно теореме 2 $$ AB = \frac{1}{2}EF\ \ ,\ \ BC = \frac{1}{2}DE\ \ ,\ \ AC = \frac{1}{2}DF $$ или $$ 2 = \frac{1}{2}EF\ \ ,\ \ 3 = \frac{1}{2}DE\ \ ,\ \ 4 = \frac{1}{2}DF $$ откуда $$ EF = 4\ \ ,\ \ DE = 6\ \ ,\ \ DF = 8 $$ и, значит, периметр треугольника DEF равен 18 см.
Пример 4. В прямоугольном треугольнике через середину его гипотенузы проведены прямые, параллельные его катетам. Найти периметр образовавшегося прямоугольника, если катеты треугольника равны 10 см и 8 см.
Решение. В треугольнике ABC (рис.6)
Рис.6
∠ А прямой, АВ = 10 см, АС = 8 см, KD и MD — средние линии треугольника ABC, откуда $$ KD = \frac{1}{2}AC = 4 см. \\ MD = \frac{1}{2}AB = 5 см. $$ Периметр прямоугольника К DMА равен 18 см.
Теорема Фалеса — WiKi
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
- Более общая формулировка, также называемая теорема о пропорциональных отрезках
Параллельные прямые отсекают на секущих пропорциональные отрезки:
- A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае не параллельных прямых
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
Таким образом (см. рис.) из того, что CB1CA1=B1B2A1A2=…{\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots } , следует, что A1B1||A2B2||…{\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots } .
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.
Лемма Соллертинского
Следующее утверждение, двойственно к лемме Соллертинского:
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть f{\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых Xf(X){\displaystyle Xf(X)} будет коника (возможно, вырожденная). |
ru-wiki.org
Теорема Фалеса — Википедия
Материал из Википедии — свободной энциклопедии
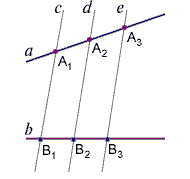
- Эта теорема о параллельных прямых. См. также Теорема Фалеса об угле, опирающемся на диаметр окружности.
Теорема Фалеса — теорема планиметрии о параллельных и секущих.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Формулировки[ | ]
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
- Более общая формулировка, также называемая теорема о пропорциональных отрезках
Параллельные прямые отсекают на секущих пропорциональные отрезки:
- A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
Замечания[ | ]
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
encyclopaedia.bid
Теорема Фалеса — Gpedia, Your Encyclopedia
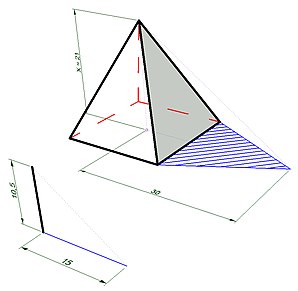
Теорема Фалеса — теорема планиметрии, о наборе параллельных секущих к паре прямых.
Эта теорема о параллельных прямых так же известная как теорема Фалеса .
Формулировки
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
- Более общая формулировка, также называемая теорема о пропорциональных отрезках
Параллельные прямые отсекают на секущих пропорциональные отрезки:
- A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае не параллельных прямых
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
История
Эта теорема приписывается греческому математику и философу Фалесу Милетскому; по легенде, Фалес Милетский рассчитывал высоту пирамиды Хеопса, измеряя длину её тени на земле и длину тени палки измеряемой высоты. Самое раннее из известных письменных доказательств этой теоремы дано в «Элементах Евклида» (предложение 2 книги VI).
Вариации и обобщения
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
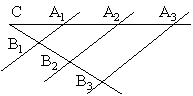В обратной теореме Фалеса важно, что равные отрезки начинаются от вершиныТаким образом (см. рис.) из того, что CB1CA1=B1B2A1A2=…{\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots }, следует, что A1B1||A2B2||…{\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots }.
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.
Лемма Соллертинского
Следующее утверждение, двойственно к лемме Соллертинского:
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть f{\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых Xf(X){\displaystyle Xf(X)} будет коника (возможно, вырожденная). |
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers[es] представила песню, посвящённую теореме[1].
Литература
- Атанасян Л. C. и др. Геометрия 7—9. — Изд. 3-е. — М.: Просвещение, 1992.
Примечания
См. также
www.gpedia.com
Теорема Фалеса
Теорема Фалеса. Средняя линия треугольника и трапеции, ее свойства
Для средних линий треугольника и трапеции оправдывается теорема, которую довел Фалес Милетский, поэтому теперь она носит его имя.
Теорема Фалеса
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Или: параллельные прямые, пересекающие две данные прямые и отсекают на одной прямой равные отрезки, отсекают равные отрезки и на другой прямой.
Обратите внимание!
По этому принципу разделяют отрезок сколь угодно равных отрезков. С одного конца заданного отрезка проводят луч, на котором откладывают необходимое количество равных отрезков определенной длины, после чего через конец последнего из отложенных отрезков и второй конец заданного отрезка проводят прямую, параллельно которой проводят прямые через деления лучи. Точки пересечения этих прямых с заданным отрезком разделяют его на необходимое количество равных отрезков.
Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
Свойства биссектрисы треугольника
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные соответствующим другим сторонам треугольника.
Средняя линия треугольника — отрезок, соединяющий середины двух его сторон. У каждого треугольника три средние линии.
Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Это свойство средней линии треугольника позволяет доказать следующие свойства геометрических фигур:
Если соединить отрезками середины сторон треугольника, то получим треугольник, периметр которого вдвое меньше периметр данного треугольника.
Если соединить отрезками середины сторон четырехугольника, то получим параллелограмм.
Медианы треугольника пересекаются в одной точке и ею делятся в отношении 2: 1, считая от вершины треугольника.
Средняя линия трапеции — отрезок, соединяющий середины боковых линий.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Если диагонали равносторонний трапеции взаимно перпендикулярны, то высота трапеции равна ее средней линии.
xn—-7sbfhivhrke5c.xn--p1ai
Теорема Фалеса про пропорційні відрізки — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Теорема Фалеса про пропорційні відрізки — одна із теорем планіметрії.
У математичній літературі країн колишнього Радянського Союзу відома як теорема Фалеса. У європейській літературі теоремою Фалеса найчастіше називають іншу теорему.
Теорема Фалеса: якщо паралельні прямі, що перетинають дві задані прямі а і b, відтинають на одній прямій рівні відрізки, то вони відтинають рівні відрізки й на іншій прямій.
- A1A2=A2A3,{\displaystyle A_{1}A_{2}=A_{2}A_{3},}
- B1B2=B2B3.{\displaystyle B_{1}B_{2}=B_{2}B_{3}.}
Узагальнена теорема Фалеса: паралельні прямі, що перетинають дві задані прямі а і b, відтинають на них пропорційні відрізки.
- A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
- Погорєлов О. В. Геометрія: Планіметрія: Підруч. для 7—9 кл. загальноосвіт. навч. закл. — 7-ме вид. — К. : Школяр, 2004. — С. 85—87.
uk.wikipedia.org