Площадь — Википедия

Пло́щадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры^[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.

Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.

Для приближённого вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.

Множество измеримо по Жордану, если внутренняя мера Жордана равна внешней мере Жордана

Площадь — функция, которая обладает следующими свойствами^[2][1]:

• Положительность, то есть площадь неотрицательна;
• Аддитивность, то есть площадь фигуры равна сумме площадей составляющих её фигур без общих внутренних точек;
• Инвариантность, то есть площади конгруэнтных фигур равны;
• Нормированность, то есть площадь единичного квадрата равна 1.

Из данного определения площади следует её монотонность, то есть площадь части фигуры меньше площади всей фигуры^[2].

Первоначально определение площади было сформулировано для многоугольников, затем оно было расширено на квадрируемые фигуры. Квадрируемой называется такая фигура, которую можно вписать в многоугольник и в которую можно вписать многоугольник, причём площади обоих многоугольников отличаются на произвольно малую величину. Такие фигуры называются также измеримыми по Жордану^[1]. Для фигур на плоскости, не состоящих из целого количества единичных квадратов, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими

[3]. Существуют неквадрируемые плоские фигуры^[1]. Предложенное выше аксиоматическое определение площади в случае плоских фигур обычно дополняют конструктивным, при котором с помощью палетки осуществляется собственно вычисление площади. При этом для более точных вычислений на последующих шагах используют палетки, у которых длина стороны квадрата в десять раз меньше длины у предыдущей палетки^[4].

Площадь квадрируемой плоской фигуры существует и единственна. Понятие площади, распространённое на более общие множества, привело к определению множеств, измеримых по Лебегу, которыми занимается теория меры. В дальнейшем возникают более общие классы, для которых свойства площади не гарантируют её единственность^[1].

Под площадью в обобщённом смысле понимают численную характеристику

k-мерной поверхности в n-мерном пространстве (евклидовом или римановом), в частности, характеристику двумерной поверхности в трёхмерном пространстве^[1].

Площадь плоской фигуры[править | править код]

На практике чаще всего требуется определить площадь ограниченной фигуры с кусочно-гладкой границей. Математический анализ предлагает универсальный метод решения подобных задач.

Декартовы координаты[править | править код]

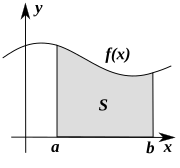Определённый интеграл как площадь фигуры Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования

Площадь, заключённая между графиком непрерывной функции на интервале [a,b]{\displaystyle [a,b]} и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:

S=∫abf(x)dx{\displaystyle S=\int \limits _{a}^{b}f(x)\,dx}

Площадь, заключённая между графиками двух непрерывных функций f(x),g(x){\displaystyle f(x),\,g(x)} на интервале [a,b]{\displaystyle [a,b]} находится как разность определённых интегралов от этих функций:

S=∫ab|f(x)−g(x)|dx{\displaystyle S=\int \limits _{a}^{b}\left|f(x)-g(x)\right|\,dx}

Полярные координаты[править | править код]

В полярных координатах: площадь, ограниченная графиком функции r=r(θ){\displaystyle r=r(\theta )} и лучами θ=θ1,θ=θ2,θ1<θ2{\displaystyle \theta =\theta _{1},\theta =\theta _{2},\theta _{1}<\theta _{2}} вычисляется по формуле:

S=12∫θ1θ2r2(θ)dθ{\displaystyle S={1 \over 2}\int \limits _{\theta _{1}}^{\theta _{2}}r^{2}(\theta )\,d\theta }.

Площадь поверхности[править | править код]

Для определения площади кусочно гладкой поверхности в трёхмерном пространстве используют ортогональные проекции к касательным плоскостям в каждой точке, после чего выполняют предельный переход. В результате, площадь искривлённой поверхности A, заданной вектор-функцией r=r(u,v),{\displaystyle \mathbf {r} =\mathbf {r} (u,v),}, даётся двойным интегралом^[1]:

S=∬A|∂r∂u×∂r∂v|dudv.{\displaystyle S=\iint \limits _{A}\left|{\frac {\partial \mathbf {r} }{\partial u}}\times {\frac {\partial \mathbf {r} }{\partial v}}\right|\,du\,dv.}

То же в координатах:

S=∬A(D(x,y)D(u,v))2+(D(y,z)D(u,v))2+(D(z,x)D(u,v))2dudv{\displaystyle S=\iint \limits _{A}{\sqrt {\left({\frac {D(x,y)}{D(u,v)}}\right)^{2}+\left({\frac {D(y,z)}{D(u,v)}}\right)^{2}+\left({\frac {D(z,x)}{D(u,v)}}\right)^{2}}}\;\mathrm {d} \,u\,\mathrm {d} \,v}

Здесь D(y,z)D(u,v)=|yu′yv′zu′zv′|,D(z,x)D(u,v)=|zu′zv′xu′xv′|,D(x,y)D(u,v)=|xu′xv′yu′yv′|{\displaystyle {\frac {D(y,z)}{D(u,v)}}={\begin{vmatrix}y’_{u}&y’_{v}\\z’_{u}&z’_{v}\end{vmatrix}},\quad {\frac {D(z,x)}{D(u,v)}}={\begin{vmatrix}z’_{u}&z’_{v}\\x’_{u}&x’_{v}\end{vmatrix}},\quad {\frac {D(x,y)}{D(u,v)}}={\begin{vmatrix}x’_{u}&x’_{v}\\y’_{u}&y’_{v}\end{vmatrix}}}.

Теория площадей[править | править код]

Теория площадей занимается изучением обобщений, связанных с распространением определения k-мерной площади с кусочно-гладкого погружения на более общие пространства. Для кусочно-гладкого погружения f площадь определяют способом, аналогичным указанному выше, при этом у площади сохраняются такие свойства как положительность, аддитивность, нормированность, а также ряд новых.

В одном квадратном сантиметре сто квадратных миллиметров

Метрические единицы[править | править код]

Русские устаревшие[править | править код]

Мерами земли при налоговых расчётах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли: коробья, верёвка, жеребья и др.

Античные[править | править код]

Другие[править | править код]

Формулы вычисления площадей простейших фигур[править | править код]

Многоугольники[править | править код]

Фигура	Формула	Переменные
Правильный треугольник	a234{\displaystyle a^{2}{\frac {\sqrt {3}}{4}}}	a{\displaystyle a} — длина стороны треугольника
Прямоугольный треугольник	ab2{\displaystyle {\frac {ab}{2}}}	a{\displaystyle a} и b{\displaystyle b} — катеты треугольника
Произвольный треугольник	12ah{\displaystyle {\frac {1}{2}}ah}	a{\displaystyle a} — сторона треугольника, h{\displaystyle h} — высота, проведённая к этой стороне
	12absin⁡α{\displaystyle {\frac {1}{2}}ab\sin \alpha }	a{\displaystyle a} и b{\displaystyle b} — любые две стороны, α{\displaystyle \alpha } — угол между ними
	p(p−a)(p−b)(p−c){\displaystyle {\sqrt {p(p-a)(p-b)(p-c)}}} (формула Герона)	a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} — стороны треугольника, p{\displaystyle p} — полупериметр (p=a+b+c2){\displaystyle \left(p={\frac {a+b+c}{2}}\right)}
	12|x0y01x1y11x2y21|{\displaystyle {\frac {1}{2}}{\begin{vmatrix}x_{0}&y_{0}&1\\x_{1}&y_{1}&1\\x_{2}&y_{2}&1\end{vmatrix}}}	(x0;y0){\displaystyle (x_{0};y_{0})}, (x1;y1){\displaystyle (x_{1};y_{1})}, (x2;y2){\displaystyle (x_{2};y_{2})} — координаты вершин треугольника (в случае обхода вершин по часовой стрелке получим положительный результат, иначе отрицательный)
Квадрат	a2{\displaystyle a^{2}}	a{\displaystyle a} — длина стороны квадрата
Прямоугольник	ab{\displaystyle ab}	a{\displaystyle a} и b{\displaystyle b} — длины сторон прямоугольника (его длина и ширина)
Ромб	12cd{\displaystyle {\frac {1}{2}}cd}	c{\displaystyle c} и d{\displaystyle d} — длины диагоналей ромба
Параллелограмм	ah{\displaystyle ah}	a{\displaystyle a} и h{\displaystyle h} — длины стороны и опущенной на неё высоты соответственно
	absin⁡α{\displaystyle ab\sin \alpha }	a{\displaystyle a} и b{\displaystyle b} — соседние стороны параллелограмма, α{\displaystyle \alpha } — угол между ними
Трапеция	12(a+b)h{\displaystyle {\frac {1}{2}}(a+b)h}	a{\displaystyle a} и b{\displaystyle b} — основания трапеции, h{\displaystyle h} — высота трапеции
Произвольный четырёхугольник	(p−a)(p−b)(p−c)(p−d)−abcdcos⁡α{\displaystyle {\sqrt {(p-a)(p-b)(p-c)(p-d)-abcd\cos \alpha }}} (формула Брахмагупты)	a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c}, d{\displaystyle d} — стороны четырёхугольника, p{\displaystyle p} — его полупериметр, α{\displaystyle \alpha } — полусумма противолежащих углов четырёхугольника
Правильный шестиугольник	a2332{\displaystyle a^{2}{\frac {3{\sqrt {3}}}{2}}}	a{\displaystyle a} — длина стороны шестиугольника
Правильный восьмиугольник	2a2(1+2){\displaystyle 2a^{2}(1+{\sqrt {2}})}	a{\displaystyle a} — длина стороны восьмиугольника
Правильный многоугольник	P2/n4tg⁡(π/n){\displaystyle {\frac {P^{2}/n}{4\operatorname {tg} (\pi /n)}}}	P{\displaystyle P} — периметр, n{\displaystyle n} — количество сторон
Произвольный многоугольник (выпуклый и невыпуклый)	12|∑i=1n(xi+1−xi)(yi+1+yi)|{\displaystyle {\frac {1}{2}}\left|\sum _{i=1}^{n}(x_{i+1}-x_{i})(y_{i+1}+y_{i})\right|} (метод трапеций)	(xi;yi){\displaystyle (x_{i};y_{i})} — координаты вершин многоугольника в порядке их обхода, замыкая последнюю с первой: (xn+1;yn+1)=(x1;y1){\displaystyle (x_{n+1};y_{n+1})=(x_{1};y_{1})}; при наличии отверстий направление их обхода противоположно обходу внешней границы многоугольника

Площади круга, его частей, описанных и вписанных в круг фигур[править | править код]

Как посчитать площадь стен: делаем расчёты првильно

Начиная ремонт, первым делом нужно определить необходимое количество строительных материалов. Провести расчеты могут специалисты, которые будут выполнять работы. Но они часто делают вычисления с большой погрешностью в свою пользу. Рассмотрим, как самостоятельно посчитать площадь стен.

Инструменты для подсчета квадратных метров

Для расчетов понадобятся:

• уровень строительный;
• рулетка с ограничителем;
• длинная линейка и угольник;
• карандаш и бумага;
• калькулятор.

Для нанесения размеров нарисуем схему комнат. Обозначим двери, окна, ниши, выступы. Результаты замеров нанесем на чертеж.

Как рассчитать площадь прямоугольных стен

Измеряем высоту (h), длину (a), ширину (b).

Площадь: S = P × h

Периметр: P = (a + b) × 2

Вдоль плинтуса измеряем длину и ширину помещений.

Высоту — по вертикальному углу.

Пример:

a = 5 м;

b = 4 м;

h = 3 м;

Р = (5 + 4) × 2 = 18 м;

S = 18 × 3 = 54 м².

Как правильно рассчитать площадь стен со сложной поверхностью

Не все помещения имеют строгую прямоугольную форму. В зданиях часто присутствуют замысловатые архитектурные элементы, усложняющие расчет.

Как посчитать квадратуру стен за вычетом проемов

При определении точного объема работ, вычтем размеры окон и дверей из общего количества квадратных метров стен комнаты. Для этого по краю рамы замеряем ширину и высоту окна, по краю коробки — габариты двери.

Перемножив длину и ширину проемов, получаем размер, который необходимо вычесть.

Аналогично действуем, если из подсчитываемой квадратуры комнаты нужно исключить печи, камины, радиаторы.

Пример:

В помещении имеется окно 2,5 м × 1,5 м и дверь 0,9 м × 2,1 м.

S окна равна 2,5 × 1,5 = 3,75 м².

S двери равна 0,9 × 2,1 = 1,89 м².

S стен за вычетом проемов составляет 54 − 3,75 − 1,89 = 48,36 м².

 Определение площади помещений неправильной формы

Для определения периметра зданий любых конфигураций сложим длины всех стен, включая выступы и ниши.

Рисунок 1. Элемент с выступом.

Проводить измерения помещений неправильной формы можно, разбив поверхность на несколько простых фигур.

Если у вас комната с прямоугольным выступом, вы имеете две фигуры, квадратуру которых легко вычислить, затем сложить.

Если элемент содержит в себе полукруг, для расчета нужно разбить его на полукруг и прямоугольник.

Рисунок 2. Элемент с полукругом.

Как считать квадратные метры стен с круглыми элементами

Встречаются круглые и полукруглые жилые здания или строения с элементами окон или дверей в виде арки.

Их периметр можно определить, умножив диаметр на число π (Пи) = 3,14.

Квадратуру вертикальных поверхностей определяем, умножив полученное значение на высоту от пола до потолка.

S круга равна квадрату радиуса, умноженному на число π; полукруга — половине этой величины.

Если необходимо из квадратуры комнаты вычесть площадь круглых колонн или полукруглых выступающих элементов, при невозможности измерить диаметр или радиус, измеряем длину окружности (P) и применяем формулу: S = P² / 4π.

Как рассчитать квадратные метры конструкций в виде треугольника

В случае наличия комнаты с треугольными элементами, мы можем применить несколько формул, в зависимости от вида фигур:

Рисунок 3. Формулы определения площади треугольников.

Где a, b, c — длины сторон треугольника; p — периметр.

Объем помещения

Для определения объема необходимо высчитать площадь пола, и полученный показатель перемножить на высоту. V = S × h.

Расчет площади стен дома на калькуляторе

Существенно облегчат расчеты специальные программы, к которым относится строительный калькулятор в онлайн-версии.

Чтобы посмотреть, сколько квадратных метров составляют стены за вычетом проемов, достаточно выбрать геометрическую форму помещения и ввести показатели:

• ширину;
• длину;
• высоту;
• количество проемов;
• размеры окон и дверей.

Строительный калькулятор рассчитает количество отделочных материалов, необходимых для вашего ремонта.

Советы и рекомендации

Необходимо помнить, что геометрические параметры зданий редко могут быть идеальными. Поэтому для определения точных величин замеры лучше производить в нескольких местах, а затем выводить среднее арифметическое. Например, рассчитывая площадь комнаты по стенам, длину лучше измерять по потолку, плинтусу и в середине вертикальной плоскости. Высоту — в углах и середине стены по отвесу.

Чтобы вычислить периметр при наличии множества выступов и ниш разных форм, необходимо проложить вдоль всех элементов шнур, затем измерить его рулеткой.

Подсчитав точные параметры, можно идти в магазин за строительными материалами. Лучше показать схемы с нанесенными размерами продавцу-консультанту. Специалист поможет рассчитать расход материалов с учетом нахлеста, подбора рисунка обоев или потерь при резке плитки.

Площадь фигуры — Википедия

Материал из Википедии — свободной энциклопедии

Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.

Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.

Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости и удовлетворяющая четырём условиям:

1. Положительность — площадь неотрицательна;
2. Нормировка — квадрат со стороной единица имеет площадь 1;
3. Конгруэнтность — конгруэнтные фигуры имеют равную площадь;
4. Аддитивность — площадь объединения двух фигур без общих внутренних точек равна сумме площадей.

При этом определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть

• Если одна фигура принадлежит другой фигуре, то площадь первой не превосходит площади второй:

Чаще всего за «определённый класс» берут множество квадрируемых фигур. Фигура F{\displaystyle F} называется квадрируемой, если для любого ε>0{\displaystyle \varepsilon >0} существует пара многоугольников P{\displaystyle P} и Q{\displaystyle Q}, такие что P⊂F⊂Q{\displaystyle P\subset F\subset Q} и S(Q)−S(P)<ε{\displaystyle S(Q)-S(P)<\varepsilon }, где S(P){\displaystyle S(P)} обозначает площадь P{\displaystyle P}.

Примеры квадрируемых фигур

• Две фигуры называются равновеликими, если они имеют равную площадь.

• Существует математически строгий, но неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. То есть на множестве всех ограниченных подмножеств плоскости существуют различные функции площади, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур, на которых площадь определяется однозначно.

Фигура	Формула	Комментарий
Правильный треугольник	34⋅a2{\displaystyle {\tfrac {\sqrt {3}}{4}}{\cdot }a^{2}}	a{\displaystyle a} — длина стороны треугольника.
Треугольник	p⋅(p−a)⋅(p−b)⋅(p−c){\displaystyle {\sqrt {p{\cdot }(p-a){\cdot }(p-b){\cdot }(p-c)}}}	Формула Герона. p{\displaystyle p} — полупериметр, a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} — длины сторон треугольника.
Треугольник	12⋅a⋅b⋅sin⁡γ{\displaystyle {\tfrac {1}{2}}{\cdot }a{\cdot }b{\cdot }\sin \gamma }	a{\displaystyle a} и b{\displaystyle b} — две стороны треугольника, а γ{\displaystyle \gamma } — угол между ними.
Треугольник	12⋅b⋅h{\displaystyle {\tfrac {1}{2}}{\cdot }b{\cdot }h}	b{\displaystyle b} и h{\displaystyle h} — сторона треугольника и высота, проведённая к этой стороне.
Квадрат	a2{\displaystyle a^{2}}	a{\displaystyle a} — длина стороны квадрата.
Прямоугольник	a⋅b{\displaystyle a{\cdot }b}	a{\displaystyle a} и b{\displaystyle b} — длины сторон прямоугольника.
Ромб	a2⋅sin⁡α,12bc{\displaystyle a^{2}{\cdot }\sin \alpha ,{\tfrac {1}{2}}bc}	a{\displaystyle a} — сторона ромба, α{\displaystyle \alpha } — внутренний угол, b,c{\displaystyle b,c} — диагонали.
Параллелограмм	b⋅h{\displaystyle b{\cdot }h}	b{\displaystyle b} — длина одной из сторон параллелограмма, а h{\displaystyle h} — высота, проведённая к этой стороне.
Трапеция	12⋅(a+b)⋅h{\displaystyle {\tfrac {1}{2}}{\cdot }(a+b){\cdot }h}	a{\displaystyle a} и b{\displaystyle b} — длины параллельных сторон, а h{\displaystyle h} — расстояние между ними (высота).
Четырёхугольник	12⋅m⋅n⋅sin⁡ϕ{\displaystyle {\tfrac {1}{2}}{\cdot }m{\cdot }n{\cdot }\sin \phi }	n{\displaystyle n} и m{\displaystyle m} — длины диагоналей, и ϕ{\displaystyle \phi } — угол между ними.
Правильный шестиугольник	3⋅32⋅a2{\displaystyle {\tfrac {3{\cdot }{\sqrt {3}}}{2}}{\cdot }a^{2}}	a{\displaystyle a} — длина стороны шестиугольника.
Правильный восьмиугольник	2⋅(1+2)⋅a2{\displaystyle 2{\cdot }(1+{\sqrt {2}}){\cdot }a^{2}}	a{\displaystyle a} — длина стороны восьмиугольника.
Правильный многоугольник	n⋅a24⋅tan⁡(π/n){\displaystyle {\frac {n{\cdot }a^{2}}{4{\cdot }\tan(\pi /n)}}}	a{\displaystyle a} — длина стороны многоугольника, а n{\displaystyle n} — количество сторон многоугольника.
	12⋅a⋅p{\displaystyle {\tfrac {1}{2}}{\cdot }a{\cdot }p}	a{\displaystyle a} — апофема (или радиус вписанной в многоугольник окружности), а p{\displaystyle p} — периметр многоугольника.
Произвольный многоугольник	12|∑i=0n−1det(xixi+1yiyi+1)|{\displaystyle {1 \over 2}\left|\sum _{i=0}^{n-1}\det {\begin{pmatrix}x_{i}&x_{i+1}\\y_{i}&y_{i+1}\end{pmatrix}}\right|}	Формула площади Гаусса. (xi,yi){\displaystyle (x_{i},y_{i})} — координаты вершин n{\displaystyle n}-угольника, (xn,yn)=(x0,y0){\displaystyle (x_{n},y_{n})=(x_{0},y_{0})}
Круг	π⋅r2{\displaystyle \pi {\cdot }r^{2}} или π⋅d24{\displaystyle {\frac {\pi {\cdot }d^{2}}{4}}}	r{\displaystyle r} — радиус окружности, а d{\displaystyle d} — её диаметр.
Сектор круга	12⋅r2⋅θ{\displaystyle {\tfrac {1}{2}}{\cdot }r^{2}{\cdot }\theta }	r{\displaystyle r} и θ{\displaystyle \theta } — соответственно радиус и угол сектора (в радианах).
Эллипс	π⋅a⋅b{\displaystyle \pi {\cdot }a{\cdot }b}	a{\displaystyle a} и b{\displaystyle b} — большая и малая полуоси эллипса.

• В. Болтянский, О понятиях площади и объёма. Квант, № 5, 1977
• Б. П. Гейдман, Площади многоугольников, Библиотека «Математическое просвещение», выпуск 16, (2002).
• Мерзон Г. А., Ященко И. В. Длина, площадь, объем. — МЦНМО, 2011. — ISBN 9785940577409.
• В. А. Рохлин, Площадь и объём, Энциклопедия элементарной математики, Книга 5, Геометрия, под редакцией П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина.

Определение площади земельного участка. Методы и погрешности

При проведении землеустроительных работ используются различные способы вычисления площадей участков земли. Применение этих способов зависит от ценности этих участков, их величины, формы границ, наличия и точности данных измерений на местности, наличия карт необходимой точности и планов участков.

Основные способы

Существует три основных способа определения площадей:

• аналитический;
• графический;
• механический.

При использовании аналитического способа определение площади производится по результатам полевых угловых и линейных измерений (или координат) характерных точек.

Для графического способа используются данные измерений на плане и карте.

Такой способ чаще всего используется при отсутствии информации полевых измерений.

Если вы хотите узнать, как решить именно Вашу проблему, обращайтесь через форму онлайн-консультанта или звоните по телефонам:

При механическом способе площадь определяется по плану с помощью специального устройства – планиметра.

Иногда используется комбинированный способ определения площади. Например, общая площадь участка определяется по координатам характерных точек аналитическим способом, а площади внутренних участков определяются по плану с помощью графического или механического методов.

Эти три метода имеют различные показатели точности.

Наиболее точным является аналитический метод. На точность этого метода влияют только погрешности полевых измерений.

Точности других методов, использующих топографическую информацию с планов, зависят еще и от погрешностей приборов, качества плана, масштаба, деформации бумаги.

Если вы хотите узнать, как решить именно Вашу проблему, обращайтесь через форму онлайн-консультанта или звоните по телефонам:

Аналитический способ

Аналитический способ позволяет по координатам характерных точек границ участка определить его площадь. При этом используются формулы аналитической геометрии.

В соответствии с ними площадь многоугольника S может быть определена по формуле:

S= 0,5*∑(Xi*(Yi+1-Yi-1), где:

• Xi и Yi – координаты i-той характерной точки участка, имеющего вид многоугольника;
• i – порядковый номер характерной точки ЗУ. Этот параметр меняется от 1 до n;
• n – число характерных точек.

Если участок имеет четырехугольную форму, то, в общем случае, для него расчет площади производится по приведенной выше формуле с учетом того, что n=4.

Если участок имеет форму трапеции и известны его стороны, то площадь такого участка можно определить по формуле:

Sт=0,5*(a+b)*h, где:

• a и b – основания фигуры;
• h – высота трапеции.

При расчете четырехугольника неправильной формы, когда известны размеры его сторон, вначале определяют величину полупериметра p:

р=0,5(а+B+c+d), где:

a,b,c,d – величины сторон.

Тогда площадь участка Sу будет равна:

Sy=√(p-a)(p-b)(p-c)(p-d).

В некоторых случаях, когда имеется много точек поворота, аналитический расчет площади участка производится с использованием данных об углах азимута.

При этом по контуру границ участка производится замер азимута каждой характерной точки. Также определяется расстояние от одной характерной точки до следующей за ней точки. Вся эта информация в дальнейшем вводится в ЭВМ, которая по специальной программе производит расчет площади ЗУ.

Графический метод

При расчете площади участка графическим методом чаще всего изображенный на плане участок сложной формы делят на участки элементарного вида (треугольники, прямоугольники, трапеции), затем вычисляют и суммируют площади этих фигур.

Точность графического метода зависит от точности графического измерения на плане. Известно, что точность измерения с помощью циркуля постоянна и равна 0,1 мм. Поэтому относительная ошибка при измерении коротких линий больше, чем при измерении длинных линий. В связи с этим желательно, чтобы простые фигуры были больших размеров и с близкими по размерам основаниями и высотами.

Такой метод удобен в случае, когда имеется небольшое количество характерных точек. В противном случае целесообразнее определять площадь участка по координатам точек, измеренных на плане.

В некоторых случаях участки имеют криволинейную форму, которую трудно аппроксимировать простыми фигурами. В таких случаях могут использоваться палетки.

Палетка представляет собой прозрачный лист, на который нанесены деления. Этот лист накладывается на план участка. Сосчитав количество делений, входящих в контур участка, и определив площадь одного деления с учетом масштаба, можно оценить площадь участка.

Недостаток такого графического метода состоит в том, что количество неполных квадратов приходится оценивать на глаз. В результате этого ухудшается точность данного метода.

Механический способ

Механический способ используется в тех случаях, когда по плану необходимо оценить площадь большого участка со сложными границами. Для осуществления этого метода используются планиметры.

Планиметр представляет собой прибор, который позволяет определить площадь плоской фигуры путем обвода ее контура. Он состоит из двух рычагов и каретки со счетным механизмом. На полюсном рычаге имеется игла, которая втыкается в план и является полюсом. Вокруг полюса по контуру участка движется обводной шпиль.
Точность метода зависит от размеров участка и свойств плана.

Погрешность определения площади

При определении площадей участков возникают неточности, которые характеризуются погрешностями. Погрешность – это разность между вычисленной величиной площади участка и ее истинной величиной.

Для различных методов определения площади такие погрешности могут быть различными.

Для аналитического метода точность расчета площади зависит исключительно от погрешностей, связанных с измерением координат поворотных точек. При этом, средняя квадратическая погрешность (СКП) аналитического метода расчета (mp) определяется формулой:

mp= mt*√ P, где:

• mt – СКП расположения поворотных точек;
• P – площадь участка.

Для примера можно взять допустимые при межевании точности mt, которые определены соответствующими нормативными актами (например, Приложением к приказу МЭР № 518). Эти точности зависят от типа земель.

Так, для населенных пунктов этот показатель равен 10 см, а для дачных участков и садоводств-20 см. Таким образом, для садового участка в 600 кв. м точность определения площади аналитическим методом может составить:

mpс= 0,2*√600=4,89 м.

При реализации графического метода на его точность влияют погрешности измерений, погрешности составления плана, деформация бумаги. Относительная погрешность такого метода составляет от 1:500 до 1:1000.

Точность механического метода также зависит от погрешностей составления плана (или карты), состояния бумаги, на которой нанесен план участка. Кроме того, на точность этого метода влияет размер участка. Этот метод не рекомендуется применять для участков размером менее 10-12 см2.

В благоприятных условиях относительная погрешность измерений площади планиметром может достигать 1:400.

Определение площади участка на ПКК

Публичная кадастровая карта (ПКК) – это онлайн-сервис, с помощью которого любой гражданин может узнать основные характеристики любого земельного участка, помещенные в кадастр недвижимости (ЕГКН).

Для того, чтобы узнать величину площади с помощью ПКК, надо зайти на страницу http://pkk5.rosreestr.ru и найти участок на карте. Для этого используется специальное меню, которое позволяет определить участок по кадастровому номеру, адресу.

Так, введя в поисковую систему ПКК адрес участка, можно получить его расположение на карте и некоторые данные.

Среди этих данных имеется площадь данного участка, которая является официальной величиной, так как она введена в ЕГРН.

Необходимо отметить, что не все участки земли можно таким образом найти по адресу. Например, при нахождении участка c кадастровым номером 50:38:0050302:130 в таблице его параметров указан адрес: “обл. Московская, р-н Зарайский, снт “Изобретатель”, уч-к 116″.

Однако при обращении к ПКК с использованием этого адреса система дает сбой. Подобный результат получается и при обращении к ПКК на других страницах.

Это говорит о том, что система поиска земельного участка на ПКК по адресу не до конца отработана Росреестром.

Чтобы определить площадь участка по координатам, вначале необходимо узнать эти координаты. Если участок уже найден на карте, то приблизительные координаты характерных точек можно определить, подводя к ним курсор. По этим координатам, в дальнейшем, можно определить площадь участка по формуле для аналитического метода.

Более точно координаты характерных точек участка можно узнать только при платном заказе выписки из ЕГРН для этого участка.

По новому закону в связи с объединением баз данных ЕГРП и ЕГРН такая выписка с 1.01 2017 года заменяет собой свидетельство на объект недвижимости, кадастровый паспорт, кадастровую выписку и выписку из ЕГРП. То есть, выписка из ЕГРН является основным документом на недвижимость.

Дорогие читатели, информация в статье могла устареть. Если вы хотите узнать, как решить именно Вашу проблему, звоните по телефонам:Или задайте вопрос юристу на сайте. Это быстро и бесплатно!

Автор статьи

Вячеслав Садчиков

Юрист. Практика в сфере недвижимости, тудового права, семейного права, защите прав потребителей.

 

Площадь — это… Что такое Площадь?

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры^[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.

Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.

Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.

Свойства

Для фигур на плоскости, не состоящих из целого количества единичных квадратов, а также для искривлённых трёхмерных поверхностей, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими^[2].

Общий метод определения площади

Площадь плоской фигуры

Декартовы координаты

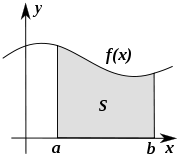Определённый интеграл как площадь фигуры 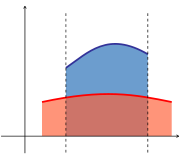Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования

Площадь, заключённая между графиком непрерывной функции на интервале и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:

Площадь, заключённая между графиками двух непрерывных функций на интервале находится как разность определённых интегралов от этих функций:

Полярные координаты

В полярных координатах: площадь, ограниченная графиком функции и лучами вычисляется по формуле:

.

Площадь поверхности

Площадь искривлённой поверхности A, заданной вектор-функцией , даётся двойным интегралом:

То же в координатах:

Здесь .

Единицы измерения площади

Метрические единицы

Русские устаревшие

Мерами земли при налоговых расчетах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли:коробья, веревка, жеребья и др.

Античные

Формулы вычисления площадей простейших фигур

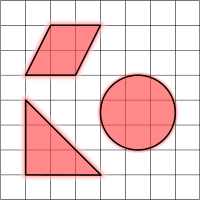
Планиметрические фигуры

Фигура	Формула	Переменные
Квадрат		— длина стороны квадрата.
Правильный треугольник		— длина стороны треугольника.
Правильный шестиугольник		— длина стороны шестиугольника.
Правильный восьмиугольник		— длина стороны восьмиугольника.
Правильный многоугольник		— периметр, а  — количество сторон.
Прямоугольный треугольник		и  — катеты треугольника.
Произвольный треугольник		— сторона треугольника,  — высота, проведенная к этой стороне.
		,  — любые две стороны,  — угол между ними.
	(формула Герона)	, ,  — стороны треугольника,  — полупериметр .
		в случае обхода вершин треугольника по часовой стрелке получим положительный результат, иначе отрицательный.
Прямоугольник		и  — длины сторон прямоугольника (его длина и ширина).
Параллелограмм		и  — длина стороны и опущенной на неё высоты соответственно.
		и  — соседние стороны параллелограмма,  — угол между ними.
Ромб		и  — длины диагоналей ромба.
Эллипс		и  — длины малой и большой полуосей.
Трапеция		та  — параллельные стороны, и  — расстояние между ними (высота трапеции).

Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур

Фигура	Формула	Переменные
Круг	или	— радиус, а  — диаметр круга.
Сектор круга		— радиус круга,  — центральный угол сектора (в радианах).
Сегмент		— радиус круга,  — центральный угол сегмента (в радианах).
Треугольник, вписанный в окружность		, ,  — стороны треугольника,  — радиус описанной окружности.
Произвольный многоугольник, описанный вокруг окружности		— радиус окружности, вписанной в многоугольник, и  — периметр многоугольника.

Формулы для вычисления площади поверхности тел в пространстве

См. также

Литература

• Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2

Ссылки

Примечания

Формула площади Гаусса — Википедия

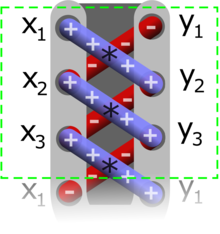Формула шнурования

Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования) — формула определения площади простого многоугольника, вершины которого заданы декартовыми координатами на плоскости. Пользователь перемножает соответствующие координаты и складывает, чтобы найти область, охватывающую многоугольник, и вычитает его из окружающего многоугольника, чтобы найти площадь многоугольника внутри. Это называется формулой шнурков, так как положительные и отрицательные слагаемые из перемножаемых координат располагаются на бумаге крест-накрест, как при завязке шнурков. Она находит применение в геодезии и лесном хозяйстве, среди других областей.

Формула была описана Мейстером (1724—1788) в 1769 году и Гауссом в 1795 году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.

Формула определения площади определяется путём взятия каждого ребра многоугольника АВ и вычисления площади треугольника АВО с вершиной в начале координат О через координаты вершин. При обходе вокруг многоугольника образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника. Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется, если она слева, и вычитается, если она справа с точки зрения из начала координат.

Формула площади верна для любого самонепересекающегося (простого) многоугольника, который может быть выпуклым или вогнутым.

Формула может быть представлена следующим выражением:

A=12|∑i=1n−1xiyi+1+xny1−∑i=1n−1xi+1yi−x1yn|==12|x1y2+x2y3+⋯+xn−1yn+xny1−x2y1−x3y2−⋯−xnyn−1−x1yn|,{\displaystyle {\begin{aligned}\mathbf {A} &={\frac {1}{2}}\left|\sum _{i=1}^{n-1}x_{i}y_{i+1}+x_{n}y_{1}-\sum _{i=1}^{n-1}x_{i+1}y_{i}-x_{1}y_{n}\right|=\\&={\frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+\dots +x_{n-1}y_{n}+x_{n}y_{1}-x_{2}y_{1}-x_{3}y_{2}-\dots -x_{n}y_{n-1}-x_{1}y_{n}|,\end{aligned}}}

где

А — площадь многоугольника,

n — количество сторон многоугольника,

(x_i, y_i), i = 1, 2, …, n — координаты вершин многоугольника.

Другое представление этой же формулы^[1][2]:

A=12|∑i=1nxi(yi+1−yi−1)|==12|∑i=1nyi(xi+1−xi−1)|==12|∑i=1nxiyi+1−xi+1yi|==12|∑i=1ndet(xiyixi+1yi+1)|,{\displaystyle {\begin{aligned}\mathbf {A} &={\frac {1}{2}}\left|\sum _{i=1}^{n}x_{i}(y_{i+1}-y_{i-1})\right|=\\&={\frac {1}{2}}\left|\sum _{i=1}^{n}y_{i}(x_{i+1}-x_{i-1})\right|=\\&={\frac {1}{2}}\left|\sum _{i=1}^{n}x_{i}y_{i+1}-x_{i+1}y_{i}\right|=\\&={\frac {1}{2}}\left|\sum _{i=1}^{n}\det {\begin{pmatrix}x_{i}&y_{i}\\x_{i+1}&y_{i+1}\end{pmatrix}}\right|,\end{aligned}}}

где

x_n+1 = x₁, x₀ = x_n,

y_n+1 = y₁, y₀ = y_n.

Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны, и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, то детерминанты будут отрицательными. Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина.

Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости. Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую координату x первой вершины и умножим её на координату y второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определён по следующей формуле^[3]:

Atri.=12|x1y2+x2y3+x3y1−x2y1−x3y2−x1y3|,{\displaystyle \mathbf {A} _{\text{tri.}}={\frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|,}

где x_i и y_i обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.

Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x₅ и y₅:

Apent.=12|x1y2+x2y3+x3y4+x4y5+x5y1−x2y1−x3y2−x4y3−x5y4−x1y5|.{\displaystyle \mathbf {A} _{\text{pent.}}={\frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|.}

А для четырехугольника — переменные до x₄ и y₄:

Aquad.=12|x1y2+x2y3+x3y4+x4y1−x2y1−x3y2−x4y3−x1y4|.{\displaystyle \mathbf {A} _{\text{quad.}}={\frac {1}{2}}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{1}y_{4}|.}

Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):

Площадь этого многоугольника:

A=12|3×11+5×8+12×5+9×6+5×4−−4×5−11×12−8×9−5×5−6×3|==602=30.{\displaystyle {\begin{aligned}\mathbf {A} &={\frac {1}{2}}|3\times 11+5\times 8+12\times 5+9\times 6+5\times 4-{}\\&\qquad -4\times 5-11\times 12-8\times 9-5\times 5-6\times 3|=\\&={\frac {60}{2}}=30.\end{aligned}}}

Формула называется «формулой шнурков» из-за общего метода, используемого для её вычисления. Этот метод использует матрицу. В качестве примера возьмём треугольник с вершинами (2, 4), (3, −8), (1, 2). Затем построим следующую матрицу, «обходя вокруг» треугольника и заканчивая начальной точкой:

[243−81224].{\displaystyle {\begin{bmatrix}2&4\\3&-8\\1&2\\2&4\end{bmatrix}}.}

Сначала проведём диагональ вниз и вправо косой чертой, как показано ниже:

и перемножим пары чисел, соединённых чертой, а затем сложим все суммы:

(2 × −8) + (3 × 2) + (1 × 4) = −6.

Зашнурованные кеды

Сделаем то же самое, проводя косую черту по диагонали вниз и влево, как показано ниже:

(4 × 3) + (−8 × 1) + (2 × 2) = 8.

Затем вычтем сумму второй группы из первой и возьмём модуль:

|(−6) − (8)| = 14.

Деление результата на два даёт площадь.

Организация чисел в матрицу с диагональными линиями упрощает запоминание формулы.

В результате проделанной операции с рисованием диагональных (косых) линий матрица с числами напоминает зашнурованную обувь, отсюда и происходит название «алгоритма шнурования».

Что такое площадь в математике? Единицы площади :: SYL.ru

Есть проблемы с элементарной геометрией? Эта статья поможет вам решить одну из них. Здесь вы узнаете о том, что такое площадь в математике, об единицах ее измерения и других важных аспектах этой темы. Разбор некоторых конкретных примеров даст вам возможность глубже изучить вопрос.

Что такое площадь в математике?

Площадь — это мера того, сколько пространства есть на плоской поверхности. Например, есть два одинаковых куска бумаги, чья суммарная площадь, очевидно, больше чем у каждого из них по отдельности.

Площади фигур в математики вычисляются разными путями, зависимо от их формы. Например, в случае с прямоугольником необходимо найти произведение его высоты и ширины. Посмотрим на рисунок.

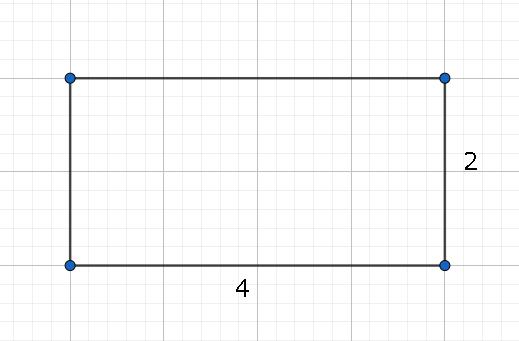
Имеем ответ: 2 × 4 = 8 см². Задача решена.

Проверить его можно вручную подсчитав количество больших квадратиков внутри прямоугольника. Подобной задачи достаточно для того чтобы объяснить, что такое площадь в математике. Но в этой теме есть еще и другие важные нюансы.

Единица измерения площади в математике

Измеряется площадь в квадратных единицах. То есть ее можно определить как некоторое количество четырехугольников, чьи стороны равны 1. При этом если поменять местами значения длины и высоты, конечный результат не изменится.

Примечание! Все величины должны быть в одинаковых единицах измерения.

Допустим, что данные заданы в сантиметрах. Как тогда правильно обозначить это на бумаге?

Вместо того чтобы писать «восемь квадратных сантиметров», можно использовать запись вида «8 см²«. Достаточно просто возвести сокращенную форму меры во вторую степень.

Перевод величин

У студента или ученика может возникнуть потребность перевести значение из одних единиц измерения в другие. Существует только один верный способ это сделать. Правда, для этого необходимо вспомнить, как правильно переводить одни единицы измерения в другие.

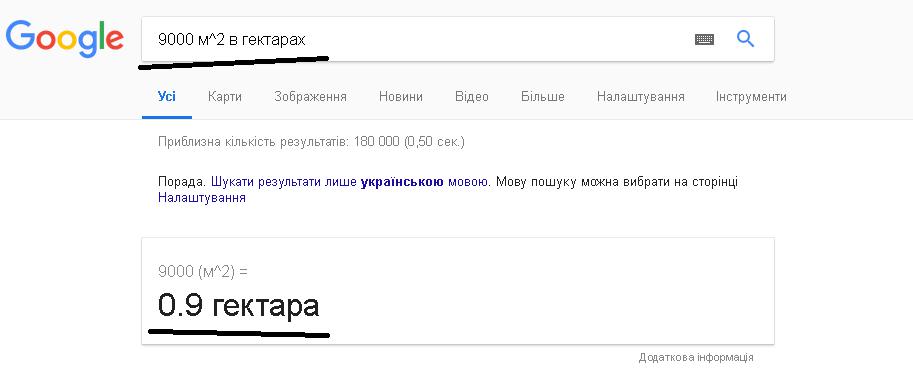
Допустим имеем 9000 м². Нужно найти, сколько это гектаров. Известно что 1 га = 10 000 м². Разделим исходную площадь на десять тысяч. В результате получим 0,9 га. Это и будет искомым значением. Главное иметь информацию об отношении двух величин между собой.

А теперь проверим.

Другие фигуры

К сожалению, для нахождения площади не всегда достаточно перемножить два числа. Ситуации бывают разные. Рабочая формула для каждой из них будет видоизменяться из раза в раз. Ниже приведены наиболее часто встречаемые вариации фигур.

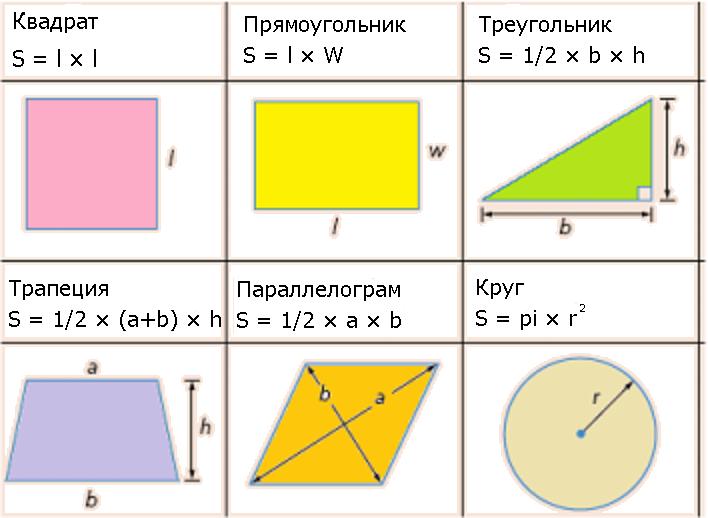
Пример

Теперь вы знаете, что такое площадь в математике. Основной теоретический материал усвоен, и можно переходить к практике. Для закрепления решим конкретную задачу.

Условие. Имеется квадрат со стороной 3 сантиметра и круг с радиусом такой же длины. Найдите, чья площадь больше и на сколько.

Решение. Для начала произведем вычисления для каждой из фигур по отдельности:

S_квад = 3 × 3 = 9. Итак, площадь квадрата равна 9 см².

А вот площадь круга вычисляется уже по другой формуле. Для ее нахождения необходимо вспомнить значение ∏:

S_круг = ∏ × 3 × 3 ≈ 28,26 см².

По результатам видим, что площадь круга в несколько раз больше. Осталось лишь посчитать на сколько. Для этого найдем разницу двух чисел.

S_круг — S_квад = 28,26 — 9 = 19,26 см².

Ответ найден.

Обычно, решая такие задачи, человек должен сводить все к готовым формулам. Затем уже искать неизвестные, выражать величины одну через другую и использовать смекалку.