Чем отличается шар от сферы

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью). Действительно, все ли из нас хорошо знают из школьной программы геометрию и могут сходу ответить на данный вопрос? Сфера имеет некоторые отличия от шара, которые нужно знать не только школьникам, чтобы получить хорошую оценку за свои продемонстрированные знания, но и многим другим людям, например, чья работа непосредственно связана с чертежами.

Определение

Шар – совокупность всех точек пространства. Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. Шар, как геометрическое тело, образуется следующим образом: происходит вращение полукруга возле его диаметра. Что касается сферы, то это и есть поверхность шара (например, замкнутый шар включает ее, открытый – нет). Вычисление площади или объема шара – это целые геометрические формулы, которые очень сложны, несмотря на кажущуюся простоту самой геометрической фигуры.

Сфера, как было отмечено выше, представляет собой поверхность шара, его оболочку. От центра сферы все точки в пространстве равноудалены. Что касается радиуса геометрического тела, то им называют любой отрезок, одна точка которого – непосредственно центр сферы, а другая может находиться в любой точке на поверхности. Можно сказать, что сфера является оболочкой шара без какого-либо содержимого (более конкретные примеры будут приведены ниже). Также как и шар, сфера является телом вращения. Кстати, многие также задаются вопросом, чем же отличаются круг и окружность от сферы и шара. Здесь все просто: в первом случае это фигуры на плоскости, во втором – в пространстве.

к содержанию ↑

Сравнение

Уже было сказано о том, что сфера является поверхностью шара, что уже дает возможность говорить об одном весомом признаке отличия. Разница между двумя геометрическими телами наблюдается и в некоторых других аспектах:

• Все точки шара находятся на одинаковом расстоянии от центра, при этом тело ограничено поверхностью (сферой, которая является пустой внутри). Иными словами, сфера полая. Обычно для простоты понимания приводят простой пример с воздушным и бильярдным шаром. Оба этих предмета называют шарами, однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.
• Сфера имеет свою площадь, но при этом у нее нет объема. Шар же наоборот: его объем можно вычислить, в то время как у него нет площади. Кто-то может сказать, что это главный признак отличия, но он проявляется только в том случае, если необходимо производить какие-то расчеты (сложные геометрические формулы). Поэтому главным отличием является то, что сфера полая, а шар – тело с содержимым внутри.
• Еще одно отличие кроется в радиусе. Например, радиусом сферы называется не только расстояние точек до центра. Радиусом может называться любой отрезок, соединяющий точку на сфере с ее центром. Все эти отрезки равны между собой. Что касается шара, то лежащие внутри него точки удалены от центра меньше, чем на радиус (как раз из-за ограничивающей его сферы).

к содержанию ↑

Выводы TheDifference.ru

1. Сфера полая, в то время как шар является заполненным внутри телом. Например, воздушный шар – это сфера, бильярдный шар – это полноценный шар.
2. Сфера имеет площадь и не имеет объем, шар же наоборот.
3. Третье отличие – это измерение радиуса двух геометрических тел.

thedifference.ru

Чем шар отличается от сферы?

Для получения грамотного ответа на вынесенный в заголовок вопрос читателю статьи потребуется хорошенько напрячь свои способности к абстрактному мышлению и как следует углубиться в определённые разделы математики, что ему доводилось изучать в школе. А для стимуляции воображения нелишним будет напомнить, что «Образование есть то, что остаётся после того, когда забывается всё, чему нас учили» (авторство фразы приписывается А.Эйнштейну).

Небольшое погружение в один из разделов математики

Для начала потребуется вспомнить о существовании науки геоме́трии (в несколько вольном переводе с греческого это слово означает «землемеренье») — обособленном разделе математики, специализирующемся на изучении пространственных структур, их отношений между собой и различных возникающих из этого обобщений. Важно, что несмотря на подобное «приземлённое» происхождения названия эта наука оперирует сугубо абстрактными понятиями, которые в привычном нам мире не существуют в прямом физическом воплощении.

Одно из таких базовых понятий — это

геометрическая точка. Напрягите своё воображение: в отличие от «точки карандашом», «точки от булавки» и так далее эта точка представляет из себя полностью абстрактный объект в воображаемом пространстве без каких-либо измеримых характеристик типа «толщины», «цвета» и так далее (математики любят при этом произносить словосочетание «нульмерный объект»). В принципе, всё остальное в геометрии будет далее определяться исходя именно из этой абстракции.

Следующее нужно для дальнейших рассуждений понятие — это «ритуальная» математическая фраза «геометри́ческое ме́сто то́чек» (ГМТ). C её помощью описывается некоторое множество (совокупность) точек, подпадающих под определённое отношение (свойство) — таким образом задаётся «геометрическая фигура». Пример: сфе́ра (от древнегреческого σφαῖρα, изначально обозначающего мяч/шар) — это геометрическое место таких точек пространства, которое можно описать как равноудалённое (находящееся на строго одном расстоянии) от некоторой заданной точки, обычно называемой «центром сферы».

Сфера

Расстояние же от центра сферы до этого ГМТ принято называть «радиусом сферы». Во время всех этих манипуляций важно продолжать помнить, что сфера — понятие более эфемерное, чем даже всем привычный и знакомый мыльный пузырь: у любого мыльного пузыря всё-таки есть вполне ощутимая стенка из водно-мыльной плёнки микроскопической толщины, которую можно физически измерить (и даже проткнуть), а у сферы — нет!

Сфера и радиус сферы

Теперь обратимся к определению шара: под шаром понимается совокупность всех таких точек пространства, что находится от определённой точки (центра шара) на расстоянии, не большем заданного (радиуса шара). Иначе говоря, шар является «геометрическим телом» — тем, что согласно первичному определению Евклида «имеет длину, ширину и глубину» (в современных учебниках это определение менее наглядно: «часть пространства, ограниченная своей образуемой формой»).

Шар

Попутно отметим, что использованные здесь способы задания сферы и шара через центр и радиус — не единственные: например, задание сферы/шара в пространстве можно выполнить посредством вращения окружности, круга и т.д. (глубоко заинтересовавшимся этим вопросом настоятельно рекомендуется ознакомиться с отдельным разделом геометрии под названием «Фигуры и тела вращения», поскольку это часто применяемый способ задания самых различных геометрических фигур и тел в пространстве).

Таким образом, и в случае сферы, и в случае шара приходится иметь дело с определённым образом заданным геометрическим местом точек (то есть геометрической фигурой), однако лишь в случае шара можно говорить о геометрическом теле. Любопытно отметить, что строго говоря сферу из шара можно «вычесть»: в этом случае математики говорят об «открытом шаре». Однако «по умолчанию» имеет место «замкнутый шар», где сфера является его естественной границей и принадлежащей ему частью.

Резюме

И шар, и сфера являются абстрактными геометрическими объектами (геометрическими фигурами), задаваемыми через некоторое геометрическое место точек пространства — например, с помощью понятия центра шара/сферы и радиуса шара/сферы. Однако только шар является полноценным геометрическим телом, поскольку включает в себя не только описание ограничивающей его поверхности, но и всей той части пространства, что в себя эта поверхность заключает. С такой точки зрения сфера — лишь внешняя абстрактная граница (поверхность) задаваемого в пространстве шара.

Ещё важно помнить, что лишь используемое по умолчанию определение «замкнутый шар» включает в себя эту границу, в случае же её исключения получается совершенно новое геометрическое тело — «открытый шар».

vchemraznica.ru

ОТЛИЧИЕ СФЕРЫ ОТ ШАРА — Сфера и шар отличия

Если взять полукруг или круг и провернуть его вокруг своей оси, получится тело, называемое шаром. Иными словами, шаром называется тело, ограниченное сферой. Сфера представляет собой оболочку шара, и ее сечением является окружность. Шар и сфера — взаимозаменяемые тела, в отличие от конуса, несмотря на то, что конус также является телом вращения. Через две точки A и B, располагающиеся в любом месте поверхности шара, может проходить бесконечное количество кругов или окружностей. Данная формула может быть полезна в том случае, если известен либо диаметр, либо радиус шара или сферы. Однако, эти параметры приведены в качестве условий не во всех геометрических задачах.

Совет 1: Как найти площадь сферы

Если известна длина диаметра сферы (d), то для нахождения площади ее поверхности (S) возводите этот параметр в квадрат и умножайте на число Пи (π): S=π∗d². Например, при длине радиуса сферы в три метра его площадь составит 4∗3,14∗3²=113,04 квадратных метров. Для вычисления площади сферы по данным, например, из второго шага поисковый запрос, который надо ввести в Google, будет выглядеть так: «4*пи*3^2». А для наиболее сложного случая с вычислением кубического корня и возведением в квадрат из третьего шага запрос будет таким: «пи*(6*500/пи)^(2/3)».

Разница между шаром и сферой

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью).

В повседневной жизни мы редко говорим сфера, чаще шар или шарик. И не все понимают какая разница между этими двумя геометрическими понятиями. Наверное можно сказать, что сфера это внешняя оболочка шара. Воздушный шарик, например, на самом деле не шар, а сфера. При условии, конечно, его абсолютной «круглости». Как я понимаю, то у шара абсолютно все точки поверхности равноудалены от его центра, а у сферф это условие не является обязательным.

Апельсин, футбольный мяч, арбуз, похожи на шар. Из всех тел заданного объёма шар имеет наименьшую поверхность. Поверхность шара называют сферой. Расстояние от точек сферы до её центра называется радиусом сферы и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку сферы с её центром.

Определение.Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Любой диаметр соответствует 2-м радиусам. Часть шара (сферы), которая отсекается от него любой плоскостью (ABC), является шаровым (сферическим) сегментом. Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота. 1/3 произведения площади поверхности шара на длину радиуса. Зачастую озвучивают так: объём шара равен 1/3 произведения поверхности шара на его радиус.

Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. От центра сферы все точки в пространстве равноудалены.

Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.

В тренде:

• Как подготовить капусту к замораживаниюЧитала, что хорошо капусту обвернуть газетами и подвесить в гараже или в погребе.У нас в Крыму капусту можно и не убирать с грядки. Когда надо, тогда и срываем.А морковку я тру на терке […]
• Льняная мука для красотыПримерно полгода назад я наткнулась на статью в интернете о том, что льняная мука чистит организм от шлаков, и при этом еще можно похудеть. Наткнулась на информацию о том, что она очищает […]
• Самый обаятельный пират всех времен и народовПри побеге Джек Воробей стащил с корабля ножны шпаги Кортеса – оружия, которое, по словам буфетчицы Арабеллы Смит, могло управлять погодой. Джек и Дэйви заключили сделку, согласно которой […]

estortenok.ru

Чем шар отличается от сферы.

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью). Действительно, все ли из нас хорошо знают из школьной программы геометрию и могут сходу ответить на данный вопрос? Сфера имеет некоторые отличия от шара, которые нужно знать не только школьникам, чтобы получить хорошую оценку за свои продемонстрированные знания, но и многим другим людям, например, чья работа непосредственно связана с чертежами.

Определение

Шар – совокупность всех точек пространства. Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. Шар, как геометрическое тело, образуется следующим образом: происходит вращение полукруга возле его диаметра. Что касается сферы, то это и есть поверхность шара (например, замкнутый шар включает ее, открытый – нет). Вычисление площади или объема шара – это целые геометрические формулы, которые очень сложны, несмотря на кажущуюся простоту самой геометрической фигуры.

Сфера , как было отмечено выше, представляет собой поверхность шара, его оболочку. От центра сферы все точки в пространстве равноудалены. Что касается радиуса геометрического тела, то им называют любой отрезок, одна точка которого – непосредственно центр сферы, а другая может находиться в любой точке на поверхности. Можно сказать, что сфера является оболочкой шара без какого-либо содержимого (более конкретные примеры будут приведены ниже). Также как и шар, сфера является телом вращения. Кстати, многие также задаются вопросом, чем же отличаются круг и окружность от сферы и шара. Здесь все просто: в первом случае это фигуры на плоскости, во втором – в пространстве.

Сравнение

Уже было сказано о том, что сфера является поверхностью шара, что уже дает возможность говорить об одном весомом признаке отличия. Разница между двумя геометрическими телами наблюдается и в некоторых других аспектах:

• Все точки шара находятся на одинаковом расстоянии от центра, при этом тело ограничено поверхностью (сферой, которая является пустой внутри). Иными словами, сфера полая. Обычно для простоты понимания приводят простой пример с воздушным и бильярдным шаром. Оба этих предмета называют шарами, однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.
• Сфера имеет свою площадь, но при этом у нее нет объема. Шар же наоборот: его объем можно вычислить, в то время как у него нет площади. Кто-то может сказать, что это главный признак отличия, но он проявляется только в том случае, если необходимо производить какие-то расчеты (сложные геометрические формулы). Поэтому главным отличием является то, что сфера полая, а шар – тело с содержимым внутри.
• Еще одно отличие кроется в радиусе. Например, радиусом сферы называется не только расстояние точек до центра. Радиусом может называться любой отрезок, соединяющий точку на сфере с ее центром. Все эти отрезки равны между собой. Что касается шара, то лежащие внутри него точки удалены от центра меньше, чем на радиус (как раз из-за ограничивающей его сферы).

Выводы сайт

1. Сфера полая, в то время как шар является заполненным внутри телом. Например, воздушный шар – это сфера, бильярдный шар – это полноценный шар.
2. Сфера имеет площадь и не имеет объем, шар же наоборот.
3. Третье отличие – это измерение радиуса двух геометрических тел.

Для получения грамотного ответа на вынесенный в заголовок вопрос читателю статьи потребуется хорошенько напрячь свои способности к абстрактному мышлению и как следует углубиться в определённые разделы математики, что ему доводилось изучать в школе. А для стимуляции воображения нелишним будет напомнить, что «Образование есть то, что остаётся после того, когда забывается всё, чему нас учили» (авторство фразы приписывается А.Эйнштейну).

Небольшое погружение в один из разделов математики

Для начала потребуется вспомнить о существовании науки геоме́трии (в несколько вольном переводе с греческого это слово означает «землемеренье») — обособленном разделе математики, специализирующемся на изучении пространственных структур, их отношений между собой и различных возникающих из этого обобщений. Важно, что несмотря на подобное «приземлённое» происхождения названия эта наука оперирует сугубо абстрактными понятиями, которые в привычном нам мире не существуют в прямом физическом воплощении.

Одно из таких базовых понятий — это геометрическая точка . Напрягите своё воображение: в отличие от «точки карандашом», «точки от булавки» и так далее эта точка представляет из себя полностью абстрактный объект в воображаемом пространстве без каких-либо измеримых характеристик типа «толщины», «цвета» и так далее (математики любят при этом произносить словосочетание «нульмерный объект»). В принципе, всё остальное в геометрии будет далее определяться исходя именно из этой абстракции.

Следующее нужно для дальнейших рассуждений понятие — это «ритуальная» математическая фраза «геометри́ческое ме́сто то́чек» (ГМТ). C её помощью описывается некоторое множество (совокупность) точек, подпадающих под определённое отношение (свойство) — таким образом задаётся «геометрическая фигура». Пример: сфе́ра (от древнегреческого σφαῖρα, изначально обозначающего мяч/шар) — это геометрическое место таких точек пространства, которое можно описать как равноудалённое (находящееся на строго одном расстоянии) от некоторой заданной точки, обычно называемой «центром сферы».

Расстояние же от центра сферы до этого ГМТ принято называть «радиусом сферы». Во время всех этих манипуляций важно продолжать помнить, что сфера — понятие более эфемерное, чем даже всем привычный и знакомый мыльный пузырь: у любого мыльного пузыря всё-таки есть вполне ощутимая стенка из водно-мыльной плёнки микроскопической толщины, которую можно физически измерить (и даже проткнуть), а у сферы — нет!

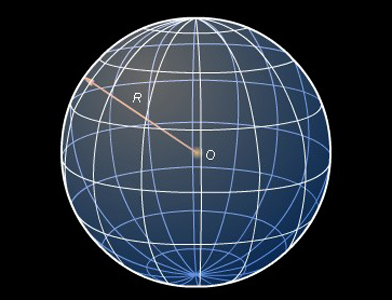
Теперь обратимся к определению шара: под шаром понимается совокупность всех таких точек пространства, что находится от определённой точки (центра шара) на расстоянии, не большем заданного (радиуса шара). Иначе говоря, шар является «геометрическим телом» — тем, что согласно первичному определению Евклида «имеет длину, ширину и глубину» (в современных учебниках это определение менее наглядно: «часть пространства, ограниченная своей образуемой формой»).

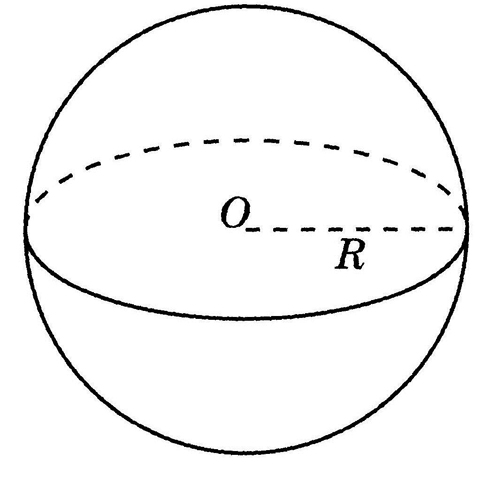
Попутно отметим, что использованные здесь способы задания сферы и шара через центр и радиус — не единственные: например, задание сферы/шара в пространстве можно выполнить посредством вращения окружности, круга и т.д. (глубоко заинтересовавшимся этим вопросом настоятельно рекомендуется ознакомиться с отдельным разделом геометрии под названием «Фигуры и тела вращения», поскольку это часто применяемый способ задания самых различных геометрических фигур и тел в пространстве).

Таким образом, и в случае сферы, и в случае шара приходится иметь дело с определённым образом заданным геометрическим местом точек (то есть геометрической фигурой), однако лишь в случае шара можно говорить о геометрическом теле. Любопытно отметить, что строго говоря сферу из шара можно «вычесть»: в этом случае математики говорят об «открытом шаре». Однако «по умолчанию» имеет место «замкнутый шар», где сфера является его естественной границей и принадлежащей ему частью.

Резюме

И шар, и сфера являются абстрактными геометрическими объектами (геометрическими фигурами), задаваемыми через некоторое геометрическое место точек пространства — например, с помощью понятия центра шара/сферы и радиуса шара/сферы. Однако только шар является полноценным геометрическим телом, поскольку включает в себя не только описание ограничивающей его поверхности, но и всей той части пространства, что в себя эта поверхность заключает. С такой точки зрения сфера — лишь внешняя абстрактная граница (поверхность) задаваемого в пространстве шара.

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впосл

slovarslov.ru

Разница между шаром и сферой. Чем шар отличается от сферы

В главе 2 мы продолжим “строительную геометрию» и расскажем о строении и свойствах важнейших пространственных фигур — шара и сферы, цилиндров и конусов, призм и пирамид. Большинство предметов, созданных руками человека, — здания, машины, мебель, посуда и т.д., и т.п., состоит из частей, имеющих форму этих фигур.

§ 4. СФЕРА И ШАР

После прямых и плоскостей сфера и шар — самые простые, но очень важные и богатые разнообразными свойствами пространственные фигуры. О геометрических свойствах шара и его поверхности — сферы — написаны целые книги. Некоторые из этих свойств были известны еще древнегреческим геометрам, а некоторые найдены совсем недавно, в последние годы. Эти свойства (вместе с законами естествознания) объясняют, почему, например, форму шара имеют небесные тела и икринки рыб, почему в форме шара делают батискафы и футбольные мячи, почему так распространены в технике шарикоподшипники и т.д. Мы можем доказать лишь самые простые свойства шара. Доказательства других, хотя и очень важных свойств, часто требуют применения совсем не элементарных методов, хотя формулировки таких свойств могут быть очень простыми: например, среди всех тел, имеющих данную площадь поверхности, наибольший объем у шара.

4.1. Определения сферы и шара.

Определяются сфера и шар в пространстве совершенно так же, как окружность и круг на плоскости. Сферой называется фигура, состоящая из всех точек пространства, удаленных от данной

ной точки на одно и то же (положительное) расстояние.

Эта точка называется центром сферы, а расстояние — ее радиусом (рис. 4.1).

Итак, сфера с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Шаром называется фигура, образованная всеми точками пространства, находящимися на расстоянии не большем данного (положительного) расстояния от данной точки. Эта точка называется центром шара, а данное расстояние — его радиусом.

Итак, шар с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Те точки X шара с центром О и радиусом R, для которых образуют сферу. Говорят, что эта сфера ограничивает данный шар или что она является его поверхностью.

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr 3 ,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью, называется большим кругом, а сечение сферы – большим кругом, а сечение сферы – большой окружностью.

Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, которая и проходит через точку А шаровой поверхности и перпендикулярна радиусу, проведённому в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Теорема. Касательная плоскость имеет с шаром только одну общую точку – точку касания.

Прямая, которая проходит через точку А шаровой поверхности перпендикулярно к радиусу, проведённому в эту точку, называется касательной.

Теорема. Через любую точку шаровой поверхности проходит бесконечно много касательных, причём все они лежат в касательной плоскости шара.

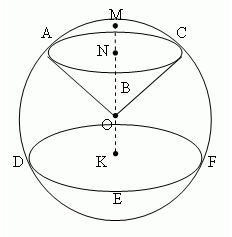Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг ABC – основание шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, – высота шарового сегмента. Точка M – вершина шарового сегмента.

Площадь поверхности шарового сегмента можно вычислить по формуле:

Объём шарового сегмента можно найти по формуле:

V = πh 2 (R – 1/3h),

где R – радиус большого круга, h – высота шарового сегмента.

Шаровой сектор получается из шарового сегмента и конуса, следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется.

Шаровой сектор – это часть шара, ограниченная кривой поверхностью сферического сегмента (на нашем рисунке – это AMCB) и конической поверхностью (на рисунке – это OABC), основанием которой служит основание сегмента (ABC), а вершиной – центр шара O.

Объем шарового сектора находится по формуле:

V = 2/3 πR 2 H.

Шаровый слой – это часть шара, заключённая между двумя параллельными плоскостями (на рисунке плоскостями ABC и DEF), пересекающими сферическую поверхность. Кривая поверхность шарового слоя называется шаровым поясом (зоной). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота.

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Определение.

Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокру

lugasat.ru

Чем сфера отличается от шара ребус. Чем отличается сфера от шара

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью). Действительно, все ли из нас хорошо знают из школьной программы геометрию и могут сходу ответить на данный вопрос? Сфера имеет некоторые отличия от шара, которые нужно знать не только школьникам, чтобы получить хорошую оценку за свои продемонстрированные знания, но и многим другим людям, например, чья работа непосредственно связана с чертежами.

Частицы, расположенные на расстоянии от центра сферы, имеют силу, направленную к центру шара, потому что из центра частица поглощает меньше гравитонов, чем с противоположной стороны. Меньше гравитонов попадает к частице из центра сферы, потому что в этом направлении количество шаровой материи больше, чем с противоположной стороны. Более толстый слой вещества поглощает больше гравитонов, которые движутся к частице, чем те, которые движутся с противоположной стороны. Результирующий импульс, передаваемый частице взаимодействующими с ней гравитонами, представляет собой вектор, направленный в центр сферы.

Определение

Шар – совокупность всех точек пространства. Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. Шар, как геометрическое тело, образуется следующим образом: происходит вращение полукруга возле его диаметра. Что касается сферы, то это и есть поверхность шара (например, замкнутый шар включает ее, открытый – нет). Вычисление площади или объема шара – это целые геометрические формулы, которые очень сложны, несмотря на кажущуюся простоту самой геометрической фигуры.

При достаточно большой массе шара силы гравитационного взаимодействия сохраняют его целиком, даже если он образован газовыми частицами. Силы гравитационного взаимодействия частиц материи с частицами пространства и остающейся материей полностью удерживают звезды, несмотря на большое внутреннее давление, вызванное высокой температурой внутренней части звезды. Внутреннее давление уравновешивается давлением, создаваемым гравитационными силами.

Возьмите тело на поверхности материальной сферы, которая имеет очень большую неподвижную массу. Если радиус сферы очень большой, его частицы расположены на очень большом расстоянии от тела и поглощают только несколько гравитонов, движущихся к телу из сферы. На тело действует относительно небольшая сила.

Сфера , как было отмечено выше, представляет собой поверхность шара, его оболочку. От центра сферы все точки в пространстве равноудалены. Что касается радиуса геометрического тела, то им называют любой отрезок, одна точка которого – непосредственно центр сферы, а другая может находиться в любой точке на поверхности. Можно сказать, что сфера является оболочкой шара без какого-либо содержимого (более конкретные примеры будут приведены ниже). Также как и шар, сфера является телом вращения. Кстати, многие также задаются вопросом, чем же отличаются круг и окружность от сферы и шара. Здесь все просто: в первом случае это фигуры на плоскости, во втором – в пространстве.

Если радиус сферы очень мал, его частицы в среднем очень близки к телу и поглощают больше гравитонов, движущихся к телу от центра сферы. В этом случае сила тяжести, действующая на тело, очень велика. Такие очень большие силы действуют на тело, расположенное на поверхности нейтронной звезды, вещество которого имеет очень высокую плотность.

Однако эти силы никогда не бесконечны. Если бы тело поглощало гравитоны только с одной стороны, то они были бы очень мощными, но конечными и ограниченными. Гравитоны, движущиеся к телу, с другой стороны, поглощаются шаром. Сила тяжести, действующая на единицу массы тела, не может уйти в бесконечность. Безграничная непроходимая величина этой силы, независимо от условий, в которых находится тело.

Сравнение

Уже было сказано о том, что сфера является поверхностью шара, что уже дает возможность говорить об одном весомом признаке отличия. Разница между двумя геометрическими телами

bogemasamara.ru

Чем отличается сфера от шара. Разница между шаром и сферой

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью). Действительно, все ли из нас хорошо знают из школьной программы геометрию и могут сходу ответить на данный вопрос? Сфера имеет некоторые отличия от шара, которые нужно знать не только школьникам, чтобы получить хорошую оценку за свои продемонстрированные знания, но и многим другим людям, например, чья работа непосредственно связана с чертежами.

Определение

Шар – совокупность всех точек пространства. Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. Шар, как геометрическое тело, образуется следующим образом: происходит вращение полукруга возле его диаметра. Что касается сферы, то это и есть поверхность шара (например, замкнутый шар включает ее, открытый – нет). Вычисление площади или объема шара – это целые геометрические формулы, которые очень сложны, несмотря на кажущуюся простоту самой геометрической фигуры.

Сфера , как было отмечено выше, представляет собой поверхность шара, его оболочку. От центра сферы все точки в пространстве равноудалены. Что касается радиуса геометрического тела, то им называют любой отрезок, одна точка которого – непосредственно центр сферы, а другая может находиться в любой точке на поверхности. Можно сказать, что сфера является оболочкой шара без какого-либо содержимого (более конкретные примеры будут приведены ниже). Также как и шар, сфера является телом вращения. Кстати, многие также задаются вопросом, чем же отличаются круг и окружность от сферы и шара. Здесь все просто: в первом случае это фигуры на плоскости, во втором – в пространстве.

Сравнение

Уже было сказано о том, что сфера является поверхностью шара, что уже дает возможность говорить об одном весомом признаке отличия. Разница между двумя геометрическими телами наблюдается и в некоторых других аспектах:

• Все точки шара находятся на одинаковом расстоянии от центра, при этом тело ограничено поверхностью (сферой, которая является пустой внутри). Иными словами, сфера полая. Обычно для простоты понимания приводят простой пример с воздушным и бильярдным шаром. Оба этих предмета называют шарами, однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.
• Сфера имеет свою площадь, но при этом у нее нет объема. Шар же наоборот: его объем можно вычислить, в то время как у него нет площади. Кто-то может сказать, что это главный признак отличия, но он проявляется только в том случае, если необходимо производить какие-то расчеты (сложные геометрические формулы). Поэтому главным отличием является то, что сфера полая, а шар – тело с содержимым внутри.
• Еще одно отличие кроется в радиусе. Например, радиусом сферы называется не только расстояние точек до центра. Радиусом может называться любой отрезок, соединяющий точку на сфере с ее центром. Все эти отрезки равны между собой. Что касается шара, то лежащие внутри него точки удалены от центра меньше, чем на радиус (как раз из-за ограничивающей его сферы).

Выводы сайт

1. Сфера полая, в то время как шар является заполненным внутри телом. Например, воздушный шар – это сфера, бильярдный шар – это полноценный шар.
2. Сфера имеет площадь и не имеет объем, шар же наоборот.
3. Третье отличие – это измерение радиуса двух геометрических тел.

другие презентации о сфере

«Задачи на шар и сферу» — Установите соответствие. Устный тест: «Тела вращения». Площадь сферы. Цилиндр, осевым сечением которого является квадрат, вписан в один шар. Шар вписан в цилиндр. Решение задач по готовым чертежам. Цели и задачи. Шар и сфера. Угол при вершине осевого сечения конуса равен 60 градусов. Конус. Работа у доски.

«Определение сферы и шара» — Планеты имеют форму шара. Точка. Каменное полушарие. Шаровой сектор. Обратная теорема. Определение сферы. Слово «сфера». Сфера. Найдите координаты центра и радиуса сферы. Закрепляем. Сечение шара плоско

bogemasamara.ru