Параллельные прямые — Википедия
Материал из Википедии — свободной энциклопедии
Параллельные прямые (от греч. παράλληλος, буквально — идущий рядом) — в планиметрии прямые, которые не пересекаются, сколько бы их не продолжали в обе стороны.
В евклидовой геометрии
На чертежах параллельные линии выделяются одинаково направленными стрелками.В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются[1]. В другом варианте определения совпадающие прямые также считаются параллельными[2][3]. Преимущество последнего определения состоит в том, что параллельность становится отношением эквивалентности[4].
Параллельность прямых m{\displaystyle m} и n{\displaystyle n} обычно обозначается:
- m∥n{\displaystyle m\parallel n}
Свойства
- Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского (см. ниже).
- Если прямая пересекает одну из параллельных прямых, то она пересекает и другую (такая прямая называется секущей). При этом образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Соответственные углы равны (Рис.1).
- Накрест лежащие углы равны (Рис.2).
- Внутренние односторонние углы в сумме составляют 180° (Рис.3).
- Если считать совпадающие прямые параллельными, то параллельность будет бинарным отношением эквивалентности, которое разбивает всё множество прямых на классы параллельных между собой прямых.
- Множество точек плоскости, расположенных на некотором фиксированном расстоянии от данной прямой, по одну сторону от неё, есть прямая, параллельная данной.
Построение параллельных прямых
В стереометрии
В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.
В геометрии Лобачевского
Параллельные прямые в модели Пуанкаре: две зелёные прямые равнобежны (асимптотически параллельны) синей прямой, а фиолетовая ультрапараллельна к нейВ геометрии Лобачевского в плоскости через точку C{\displaystyle C} вне данной прямой AB{\displaystyle AB} проходит бесконечное множество прямых, не пересекающих AB{\displaystyle AB}. Прямая CE{\displaystyle CE} называется равнобежной прямой AB{\displaystyle AB} в направлении от A{\displaystyle A} к B{\displaystyle B}, если:
- точки B{\displaystyle B} и E{\displaystyle E} лежат по одну сторону от прямой AC{\displaystyle AC};
- прямая CE{\displaystyle CE} не пересекает прямую AB{\displaystyle AB}, но всякий луч, проходящий внутри угла ACE{\displaystyle ACE}, пересекает луч AB{\displaystyle AB}.
Аналогично определяется прямая, равнобежная AB{\displaystyle AB} в направлении от B{\displaystyle B} к A{\displaystyle A}.
Равнобежные прямые называются также асимптотически параллельными или просто параллельными. Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися[5].
Свойства
Расходящиеся параллельные прямые имеют единственный общий перпендикуляр. Этот перпендикуляр соединяет ближайшую пару точек на этих прямых.
Несмотря на то, что асимптотически параллельные прямые не пересекаются, на любой паре асимптотически параллельных прямых можно выбрать произвольно близкие точки.
См. также
Примечания
Параллельность прямых и плоскостей [wiki.eduVdom.com]
subjects:stereometry:параллельность_прямых_и_плоскостей
Прямые
Параллельные прямые — прямые в пространстве, которые лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Прямая и плоскость
Три случая взаимного расположения прямой и плоскости в пространстве:
Прямая лежит в плоскости.
Прямая и плоскость имеют только одну общую точку (т.е. пересекаются).
Прямая и плоскость не имеют ни одной общей точки.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости:
Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости
Рис.1
Свойство прямой, параллельной плоскости:
Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей. См.Рис.2.
Рис.2
Плоскости
Параллельные плоскости – плоскости, не имеющие общих точек.
Признаки параллельности плоскостей:
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. См.Рис.3.
Рис.3
Рис.4
Свойства параллельных плоскостей:
Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны. См.Рис.5
Рис.5
Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны. См.Рис.6
Рис.6
Рекомендуем
subjects/stereometry/параллельность_прямых_и_плоскостей.txt · Последние изменения: 2015/12/26 14:25 — ¶
Асимптотически параллельные прямые — Википедия
Материал из Википедии — свободной энциклопедии
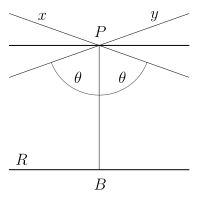
В нейтральной или абсолютной геометрии и в геометрии Лобачевского могут иметься много прямых, параллельных данной прямой R{\displaystyle R} и проходящих через точку P{\displaystyle P} вне этой прямой. Однако две параллельные могут быть ближе к R{\displaystyle R}, чем остальные (по одной с каждой стороны).
Имеет смысл в этом случаен дать другое определение параллельности для нейтральной геометрии. Если имеются очень близкие параллельные к данной прямой, их называют асимптотически параллельными или параллельными в пределе.
Для лучей отношение асимптотической параллельности является отношением эквивалентности, которое включает терминальное отношение эквивалентности.
Асимптотические параллельные могут образовывать две или три стороны асимптотического треугольника.
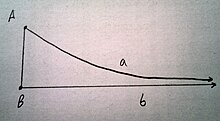 Луч Aa является асимптотически параллельным лучу Bb, что записывается как Aa|||Bb{\displaystyle Aa|||Bb}
Луч Aa является асимптотически параллельным лучу Bb, что записывается как Aa|||Bb{\displaystyle Aa|||Bb}Луч Aa{\displaystyle Aa} является асимптотически параллельным лучу Bb{\displaystyle Bb}, если они котерминальны или если они лежат на различных прямых, не равных прямой AB{\displaystyle AB}, не пересекаются и любой луч внутри угла BAa{\displaystyle BAa} пересекает луч Bb{\displaystyle Bb}[1].
Различные прямые, содержащие асимптотические параллельные лучи, не пересекаются.
Доказательство[править | править код]
Предположим, что прямые, содержащие различные параллельные лучи, пересекаются. По определению они не могут пересечься на стороне AB{\displaystyle AB}, в которой находится луч a{\displaystyle a}. Тогда они должны пересекаться на стороне AB{\displaystyle AB}, противоположной лучу a{\displaystyle a}, обозначим эту точку C{\displaystyle C}. Тогда (здесь P = прямой угол) ∠CAB+∠CBA<2P⇒∠aAB+∠bBA>2P{\displaystyle \angle CAB+\angle CBA<2P\Rightarrow \angle aAB+\angle bBA>2P}. Противоречие.
Параллельность прямых и плоскостей. Свойства и признаки
Категория: Справочные материалы
Елена Репина 2013-08-12 2016-10-22Параллельные прямые
Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.

Признак параллельности прямых
Две прямые, параллельные третьей, параллельны между собой.

Параллельные прямая и плоскость
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости
Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.

Свойство прямой, параллельной данной плоскости
Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a.

Параллельные плоскости
Параллельные плоскости – плоскости, которые не пересекаются.
Признаки параллельности плоскостей
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.
Свойства параллельных плоскостей
Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

Автор: egeMax | Нет комментариев
Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости
Тема: Перпендикулярность прямой и плоскости
Урок: Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости
На этом уроке мы рассмотрим перпендикулярность прямых в пространстве, перпендикулярность прямой и плоскости и параллельные прямые, которые перпендикулярны к плоскости.
Определение. Две прямые называются перпендикулярными, если угол между ними равен 90°.
Обозначение. 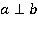 .
.
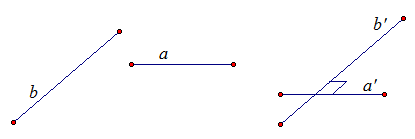
Рис. 1.
Рассмотрим прямые а и b. Прямые могут пересекаться, скрещиваться, быть параллельными. Для того, чтобы построить угол между ними нужно выбрать точку и через нее провести прямую 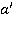 , параллельную прямой а, и прямую
, параллельную прямой а, и прямую 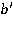 , параллельную прямойb. Прямые
, параллельную прямойb. Прямые 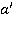 и
и 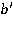 пересекаются. Угол между ними и есть угол между прямыми а и b. Если угол равен 90°, то прямые а и b перпендикулярны.
пересекаются. Угол между ними и есть угол между прямыми а и b. Если угол равен 90°, то прямые а и b перпендикулярны.
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Доказательство:
Пусть даны две параллельные прямые а и b, и прямая с,причем 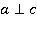 . Нужно доказать, что
. Нужно доказать, что 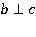 .
.
Возьмем произвольную точку М. Через точку М проведем прямую 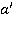 , параллельную прямой а и прямую
, параллельную прямой а и прямую  , параллельную прямой c (рис. 2). Тогда угол АМС равен 90°.
, параллельную прямой c (рис. 2). Тогда угол АМС равен 90°.
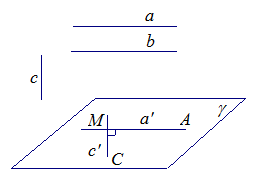
Рис. 2.
Прямая b параллельна прямой а по условию, прямая 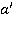 параллельна прямой а по построению. Значит, прямые
параллельна прямой а по построению. Значит, прямые 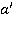 и b параллельны.
и b параллельны.
Имеем, прямые 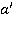 и b параллельны, прямые с и
и b параллельны, прямые с и  параллельны по построению. Значит, угол между прямыми b и с – это угол между прямыми
параллельны по построению. Значит, угол между прямыми b и с – это угол между прямыми 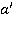 и
и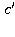 , то есть угол АМС, равный 90°. Значит, прямые b и с перпендикулярны, что и требовалось доказать.
, то есть угол АМС, равный 90°. Значит, прямые b и с перпендикулярны, что и требовалось доказать.
Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Обозначение.  .
.
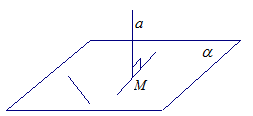
Рис. 3.
Если  , то
, то 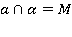 . (пересечение а и
. (пересечение а и 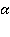 )
)
Доказательство:
Напоминание. Прямая и плоскость или пересекаются в одной точке, или параллельны, или прямая лежит в плоскости.
Если прямая а параллельна плоскости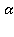 (рис. 4), то в плоскости
(рис. 4), то в плоскости 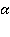 можно провести прямую
можно провести прямую 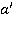 , параллельную прямой а. Получаем противоречие с определением перпендикулярности прямой и плоскости.
, параллельную прямой а. Получаем противоречие с определением перпендикулярности прямой и плоскости.
Если прямая а лежит в плоскости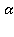 (рис. 5), то в плоскости
(рис. 5), то в плоскости 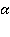 можно провести прямую
можно провести прямую 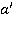 , параллельную прямой а. Опять получаем противоречие с определением перпендикулярности прямой и плоскости.
, параллельную прямой а. Опять получаем противоречие с определением перпендикулярности прямой и плоскости.
Значит, если прямая а перпендикулярна плоскости 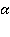 , то она пересекается с ней.
, то она пересекается с ней.
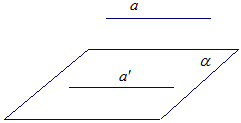
Рис. 4
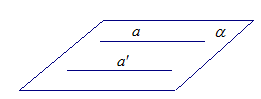
Рис. 5
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перепедикуляная к этой плоскости.
Доказательство.
Пусть прямая а параллельна прямой а1. Прямая а перепендикулярна плоскости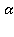 . Докажем, что и прямая а1 перпендикулярна плоскости
. Докажем, что и прямая а1 перпендикулярна плоскости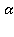 .
.
Прямая а перпендикулярна плоскости 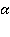 . Значит, она перпендикулярна любой прямой, лежащей в этой плоскости. Прямая х лежит в плоскости
. Значит, она перпендикулярна любой прямой, лежащей в этой плоскости. Прямая х лежит в плоскости 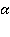 , значит,
, значит, 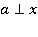 (см. рис. 6).
(см. рис. 6).
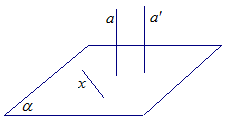
Рис 6.
Прямая а перпендикулярна прямой х, а прямая а1 параллельна прямой а. Значит, прямая а1 перпендикулярна прямой х по лемме. Прямую х мы выбирали произвольно. Значит, прямая а1 перпендикулярна любой прямой в плоскости 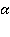 , то есть прямая х перпендикулярна плоскости
, то есть прямая х перпендикулярна плоскости 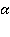 , что и требовалось доказать.
, что и требовалось доказать.
Если две прямые перпендикулярны к плоскости, то они параллельны.
Доказательство.
Пусть прямая а перепендикулярна плоскости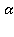 и прямая b перепендикулярна плоскости
и прямая b перепендикулярна плоскости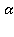 . Докажем, что прямая а параллельна прямой b.
. Докажем, что прямая а параллельна прямой b.
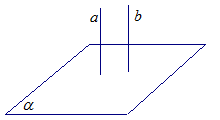
Рисунок 7.
Предположим, что прямая b не параллельна прямой а. Через точку М прямой b проведем прямую 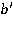 , параллельно прямой а (рис. 8).
, параллельно прямой а (рис. 8).
Прямые 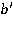 и а параллельны, прямая а перпендикулярна плоскости
и а параллельны, прямая а перпендикулярна плоскости 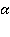 . По теореме, прямая
. По теореме, прямая 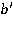 также перпендикулярна плоскости
также перпендикулярна плоскости 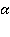 .
.
Прямые b и 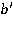 пересекаются, а значит через них проходит некоторая плоскость. Пусть эта плоскость пересекает плоскость
пересекаются, а значит через них проходит некоторая плоскость. Пусть эта плоскость пересекает плоскость 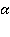 по прямой с. Тогда прямая
по прямой с. Тогда прямая 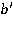 перпендикулярна прямой с, так как прямая с лежит в плоскости
перпендикулярна прямой с, так как прямая с лежит в плоскости 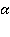 , а прямая
, а прямая 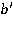 ей перпендикулярна.
ей перпендикулярна.
Но тогда в плоскости, определенной пересекающимися прямыми b и 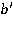 через точку М проходят два перпендикуляра b и
через точку М проходят два перпендикуляра b и 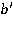 к прямой с. Получаем противоречие. Значит, прямая b параллельна прямой а, что и требовалось доказать.
к прямой с. Получаем противоречие. Значит, прямая b параллельна прямой а, что и требовалось доказать.
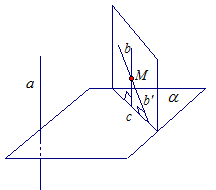
Рис. 8.
Дан параллелепипед ABCDA1B1C1D1 (рис. 9). Докажите, что 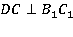 и
и 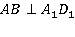 , если
, если 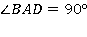 .
.
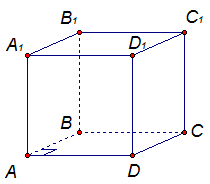
Рис. 9.
Доказательство.
ABCD – прямоугольник, так как в параллелограмме ABCD угол 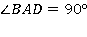 .
.
Прямая В1С1 параллельна прямой ВС, а прямая ВС перпендикулярна прямой DС. Значит, по лемме, прямая DС перпендикулярна В1С1.
Прямая АВ перпендикулярна прямой ВС, а ВС параллельна прямой A1D1. Значит, по лемме, прямая АВ перпендикулярна A1D1. Задача доказана.
Рассмотрим другое доказательство факта, что 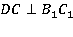 .
.
Угол DCB равен углу между прямыми DC и В1С1. Угол DCB – прямой. Значит, прямые DС и В1С1 перпендикулярны.
В тетраэдре ABCD — 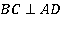 . Докажите, что
. Докажите, что 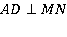 , где М и N середины ребер АВ и АС.
, где М и N середины ребер АВ и АС.
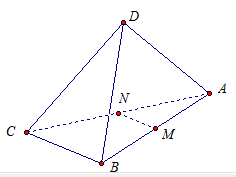
Рис. 10.
Доказательство.
MN – средняя линия треугольника АВС. По свойству средней линии, ВС параллельна MN.
Прямые ВС и MN параллельны, а прямые ВС и AD перпендикулярны. Значит, по лемме, прямые AD и MN перпендикулярны, что и требовалось доказать.
Итак, мы рассмотрели перпендикулярность прямых в пространстве, перпендикулярность прямой и плоскости, перпендикулярность к плоскости параллельных прямых. На следующем уроке мы рассмотрим признак перпендикулярности прямой и плоскости.
Список рекомендованной литературы
1. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил.
2. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
3. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М. : Дрофа, 008. – 233 с. :ил.
Рекомендованные ссылки на ресурсы интернет
1. Fizma.net (Источник)
2. Хvatit.com (Источник)
3. Якласс (Источник)
4. 900igr.net Источник
Рекомендованное домашнее задание
1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.: ил.
Задания 5, 6, 7 стр. 54
2. Дайте определение перпендикулярности прямых в пространстве.
3. Равные стороны АВ и CD четырехугольника ABCD перпендикулярны некоторой плоскости. Определите вид четырехугольника.
4. Сторона треугольника перпендикулярна некоторой прямой а. Докажите, что одна из средних линий треугольника перпендикулярна прямой а.
Параллельные прямые — это… Что такое Параллельные прямые?
Параллельные прямые
Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается.
Свойства
- Параллельность — бинарное отношение эквивалентности, поэтому разбивает всё множество прямых на классы параллельных между собой прямых.
- Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две)
- 2 параллельные прямые в пространстве лежат в одной плоскости.
- При пересечении 2 параллельных прямых третьей, называемой секущей:
- Секущая обязательно пересекает обе прямые.
- При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Накрест лежащие углы равны.
- Соответственные углы равны.
- Односторонние углы в сумме составляют 180°.
В геометрии Лобачевского в плоскости через точку Невозможно разобрать выражение (лексическая ошибка): C</math¹> вне данной прямой <math>AB
проходит бесконечное множество прямых, не пересекающих AB. Из них параллельными к AB называются только две.
Прямая CE называется равнобежной (параллельной) прямой AB в направлении от A к B, если:
- точки B и E лежат по одну сторону от прямой AC;
- прямая CE не пересекает прямую AB, но всякий луч, проходящий внутри угла ACE, пересекает луч AB.
Аналогично определяется прямая, равнобежная AB в направлении от B к A.
Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися.
См. также
Параллельные прямые — это… Что такое Параллельные прямые?
Параллельные прямые
Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается.
Свойства
- Параллельность — бинарное отношение эквивалентности, поэтому разбивает всё множество прямых на классы параллельных между собой прямых.
- Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две)
- 2 параллельные прямые в пространстве лежат в одной плоскости.
- При пересечении 2 параллельных прямых третьей, называемой секущей:
- Секущая обязательно пересекает обе прямые.
- При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Накрест лежащие углы равны.
- Соответственные углы равны.
- Односторонние углы в сумме составляют 180°.
В геометрии Лобачевского в плоскости через точку Невозможно разобрать выражение (лексическая ошибка): C</math¹> вне данной прямой <math>AB
проходит бесконечное множество прямых, не пересекающих AB. Из них параллельными к AB называются только две.
Прямая CE называется равнобежной (параллельной) прямой AB в направлении от A к B, если:
- точки B и E лежат по одну сторону от прямой AC;
- прямая CE не пересекает прямую AB, но всякий луч, проходящий внутри угла ACE, пересекает луч AB.
Аналогично определяется прямая, равнобежная AB в направлении от B к A.
Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися.