Признаки параллельности прямых . Видеоурок. Геометрия 7 Класс
Две прямые на плоскости называются параллельными, если они не пересекаются. Обозначается это так:  .
.
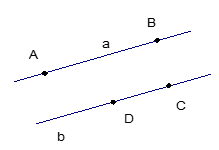
Рис. 1
Отрезки AB и CD, лежащие на параллельных прямых, называются параллельными.
Лучи, лежащие на параллельных прямых, также называются параллельными.
Задумаемся, неужели а и b нигде не пересекутся? И существуют ли такие прямые? Ведь а и b не ограничены. И в соседней комнате не пересекутся? И на луне?
Оказывается, такие прямые существуют.
Мы доказывали, что перпендикулярная прямая а к прямой с и перпендикулярная прямая b к прямой с нигде не пересекаются (Рис. 2).
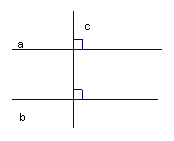
Рис. 2
То есть две перпендикулярные прямые к одной и той же третьей прямой нигде не пересекутся. Оказывается, для этих прямых есть термин.
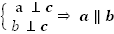 .
.
Рассмотрим важную геометрическую конструкцию, в которой две прямые а и b рассекаются прямой с (Рис. 3).
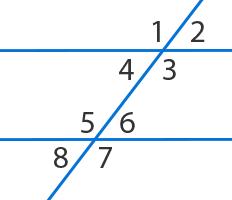
Рис. 3
с – секущая а и b. Это означает, что она пересекает и а, и b.
Возникает много углов (1, 2, 3, 4, 5, 6, 7, 8).
Эти углы называются:
— накрест лежащие углы:  ,
, 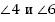 ;
;
— односторонние углы: 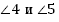 , ∠3 и ∠6;
, ∠3 и ∠6;
— соответственные углы: 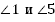 ,
,  ,
, 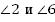 ,
, 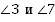
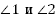 – смежные углы.
– смежные углы.
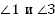 – вертикальные углы.
– вертикальные углы.
Сформулируем и докажем первый признак параллельности прямых.
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Итак, даны две прямые а и b. Прямая АВ рассекает эти прямые и 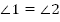 (Рис. 4).
(Рис. 4).
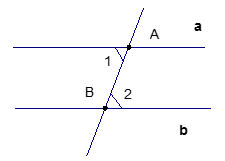
Рис. 4
Докажем, что 
Доказательство:
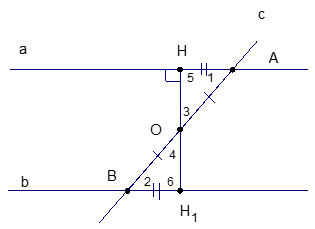
Рис. 5
Возьмем середину отрезка АВ – точку О – и опустим перпендикуляр ОН на прямую а. Получим точку Н. Получим отрезок АН. Отложим от точки В по прямой b отрезок, равный длине отрезка АН. Получим точку  , причем
, причем 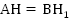 .
.
Имеем два треугольника 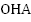 и
и 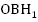
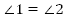 (по условию),
(по условию), 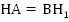 (по построению), ОА = ОВ (по построению).
(по построению), ОА = ОВ (по построению).
Из равенства треугольников следует, что 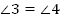 . А значит
. А значит – это продолжение ОН, то есть точки О, Н и
– это продолжение ОН, то есть точки О, Н и 
Также 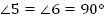 . Значит, прямая Н
. Значит, прямая Н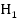 перпендикулярна к прямой b.
перпендикулярна к прямой b.
Итак, мы имеем, что 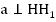 ,
, 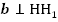 . А значит,
. А значит,  , что и требовалось доказать.
, что и требовалось доказать.
Второй признак параллельности прямых
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Имеем: а, b, с – прямые; с – секущая, .
.
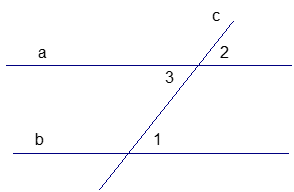
Рис. 6
Доказательство:
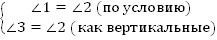
Значит, 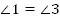 .
.
Применим первый признак параллельности прямых и получим, что  .
.
Третий признак параллельности прямых
Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Имеем: а, b, с – прямые; с – секущая,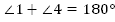 (Рис. 7).
(Рис. 7).
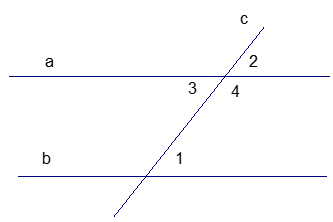
Рис. 7
Доказательство:
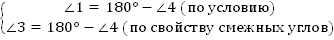
Значит, 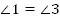 .
.
Применим первый признак параллельности прямых и получим, что 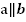
Признаки параллельности прямых используются для решения разных задач.
Рассмотрим пример:
а, b, с – прямые; с – секущая,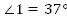 ,
, 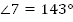 (Рис. 8)
(Рис. 8)
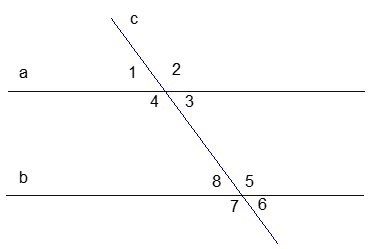
Рис. 8
Сведем к одному из признаков параллельности прямых.
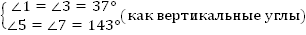
Следовательно,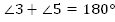 . По третьему признаку параллельности прямых
. По третьему признаку параллельности прямых
На этом уроке мы рассмотрели понятие параллельных и прямых и разобрали признаки параллельности прямых, научились их применять. На следующем занятии мы разберем свойства параллельных прямых.
Список рекомендованной литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5 изд. – М.: Просвещение.
- Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
Рекомендованные ссылки на интернет-ресурсы
- Параллельные прямые (Источник).
- Параллельные прямые (Источник).
- Признаки параллельности двух прямых (Источник).
Рекомендованное домашнее задание
- Нарисуйте произвольный треугольник АВС. Отметьте точку М на стороне АВ. Через точку М проведите прямые, параллельные двум другим сторонам.
- Прямая АВ пересекает прямую CD в точке А, а прямую MN в точке В.
 . Параллельны ли прямые CD и MN?
. Параллельны ли прямые CD и MN? - В треугольнике АВС ВК – биссектриса. Точка К принадлежит АС. Точка М – середина стороны ВС. Доказать, что
 .
.
Параллельные прямые | Формулы с примерами
Правило
Секущая с — прямая, пересекающая прямые а и b в различных точках.
При пересечении двух прямых и секущей образуется восемь углов.
Соответственные углы: ? 1 и ? 5; ? 2 и ? 6; ? 3 и ? 7; ? 4 и ? 8.
Внутренние односторонние: ? 4 и ? 5; ? 3 и ? 6.
Внешние односторонние: ? 1 и ? 8; ? 2 и ? 7.
Внутренние накрест лежащие: ? 3 и ? 5 и ? 4 и ? 6.
Внешние накрест лежащие: ? 1 и ? 7; ? 2 и ? 8.
Аксиома
Аксиома параллельных: через точку, не лежащую на данной прямой, можно провести на плоскости прямую, параллельную данной, и только одну.
Теорема 1
Теорема 1: две прямые, параллельные третьей, параллельны: a || c, b || c => a || b.
Теорема 2
Теорема 2: Две прямые, перпендикулярные третьей,
параллельны: a ? c, b ? c => a || b.
Признаки параллельности прямых
ПравилоI. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны: ? 1 = ? 2 => a || b.

II. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны: ? 1 = ? 2 => a || b.

III. Если при пересечении двух прямых секущей сумма односторонних углов равна 180?, то прямые параллельны: ? 1 + ? 2 = 180? => a || b.

Урок 4: Параллельные прямые — 100urokov.ru
План урока:
Определение параллельных прямых
Аксиома параллельности
Секущая
Теорема о прямых, перпендикулярных секущей
Признаки параллельности прямых
Расстояние между параллельными прямыми
Способы построения параллельных прямых
Определение параллельных прямых
Из аксиом геометрии известно, что две прямые могут иметь единственную общую точку. В этом случае их называют пересекающимися. Как пример приведем рисунок:

Здесь a и c пересекаются в А. Однако прямые на плоскостиможно расположитьтак, что они не будут пересекаться:

Как бы далеко мы не продолжали а и с, они никогда не пересекутся. В подобном случае говорят, что a и cпараллельны.
Дадим определение параллельных прямых:

Для подобного отношения существует специальный значок, который выглядит как две вертикальные черточки: a||c.
Параллельными бывают и другие геометрические фигуры: отрезки, лучи. Для этого они должны лежать на параллельных прямых:

Здесь АВ||CD. У многих геометрических фигур параллельны противоположные стороны. Достаточно вспомнить квадрат или прямоугольник.

Представим себе кубик с шестью гранями. Обозначим буквами его вершины:

Несложно заметить, что отрезки TEи UJи их продолжения не пересекаются. Но это не значит, что TE||UJ. Дело в том, что ребра TEи UJ не лежат в одной плоскости. Для подобных случаев используется термин «скрещивающиеся» отрезки.
Аксиома параллельности
Ясно, что через точку, лежащую на прямой, не получится провести другую прямую, которая будет ей параллельна. Но в противном случае это возможно. В древности Евклид, великий древнегреческий ученый, создавший классическую геометрию, сформулировал знаменитую аксиому параллельности, известную как пятый постулат:


На рисунке черезА проходитс, которая параллельна а. Любая другая прямая, которой принадлежит А (в данном случае d), обязательно будет пересекать а.
Это утверждение кажется очевидным, но в реальностипятый постулат веками будоражил умы величайших математиков мира. Дело в том, что аксиомой считается утверждение, которое считается очевидным и не может быть доказано. Они являются основанием всех логических умозаключений, которые используются при доказательстве теорем. Однако многие ученые полагали, что пятый постулат можно вывести из других аксиом.Но за две тысячи лет никому так и не удалось сделать это.
В XIX веке россиянин Лобачевский попробовал построить доказательство пятого постулата методом «от противного». Он предположил, что пятый постулат неверен, и на основе этого утверждения стал доказывать теоремы, ожидая, что когда-нибудь получится прийти к противоречию. В результате ученый создал отдельную геометрию, которую сегодня называют геометрией Лобачевского, однако к противоречию он так и не пришел. Тем самым он доказал, что всем известная евклидовая геометрия является не единственно возможной. Существуют альтернативные ей геометрические системы, которые сегодня называют неевклидовыми. Это одно из величайших открытий в истории математики, которое позже легло в основу теории относительности, созданной Альбертом Эйнштейном.
Но вернемся к евклидовой геометрии. Из аксиомы параллельности следует следующее утверждение:

Такое свойство называют транзитивностью. Докажем его методом «от противного». Пусть а||c и a||b. Предположим, чтоbи с пересекаются в D:

В результате через D проходят сразу две различные прямые, которые параллельны a. Но попятому постулату это невозможно. Получается противоречие. Значит, исходное утверждение (о том, что bи с пересекаются) ошибочно, а поэтому b||c.
Секущая

При этом она образует 8 углов:

Здесь с – это секущая, а||b. Образованные углы можно разбить на пары, которые имеют особое название. Накрест секущими называют пары ∠1 и ∠5, ∠3 и ∠7, ∠4 и ∠6, ∠2 и ∠8:

Еще 4 пары называют соответственными углами. Это ∠1 и ∠7, ∠2 и ∠6, ∠3 и ∠5, ∠4 и ∠8:

Третья группа углов носит название односторонних. К ним относят пары∠1 и ∠6, ∠2 и ∠7, ∠4 и ∠5, ∠3 и ∠8:

Те углы, которые расположены между параллельными прямыми, носят название внутренних. На рисунке таковыми являются ∠1, ∠4, ∠5 и ∠6. Остальные углы считаются внешними. Можно заметить, что пары накрест лежащих и односторонних углов образуются либо двумя внешними (на рисунке расположены справа), либо двумя внутренними углами. А вот пара соответственных углов всегда состоит из одного внешнего и одного внутреннего угла.
Теорема о прямых, перпендикулярных секущей
Докажем следующее утверждение:

На рисунке это будет выглядеть так:

Кажется очевидным, что aи b никогда не пересекутся, однако доказать это на основе аксиом геометрии не так-то просто! Попробуйте сначала сделать это самостоятельно, а если не получилось, то смотрите сюда:

Доказательство построено на методе «от противного». Допустим, чтоaи b пересекутся в точке, которую мы обозначимкак А. Теперь отобразим (как будто в зеркале) полученный треугольник DKA симметрично относительно c. При этом отражение А обозначим как А’. ∠ADK равен 90°, поэтому и угол ∠A’DK также равен 90°. Тогда ∠А’DА=∠ADK+∠A’DK=90°+90°=180°. Это означает, что линия АDА’) является прямой. Тоже самое можно доказать и для линии АKА’.
Получаем, что через А и A’ проходит две разных прямых. Однако одна из аксиом геометрии гласит, что через две точки можно провести единственную прямую. Полученное противоречие говорит о том, что изначальное утверждение ошибочно, и aи b не пересекаются.
Признаки параллельности прямых
По характерным углам, которые образуются секущей, можно определить параллельность прямых. Первый из признаков параллельности двух прямых звучит так:

Попробуем доказать это. Пусть c – секущая для aи b, и ∠1 равен∠5.

Сначала рассмотрим простейший случай, когда эти углы прямые. Тогдаaи b перпендикулярны c,а потому a||b. В более сложном случае ∠1 и ∠5 не равны 90°. Тогда с середины отрезка АВ (обозначим ее как О), опустим перпендикуляр на a, а точку их пересечения обозначим как H. Далее построим отрезок АК, который лежит на b и равен по длине BH:

Теперь рассмотрим треугольники АОК и ВОН. ∠ОАК и ∠НВО равны друг другу, также равны и две прилегающие к нему стороны: ОА=ОВ (так как О – середина отрезка АВ) и HB=АК. Получаем, что эти треугольники равны друг другу по 1-ому признаку равенства треугольников (смотри урок 3).
Из этого можно сделать два вывода. Во-первых, равны ∠АОК и ∠НОВ, поэтому они являются вертикальными.Это означает, что Н, О и Красполагаются на одной прямой. Во-вторых, угол ∠ОКА=∠ВНО=90°. Следовательно, отрезок HK перпендикулярен и к a, и к b. Поэтому a||b.
Второй признак формулируется так:

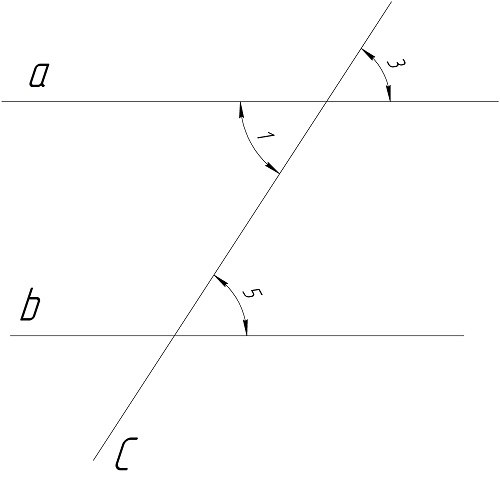
Действительно, пусть ∠3 и ∠5 равны друг другу. Тогда∠1 равен∠3, так как они вертикальные. Получаем, что ∠5=∠3=∠1. Но ∠5 и ∠1 накрест лежащие. Их равенстворанее доказанному1-ому признаку параллельности означает, a||b.
Третий признак звучит так:


Пусть ∠5+∠4=180° (1). Так как ∠4 и ∠1 являются смежными, то для них можно записать равенство: ∠4+∠1=180°. Отсюда можно получить значение угла 4: ∠4=180°-∠1. Подставляя это уравнение в выражение (1), получаем:
∠5+(180°-∠1)=180. Раскрывая скобки и перенося слагаемые в правую часть, можно получить равенство ∠5=∠1. Но эти углы являются накрест лежащими, а потому их равенство означает, что a||b.
Расстояние между параллельными прямыми
Дадим определение расстояния между параллельными прямыми:


На этом рисунке a||b, из D опущен перпендикуляр на b. Длина полученного отрезка DK и является расстоянием между aи b. Несложно убедиться, что его величина не зависит от выбора точки D. Докажем это утверждение:

Опустим из двух произвольных точек D и D’, принадлежащих a, перпендикуляры на b. Обозначим точки, в которых они пересекут b, как K и K’. Kи D’ соединим отрезком, который окажется секущим. А теперь внимательно изучим треугольники DKD’и KK’D’. У них есть общая сторона KD’. ∠D’KK’ и ∠KD’D равны друг другу как накрест лежащие. По той же причине можно записать равенство ∠DKD’=∠KD’K’. Получается, что эти треугольники равны друг другу по стороне и двум прилегающим углам. Из это следует, что DK=D’K’.
Заметим, что если прямые не параллельны, то длина перпендикуляра будет меняться в зависимости от выбора исходной точки. Поэтому понятие расстояния для пересекающихся прямых теряет смысл.
Способы построения параллельных прямых
На уроках геометрии обязательно придется строить параллельные отрезки. Как это делать быстро с помощью подручных инструментов? Самый простой практический способ построения параллельных прямых требует наличия только линейки и угольника.
Сначала надо приложить угольник к исходномуотрезку. Далее к боковой грани угольникаприкладывают линейку. После этого треугольник можно двигать по линейке, которую надо удерживать неподвижно. Когда угольник займет новое положение, можно будет построить отрезок, параллельныйисходному:

Источник
В геометрии ещё с античных времен существуют так называемые задачи на построение. В них требуется построить требуемый рисунок, используя только два предмета: циркуль и линейку. При этом на линейке нет никаких делений. Как же построить параллельные отрезки с помощью этих двух инструментов?
Рассмотрим такую задачу: дана прямая aи точка D, не лежащая на ней. Требуется построить через D такую b, что a||b:

Решение состоит из нескольких шагов. Сначала надо провести из Dокружность произвольного радиуса, но достаточно большую, чтобы, она пересекла aв двух точках. Обозначим их как K и K’.

Далее из этих точек мы проводим две окружности равных радиусов, при этом также таких, чтобы они пересекались в двух точках. Для определенности в качестве радиуса можно взять длину отрезка KK’. Точки пересечения этих окружностей обозначим как Fи F’:

Соединяя эти две точки, мы получим перпендикуляр к a, который проходит через D. В принципе, для построения достаточно использовать одну точку(либо F, либо F’):

На следующем шаге проводится окружность любого радиуса с центром в D. Обозначим буквами M и M’ точки, где она пересекается с FF’:

Последний шаг. Проводим из M и M’ окружности, чьи радиусы равныMM’. Они пересекутся в двух точках, V и V’. Прямая VV’ будет параллельна исходной прямой a:

Из этого урока вы узнали, какие прямые именуются параллельными, и по каким признакам их можно определить. Эти знания очень пригодятся не только при изучении геометрии, но и в других областях. При построении инженерами чертежей и 3D моделей именно параллельные отрезки играют ключевую роль.
Посмотрите на окружающий мир и оцените, сколько в нем параллельных линий. Можно вспомнить:
- рельсы, по которым ездят локомотивы и поезда;
- шпалы, лежащие под этими рельсами;
- полосы движения на автомагистралях
- колонны, поддерживающие фасады зданий.
Это доказывает, что геометрия – не сухая бумажная наука, рассуждающая об абстрактных понятиях, а практически важная дисциплина. Её изучение обязательно пригодится в будущем. Ждем вас на следующем уроке!
Параллельные и перпендикулярные прямые. Видеоурок. Геометрия 7 Класс
Земля имеет форму, похожую на шар. Но ее размеры огромны по сравнению с тем участком поверхности, который видит человек. Поэтому для нас видимая часть Земли кажется плоской.
Математика занимается изучением идеальных объектов, приближенных к реальным.
Для многих практических задач кривизна поверхности Земли существенно не влияет на точность решения, поэтому мы можем считать видимую часть Земли плоской. Изучением такой идеальной модели занимается планиметрия – геометрия на плоскости.
Точка, прямая и плоскость – это основные, неопределяемые понятия в геометрии. Т. к. в ближайшее время мы будем заниматься планиметрией (т. е. геометрией на плоскости), то у нас будет одна плоскость, на которой будут лежать все остальные фигуры. Из основных фигур остаются точки и прямые.
Взаимное расположение точки и прямой допускает два варианта: точка принадлежит прямой или не принадлежит (см. рис. 1).
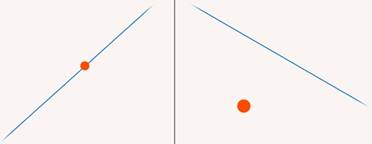
Рис. 1. Взаимное расположение точки и прямой (слева направо): точка принадлежит прямой, точка не принадлежит прямой
А вот про взаимное расположение прямых мы поговорим на этом уроке.
Две прямые на плоскости могут пересекаться или не пересекаться. Если прямые не пересекаются, их называют параллельными (см. рис. 2).

Рис. 2. Параллельные прямые
Важное свойство параллельных прямых: расстояние между ними везде будет одинаковым (см. рис. 3). Рельсы железной дороги делают параллельными, поскольку расстояние между колесами поезда постоянно.

Рис. 3. Расстояние между параллельными прямыми везде одинаково
Расстояние между прямыми
Понятие расстояния между двумя прямыми на плоскости имеет смысл только для параллельных прямых.
Действительно, говорить о расстоянии между пересекающимися прямыми бессмысленно – в точке пересечения оно равно 0, а с удалением от этой точки стремится к бесконечности (см. рис. 4).
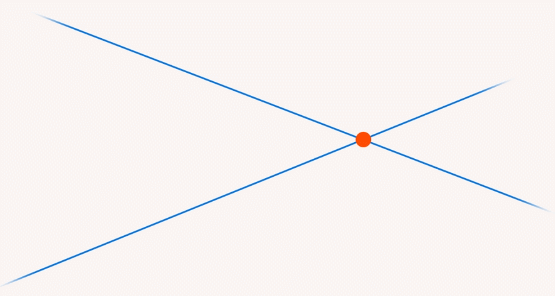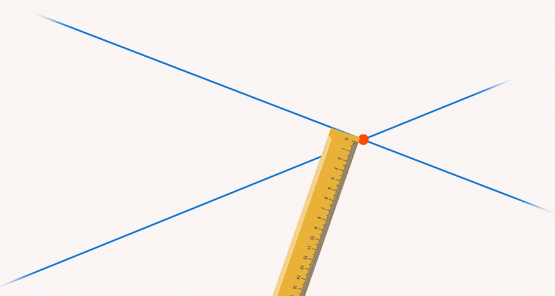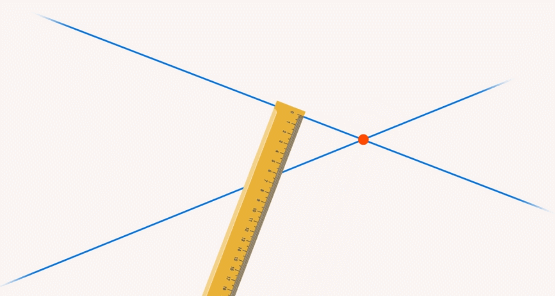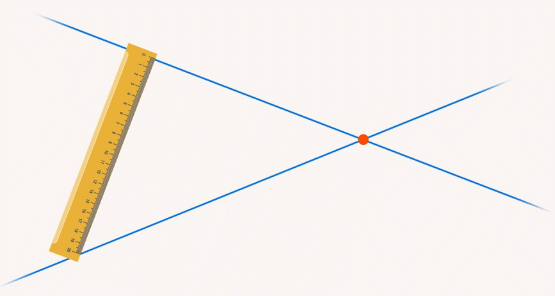
Рис. 4. Расстояние в точке пересечения прямых равно 0, а с удалением от этой точки стремится к бесконечности
Для параллельных прямых расстоянием называется длина отрезка, перпендикулярного обеим прямым (см. рис. 5).
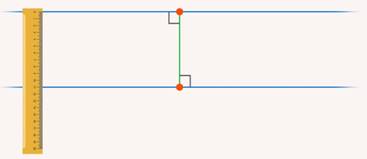
Рис. 5. Расстояние между параллельными прямыми – длина отрезка, перпендикулярного им обеим
Если вернуться к примеру с рельсами, то расстояние между рельсами – это длина шпалы (или длина оси, соединяющей колеса поезда).
Если говорить не о прямых, а об отрезках или лучах, то нельзя называть их параллельными только потому, что они не пересекаются: на рисунке ниже изображены примеры непересекающихся, но непараллельных отрезков и лучей (см. рис. 6).

Рис. 6. Примеры непересекающихся, но непараллельных отрезков и лучей
Если отрезки и лучи продолжить до прямых и эти прямые окажутся параллельными, то и сами отрезки и лучи называются параллельными. Или короче: отрезки и лучи, лежащие на одной прямой или на параллельных прямых, называются параллельными (см. рис. 7).
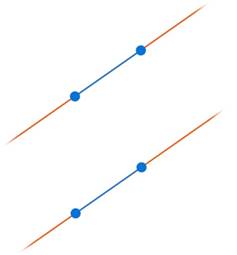
Рис. 7. Если отрезки и лучи лежат на одной прямой или на параллельных прямых, то они параллельны
Пересекающиеся прямые и отрезки встречаются гораздо чаще. Мы знаем, что перекресток – это место, где пересекаются две и больше улиц. У пересекающихся прямых перекресток называется точкой пересечения. Причем, у двух прямых общая точка может быть только одна (если они непараллельны).
Две пересекающиеся прямые образуют 4 угла. Обозначим их как 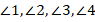 (см. рис. 8).
(см. рис. 8).
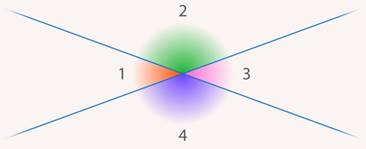
Рис. 8. Нумерация углов, образованных пересечением двух прямых
Если поворачивать одну прямую вокруг точки пересечения, то углы меняются (см. рис. 9). Но легко заметить, что углы 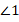 и
и 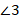 , а также
, а также 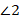 и
и 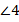 равны, независимо от положения второй прямой.
равны, независимо от положения второй прямой.
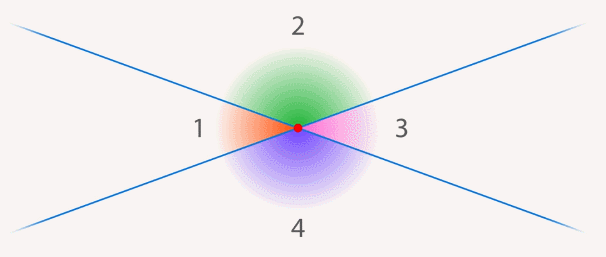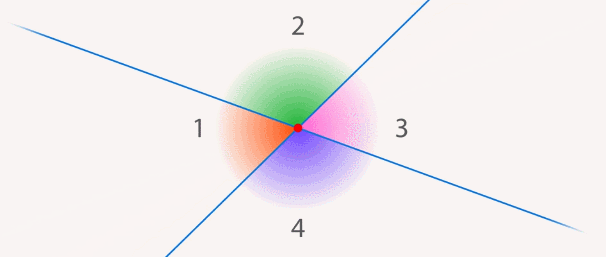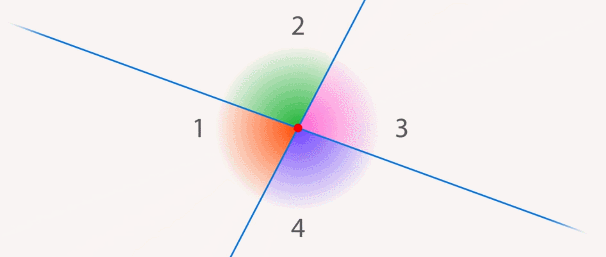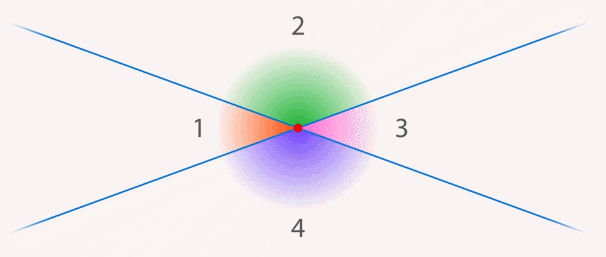
Рис. 9. Углы меняются при повороте прямой вокруг точки пересечения
Пары противоположных углов, которые образуются при пересечении прямых, называются вертикальными. Пары углов  и
и  или
или 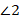 и
и 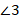 , образующих вместе развернутый угол, называют смежными.
, образующих вместе развернутый угол, называют смежными.
Итак, мы видим два свойства:
- сумма смежных углов равна
 , т. к. два смежных угла всегда вместе образуют развернутый угол, градусная мера которого равна
, т. к. два смежных угла всегда вместе образуют развернутый угол, градусная мера которого равна  ;
; - вертикальные углы равны (мы это заметили, но, как мы договаривались, очевидность не является доказательством – требуется доказать это утверждение).
Теорема.
Вертикальные углы равны.
Доказательство.
Итак, смежные углы 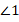 и
и 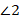 вместе составляют развернутый угол, значит, их сумма равна
вместе составляют развернутый угол, значит, их сумма равна 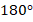 (см. рис. 10).
(см. рис. 10).
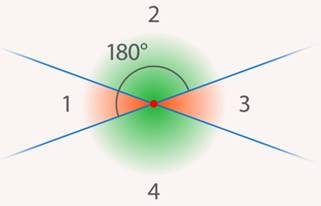
Рис. 10. Смежные углы 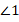 и
и 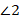 составляют развернутый угол, равный
составляют развернутый угол, равный 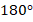
Углы 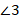 и
и 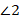 также являются смежными и составляют развернутый угол, значит, их сумма также равна
также являются смежными и составляют развернутый угол, значит, их сумма также равна 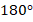 (см. рис. 11).
(см. рис. 11).
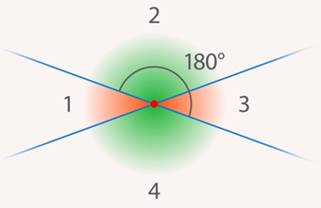
Рис. 11. Смежные углы 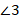 и
и 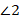 составляют развернутый угол, равный
составляют развернутый угол, равный 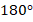
Получаем:
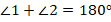
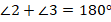
Вычтем из одного уравнения второе, получим:
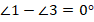
Откуда:
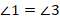
Можно было рассуждать и по-другому: к углам 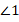 и
и 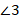 добавили один и тот же угол
добавили один и тот же угол 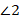 и получили одинаковые суммы,
и получили одинаковые суммы, 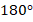 . Значит, сами углы были равны друг другу.
. Значит, сами углы были равны друг другу.
Теорема доказана.
Посмотрим на смежные углы. На всех представленных рисунках один из них меньше другого (см. рис. 12).
Рис. 12. Углы при пересекающихся прямых
Но всегда ли это так? Начнем вращать прямую, увеличивая меньший угол и уменьшая больший. В определенный момент углы с двух сторон от прямой, которую мы вращаем, станут одинаковыми. Полученные углы называют прямыми, а прямые называют перпендикулярными (см. рис. 13).
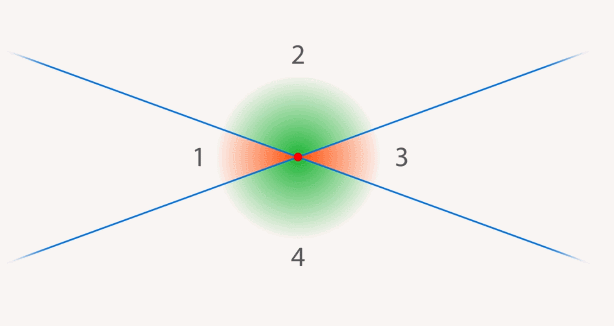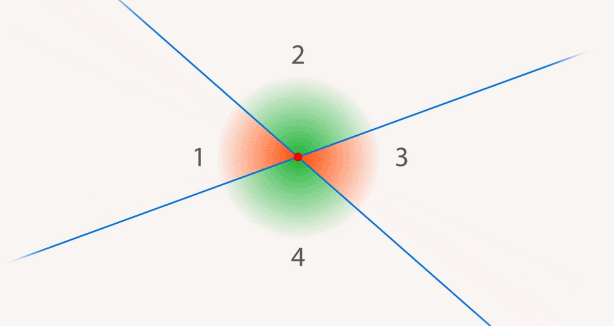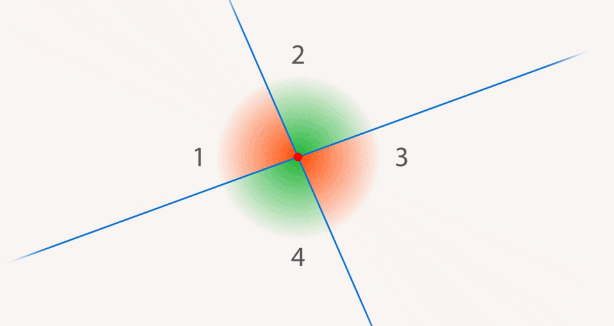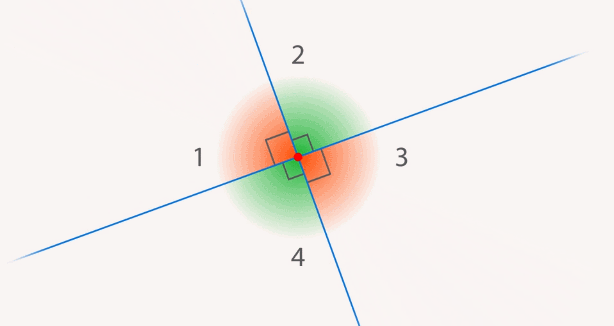
Рис. 13. Перпендикулярные прямые образуют прямые углы
Почему прямые называют перпендикулярными?
Когда каменщики в Древнем Риме строили стены, то, конечно, хотели сделать их устойчивыми и прочными. Но если стену сделать такой – она обвалится вперед, если такой – назад (см. рис. 14).

Рис. 14. Положения стены, при которых она обвалится
Нужно сделать так, чтобы она стояла прямо (отсюда прямые углы), т. е. чтобы углы слева и справа от нее были равны (см. рис. 15).

Рис. 15. Стена стоит прямо – углы слева и справа от нее равны
Как это можно сделать без угольника, циркуля, линейки прямо на улице? Для этого использовали отвес (см. рис. 16).

Рис. 16. Отвес
А линию и стену назвали, соответственно, отвесной. От лат. perpendicular – «отвес», отсюда и название прямых – перпендикулярные.
Поскольку углы 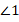 и
и 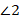 при пересечении перпендикулярных прямых равны, а также являются смежными, т. е. в сумме составляют развернутый угол, то прямой угол равен половине развернутого угла, или, если говорить о градусной мере, то:
при пересечении перпендикулярных прямых равны, а также являются смежными, т. е. в сумме составляют развернутый угол, то прямой угол равен половине развернутого угла, или, если говорить о градусной мере, то:
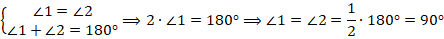
Во всех остальных случаях прямая стоит косо и углы по обе стороны от нее косые – один острый (меньше прямого), другой тупой (больше прямого) (рис. 17).
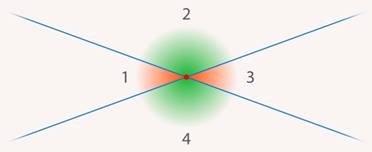
Рис. 17. Углы 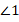 и
и 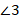 – острые, а
– острые, а  и
и 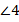 – тупые
– тупые
Острым, соответственно, будет угол от 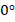 до
до 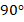 градусов (не включая), а тупым – от
градусов (не включая), а тупым – от 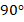 до
до 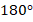 градусов (также не включая).
градусов (также не включая).
Угол между прямыми
Вернемся еще раз к смежным непрямым углам. Понятно, что один из них – острый, второй – тупой. И понятно, что любой из них однозначно задает угол, под которым пересекаются прямые, т. е., зная любой из четырех углов, можно восстановить значения трех остальных, используя свойства вертикальных и смежных углов (см. рис. 18).
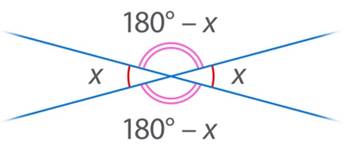
Рис. 18. Зная один из углов, при помощи свойств вертикальных и смежных углов можно восстановить значения трех остальных
Но, чтобы не было путаницы, договорились называть углом между прямыми именно острый угол, который образуется при их пересечении. Например, если при пересечении прямых получаются смежные углы 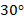 и
и 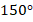 , то говорят, что угол между прямыми равен
, то говорят, что угол между прямыми равен 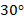 .
.
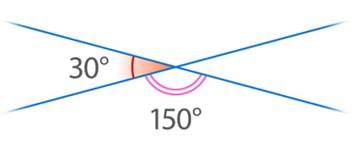
Рис. 19. Угол между пересекающимися прямыми равен 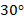
Угол между перпендикулярными прямыми равен 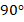 , а между параллельными считается равным
, а между параллельными считается равным 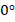 .
.
Итак, перпендикулярность – это особый, предельный случай пересечения двух прямых.
Обычно предельные случаи оказываются очень важными базовыми и им уделяют много внимания. Подробнее об этом ниже.
Предельные случаи
С предельными случаями мы сталкиваемся в разных ситуациях. Например, предельным случаем прямоугольника является квадрат – прямоугольник, у которого все стороны равны.
Другой пример. У каждого числа есть противоположное. У числа 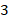 – число
– число 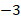 , у числа
, у числа 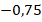 – число
– число 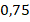 . Обычно число и ему противоположное – разные числа. И есть один предельный случай, когда число совпадает со своим противоположным, или можно сказать, у него нет противоположного. Это, конечно, число
. Обычно число и ему противоположное – разные числа. И есть один предельный случай, когда число совпадает со своим противоположным, или можно сказать, у него нет противоположного. Это, конечно, число 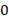 . Мы понимаем, что ноль очень важное число в математике.
. Мы понимаем, что ноль очень важное число в математике.
Так и перпендикулярность, как предельный случай пересечения, часто встречается в геометрических задачах.
Понятие перпендикуляра связано с ответом на вопрос о кратчайшем расстоянии от точки до прямой.
Вы плаваете, устали и собираетесь плыть назад к берегу. Конечно, вам хочется плыть по кратчайшему пути. Кратчайшим путем будет перпендикуляр, проведенный от точки вашего нахождения до берега (см. рис. 20).

Рис. 20. Кратчайший путь – перпендикуляр, проведенный от точки вашего нахождения до берега
Если же вы находитесь на берегу (будем считать его прямой линией) и на вас движется волна, то убегать от нее нужно по линии, перпендикулярной фронту волны (см. рис. 21).

Рис. 21. При нахождении на берегу от волны нужно убегать по линии, перпендикулярной фронту волны
Действительно, если за 10 секунд вы пробежите 50 метров вот так, то окажетесь ближе к волне, чем, если бы бежали так (см. рис. 22).

Рис. 22. Если бежать по первой линии, то вы окажетесь ближе к волне, чем, если бежать по второй
Рассмотрим точку, которая не лежит на прямой. Проведем через нее перпендикулярную прямую. Отрезок 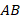 называется перпендикуляром. Будем говорить, что мы опустили перпендикуляр из точки
называется перпендикуляром. Будем говорить, что мы опустили перпендикуляр из точки 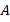 на прямую
на прямую  (рис. 23).
(рис. 23).
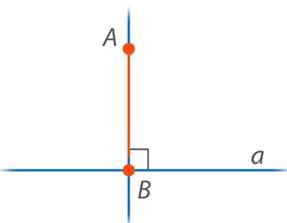
Рис. 23. Перпендикуляр  , опущенный из точки
, опущенный из точки  на прямую
на прямую 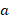
Длиной перпендикуляра будем называть расстояние от точки 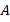 до прямой
до прямой 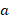 .
.
Любой отрезок, соединяющий точку 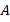 с другой точкой на прямой (не
с другой точкой на прямой (не 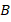 ), называется наклонной. Например,
), называется наклонной. Например,  – наклонная (см. рис. 24).
– наклонная (см. рис. 24).
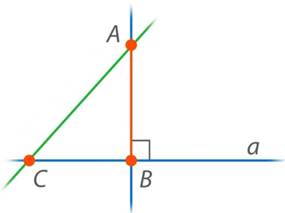
Рис. 24. Наклонная 
Рассуждения про кратчайшее расстояние до берега или от волны теперь можно сформулировать так: перпендикуляр всегда короче наклонной, проведенной из той же точки (см. рис. 25).
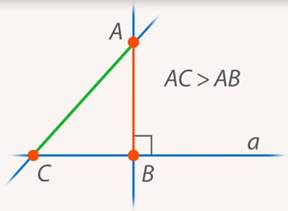
Рис. 25. Наклонная 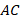 длиннее перпендикуляра
длиннее перпендикуляра 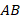
Факт очевидный, но строго доказать мы его пока не можем, нам не хватает инструментов. Но скоро мы это сделаем.
Две прямые на плоскости, взятые случайным образом, будут пересекаться, причем не под прямым углом. Иначе говоря: если вы бросите две спицы на стол и продлите их до прямых, то полученные прямые не будут параллельными или перпендикулярными. Вероятность этого события можно считать равной 0 – как выпадения монеты на ребро.
Это два предельных случая расположения прямых. Связаны ли они друг с другом? Если все сосны в лесу растут вертикально (перпендикулярно земле), то они параллельны друг другу.
Это наблюдение можно сформулировать в виде признака параллельности прямых: если две прямые перпендикулярны третьей, то они параллельны друг другу (см. рис. 26). Факт очевидный, но строго докажем его чуть позже:
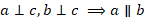
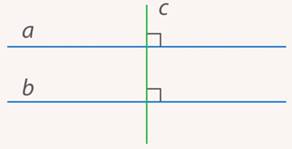
Рис. 26. Если две прямые перпендикулярны третьей, то они параллельны друг другу
Что можно сказать про три прямые, какие для них возможны варианты взаимного расположения?
Поскольку любые две прямые могут либо быть параллельными, либо пересекаться, то для трех прямых возможны различные комбинации этих случаев.
1. Все три прямые параллельны друг другу (см. рис. 27).

Рис. 27. Три параллельные прямые
2. Две прямые параллельны, третья прямая их пересекает (см. рис. 28).
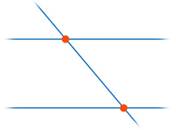
Рис. 28. Прямая пересекает две другие параллельные прямые
3. Все три прямые пересекаются, причем в одной точке (см. рис. 29).
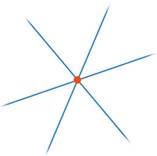
Рис. 29. Три прямые пересекаются в одной точке
4. Все три прямые пересекаются друг с другом попарно (см. рис. 30).
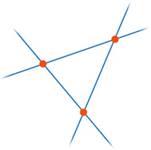
Рис. 30. Три прямые пересекаются друг с другом попарно
Поговорим о каждом из этих случаев подробнее.
1. Все три прямые параллельны друг другу.
Проведем прямую 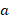 , затем – прямую
, затем – прямую 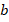 параллельно
параллельно 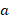 и прямую
и прямую 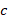 параллельно
параллельно 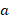 . Мы догадываемся, что
. Мы догадываемся, что 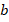 и
и 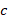 параллельны друг другу (см. рис. 31). Такое свойство называется транзитивностью:
параллельны друг другу (см. рис. 31). Такое свойство называется транзитивностью:
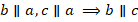

Рис. 31. Если провести прямые 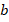 и
и 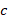 , параллельные прямой
, параллельные прямой 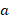 , то они также будут параллельными
, то они также будут параллельными
Вспомните другие известные нам примеры транзитивности:
-
 ;
; -
 ;
; - яблоко весит больше груши, а груша – больше сливы, значит, яблоко весит больше сливы (см. рис. 32).
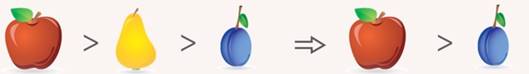
Рис. 32. Пример транзитивности
Рассмотрим доказательство признака параллельности. Оно основывается на пятом постулате Евклида: через точку, не лежащую на прямой, можно провести только одну прямую, параллельную данной.
Доказательство.
Итак, 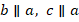 . Докажем, что
. Докажем, что 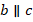 . Предположим, что это не так (используем метод от противного). Они непараллельны, значит, они пересекаются в некоторой точке
. Предположим, что это не так (используем метод от противного). Они непараллельны, значит, они пересекаются в некоторой точке 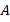 (см. рис. 33).
(см. рис. 33).
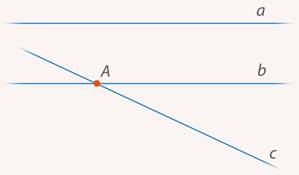
Рис. 33. Прямые 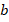 и
и 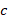 пересекаются в точке
пересекаются в точке 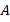
Эта точка не лежит на прямой 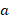 , т. к. прямые
, т. к. прямые 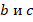 не имеют общих точек с прямой
не имеют общих точек с прямой 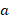 в силу параллельности. Значит, через точку
в силу параллельности. Значит, через точку 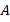 , не лежащую на прямой
, не лежащую на прямой 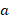 , проходят две прямые, параллельные
, проходят две прямые, параллельные 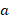 . Это противоречит пятому постулату Евклида. Таким образом,
. Это противоречит пятому постулату Евклида. Таким образом, 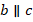 .
.
Доказано.
- Окончательная формулировка признака параллельности: если две прямые параллельны третьей, то они параллельны друг другу.
- Все три прямые могут пересекаться в одной точке, образовывать пучок. Это предельный случай, но пока он нам не очень интересен.
- Две прямые параллельны, третья прямая их пересекает.
Рассмотрим острые углы 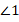 и
и 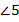 (см. рис. 34). Такие углы называются соответственными. Мы догадываемся, что они равны.
(см. рис. 34). Такие углы называются соответственными. Мы догадываемся, что они равны.
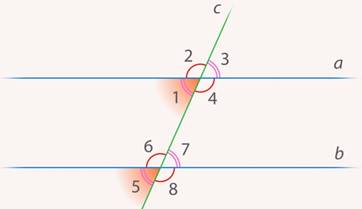
Рис. 34. Соответственные углы 
В самом деле, если прямую  сдвигать вниз параллельно самой себе, то, когда прямая
сдвигать вниз параллельно самой себе, то, когда прямая  совпадет с прямой
совпадет с прямой 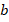 ,
, 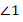 совпадет с
совпадет с 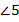 (рис. 35).
(рис. 35).
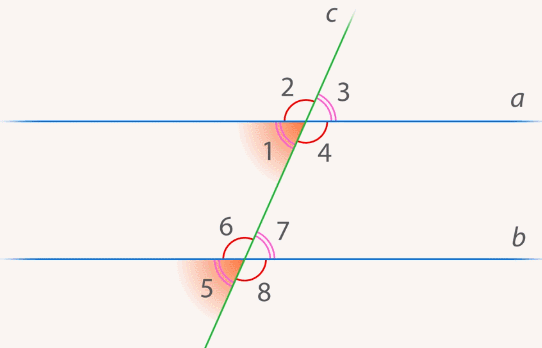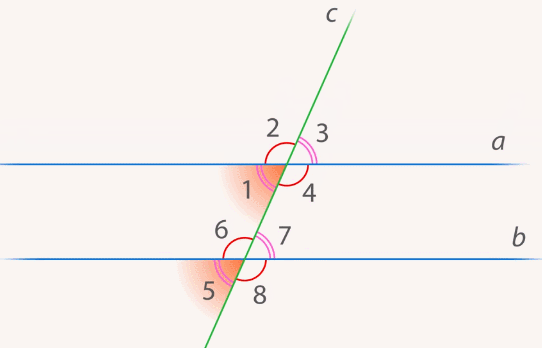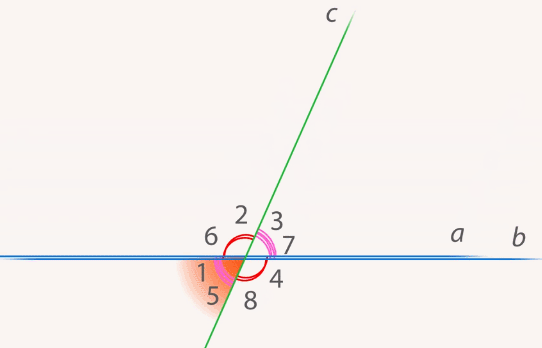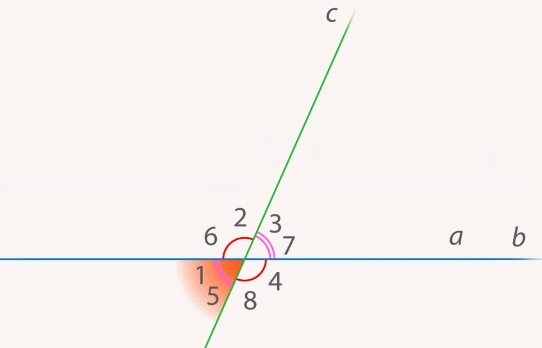
Рис. 35. Когда при сдвиге прямой  вниз параллельно самой себе, прямая
вниз параллельно самой себе, прямая 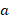 совпадет с прямой
совпадет с прямой 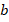 , то
, то 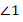 совпадет с
совпадет с 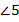
Такое рассуждение не является строгим доказательством (докажем мы его позже), но оно дает нам понимание, что параллельные прямые – это по сути две одинаковые прямые.
Аналогично мы видим еще 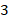 пары соответственных углов:
пары соответственных углов: 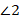 и
и 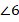 ,
, 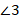 и
и 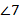 ,
, 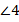 и
и 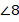 . Они тоже равны между собой.
. Они тоже равны между собой.
Поскольку мы доказали, что вертикальные углы равны, то можем записать такие цепочки равенств:
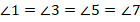
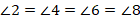
Это совсем не удивительно. Две пер
Построение параллельных прямых
В основе способов построения параллельных прямых с помощью различных инструментов лежат признаки параллельности прямых.
Построение параллельных прямых с помощью циркуля и линейки
Рассмотрим принцип построения параллельной прямой, проходящей через заданную точку, с помощью циркуля и линейки.
Пусть дана прямая и некоторая точка А, которая не принадлежит данной прямой.
Необходимо построить прямую, проходящую через заданную точку $А$ параллельно данной прямой.
На практике зачастую требуется построить две или более параллельных прямых без данной прямой и точки. В таком случае необходимо начертить прямую произвольно и отметить любую точку, которая не будет лежать на данной прямой.
Рассмотрим этапы построения параллельной прямой:
- Выберем произвольную точку на данной прямой и назовем ее $В$. обратим внимание, что выбор точки абсолютно произвольный, т.к. не влияет на результат построения.
- С помощью циркуля и начертим окружность радиуса $АВ$ с центром в точке $В$.
На пересечении окружности и прямой отметим точку и назовем ее $С$.
С тем же радиусом $АВ$ построим окружность с центром в точке $С$. Обратим внимание, что вторая построенная окружность обязательно должна пройти через точку В при правильном выполнении построения.
С прежним радиусом $АВ$ построим третью окружность с центром в точке $А$.
Отметим точку пересечения второй и третьей построенных окружностей и назовем ее $D$. Отметим, что третья окружность при правильном построении также должна пройти через точку $В$.
Через точки $А$ и $D$ проведем прямую, которая будет параллельной заданной.
Таким образом, получили параллельные прямые $ВС$ и $АD$:
$BC \parallel AD$, т. $A \in AD$.
На практике также применяют метод построения параллельных прямых с помощью чертежного угольника и линейки.
Построение параллельных прямых с помощью угольника и линейки
Для построения прямой, которая будет проходить через точку М параллельно данной прямой а, необходимо:
- Угольник приложить к прямой $а$ диагональю (смотрите рисунок), а к его большему катету приложить линейку.
- Передвинуть угольник по линейке до тех пор, пока данная точка $М$ не окажется на диагонали угольника.
- Провести через точку $М$ искомую прямую $b$.
Мы получили прямую, проходящую через заданную точку $М$, параллельную данной прямой $а$:
$a \parallel b$, т. $M \in b$.
Параллельность прямых $а$ и $b$ видна из равности соответственных углов, которые отмечены на рисунке буквами $\alpha$ и $\beta$.
Построение параллельной прямой, отстоящей на заданное расстояние от данной прямой
В случае необходимости построения прямой, параллельной заданной прямой и отстоящей от нее на заданном расстоянии можно воспользоваться линейкой и угольником.
Пусть дана прямая $MN$ и расстояние $а$.
- Отметим на заданной прямой $MN$ произвольную точку и назовем ее $В$.
- Через точку $В$ проведем прямую, перпендикулярную к прямой $MN$, и назовем ее $АВ$.
- На прямой $АВ$ от точки $В$ отложим отрезок $ВС=а$.
- С помощью угольника и линейки проведем прямую $CD$ через точку $С$, которая и будет параллельной заданной прямой $АВ$.
Если отложить на прямой $АВ$ от точки $В$ отрезок $ВС=а$ в другую сторону, то получим еще одну параллельную прямую к заданной, отстоящую от нее на заданное расстояние $а$.
Другие способы построения параллельных прямых
Еще одним способом построения параллельных прямых является построение с помощью рейсшины. Чаще всего данный способ используют в чертежной практике.
При выполнении столярных работ для разметки и построения параллельных прямых, используется специальный чертежный инструмент – малка – две деревянные планки, которые скрепляются шарниром.
Параллельные прямые — это… Что такое Параллельные прямые?
Параллельные прямые
Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается.
Свойства
- Параллельность — бинарное отношение эквивалентности, поэтому разбивает всё множество прямых на классы параллельных между собой прямых.
- Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две)
- 2 параллельные прямые в пространстве лежат в одной плоскости.
- При пересечении 2 параллельных прямых третьей, называемой секущей:
- Секущая обязательно пересекает обе прямые.
- При пересечении образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
- Накрест лежащие углы равны.
- Соответственные углы равны.
- Односторонние углы в сумме составляют 180°.
В геометрии Лобачевского в плоскости через точку Невозможно разобрать выражение (лексическая ошибка): C</math¹> вне данной прямой <math>AB
проходит бесконечное множество прямых, не пересекающих AB. Из них параллельными к AB называются только две.
Прямая CE называется равнобежной (параллельной) прямой AB в направлении от A к B, если:
- точки B и E лежат по одну сторону от прямой AC;
- прямая CE не пересекает прямую AB, но всякий луч, проходящий внутри угла ACE, пересекает луч AB.
Аналогично определяется прямая, равнобежная AB в направлении от B к A.
Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися.
См. также
Параллельные прямые
Понятие параллельных прямых
Определение 1
Параллельные прямые – прямые, которые лежат в одной плоскости, не совпадают и не имеют общих точек.
Если у прямых есть общая точка, тогда они пересекаются.
Если все точки прямых совпадают, то имеем по сути одну прямую.
Если прямые лежат в разных плоскостях, то условий их параллельности несколько больше.
При рассмотрении прямых на одной плоскости можно дать следующее определение:
Определение 2
Две прямые на плоскости называют параллельными, если они не пересекаются.

В математике параллельные прямые принято обозначать с помощью знака параллельности « $\parallel$ ». Например, тот факт, что прямая $c$ параллельна прямой $d$ обозначается следующим образом:
$c \parallel d$.
Зачастую рассматривается понятие параллельных отрезков.
Определение 3
Два отрезка называют параллельными, если они лежат на параллельных прямых.
Например, на рисунке параллельными являются отрезки $AB$ и $CD$, т.к. они принадлежат параллельным прямым:
$AB \parallel CD$.

Вместе с тем, отрезки $MN$ и $AB$ или $МN$ и $CD$ параллельными не являются. Этот факт можно записать с помощью символов следующим образом:
$MN ∦ AB$ и $MN ∦ CD$.
Аналогичным образом определяется параллельность прямой и отрезка, прямой и луча, отрезка и луча или двух лучей.
Историческая справка
С греческого языка понятие «параллелос» переводится «рядом идущий» или «проведенный друг возле друга». Этот термин использовался в древней школе Пифагора еще до того, как параллельные прямые получили свое определение. Согласно историческим фактам Евклидом в $III$ в. до н.э. в его трудах все же был раскрыт смысл понятия параллельных прямых.
В древности знак для обозначения параллельных прямых имел отличный вид того, что мы используем в современной математике. Например, древнегреческим математиком Паппом в $III$ в. н.э. параллельность обозначалась с помощью знака равенства. Т.е. тот факт, что прямая $l$ параллельна прямой $m$ ранее обозначался «$l=m$». Позднее для обозначения параллельности прямых стали использовать привычный нам знак «$\parallel$, а знак равенства стали использовать для обозначения равенства чисел и выражений.
Параллельные прямые в жизни
Зачастую мы не замечаем, что в обычной жизни нас окружает огромное число параллельных прямых. Например, в нотной тетради и сборнике песен с нотами нотный стан выполнен с помощью параллельных линий. Также параллельные линии встречаются и в музыкальных инструментах (например, струны арфы, гитары, клавиши фортепиано и т.п.).
Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно. Рельсы линий метро и железных дорог располагаются параллельно.
Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий.
Параллельные прямые в архитектуре
На представленных изображениях архитектурные сооружения содержат параллельные прямые. Использование параллельности прямых в строительстве помогает увеличить срок службы таких сооружений и придает им необычайную красоту, привлекательность и величие. Линии электропередач также умышленно проводятся параллельно, чтобы избежать их пересечения или соприкосновения, что привело бы к замыканию, перебоям и отсутствию электричества. Чтобы поезд мог беспрепятственно перемещаться рельсы также выполнены параллельными линиями.
В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.
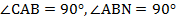 . Параллельны ли прямые CD и MN?
. Параллельны ли прямые CD и MN?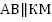 .
.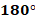 , т. к. два смежных угла всегда вместе образуют развернутый угол, градусная мера которого равна
, т. к. два смежных угла всегда вместе образуют развернутый угол, градусная мера которого равна 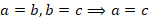 ;
;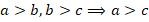 ;
;