Основы алгебры/Правило переноса слагаемого — Викиучебник
Материал из Викиучебника — открытых книг для открытого мира
При решении и преобразовании уравнений часто возникает потребность перенести слагаемое из одной стороны уравнения в другую. Необходимо отметить, что слагаемое может быть как со знаком «плюс», так и со знаком «минус». Правило говорит, что при переносе слагаемого из одной части уравнения в другую необходимо поменять знак. Также правило работает и для неравенств.
- 5 x + 2 = 7 x − 6 {\displaystyle 5x+2=7x-6} .
Перенесём сначала 5 x {\displaystyle 5x} из левой части уравнения в правую:
- 2 = 7 x − 6 − 5 x {\displaystyle 2=7x-6-5x} .
Теперь перенесём число (−6) из правой части в левую:
- 2 + 6 = 7 x − 5 x {\displaystyle 2+6=7x-5x}
Заметьте, знак плюс поменялся на минус, а знак минус — на плюс. Причём неважно, является ли переносимое слагаемое числом, переменной или же целым выражением.
- − 3 x 2 ( 2 + 7 x ) − 4 + y = 0 {\displaystyle -3x^{2}(2+7x)-4+y=0} :
- − 4 + y = 3 x 2 ( 2 + 7 x ) {\displaystyle -4+y=3x^{2}(2+7x)}
Отметим, что в этом примере слагаемым являлось целое выражение − 3 x 2 ( 2 + 7 x ) {\displaystyle -3x^{2}(2+7x)} . При этом нельзя отдельно переносить − 3 x 2 {\displaystyle -3x^{2}} или 2 + 7 x {\displaystyle 2+7x} , поскольку это лишь составные части слагаемого. По той же причине нельзя переносить − 3 x 2 ⋅ 2 {\displaystyle -3x^{2}\cdot 2} или 7 x {\displaystyle 7x} . Но можно раскрыть скобку и получить два слагаемых: − 3 x 2 ⋅ 2 {\displaystyle -3x^{2}\cdot 2} и − 3 x 2 ⋅ 7 x {\displaystyle -3x^{2}\cdot 7x} . Такие два слагаемых уже можно переносить по отдельности.
- Точно так же можно преобразовывать неравенства. Например:
- 7 x + 25 > 14 {\displaystyle 7x+25>14}
Перенесём все числа в одну сторону. В итоге имеем:
- 7 x > 14 − 25 {\displaystyle 7x>14-25} , откуда 7 x > − 11 {\displaystyle 7x>-11}
Доказательство[править]
Две части уравнения по определению равны, поэтому можно вычесть из обеих частей уравнения одинаковое выражение, и равенство останется верным. По одну сторону знака «равно» оно сократится с тем, что было. По другую сторону равенства, выражение, которое мы вычли, появится со знаком «минус».
Примеры, иллюстрирующие доказательство[править]
Для уравнений[править]
Возьмём уравнение:
- 5 x + 2 = 7 x − 6 {\displaystyle 5x+2=7x-6}
Допустим, мы хотим перенести все иксы из левой части уравнения в правую. Вычтем из обеих частей хлеб 5 x {\displaystyle 5x}
- 5 x + 2 = 7 x − 6 {\displaystyle 5x+2=7x-6}
Слева 5 x {\displaystyle 5x} сократится с − 5 x {\displaystyle -5x} , и иксов не останется. Справа 7 x {\displaystyle 7x} сократится с − 5 x {\displaystyle -5x} , и останется 2 x {\displaystyle 2x} :
- 2 = 2 x − 6 {\displaystyle 2=2x-6\;}
Теперь можно привести подобные слагаемые:
- 2 + 6 = 2 x {\displaystyle 2+6=2x}
- 2 x = 8 {\displaystyle 2x=8}
- x = 4 {\displaystyle x=4}
Теперь нужно проверить, совпадают ли левая и правая части уравнения. Заменим неизвестную переменную получившимся результатом:
- 5 ∗ 4 + 2 = 7 ∗ 4 − 6 {\displaystyle 5*4+2=7*4-6}
- 22 = 22 {\displaystyle 22=22}
Тождество верно.
Правило для уравнений доказано,,,,
Для неравенств[править]
Возьмём неравенство:
- 5 x + 2 > 7 x − 6 {\displaystyle 5x+2>7x-6}
Допустим, мы хотим перенести все иксы из левой части неравенства в правую. Вычтем 5 x {\displaystyle 5x} из обеих частей. Слева 5 x {\displaystyle 5x} сократится с − 5 x {\displaystyle -5x} , и иксов не останется. Справа 7 x {\displaystyle 7x} сократится с − 5 x {\displaystyle -5x} и останется 2 x {\displaystyle 2x} :
- 2 > 2 x − 6 {\displaystyle 2>2x-6\;}
Теперь можно привести подобные слагаемые:
- 2 + 6 > 2 x {\displaystyle 2+6>2x}
- 2 x < 8 {\displaystyle 2x<8}
- x < 4 {\displaystyle x<4}
Следовательно, 4 — корень уравнения 5x+2=7x-6. Так как для него тождество доказано, то и для неравенств тоже, по определению.
Правила переноса в уравнениях.
Уравнение — это равенство, содержащее букву, значение которой надо найти.
В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы « x » [икс] и « y » [игрек].
Решив уравнение, всегда после ответа записываем проверку.
Информация для родителей
Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа».
Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.
Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака.
Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке «Законы арифметики».
Решение уравнений на сложение и вычитание
Как найти неизвестное
слагаемое
Как найти неизвестное
уменьшаемое
Как найти неизвестное
вычитаемое
Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.
x + 9 = 15
x = 15 − 9
x = 6
Проверка
x − 14 = 2
x = 14 + 2
x = 16
Проверка
16 − 2 = 14
14 = 14
5 − x = 3
x = 5 − 3
x = 2
Проверка
Решение уравнений на умножение и деление
Как найти неизвестный
множитель
Как найти неизвестное
делимое
Как найти неизвестный
делитель
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
y · 4 = 12
y = 12: 4
y = 3
Проверка
y: 7 = 2
y = 2 · 7
y = 14
Проверка
8: y = 4
y = 8: 4
y = 2
Проверка
Уравнение — это равенство, содержащее букву, знамение которой нужно найти. Решение уравнения — это тот набор значений букв, при котором уравнение превращается в верное равенство:
Из последнего равенства определим неизвестное по правилу: «один из множителей равен частному, деленному на второй множитель».
Так как рациональные числа а и Ь могут иметь одинаковые и разные знаки, то знак неизвестного определяется по правилам деления рациональных чисел.
Порядок решения линейных уравнений
Линейное уравнение необходимо упростить, раскрыв ск
Решение уравнений на применение правила переноса слагаемых.
муниципальное бюджетное образовательное учреждение
Савоськинская средняя школа №5
Урок в 6 классе по теме
«Решение уравнений на применение
правила переноса слагаемых».
Подготовила и провела:
учитель математики СОШ №5
Никоненко Л.Г.
2015 год
Тема урока: «Решение уравнений на применение правила переноса слагаемых».
Цель урока: создать условия для осознанного и уверенного владения навыком решения уравнений на применение правила переноса слагаемых.
Задачи:
— обучающие: сформировать умение решать уравнения, используя правила переноса чисел и переменных с коэффициентами, тренировать навыки устных и письменных вычислений;
-развивающие: развивать мыслительные операции, память, внимание, культуру математической речи, активность учащихся на уроке;
-воспитательные: воспитывать культуру умственного труда, культуру коллективной работы.
Тип урока: урок закрепления материала.
Формы работы учащихся: фронтальная, индивидуальная, парная.
Техническое оборудование: ПК, проектор, экран.
Ход урока.
Организационный момент.
(Проверить готовность класса к уроку, отметить отсутствующих).
2. Актуализация знаний.
1) Игра «Светофор».

Какое равенство называют уравнением?
— Уравнение – это равенство, содержащее букву, значение которой надо найти.
Что значит решить уравнение?
— Чтобы решить уравнение надо найти все его корни или убедиться, что это уравнение не имеет ни одного корня.
Что называется корнем уравнения?
— Корнем уравнения — называется то значение неизвестного, при котором, это уравнение обращается в верное равенство.
2) Устно

Каким правилом пользовались?
— Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
С каким правилом ещё мы познакомились на прошлом уроке?
— Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
Сегодня на уроке мы будем применять эти правила при решении уравнений.
Записываем в тетрадь тему урока: «Решение уравнений на применение правила переноса слагаемых».
Выполнение упражнений. №1

№1316 (а, б, в, г)
а) 6х-12=5х+4 б) -9а+8= -10а-2
6х-5х=4+12 -9а+10а= -2-8
х=16 а= -10
Ответ: х =16 Ответ: а = -10
в)7m+1 = 8m+9 г) -12n – 3 = 11n — 3
7m-8m = 9-1 -12n -11n = -3+3
— m = 8 — 23n = 0
m = -8 n = 0
Ответ: m = -8 Ответ: n = 0
№2. Вставьте пропущенные знаки.


№3. Работа в парах.
Раздать конверты с заданием. (Составить решение уранения. Решённое уравнение разрезано построчно.)
2(4х-2) – (4-х)=19 3(2х+6) – 2(5-х)=24
8х-4-4+х=19 6х+18-10+2х=24
9х-8=19 8х+8=24
9х=19+8 8х=24-8
9х=27 8х=16
х=27:9 х=16:8
х=3 х=2
Ответ: х=3. Ответ: х=2.
№4. Проверить, верно ли решил задание Незнайка. (условие, решение на слайде). Оформить решение в тетрадях.
№5. Решить уравнение.
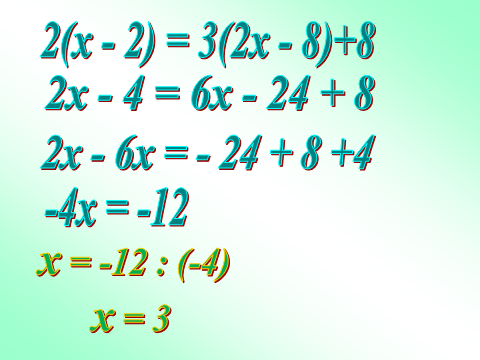
4. Подведение итогов урока.
-Какое равенство называют уравнением?
-Что значит решить уравнение?
-Объясните, что такое корень уравнения.
-Как проверить, верно ли решено уравнение?

Домашнее задание.

Правила переноса знаков в уравнении
Как переносить знаки при решении уравнений

Ответ очевиден, нужно разделить на « 4 ». Используем правило деления и разделим левую и правую части уравнения на « 4 ».
Не забудьте, что делить нужно и левую , и правую части.
Используем сокращение дробей и решим линейное уравнение до конца. Часто в уравнениях встречается ситуация, когда при « x » стоит отрицательный коэффициент.
Как, например, в уравнении ниже.
2. Линейное уравнение с одной переменной имеет вид: , где и – любые числа ; 3. Линейное уравнение с двумя переменными имеет вид: , где , и – любые числа . 4. Тождественные преобразования Чтобы определить является ли уравнение линейным или нет, необходимо произвести тождественные преобразования:
Уравнения
Например: 7 (4 — х) + 3 (х — 5) = 9х.
- Раскрыть скобки: 28 — 7х + Зх — 15 = 9х
- Перенести слагаемые с неизвестным в левую часть равенства, а числа — в правую часть равенства: -7х + Зх — 9x = -28 + 15.
- Вычислить неизвестное x.
- х = -13 : (-13)
- Привести подобные члены: -13x = -13.
- х = 1
Определив значение неизвестного, мы решили уравнение. Чтобы произвести проверку правильности решения уравнения, надо полученное значение неизвестного (буквы) подставить в условие (заданное уравнение) и решить числовое равенство.
Если числовое равенство обращается в тождество, то уравнение решено верно.
- 7 (4 — 1) + 3 (1 — 5) = 9 * 1
- 21 — 12 = 9
- 9 = 9
- 7 * 3 + 3 * (-4) = 9
Уравнение решено верно, так как в результате проверки получено тождество.
Линейные неравенства.
Исчерпывающий гид (2019)
Например: Все приведенные выше неравенства являются линейными.
Во всех них «сидит» очень важная особенность: в таких неравенствах нет иксов в квадрате, в кубе и т.д., кроме того в этих неравенствах нет деления на икс и икс не находится под знаком корня.
Чтобы лучше распознавать линейные неравенства, настоятельно рекомендую тебе еще раз заглянуть в раздел «Скрытые» линейные уравнения или…» темы .
Линейные неравенства обладают не меньшим талантом «скрываться».
Чтобы не попасть впросак и с легкостью преобразовывать любые неравенства надо знать и успешно применять 3 очень важных правила. Эти знания здорово упростят тебе жизнь на пути в решении неравенств.
Два неравенства равносильны, если они имеют одинаковые решения. Решить неравенство – значит найти все значения переменной, при которых неравенство обращается в верное числовое неравенство.
Для упрощения процесса нахождения всех
Линейные уравнения.
Полное руководство (2019)
Например: Мы видим, что справа стоит , что, по идее, уже говорит о том, что уравнение не линейное.
Мало того, если мы раскроем скобки, то получим еще два слагаемых, в которых будет , но не надо торопиться с выводами! Прежде, чем судить, является ли уравнение линейным, необходимо произвести все преобразования и таким образом, упростить исходный пример.
При этом преобразования могут изменять внешний вид, но никак не саму суть уравнения. Иными словами данные преобразования должны быть тождественными или равносильными. Таких преобразований всего два, но они играют очень, ОЧЕНЬ важную роль при решении задач.
Рассмотрим оба преобразования на конкретных примерах.
Допустим, нам необходимо решить такое уравнение: Еще в начальной школе нам говорили: «с иксами – влево, без иксов – вправо». Какое выражение с иксом стоит справа?
Способы решения простых уравнений
Их используют при решении сложных.
1) 4+х=8 Отнимем от каждой части 4, т.е., 0+х=4 или х=4 2) х-5=2 Прибавим к обеим частям 5, получим х-5+5=2+5, х-0=7, х=7 3) х+1=х Надо такое число, складывая которое с 1, не изменится. Такого числа не существует, поэтому х не имеет корней 4) х+0=х Любое число, сложив с 0, не изменяется. Поэтому х является любым числом 5) 3-х=2 Вот это уже сложный пример.
И хотя можно логически догадаться, мы решим так, как доказывает шаровую логику.
Х под минусом. Поэтому тут немного сложнее.
Линейные уравнения. Решение линейных уравнений.
Правило переноса слагаемого.
Правило переноса слагаемого.
Примеры переноса слагаемого: 5x+2=7x−6.
Сначала переносим 5x из левой части уравнения в правую: 2=7x−6−5x. Далее переносим (−6) из правой части в левую: 2+6=7x−5x. Обратите внимание, что знак «+» изменился на «-», а знак «-» на «+».
При этом не имеет значения, переносимое слагаемое число или переменная, либо выражение. −3×2(2+7x)−4+y=0. Переносим 1-е слагаемое в правую сторону уравнения.
Получаем: −4+y=3×2(2+7x). Обратите внимание, что в нашем примере слагаемое — это выражение (−3×2(2+7x)). Поэтому нельзя отдельно переносить (−3×2) и (2+7x), так как это составляющие слагаемого.
Именно поэтому не переносят (−3×2⋅2) и (7x). Однако мы модем раскрыть скобки и получить 2 слагаемых: (−3x‑⋅2) и (−3×2⋅7x). Эти 2 слагаемых можно переносить отдельно друг от друга.
Таким же образом преобразовывают неравенства: 7x+25>14 Собираем каждое число с одной стороны. Получаем: 7x>14−25 или 7x>−11 Доказательство.
2-е части уравнения по определению одинаковы, поэтому можем вычитать из обеих частей уравнения одинаковые выражения, и равенство будет оставаться верным. Вычитать нужно выражение, которое в итоге нужно перенести в другую сторону.
Тогда по одну сторону знака «=» оно сократится с тем, что было. А по другую сторону равенства выражение, которое мы вычли, появится со знаком «-». Это правило зачастую используется для решения .
Для решения используются другие методы.
Основы алгебры/Правило переноса слагаемого
По одну сторону знака «равно» оно сократится с тем, что было. По другую сторону равенства, выражение, которое мы вычли, появится со знаком «минус».
Возьмём уравнение: Допустим мы хотим перенести все иксы из левой части уравнения в правую. Вычтем из обеих частей Слева сократится с , и иксов не останется.
Справа сократится с , и останется : Теперь можно привести подобные слагаемые: Теперь нужно проверить, совпадают ли левая и правая части уравнения. Заменим неизвестную переменную получившимся результатом: Тождество верно.
Правило для уравнений доказано, Возьмём неравенство: Допустим, мы хотим перенести все иксы из левой части неравенства в правую. Вычтем из обеих частей. Слева сократится с , и иксов не останется. Справа сократится с и останется : Теперь можно привести подобные слагаемые: Следовательно, 4 — корень уравнения 5x+2=7x-6.
Так как для него тождество доказано, то и
Решение линейных уравнений 7 класс
Но нельзя делить на неизвестное!
Разберемся на примере, как использовать правило деления при решении линейных уравнений.
Число «4», которое стоит при «x», называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение. Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент «1».
Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы получить «1»?». Ответ очевиден, нужно разделить на «4». Используем и разделим левую и правую части уравнения на «4».
Не забудьте, что делить нужно и левую, и правую части.
Используем и решим линейное уравнение до конца.
Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент.
Решение уравнений
слагаемые, содержащие переменную, перенести в левую часть уравнения, а числа – в его правую часть, не забывая при переносе менять знаки на противоположные; 2) привести подобные слагаемые в левой и правой частях уравнения; 3) разделить число в правой части на коэффициент при переменной. Во всех рассмотренных нами примерах мы уравнения приводили к виду: Определение Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнением с одним неизвестным.
Итоги Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число.
Источник: //econsalting.ru/kak-perenosit-znaki-pri-reshenii-uravnenij-62471/
Меняется ли знак при переносе отрицательного числа в уравнении

Правило переноса слагаемого.
При решении и преобразовании уравнений зачастую возникает необходимость переноса слагаемого на другую сторону уравнения.
Заметим, что слагаемое может иметь как знак «плюс», так и знак «минус». Согласно правилу, перенося слагаемое в другую часть уравнения, нужно изменить знак на противоположный. Кроме того, правило работает и для неравенств.
Примеры переноса слагаемого: 5x+2=7x−6. Сначала переносим 5x из левой части уравнения в правую: 2=7x−6−5x. Далее переносим (−6) из правой части в левую: 2+6=7x−5x.
Обратите внимание, что знак «+» изменился на «-», а знак «-» на «+».
При этом не имеет значения, переносимое слагаемое число или переменная, либо выражение.
Правило переноса знака в уравнении
Если 3) Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство, т.е. Если 4) Если из одной части верного неравенства перенести в другую какое-либо слагаемое, изменив его знак на противоположный, то получится верное неравенство, т.е.
Если 5) Если обе части верного неравенства умножить на одно и то же положительное число, то получится верное неравенство.
Например, если 6) Если обе части верного неравенства умножить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
Например, если 7) Аналогично правилам 5) и 6) действуют правила для деления на одно и то же число.
Или 3) Неравенства одинаковых знаков с положительными членами можно почленно умножать.
Линейные неравенства. Исчерпывающий гид (2019)
Важное замечание!
Итак, надеюсь, ты уже знаком с линейными уравнениями, поэтому можно смело покорять неравенства! Если ты ознакомился с линейными уравнениями, то уже знаком с Васей, который раздавал яблоки своим друзьям.
Давай вернемся к примеру с Васей (может, и нам что-то перепадет?). Так вот, предположим, что у Васи больше, чем яблок. Все свои яблоки он хочет раздать поровну троим друзьям.
По сколько яблок получит каждый друг?
Если обозначить через количество яблок, которое достанется каждому из трех друзей, то получим следующее
Правило переноса знака в уравнении

Если 3) Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство, т.е.Если 4) Если из одной части верного неравенства перенести в другую какое-либо слагаемое, изменив его знак на противоположный, то получится верное неравенство, т.е.
Если 5) Если обе части верного неравенства умножить на одно и то же положительное число, то получится верное неравенство.
Например, если 6) Если обе части верного неравенства умножить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.Например, если 7) Аналогично правилам 5) и 6) действуют правила для деления на одно и то же число.
Если 1) Неравенства одинакового знака можно почленно складывать.Или 2) Неравенства противоположных знаков можно почленно вычитать, оставляя знак того неравенства, из которого производится вычитание.
Как решать линейные уравнения
Или 3) Неравенства одинаковых знаков с положительными членами можно почленно умножать.
4) Обе части неравенства с положительными членами можно возводить в одну и ту же натуральную степень.
Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на Раскрываем скобки.
Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках.
Если перед скобками стоит знак « », знаки не меняем.
Рассмотрим примеры решения таких линейных уравнений в 6 классе. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки: 5x-2x=7 11 (Чтобы лучше запомнить это правило, предлагаю следующую ассоциацию. В левой части «хозяин» — слагаемое с переменной, 5x.
«В гости» к нему приходит из правой части уравнения 2x. В левой части 2x имело знак « », при переносе знак изменяем на «-«. Его знак не меняем, так как это слагаемое остается в правой части. Его знак меняем на противоположный — был «-«, при переносе меняем его на « ».
) 3x=18 Это — 2) 12 — 7x=16x 3 Это — линейное уравнение.
Гостю надо снять обувь, в которой он пришел — не будет же он ходить в доме в обуви, в которой ходил по улице.
Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки: -7x-16x=3-12 -23x=-9 обе части уравнения делим на число, стоящее перед иксом: x=-9:(-23) При Ответ: 9/23.
Неизвестные переносим в одну сторону, известные — в другую с противоположными знаками: 15x-10x=-7-11 5x=-18 Обе части уравнения делим на число, стоящее перед иксом: x=-18:5 При делении чисел с разными знаками получаем отрицательное число.
При делении на 5 ответ записываем в виде десятичной дроби. Неизвестные переносим в одну сторону, известные — в другую, изменяя при переносе их знаки: -3y-4y=72-54 -7y=18 Обе части уравнения делим на число, стоящее перед игреком: y=18:(-7) При делении чисел с разными знаками получаем отрицательное число.
Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров.
В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число.
Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д.
Именно об уравнениях такого типа мы с вами поговорим.
Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др.
Все теоретические положения будем сразу пояснять на конкретных примерах.
RTB R-A-339285-1 В данном случае мы придаем вычитанию смысл, который является обратным смыслу сложения.
Иначе говоря, есть определенная связь между действиями сложения и вычитания, которую можно в буквенном виде выразить так: если .
Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму.
Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно.
Посмотрим, как применить данное правило на практике.
Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня.
Решение нашего простого уравнения, приведенного выше, правильно будет записать так: верное, значит, неизвестное слагаемое было найдено правильно.
Если бы равенство оказалось неверным, то нам следовало бы вернуться к решению и перепроверить его, поскольку это знак допущенной ошибки.
Как правило, чаще всего это бывает вычислительная ошибка или применение неверного правила.
Правила переноса знаков в уравнении

Слайд 5)
Какое правило мы используем при решении?
— Нахождение неизвестного множителя.
Запишем несколько уравнений в тетрадь и решим их используя правила нахождения неизвестного слагаемого и уменьшаемого: (Слайд 7)
А как решить такое уравнение?
х + 5 = — 2х – 7 (Слайд 8)
Упростить мы не можем, т. к. подобные слагаемые находятся в разных частях уравнения, следовательно, необходимо их перенести.
Горят причудливо краски, И как ни мудра голова, Вы все-таки верьте в сказки Сказка всегда права.
Давным-давно жили-были 2 короля: черный и белый. Черный король жил в Черном королевстве на правом берегу реки, а Белый король – в Белом на левом берегу. Между королевствами протекала очень бурная и опасная река. Переправиться через эту реку ни вплавь, ни на лодке было невозможно.
Внимание
Одним из наиболее часто используемых действий при решении уравнений в алгебре является перенос слагаемого. Общее правило гласит, что слагаемое можно перенести из одной части равенства в другую с переменой знака.
Так, для равенства
a+b=c-d
перенос разных слагаемых выглядит следующим образом:
a=c-d-b
b=c-d-a
a+b-c=-d
a+b+d=c
a+b-c+d=0
В исходном равенстве у a, b и c положительный знак, и они переносятся со знаком «минус», а d имеет отрицательный знак, поэтому, при переносе знак меняется на противоположный, «плюс».
Правила переноса слагаемых в уравнении
Примеры.
Вот тебе еще пару примеров для самостоятельной тренировки – определи, является ли уравнение линейным и если да, найди его корни:
Ответы:
1. Является.
2. Не является.
Раскроем скобки и приведем подобные слагаемые:
Произведем тождественное преобразование – разделим левую и правую часть на :
Мы видим, что уравнение не является линейным, так что искать его корни не нужно.
3. Является.
Произведем тождественное преобразование – умножим левую и правую часть на , чтобы избавиться от знаменателя.
Подумай, почему так важно, чтобы ? Если ты знаешь ответ на этот вопрос, переходим к дальнейшему решению уравнения, если нет – обязательно загляни в тему «ОДЗ», чтобы не наделать ошибок в более сложных примерах.
Важно
Ответ очевиден, нужно разделить на «4».
Используем правило деления и разделим левую и правую части уравнения на «4». Не забудьте, что делить нужно и левую, и правую части.
Используем сокращение дробей и решим линейное уравнение до конца.
Как решить уравнение, если «x» отрицательное
Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент.
Как, например, в уравнении ниже.
Чтобы решить такое уравнение, снова зададим себе вопрос: «На что нужно разделить «−2», чтобы получить «1»?». Нужно разделить на «−2».
Важно!
При делении на отрицательное число помните про правило знаков.
Примеры решения линейных уравнений
Рассмотрим другие примеры решения линейных уравнений.
Правила переноса знаков в уравнении реакции
По правилу переноса перенесем «4x» из левой части уравнения в правую, поменяв знак на противоположный.
Несмотря на то, что перед «4x» не стоит никакого знака, мы понимаем, что перед «4x» стоит знак «+».
Теперь приведем подобные и решим уравнение до конца.
Свойство № 2 или правило деления
Запомните!
В любом уравнении можно разделить левую и правую часть на одно и то же число.
Но нельзя делить на неизвестное!
Разберемся на примере, как использовать правило деления при решении линейных уравнений.
Число «4», которое стоит при «x», называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение.
Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент «1».
Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы получить «1»?».
1)
2) Пусть дано линейное уравнение: 5x + 2(10x + 32) = 100. Для того, чтобы его решить необходимо определить величину неизвестной x.
3) Первым шагом раскрываем скобки: 5x + 20x + 64 = 100.
4) Перенесем свободный член в правую часть с противоположным знаком, то есть если было 64, то станет — 64.
А также приведем подобные слагаемые в левой части уравнения (5x + 20x). Получаем: 25x = 100 — 64.
5) Считаем значение в правой части уравнения.
Получаем: 25x = 36.
6) Поделим обе части уравнения на коэффициент перед неизвестной, то есть на 25.
Правила переноса цифр в уравнении
Иначе говоря, f(x) = g(x) f(x) — g(x) = 0 что является частным случаем эквивалентности (1)(2).
Мы видим, что любое уравнение с одним неизвестным можно заменить эквивалентным уравнением вида h(х) = 0, т. е. уравнением, в левой части которого стоит некоторая функция, а правая часть равна нулю. Указанное преобразование (перенос членов из одной части уравнения в другую) применяется при решении уравнений чрезвычайно часто.
Линейные неравенства
Исчерпывающий гид (2019)
Ну вот и справились с неравенством! Сейчас я введу формализованное определение линейного неравенства и будем разбираться с ним дальше.
Линейные неравенства — это неравенства вида:
где и – любые числа, причем ; — неизвестная переменная.
Например: Все приведенные выше неравенства являются линейными.
Черное, то попадал в немилость Черного короля. Жителям королевств надо было что-то придумать, чтобы не гневить своих королей. Как вы считаете, что они придумали?
— Переходя мост они меняли цвет одежды на противоположный!
А теперь вернемся к нашим уравнениям и посмотрим, что происходит с числами при переходе через «мост» — из одной части равенства в другую.
— Числа меняют свои знаки на противоположные!
При переносе слагаемых из одной части уравнения в другую, знаки изменяем на противоположные!
Используя это правило, решим наше уравнение.
Договоримся, что в левой части у нас будут жить слагаемые, содержащие неизвестное, а в правой части, числа не содержащие буквенного множителя.
Смотрите еще:
- Средства тушения пожара и правила пользования ими § 6.
Основные понятия: уравнение, корень уравнения, решение
Правило переноса запятой в делении

Если дробь меньше единицы, значит, она описывает часть чего-то, если больше — несколько целых частей и еще кусочек. Дроби описываются 2 значениями: знаменателем, объясняющим, на сколько равных частей поделено число и числителем, который говорит о том, сколько таких частей мы имеем в виду.
В десятичной системе счисления значение каждой цифры зависит от разряда, в котором она записана. При этом единицы соседних разрядов отличаются в 10 раз.
Деление десятичных дробей столбиком
Задача перевода числа с основанием q1 в число с основанием q2 сводится к отыскиванию коэффициентов полинома нового основания.
Сразу скажем, что в результате деления конечной десятичной дроби на натуральное число может получиться или конечная десятичная дробь или бесконечная периодическая десятичная дробь.
Действительно, после того, как закончится деление всех отличных от 0 десятичных знаков делимой дроби, может получиться либо остаток 0 , и мы получим конечную десятичную дробь, либо остатки начнут периодически повторяться, и мы получим периодическую десятичную дробь.
При делении десятичной дроби на 10, 100, 1000 и т.д. просто переносим запятую влево настолько же знаков, сколько нулей в делителе.
Причем, если одним из чисел, с которыми проводится деление, является конечная или периодическая десятичная дробь, то она тоже округляются до того же разряда, что и непериодическая десятичная дробь.
В примере с пирогом знаменатель — 4, а в выражении «1 день — 1/7 недели» — 7. Дробное выражение с любым знаменателем представляет собой обыкновенную дробь.
При решении и преобразовании уравнений часто возникает потребность перенести слагаемое из одной стороны уравнения в другую. Необходимо отметить, что слагаемое может быть как со знаком «плюс», так и со знаком «минус».
Правило говорит, что при переносе слагаемого из одной части уравнения в другую необходимо поменять знак. Также правило работает и для неравенств.
Если ваш ребенок никак не может усвоить, как делить десятичные дроби, то это не повод считать его не способным к математике.
Две части уравнения по определению равны, поэтому можно вычесть из обеих частей уравнения одинаковое выражение, и равенство останется верным. По одну сторону знака «равно» оно сократится с тем, что было.
По другую сторону равенства, выражение, которое мы вычли, появится со знаком «минус».
Остаток сдвигается на один разряд влево (просто знаковую точку перенести вправо на один разряд), сносится последующий разряд делимого не участвующий до этого в делении.
Суть подхода к делению натурального числа на десятичную дробь и к делению десятичной дроби на натуральное число ничем не отличается от сути деления десятичных дробей. То есть, конечные и периодические дроби заменяются обыкновенными дробями, а бесконечные непериодические дроби округляются.
Работа с текстом учебника. Найдите и прочитайте в пункте 4.4 правила увеличения и уменьшения десятичных дробей в 10, 100, 1000.. раз.
В тех случаях, когда мат.
текст носит вспомогательный, справочный характер (например, теоретический материал в задачнике), нередко оказывается полезным перевести группу формул в таблицу, более наглядную и компактную по структуре.
В таблице 13.
1 вертикальными стрелками показаны сносы последующих разрядов делимого в промежуточные остатки. Горизонтальные стрелки отражают разряды записи результата в регистр частного Рг.С. Единицы переполнения, получаемые после суммирования, пропадают, т. к.
используется сумматор дополнительного кода. Вместо выполнения операции левого сдвига остатков, переносится на один разряд вправо точка, отделяющая знак числа, при этом, первый разряд знака пропадает. Что равносильно сдвигу.
Произведением десятичной дроби и натурального числа называется сумма слагаемых, равных этой десятичной дроби, а количество слагаемых равно натуральному числу.
Умножение двух десятичных дробей выполняется так:Числа перемножаются без учета запятых.Запятая в произведении ставится так, чтобы отделить справа столько же знаков, сколько отделено в обоих множителях вместе взятых.
Скорее всего, ему просто непонятно объяснили, как это делается. Нужно помочь ребенку и в максимально простой, почти игровой, форме рассказать ему о дробях и операциях с ними. А для этого надо и самим кое-что вспомнить.
Деление чисел с фиксированной запятой с восстановлением остатка — раздел Компьютеры, Компьютерная арифметика. Прикладная теория цифровых автоматов Деление Выполняется По Алгоритму С Восстановлением Остатка На Сумматоре Допол…
Из изложенных выше правил переноса следует, что многие слова можно переносить различными способами; при этом следует предпочитать такие переносы, при которых не разбиваются значащие части слова.
Найдем периметр квадрата со стороной 2,33 м. Он равен 2,33 + 2,33 + 2,33 + 2,33, то есть 9,32 м. Периметр равен сумме четырех слагаемых, каждое из которых равно 2,33 , или произведению числа 2,33и натурального числа 4.
Основы информатики. М. Высшая школа, 1991-235 с. 2.Савельев А.Я. Арифметические и логические основы цифровых автоматов. М.
В какую сторону и на сколько цифр надо перенести запятую, чтобы увеличить (уменьшить) десятичную дробь: в 10 раз; в 100 раз; в 1000 раз?
Деление конечных десятичных дробей на натуральные числа удобно проводить столбиком по аналогии с делением столбиком натуральных чисел . Приведем правило деления.
При умножении десятичной дроби на натуральное число, мы должны: перемножить числа, не обращая внимания на запятую;в полученном произведении поставить запятую так, чтобы справа от нее было столько же цифр, сколько в десятичной дроби.
Деление десятичных дробей на 0,1, 0,01, 0,001 и т.д
Допустим, вы разрезали пирог на 4 равных части и 1 из них отдали соседям. Знаменатель будет равен 4. А числитель зависит от того, что мы хотим описать.
Если мы рассказываем о том, сколько было отдано соседям, то числитель равен 1, а если речь идет о том, сколько осталось, то 3.
Сначала нужно округлить десятичные дроби, чтобы от деления бесконечной непериодической десятичной дроби перейти к делению конечных десятичных дробей. Мы можем провести округление до сотых: 0,779…≈0,78 и 1,5602≈1,56 .
В итоге решения примеров на умножение и деление десятичной дроби на разрядную единицу 10, 100, 1000 и т. д., учащиеся самостоятельно выводят правила;2.
Источник: //matrix66.ru/pravovye-stati/3311-pravilo-perenosa-zapyatoy-v-delenii.html
Уравнение правило переноса
Причём неважно, является ли переносимое слагаемое числом, переменной или же целым выражением. Перенесём первое слагаемое в правую сторону уравнения. Получим: Перенесём все числа в одну сторону. В итоге имеем: Допустим мы хотим перенести все иксы из левой части уравнения в правую.
Вычтем из обеих частей 5 x Теперь нужно проверить, совпадают ли левая и правая части уравнения.
Заменим неизвестную переменную получившимся результатом: Теперь можно привести подобные слагаемые: Следовательно, 4 — корень уравнения 5x+2=7x-6. Так как для него тождество доказано, то и для неравенств тоже, по определению. Две части уравнения по определению равны, поэтому можно вычесть из обеих частей уравнения одинаковое выражение, и равенство останется верным.
Линейные уравнения.
Решение линейных уравнений. Правило переноса слагаемого.
Именно поэтому не переносят (−3×2⋅2) и (7x).
Вычитать нужно выражение, которое в итоге нужно перенести в другую сторону.
Тогда по одну сторону знака «=» оно сократится с тем, что было. А по другую сторону равенства выражение, которое мы вычли, появится со знаком «-». Это правило зачастую используется для решения .
Для решения используются другие методы.
Основные приемы решения уравнений
Таким образом, (4) есть верное числовое равенство.
Но это означает, что a есть корень уравнения (2). Итак, каждый корень уравнения (1) является также корнем уравнения (2), т.
е. (1)
(2). Аналогично доказывается, что (2)(1).
Итак, мы доказали, что при переносе любого слагаемого из одной части уравнения в другую с противоположным знаком получается равносильное уравнение. В частности, мы можем, если нужно, перенести все слагаемые в одну часть уравнения. Иначе говоря, f(x) = g(x) f(x) — g(x) = 0 что является частным случаем эквивалентности (1)(2).
Мы видим, что любое уравнение с одним неизвестным можно заменить эквивалентным уравнением вида h(х) = 0, т. е. уравнением, в левой части которого стоит некоторая функция, а правая часть равна нулю. Указанное преобразование (перенос членов из одной части уравнения в другую) применяется при решении уравнений чрезвычайно часто.
Конспект урока по теме «Решение уравнений с переносом слагаемых из одной части в другую»
Задачи урока:- образовательные: создание условий для усвоения формирование вычислительных навыков с рациональными числами, формирование общеучебных и общекультурных навыков работы с информацией, формирование навыка применения решения уравнений.
— воспитательные: умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность, оценивать себя и своих товарищей- развивающие :развитие зрительной памяти, внимания, смысловой памяти, умение обрабатывать информацию и ранжировать ее по указанным основаниям, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Основные понятия: уравнение, корень уравнения, решение
Правила переносов
от слова, к которому он относится, но не от точки или запятой.
В тексте сноски знаки выравнивают и отбивают от начала текста на полукегельную.
Знак номера и параграфа применяют только к относящимся к ним числам и отбивают на полукегельную. Сдвоенные знаки между собой не отбивают.
Если к знаку относится несколько чисел, то между собой их отбивают на полукегельную, а если эти числа разделены запятыми — пробелом в 3 п.
В журнальных, газетных, информационных изданиях и изданиях оперативной полиграфии во всех перечисленных случаях допустимы отбивки междусловными пробелами. Знаки процента и промилле применяют только с относящимися к ним числами без отбивки.
Источник: //27advokat.ru/pravila-perenosa-znakov-v-uravnenii-48094/
Перенос знаков в уравнении правило 5 класс
Основы алгебры/Правило переноса слагаемого
При решении и преобразовании уравнений часто возникает потребность перенести слагаемое из одной стороны уравнения в другую. Необходимо отметить, что слагаемое может быть как со знаком «плюс», так и со знаком «минус». Правило говорит, что при переносе слагаемого из одной части уравнения в другую необходимо поменять знак.
Перенесём сначала из левой части уравнения в правую: .

Также правило работает и для неравенств.

Теперь перенесём число (−6) из правой части в левую: 2+6=7x-5x Заметьте, знак плюс поменялся на минус, а знак минус — на плюс. Причём неважно, является ли переносимое слагаемое числом, переменной или же целым выражением. Перенесём первое слагаемое в правую сторону уравнения. Получим: Отметим, что в этом примере слагаемым являлось целое выражение .
При этом нельзя отдельно переносить или , поскольку это лишь составные части слагаемого. По той же причине нельзя переносить или .
Но можно раскрыть скобку и получить два слагаемых: и . Такие два слагаемых уже можно переносить по отдельности.
- Точно также можно преобразовывать неравенства. Например:
Перенесём все числа в одну сторону.
В итоге имеем: или Две части уравнения по определению равны, поэтому можно вычесть из обеих частей уравнения одинаковое выражение, и равенство останется верным.
По одну сторону знака «равно» оно сократится с тем, что было. По другую сторону равенства, выражение, которое мы вычли, появится со знаком «минус». Возьмём уравнение: Допустим мы хотим перенести все иксы из левой части уравнения в правую.
Вычтем из обеих частей хлеб Слева сократится с , и иксов не останется.
Справа сократится с , и останется : Теперь можно привести подобные слагаемые: Теперь нужно проверить, совпадают ли левая и правая части уравнения.
Заменим неизвестную переменную получившимся результатом: Тождество верно. Правило для уравнений доказано, Возьмём неравенство: Допустим, мы хотим перенести все иксы из левой части неравенства в правую. Вычтем из обеих частей. Слева сократится с , и иксов не останется.
Справа сократится с и останется : Теперь можно привести подобные слагаемые: Следовательно, 4 — корень уравнения 5x+2=7x-6. Так как для него тождество доказано, то и для неравенств тоже, по определению.
Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач. С помощью уравнений описываются различные процессы, протекающие в природе.
Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Предварительные навыки Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти.
Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство. Например выражение 3 + 2 = 5 является равенством.
При вычислении левой части получается верное числовое равенство 5 = 5. А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x, значение которой можно найти.
Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство. Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет Говорят, что число 2 является корнем или решением уравнения 3 + x = 5 Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет. Переменную, входящую в уравнение, иначе называют неизвестным.
Вы вправе называть как вам удобнее. Это синонимы. Примечание. Словосочетание «решить уравнение» говорит самó за себя.

Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части. Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Рассмотрим следующее выражение: 8 + 2 Данное выражение является суммой чисел 8 и 2.
Значение данного выражения равно 10 8 + 2 = 10 Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство.
К примеру, выразим число 2. Чтобы выразить число 2, нужно задать вопрос:
«что нужно сделать с числами 10 и 8, чтобы получить число 2»
.
Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8. Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8: 2 = 10 − 8 Мы выразили число 2 из равенства 8 + 2 = 10.
Как видно из примера, ничего сложного в этом нет. При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть».
Решение уравнений
Меню
Вход / / / / В этом уроке мы закрепим навыки решения уравнений.
Покажем решение уравнения способом переноса слагаемых из одной части в другую, изменив при этом их знаки. Сформулируем алгоритм решения уравнения, содержащего подобные слагаемые.
Введем понятие линейного уравнения. Вам уже много раз приходилось решать различные уравнения. Давайте вспомним, что же называется уравнением.
Определение Уравнение – это равенство, содержащее переменную, значение которой надо найти. Значение переменной, при котором из уравнения получается верное числовое равенство, называют корнем уравнения. Решить уравнение – значит найти все его корни, или убедиться, что уравнение не имеет корней.
Разберёмся, как же решают уравнения. Итак, первое уравнение Но можно решить это уравнение другим способом. Обычно в таком случае говорят, что обе части уравнения разделили на 5.
Второе уравнение: То же самое мы бы получили, если бы воспользовались правилом отыскания неизвестного множителя.
Сделаем вывод: Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число. Третье уравнение: Это уравнение можно переписать так: Следующее уравнение:

Сделаем вывод: Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак. И решим ещё одно уравнение: Чтобы решить уравнение, содержащее подобные слагаемые нужно: 1) слагаемые, содержащие переменную, перенести в левую часть уравнения, а числа – в его правую часть, не забывая при переносе менять знаки на противоположные; 2) привести подобные слагаемые в левой и правой частях уравнения; 3) разделить число в правой части на коэффициент при переменной.
Во всех рассмотренных нами примерах мы уравнения приводили к виду: Определение Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнением с одним неизвестным. Итоги Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число.
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
Чтобы решить уравнение, содержащее подобные слагаемые нужно: 1) слагаемые, содержащие переменную, перенести в левую часть уравнения, а числа – в его правую часть, не забывая при переносе менять знаки на противоположные; 2) привести подобные слагаемые в левой и правой частях уравнения; 3) разделить число в правой части на коэффициент при переменной.
Уравнение вида ах = b, где а ≠ 0 называют линейным уравнением.
0
4111
Уравнение правило переноса
Оглавление: Уравнение — это равенство, содержащее букву, значение которой надо найти. В уравнениях неизвестное обычно обозначается строчной латинской буквой.
Чаще всего используют буквы « x » [икс] и « y » [игрек].
- Решить уравнение — значит найти все его корни или убедиться, что корней нет.
- Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.
Решив уравнение, всегда после ответа записываем проверку. Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа». Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления.

Методы решения уравнений для 5 класса приведены ниже. Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака. Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке «Законы арифметики».
Как найти неизвестноеслагаемое Как найти неизвестноеуменьшаемое Как найти неизвестноевычитаемое Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность. x + 9 = 15x = 15 − 9x = 6 Проверка x − 14 = 2x = 14 + 2x = 16 Проверка 16 − 2 = 1414 = 14 5 − x = 3x = 5 − 3x = 2 Проверка Как найти неизвестныймножитель Как найти неизвестноеделимое Как найти неизвестныйделитель Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Чтобы найти неизвестный делитель, надо делимое разделить на частное. y · 4 = 12y = 12 : 4y = 3 Проверка y : 7 = 2y = 2 · 7y = 14 Проверка 8 : y = 4y = 8 : 4y = 2 Проверка Перенесём сначала 5x из левой части уравнения в правую: Теперь перенесём число (−6) из правой части в левую: Заметьте, знак плюс поменялся на минус, а знак минус — на плюс.
Причём неважно, является ли переносимое слагаемое числом, переменной или же целым выражением. Перенесём первое слагаемое в правую сторону уравнения. Получим: Перенесём все числа в одну сторону.
В итоге имеем: Допустим мы хотим перенести все иксы из левой части уравнения в правую.
Вычтем из обеих частей 5 x Теперь нужно проверить, совпадают ли левая и правая части уравнения.
Заменим неизвестную переменную получившимся результатом: Теперь можно привести подобные слагаемые: Следовательно, 4 — корень уравнения 5x+2=7x-6. Так как для него тождество доказано, то и для неравенств тоже, по определению. Две части уравнения по определению равны, поэтому можно вычесть из обеих частей уравнения одинаковое выражение, и равенство останется верным.
По одну сторону знака «равно» оно сократится с тем, что было. По другую сторону равенства, выражение, которое мы вычли, появится со знаком «минус».
Правило для уравнений доказано. Внимание! Предварительный
Правила переноса знаков в уравнении
» Жилищное право Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш.
Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера». Раз уж ты оказался на этой теме, то ты наверняка уже знаком с темой «Линейные уравнения».
Если нет, то лучше скорей отправляйся исправлять это недоразумение. Без усвоенной темы «Линейные уравнения» спокойное плавание в «Линейных неравенствах» не гарантировано.
Итак, надеюсь, ты уже знаком с линейными уравнениями, поэтому можно смело покорять неравенства!
Если ты ознакомился с линейными уравнениями, то уже знаком с Васей, который раздавал яблоки своим друзьям. Давай вернемся к примеру с Васей (может, и нам что-то перепадет?). Так вот, предположим, что у Васи больше, чем яблок.
Все свои яблоки он хочет раздать поровну троим друзьям. По сколько яблок получит каждый друг? Если обозначить через количество яблок, которое достанется каждому из трех друзей, то получим следующее линейное неравенство: Дальше мы делим обе части составленного неравенства на и получаем: Таким образом, каждый друг щедрого Васи получит больше, чем яблока.
Ну вот и справились с неравенством!
Сейчас я введу формализованное определение линейного неравенства и будем разбираться с ним дальше. Линейные неравенства – это неравенства вида:где и – любые числа, причем ; – неизвестная переменная. Например: Все приведенные выше неравенства являются линейными.
Во всех них «сидит» очень важная особенность: в таких неравенствах нет иксов в квадрате, в кубе и т.д., кроме того в этих неравенствах нет деления на икс и икс не находится под знаком корня. Чтобы лучше распознавать линейные неравенства, настоятельно рекомендую тебе еще раз заглянуть в раздел «Скрытые» линейные уравнения или…» темы «Линейные уравнения.
Начальный уровень.». Линейные неравенства обладают не меньшим талантом «скрываться». Чтобы не попасть впросак и с легкостью преобразовывать любые неравенства надо знать и успешно применять 3 очень важных правила. Эти знания здорово упростят тебе жизнь на пути в решении неравенств.
Два неравенства равносильны, если они имеют одинаковые решения.
Решить неравенство – значит найти все значения переменной, при которых неравенство обращается в верное числовое неравенство.
Для упрощения процесса нахождения всех корней неравенства проводятся равносильные преобразования, то есть проводится замена данного неравенства более простым, при этом не должны потеряться никакие решения и не должно возникнуть никаких посторонних корней.
В общем, это все пока только слова. Давай разбираться прямо на правилах.

ПРАВИЛО 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные). Например, Таким образом, можно с уверенностью сказать, что равносильно . Или вот такой пример: В теме «Линейные уравнения» говорилось, что для удобства принято переносить слагаемые с переменной в левую часть, а остальные в правую – так и поступим: Здесь все должно быть понятно, перейдем к следующему правилу.
ПРАВИЛО 2.
Правила переноса в уравнениях
Оглавление: Для решения линейных уравнений используют два основных правила (свойства). При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный . Давайте разберём правило переноса на примере.
Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть. Перенесем число « 3 » из левой части уравнения в правую. Так как в левой части уравнения у числа « 3 » был знак « + », значит в правую часть уравнения « 3 » перенесется со знаком « − ».
Полученное числовое значение « x = 2 » называют корнем уравнения. Не забывайте после решения любого уравнения записывать ответ. Рассмотрим другое уравнение. По правилу переноса перенесем « 4x » из левой части уравнения в правую, поменяв знак на противоположный.
Несмотря на то, что перед « 4x » не стоит никакого знака, мы понимаем, что перед « 4x » стоит знак « + ». Теперь приведем подобные и решим уравнение до конца.
В любом уравнении можно разделить левую и правую часть на одно и то же число .
Но нельзя делить на неизвестное! Разберемся на примере, как использовать правило деления при решении линейных уравнений. Число « 4 », которое стоит при « x », называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение. Чтобы решить уравнение необходимо сделать так, чтобы при « x » стоял коэффициент « 1 ».
Давайте зададим себе вопрос: «На что нужно разделить « 4 », чтобы получить « 1 »?». Ответ очевиден, нужно разделить на « 4 ».
Используем правило деления и разделим левую и правую части уравнения на « 4 ». Не забудьте, что делить нужно и левую , и правую части.
Используем сокращение дробей и решим линейное уравнение до конца.
Часто в уравнениях встречается ситуация, когда при « x » стоит отрицательный коэффициент. Как, например, в уравнении ниже.
Чтобы решить такое уравнение, снова зададим себе вопрос: «На что нужно разделить « −2 », чтобы получить « 1 »?». Нужно разделить на « −2 ». Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ? 1. Линейное уравнение Это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна .
2. Линейное уравнение с одной переменной имеет вид: , где и – любые числа ; 3. Линейное уравнение с двумя переменными имеет вид: , где , и – любые числа . 4. Тождественные преобразования Чтобы определить является ли уравнение линейным или нет, необходимо произвести тождественные преобразования: перенести влево/вправо подобные члены, не забыв изменить знак; умножить/разделить обе части уравнения на одного и тоже число.
Все мы с детства знаем такую задачу: «У Васи есть яблок.
Мальчик решил поделиться яблоками с друзьями.
Сколько яблок досталось каждому другу?» Каждый из нас, не задумываясь, ответит: «Каждому другу досталось по яблока».
А вот теперь я предлагаю все же задуматься… Да-да.
Оказывается, отвечая на такой простой вопрос ты в голове решаешь линейное уравнение!
Смотри:
Решение уравнений, правило переноса слагаемых
с – 3,6 = — 8 А как решить такое уравнение? х + 5 = — 2х – 7 (Слайд 8) Упростить мы не можем, т. к. подобные слагаемые находятся в разных частях уравнения, следовательно, необходимо их перенести.
(Слайд 9) Горят причудливо краски, И как ни мудра голова, Вы все-таки верьте в сказки Сказка всегда права. Асадов СКАЗКА. Давным-давно жили-были 2 короля: черный и белый.
Черный король жил в Черном королевстве на правом берегу реки, а Белый король – в Белом на левом берегу. Между королевствами протекала очень бурная и опасная река.
Переправиться через эту реку ни вплавь, ни на лодке было невозможно.
Нужен был мост! Строительство моста шло очень долго, и вот, наконец, мост построили. Всем бы радоваться и общаться друг с другом, но вот беда: Белый король не любил черный цвет, все жители его королевства носили светлые одежды, а Черный король не любил белый цвет и, жители его королевства носили одежды темного цвета. Если кто-то из Черного королевства переходил в Белое, то сразу попадал в немилость Белого короля, а, если кто-то из Белого королевства переходил в Черное, то попадал в немилость Черного короля.
Жителям королевств надо было что-то придумать, чтобы не гневить своих королей. Как вы считаете, что они придумали?
(Ответы детей) — Переходя мост они меняли цвет одежды на противоположный!
А теперь вернемся к нашим уравнениям и посмотрим, что происходит с числами при переходе через «мост» — из одной части равенства в другую. — Числа меняют свои знаки на противоположные!
Правило. При переносе слагаемых из одной части уравнения в другую, знаки изменяем на противоположные! Используя это правило, решим наше уравнение.
Договоримся, что в левой части у нас будут жить слагаемые, содержащие неизвестное, а в правой части, числа не содержащие буквенного множителя.
х + 5 = — 2х – 7 х + 2х = — 7 – 5 3х = -12 х = -12 : 3 х = — 4 Решим еще несколько уравнений: (Слайд 12) 7х = х – 12 8у + 9 = 33 6х – 5 = 4х + 8 27 + 3у = 10 у + 6 Во всех рассмотренных примерах мы приводили данные уравнения к виду ах= в, где а≠ 0. Уравнение вида ах = в, где а ≠0 называется линейным уравнением с одним неизвестным. Решаем N 1316 Домашнее задание §8 п.
42 N 1342 (а, б) Итог урока (Слайд 16) я познакомился с .- было непросто .- я добился .- у меня получилось .- хотелось бы .- мне запомнилось .- я попробую .
«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать уравнения, то решайте их»
Д.Пойа Упростить выражения: 1).
3х + х 2). 4а + 3а – а 3). 7m + 8n – 5 m – 3n 4).
– 6a + 12 b – 5a – 12b 5). 9x – 0,6y – 14x + 1,2y = 4x = 6a = 2 m +5n = — 11a = — 5x + 0,6y Уравнение пришло, тайн немало принесло.
Какие выражения являются уравнениями? 3,6 + k = 40 2х – 0,7 = 3,5 9,8 + ( 13,5 + x) 8,2 + 1,6 m – 10 3(4,8 – 1,6) = 9,6 3(a + 4) = 6,4 — 5 x 0,4 y Уравнение равенство, содержащее неизвестное число.
Решить уравнение – значит найти его корни или доказать, что их нет. Решить уравнение.
Основы алгебры/Правило переноса слагаемого
При решении и преобразовании уравнений часто возникает потребность перенести слагаемое из одной стороны уравнения в другую. Необходимо отметить, что слагаемое может быть как со знаком «плюс», так и со знаком «минус».
Правило говорит, что при переносе слагаемого из одной части уравнения в другую необходимо поменять знак. Также правило работает и для неравенств.
Перенесём сначала из левой части уравнения в правую: . Теперь перенесём число (−6) из правой части в левую: 2+6=7x-5x Заметьте, знак плюс поменялся на минус, а знак минус — на плюс.
Причём неважно, является ли переносимое слагаемое числом, переменной или же целым выражением. Перенесём первое слагаемое в правую сторону уравнения.
Получим: Отметим, что в этом примере слагаемым являлось целое выражение . При этом нельзя отдельно переносить или , поскольку это лишь составные части слагаемого.
По той же причине нельзя переносить или .
Но можно раскрыть скобку и получить два слагаемых: и . Такие два слагаемых уже можно переносить по отдельности.
- Точно также можно преобразовывать неравенства. Например:
Перенесём все числа в одну сторону.
В итоге имеем: или Две части уравнения по определению равны, поэтому можно вычесть из обеих частей уравнения одинаковое выражение, и равенство останется верным. По одну сторону знака «равно» оно сократится с тем, что было. По другую сторону равенства, выражение, которое мы вычли, появится со знаком «минус».
Возьмём уравнение: Допустим мы хотим перенести все иксы из левой части уравнения в правую. Вычтем из обеих частей хлеб Слева сократится с , и иксов не останется.
Справа сократится с , и останется : Теперь можно привести подобные слагаемые: Теперь нужно проверить, совпадают ли левая и правая части уравнения. Заменим неизвестную переменную получившимся результатом: Тождество верно.
Правило для уравнений доказано, Возьмём неравенство: Допустим, мы хотим перенести все иксы из левой части неравенства в правую.
Вычтем из обеих частей. Слева сократится с , и иксов не останется.
Справа сократится с и останется : Теперь можно привести подобные слагаемые: Следовательно, 4 — корень уравнения 5x+2=7x-6. Так как для него тождество доказано, то и для неравенств тоже, по определению.
Основы алгебры/Правило переноса слагаемого
При решении и преобразовании уравнений часто возникает потребность перенести слагаемое из одной стороны уравнения в другую.
Необходимо отметить, что слагаемое может быть как со знаком «плюс», так и со знаком «минус».
Правило говорит, что при переносе слагаемого из одной части уравнения в другую необходимо поменять знак. Также правило работает и для неравенств.
Перенесём сначала из левой части уравнения в правую: .
Теперь перенесём число (−6) из правой части в левую: 2+6=7x-5x Заметьте, знак плюс поменялся на минус, а знак минус — на плюс.
Причём неважно, является ли переносимое слагаемое числом, переменной или же целым выражением.
Перенесём первое слагаемое в правую сторону уравнения.
Получим: Отметим, что в этом примере слагаемым являлось целое выражение . При этом нельзя отдельно переносить или , поскольку это лишь составные части слагаемого.
По той же причине нельзя переносить или . Но можно раскрыть скобку и получить два слагаемых: и . Такие два слагаемых уже можно переносить по отдельности.
- Точно также можно преобразовывать неравенства. Например:
Перенесём все числа в одну сторону.
В итоге имеем: или Две части уравнения по определению равны, поэтому можно вычесть из обеих частей уравнения одинаковое выражение, и равенство останется верным. По одну сторону знака «равно» оно сократится с тем, что было. По другую сторону равенства, выражение, которое мы вычли, появится со знаком «минус».
Возьмём уравнение: Допустим мы хотим перенести все иксы из левой части уравнения в правую.
Вычтем из обеих частей хлеб Слева сократится с , и иксов не останется.
Справа сократится с , и останется : Теперь можно привести подобные слагаемые: Теперь нужно проверить, совпадают ли левая и правая части уравнения.
Заменим неизвестную переменную получившимся результатом: Тождество верно. Правило для уравнений доказано, Возьмём неравенство: Допустим, мы хотим перенести все иксы из левой части неравенства в правую.
Вычтем из обеих частей. Слева сократится с , и иксов не останется.
Справа сократится с и останется : Теперь можно привести подобные слагаемые: Следовательно, 4 — корень уравнения 5x+2=7x-6. Так как для него тождество доказано, то и для неравенств тоже, по определению.
Линейные уравнения для 5 класса
Одним из самых важных навыков при поступлении в 5 класс является умение решать простейшие уравнения. Так как 5 класс ещё не так далек от начальной школы, то и видов уравнений, которые может решать ученик не так уж и много. Мы познакомим Вас со всеми основными видами уравнений, которые необходимо уметь решать, если Вы хотите поступить в физико-математическую школу.
1 тип: «луковичные» Это уравнения, которые почти со

вероятностью встретятся Вам при поступлении в любую школу или кружок 5 класса как отдельное задание. Их легко отличить от других: в них переменная присутствует только 1 раз.
Например,

или

.
Решаются они очень просто: необходимо просто «добраться» до неизвестной, постепенно «снимая» всё лишнее, что окружает её — как будто почистить луковицу — отсюда и такое название. Для решения достаточно помнить несколько правил из второго класса.
Перечислим их все: Сложение
- слагаемое1 + слагаемое2 = сумма
- слагаемое1 = сумма — слагаемое2
- слагаемое2 = сумма — слагаемое1
Вычитание
- уменьшаемое — вычитаемое = разность
- уменьшаемое = вычитаемое + разность
- вычитаемое = уменьшаемое — разность
Умножение
- множитель1 = произведение : множитель2
- множитель2 = произведение : множитель1
- множитель1 * множитель2 = произведение
Деление
- делимое = делитель * частное
- делитель = делимое : частное
- делимое : делитель = частное
Разберём на примере, как применять данные правила.

Заметим, что мы делим

на

и получаем . В этой ситуации мы знаем делитель и частное.
Чтобы найти делимое, нужно делитель умножить на частное:

Мы стали немного ближе к самому

. Теперь мы видим, что к

прибавляется

и получается

.
Значит, чтобы найти одно из слагаемых, нужно из суммы вычесть известное слагаемое:

И ещё один «слой» снят с неизвестной!
Теперь
Решение линейных уравнений 7 класс
Для решения линейных уравнений используют два основных правила (свойства). Запомните!
При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный. Давайте разберём правило переноса на примере.
Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть.
Перенесем число «3» из левой части уравнения в правую. Так как в левой части уравнения у числа «3» был знак «+», значит в правую часть уравнения «3» перенесется со знаком «−».
Полученное числовое значение «x = 2» называют корнем уравнения. Важно!
Не забывайте после решения любого уравнения записывать ответ. Рассмотрим другое уравнение. 5x = 4x + 9 По перенесем «4x» из левой части уравнения в правую, поменяв знак на противоположный.
Несмотря на то, что перед «4x» не стоит никакого знака, мы понимаем, что перед «4x» стоит знак «+». 5x = 4x + 9 5x = +4x + 9 5x − 4x = 9 Теперь и решим уравнение до конца.
5x − 4x = 9 x = 9 Ответ: x = 9 Запомните! В любом уравнении можно разделить левую и правую часть на одно и то же число.
Но нельзя делить на неизвестное! Разберемся на примере, как использовать правило деления при решении линейных уравнений.
Число «4», которое стоит при «x», называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение. Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент «1».
Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы получить «1»?».
Ответ очевиден, нужно разделить на «4».
Используем и разделим левую и правую части уравнения на «4».
Не забудьте, что делить нужно и левую, и правую части.
Используем и решим линейное уравнение до конца.
Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент.
Как, например, в уравнении ниже.
−2x = 10 Чтобы решить такое уравнение, снова зададим себе вопрос: «На что нужно разделить «−2», чтобы получить «1»?». Нужно разделить на «−2». −2x = 10 |:(−2) −2x−2 = 10−2 x = −5 Ответ: x = −5 Важно!
При делении на отрицательное число помните про . Рассмотрим другие примеры решения линейных уравнений.
Обычно для решения уравнений нужно применять оба свойства ( и ).
Также требуется вспомнить и .
25x − 1 = 9 25x = 9 + 1 25x = 10 |: 25 25×25 = 1025 x = 25 Ответ: x = 25 11(y − 4) + 10(5 − 3y) − 3(4 − 3y) =
Решение линейных уравнений 7 класс
Для решения линейных уравнений используют два основных правила (свойства). Запомните!
При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный.
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть.
Перенесем число «3» из левой части уравнения в правую.
Так как в левой части уравнения у числа «3» был знак «+», значит в правую часть уравнения «3» перенесется со знаком «−».
Полученное числовое значение «x = 2» называют корнем уравнения. Важно!
Не забывайте после решения любого уравнения записывать ответ.
Рассмотрим другое уравнение. 5x = 4x + 9 По перенесем «4x» из левой части уравнения в правую, поменяв знак на противоположный.
Несмотря на то, что перед «4x» не стоит никакого знака, мы понимаем, что перед «4x» стоит знак «+». 5x = 4x + 9 5x = +4x + 9 5x − 4x = 9 Теперь и решим уравнение до конца.
5x − 4x = 9 x = 9 Ответ: x = 9 Запомните!
В любом уравнении можно разделить левую и правую часть на одно и то же число. Но нельзя делить на неизвестное! Разберемся на примере, как использовать правило деления при решении линейных уравнений.
Число «4», которое стоит при «x», называют числовым коэффициентом при неизвестном.
Между числовым коэффициентом и неизвестном всегда стоит действие умножение. Чтобы решить уравнение необходимо сделать так, чтобы при «x» стоял коэффициент «1».
Давайте зададим себе вопрос: «На что нужно разделить «4», чтобы получить «1»?». Ответ очевиден, нужно разделить на «4». Используем и разделим левую и правую части уравнения на «4».
Не забудьте, что делить нужно и левую, и правую части.
Используем и решим линейное уравнение до конца.
Часто в уравнениях встречается ситуация, когда при «x» стоит отрицательный коэффициент.
Как, например, в уравнении ниже. −2x = 10 Чтобы решить такое уравнение, снова зададим себе вопрос: «На что нужно разделить «−2», чтобы получить «1»?». Нужно разделить на «−2». −2x = 10 |:(−2) −2x−2 = 10−2 x = −5 Ответ: x = −5 Важно!
При делении на отрицательное число помните про .
Рассмотрим другие примеры решения линейных уравнений.
Обычно для решения уравнений нужно применять оба свойства ( и ).
Как переносить знаки при решении уравнений
Как в уравнениях переносить знаки

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: Раз уж ты оказался на этой теме, то ты наверняка уже знаком с темой «Линейные уравнения».
Если нет, то лучше скорей отправляйся исправлять это недоразумение. Без усвоенной темы спокойное плавание в «Линейных неравенствах» не гарантировано. Итак, надеюсь, ты уже знаком с линейными уравнениями, поэтому можно смело покорять неравенства!
Если ты ознакомился с линейными уравнениями, то уже знаком с Васей, который раздавал яблоки своим друзьям. Давай вернемся к примеру с Васей (может, и нам что-то перепадет?).
Так вот, предположим, что у Васи больше, чем яблок. Все свои яблоки он хочет раздать поровну троим друзьям.
По сколько яблок получит каждый друг? Если обозначить через количество яблок, которое достанется каждому из трех друзей, то получим следующее
Решение линейных уравнений 7 класс
Для решения линейных уравнений используют два основных правила (свойства). Запомните!
При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный.
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть.
Перенесем число «3» из левой части уравнения в правую. Так как в левой части уравнения у числа «3» был знак «+», значит в правую часть уравнения «3» перенесется со знаком «−».Полученное числовое значение «x = 2» называют корнем уравнения. Важно!
Не забывайте после решения любого уравнения записывать ответ.Линейные уравнения. Решение линейных уравнений.Правило переноса слагаемого.
Правило переноса слагаемого.
При решении и преобразовании уравнений зачастую возникает необходимость переноса слагаемого на другую сторону уравнения. Заметим, что слагаемое может иметь как знак «плюс», так и знак «минус». Согласно правилу, перенося слагаемое в другую часть уравнения, нужно изменить знак на противоположный. Кроме того, правило работает и для неравенств.
Примеры переноса слагаемого: 5x+2=7x−6. Сначала переносим 5x из левой части уравнения в правую: 2=7x−6−5x.
Далее переносим (−6) из правой части в левую: 2+6=7x−5x. Обратите внимание, что знак «+» изменился на «-», а знак «-» на «+». При этом не имеет значения, переносимое слагаемое число или переменная, либо выражение.
−3×2(2+7x)−4+y=0. Переносим 1-е слагаемое в правую сторону уравнения.
Получаем: −4+y=3×2(2+7x). Обратите внимание, что в нашем примере слагаемое — это выражение (−3×2(2+7x)).
Поэтому нельзя отдельно переносить (−3×2) и (2+7x), так как это составляющие слагаемого.
Правила переноса в уравнениях
Для решения линейных уравнений используют два основных правила (свойства). При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный .
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть. Перенесем число « 3 » из левой части уравнения в правую. Так как в левой части уравнения у числа « 3 » был знак « + », значит в правую часть уравнения « 3 » перенесется со знаком « − ». Полученное числовое значение « x = 2 » называют корнем уравнения.
Не забывайте после решения любого уравнения записывать ответ.Рассмотрим другое уравнение. По правилу переноса перенесем « 4x » из левой части уравнения в правую, поменяв знак на противоположный. Несмотря на то, что перед « 4x » не стоит никакого знака, мы понимаем, что перед « 4x » стоит знак « + ».
Решение уравнений, правило переноса слагаемых
с – 3,6 = — 8 А как решить такое уравнение? х + 5 = — 2х – 7 (Слайд 8) Упростить мы не можем, т.
к. подобные слагаемые находятся в разных частях уравнения, следовательно, необходимо их перенести.
(Слайд 9) Горят причудливо краски, И как ни мудра голова, Вы все-таки верьте в сказки Сказка всегда права. Асадов СКАЗКА. Давным-давно жили-были 2 короля: черный и белый. Черный король жил в Черном королевстве на правом берегу реки, а Белый король – в Белом на левом берегу. Между королевствами протекала очень бурная и опасная река.
Переправиться через эту реку ни вплавь, ни на лодке было невозможно. Нужен был мост! Строительство моста шло очень долго, и вот, наконец, мост построили.
Всем бы радоваться и общаться друг с другом, но вот беда: Белый король не любил черный цвет, все жители его королевства носили светлые одежды, а Черный король не любил белый цвет и, жители его королевства носили одежды темного цвета.
Как репетитор по математике борется с ошибками переноса слагаемых
Мне очень часто доводилось исправлять ученические ошибки, казалось бы не поддающихся какому-либо разумному объяснению и анализу. Опытному репетитору по математике хорошо знакомы ситуации, когда дети совершают промахи в казалось бы, в совершенно простых ситуациях.
«Как тут можно ошибиться», — спросит начинающий репетитор? Кажется, что выполнить задание правильно куда проще, чем вносить какие-то необъяснимые и нелогичные изменения в записанное.
Профессия «репетитор по математике» — очень сложное ремесло, однако это не должно пугать или оправдывать неудачи.
Хороший репетитор находиться в постоянном поиске причин появления ошибок, пробует новые и совершенствует испытанные подходы к их устранению.
Как минимизировать частоту появления ошибок? Рассмотрим типичную проблему при работе репетитора по математике в 6 классе с очень слабым учеником: при решении линейного уравнения школьник хронически ошибается в переносах слагаемых из одной части равенства в другую.
Основы алгебры/Правило переноса слагаемого
При решении и преобразовании уравнений часто возникает потребность перенести слагаемое из одной стороны уравнения в другую.
Необходимо отметить, что слагаемое может быть как со знаком «плюс», так и со знаком «минус». Правило говорит, что при переносе слагаемого из одной части уравнения в другую необходимо поменять знак.
Также правило работает и для неравенств.
Перенесём сначала из левой части уравнения в правую: .
Теперь перенесём число (−6) из правой части в левую: 2+6=7x-5x Заметьте, знак плюс поменялся на минус, а знак минус — на плюс. Причём неважно, является ли переносимое слагаемое числом, переменной или же целым выражением.
Перенесём первое слагаемое в правую сторону уравнения. Получим: Отметим, что в этом примере слагаемым являлось целое выражение . При этом нельзя отдельно переносить или , поскольку это лишь составные части слагаемого.По той же причине нельзя переносить или .
Линейные уравнения. Полное руководство (2019)
Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш.
Как это сделать в твоем браузере написано здесь: Все мы с детства знаем такую задачу: «У Васи есть яблок. Мальчик решил поделиться яблоками с друзьями.
Сколько яблок досталось каждому другу?» Каждый из нас, не задумываясь, ответит: «Каждому другу досталось по яблока». А вот теперь я предлагаю все же задуматься… Да-да.
Оказывается, отвечая на такой простой вопрос ты в голове решаешь линейное уравнение! Смотри: или в устной форме – трем друзьям дали по яблок из расчета, что всего в наличии у Васи яблок. Соответственно, дальше ты находишь путем деления произведения на известный тебе множитель: И вот ты уже решил линейное уравнение Теперь дадим этому термину математическое определение.
Линейное уравнение – это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна .
Решение уравнений
Меню
Вход / / / / В этом уроке мы закрепим навыки решения уравнений.
Покажем решение уравнения способом переноса слагаемых из одной части в другую, изменив при этом их знаки. Сформулируем алгоритм решения уравнения, содержащего подобные слагаемые.
Введем понятие линейного уравнения.
Вам уже много раз приходилось решать различные уравнения. Давайте вспомним, что же называется уравнением. Определение Уравнение – это равенство, содержащее переменную, значение которой надо найти.
Значение переменной, при котором из уравнения получается верное числовое равенство, называют корнем уравнения. Решить уравнение – значит найти все его корни, или убедиться, что уравнение не имеет корней. Разберёмся, как же решают уравнения.
Источник: profjurist.ru
Как переносить знаки при решении уравнений

Например: 7 (4 — х) + 3 (х — 5) = 9х.
- Раскрыть скобки: 28 — 7х + Зх — 15 = 9х
- Перенести слагаемые с неизвестным в левую часть равенства, а числа — в правую часть равенства: -7х + Зх — 9x = -28 + 15.
- Вычислить неизвестное x.
- х = -13 : (-13)
- Привести подобные члены: -13x = -13.
- х = 1
Определив значение неизвестного, мы решили уравнение. Чтобы произвести проверку правильности решения уравнения, надо полученное значение неизвестного (буквы) подставить в условие (заданное уравнение) и решить числовое равенство.
Если числовое равенство обращается в тождество, то уравнение решено верно.
- 7 (4 — 1) + 3 (1 — 5) = 9 * 1
- 21 — 12 = 9
- 9 = 9
- 7 * 3 + 3 * (-4) = 9
Уравнение решено верно, так как в результате проверки получено тождество.
Линейные неравенства.Исчерпывающий гид (2019)
Например: Все приведенные выше неравенства являются линейными.
Во всех них «сидит» очень важная особенность: в таких неравенствах нет иксов в квадрате, в кубе и т.д., кроме того в этих неравенствах нет деления на икс и икс не находится под знаком корня.
Чтобы лучше распознавать линейные неравенства, настоятельно рекомендую тебе еще раз заглянуть в раздел «Скрытые» линейные уравнения или…» темы .
Линейные неравенства обладают не меньшим талантом «скрываться».
Чтобы не попасть впросак и с легкостью преобразовывать любые неравенства надо знать и успешно применять 3 очень важных правила. Эти знания здорово упростят тебе жизнь на пути в решении неравенств.
Два неравенства равносильны, если они имеют одинаковые решения. Решить неравенство – значит найти все значения переменной, при которых неравенство обращается в верное числовое неравенство.Для упрощения процесса нахождения всех
Линейные уравнения.Полное руководство (2019)
Например: Мы видим, что справа стоит , что, по идее, уже говорит о том, что уравнение не линейное.
Мало того, если мы раскроем скобки, то получим еще два слагаемых, в которых будет , но не надо торопиться с выводами! Прежде, чем судить, является ли уравнение линейным, необходимо произвести все преобразования и таким образом, упростить исходный пример.
При этом преобразования могут изменять внешний вид, но никак не саму суть уравнения. Иными словами данные преобразования должны быть тождественными или равносильными. Таких преобразований всего два, но они играют очень, ОЧЕНЬ важную роль при решении задач.
Рассмотрим оба преобразования на конкретных примерах.
Допустим, нам необходимо решить такое уравнение: Еще в начальной школе нам говорили: «с иксами – влево, без иксов – вправо». Какое выражение с иксом стоит справа?
Способы решения простых уравнений
Их используют при решении сложных.
1) 4+х=8 Отнимем от каждой части 4, т.е., 0+х=4 или х=4 2) х-5=2 Прибавим к обеим частям 5, получим х-5+5=2+5, х-0=7, х=7 3) х+1=х Надо такое число, складывая которое с 1, не изменится. Такого числа не существует, поэтому х не имеет корней 4) х+0=х Любое число, сложив с 0, не изменяется. Поэтому х является любым числом 5) 3-х=2 Вот это уже сложный пример.
И хотя можно логически догадаться, мы решим так, как доказывает шаровую логику.
Х под минусом. Поэтому тут немного сложнее.
Линейные уравнения. Решение линейных уравнений.Правило переноса слагаемого.
Правило переноса слагаемого.
Примеры переноса слагаемого: 5x+2=7x−6.
Сначала переносим 5x из левой части уравнения в правую: 2=7x−6−5x. Далее переносим (−6) из правой части в левую: 2+6=7x−5x. Обратите внимание, что знак «+» изменился на «-», а знак «-» на «+».
При этом не имеет значения, переносимое слагаемое число или переменная, либо выражение. −3×2(2+7x)−4+y=0. Переносим 1-е слагаемое в правую сторону уравнения.
Получаем: −4+y=3×2(2+7x). Обратите внимание, что в нашем примере слагаемое — это выражение (−3×2(2+7x)). Поэтому нельзя отдельно переносить (−3×2) и (2+7x), так как это составляющие слагаемого.
Именно поэтому не переносят (−3×2⋅2) и (7x). Однако мы модем раскрыть скобки и получить 2 слагаемых: (−3x‑⋅2) и (−3×2⋅7x). Эти 2 слагаемых можно переносить отдельно друг от друга.Таким же образом преобразовывают неравенства: 7x+25>14 Собираем каждое число с одной стороны. Получаем: 7x>14−25 или 7x>−11 Доказательство.
2-е части уравнения по определению одинаковы, поэтому можем вычитать из обеих частей уравнения одинаковые выражения, и равенство будет оставаться верным. Вычитать нужно выражение, которое в итоге нужно перенести в другую сторону.
Тогда по одну сторону знака «=» оно сократится с тем, что было. А по другую сторону равенства выражение, которое мы вычли, появится со знаком «-». Это правило зачастую используется для решения .
Для решения используются другие методы.
zakondostatka.ru

« Бюро медико социальной экспертизы в тамбове Продлено действие патента на промышленный образец » admin | 20.05.2020 — 13:38 |20.05.2020 Статьи Решение простых уравнений. 5 класс Уравнение — это равенство, содержащее букву, значение которой надо найти. Решив уравнение, всегда после ответа записываем проверку.
Информация для родителей Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа». Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления.
Уравнение правило переноса
Уравнение — это равенство, содержащее букву, значение которой надо найти.
В уравнениях неизвестное обычно обозначается строчной латинской буквой.
- Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.
- Решить уравнение — значит найти все его корни или убедиться, что корней нет.
Решив уравнение, всегда после ответа записываем проверку.
Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа».
Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.
Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака.
Цели урока Образовательные: Закрепить понятие корня уравнения, правила переноса слагаемого из одной части уравнения в другую, умножения и деления обеих.— презентация
Мы предполагаем, что вам понравилась эта презентация. Чтобы скачать ее, порекомендуйте, пожалуйста, эту презентацию своим друзьям в любой соц.
сети. Кнопочки находятся чуть ниже. Спасибо. Кнопки: Назад Скачать презентацию Идет загрузка презентации. Пожалуйста, подождите
Презентация была опубликована 3 года назад пользователем Получить код презентации Скачать Показать еще Цели урока Образовательные: Закрепить понятие корня уравнения, правила переноса слагаемого из одной части уравнения в другую, умножения и деления обеих частей уравнения на одно и то же число неравное нулю, умения решать задачи с помощью уравнений.
Воспитательные: воспитывать навыки самоконтроля, взаимоконтроля, самооценки; к предмету и уверенность в своих силах.
воспитывать чувства гражданственности и патриотизма,
Правила умножения и деления
После того, как выучена таблица умножения, школьникам объясняют правила умножения и деления, учат использовать их при вычислении математических выражений.
При сложении и вычитании, умножении и делении чисел в простых выражениях у детей не возникает трудностей:
- 86 – 9 = 77;
- 5 × 3 = 15;
- 81 : 9 = 9.
В таких вычислениях необходимо только знать правила сложения и вычитания и Когда начинаются более сложные упражнения, примеры состоят из двух и более действий, да еще и со скобками, при решении у детей появляются ошибки.
И главная из них – неправильный порядок действий.
Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?
10 – 5 + 2 = ? Если мы будем выполнять действия по порядку, получим:
Попробуем иначе:
Получили два разных ответа.
Коллегия адвокатов
Уравнение — это равенство, содержащее букву, знамение которой нужно найти.
Решение уравнения — это тот набор значений букв, при котором уравнение превращается в верное равенство: Напомним, что для решения уравнении надо слагаемые с неизвестным перенести в одну часть равенства, а числовые слагаемые в другую, привести подобные и получить такое равенство: Из последнего равенства определим неизвестное по правилу:
«один из множителей равен частному, деленному на второй множитель»
.
Так как рациональные числа а и Ь могут иметь одинаковые и разные знаки, то знак неизвестного определяется по правилам деления рациональных чисел.
Линейное уравнение необходимо упростить, раскрыв скобки и выполнив действия второй ступени (умножение и деление).Перенести неизвестные в одну сторону от знака равенства, а числа — в другую сторону от знака равенства, получив тождественное заданному равенство, Привести подобные слева и справа от знака равенства, получив равенство вида ax = b.
Линейные неравенства. Подробная теория с примерами

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Раз уж ты оказался на этой теме, то ты наверняка уже знаком с темой «Линейные уравнения».
Если нет, то лучше скорей отправляйся исправлять это недоразумение.
Без усвоенной темы «Линейные уравнения» спокойное плавание в «Линейных неравенствах» не гарантировано.
Итак, надеюсь, ты уже знаком с линейными уравнениями, поэтому можно смело покорять неравенства!
Что такое «линейные неравенства»?
Если ты ознакомился с линейными уравнениями, то уже знаком с Васей, который раздавал яблоки своим друзьям. Давай вернемся к примеру с Васей (может, и нам что-то перепадет?).
Так вот, предположим, что у Васи больше, чем яблок. Все свои яблоки он хочет раздать поровну троим друзьям. По сколько яблок получит каждый друг?
Если обозначить через количество яблок, которое достанется каждому из трех друзей, то получим следующее линейное неравенство:
Дальше мы делим обе части составленного неравенства на и получаем:
Таким образом, каждый друг щедрого Васи получит больше, чем яблока.
Ну вот и справились с неравенством!
Сейчас я введу формализованное определение линейного неравенства и будем разбираться с ним дальше.
Линейные неравенства – это неравенства вида: где и – любые числа, причем ; – неизвестная переменная. |
Например:
Все приведенные выше неравенства являются линейными.
Во всех них «сидит» очень важная особенность: в таких неравенствах нет иксов в квадрате, в кубе и т.д., кроме того в этих неравенствах нет деления на икс и икс не находится под знаком корня.
Чтобы лучше распознавать линейные неравенства, настоятельно рекомендую тебе еще раз заглянуть в раздел «Скрытые» линейные уравнения или…» темы «Линейные уравнения. Начальный уровень.».
Линейные неравенства обладают не меньшим талантом «скрываться».
Чтобы не попасть впросак и с легкостью преобразовывать любые неравенства надо знать и успешно применять 3 очень важных правила. Эти знания здорово упростят тебе жизнь на пути в решении неравенств.
Правила преобразования неравенств
Два неравенства равносильны, если они имеют одинаковые решения.
Решить неравенство – значит найти все значения переменной, при которых неравенство обращается в верное числовое неравенство.
Для упрощения процесса нахождения всех корней неравенства проводятся равносильные преобразования, то есть проводится замена данного неравенства более простым, при этом не должны потеряться никакие решения и не должно возникнуть никаких посторонних корней.
В общем, это все пока только слова. Давай разбираться прямо на правилах.
| ПРАВИЛО 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные). |
Например,
Таким образом, можно с уверенностью сказать, что равносильно .
Или вот такой пример:
В теме «Линейные уравнения» говорилось, что для удобства принято переносить слагаемые с переменной в левую часть, а остальные в правую – так и поступим:
Здесь все должно быть понятно, перейдем к следующему правилу.
| ПРАВИЛО 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному. |
Вернемся к нашим двум предыдущим примерам.
В первом примере мы остановились на . Применим правило 2, разделив обе части неравенства на положительное число :
Заметил, знак неравенства как был «больше», так и сохранился? Все это потому, что мы делили на положительное число.
Давай закрепим на втором примере, где мы остановились на . Разделим обе части неравенства на :
Делили на положительное число , поэтому знак неравенства сохранился.
Почему так акцентируется внимание на том, что знак неравенства сохраняется? А вот потому, что в отличие от преобразований линейных уравнений, преобразования линейных неравенств имеют свою особенность, можно даже сказать «подводный камень». Что это за «камень» должно прояснить правило 3.
| ПРАВИЛО 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак на знак , и наоборот; знак на знак , и наоборот). |
Заметил важное отличие от правила 2? Все верно:
- При умножении/делении на положительное число знак неравенства сохраняется
- При умножении/делении на отрицательное число знак неравенства меняется на противоположный
Например:
Делим на отрицательное число , тогда знак неравенства меняется на противоположный:
Заметил, знак (меньше) заменили на знак (больше)?
Или вот такой пример:
Делим обе части на отрицательное число , меняя при этом знак неравенства на противоположный:
Усвоил? Тогда давай закреплять на примерах
Не пугайся, что примеры, на первый взгляд, сложней, чем мы с тобой разбирали. Мы ведь знаем все необходимые правила преобразования линейных неравенств, а значит, не пропадем.
Ну что, приступим? Как-никак, это не Эверест покорять.
1.
Раскроем для начала скобки и приведем подобные слагаемые:
А теперь можем применять наши правила преобразования линейных неравенств:
Ну вот, мы почти решили наше неравенство – осталось записать ответ в виде промежутка. Неравенство у нас нестрогое, поэтому число включается в наш промежуток. Для наглядности изображу решения на оси:
Запишем ответ: .
2.
Все, как в первом примере: раскрываем скобки, приводим подобные слагаемые, осуществляем необходимые преобразования:
Неравенство у нас нестрогое, поэтому число включается в наш промежуток:
Ответ:
3.
Думаешь это не линейное неравенство? А что мы говорили в теме Линейные уравнений об их «скрытности»?Поспешных выводов делать не стоит, давай лучше проведем все возможные преобразования и убедимся, что это линейное неравенство, либо докажем обратное.
Сейчас будем делить обе части неравенства на отрицательное число . Что же тогда произойдет со знаком неравенства? Все верно – он поменяется на противоположный!
Неравенство нестрогое, значит, включается в наш промежуток.
Ответ:
4.
Проводим соответствующие преобразования:
Делим обе части на отрицательное число , не забывая поменять знак неравенства на противоположный:
Неравенство нестрогое, поэтому – не включается в промежуток:
Ответ:
5.
Этот пример проще, поэтому сразу запишу ход решения без комментариев:
Ответ:
Линейные неравенства с двумя переменными
В теме Линейные уравнения достаточно подробно разобрано понятие линейного уравнения с двумя переменными. Линейное неравенство представляет собой практически то же самое, только знак равенства меняется на знак неравенства .
Линейные неравенства с двумя переменными имеют вид: где , и – любые числа, . |
А вся разница с линейным неравенством с одной переменной только в том, что в неравенство добавляется еще одна переменная .
Решением неравенства с двумя переменными называется множество пар чисел , которые удовлетворяют этому неравенству (т.е. при подстановке этих точек неравенство верно).
Для решения линейных неравенств с двумя переменными, используется графический способ.
Давай разберем вот такой пример:
Решение:
Как уже упоминалось, решается такое неравенство графически.
Построим график уравнения . Как ты уже должен был знать из темы «Линейные уравнения», графиком будет прямая.
Строим график по двум точкам, через которые проходит прямая, к примеру, и . Вот, что у меня получилось:
Так как неравенство в этом примере у нас строгое, то координаты точек самого графика прямой не будут являться решением исходного неравенства. Поэтому обозначим линию пунктиром на графике:
Как можно заметить, прямая разбила плоскость на две полуплоскости. Все точки одной из полуплоскостей будут являться решением исходного неравенства.
Так как в исходном неравенстве у нас стоит знак , то мы должны выбрать те точки, которые лежат выше графика прямой. Изобразим все решения неравенства на графике:Все решения «затушеваны» голубым цветом. Вот и все, неравенство с двумя переменными решено. Это значит, что координаты и любой точки из закрашенной области – решения неравенства.
Линейные неравенства. коротко о главном
Линейными неравенствами называются неравенства вида:
где и – любые числа, причем ; – неизвестная переменная.
Правила преобразования неравенств:
Правило 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные).
Правило 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.
Правило 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак на знак , и наоборот; знак на знак , и наоборот).
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике,
А также получить доступ к учебнику YouClever без ограничений…
Как меняются знаки при переносе в уравнении — kak.glivec.su
Содержание статьи:
Уравнение правило переноса
Оглавление: Уравнение — это равенство, содержащее букву, значение которой надо найти. В уравнениях неизвестное обычно обозначается строчной латинской буквой.
- Решить уравнение — значит найти все его корни или убедиться, что корней нет.
- Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.
Решив уравнение, всегда после ответа записываем проверку.
Чаще всего используют буквы « x » [икс] и « y » [игрек].
Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему «Отрицательные числа». Поэтому они должны решать уравнения, используя только свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже. Не пытайтесь объяснить решение уравнений через перенос чисел и букв из одной части уравнения в другую с изменением знака.
Правила переносов.
строки над иллюстрацией. Знаки препинания от предшествующих слов не отбивают.
Многоточие в начале предложения не отбивают от следующего за ним слова.
При наборе вразрядку отбивку знаков и цифр не увеличивают.
Дефис от предшествующих и последующих элементов набора не отбивают; исключение составляет набор вразрядку, при котором дефис отбивается на величину разрядки. Тире в начале абзацного отступа отделяют от последующего слова на полукегельную.
Тире за запятой или точкой, а также между числами в значении «от-до» располагают без отбивки. Во всех остальных случаях тире отбивают пробелом в 2 п. Кавычки и скобки от заключенных в них слов, а также знаки препинания от скобок и кавычек не отбиваются.
Кавычки должны иметь то же начертание, что и заключенный в них текст. Начертание скобок должно соответствовать начертанию шрифта основного текста.
Скобки внутри выделенного текста должны соответствовать начертанию выделения.
Правила переноса в уравнениях
Оглавление: Для решения линейных уравнений используют два основных правила (свойства).
Знак ссылки на сноску (цифры или звездочки) в основном тексте отбивают на 2 п.
При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный .
Давайте разберём правило переноса на примере. Пусть нам требуется решить линейное уравнение. Вспомним, что у любого уравнения есть левая и правая часть. Перенесем число « 3 » из левой части уравнения в правую. Так как в левой части уравнения у числа « 3 » был знак « + », значит в правую часть уравнения « 3 » перенесется со знаком « − ».
Полученное числовое значение « x = 2 » называют корнем уравнения.
Не забывайте после решения любого уравнения записывать ответ. Рассмотрим другое уравнение. По правилу переноса перенесем « 4x » из левой части уравнения в правую, поменяв знак на противоположный.
Несмотря на то, что перед « 4x » не стоит никакого знака, мы понимаем, что перед « 4x » стоит знак « + ».
Решение линейных уравнений 7 класс
Для решения линейных уравнений используют два основных правила (свойства). Запомните!
При переносе из одной части уравнения в другую член уравнения меняет свой знак на противоположный. Давайте разберём правило переноса на примере.
Пусть нам требуется решить линейное уравнение.
Вспомним, что у любого уравнения есть левая и правая часть.
Перенесем число «3» из левой части уравнения в правую. Так как в левой части уравнения у числа «3» был знак «+», значит в правую часть уравнения «3» перенесется со знаком «−».
Полученное числовое значение «x = 2» называют корнем уравнения.
Важно!
Не забывайте после решения любого уравнения записывать ответ.
Конспект урока по теме «Решение уравнений с переносом слагаемых из одной части в другую».
Тема: Решение уравнений с переносом слагаемых из одной части в другую.Класс: 6Предмет: Математика.Средства обучения: УМК: Математика. 6 класс, С.М. Никольский, М. К.
ПотаповТип урока: изучение и первичное закрепление новых знаний и способов действий.Планируемые образовательные результаты:Предметные: изучить правило решения уравнения переносом слагаемых из одной части уравнения в другую.
Тренировать способность к использованию выведенного алгоритма; закрепить изучаемый материал в процессе выполнения заданий, осуществить первичный контроль, совершенствовать вычислительные навыки.Личностные: формирование культуры общения; формирование умения вести диалог друг с другом; формирование умения отстаивать свою точку зрения и приводить свои аргументы или контраргументы; формирование умения признавать собственные ошибки.Метапредметные:регулятивные – уметь определять и формулировать цель на уроке
Основы алгебры/Правило переноса слагаемого
При решении и преобразовании уравнений часто возникает потребность перенести слагаемое из одной стороны уравнения в другую. Необходимо отметить, что слагаемое может быть как со знаком «плюс», так и со знаком «минус».
Правило говорит, что при переносе слагаемого из одной части уравнения в другую необходимо поменять знак.
Также правило работает и для неравенств.
- .
Перенесём сначала из левой части уравнения в правую: . Теперь перенесём число (−6) из правой части в левую: 2+6=7x-5x Заметьте, знак плюс поменялся на минус, а знак минус — на плюс.
Причём неважно, является ли переносимое слагаемое числом, переменной или же целым выражением.
Решение уравнений, правило переноса слагаемых
с – 3,6 = — 8 А как решить такое уравнение?
Перенесём первое слагаемое в правую сторону уравнения. Получим: Отметим, что в этом примере слагаемым являлось целое выражение . При этом нельзя отдельно переносить или , поскольку это лишь составные части слагаемого. По той же причине нельзя переносить или .
х + 5 = — 2х – 7 (Слайд 8) Упростить мы не можем, т. к. подобные слагаемые находятся в разных частях уравнения, следовательно, необходимо их перенести.
(Слайд 9) Горят причудливо краски, И как ни мудра голова, Вы все-таки верьте в сказки Сказка всегда права.
Асадов СКАЗКА. Давным-давно жили-были 2 короля: черный и белый.
Черный король жил в Черном королевстве на правом берегу реки, а Белый король – в Белом на левом берегу. Между королевствами протекала очень бурная и опасная река.
Переправиться через эту реку ни вплавь, ни на лодке было невозможно.
Нужен был мост! Строительство моста шло очень долго, и вот, наконец, мост построили. Всем бы радоваться и общаться друг с другом, но вот беда: Белый король не любил черный цвет, все жители его королевства носили светлые одежды, а Черный король не любил белый цвет и, жители его королевства носили одежды темного цвета.
Уравнения
Уравнение — это равенство, содержащее букву, знамение которой нужно найти. Решение уравнения — это тот набор значений букв, при котором уравнение превращается в верное равенство: Напомним, что для решения уравнении надо слагаемые с неизвестным перенести в одну часть равенства, а числовые слагаемые в другую, привести подобные и получить такое равенство: ах = Ь Из последнего равенства определим неизвестное по правилу:
«один из множителей равен частному, деленному на второй множитель»
.
x = b : a Так как рациональные числа а и Ь могут иметь одинаковые и разные знаки, то знак неизвестного определяется по правилам деления рациональных чисел. Линейное уравнение необходимо упростить, раскрыв скобки и выполнив действия второй ступени (умножение и деление).
Перенести неизвестные в одну сторону от знака равенства, а числа — в другую сторону от знака равенства, получив тождественное заданному равенство,
Основные приемы решения уравнений.
1. Перенос слагаемых из одной части уравнения в другую. Переход от уравнения f(x) = g(x) + m(x) (1)к уравнению f(x) — m(x) = g(x) (2)называют переносом слагаемых из одной части уравнения в другую.Перенос слагаемых из одной части уравнения в другую — это преобразование уравнения всегда приводит к равносильному уравнению, т.
е., каковы бы ни были функции f(х), m(х), g(x), мы имеем (1)
(2).
В самом деле, пусть a — корень уравнения (1), т. е. соотношение f(a) + m(a) = g(a) = g(a) + m(a) (3)представляет собой верное числовое равенство.
Это означает, что ринадлежит области определения каждой из функций f{x), m(x), g(x), т. е. определены числа f(a), m(a), g(a), и2) эти числа связаны соотношением (3).
Источник: help-avto76.ru
Читайте также
Конвективная теплопередача
Тепловая энергия, передаваемая между поверхностью и движущейся жидкостью с разными температурами, известна как конвекция .
На самом деле это комбинация диффузии и объемного движения молекул. Вблизи поверхности скорость жидкости мала, и преобладает диффузия. На расстоянии от поверхности объемное движение усиливает влияние и преобладает.
Конвективная теплопередача может быть
- принудительной или вспомогательной конвекцией
- естественной или свободной конвекцией
принудительной или вспомогательной конвекцией
принудительной конвекцией, когда поток жидкости индуцируется внешняя сила, такая как насос, вентилятор или смеситель.
Естественная или свободная конвекция
Естественная конвекция вызывается выталкивающими силами из-за разницы плотности, вызванной колебаниями температуры в жидкости. При нагревании изменение плотности в пограничном слое заставит жидкость подниматься и заменяться более холодной жидкостью, которая также будет нагреваться и подниматься. Это продолжающееся явление называется свободной или естественной конвекцией.
Процессы кипения или конденсации также называют конвективными процессами теплопередачи.
- Теплопередача на единицу поверхности за счет конвекции была впервые описана Ньютоном, и это соотношение известно как закон охлаждения Ньютона .
Уравнение конвекции может быть выражено как:
q = h c A dT (1)
, где
q = теплопередача за единицу времени (Вт, БТЕ / ч)
A = площадь теплообмена поверхности (м 2 , футы 2 )
h c = коэффициент конвективной теплопередачи процесса ( Вт / (м 2o C, Btu / (фут 2 h o F) )
dT = разница температур между поверхностью и основной жидкостью ( o C, F)
Коэффициенты теплопередачи — единицы
Коэффициенты конвективной теплопередачи
Коэффициенты конвективной теплопередачи — ч c — в зависимости от тип среды, газ или жидкость, и свойства потока, такие как скорость, вязкость и другие свойства, зависящие от потока и температуры.
Типичные коэффициенты конвективной теплопередачи для некоторых распространенных применений потока жидкости:
- Свободная конвекция — воздух, газы и сухие пары: 0,5 — 1000 (Вт / (м 2 K))
- Свободная конвекция — вода и жидкости: 50 — 3000 (Вт / (м 2 K))
- Принудительная конвекция — воздух, газы и сухие пары: 10 — 1000 (Вт / (м 2 K))
- Принудительная конвекция — вода и жидкости: 50 — 10000 (Вт / (м 2 K))
- Принудительная конвекция — жидкие металлы: 5000 — 40000 (Вт / (м 2 K))
- Кипящая вода: 3.000 — 100,000 (Вт / (м 2 K))
- Водяной пар конденсата: 5.000 — 100,000 (Вт / (м 2 K))
Коэффициент конвективной теплопередачи для воздуха
Коэффициент конвективной теплопередачи для потока воздуха может быть приблизительно равен
ч c = 10,45 — v + 10 v 1/2 (2)
где
h c = коэффициент теплопередачи (кКал / м 2 ч ° C)
v = относительная скорость между поверхностью объекта и воздухом (м / с)
Начиная с
1 ккал / м 2 ч ° С = 1.16 Вт / м 2 ° C
— (2) можно изменить на
ч cW = 12,12 — 1,16 v + 11,6 v 1/2 (2b)
где
ч cW = коэффициент теплопередачи (Вт / м 2 ° C )
Примечание! — это эмпирическое уравнение, которое может использоваться для скоростей от 2 до 20 м / с .
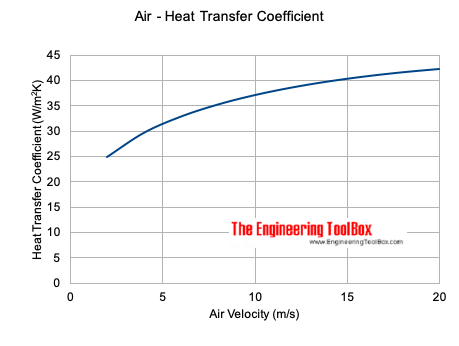
Пример — конвективная теплопередача
Жидкость течет по плоской поверхности 1 м на 1 м. Температура поверхности 50 o C , температура жидкости 20 o C и коэффициент конвективной теплопередачи 2000 Вт / м 2o С . Конвективную теплопередачу между более горячей поверхностью и более холодным воздухом можно рассчитать как
q = (2000 Вт / (м 2o C)) ((1 м) (1 м)) ((50 o C) — (20 o C))
= 60000 (Вт)
= 60 (кВт)
Калькулятор конвективной теплопередачи
Таблица конвективной теплопередачи
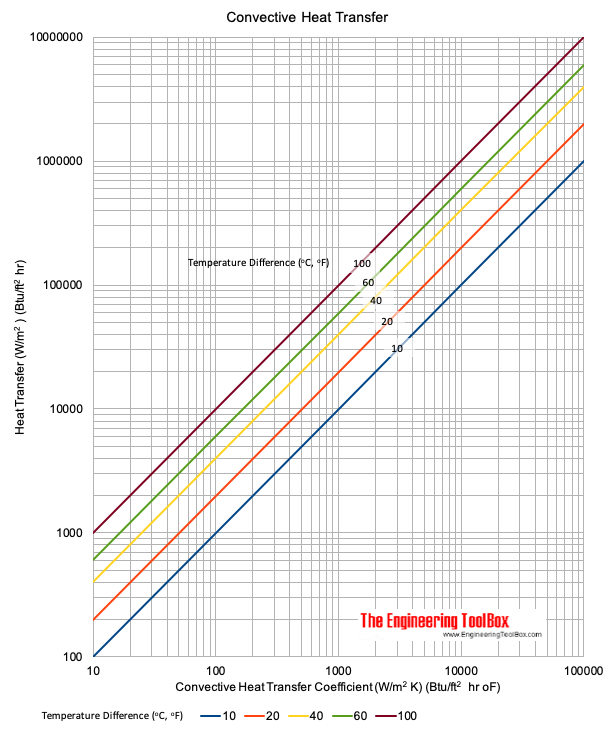
Создание, нумерация и перекрестные ссылки в уравнениях в Microsoft Word | Информационные системы и технологии
Начало работы
С помощью редактора формул, поставляемого с Microsoft Word, формулы можно вставлять в Word, PowerPoint или любое приложение, поддерживающее связывание и встраивание объектов (OLE).
Хотя большая часть этого документа содержит инструкции, относящиеся к Word, процедуры вставки и редактирования формул в Word такие же, как и для PowerPoint.Некоторые примечания к PowerPoint можно найти в конце этого документа.
Обучение работе с редактором формул
Пожалуйста, посмотрите вводное видео.
Полное описание использования редактора формул доступно в разделе « Help » в окне редактора формул.
Вставка уравнения
Пожалуйста, посмотрите видео о создании уравнения (примеры в этом видео немного отличаются от примеров в этом тексте).
Упражнение 1:
- Откройте Microsoft Word.
- Чтобы вставить уравнение, выберите Insert, Object, Microsoft Equation 3.0 и нажмите OK . Произойдет одно из двух:
- Появится выделенная область вместе с палитрами редактирования формул. Это называется редактированием на месте. Может быть очень сложно увидеть, что вводится, или
- Откроется отдельное окно с палитрами вверху. Это намного проще для ввода уравнений. Это выглядит следующим образом.

- Чтобы выйти и вернуться в документ Word, вы можете выбрать Файл / Выход и вернуться в ( DocumentName ) ; чтобы обновить документ Word, но остаться в редакторе формул, вы можете выбрать File / Update.
- Редактирование на месте по умолчанию, но можно сделать редактирование окна по умолчанию.
Размещение кнопки уравнения на панели инструментов
Пожалуйста, посмотрите видео об автоматизации.
Упражнение 2:
Если вы вводите много уравнений, вам может быть удобно иметь кнопку «Вставить уравнение» прямо на панели инструментов. Это можно сделать по:
- щелкнув правой кнопкой мыши на панели инструментов (или открыв меню Инструменты ) и выбрав Настроить
- Откроется окно. Щелкните вкладку Commands , если она еще не выбрана.
- Выберите Вставить слева, а затем Редактор формул справа.
- Щелкните и перетащите кнопку рядом с Редактор формул (символ квадратного корня с альфой в нем) на панель инструментов. С этого момента при нажатии на эту кнопку будет вставлено уравнение.
Введите уравнение
Чтобы ввести уравнение, просто начните печатать. Все символы с клавиатуры можно вводить напрямую. (Скобки, квадратные скобки и фигурные скобки можно вводить с клавиатуры, но они имеют фиксированный размер. Скобки, которые будут «увеличиваться», должны быть выбраны из соответствующего шаблона).
Ввод символов
Имеется 10 палитр символов, весь верхний ряд кнопок. Символы, напечатанные на кнопках, указывают на символы, доступные под каждой кнопкой. Две крайние правые палитры символов — это (1) строчные греческие буквы и (2) греческие буквы верхнего регистра.
Чтобы выбрать элемент из палитры символов, щелкните кнопку палитры, а затем щелкните нужный символ.
Ввод шаблонов
Второй ряд кнопок палитры — это палитры шаблонов. Они предоставляют заполнители для ввода информации. Например,  предоставляет несколько палитр интеграции. Некоторые из них имеют местозаполнитель только для подынтегрального выражения, некоторые для подынтегрального выражения плюс нижний предел, некоторые для подынтегрального выражения плюс нижний плюс верхний пределы.
предоставляет несколько палитр интеграции. Некоторые из них имеют местозаполнитель только для подынтегрального выражения, некоторые для подынтегрального выражения плюс нижний предел, некоторые для подынтегрального выражения плюс нижний плюс верхний пределы.
Палитра  содержит шаблоны для дробей и радикалов.
содержит шаблоны для дробей и радикалов.
Чтобы вставить шаблон, выберите нужный шаблон из соответствующей кнопки палитры и заполните поля шаблона.Заполнители могут содержать символы клавиатуры, символы из палитр символов или другие шаблоны. Например, подынтегральное выражение может быть шаблоном дроби, а числитель дроби может быть шаблоном квадратного корня.
Обход уравнения
Мигающий курсор под прямым углом указывает, где вы собираетесь ввести информацию в уравнение. Горизонтальная полоса курсора отмечает базовую линию вводимых символов. Вертикальная полоса указывает высоту. Вы можете установить точку вставки, щелкнув мышью или с помощью клавиатуры.
Размещение точки вставки в уравнении с помощью клавиш.
Пресс | Перемещает точку вставки |
|---|---|
| Выступ | До конца прорези. Если точка вставки находится в конце слота, она перемещается в следующий логический слот. |
| Shift + Tab | До конца предыдущего слота. |
| Стрелка вправо | Право на один юнит в текущем слоте или шаблоне. |
| Стрелка влево | Остался один отряд в текущем слоте или шаблоне. |
| Стрелка вверх | На одну строку вверх. |
| Стрелка вниз | На одну строку ниже. |
| Дом | В начало текущего слота. |
| конец | До конца текущего слота. |
Примечание: Чтобы вставить символ табуляции в слот, нажмите CTRL + TAB.
Упражнение 3:
Чтобы ввести уравнение  , запустите редактор формул и:
, запустите редактор формул и:
- Наберите «x =» с клавиатуры
- Выберите дробь из шаблона
 .
. - Выберите скобки из числа
 . (На самом деле в этом уравнении можно было бы вводить круглые скобки с клавиатуры).
. (На самом деле в этом уравнении можно было бы вводить круглые скобки с клавиатуры). - Введите «-b» с клавиатуры.
- Выберите «плюс или минус» из палитры
 .
. - Выберите корень из палитры
 .
. - Наберите «b» с клавиатуры.
- Выберите верхний индекс из палитры
 .
. - Введите «2».
- Tab, чтобы перейти на уровень ниже, и введите «-4ac».
- Нажмите табуляцию 3 раза, чтобы перейти к знаменателю, и введите «2a».
Удаление из уравнений
Когда вы вводите уравнение, вы можете вернуться назад в любой момент. Вы также можете выбрать части уравнения с помощью мыши и удалить.
Кронштейны для выращивания
Скобки, круглые скобки и фигурные скобки, которые увеличиваются вместе с заключенным текстом, должны быть выбраны из шаблона  .
.
Матрицы
Матрицы любого размера могут быть созданы из шаблона  .
.
Укладка и выравнивание уравнений
Пожалуйста, посмотрите видео о штабелировании и матрицах.
Уравнения можно складывать в стопку. Для этого просто нажмите клавишу Return, чтобы начать новую строку. Чтобы выровнять эту стопку по символу, например по знаку равенства, выберите «Выровнять по» в меню Формат .

Упражнение 4:
- Попробуйте ввести следующую матрицу:

Введите следующие уравнения и выровняйте их по знаку = , выбрав Формат / Выровнять по = после их ввода.Также попробуйте использовать символ выравнивания
 для выравнивания уравнений.
для выравнивания уравнений.

Вставка интервала в уравнение
Пробелы можно вставить в уравнение следующим образом.
| Тип помещения | Клавиши для нажатия |
|---|---|
| Нулевое пространство | Shift + пробел |
| 1-точечный интервал | Ctrl + Alt + пробел |
| Тонкое пространство (одна шестая em) | Ctrl + пробел |
| Толстое пространство (одна треть em) | Ctrl + Shift + пробел |
| Em-пространство (четырехъядерный) | Без сочетания клавиш |
Редактирование существующего уравнения
Пожалуйста, посмотрите видео, редактирующее существующее уравнение.
Существующее уравнение можно отредактировать либо двойным щелчком по нему, либо щелкнув его правой кнопкой мыши и выбрав Equation Object или Open или Edit .
Сочетания клавиш
Большинство людей не хотят постоянно перемещать руки от клавиатуры к мыши, чтобы выбрать палитры. Доступен ряд сочетаний клавиш.
Чтобы узнать больше о сочетаниях клавиш для уравнений, откройте редактор формул и выберите:
- Справка / Разделы справки редактора формул
- Выберите вкладку Указатель
- Тип клавиатура в отведенном месте и в нижней части,
- Дважды щелкните сочетание клавиш .
Вставка шаблонов в уравнение с помощью клавиш
- Шаблоны можно вставлять с помощью комбинации символов Ctrl +.
| Для вставки | Шаблон | Пресс |
|---|---|---|
| () | Круглые скобки | Ctrl + 9 или Ctrl + 0 |
| [] | Кронштейны | Ctrl + [или Ctrl +] |
| {} | Подтяжки | Ctrl + {или Ctrl +} |
| — | Фракция | Ctrl + F |
| / | Слэш фракция | Ctrl + / |
| ` | Верхний индекс (высокий) | Ctrl + H |
| _ | Верхний индекс (нижний) | Ctrl + L |
 | Подстрочный / верхний индекс | Ctrl + J |
 | Интегральный | Ctrl + I |
| | | | Абсолютное значение | Ctrl + Shift + T |
| √ | Корень | Ctrl + R |
 | n -й корень | Ctrl + T, N |
| ∑ | Суммирование | Ctrl + T, S |
| ∏ | Товар | Ctrl + T, P |
 | Матричный шаблон 3X3 | Ctrl + T, M |
| _ | Underscript (ограничение) | Ctrl + T, U |
Вставка символов в уравнение с помощью клавиш
- Многие символы могут быть вставлены с помощью последовательности Ctrl + K, символов .
- Примечание : Эти комбинации клавиш недоступны в Windows NT.
| Для вставки | Представляет | Нажмите CTRL + K, |
|---|---|---|
| ∞ | бесконечность | I |
| → | Стрела | А |
| ∂ | Производная (частичная) | D |
| ≤ | Меньше или равно | < |
| ≥ | Больше или равно | > |
| х | раз | Т |
| ∈ | Элемент | E |
| ∉ | Не является элементом | SHIFT + E |
| С | Содержится в | С |
| ⊄ | Не содержится в | SHIFT + C |
Добавление украшений в уравнение с помощью клавиш
- Можно добавить украшение к символу слева от точки вставки с помощью сочетаний клавиш.
| Применить | Описание | Пресс |
|---|---|---|
 | Перекладина | Ctrl + Shift + дефис |
 | Тильда | Ctrl + ~ (Ctrl + Shift + «на некоторых клавиатурах) |
 | Стрелка (вектор) | Ctrl + Alt + дефис |
Перестановка уравнений
Уравнения как важный геологический инструмент

Профессор говорит «математику», которая может показаться другим языком! , фото Дженнифер М. Веннер.
Иногда может показаться, что ваш инструктор по геофизическим наукам говорит на другом языке, когда говорит об уравнениях или формулах. Особенно, если он / она ожидает, что вы будете «манипулировать» или переставлять их! Но уравнения могут предоставить мощные инструменты для описания мира природы.В науках о Земле мы можем описать поведение многих природных явлений, написав уравнение для линии ( y = mx + b ) или с помощью экспоненциальных функций ( y = e xt ). И с небольшой алгеброй мы можем изменить эти уравнения, чтобы решить для ЛЮБОЙ из переменных в них.Хотя это может показаться волшебством, для этого не нужно быть «математиком». Эта страница предназначена для того, чтобы предоставить вам некоторые инструменты, которые помогут вам изучить некоторые простые шаги, которые помогут вам решить уравнение для любой из переменных (буквы, которые представляют интересующий элемент или количество).
Зачем мне манипулировать уравнениями?
 Фотография Кена Эндрюса (ученого из JPL) жонглирования. Изменено Джен Веннер.
Фотография Кена Эндрюса (ученого из JPL) жонглирования. Изменено Джен Веннер.Вы не поверите, но есть много веских причин для развития вашей способности переставлять уравнения, важные для наук о Земле. Это может сэкономить время, помочь вам с юнитами и сэкономить место для мозга! Вот несколько причин для развития навыков манипулирования уравнениями (в произвольном порядке):
- Уравнения легче обрабатывать до , вставляя числа! И, если вы можете изолировать переменную на одной стороне уравнения, она применима к любой подобной проблеме, которую вам нужно решить для этой переменной!
- Если вы знаете, как манипулировать уравнениями, вам нужно запомнить только одно уравнение, в котором есть все рассматриваемые переменные — вы можете манипулировать им, чтобы найти любую другую переменную! Это означает меньше запоминания!
- Манипулирование уравнениями может помочь вам отслеживать (или вычислять) единицы числа.Поскольку единицы измерения определяются уравнениями, если вы манипулируете, вставляете числа и отменяете единицы измерения, вы в конечном итоге получите именно те единицы измерения (для данной переменной)!
Где это используется в науках о Земле?
Если честно, манипуляции с уравнениями имеют место почти во всех аспектах наук о Земле. Каждый раз, когда вы видите P, T, ρ или x (или даже =), есть уравнение, которым вы можете манипулировать. Поскольку уравнения можно использовать для описания множества важных природных явлений, возможность манипулировать ими дает вам мощный инструмент для понимания мира вокруг вас!
См. Только несколько примеров на странице «Практика управления уравнениями».
Обзор важных правил преобразования уравнений

Решение для y Дженнифер М. Веннер.
Вы, вероятно, выучили ряд правил работы с уравнениями в предыдущем курсе алгебры. Никогда не помешает напоминать себе о правилах. Итак, давайте рассмотрим:
- ПРАВИЛО №1: вы можете складывать, вычитать, умножать и делить на что угодно, , если вы делаете то же самое с обеими сторонами знака равенства. В уравнении знак равенства действует как точка опоры баланса: если вы добавляете 5 единиц чего-либо к одной стороне баланса, вы должны прибавить такую же сумму к другой стороне, чтобы баланс оставался устойчивым. То же самое и с уравнением — выполнение одной и той же операции с обеими сторонами сохраняет смысл уравнения от изменения.
Давайте использовать уравнение для линии, чтобы проиллюстрировать пример того, как использовать Правило №1. Общее уравнение для линии:

Если мы хотим найти b в этом уравнении, мы должны вычесть mx из обеих частей.
Если мы выполним математические вычисления с каждой стороны (то есть вычтем mx из mx справа), мы получим уравнение, которое выглядит следующим образом:
Это уравнение также можно записать в виде b = y — mx, если вы предпочитаете, чтобы решаемая переменная находилась слева. - ПРАВИЛО № 2: чтобы переместить или отменить величину или переменную на одной стороне уравнения, выполните «противоположную» операцию с ней на обеих сторонах уравнения. Например, если у вас было g-1 = w и вы хотите изолировать g, добавьте 1 к обеим сторонам (g-1 + 1 = w + 1).Упростим (потому что (-1 + 1) = 0) и получим g = w + 1.
Давайте воспользуемся более сложным уравнением, которое геологи могут использовать, чтобы выяснить отношение толщины к плотности плавающих веществ (например, кора в мантии, айсберги в воде):
, где H над = высота объекта над поверхностью жидкости, в которой он плавает,
H total = общая высота (или толщина) плавающего объекта
ρ объекта = плотность объекта
и ρ жидкости = плотность жидкости
Представим, что мы изучаем айсберг и хотим знать, какова его плотность.Как нам изменить уравнение для решения этой переменной? Чтобы выделить объект с ρ на одной стороне уравнения, необходимо предпринять несколько шагов. С чего начать?- Давайте начнем с выделения части уравнения в круглые скобки. Для этого нам нужно обе стороны разделить на H итого :

Разделенная на себя сущность равна 1:
и, поскольку 1, умноженная на что-то, равно этому чему-то, мы можем упростить и получить:
- Мы все еще не совсем там.Что еще нужно переместить, чтобы изолировать объект с ρ ? Давайте выделим содержащую его дробь, поэтому мы хотим вычесть 1 с обеих сторон:

и, 1 минус 1 равно 0, поэтому мы можем избавиться от единиц в левой части.
- Нам все еще нужно сделать еще несколько операций, чтобы выделить объект с ρ . Сначала умножьте обе части на ρ жидкость , чтобы очистить дробь:

Мы можем исключить ρ жидкость с каждой стороны:
- Тогда нам нужно избавиться от знака минус:
Умножьте обе стороны на -1, чтобы получить -ρ жидкость положительная:

Отрицательное число (или символ), умноженное на отрицательное число, является положительным числом.Поскольку мы умножаем на -1, мы просто меняем знак у всех чисел и символов с обеих сторон и получаем:
- Немного изменив правую часть уравнения, мы получим уравнение для определения плотности айсберга!

Несколько простых шагов для работы с уравнениями

Вот несколько простых шагов для работы с уравнениями.Под каждым шагом вы найдете пример того, как это сделать, с примером, который использует геологический контекст плотности (мера массы на единицу объема).
- Оцените, что у вас есть (для каких переменных у вас есть значения? Какие единицы присутствуют? И т. Д.). НИКАКИХ номеров пока НЕ подключайте!
 Например: у вас есть куб пирита размером 3 см x 3 см x 3 см. Вы знаете, что плотность пирита 5,02 г / см 3 .Можете ли вы выяснить, сколько весит этот кубик пирита (без весов)?
Например: у вас есть куб пирита размером 3 см x 3 см x 3 см. Вы знаете, что плотность пирита 5,02 г / см 3 .Можете ли вы выяснить, сколько весит этот кубик пирита (без весов)?Во-первых, вам нужно знать, что плотность (ρ) равна массе (m), деленной на объем (v). Мы можем записать это в виде математического выражения (или уравнения, если хотите):

Какие из этих значений указаны в вопросе выше? У вас есть плотность (5,02 г / см 3 ). И с помощью информации вы можете определить объем (длина x ширина x высота). - Определите, какие из переменных вы хотите использовать в качестве ответа.(Какой вопрос вас просят вычислить? Что такое неизвестная переменная?)
- Давайте начнем с выделения части уравнения в круглые скобки. Для этого нам нужно обе стороны разделить на H итого :
Подстрочный индекс математического уравнения в документации R
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- реклама Обратитесь к разработчикам и технологам со всего мира
- О компании



 .
. .
. .
. .
. для выравнивания уравнений.
для выравнивания уравнений.














 Например: у вас есть куб пирита размером 3 см x 3 см x 3 см. Вы знаете, что плотность пирита 5,02 г / см 3 .Можете ли вы выяснить, сколько весит этот кубик пирита (без весов)?
Например: у вас есть куб пирита размером 3 см x 3 см x 3 см. Вы знаете, что плотность пирита 5,02 г / см 3 .Можете ли вы выяснить, сколько весит этот кубик пирита (без весов)?