Формулы периметра, Периметр
Периметр фигуры это длина всех ее сторон. Не все фигуры имеют периметр, например, шар не имеет периметра.
Стандартное обозначение периметра в математике — буква P
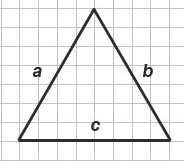
Периметр треугольника
P = a + b + c
Периметр квадрата
Пусть длина стороны квадрата равна a. Квадрат имеет четыре равных стороны, поэтому периметр квадрата есть P = a + a + a +a или:
P = 4 ⋅ a
Периметр прямоугольника
Пусть длины сторон прямоугольника равны a иb.
Длина всех его сторон есть P = a + b + a + b или:
P = 2 ⋅ a + 2 ⋅ b
Периметр параллелограмма
Пусть длины сторон параллелограмма равны a и b
Длина всех его сторон есть P = a + b + a + b, поэтому периметр параллелограмма есть:
P = 2 ⋅ a + 2 ⋅ b
Как видно, периметр параллелограмма равен периметру прямоугольника.
Периметр ромба
P = 4 ⋅ a
Периметр равнобедренной трапеции
Пускай длины параллельных сторон трапеции a и b, а длины двух других сторон равна c(Как известно, равнобедренная трапеция имеет две равные стороны).
P = a + b + c + c = a + b + 2 ⋅ c
Периметр равностороннего треугольника
Как известно, равносторонний треугольник имеет 3 равные стороны. Если длина стороны равна a, тогда формула нахождения периметра есть P = a + a + a
P = 3 ⋅ a
Длина окружности(периметр круга)
Обозначим длину окружности буквой l.
$l = d \cdot \pi = 2\cdot r \cdot \pi$
Где:
$\pi = 3,14$
r радиус круга (окружности)
d диаметр круга.
Правильный многоугольник
$P = 2nb\sin\frac{\pi}{n}$
n число ребер(вершин).
$\pi = 3,14159265359$
Периметр — Википедия
 Периметр — длина контура замкнутой плоской фигуры, длина границы.
Периметр — длина контура замкнутой плоской фигуры, длина границы.Пери́метр (др.-греч. περίμετρον — окружность, др.-греч. περιμετρέο — измеряю вокруг) — общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина.
Иногда периметром называют границу геометрической фигуры.Вычисление периметра имеет существенное практическое значение. Например, для вычисления длины ограды вокруг сада или участка. Периметр колеса (окружности) определяет, насколько далеко оно продвинется при полном обороте. Таким же образом, длина нитки, намотанной на катушку, тесно связана с периметром катушки.
 Периметр прямоугольника.
Периметр прямоугольника.Многоугольники являются основными фигурами для определения периметров, и не только потому, что они являются простейшими фигурами, но и потому, что периметры многих фигур вычисляются путём аппроксимации их последовательностью многоугольников. Первым известным математиком, который использовал этот подход, был Архимед, который аппроксимировал периметр окружности путём описывания около неё правильных многоугольников.
Периметр многоугольника равен сумме длин его сторон. В частности, периметр прямоугольника, имеющего ширину w{\displaystyle w} и длину ℓ{\displaystyle \ell }, равен 2w+2ℓ{\displaystyle 2w+2\ell }.
Равносторонний многоугольник — это многоугольник, имеющий равные длины сторон (например ромб — это равносторонний многоугольник с 4 сторонами). Чтобы вычислить периметр равностороннего многоугольника, нужно умножить число сторон на общую длину стороны.
Периметр правильного многоугольника можно вычислить по числу сторон и его радиусу, то есть расстоянию от центра до вершин. Длину стороны можно вычислить, используя тригонометрию. Если R — радиус многоугольника, а n — число сторон, периметр равен
- 2nRsin(180∘n).{\displaystyle 2nR\sin \left({\frac {180^{\circ }}{n}}\right).}
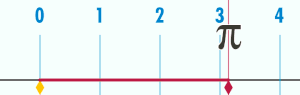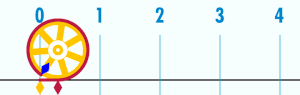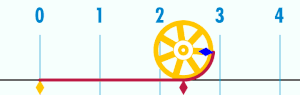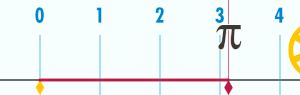 Если диаметр окружности равен 1, её периметр равен π.
Если диаметр окружности равен 1, её периметр равен π.Периметр окружности пропорционален её диаметру (и радиусу). То есть, существует константа π такая, что если P — периметр окружности, а D — её диаметр, то:
- P=π⋅D.{\displaystyle P=\pi \cdot {D}.}
Для радиуса r окружности формула превращается в
- P=2π⋅r.{\displaystyle {P}={2}\pi \cdot {r}.}
Для вычисления периметра окружности знание радиуса или диаметра и числа π достаточно. Проблема заключается в том, что π не является рациональным (его нельзя выразить в виде дроби двух целых чисел) и даже не является алгебраическим (оно не является корнем никакого полиномиального уравнения с рациональными коэффициентами). Таким образом, получение точного приближения к π важно для вычислений. Нахождение знаков π относится ко многим областям, таким как математический анализ и теория алгоритмов.
 Чем мельче структура фигуры, тем меньше площадь и тем больше периметр. Выпуклая оболочка остаётся той же самой.
Чем мельче структура фигуры, тем меньше площадь и тем больше периметр. Выпуклая оболочка остаётся той же самой. 
Периметр и площадь являются двумя основными измерениями геометрических фигур, их часто путают. Нередко также считают, что увеличение одной из этих величин приводит к увеличению другой. Действительно, увеличение (или уменьшение) размера фигуры приводит к увеличению (или уменьшению) её площади, так же как и её периметра. Так, например, если нарисовать карту поля в масштабе 1/10 000, действительные размеры периметра можно вычислить простым умножением на 10 000. Действительная площадь будет в 10 0002 раз больше площади фигуры на карте.
Тем не менее, нет никакой связи между площадью и периметром фигур. Например, периметр прямоугольника шириной 0,001 и длиной 1000 чуть больше 2000, в то время, как периметр прямоугольника шириной 0,5 и длиной 2 равен 5. Площади обеих фигур равны 1.
Прокл (V-й век) писал, что греческие крестьяне делили поля, опираясь на периметры[1], однако урожай с поля пропорционален площади, а не периметру, и много наивных крестьян получали поля с большим периметром, но малой площадью.
Если удалить часть фигуры, её площадь уменьшится, а вот периметр может и не уменьшиться. В случае очень неправильных фигур некоторые могут спутать периметр с выпуклой оболочкой. Выпуклую оболочку визуально можно представить как резинку, натянутую вокруг фигуры. На рисунке слева все фигуры имеют одну выпуклую оболочку (шестиугольник).
Изопериметрическая задача — это задача нахождения фигуры с максимальной площадью среди фигур, имеющих заданный периметр. Решение интуитивно — это окружность. В частности поэтому капли жира в бульоне имеют форму кружочков.
Задача выглядит простой, но строгое математическое доказательство сложно. Изопериметрическая задача иногда упрощается — найти четырёхугольник, треугольник или другую определённую фигуру с наибольшей площадью среди имеющих заданный периметр. Решение изопериметрической задачи для четырёхугольников — квадрат, для треугольников — правильный треугольник. В общем случае, многоугольник с n сторонами имеет максимальную площадь при заданном периметре, если он является правильным, что ближе к окружности по сравнению с неправильными многоугольниками.
Периметр треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Так как изначально периметр для любой фигуры – это сумма длин всех ее сторон, то периметр треугольника найти проще всего, зная все три стороны: P=a+b+c. Для равнобедренного треугольника формула периметра будет выглядеть несколько иначе в силу того, что две из сторон у него конгруэнтны, то есть равны по значению: P=2a+b. С равносторонним треугольником все еще незатейливей – у него все три стороны одинаковые, поэтому периметр будет равен утроенной стороне: P=3a.
Для треугольников, обладающих особыми свойствами, как например, вышеупомянутые равнобедренный и равносторонний треугольники, могут быть выведены и другие формулы. Например, периметр равнобедренного треугольника можно найти и через высоту. Высота в данном случае делит основание пополам, исходя из чего можно найти неизвестную сторону по теореме Пифагора из получившихся прямоугольных треугольников. Если дана боковая сторона, то половина основания будет равна  , а само основание, соответственно,
, а само основание, соответственно,  . Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим
. Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим  . Если дано основание, то по той же теореме Пифагора находим боковую сторону
. Если дано основание, то по той же теореме Пифагора находим боковую сторону 
 .
. Найти периметр равностороннего треугольника становится возможным, уже зная одну лишь высоту. Используя теорему Пифагора, выражаем сторону треугольника через высоту  . Подставляем в формулу периметра равностороннего треугольника и получаем
. Подставляем в формулу периметра равностороннего треугольника и получаем 
Периметр прямоугольного треугольника можно найти, зная две стороны из трех. Если известны два катета a и b, то гипотенуза c по теореме Пифагора равна 
 . Если дана гипотенуза и один из катетов, формула периметра прямоугольного треугольника принимает уже другой вид:
. Если дана гипотенуза и один из катетов, формула периметра прямоугольного треугольника принимает уже другой вид: 
решение задачи по 2 сторонам, средней линии и известной высоте
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю, дизайнеру.
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Классическая формула
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
P = a + b + c.
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.


Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Это интересно! Что значит вертикально и как выглядит вертикальная линия
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:

 .
.Далее рассчитывайте Р по такой формуле:

 .
.Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Это интересно! Основы геометрии: что это такое биссектриса треугольника
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольнике является наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла;
- медиана к основанию;
- высота треугольника;
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
P = 2a + b.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
P = 3a.
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Это интересно! Изучаем символы: как обозначается в математике площадь
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.

 .
.На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.

 .
.Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:

 .
.Также периметр описанного вида фигуры определяется и без данных о размерах катетов.

 .
.Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:

 .
.Это интересно! Как найти и чему будет равна длина окружности
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:

 .
.Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Полезное видео: нахождение периметра треугольника
Вконтакте
Одноклассники
Мой мир
Как найти периметр треугольника: решение задачи по 2 сторонам, средней линии и известной высоте
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых. Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю, дизайнеру.
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Классическая формула
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
P = a + b + c.
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Это интересно! Что значит вертикально и как выглядит вертикальная линия
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
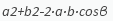 .
.
Далее рассчитывайте Р по такой формуле:
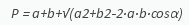 .
.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Это интересно! Основы геометрии: что это такое биссектриса треугольника
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольнике является наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла,
- медиана к основанию,
- высота треугольника,
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
P = 2a + b.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
P = 3a.
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Это интересно! Изучаем символы: как обозначается в математике площадь
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
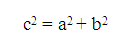 .
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
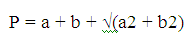 .
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
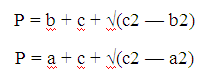 .
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
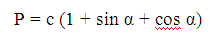 .
.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
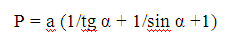 .
.
Это интересно! Как найти и чему будет равна длина окружности
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
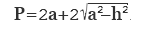 .
.
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Полезное видео: нахождение периметра треугольника
Периметр и площадь треугольника
Периметр
Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:P = a + b + c
где P – это периметр треугольника, a, b и c – его стороны.

Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
P = 2a + b
где P – это периметр равнобедренного треугольника, a – любая из боковых сторон, b – основание.

Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
P = 3a
где P – это периметр равностороннего треугольника, a – любая из его сторон.

Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2. Общая формула для нахождения площади треугольников будет выглядеть так:
где S – это площадь треугольника, a – его основание, ha – высота, опущенная на основание a.
Периметр равнобедренного треугольника | Треугольники
Чтобы найти периметр равнобедренного треугольника, нужно знать всего две его стороны — основание и боковую сторону.
В общем случае формула для нахождения периметра треугольника выглядит так:
где a, b и c — длины сторон треугольника.
Поскольку у равнобедренного треугольника
две стороны равны (боковые),
формулу можно упростить:
Таким образом, периметр равнобедренного треугольника равен сумме длин основания и удвоенной боковой стороны:
Соответственно, периметр равнобедренного треугольника ABC можно найти по формуле:
(здесь AC — основание, AB — боковая сторона).
Примеры.
1) Найти периметр равнобедренного треугольника, если его основание равно 4 см, а боковая сторона — 9 см.
Решение:
Здесь а=4 см, b=9 см. По формуле Р=а+2b имеем: P=4+2∙9=22 (cм).
2) Периметр равнобедренного треугольника равен 170 см, а его основание — 60 см. Найти боковую сторону треугольника.
Решение:
Здесь а=60 см, Р=170 см. По формуле Р=а+2b, 2b=Р-а, b=(Р-а):2, b=(170-60):2=55 (см).
Задача нахождения периметра равностороннего треугольника решается еще проще. Её мы рассмотрим в следующий раз.