Площади подобных треугольников | Треугольники
Утверждение
Площади подобных треугольников относятся как квадраты их соответствующих сторон, то есть отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Дано:
Доказать:
Площадь треугольника ABC может быть найдена, например, по двум сторонам и углу между ними:
Аналогично,
Так как углы подобных треугольников равны, а стороны — пропорциональны, то ∠A=∠A1,
то есть
Теперь можем найти, как относятся площади подобных треугольников:
Так как
то
то есть
Что и требовалось доказать.
Поскольку отношение любых линейных размеров (высот, медиан, биссектрис, периметров) подобных треугольников равно коэффициенту подобия, площади подобных треугольников относятся как квадраты их соответствующих линейных размеров.
Урок 32. Отношение площадей подобных треугольников
Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников. Вернуться к Списку уроков Тематического планирования.
Урок 32. Отношение площадей
подобных треугольников
Основные дидактические цели урока: закрепить понятия пропорциональных отрезков и подобных треугольников; совершенствовать навыки решения задач на применение свойства биссектрисы треугольника и определения подобных треугольников; рассмотреть теорему об отношении площадей подобных треугольников и показать ее применение в процессе решения задач.
Ход урока
I. Организационный момент
(Учитель сообщает тему урока, формулирует цели урока.)
II. Актуализация знаний учащихся. Мотивация к учебной деятельности
1. Теоретический опрос.
(Один ученик оформляет доказательство теоремы на доске.)
2) Доказать свойство биссектрисы треугольника.
2. Проверка домашнего задания.
(Учитель проверяет решение задач № 538, 542. Два ученика готовят решение на доске.)
Задача № 538

Наводящие вопросы.
- В каком отношении биссектриса AD треугольника АВС делит сторону ВСР.
- Что можно сказать об отношении отрезков АВ и АС?
- Составьте уравнение, используя отношение отрезков АВ и АС и значение периметра треугольника АВС.
Задача № 542

Наводящие вопросы.
- Какие треугольники называются подобными?
- Чему равно отношение сходственных сторон MN и ВС, KN и AC?
- Чему равны стороны треугольника KMN?
3. Работа по индивидуальным карточкам.
(3—6 учеников работают по карточкам.)
I уровень сложности
- Треугольники KPF и ЕМТ подобны, причем КР : ME = PF : МТ = КЕ : ЕТ, ∠F = 30°, ∠Е = 49°. Найдите остальные углы этих треугольников.
- Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см. Найдите периметр треугольника АВС, если известно, что АВ = 9 см.
II уровень сложности
- ΔВВС подобен ΔАВС (рис. 7.3), AD = 16 см, DC = 9 см. ∠ABC и ∠BDA — тупые. Найдите ВС.
- Периметр треугольника равен 70 см, две его стороны равны 24 см и 32 см. Найдите отрезки, на которые биссектриса треугольника делит его третью сторону.

III уровень сложности
- Диагональ АС делит трапецию ABCD на два подобных треугольника АВС и ACD, ВС = 8 см, AD = 18 см. Найдите АС.
- В равнобедренном треугольнике точка Е — середина основания АС, а точка К делит сторону ВС в отношении 2:5, считая от вершины С. Найдите отношение, в котором прямая BE делит отрезок АК.
- Решение задач по готовым чертежам для подготовки к восприятию нового материала (работа в парах).


Ответы и указания к задачам по готовым чертежам:

(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:
- оценка «5» — правильно решены три-четыре задачи;
- оценка «4» — правильно решены две задачи;
- оценка «3» — правильно решена одна задача;
- оценка «2» — не ставится.
III. Работа по теме урока
(Учитель делит класс на группы для решения задания творческого характера. После завершения работы заслушиваются и обсуждаются варианты решений.)
Задание. Треугольники АВС и А1В1С1 подобны с коэффициентом подобия k. Найти отношение их площадей.

Вывод. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
IV. Закрепление изученного материала
- Работа в рабочих тетрадях. Решить задачу № 54. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)
- Решить задачу № 545 (работа в парах). (После завершения работы заслушиваются и обсуждаются варианты решений.)
Задача № 545
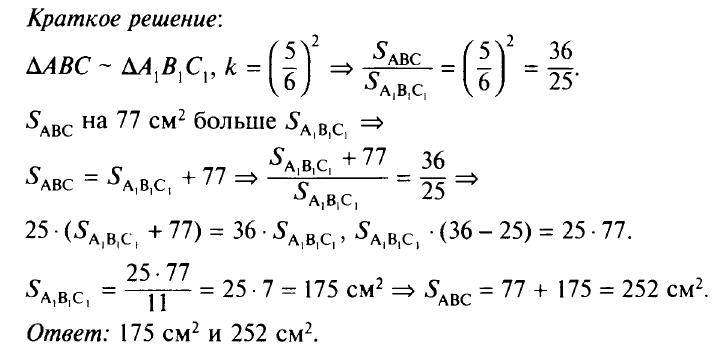
Вопросы для обсуждения.
- Чему равно отношение площадей подобных треугольников, если их сходственные стороны относятся как 6 : 5?
- Верно ли составлено уравнение исходя из условий задачи?
- Решить задачи № 547, 548 (работа в группах). (После завершения работы заслушиваются и обсуждаются варианты решений.)

V. Самостоятельная работа
I уровень сложности

II уровень сложности

III уровень сложности

VI. Рефлексия учебной деятельности
- Какие треугольники называются подобными?
- Сформулируйте свойство биссектрисы треугольника.
- Что можно сказать о площадях подобных треугольников?
Домашнее задание
- П. 60, вопросы 4 (учебник, с. 158).
- Решить задачи № 543, 544, 546, 549.
- Решить дополнительные задачи.
I уровень сложности: В подобных треугольниках АВС и KMN равны углы В и М, С и N, АС = 3 см, KN = 6 см, MN = 4 см, ∠AX = 30°. Найдите ВС, ∠K; отношение площадей треугольников AВС и KMN; АЕ и BE, если известно, что СЕ — биссектриса треугольника АВС, АВ = 3,5 см.
II уровень сложности: В прямоугольном треугольнике ABC ∠C = 90°, ∠B = 30°, АВ = 12 см, CD — высота. Докажите, что ΔACD подобен ΔАВС, найдите отношение их площадей и отрезки, на которые биссектриса угла А делит катет ВС.
Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников.
Вернуться к Списку уроков Тематического планирования.
Отношение площадей подобных треугольников / Подобные треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Отношение площадей подобных треугольников
Теорема
Доказательство
Дано:  АВС
АВС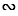
 А1В1С1, — коэффициент подобия,
А1В1С1, — коэффициент подобия, 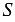 и — площади
и — площади  АВС и
АВС и  А1В1С1.
А1В1С1.
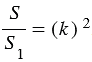 .
.
Доказательство:

1.  АВС
АВС
 А1В1С1, следовательно,
А1В1С1, следовательно, 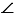 А =
А =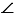 А1, значит,
А1, значит, 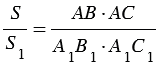 (т.к. площади треугольников, имеющих по равному углу, относятся как произведения сторон, заключающих равные углы). При этом, из подобия треугольников АВС и А1В1С1 следует то, что
(т.к. площади треугольников, имеющих по равному углу, относятся как произведения сторон, заключающих равные углы). При этом, из подобия треугольников АВС и А1В1С1 следует то, что 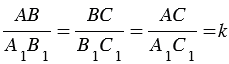 , значит,
, значит, 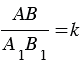 и , тогда,
и , тогда,  .
.
Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 543, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 544, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 545, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 546, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 622, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 627, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1077, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1143, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1209*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1308, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Отношение площадей подобных треугольников
На прошлом уроке мы с вами говорили, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Напомним, что подобие треугольников обозначается
следующим образом  .
.
На этом уроке мы докажем теорему об отношении площадей двух подобных треугольников.
Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство.

 ,
,
 –
коэффициент подобия.
–
коэффициент подобия.
 ,
,
 .
.
 ,
,
 .
.
 ,
,
 ,
,

Следовательно,  .
.
Что и требовалось доказать.
Задача. Площади подобных
треугольников  и
и
 равны
соответственно
равны
соответственно  см2
и
см2
и  см2.
Сторона
см2.
Сторона  см.
Найдите сходственную ей сторону
см.
Найдите сходственную ей сторону  треугольника
треугольника
 .
.
Решение.

Выше мы доказали, что отношение площадей двух
подобных треугольников равно квадрату коэффициента подобия.  ,
,  ,
,
 .
.
 ,
,
 ,
,
 (см).
(см).
Ответ:  см.
см.
Задача. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство.
 ,
,
 –
коэффициент подобия.
–
коэффициент подобия.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 ,
,
 .
.
 ,
,
 ,
,
 .
.
Что и требовалось доказать.
Задача. Треугольники  и
и
 подобны.
Сходственные стороны
подобны.
Сходственные стороны  и
и
 соответственно
равны
соответственно
равны  см
и
см
и  м.
Найдите отношение периметров треугольников
м.
Найдите отношение периметров треугольников  и
и
 .
.
Решение:

 м
м см.
см.
 .
.
 .
.
Ответ:  .
.
Итак, на этом уроке мы доказали, что отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. А также решили несколько задач. Причём при решении одной из них установили, что отношение периметров двух подобных треугольников равно коэффициенту подобия.
Решение задач по теме «Отношение площадей подобных треугольников»

ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ

Свойство
Если высоты треугольников равны, то площади относятся как основания .

Свойство
Медиана делит треугольник на два равновеликих треугольника.
Три медианы делят треугольник на 6 равновеликих треугольников.

Теорема
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведение сторон, заключающих равные углы

Доказать:
Дано:

Дайте ответы на вопросы:
1. Что называют отношением отрезков AB и CD?
2. При каком условии отрезки AB, CD и A 1 B 1 , C 1 D 1 называют пропорциональными?
3. Назовите сходственные стороны треугольников ∆MKL и ∆PZD, если
∠ M=∠Z, ∠K=∠D, ∠L=∠P.
4. Используя свойство биссектрисы треугольника, найдите KN, если OC=4см, CN=3см, OK=2см.
K
M L
Z
P
D
C
O K N

Теорема: «Об отношении площадей подобных треугольников» Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Дано: ∆ABC ∾ ∆A 1 B 1 C 1
Доказать:
Доказательство:
1. Так как по условию ∆ABC ∾ ∆A 1 B 1 C 1 , то
∠ A=∠A 1 , по теореме об отношении площадей треугольников (п.53), значит
2. Так как
ч.т.д.
C
A B
C 1
A 1 B 1

Реши задачи
- Две сходственные стороны подобных треугольников равны
8 см и 4 см. Периметр второго треугольника равен 12 см.
Чему равен периметр первого треугольника ?
24 см
2. Две сходственные стороны подобных треугольников равны
9 см и 3 см. Площадь второго треугольника равна 9 см 2 .
Чему равна площадь первого треугольника ?
81 см 2
3. Две сходственные стороны подобных треугольников равны
5 см и 10 см. Площадь второго треугольника равна 32 см 2 .
Чему равна площадь первого треугольника ?
8 см 2
4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 .
Одна из сторон первого треугольника равна 4 см. Чему равна
сходственная сторона второго треугольника ?
8 см

Закрепление. № 544
Дано : ∆ABC ∾ ∆A 1 B 1 C 1 ,
Найти : AC
Решение :
1.Так как по условию
то по т . «Об отношении площадей подобных треугольников»:
2.Так как : ∆ABC ∾ ∆A 1 B 1 C 1 , а также
AC и A 1 C 1 – сходственные стороны, k=2, то
Ответ: AC=4,5 (м)
B
A C
B 1
A 1 C 1

Закрепление. № 54 5
Дано : ∆ABC ∾ ∆A 1 B 1 C 1 , AC: A 1 C 1 =6:5
Найти :
Решение :
1.Пусть S A1B1C1 =x см 2 , S ABC =(x+77) см 2
2.Так как AC: A 1 C 1 =6:5 , то
3.По теореме об отношении площадей подобных треугольников:
Значит S A 1 B 1 C 1 = 175 см 2 , S ABC = 252 см 2
Ответ: S A 1 B 1 C 1 = 175 см 2 , S ABC = 252 см 2
B
A C
B 1
A 1 C 1

Закрепление. № 537
A
C D B
Дано : ∆ABC, AD – биссектриса ∆ABC, AB=14см, AC=21см, BC=20см
Найти : BD, DC
Решение :
1.Так как по условию BC=20см, BC=CD+DB, то пусть BD=x см , CD=(20-x) см .
2.Так как по условию AD – биссектриса ∆ABC, то по свойству биссектрисы треугольника BD:AB=CD:AC (1).
3.Так как по условию AB=14см, AC=21см, то (1) – примет вид:
Значит BD=8 см , DC=12 см .
Ответ: BD=8 см , DC=12 см .

Домашнее задание:
п.п. 1 — 60 ;
№ 538, №548 (воспользоваться условием № 547)

Самопроверка домашнего задания по образцу № 538
A
C D B
Дано : ∆ABC, AD – биссектриса ∆ABC, CD=4,5 см , BD=13,5 см , P ABC =42 см.
Найти : AB и AC
Решение :
1.Так как CB=CD+DB, CD=4,5 см , BD=13,5 см, то CB=18 см.
2.Пусть AB = х. Так как P ABC =42 см , CB=18 см ,
то AC = 42-(18+х) = 24-х ( см).
3.По свойству биссектрисы треугольника:
т.е.
Значит AB=18 см и AC =6 см .
Ответ: AB=18 см и AC =6 см .

Самопроверка домашнего задания по образцу № 5 47
B
A C
B 1
A 1 C 1
Дано : ∆ABC ∾ ∆A 1 B 1 C 1
Доказать :
Доказательство :
1. Так как по условию ∆ABC ∾ ∆A 1 B 1 C 1 , то
2.
ч.т.д.
Итак если ∆ABC ∾ ∆A 1 B 1 C 1 , то

Самопроверка домашнего задания по образцу № 5 48
Дано : ∆ABC ∾ ∆A 1 B 1 C 1 ,
BC и B 1 C 1 – сходственные стороны,
BC = 1,4 м = 140 см , B 1 C 1 = 56 см .
Найти :
Решение :
Ответ:
Треугольники — Part 24
Выясним, в каких случаях равнобедренные треугольники подобны.
Признаки подобия равнобедренных треугольников
1) Если угол между боковыми сторонами одного равнобедренного треугольника равен углу между боковыми сторонами другого равнобедренного треугольника, то такие треугольники подобны.
Читать далее
Подобие треугольников, Равнобедренный треугольникУтверждение
Если в треугольник вписан ромб так, что один угол у них — общий, а противоположная ему вершина ромба принадлежит третьей стороне треугольника, то ромб отсекает два треугольника, подобные данному.
Дано: ∆ ABC,
AMNK — ромб, N∈BC.
Доказать:
Доказательство:
Читать далее
Подобие треугольниковУтверждение
Если в треугольник вписан параллелограмм таким образом, что один угол у них общий, а три другие вершины параллелограмма лежат на сторонах треугольника, то параллелограмм отсекает два треугольника, подобных данному.
Дано: ∆ ABC, ADEF — параллелограмм,
D∈AB, E∈BC, F∈AC.
Читать далее
Подобие треугольниковУтверждение
Площади подобных треугольников относятся как квадраты их соответствующих сторон, то есть отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Дано:
Доказать:
Читать далее
Найти площадь треугольника, Подобие треугольниковДиагонали трапеции пересекаются в точке. Что можно сказать об образовавшихся треугольниках, прилежащих к основаниям?
Утверждение.
Если диагонали трапеции пересекаются в точке, то образованные при этом прилежащие к основаниям треугольники подобны.
Дано: ABCD — трапеция,
Доказать:
Читать далее
Подобие треугольников, ТрапецияПодобие прямоугольных треугольников обычно доказывают, используя не общие признаки, а специальные признаки подобия для прямоугольных треугольников.
Признаки подобия прямоугольных треугольников
1- й признак подобия прямоугольных треугольников
( подобие прямоугольных треугольников по острому углу)
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Читать далее
Подобие треугольников