Линейные операции над векторами. Примеры решения задач. Часть 1
Задача № 1. По данным векторам 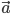 и
и 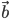 построить каждый из следующих векторов:
построить каждый из следующих векторов:
1) 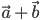 ; 2)
; 2) .
.
Решение. Пусть даны такие два вектора 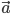 и
и 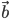 .
.
1) 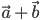
I способ. Помещаем начало векторов
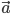 и
и 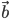 в точку О и строим параллелограмм ОВСА. Диагональ ОС изображает сумму
в точку О и строим параллелограмм ОВСА. Диагональ ОС изображает сумму 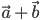 .
.
Рис.1
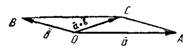
Рис.2
II способ. Помещаем начало вектора 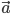
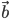 совмещаем с концом вектора
совмещаем с концом вектора 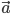 . Замыкающий вектор есть
. Замыкающий вектор есть 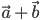 . Его начало — в точке О, а конец совпадает с концом вектора
. Его начало — в точке О, а конец совпадает с концом вектора 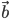 .
.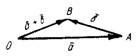
Рис.3
2)  .
.
I способ.
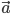 помещаем в точку О и строим вектор
помещаем в точку О и строим вектор 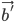 по длине равный вектору
по длине равный вектору 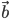 , но противоположного направления.
, но противоположного направления.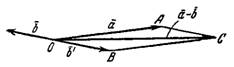
Рис.4
Теперь находим сумму векторов 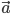 и
и 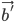 по правилу параллелограмма. Искомый вектор
по правилу параллелограмма. Искомый вектор 
II способ. Начало векторов
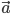 и
и 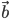 помещаем в одну точку О. Концы векторов соединяем. Замыкающий вектор есть
помещаем в одну точку О. Концы векторов соединяем. Замыкающий вектор есть  ; его начало — в конце вектора
; его начало — в конце вектора 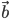 , конец — в конце вектора
, конец — в конце вектора 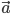 .
.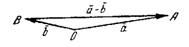
Рис.5
Задача № 2. В треугольнике ABC вектор 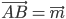 и вектор
и вектор 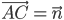 . Построить каждый из следующих векторов:
. Построить каждый из следующих векторов:
1) 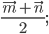 2)
2)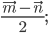 3)
3) 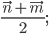 4)
4) 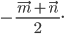
Решение задачи №2 подробно изложено в следующем видео
Задача № 3. Точка О является центром тяжести треугольника ABC. Доказать, что 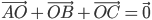 .
.
Задача № 4. В правильном пятиугольнике ABCDE заданы векторы, совпадающие с его сторонами: 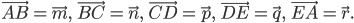
Построить вектор: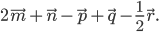
Решения этих задач подробно изложено в следующем видео
Разложение вектора по трём некомпланарным векторам. Задачи
Тема: Векторы в пространстве
Урок: Разложение вектора по трем некомпланарным векторам. Задачи
Определение:
Вектором называется направленный отрезок. У вектора 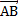 точка А – начало вектора, точка В – конец.
точка А – начало вектора, точка В – конец.
Для вектора важна не только длина, но и направление.
Определение:
Коллинеарными называют векторы, принадлежащие одной и той же или параллельным прямым.
Коллинеарные векторы могут быть сонаправленными и противонаправленными.
Определение:
Равными называют коллинеарные сонаправленные векторы, длины которых равны.
Любой вектор можно единственным образом отложить от произвольной точки.
Для сложения векторов применяются правила треугольника, параллелограмма, многоугольника и параллелепипеда.
При умножении вектора на положительное число его длина умножается на это число, а направление остается неизменным. При умножении вектора на отрицательное число его длина умножается на это число, а направление меняется на противоположное.
Новым для векторов в пространстве относительно векторов на плоскости является понятие компланарности.
Определение:
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Мы знаем, что если заданы два неколлинеарных вектора на плоскости, то любой третий вектор на той же плоскости можно однозначно разложить по этим векторам (рис. 1, 2):
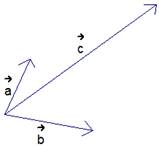
Рис. 1. Векторы на плоскости
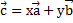
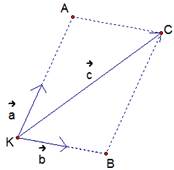
Рис. 2. Разложение вектора через два неколлинеарных
Данный факт легко доказывается. Пусть 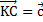 . Из точки С проводим прямую CB, параллельно вектору
. Из точки С проводим прямую CB, параллельно вектору 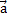
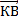 , коллинеарный вектору
, коллинеарный вектору 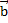 . Аналогично из точки С проводим прямую CА, параллельно вектору
. Аналогично из точки С проводим прямую CА, параллельно вектору 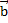 . Получаем вектор
. Получаем вектор 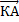 , коллинеарный вектору
, коллинеарный вектору 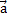
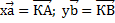
Вопрос на понимание компланарности векторов. Если вектор 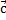 можно представить в виде
можно представить в виде 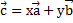 , где х и у – конкретные числа, то векторы
, где х и у – конкретные числа, то векторы 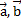 и
и 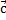 компланарны.
компланарны.
Если заданы три некомпланарных вектора, то мы можем однозначно разложить любой заданный четвертый вектор через три заданных. Например, заданы некомпланарные векторы 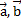 и
и 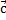 . Тогда любой вектор
. Тогда любой вектор 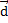 можно представить в виде суммы:
можно представить в виде суммы: 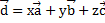 , где х, у и z – конкретные числа, причем для заданного вектора единственные. Эти числа называются коэффициентами разложения.
, где х, у и z – конкретные числа, причем для заданного вектора единственные. Эти числа называются коэффициентами разложения.
Задача 1: дан куб  с ребром m. Точка К – середина ребра
с ребром m. Точка К – середина ребра  . Разложить вектор
. Разложить вектор 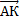 по векторам
по векторам 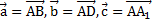 и найти его длину.
и найти его длину.
Решение: построим заданный куб (рис. 3).
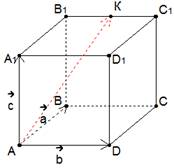
Рис. 3. Куб, задача 1
Векторами 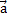 и
и 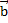 задается плоскость квадрата
задается плоскость квадрата 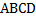 . Третий вектор
. Третий вектор 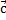 не лежит в этой плоскости, отсюда заключаем, что три заданных вектора
не лежит в этой плоскости, отсюда заключаем, что три заданных вектора 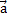 ,
, 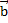 и
и 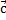 некомпланарны, и мы можем выразить через них искомый вектор
некомпланарны, и мы можем выразить через них искомый вектор 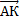 . Найдем вектор
. Найдем вектор 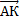 по правилу многоугольника. Очевидно, что в данной задаче для этого есть множество способов, но мы выбираем самый короткий путь:
по правилу многоугольника. Очевидно, что в данной задаче для этого есть множество способов, но мы выбираем самый короткий путь: 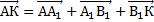 . вектор
. вектор 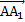 мы по условию обозначили как вектор
мы по условию обозначили как вектор 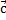 . Вектор
. Вектор 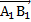 согласно свойствам куба равен вектору
согласно свойствам куба равен вектору 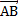 , обозначенному за вектор
, обозначенному за вектор 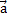 .
.
вектор 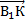 составляет половину вектора
составляет половину вектора 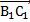 , так как точка К – середина ребра
, так как точка К – середина ребра  по условию:
по условию: 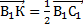 . Вектор
. Вектор 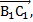 согласно свойствам куба, равен вектору
согласно свойствам куба, равен вектору 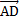 , обозначенному как вектор
, обозначенному как вектор 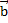 . Имеем:
. Имеем: 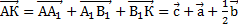
Так, заданный вектор выражен через три некомпланарных вектора. Осталось найти его длину. Здесь нужно применить теорему Пифагора. Рассмотрим прямоугольный треугольник 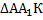 . Он прямоугольный потому, что ребро
. Он прямоугольный потому, что ребро 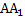 перпендикулярно всей плоскости основания
перпендикулярно всей плоскости основания 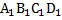 , значит и любой прямой в этой плоскости, значит прямой
, значит и любой прямой в этой плоскости, значит прямой 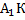 . Один из катетов
. Один из катетов 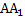 равен m как ребро куба. Катет
равен m как ребро куба. Катет 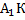 найдем из другого прямоугольного треугольника –
найдем из другого прямоугольного треугольника – 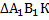 , где он уже является гипотенузой. Здесь катет
, где он уже является гипотенузой. Здесь катет 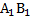 равен m как ребро куба. Катет
равен m как ребро куба. Катет 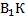 равен
равен 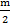 , так как точка К – середина ребра
, так как точка К – середина ребра  . Имеем:
. Имеем: 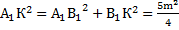
Вернемся к первому треугольнику: 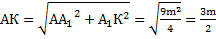
Задача 2: векторы 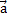 ,
, 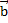 и
и 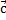 компланарны. Компланарны ли векторы
компланарны. Компланарны ли векторы 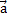 ,
, 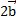 и
и 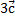 ? Компланарны ли векторы
? Компланарны ли векторы 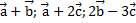 ?
?
Решение: тот факт, что векторы 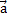 ,
, 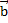 и
и 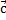 компланарны, означает, что, будучи отложенными от одной точки, они расположены в одной плоскости (рисунок 4.а). Это значит, что один из векторов, например, вектор
компланарны, означает, что, будучи отложенными от одной точки, они расположены в одной плоскости (рисунок 4.а). Это значит, что один из векторов, например, вектор 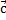 , можно однозначно разложить по двум другим:
, можно однозначно разложить по двум другим: 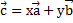 . Очевидно, что векторы
. Очевидно, что векторы 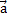 ,
, 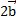 и
и 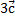 тоже компланарны, т. к. умножение вектора на положительное число не меняет его направления, а меняет только длину, и векторы останутся в той же плоскости (рисунок 4.б).
тоже компланарны, т. к. умножение вектора на положительное число не меняет его направления, а меняет только длину, и векторы останутся в той же плоскости (рисунок 4.б).
|
Рис. 4. а |
Рис. 4. б |
Очевидно, что тройка векторов 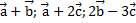 также компланарна, потому что всякая линейная комбинация компланарных векторов есть вектор, им компланарный. Мы имеем три вектора, компланарных заданным векторам, очевидно, что они компланарны между собой.
также компланарна, потому что всякая линейная комбинация компланарных векторов есть вектор, им компланарный. Мы имеем три вектора, компланарных заданным векторам, очевидно, что они компланарны между собой.
Итак, мы вспомнили все основные определения и теоремы касательно векторов в пространстве, подробно остановились на понятии компланарности векторов и рассмотрели типовые задачи на эту тему.
Список литературы
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
- Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Домашнее задание
 – параллелепипед. М – точка пересечения
– параллелепипед. М – точка пересечения  и
и  .
.  . Разложите вектор
. Разложите вектор  по трем заданным векторам.
по трем заданным векторам.- в тетраэдре DABC O – точка пересечения медиан треугольника АВС, точка F принадлежит ребру AD, причем
 . Разложите вектор
. Разложите вектор  по векторам
по векторам  .
. - используя векторы, докажите, что диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Webmath.exponenta.ru (Источник).
- СтудопедиЯ (Источник).
- Научная библиотека (Источник).
Глава 30. Линейные операции над векторами
Глава 30. Линейные операции над векторами
Суммой двух векторов и называется вектор, который идет из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правильно треугольника). Построение суммы изображено на рис. 1.
Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограма: если векторы и приведены к общему началу и на них построен параллелограмм, то сумма есть вектор, совпадающий с диагональю этого паралеллограмма, идущей из общего начала и (рис. 2). Отсюда сразу следует, что .
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 3, где изображено построение суммы четырех векторов , , , ).
Разность двух векторов и называется вектор, который в сумме с вектором составляет вектор . Если два вектора и приведены к общему началу, то разность их есть вектор, идущий из конца («вычитаемого») к концу («уменьшаемого»). Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются взаимно обратными: если один из них обозначен символом , то другой обозначается символом . Легко видеть, что . Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».
Произведение (или также ) вектора на число называется вектор, модуль которого равен произведению модуля вектора на модуль числа ; он параллелен вектору или лежит с ним на одной прямой и направлен так же, как вектор , если — число положительное, и противоположно вектору , если — число отрицательное.
Сложение векторов и умножение вектора на число называются линейными операциями над векторами.
Имеют место следующие две основные теоремы о проекциях векторов:
1). Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось:
2). При умножении вектора на число его проекция умножается на то же число:
.
В частности, если
, ,
то
,
и
.
Если , то для любого числа
.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов
, ,
является пропорциональность их координат:
.
Тройка векторов , , называется координатным базисом, если эти векторы удовлетворяют следующим условиям:
1). Вектор лежит на оси Ох, вектор — на оси Оу, вектор — на оси Oz;
2). Каждый из векторов , , направлен по своей оси в положительную сторону;
3). Векторы , , единичные, то есть , , .
Каким бы ни был вектор , он всегда может быть разложен по базису , , , то есть может быть представлен в виде
;
коэффициенты этого разложения являются координатами вектора (то есть X, Y, Z суть проекции вектора на координатные оси).
| 761 | По данным векторам и построить каждый из следующих векторов: 1). , 2). , 3). , 4). . | |
| 762 | Даны =13, =19 и =24. Вычислить . | |
| 763 | Даны =11, =23 и =30. Определить . | |
| 764 | Векторы и взаимно перпендикулярны, причем =5, =12. Определить и . | |
| 765 | Векторы и образуют угол =600, причем=5 и =8. Определить и . | |
| 766 | Векторы и образуют угол =1200, причем =3 и =5. Определить и . | |
| 767 | Какому условию должны удовлетворять векторы и , чтобы имели место следующие соотношения: | |
| 767.1 | ; | |
| 767.2 | ; | |
| 767.3 | . | |
| 768 | Какому условию должны удовлетворять векторы и , чтобы вектор делил пополам угол между векторами и . | |
| 769 | По данным векторам и построить каждый из следующих векторов: | |
| 769.1 | ; | |
| 769.2 | ; | |
| 769.3 | ; | |
| 769.4 | . | |
| 770 | В треугольнике АВС вектор и вектор . Построить каждый из следующих векторов. Принимая в качестве масштабной единицы , построить также векторы: | |
| 770.1 | ; | |
| 770.2 | ; | |
| 770.3 | ; | |
| 770.4 | ; | |
| 770.5 | ; | |
| 770.6 | . | |
| 771 | Точка О является центром масс треугольника АВС. Доказать, что . | |
| 772 | В правильном пятиугольнике ABCDE заданы векторы, совпадающие с его ребрами: , , , , . Построить векторы: | |
| 772.1 | ; | |
| 772.2 | ; | |
| 772.3 | . | |
| 773 | В параллелепипеде ABCDA’B’C’D’ (рис.) заданы векторы, совпадающие с его ребрами: , , . Построить каждый из следующих векторов: | |
| 773.1 | ; | |
| 773.2 | ; | |
| 773.3 | ; | |
| 773.4 | ; | |
| 773.5 | . | |
| 774 | Три силы , , , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей , если известно, что =2Н, =10Н, =11Н. | |
| 775 | Даны два вектора ={3; -2; 6}, ={-2; 1; 0}. Определить проекции на координатные оси следующих векторов: | |
| 775.1 | ; | |
| 775.2 | ; | |
| 775.3 | ; | |
| 775.4 | ; | |
| 775.5 | ; | |
| 775.6 | . | |
| 776 | Проверить коллинеарность векторов ={2; -1; 3} и ={-6; 3; -9}. Установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. | |
| 777 | Определить, при каких значениях , векторы и коллинеарны. | |
| 778 | Проверить, что четыре точки A(3; -1; 2), B(1; 2; -1), C(2; 2; -7), D(3; -5; 3) служат вершинами трапеции. | |
| 779 | Даны точки A(-1; 5; -10}, B(5; -7; 8), C(2; 2; -7), D(5; -4; 2). Проверить, что векторы и коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны. | |
| 780 | Найти орт вектора ={6; -2; -3}. | |
| 781 | Найти орт вектора ={3; 4; -12}. | |
| 782 | Определить модули суммы и разности векторов ={3; -5; 8} и ={-1; 1; -4}. | |
| 783 | Дано разложение вектора по базису , , : . Определить разложение по этому же базису вектора , параллельного вектору и противоположного с ним направления, при условии, что =75. | |
| 784 | Два вектора ={2; -3; 6} и ={-1; 2; -2} приложены к одной точке. Определить координаты вектора направленного по биссектрисе угла между векторами и , при условии, что . | |
| 785 | Векторы ={2; 6; -4} и ={4; 2; -2} совпадают со сторонами теругольника АВС. Определить координаты векторов, приложенных к вершинам треугольника и совпадающими с его медианами AM, BN, CP. | |
| 786 | Доказать, что если и — какие угодно неколлинеарные векторы, то всякий вектор, лежащих в их плоскости, может быть представлен в виде . Доказать, что числа и однозначно определяются векторами , и . | |
| 787 | На плоскостиданы два вектора ={2; -3}, ={1; 2}. Найи разложение вектора ={9; 4} по базису , . | |
| 788 | На плоскости даны три вектора ={3; -2}, ={-2; 1}, ={7; -4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других. | |
| 789 | Даны три вектора ={3; -1}, ={1; -2}, ={-1; 7}. Определить разложение вектора по базису , . | |
| 790 | Принимая в качестве базиса векторы и , совпадающие со сторонами треугольника АВС, опреедлить разложение векторов, приложенных в вершинах треугольника и совпадающие с его медианами. | |
| 791 | На плоскости даны етыре точки A(1; -2), B(2; 1), C(3; 2), D(-2; 3). Определить разложение векторов , , и , принимая в качестве базиса векторы и . | |
| 792 | Доказать, что если , , — какие угодно некомпланарные векторы, то всякий вектор пространства может быть представлен в виде . Доказать, что числа , , однознчно определяются векторами , , , . (Представление вектора в виде называется разложением его по базису , , . Числа , , называются коэффициентами этого разложения. | |
| 793 | Даны три вектора ={3; -2; 1}, ={-1; 1; -2}, ={2; 1; -3}. Найти разложение вектора ={11; -6; 5} по базису , , . | |
| 794 | Даны четыре вектора ={2; 1; 0}, ={1; -2; 2}, ={2; 2; -1}, ={3; 7; -7}. Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных. |
Смешанное произведение трёх векторов и его приложения
Задача 12. Даны
координаты вершин параллелепипеда 
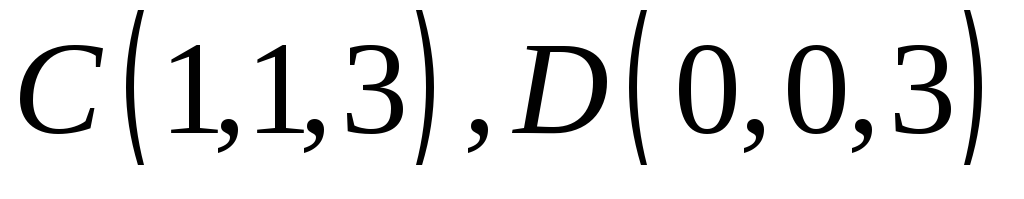 .
Найти: 1) объём параллелепипеда; 2) высоту,
опущенную из вершины C;
3) угол между вектором
.
Найти: 1) объём параллелепипеда; 2) высоту,
опущенную из вершины C;
3) угол между вектором  и гранью, в которой лежат векторы
и гранью, в которой лежат векторы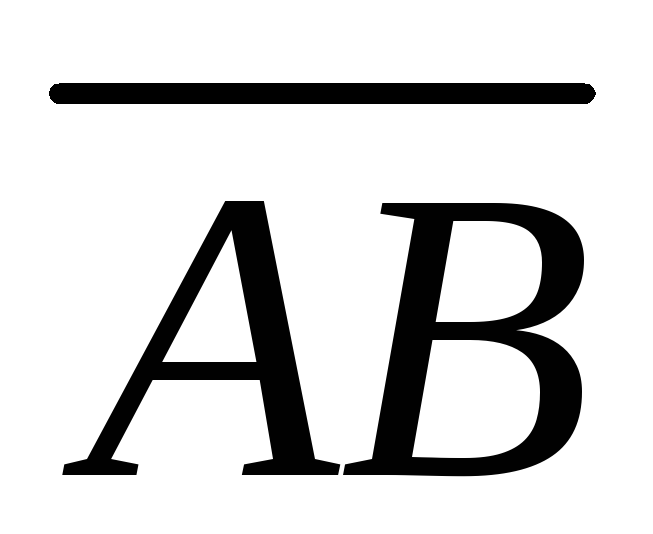 и
и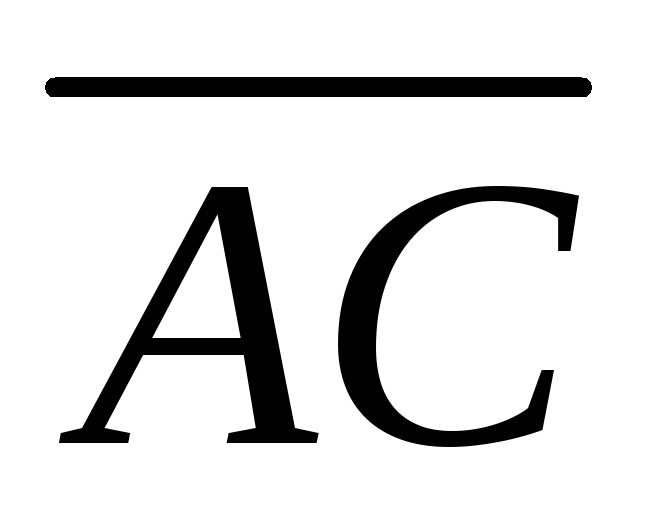 .
.
Решение.
Определим векторы 
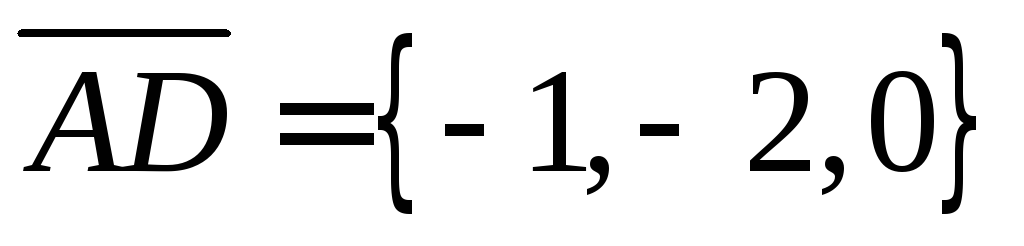 .
.
1
 ).
).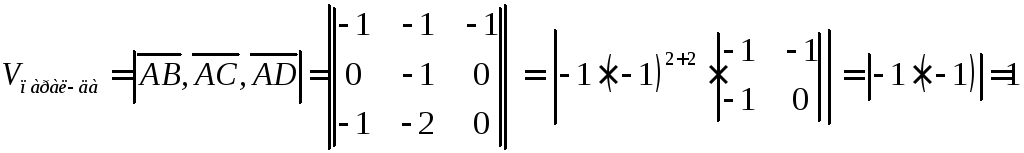 .
.
2). 
 ?
? ,
,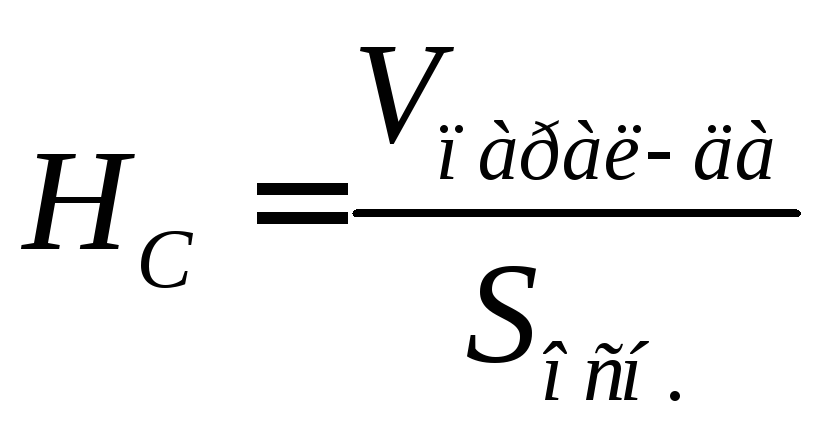 .
.
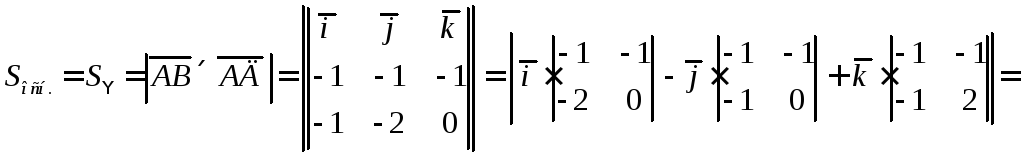
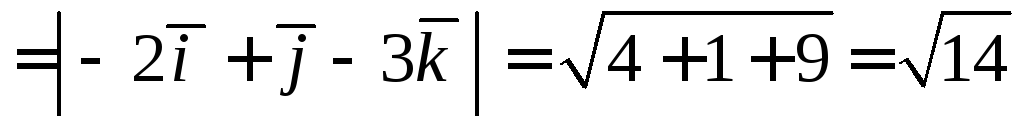 .
Тогда
.
Тогда  .
.
|
Для этого определим
угол между вектором |
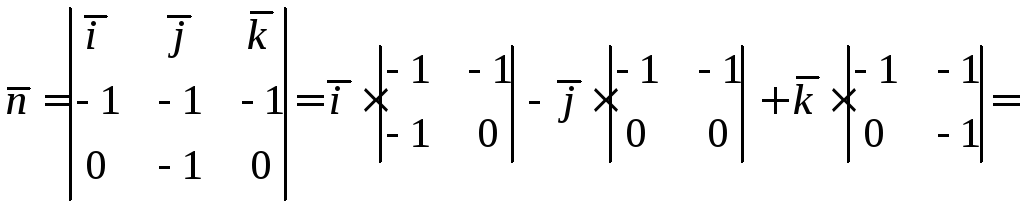
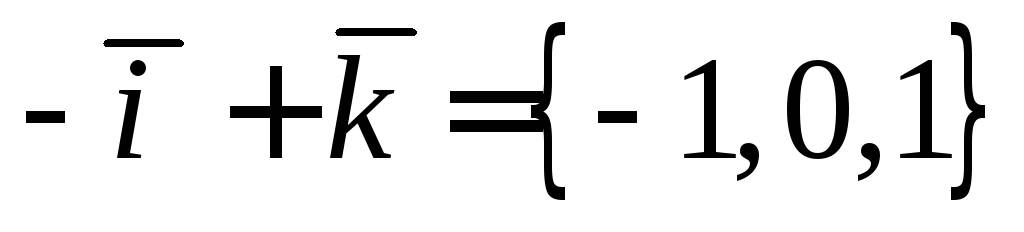 .
.
Тогда 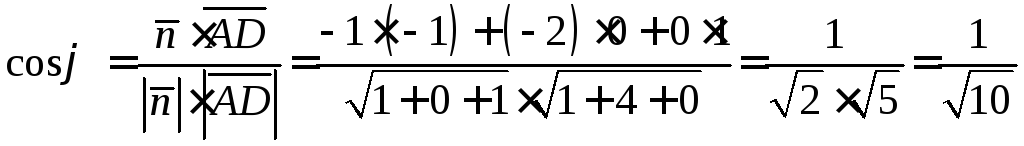 .
. .
.
Угол 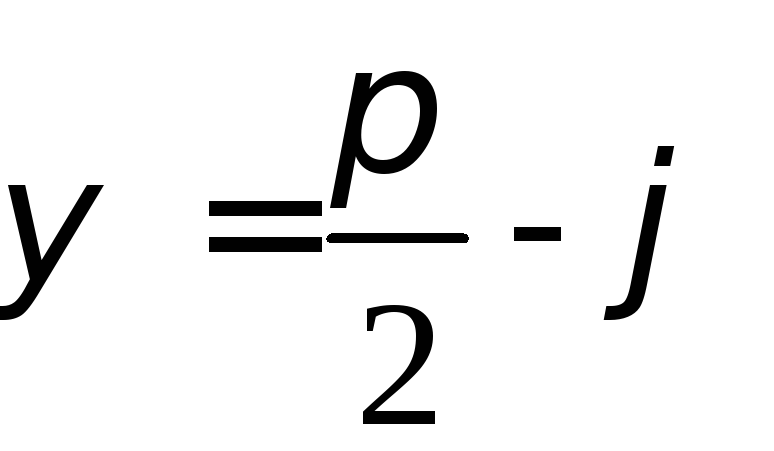 ,
т.е.
,
т.е. .
.
Задача 13. Проверить
лежат ли четыре точки 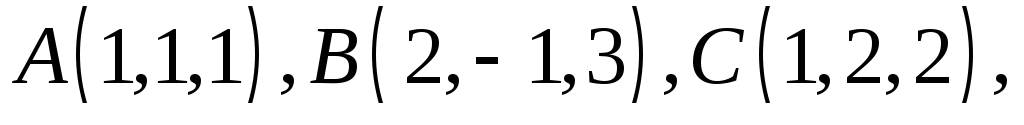
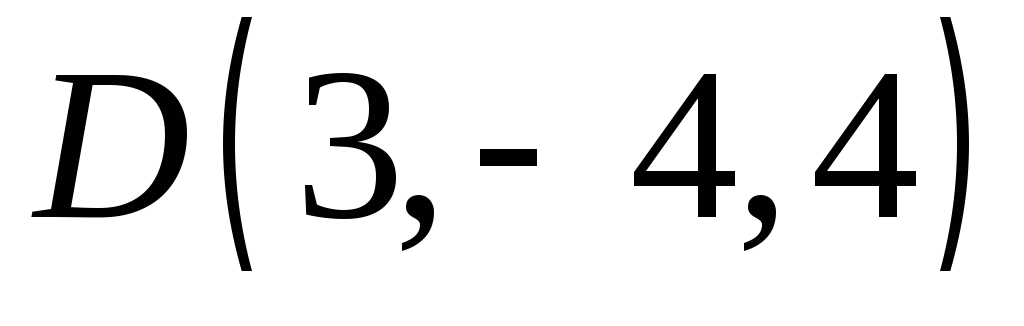 в одной плоскости.
в одной плоскости.
Решение. Если точки лежат в одной плоскости, то
и векторы, например, 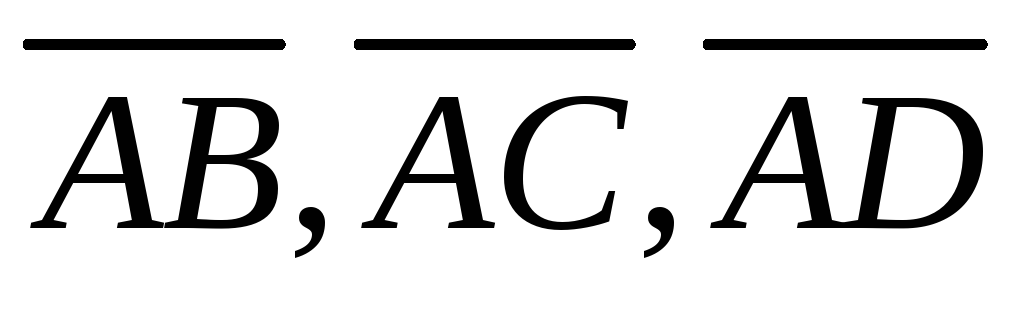 лежат в одной плоскости, т.е. компланарны,
следовательно, их смешанное произведение
равно 0. Определим векторы:
лежат в одной плоскости, т.е. компланарны,
следовательно, их смешанное произведение
равно 0. Определим векторы: ,
,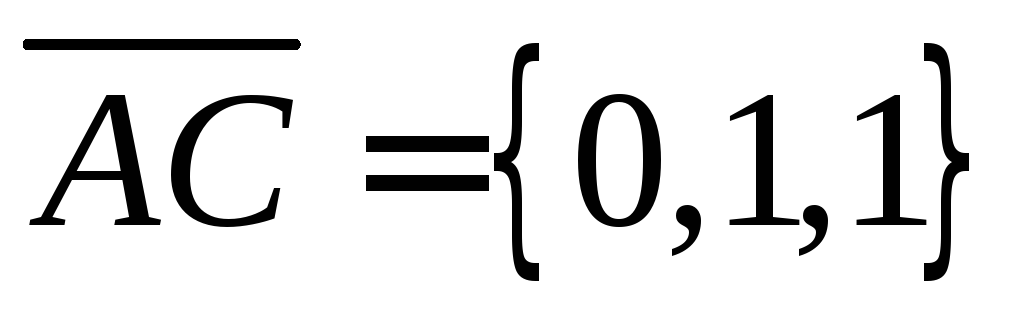 ,
,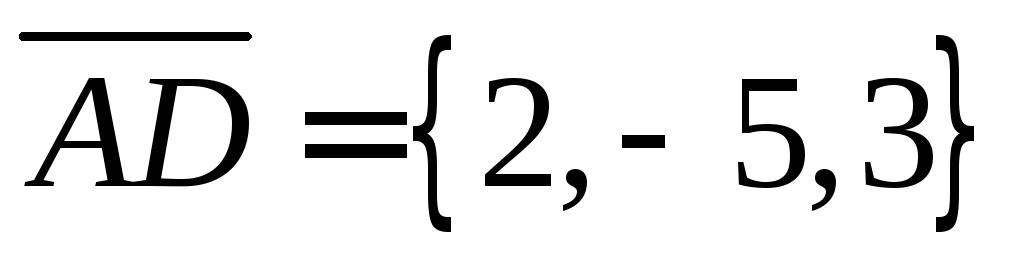 .
.
С оставим
определитель:
оставим
определитель:
Определитель
равен нулю, следовательно, векторы
линейно зависимы. Найдём линейную
зависимость, например, вектора  от
от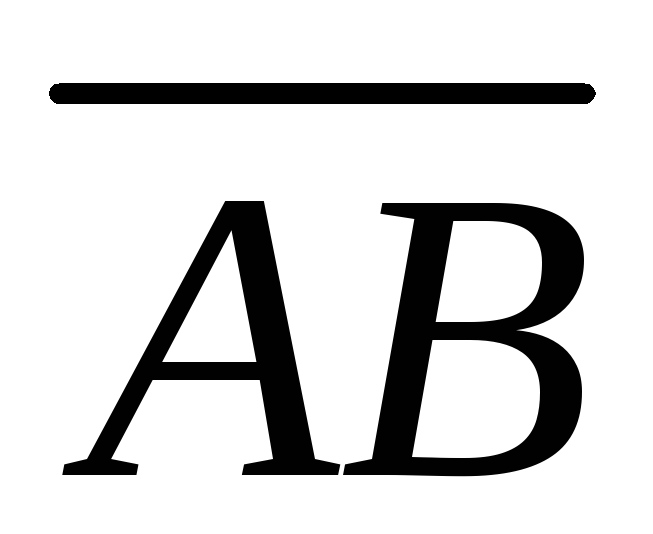 и
и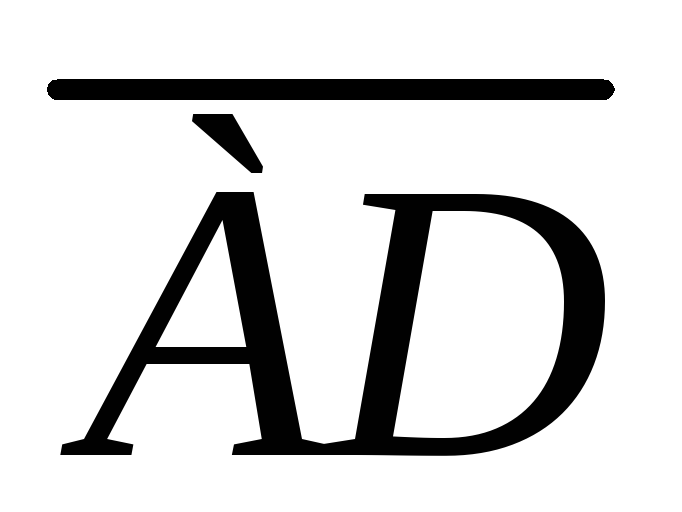 .
.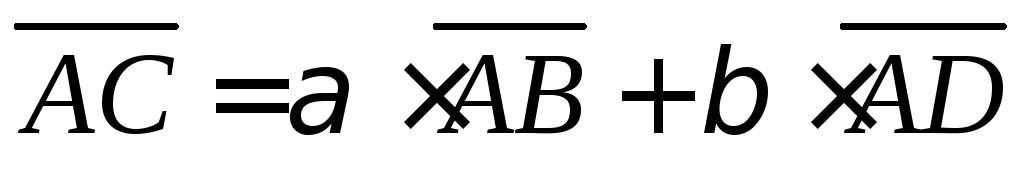 .
.

 .
Тогда
.
Тогда  .
.
Получим 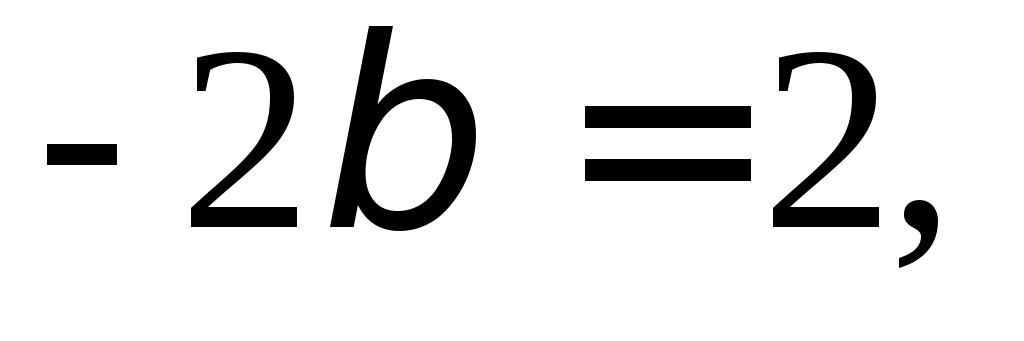
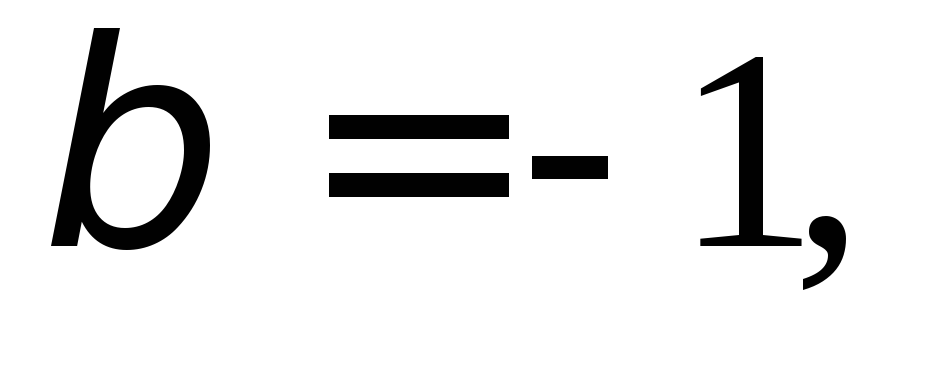
 .
Тогда
.
Тогда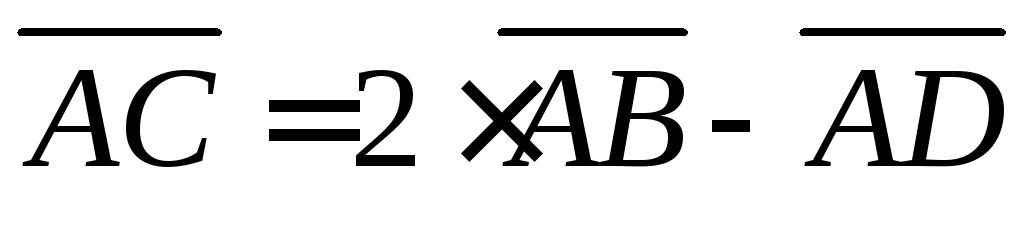 .
.
7. Индивидуальные домашние задания
Индивидуальные домашние задания выполняется по графику, разработанному кафедрой «Высшая математика», и соответствуют обязательной части практической работы второго раздела программы первого семестра.
Решения задач необходимо представлять в письменном виде в отдельных тетрадях. Нумерация задач должна совпадать с их нумерацией в задании.
В работе должны быть указаны условия задач и развёрнутое решение с пояснениями.
Защита ИДЗ для студентов дневной формы обучения проводится в виде контрольных работ на практических занятиях или на консультациях.
Во время защиты студент должен ответить на контрольные вопросы, пояснить решения задач из заданий, решить аналогичные задачи.
Повторная защита для студентов дневной формы обучения проводится на консультациях.
Студенты, не защитившие ИДЗ повторно, защищают их по графику,
составленному преподавателем.
Студенты заочной формы обучения сдают ИДЗ на проверку в межсессионный период.
Защита ИДЗ для студентов заочной формы обучения проводится на консультациях и в экзаменационную сессию.
№ | Тема | для ДО | для ЗО |
1 | Линейные операции над векторами | Задачи 1, 2 | Задачи 1, 2 |
2 | Скалярное произведение двух векторов и его приложения | Задачи 3, 4, 5 | Задачи 4, 5 |
3 | Векторное произведение двух векторов и его приложения | Задачи 6, 7, 8 | Задачи 7, 8 |
4 | Смешанное произведение трёх векторов и его приложения | Задачи 9, 10 | Задачи 9, 10 |
З а д а ч а 1
1. Дан параллелограмм
ABCD.
Доказать, что  ,
где
,
где

 произвольная точка
пространства.
произвольная точка
пространства.
2. В параллелограмме ABCD: 
 точка пересечения диагоналей. Найти
точка пересечения диагоналей. Найти  ,
если а)
,
если а)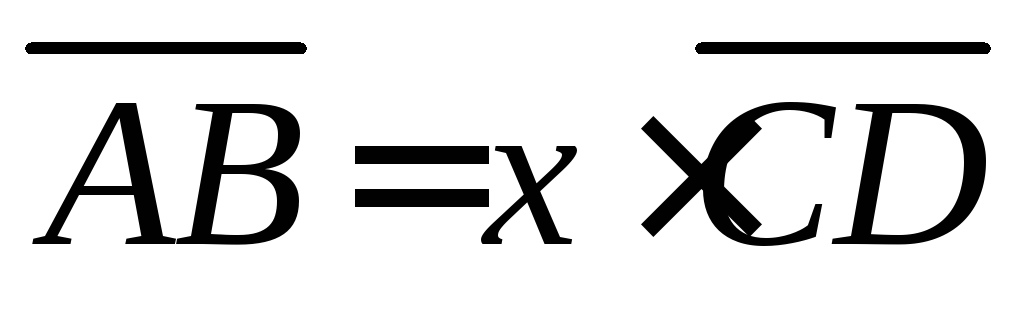 ,
б)
,
б) ,
в)
,
в)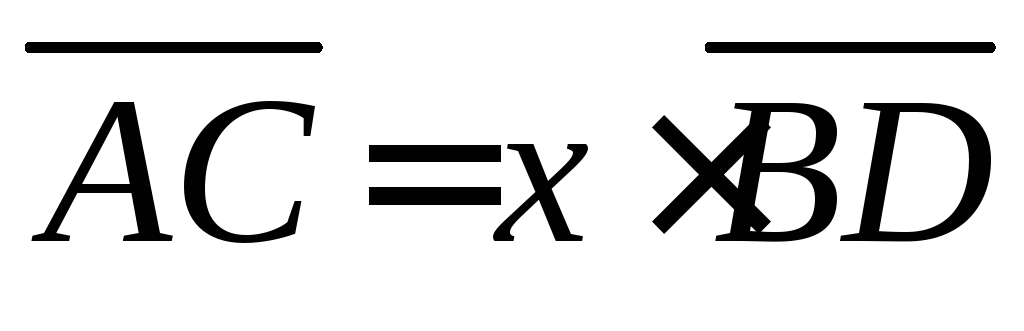 ,
г)
,
г)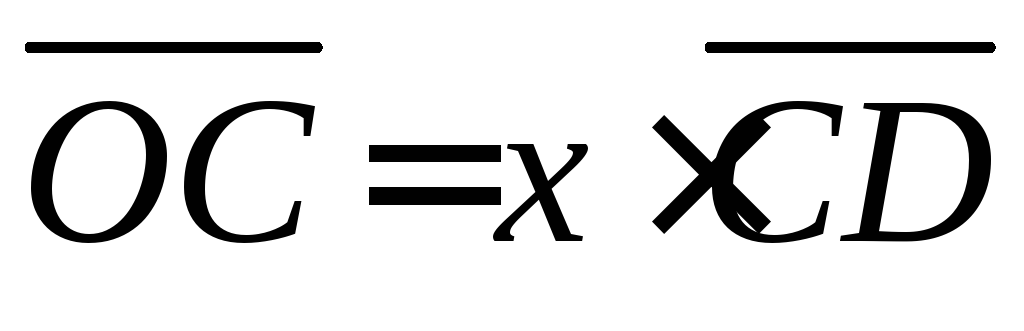 .
.
3. В ромбе ABCD диагонали 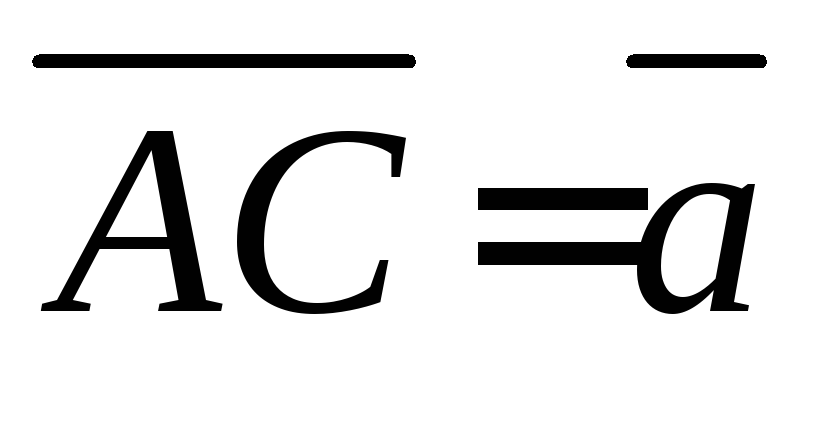 ,
, .
Разложить по этим двум
.
Разложить по этим двум
векторам векторы 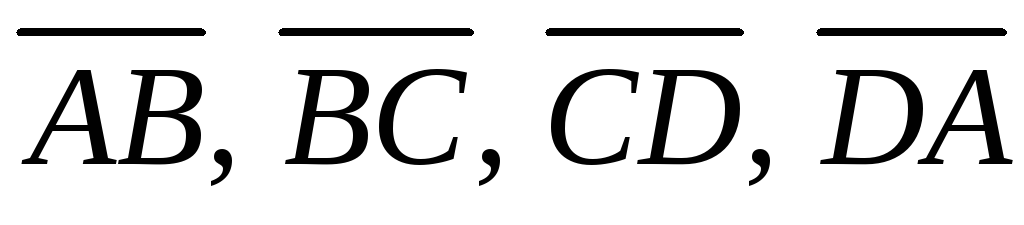 .
.
4. В треугольнике
PQR: 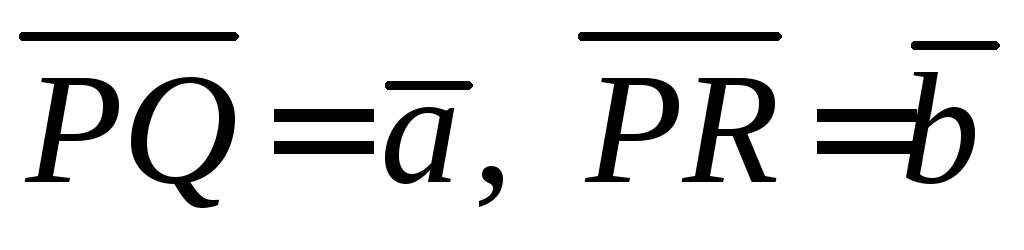 ,
точка
,
точка
 середина стороныQR. Выразить вектор
середина стороныQR. Выразить вектор  через векторы
через векторы и
и .
.
5. На сторонах ОА и ОВ в прямоугольнике ОАСВ отложены единичные векторы 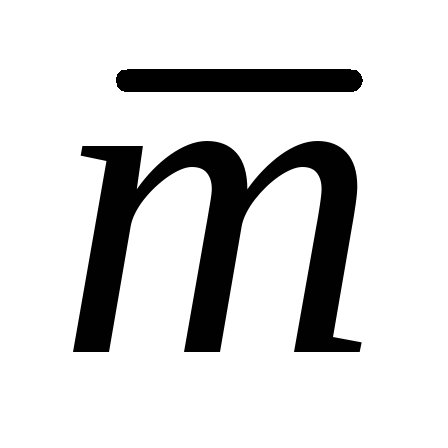 и
и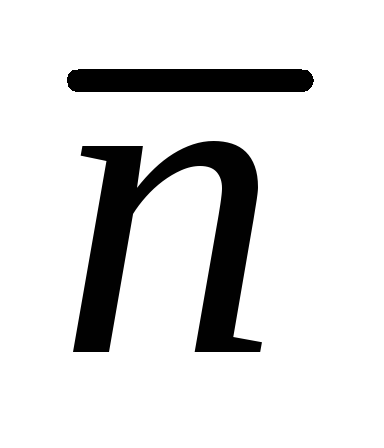 .
Выразить векторы
.
Выразить векторы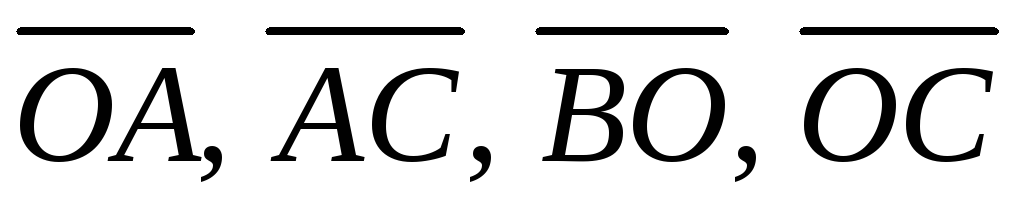 и
и через векторы
через векторы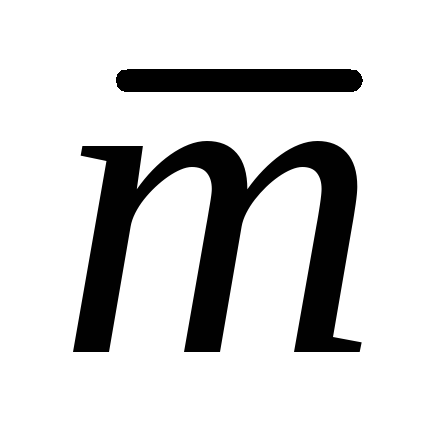 и
и ,
если
,
если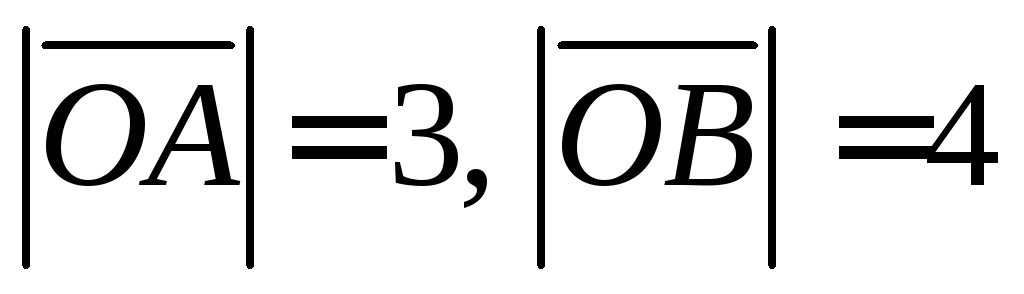 .
.
6. В треугольнике АВС: М – точка пересечения медиан треугольника, 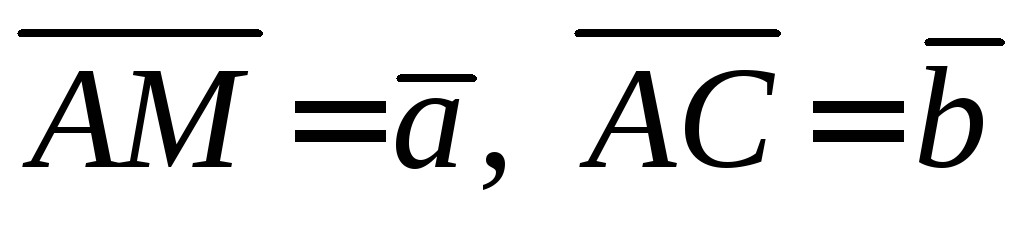 .
Разложить
.
Разложить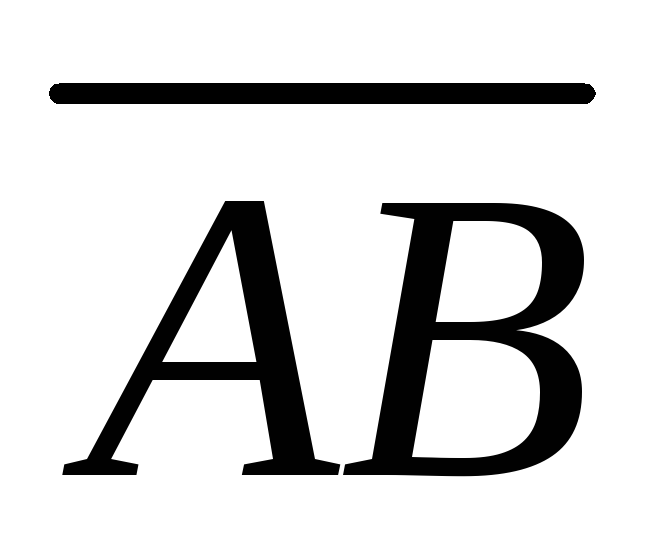 и
и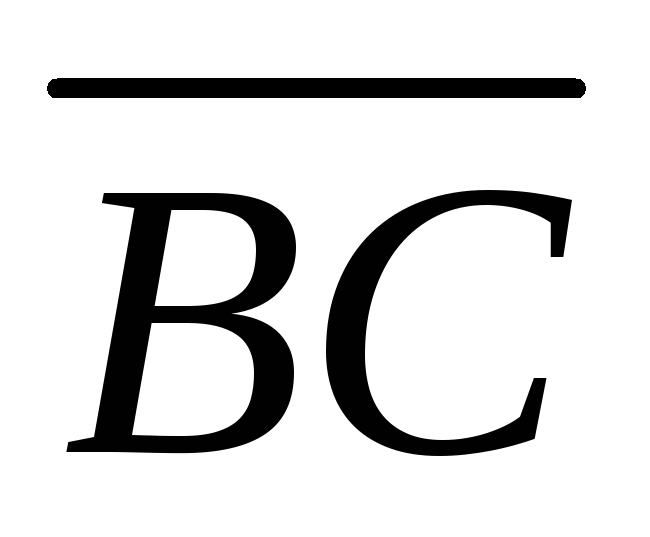 по векторам
по векторам и
и .
.
7. В параллелограмме ABCD точки K и М  середины сторонBC и CD,
середины сторонBC и CD,  .
Выразить векторы
.
Выразить векторы и
и через векторы
через векторы и
и .
.
8. Точка O является центром тяжести (точка
пересечения медиан) треугольника АВС.
Доказать, что  .
.
9. В четырёхугольнике ABCD диагонали в точке пересечения делятся пополам. Доказать, что этот четырёхугольник параллелограмм.
10. Четырехугольник ABCD – параллелограмм, O – точка пересечения диагоналей, 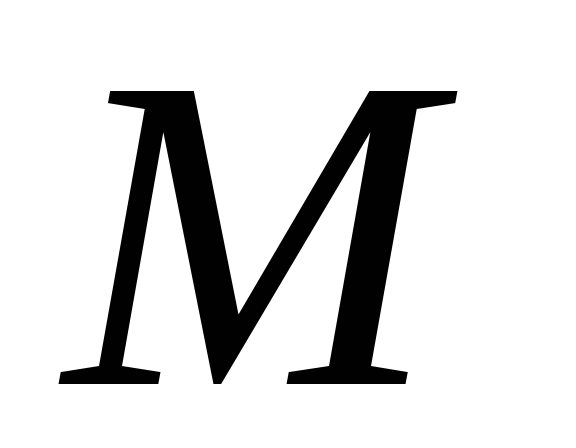 и
и
 середины параллельных сторонBC и AD соответственно. Построить векторы: а)
середины параллельных сторонBC и AD соответственно. Построить векторы: а)  ,
б)
,
б)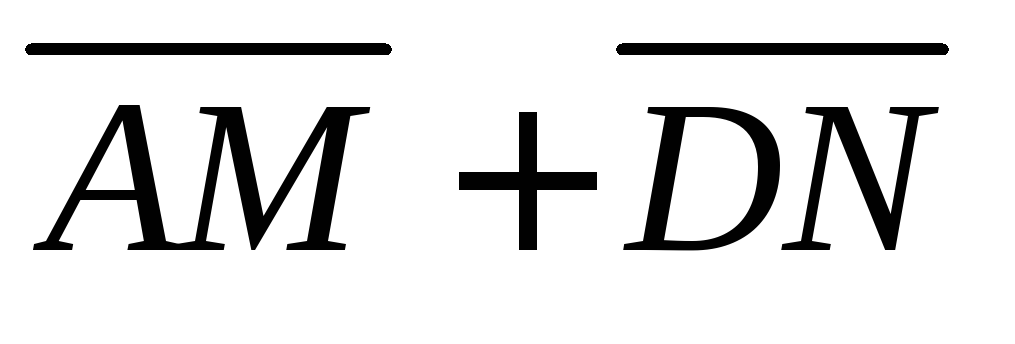 ,
в)
,
в)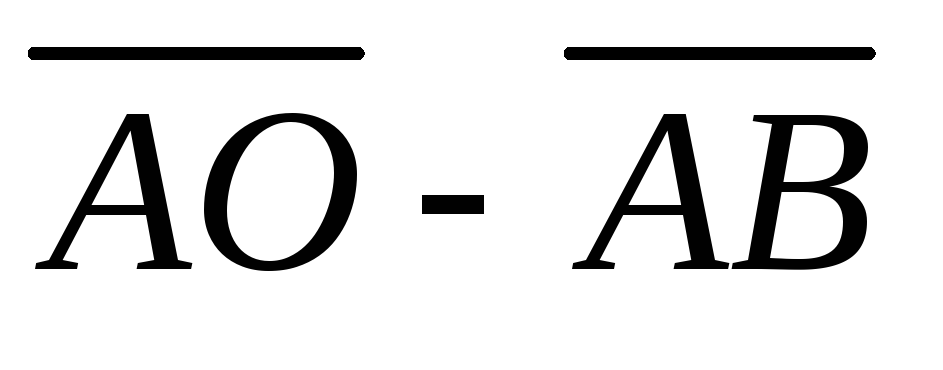 ,
г)
,
г) ,
,
д)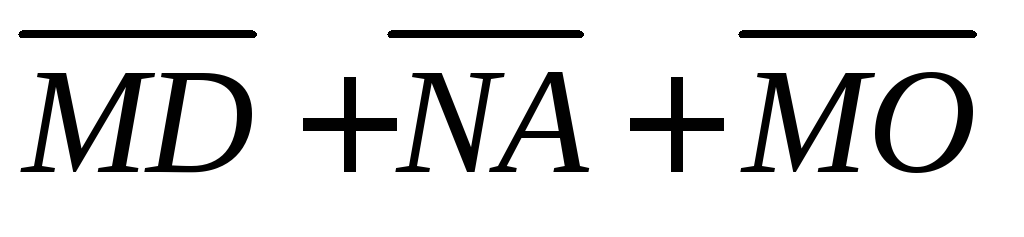 ,
е)
,
е) .
.
11. В треугольнике АВС: 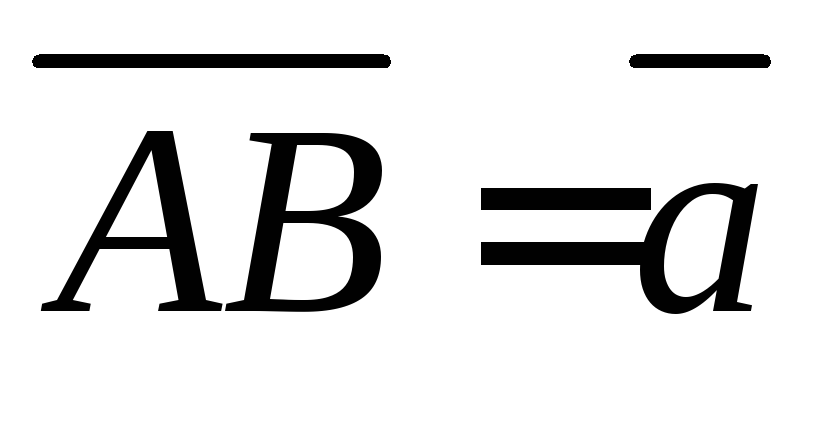 ,
, ,
точки
,
точки
 середины сторонАВ, BC и АС соответственно. Выразить через векторы
середины сторонАВ, BC и АС соответственно. Выразить через векторы  и
и медианы
медианы
треугольника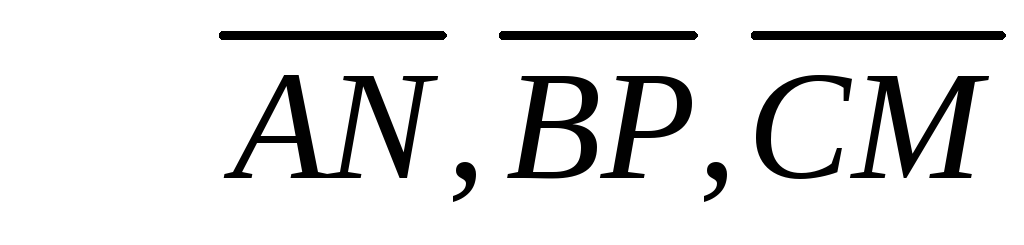 .
.
12. В треугольнике  вектор
вектор и вектор
и вектор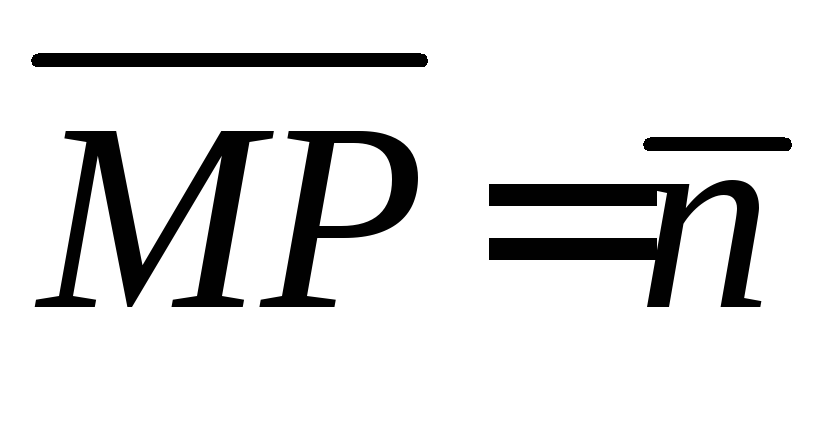 .
Построить каждый из следующих векторов:
1)
.
Построить каждый из следующих векторов:
1)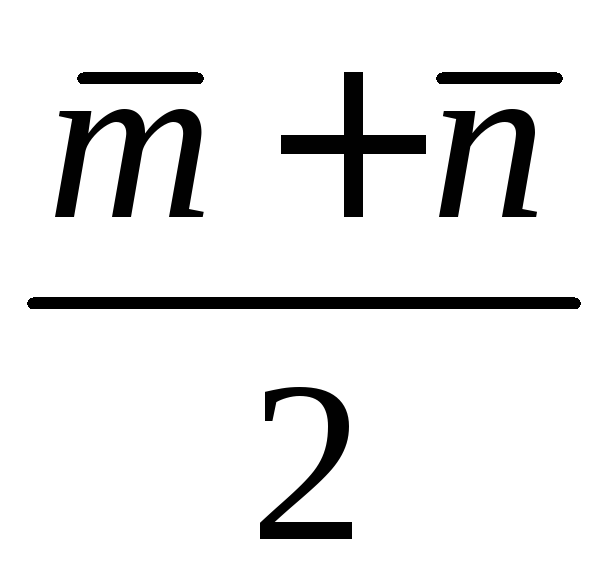 ;
2)
;
2)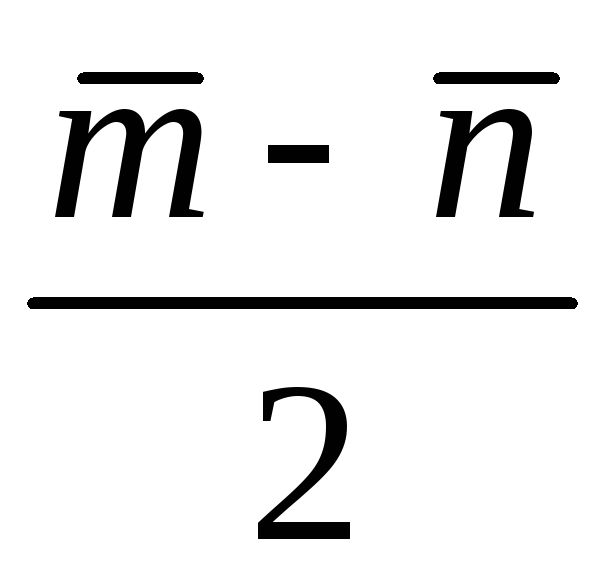 ;
3)
;
3)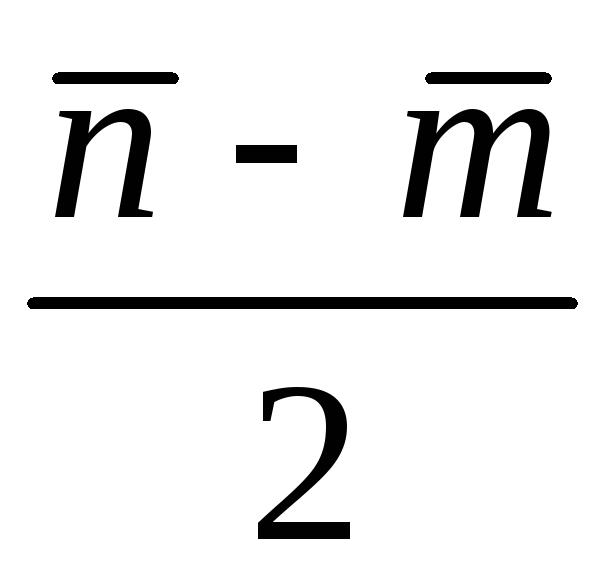 ;
4)
;
4)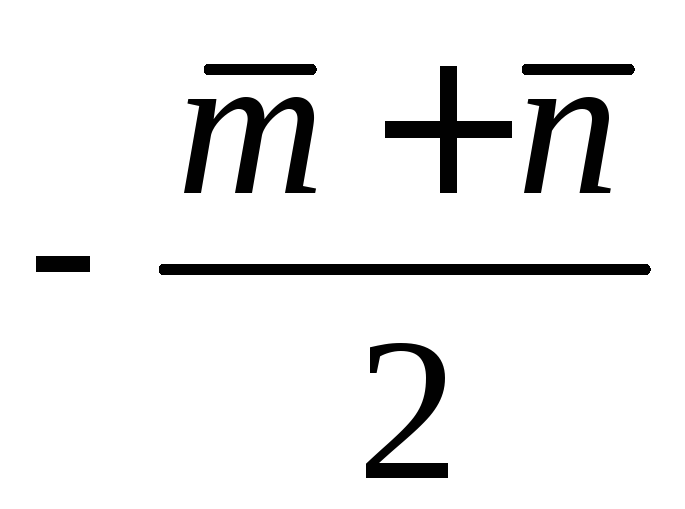 .
.
13. По данным векторам  и
и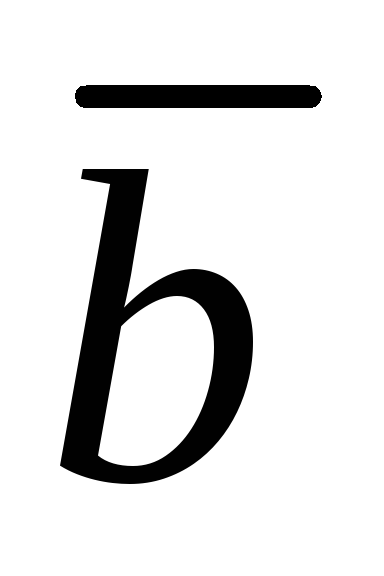 построить каждый из следующих векторов:
1)
построить каждый из следующих векторов:
1)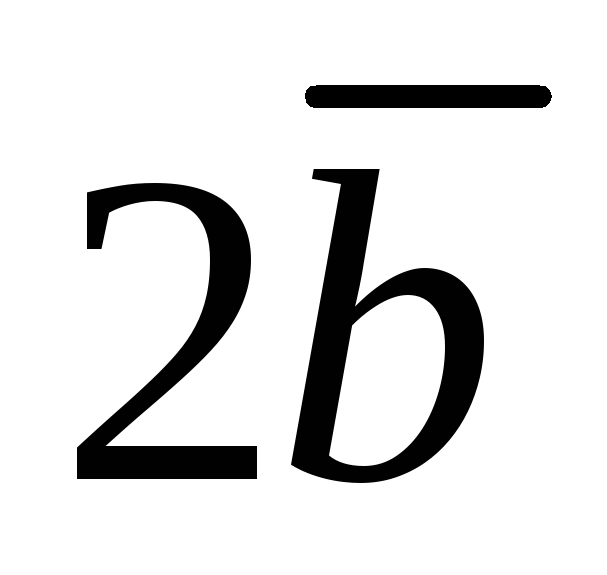 ;
2)
;
2) ;
3)
;
3)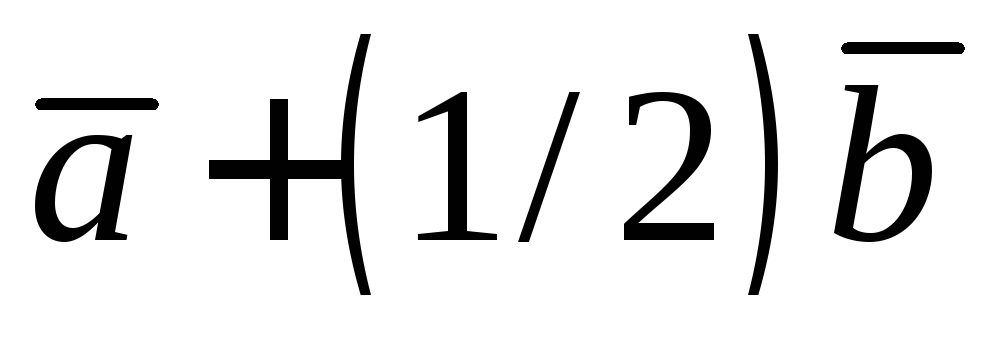 ;
4)
;
4) .
.
14. Какому условию
должны удовлетворять векторы  и
и ,
чтобы вектор
,
чтобы вектор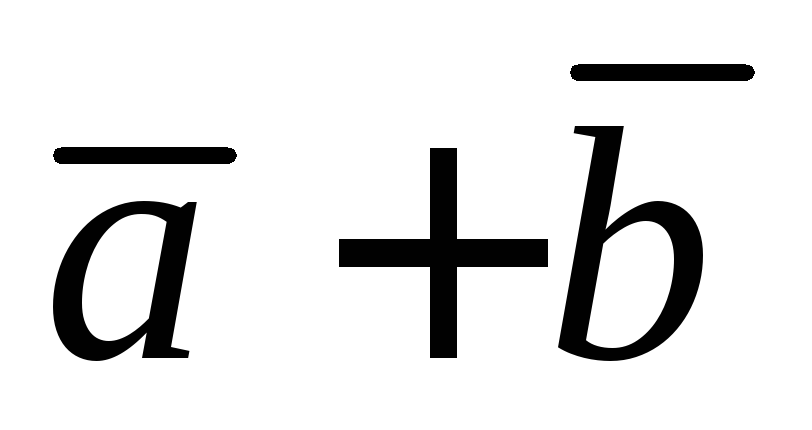 делил пополам угол между векторами
делил пополам угол между векторами и
и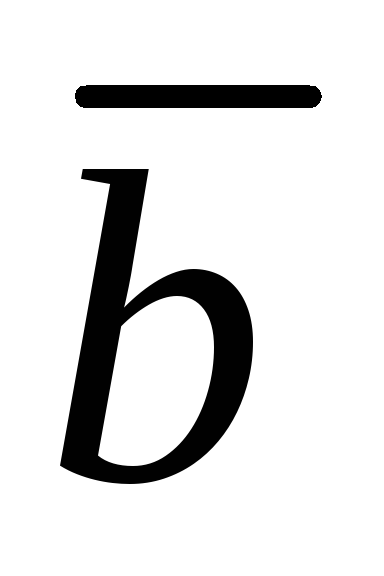 ?
?
15. Три силы  ,
приложенные к одной точке, имеют взаимно
перпендикулярные направления. Определить
величину их равнодействующей, если
известно, что
,
приложенные к одной точке, имеют взаимно
перпендикулярные направления. Определить
величину их равнодействующей, если
известно, что ,
,
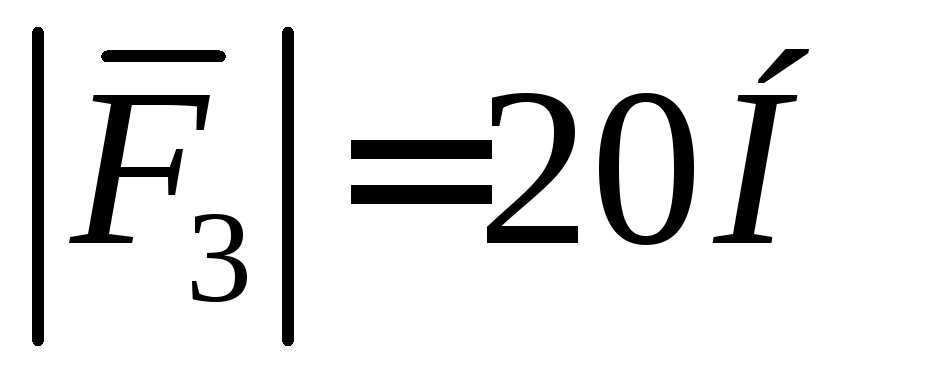 .
.
16. В тетраэдре ABCD:  ,
,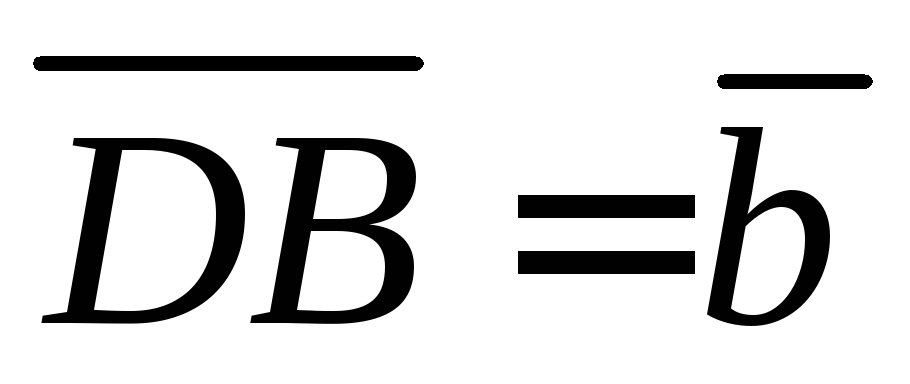 ,
, ,
точка
,
точка
 центр тяжести треугольникаАВС.
Выразить вектор
центр тяжести треугольникаАВС.
Выразить вектор  через векторы
через векторы ,
, ,
, .
.
17. Даны точки A,
В и С.
Построить точку  так, чтобы
так, чтобы .
.
18. В треугольнике АВС проведена биссектриса AD.
Выразить вектор  через векторы
через векторы и
и .
.
19. В трапеции ABCD  точки
точки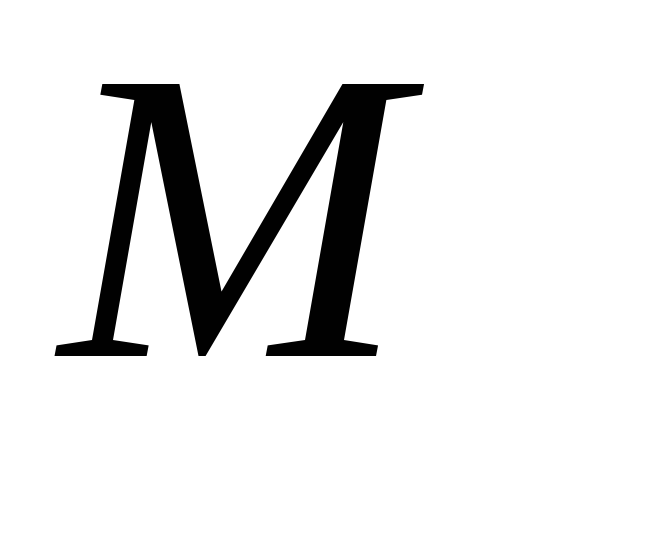 и
и
 середины оснований
середины оснований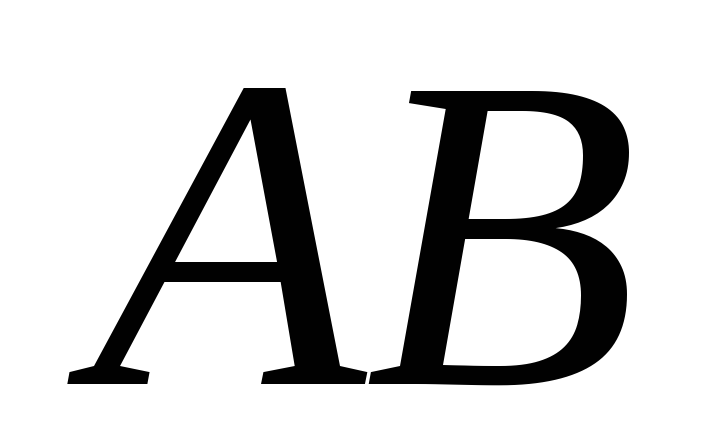 и
и ,
,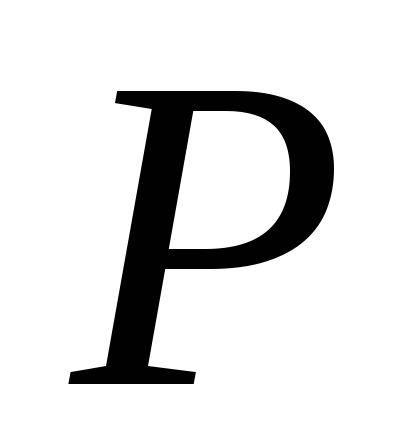
 точка пересечения диагоналей. Выразить
векторы
точка пересечения диагоналей. Выразить
векторы и
и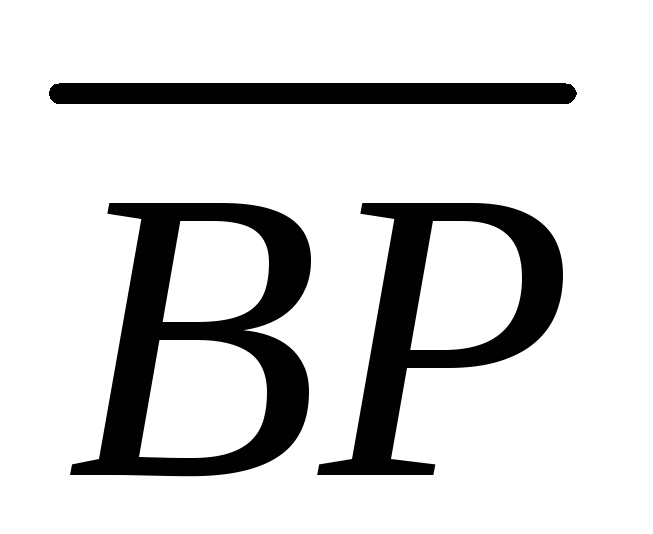
через 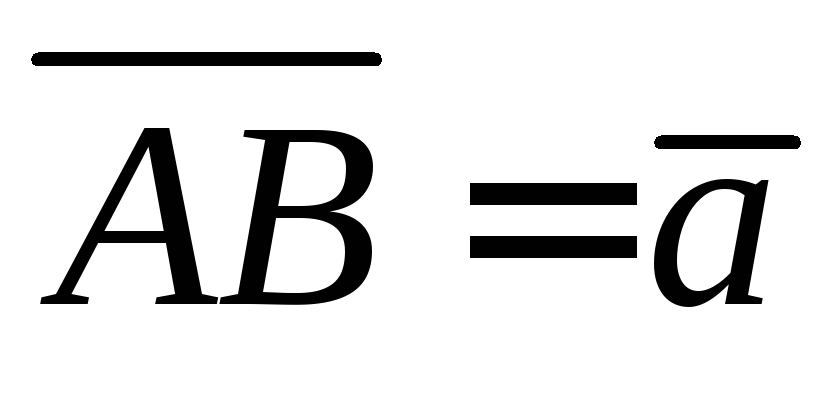 и
и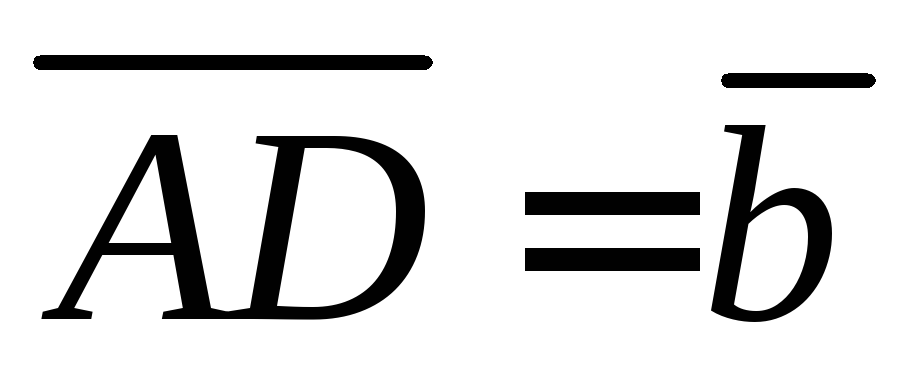 .
.
20. В трапеции ABCD  точки
точки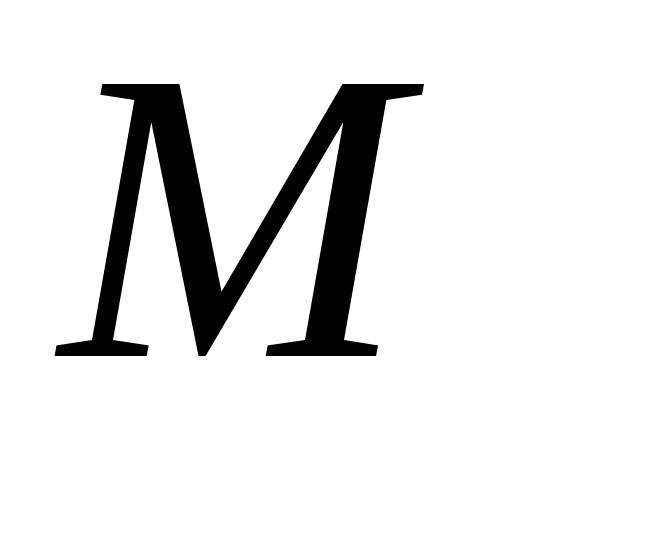 и
и
 середины оснований
середины оснований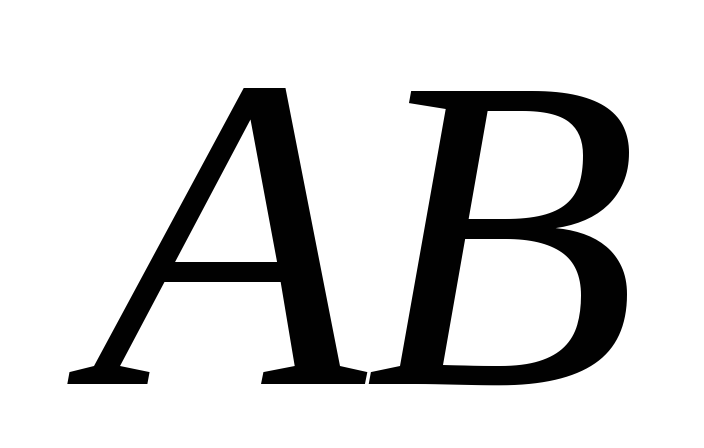 и
и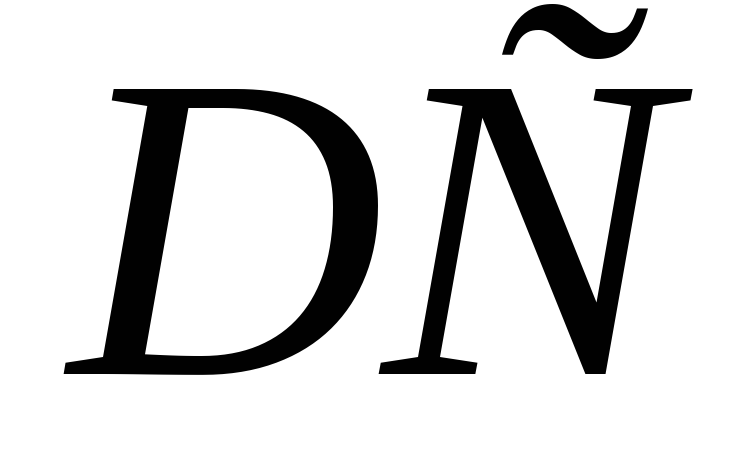 ,
,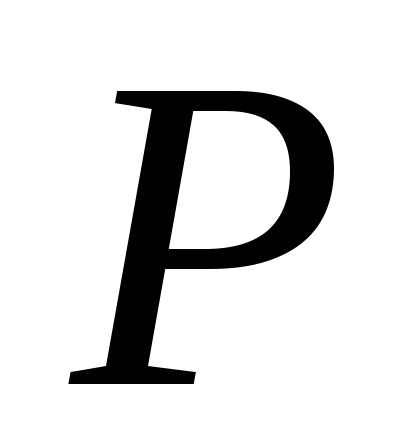
 точка пересечения диагоналей. Выразить
векторыи
точка пересечения диагоналей. Выразить
векторыи
через 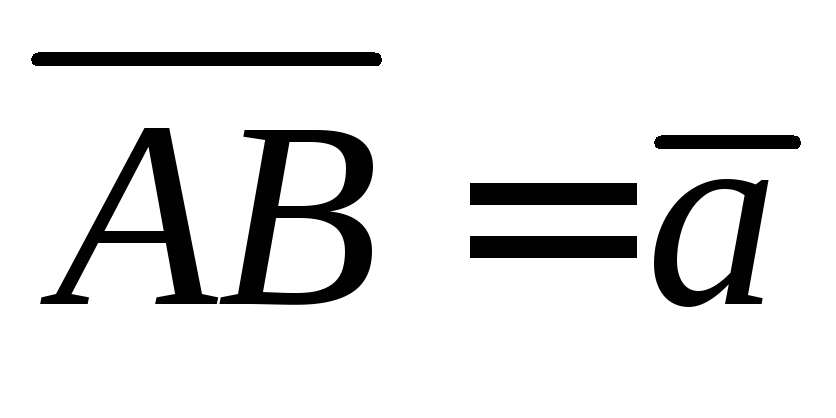 и
и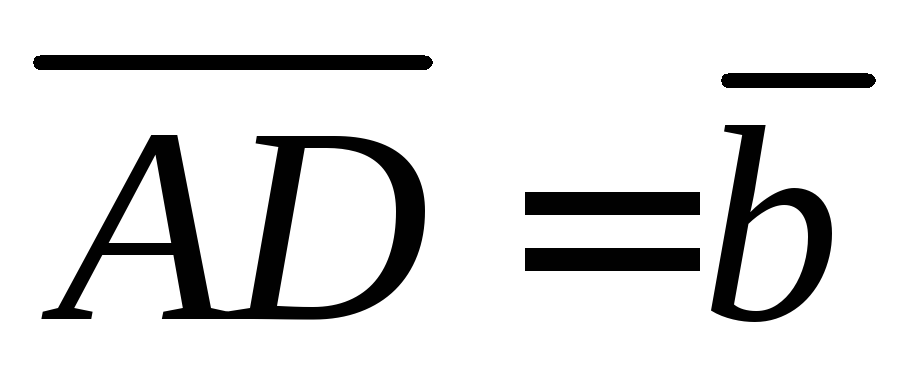 .
.
21. В трапеции ABCD 
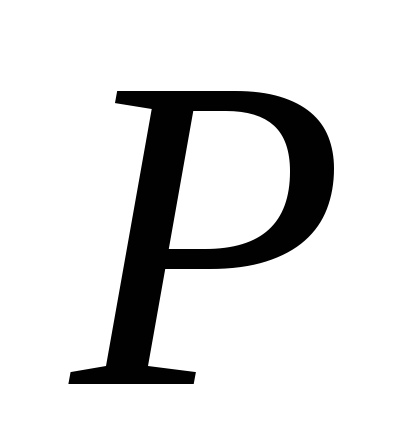
 точка пересечения диагоналей,
точка пересечения диагоналей, и
и .
Выразить векторы
.
Выразить векторы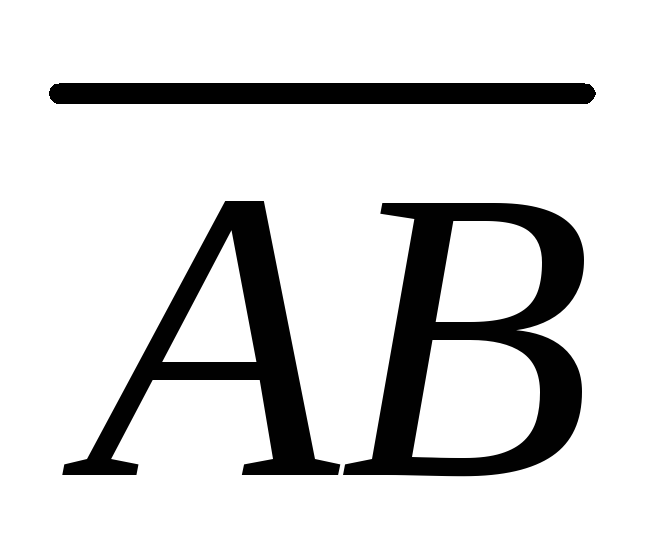 и
и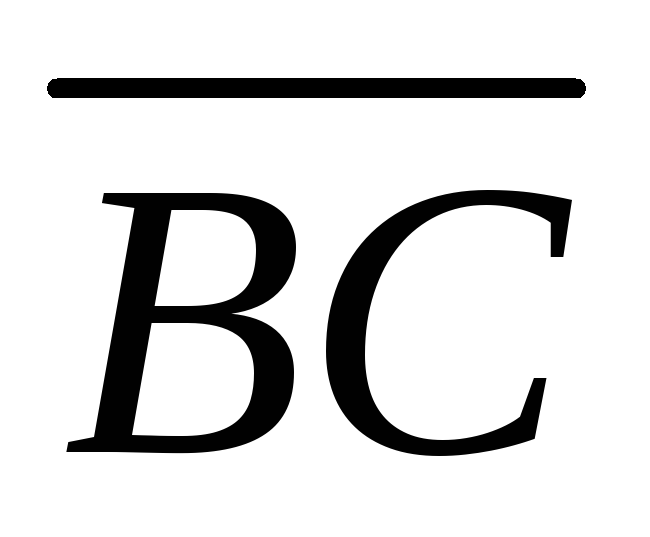 через векторы
через векторы и
и .
.
22. В трапеции ABCD 

 точка пересечения диагоналей,
точка пересечения диагоналей,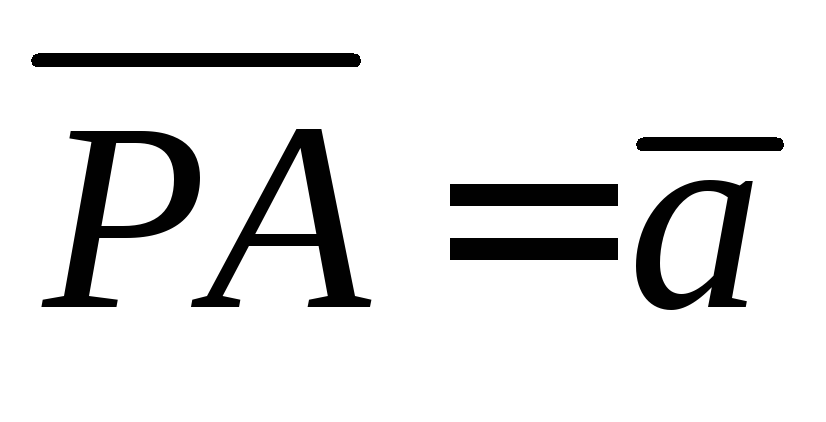 и
и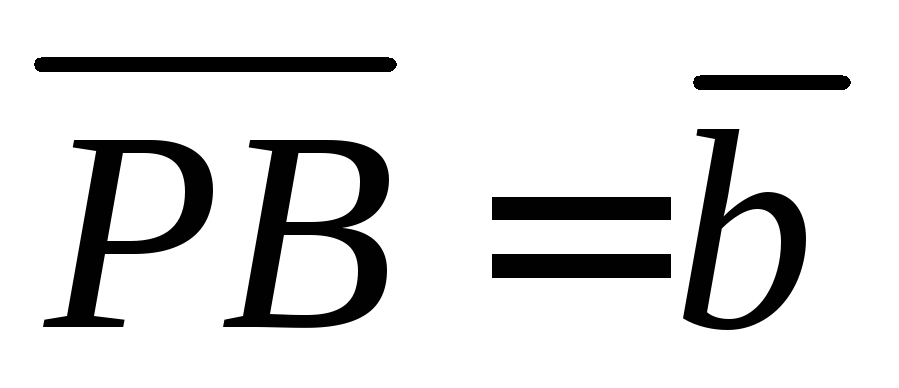 .
Выразить векторы
.
Выразить векторы и
и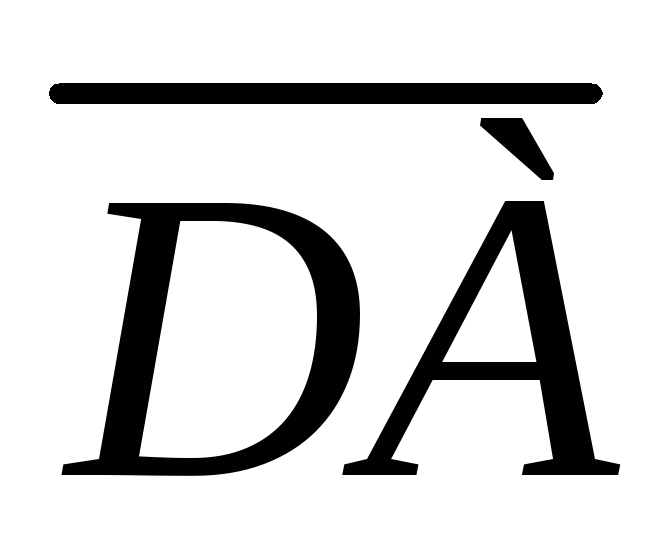 через векторы
через векторы и
и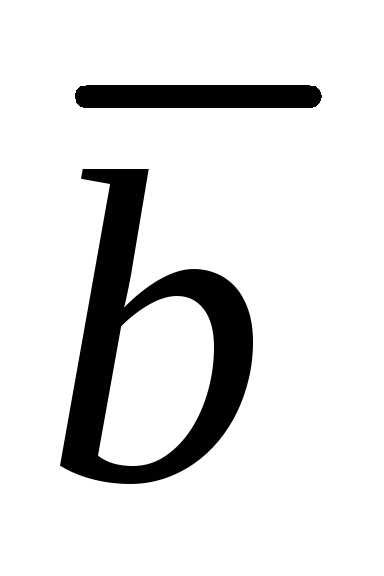 .
.
23. В произвольном
треугольнике АВС точки 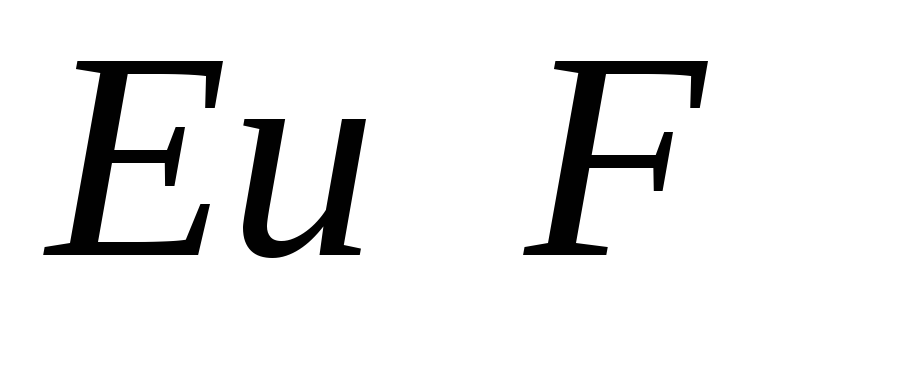
 середины
сторон
середины
сторон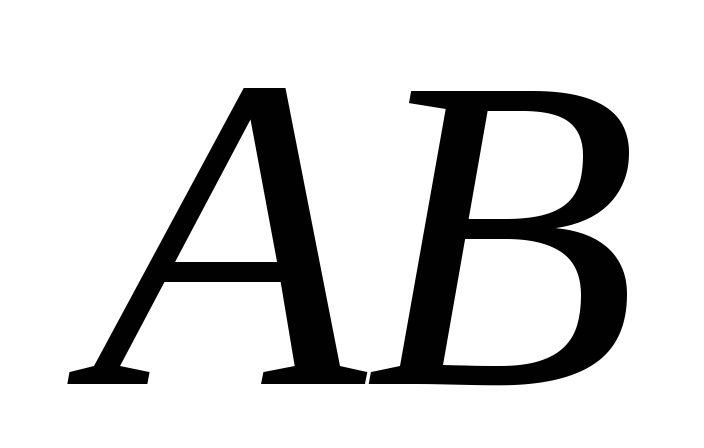 и
и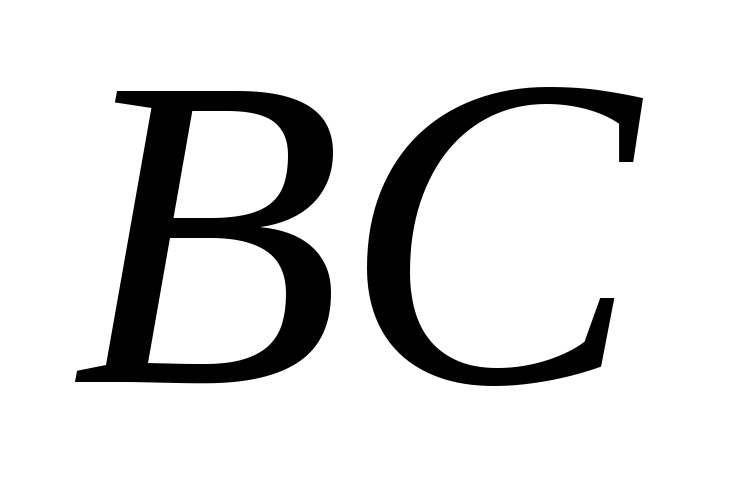 .
Выразить векторы
.
Выразить векторы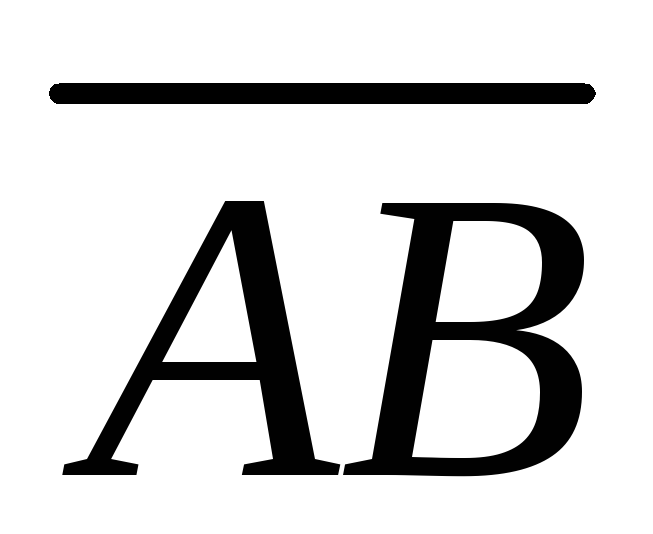 ,
,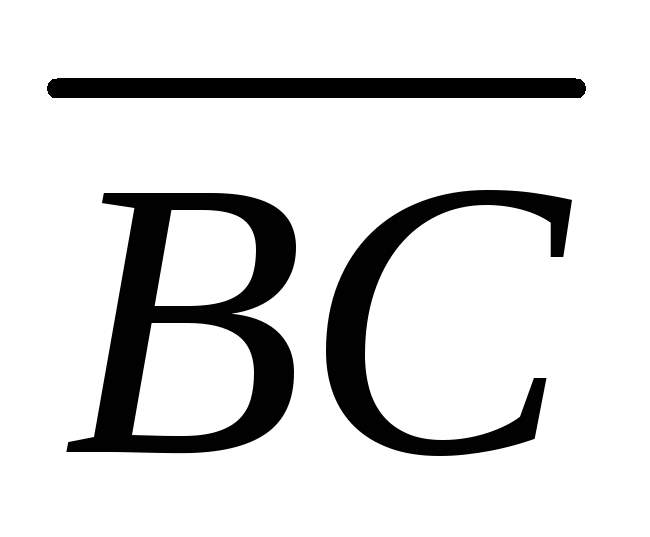 и
и через векторы
через векторы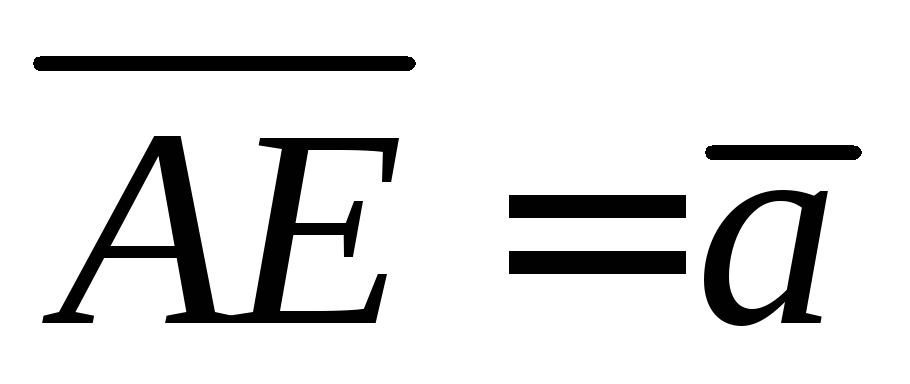 и
и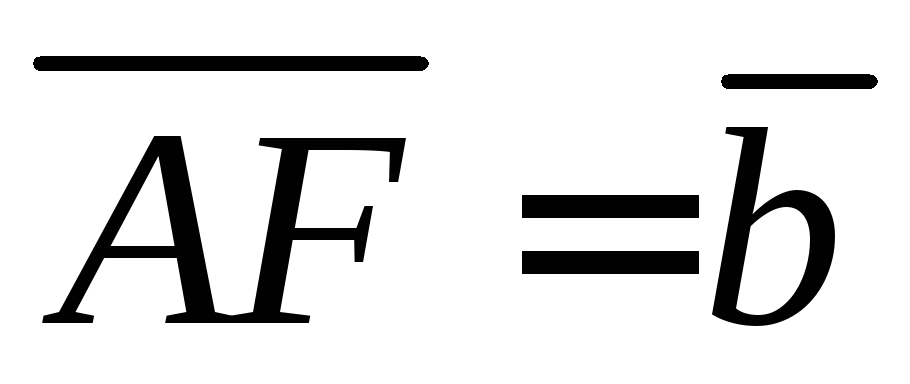 .
.
24. В треугольнике  проведена средняя линия
проведена средняя линия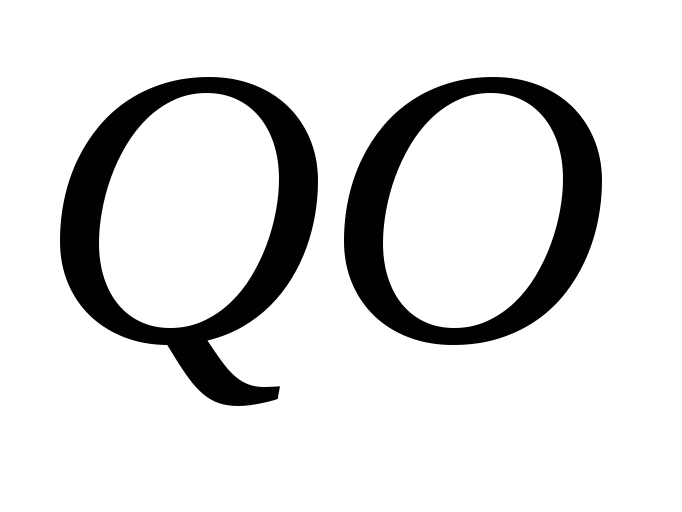 параллельная стороне
параллельная стороне .
Выразить векторы
.
Выразить векторы и
и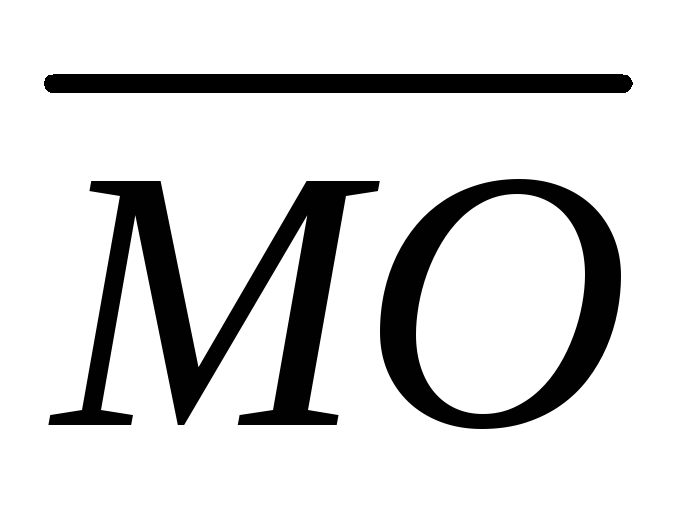 через векторы
через векторы и
и .
.
25. Пусть ABCD – параллелограмм, O точка пересечения его диагоналей.
Полагая
точка пересечения его диагоналей.
Полагая  и
и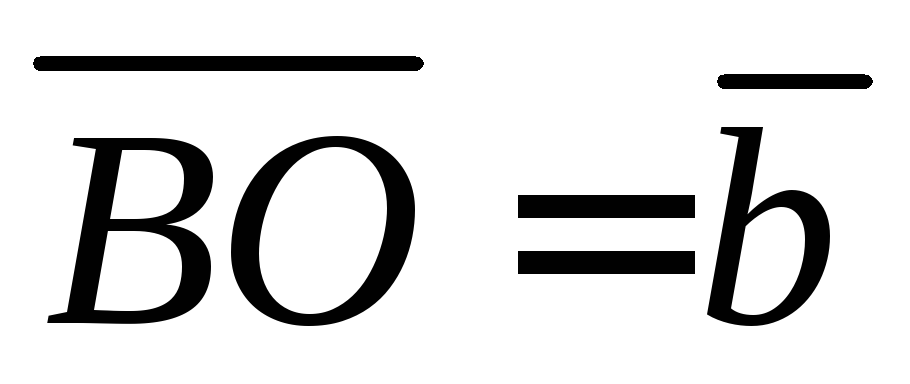 ,
выразить через
,
выразить через и
и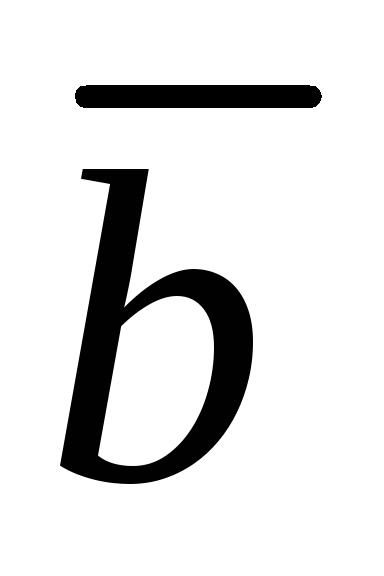 векторы
векторы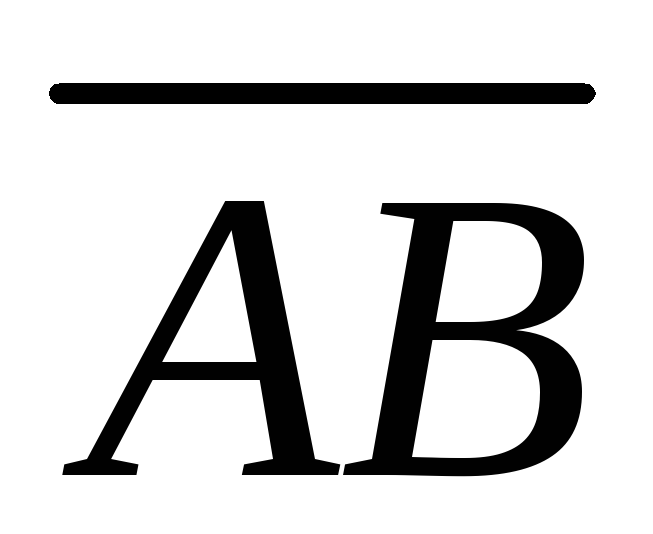 ,
,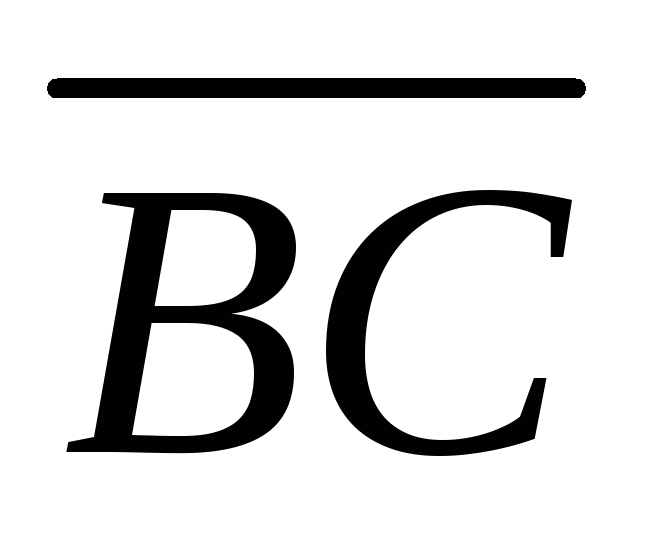 ,
, ,
, .
.
26. Точка 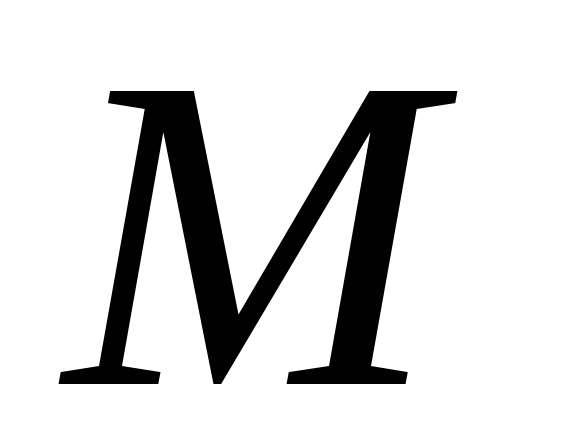
 центр тяжести треугольникаАВС.
Выразить: 1) вектор
центр тяжести треугольникаАВС.
Выразить: 1) вектор 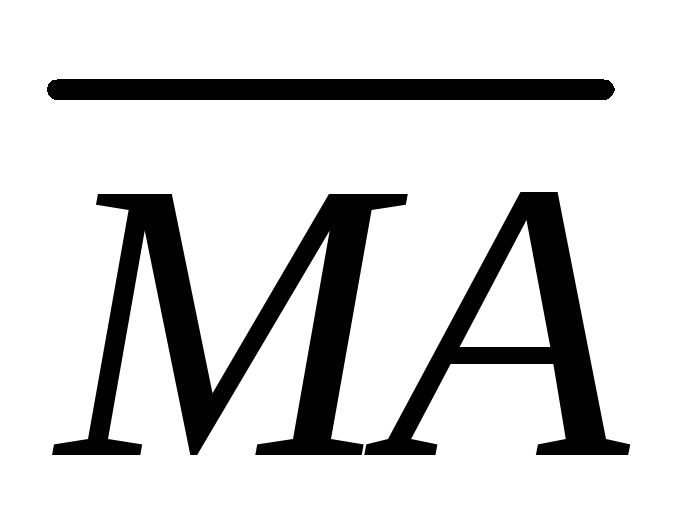 через
через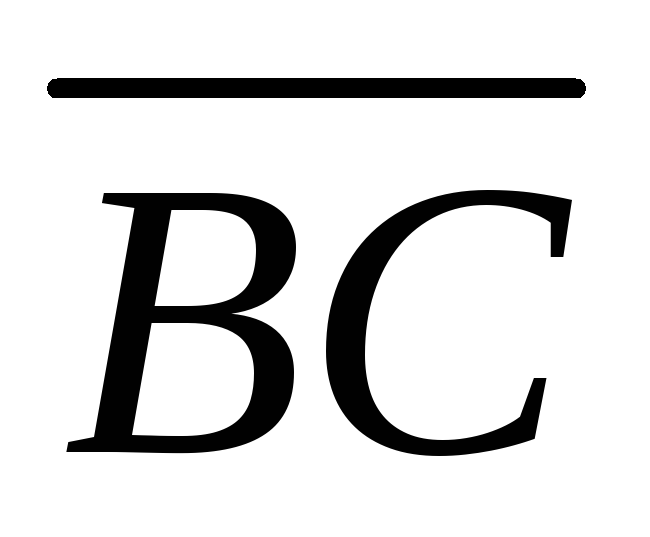 и;
2) вектор
и;
2) вектор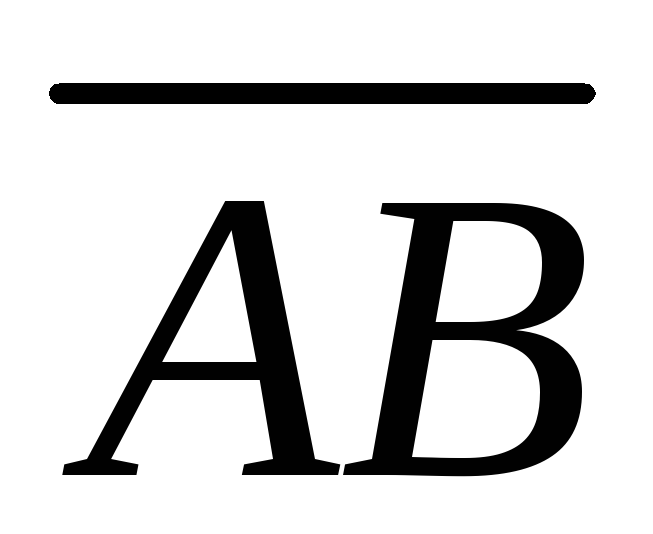 через векторы
через векторы и
и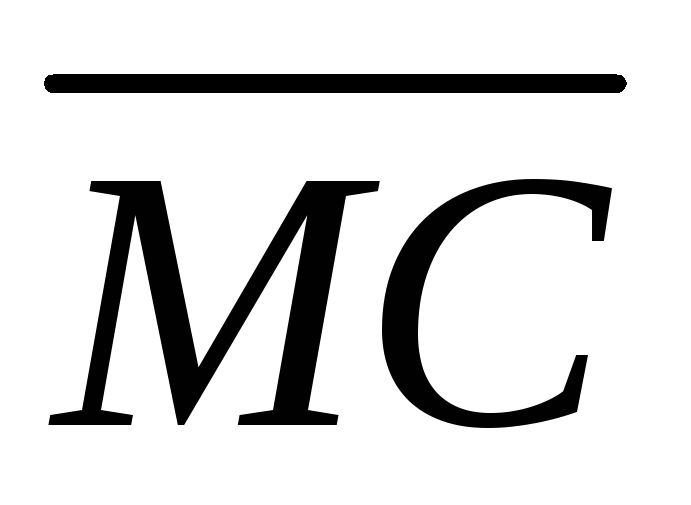 .
.
27. В тетраэдре ABCD точка  лежит на ребре
лежит на ребре и делит отрезок
и делит отрезок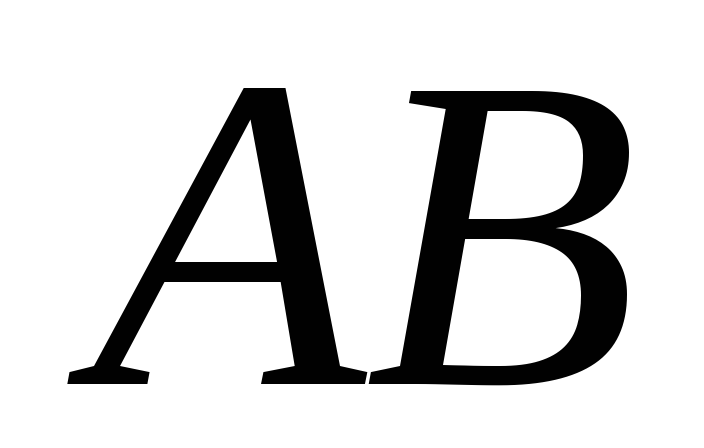 в отношении
в отношении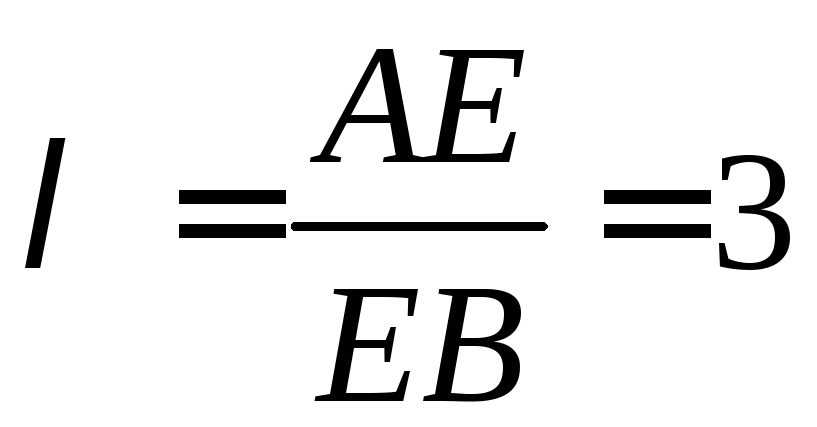 ,
,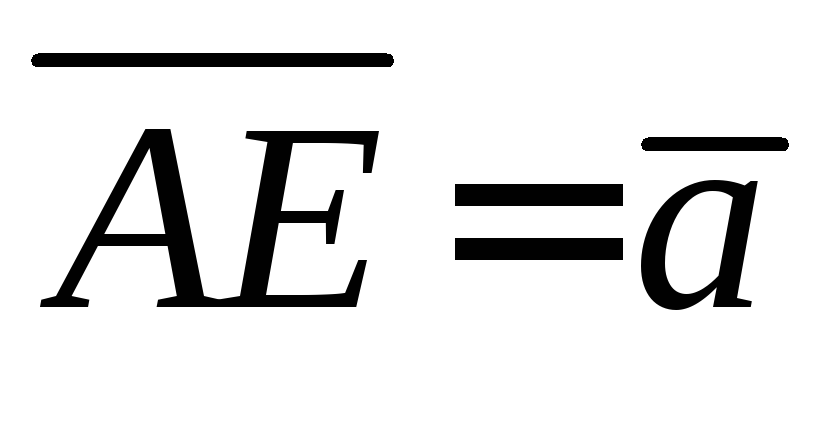 ,
, ,
,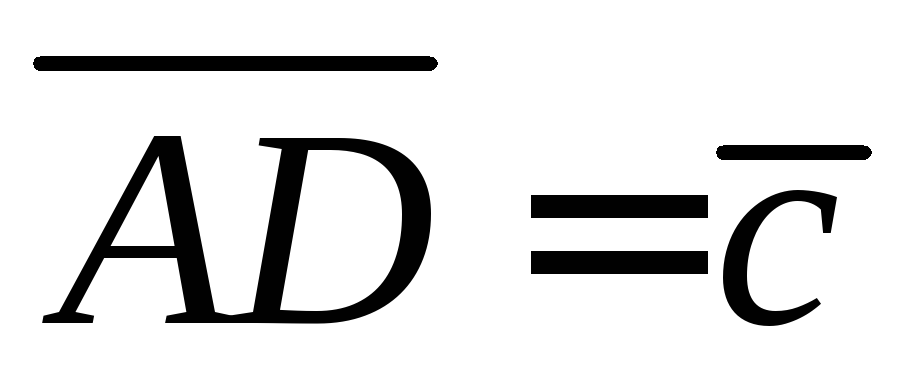 .
Выразить векторы
.
Выразить векторы ,
, ,
,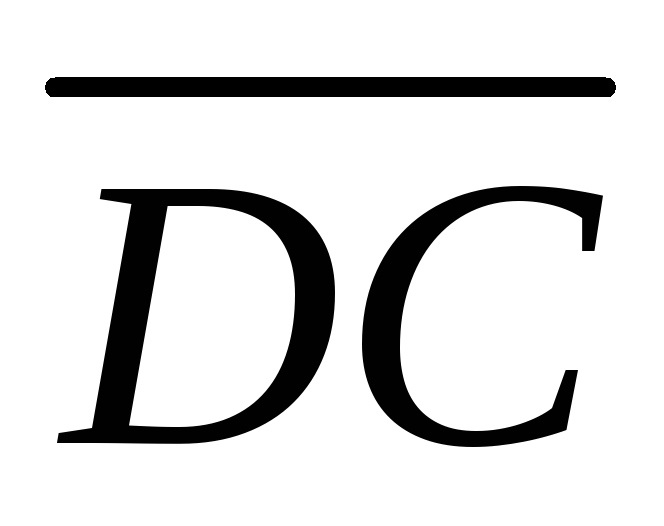 через векторы
через векторы ,
, ,
, .
.
28. В тетраэдре ABCD точка  делит сторону
делит сторону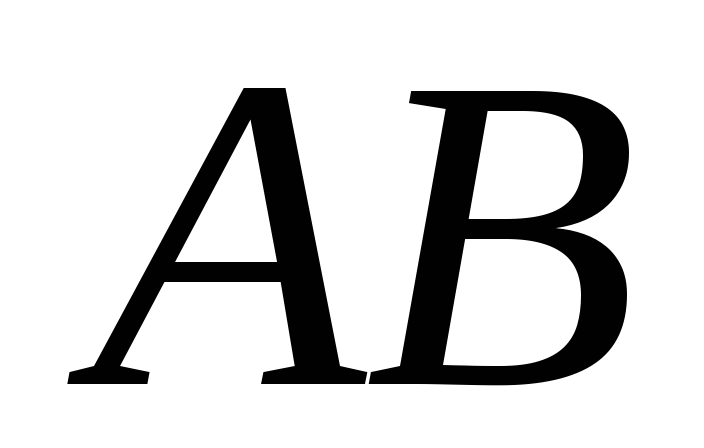 в отношении
в отношении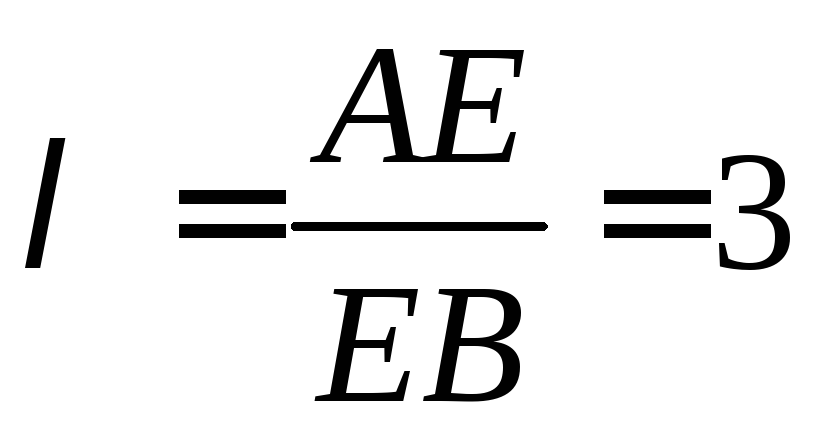 .
Выразить векторы
.
Выразить векторы ,
, ,
, через векторы
через векторы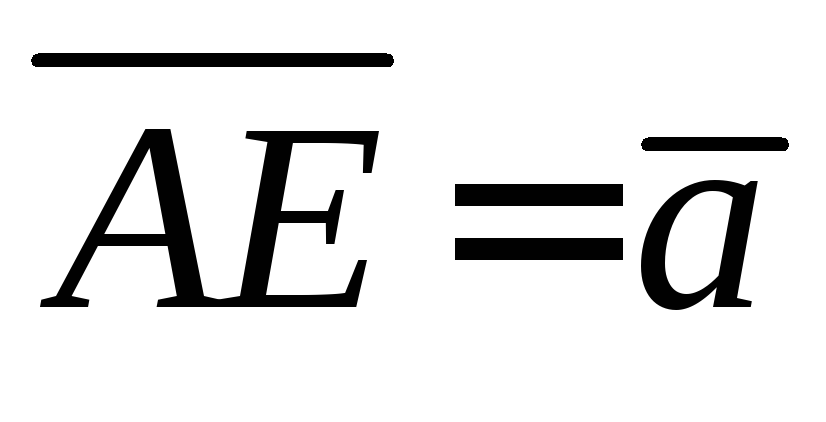 ,
,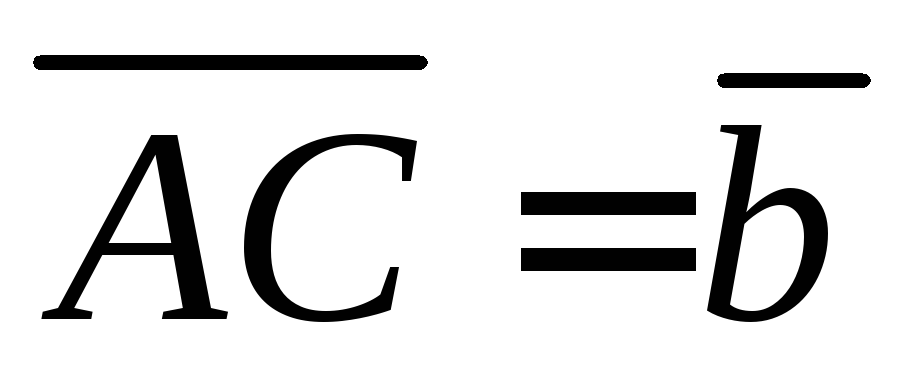 ,
,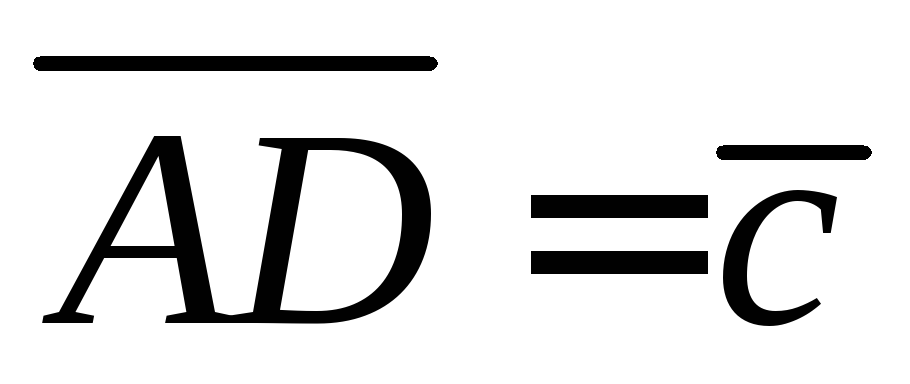 .
.
29. Дан треугольник АВС и
произвольная точка  .
.
 середины сторон
середины сторон и
и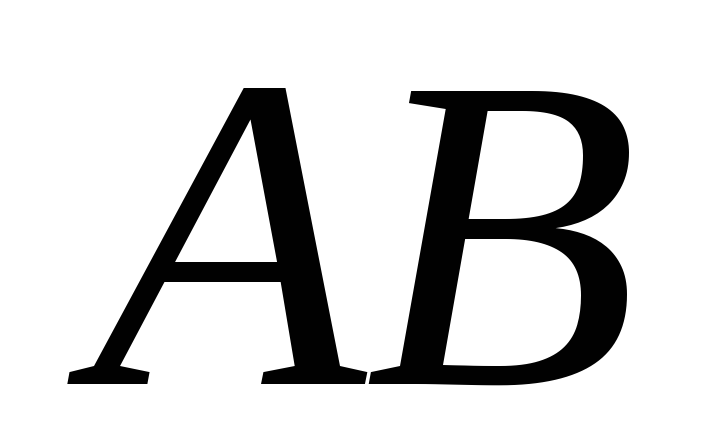 соответственно. Доказать, что
равнодействующая сил
соответственно. Доказать, что
равнодействующая сил
 ,
,  и
и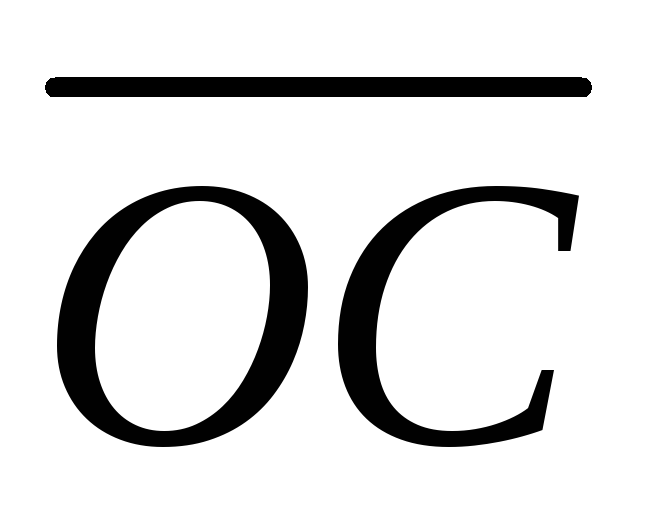 равна равнодействующей сил
равна равнодействующей сил ,
, и
и .
.
30. В параллелограмме ABCD  и
и 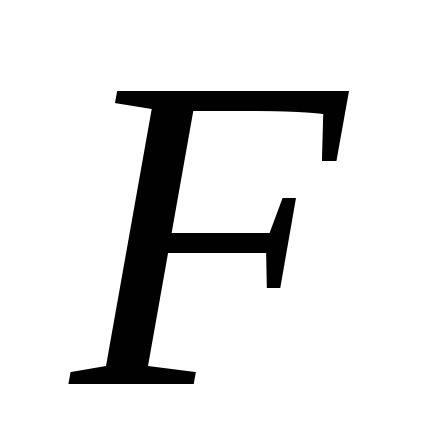
 середины противоположных сторон
середины противоположных сторон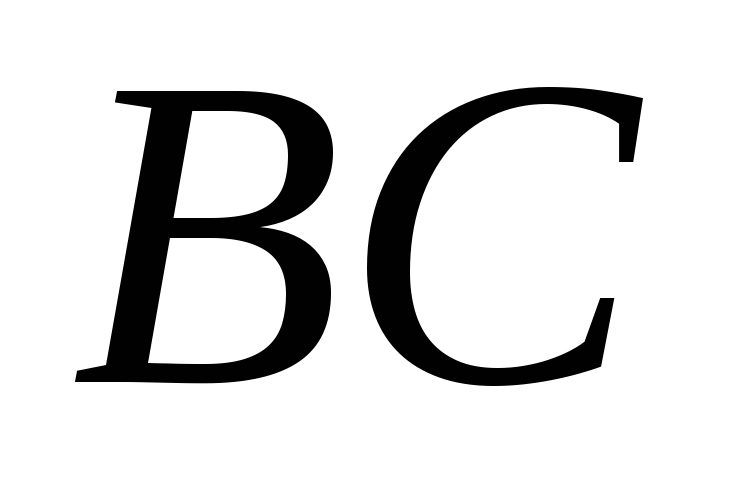 и
и ,
,
 точка пересечения диагоналей. Выразить
векторы
точка пересечения диагоналей. Выразить
векторы ,,
,, ,
,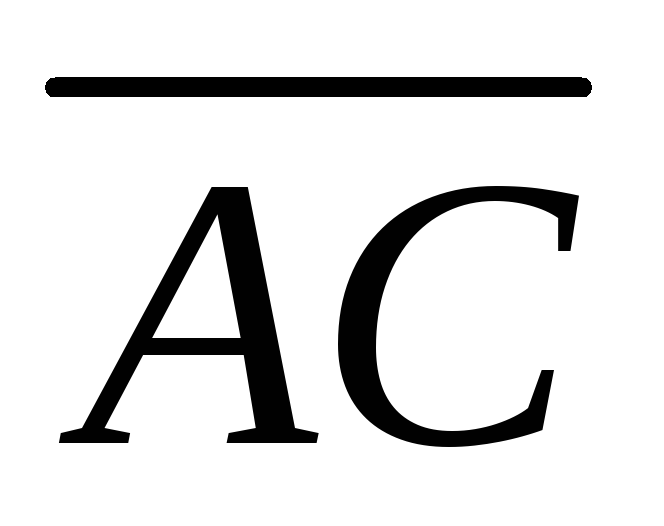 через векторыи
через векторыи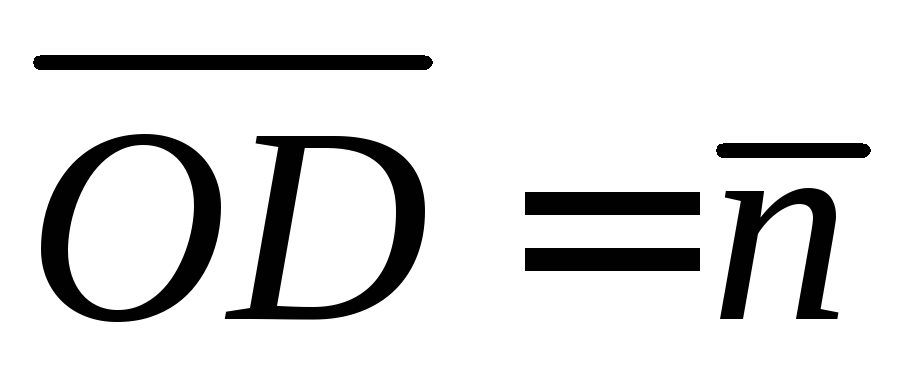 .
.

 и
и 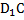 .
. 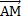 по трем заданным векторам.
по трем заданным векторам.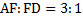 . Разложите вектор
. Разложите вектор 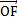 по векторам
по векторам 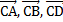 .
.
 .
. и вектором
и вектором ,
где
,
где ,
т.е.
,
т.е.