Понятие функции. Способы задания функции
Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут , при этом x называют аргументом функции, y называют значением функции.
, при этом x называют аргументом функции, y называют значением функции.Существуют разные способы задания функций.
1. Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции.
Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например  .
.
Рассмотрим первый пример —  . Здесь значению x = 1 соответствует
. Здесь значению x = 1 соответствует  , значению x = 3 соответствует
, значению x = 3 соответствует 
Функция может быть задана на разных частях множества X разными функциями.
Например:

Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а слева формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.
Например  . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:
. Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:
 . То есть, значение функции при х = 3 равно -4/3.
. То есть, значение функции при х = 3 равно -4/3.
При аналитическом способе задания, функция может быть задана параметрически — это, когда х и у выражены через некоторый параметр t. Например,

Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.
2. Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом  . Пример:
. Пример:

3. Словесный способ.
Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
4. Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Пример:

Табличный способ задания функции очень удобен при обработке результатов исследований. Например, при выявлении зависимости между уровнем загрязнения окружающей среды и количеству людей, заболевших раком.
1. Понятие функции. Способы задания, свойства, классификация функций.
Определение: если одному значению независимой переменной x соответствует одно (много) значений y, то y назыв однозначной (многозначной) функцией аргумента x и обозн y=f(x)
Определение: множество значений аргумента x, для которых функция существует, определена, назыв областью определения функции. D(f)
Определение: множество значений переменной y, соответствующих значений x из области определения, назыв областью значения ф-ции. E(f)
Для нахождения нулей функции нужно решить уравнение
f (x) = 0, а для нахождения промежутков знакопостоянства нужно решить неравенства f (x) > 0 и f (x) < 0.Если на некотором промежутке функция непрерывна и не имеет корней, то она сохраняет знак на этом промежутке.
Определение: ф-ция f(x) называется возрастающей, если большему значению аргумента соответствует большее значение ф-ции, т.е. для x1<x2: f(x1)<f(x2)
Определение: ф-ция f(x) назыв убывающей, если большему значению аргумента соответствует меньшее значение ф-ции, т.е. для x1<x2: f(x1)>f(x2)
Определение: ф-ция f(x) называется чётной, если выполняется f(-x)= f(x)
Ф-ция назыв нечётной, если выполняется
f(-x)= -f(x)
Определение: ф-ция y=f(x) назыв. периодической с периодом Т, еси выполняется соотношение f(x+T)=f(x) основные элементарные ф-ции: y=xn, y=an
Определение: если ф-ция задана звеньями элементарных ф-ций на определённых интервалах, назыв. сложной ф-цией.
Определние: ф-ция x=φ(y) назыв. обратной для ф-ции y=f(x), если первая ф-ция будучи подставлена во вторую, превращает её в тождество: y=f[φ(y)]
2. Числовые последовательности. Предел последовательности. Предел функции.
Определение: Числовой последовательностью назыв множество чисел, пронумерованных с помощью натуральных чисел и расположенных в порядке возрастания их номеров.
у1, у2, …, уn={yn}→yn=f(n), где у1, у2 –члены, yn=f(n) –общий член последов.
Определение: Число
а назыв пределом последов, если 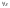 >0,
сколь угодно малого
>0,
сколь угодно малого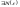 ,
что для всехn>
N(
,
что для всехn>
N(
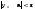 ,
при этом
,
при этом 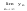 =a,
(a-ε;a+ε)
— окрестность
=a,
(a-ε;a+ε)
— окрестность
Геометрическая интерпретация
y=f(x) – ф-ция, х — аргумент ф-ции, х→а, f(x) →А, А предел ф-ции
Определение: числа
А назыв. пределом ф-ции f(x)
при х→а, если 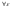 >0,
сколь угодно малого,
>0,
сколь угодно малого,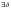 >0,
что для всехx,
для которых выполняется условие
>0,
что для всехx,
для которых выполняется условие 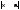 <
< ,
имеет место
,
имеет место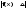

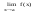 =A
=AЗамечание: 1) х→а как угодно; 2) f(x) в точке а может быть и не определена.
Определение: числа А назыв. пределом ф-ции f(x)
при х→∞, если 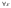 >0,
сколь угодно малого,
>0,
сколь угодно малого, 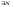 ,
что для всехx,|x|>N
, выполняется.
,
что для всехx,|x|>N
, выполняется.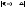 <
<
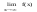
Теорема: Любая функция, имеющая предел, является ограниченной.
3. Теоремы о пределах. Односторонние пределы.
Теорема 1: Пусть lim{x→a}f(x)=А и lim{x→a}g(x)=В, тогда 1)lim{x→a}(f(x)+g(x)) = А+В; 2)lim{x→a}(f(x)*g(x)) = А*В; 3)lim{x→a}(f(x)/g(x)) =А/В
Теорема 2: lim f1(x)= А1
lim f2(x) = А2,
f1(x)<=f2(x),  x
x D(f)
=> A1<A2
D(f)
=> A1<A2
Теорема 3: lim f1(x)=А, lim f2(x) = А, f1(x)<f(x)<f2(x) => lim f(x) =A
Определение: если при вычислении предела lim{x→a}f(x) при х→а, Х остаётся всё время меньше (больше) а, то предел называется левым(правым) – оба односторонние.
Замечание: 1) Если сущ-ют и равны м/у собой односторонние пределы, то они равны пределу f(x), при х→а. 2) Если существует предел данной функции, то существует и его односторонние пределы.
1. Понятие функции одного переменного. Виды и способы задания функции.
Если каждому элементу х множ-ва Х (х є Х) ставится в соответствие вполне определённый элемент у множ-ва У (у є У), то говорят, что на множ-ве Х задана функция у = f(x). При этом х назыв. независимой переменной (или аргументом), у – зависимой переменной, а буква f обозначает закон соответсвия. Множ-во Х назыв. областью определения, а множ-во У – областью значений функции.
Способы задания фун-ий.
а)аналитический, если фун-ия задана формулой у = f(x)
б)табличный способ. Состоит в том, что фун-ия задаётся таблицей, содержащей значения аргумента х и соответствующие значения фун-ии f(x).
в)графический. Состоит в изображении графика фун-ии – множества точек (х,у) плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие им значения фун-ии f(x).
г)логический
3. Односторонний предел. Существование предела в точке.
Число 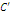 назыв. односторонним пределом слева
фун-ии f(x)
в точке сгущения x0, если
для ∀ε>0
∃δ>0,
такое, что x∈(x0-δ,
x0]
=> f(x)
назыв. односторонним пределом слева
фун-ии f(x)
в точке сгущения x0, если
для ∀ε>0
∃δ>0,
такое, что x∈(x0-δ,
x0]
=> f(x) 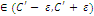
Число  назыв. односторонним пределом справа
фун-ии f(x)
в точке сгущения х0,
если если
∀ε>0
назыв. односторонним пределом справа
фун-ии f(x)
в точке сгущения х0,
если если
∀ε>0
∃δ>0, такое, что x∈(x0-δ, x0] => f(x)

Число  назыв. односторонним пределом справа
фун-ии f(x)
в точке сгущения х0,
если если
∀ε>0
∃δ>0,
такое ,что х ∈[ x0, x0 +
δ) =>
назыв. односторонним пределом справа
фун-ии f(x)
в точке сгущения х0,
если если
∀ε>0
∃δ>0,
такое ,что х ∈[ x0, x0 +
δ) => 
Сущ-ие
предела в точке. Число А назыв. пределом
фун-ии f(x)
при х, стремящемся к х0 (или точке х0),
если для любого, даже сколь угодно малого
положительного числа ε>0, найдётся
такое положительное число δ>0 (зависящее
от ε, δ=δ(ε)), что для всех х, не равных х0 и удовлетворяющее условию 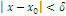 ,
выполняется неравенство
,
выполняется неравенство 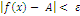
Обозначается 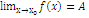 или
или 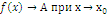
2. Предел функции и его свойства.
Предельной точной сгущения множества A называется точка x0, если в любой окрестности этой точки найдутся такие множества, отличные от x0.
Определение предела по Коши. Функция y=f(x), определенная в A, имеет предел С в точке сгущения x0, если ∀ε>0 ∃δ>0, такое, что x∈(x0-δ, x0) ∪(x0, x0+δ) ⇒ f(x)∈(C-ε, С+ε). Существование предела записывают в виде limx→x0 f(x)=C или |x-x0|<δ⇒|f(x)-C|< ε.
Определение предела по Гейне. Если для различных последовательностей {xn}, стремящихся к x0, последовательность значений функции {f(xn)} сходится к некоторому числу C, то это число называется пределом функции f(x).
Определение Коши используется для обоснования существования предела, а опред-ие Гейна – для обоснования отсутствия предела.
Свойства предела : предел единственен и фун-ия в некоторой окрестности предельной точки ограничена.
1)Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
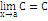
2)Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
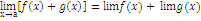
3) Предел произведения функции на постоянную величину
Постоянный коэффициент можно выносить за знак предела:
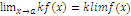
4)Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:
5)Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
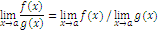
если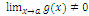
1. Функции. Основные определения и свойства. Способы задания. Классификация.
Вещественные
функции вещественного аргумента делят
на два класса: элементарные и не
элементарные. ОПРЕДЕЛЕНИЕ. Элементарной
функцией называется функция, которая
может быть задана одной формулой  ,
где
,
где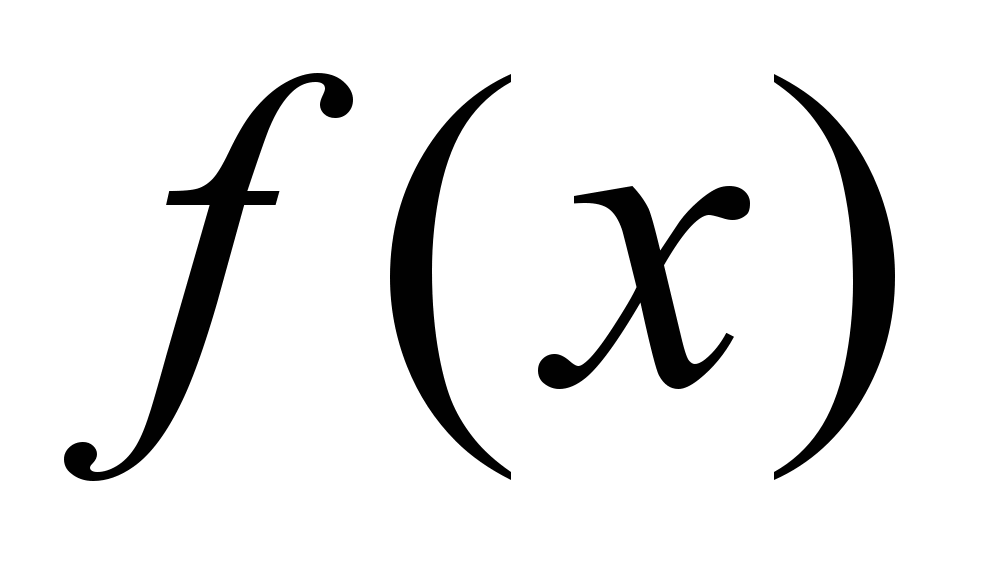 –
выражение, составленное из основных
элементарных функций и действительных
чисел с помощью конечного числа операций
сложения, вычитания, умножения, деления
и взятия функции от функции.Основными
элементарными функциями называются
следующие функции:
–
выражение, составленное из основных
элементарных функций и действительных
чисел с помощью конечного числа операций
сложения, вычитания, умножения, деления
и взятия функции от функции.Основными
элементарными функциями называются
следующие функции:
степенная функция
 ,
где
,
где R;
R;показательная функция
 ,
где
,
где и
и ;
;логарифмическая функция
 ,
где
,
где и
и ;
;тригонометрические функции
 ,
, ,
, ,
, ;
;обратные тригонометрические функции
 ,,
,, ,
,  .
.
Областью
определения функции 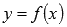 (выраженияf(x)
) называют множество всех значений x
, для которых функция (выражение) имеет
смысл.
(выраженияf(x)
) называют множество всех значений x
, для которых функция (выражение) имеет
смысл.
Область
определения функции 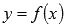 обозначается
как
обозначается
как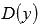 или
или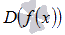 .
.
Способы задания функции
1)Аналитический способ
Закон, устанавливающий связь между аргументом и функцией, задается посредством формул.
2)Табличный способ
Функцию можно задать, перечислив все её возможные аргументы и значения для них.
3)Графический способ
Функцию можно задать графически, отобразив множество точек её графика на плоскости.
| Обратная функция Обратная функция, функция, обращающая зависимость, выражаемую данной функцией. Так, еслиу = f (x) — данная функция, то переменная х, рассматриваемая как функция переменной у, х = j (y), является обратной по отношению к данной функции у = f (x). Например, О. ф. для у = ax + b (а¹0) является х = (у—b)/a. |
Сложная функция Сложная функция, функция от функции. Если величина y является функцией от u, то есть у = f (u), а u, в свою очередь, функцией от х, то есть u = j(х), то у является С. ф. от х, то есть y = f [(x)], определённой для тех значений х, для которых значения j(х) входят в множество определения функции f (u). В таком случае говорят, что у является С. ф. независимого аргумента х, а u — промежуточным аргументом. Например, если у = u2, u = sinx, то у = sin2х для всех значений х. |
2. Предел функции точке. Односторонние пределы.
Предел функции в точке
Пусть
задано некоторое числовое множество 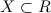 и
каждому
и
каждому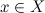 поставлено
в соответствие число
поставлено
в соответствие число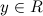 ,
тогда говорят, что на множестве
,
тогда говорят, что на множестве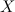 задана
функция
задана
функция ,
, .
.
Определение предела функции по Коши
Определение
Число  называетсяпределом
функции
называетсяпределом
функции 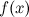 в
точке
в
точке  ,
если для
,
если для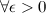
 такое,
что для
такое,
что для из
того, что
из
того, что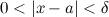 следует,
что
следует,
что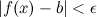 :
: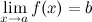 или
или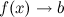 при
при .
.
Односторонние пределы
Определение
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Левый и правый пределы функции
Определение
Число  называетсяправым
пределом функции
называетсяправым
пределом функции 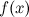 в
точке
в
точке  ,
если для
,
если для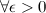
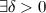 такое,
что для любого
такое,
что для любого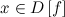 и
и ,
выполняется неравенство
,
выполняется неравенство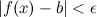 (рис.
1). Правый предел обозначается
(рис.
1). Правый предел обозначается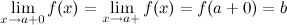
Число  называетсялевым
пределом функции
называетсялевым
пределом функции 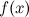 в
точке
в
точке  ,
если для
,
если для
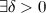 такое,
что для любого
такое,
что для любого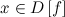 и
и ,
выполняется неравенство
,
выполняется неравенство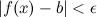 (рис.
2). Левый предел обозначается
(рис.
2). Левый предел обозначается

Левый и правый пределы функции называются односторонними пределами.
Теорема
Если
существуют 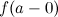 и
и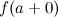 ,
причем
,
причем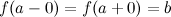 ,
то существует и
,
то существует и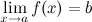 .
Обратное утверждение также верно.
.
Обратное утверждение также верно.
В
случае, если 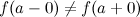 ,
то предел
,
то предел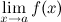 не
существует.
не
существует.
3. Предел функции в точке. Предел на бесконечности. Первая часть в предыдущем вопросе.
Понятие функции, ее области определения и множества значений. Способы задания функции
Пусть D – произвольное подмножество действительных
чисел (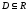 ).
).
Определение
5. Если каждому числу 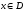 поставлено в
соответствие по некоторому правилу или
закону одно вполне определенное значение y = f(x),
то говорят, что на множестве D определена числовая
функция f.
поставлено в
соответствие по некоторому правилу или
закону одно вполне определенное значение y = f(x),
то говорят, что на множестве D определена числовая
функция f.
В
определении речь идет об однозначной функции.
Если допускать, что каждому 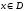 отвечает не одно, а несколько (или даже
бесконечное множество) значений y,
то функцию называют многозначной.
В дальнейшем будем рассматривать
однозначные функции.
отвечает не одно, а несколько (или даже
бесконечное множество) значений y,
то функцию называют многозначной.
В дальнейшем будем рассматривать
однозначные функции.
Множество D называется областью определения функции f и обозначается D(f),
а множество  –
множеством значений функции и
обозначается Е(f).
–
множеством значений функции и
обозначается Е(f).
Для
записи функции применяются следующие
обозначения: y = f(x), 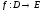 ,
, 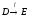 .
.
Величина х называется независимой переменной или аргументом функции, а величина у – зависимой переменной или функцией.
Способы задания функции: аналитический, табличный, графический.
Аналитический
способ задания
функции состоит в том, что с помощью формулы,
или нескольких формул, или уравнений
устанавливается алгоритм вычисления
значений функции f(x)
для каждого из значений 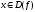 .
.
Под областью определения понимают множество x, при которых данная формула имеет смысл.
Табличный
способ задания
функции осуществляется табличным перечислением n значений аргумента 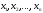 и
соответствующих им значений функции
и
соответствующих им значений функции 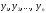 .
.
Графический способ задания функции состоит в представлении функции y = f(x) графиком в некоторой системе координат.
Определение 6. Графиком
функции y = f(x)
называется
множество всех точек плоскости 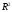 с
координатами (х; f(x)),
где х
с
координатами (х; f(x)),
где х  D(f).
D(f).
Основные свойства функции
Средствами элементарной математики для функции y = f(x) с областью определения D(f) в большинстве случаев можно определить следующие характеристики:
1. Нули и знак функции.
Значения 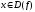 ,
при которых функция f обращается в нуль, называются нулями
функции, т.е.
нули функции являются корнями уравнения f(x)=0.
,
при которых функция f обращается в нуль, называются нулями
функции, т.е.
нули функции являются корнями уравнения f(x)=0.
Если f(x)>0 на некотором интервале, то говорят, что функция на этом интервале положительная и график функции расположен выше оси Ox.
Если f(x)<0 на некотором интервале, то говорят, что функция на этом интервале отрицательная и график функции расположен ниже оси Ox.
В нуле функции график имеет общую точку с осью Ox.
2. Четность или нечетность функции.
Определение
7. Числовая
функция f называется четной (нечетной),
если  .
.
График четной функции симметричен относительно оси Оу, а график нечетной функции симметричен относительно начала координат.
Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида.
3. Периодичность функции.
Определение 8. Функция f называется периодической,
если существует такое число Т  0,
что для
0,
что для выполняются
условия:
выполняются
условия:
1) 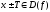 ;
;
2) f(x – Т) = f(x + Т) = f(x).
Число Т называется периодом функции.
Заметим,
что если Т является периодом функции f(x),
то число nT , где 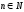 –
также период этой функции. Если
существует наименьший положительный
период функции, то его называют основным
периодом.
–
также период этой функции. Если
существует наименьший положительный
период функции, то его называют основным
периодом.
4. Интервалы возрастания, убывания функции.
Определение 9. Функция f называется возрастающей (убывающей)
на
множестве Х D(f),
если для любых значений
D(f),
если для любых значений  таких,
что
таких,
что 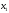 <
< 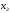 ,
справедливо неравенство f(x1) < f(x2)
(f(x1) > f(x2)).
,
справедливо неравенство f(x1) < f(x2)
(f(x1) > f(x2)).
Возрастающие и убывающие на множестве Х функции называются монотонными функциями на этом множестве.
5. Ограниченность функции.
Определение 10. Функция y = f(x)
называется ограниченной на множестве Х  D(f),
если существует такое число М > 0,
что для
D(f),
если существует такое число М > 0,
что для 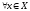 выполняется: |f(x)|
выполняется: |f(x)|  M.
M.
Из определения следует, что график ограниченной функции располагается между прямыми y=M и y= –M.
§ 5. Определение числовой функции. Способы задания функций. Свойства функций
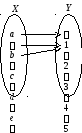
На рисунке дан граф соответствия между множествами Х = {а;b;с;d;е},Y = {1; 2; 3; 4; 5}. Данное соответствие таково, что не у каждого элемента множестваХесть соответствующий элемент множестваY, но если есть, то он единственный.
А= {а;b;с} – множество тех элементов, для которых есть соответствующий элемент в множествеY. Заметим, что каждому элементу множестваАсоответствует единственный элемент множестваY.
Определение. Соответствие между множествамиХ иY, где каждому элементу множестваХ соответствует не более одного элемента множестваY, называетсяфункциональнымсоответствиемилифункцией.
Функции обозначают буквами латинского алфавита f,g,hи др. и пишут:у=f(х).
х– независимая переменная или аргумент, все значения, которые принимает независимая переменная – область определения функции.
Пусть дана функция fс областью определенияАХ, гдеХ– множество отправления функцииf. Множество прибытия обозначимY.
Элемент у Y, соответствующий элементух А, называют значением функцииf и пишуту=f(х).
Определение.Множество всеху Y, которые являются значениями функцииf, называютмножеством значенийфункцииf.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Пример. Пусть
дана функцияf(х)
=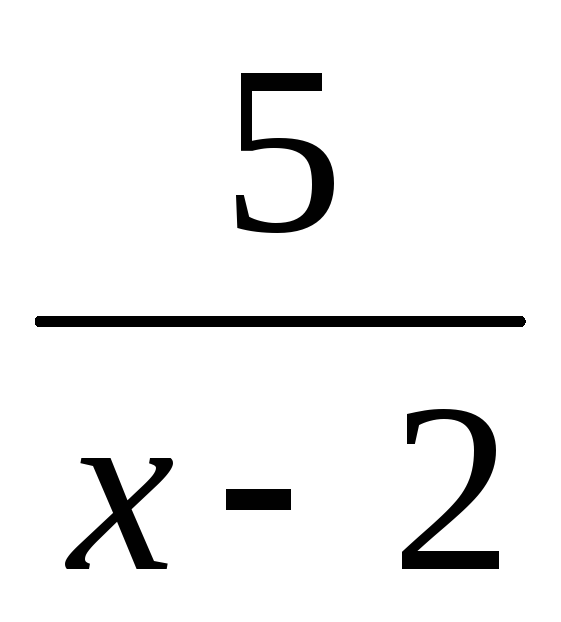 .
Областью определения функцииf(х) является множествоR \ {2}.
.
Областью определения функцииf(х) является множествоR \ {2}.
Способы задания функций
Аналитическоезадание функции – задание функции с помощью формулыу=f(х), гдеf(х) – некоторое выражение в переменнойх.
Табличноезадание функции – приводится таблица, указывающая значение функции для имеющихся в таблице значениях аргумента. Этот способ часто используется на практике, когда зависимость одной величины от другой находят опытным путем; оказывается удобным, т.к. позволяет найти значение функции для имеющихся в таблице значений аргумента без вычислений.
Графическоезадание функции. Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Свойства функций
Четные и нечетные функции
Определение. Функцияу=f(х) называетсячетной, если для любого элементахиз области определения функции выполняется равенство f(–х) = f(х).
Определение. Функцияу=f(х) называетсянечетной, если для любого элементахиз области определения функции выполняется равенство f(–х) = – f(х).
Из определений следует, что область определения Х как четной, так и нечетной функции должна обладать следующим свойством: еслихХ, то – хХ.
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Возрастающие и убывающие функции
Определение. Функцияу=f(х) называетсявозрастающейна промежуткеХ, еслих1,х2Х, таких, чтох1 <х2, выполняется неравенствоf(х1) < f(х2).
Определение. Функцияу=f(х) называетсяубывающейна промежуткеХ, еслих1,х2Х, таких, чтох1 <х2, выполняется неравенствоf(х1) > f(х2).
Определение. Функция называетсямонотоннойна некотором промежуткеА, если она на этом промежутке возрастает или убывает.
Способы задания функции
Доклад
на тему: Способы задания функции
Выполнила: Ковалёва Юлия
211 группа «Лечебное дело»
Преподаватель: Пушкарская
Ольга Владимировна
2015
Функция — одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r2. Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции — теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.
1. Функция и её свойства
Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.
Переменная х- независимая переменная или аргумент.
Переменная у- зависимая переменная
Значение функции- значение у, соответствующее заданному значению х.
Область определения функции- все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- все значения, которые принимает функция.
Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)
Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x)
Возрастающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2)
Убывающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
2. Способы задания функции
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)- с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.
3. Виды функций и их свойства
1) Постоянная функция- функция, заданная формулой у=b, где b-некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат
2) Прямая пропорциональность- функция, заданная формулой у=kx, где к¹0. Число k называется коэффициентом пропорциональности.
Cвойства функции y=kx:
1. Область определения функции- множество всех действительных чисел
2. y=kx — нечетная функция
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
3)Линейная функция- функция, которая задана формулой y=kx+b, где k и b-действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.
Свойства функции y=kx+b:
1. Область определения- множество всех действительных чисел
2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
Графиком функции является прямая.
4) Обратная пропорциональность- функция, заданная формулой y=k/х, где k¹0 Число k называют коэффициентом обратной пропорциональности.
Свойства функции y=k/x:
1. Область определения- множество всех действительных чисел кроме нуля
2. y=k/x- нечетная функция
3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке (-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на промежутке (0;+¥).
Графиком функции является гипербола.
5)Функция y=x2
Свойства функции y=x2:
1. Область определения- вся числовая прямая
2. y=x2 — четная функция
3. На промежутке [0;+¥) функция возрастает
4. На промежутке (-¥;0] функция убывает
Графиком функции является парабола.
6)Функция y=x3
Свойства функции y=x3:
1. Область определения- вся числовая прямая
2. y=x3 —нечетная функция
3. Функция возрастает на всей числовой прямой
Графиком функции является кубическая парабола
7)Степенная функция с натуральным показателем- функция, заданная формулой
y=xn, где n— натуральное число. При n=1 получаем функцию
y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x2;
y=x3. Их свойства рассмотрены выше.
Пусть n- произвольное четное число, большее двух: 4,6,8… В этом случае функция
y=xn обладает теми же свойствами, что и функция y=x2.
График функции напоминает параболу y=x2, только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем “теснее прижимаются” к оси Х, чем больше n.
Пусть n- произвольное нечетное число, большее трех: 5,7,9… В этом случае функция y=xn обладает теми же свойствами, что и функция y=x
График функции напоминает кубическую параболу.
8)Степенная функция с целым отрицательным показателем- функция, заданная формулой y=x-n, где n— натуральное число.
При n=1 получаем y=1/х, свойства этой функции рассмотрены в п.4.
Пусть n- нечетное число, большее единицы: 3,5,7… В этом случае функция y=x-n обладает в основном теми же свойствами, что и функция y=1/х.
Пусть n- четное число, например n=2.
Свойства функции y=x-2:
1. Функция определена при всех x¹0
2. y=x-2 — четная функция
3. Функция убывает на (0;+¥) и возрастает на (-¥;0).
Теми же свойствами обладают любые функции при четном n, большем двух.
9)Функция y=Öх
Свойства функции y=Öх:
1. Область определения — луч [0;+¥).
2. Функция y=Öх — общего вида
3. Функция возрастает на луче [0;+¥).
10)Функция y=3Öх
Свойства функции y=3Öх:
1. Область определения- вся числовая прямая
2. Функция y=3Öх нечетна.
3. Функция возрастает на всей числовой прямой.
11)Функция y=nÖх
При четном n функция обладает теми же свойствами, что и функция y=Öх. При нечетном n функция y=nÖх обладает теми же свойствами, что и функция y=3Öх.
12)Степенная функция с положительным дробным показателем- функция, заданная формулой y=xr, где r— положительная несократимая дробь.
Свойства функции y=xr:
1. Область определения- луч [0;+¥).
2. Функция общего вида
3. Функция возрастает на [0;+¥).
На рисунке изображен график функции y=x5/2. Он заключен между графиками функций y=x2 и y=x3, заданных на промежутке [0;+¥).Подобный вид имеет любой график функции вида y=xr, где r>1.
На рисунке изображен график функции y=x2/3. Подобный вид имеет график любой степенной функции y=xr, где 0<r<1
13)Степенная функция с отрицательным дробным показателем-функция, заданная формулой y=x-r, где r— положительная несократимая дробь.
Свойства функции y=x-r:
1. Обл. определения -промежуток (0;+¥)
2. Функция общего вида
3. Функция убывает на (0;+¥)
14)Обратная функция
Если функция y=f(x) такова, что для любого ее значения yo уравнение f(x)=yo имеет относительно х единственный корень, то говорят, что функция f обратима.
Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и областью ее значений является промежуток Y, то у нее существует обратная функция, причем обратная функция определена и возрастает(убывает) на Y.
Таким образом, чтобы построить график функции, обратной к функции y=f(x), надо график функции y=f(x) подвергнуть преобразованию симметрии относительно прямой y=x.
15)Сложная функция- функция, аргументом которой является другая любая функция.
Возьмем, к примеру, функцию y=x+4. Подставим в аргумент функцию y=x+2. функция графический аналитический табличный
Получается: y(x+2)=x+2+4=x+6. Это и будет являться сложной функцией.
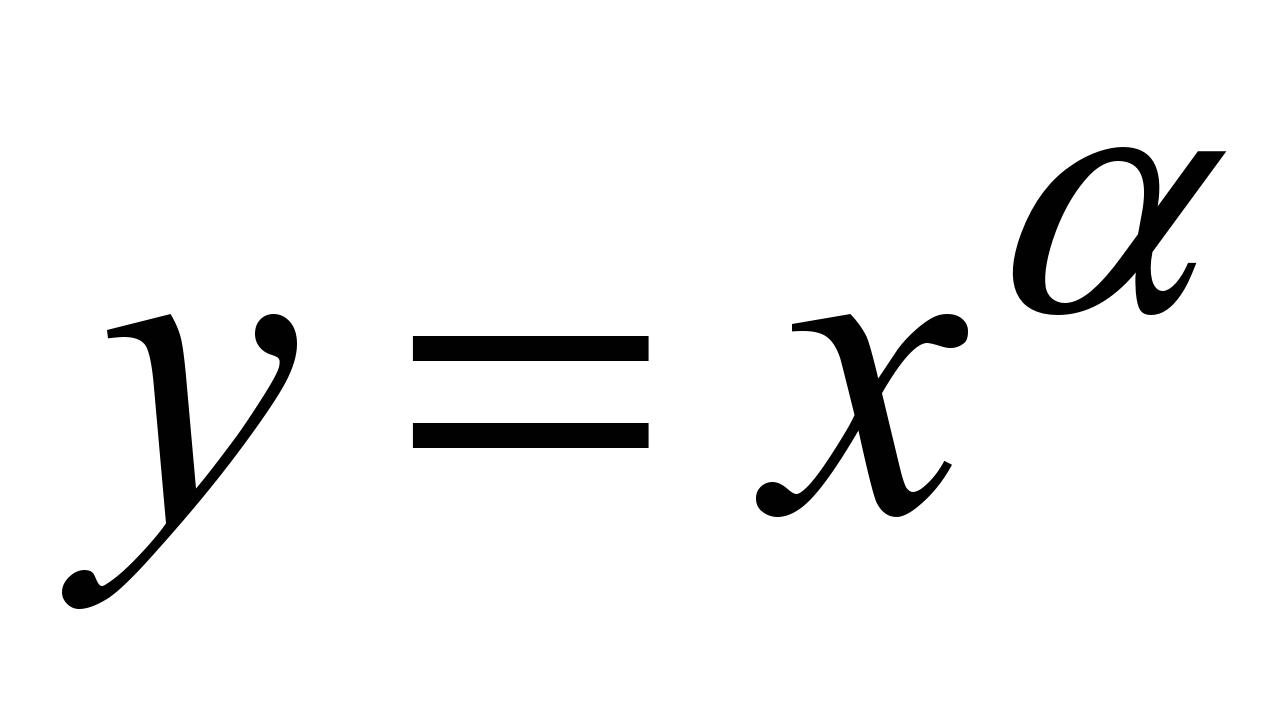 ,
где
,
где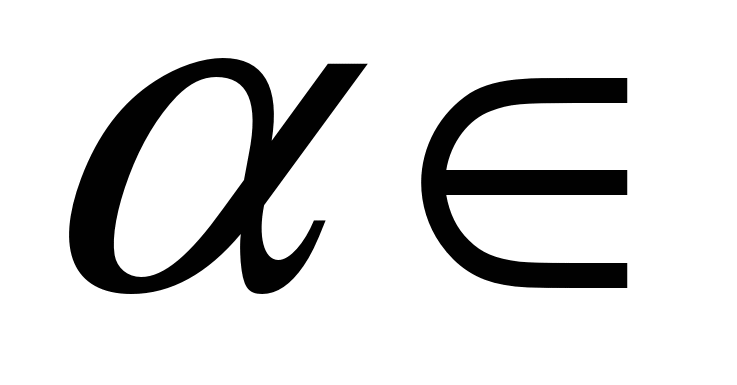 R;
R;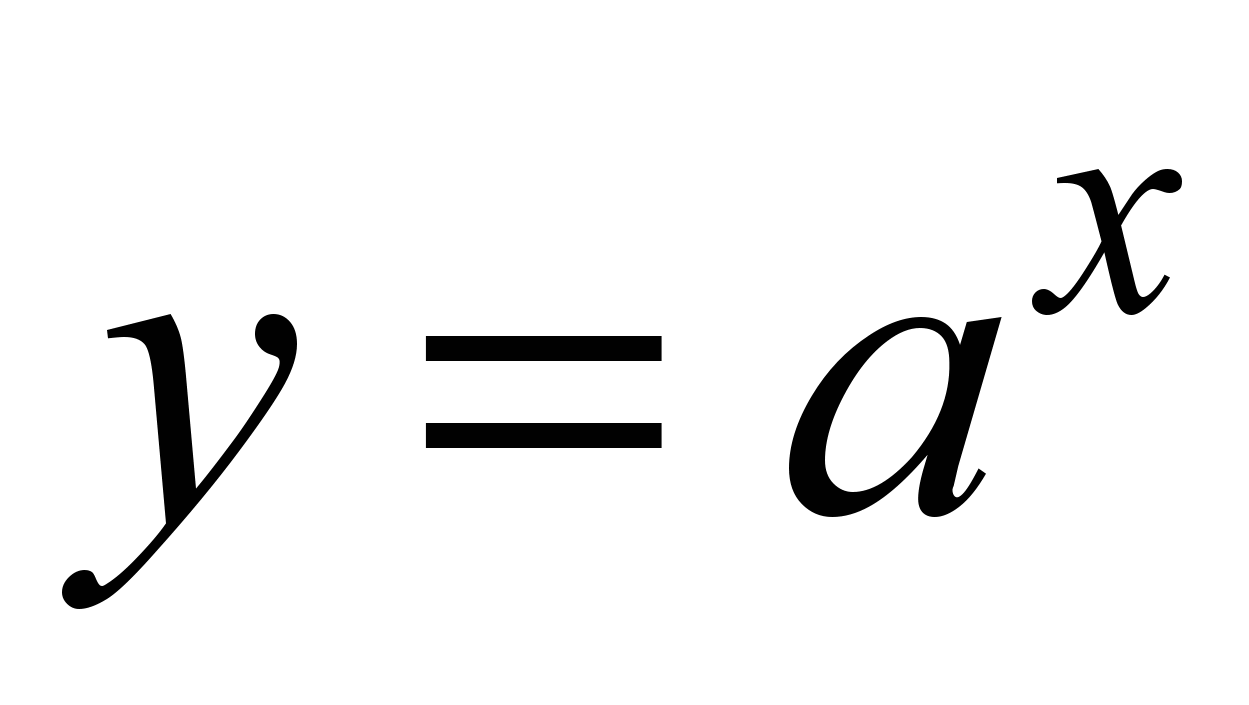 ,
где
,
где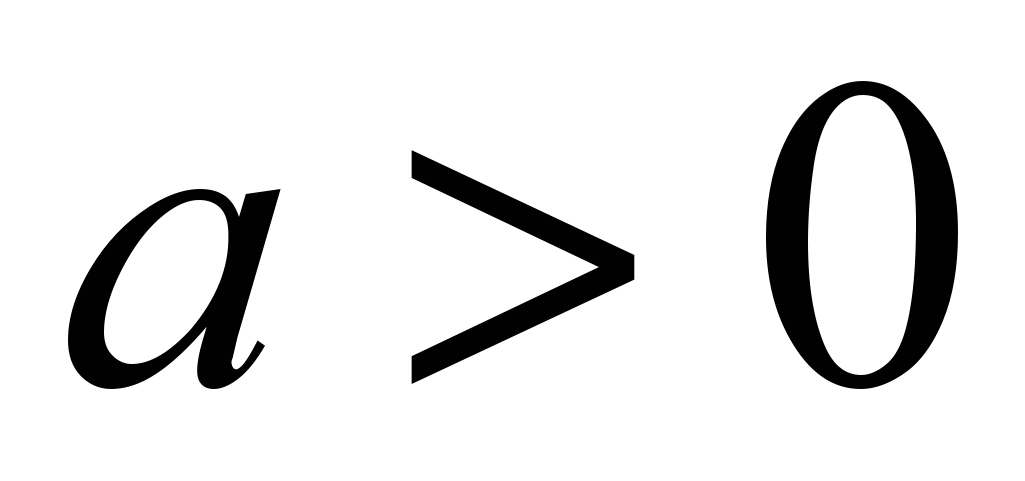 и
и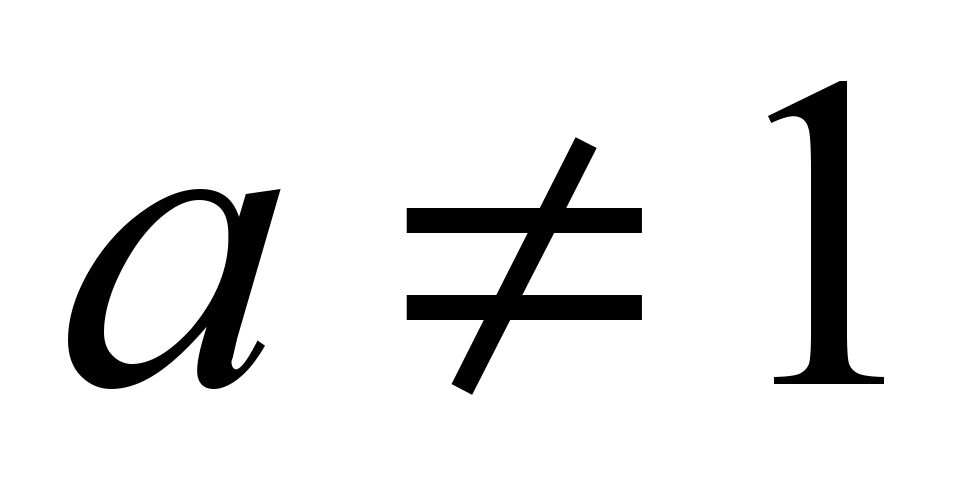 ;
;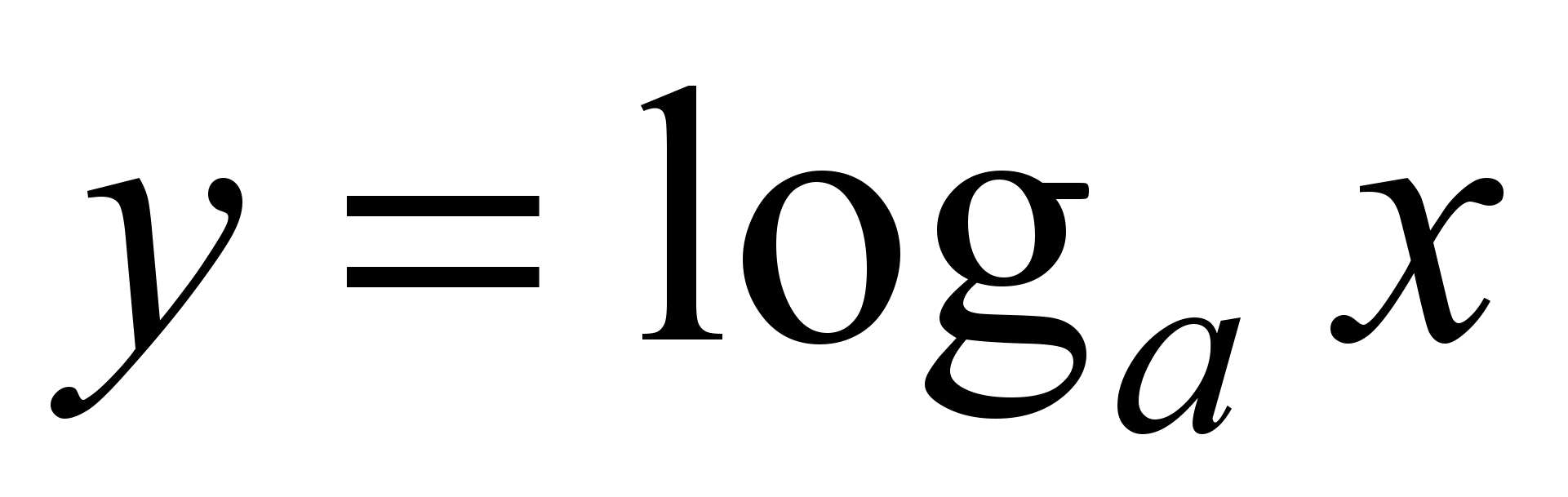 ,
где
,
где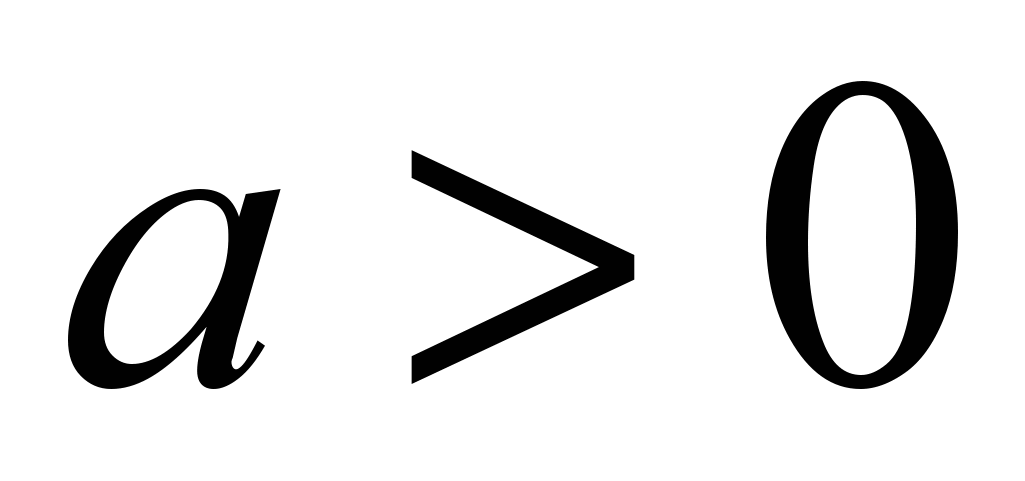 и
и ;
;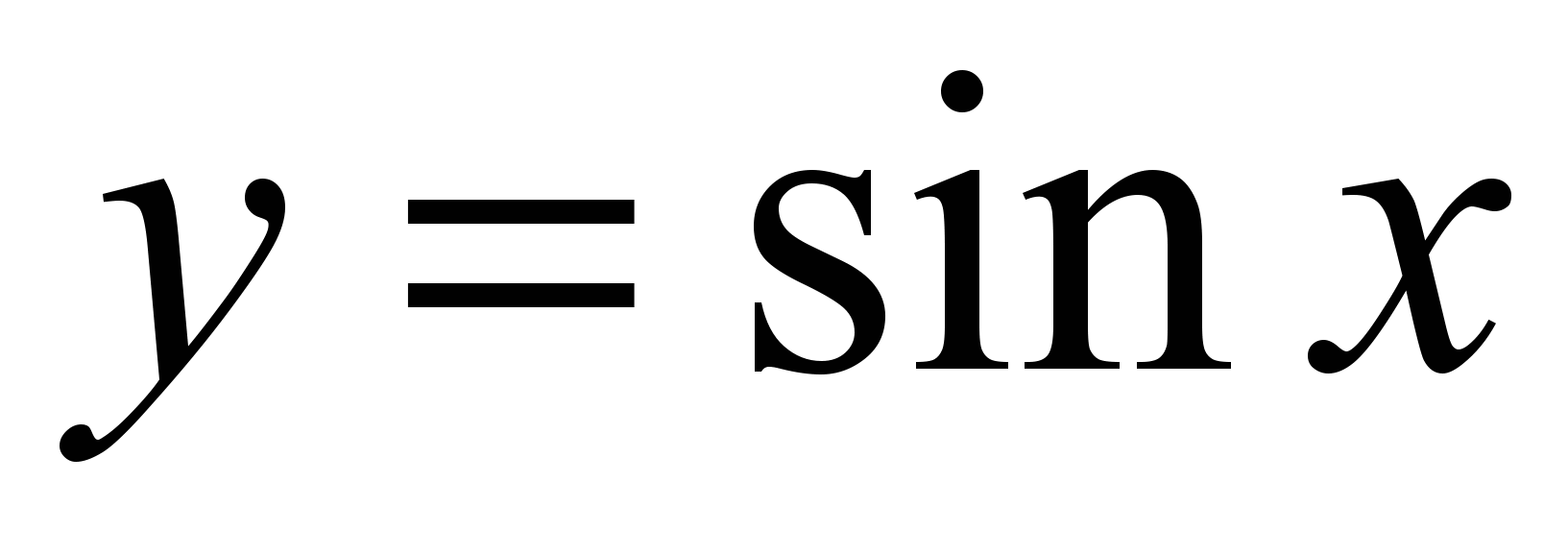 ,
,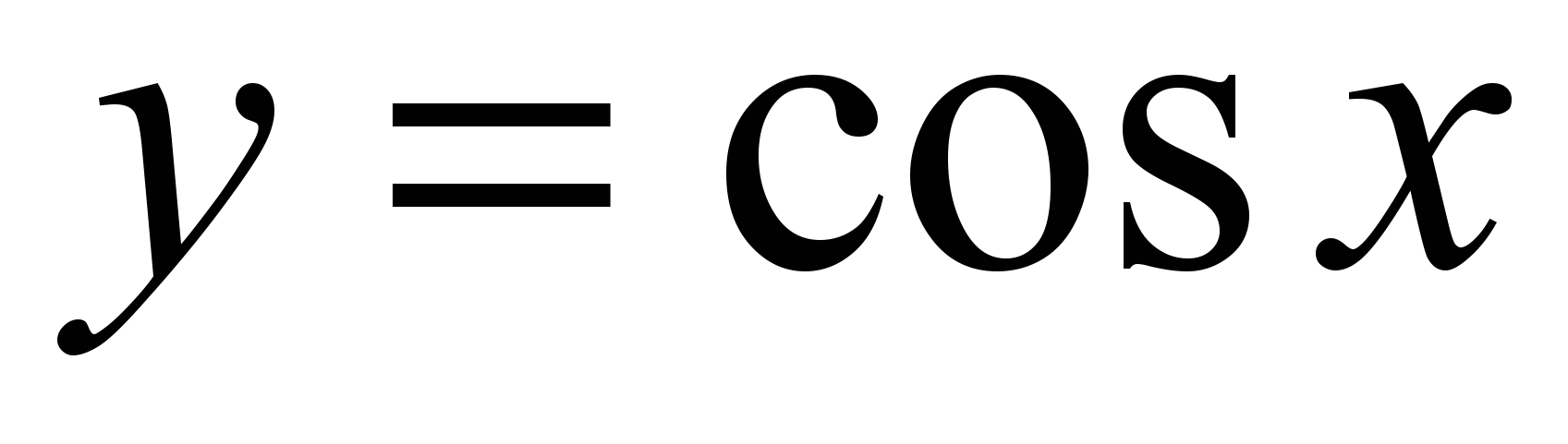 ,
, ,
,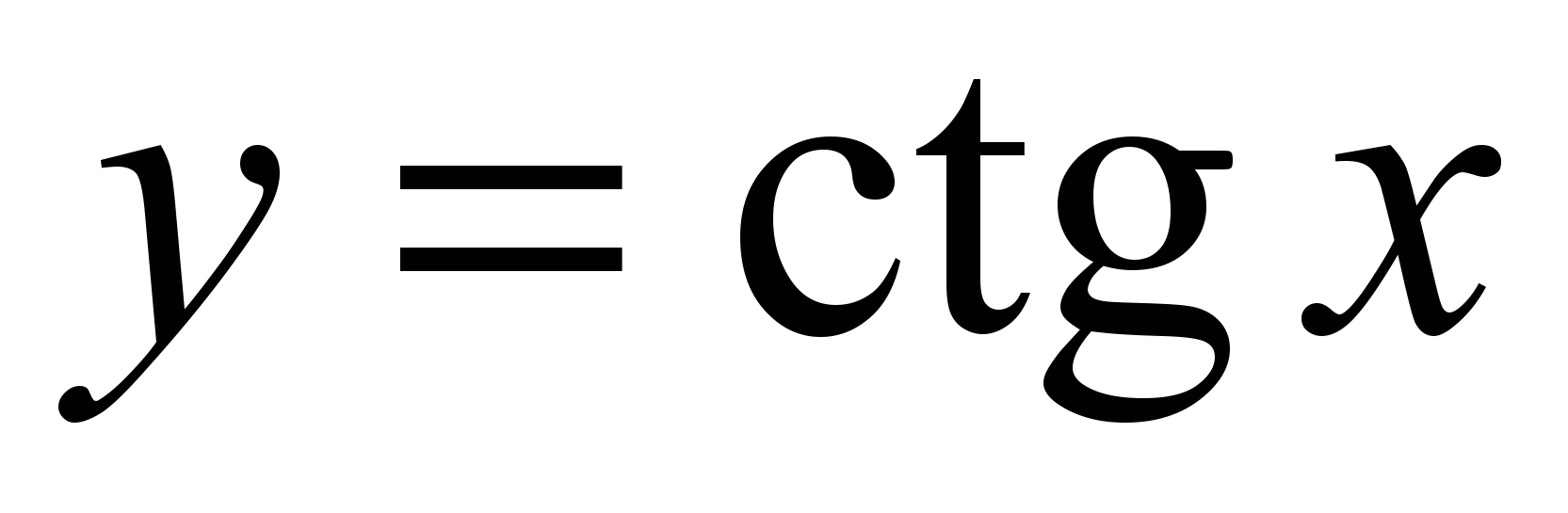 ;
; ,,
,,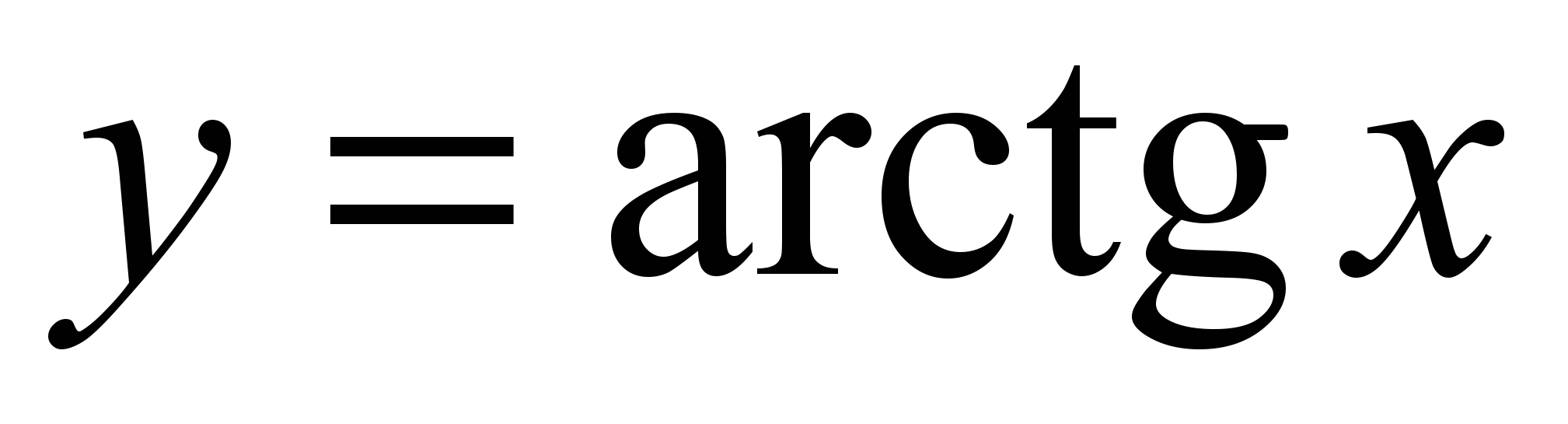 ,
, 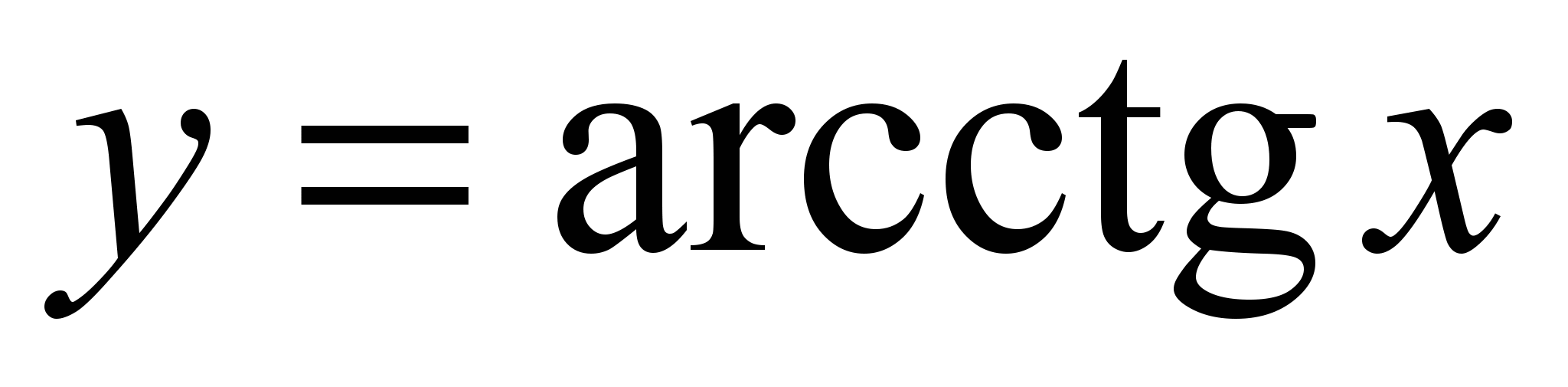 .
.