Функция y = √x. Её свойства и график. Видеоурок. Алгебра 8 Класс
Квадратным корнем из неотрицательного числа  называют такое неотрицательное число, квадрат которого равен
называют такое неотрицательное число, квадрат которого равен  . Это число обозначают
. Это число обозначают 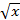 , число
, число  называют подкоренным числом.
называют подкоренным числом.
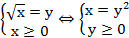
Примеры:
1. 
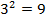 ,
,  )
)2. 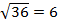 (
(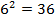 ,
,  )
)
Обратите внимание:
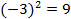
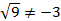 – корень не может быть равен отрицательному числу.
– корень не может быть равен отрицательному числу.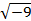 – нельзя вычислить. Корня квадратного из отрицательного числа не существует.
– нельзя вычислить. Корня квадратного из отрицательного числа не существует.
Функцией 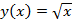 , где
, где 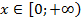 , называется закон, который каждому неотрицательному числу
, называется закон, который каждому неотрицательному числу  сопоставляет число
сопоставляет число 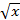
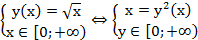
Функция 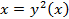 нам уже известна. Это функция типа
нам уже известна. Это функция типа  . Таким образом, изучать функцию
. Таким образом, изучать функцию 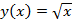 мы будем на базе функции
мы будем на базе функции 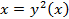 , где
, где 
Графиком функции 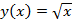 является ветвь параболы. Проверим это, составив таблицу.
является ветвь параболы. Проверим это, составив таблицу.
|
x |
0 |
1 |
4 |
6,25 |
9 |
|
|
0 |
1 |
2 |
2,5 |
3 |
Построим найденные точки на координатной плоскости (см. Рис. 1).
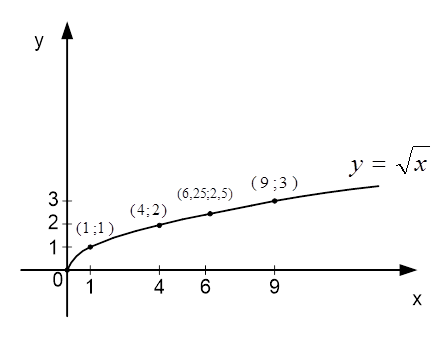
Рис. 1. График функции 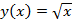
Прочтем график:
Если аргумент возрастает от 0 до 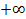 , функция возрастает от 0 до
, функция возрастает от 0 до 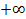
1. Множество значений функции 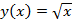 – это луч
– это луч 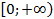 .
.
Докажем это свойство
Доказательство
Пусть  – это произвольное число из промежутка
– это произвольное число из промежутка 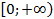 . Найдется ли такое
. Найдется ли такое 
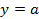 ? Чтобы узнать это, решим уравнение:
? Чтобы узнать это, решим уравнение:


Число  достигается, когда аргумент равен
достигается, когда аргумент равен 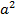 (см. Рис. 2).
(см. Рис. 2).

Рис. 2. Иллюстрация к доказательству
Следовательно:
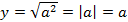
Что и требовалось доказать.
Следствия из данного свойства
а) Функция 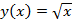 не ограничена сверху. То есть на оси
не ограничена сверху. То есть на оси 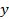 для этой функции нет самого большого положительного числа.
для этой функции нет самого большого положительного числа.
б) Функция ограничена снизу и имеет наименьшее значение.
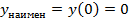
в)  при всех
при всех 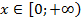 .
.
2. Функция 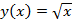 монотонно возрастает на всей области определения, то есть при
монотонно возрастает на всей области определения, то есть при 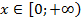 .
.

Функция называется монотонно возрастающей на всей области определения, если для любых 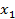 и
и  , принадлежащих области определения, из неравенства
, принадлежащих области определения, из неравенства 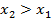 следует неравенство
следует неравенство 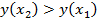 .
.
Рисунок 3 иллюстрирует нам, что функция 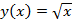

Рис. 3. Функция 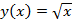 монотонно возрастающая
монотонно возрастающая
3. Функция 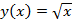 выпукла вверх на всей области определения.
выпукла вверх на всей области определения.
Для любых двух точек, например 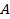 и
и 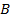 (см. Рис. 4), дуга, лежащая между этими точками, будет находиться над отрезком, соединяющим эти две точки, следовательно, функция выпуклая вверх.
(см. Рис. 4), дуга, лежащая между этими точками, будет находиться над отрезком, соединяющим эти две точки, следовательно, функция выпуклая вверх.
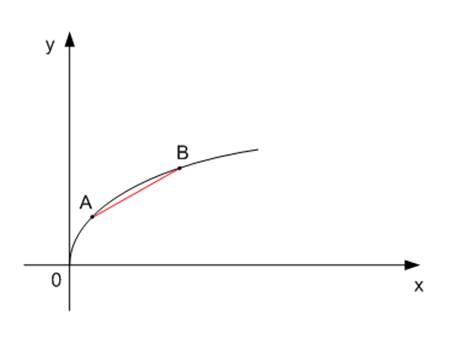
Рис. 4. Функция 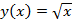 выпуклая вверх
выпуклая вверх
Список литературы
1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010.
3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2010.
4. Мордкович А.Г. Алгебра 8 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет портал «Гипермаркет знаний» (Источник)
2. Интернет портал «FizMat» (Источник)
3. Видеохостинг «YouTube» (Источник)
4. Интернет портал «UzTest» (Источник)
Домашнее задание
1. Упражнения 487, 488, 494 (стр. 146) – Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра 8 класс
2. Пересекает ли график функции 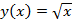 прямая: а)
прямая: а) 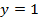 ; б)
; б) 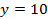 ; в)
; в) 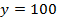 ; г)
; г) 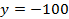 ?
?
Презентация к уроку по алгебре (8 класс) по теме: Презентация «Функции и графики»
Слайд 1
Функции и графики Методическая разработка к учебнику Ю. Макарычева «Алгебра – 8» углубленное изучение Драгунова Е. Ю. учитель математики МОУ СОШ № 10 г.о. ЖуковскийСлайд 2
Функция, область определения и область значений функции. Х Х У У f f f- функция Каждому х соответствует единственный у f f- не функция -Не каждому х — не единственный у
Слайд 3
Функцией (функциональной зависимостью) называется зависимость переменной у от переменной х , при которой каждому значению х соответствует единственное значение у. Переменная х- независимая – аргумент. Переменная у – зависимая – значение функции( функция) х у f или у = f (х)
Слайд 4
Все значения, которые может принимать аргумент (независимая переменная) образуют область определения функции. D (f) Все значения, которые может принимать функция (зависимая переменная) образуют область (множество) значений функции. E (f) Свойства функции
Слайд 5
Свойства функции Значения аргумента, при которых функция обращается в нуль , называются нулями функции Промежутки, в которых функция принимает только положительные или только отрицательные значения, называются промежутками знакопостоянства функции
Слайд 6
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 о х -1 -2 -3 -4 -5 -6 у 9 8 7 6 5 4 3 2 1 у = 0 при х = -2 и х = 3
Слайд 7
Повторение. № 1.Какие из данных графиков являются графиками каких-либо функций?
Слайд 10
Укажите по графику: а) область определения; б) область значений; в) нули функции; г) промежутки знакопостоянства
Слайд 11
у= f(x) – данная функция (уравнение с двумя переменными) Пара (х 0 ; f (х 0 )) – решение уравнения и одновременно точка на координатной плоскости. Графиком функции называется множество точек координатной плоскости , абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Слайд 12
y = f(x) у = -f(x) y = f(-x) y = f(x-1) у = f(x) — 1 у = 2f(x) y = f(3x) x = f(y)
Слайд 13
Построение графика функции с помощью геометрических преобразований Растяжение и сжатие Дано : Построить: y = f(x) y = kf(x) , к = 0 Берем х из области определения Берем х из области определения Вычисляем у = f(x) Вычисляем у 1 = f(x) , а затем у = к f (х)
Слайд 14
y x 0 y= к f(x) y=f(x) к >1 0
Слайд 15
y x 0 y=f(x) y=-f(x)
Слайд 16
для построения графика у = -к f (х) Сначала сжатие или растяжение Затем симметрия
Слайд 17
Параллельный перенос графика Дано : Построить: y = f(x) y = f(x) + n Берем х из области определения Берем х из области определения Вычисляем у = f(x) Вычисляем у 1 = f(x) , а затем у = f (х) +n При одинаковых значениях х , у отличаются на одно и тоже число. График «сдвигается» вдоль оси у на n единичных отрезков
Слайд 18
y x 0 y=f(x)+n n0 y=f(x)
Слайд 19
Параллельный перенос графика Дано : Построить: y = f(x) y = f(x — m) Берем х из области определения Берем х из области определения, затем вычисляем ( х- m) Вычисляем у = f(x) Вычисляем у = f (х -m ) При одинаковых значениях у , х отличаются на одно и тоже число. График «сдвигается» вдоль оси х на m единичных отрезков
Слайд 20
y x 0 y=f(x — m) m > 0 m
Слайд 21
Для построения графика у = f(x-m)+n Сначала параллельный перенос вдоль оси Х Затем параллельный перенос вдоль оси У
План-конспект урока по математике (8 класс) по теме: Функции и их графики
Тема урока: «Функции и их графики».
8 класс
Цель урока: закрепление знаний и формирование практических навыков.
Задачи урока:
Образовательные:
правильно употреблять функциональную терминологию;
уметь распознавать графики функций;
иметь наглядное представление о некоторых свойствах функций;
закрепить навыки построения простейших графиков функций,
использование их при решении уравнений.
Развивающие:
расширение кругозора;
быстрота реакции;
развитие математической речи при комментировании решений.
Воспитательные:
воспитание взаимопомощи в процессе выполнения работы в парах;
воспитание внимания, собранности и аккуратности;
формирование адекватной самооценки.
Оборудование:
1. Мультимедийная установка.
2. Карточки с индивидуальными заданиями.
(Вступительное слово учителя)
Идея функциональной зависимости восходит к древности, она содержится уже в первых формулах для нахождения объемов и площадей фигур (4-5 тысяч лет назад).
Начиная с 17 века понятие «функция» становится одним из важнейших. Функция сыграла и поныне играет большую роль в познании реального мира.
Функция – это математическая модель, позволяющая изучать и описывать разнообразные зависимости между реальными величинами.
Умение анализировать эти зависимости сделает вас в дальнейшем успешными в своем поле деятельности.
В настоящее время построение графиков функций, использование свойств функций при решении уравнений необходимо для успешной сдачи экзаменов.
Сегодня на уроке мы повторим все ранее изученные функции, их графики и некоторые свойства.
I. Устная работа (задания проектируются на экран):
1) Установите соответствие между графиками функций и формулами, задающими эти функции: (ученик должен сказать название функции и графика)
II. (Задание выполняет весь класс. Нужно выписать буквы, соответствующие верным ответам. Получится слово «Лейбниц». Учитель контролирует выполнение задания, при необходимости оказывает помощь.)
Установите соответствие между графиками функций и формулами.
III. (Сообщение учителя. На экран проектируется портрет Вильгельма Лейбница.)
Вильгельм Лейбниц – выдающийся немецкий математик, физик, философ, языковед в 1673 году ввел слово «функция», от латинского function – совершение, выполнение.
IV. (Работа в парах. Учащиеся, по желанию, решение выполняют на листочках, чтобы сдать на проверку. Правильность выполнения задания проверяется с помощью проектора.)
Изобразив схематически графики функций, выясните, имеет ли корни уравнение, и сколько?
1) 2) 3)
V. (Задание учащиеся выполняют по вариантам. Два ученика решают уравнения с обратной стороны доски. Правильность выполнения и оформления проверяется с помощью проектора. Учитель контролирует выполнение задания, при необходимости помогает учащимся.)
Решите графически уравнение:
I вариант II вариант
VI. Минута отдыха.
(Задание выполняется устно.)
Установите соответствие между пословицами и графиками функций:
Учитель комментирует все ответы. ( 1)По оси абсцисс – дела, по оси ординат – слава: если дела и поступки положительные, то и слава о человеке идет добрая.
3) По оси абсцисс – семена, по оси ординат – урожай. Для получения высокого урожая необходимо посеять оптимальное количество семян.)
VII. (Тест учащиеся выполняют по вариантам. Учащиеся, по желанию, сдают ответы на листочках. Учитель контролирует выполнение задания. Проверка осуществляется после выполнения задания большинством. Задания, где больше всего встречалось ошибок, разбираются вместе с классом.)
II вариант
Выберите верный ответ:
1)На рисунке изображен график функции вида у=kx+m.
Определите знаки k и m.
А) k>0; m>0 Б) k0
2)Укажите график функции убывающей на
3)Укажите график функции ограниченной снизу.
4)Дан график функции. Какие из утверждений верны?
1.Функция ограничена сверху.
2.
3.Выпукла вверх.
4.Непрерывна.
I вариант
Выберите букву, соответствующую верному ответу:
1) На рисунке изображен график функции вида у=kх+m.
Определите знаки к и m.
А) k>0; m>0 Б) k>0; m0
2)Укажите график функции возрастающей на .
3)Укажите график функции ограниченной сверху.
4)Дан график функции у=.Какие из утверждений верны:
1.Функция ограничена снизу.
2.
3.Функция непрерывна.
4.Выпукла вниз.
А) 1 и 2 Б) 2 и 3 В) 1 и 3
Ответы
I вариант II вариант
Б А Б В Б Б В А
VIII. (Задание повышенной сложности. Выполняет весь класс. Ученик решает у доски с подробными комментариями.)
Постройте график функции:
IX. Дополнительное задание. ( Для тех, кто быстро справился с основными заданиями. Проверяем с помощью пректора.)
Постройте графики функций:
а); б)
ХI.Домашнее задание.
Составьте уравнения, имеющие три, два, одно решение и не имеющее решения. Подтвердите ваши предположения, схематически изобразив графики.
XII. Итог урока подводит учитель.
Сегодня на уроке мы повторили все ранее изученные функции, их графики и некоторые свойства. На следующих уроках будем изучать более сложные функции, графики которых получаются из данных путем сдвига вдоль оси х и оси у.
(На экране пример квадратичной функции, которая получается из графика функции у=хс помощью : а) параллельного переноса вдоль оси х; б) параллельного переноса вдоль оси х и оси у.)
Подведение итогов урока, заполнение учащимися листа самооценки.
Степень сложности урока Степень освоенности материала
Легко | Обычно | Сложно |
Усвоен полностью | Усвоен частично | Неусвоен |
Степень интереса познания
Интересно | Не очень интересно | Скучно |
I вариант
I. Cхематически изобразив графики функций, выясните, имеет ли уравнение корни, и сколько?
1) 2) 3)
II. Решите графически уравнение:
III. Выберите букву, соответствующую верному ответу:
1) На рисунке изображен график функции вида у=kх+m.
Определите знаки к и m.
А) k>0; m>0 Б) k>0; m0
2)Укажите график функции возрастающей на .
3)Укажите график функции ограниченной сверху.
4)Дан график функции у=.Какие из утверждений верны:
1.Функция ограничена снизу.
2.
3.Функция непрерывна.
4.Выпукла вниз.
А) 1 и 2 Б) 2 и 3 В) 1 и 3
IV. Постройте график функции:
Дополнительные задания:
V.Дана функция у=f(х), где f(х)=. Решите уравнение
f(x-1)-f(x+1)=1.
VI.Постройте графики функций:
а);
б)
II вариант
I. Cхематически изобразив графики функций, выясните, имеет ли уравнение корни, и сколько?
1) 2) 3)
II.Решите графически уравнение:
III. Выберите верный ответ:
1)На рисунке изображен график функции вида у=kx+m.
Определите знаки k и m.
А) k>0; m>0 Б) k0
2)Укажите график функции убывающей на
3)Укажите график функции ограниченной снизу.
4)Дан график функции. Какие из утверждений верны?
1.Функция ограничена сверху.
2.
3.Выпукла вверх.
4.Непрерывна.
IV. Постройте график функции:
Дополнительные задания:
V. Дана функция у=f(х), где f(х)=. Решите уравнение
f(x-1)-f(x+1)=1.
VI. Постройте графики функций:
а);
б)
Список литературы
1.Мордкович А.Г. Алгебра. 9 кл.: В двух частях. – М.: Мнемозина, 2008.
2.Программы. Математика.5-6 классы. Алгебра.7-9 классы. Алгебра и начала анализа. 10-11 классы./авт.-сост. И.И.Зубарева, А.Г.Мордкович. – М.: Мнемозина, 2007.
3.Мордкович А.Г., Тульчинская Е.Е. Алгебра: Тесты для 7-9 кл. общеобразоват. учреждений. — М.: Мнемозина, 2000.
4.Глайзер Г.Д. Повышение эффективности обучения математике в школе. — М.: Просвящение,1989.
5. Мордкович А.Г. Алгебра. 7-9 кл.: Методическое пособие для учителя. – М.: Мнемозина, 2001.
Урок алгебры в 8 классе на тему «График функции»
Автор: Краснова Надежда Николаевна, учитель математики МОБУ СОШ № 1 имени И.Д. Бувальцева МО Кореновский район г. Кореновска
Предмет: Алгебра
Класс: 8
Тип урока: урок комплексного применения знаний и умений.
Технологическая карта изучения темы «График функции».
Тема
Развертки
Цели
Образовательные: учащиеся должны:
знать: что такое функция, область определения и область значений функции, знать графики функций, числовые промежутки;
уметь: работать с графиками функций, строить графики, составлять таблицы, работать с числовыми промежутками.
Развивающие: развивать внимание, пространственное мышление, воображение, умение анализировать, сравнивать, творческие способности учащихся, навыков самостоятельной работы, поддержание интереса к предмету.
Воспитательные: воспитание аккуратности, культуры общения, воспитание потребности к самообразованию, умение организовать свою работу и поэтапное её выполнение, формирование адекватной самооценки, воспитание трудолюбия, интереса к предмету при помощи интересного и наглядного материала.
Формировать УУД:
—Личностные: потребность в самовыражении и самореализации, социальном признании; готовности к самообразованию и самовоспитанию; способность к самооценке на основе критерия успешности учебной деятельности.
— Регулятивные: планировать пути достижения целей; устанавливать целевые приоритеты; при планировании достижения целей самостоятельно, полно и адекватно учитывать условия и средства их достижения; осуществлять познавательную рефлексию в отношении действий по решению учебных и познавательных задач; прилагать волевые усилия и преодолевать трудности и препятствия на пути достижения целей.
— Коммуникативные: формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром; осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь; работать в паре — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации.
— Познавательные: реализация проектно-исследовательской деятельности;
создавать и преобразовывать модели и схемы для решения задач; давать определение понятиям.
Планируемый результат
Предметные: распознавать графики функций, находить и изображать числовые промежутки на координатной плоскости; строить графики ; углубить и развить представления о графиках; научиться применять понятие функции и графиков для выполнения практических расчётов и построений.
Личностные: уметь самовыражаться и самореализовываться; уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь планировать пути достижения целей; устанавливать целевые приоритеты; при планировании достижения целей самостоятельно, полно и адекватно учитывать условия и средства их достижения; осуществлять познавательную рефлексию в отношении действий по решению учебных и познавательных задач; прилагать волевые усилия и преодолевать трудности и препятствия на пути достижения целей. (Регулятивные УУД)
Уметь формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром; осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь; работать в паре — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации. (Коммуникативные УУД)
Уметь реализовать проектно-исследовательскую деятельность;
создавать и преобразовывать модели и схемы для решения задач; давать определение понятиям.
Основные понятия
Функции, графики функций, числовые промежутки, зависимые и не зависимые переменные.
Межпредметные связи
Математика
Ресурсы:
— основные
— дополнительные
Учебник “Алгебра 8” под редакцией Г.В. Дорофеева, стр.216-222.
Рабочая тетрадь по алгебре для 8 класса, часть вторая, С.С. Минаева, Л.О. Рослова, стр. 36-38.
Дидактические материалы по алгебре для 8 класса, Л.П. Евстафьева, А.П. Карп, стр. 133-134.
Мультимедийная презентация к уроку, выполненная в Microsoft Power Point, режим интерактивной доски NTERWRAITETM,тетради, личные карточки, задания с использованием интерактивной доски, карточки с дополнительными заданиями.
Организация пространства
Фронтальная работа, работа в парах, индивидуальная работа.
Технология проведения
Деятельность учеников
Деятельность учителя
Задания для учащихся, выполнение которых приведет к достижению запланированных результатов
Планируемые результаты УУД
Предметные
УУД
1. Мотивация к учебной деятельности (2 мин.)
Цели:
— актуализировать требования к ученику со стороны учебной деятельности;
— создать условия для возникновения у учеников внутренней потребности включения в учебную деятельность;
— установить тематические рамки;
— уточнить тип урока и наметить шаги учебной деятельности.
Приветствуют учителя.
Слушают.
Записывают в тетрадях дату и тему урока. Заполняют личные карточки.
Организует актуализацию требований к ученику со стороны учебной деятельности.
Создает условия для возникновения у учеников внутренней потребности включения в учебную деятельность.
Устанавливает тематические рамки.
Организует уточнение типа урока и название шагов учебной деятельности.
Показывает данный этап на слайде.
-Добрый день. Наш урок сегодня необычный. У нас в классе будет работать астрономическая лаборатория. И нам необходимы новые работники. А вы знаете, кто такие астрономы? Сегодня каждый из вас узнает, какие знания потребуются настоящим астрономам. Чтобы попасть в лабораторию необходимо проверить свои знания. Результаты испытаний вы будете заносить в личную карточку. Подведя итоги в конце урока, мы узнаем, кто же из вас получит квалификацию: «высокий уровень» – ученый; «достаточный уровень» – лаборант; «средний уровень» – помощник лаборанта. Запишите свои данные в личную карточку. Настроение в начале урока: рисуют смайлики. Также хотелось бы узнать, кем бы вы хотели работать в данной лаборатории. Запишите в личную карточку. Желаю успеха! слайд№1
Уметь самостоятельно сформулировать цель урока, правильно излагать свои мысли.
Уметь придерживаться правил поведения в школе и следовать им. (Коммуникативные УУД)
Уметь ориентироваться в своей системе знаний: ставить перед собой цели и задачи с помощью учителя. (Познавательные УУД.)
Уметь слушать учителя. (Коммуникативные УУД)
2. Актуализация знаний. (5 мин.)
Цели:
-организовать актуализацию устного счета;
-организовать у учащихся внимание и самоконтроль;
-организовать фиксирования учащимися индивидуального затруднения.
Смотрят на доску. Устно, по цепочке, отвечают на вопросы, выполняют арифметические действия.
Производят самоконтроль.
Ставит цель перед учащимися.
Показывает данный этап на слайде.
Контролирует правильность выполнения.
Ученые должны уметь точно выполнять математические расчеты. Вот это мы сейчас и проверим. слайд№2
-Молодцы, вы справились с этой задачей. И теперь все достойны работать в лаборатории.
Уметь быстро и правильно вычислять и отвечать на вопросы.
Уметь контролировать последовательность действий. (Регулятивные УУД)
Уметь производить арифметические действия. (Познавательные УУД.)
Уметь оформлять свои мысли в устной форме. (Коммуникативные УУД)
3. Теоретическое обоснование графиков функций. (3 мин.)
Цели:
-организовать постановку цели урока;
— организовать составление совместного плана действий;
— организовать проверку знаний по изученной теме «Что такое функция»
— закрепить, на основе повторения теории, тему «График функции»;
-организовать у учащихся внимание и самоконтроль;
-организовать устранение и фиксирование преодоления затруднения.
Слушают учителя.
Работают с интерактивной доской.
Отвечают на вопросы. Высказывают свое мнение.
Выявляют места затруднений, исправляют с помощью учителя ошибки.
Показывает данный этап на слайде.
Организует теоретическое обоснование функции и графиков в соответствии с планом.
Организует диалог. Контролирует правильность ответов.
Организует усвоение и закрепление учениками темы «График функции».
-Ученые очень умны, давайте проверим на сколько прочны ваши знания. Вы должны ответить на вопросы. Задания на слайдах №3,4
Идет фронтальный и индивидуальный опрос, устная или непосредственная работа с интерактивной доской.
-Молодцы, ребята, справились с этой задачей.
(В соответствии с критериями учащиеся выставляют баллы.)
Уметь правильно излагать свои мысли.
Уметь решать простейшие задачи.
Иметь наглядные представления о числовых промежутках, о функции, о графиках.
Уметь высказывать свое предположение; контролировать последовательность действий. (Регулятивные УУД)
Уметь оформлять мысли в устной и письменной форме; слушать других. (Коммуникативные УУД)
Уметь добывать новые знания; ориентироваться в своей системе знаний; находить ответы на вопросы, используя свой жизненный опыт и информацию, полученную на уроках. (Познавательные УУД.)
4. Практическая работа. (10 мин.)
Цели:
— организовать самостоятельное выполнение учащимися построения графиков знаков зодиака
— организовать самопроверку и самооценку;
— организовать работу в парах;
— развить пространственное мышление,
воображение, творческие способности учащихся;
— воспитать трудолюбие, аккуратность, культуру общения, потребность к самообразованию, умение организовать свою работу и поэтапное её выполнение, интерес к предмету при помощи знаков зодиака.
В парах выполняют построение графиков. Обсуждают, делают вывод
Выполняют самооценку, выставляют баллы.
Объясняет задания для практической работы.
Следит за выполнением учащимися построения графиков. Организует самооценку учебной деятельности.
А теперь, каждый из вас будет строить один из знаков зодиака на координатной плоскости.
— Каждая парта (работа происходит в парах) получает карточку. Построив, определите, какой знак зодиака у вас получился. Сделав вывод, составьте алгоритм построения графиков.
(Группа, которая справилась с заданием быстрее всех, получает дополнительное задание на карточке, оценивающееся в 3 балла.)
— А сейчас подведем итоги, что у вас получилось и к какому выводу вы пришли. слайд№5,6. (В соответствии с критериями учащиеся выставляют баллы.)
Уметь строить графики функций, отмечать числовые промежутки на координатной плоскости.
Уметь планировать свое действие в соответствии с поставленной задачей.
Уметь оценивать правильность выполнения действия на уровне адекватной оценки. (Регулятивные УУД)
Уметь оформлять мысли в устной и письменной форме; уметь работать в парах. (Коммуникативные УУД)
Способность к самооценке на основе критерия успешности учебной деятельности. Способствовать развитию пространственного мышления,
воображения, творческих способностей учащихся.
Способствовать воспитанию трудолюбия, аккуратности, культуры общения, потребности к самообразованию. (Личностные УУД)
5. Физкультминутка. (1 мин.)
Цели:
— снять напряжение,
— настроить учащихся на письменную работу.
Под руководством учителя выполняют физические упражнения.
Организует проведение физкультминутки.
-Ребята, во время работы вы засиделись, нужна разминка.
Проведем небольшую зарядку.
Чтоб глаза твои зоркие были,
Чтоб в очках тебе не ходить,
Эти лёгкие движенья
Предлагаю повторить.
Вдаль посмотри и под ноги,
Вправо, влево побыстрей.
Удивимся, что такое?
И закроем их скорей.
А теперь по кругу быстро,
Словно стрелочка часов,
Проведём глазами дружно,
Ну, а дальше будь здоров!
Уметь придерживаться правил поведения на уроке. (Коммуникативные УУД)
Уметь контролировать последовательность действий. (Регулятивные УУД)
6. Закрепление темы «График функции». (6 мин.)
Цели:
— организовать выполнение учащимися самостоятельную работу с учебником;
— организовать самопроверку и самооценку;
— организовать выявление места и причины затруднений, работу над ошибками.
Выполняют самостоятельно задания в тетради, у доски.
Выполняют самопроверку.
Ведут контроль за доской.
Называют место своего затруднения, причину; исправляют ошибки.
Выполняют самооценку по алгоритму, выставляют баллы.
Организует выполнение учащимися работы в тетрадях, у доски.
Помогает в выявлении места и причины затруднений; контролирует работу над ошибками.
Организует самооценку учебной деятельности.
-А теперь давайте проверим на сколько хорошо вы изучили тему «График функции».
В тетрадях и у доски, выполнить задания по учебнику: № 769, 772, 773, стр. 221. (Учащиеся читают задание, дается время на выполнение, а так же три ученика, выполняют решение на доске.)
-Давайте подведем итоги. (В соответствии с критериями учащиеся выставляют баллы.)
Уметь решать и оформлять задания на тему: «График функции».
Уметь проговаривать последовательность действий на уроке; планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; уметь оценивать правильность выполнения действия на уровне адекватной оценки. (Регулятивные УУД)
Способность к самооценке на основе критерия успешности учебной деятельности. (Личностные УУД)
Уметь оформлять мысли в устной и письменной форме. (Коммуникативные УУД)
7. Самостоятельная работа. (10 мин.)
Цели:
— организовать выполнение учащимися самостоятельную работу.
— организовать самопроверку и самооценку;
— развить пространственное мышление, воображение, творческие способности учащихся;
— воспитать трудолюбие, аккуратность, потребность к самообразованию, умение организовать свою работу и поэтапное её выполнение.
Выполняют самостоятельно задания в тетради, у доски.
Выполняют самопроверку.
Ведут контроль за доской.
Называют место своего затруднения, причину; исправляют ошибки.
Выполняют самооценку по алгоритму, выставляют баллы.
Объясняет задания для самостоятельной работы.
Организует выполнение учащимися заданий. Организует самооценку учебной деятельности.
-Следующим заданием для каждого будет самостоятельная работа. Каждый из вас по вариантам выполняет задания из дидактического материала (стр. 133 П-45. График функции.). слайд№7.
По окончанию работы тетради сдаются на проверку.
(В соответствии с критериями учащиеся выставляют баллы.)
Бонус 1 балл – за чистоту записей в рабочей тетради.
Уметь самостоятельно решать и оформлять задания на тему: «График функции».
Уметь планировать свое действие в соответствии с поставленной задачей.
Уметь оценивать правильность выполнения действия на уровне адекватной оценки. (Регулятивные УУД)
Уметь оформлять мысли в письменной форме. (Коммуникативные УУД)
Способность к самооценке на основе критерия успешности учебной деятельности. Способствовать развитию мышления. (Личностные УУД)
8. Рефлексия учебной деятельности на уроке. (3 мин.)
Цели:
— организовать рефлексию и самооценку учениками собственной учебной деятельности.
Слушают учителя.
Записывают домашнее задание. Заполняют личные карточки.
Показывает данный этап на слайде. Объясняет домашнее задание.
Организует рефлексию.
Благодарит за урок.
— Вы прошли все испытания. Пришла пора узнать, какую квалификацию вы можете получить.
Выставляем себе оценки — сумма баллов делится на 2.
-Что мы с вами сегодня узнали? Повторите алгоритм построения графиков.
Довольны ли вы своей работой на уроке? Изобразите свое настроение в конце урока. (рисуют смайлики).
-Что понравилось?
-Что вызвало затруднение?
-За что можете себя похвалить?
-Кто получил ту квалификацию, которую планировал в начале урока?
Все знания, которые вы прибрели на уроке помогут вам постичь тайны и законы математики.
— Давайте запишем домашнее задание. слайд№8. (Прочитать в учебнике и разобрать п. 5.3,выполнить задания в рабочей тетради, часть 2, № 204, 205, 206, стр. 36-37.)
-А завершить урок я хотела бы небольшой притчей.
«Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и каждому задал по вопросу. У первого спросил: «Что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»».
-Ребята! Давайте мы попробуем оценить каждый свою работу за урок.
-Кто работал так, как первый человек, изобразите в личной карточке «…».
-Кто работал добросовестно, «!?».
-Кто принимал участие в строительстве храма «Знаний», «!».
Давайте поблагодарим друг друга за хорошую работу и скажем «Спасибо за урок!»
Способность к самооценке на основе критерия успешности учебной деятельности. (Личностные УУД)
Уметь оценивать правильность выполнения действия на уровне адекватной оценки. (Регулятивные УУД)
Функции, их свойства, графики, 8 класс
Просмотр содержимого документа
«Функции, их свойства, графики, 8 класс»

5
4
2
1
3
6
№ 1
Как называется соответствие, установленное по правилу, согласно которому каждому значению х из множества Х соответствует определённое значение у

5
4
2
1
ф
3
6
у
н
к
ц
и
я
№ 2
Как называется независимая переменная?

5
4
2
а
р
1
г
у
ф
3
м
6
у
е
н
н
к
ц
т
и
я
№ 3
Как называют процесс описания свойств функции?
 m и f(x) то функция у=f(x) — … «
m и f(x) то функция у=f(x) — … «
5
4
2
а
р
1
г
3
ф
у
м
и
6
у
е
н
с
н
к
с
т
ц
л
е
и
д
я
о
в
а
н
и
е
№ 4
Если для любого х из области определения выполняются условия f(х)m и f(x)
то функция
у=f(x) — …

5
4
о
2
г
а
р
р
г
а
1
ф
у
3
н
6
и
м
и
у
ч
е
н
с
н
с
к
е
н
т
ц
л
и
е
н
а
д
я
я
о
в
а
н
и
е
№ 5
Для любых двух элементов и
из области определения, если
при условии
f( )

5
4
в
2
о
о
а
г
з
р
р
р
1
г
а
а
у
н
ф
3
с
м
и
6
и
у
т
ч
е
с
н
а
н
ю
с
к
е
л
ц
н
щ
т
н
е
и
а
д
а
я
я
я
о
в
а
н
и
е
№ 6
Как называют число, от знака которого зависит направление ветвей параболы, возрастание или убывание линейной функции и т.д.

5
4
в
2
о
о
а
г
з
р
р
р
1
г
а
а
у
н
ф
3
с
м
и
6
и
у
т
ч
е
к
с
н
а
н
ю
о
с
к
е
л
э
ц
н
щ
т
н
ф
е
и
а
д
а
ф
я
я
я
и
о
в
ц
и
а
е
н
н
и
т
е
Если у= f (x), то множество точек (х; у) координатной плоскости называют …
7

5
4
в
о
2
о
г
а
з
р
р
р
г
а
а
1
ф
у
3
н
с
и
6
м
и
у
т
ч
к
е
н
с
а
н
с
о
к
ю
е
н
т
щ
л
ц
э
н
и
ф
е
а
ф
д
а
я
я
и
я
о
в
ц
а
и
е
н
н
и
т
е
7

Функции,
их свойства
и
графики

Задания ГИА
 0, k= . m= 4 Ответ: 4 «
0, k= . m= 4 Ответ: 4 «
Функция возрастающая – k0, k= . m= 4
Ответ: 4

Ответ:
431

Ответ: 3
Функция убывающая, k
b

Ответ: -3

5
2
Ответ: 2,5

(2;2)
Ответ: 1
 0, т.к. ветви параболы направлены вверх, с0) «
0, т.к. ветви параболы направлены вверх, с0) «
с
Ответ: 4
(а0, т.к. ветви параболы направлены вверх, с0)

с
Ответ: 4

Решение задач
Уровень А – Найти область определения функции:
А) , б)
В) .
Уровень В – 1) Построить график функции
и выяснить, при каких значениях с прямая у=с имеет с графиком функции: а) 1 общую точку, б) 2 общие точки
2) Описать свойства функции (по готовому рисунку).
Уровень С —

У=4, с=4 1 общая точка
У=2, с=2 1 общая точка
У=0, с=0 2 общие точки
3 общие точки
У=-3, с=3 2 общие точки

Домашнее задание
Уровень АВ – по карточкам
Уровень С —

Дополнительное задание
Решить уравнение:

Алгебра 8: С-52. Понятие функции
Алгебра 8: С-52. Понятие функции
РЕШЕНИЯ и ОТВЕТЫ на самостоятельную работу «С-52. Понятие функции. График функции (повторение)» из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение». Представленные ниже образец варианта № 1 самостоятельной работы по алгебре 8 класса и ответы на оба варианта этой работы ориентированы на учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы на самостоятельную работу по алгебре адресованы учителям и родителям, которые смогут проконтролировать правильность выполнения задания.
Самостоятельная работа Понятие функции.
График функции (повторение) (С-52 В-1).
Нажмите на картинку, чтобы увеличить!Ключевые слова самостоятельной работы № 52 (В-1):
1. Функция задана формулой у(х) = … Найдите…
2. Функция задана формулой. 1) Найдите значение функции при х, равном: 2) При каком значении х значение функции равно:
3. Одна сторона прямоугольника равна х см, а другая — в 3 раза больше. Выразите через х периметр Р (в сантиметрах) и площадь S (в квадратных сантиметрах). Найдите значение каждой из функций Р от х и S от х при х, равном 12.
5. Функция задана графиком (рис. 5). а) Найдите б) При каком значении х значение функции равно ? в) При каких значениях х функция принимает положительные значения? г) При каких значениях х функция принимает отрицательные значения?
6. Постройте график функции.
7. Принадлежит ли графику функции точка ?
8. Докажите, что графики функций проходят через одну и ту же точку.
9. Найдите значения k и b, если известно, что график функции проходит через точки .
10. Задайте формулой линейную функцию, графиком которой служит прямая, проходящая через точку и параллельная прямой.
Ответы на самостоятельную работу № 52
Вариант 1.
Вариант 2
Вы смотрели ГДЗ на контрольную работу по алгебре 8 класс «Понятие функции. График функции (повторение)» из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.: Просвещение» (учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского).
Вернуться к Списку самостоятельных работ по алгебре 8 класс (УМК Макарычев и др.)
План-конспект урока по алгебре (8 класс) на тему: Функция y=k/x и ее график
Урок-открытие новых знаний
(Алгебра. 8 класс: учебник. Ю. Н. Макарычев)
Тема урока «Функция k/x и ее график »
Тип урока: изучение нового материала
ЦЕЛИ УРОКА:
Образовательная цель:
— научить строить график функции y= k/x опираясь на свойства функции;
— ввести понятие функции обратной пропорциональности;
— сформировать чёткое представление о различиях свойств и расположения графика функции при различных значениях k;
— расширить представления учащихся о функциях.
Развивающая цель:
— продолжить развитие познавательного интереса к изучению понятия функции;
— развивать умение анализировать, наблюдать, сопоставлять, логически мыслить;
— продолжить развитие элементов творческой деятельности учащихся, через вовлечение их в работу частично поискового характера, развитие навыков взаимоконтроля и самоконтроля.
Воспитывающая цель:
— воспитание навыков коммуникативности в работе, умение слушать и слышать другого, уважение к мнению товарища;
— воспитание у учащихся таких нравственных качеств, как настойчивость, аккуратность, инициативность, точность, привычка к систематичному труду, самостоятельность, активность;
— воспитание культуры общения.
Оборудование:
— проектор, компьютер, экран, раздаточный материал.
— Презентация к уроку.
ХОД УРОКА
1. Организационный момент
2. Повторение изученного
Учитель: Сегодня на уроке мы продолжаем знакомиться с новыми функциями, их свойствами и графиком.
Чтобы определить учебные задачи нашего урока выполним следующую работу.
(У каждого ученика на парте раздаточный материал с заданием, необходимо ответить на вопрос, найти верный ответ среди предложенных,
соответствующую букву записать в таблицу под правильным ответом).
Учитель: Какое слово получили? (Гипербола)
Что это за слово в математике?
3. Изучение нового материала
Ученик выступает с сообщением: (это график некоторой функции. Одним из первых, кто начал изучать эту кривую был ученик знаменитого Платона, древнегреческий математик Менехм в IV в. до н.э., но так и не сумел её полностью изучить. А вот полностью исследовал свойства гиперболы и дал ей название крупнейший геометр древности Аполоний Пергский в III в. до н.э.).
Учитель: Сегодня мы с вами побываем в роли древнегреческих ученых.
Как вы думаете, какие задачи мы должны поставить и решить на уроке?
(Учащиеся пытаются сформулировать эти задачи с помощью учителя).
Выяснить графиком какой функции является гипербола.
Рассмотреть расположение графика функции в системе координат.
Изучить свойства функции
Помогут ответить на вопросы следующие задания:
Закончите предложения:
а) С увеличением цены за единицу товара количество товара, которое можно закупить на данную сумму денег … уменьшится
б) С уменьшением скорости движения на данном отрезке пути время движения … увеличится
в) С увеличением производительности труда при выполнении данного объёма работы количество рабочих … уменьшится
(Учитель читает задачу, учащиеся отвечают на вопрос, учащиеся записывают в тетради, один ученик на доске)
Пешеход проходит путь S со скоростью v за t часов. Выразите время пешехода через путь и скорость.
Найдите значение t при S=60 и V=0,5; 1; 2; 4; 16; 60; 120.
Учитель:
Какая зависимость между временем нахождения в пути и скоростью?
Как можем записать формулу в общем виде?
Определение.
Функция, заданная формулой где k 0, называется обратной пропорциональностью.
Учитель: Детально рассмотрим эту зависимость с помощью графика на примере функции .
Как построить график незнакомой нам функции?
А как вы думаете, как будет называться график этой функции?
Построение графика функции.
Составить таблицу значений (взять значения аргумента с расчетом, чтобы положение графика определялось с достаточной полнотой).
Отметить точки на координатной плоскости.
Соединить точки линией.
(Все учащиеся строят в тетради, один ученик на доске)
Учитель: Давайте перечислим свойства этой функции.
(Учащиеся с помощью учителя перечисляют свойства построенной функции).
Учитель: А как вы думаете, если мы возьмем отрицательное число k,
Что произойдет с расположением графика в системе координат?
Исследовательская работа в парах.
Задание. Построить график функции и описать свойства?
(Учащиеся выполняют задания в парах, после выполнения один из учеников записывает свойства на доске).
Учитель: Что произошло с графиком функции, при изменении коэффициента?
4. Первичное закрепление
Выполнение номеров: 182, 185, 181, 257 (а, д) (на доске и в тетрадях)
5. Итог урока
— О какой функции сегодня шла речь?
— Что является графиком функции
— В каких координатных четвертях расположен график функции?
— Какова область определения функции
6. Домашнее задание
180, 184, 193
— Спасибо, урок окончен.