Последовательность — это… Что такое Последовательность?
Последовательность — это набор элементов некоторого множества:
- для каждого натурального числа можно указать элемент данного множества;
- это число является номером элемента и обозначает позицию данного элемента в последовательности;
- для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма.
Последовательность по своей природе — отображение, поэтому его не следует смешивать с множеством, которое «пробегает» последовательность.
В математике рассматривается множество различных последовательностей:
Целью изучения всевозможных последовательностей является поиск закономерностей, прогноз будущих состояний и генерация последовательностей.
Определение
Пусть задано некоторое множество элементов произвольной природы. | Всякое отображение множества натуральных чисел в заданное множество называется последовательностью (элементов множества ).
Образ натурального числа , а именно, элемент , называется —ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом.
Связанные определения
- Подмножество множества , которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
- Если взять возрастающую последовательность натуральных чисел, то её можно рассматривать как последовательность индексов некоторой последовательности: если взять элементы исходной последовательности с соответствующими индексами (взятыми из возрастающей последовательности натуральных чисел), то можно снова получить последовательность, которая называется подпоследовательностью заданной последовательности.
Комментарии
- Не следует смешивать носитель последовательности и саму последовательность! Например, точка как одноточечное подмножество является носителем стационарной последовательности вида .
- Любое отображение множества в себя также является последовательностью.
Обозначения
Последовательности вида
принято компактно записывать при помощи круглых скобок:
- или
иногда используются фигурные скобки:
Допуская некоторую вольность речи, можно рассматривать и конечные последовательности вида
- ,
которые представляют собой образ начального отрезка последовательности натуральных чисел.
См. также
| 1. |
Нахождение членов последовательности, дана общая формула
Сложность: лёгкое |
1,5 |
| 2. |
Нахождение членов последовательности, даны предыдущие члены
Сложность: лёгкое |
1 |
| 3. |
Аналитически заданная последовательность
Сложность: лёгкое |
1,5 |
| 4. |
Рекуррентно заданная последовательность
Сложность: лёгкое |
2 |
| 5. | Определение вида последовательности Сложность: лёгкое | 2 |
| 6. |
Нахождение членов последовательности (аналитическая формула)
Сложность: лёгкое |
3 |
| 7. |
Нахождение номера члена последовательности, равного данному числу
Сложность: среднее |
3 |
| 8. |
Вычисление члена последовательности, если дана нижняя граница
Сложность: среднее |
3 |
| 9. |
Выяснение ограниченности последовательностей
Сложность: среднее |
1 |
| 10. |
Использование свойств функции в вычислении членов последовательности
Сложность: сложное |
4 |
| 11. |
Вычисление значения параметра р в ограниченной последовательности
Сложность: сложное |
3 |
| 12. |
Доказательство монотонности последовательности
|
6,5 |
Ряд (математика) — Википедия
Ряд, называемый также бесконечная сумма — одно из центральных понятий математического анализа. В простейшем случае ряд записывается как бесконечная сумма чисел[1]:
- a1+a2+a3+…+an+…{\displaystyle a_{1}+a_{2}+a_{3}+\ldots +a_{n}+\ldots \quad } Краткая запись: ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}}
Здесь a1,a2,a3…{\displaystyle a_{1},a_{2},a_{3}\dots } — последовательность вещественных или комплексных чисел; эти числа называются членами ряда.
Чтобы присвоить числовому ряду значение суммы, рассмотрим последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:
- S1=a1{\displaystyle S_{1}=a_{1}}
- S2=a1+a2{\displaystyle S_{2}=a_{1}+a_{2}}
- S3=a1+a2+a3{\displaystyle S_{3}=a_{1}+a_{2}+a_{3}}
- ⋯{\displaystyle \cdots }
- Sn=a1+a2+a3+⋯+an{\displaystyle S_{n}=a_{1}+a_{2}+a_{3}+\dots +a_{n}}
- ⋯{\displaystyle \cdots }
Если последовательность частичных сумм имеет предел S{\displaystyle S} (конечный или бесконечный), то говорят, что сумма ряда равна S.{\displaystyle S.} При этом, если предел конечен, то говорят, что ряд сходится. Если предел не существует или бесконечен, то говорят, что ряд расходится[1].
Числовые ряды и их обобщения (см. ниже о нечисловых рядах) используются повсеместно в математическом анализе для вычислений, для анализа поведения разнообразных функций, при решении алгебраических или дифференциальных уравнений. Разложение функции в ряд можно рассматривать как обобщение задания вектора координатами, эта операция позволяет свести исследование сложной функции к анализу элементарных функций и облегчает численные расчёты[2]. Ряды — незаменимый инструмент исследования не только в математике, но и в физике, астрономии, информатике, статистике, экономике и других науках.
Примеры[править | править код]
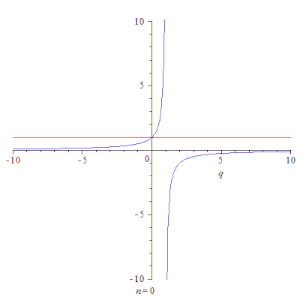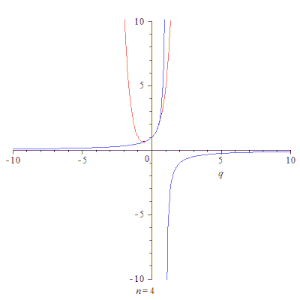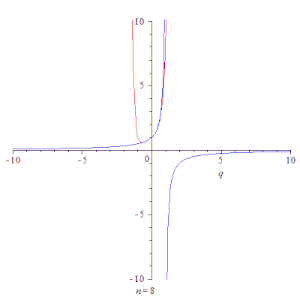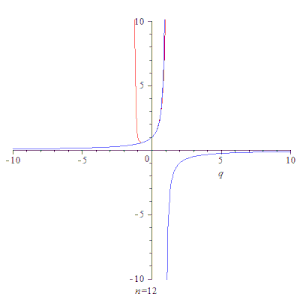 Анимация, показывающая сходимость частичных сумм геометрической прогрессии ∑k=0nqk{\displaystyle \sum \limits _{k=0}^{n}q^{k}} (красная линия) к её сумме 11−q{\displaystyle {1 \over 1-q}} (синяя линия) при |q|<1{\displaystyle |q|<1}.
Анимация, показывающая сходимость частичных сумм геометрической прогрессии ∑k=0nqk{\displaystyle \sum \limits _{k=0}^{n}q^{k}} (красная линия) к её сумме 11−q{\displaystyle {1 \over 1-q}} (синяя линия) при |q|<1{\displaystyle |q|<1}.Простейшим примером сходящегося ряда является сумма членов бесконечной геометрической прогрессии[3] со знаменателем q<1{\displaystyle q<1}:
- a+aq+aq2+aq3+…{\displaystyle a+aq+aq^{2}+aq^{3}+\dots }
Частичная сумма Sn=a1−qn1−q.{\displaystyle S_{n}=a{\frac {1-q^{n}}{1-q}}.} Предел этого выражения limn→∞Sn=a1−q,{\displaystyle \lim _{n\to \infty }S_{n}={\frac {a}{1-q}},} это и есть сумма бесконечной геометрической прогрессии[1]. Например, при a=1,q=12{\displaystyle a=1,q={\frac {1}{2}}} получается ряд, сумма которого равна 2:
- 1+12+14+18+…{\displaystyle 1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+\dots }
Десятичную дробь с бесконечной дробной частью можно рассматривать как сумму ряда[3]; например, число π=3,1415926…{\displaystyle \pi =3{,}1415926\dots } есть сумма следующего ряда:
- 3+1101+4102+1103+5104+9105+…{\displaystyle 3+{\frac {1}{10^{1}}}+{\frac {4}{10^{2}}}+{\frac {1}{10^{3}}}+{\frac {5}{10^{4}}}+{\frac {9}{10^{5}}}+\dots }
Более сложным примером является ряд обратных квадратов, сумму которого лучшие математики Европы не могли найти более 100 лет[4]:
- ∑n=1∞1n2=π26{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}}
Ряд 1+1+1+…{\displaystyle 1+1+1+\dots } расходится, сумма его бесконечна. Расходится и гармонический ряд:∑n=1∞1n=∞.{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}={\infty }.} «Ряд Гранди» 1−1+1−1+1−1…{\displaystyle 1-1+1-1+1-1\dots } расходится, его частичные суммы колеблются от 1 до 0, поэтому предела частичных сумм не существует, суммы у этого ряда нет[5].
Классификация[править | править код]
Положительный ряд — вещественный ряд, все члены которого неотрицательны. У положительных рядов сумма всегда существует, но может быть бесконечна[6].
Знакочередующийся ряд — вещественный ряд, в котором знаки членов чередуются: плюс, минус, плюс, минус и т. д. Для таких рядов существует простой признак сходимости Лейбница. Знакочередующийся вариант приведенного выше гармонического ряда, в отличие от последнего, сходится[7]:
- 1−12+13−14+15−⋯=ln(2){\displaystyle 1-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-\cdots =\ln(2)}
Абсолютная и условная сходимость[править | править код]
Говорят, что вещественный или комплексный ряд сходится абсолютно, если сходится ряд из модулей (абсолютных величин) его членов[7]:
- ∑n=1∞|an|{\displaystyle \sum _{n=1}^{\infty }|a_{n}|}
Абсолютно сходящийся ряд сходится и в обычном смысле этого понятия. При этом всякий такой ряд обладает важным свойством переместительности: при любой перестановке членов абсолютно сходящегося ряда получается сходящийся ряд с той же суммой[8].
Если числовой ряд сходится, но не абсолютно, он называется условно сходящимся. Пример:
- 1−12+13−14+15…{\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}\dots } Сам ряд сходится, но ряд его абсолютных величин (гармонический ряд) расходится[7].
Свойства условно сходящихся рядов[7].
- Если ряд сходится условно, то как ряд из его положительных членов, так и ряд из его отрицательных членов расходятся.
- Следствие (критерий абсолютной сходимости): ряд из вещественных чисел сходится абсолютно тогда и только тогда, когда сходятся как ряд из положительных его членов, так и ряд из отрицательных членов.
- (теорема Римана): Перестановкой членов условно-сходящегося ряда можно получить ряд с любой заданной вещественной суммой.
Операции над рядами[править | править код]
Пусть заданы сходящиеся ряды ∑n=1∞an{\displaystyle \sum _{n=1}^{\infty }a_{n}} и ∑n=1∞bn{\displaystyle \sum _{n=1}^{\infty }b_{n}}. Тогда:
- Их суммой называется ряд ∑n=1∞(an+bn),{\displaystyle \sum _{n=1}^{\infty }(a_{n}+b_{n}),} разностью — ряд ∑n=1∞(an−bn).{\displaystyle \sum _{n=1}^{\infty }(a_{n}-b_{n}).}
- Их произведением Коши[en] называется ряд ∑n=1∞cn{\displaystyle \sum _{n=1}^{\infty }c_{n}}, где:
- cn=∑k=1nakbn−k+1=a1b1+(a1b2+a2b1)+(a1b3+a2b2+a3b1)+⋯+(a1bn+a2bn−1+⋯+anb1){\displaystyle c_{n}=\sum _{k=1}^{n}a_{k}b_{n-k+1}=a_{1}b_{1}+(a_{1}b_{2}+a_{2}b_{1})+(a_{1}b_{3}+a_{2}b_{2}+a_{3}b_{1})+\dots +(a_{1}b_{n}+a_{2}b_{n-1}+\dots +a_{n}b_{1})}
Если оба ряда сходятся, то их сумма и разность также сходятся. Если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из исходных рядов сходится абсолютно, то произведение рядов сходится.
Необходимый признак сходимости числового ряда[править | править код]
Ряд a1+a2+a3+…+an+…{\displaystyle {a}_{1}+{a}_{2}+{a}_{3}+\ldots +{a}_{n}+\ldots } может сходиться лишь в том случае, когда член an{\displaystyle {a}_{n}} (общий член ряда) с возрастанием его номера стремится к нулю[9]:
- limn→∞an=0.{\displaystyle \lim _{n\rightarrow \infty }{a}_{n}=0.}
Это необходимый признак сходимости ряда, но он не является достаточным — у гармонического ряда, например, общий член с ростом номера неограниченно уменьшается, тем не менее ряд расходится. Если же общий член ряда не стремится к нулю, то ряд заведомо расходится[9].
Сходящиеся ряды[править | править код]
Свойство 1. Если ряд
- ∑n=1∞an=a1+a2+a3+a4+…{\displaystyle \sum _{n=1}^{\infty }{a}_{n}={a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}+\ldots } (1.1)
сходится и его сумма равна S, то ряд
- ∑n=1∞can=ca1+ca2+ca3+ca4+…{\displaystyle \sum _{n=1}^{\infty }c{a}_{n}=c{a}_{1}+c{a}_{2}+c{a}_{3}+c{a}_{4}+\ldots } (1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд (1.2) расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
- ∑n=1∞bn{\displaystyle \sum _{n=1}^{\infty }{b}_{n}},
а их суммы равны S1{\displaystyle {S}_{1}} и S2{\displaystyle {S}_{2}} соответственно, то сходятся и ряды
- ∑n=1∞(an±bn){\displaystyle \sum _{n=1}^{\infty }({a}_{n}\pm {b}_{n})},
причём сумма каждого равна соответственно S1±S2{\displaystyle {S}_{1}\pm {S}_{2}}.
Для выяснения ключевого в анализе вопроса, сходится или нет заданный ряд, предложены многочисленные признаки сходимости (см. список).
Нерешённые проблемы[править | править код]
До сих пор неизвестно, сходится ли «ряд Флинт Хиллз» (Flint Hills Series)[10]:
- ∑n=1∞cosec2(n)n3{\displaystyle \sum _{n=1}^{\infty }{\frac {\operatorname {cosec} ^{2}(n)}{n^{3}}}}
Если удастся доказать, что этот ряд сходится, то как следствие получится важный факт: мера иррациональности числа π{\displaystyle \pi } меньше, чем 2,5.
Известно, что сумма ряда обратных квадратов и суммы других рядов с обратными чётными степенями выражаются через степени числа π,{\displaystyle \pi ,} но мало что известно про сумму обратных кубов («константу Апери»):
- 113+123+133+143+⋯≈1,2020569{\displaystyle {\frac {1}{1^{3}}}+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+\dots \approx 1{,}2020569}.
Никто пока не сумел связать это значение с классическими константами или элементарными функциями[11].
Понятие бесконечного ряда и его суммы можно ввести не только для чисел, но и для других математических объектов, для которых определены сложение и понятие близости, позволяющее определить предел. Например, в анализе широко используются ряды из функций: степенные ряды, ряды Фурье, ряды Лорана. Членами ряда могут быть также векторы, матрицы и др.
Общее определение[править | править код]
Ряд (или бесконечная сумма) в математике — последовательность элементов (членов данного ряда) a1,a2,a3…{\displaystyle a_{1},a_{2},a_{3}\dots } некоторого топологического векторного пространства, рассматриваемая вместе с множеством частичных сумм членов ряда (частичные суммы определяются так же, как и в числовых рядах). Если для последовательности частичных сумм определён предел: S=limn→∞Sn,{\displaystyle S=\lim _{n\rightarrow \infty }S_{n},} то значение S{\displaystyle S} называется суммой данного ряда, а сам ряд называется сходящимся (в противном случае — расходящимся)[12].
Ряды всегда можно почленно складывать или вычитать, причём сумма и разность сходящихся рядов также сходятся. Если члены рядов берутся из кольца или поля, то ряды сами образуют кольцо относительно сложения и произведения Коши[en].
Функциональные ряды[править | править код]
Определение и свойства[править | править код]
Ряд называется функциональным, если все его члены — функции, определённые на некотором множестве:
- a1(x)+a2(x)+a3(x)+…+an(x)+…;{\displaystyle a_{1}(x)+a_{2}(x)+a_{3}(x)+\ldots +a_{n}(x)+\ldots ;\quad } краткая запись: ∑n=1∞an(x){\displaystyle \sum _{n=1}^{\infty }a_{n}(x)}
Частичные суммы в этом случае также являются функциями, заданными на том же множестве. Ряд называется сходящимся на множестве X{\displaystyle X}, если при любом фиксированном x0∈X{\displaystyle x_{0}\in X} сходится числовой ряд[2]:
- a1(x0)+a2(x0)+a3(x0)+…+an(x0)+…{\displaystyle a_{1}(x_{0})+a_{2}(x_{0})+a_{3}(x_{0})+\ldots +a_{n}(x_{0})+\ldots }
Множество X{\displaystyle X} называется областью сходимости ряда. Сумма ряда, очевидно, также является функцией на X.{\displaystyle X.} Кроме так определённой «поточечной» сходимости, в разных пространствах могут быть использованы и другие нормы близости, от которых зависит существование предела частичных сумм.
Пример — разложение в ряд рациональной дроби:
- 11+x2=1−x2+x4−x6+…{\displaystyle {\frac {1}{1+x^{2}}}=1-x^{2}+x^{4}-x^{6}+\ldots }
Этот ряд сходится в интервале (−1;1){\displaystyle (-1;\;1)}.
Среди основных типов функциональных рядов:
Равномерная сходимость[править | править код]
Вообще говоря, свойства суммы могут отличаться от свойств членов ряда — например, сумма ряда непрерывных функций может не быть непрерывной.
Говорят, что сходящийся на множестве X{\displaystyle X} функциональный ряд равномерно сходится (на этом множестве)[13], если последовательность частичных сумм ряда равномерно сходится на X{\displaystyle X}.
Существуют несколько признаков, позволяющих убедиться в равномерной сходимости ряда[13]:
Важность понятия равномерной сходимости ряда показывают следующие теоремы (все функции считаются вещественными).
- Сумма ряда из функций, непрерывных в некоторой точке x0{\displaystyle x_{0}}, будет и сама непрерывна в этой точке при условии, что функциональный ряд в точке x0{\displaystyle x_{0}} сходится равномерно. В частности, сумма равномерно сходящегося ряда вещественных функций, непрерывных на отрезке [a,b],{\displaystyle [a,b],} также будет непрерывна на этом отрезке[14].
- Если функции fn(x){\displaystyle f_{n}(x)} непрерывно дифференцируемы на отрезке [a,b]{\displaystyle [a,b]} и оба ряда:
- f1(x)+f2(x)+f3(x)+…{\displaystyle f_{1}(x)+f_{2}(x)+f_{3}(x)+\dots }
- df1(x)dx+df2(x)dx+df3(x)dx+…{\displaystyle {\frac {df_{1}(x)}{dx}}+{\frac {df_{2}(x)}{dx}}+{\frac {df_{3}(x)}{dx}}+\dots }
- сходятся на [a,b]{\displaystyle [a,b]}, причём ряд производных сходится равномерно, то сумма ряда имеет производную, и дифференцировать ряд можно почленно[15]:
- ddx(f1(x)+f2(x)+f3(x)+…)=df1(x)dx+df2(x)dx+df3(x)dx+…{\displaystyle {\frac {d}{dx}}(f_{1}(x)+f_{2}(x)+f_{3}(x)+\dots )={\frac {df_{1}(x)}{dx}}+{\frac {df_{2}(x)}{dx}}+{\frac {df_{3}(x)}{dx}}+\dots }
- ∫abF(x)dx=∑n=1∞∫abfn(x)dx{\displaystyle \int \limits _{a}^{b}F(x)dx=\sum _{n=1}^{\infty }\int \limits _{a}^{b}{f_{n}}(x)dx}
- Условие равномерной сходимости гарантирует, что ряд справа сходится.
Пример неравномерно сходящегося степенного ряда — геометрическая прогрессия 1+x+x2+x3+…{\displaystyle 1+x+x^{2}+x^{3}+\dots } В промежутке [0,1){\displaystyle [0,1)} она сходится к функции 11−x,{\displaystyle {\frac {1}{1-x}},} но не равномерно (о чём свидетельствует бесконечный скачок суммы при приближении к 1)[17].
Ряды матриц[править | править код]
В кольце числовых квадратных матриц фиксированного порядка n
Числовая последовательность — это… Что такое Числовая последовательность?
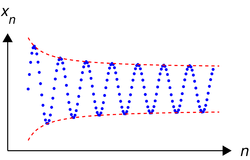 Последовательность
ПоследовательностьЧисловая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Определение
Пусть множество — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества называется числовой последовательностью.
Примеры
- Функция является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид .
- Функция является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид .
- Функция, сопоставляющая каждому натуральному числу одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида . В частности, пятым членом этой последовательности является слово «май».
Операции над последовательностями
На множестве всех последовательностей элементов множества можно определить арифметические и другие операции, если таковые определены на множестве . Такие операции обычно определяют естественным образом, т. е. поэлементно.
Например, так определяются арифметические операции для числовых последовательностей.
Суммой числовых последовательностей и называется числовая последовательность такая, что .
Разностью числовых последовательностей и называется числовая последовательность такая, что .
Произведением числовых последовательностей и называется числовая последовательность такая, что .
Частным числовой последовательности и числовой последовательности , все элементы которой отличны от нуля, называется числовая последовательность . Если в последовательности на позиции всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность .
Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.
Подпоследовательности
Подпоследовательность последовательности — это последовательность , где — возрастающая последовательность элементов множества натуральных чисел.
Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.
Примеры
- Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел.
- Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.
Свойства
- Всякая последовательность является своей подпоследовательностью.
- Для всякой подпоследовательности верно, что .
- Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.
- Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.
- Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.
- Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
- Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
Предельная точка последовательности
Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности. Для сходящихся числовых последовательностей предельная точка совпадает с пределом.
Предел последовательности
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.
Верхний предел последовательности — это наибольшая предельная точка этой последовательности.
Нижний предел последовательности — это наименьшая предельная точка этой последовательности.
Некоторые виды последовательностей
- Стационарная последовательность — это последовательность, все члены которой, начиная с некоторого, равны.
- стационарная
Ограниченные и неограниченные последовательности
В предположении о линейной упорядоченности множества элементов последовательности можно ввести понятия ограниченных и неограниченных последовательностей.
Критерий ограниченности числовой последовательности
Числовая последовательность является ограниченной тогда и только тогда, когда существует такое число, что модули всех членов последовательности не превышают его.
- ограниченная
Свойства ограниченных последовательностей
Бесконечно большие и бесконечно малые последовательности
Свойства бесконечно малых последовательностей
Бесконечно малые последовательности отличаются целым рядом замечательных свойств, которые активно используются в математическом анализе, а также в смежных с ним и более общих дисциплинах.
- Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
- Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
- Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
- Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
- Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
- Любая бесконечно малая последовательность ограничена.
- Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.
- Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.
- Если — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно малой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно малой.
- Если — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно большой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно большой.
Сходящиеся и расходящиеся последовательности
- Сходящаяся последовательность — это последовательность элементов множества , имеющая предел в этом множестве.
- Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.
Свойства сходящихся последовательностей
- Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.
- Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.
- Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел.
- Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.
- Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.
- Если последовательность сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность , которая является ограниченной.
- Сумма сходящихся последовательностей также является сходящейся последовательностью.
- Разность сходящихся последовательностей также является сходящейся последовательностью.
- Произведение сходящихся последовательностей также является сходящейся последовательностью.
- Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.
- Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.
- Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.
- Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.
- Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.
- Любую сходящуюся последовательность можно представить в виде , где — предел последовательности , а — некоторая бесконечно малая последовательность.
- Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).
Монотонные последовательности
Монотонная последовательность — это невозрастающая, либо неубывающая последовательность. При этом предполагается, что на множестве, из которого берутся элементы последовательности, введено отношение порядка.
Фундаментальные последовательности
Фундаментальная последовательность (сходящаяся в себе последовательность, последовательность Коши) — это последовательность элементов метрического пространства, в которой для любого наперёд заданного расстояния найдётся такой элемент, расстояние от которого до любого из следующих за ним элементов не превышает заданного. Для числовых последовательностей понятия фундаментальной и сходящейся последовательностей эквивалентны, однако в общем случае это не так.
Вариации и обобщения
Примечания
См. также
Математическая последовательность — это… Что такое Математическая последовательность?
- Математическая последовательность
Последовательность — функция
 одного натурального переменного, обладающая следующим свойством:
одного натурального переменного, обладающая следующим свойством:Областью значений функции
 может при этом быть произвольное множество X. Желая уточнить характер этой области, нередко говорят о «последовательности элементов множества X».
может при этом быть произвольное множество X. Желая уточнить характер этой области, нередко говорят о «последовательности элементов множества X».Значение
 обычно называют членом последовательности
обычно называют членом последовательности  , имеющим номер
, имеющим номер  .
.Упорядоченные наборы
 первых
первых  членов последовательности (рассматриваемые в предположении о существовании члена
членов последовательности (рассматриваемые в предположении о существовании члена  ) называют начальными отрезками последовательности.
) называют начальными отрезками последовательности.Символика
При записи членов последовательностей номер обычно пишут не в скобках после символа функции, а в качестве нижнего индекса при этом символе. Например, вместо записи x(n) для n-го члена последовательности x применяют запись xn.
Чаще всего рассматриваются последовательности, областью определения которых является весь натуральный ряд. С целью указать на такой характер области определения функции x используют обозначение
 . Аналогично, для последовательностей, областью определения которых является отрезок натурального ряда вида
. Аналогично, для последовательностей, областью определения которых является отрезок натурального ряда вида ,
,
используют обозначение
 .
.Примеры
- Функция
 является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид
является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид  .
. - Функция
 является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид
является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид  .
. - Функция, сопоставляющая каждому натуральному числу
 одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида
одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида  . В частности, пятым членом x5 этой последовательности является слово «май».
. В частности, пятым членом x5 этой последовательности является слово «май».
Типы последовательностей
- Бесконечно малая — последовательность, предел которой равен 0.
- Бесконечно большая — последовательность, предел которой равен бесконечности.
- Стационарная — последовательность, все члены которой, начиная с некоторого, равны.
Вариации и обобщения
См. также
Wikimedia Foundation. 2010.
- Математика Древнего Востока
- Математическая сингулярность
Смотреть что такое «Математическая последовательность» в других словарях:
ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ — ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ, математическая ПОСЛЕДОВАТЕЛЬНОСТЬ, каждый член которой является суммой двух предыдущих. Таким образом, если энный член последовательности обозначается хn, то для всей последовательности справедливым будет уравнение:… … Научно-технический энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА — математическая дисциплина, предметом к рой являются модели экономич. объектов и процессов и методы их исследования. Однако понятия, результаты, методы М. э. удобно и принято излагать в тесной связи с их экономич. происхождением, интерпретацией и… … Математическая энциклопедия
МАТЕМАТИЧЕСКАЯ (АНАЛИТИЧЕСКАЯ) ГЕОЛОГИЯ , — Вистелиус, 1944, 1969, научная дисциплина, занимающаяся математическим моделированием геол. процессов и примыкающими к этому вопросу задачами. Термин предложен в 1944 г. в русской лит., поддержан акад. В. И. Вернадским; в 1947 г. появился в англ … Геологическая энциклопедия
последовательность проверки кадра — Любая математическая формула, определяющая числовое значение на основе последовательности битов переданного блока информации и использующая это значение на приемном конце для обнаружения ошибок передачи. В сетях FDDI и Token Ring FCS использует… … Справочник технического переводчика
Математическая индукция — Математическая индукция один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала пров … Википедия
Математическая константа — У этого термина существуют и другие значения, см. Константа. Математическая константа величина, значение которой не меняется; в этом она противоположна переменной. В отличие от физических констант, математические константы определены… … Википедия
E (математическая константа) — e математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия
Е (математическая константа) — e математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия
Подпоследовательность — (математическая) последовательность x1, x2,…, xn,… с соблюдением порядка, т. е. при условии, что n1 … Большая советская энциклопедия
Теория волн Эллиотта — (Elliott Wave Theory) Теория волн Эллиотта это математическая теория об изменении поведения общества или финансовых рынков Все о волновой теории Эллиотта: видео, книги, статьи о теории волн, информация о советниках и индикаторах волн Эллиотта… … Энциклопедия инвестора
Книги
- Алгебра. 7 класс. Учебник. В 2-х частях. ФГОС, Мордкович Александр Григорьевич, Александрова Лидия Александровна, Мишустина Татьяна Николаевна. Учебник написан в соответствии с ФГОС ООО, реализует авторскую концепцию, в которой приоритетной содержательно-методической основой является функционально-графическая линия, а идейным… Подробнее Купить за 1191 руб
- Алгебра. 8 класс. Учебник + задачник. ФГОС (количество томов: 2), Мордкович А.Г.. Учебник написан в соответствии с ФГОС ООО, реализует авторскую концепцию, в которой приоритетной содержательно-методической основой является функционально-графическая линия, а идейным… Подробнее Купить за 730 руб
- Медицинская статистика, А. Н. Герасимов. В книге, подготовленной заведующим кафедрой медицинской информатики и статистики ММА им. И. М. Сеченова, речь идет о статистической обработке медицинских данных с помощью пакетов… Подробнее Купить за 580 руб
Понятие числовой последовательности
Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел.
Если
функцию 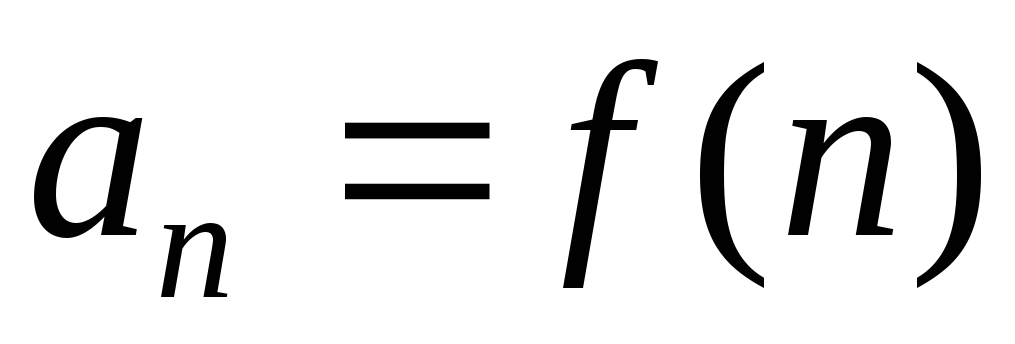 задать на множестве натуральных чисел
задать на множестве натуральных чисел ,
то множество значений функции будет
счетным и каждому номеру
,
то множество значений функции будет
счетным и каждому номеру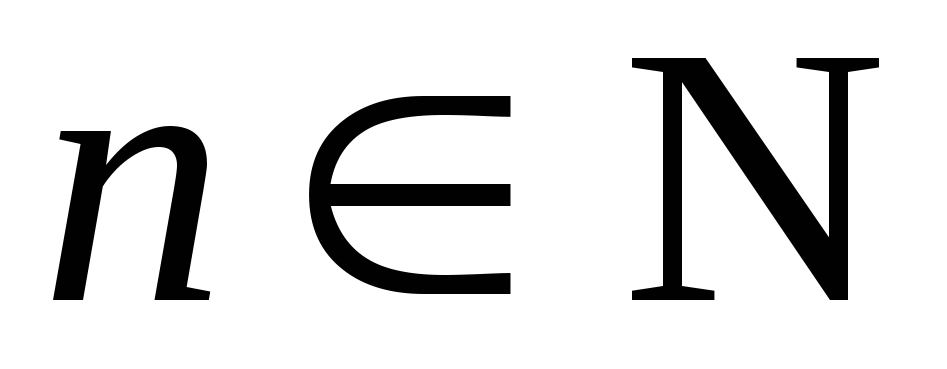 ставится в соответствие число
ставится в соответствие число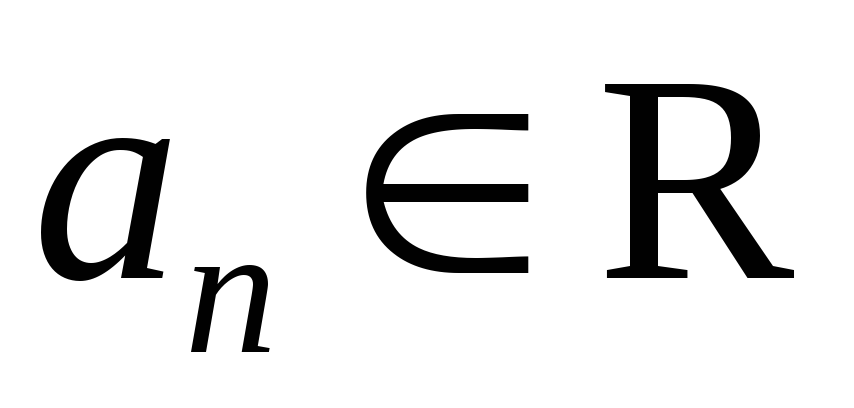 .
В этом случае говорят, что заданачисловая
последовательность. Числа
.
В этом случае говорят, что заданачисловая
последовательность. Числа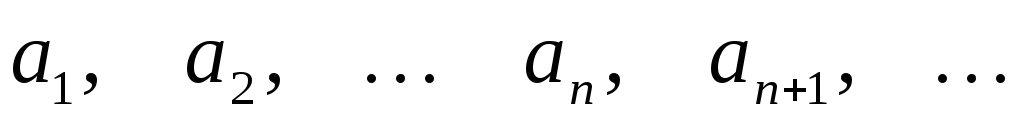 называютэлементамиили членами
последовательности, а число
называютэлементамиили членами
последовательности, а число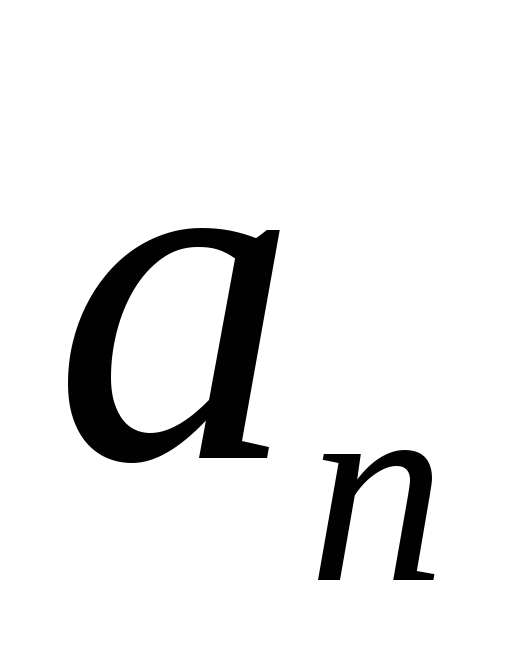 – общим или
– общим или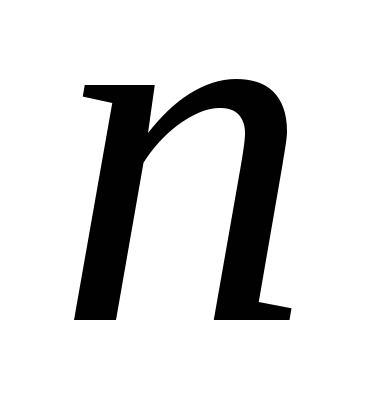 –м
членом последовательности. Каждый
элемент
–м
членом последовательности. Каждый
элемент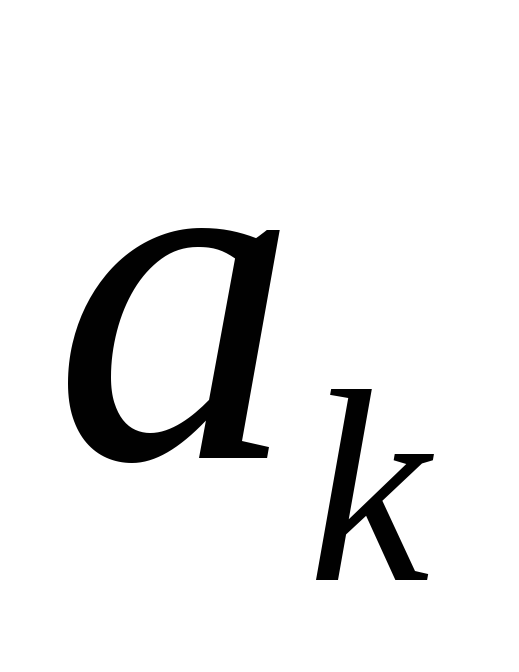 имеет последующий элемент
имеет последующий элемент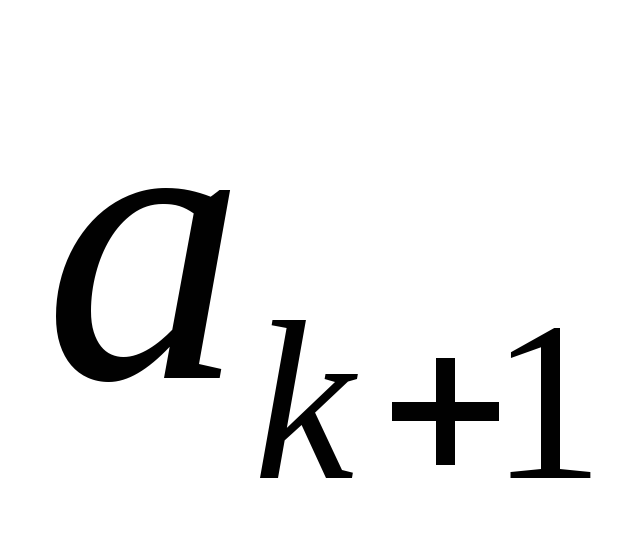 .
Это объясняет употребление термина
«последовательность».
.
Это объясняет употребление термина
«последовательность».
Задают
последовательность обычно либо
перечислением ее элементов 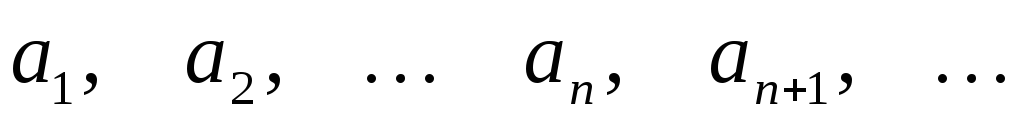 ,
либо указанием закона, по которому
вычисляется элемент с номером
,
либо указанием закона, по которому
вычисляется элемент с номером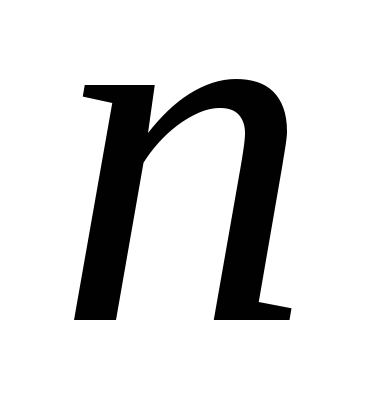 ,
т.е. указанием формулы ее
,
т.е. указанием формулы ее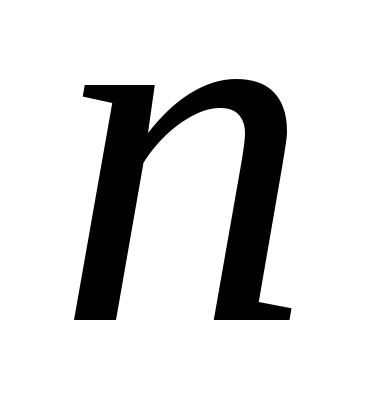 ‑го
члена
‑го
члена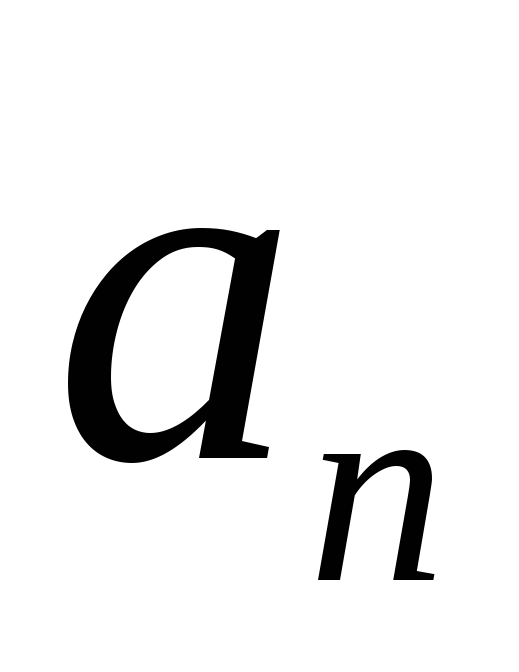 .
.
Пример. Последовательность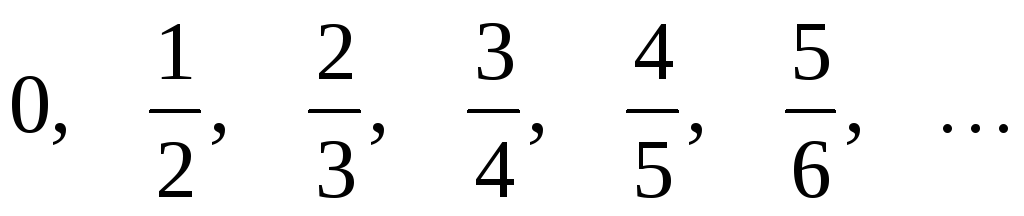 может быть задана формулой:
может быть задана формулой: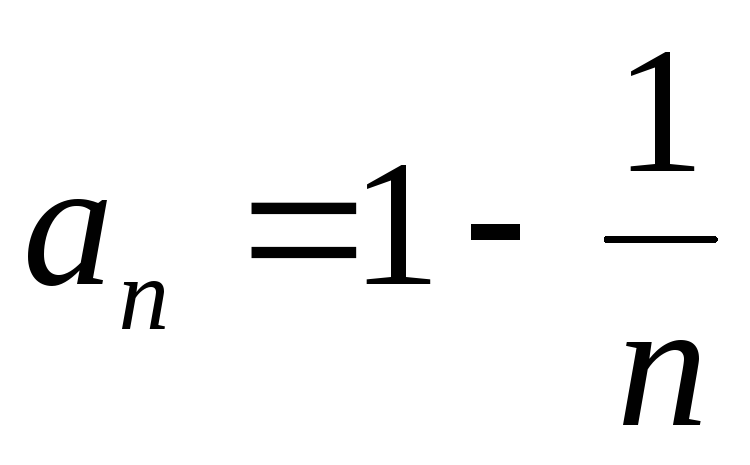 .
.
Обычно
последовательности обозначаются так: 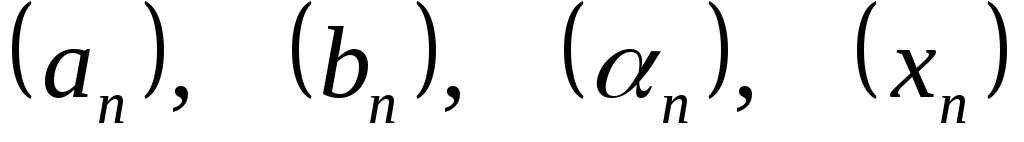 и т.п., где в скобках указывается формула
ее
и т.п., где в скобках указывается формула
ее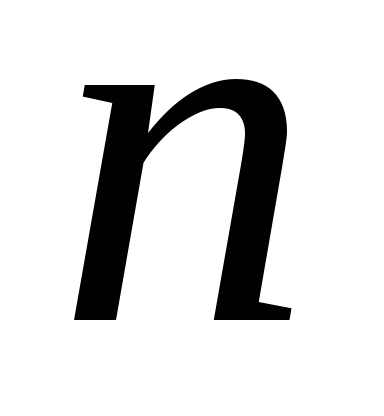 -го
члена.
-го
члена.
Пример. Последовательность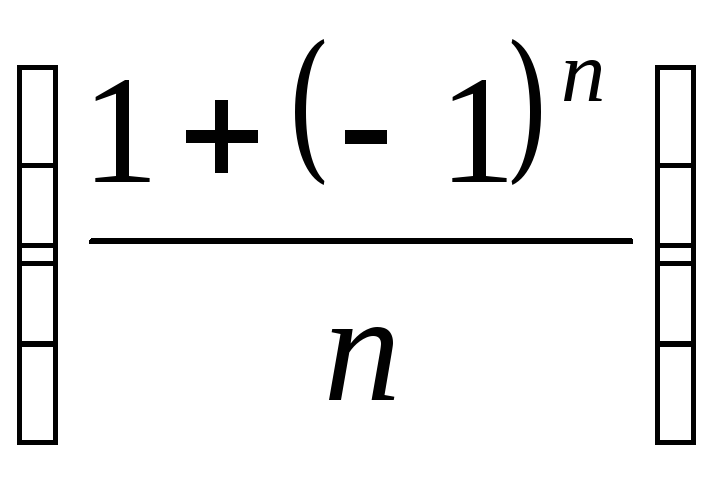 ‑это последовательность
‑это последовательность 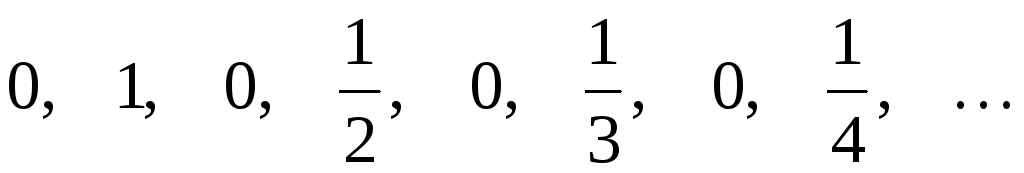
Множество
всех элементов последовательности 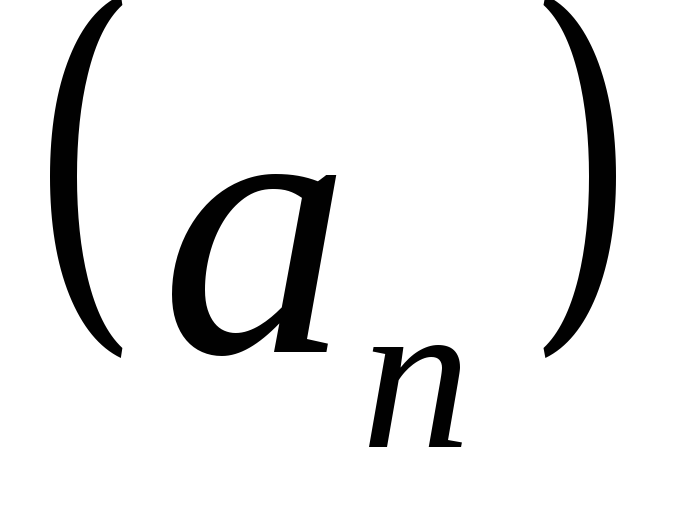 обозначается
обозначается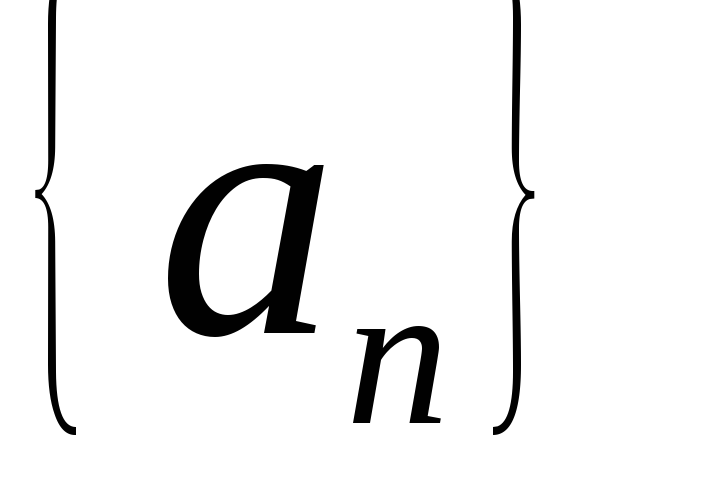 .
.
Пусть 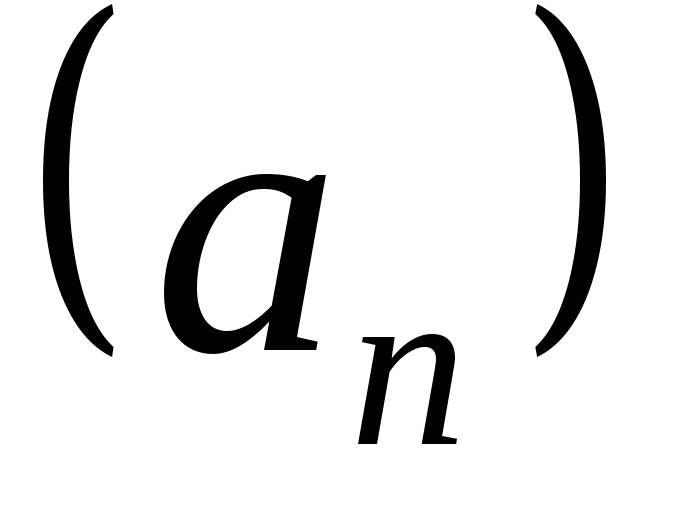 и
и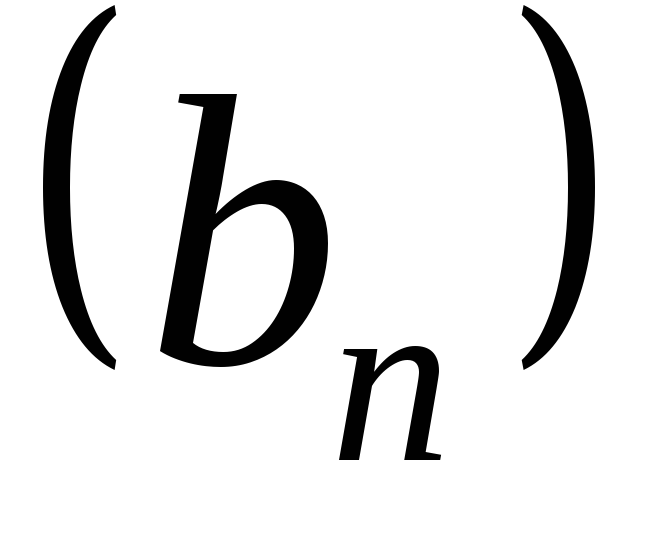 ‑ две последовательности.
‑ две последовательности.
Суммой последовательностей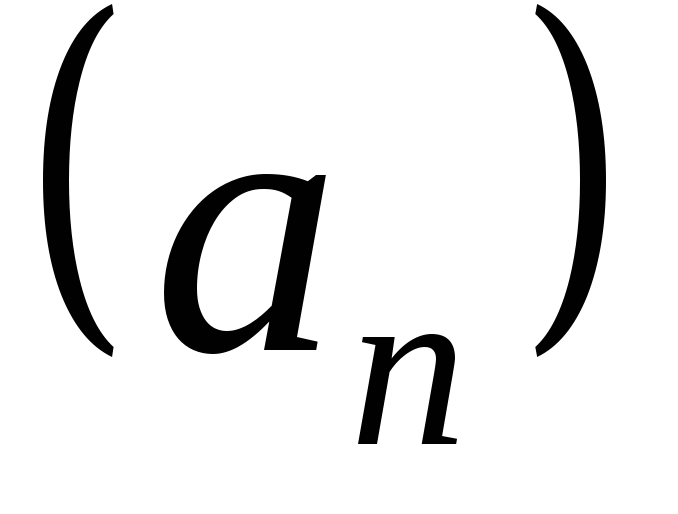 и
и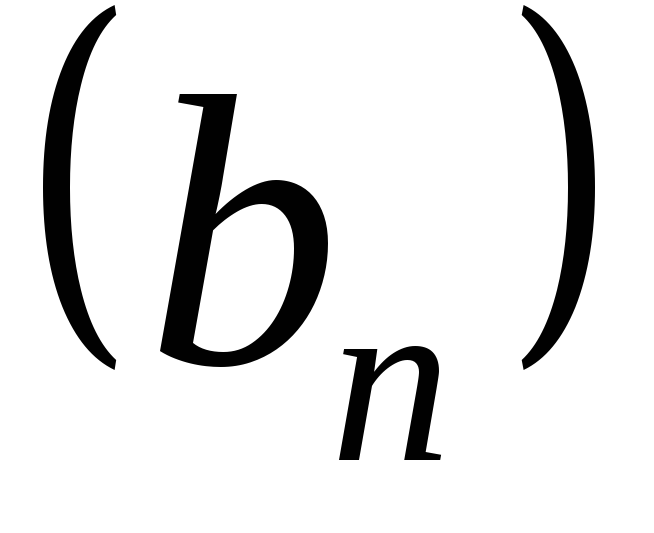 называют последовательность
называют последовательность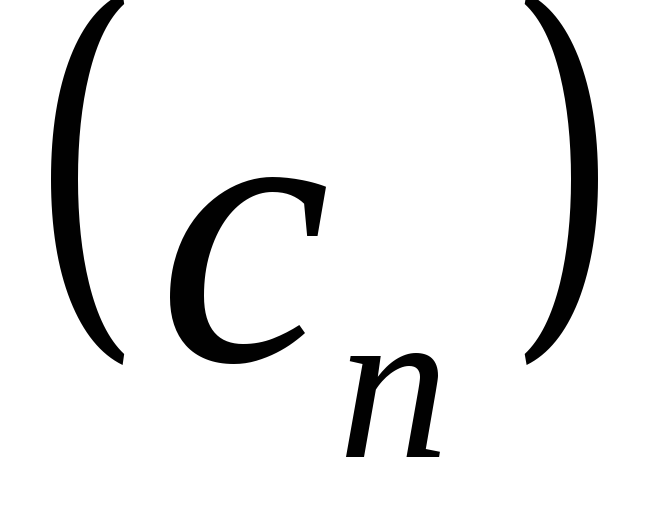 ,
где
,
где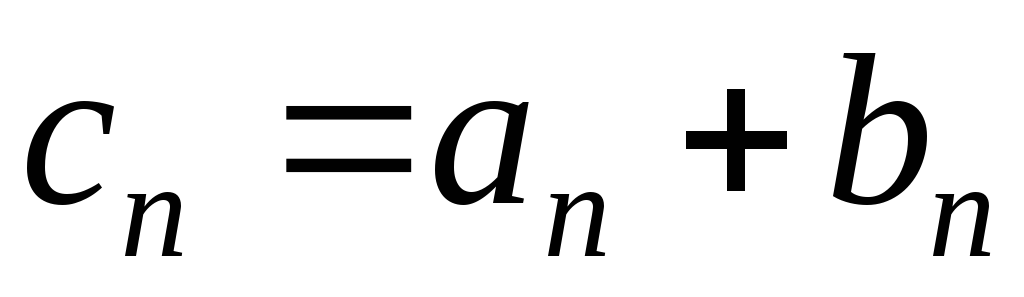 ,
т.е.
,
т.е.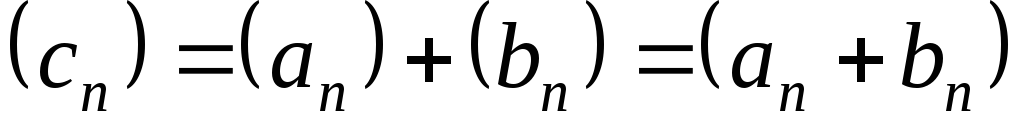 .
.
Разностьюэтих последовательностей называют
последовательность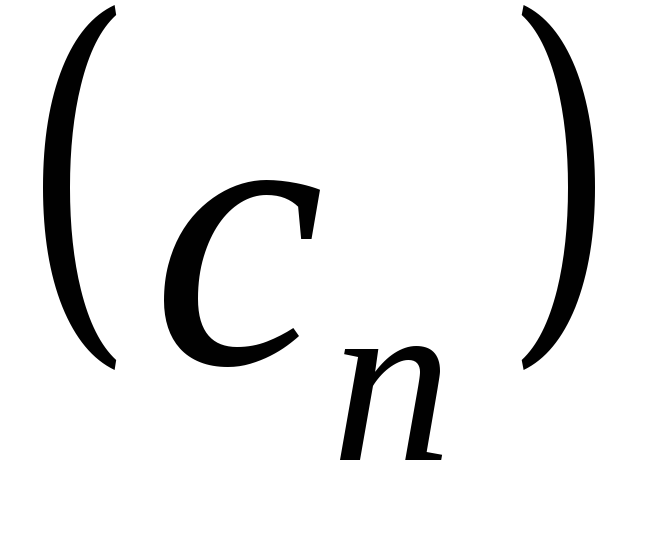 ,
где
,
где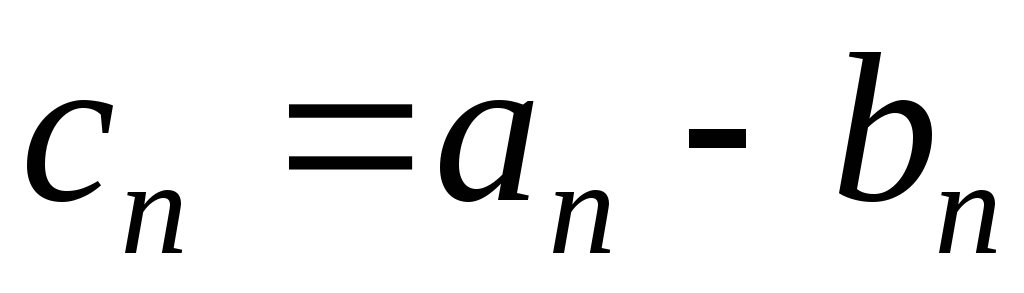 ,
т.е.
,
т.е.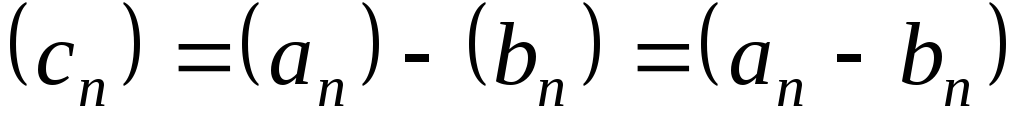 .
.
Если  и
и 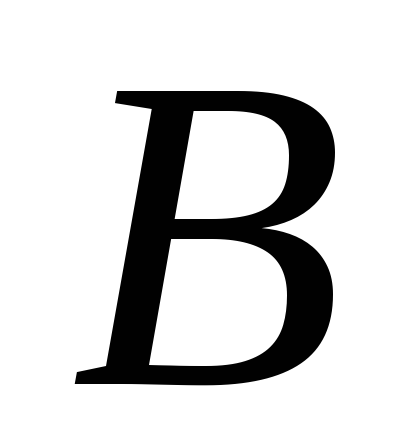 ‑постоянные, то последовательность
‑постоянные, то последовательность 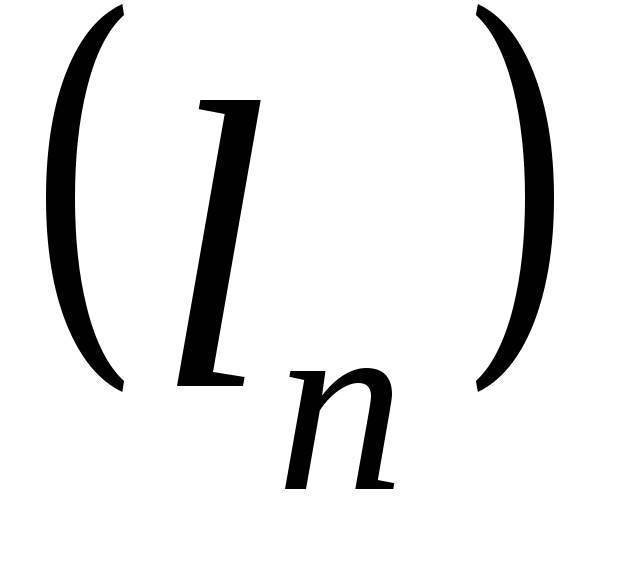 ,
,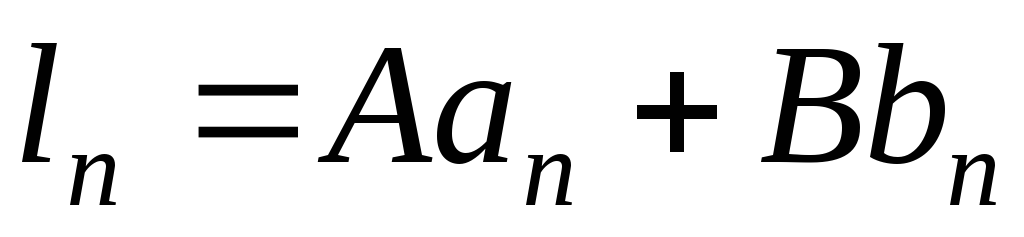 называютлинейной комбинациейпоследовательностей
называютлинейной комбинациейпоследовательностей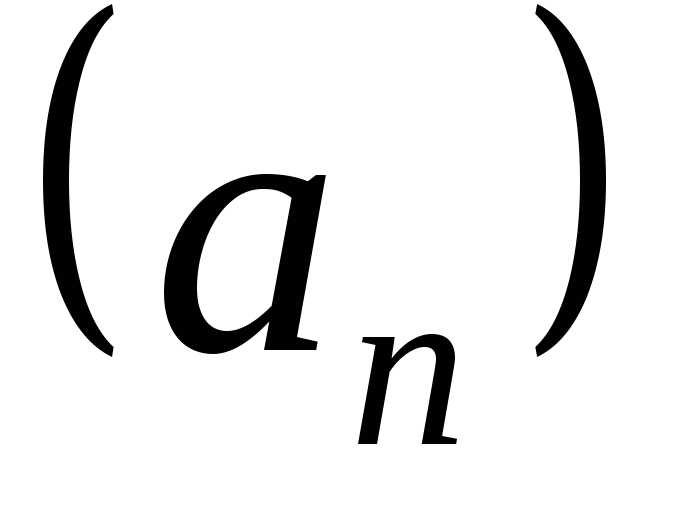 и
и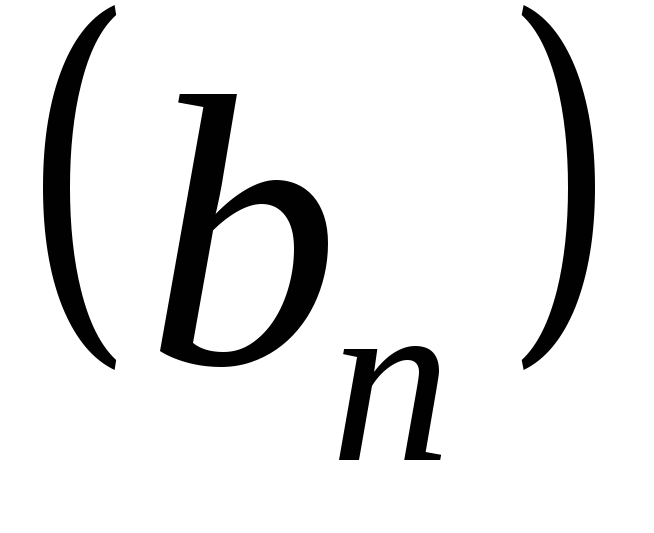 ,
т.е.
,
т.е.
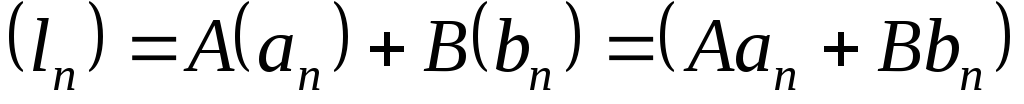 .
.
Произведениемпоследовательностей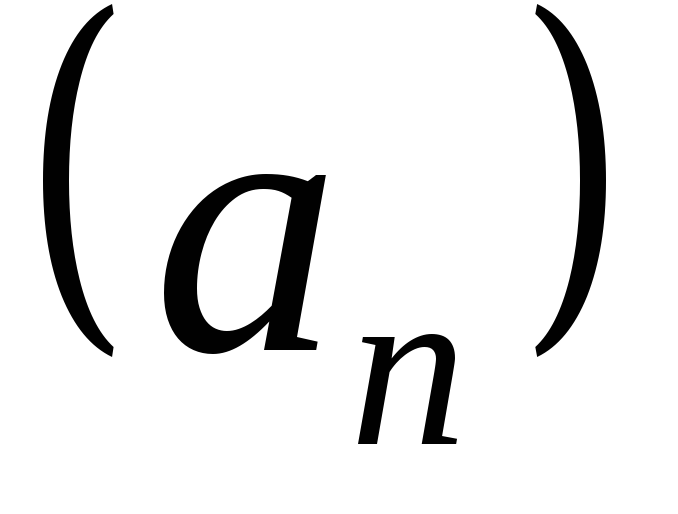 и
и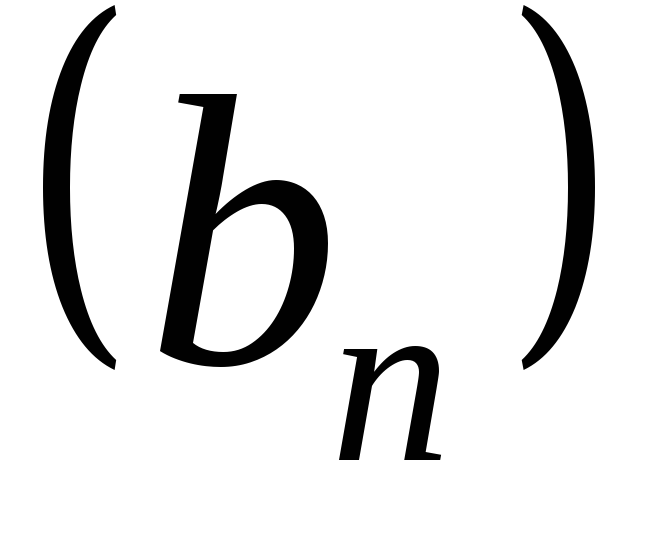 называют последовательность с
называют последовательность с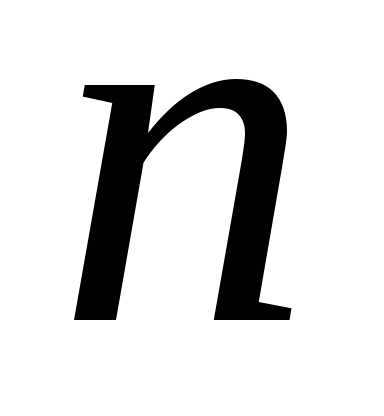 -м
членом
-м
членом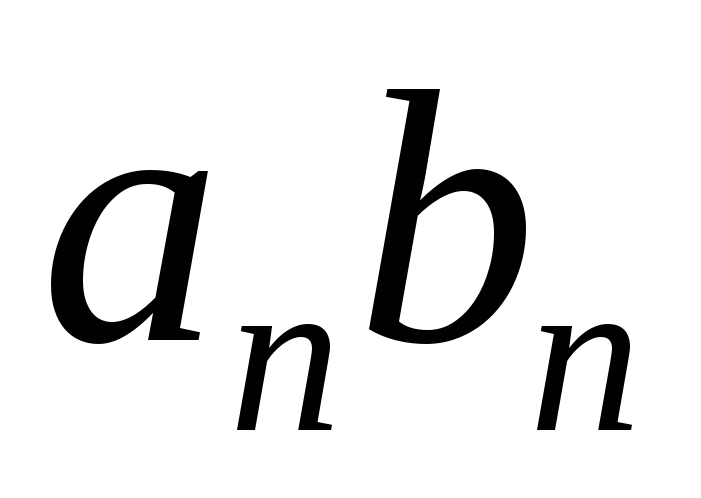 ,
т.е.
,
т.е.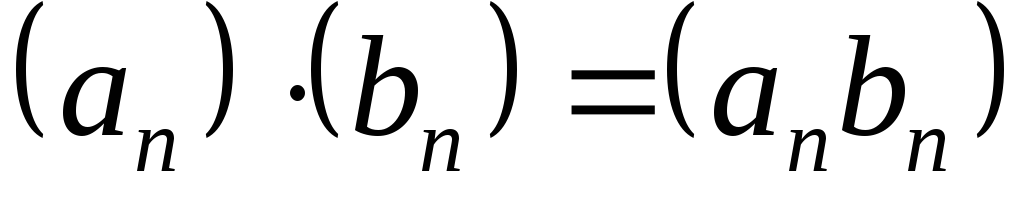 .
.
Если 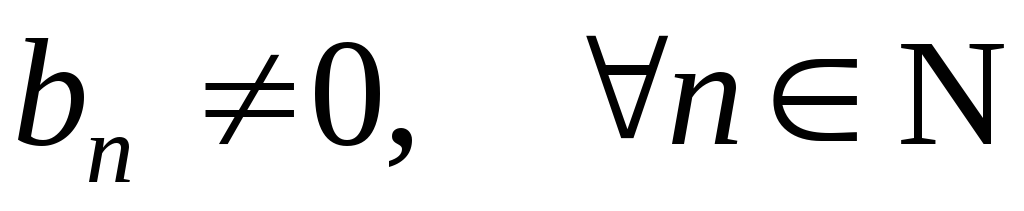 ,
то можно определитьчастное
,
то можно определитьчастное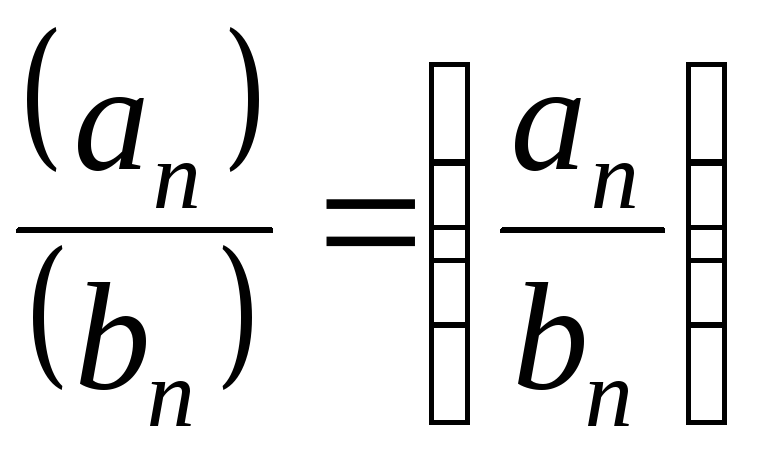 .
.
Сумма,
разность, произведение и частное
последовательностей 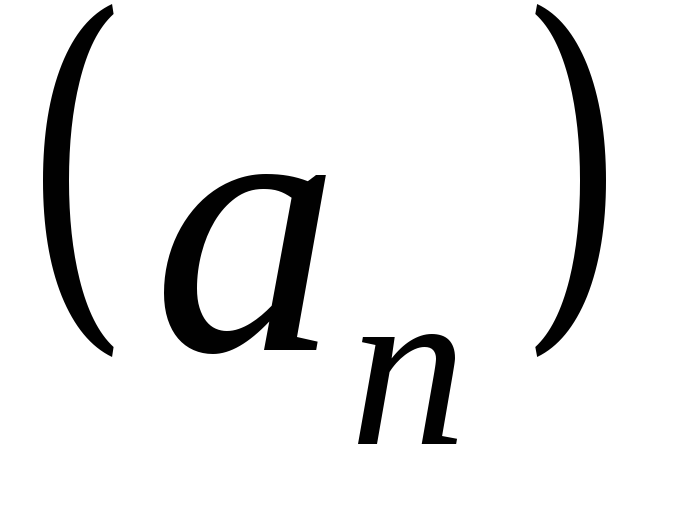 и
и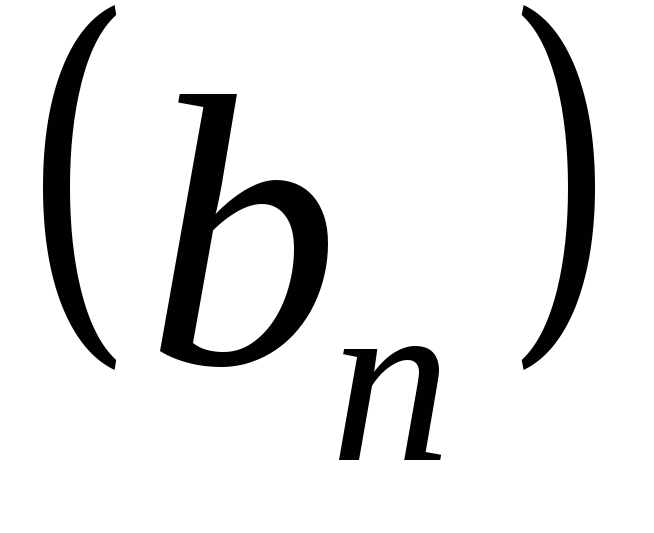 называются ихалгебраическимикомпозициями.
называются ихалгебраическимикомпозициями.
Пример. Рассмотрим последовательности 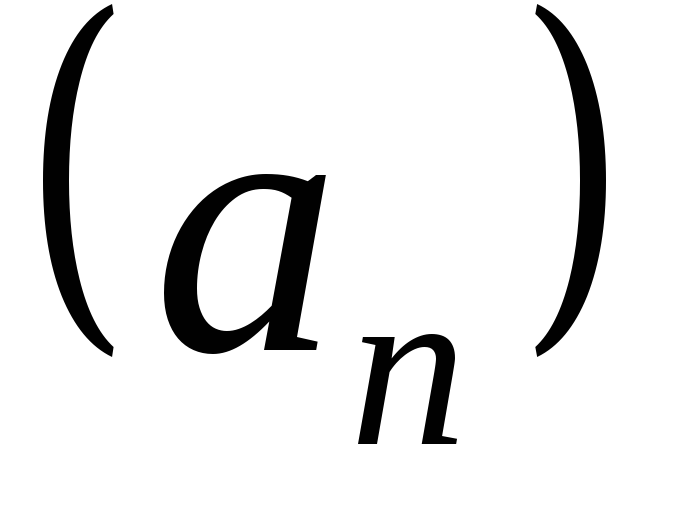 и
и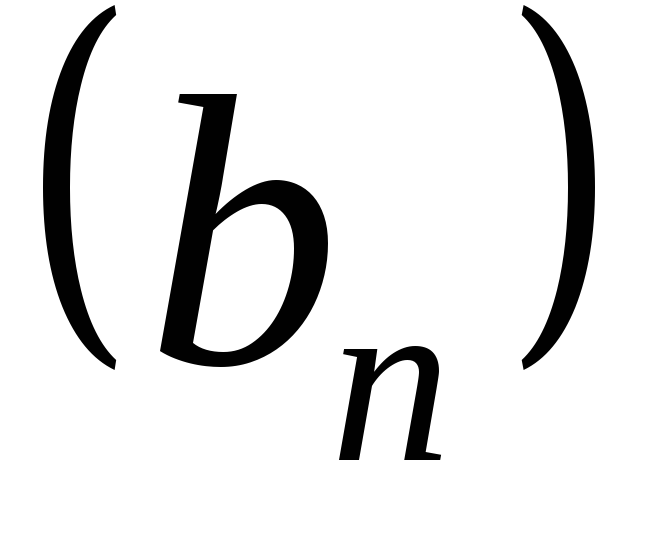 ,
где
,
где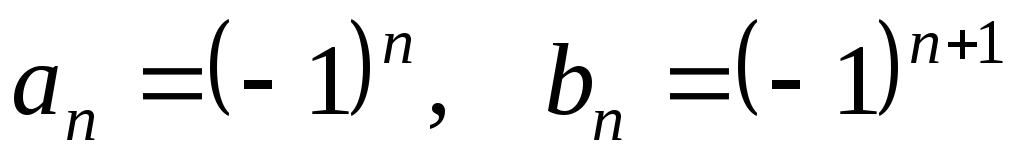 .
Тогда
.
Тогда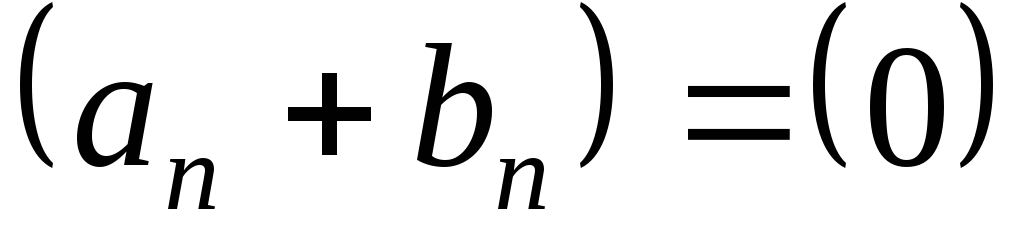 ,
т.е. последовательность
,
т.е. последовательность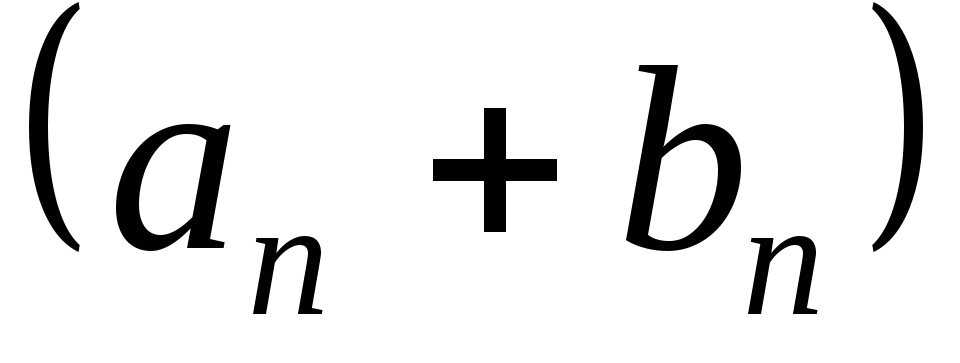 имеет все элементы, равные нулю.
имеет все элементы, равные нулю.
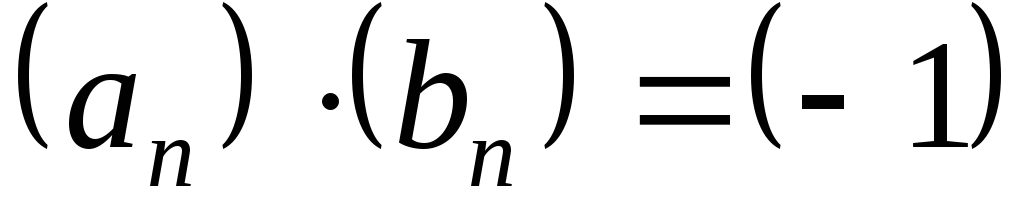 ,
, 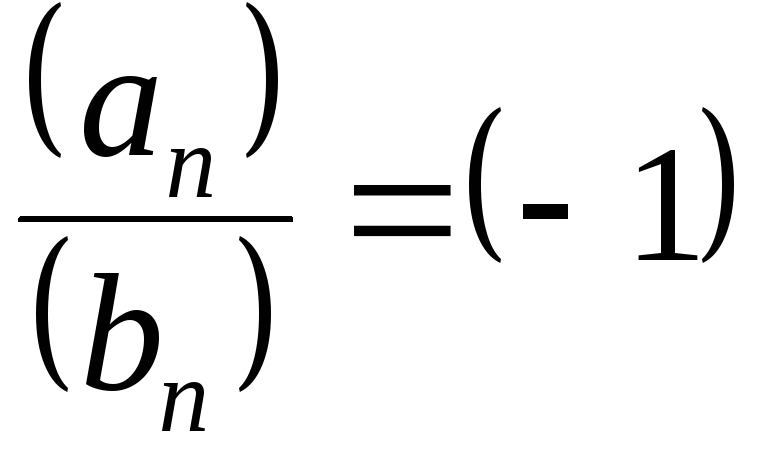 ,
т.е. все элементы произведения и частного
равны
,
т.е. все элементы произведения и частного
равны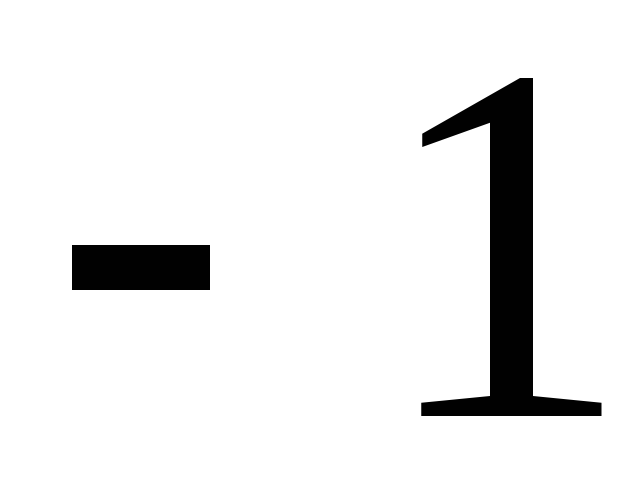 .
.
Если
вычеркнуть некоторые элементы
последовательности 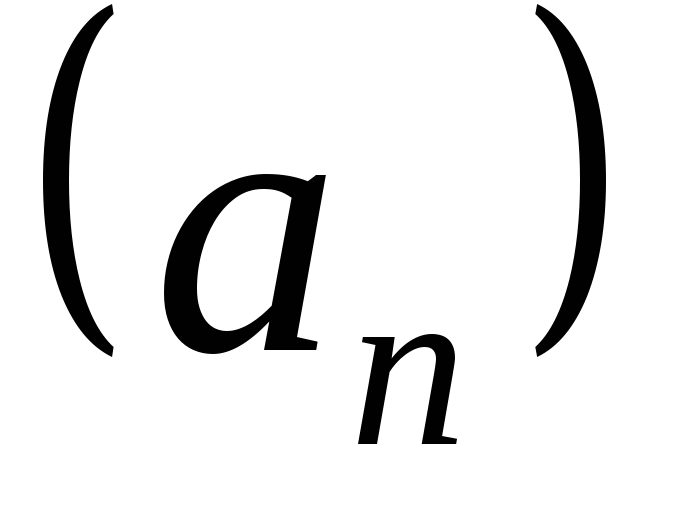 так, чтобы осталось бесконечное множество
элементов, то получим другую
последовательность, называемуюподпоследовательностьюпоследовательности
так, чтобы осталось бесконечное множество
элементов, то получим другую
последовательность, называемуюподпоследовательностьюпоследовательности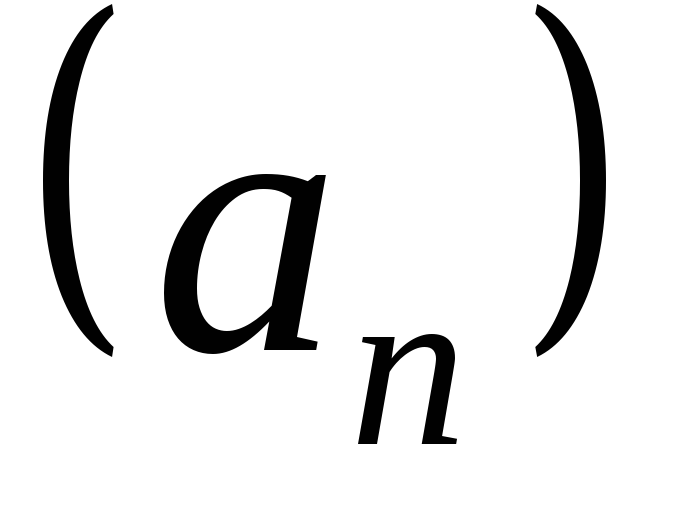 .
Если вычеркнуть несколько первых
элементов последовательности
.
Если вычеркнуть несколько первых
элементов последовательности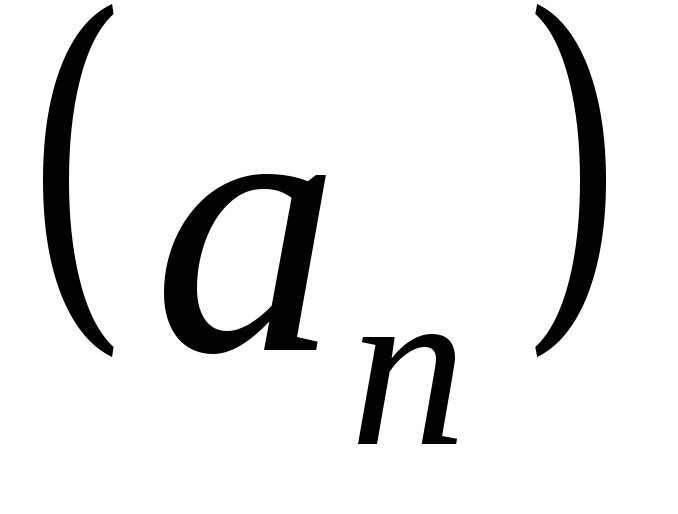 ,
то новую последовательность называютостатком.
,
то новую последовательность называютостатком.
Последовательность ограниченасверху(снизу),
если множество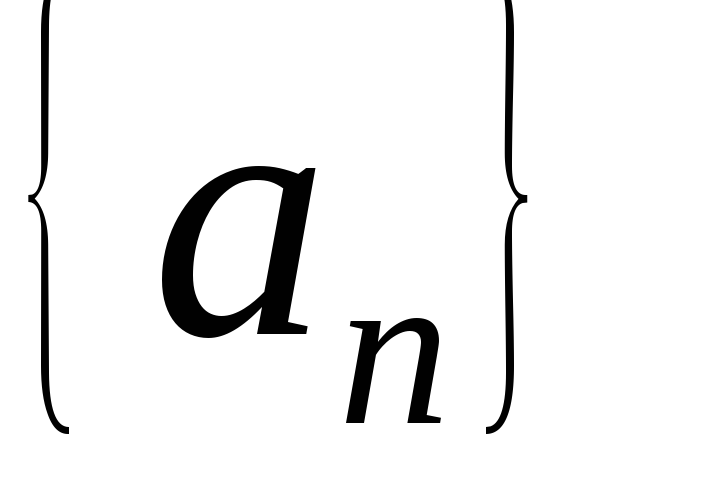 ограничено сверху (снизу). Последовательность
называютограниченной, если она
ограничена сверху и снизу. Последовательность
ограничена тогда и только тогда, когда
ограничен любой ее остаток.
ограничено сверху (снизу). Последовательность
называютограниченной, если она
ограничена сверху и снизу. Последовательность
ограничена тогда и только тогда, когда
ограничен любой ее остаток.
Сходящиеся последовательности
Говорят,
что последовательность 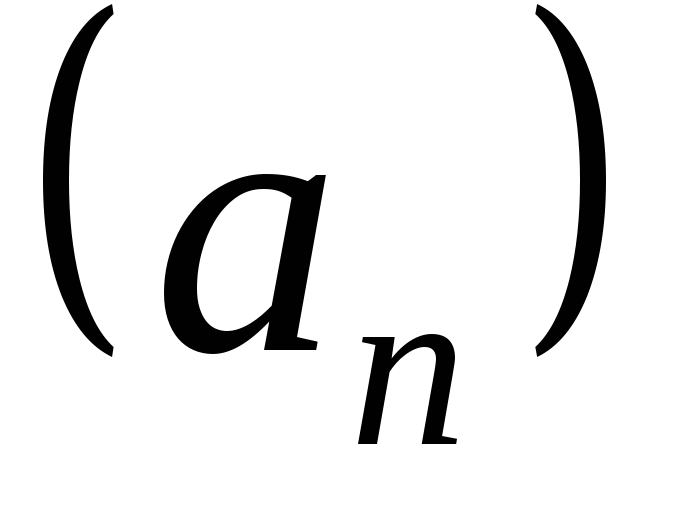 сходится, если существует число
сходится, если существует число такое, что для любого
такое, что для любого существует такое
существует такое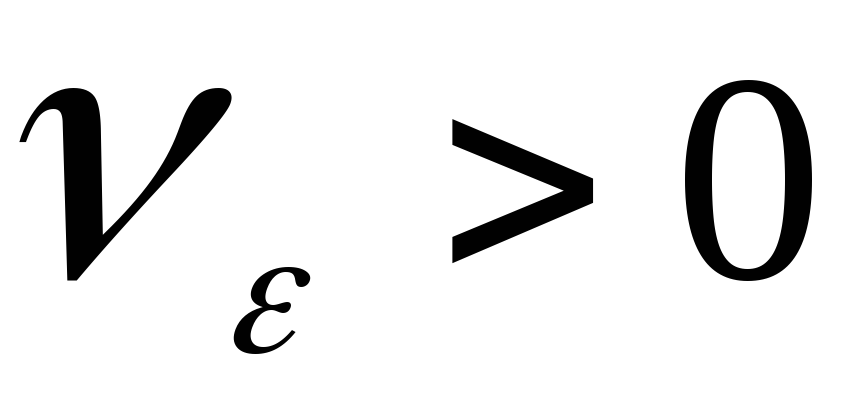 ,
что для любого
,
что для любого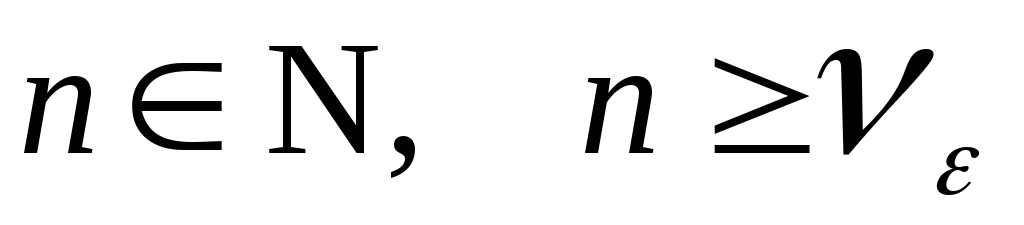 ,
выполняется неравенство:
,
выполняется неравенство: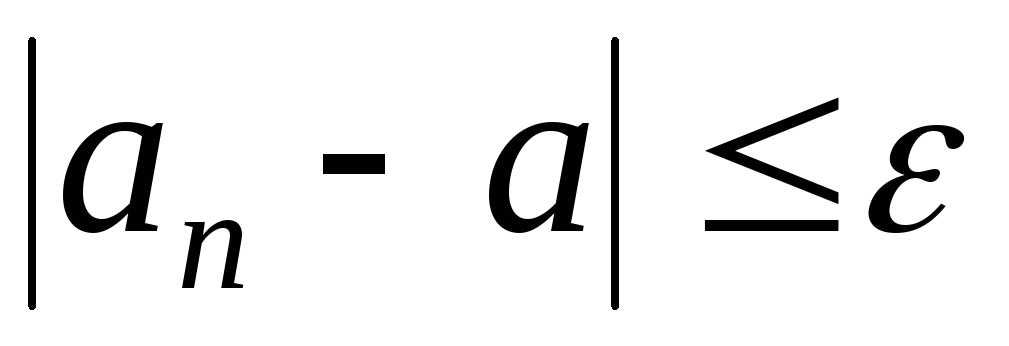 .
.
Число  называютпределом последовательности
называютпределом последовательности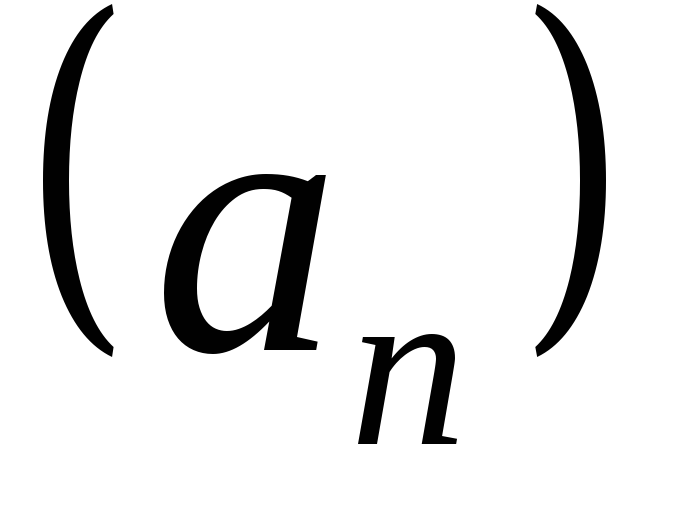 .
При этом записывают
.
При этом записывают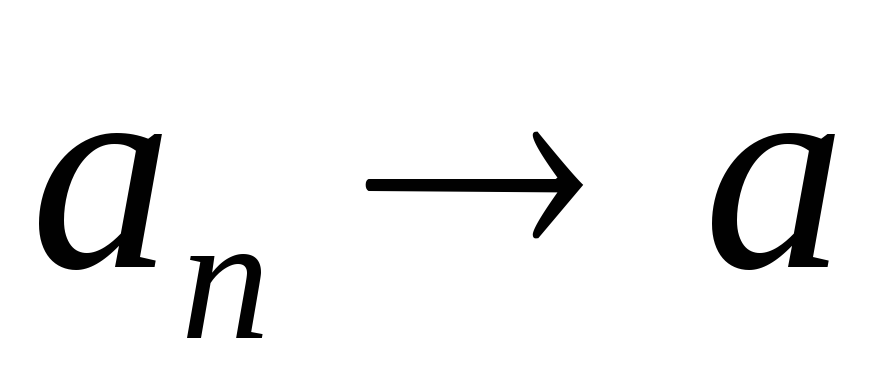 или
или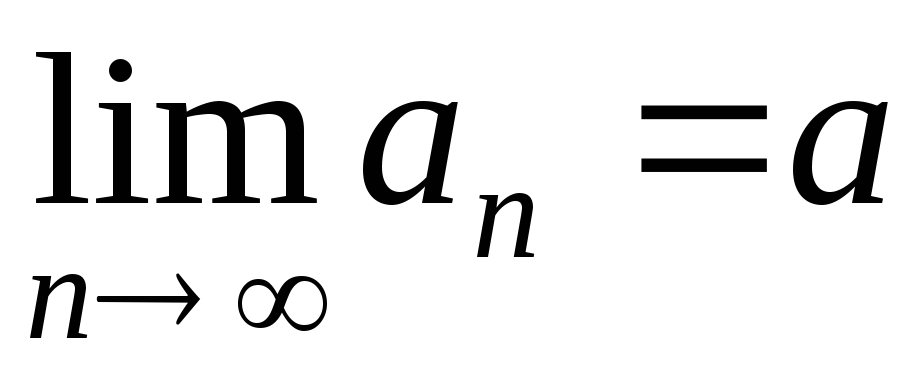 .
.
Пример.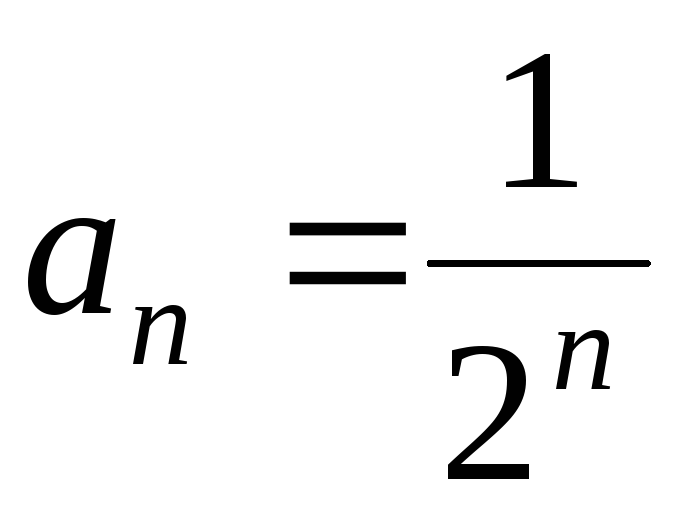 .
.
Покажем,
что 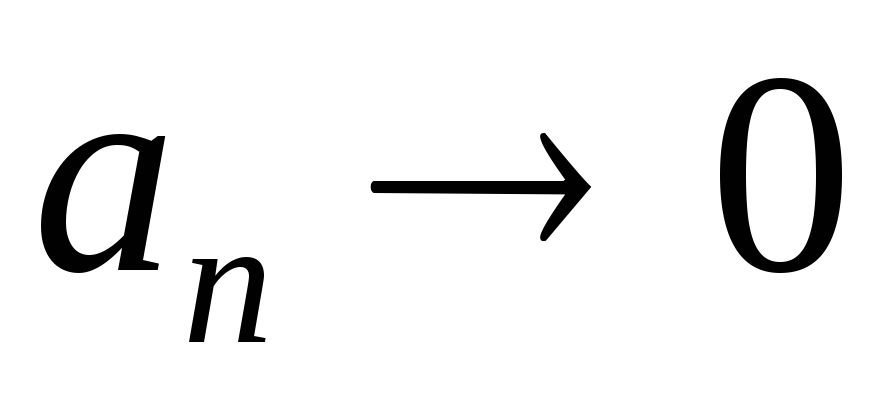 .
Зададим любое число
.
Зададим любое число .
Неравенство
.
Неравенство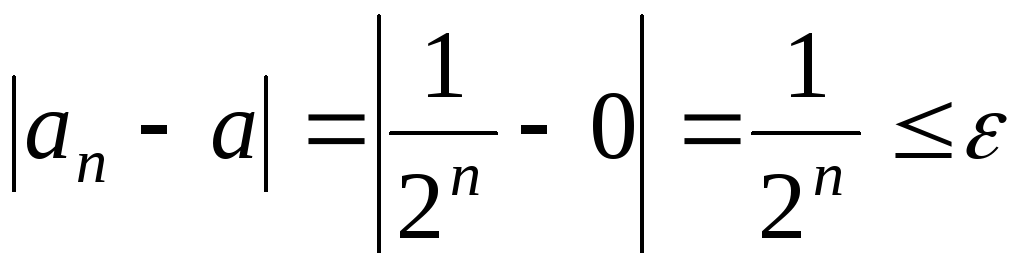 выполняется для
выполняется для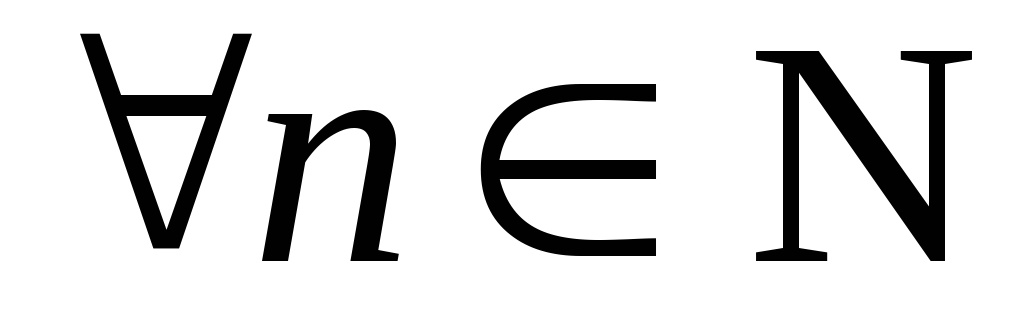 ,
такого, что
,
такого, что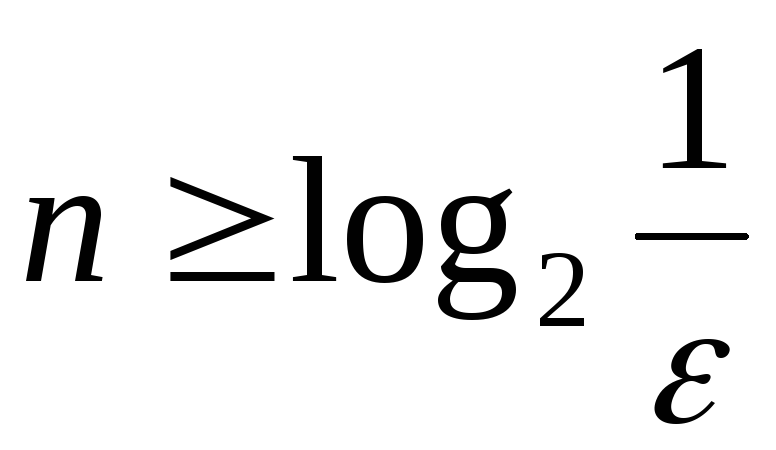 ,
что определение сходимости выполняется
для числа
,
что определение сходимости выполняется
для числа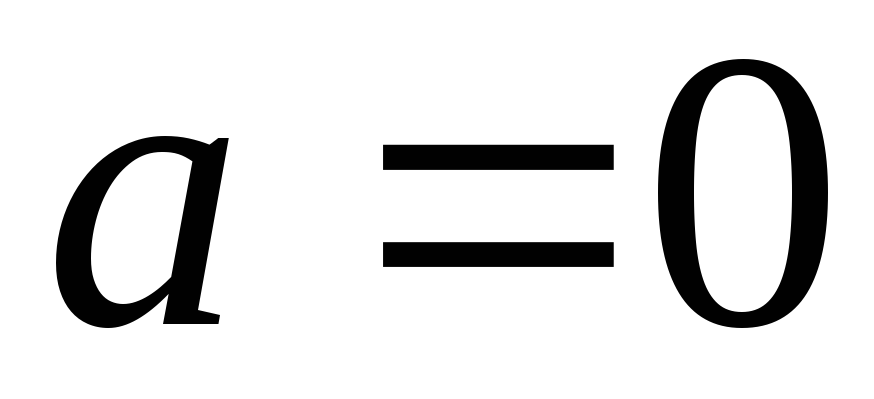 .
Значит,
.
Значит,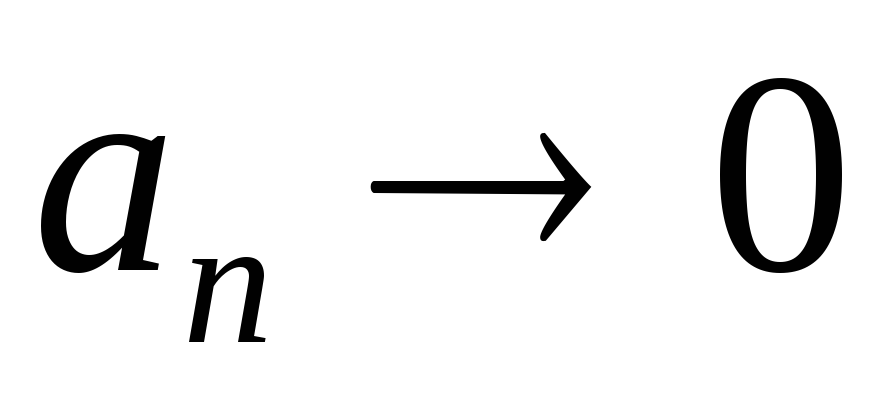 .
.
Иными
словами 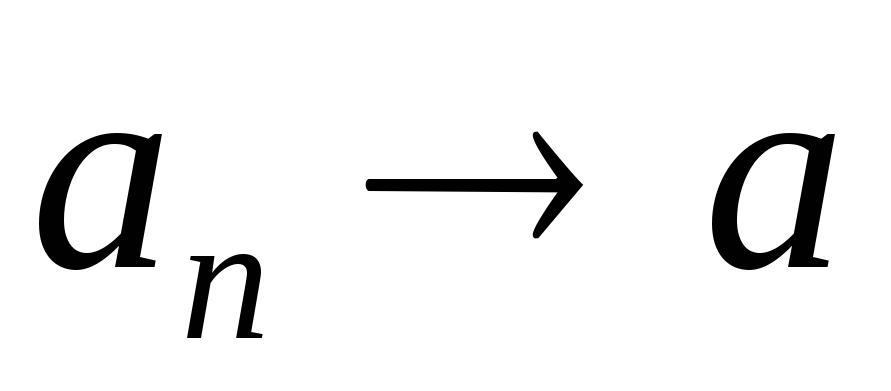 означает, что все члены последовательности
означает, что все члены последовательности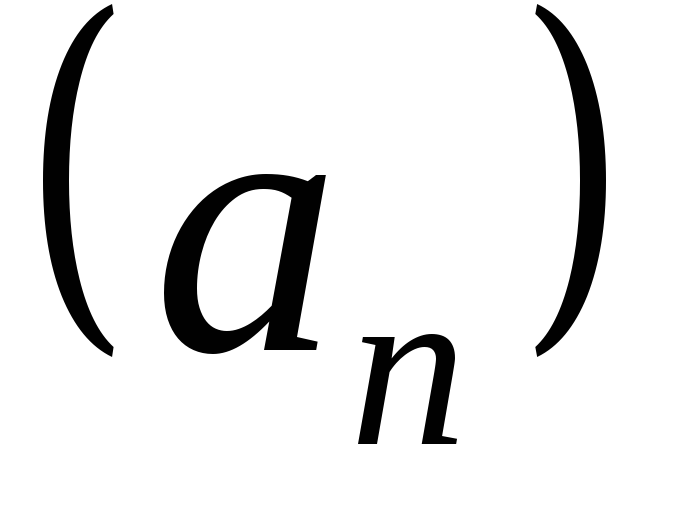 с достаточно большими номерами мало
отличается от числа
с достаточно большими номерами мало
отличается от числа ,
т.е. начиная с некоторого номера
,
т.е. начиная с некоторого номера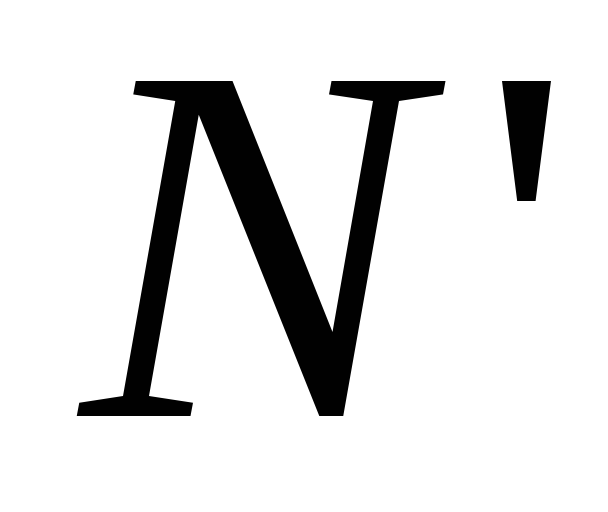 (при
(при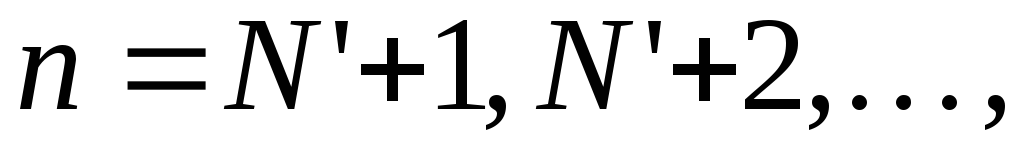 )
элементы последовательности находятся
в интервале
)
элементы последовательности находятся
в интервале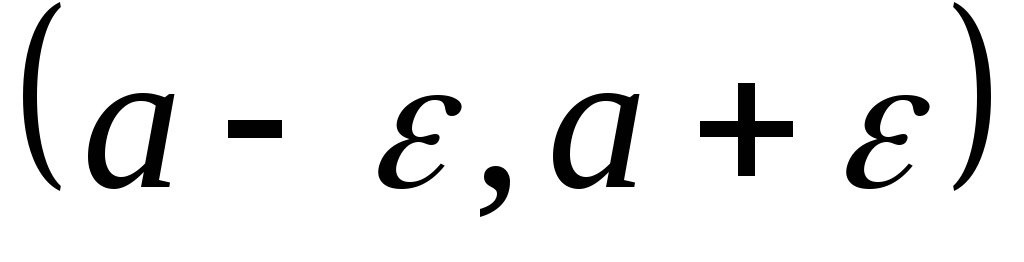 ,
который называется
,
который называется –окрестностью
точки
–окрестностью
точки .
.
Последовательность 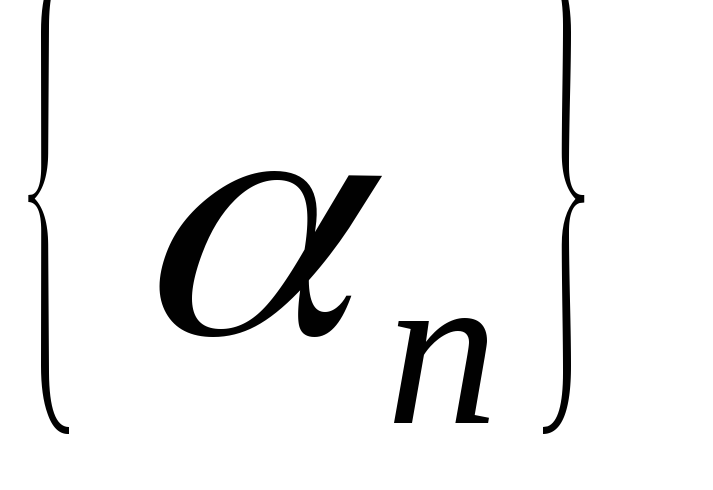 ,
предел которой равен нулю (
,
предел которой равен нулю (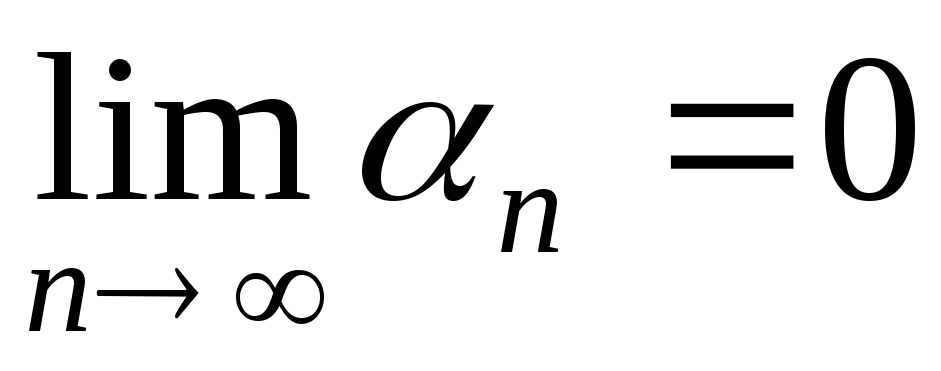 ,
или
,
или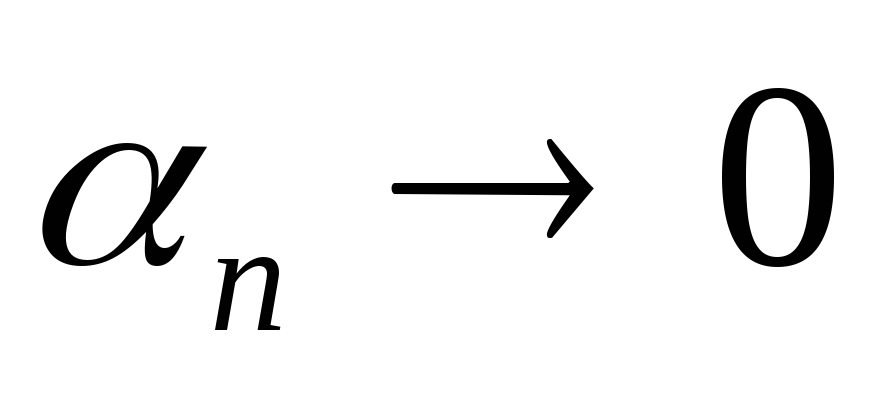 при
при )
называетсябесконечно малой.
)
называетсябесконечно малой.
Применительно к бесконечно малым справедливы утверждения:
Сумма двух бесконечно малых является бесконечно малой;
Произведение бесконечно малой на ограниченную величину является бесконечно малой.
Теорема.Для того чтобы последовательность 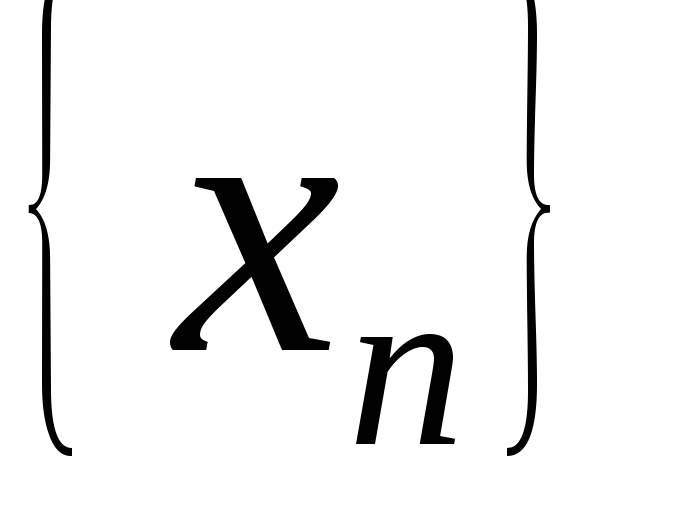 имела предел, необходимо и достаточно
чтобы
имела предел, необходимо и достаточно
чтобы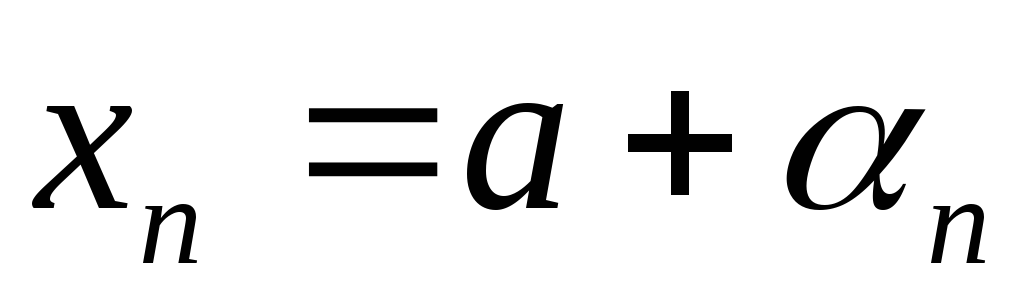 ,
где
,
где – постоянная;
– постоянная;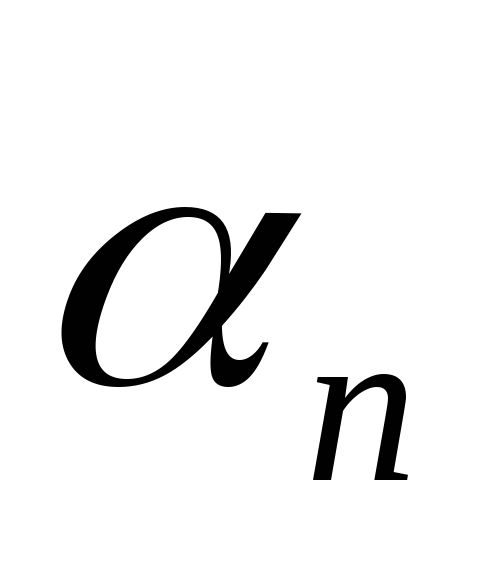 –
бесконечно малая.
–
бесконечно малая.
Основные свойства сходящихся последовательностей:
Сходящаяся последовательность имеет только один предел;
Сходящаяся последовательность ограничена;
Если
 ,
то
,
то ;
;При любых постоянных
 и
и
 ;
; ;
;Если
 ,
, и
и ,
то
,
то ;
;Если
 ,
то
,
то ;
;Если
 и
и ,
то
,
то ;
;Если
 ,
то
,
то .
.
Свойства 3. и 4. обобщаются на случай любого числа сходящихся последовательностей.
Отметим,
что при вычислении предела дроби,
числитель и знаменатель которой
представляют собой линейные комбинации
степеней 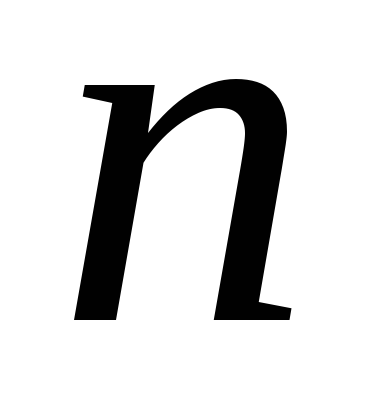 ,
предел дроби равен пределу отношения
старших членов (т.е. членов, содержащих
наибольшие степени
,
предел дроби равен пределу отношения
старших членов (т.е. членов, содержащих
наибольшие степени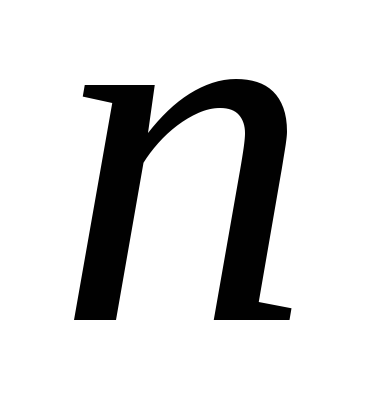 числителя и знаменателя).
числителя и знаменателя).
Последовательность 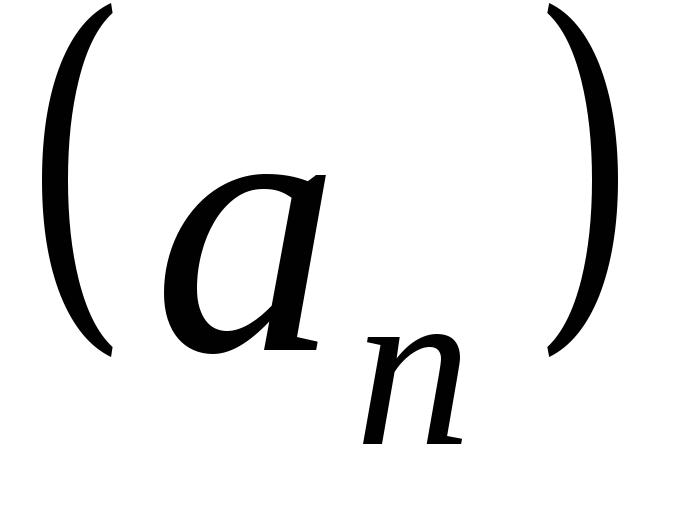 называется:
называется:
возрастающей, если
 ;
;строго возрастающей, если
 ;
;убывающей, если
 ;
;строго убывающей, если
 .
.
Все такие последовательности называют монотонными.
Теорема.Если последовательность 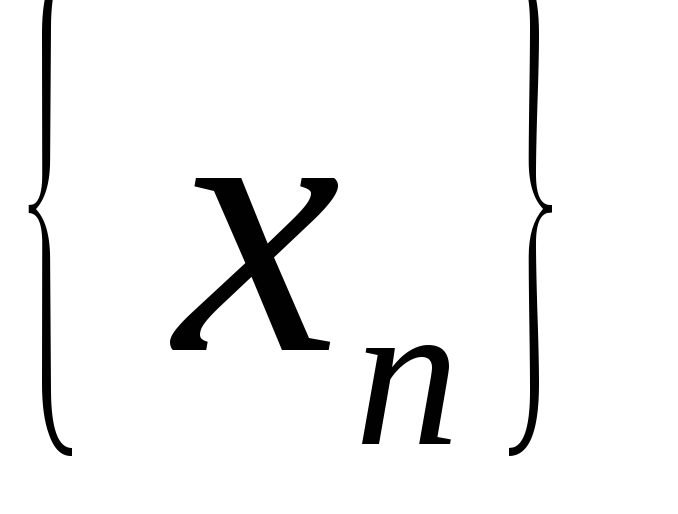 монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани.
монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани.
Монотонная последовательность — Википедия
Материал из Википедии — свободной энциклопедии
Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.
Пусть имеется множество X{\displaystyle X}, на котором введено отношение порядка.
Последовательность {xn}{\displaystyle \{x_{n}\}} элементов множества X{\displaystyle X} называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.
- {xn}{\displaystyle \{x_{n}\}} — неубывающая ⇔ ∀n∈N:xn⩽xn+1{\displaystyle \Leftrightarrow ~\forall n\in \mathbb {N} \colon x_{n}\leqslant x_{n+1}}
Последовательность {xn}{\displaystyle \{x_{n}\}} элементов множества X{\displaystyle X} называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
- {xn}{\displaystyle \{x_{n}\}} — невозрастающая ⇔ ∀n∈N:xn⩾xn+1{\displaystyle \Leftrightarrow ~\forall n\in \mathbb {N} \colon x_{n}\geqslant x_{n+1}}
Последовательность {xn}{\displaystyle \{x_{n}\}} элементов множества X{\displaystyle X} называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.
- {xn}{\displaystyle \{x_{n}\}} — возрастающая ⇔ ∀n∈N:xn<xn+1{\displaystyle \Leftrightarrow ~\forall n\in \mathbb {N} \colon x_{n}<x_{n+1}}
Последовательность {xn}{\displaystyle \{x_{n}\}} элементов множества X{\displaystyle X} называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.
- {xn}{\displaystyle \{x_{n}\}} — убывающая ⇔ ∀n∈N:xn>xn+1{\displaystyle \Leftrightarrow ~\forall n\in \mathbb {N} \colon x_{n}>x_{n+1}}
Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.[1]
Последовательность называется строго монотонной, если она является возрастающей, либо убывающей.
Очевидно, что строго монотонная последовательность является монотонной.
Иногда используется вариант терминологии, в котором термин «возрастающая последовательность» рассматривается в качестве синонима термина «неубывающая последовательность», а термин «убывающая последовательность» — в качестве синонима термина «невозрастающая последовательность». В таком случае возрастающие и убывающие последовательности из вышеприведённого определения называются «строго возрастающими» и «строго убывающими», соответственно.
Может оказаться, что вышеуказанные условия выполняются не для всех номеров n∈N{\displaystyle n\in \mathbb {N} }, а лишь для номеров из некоторого диапазона
- I={n∈N∣N−⩽n<N+}{\displaystyle I=\{n\in \mathbb {N} \mid N_{-}\leqslant n<N_{+}\}}
(здесь допускается обращение правой границы N+{\displaystyle N_{+}} в бесконечность). В этом случае последовательность называется монотонной на промежутке I{\displaystyle I}, а сам диапазон I{\displaystyle I} называется промежутком монотонности последовательности.
- Последовательность натуральных чисел.
- ∀n∈N:xn=n{\displaystyle \forall n\in \mathbb {N} \colon x_{n}=n}.
- Начальные отрезки: (1,2,3,4,5,6,7,8,⋯){\displaystyle (1,2,3,4,5,6,7,8,\cdots )}.
- Возрастающая последовательность.
- Состоит из натуральных чисел.
- Ограничена снизу, сверху не ограничена.
- Последовательность Фибоначчи.
- xn={1,n=1∨n=2xn−1+xn−2,n⩾3{\displaystyle x_{n}={\begin{cases}1,&n=1\lor n=2\\x_{n-1}+x_{n-2},&n\geqslant 3\end{cases}}}
- Начальные отрезки: (1,1,2,3,5,8,13,21,⋯){\displaystyle (1,1,2,3,5,8,13,21,\cdots )}.
- Неубывающая последовательность.
- Состоит из натуральных чисел.
- Ограничена снизу, сверху не ограничена.
- Геометрическая прогрессия с основанием 1/2{\displaystyle 1/2}.
- ∀n∈N:xn=12n−1{\displaystyle \forall n\in \mathbb {N} \colon x_{n}={\frac {1}{2^{n-1}}}}.
- Начальные отрезки: (1,1/2,1/4,1/8,1/16,⋯){\displaystyle (1,1/2,1/4,1/8,1/16,\cdots )}.
- Убывающая последовательность.
- Состоит из рациональных чисел.
- Ограничена с обеих сторон.
- Последовательность, сходящаяся к числу e.
- ∀n∈N:xn=(1+1n)n{\displaystyle \forall n\in \mathbb {N} \colon x_{n}=\left(1+{\frac {1}{n}}\right)^{n}}.
- Начальные отрезки: (2,9/4,64/27,625/256,⋯){\displaystyle (2,9/4,64/27,625/256,\cdots )}.
- Возрастающая последовательность.
- Состоит из рациональных чисел, но сходится к трансцендентному числу.
- Ограничена с обеих сторон.
- Последовательность рациональных чисел вида xn=(n−5)2{\displaystyle x_{n}=\,\!(n-5)^{2}} не является монотонной. Тем не менее, она (строго) убывает на отрезке {1,2,3,4}{\displaystyle \{1,\,\!2,3,4\}} и (строго) возрастает на промежутке {n∈N∣n⩾5}{\displaystyle \{n\in \mathbb {N} \mid n\geqslant 5\}}.
- Ограниченность.
- Всякая неубывающая последовательность ограничена снизу.
- Всякая невозрастающая последовательность ограничена сверху.
- Всякая монотонная последовательность ограничена по крайней мере с одной стороны.
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 68 — 105. — 672 с. — ISBN 5-482-00445-7.
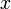 одного натурального переменного, обладающая следующим свойством:
одного натурального переменного, обладающая следующим свойством: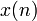 обычно называют членом последовательности
обычно называют членом последовательности 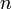 .
.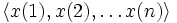 первых
первых 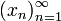 . Аналогично, для последовательностей, областью определения которых является отрезок натурального ряда вида
. Аналогично, для последовательностей, областью определения которых является отрезок натурального ряда вида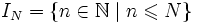 ,
,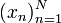 .
.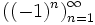 является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид
является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид 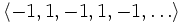 .
.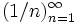 является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид
является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид 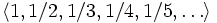 .
.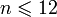 одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида
одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида 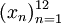 . В частности, пятым членом x5 этой последовательности является слово «май».
. В частности, пятым членом x5 этой последовательности является слово «май».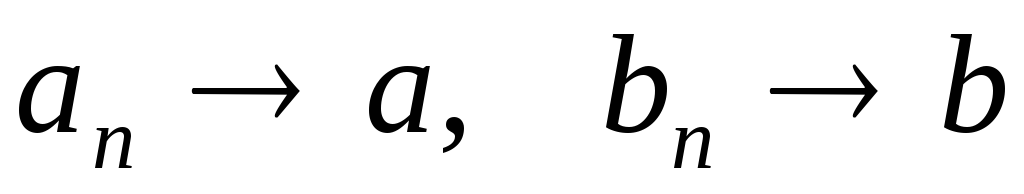 ,
то
,
то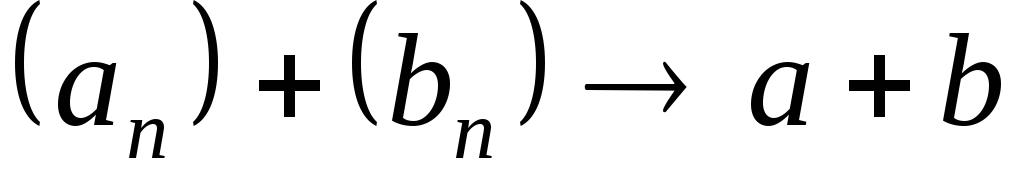 ;
; и
и
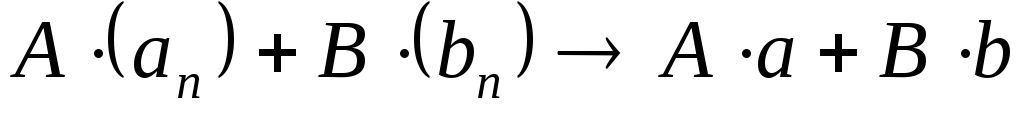 ;
;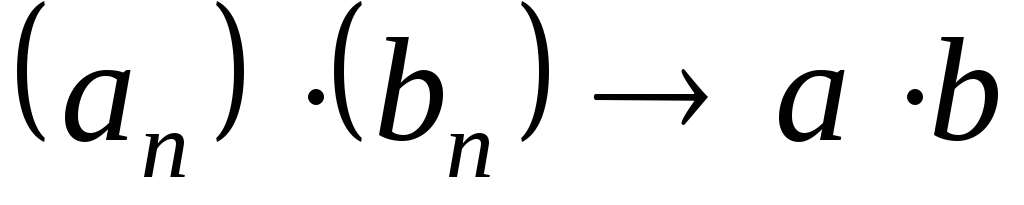 ;
;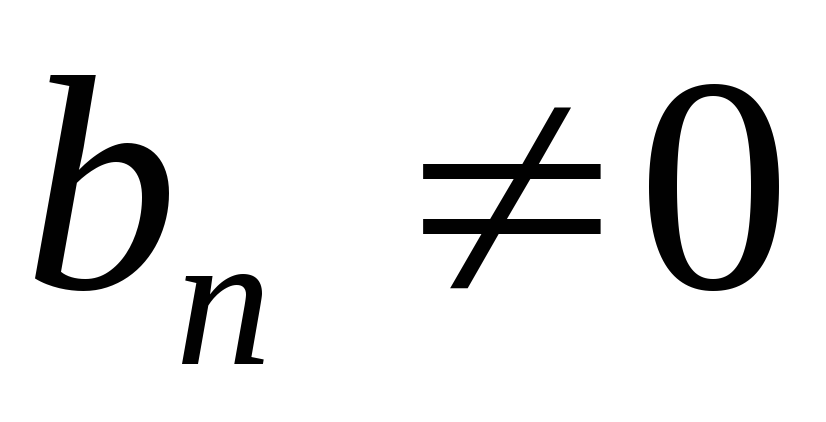 ,
,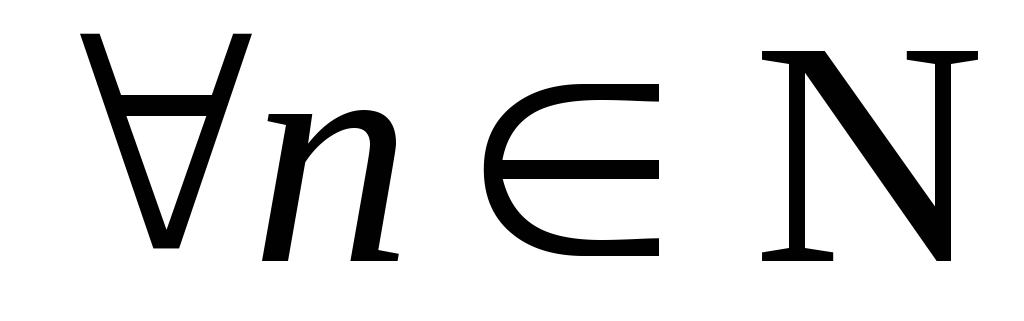 и
и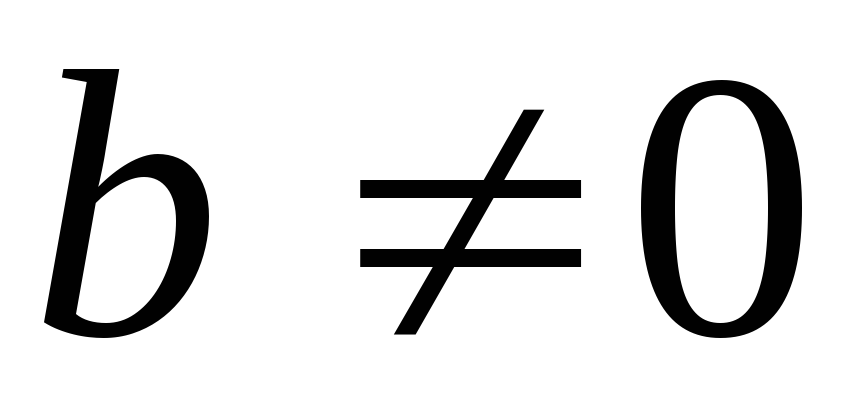 ,
то
,
то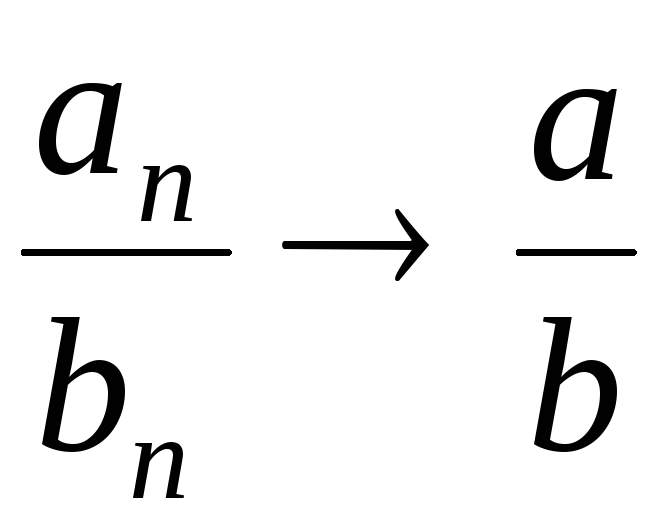 ;
;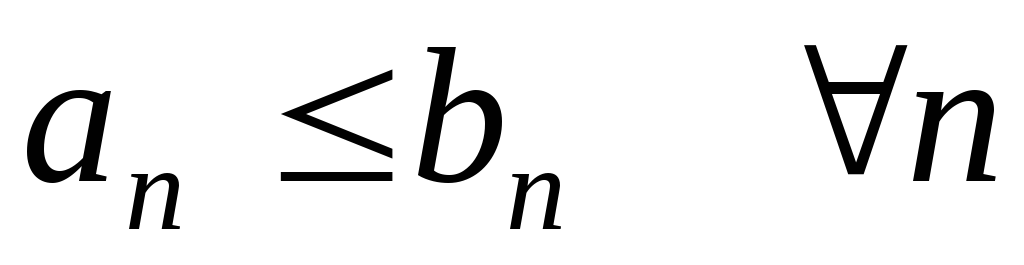 ,
то
,
то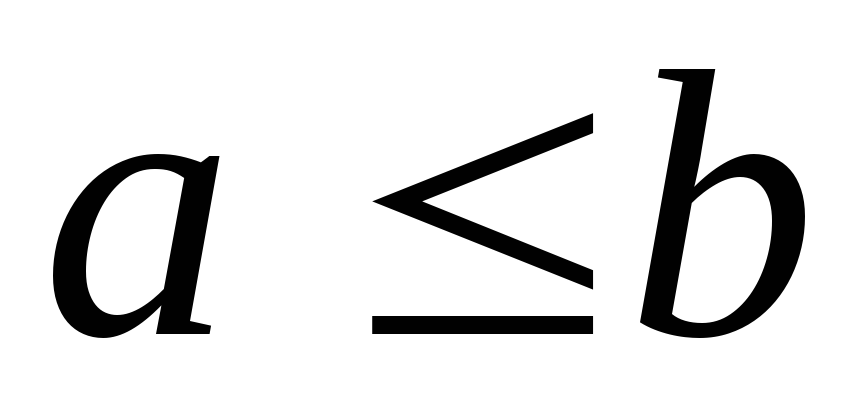 ;
;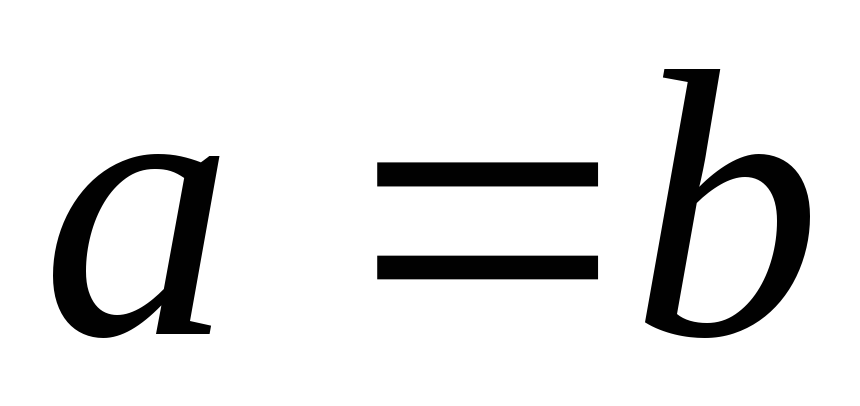 и
и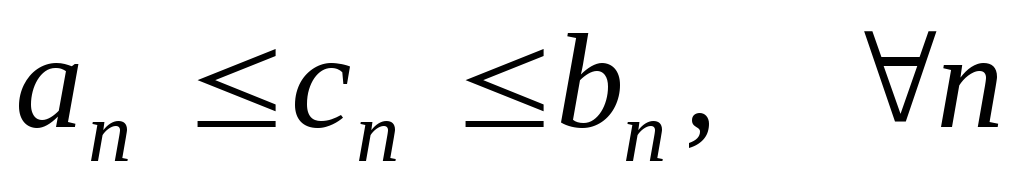 ,
то
,
то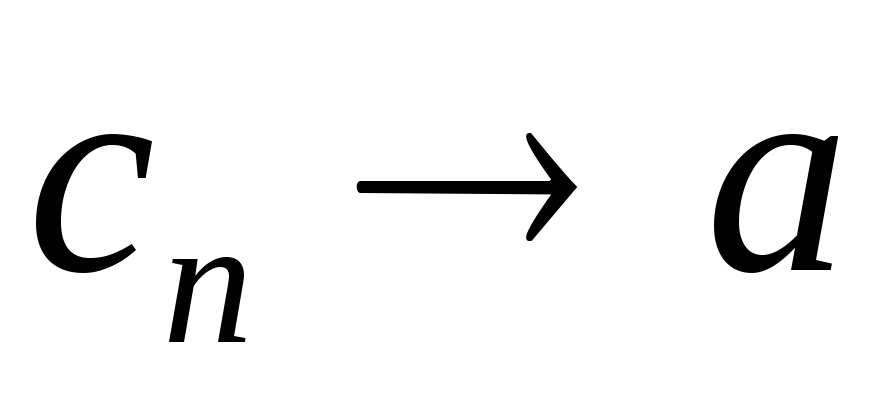 ;
;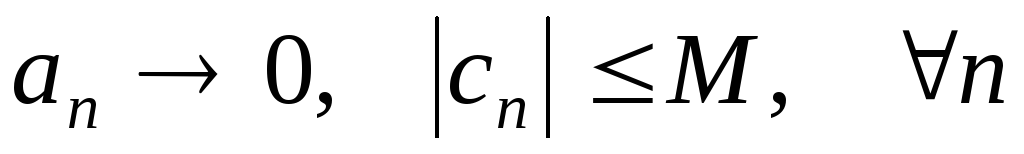 ,
то
,
то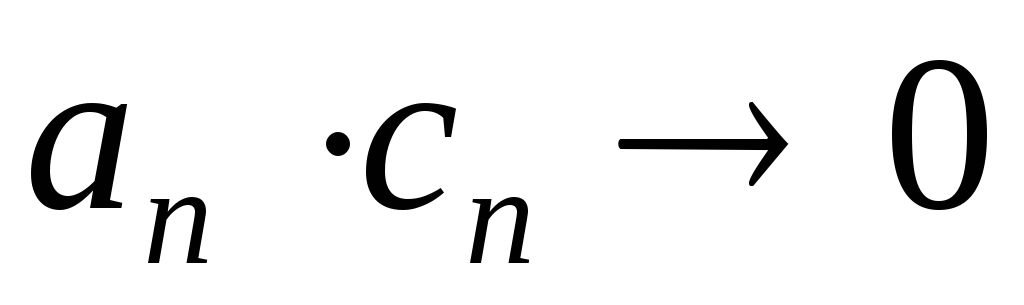 .
.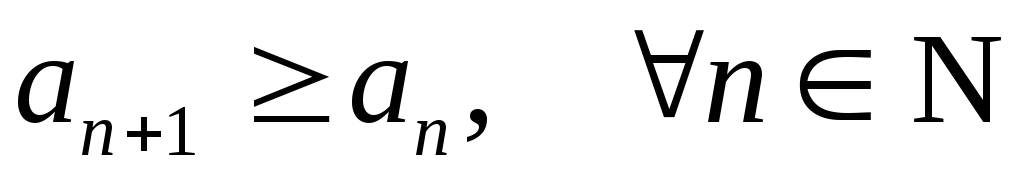 ;
;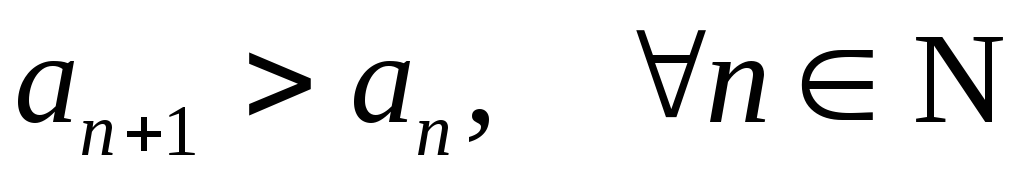 ;
;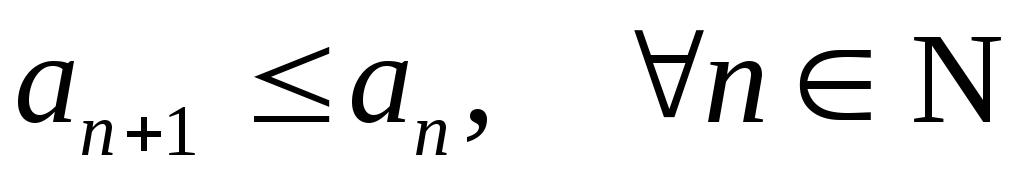 ;
;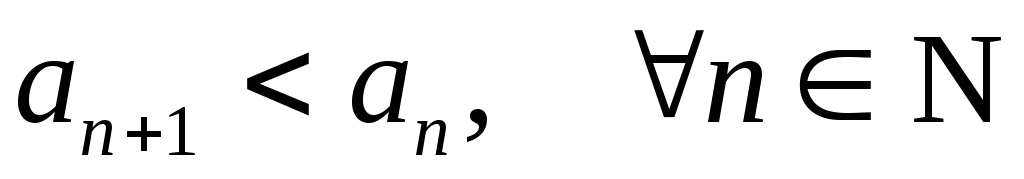 .
.