Презентация к уроку по алгебре (9 класс) на тему: построение графиков функций с модулем 9 класс
Слайд 2
График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х
Слайд 3
y =
Слайд 4
у = | х ² — х -6 | Проверь 1.Построим график функции у =х ² — х -6 2 . Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.
Слайд 6
Для построения графика функции у = |f(х) | достаточно : 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
Слайд 7
График функции у = f |(х)|
Слайд 8
Для построения графика функции у = f |(х)| достаточно: 1. построить график функции у = f(х) для х>0; 2. Для х
Слайд 10
Построить график функции у=0,25 х ² — | х | -3. 1) Поскольку | х | = х при х≥0, требуемый график совпадает с параболой у=0,25 х² — х — 3. Если х
Слайд 11
Построить график функции у = | 2|х | — 3| 1. Построить у = 2|х | — 3 , для 2 |х| — 3 > 0 , |х | >1,5 т.е. х 1,5 а) у = 2х — 3 , для х > 0 б) д ля х 0 б) д ля х
Слайд 12
1. у = | 2|х | — 3| 1) Построить у = 2х-3, для х>0. 2) Построить прямую, симметричную построенной относительно оси ОУ. 3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Слайд 13
у = | х ² – 5|х| | 1. Построим у = х ² – 5 |х|, для х ² – 5 |х| > 0 т.е. х > 5 и х 0 б) д ля х 0 б) д ля х
Слайд 14
2. у = | х ² – 5|х| | а ) Построим график функции у = х ² – 5 х для х>0. б) Построим часть графика, симметричную построенной относительно оси ОУ в) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Слайд 15
о х 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 у 9 8 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 Найдите все положительные значения к , при которых прямая у=кх пересекает в одной точке ломанную, заданную условиями: Х >3 Х
Слайд 16
-1 -2 -3 -4 -5 -6 1 2 3 4 5 6 7 1. у = I х I 2. у = I х +1 I Ответ: (- 1 ; 4 ) , (-4;-1), (4;1). Построить о -7 -6 -5 -4 -3 -2 -1 9 8 7 6 5 4 3 2 1 у х 2. у = I х +1 I – 4 Решить систему уравнений
nsportal.ru
Презентация к уроку по алгебре (9 класс) по теме: Построение графиков функций с модулем
Слайд 6
График функции у = |x+a| получается параллельным переносом графика y=|x| в отрицательном направлении от оси х на |а| при а>0 и в положительном направлении на |a| при a
Слайд 7
Построить график функции у = х ² — 4 | х | + 3. 1 способ. Раскрываем | х | = х при х≥0, получаем график у = х² — 4х + 3. При х
Слайд 9
2 способ. Если рассмотрим график у = х² — 4х + 3 при х≥0 и отобразить его относительно оси ОУ мы получим тот же самый график.
Слайд 10
Для построения графика функции у = |f(х) | достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
Слайд 11
Построить график функции у = | х ² — х -6 | 1.Построим график функции у =х ² — х -6 2 . Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.
Слайд 12
Построить график функции у = | х + 3 | + |2x + 1| — x Строить график будем с помощью раскрытия модуля. Алгоритм построения: Приравняем каждое подмодульное выражение к нулю и находим точки, в которых подмодульные выражения, входящие в уравнение функции меняют знак. Наносим эти точки на ось х и выделяем промежутки, в которых подмодульные выражения сохраняют знак. Раскрываем модуль на каждом промежутке и получаем соответствующие уравнения функции. Строим график на каждом промежутке.
Слайд 13
у = | х + 3 | + |2x + 1| — x Приравниваем каждое подмодульное выражение к нулю и находим точки, в которых происходит смена знака: Наносим точки на ось х:
Слайд 14
3. При
Слайд 16
у = | х + 3 | + |2x + 1| — x
Слайд 17
Построить график функции у = | 2|х | — 3| 1. Построить у = 2|х | — 3 , для 2 |х| — 3 > 0 , | х | >1,5 т.е. х 1,5 а) у = 2х — 3 , для х > 0 б) для х 0 б) для х
Слайд 18
у = | 2|х | — 3| 1) Построить у = 2х-3, для х>0. 2) Построить прямую, симметричную построенной относительно оси ОУ. 3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Слайд 19
у = | х ² – 5|х| | Построим у = х ² – 5 х, для х>0. Вершина параболы в (2,5; -6,25) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. 3. Для х
Слайд 20
Найти корни уравнения ||x-2|-5| = 3. Выполняем построение первого (внутреннего) модуля y = |x-2| Параллельно переносим линии вниз на 5 , чтобы получить график функции y = |x-2|- 5 Отражаем все что находится ниже оси абсцисс. Это и будет искомая функция y=||x-2|-5| . Также выполняем построение прямой у=3
Слайд 21
Найти корни уравнения ||x-2|-5|=3. Нетрудно определить по графику, что решениями уравнения с модулями будут значения x = — 6; x = 0; x = 4; x = 10 .
Слайд 22
Построить график функции у = | (|х| — 2) 2 – 3 | Строим график функции у = (х — 2) 2 – 3 Совершаем преобразование: для этого часть графика, расположенную левее оси оу стираем.
Слайд 23
Построить график функции у = | (|х| — 2) 2 – 3 | Часть графика, расположенную правее оси оу достраиваем симметрично относительно этой оси. Получаем график функции у = (|х| — 2) 2 – 3
Слайд 24
Построить график функции у = | (|х| — 2) 2 – 3 | Часть графика, расположенную ниже оси ох отображаем симметрично относительно этой оси.
Слайд 25
График неравенства | у — 2х -1| + 2|х| ≤ 3 Задача. Изобразите на координатной плоскости множество решений неравенства. Раскроем модули. Для этого каждое подмодульное выражение приравняем к нулю: у – 2х – 1 = 0; у = 2х + 1 х = 0 Подмодульные выражения меняют знак при переходе через прямые у = 2х + 1 и х = 0.
Слайд 26
Выводы: Для построения графика функции у = f |(х)|: 1.Построить график функции у = f (х) для х>0; 2.Построить для х0. 2. Строим вторую часть графика, т. е. построенный график симметрично отражаем относительно ОУ 3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.
Слайд 27
у = f |(х)| у = | f (х)| у = | f |(х)| | у = f (х), х>0 Построить часть для х0
nsportal.ru
Построение функций, содержащих модули
Здравствуйте, уважаемые посетители! В этой статье мы попробуем подробно разобраться, как построить график функции, если эта функция содержит модуль. В статье разобраны различные примеры с пошаговым построением и подробным объяснением, как получен тот или иной график.
1. Начнем с построения графика

В “основе” его лежит график функции

и все мы знаем, как он выглядит:

Теперь построим график


Теперь необходимо умножить на два все ординаты, чтобы получить график функции


Наконец, сдвигаем график вверх на две единицы:


Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):

2. Теперь построим график функции

Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:

При х>2/3 функция запишется так:

То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (правее) мы строим функцию

а в другой (левее) – график функции

Строим:

3. Следующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:

Посмотрим, в каких точках подмодульные выражения меняют знак:

Расставим знаки для подмодульных выражений на координатной прямой:

Раскрываем модули на первом интервале:

На втором интервале:

На третьем интервале:

Таким образом, на интервале (-∞; 1.5] имеем график, записанный первым уравнением, на интервале [1.5; 2] – график, записанный вторым уравнением, и на интервале [2;∞) – график по третьему уравнению:

Строим:

4. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:

В основе опять знакомый нам график функции

но, если в знаменателе x стоит под знаком модуля,

то график имеет вид:

Теперь произведем сдвиг на три единицы,

при этом сдвинутся обе части: правая – вправо, левая – влево (своеобразное зеркало : отходишь дальше – видно больше)

График этой функции, умноженной на два,

выглядит так:

Теперь можно поднять график по оси у:

и тогда он будет таким:
Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:


5.Очень интересно выглядит график функции

В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) – второе:


6. Две следующие функции отличаются знаком, и графики их выглядят по-разному:




7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:
Первый:


Второй:


8.Теперь построим график такой функции:

Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:

А на интервале [4; ∞) так:

Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:

9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:

Однако многочлен в числителе раскладывается на множители:

Точки перемен знака подмодульных выражений – 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:
На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

Строим:

Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:

Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:
На первом интервале (-∞; -2):

На втором интервале (-2;4):

На третьем интервале (4;∞):

График изменится:

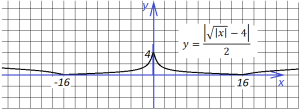
10. Наконец, последний график мы построим для функции

Начнем построение с “базовой” для этого графика функции

она выглядит так:

Далее добавим знак модуля под корень:


Теперь опустим этот график вниз на 4 единицы по оси у:


“Опрокинем” все, что ниже оси х, вверх,

и не забудем поделить все ординаты на 2:


easy-physic.ru
Разработка элективного курса по математике для предпрофильной подготовки в 9-м классе «Графики функций с модулем»
Пояснительная записка
Математика уже давно стала основным аппаратом физики и техники. Последние годы математические методы все настойчивее проникают в различные науки. Современная жизнь требует от человека гибкости и скорости нахождения решений, основанных на рациональности. Данный элективный курс предназначен для учащихся 9-х классов, желающих повысить уровень своих математических умений, а также усвоить дополнительные сведения при построении графиков, выражения которых содержат знак абсолютной величины. Практика решения таких задач полезна для развития и укрепления способности к самостоятельному логическому мышлению, для обогащения математической и графической культуры и может быть использована для графического решения уравнений и неравенств с модулем.
Цели обучения:
- создание условий для обоснованного выбора профиля обучения в старшей школе через оценку собственных возможностей в усвоении математического материала при построении графиков с модулем;
- оказание помощи учащимся в поиске и приобретении индивидуального стиля и темпа учебной деятельности, раскрытии индивидуальных, познавательных процессов и интересов.
Учащиеся должны знать:
- графики основных функций школьной программы.
Учащиеся должны уметь:
- строить графики основных функций школьной программы.
Тематическое планирование учебного материала
Тема |
Количество часов |
Вид деятельности |
Вводное занятие |
1 |
Беседа, тестирование |
График функции |
1 |
Беседа, практикум |
График функции |
1 |
Беседа, практикум |
График функции |
1 |
Беседа, практикум |
График функции где |
1 |
Беседа, практикум |
График функции |
1 |
Беседа, практикум |
Графики некоторых простейших функций, заданных явно. |
2 |
Беседа, практикум, семинар |
Занятие 1. Вводное занятие
Цель: установление владения базовыми умениями в области построения графиков элементарных функций.
Ход занятия
1. Вводная беседа
На практике мы часто встречаемся с зависимостями между различными величинами не только в математике, но и в других сферах деятельности. С помощью графиков наиболее естественно отражаются функциональные зависимости одних величин от других. Преобразование графиков, построение кусочно заданной функции, а особенно графики, содержащие переменную под знаком модуля, позволяют передать красоту математики.
С помощью таблицы повторим графики основных функций (Рисунок 1), изученных вами.
Проверку базовых знаний осуществляется за счет тестирования. (Приложение 1)
Занятие 2. График функции
Цель: научиться строить график функции .
Ход занятия
I. Беседа
Определение: Абсолютной величиной (модулем) действительного числа а называется неотрицательное число.
Нетрудно показать, что функция является четной.
В самом деле, так как , то .
Следовательно, график этой функции симметричен относительно оси ОУ. Отсюда следует, что достаточно построить график функции у = f (х) для х > 0, а затем достроить его левую часть, симметричную правой относительно оси ОУ.
Давайте запишем алгоритм построения такого графика.
Алгоритм:
- Построить график функции у = f (х), для х > 0.
- Достроить симметричный ему относительно оси ОУ.
Примеры.
1) Построить график функции
а) Строим график функции у = х для х > 0
б) Строим для x < 0 часть графика, симметричную построенной относительно оси ОУ. (Рисунок 2)
Рисунок 2
2), здесь .
а) Для х > 0 строим график функции .
Известно, что это парабола, ветви которой направлены вверх. Ось ОУ она пересекает в точке (0; –3). Ось ОХ пересекает в точках (–2; 0) и (6; 0), что следует из уравнения . Вершина параболы находится в точке (2; –4).
б) Достраиваем для x < 0 часть графика (левую половину), симметричную построенной (правой части) относительно оси ОУ. (Рисунок 3)
Рисунок 3
II. Практическая часть
Задание: из предложенного списка функций выбрать по желанию и построить графики двух:
а) ;
б) ;
в) ;
г) ;
д) .
Решение см. Рисунок 4.
Рисунок 4
Занятие 3. График функции
Цель: научиться строить график функции .
Ход занятия
I. Беседа
Под абсолютной величиной функции f (х) (т. е. под записью принято понимать функцию вида:
.
Отсюда вытекает практическое правило построения графика функции.
Алгоритм:
- Строим график функции у = f (х).
- На участках, где график расположен в нижней полуплоскости, т. е. где f (х) <0, строим кривые, симметричные построенным относительно оси ОХ.
Пример.
Построить график функции .
а) Строим график функции у = х — 2.
б) График нижней полуплоскости преобразовываем вверх симметрично оси ОХ. (Рисунок 5) Ломаная АBC является графиком данной функции.
Рисунок 5
II. Практическая часть
Задание: из предложенного списка функций выбрать по желанию и построить графики двух:
а) ;
б) ;
в) ;
г) ;
д) .
Решение см. Рисунок 6.
Рисунок 6
Занятие 4. График функции
Цель: научиться строить график функции .
Ход занятия
I. Лекция
Так как функция совмещает двойное применение модуля, то график данной функции может быть построен в следующем порядке.
Алгоритм:
1. Строим график функции у =f (х), для х ≥ 0.
2. Строим график функции y=f (–х), для х < 0 (или строим кривую графика, симметричную построенной относительно оси ОУ, так как данная функция четная).
3. Участки графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.
Пример.
Построить график функции . Рисунок 7
Рисунок 7
II. Практическая часть
Задание: из предложенного списка функций выбрать по желанию и построить графики двух:
а) ;
б) ;
в) ;
г) ;
д) .
Решение см. Рисунок 8.
Рисунок 8
Занятие 5. График функции где
Цель: научиться строить графики функции вида где .
Ход занятия
I. Беседа
По определению абсолютной величины будем иметь: , где .
Следовательно, данная функция является двузначной, а график ее будет симметричен относительно оси ОХ.
Областью определения данной функции являются промежутки значений аргумента х, на которых функция у = f (х) неотрицательна.
Алгоритм:
- Установить область определения функции из условия: .
- На промежутках определения функции построить график функции у = f (х).
- Построить кривые, симметричные построенному графику относительно оси ОХ.
Примеры.
1. Построить график функции .
а) Область определения: или .
б) Для строим график функции .
в) Строим кривую, симметричную построенной, относительно оси ОХ. (Рисунок 9)
Рисунок 9
2. Построить график функции .
а) Область определения: или и .
б) По определению абсолютной величины, у — 2 = ± (х2 – 1), или у = 2 ± (х2 – 1), или . (Рисунок 10)
Рисунок 10
II. Практическая часть
Задание: из предложенного списка функций выбрать по желанию и построить графики двух:
а) ;
б) ;
в) ;
г) ;
д) .
Решение см. Рисунок 11.
Рисунок 11
Занятие 6. График функции .
Цель: научиться строить графики функции вида .
Ход занятия
I. Беседа
Алгоритм построения графика данной функции:
- Строим график функции .
- Строим график функции . Он будет представлять собой кривую, симметричную графику функции относительно оси ОХ.
Примеры.
1. Построить график функции .
- Строим график функции .
- Достраиваем график функции . (Рисунок 12)
Рисунок 12
2. Построить график функции .
- Строим график функции .
- Достраиваем график функции . (Рисунок 13)
Рисунок 13
II. Практическая часть
Задание: из предложенного списка функций выбрать по желанию и построить графики двух:
а) ;
б) ;
в) ;
г) ;
д) .
Решение см. Рисунок 14.
Рисунок 14
Занятие 7. Графики некоторых простейших функций, заданных явно.
Цель: научиться строить графики функций, заданных явно; создание ситуации успеха в процессе оценки и самооценки знаний по темам курса.
Ход занятия
I. Беседа
Построим график функции .
По определению абсолютной величины функции .
Строим прямые на двух участках. (Рисунок 15)
Рисунок 15
Примеры.
1) Построим график функции .
а) Строим график функции у = 2х – 4 для х ≥2.
б) Проводим ось симметрии: х = 2.
в) Достраиваем график: проводим прямую, симметричную первой относительно оси симметрии. (Рисунок 16)
Рисунок 16
Рассмотрим другой порядок построения· графиков подобных функций, который будет более удобным и общим для построения графиков в дальнейшем.
2) Построить график функции .
а) Из условий и находим абсциссы точек перелома графика: хl = 1 и х2 = 3.
Следовательно, данную функцию следует рассматривать на трех промежутках: , (1; 3] и и на них по частям строить график.
б) На .
На (1; 3] .
На ,
т.е. (Рисунок 17)
Рисунок 17
II. Практическая часть
Задание: из предложенного списка функций выбрать по желанию и построить графики двух:
а) ;
б) ;
в) ;
г) ;
д) ;
е) .
Решение см. Рисунок 18.
Рисунок 18
III. Презентация учащимися собственных графиков, созданных для портфолио
IV. Проверка построенных графиков через программу Advanced Grapher
Литература для учителя
- И.И. Гайдуков. Абсолютная величина. М.: Просвещение, 1968.
- Фальке Л.Я. Изучение сложных тем курса алгебры в средней школе. М.: Илекса; Ставрополь: Сервисшкола, 2002.
- М.Е. Козина. Математика 8-9 классы. Выпуск 2. Сборник элективных курсов. Волгоград: Учитель, 2007
- А.В. Коркуев, Л.Д. Арестова. Построение графиков некоторых функций. Журнал «Математика в школе», №3-1995г.
urok.1sept.ru
Рабочая программа по алгебре (9 класс): Построение графиков функций с модулем
Пояснительная записка
Предлагаемый элективный курс по предпрофильной подготовке учащихся 9 классов посвящен одному из основных понятий современной математики — функциональной зависимости. Понятие функциональной зависимости, являясь одним из центральных в математике, пронизывает все ее приложения, оно, как ни одно другое, приучает воспринимать величины в их живой изменчивости, во взаимной связи и обусловленности. Изучение поведения функций и построение их графиков являются важным разделом школьного курса. Существуют различные способы задания функции: аналитический, табличный, словесный, а также графический. Иногда график является единственно возможным способом задания функции. Он широко используется в технике, лежит в основе работы многих самопишущих автоматических приборов. Свободное владение техникой построения графиков часто помогает решать сложные задачи, а порой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой интерес для самих учащихся. Однако на базе основной школы материал, связанный с этим вопросом, представлен несколько хаотично, изучается недостаточно полно, многие важные моменты не входят в программу и, следовательно, не изучаются.
Цель данного элективного курса — прояснить и дополнить школьный материал, связанный с функциями и их графиками, представить систематизацию функций не по видам, а по методам построения их графиков.
Задачи курса:
— Показать значимость представления зависимостей в графическом изображении;
— Сформировать умения упрощать процедуру построения графиков, используя различные преобразования;
— Ввести понятие выполнения арифметических действий над функциями;
В курсе заложена возможность дифференцированного обучения, как путем использования задач различного уровня сложности, так и на основе различной степени самостоятельности осваивания нового материала. Следовательно, программа применима для самых разных групп школьников, в том числе не имеющих хорошей подготовки.
На изучение всего курса отводится 15 ч, по окончании предусмотрено зачетное мероприятие на 2 ч в виде контрольной или тестовой работы, возможны также другие, даже комбинированные формы диагностики
Тема | Количество часов | Форма контроля | ||
всего | теория | практика | ||
1. Понятия функции и графика | 3 | 2 | 1 | Устный опрос |
2. Преобразование графиков | 5 | 2 | 3 | Составление табли-цы, самостоятель-ная работа |
3. Действия над функциями | 4 | 2 | 2 | Математический диктант, взаимопроверка |
4. Дополнительный материал | 3 | 2 | 1 | Домашняя конт-рольная работа |
5. Итоговая диагностика | 2 | — | 2 | Зачет |
Итого | 17 | 8 | 9 | |
Содержание программы
Тема 1. Понятия функции и графика.
Учащимся сообщается цель и значение данного элективного курса. Выявляются и систематизируются их знания о функциональной зависимости. Определяется понятийный аппарат, круг доступных задач, предоставляется дополнительная информация для расширения возможностей учащихся. При этом целесообразно использование разнообразного наглядного материала.
Занятие 1 «Введение. Понятие функциональной зависимости».
Занятие 2 «График функции».
Занятие 3 «Способы задания функции».
Тема 2. Преобразование графиков.
При построении графиков многих функций можно избежать проведения подробного исследования. Изложению методов, упрощающих аналитическое выражение функции и облегчающих построение графиков, посвящены уроки данной темы. В результате учащиеся получают практическое руководство для построения эскизов графиков многих функций.
Занятие 1 «Перенос вдоль оси ординат и вдоль оси абсцисс».
Занятие 2 «Построение графиков функций с помощью переноса вдоль оси ординат и вдоль оси абсцисс».
Занятие 3 «Сжатие (растяжение) вдоль оси ординат и вдоль оси абсцисс».
Занятие 4 «Построение графиков функций с помощью сжатия (растяжения) вдоль оси ординат и вдоль оси абсцисс».
Занятие 5 «Построение графиков функций с помощью нескольких преобразований».
Тема 3. Действия над функциями.
Графики суммы (разности), произведения и частного двух функций также можно построить без применения методов математического анализа, используя определенные правила. Особенно эффективен этот метод в случае, когда исходные функции являются элементарными. В этой же теме рассматривается построение графиков функций, содержащих знак модуля.
Занятие 1 «Сумма и разность функций».
Занятие 2 «Произведение и частное функций».
Занятие 3 «Построение графиков функций».
Занятие 4 «Функции, содержащие операцию взятия модуля».
Тема 4. Дополнительный материал.
В качестве дополнительного материала рассматриваются приемы построения графиков суперпозиций простейших функций и их свойства. Вводится понятие обратной функции, определяются ее область определения и множество значений и устанавливается связь графиков прямой и обратной функций.
Занятие1 «Понятие суперпозиции функций».
Занятие 2 «Построения графиков суперпозиций простейших функций и их свойства».
Занятие 3 «Понятие обратной функции. Связь графиков прямой и обратной функций».
Литература
Виленкин Н.Я. Функции в природе и технике. М., 1978.
Вирченко Н.А., Ляшко И. И., Швецов К.И. Графики функций: Справочник. Киев, 1981.
Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э. Функции и графики (основные приемы). М., 1985.
Ершов Л.В., Райхмист Р.Б. Построение графиков функций: Книга для учителя. М., 1994.
Егерев В.К., Радунский Б.А., ТальскийД.А. Методика построения графиков функций. М., 1967.
Крейнин Я.Л. Функции, пределы, уравнения и неравенства с параметрами. М., 1995.
Сивашинский И.Х. Элементарные функции и графики. М., 1965.
Шилов Г.Е. Как строить графики? М., 1982.
Яремчук Ф.П., Рудченко П.А. Алгебра и элементарные функции: Справочник. Киев, 1987.
Программа курса по выбору
«Преобразование графиков элементарных функций»
для учащихся 9 классов
Предмет: математика;
Учитель: Дубровина Ольга Викторовна;
Квалификация: 1 квалификационная категория.
Казань-2015
nsportal.ru
Обучение учащихся построению графиков функций с модулем
Обучение учащихся построению графиков функций с модулем
Построение графиков, содержащих модуль, осуществляется двумя способами:
На основании определения модуля
Построение графика функции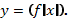
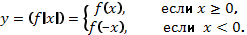
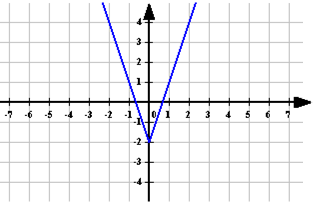
Приведем пример построения графика функции 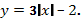
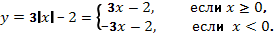
П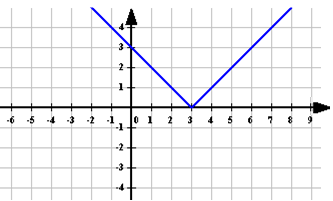 остроение графика функции
остроение графика функции 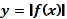
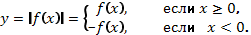
Приведем пример построения графика функции 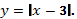
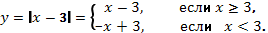
На основании правил геометрического преобразования графиков функций.
Какие геометрические преобразования, можно использовать при построении графиков функций? (параллельный перенос вдоль осей ОХ и ОУ, симметричное отображение относительно осей или точки)
Построение графика 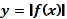 .
.
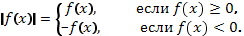
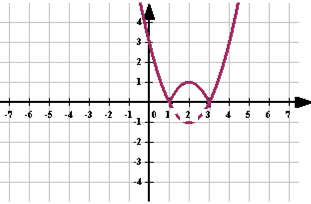 Чтобы построить график функции
Чтобы построить график функции 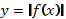 , если известен график функции
, если известен график функции 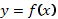 , нужно оставить на месте ту его часть, где
, нужно оставить на месте ту его часть, где 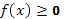 , и симметрично отобразить относительно оси Х другую его часть, где
, и симметрично отобразить относительно оси Х другую его часть, где 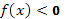 .
.
Алгоритм построения графика:
1. Построить график функции 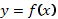 ,
,
2. Часть графика 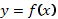 , лежащая над осью ОХ, сохраняется, а часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ.
, лежащая над осью ОХ, сохраняется, а часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ.
Построение графика 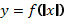 .
.
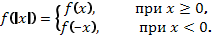
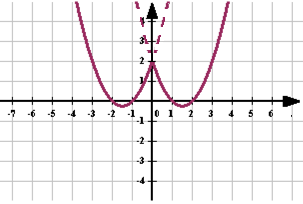 Чтобы построить график функции
Чтобы построить график функции 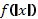 , если известен график функции
, если известен график функции 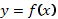 , нужно оставить на месте ту его часть, где
, нужно оставить на месте ту его часть, где 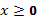 , а при
, а при 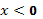 отобразить построенную часть симметрично относительно оси ОУ.
отобразить построенную часть симметрично относительно оси ОУ.
Алгоритм построения графика:
Построить график функции 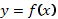 ,
,
При 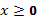 график сохраняется, а при
график сохраняется, а при 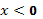 отображается построенная часть симметрично относительно оси ОУ.
отображается построенная часть симметрично относительно оси ОУ.
В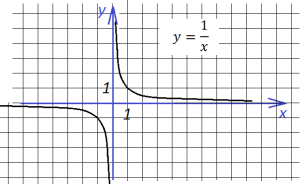 “основе” его лежит график функции
“основе” его лежит график функции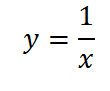 , он выглядит так :
, он выглядит так :
Теперь построим график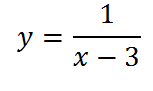
Ч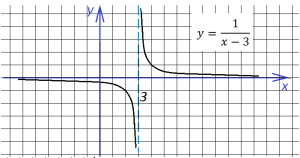 тобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:
тобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:
Т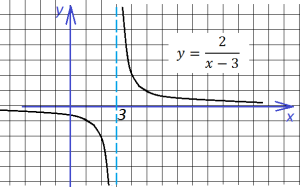 еперь необходимо умножить на два все ординаты, чтобы получить график функции
еперь необходимо умножить на два все ординаты, чтобы получить график функции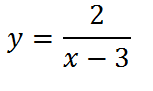
Наконец, сдвигаем график вверх на две единицы:
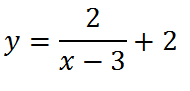
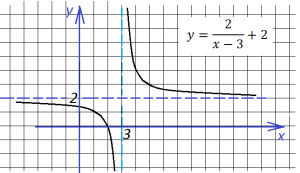
Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):
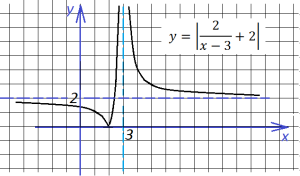
В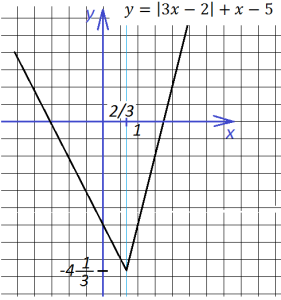 ыражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:
ыражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так: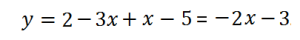
При х>2/3 функция запишется так: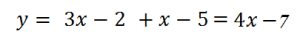
То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (правее) мы строим функцию 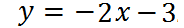 ,
,
а в другой (левее) – график функции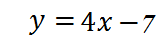
С
 ледующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:
ледующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля: 
Посмотрим, в каких точках подмодульные выражения меняют знак:
Расставим знаки для подмодульных выражений на координатной прямой:
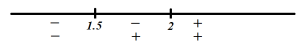
Раскрываем модули на первом интервале: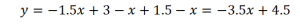
На втором интервале: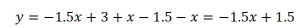
На третьем интервале: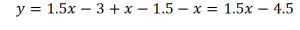
Таким образом, на интервале (-∞; 1.5] имеем график, записанный первым уравнением, на интервале [1.5; 2] – график, записанный вторым уравнением, и на интервале [2;∞) — график по третьему уравнению:
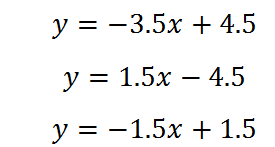
Строим:
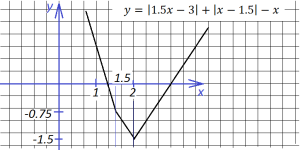
4. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:
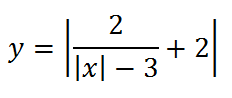
В основе опять знакомый нам график функции
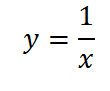
но, если в знаменателе x стоит под знаком модуля,
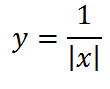
то график имеет вид:
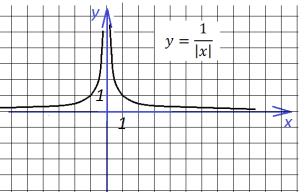
Теперь произведем сдвиг на три единицы,
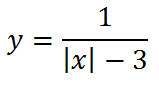
при этом сдвинутся обе части: правая — вправо, левая — влево (своеобразное зеркало : отходишь дальше — видно больше)
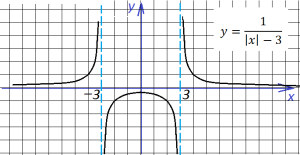
График этой функции, умноженной на два,
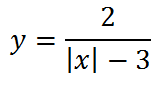
выглядит так:
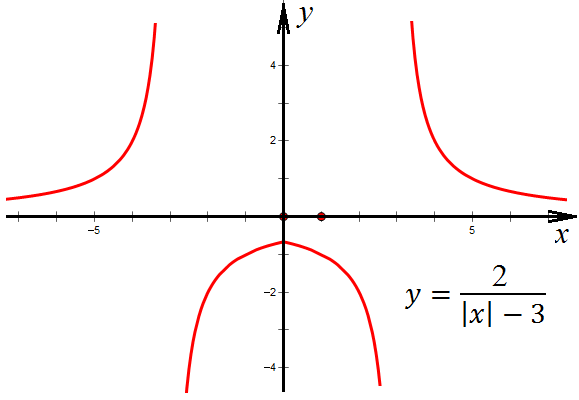
Теперь можно поднять график по оси у:
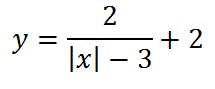
и тогда он будет таким: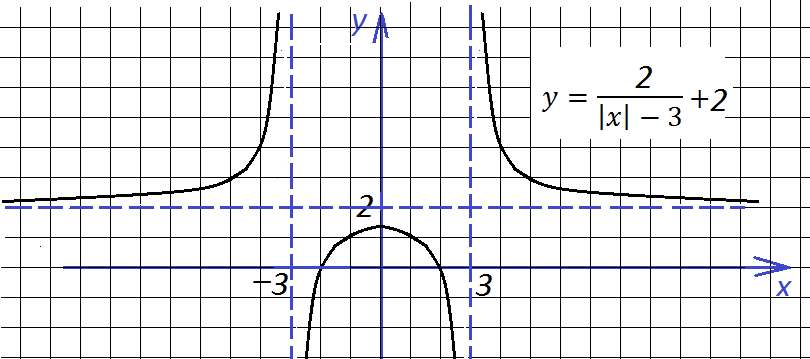
Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:
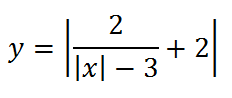
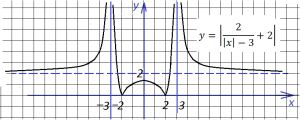
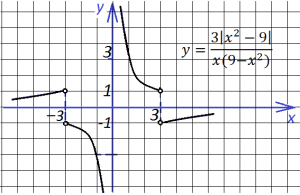
5.Очень интересно выглядит график функции
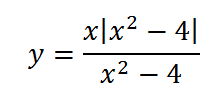
В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) — второе:
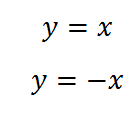
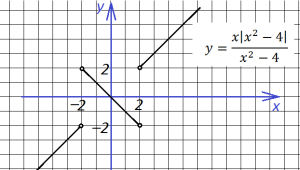
6. Две следующие функции отличаются знаком, и графики их выглядят по разному:
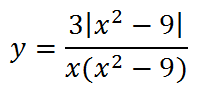
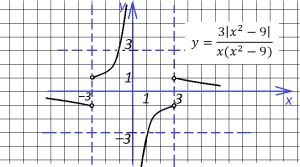
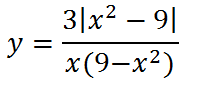
7. Еще два похожих графика, вид которых меняется в зависимости от х в показателе степени:
Первый:
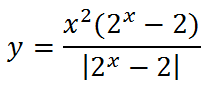
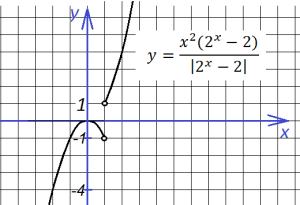
Второй:
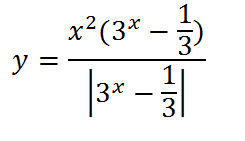
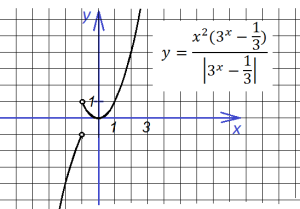
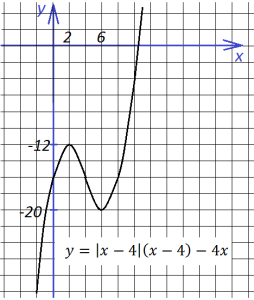
8.Теперь построим график такой функции:
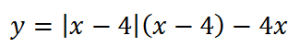
Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так:
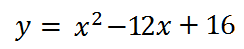
А на интервале [4; ∞) так:
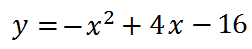
Точка вершины первой параболы (2;-12), она обращена вниз ветвями, точка вершины второй параболы (6, -20), ветви ее обращены вверх. В итоге имеем:
9. Построим график функции, которая, на первый взгляд, выглядит устрашающе:
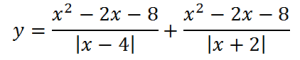
Однако многочлен в числителе раскладывается на множители:
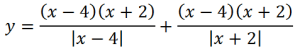
Точки перемен знака подмодульных выражений – 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть:
На первом интервале (-∞; -2):
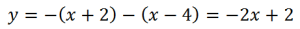
На втором интервале (-2;4):
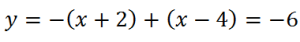
На третьем интервале (4;∞):
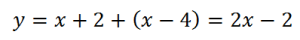
Строим:
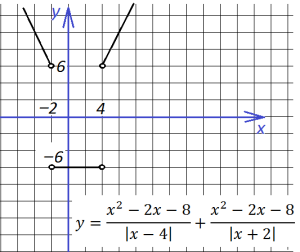
Внесем небольшие изменения, добавив двойку в знаменатель исходной функции:
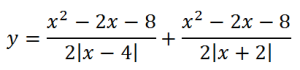
Тогда точки перемены знака остаются те же, но функция выглядит иначе на разных интервалах:
На первом интервале (-∞; -2):
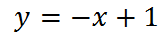
На втором интервале (-2;4):
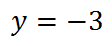
На третьем интервале (4;∞):
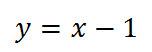
График изменится:
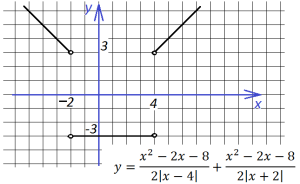
10. Наконец, последний график мы построим для функции
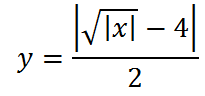
Начнем построение с “базовой” для этого графика функции
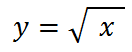
она выглядит так:
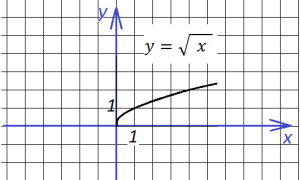
Далее добавим знак модуля под корень:
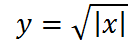
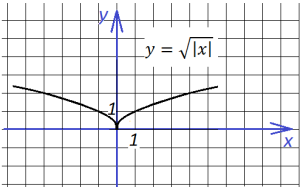
Теперь опустим этот график вниз на 4 единице по оси у:
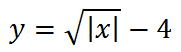
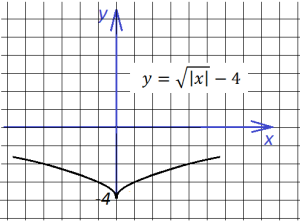
“Опрокинем” все, что ниже оси х, вверх,
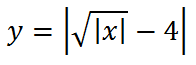
и не забудем поделить все ординаты на 2:
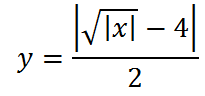
infourok.ru
Методическая разработка по алгебре (9 класс) по теме: Методическая разработка урока в 9 классе «Построение графиков функций содержащих модуль «
9 класс. Урок алгебры в классе с углубленным изучением предмета.
Учитель: Семакина Н.В.
Тема: построение и чтение графиков функций содержащих модуль.
К уроку подготовлена презентация. (Слайды с заданием математического диктанта. Слайды с ответами для самопроверки)
Цель: совершенствовать у обучающихся графическое представление.
Задачи:
— проверить уровень усвоения учащимися темы;
— углубить знания учащихся по материалу «Понятие модуля числа (выражения) и его применение при построении графиков функции содержащих модуль»; развивать умения применять алгоритмы при построении графиков функций;
— создать условия для развития памяти, мышления, воспитания самостоятельности и трудолюбия.
Ход урока
1 Организационный момент (сообщить тему урока, сформулировать цели урока)
— Сегодня у нас урок самостоятельной работы, большую часть времени урока вы будете работать самостоятельно или в парах
— работу выполняем в тетрадях, которые раздали,
— записываем число, тему.(один из учеников читает тему )
(вопрос-ответ)
— Чем будем заниматься на уроке (строить графики, функций содержащие модуль и использовать полученные знания при решении различного рода заданий )
— что для этого надо знать(понятие модуля, свойства модуля, алгоритм построения графиков различных функций )
— эта тема новая для вас (нет)
— для чего повторяем эту тему (подготовится к самостоятельной работе; чтобы справится с заданиями второй части экзаменационной работы )
— каждый из вас сегодня в ходе работы должен выявить для себя не понятные вопросы, связанные с темой записать их на листочек передать мне в конце урока.
2.Актуализация знаний учащихся
— два ученика оформляют решение домашнего задания на доске
№ 1.Постройте график функции y = |x|(х-3) используя определение модуля.
№ 2. Постройте график функции y = x + 4|х| -5 используя алгоритм.
— остальные выполняют задания математического диктанта. Работаем на два варианта. Не отвлекаемся, не отстаем.
Математический диктант (презентация)
Математический диктант
1 вариант
- Решить уравнение |x — 3| = 4
- Решить уравнение |x — 3|=2х-6
- Вычислите
- Вычислить
- Схематично постройте график
функции y = — |x| + 2
- Схематично постройте график
функции y = |x- 2|
2 вариант
- Решить уравнение |x — 3| = 4
2.Решить уравнение |x — 3|=2х-6
- Вычислите
- Вычислить
- Схематично постройте график
функции y = |x| + 2
- Схематично постройте график
функции y = |x+ 2|
— решение
— самопроверка 3 –заданий – оценка 3; 4 заданий –оценка 4;
5-6 заданий оценка 5
— сделайте запись на листочках по непонятным вопросам.
— рассказать алгоритм построения графика функции у=|f(х)|, у=f|х|
3. Домашнюю работу разбираем всем классом.
Задаем вопросы, готовимся к самостоятельной работе.
Дополнительные вопросы учащимся, выполнявшим домашнее задание:
— прочитать график :область определения, область значения, промежутки монотонности, наибольшее, наименьшее значение функции.
4. Работа в парах. Самостоятельная работа по индивидуальным карточкам, разного уровня сложности. В паре карточки одного уровня, можно работать в паре. Если задание сложное поднимите руку, можно получить задание базового уровня. Помощники: памятки с алгоритмом построения графиков.
5.Подвидение итогов.
Работу закончили, кто не справился, возьмите карточки домой. Запомните номер карточки. Ответы можете посмотреть на стенде «Проверь себя». Запишите непонятные вопросы для разбора на следующем уроке.
6. Домашнее задание.
Повторить&7-13, Вариант № 11 задание №22. Примеры на доске запишите в тетрадь. Решаем на выбор 2 примера .
Листочки с вопросами передали.
Спасибо за урок! До свидание!
Приложение № 1
(Карточки с заданием для самостоятельной работы)
Карточка № 1
Постройте график функции y = |x + 6х + 5| и найдите, при каких значениях m прямая y = m пересекает построенный график ровно в трех точках.
Карточка № 1а
Постройте график функции y = |x + 2х — 3| и найдите, при каких значениях m прямая y = m пересекает построенный график ровно в двух точках.
Карточка № 2
Постройте график функции y = x — 2|х| — 3 и найдите, при каких значениях m прямая y = m пересекает построенный график ровно в трех точках.
Карточка № 2а
Постройте график функции y = x — 2|х| и найдите, при каких значениях m прямая y = m пересекает построенный график ровно в двух точках.
Карточка № 3
Постройте график функции y = x + 4|х| -5 и найдите, при каких значениях m прямая y = m и построенный график имеют ровно одну общую точку
Карточка № 3а
Постройте график функции y = x + |х| и найдите, при каких значениях m прямая y = m и построенный график имеют две общие точки.
Карточка № 4
Постройте график функции и определите, при каком значении m
прямая у = m имеет с графиком две общие точки.
Карточка № 5
Постройте график функции ,и определите, при каком значении m прямая у = m имеет с графиком две общие точки.
Карточка № 6
Постройте график функции ,и определите, при каком значении m прямая у = m имеет с графиком две общие точки.
Карточка № 6а
Постройте график функции ,и определите, при каком значении m прямая у = m имеет с графиком три общие точки.
Карточка № 9
Постройте график функции ,и определите, при каком значении m прямая у = m имеет с графиком три общие точки.
Карточка № 7
Постройте график функции ,и определите, при каком значении m прямая у = m имеет с графиком ровно одну общую точку.
Карточка № 8
Постройте график функции y = |x|(х-3)
и определите, при каких значениях m прямая
y = m имеет с графиком ровно одну общую точку.
Приложение № 2
Алгоритм построения графика функции у = f(|x|)
- Построить график функции у = f(x) при х > 0.
- Добавить ветви, симметричные построенным
относи тельно оси у
Алгоритм построения графика функции
у = |f(x)|
1.Построить график функции у = f(x).
2.Оставить без изменения те части графика функции у = f(x), которые лежат не ниже оси х.
3.Части графика функции у = f(x), которые лежат ниже оси х, заменить на симметричные им относительно оси х.
Алгоритм построения параболы у = ах2 + bх + с
- Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось параболы.
- Отметить на оси х две точки, симметричные относи тельно оси параболы (чаще всего в качестве одной из таких точек берут точку с абсциссой х = 0), найти значения функ ции в этих точках; построить на координатной плоскости соответствующие точки.
- Через полученные три точки провести параболу (в случае необходимости берут еще одну пару точек, симметричных относительно оси параболы, и строят параболу по пяти точкам).
- Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось параболы.
- Отметить на оси х две точки, симметричные относи тельно оси параболы (чаще всего в качестве одной из таких точек берут точку с абсциссой х = 0), найти значения функ ции в этих точках; построить на координатной плоскости соответствующие точки.
- Через полученные три точки провести параболу (в случае необходимости берут еще одну пару точек, симметричных относительно оси параболы, и строят параболу по пяти точкам).
nsportal.ru
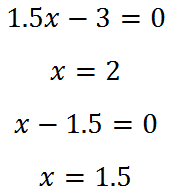 ледующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля:
ледующий график – также ломаная, но имеет две точки излома, так как содержит два выражения под знаками модуля: