Преобразование графиков функций
 Преобразование графиков функций
Преобразование графиков функций
В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции  получить график функции
получить график функции 
Линейным преобразованием функции  называется преобразование самой функции и/или ее аргумента к виду
называется преобразование самой функции и/или ее аргумента к виду 
Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:
- Вычленение базовой функции, собственно, график которой мы и преобразовываем.
- Определения порядка преобразований.
Именно на этих моментах мы и остановимся подробнее.
Рассмотрим внимательно функцию

В ее основе лежит функция  . Назовем ее базовой функцией.
. Назовем ее базовой функцией.
При построении графика функции 
 .
.Если бы мы совершали преобразования функции  в том же порядке , в каком находили ее значение при определенном значении аргумента, то
в том же порядке , в каком находили ее значение при определенном значении аргумента, то
Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.
Преобразования аргумента.
1. f(x) 
1. Строим график фунции 
2. Сдвигаем график фунции  вдоль оси ОХ на |b| единиц
вдоль оси ОХ на |b| единиц
- влево, если b>0
- вправо, если b<0
Построим график функции 
1. Строим график функции 
2. Сдвигаем его на 2 единицы вправо:

2. f(x)  f(kx)
f(kx)
1. Строим график фунции 
2. Абсциссы точек графика  делим на к, ординаты точек оставляем без изменений.
делим на к, ординаты точек оставляем без изменений.
Построим график функции  .
.
1. Строим график функции 
2. Все абсциссы точек графика  делим на 2, ординаты оставляем без изменений:
делим на 2, ординаты оставляем без изменений:

3. f(x)  f(-x)
f(-x)
1. Строим график фунции 
2. Отображаем его симметрично относительно оси OY.
Построим график функции  .
.
1. Строим график функции 
2. Отображаем его симметрично относительно оси OY:

4. f(x)  f(|x|)
f(|x|)
1. Строим график функции 
2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:
График функции  выглядит так:
выглядит так:

Построим график функции 
1. Строим график функции  (это график функции
(это график функции 

2. Часть графика, расположенную левее оси OY (x<0) стираем:

3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:

Важно! Два главных правила преобразования аргумента.
1. Все преобразования аргумента совершаются вдоль оси ОХ
2. Все преобразования аргумента совершаются «наоборот» и «в обратном порядке».
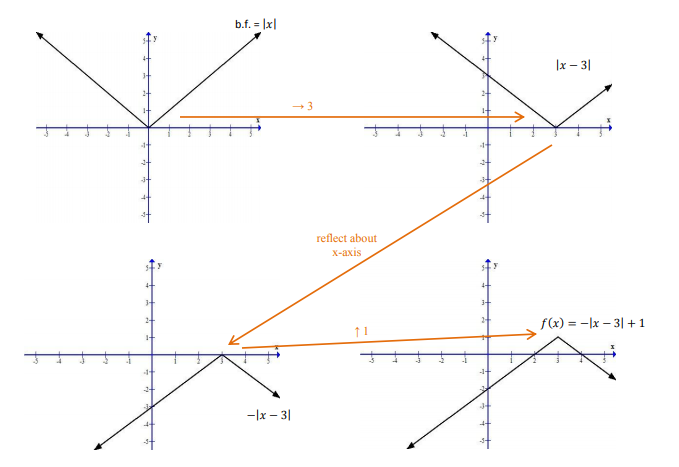
Например, в функции 
1. Берем модуль от х.
2. К модулю х прибавляем число 2.
Но построение графика мы совершали в обратном порядке:
Сначала выполнили преобразование 2. — сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы «наоборот»)
Затем выполнили преобразование f(x)  f(|x|).
f(|x|).
Коротко последовательность преобразований записывается так:

Теперь поговорим о преобразовании функции. Преобразования совершаются
1. Вдоль оси OY.
2. В той же последовательности, в какой выполняются действия.
Вот эти преобразования:
1. f(x) f(x)+D
f(x)+D1. Строим график функции y=f(x)
2. Смещаем его вдоль оси OY на |D| единиц
- вверх, если D>0
- вниз, если D<0
Построим график функции 
1. Строим график функции 
2. Смещаем его вдоль оси OY на 2 единицы вверх:

2. f(x)
1. Строим график функции y=f(x)
2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.
Построим график функции 
1. Построим график функции 
2. Ординаты всех точек графика умножим на 2:

3. f(x) -f(x)
-f(x)
1. Строим график функции y=f(x)
2. Отображаем его симметрично относительно оси ОХ.
Построим график функции  .
.
1. Строим график функции  .
.
2. Отображаем его симметрично относительно оси ОХ.

4. f(x) |f(x)|
|f(x)|
1. Строим график функции y=f(x)
2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.
Построим график функции 
1. Строим график функции  . Он получается смещением графика функции
. Он получается смещением графика функции  вдоль оси OY на 2 единицы вниз:
вдоль оси OY на 2 единицы вниз:

2. Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:

И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:
y=f(x)  |y|=f(x)
|y|=f(x)
1. Строим график функции y=f(x)
2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
Построим график уравнения 
1. Строим график функции  :
:

2. Часть графика, расположенную ниже оси ОХ стираем:

3. Часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.

И, наконец, предлагаю вам посмотреть ВИДЕОУРОК в котором я показываю пошаговый алгоритм построения графика функции

График этой функции выглядит так:

И.В. Фельдман, репетитор по математике.
ege-ok.ru
параллельный перенос (сдвиг), отображение, растяжение, сжатие, отражение. Курсы по математике
Тестирование онлайн
Преобразование графиков
Параллельный перенос
График функции y=f(x)+B получается параллельным переносом графика функции y=f(x) в положительном направлении вдоль оси Оу на расстояние В, если В>0 и в отрицательном направлении вдоль оси Оу, если B.
График функции y=f(x+b) получается параллельным переносом графика функции y=f(x) в положительном направлении вдоль оси Оx на расстояние b, если b и в отрицательном направлении вдоль оси Оx, если b>0.
Отображение
График функции y=-f(x) получается симметричным отображением графика y=f(x) относительно оси Ох.
График функции y=f(-x) получается симметричным отображением графика y=f(x) относительно оси Оу.
Деформация (растяжение и сжатие) графика
График функции y=Af(x), получается растяжением графика y=f(x) вдоль оси Оу от оси Ох в A раз при A>1 или сжатием вдоль оси Оу к оси Ох в раз при A.
График функции y=f(ax), получается сжатием графика y=f(x) вдоль оси Ох к оси Оу в а раз при а>1 или растяжением вдоль оси Ох к оси Оу в раз при а.
Отражение
График функции получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), лежащая над осью Ох и на оси, остается без изменений, а часть графика, лежащая под осью Ох, отражается симметрично относительно оси Ох на верхнюю полуплоскость.
График функции получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), соответствующая неотрицательным значениям аргумента , остается без изменений, а отрицательным значениям аргумента будет соответствовать график, полученный путем симметричного относительно оси Оy отображения части графика, оставленной без изменений.
Примеры
fizmat.by
Преобразование графиков функций — подготовка к ЕГЭ по Математике
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.

1. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.

Теперь растяжение графика. Или сжатие.
2. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если

3. Растяжение (сжатие) по вертикали
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если

И отражение по горизонтали.
4. Отражение по горизонтали
График функции симметричен графику функции относительно оси Y.


5. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.

Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
6. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.

Построим график функции
Конечно же, мы пользуемся определением модуля.

Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.

Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.

Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке

2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка

Продолжение — в статье «Построение графиков функций».
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Преобразование графиков
Параллельный перенос.
ПЕРЕНОС ВДОЛЬ ОСИ ОРДИНАТ
f(x) => f(x) — b
Пусть требуется построить график функции у = f(х) — b. Нетрудно заметить, что ординаты этого графика для всех значений x на |b| единиц меньше соответствующих ординат графика функций у = f(х) при b>0 и на |b| единиц больше — при b0 или вверх при bДля построения графика функции y + b = f(x) следует построить график функции y = f(x) и перенести ось абсцисс на |b| единиц вверх при b>0 или на |b| единиц вниз при b
ПЕРЕНОС ВДОЛЬ ОСИ АБСЦИСС
f(x) => f(x + a)
Пусть требуется построить график функции у = f(x + a). Рассмотрим функцию y = f(x), которая в некоторой точке x = x1 принимает значение у1 = f(x1). Очевидно, функция у = f(x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.е. x2 = x1 — a, причем рассматриваемое равенство справедливо для совокупности всех значений из области определения функции. Следовательно, график функции у = f(x + a) может быть получен параллельным перемещением графика функции y = f(x) вдоль оси абсцисс влево на |a| единиц при a > 0 или вправо на |a| единиц при a Для построения графика функции y = f(x + a) следует построить график функции y = f(x) и перенести ось ординат на |a| единиц вправо при a>0 или на |a| единиц влево при a
Примеры:
2.y=f(x)+b
Отражение.
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = F(-X)
f(x) => f(-x)
Очевидно, что функции y = f(-x) и y = f(x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Иначе говоря, ординаты графика функции y = f(-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f(x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х. Таким образом, получаем следующее правило.
Для построения графика функции y = f(-x) следует построить график функции y = f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f(-x)
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = — F(X)
f(x) => — f(x)
Ординаты графика функции y = — f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f(x) при тех же значениях аргумента. Таким образом, получаем следующее правило.
Для построения графика функции y = — f(x) следует построить график функции y = f(x) и отразить его относительно оси абсцисс.
Примеры:
2.y=f(-x)
3.y=-f(-x)
Деформация.
ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ ОРДИНАТ
f(x) => k•f(x)
Рассмотрим функцию вида y = k•f(x), где k > 0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в k раз больше ординат графика функции у = f(x) при k > 1 или 1/k раз меньше ординат графика функции y = f(x) при kДля построения графика функции y = k•f(x) следует построить график функции y = f(x) и увеличить его ординаты в k раз при k > 1(произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 1/k раз при k
k > 1 — растяжение от оси Ох
0 — сжатие к оси OX
ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ АБСЦИСС
f(x) => f(k•x)
Пусть требуется построить график функции y = f(kx), где k>0. Рассмотрим функцию y = f(x), которая в произвольной точке x = x1 принимает значение y1 = f(x1). Очевидно, что функция y = f(kx) принимает такое же значение в точке x = x2, координата которой определяется равенством x1 = kx2, причем это равенство справедливо для совокупности всех значений х из области определения функции. Следовательно, график функции y = f(kx) оказывается сжатым (при k1) вдоль оси абсцисс относительно графика функции y = f(x). Таким образом, получаем правило.
Для построения графика функции y = f(kx) следует построить график функции y = f(x) и уменьшить его абсциссы в k раз при k>1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в 1/k раз при k
k > 1 — сжатие к оси Оу
0 — растяжение от оси OY
Работу выполнили Чичканов Александр, Леонов Дмитрий под руководством Ткач Т.В, Вязовова С.М, Островерховой И.В.
©2014
tofmal.ru
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок: 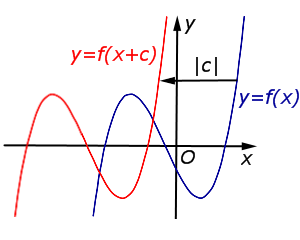 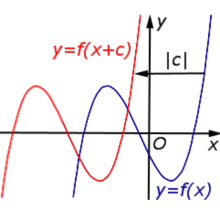 |
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок: 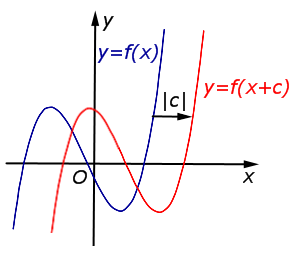 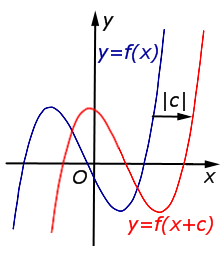 |
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок: 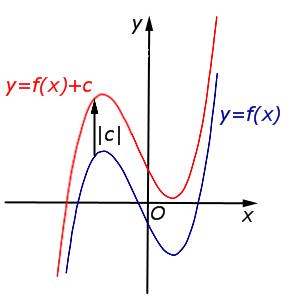 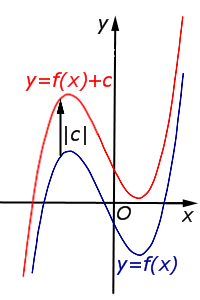 |
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок: 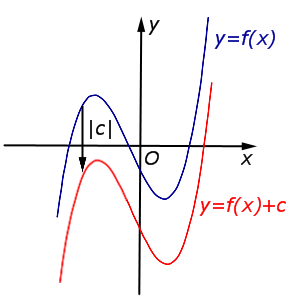 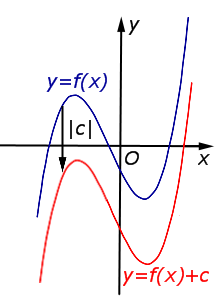 |
| Преобразование y = – f (x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок: 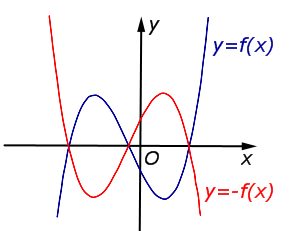 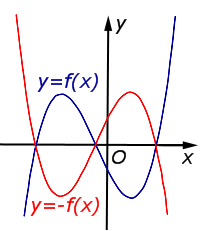 |
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок: 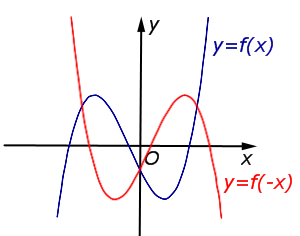 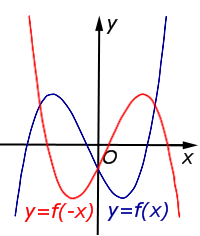 |
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок: 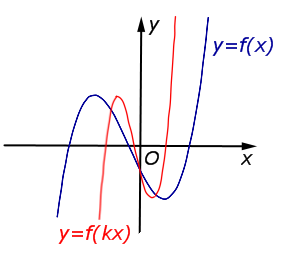 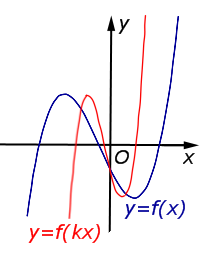 |
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в Рисунок: 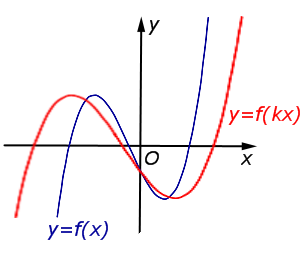 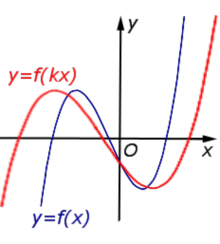 |
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в Рисунок: 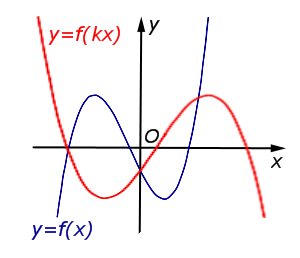 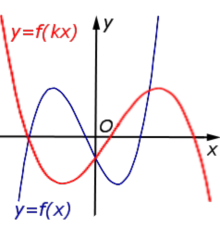 |
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: 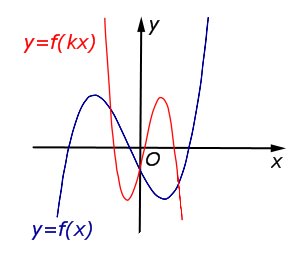 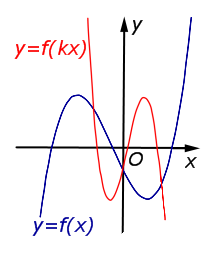 |
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок: 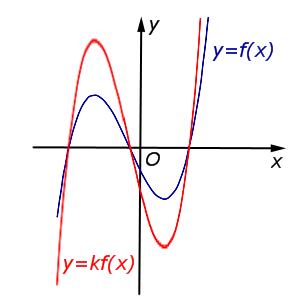 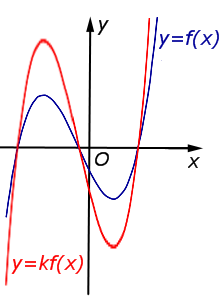 |
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в Рисунок: 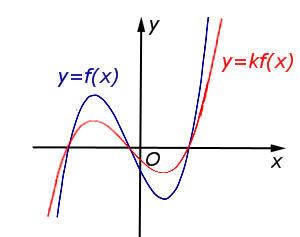 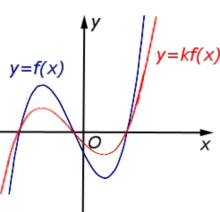 |
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в Рисунок: 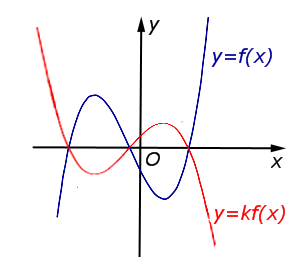 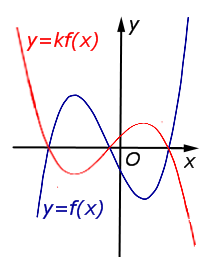 |
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: 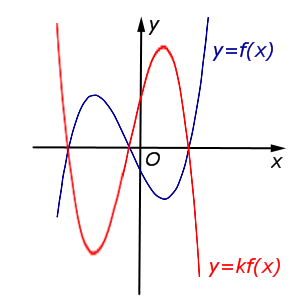 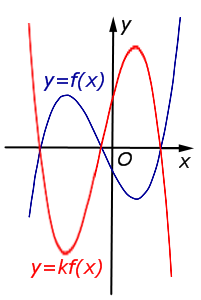 |
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области Рисунок: 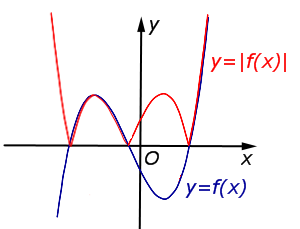 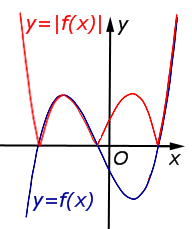 |
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области Рисунок: 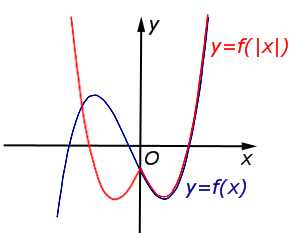 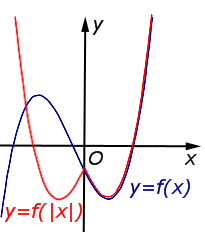 |
www.resolventa.ru
Смещение графиков функций. Изменение графиков функций.
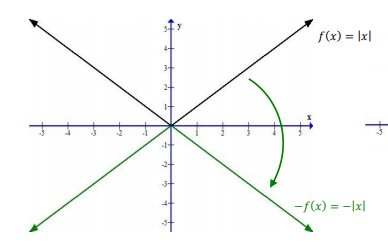
Смещение графика \(f(x)=|x|\) по вертикали
График функции \(f(x)=|x|\) и \(-f(x)=-|x|\):
Графики функций \(f(x)=x^3\) и \(f(-x)=(-x^3)\). Графики \(f(x)=\sqrt{x}\) и \(f(-x)=\sqrt{-x}\)
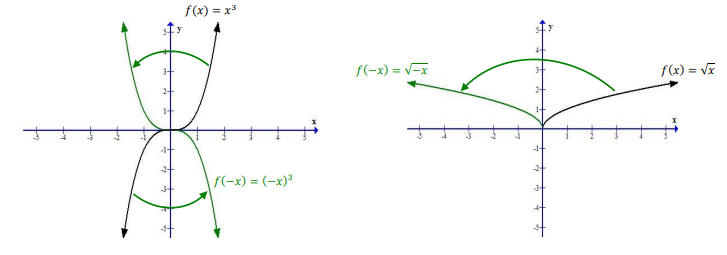
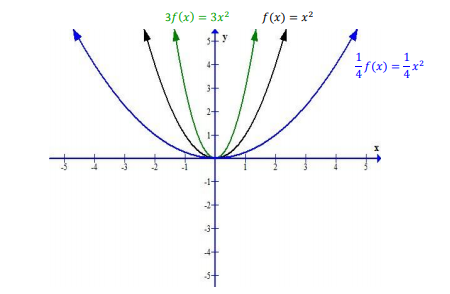
Изменение графика параболы по мере увеличения и уменьшения числового коэффициента:
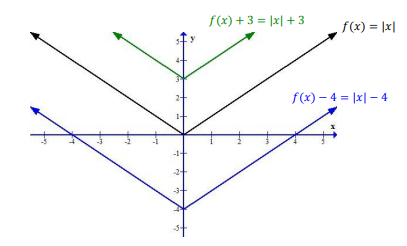
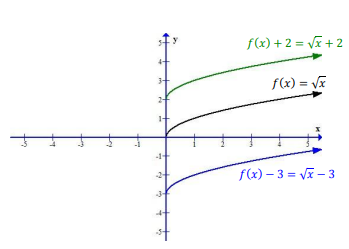
Если мы прибаляем к функции \(f(x)=|x|\) число \(f(x)=|x|+3\) , то график смещается по оси \(0Y\) на \(+3\) еденицы вверх, а если мы вычитаем число \(-4\)
\(f(x)=|x|-4\), то график сместиться вниз на 4 вниз:
То же самое с графиком \(f(x)=\sqrt{x}\):
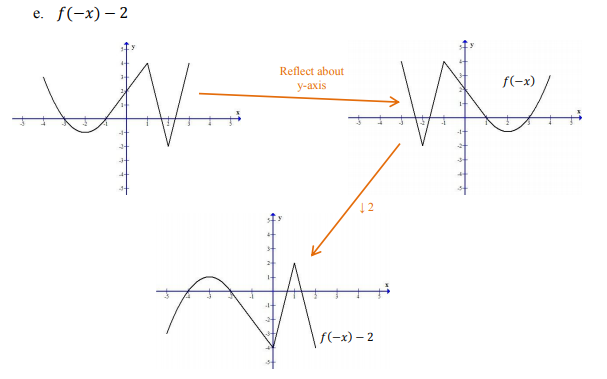
\(f(-x)-\)отражение относительно \(OY\):
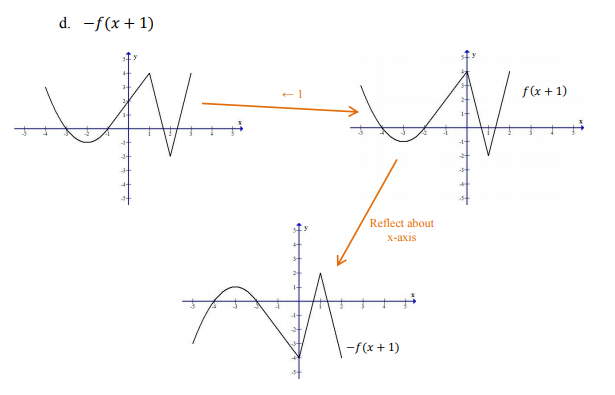
\(-f(x)- \)отражение относительно \(OX\) :
Изменение графиков функций
\(f(x)+c-\) сдвиг \(f(x)\) вверх относительно \(OY\)
\(f(x)-c-\) сдвиг \(f(x)\) вниз относительно \(OY\)
\(f(x+c)-\)сдвиг \(f(x)\) влево относительно \(OX\)
\(f(x-c)-\)сдвин \(f(x)\) вправо относительно \(OX\)
\(f(-x)-\) отражение относительно \(OY\)
\(-f(x)- \)отражение относительно \(OX\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Пишкова Наталья Евгеньевна Основные методы построения графиков функций
11
Статьи по математике из журнала МИФ-2 за 2002-2003 годыМатематика, 11 класс
График функции – это множество точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты — соответствующими значениями функции y.
Если буквально следовать определению, то для построения графика некоторой функции нужно найти в с е пары соответствующих значений аргумента и функции и построить все точки с этими координатами. В большинстве случаев это сделать практически невозможно, так как таких точек бесконечно много. Поэтому обычно исследуют функцию, что даёт возможность найти область определения и область изменения функции, области её убывания или возрастания, асимптоты, интервалы знакопостоянства и т.д.; находят несколько точек, принадлежащих графику, и соединяют их плавной кривой. Однако при построении графиков многих функций часто можно избежать проведение подобного исследования, используя ряд методов, упрощающих аналитическое выражение функции и облегчающих построение графика. Изложению именно таких методов и посвящается эта статья, которая может служить практическим руководством при построении графиков многих функций.
1.Параллельный перенос
Перенос (сдвиг) вдоль оси ординат
Пусть требуется построить график функции y=f(x)+b. Нетрудно заметить, что ординаты этого графика для всех значений аргумента на b единиц больше соответствующих ординат графика y=f(x) при b>0 и на b единиц меньше при b<0. Следовательно, график функции y=f(x)+b можно получить параллельным переносом вдоль оси ординат графика функции y=f(x) на b единиц вверх при b>0 или вниз при b<0.
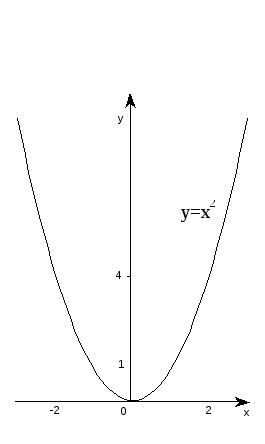

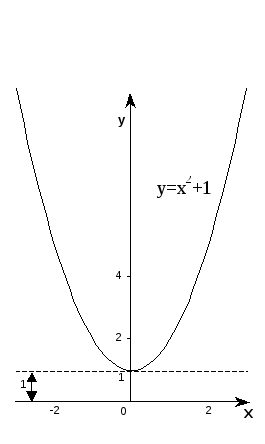 Рассмотрим
это на примере построения графика
функцииy=
x2 +1. Воспользуемся уже хорошо известным
нам графиком функции y=x2 (рис.1), назвав его исходным графиком.
Сравнивая функцию y=x2 +1 с функцией y=x2 , видим, что ординаты y
графика заданной функции на 1 больше
ординат исходного графика. Следовательно,
исходный график надо перенести на 1
вверх, как это и показано на рисунке 2.
Рассмотрим
это на примере построения графика
функцииy=
x2 +1. Воспользуемся уже хорошо известным
нам графиком функции y=x2 (рис.1), назвав его исходным графиком.
Сравнивая функцию y=x2 +1 с функцией y=x2 , видим, что ординаты y
графика заданной функции на 1 больше
ординат исходного графика. Следовательно,
исходный график надо перенести на 1
вверх, как это и показано на рисунке 2.
Рис.1 Рис.2 Рис.3
Однако перемещение графика связано с его перерисовыванием, что бывает затруднительно, особенно в случае сложных графиков. Перенос же графика на b единиц вверх или вниз вдоль оси ординат эквивалентен соответствующему, противоположному переносу оси абсцисс на столько же единиц.
Вернёмся к нашему примеру и покажем, что график функции y=x2+1 можно построить ещё проще, если воспользоваться тем же исходным графиком y=x2, но вместо перенесения всей кривой вверх на 1 перенести ось x-ов на ту же единицу вниз, как показано на рисунке 3. Тем самым относительно новой оси x-ов все ординаты кривой увеличиваются на 1, и получается график заданной функции.
Именно этим способом и следует пользоваться, поэтому сформулируем следующее правило.
Для построения графика функции y=f(x)+b (где y=f(x) — простейшая функция, график которой нам известен) следует построить график функции y=f(x), причём горизонтальную ось начертить штриховой линией и затем сдвинуть её на b единиц вниз, если b>0 и на b единиц вверх, если b<0. Это и будет истинная ось х-ов; полученный в новой системе координат график является графиком функции y=f(x)+b.
Пример 1. Построить график функции y=2x+3.
Р е ш е н и е:
С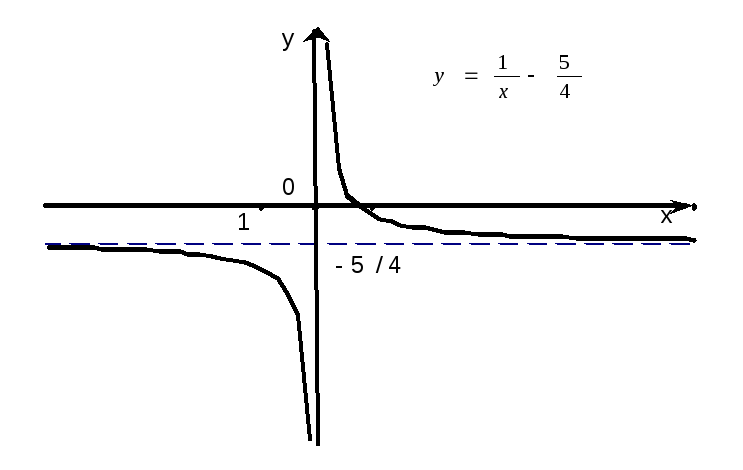 троим
график функцииy=2x и переносим ось абсцисс на 3 единицы
вниз. Получаем график функции y=2x+3
( рис.4 ). Прямая y=3
является горизонтальной асимптотой.
График пересекает ось ординат в точке
( 0;4 ).
троим
график функцииy=2x и переносим ось абсцисс на 3 единицы
вниз. Получаем график функции y=2x+3
( рис.4 ). Прямая y=3
является горизонтальной асимптотой.
График пересекает ось ординат в точке
( 0;4 ).
 Рис.4 Рис.5
Рис.4 Рис.5
Пример 2. Построить
график функции 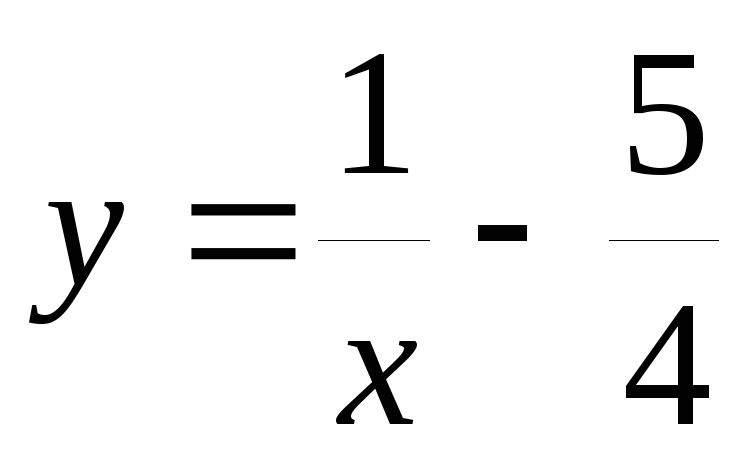
Р е ш е н и е :
Строим график
функции 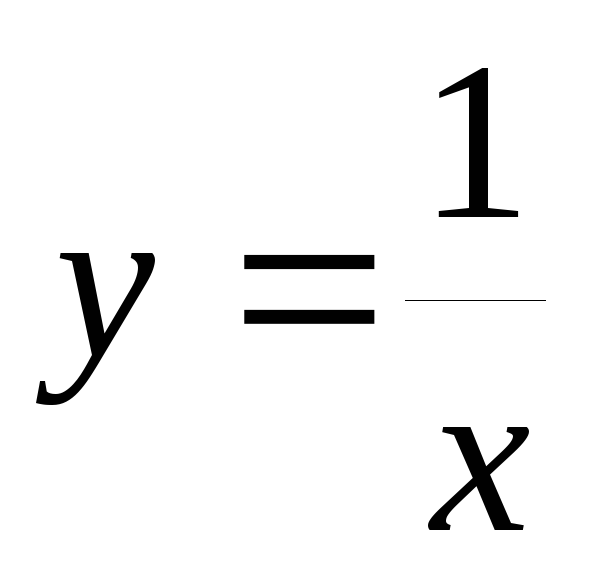 и переносим ось абсцисс на
и переносим ось абсцисс на единиц
вверх. Получаем график функции
единиц
вверх. Получаем график функции ( рис.5 ). Прямая
( рис.5 ). Прямая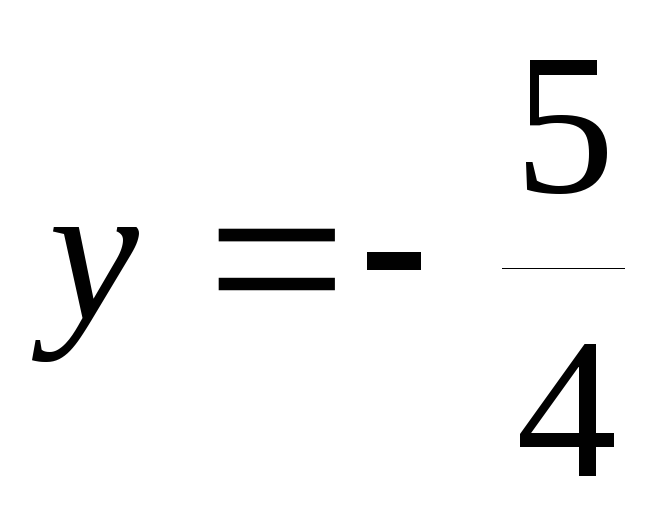 является горизонтальной асимптотой.
График пересекает ось абсцисс в точке
(
является горизонтальной асимптотой.
График пересекает ось абсцисс в точке
(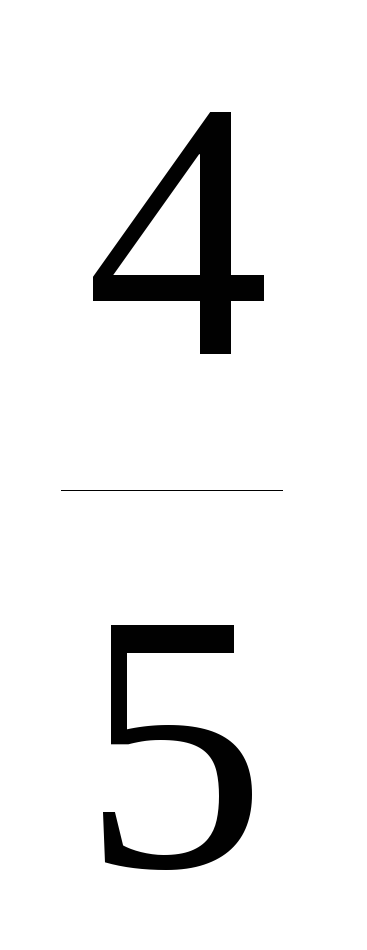 ;0 ).
;0 ).
studfile.net
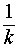 раз от оси Oy.
раз от оси Oy.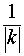 раз от оси Oy с последующим симметричным отражением графика относительно оси Oy.
раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. , остаётся на месте. Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
, остаётся на месте. Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.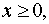 остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области
остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области